Inherent Structure Based Multi-view Learning with Multi-template Feature Representation for Alzheimer’s Disease Diagnosis

Abstract

Multi-template based brain morphometric pattern analysis using magnetic resonance imaging (MRI) has been recently proposed for automatic diagnosis of Alzheimer’s disease (AD) and its prodromal stage (i.e., mild cognitive impairment or MCI). In such methods, multi-view morphological patterns generated from multiple templates are used as feature representation for brain images. However, existing multi-template based methods often simply assume that each class is represented by a specific type of data distribution (i.e., a single cluster), while in reality the underlying data distribution is actually not pre-known. In this paper, we propose an inherent structure based multi-view leaning (ISML) method using multiple templates for AD/MCI classification. Specifically, we first extract multi-view feature representations for subjects using multiple selected templates, and then cluster subjects within a specific class into several sub-classes (i.e., clusters) in each view space. Then, we encode those sub-classes with unique codes by considering both their original class information and their own distribution information, followed by a multi-task feature selection model. Finally, we learn an ensemble of view-specific support vector machine (SVM) classifiers based on their respectively selected features in each view, and fuse their results to draw the final decision. Experimental results on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database demonstrate that our method achieves promising results for AD/MCI classification, compared to the state-of-the-art multi-template based methods.

I. Introduction

Alzheimer’s Disease (AD), characterized by progressive impairment of cognitive and memory function, is the sixth leading cause of death in the United States for Americans aged 65 years or older. According to a recent report from Alzheimer’s Association [1], the total estimated prevalence of AD is expected to be 13.8 million in the United States by 2050. As there is no cure for AD to reverse its progression, it is of vital importance for early diagnosis and monitoring of AD at its early prodromal stage, i.e., mild cognitive impairment (MCI).

In the literature, many brain morphometric pattern analysis methods have been developed for computer-aided AD/MCI diagnosis, by identifying differences in shape and neuroanatomical configuration of different brains provided by magnetic resonance imaging (MRI) [2-10]. Most of early works use regional measurement of anatomical volumes in pre-defined regions of interest (ROIs) (e.g., hippocampus, entorhinal cortex, or neocortex) to investigate abnormal tissue structure caused by AD or MCI. However, it is difficult to accurately label those ROIs, since the prior knowledge about abnormal regions is not always available in practice. More recently, with the development of deformable image registration techniques, automatic spatial normalization proves to be a fundamental procedure in brain morphometric pattern analysis, which allows quantitative comparisons among different subjects in a common space. Within the spatial normalization framework, a large number of brain morphometric analysis methods are developed for automatic AD/MCI diagnosis, e.g., deformation-based morphometry (DBM) [4, 11-14], tensor-based morphometry (TBM) [6, 15-20], and voxel-based morphometry (VBM) [21-26]. Particularly, DBM uses deformation fields to identify relative shape differences between groups of individual brains; TBM measures the Jacobian of deformation fields to localize local differences of brain structures, whereas VBM compares brain images on a voxel basis, after deformable registration of individual brain images. For instance, Teipel et al. [13] develop a multivariate DBM method to predict Alzheimer’s disease in mild cognitive impairment, while Lau et al. [27] propose to use DBM method to determine longitudinal neuroanatomical changes in AD. Hua et al. [20] develop several TBM methods to characterize brain atrophy in AD and MCI, which shows high statistical power to track brain changes in large neuroimaging studies. Shen et al. [28] propose a high-resolution VBM method by using a mass-preserving deformation mechanism and an automatic spatial normalization approach, achieving a high accuracy of registration. Fan et al. [29] design a COMPARE (Classification Of Morphological Patterns using Adaptive Regional Elements) algorithm to extract volumetric features from spatially adaptive local regions, which overcomes the limitation of traditional voxel-based methods often with very high feature dimensionality and noisy features, and has been successfully applied to several MRI-based applications (e.g., AD classification and gender classification [29, 30]).

In general, existing brain morphometric studies usually focus on using only one template as the benchmark space to compare anatomic differences among different brains. Actually, using only a single template may cause a bias in registration, as the template may have shape and intensity distributions that are closer to some subjects, but not close to other subjects. For instance, it is reported that the statistical power of TBM using only a single template depends on the particular template selected [18, 20]. To address this issue, several multi-template based brain morphometric methods have been recently proposed [17, 19, 31-33], where all studied MR images are non-linearly registered onto multiple pre-defined templates. Compared with single-template based methods, multi-template based methods could achieve overall lower registration error, which leads to less noisy feature representation for subjects [33]. Also, with each template as a specific view, multi-view feature representation generated from different templates for a brain image can better represent each subject, and could promote the performance of the subsequent learning models. For instance, Leporé et al. [17] develop a multi-template based approach for AD classification, and achieve better results than single-template based methods. Koikkalainen et al. [19] and Min et al. [31, 34] propose to extract multi-view features from multiple templates for all studied subjects, where features are averaged and concatenated for AD/MCI classification, respectively. To better use multi-view features, Liu et al. [32] develop a view-centralized multi-template classification method by focusing on features from a specific view (i.e., template) with the guidance information from features of other views, and achieve promising results for AD/MCI classification.

However, most of existing multi-template based methods simply assume that each class is represented by a specific type of data distribution (e.g., Gaussian distribution) [17, 19, 31, 32]. Although such assumption may simplify the problem at hand, it will definitely degrade the learning performance, because the underlying distribution structure of data is actually not pre-known. In practice, the potentially complicated distribution structure of neuroimaging data within a specific class could result from several facts [35], e.g., 1) different sub-types of a specific disease, and 2) inaccurate clinical diagnosis. Intuitively, modeling the inherent distribution structure information of data can bring more prior information to the learning process, and, thus, could further promote the diagnosis performance. To the best of our knowledge, no previous multi-template based methods employ such distribution structure information of data in their learning models.

To this end, in this paper, we propose an inherent structure based multi-view learning (ISML) method for AD/MCI classification. Specifically, we first non-linearly register each brain MR image onto multiple selected templates, through which multi-view feature representation for each subject can be obtained from different templates. To uncover the inherent distribution structure of data, we partition subjects in each original class into several sub-classes (i.e., clusters) by using a clustering algorithm. Then, we re-label each sub-class with a unique code vector by considering both its original class label and its distribution information. Afterwards, we adopt a multi-task feature selection method to select informative features in each view space. Based on those selected features, we then learn multiple support vector machine (SVM) classifiers, with each SVM corresponding to a specific view space. Finally, we fuse these SVMs by an ensemble classification method with a simple majority voting strategy. Experiments on the ADNI database demonstrate that our method outperforms the state-of-the-art multi-template based methods for AD/MCI classification. The major contributions of this paper are two-fold. First, we propose to mine the underlying distribution structure information of data for multi-template based methods, by using a sub-class clustering algorithm. Second, we develop an ensemble classification method to better take advantage of multi-view feature representation generated from multiple templates.

It is worth indicating the difference between this work and our previous study [32]. First, the method proposed in [32] focuses on using the representation from the main view (i.e., template) with extra guidance from other views, where the inherent data structure of multi-view data is not considered. In contrast, this study focuses on exploiting the data distribution structure information within each view space, where a clustering based algorithm is adopted to partition the original data into several sub-classes. In addition, feature selection in [32] is performed in each individual view space, where the inherent relationships among different views are not considered. Different from [32], feature selection in this work is under a multi-task learning framework, where the relationships among different tasks (with each task corresponding to a specific view) can be modeled implicitly.

The rest of the paper is organized as follows. We first present the details of our proposed approach in the Method section. Then, we describe the experiments and comparative results in the Results section. In the Discussion section, we investigate the influence of parameters, analyze the diversity of classifiers, and discuss the limitations of our method. Finally, we conclude this paper in the Conclusion section.

II. Method

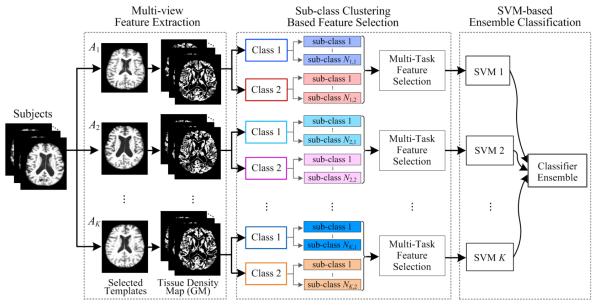
Figure 1 shows the flowchart of our proposed inherent structure based multi-view learning (ISML) method for AD/MCI classification. From Fig. 1, we can observe that there are three main steps in ISML, including 1) multi-view feature extraction, 2) sub-class clustering based feature selection, and 3) SVM-based ensemble classification. In what follows, we will elaborate each step in details.

Fig. 1.

The flowchart of our proposed method, including three main steps: 1) multi-view feature extraction, 2) sub-class clustering based feature selection, and 3) SVM-based ensemble classification.

A. Multi-view Feature Extraction

In this study, we develop a multi-view feature extraction method using multiple templates, with each template regarded as a specific view representation. In brief, we first develop a study-specific template selection strategy to obtain multiple templates from data, and then extract multi-view regional feature representation for each subject from multiple template spaces.

1) Template Selection

In multi-template based methods, each brain MR image is usually first non-linearly registered onto multiple selected templates, through which multi-view feature representation can be extracted by regarding each template as a specific view. In the literature, existing multi-template based studies either employ templates in a pre-defined template library [17], or select templates randomly from all studied subjects [19]. However, due to differences between populations (e.g., age, disease, etc.) or changes in scanner and imaging technology, MR images in two different studies might be significantly different [19, 35]. Thus, pre-defined templates and those obtained by random selection strategy may be not representative enough for the whole population in a specific study, which may induce large registration errors and reduce the discriminative ability of the features. Different from previous template selection strategies, we now develop a study-specific template selection approach that can capture population variability as much as possible. In brief, we adopt an affinity propagation (AP) clustering algorithm [36] to partition the studied subjects into several clusters. Thereupon, the corresponding cluster centers (i.e., exemplars) are called and used as templates.

AP starts with a similarity matrix with each element defining the similarity between a pair of data points, and keeps passing real-valued messages between data points until a high-quality set of representative points (i.e., exemplars) and corresponding clusters are found [36]. The advantage of the AP algorithm over traditional clustering algorithms (e.g., k-means [37]) is that AP is independent of the quality of initial sets of cluster centers by considering all data points as cluster centers, simultaneously. In AP clustering process, we apply a bi-section method to find an appropriate preference value [36], while the similarity between two data points are computed as the negative normalized mutual information. In this work, there are a total of 10 templates selected from AD and normal controls (NC) subjects (shown in Fig. 2). Although it is possible to select more templates from data, those additional templates could bring more computation burden in image registration process. On the other hand, the number of our selected templates is similar to existing multi-template based studies [17, 19].

Fig. 2.

Selected templates (i.e., exemplars) achieved by affinity propagation algorithm.

2) Feature Extraction

Following [22], we adopt a mass-preserving shape transformation framework to capture the morphometric patterns of all studied subjects using multiple templates, by first performing segmentation and registration to extract volumetric features, then adaptively clustering voxels into regions of interest (ROIs) in each specific template space, and finally extracting features from each ROI. Specifically, we first adopt a brain tissue segmentation method [38] to segment each skull-stripped MR brain image into three tissues, i.e., gray matter (GM), while matter (WM), and cerebrospinal fluid (CSF). Since GM is most affected by AD [39, 40], we only use GM tissues for feature extraction and classification in this study. Afterwards, the tissue-segmented brain image (i.e., GM) is spatially normalized onto each of multiple template spaces, by using a high-dimensional image warping method called HAMMER [41]. Given K templates, a total of K GM tissue density maps, each reflecting the local volumetric measurement, are generated from multi-template spaces for each subject.

The above mass-preserving transformation procedure generates millions of volumetric features for each brain that could be redundant and noisy for subsequent learning model, especially for only a relatively small number of training samples [29, 31, 42]. At the same time, traditional methods for obtaining regional features using pre-defined ROIs are not suitable for multi-template based methods, because different templates may provide complementary representation for a brain image from different views. Following [29], we adopt a watershed segmentation algorithm [43] to obtain a regional grouping of volumetric features in each of multiple template spaces, individually. In this way, different templates will yield different ROI partitions, due to the fact that different tissue density maps of the same subject are generated in different template spaces. Furthermore, other than using all voxels in each region for total regional volumetric measurement, we adopt a regional feature aggregation method to aggregate only a sub-region in each region to further optimize the discriminative power of the obtained regional features, by using an iterative voxel selection algorithm proposed in [29]. Finally, in each template space, D regional features are extracted for each subject. Using K templates, we can obtain K sets of D-dimensional features for each studied subject, while each set of features represent a subject from a specific view (i.e., template). It is worth noting that, compared with the single-view feature extraction method, our multi-view feature extraction method has relatively higher computational cost. That is mainly because of using multiple templates for image registration using HAMMER [41]. But this is reasonable, since we are incorporating more information and potentially selecting better and more relevant features. Thus, there is a trade-off between the quality of feature representation and the computational cost. One possible solution in the future is to parallelize the image registration process by using multiple CPUs, which will speed up multi-view feature extraction process.

B. Sub-class Clustering Based Feature Selection

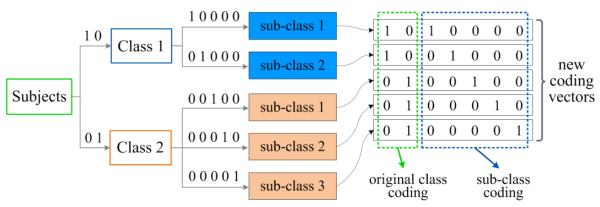
Although we perform voxel selection in the feature extraction stage to improve the discriminative power of features, many regional features could be still redundant or noisy for subsequent classification models because of the limited number of training subjects. Hence, feature selection is an essential step to eliminate those redundant or noisy features. On the other hand, since the data distribution structure of a particular class may be complicated, we believe that mining and utilizing such structure information in the feature selection stage can help find informative features. Accordingly, we first propose to mine the inherent structure of data in each template space, by employing a sub-class clustering algorithm. Based on the clustering results, we then encode those sub-classes with unique codes by considering both their original class information and their own distribution information, with a popular one-versus-all (OVA) encoding strategy [44]. Afterwards, we utilize a multi-task feature selection model to select the most informative features, through which the structure information of data is used to guide the feature selection process.

To uncover the underlying structure of a specific class, we exploit the affinity propagation (AP) algorithm [36] again to partition the subjects within this class into several sub-classes (i.e., clusters) in each of multi-view spaces. As an example, Fig. 3 shows the sub-class clustering results with subjects belonging to two original classes (i.e., Class 1 and Class 2). Using the AP algorithm, we partition the subjects in Class 1 into two sub-classes, while divide subjects in Class 2 into three sub-classes (see Fig. 3). Then, we re-label all sub-classes with unique codes by encoding the original classes and those sub-classes using the OVA encoding strategy, respectively. As illustrated in Fig. 3, each original class is now represented by a unique OVA coding vector (i.e., [1 0] for Class 1 and [0 1] for Class 2). For those five sub-classes in both Class 1 and Class 2, we encode them with similar OVA encoding strategy. Specifically, sub-class 1 and sub-class 2 in Class 1 are encoded as [1 0 0 0 0] and [0 1 0 0 0], respectively, while those three sub-classes in Class 2 are encoded as [0 0 1 0 0], [0 0 0 1 0], and [0 0 0 0 1], respectively. In this way, subjects in sub-class 1 of Class 1 are finally labeled as [1 0 1 0 0 0 0], where the first two bits denote the OVA coding for its original class (i.e., Class 1), and the last five bits represent its unique OVA coding among five sub-classes of all original classes.

Fig. 3.

An example illustration of our proposed sub-class clustering based encoding method in a specific view space, where subjects in Class 1 are partitioned into two sub-classes, while subjects in Class 2 are divided into three sub-classes.

Throughout the paper, we denote matrices as boldface uppercase letters, vectors as boldface lowercase letters, and scalars as normal italic letters. Denote $\mathbf{X}\in {\mathbb{R}}^{N\times D}$ as the data matrix with N subjects and D-dimensional features in a specific view space. Let $\mathbf{Y}\in {\mathbb{R}}^{N\times C}$ represent the new class label matrix for N subjects by employing the above sub-class clustering based encoding strategy, where each subject is labeled by a C-bit row vector, and C is the sum of the number of original classes and the number of sub-classes of all original classes. Since each column of Y partitions all studied subjects into two categories in a new label space, the original problem can be transformed into C binary sub-problems, where subjects labeled as 1 are treated as positive samples, and those labeled as 0 are used as negative samples. Therefore, we can transform the original problem into a multi-task learning problem (e.g., 7 tasks in Fig. 3) with each task corresponding to a specific column of Y.

After the sub-class clustering and the encoding process, we then adopt a multi-task feature selection model to select informative features in each view space individually. Let a_i and a^j represent the i^th row and the j^th column of a matrix A, respectively. We further denote the Frobenius norm and the l_2,1 norm of A as ${\Vert \mathbf{A}\Vert }_F=\sqrt{{\sum }_i{\Vert {\mathbf{a}}_i\Vert }_2^2}$ and ${\Vert \mathbf{A}\Vert }_{2,1}={\sum }_i{\Vert {\mathbf{a}}_i\Vert }_2$, respectively. Also, let $\mathbf{W}=[{\mathbf{w}}^1,{\mathbf{w}}^2,\cdots ,{\mathbf{w}}^c,\cdots ,{\mathbf{w}}^C]\in {\mathbb{R}}^{D\times C}$ represent the weight for C learning tasks, and w^c is a column weight vector corresponding to the c-th task. To jointly select common features among different tasks, we adopt a multi-task feature selection model [45], which is defined as

$${\min }_{\mathbf{W}}{\Vert \mathbf{Y}-\mathbf{XW}\Vert }_F^2+\lambda {\Vert \mathbf{W}\Vert }_{2,1}$$ (1)

where the first term is the empirical loss on the training data, the second term is a group sparsity regularizer, and λ is a parameter used to trade off the balance between the two terms in (1). Due to the group sparsity nature of l_2,1 norm [45], the estimated optimal coefficient matrix $\widehat{\mathbf{W}}$ will have some zero-value row vectors, implying that the corresponding features are not informative in predicting any of the class labels of the training data. Unlike conventional methods that only learn a single mapping function between the input data and corresponding class labels, our sub-class clustering based multi-task learning aims to learn multiple mapping vectors (i.e., {w¹,w²,⋯,w^c⋯,w^C}) jointly, which allows us to explicitly take advantage of the distribution structure of original classes in the feature selection process. In this study, we used the SLEP toolbox [46] for solving the proposed problem in (1).

C. SVM-based Ensemble Classification

To better take advantage of multi-view feature representation generated from different templates, we further propose an SVM-based ensemble classification approach. Specifically, we first learn a view-specific linear SVM classifier based on the selected features in each view space. Due to the max-margin classification characteristic, the SVM has good generalization capability across different training data (e.g., produced in each 10-fold cross-validation case in our experiments), as extensively shown in existing AD diagnosis studies [10, 32, 47]. Given K different views (i.e., templates), we therefore obtain K different SVMs. Note that those SVMs for K views are trained individually, with each one learned by using all studied subjects with feature representation from a specific view space and their original class labels. Then, a majority voting strategy [48], a simple but effective classifier fusion method, is employed to combine the outputs of those view-specific SVMs. Given a new test sample, its class label is determined through the same majority voting of the outputs of K SVM classifiers.

III. Experimental Results

A. Subjects and Image Pre-processing

1) Subjects

In this study, we evaluate the efficiency of our proposed method on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database available at http://adni.loni.usc.edu/. We only consider the T1-weighted MRI baseline data in ADNI-1 database, acquired from 97 AD, 128 NC, and 234 MCI subjects. For those MCI subjects, they were further clinically divided into 117 progressive MCI (pMCI) subjects who progressed to AD in 18 months, and 117 stable MCI (sMCI) subjects who did not progress to AD in 18 months. In Table I, we show the demographic and clinical information of the studied subjects.

TABLE I.

Demographic information of 459 studied subjects from the ADNI database

Diagnosis	AD	pMCI	sMCI	NC
Subject number	97	117	117	128
Male/Female	48/49	67/50	79/38	63/65
Age (Mean±SD)	75.90±6.84	75.18±6.97	75.09±7.65	76.11±5.10
MMSE (Mean±SD)	23.37±1.84	26.45±1.66	27.42±1.78	29.13±0.96

Note: Values are denoted as mean ± deviation; MMSE means mini-mental state examination; M and F represent male and female, respectively.

In the ADNI database, subjects were 55-90 years old with a study partner who can provide an independent evaluation of functioning. General inclusion/exclusion criteria are briefly listed as follows (see http://www.adni-info.org/Home.aspx). (1) Normal control subjects: Mini-Mental State Examination (MMSE) scores between 24 and 30 (inclusive), a Clinical Dementia Rating (CDR) of 0, non-depressed, non-MCI, and non-demented; (2) MCI subjects: MMSE scores between 24 and 30 (inclusive), a memory complaint, objective memory loss measured by education adjusted scores on Wechsler Memory Scale Logical Memory II, a CDR of 0.5, absence of significant levels of impairment in other cognitive domains, essentially preserved activities of daily living, and an absence of dementia; and (3) AD subjects: MMSE scores between 20 and 26 (inclusive), CDR of 0.5 or 1.0, and meets the National Institute of Neurological and Communicative Disorders and Stroke and the Alzheimer’s Disease and Related Disorders Association (NINCDS/ADRDA) criteria for probable AD.

The MR images for all studied subjects were pre-processed by a standard procedure. Specifically, to correct intensity inhomogeneity, we first perform a non-parametric non-uniform bias correction proposed in [49] for each MR image. Then, skull stripping [3] and manual review or correction are performed to remove both skull and dura, followed by cerebellum removal. Next, each brain image is segmented into three tissues (i.e., GM, WM, and CSF) by using FAST [38]. Finally, all brain images are affine aligned by FLIRT [50, 51].

2) Experimental Setting

The evaluation of our method is conducted on three binary classification problems, including AD vs. NC classification, pMCI vs. NC classification, and pMCI vs. sMCI classification. In the experiments, we use a 10-fold cross-validation strategy to evaluate the performance of our method and those compared methods. We randomly partition the studied subjects in each class into 10 sub-sets with approximately equal size without replacement. Afterwards, one sub-set is used as testing data, while the others are employed as training data. We then report the performances of different methods by averaging the results of those 10 folds in cross-validation.

We compare the proposed sub-class clustering feature selection method with six well-known feature selection methods, including t-test [52], Laplacian Score (LS) [53], Fisher Score (FS), Pearson Correlation (PC) [54], COMPARE [29], and LASSO [55]. For LS/FS/PC methods, we first select the first d features from the ranking list of features generated by the corresponding algorithms on the training set, where d is the desired number of selected features specified as d={1, 2, …, D} in the experiments. Then, we report the highest classification accuracy achieved by LS/FS/PC on the testing set. For t-test, COMPARE, LASSO, and our method, the optimal feature subset is determined through corresponding algorithms on the training set via inner cross validation, and the classification results on the testing set are reported using such fixed feature subset. In this study, K=10 templates are selected from AD and NC subjects using the AP clustering algorithm, and each subject is represented by a D-dimensional (D=1500 in this study) feature vector in each of templates (i.e., views). For fair comparison, all competing methods share the same multi-view feature representation for each training (or testing) subject.

In addition, we deal with multi-view features generated from different templates via three different ways. First, we employ single-view features in the first group of experiments. That is, we first perform feature selection in a specific view space (i.e., only features from this view are used), and construct a view-specific SVM classifier using those selected features. We then average the results among multiple single-views achieved by different methods. Second, we simply concatenate multi-view features generated from multiple templates as a long feature vector, and then use different feature selection algorithms to perform feature selection, followed by a SVM classifier. Finally, we make use of multi-view features through the proposed SVM-based ensemble classification strategy, where we perform feature selection in each of multi-view spaces individually, and construct multiple SVMs (each SVM corresponding to a specific view). This would be followed by a majority voting strategy to combine the outputs of those SVMs for making a final decision.

Following [56], the sub-class number of positive classes, i.e., (1) AD in AD vs. NC classification, (2) pMCI in pMCI vs. NC classification, and (3) pMCI in pMCI vs. sMCI classification, in our method is empirically set as 2, while that for negative classes is set as 3. In Section 4, we further investigate the influence of sub-class numbers on the learning performance of our method. For model selection, the regularization parameter (i.e., λ) in our sub-class clustering based feature selection model as defined in (1), as well as the parameter for l₁-norm regularizer in LASSO, are both chosen from the range {2⁻¹⁰, 2⁻⁹, ⋯, 2⁰} through inner 10-fold cross validation on the training data. Specifically, the training data are further divided into 10 subsets, with one subset for testing and the other nine subsets for training. Finally, we select the parameter values with which the learning method can achieve the best average validation classification accuracy among 10 folds. For the t-test method, the p-value is chosen from {0.05, 0.08, 0.10, 0.12, 0.15} via inner cross validation on training data. Also, the soft margin parameter of linear SVM is chosen from the range {2⁻¹⁰, 2⁻⁹, ⋯, 2⁵}. Here, we resort to the LIBSVM toolbox [57] for SVM classifier learning, and the SLEP toolbox [46] for multi-task feature learning.

We evaluate the performance of different methods via seven evaluation metrics: classification accuracy (ACC), sensitivity (SEN), specificity (SPE), balanced accuracy (BAC), positive predictive value (PPV), negative predictive value (NPV) [58], and the area under the receiver operating characteristic curve (AUC). Denote TP, TN, FP and FN as True Positive, True Negative, False Positive, and False Negative, respectively. Those evaluation metrics are defined as: (1) ACC=(TP+TN)/(TP+TN+FP+FN); (2) SEN=TP/(TP+FN); (3) SPE=TN/(TN+FP); (4) BAC=(SEN+SPE)/2; (5) PPV=TP/(TP+FP); (6) NPV=TN/(TN+FN). In addition, the receiver operating characteristic (ROC) curve, a plot of true positive rate vs. false positive rate, is also used to evaluate the performance of brain disease diagnosis, while the area under the ROC Curve (AUC) that is a metric for measuring the overall performance of a diagnostic test.

3) Results using Single-view Features

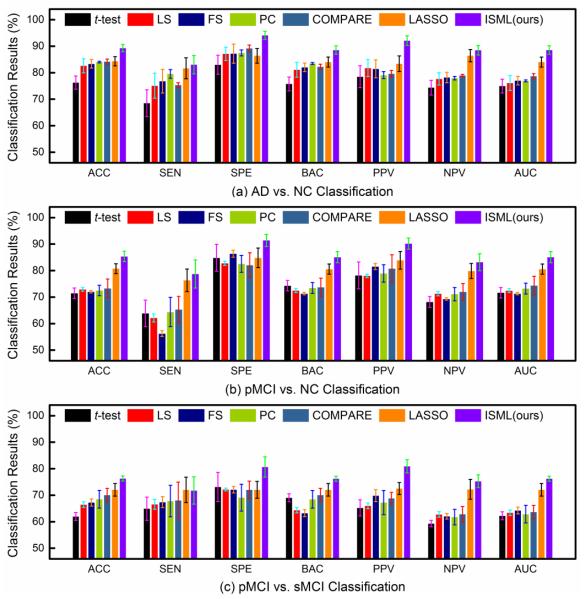
To demonstrate the superiority of our proposed sub-class clustering based feature selection method, we first perform experiments by using single-view feature representation. Specifically, we first select features in a specific view space using a feature selection algorithm, and then construct an SVM classifier with those selected features. Given K sets of single-view features, we report the averaged classification results among K views achieved by different methods in three classification tasks in Fig. 4.

Fig. 4.

Averaged classification results achieved by different methods using different single-view features in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

From Fig. 4, one can observe that, in most cases, our method achieves better performance than the compared methods in terms of seven evaluation metrics in three classification problems. Specifically, our ISML method consistently outperforms the compared methods in both the AD vs. NC and the pMCI vs. NC classification. In pMCI vs. sMCI classification, our method is superior to the compared methods in six out of seven evaluation metrics. This indicates that, compared with methods performing direct feature selection according to the original labels, our sub-class clustering based feature selection method helps promote the performance of AD classification. The advantage of our method could be due to the fact that our method utilizes the structure information of data.

4) Results using Multi-view Features via Feature Concatenation

In the second group of experiments, we employ multi-view features and feature concatenation strategy to preform classification. That is, we first concatenate multi-view features generated from different templates as a long feature vector for each subject, and then perform feature selection using different algorithms, followed by a SVM classifier. Figure 5 shows the classification results of different methods using multi-view features and the feature concatenation strategy.

Fig. 5.

Classification results achieved by different methods using multi-view features and feature concatenation strategy in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

As could be seen in Fig. 5, the proposed ISML method outperforms all competing methods, in most cases. For instance, in terms of the classification accuracy, ISML achieves an improvement of 1.44% compared with the second best method (LASSO) in AD vs. NC classification, an improvement of 2.03% compared with the second best method (LASSO) in pMCI vs. NC classification, and an improvement of 2.78% compared with the second best method (COMPARE) in pMCI vs. sMCI classification. On the other hand, from Fig. 4 and Fig. 5, one can see that methods using multi-view features usually outperform their counterparts using single-view features. This implies that, compared with single-view features, multi-view feature representation can facilitate subsequent classification tasks by comprehensively representing each subject.

5) Results using Multi-view Features via Ensemble Classification

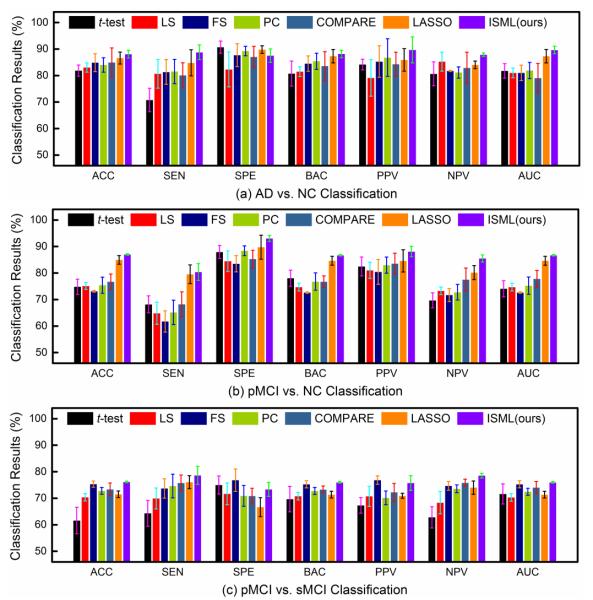
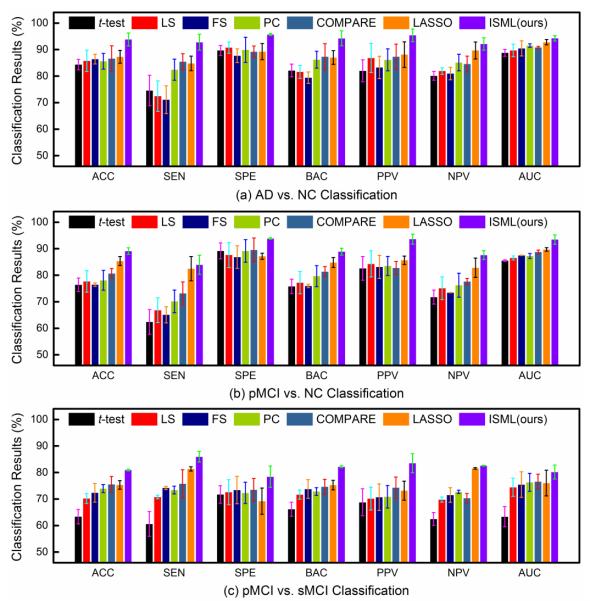
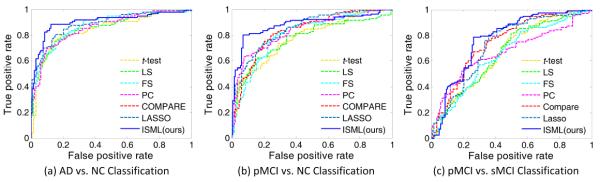
In the third group of experiments, we make use of multi-view features via our proposed SVM-based ensemble classification strategy. Briefly, we first perform feature selection using a specific feature selection algorithm in each of multi-view (i.e., multi-template) spaces, and then construct multiple view-specific SVMs (with each one corresponding to a specific view), followed by a majority voting strategy to combine the outputs of those SVMs for making a final decision. We report the experimental results achieved by different methods in three classification tasks in Fig. 6, and further plot the corresponding ROC curves in Fig. 7.

Fig. 6.

Classification results achieved by different methods using multi-view features and ensemble classification strategy in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

Fig. 7.

ROC curves achieved by different methods using the proposed ensemble classification strategy in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

As shown in both Fig. 6 and Fig. 7, our ISML method achieves significantly better performance than other methods in three classification tasks, especially in terms of ACC, SEN, SPE, BAC, PPV and AUC. In particular, ISML obtains the best sensitivity in AD vs. NC classification (7.34% higher than the second best sensitivity achieved by LASSO), indicating that our method can effectively identifies AD (or pMCI) patients. Higher sensitivity values indicate high confidence in disease diagnosis, which is potentially very useful in real-world applications. Thus, from a clinical point of view, ISML is less likely to misdiagnose subjects with diseases, in comparison to those compared methods. In terms of AUC (as shown in Fig. 6 and Fig. 7), ISML is apparently superior to all other methods in three classification tasks. In addition, it can be seen from Fig. 5 and Fig. 6 that methods using our ensemble classification method generally achieve more promising results, compared with their counterparts using feature concatenation strategy. It implies that the ensemble-based method provides a better way to make use of multi-view feature representation, compared with the feature concatenation strategy. Better performance of our ensemble-based method is mainly due to the fact that the rich anatomical structures of multi-templates that are treated as specific views individually, while such structure information could be lost in the feature concatenation method.

6) Comparison with State-of-the-art Methods

Furthermore, we compare the results achieved by our ISML method (using multi-view features and ensemble classification strategy) with those of the state-of-the-art methods that use MRI data of ADNI subjects. Since very limited studies report the pMCI vs. NC classification results, we only report the results of AD vs. NC classification and pMCI vs. sMCI classification in Table II, respectively. Also, we further list the details of each method in Table II, including the type of features and classifiers. It is worth noting that 30 templates are randomly selected from all studied subjects in [8, 19], while 10 templates are determined by the AP clustering algorithm from AD and NC subjects in [31, 32, 34] and our method.

TABLE II.

Comparison with state-of-the-art methods using multiple templates in AD vs. NC and pMCI vs. sMCI classification

Method	Feature Type	Classifier	AD vs. NC			pMCI vs. sMCI
			ACC (%)	SEN (%)	SPE (%)	ACC (%)	SEN (%)	SPE (%)
Koikkalainen et al. [19]	TBM	Linear regression	86.00	81.00	91.00	72.10	77.00	71.00
Wolz et al. [8]	TBM	Linear discriminant analysis	87.00	84.00	90.00	64.00	65.00	62.00
Min et al. [31]	Data-Driven ROI GM	SVM	91.64	88.56	93.85	72.41	72.12	72.58
Min et al. [34]	Data-Driven ROI GM	SVM	90.69	87.56	93.01	73.69	76.44	70.76
Liu et al. [32]	Data-Driven ROI GM	SVM ensemble	92.51	92.89	88.33	78.88	85.45	76.06
ISML (ours)	Data-Driven ROI GM	SVM ensemble	93.83	92.78	95.69	80.90	85.95	78.41

It can be seen from Table II that our ISML method generally outperforms the compared methods in AD vs. NC classification. More specifically, ISML achieves much higher accuracy (i.e., 93.83%) and much better specificity (i.e., 95.69%) compared with the other methods, and obtains a comparable sensitivity (i.e., 92.78%) compared with the second best method proposed by Liu et al. in [32]. From Table II, one can also observe that, in pMCI vs. sMCI classification, ISML achieves an accuracy of 80.90%, a sensitivity of 85.95%, and a specificity of 78.41%, while the best accuracy, the best sensitivity, and the best specificity obtained by the compared methods are only 78.88%, 85.45%, and 76.06%, respectively. Note that our method is the first one to mine and utilize the underlying complex data distribution structure for feature selection in multi-template based methods, while the conventional methods simply assume that data is represented by a specific type of distribution (e.g., Gaussian distribution) [8, 19, 31, 32, 34].

IV. Discussion

Since there are two key stages (i.e., sub-class clustering based feature selection and SVM-based ensemble classification) in our ISML method, we further investigate the influence of sub-class number on the learning performance, and analyze the diversity of classifiers in the classifier ensemble.

1) Influence of Sub-class Number

First, we evaluate the influence of different sub-class numbers on the learning performance of our ISML method in three classification tasks using multi-view feature representation. Following [56], the sub-class number for a specific original class (e.g., AD, NC, pMCI, or sMCI) varies from 1 to 5 in our experiments, and the corresponding AP clustering algorithm is performed to partition the subjects within each class into a specific number of clusters. In Fig. 8 and Fig. 9, we plot the classification accuracies achieved by ISML with different sub-class numbers, using the feature concatenation and the ensemble classification strategies, respectively.

Fig. 8.

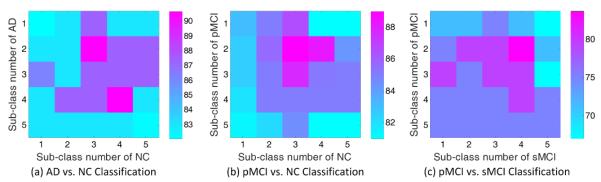
Classification accuracy vs. sub-class number, achieved by our ISML method using feature concatenation strategy in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

Fig. 9.

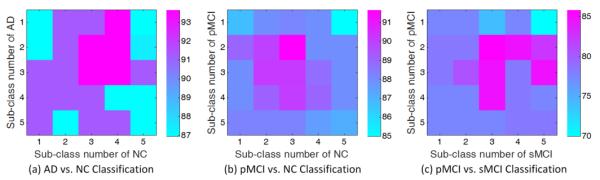
Classification accuracy vs. sub-class number, achieved by our ISML method using ensemble classification strategy in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

From Fig. 8 (a) and Fig. 9 (a), we can draw the conclusion that ISML achieves the best performance when the sub-class number is 2 or 3 for AD, and 3 or 4 for NC. When the sub-class number is smaller than 2 or larger than 4, the performance of ISML is not so satisfying. Similar trend can be found in pMCI vs. NC classification as shown in Fig. 8 (b) and Fig. 9 (b), and also in pMCI vs. sMCI classification as shown in Fig. 8 (c) and Fig. 9 (c). The underlying reason for those results could be that the inherent structure of an original class (e.g., AD, pMCI, sMCI, and NC) is not very complex; also, our experimental results are consistent with the results reported in [56] for AD/MCI classification. On the other hand, we can clearly see from Fig. 8 and Fig. 9 that the underlying data distribution may be not simple Gaussian distribution, as assumed by the conventional multi-template based methods, which justifies the proposed method.

2) Analysis of Classifier Diversity

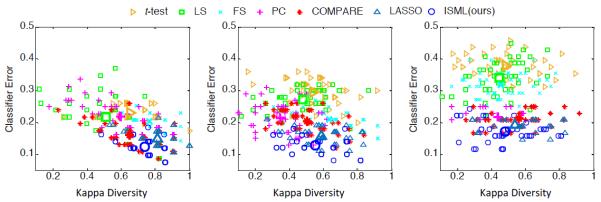
In this study, we propose an SVM-based ensemble classification method to better use multi-view feature representation generated from multiple templates. To understand how the ensemble classification approach works, we now quantitatively measure the diversity and the mean classification error between any two different SVM classifiers, where each SVM is learned in a specific view space. Here, we use Kappa index to measure the diversity [59] of two classifiers, where a small Kappa value indicates a better diversity of two classifiers. Also, small mean classification errors imply better accuracies achieved by a pair of classifiers. In Fig. 10, we plot the Kappa-error diagrams and the corresponding centroids of point clouds achieved by seven ensemble-based methods in three classification tasks, where the most desired points lie on the bottom left of the Kappa-error diagram [59].

Fig. 10.

Diversities and mean classification errors achieved by seven ensemble-based methods in (a) AD vs. NC, (b) pMCI vs. NC, and (c) pMCI vs. sMCI classification tasks.

It can be seen from Fig. 10 that our ISML method consistently outperforms the compared methods in terms of the mean classification error in AD vs. NC, pMCI vs. NC, and pMCI vs. sMCI classification tasks. Although LS, PC and COMPARE usually achieve smaller Kappa values compared with ISML, their classification errors are much higher than those of ISML. These results indicate that the proposed ISML method makes a better trade-off between the diversity and the classification error for achieving a better classification performance, compared with the other methods.

3) Limitations

In this study, we validate the efficacy of the proposed method via three groups of experiments and three binary classification tasks (i.e., the classifications of AD vs. NC, pMCI vs. NC, and pMCI vs. sMCI). However, there are several limitations in our method.

First, using the proposed sub-class clustering based encoding method, we transform the original binary learning problem into a multi-task learning problem. Here, we employ the one-versus-all (OVA) encoding strategy to re-label subjects, while there are still many other types of efficient encoding strategies for dealing with multi-class learning problems in machine learning domain (e.g., ternary encoding method and data-driven encoding strategy [60]). It is interesting to investigate whether other complex sub-class encoding strategies can further boost the performance of AD/MCI classification.

Second, in the feature selection stage, we only use the naïve multi-task sparse feature selection method with a l_2,1 norm based regularizer, where relationships among subjects are not considered at all. As one type of prior information, the relationship information among subjects in each of multiple tasks can also be used to guide the feature selection procedure. For instance, it is possible to adopt the manifold regularized multi-task feature selection model [47] to identify informative features, which is expected to further promote the performance of AD/MCI classification.

Third, we currently extract regional features in multiple template spaces, where the partitions of ROIs in different templates may be different from each other. The advantage of such feature extraction method is that the unique characteristics of different templates can be preserved naturally. However, at the same time, it is also difficult to directly compare subjects in two template spaces because of anatomical structure differences among templates. To facilitate direct comparison between subjects in two different template spaces, it could be interesting to further register those selected templates into a common space, and then perform ROI partition jointly.

V. Conclusion

In this paper, we propose an inherent structure based multi-view leaning (ISML) method with feature representation generated from multiple templates for AD/MCI classification. Specifically, we first select multiple templates from data, and then extract multi-view feature representation for subjects using those templates, where each template is treated as a specific view. Afterwards, we cluster subjects within each class into several sub-classes in each view space, and encode those sub-classes with unique codes by considering both their original class information and their own distribution information, followed by a multi-task feature selection procedure. Finally, we learn a view-specific SVM classifier using selected features in each view space, and fuse results of multiple SVMs together by a majority voting strategy. We evaluate the efficacy of the proposed method on 459 subjects with MRI baseline data from the ADNI database, and obtain the accuracies of 93.83%, 89.09%, and 80.90% for AD vs. NC, pMCI vs. NC, and pMCI vs. sMCI classification tasks, respectively.