Abstract
Previous studies have shown that a greater number of ovulatory cycles, cumulatively summed as lifetime number of ovulatory cycles (LOC), increases ovarian cancer risk, but there is no uniform algorithm with which to compute LOC. The association between LOC and endometrial cancer is less certain. Accordingly, we identified 14 different LOC algorithms in a literature review and calculated LOCs in the Polish Cancer Study (2001–2003). We evaluated the associations of LOC with ovarian and endometrial cancer risks using unconditional logistic regression, with and without adjustment for individual risk factors used in the LOC computations. Our analysis included 302 ovarian cancer cases with 1,356 controls and 532 endometrial cancer cases with 1,286 controls. We found a high correlation between LOC values among the combined controls (r ≥ 0.88) and identified 5 groups of similar LOC algorithms. A LOC value in the highest quartile was associated with ovarian cancer risk as computed by 2 algorithms (odds ratio (OR) = 2.22 (95% confidence interval (CI): 1.07, 4.62) and OR = 2.44 (95% CI: 1.22, 4.87)) and with endometrial cancer risk as computed by 1 algorithm (OR = 1.95, 95% CI: 1.11, 3.44). LOC algorithms using a core set of variables widely available in epidemiologic studies may be independently associated with risk of gynecological cancers beyond the contribution of the individual risk factors, such as ages at menopause and menarche.
Keywords: age at menarche, age at menopause, endometrial cancer, incessant ovulation, lifetime ovulatory cycles, ovarian cancer, ovulation
Epidemiologic studies have consistently observed protective associations with increased number of births and use of oral contraceptives and have provided some evidence for protective associations with later age at menarche and earlier age at menopause in relation to risks of ovarian (1) and endometrial (2) cancer. In line with this evidence, Fathalla (3), and subsequently others (4–7), suggested that repeated trauma to and repair of the ovarian epithelium caused by “incessant ovulation” is a major risk factor for ovarian cancer. The “incessant ovulation” hypothesis postulates that increased numbers of active ovulatory cycles might also be associated with increased endometrial cancer risk (8).
Supporting this, a greater lifetime number of ovulatory cycles (LOC) has been shown in numerous studies to be associated with increased risk of ovarian cancer (4, 9–20) and, to a lesser degree, endometrial cancer (21, 22). LOC generally estimates the cumulative number of a woman's ovulatory cycles based on mathematical algorithms that typically take into account the time between menopause and menarche. Additionally, the duration of any anovulatory cycles during times of oral contraceptive use, pregnancy, and breastfeeding is subtracted from the menstrual span duration. Thus, the calculated LOC measure reflects a specific biological process that is captured in multiple individual variables. However, previous epidemiologic studies have shown positive associations between LOC and ovarian cancer, with a wide range of estimates (odds ratios ranging from 1.81 (11) to 5.01 (12) when comparing the highest categories of ovulatory cycles or years of ovulation with the lowest), and it is unclear whether these variations in estimates are related to differences between study populations or to differences between algorithms used to calculate LOC, since no uniform LOC algorithm has been established. Furthermore, many of the previous ovarian cancer studies evaluated LOC unadjusted for any of the individual risk factors used to compute it, such as age at menarche, age at menopause, ever use of oral contraceptives, and pregnancy history (10–12, 14–16, 19, 23); while some studies adjusted for at least 1 risk factor, not all of these studies allowed for comparison of risk estimates before and after adjustments (9, 18, 24). Thus, it is not well established that LOC is associated with cancer risk beyond the contributions made by its individual components.
To further assess these putative relationships, we identified various LOC algorithms previously employed and then applied each algorithm to assess the relationship of LOC to ovarian and endometrial cancer risks in the Polish Cancer Study (25, 26), which has detailed information on hormonal and reproductive factors.
METHODS
Identification of LOC algorithms
We identified relevant articles by searching PubMed through the end of June 2013 using the search terms “lifetime ovulatory cycles” OR “ovulatory cycles” OR “incessant ovulation” AND “cancer.” The reference lists of relevant articles were also searched for additional eligible studies. In our evaluation of the articles, we included studies that would allow us to quantify ovulation over a lifetime or total number of years of ovulation. We did not limit our evaluation to studies of ovarian and endometrial cancer. We selected the first article we found for each unique algorithm.
Calculating LOCs and estimating associations with cancer risk
Study population
We calculated LOC by means of different algorithms identified in the literature review using data from the Polish Cancer Study, which has been described elsewhere in detail (25, 26). Briefly, eligible case women were diagnosed between June 1, 2001, and December 30, 2003, resided in Warsaw or Lodz, Poland, and were aged 20–74 years at the time of diagnosis. Incident and invasive endometrial (n = 551) and ovarian (n = 317) cancer cases were ascertained through a rapid identification system coordinated by 5 participating Polish hospitals that cover approximately 85% of all cases diagnosed in the 2 cities. Additionally, cancer registries in Warsaw and Lodz were used to identify cases missed by the rapid identification system. Eligible controls with no prior breast or ovarian cancer (for ovarian cancer cases) or no prior breast or endometrial cancer (for endometrial cancer cases) at the time of enrollment and with one or both ovaries intact (for ovarian cancer cases) or with an intact uterus (for endometrial cancer cases) were randomly selected from a database of all Polish residents, with some controls being shared between breast, endometrial, and ovarian cancer cases in the Polish Cancer Study. Information on demographic factors, anthropometric factors, menstrual characteristics, oral contraceptive use, menopausal hormone use, and cigarette smoking was collected through interviewer-administered questionnaires. The study protocol was reviewed and approved by local Polish and US National Cancer Institute institutional review boards. All participants provided written informed consent.
We focused our analysis on women who reported being postmenopausal (i.e., no longer having menstrual periods) in order to evaluate the complete menstrual time span (i.e., years between age at menarche and age at menopause). For women with surgically induced menopause (mean age at surgically induced menopause was 42.9 years; range, 25–52 years), age at menopause was assigned as the age of surgery if a woman had undergone bilateral oophorectomy. Age at menopause was assigned as 50 years if a woman had undergone partial oophorectomy or hysterectomy, since she would have continued to have ovulatory cycles after her surgery. We excluded women with ages at menopause of <40 years and >60 years to minimize potential misreporting. The resulting analytical population consisted of 302 ovarian cancer cases and 1,356 ovarian controls and 532 endometrial cancer cases and 1,286 endometrial controls. The combined control set contained 1,365 women, and 1,277 controls overlapped between the ovarian and endometrial cancer analyses.
Computation of LOC
Of the 18 unique algorithms identified from the literature review, we did not have sufficient data on the required variables (i.e., “months of postpartum amenorrhea,” “months of missed or irregular periods,” and “amenorrheic time”) to evaluate 4 algorithms in the Polish Cancer Study. For the remaining 14 algorithms, we attempted to code variables as defined in the original report. For example, some studies specified using the average menstrual cycle length reported in the risk factor questionnaire; others relied on certain assumptions. Based on an average cycle length of 28 days, the number of menstrual cycles per year was 13. We were unable to calculate a woman's LOC if she was missing data for one or more of the variables included in the LOC algorithm. Duration of ovulation was transformed to number of ovulatory cycles by dividing the duration of ovulation by average cycle length, where an average cycle length of 28 days was assumed.
Statistical analysis
In the combined control set, we compared LOCs computed from the different algorithms using Pearson's pairwise correlation and used histograms to evaluate the distributions of the LOC values. Quartile categories (quartiles 1–4) for each LOC were determined on the basis of the distribution among the combined controls, with the lowest quartile (quartile 1) used as the referent group. We also compared the LOC algorithms with key individual risk factors that were used in LOC computation using Spearman rank pairwise correlation.
We evaluated the LOC from each algorithm in relation to ovarian and endometrial cancer risk by calculating odds ratios and 95% confidence intervals using adjusted unconditional logistic regression. Statistical heterogeneity in the odds ratios across the categories of individual risk factors was assessed using the Wald χ2 test (P value). To test for linear trends, we entered the ordinal values representing categories of risk factors as a continuous variable in the models (P for trend). We also evaluated whether individual risk factors in the LOC algorithms, particularly age at menopause, age at menarche, oral contraceptive use, and number of live births, would remain statistically significant after adjustment for LOC. The likelihood ratio test was used to determine the significance of the model results with and without the LOC term (P for heterogeneity). For all analyses, P values less than 0.05 were considered statistically significant. All statistical tests (P values presented) were 2-sided. Statistical analyses were performed in Stata 13.1 (StataCorp LP, College Station, Texas) and SAS 9.3 (SAS Institute, Inc., Cary, North Carolina).
RESULTS
Identifying LOC algorithms
The primary literature search identified 449 articles. After review of the abstracts and the Methods sections, we identified 18 unique LOC algorithms using different variables, with different definitions for one or more of the factors (4, 9–12, 14–17, 19, 21–24, 27–30). For example, the period after childbirth, generally considered a period when women are not ovulating, was captured differently across algorithms. Some studies reported this period as the 12 months after any full-term birth, regardless of breastfeeding duration (9, 24). Other studies relied on information collected on duration of breastfeeding (9, 11, 12, 14–17, 19, 23, 29) or on postpartum amenorrheic time (10, 12, 30). We present the 18 LOC algorithms (labeled A–R) and the variables used in each calculation in Web Tables 1 and 2 (available at http://aje.oxfordjournals.org/). Fourteen different variables were reported across the algorithms, and 6 variables were used in at least half of the models. All of the models contained the variables age at menopause and age at menarche.
Estimating LOC
The simplest LOC models (algorithms C and F), which incorporated 3 variables (age at menarche, age at menopause, and parity (calculated as the product of number of births and 1.5 in algorithm C and as months of pregnancy in algorithm F)), and the most complex model (algorithm O), which included 9 variables (additionally included: duration of oral contraceptive use, average cycle length, duration of breastfeeding, and numbers of abortions, miscarriages, and stillbirths), produced similar ranges of LOC with high correlation (r = 0.93; Web Table 3) in the controls of the Polish Cancer Study.
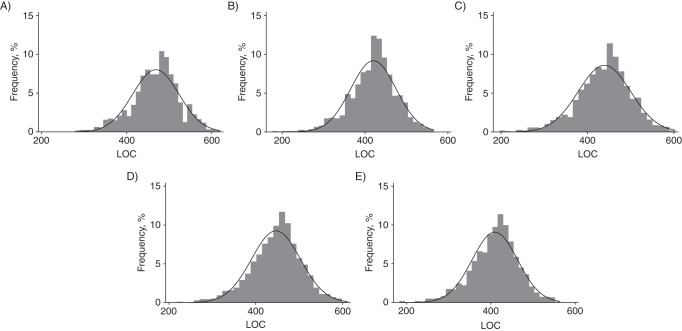
In Figure 1, we present the LOC distribution among controls from the Polish Cancer Study (n = 1,365) as computed by the 5 major groups of algorithms (represented by algorithms C, D, G, M, and R) with pairwise correlation less than 0.98. LOC values ranged from 176.0 to 565.7 for algorithm D and from 279.5 to 619.1 for algorithm C. All other models were highly correlated with one of these 5 algorithms (r ≥ 0.98; Web Table 3). Correlation between key individual risk factors used to compute LOCs and LOC values from the 5 major groups were also evaluated (Web Table 4). In general, individual correlation was low (ρ range: −0.04 to −0.30), except for age at menopause, which was positively correlated with LOC (ρ ≥ 0.72).
Figure 1.
Distributions of lifetime number of ovulatory cycles (LOC) among combined controls (n = 1,365) from the Polish Cancer Study (2001–2003) for 5 LOC algorithms with pairwise correlation less than 0.98. A) Algorithm C: LOC range, 279.5–619.1 (mean = 468.4); B) algorithm D: LOC range, 176.0–565.7 (mean = 420.1); C) algorithm G: LOC range, 196.3–602.3 (mean = 439.3); D) algorithm M: LOC range, 218.8–611.0 (mean = 446.6); E) algorithm R: LOC range, 183.5–564 (mean = 409.5). Other algorithms were highly correlated with one of the above models (r ≥ 0.98): Algorithm C was correlated with algorithm F; algorithm D was correlated with algorithms E, H, J, N, O, and R; algorithm G was correlated with algorithm B; and algorithm R was correlated with algorithms A, B, D, E, H, J, N, O, and Q.
Estimating cancer risk related to LOC
Web Table 5 shows the distribution of selected characteristics among ovarian and endometrial cancer cases and controls. Characteristics significantly differed between cases and controls for several factors. For the most part, both endometrial and ovarian cancer cases tended to have had younger ages at menarche and fewer pregnancies and births than controls.
LOC values in the highest quartile were significantly associated with increased ovarian cancer risk as computed by 2 of the 5 major groups of algorithms (odds ratios ranged from 2.22 (95% confidence interval (CI): 1.07, 4.62) for algorithm D to 2.44 (95% CI: 1.22, 4.87) for algorithm G) and with endometrial cancer risk as computed by 1 (algorithm G) of the 5 major groups of algorithms (odds ratio = 1.95, 95% CI: 1.11, 3.44) in models that adjusted for key risk factors used to compute LOC, including age at menopause (Tables 1 and 2). Being in the highest LOC quartile category for the other groups (algorithms C, M, and R for ovarian cancer risk and algorithms D, M, and R for endometrial cancer risk) was associated with elevated cancer risk, albeit not significantly. Furthermore, we observed overall similar associations for both ovarian and endometrial cancer risk only after adjusting for age and site, though the associations tended to be generally attenuated before full adjustment for ovarian cancer risk and attenuated after full adjustment for endometrial cancer risk. Risk factor associations for individual risk factors used to compute LOC, including ages at menopause and menarche, oral contraceptive use, and number of live births, changed most noticeably after results were adjusted for LOC as computed by algorithms D (P for heterogeneity = 0.02) and G (P for heterogeneity = 0.08) for ovarian cancer risk and as computed by algorithm D for endometrial cancer risk (P for heterogeneity = 0.12), albeit not statistically significantly for all of the algorithms (Tables 3 and 4). Furthermore, in general, ovarian and endometrial cancer risk associations with each individual component of LOC seemed to be slightly attenuated after adjustment for LOC. The exception was age at menopause, a risk factor positively correlated with LOC; we observed qualitative changes in the association from increased to decreased risk with increase age at menopause.
Table 1.
Association Between Lifetime Number of Ovulatory Cycles, As Calculated by 5 Different Algorithms, and Ovarian Cancer in the Polish Cancer Study, 2001–2003a
| Algorithm and Quartile of LOCb | No. of Cases | No. of Controls | Model 1c |
Model 2d |
||
|---|---|---|---|---|---|---|
| OR | 95% CI | OR | 95% CI | |||
| Algorithm C | ||||||
| Q1 | 86 | 301 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 76 | 333 | 1.04 | 0.71, 1.54 | 1.05 | 0.64, 1.72 |
| Q3 | 51 | 314 | 0.92 | 0.60, 1.39 | 1.03 | 0.53, 2.00 |
| Q4 | 75 | 343 | 1.45 | 0.98, 2.15 | 1.75 | 0.82, 3.75 |
| P valuee | 0.11 | 0.13 | ||||
| P for trendf | 0.11 | 0.16 | ||||
| Algorithm D | ||||||
| Q1 | 86 | 319 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 67 | 315 | 1.02 | 0.68, 1.52 | 1.06 | 0.65, 1.73 |
| Q3 | 53 | 315 | 0.99 | 0.66, 1.50 | 1.08 | 0.58, 2.01 |
| Q4 | 76 | 320 | 1.70 | 1.14, 2.52 | 2.22 | 1.07, 4.62 |
| P value | 0.02 | 0.03 | ||||
| P for trend | 0.02 | 0.02 | ||||
| Algorithm G | ||||||
| Q1 | 72 | 308 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 78 | 322 | 1.39 | 0.92, 2.09 | 1.44 | 0.89, 2.33 |
| Q3 | 59 | 318 | 1.46 | 0.95, 2.26 | 1.58 | 0.89, 2.81 |
| Q4 | 71 | 315 | 2.00 | 1.31, 3.07 | 2.44 | 1.22, 4.87 |
| P value | 0.01 | 0.02 | ||||
| P for trend | 0.002 | 0.08 | ||||
| Algorithm M | ||||||
| Q1 | 84 | 301 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 66 | 301 | 0.95 | 0.64, 1.42 | 0.89 | 0.53, 1.47 |
| Q3 | 49 | 282 | 0.94 | 0.61, 1.45 | 0.84 | 0.45, 1.59 |
| Q4 | 72 | 325 | 1.47 | 0.99, 2.20 | 1.28 | 0.60, 2.71 |
| P value | 0.09 | 0.52 | ||||
| P for trend | 0.07 | 0.36 | ||||
| Algorithm R | ||||||
| Q1 | 80 | 330 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 75 | 304 | 1.19 | 0.80, 1.77 | 1.12 | 0.69, 1.83 |
| Q3 | 52 | 311 | 1.08 | 0.71, 1.64 | 0.95 | 0.52, 1.74 |
| Q4 | 75 | 323 | 1.70 | 1.14, 2.53 | 1.48 | 0.72, 3.04 |
| P value | 0.04 | 0.38 | ||||
| P for trend | 0.02 | 0.31 | ||||
Abbreviations: CI, confidence interval; LOC, lifetime ovulatory cycles; OR, odds ratio; Q, quartile.
a Factors were evaluated among cases/controls without missing LOC values for each given algorithm.
b Quartile categories for each LOC algorithm were based on the distribution among the combined controls. Quartile cutpoints—algorithm C: Q1, 279.5–438; Q2, 439–467; Q3, 468–504; Q4, 505–619.1; algorithm D: Q1, 176.0–389.5; Q2, 389.6–425.8; Q3, 425.9–453.35; Q4, 453.36–565.7; algorithm G: Q1, 196.3–402; Q2, 403–444.5; Q3, 444.6–479.9; Q4, 480.0–602.3; algorithm M: Q1, 218.8–412; Q2, 413–452.5; Q3, 452.6–480; Q4, 481–611; algorithm R: Q1, 183.5–377.525; Q2, 377.526–413.525; Q3, 413.526–443.52; Q4, 443.53–564.
c Adjusted for age (in 5-year age categories) and study site (Lodz or Warsaw).
d Additionally adjusted for age at menopause (<45, 45–49, 50–54, or ≥55 years), age at menarche (<13, 13, 14, 15, or ≥16 years), oral contraceptive use (never, ever), and number of live births (0, 1, 2, or ≥3).
e Statistical heterogeneity in the ORs across the categories of the risk factors was assessed using the Wald χ2 test.
f To test for linear trends, we entered the ordinal values representing categories of risk factors as a continuous variable in the models.
Table 2.
Association Between Lifetime Number of Ovulatory Cycles, As Calculated by 5 Different Algorithms, and Endometrial Cancer in the Polish Cancer Study, 2001–2003a
| Algorithm and Quartile of LOCb | No. of Cases | No. of Controls | Model 1c |
Model 2d |
||
|---|---|---|---|---|---|---|
| OR | 95% CI | OR | 95% CI | |||
| Algorithm C | ||||||
| Q1 | 92 | 297 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 94 | 302 | 1.04 | 0.71, 1.54 | 0.71 | 0.46, 1.10 |
| Q3 | 116 | 285 | 0.92 | 0.60, 1.40 | 0.68 | 0.40, 1.16 |
| Q4 | 208 | 338 | 1.45 | 0.98, 2.15 | 0.89 | 0.47, 1.57 |
| P valuee | 0.11 | 0.98 | ||||
| P for trendf | 0.07 | 0.21 | ||||
| Algorithm D | ||||||
| Q1 | 88 | 316 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 103 | 281 | 1.02 | 0.69, 1.52 | 1.07 | 0.70, 1.63 |
| Q3 | 106 | 292 | 0.99 | 0.66, 1.50 | 0.85 | 0.52, 1.41 |
| Q4 | 207 | 312 | 1.70 | 1.14, 2.52 | 1.29 | 0.73, 2.32 |
| P value | 0.02 | 0.44 | ||||
| P for trend | 0.08 | 0.11 | ||||
| Algorithm G | ||||||
| Q1 | 69 | 286 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 99 | 293 | 1.39 | 0.92, 2.09 | 1.30 | 0.85, 2.00 |
| Q3 | 129 | 305 | 1.46 | 0.95, 2.26 | 1.49 | 0.92, 2.42 |
| Q4 | 205 | 311 | 2.00 | 1.31, 3.07 | 1.95 | 1.11, 3.44 |
| P value | 0.02 | 0.02 | ||||
| P for trend | 0.10 | 0.13 | ||||
| Algorithm M | ||||||
| Q1 | 75 | 299 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 94 | 273 | 0.95 | 0.64, 1.42 | 0.98 | 0.63, 1.53 |
| Q3 | 104 | 258 | 0.94 | 0.61, 1.44 | 0.90 | 0.54, 1.51 |
| Q4 | 200 | 316 | 1.47 | 0.99, 2.20 | 1.09 | 0.60, 1.98 |
| P value | 0.75 | 0.75 | ||||
| P for trend | 0.07 | 0.75 | ||||
| Algorithm R | ||||||
| Q1 | 83 | 327 | 1.00 | Referent | 1.00 | Referent |
| Q2 | 100 | 273 | 1.19 | 0.80, 1.77 | 1.16 | 0.76, 1.76 |
| Q3 | 113 | 286 | 1.08 | 0.71, 1.64 | 1.11 | 0.69, 1.79 |
| Q4 | 208 | 314 | 1.70 | 1.14, 2.53 | 1.47 | 0.84, 2.58 |
| P value | 0.21 | 0.21 | ||||
| P for trend | 0.08 | 0.40 | ||||
a Factors were evaluated among cases/controls without missing LOC values for each given algorithm.
b Quartile categories for each LOC algorithm were based on the distribution among the combined controls. Quartile cutpoints—algorithm C: Q1, 279.5–438; Q2, 439–467; Q3, 468–504; Q4, 505–619.1; algorithm D: Q1, 176.0–389.5; Q2, 389.6–425.8; Q3, 425.9–453.35; Q4, 453.36–565.7; algorithm G: Q1, 196.3–402; Q2, 403–444.5; Q3, 444.6–479.9; Q4, 480.0–602.3; algorithm M: Q1, 218.8–412; Q2, 413–452.5; Q3, 452.6–480; Q4, 481–611; algorithm R: Q1, 183.5–377.525; Q2, 377.526–413.525; Q3, 413.526–443.52; Q4, 443.53–564.
c Adjusted for age (in 5-year age categories) and study site (Lodz or Warsaw).
d Additionally adjusted for age at menopause (<45, 45–49, 50–54, or ≥55 years), age at menarche (<13, 13, 14, 15, or ≥16 years), oral contraceptive use (never, ever), and number of live births (0, 1, 2, or ≥3).
e Statistical heterogeneity in the ORs across the categories of the risk factors was assessed using the Wald χ2 test.
f To test for linear trends, we entered the ordinal values representing categories of risk factors as a continuous variable in the models.
Table 3.
Associations Between Key Components of the Lifetime Number of Ovulatory Cycles (LOC) Measure (As Calculated by 5 Different Algorithms) and Ovarian Cancer, With and Without Adjustment for LOC, Polish Cancer Study, 2001–2003a
| Component of LOC | No. of Cases | No. of Controls | Without LOCb |
With LOCc |
||
|---|---|---|---|---|---|---|
| OR | 95% CI | OR | 95% CI | |||
| Algorithm C | ||||||
| Age at menopause, years | ||||||
| <45 | 38 | 109 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 106 | 355 | 1.23 | 0.71, 2.14 | 1.21 | 0.65, 2.23 |
| 50–54 | 112 | 647 | 1.05 | 0.62, 1.80 | 0.86 | 0.39, 1.89 |
| ≥55 | 32 | 180 | 1.17 | 0.62, 2.22 | 0.70 | 0.27, 1.86 |
| P valued | 0.97 | 0.36 | ||||
| P for trende | 0.77 | 0.46 | ||||
| Age at menarche, years | ||||||
| <13 | 81 | 270 | 1.00 | Referent | 1.00 | Referent |
| 13 | 61 | 298 | 0.68 | 0.45, 1.01 | 0.72 | 0.48, 1.07 |
| 14 | 89 | 347 | 0.86 | 0.59, 1.24 | 0.95 | 0.64, 1.43 |
| 15 | 29 | 145 | 0.71 | 0.43, 1.20 | 0.82 | 0.47, 1.43 |
| ≥16 | 28 | 231 | 0.47 | 0.28, 0.77 | 0.57 | 0.32, 1.01 |
| P value | 0.01 | 0.16 | ||||
| P for trend | 0.03 | 0.15 | ||||
| Oral contraceptive use | ||||||
| Never | 265 | 1,207 | 1.00 | Referent | 1.00 | Referent |
| Ever | 20 | 70 | 0.87 | 0.48, 1.59 | 0.85 | 0.46, 1.56 |
| No. of live births | ||||||
| 0 | 51 | 141 | 1.00 | Referent | 1.00 | Referent |
| 1 | 114 | 390 | 0.90 | 0.59, 1.36 | 0.90 | 0.59, 1.37 |
| 2 | 104 | 564 | 0.53 | 0.35, 0.81 | 0.53 | 0.35, 0.80 |
| ≥3 | 19 | 196 | 0.27 | 0.14, 0.49 | 0.27 | 0.15, 0.51 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm D | ||||||
| Age at menopause, years | ||||||
| <45 | 38 | 104 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 105 | 351 | 1.17 | 0.68, 2.04 | 1.14 | 0.62, 2.09 |
| 50–54 | 107 | 636 | 0.98 | 0.57, 1.67 | 0.73 | 0.33, 1.56 |
| ≥55 | 32 | 178 | 1.13 | 0.60, 2.14 | 0.54 | 0.21, 1.40 |
| P value | 0.84 | 0.12 | ||||
| P for trend | 0.72 | 0.20 | ||||
| Age at menarche, years | ||||||
| <13 | 78 | 268 | 1.00 | Referent | 1.00 | Referent |
| 13 | 60 | 292 | 0.68 | 0.45, 1.02 | 0.74 | 0.49, 1.12 |
| 14 | 88 | 342 | 0.88 | 0.61, 1.28 | 1.04 | 0.69, 1.54 |
| 15 | 29 | 139 | 0.75 | 0.45, 1.26 | 0.92 | 0.53, 1.62 |
| ≥16 | 27 | 228 | 0.48 | 0.29, 0.79 | 0.63 | 0.36, 1.11 |
| P value | 0.02 | 0.35 | ||||
| P for trend | 0.03 | 0.21 | ||||
| Oral contraceptive use | ||||||
| Never | 263 | 1,205 | 1.00 | Referent | 1.00 | Referent |
| Ever | 19 | 64 | 0.87 | 0.47, 1.63 | 0.97 | 0.50, 1.87 |
| No. of live births | ||||||
| 0 | 48 | 135 | 1.00 | Referent | 1.00 | Referent |
| 1 | 113 | 383 | 0.91 | 0.60, 1.39 | 0.96 | 0.63, 1.48 |
| 2 | 103 | 554 | 0.55 | 0.36, 0.83 | 0.58 | 0.38, 0.89 |
| ≥3 | 18 | 197 | 0.27 | 0.15, 0.50 | 0.31 | 0.16, 0.58 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm G | ||||||
| Age at menopause, years | ||||||
| <45 | 38 | 103 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 105 | 349 | 1.18 | 0.68, 2.04 | 0.93 | 0.50, 1.72 |
| 50–54 | 106 | 634 | 0.96 | 0.56, 1.65 | 0.59 | 0.29, 1.19 |
| ≥55 | 31 | 177 | 1.09 | 0.57, 2.06 | 0.50 | 0.20, 1.21 |
| P value | 0.71 | 0.04 | ||||
| P for trend | 0.69 | 0.15 | ||||
| Age at menarche, years | ||||||
| <13 | 77 | 266 | 1.00 | Referent | 1.00 | Referent |
| 13 | 60 | 290 | 0.69 | 0.46, 1.03 | 0.73 | 0.48, 1.10 |
| 14 | 87 | 342 | 0.88 | 0.60, 1.27 | 1.02 | 0.69, 1.52 |
| 15 | 29 | 139 | 0.75 | 0.45, 1.26 | 0.92 | 0.53, 1.59 |
| ≥16 | 27 | 226 | 0.49 | 0.29, 0.80 | 0.65 | 0.37, 1.12 |
| P value | 0.02 | 0.36 | ||||
| P for trend | 0.04 | 0.22 | ||||
| Oral contraceptive use | ||||||
| Never | 261 | 1,199 | 1.00 | Referent | 1.00 | Referent |
| Ever | 19 | 64 | 0.88 | 0.47, 1.64 | 1.03 | 0.54, 1.97 |
| No. of live births | ||||||
| 0 | 48 | 134 | 1.00 | Referent | 1.00 | Referent |
| 1 | 111 | 379 | 0.90 | 0.59, 1.38 | 1.00 | 0.65, 1.54 |
| 2 | 103 | 554 | 0.55 | 0.36, 0.83 | 0.64 | 0.41, 0.99 |
| ≥3 | 18 | 196 | 0.27 | 0.15, 0.50 | 0.35 | 0.18, 0.67 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | 0.0003 | ||||
| Algorithm M | ||||||
| Age at menopause, years | ||||||
| <45 | 37 | 99 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 105 | 331 | 1.24 | 0.70, 2.18 | 1.32 | 0.70, 2.49 |
| 50–54 | 100 | 609 | 0.94 | 0.54, 1.64 | 0.94 | 0.43, 2.06 |
| ≥55 | 29 | 170 | 1.09 | 0.56, 2.11 | 0.90 | 0.34, 2.41 |
| P value | 0.56 | 0.57 | ||||
| P for trend | 0.46 | 0.42 | ||||
| Age at menarche, years | ||||||
| <13 | 76 | 252 | 1.00 | Referent | 1.00 | Referent |
| 13 | 57 | 281 | 0.67 | 0.43, 1.01 | 0.69 | 0.45, 1.06 |
| 14 | 83 | 323 | 0.83 | 0.57, 1.22 | 0.88 | 0.59, 1.33 |
| 15 | 28 | 136 | 0.73 | 0.43, 1.23 | 0.77 | 0.44, 1.37 |
| ≥16 | 27 | 218 | 0.47 | 0.28, 0.79 | 0.51 | 0.29, 0.91 |
| P value | 0.02 | 0.08 | ||||
| P for trend | 0.04 | 0.13 | ||||
| Oral contraceptive use | ||||||
| Never | 248 | 1,132 | 1.00 | Referent | 1.00 | Referent |
| Ever | 20 | 64 | 0.93 | 0.50, 1.73 | 0.91 | 0.49, 1.69 |
| No. of live births | ||||||
| 0 | 50 | 135 | 1.00 | Referent | 1.00 | Referent |
| 1 | 103 | 356 | 0.88 | 0.58, 1.35 | 0.92 | 0.59, 1.43 |
| 2 | 99 | 532 | 0.53 | 0.35, 0.81 | 0.56 | 0.35, 0.88 |
| ≥3 | 19 | 186 | 0.28 | 0.15, 0.52 | 0.30 | 0.15, 0.58 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm R | ||||||
| Age at menopause, years | ||||||
| <45 | 38 | 106 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 105 | 350 | 1.23 | 0.71, 2.14 | 1.18 | 0.63, 2.18 |
| 50–54 | 108 | 634 | 1.03 | 0.60, 1.77 | 0.89 | 0.42, 1.90 |
| ≥55 | 31 | 178 | 1.13 | 0.60, 2.15 | 0.81 | 0.32, 2.07 |
| P value | 0.85 | 0.45 | ||||
| P for trend | 0.73 | 0.61 | ||||
| Age at menarche, years | ||||||
| <13 | 78 | 267 | 1.00 | Referent | 1.00 | Referent |
| 13 | 61 | 290 | 0.69 | 0.46, 1.04 | 0.72 | 0.48, 1.09 |
| 14 | 87 | 344 | 0.86 | 0.59, 1.25 | 0.93 | 0.62, 1.38 |
| 15 | 29 | 140 | 0.74 | 0.44, 1.24 | 0.80 | 0.46, 1.39 |
| ≥16 | 27 | 227 | 0.48 | 0.29, 0.79 | 0.54 | 0.31, 0.95 |
| P value | 0.02 | 0.10 | ||||
| P for trend | 0.04 | 0.15 | ||||
| Oral contraceptive use | ||||||
| Never | 263 | 1,202 | 1.00 | Referent | 1.00 | Referent |
| Ever | 19 | 66 | 0.86 | 0.45, 1.59 | 0.89 | 0.47, 1.69 |
| No. of live births | ||||||
| 0 | 50 | 139 | 1.00 | Referent | 1.00 | Referent |
| 1 | 111 | 379 | 0.89 | 0.58, 1.34 | 0.93 | 0.61, 1.41 |
| 2 | 103 | 554 | 0.54 | 0.35, 0.81 | 0.57 | 0.37, 0.89 |
| ≥3 | 18 | 196 | 0.27 | 0.14, 0.49 | 0.29 | 0.15, 0.57 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
a Factors were evaluated among cases/controls without missing LOC values for each given algorithm.
b Adjusted for age (in 5-year age categories) and study site (Lodz or Warsaw), age at menopause (<45, 45–49, 50–54, or ≥55 years), age at menarche (<13, 13, 14, 15, or ≥16 years), oral contraceptive use (never, ever), and number of live births (0, 1, 2, or ≥3).
c Additionally adjusted for LOC (quartiles among combined controls). Quartile cutpoints—algorithm C: Q1, 279.5–438; Q2, 439–467; Q3, 468–504; Q4, 505–619.1; algorithm D: Q1, 176.0–389.5; Q2, 389.6–425.8; Q3, 425.9–453.35; Q4, 453.36–565.7; algorithm G: Q1, 196.3–402; Q2, 403–444.5; Q3, 444.6–479.9; Q4, 480.0–602.3; algorithm M: Q1, 218.8–412; Q2, 413–452.5; Q3, 452.6–480; Q4, 481–611; algorithm R: Q1, 183.5–377.525; Q2, 377.526–413.525; Q3, 413.526–443.52; Q4, 443.53–564.
d Statistical heterogeneity in the ORs across the categories of the risk factors was assessed using the Wald χ2 test.
e To test for linear trends, we entered the ordinal values representing categories of risk factors as a continuous variable in the models.
Table 4.
Associations Between Key Components of the Lifetime Ovulatory Cycles (LOC) Measure (As Calculated by 5 Different Algorithms) and Endometrial Cancer, With and Without Adjustment for LOC, Polish Cancer Study, 2001–2003a
| Component of LOC | No. of Cases | No. of Controls | Without LOCb |
With LOCc |
||
|---|---|---|---|---|---|---|
| OR | 95% CI | OR | 95% CI | |||
| Algorithm C | ||||||
| Age at menopause, years | ||||||
| <45 | 33 | 110 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 111 | 355 | 1.19 | 0.72, 1.96 | 1.44 | 0.83, 2.48 |
| 50–54 | 252 | 579 | 2.04 | 1.27, 3.27 | 2.71 | 1.38, 5.35 |
| ≥55 | 114 | 179 | 3.00 | 1.80, 5.00 | 3.59 | 1.62, 7.96 |
| P valued | <0.0001 | 0.001 | ||||
| P for trende | <0.0001 | 0.006 | ||||
| Age at menarche, years | ||||||
| <13 | 143 | 256 | 1.00 | Referent | 1.00 | Referent |
| 13 | 128 | 280 | 0.77 | 0.56, 1.04 | 0.77 | 0.56, 1.05 |
| 14 | 123 | 327 | 0.66 | 0.49, 0.90 | 0.67 | 0.48, 0.92 |
| 15 | 54 | 138 | 0.73 | 0.49, 1.07 | 0.73 | 0.48, 1.12 |
| ≥16 | 62 | 222 | 0.50 | 0.35, 0.72 | 0.49 | 0.32, 0.76 |
| P value | <0.0001 | 0.002 | ||||
| P for trend | 0.003 | 0.02 | ||||
| Oral contraceptive use | ||||||
| Never | 480 | 1,146 | 1.00 | Referent | 1.00 | Referent |
| Ever | 27 | 63 | 0.97 | 0.59, 1.58 | 0.95 | 0.58, 1.55 |
| No. of live births | ||||||
| 0 | 94 | 140 | 1.00 | Referent | 1.00 | Referent |
| 1 | 169 | 359 | 0.71 | 0.51, 0.99 | 0.71 | 0.51, 0.99 |
| 2 | 201 | 536 | 0.57 | 0.41, 0.78 | 0.57 | 0.41, 0.78 |
| ≥3 | 46 | 188 | 0.36 | 0.23, 0.56 | 0.35 | 0.23, 0.55 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm D | ||||||
| Age at menopause, years | ||||||
| <45 | 33 | 105 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 109 | 351 | 1.13 | 0.69, 1.87 | 1.13 | 0.65, 1.96 |
| 50–54 | 249 | 569 | 1.95 | 1.21, 3.12 | 1.57 | 0.98, 3.58 |
| ≥55 | 113 | 176 | 2.89 | 1.73, 4.83 | 2.30 | 1.07, 4.96 |
| P value | <0.0001 | 0.02 | ||||
| P for trend | <0.0001 | 0.05 | ||||
| Age at menarche, years | ||||||
| <13 | 142 | 253 | 1.00 | Referent | 1.00 | Referent |
| 13 | 127 | 275 | 0.77 | 0.57, 1.05 | 0.80 | 0.58, 1.09 |
| 14 | 121 | 322 | 0.67 | 0.49, 0.91 | 0.71 | 0.51, 0.98 |
| 15 | 53 | 132 | 0.73 | 0.49, 1.08 | 0.77 | 0.51, 1.18 |
| ≥16 | 61 | 219 | 0.50 | 0.35, 0.72 | 0.54 | 0.36, 0.83 |
| P value | <0.001 | 0.009 | ||||
| P for trend | 0.003 | 0.07 | ||||
| Oral contraceptive use | ||||||
| Never | 478 | 1,144 | 1.00 | Referent | 1.00 | Referent |
| Ever | 26 | 57 | 1.05 | 0.63, 1.74 | 1.08 | 0.63, 1.85 |
| No. of live births | ||||||
| 0 | 93 | 134 | 1.00 | Referent | 1.00 | Referent |
| 1 | 168 | 353 | 0.70 | 0.50, 0.98 | 0.72 | 0.52, 1.01 |
| 2 | 199 | 526 | 0.56 | 0.40, 0.77 | 0.57 | 0.41, 0.79 |
| ≥3 | 44 | 188 | 0.34 | 0.22, 0.53 | 0.36 | 0.23, 0.57 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm G | ||||||
| Age at menopause, years | ||||||
| <45 | 32 | 104 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 109 | 349 | 1.17 | 0.71, 1.95 | 0.98 | 0.55, 1.72 |
| 50–54 | 249 | 567 | 2.00 | 1.24, 3.23 | 1.31 | 0.70, 2.46 |
| ≥55 | 112 | 175 | 2.93 | 1.74, 4.94 | 1.60 | 0.76, 3.34 |
| P value | <0.0001 | 0.08 | ||||
| P for trend | <0.0001 | 0.28 | ||||
| Age at menarche, years | ||||||
| <13 | 141 | 251 | 1.00 | Referent | 1.00 | Referent |
| 13 | 127 | 273 | 0.77 | 0.57, 1.06 | 0.82 | 0.60, 1.12 |
| 14 | 120 | 322 | 0.66 | 0.49, 0.91 | 0.75 | 0.54, 1.03 |
| 15 | 53 | 132 | 0.73 | 0.49, 1.09 | 0.85 | 0.56, 1.29 |
| ≥16 | 61 | 217 | 0.50 | 0.35, 0.72 | 0.62 | 0.41, 0.94 |
| P value | <0.0001 | 0.04 | ||||
| P for trend | 0.004 | 0.21 | ||||
| Oral contraceptive use | ||||||
| Never | 476 | 1,138 | 1.00 | Referent | 1.00 | Referent |
| Ever | 26 | 57 | 1.05 | 0.63, 1.75 | 1.25 | 0.73, 2.12 |
| No. of live births | ||||||
| 0 | 93 | 133 | 1.00 | Referent | 1.00 | Referent |
| 1 | 167 | 349 | 0.71 | 0.51, 0.99 | 0.74 | 0.52, 1.05 |
| 2 | 198 | 526 | 0.56 | 0.40, 0.77 | 0.61 | 0.44, 0.86 |
| ≥3 | 44 | 187 | 0.35 | 0.22, 0.54 | 0.41 | 0.26, 0.65 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | 0.001 | ||||
| Algorithm M | ||||||
| Age at menopause, years | ||||||
| <45 | 28 | 100 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 101 | 331 | 1.23 | 0.72, 2.10 | 1.26 | 0.70, 2.29 |
| 50–54 | 239 | 547 | 2.21 | 1.33, 3.68 | 2.23 | 1.11, 4.46 |
| ≥55 | 105 | 168 | 3.21 | 1.85, 5.58 | 3.04 | 1.35, 6.84 |
| P value | <0.0001 | 0.002 | ||||
| P for trend | <0.0001 | 0.01 | ||||
| Age at menarche, years | ||||||
| <13 | 134 | 236 | 1.00 | Referent | 1.00 | Referent |
| 13 | 120 | 263 | 0.76 | 0.51, 1.04 | 0.77 | 0.55, 1.07 |
| 14 | 114 | 306 | 0.64 | 0.47, 0.88 | 0.66 | 0.47, 0.91 |
| 15 | 49 | 130 | 0.69 | 0.46, 1.03 | 0.71 | 0.46, 1.10 |
| ≥16 | 56 | 211 | 0.47 | 0.32, 0.69 | 0.49 | 0.32, 0.76 |
| P value | <0.0001 | 0.002 | ||||
| P for trend | 0.002 | 0.02 | ||||
| Oral contraceptive use | ||||||
| Never | 443 | 1,076 | 1.00 | Referent | 1.00 | Referent |
| Ever | 27 | 58 | 1.07 | 0.65, 1.77 | 1.07 | 0.64, 1.77 |
| No. of live births | ||||||
| 0 | 92 | 134 | 1.00 | Referent | 1.00 | Referent |
| 1 | 155 | 330 | 0.71 | 0.51, 1.00 | 0.72 | 0.51, 1.03 |
| 2 | 186 | 505 | 0.56 | 0.40, 0.78 | 0.57 | 0.40, 0.80 |
| ≥3 | 40 | 177 | 0.33 | 0.21, 0.52 | 0.34 | 0.21, 0.55 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | <0.0001 | ||||
| Algorithm R | ||||||
| Age at menopause, years | ||||||
| <45 | 32 | 107 | 1.00 | Referent | 1.00 | Referent |
| 45–49 | 110 | 350 | 1.24 | 0.75, 2.05 | 1.15 | 0.65, 2.00 |
| 50–54 | 250 | 567 | 2.10 | 1.30, 3.39 | 1.71 | 0.90, 3.24 |
| ≥55 | 112 | 176 | 3.05 | 1.82, 5.13 | 2.16 | 1.01, 4.58 |
| P value | <0.0001 | 0.02 | ||||
| P for trend | <0.0001 | 0.10 | ||||
| Age at menarche, years | ||||||
| <13 | 141 | 252 | 1.00 | Referent | 1.00 | Referent |
| 13 | 127 | 273 | 0.78 | 0.57, 1.06 | 0.81 | 0.60, 1.11 |
| 14 | 120 | 324 | 0.66 | 0.49, 0.90 | 0.71 | 0.52, 0.99 |
| 15 | 54 | 133 | 0.74 | 0.50, 1.10 | 0.82 | 0.54, 1.24 |
| ≥16 | 62 | 218 | 0.51 | 0.35, 0.73 | 0.58 | 0.38, 0.88 |
| P value | <0.0001 | 0.02 | ||||
| P for trend | 0.004 | 0.11 | ||||
| Oral contraceptive use | ||||||
| Never | 478 | 1,141 | 1.00 | Referent | 1.00 | Referent |
| Ever | 26 | 59 | 1.01 | 0.61, 1.67 | 1.10 | 0.65, 1.87 |
| No. of live births | ||||||
| 0 | 94 | 138 | 1.00 | Referent | 1.00 | Referent |
| 1 | 167 | 349 | 0.72 | 0.52, 1.00 | 0.75 | 0.53, 1.05 |
| 2 | 198 | 526 | 0.57 | 0.41, 0.78 | 0.61 | 0.43, 0.85 |
| ≥3 | 45 | 187 | 0.36 | 0.23, 0.56 | 0.40 | 0.25, 0.64 |
| P value | <0.0001 | <0.0001 | ||||
| P for trend | <0.0001 | 0.001 | ||||
a Factors were evaluated among cases/controls without missing LOC values for each given algorithm.
b Adjusted for age (in 5-year age categories) and study site (Lodz or Warsaw), age at menopause (<45, 45–49, 50–54, or ≥55 years), age at menarche (<13, 13, 14, 15, or ≥16 years), oral contraceptive use (never, ever), and number of live births (0, 1, 2, or ≥3).
c Additionally adjusted for LOC (quartiles among combined controls). Quartile cutpoints—algorithm C: Q1, 279.5–438; Q2, 439–467; Q3, 468–504; Q4, 505–619.1; algorithm D: Q1, 176.0–389.5; Q2, 389.6–425.8; Q3, 425.9–453.35; Q4, 453.36–565.7; algorithm G: Q1, 196.3–402; Q2, 403–444.5; Q3, 444.6–479.9; Q4, 480.0–602.3; algorithm M: Q1, 218.8–412; Q2, 413–452.5; Q3, 452.6–480; Q4, 481–611; algorithm R: Q1, 183.5–377.525; Q2, 377.526–413.525; Q3, 413.526–443.52; Q4, 443.53–564.
d Statistical heterogeneity in the ORs across the categories of the risk factors was assessed using the Wald χ2 test.
e To test for linear trends, we entered the ordinal values representing categories of risk factors as a continuous variable in the models.
DISCUSSION
Despite differences in computation and data interpretation, LOC values calculated in our analysis using different algorithms were highly correlated, with similar LOC rankings (i.e., quartiles 1, 2, and 3 vs. quartile 4) across algorithms. The LOC values for the combined controls in the Polish Cancer Study ranged from 176.0 to 565.7 on the lower end and from 279.5 to 619.1 on the higher end. These LOC ranges are similar to the quartiles of LOC values presented in the largest LOC–ovarian cancer study to date, based on data from 2 case-control studies with 1,822 pre- and postmenopausal ovarian cancer cases: <357, 357–428, 429–480, and ≥481 (11).
Our results are generally consistent with previous studies showing that there are increases in ovarian and endometrial cancer risk with increasing LOC (4, 9–19, 21, 22), although not all of the LOC algorithms resulted in LOCs that were statistically significantly associated with the 2 gynecological cancers. In our study, LOC values from algorithms D and G showed positive associations with ovarian cancer risk and LOC from algorithm G showed positive associations with endometrial cancer risk. In comparing the algorithms that showed strong associations with cancer risk (i.e., algorithms D and G) with those that did not, the main difference was the use of pregnancy durations by algorithms D and G versus number of births by others. It is unclear whether incomplete pregnancies have certain implications for mechanisms or for better estimation of anovulatory cycles.
We also evaluated LOC in relation to risk of these tumors while adjusting for several key risk factors in the LOC computation (namely age at menopause, age at menarche, oral contraceptive use, and number of live births), albeit not all risk factors. The estimates for LOC did not change. This indicates that LOC contributes information in addition to the individual components and provides justification for evaluating LOC as an exposure separately from individual components of LOC. Conversely, associations with individual factors were attenuated, except for age at menopause, when LOC was added to the model. Age at menopause is most likely the central component of LOC, and its biological effect may be fully explained through LOC, which could lead to problems when adjusting for 2 highly correlated variables that are both strongly associated with the outcome. Other individual components, such as oral contraceptive use, may work through non-LOC-related mechanisms like the hormonal pathway. Additional LOC analyses in other studies with different population characteristics (e.g., higher prevalence of oral contraceptive use) are needed to fully understand the extent to which individual components of LOC should be included in the model in addition to the LOC measure.
In examining LOC as a covariate, the inclusion of the LOC variable may be an efficient way, by increasing statistical power (i.e., saving degrees of freedom), to adjust for several important reproductive factors in a single variable in a biologically meaningful manner. In our study, additional adjustment for age at menopause, age at menarche, and oral contraceptive use could have been avoided by including LOC in the model. The caveat is that in models without individual LOC components, it is not possible to distinguish whether an individual risk factor is an effect modifier, since 2 women with the same LOC value could have very different risk profiles (e.g., one could have had a longer duration of oral contraceptive use while the other had a longer duration of pregnancy). However, these questions can be addressed in more focused secondary analyses.
We limited our analysis to postmenopausal women, which allowed us to compute reliable estimates of the lifetime number of menstrual cycles. Investigators in some previous studies have reported that lifetime years of ovulation were more strongly associated with ovarian cancer among premenopausal women than among postmenopausal women (12, 18). Thus, we cannot exclude the possibility that we did not observe statistically significant associations with all the LOCs as computed by the algorithms we identified in our literature review, because our analysis was limited to postmenopausal women. Larger studies of pre- and postmenopausal women are needed to explore whether ovulation may be more important in the etiology of premenopausal cancer.
Several underlying mechanisms have been proposed to explain the relationship between incessant ovulation and ovarian cancer, including the development of genetically damaged cells caused by proliferation of ovarian surface epithelial cells to repair the ruptured ovarian surface and the production of stromal inclusion cysts, which undergo carcinogenic transformation (8, 14, 31). For endometrial cancer, the proposed mechanism is that incessant ovulation largely equates with incessant menstruation and that the increased number of cycles may increase the probability of random genetic mutations associated with repeated disruption and regeneration of the uterine lining (8). It is well established that endometrial cancer risk is associated with unopposed estrogen stimulation (2); thus, it is possible that LOC is a composite variable reflecting lifetime endogenous estrogen exposure instead of the amount of genotoxic insults associated with repeated disruption and regeneration of the uterine lining.
The major strength of our study was the availability of a detailed study questionnaire, which allowed us to examine many of the LOC algorithms in 1 target population with a limited number of women with surgically induced menopause. However, a potential limitation of using this study population is the low level of oral contraceptive use in Poland. The frequency of some exposures may vary between populations and may differentially impact LOC estimates from different models and limit the generalizability of the results. In addition, we relied on self-reported data, so misclassification may have occurred in our estimation of LOC. Misclassification error may have also been present because of the absence of other important details on each woman's menstrual characteristics, such as menstrual cycle length and bleeding patterns. Both short (<26 days) and long (>35 days) cycles, as compared with normal-length cycles (26–35 days), were associated with an increased probability of anovulation in the BioCycle Study, a prospective cohort study of 259 regularly menstruating healthy women aged 18–44 years (32). Additionally, in the same study, it was reported that bleeding duration and volume were reduced after anovulatory cycles as compared with ovulatory cycles (33). However, any approach to calculating the number of ovulations will inherently be imprecise, because not all menstrual cycles are ovulatory, and there is variation in menstrual cycles within and between women according to age and other characteristics (34).
In conclusion, LOC algorithms using a core set of variables widely available in epidemiologic studies may be independently associated with risk of gynecological cancers beyond the contribution by the individual risk factors such as age at menopause and age at menarche, although interpretation of risk estimates for individual factors, such as age at menopause, must be done cautiously. We also observed similar risk associations for LOC in risk models that did not additionally include individual components of LOC. The inclusion of the LOC variable could be an efficient way to adjust for several important reproductive factors in a single variable in a biologically meaningful manner. The methods used in this analysis should be repeated in a larger pooled data set. Pooling efforts among studies with detailed reproductive and menstrual history data for large numbers of pre- and postmenopausal women might help to further characterize how these reproductive factors mediate gynecological cancer risks. However, the utility of LOC algorithms in epidemiologic studies ultimately depends on the assumption that these measures are correlated with more direct measures of LOC that would account for which cycles might truly be ovulatory (10). Further evaluation of better assessment of cumulative length of ovulatory cycling is needed to evaluate whether LOC itself increases the risks of ovarian and endometrial cancer.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Division of Cancer Epidemiology and Genetics, National Cancer Institute, Bethesda, Maryland (Hannah P. Yang, Kelsey R. Murphy, Ruth M. Pfeiffer, Montserrat Garcia-Closas, Louise A. Brinton, Nicolas Wentzensen); Department of Epidemiology and Biostatistics, Dornsife School of Public Health, Drexel University, Philadelphia, Pennsylvania (Neena George); and Department of Cancer Epidemiology and Prevention, M. Sklodowska-Curie Cancer Center, Warsaw, Poland (Jolanta Lissowska).
This research was supported by the Division of Cancer Epidemiology and Genetics Intramural Research Program of the National Institutes of Health, National Cancer Institute.
Conflict of interest: none declared.
REFERENCES
- 1.Hankinson SE, Danforth KN. Ovarian cancer. In: Schottenfeld D, Fraumeni JF, eds. Cancer Epidemiology and Prevention. New York, NY: Oxford University Press; 2006:1013–1026. [Google Scholar]
- 2.Cook LS, Weiss NS, Doherty JA et al. Endometrial cancer. In: Schottenfeld D, Fraumeni JF, eds. Cancer Epidemiology and Prevention. New York, NY: Oxford University Press; 2006:1027–1043. [Google Scholar]
- 3.Fathalla MF. Incessant ovulation—a factor in ovarian neoplasia? [letter] Lancet. 1971;27716:163. [DOI] [PubMed] [Google Scholar]
- 4.Casagrande JT, Louie EW, Pike MC et al. “Incessant ovulation” and ovarian cancer. Lancet. 1979;28135:170–173. [DOI] [PubMed] [Google Scholar]
- 5.Cramer DW, Welch WR. Determinants of ovarian cancer risk. II. Inferences regarding pathogenesis. J Natl Cancer Inst. 1983;714:717–721. [PubMed] [Google Scholar]
- 6.Fleming JS, Beaugié CR, Haviv I et al. Incessant ovulation, inflammation and epithelial ovarian carcinogenesis: revisiting old hypotheses. Mol Cell Endocrinol. 2006;247(1-2):4–21. [DOI] [PubMed] [Google Scholar]
- 7.Risch HA. Hormonal etiology of epithelial ovarian cancer, with a hypothesis concerning the role of androgens and progesterone. J Natl Cancer Inst. 1998;9023:1774–1786. [DOI] [PubMed] [Google Scholar]
- 8.Cramer DW. The epidemiology of endometrial and ovarian cancer. Hematol Oncol Clin North Am. 2012;261:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gates MA, Rosner BA, Hecht JL et al. Risk factors for epithelial ovarian cancer by histologic subtype. Am J Epidemiol. 2010;1711:45–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Moorman PG, Schildkraut JM, Calingaert B et al. Ovulation and ovarian cancer: a comparison of two methods for calculating lifetime ovulatory cycles (United States). Cancer Causes Control. 2002;139:807–811. [DOI] [PubMed] [Google Scholar]
- 11.Pelucchi C, Galeone C, Talamini R et al. Lifetime ovulatory cycles and ovarian cancer risk in 2 Italian case-control studies. Am J Obstet Gynecol. 2007;1961:83.e1–83.e7. [DOI] [PubMed] [Google Scholar]
- 12.Purdie DM, Bain CJ, Siskind V et al. Ovulation and risk of epithelial ovarian cancer. Int J Cancer. 2003;1042:228–232. [DOI] [PubMed] [Google Scholar]
- 13.Robbins CL, Whiteman MK, Hillis SD et al. Influence of reproductive factors on mortality after epithelial ovarian cancer diagnosis. Cancer Epidemiol Biomarkers Prev. 2009;187:2035–2041. [DOI] [PubMed] [Google Scholar]
- 14.Schildkraut JM, Bastos E, Berchuck A. Relationship between lifetime ovulatory cycles and overexpression of mutant p53 in epithelial ovarian cancer. J Natl Cancer Inst. 1997;8913:932–938. [DOI] [PubMed] [Google Scholar]
- 15.Schildkraut JM, Moorman PG, Bland AE et al. Cyclin E overexpression in epithelial ovarian cancer characterizes an etiologic subgroup. Cancer Epidemiol Biomarkers Prev. 2008;173:585–593. [DOI] [PubMed] [Google Scholar]
- 16.Terry KL, Titus-Ernstoff L, McKolanis JR et al. Incessant ovulation, mucin 1 immunity, and risk for ovarian cancer. Cancer Epidemiol Biomarkers Prev. 2007;161:30–35. [DOI] [PubMed] [Google Scholar]
- 17.Tung KH, Goodman MT, Wu AH et al. Reproductive factors and epithelial ovarian cancer risk by histologic type: a multiethnic case-control study. Am J Epidemiol. 2003;1587:629–638. [DOI] [PubMed] [Google Scholar]
- 18.Tung KH, Wilkens LR, Wu AH et al. Effect of anovulation factors on pre- and postmenopausal ovarian cancer risk: revisiting the incessant ovulation hypothesis. Am J Epidemiol. 2005;1614:321–329. [DOI] [PubMed] [Google Scholar]
- 19.Webb PM, Green A, Cummings MC et al. Relationship between number of ovulatory cycles and accumulation of mutant p53 in epithelial ovarian cancer. J Natl Cancer Inst. 1998;9022:1729–1734. [DOI] [PubMed] [Google Scholar]
- 20.Whittemore AS, Harris R, Itnyre J. Characteristics relating to ovarian cancer risk: collaborative analysis of 12 US case-control studies. IV. The pathogenesis of epithelial ovarian cancer. Collaborative Ovarian Cancer Group. Am J Epidemiol. 1992;13610:1212–1220. [DOI] [PubMed] [Google Scholar]
- 21.McPherson CP, Sellers TA, Potter JD et al. Reproductive factors and risk of endometrial cancer. The Iowa Women's Health Study. Am J Epidemiol. 1996;14312:1195–1202. [DOI] [PubMed] [Google Scholar]
- 22.Pettersson B, Adami HO, Bergström R et al. Menstruation span—a time-limited risk factor for endometrial carcinoma. Acta Obstet Gynecol Scand. 1986;653:247–255. [DOI] [PubMed] [Google Scholar]
- 23.Odukogbe AA, Adebamowo CA, Adeniji AO et al. Total ovulating period: any contribution to ovarian carcinogenesis? Afr J Med Med Sci. 2005;343:307–309. [PubMed] [Google Scholar]
- 24.La Vecchia C, Franceschi S, Gallus G et al. Incessant ovulation and ovarian cancer: a critical approach. Int J Epidemiol. 1983;122:161–164. [DOI] [PubMed] [Google Scholar]
- 25.Brinton LA, Sakoda LC, Lissowska J et al. Reproductive risk factors for endometrial cancer among Polish women. Br J Cancer. 2007;969:1450–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Garcia-Closas M, Brinton LA, Lissowska J et al. Ovarian cancer risk and common variation in the sex hormone-binding globulin gene: a population-based case-control study. BMC Cancer. 2007;7:60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cramer DW, Xu H. Predicting age at menopause. Maturitas. 1996;233:319–326. [DOI] [PubMed] [Google Scholar]
- 28.Cramer DW, Xu H, Harlow BL. Does “incessant” ovulation increase risk for early menopause? Am J Obstet Gynecol. 1995;1722:568–573. [DOI] [PubMed] [Google Scholar]
- 29.Kotsopoulos J, Lubinski J, Lynch HT et al. Oophorectomy after menopause and the risk of breast cancer in BRCA1 and BRCA2 mutation carriers. Cancer Epidemiol Biomarkers Prev. 2012;217:1089–1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Siskind V, Green A, Bain C et al. Beyond ovulation: oral contraceptives and epithelial ovarian cancer. Epidemiology. 2000;112:106–110. [DOI] [PubMed] [Google Scholar]
- 31.Fathalla MF. Incessant ovulation and ovarian cancer—a hypothesis re-visited. Facts Views Vis Obgyn. 2013;54:292–297. [PMC free article] [PubMed] [Google Scholar]
- 32.Mumford SL, Steiner AZ, Pollack AZ et al. The utility of menstrual cycle length as an indicator of cumulative hormonal exposure. J Clin Endocrinol Metab. 2012;9710:E1871–E1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dasharathy SS, Mumford SL, Pollack AZ et al. Menstrual bleeding patterns among regularly menstruating women. Am J Epidemiol. 2012;1756:536–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mihm M, Gangooly S, Muttukrishna S. The normal menstrual cycle in women. Anim Reprod Sci. 2011;124(3-4):229–236. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.