Microelastic mapping of the rat dentate gyrus

Abstract

The lineage commitment of many cultured stem cells, including adult neural stem cells (NSCs), is strongly sensitive to the stiffness of the underlying extracellular matrix. However, it remains unclear how well the stiffness ranges explored in culture align with the microscale stiffness values stem cells actually encounter within their endogenous tissue niches. To address this question in the context of hippocampal NSCs, we used atomic force microscopy to spatially map the microscale elastic modulus (E) of specific anatomical substructures within living slices of rat dentate gyrus in which NSCs reside during lineage commitment in vivo. We measured depth-dependent apparent E-values at locations across the hilus (H), subgranular zone (SGZ) and granule cell layer (GCL) and found a two- to threefold increase in stiffness at 500 nm indentation from the H (49 ± 7 Pa) and SGZ (58 ± 8 Pa) to the GCL (115 ± 18 Pa), a fold change in stiffness we have previously found functionally relevant in culture. Additionally, E exhibits nonlinearity with depth, increasing significantly for indentations larger than 1 µm and most pronounced in the GCL. The methodological advances implemented for these measurements allow the quantification of the elastic properties of hippocampal NSC niche at unprecedented spatial resolution.

1. Introduction

Neural stem cells (NSCs), which reside in the hippocampus and the subventricular zone of the adult mammalian brain, continually generate neurons throughout adult life [1,2]. Hippocampal NSCs reside in the subgranular cell layer (SGZ) of the dentate gyrus (DG), undergo self-renewal and neuronal differentiation throughout adult life and play key roles in learning and memory. Differentiation is a coordinated process involving migration over several cell diameters into the granule cell layer (GCL), extension of axons through the hilus (H) and into CA3, and development of dendrites through the GCL and into the molecular layer [1,3,4].

Importantly, this process is not static but dynamically responds to numerous cellular and molecular inputs. For instance, key biochemical signalling factors within the SGZ microenvironment have been found to regulate both neural stem and progenitor cell proliferation—such as sonic hedgehog [5], fibroblast growth factor-2, heparin-binding EGF-like growth factor [6] and vascular endothelial growth factor [7]—and neuronal differentiation—such as Wnt3a [8,9] and ephrin-B2 [10]. Additionally, not only the biochemical but also the biophysical microenvironment may regulate stem cell function. For example, mechanical signalling through cell–extracellular matrix (ECM) interactions has been shown to play a role in regulating NSC differentiation. In particular, the elastic modulus (E) of the ECM substrate has been shown to regulate NSC lineage in vitro [11,12], with soft ECMs promoting NSC neurogenesis and stiff ECMs suppressing it [12,13]. Despite the clear instructive effects of elastic modulus on stem cell behaviour in vitro, and the in vivo regulation of stem cell behaviour by signals that are modulated in vitro by stiffness differences [13], the degree to which E may vary in the in vivo niche is unknown.

Atomic force microscopy (AFM) indentation has facilitated direct measurement of E with higher (up to sub-micrometre) spatial resolution compared with other methods such as optical coherence tomography [14] and stress-relaxation micro-indentation [15], and has been used notably by Morrison and co-workers to map and report stiffness across the rat hippocampus bulk from the CA1 to CA3 pyramidal cell layers and across the DG [16]. Such measurements have informed the design of in vitro assay platforms capable of recapitulating in vivo behaviour. Synthetic polyacrylamide matrix culture systems have shown stiffness-dependent instruction of NSC differentiation [12,13], neurogenic instruction of pluripotent stem cell differentiation [17] and full neuronal maturation and subtype differentiation with physiological stiffness values [18]. That said, these seminal AFM indentation measurements focused on large size scale variations in stiffness across the entire hippocampus, rather than high-resolution investigation of the specific regions in which hippocampal NSCs reside. While technically challenging, obtaining higher resolution mechanical maps of portions the hippocampal NSC niche relevant to neurogenesis could provide valuable insight into potential mechanical influences on NSCs during proliferation and differentiation in vivo. To address this unmet need, we conducted AFM measurements of the elastic modulus of the DG between the GCL and H, a region that directly encompasses the stem cell niche.

2. Results

2.1. Preparation of hippocampal slices for atomic force microscopy stiffness mapping

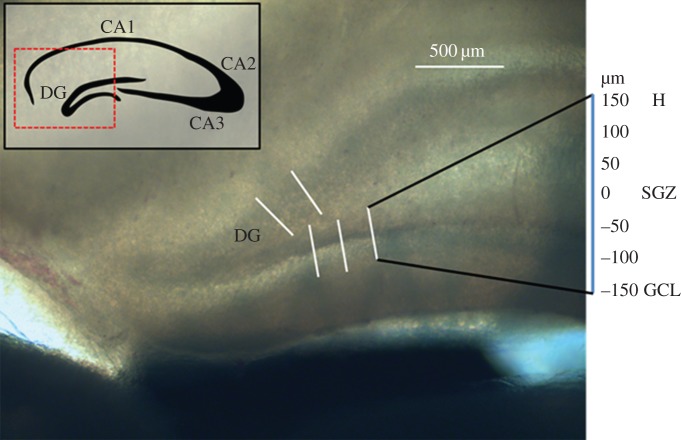
To maximally preserve physiological biomechanical properties of brain tissue, we designed a protocol for much more rapid (less than 1 h after sacrifice), fixative-free AFM measurements of hippocampal slices. Briefly, we extracted brains from freshly sacrificed rats and immersed them in 0°C cutting solution. We used a vibratome to generate 400 µm thick coronal sections, and quickly transported sections to the AFM stage. To save time that would normally be needed to allow adhesive bonding of the sample to the substrate, we secured the slices by placing them under a nylon mesh secured by a metal ring. A compliant nylon mesh with wide spacing (2 mm) was used to minimize tissue deformation and strain near the point of measurement. AFM measurements were performed between 30 and 60 min after sacrifice (figure 1). Importantly, our protocol uses no chemical fixatives and minimal embedding, and the AFM tip is allowed to directly contact the tissue surface. A thick sample (400 µm) and small indentation depths (less than 2 µm) were used to prevent the underlying polystyrene dish from contributing to measurements.

Figure 1.

Transmitted light image of a representative coronal hippocampal section. Measurements were taken in the DG, at 7 points along a 300 µm linear profile from the GCL to the H. Five profiles for each slice were taken, and representative measurement locations are indicated.

2.2. Stiffness is variable across the stem cell niche

Five linear profiles of force curves were acquired in six samples (figure 1), up to an estimated indentation of 2 µm. The contact point was algorithmically estimated, and force curves were fitted to the Hertz contact model for a sphere indenting up to a maximum indentation (δ_max) of 500 nm. Owing to the large polystyrene bead (25 µm) used as a tip, measurements incorporate both cell and matrix mechanical properties. Two iterations of a nonlinear fit were used to obtain E (figure 2a). The mean at 500 nm indentation was 49 ± 7 Pa (mean ± s.e., N = 6) for the H, 58 ± 8 Pa in the SGZ and 115 ± 18 Pa in the GCL (figure 2a). These values are comparable with previous reports of E as approximately 100 Pa in the DG for a 500 nm indentation [16]. However, we discovered that the GCL stiffness was significantly (p < 0.01, two- to threefold increase) higher than the SGZ and the H, whereas comparisons between the SGZ and H showed no significant difference (p > 0.05). The measurements thus indicate a gradient of increasing stiffness between the SGZ and the GCL (figure 2a), which has not been previously observed.

Figure 2.

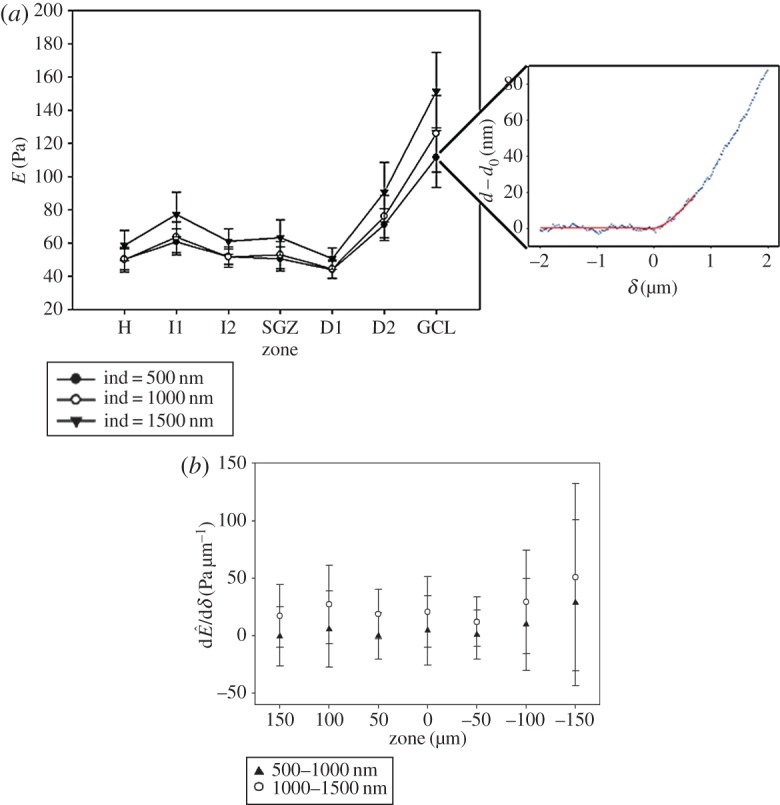
(a) Average E from six brain samples with representative force curve. In the inset representative force curve, points depict experimental data for z, cantilever vertical position and d, cantilever deflection, and the trend line is a two-part fitted model: a straight line for the non-contact zone and a 3/2 power of δ for the contact region. In the graph, each point is the average of five force curves, and shown for three different indentation depths. The tissue is slightly nonlinear with indentation depth. Standard error is indicated. Stiffnesses in H and SGZ are significantly different from GCL (p < 0.05). SGZ and GCL both showed significant differences between δ = 1000 nm and δ = 1500 nm. SGZ showed significant difference between δ = 500 nm and δ = 1000 nm. (b) Graph of derivative of Ê with respect to indentation depth, indicating the depth dependence of strain stiffening.

2.3. Dentate gyrus stiffness exhibits slight nonlinearity for indentations greater than 1 µm

Tissue behaviour (linear or nonlinear) at supraphysiological strains is a critical component for understanding response to injury, and the hippocampus in particular is uniquely sensitive to mechanical strain [19]. We therefore computed a pointwise, depth-dependent apparent Young's modulus (Ê) at indentations of 0.5, 1 and 1.5 µm. At a greater indentation depth, the sample exhibited higher stiffness values than at lower depths for particular locations. Specifically, Ê (δ = 500 nm) was 50 ± 6 Pa (H), 51 ± 7 Pa (SGZ) and 111 ± 18 Pa (GCL), but with δ = 1500 nm these values increased to 59 ± 9 Pa, 63 ± 11 Pa and 151 ± 24 Pa, respectively (figure 2a,b). Both the SGZ and the GCL exhibited significant differences (p < 0.05) in Ê between 1 and 1.5 µm indentations, but only the SGZ showed a difference between 0.5 and 1 µm. While tissue nonlinearity has been previously reported for the DG bulk as between 90 and 130 Pa [16], differences in nonlinearity have not been observed within the sub-anatomical regions of the hippocampus and NSC niche.

3. Discussion

In this study, we spatially mapped the elastic modulus of the hippocampal NSC niche using AFM. Our work both represents a key methodological advance and reveals new insight into the micromechanical properties of the endogenous NSC niche, thereby providing crucial design input for systems to recapitulate NSC neurogenesis in vitro. Methodologically, our approach is expected to preserve key mechanical properties of brain tissue by employing no chemical fixation and only minimal embedding, as well as by reducing preparation time by physically anchoring rather than adhesively bonding the tissue to the substrate. Additionally, our approach incorporates automated identification AFM tip contact points, similar to methods previously reported [20,21], which have typically been identified by visual examination. This invites error and observer bias that may significantly affect the resulting curve fit and extraction of E and Ê. While important advances have been made to automate this process through the use of algorithmic models, these approaches rely on empirically determined criteria to define the contact point. Moreover, these models are suited for samples at least an order of magnitude stiffer than brain tissue and have difficulty identifying contact points for very soft gels <3 kPa [22]. To remedy this concern, we used an algorithmic, iterative fitting procedure that defines a contact point based on contact theory, which allowed us to identify the contact point more reproducibly and systematically.

These advances in sample preparation, together with the high spatial resolution of AFM, allowed us to spatially map DG substructures and identify differences in stiffness across regions of the DG, which has not been yet evaluated with high resolution. The SGZ, where the progenitor pool is maintained, and the H, through which new axons grow and project to the CA3, both show stiffness near 50 Pa. The GCL, through which newly differentiated neurons migrate and extend dendrites, shows twofold higher stiffness. The difference in stiffness in the GCL may be due to the densely packed mature granule cells, whereas the lower stiffness in the SGZ and H may be due to differences in cell body density, or even possibly different mechanical properties of immature progenitors. These measurements show that among these anatomical features, there are stiffness gradients that are in a position to influence cell differentiation and axonal and dendritic growth. Additionally, we have identified substructure specific nonlinear stiffening for indentations higher than a micrometre, which indicates possible heterogeneities between tissue substructures, such as differences in cell body and nuclei density between regions. Previous work has identified the hippocampus bulk as possessing strain-stiffening properties, we have shown and characterized precise values for the DG, and notably see this behaviour in the SGZ and GCL but not in the H. While these results are compatible with the observation that many biopolymers can exhibit strain-stiffening behaviour, the reason for this and its physiological implications are unknown and may be the subject of future work [23]. Finally, synthetic systems used to study NSC differentiation have to date been uniform in stiffness, and future work with new culture platforms may explore whether microscale stiffness gradients could serve an informative role in neural stem cell development.

Our measurements also validate the physiological relevance of engineered ECM substrates to drive NSC neurogenesis in culture. We show that the stiffness of living DG tissue lies within a range of 50–150 Pa, which is consistent with past AFM measurements of bulk hippocampal tissue [16] and closely matches stiffness regimes previously identified (200 Pa in two-dimensional culture [12,13] and 180 Pa in three-dimensional culture [24]) to be pro-neurogenic in vitro for NSCs, mesenchymal stem cells [11] and human pluripotent stem cells [17]. However, it is important to note some caveats that accompany our measurements. While reducing sample preparation time and removing fixation steps are expected to preserve physiological properties of brain, indentation measurements are still taken on a cut surface of a brain slice. This can cause significant cell death and relaxation in the brain matrix in the plane of indentation. Additionally, in order to better preserve tissue properties, measurements were obtained in buffer at refrigerant temperature (4°C) rather than body temperature, which may produce some artefactual stiffening due to tissue contraction. Last, our study examines only juvenile rats at P18–22, while neurogenesis is an ongoing process, especially in adults. Indeed, the stiffness of bulk hippocampus has been shown to vary by more than 100% between P10 and adulthood [25]. Nevertheless, our measurements therefore offer key, novel validation to these materials strategies by demonstrating that these pro-neurogenic stiffness values match well with the stiffness of microscale regions associated with NSC proliferation (SGZ) and differentiation (GCL) in the hippocampus.

It is anticipated that further methodological refinements may enable even higher-resolution mapping of these niches, which in turn may yield more sophisticated input into the design of neurogenic culture scaffolds. Additionally, it would be useful to revisit these measurements with specific hippocampal disease models to investigate potential biomechanical changes in the NSC niche that may influence neurogenesis in currently unappreciated ways. Finally, by coupling these AFM measurements with live cell markers that track specific stages of neural lineage commitment maturation, it may be possible to correlate changes in microscale tissue mechanics within the DG with the dynamics of neurogenesis. With the emergence of increasingly sophisticated materials strategies that enable patterning of ECM stiffness in time and space, such measurements help the field discover and recapitulate subtleties of the NSC niche.

4. Material and methods

4.1. Murine hippocampus preparation

Coronal hippocampal sections were prepared as described previously [26]. Briefly, juvenile (p18–p22) Sprague–Dawley rats were anaesthetized with isoflurane and sacrificed by decapitation. The brain was extracted and kept in a low-sodium, bicarbonate-buffered cutting solution at ambient temperature with constant bubbling with 95% O₂ and 5% CO₂, and 400 μm coronal sections were cut with a Leica VT1000S vibratome at 0°C. The sections were stored in Ringer's solution at ambient temperature and bubbling with 95% O₂ and 5% CO₂ and were quickly transported to the AFM stage. Sections were gently weighed down for measurement on a Petri dish with parallel nylon fibres (approx. 2 mm spacing) attached to a metal ring, and measured within 30–60 min after sacrifice. Cutting solution composition was 75 mM sucrose, 85 mM NaCl, 25 mM NaHCO₃, 25 mM d-(+)-glucose, 2.5 mM KCl, 1.25 mM NaH₂PO₄–H₂O, 0.5 mM ascorbic acid, 4 mM MgCl₂, 0.5 mM CaCl₂, 320 mOsm l⁻¹, pH 7.2.

4.2. Atomic force microscopy measurements

Indentation measurements were obtained with a NanoScope Catalyst (Bruker Corporation, Billerica, MA, USA) atomic force microscope mounted on an inverted optical microscope (Eclipse Ti-E, Nikon Corporation, Chiyoda, Tokyo, Japan). A 25 µm diameter polystyrene bead (Polysciences, Inc., Warrington, PA, USA) was epoxied to the end of a soft (k = 0.01 N m⁻¹) tipless cantilever (MLCT-O10, Bruker). The combination of a soft cantilever and a large bead (compared with the indentation) allowed us to measure the small deflections that such soft samples caused on the cantilever. Fabrication was validated with scanning electron microscopy, and cantilever spring constants (k) were measured via thermal oscillation [27] using an Asylum MFP-3D Infinity AFM (Asylum Research, Santa Barbara, CA, USA).

For each sample, five linear profiles transverse to the DG layers were acquired (indicated by lines in figure 1). Seven measurements were taken across each profile, with the centre point directly on the SGZ and a lateral spacing of 50 µm. Each measurement was the average of five force curves, obtained with ramp amplitude of 10 µm and frequency of 0.5 Hz, resulting in tip velocity of 10 µm s⁻¹.

4.3. Data processing

The force F exerted on the cantilever was calculated as a Hookean linear spring:

$$F=k(d-d_0)$$ 4.1

and indentation depth δ was defined as

$$\delta =(z-z_{\mathrm{c}})-(d-d_0)$$ 4.2

with d as cantilever deflection, d₀ as deflection offset, z as cantilever vertical position, and z_c as cantilever vertical position at the contact point. These data were fitted to the Hertz contact model for a sphere indenting an infinite sphere using a nonlinear least-squares method [19]:

$$F=\frac{4\hat{\mathrm{E}}}{3(1-v^2)}{R}^{1/2}{\delta }^{3/2}$$ 4.3

with R defined as bead radius (12.5 µm) and v as Poisson's ratio. We assumed a Poisson's ratio of 0.5, which agrees closely with simulation [28] and past measurements [29]. We fitted a two-part equation (a line for the non-contact zone and the Hertz elastic model for the contact zone) to the entire dataset using a nonlinear least-squares method (Matlab, The MathWorks, Natick, MA, USA) to obtain an estimation of the contact point (z_c, d₀). We iterated the fit using a defined maximum indentation (δ_max) to refine our estimation of the contact point and E. Additional fittings did not appreciably improve the error. We report a pointwise apparent Young's modulus (Ê(δ)), reported at three chosen indentations (500 nm, 1 µm and 1.5 µm). Statistical analysis was performed with a two-way repeated measures analysis of variance (Sigma Plot, Systat Software), with factors region and indentation.

Ethics

Live vertebrate experiments were carried out in accordance with approved guidelines (animal use protocol R261).

Data accessibility

Elastic moduli from atomic force microscopy curves are available at doi:10.5061/dryad.tv41g.

Authors' contributions

T.L.: conception and design, collection and/or assembly of data, data analysis and interpretation; M.S.K: manuscript writing; D.V.S. and S.K.: financial support, conception and design, data analysis and interpretation, manuscript writing and final approval of manuscript.

Competing interests

The authors claim no competing financial interests.

Funding

This work was supported by a grant from the NIH (1R01NS074831 to D.V.S. and S.K.) and from the Spanish Ministry of Education (FPU grant with BOE 28 October 2008 to T.L).