Abstract
We have extended a conventional photosynthesis model to simulate field and laboratory measurements of chlorophyll fluorescence at the leaf scale. The fluorescence paramaterization is based on a close nonlinear relationship between the relative light saturation of photosynthesis and nonradiative energy dissipation in plants of different species. This relationship diverged only among examined data sets under stressed (strongly light saturated) conditions, possibly caused by differences in xanthophyll pigment concentrations. The relationship was quantified after analyzing data sets of pulse amplitude modulated measurements of chlorophyll fluorescence and gas exchange of leaves of different species exposed to different levels of light, CO2, temperature, nitrogen fertilization treatments, and drought. We used this relationship in a photosynthesis model. The coupled model enabled us to quantify the relationships between steady state chlorophyll fluorescence yield, electron transport rate, and photosynthesis in leaves under different environmental conditions.
Key Points
Light saturation of photosynthesis determines quenching of leaf fluorescence
We incorporated steady state leaf fluorescence in a photosynthesis model
Keywords: chlorophyll fluorescence, photosynthesis, electron transport
1. Introduction
During photosynthesis, part of the solar radiation absorbed by chlorophyll is reemitted at longer wavelengths (fluorescence). In plants, chlorophyll fluorescence can be considered as an unavoidable leak in the energy processing in photosystems [Fleming et al., 2012], a process that is otherwise very efficient [Mohseni et al., 2008; Rebentrost et al., 2009; Hildner et al., 2013]. Typically, less than 5% of absorbed photons are reemitted by plants as fluorescence. Although the reemission is a physical process, it is regulated by the biology of living cells. By measuring fluorescence, one can diagnose aspects of this regulation and assess the efficiency of the exciton use by photosystems.
Active measurements of fluorescence with dedicated, laboratory, and portable instruments have been used to assess the status of the photosynthetic apparatus in terrestrial plants for several decades [Bilger et al., 1995]. Such measurements make it possible to quantify the probability of each of the three alternative fates of absorbed photons in the pigment bed: photochemistry, heat dissipation, and fluorescence [Kitajima and Butler, 1975; Genty et al., 1989]. These measurements, in combination with measurements of gas exchange between leaves and the atmosphere, have lead to substantially improved knowledge of the process of photosynthesis [Papageorgiou et al., 2004; Porcar-Castell et al., 2014] and to a quantitative basis for relating fluorescence measurements to the rate of electron transport [Butler, 1978; Weis and Berry, 1987a; Genty et al., 1989; Loriaux et al., 2013].
The detection of solar-induced fluorescence (SIF) has more recently become feasible too. The detection of SIF requires instruments of high spectral resolution and high accuracy due to the fact that the weak fluorescence light has to be differentiated from the much stronger reflected ambient light (for a review of techniques, see Meroni et al. [2009]). An advantage of SIF is that the technique does not have limitations imposed by the strength of an artificial excitation source. During the last decade and especially in the 2010s, field measurements [Moya et al., 2004; Mazzoni et al., 2012], airborne measurements [Guanter et al., 2007; Zarco-Tejada et al., 2013], and spaceborne measurements [Frankenberg et al., 2011; Joiner et al., 2011] have been developed.
Triggered by the increase in SIF measurements, we are interested in characterizing the sensitivity of steady state fluorescence to physiological and biophysical states of the vegetation and in being able to simulate steady state fluorescence as an output of a photosynthesis model [e.g., van der Tol et al., 2009a]. The degree to which SIF can be coupled to photosynthesis determines the opportunities we have for using it in carbon cycle models.
To achieve these goals, we need to dive down into the mechanisms of light harvesting and photon processing in the reaction centers of higher plants. In this study we will draw upon measurements conducted in a laboratory setting in which photosynthesis measurements by CO2 exchange were combined with fluorescence, using the pulse amplitude modulation (PAM) measuring principle. This provides a highly selective measure of the relative chlorophyll fluorescence quantum yield. In conjunction with the saturating pulse method, PAM fluorometers allow assessment of photosynthetic energy conversion—information that we will need to build an understanding of remote sensing observations.
2. Theoretical Background
In this paper we distinguish fluorescence levels as measured with a PAM, with the symbol F (Figure 1), coefficients for probabilities of excitons to follow a certain pathway with K, or quantum yields with Φ. We use in subscripts the symbols P for photochemistry and D and N for heat dissipation, a constitutive thermal dissipation (D) that is present in dark adapted plants and a variable, energy-dependent heat dissipation (N) controlled by mechanisms that regulate the electron transport of the photosystems. Although this differentiation into two terms is only a simplified view, it is sufficient for our purpose and it prevents equifinality of the model.
Figure 1.
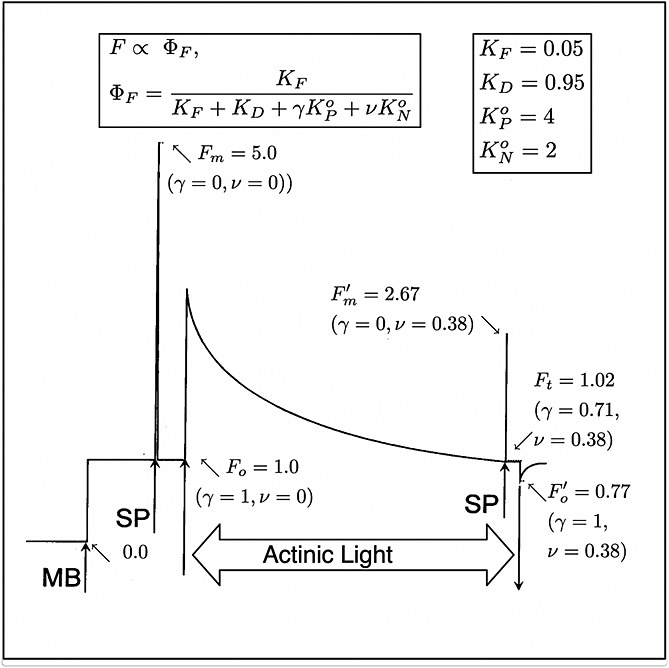
A sample trace of a measurement of fluorescence from a leaf with a PAM fluorometer [after Maxwell and Johnson, 2000]. The measuring light is turned on at MB; saturating pulses (1 s) are applied at SP. Note that γ→0 during a SP while ν is unchanged. The experiment shows changes in fluorescence that occur when actinic light is provided. The fluorescence levels (F) are normalized to the Fo level. The photochemical yield of the leaf under dark adapted conditions 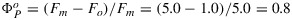 and after a period of illumination
and after a period of illumination 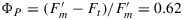 . These arbitrary fluorescence levels can be related to absolute yields with the equations and probability constants shown in the boxes and the values of γ and ν. We used equations (8) and (9) to estimate KN and KP, respectively, and
. These arbitrary fluorescence levels can be related to absolute yields with the equations and probability constants shown in the boxes and the values of γ and ν. We used equations (8) and (9) to estimate KN and KP, respectively, and  and
and 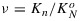 .
.
An example of measurements of a leaf with a PAM fluorometer is illustrated in Figure 1. At the start (left), the leaf which has been in the dark for some time is illuminated by a dim beam of modulated light from a light-emitting diode (MB). The fluorescence elicited is also modulated and can be selectively detected by a special circuit. Application of an ≈1 s pulse of unmodulated light more than sufficient to saturate photosynthesis, a so called saturating pulse (SP), will elicit a large pulse of fluorescence, but the detector sees only the effect of that light on the yield of fluorescence from the constant modulated light. This yield goes up several fold because the added light results in nearly complete closure of the PSII reaction centers (γ→0), blocking the photochemical deexcitation pathway and increasing the lifetime of the excitation. The level of fluorescence with only the measuring light is termed the Fo level. The peak level of fluorescence that is reached during the pulse is termed Fm. Since the information from PAM experiments is contained in the ratio of the fluorescence levels rather than in the absolute power, the signals are generally normalized to Fo=1 or Fm = 5.0 (Figure 1). The variable component of fluorescence (Fv/Fm = (Fm−Fo)/Fm) is related to the efficiency of photochemical trapping in the dark adapted state 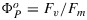 when the traps are fully open [Butler, 1978]. This ratio is typically about 0.8 and is very similar among healthy plants [Björkman and Demmig, 1987].
when the traps are fully open [Butler, 1978]. This ratio is typically about 0.8 and is very similar among healthy plants [Björkman and Demmig, 1987].
In the next manipulation (Figure 1), a constant actinic light of an intensity sufficient to drive photosynthesis is turned on. This also elicits an increase in fluorescence, but this level, Ft, varies with time as the levels of photochemical and nonphotochemical tapping change in response to metabolic feedback processes, eventually reaching a steady state after several minutes. Applying a saturation pulse at this point results in a new, lower maximum fluorescence (2.67 in the example of Figure 1). To distinguish this from the dark adapted state, it is designated as 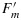 . Turning all light except the measuring light off yields a new lower minimum
. Turning all light except the measuring light off yields a new lower minimum 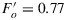 . The fact that the fluorescence level under steady state illumination Ft is higher than
. The fact that the fluorescence level under steady state illumination Ft is higher than  and lower than
and lower than 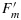 indicates that in steady state some of the photochemical traps were closed. However, the levels
indicates that in steady state some of the photochemical traps were closed. However, the levels 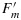 and
and 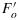 are substantially lower than their dark adapted values. This SP measurement takes advantage of the property that nonphotochemical traps do not change during the 1 s pulse, but the photochemical traps can be nearly completely closed by the pulse. This difference in relaxation time makes it possible to use PAM fluorometry to distinguish and evaluate the two types of trapping [Weis and Berry, 1987a] on the processing of excitations at Ft.
are substantially lower than their dark adapted values. This SP measurement takes advantage of the property that nonphotochemical traps do not change during the 1 s pulse, but the photochemical traps can be nearly completely closed by the pulse. This difference in relaxation time makes it possible to use PAM fluorometry to distinguish and evaluate the two types of trapping [Weis and Berry, 1987a] on the processing of excitations at Ft.
Bernard Genty, Jean-Marie Briantais, and Neil R. Baker [Genty et al., 1989] proposed in highly cited paper that ΦP at the steady state could be calculated from the ratio of the variable to the total fluorescence 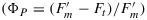 . This is a very important concept as it makes it possible to use fluorescence and knowledge of the flux of photosynthetically active radiation (PAR) that is absorbed (JaPAR) to estimate the rate of photosynthetic electron transport (Je).
. This is a very important concept as it makes it possible to use fluorescence and knowledge of the flux of photosynthetically active radiation (PAR) that is absorbed (JaPAR) to estimate the rate of photosynthetic electron transport (Je).
| (1) |
While this equality portends great promise for using fluorescence to measure photosynthetic rate, it is important to note that most of the information is in the  level. Ft is very similar to the Fo level, yet ΦP at the steady state is substantially lower than in the dark adapted state (0.62 versus 0.8). Observations of SIF will only see the steady state level. Information on
level. Ft is very similar to the Fo level, yet ΦP at the steady state is substantially lower than in the dark adapted state (0.62 versus 0.8). Observations of SIF will only see the steady state level. Information on 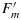 is beyond the reach of the method. We will show that there are significant, albeit small, changes in the Ft level that can be related to photosynthetic rate.
is beyond the reach of the method. We will show that there are significant, albeit small, changes in the Ft level that can be related to photosynthetic rate.
Here we are finally interested in understanding the absolute yield of fluorescence, while PAM measurements are only concerned with the ratio of the levels. To make this transition, we adopt a formalism developed by Butler [1978] of using rate coefficients (K) to express the probability of the different fates of the excitations. The yields expressed with rate coefficients K as follows:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Because they are mutually exclusive, the sum of the yields of all processes is unity
| (7) |
Because of the normalization by 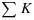 , the coefficients K are unitless and can all be multiplied by the same scalar without any effect on the yields. The values used here (KD = 0.95 and KF = 0.05) have the useful property that KN≡NPQ (nonphotochemical quenching), a commonly reported parameter obtained from PAM fluorometry. The rate coefficients KN and KP vary with the metabolic state, and we will define these by reference to their respective maximum values. Thus,
, the coefficients K are unitless and can all be multiplied by the same scalar without any effect on the yields. The values used here (KD = 0.95 and KF = 0.05) have the useful property that KN≡NPQ (nonphotochemical quenching), a commonly reported parameter obtained from PAM fluorometry. The rate coefficients KN and KP vary with the metabolic state, and we will define these by reference to their respective maximum values. Thus, 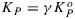 and
and  .
. 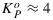 and (as we will show later)
and (as we will show later) 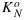 varies from about 2 to 6 depending on the stress history of the vegetation. These dynamically changing rate coefficients for NPQ and for photochemistry KN and KP can be calculated as follows:
varies from about 2 to 6 depending on the stress history of the vegetation. These dynamically changing rate coefficients for NPQ and for photochemistry KN and KP can be calculated as follows:
| (8) |
| (9) |
These equations have been derived from equations (2) to (6) using that KP is (by definition) zero at  and at Fm and that KN is zero at Fm. These transformations are also illustrated in Figure 1.
and at Fm and that KN is zero at Fm. These transformations are also illustrated in Figure 1.
An additional constraint on this system is that the flux of electrons produced by PSII photochemistry must equal the rate of reactions which consume electrons, and thus, ΦP is constrained by the rate of CO2 fixation. In equation (1) we already mentioned that
| (10) |
The rate of electron transport Je in this equation can be obtained from the rate of gross CO2 assimilation, JA (corrected for dark respiration), as follows:
| (11) |
where Γ∗ is the CO2 compensation point and Cc is the chloroplast CO2 partial pressure estimated from gas exchange. The ratio on the right-hand side of equation (11) corrects for the effect that photorespiration, the competition of O2 with CO2, has on the stoichiometry linking Je to photosynthesis. Equation (11) bridges CO2 gas exchange through stomata and cell walls with the photochemical electron transport. Following the assumption of Farquhar et al. [1980] feedback on ΦP should be small when the energy supply for photosynthesis is limiting, for example, at low irradiance levels. As illumination increases, other factors such as resistance to CO2 diffusion into the mesophyll or Rubisco limit the rate of photosynthesis and ΦP becomes the dependent variable, and regulatory sequences [Woodrow and Berry, 1988] should limit the probability of photochemistry to maintain the equality of source and sink. This can occur in two ways: (a) by simple mass action when reduced electron carriers backup causing the photosystems to accumulate in the reduced (in active) form (γ↓) or (b) by opening competing nonphotochemical traps (ν↑). It is thought that the pH gradient across the chloroplast membrane increases when turnover of the energy carrier adenosine triphosphate (ATP) becomes restricted and the reduced pH activates nonphotochemical traps. The change in the pH is also responsible for the conversion of violaxanthin into zeaxanthin, an effective nonphotochemical quencher of the excitons [Gilmore, 1997]. The mechanisms of NPQ and the their regulation are still an area of active research (for reviews, see Ruban et al. [2012] and Zaks et al. [2013]).
3. A Model for 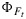
All else being equal closure of photochemical traps will cause 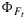 to increase, and opening of nonphotochemical traps will cause
to increase, and opening of nonphotochemical traps will cause 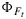 to decrease, yet both will have the effect of causing ΦP to decrease. Regardless of the mechanism, however, the yield should follow the Genty relationship,
to decrease, yet both will have the effect of causing ΦP to decrease. Regardless of the mechanism, however, the yield should follow the Genty relationship,
| (12) |
Here we will assume that we can know ΦP independently, for example, from a photosynthesis model. Our next step is to find an independent approach to evaluate 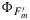 . Following equation (3) and recalling that KP→0 in SP, one may write that
. Following equation (3) and recalling that KP→0 in SP, one may write that
| (13) |
in which only KN is unknown. While there is no theoretical basis to constrain KN, we have sought an empirical relationship to relate KN to changes in ΦP. The central point of our approach is therefore to relate KN which controls 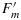 to the relative decrease in the yield of photochemistry. To quantify the strength of the feedback, we define a factor x on a scale of 0 (photochemistry operating at full efficiency) to 1 (photochemistry totally blocked by feedback), x is defined as follows:
to the relative decrease in the yield of photochemistry. To quantify the strength of the feedback, we define a factor x on a scale of 0 (photochemistry operating at full efficiency) to 1 (photochemistry totally blocked by feedback), x is defined as follows:
| (14) |
where 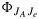 is the quantum yield for electron transport linked to CO2 fixation at steady state and
is the quantum yield for electron transport linked to CO2 fixation at steady state and  in the limit as JaPAR→0. This is equivalent to
in the limit as JaPAR→0. This is equivalent to
| (15) |
or, alternatively, after normalization of the fluxes by aPAR
| (16) |
where 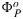 is the maximum photochemical yield as observed under dark adapted, low light conditions. Substituting equation (16) into equation (12) results in the following:
is the maximum photochemical yield as observed under dark adapted, low light conditions. Substituting equation (16) into equation (12) results in the following:
| (17) |
The aim here is to assess to what extent a general relationship 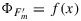 exists that can substitute
exists that can substitute 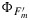 in this equation, thus enabling the modeling of steady state fluorescence from a gas exchange measurement or vice versa. We used a collection of PAM data sets to assess this further. Our strategy is to make use of a large comprehensive data set obtained with cotton to develop a modeling approach and then to extend the analysis to other data sets that span different species, different environmental conditions, and different photosynthetic types. These additional data sets provided an opportunity to test our model and obtain additional information useful to make our model more general.
in this equation, thus enabling the modeling of steady state fluorescence from a gas exchange measurement or vice versa. We used a collection of PAM data sets to assess this further. Our strategy is to make use of a large comprehensive data set obtained with cotton to develop a modeling approach and then to extend the analysis to other data sets that span different species, different environmental conditions, and different photosynthetic types. These additional data sets provided an opportunity to test our model and obtain additional information useful to make our model more general.
4. Data Description
Four sets of measurements with a PAM fluorescence sensor [Schreiber et al., 1986] in combination with a leaf gas exchange chamber were used. The data sets were chosen to represent variations in the main driving variables. Three data sets concerned light and CO2 response curves (cotton, tobacco, and maize), two of these had additional measurements at different temperatures and one at different nitrogen fertilization. Measured Ci [LI-COR Biosciences Inc., 2004] rather than Cc (equation (14)) was used to calculate Je lacking measurements of mesophyll conductance in these studies. Also, note that all of the active fluorescence measurements were made using a single-intensity saturating flash. The resulting values for Fm and  might be underestimated in this way [Markgraf and J. Berry, 1990]. A recent paper [Loriaux et al., 2013] suggests an alternative method for measurement. We have not evaluated the impact of this alternative method on our analysis. Another limitation of our study is that the broadband active fluorescence data include a portion of photosystem I (PSI) [Franck et al., 2002]. In order to estimate the PSI contribution accurately, we would need to account for wavelength and leaf structure dependent reabsorption of the emitted fluorescence in the leaf (because PSI and PSII emit at different wavelengths and the PAM detector is sensitive to a part of the fluorescence spectrum that overlaps with the chlorophyll absorption spectrum). Because we did not have concurrent spectrometry data, we decided not to correct for the PSI fraction in this study but to use the measurements as they are instead. The fluorescence yields thus refer to the total fluorescence of both photosystems. C4 species have a slightly larger PSI contribution [Genty et al., 1989]. We intend to address the separation of PSI and PSII fluorescence by incorporating spectral measurements and a radiative transfer model for the leaf in a separate study.
might be underestimated in this way [Markgraf and J. Berry, 1990]. A recent paper [Loriaux et al., 2013] suggests an alternative method for measurement. We have not evaluated the impact of this alternative method on our analysis. Another limitation of our study is that the broadband active fluorescence data include a portion of photosystem I (PSI) [Franck et al., 2002]. In order to estimate the PSI contribution accurately, we would need to account for wavelength and leaf structure dependent reabsorption of the emitted fluorescence in the leaf (because PSI and PSII emit at different wavelengths and the PAM detector is sensitive to a part of the fluorescence spectrum that overlaps with the chlorophyll absorption spectrum). Because we did not have concurrent spectrometry data, we decided not to correct for the PSI fraction in this study but to use the measurements as they are instead. The fluorescence yields thus refer to the total fluorescence of both photosystems. C4 species have a slightly larger PSI contribution [Genty et al., 1989]. We intend to address the separation of PSI and PSII fluorescence by incorporating spectral measurements and a radiative transfer model for the leaf in a separate study.
4.1. Cotton Data Set
This data set consists of measurements on cotton leaves over a temperature range from 14 to 40°C, including light responses, CO2 responses, and measurements at low (to minimize photorespiration) and normal O2 concentration. The experiment is described in Weis and Berry [1987b]. The original measurements, which were normalized to an Fm, were rescaled to fluorescence data normalized to Fo. Gas exchange measurements were taken simultaneously.
4.2. Tobacco Data Set
We used unpublished experimental data of greenhouse grown Nicotiana tabacum plants collected by A. Moersch at the Forschungszentrum Jülich in 2009. Measurements were carried out on attached leaves in a climatized cuvette under three leaf temperature regimes, 10, 20, and 30°C, with relative humidity of 94, 86, and 77% for the respective treatments. Gas exchange was measured with a CMS-400 gas exchange measurement system (Walz, Germany), concurrent with Mini-PAM fluorescence (Walz, Germany). Reflectance, water content, specific mass, and pigment composition were measured as well, but these data are not considered in the present study. The measurement sequence was as follows. A single leaf was clamped in a dark leaf cuvette, while gas exchange was measured continuously. After 30 min of acclimation, the gas exchange measurements were recorded, and Fo and Fm measurements were taken with the Mini-PAM. The measurements were repeated at light intensities of 77, 165, 310, 561, and 1051 μmol m−2s−1, each time after 30 min of acclimation. The whole measurement sequence was repeated 5 times in a period of 20 days but with the light intensity changes in a variable order (always starting with a dark adapted measurement).
4.3. Drought Stress of Several Species
Data published by Flexas et al. [2002] of the following C3 species were used: Vitis vinifera L (grape) in the field, Solanum melongena L. plants (herbaceous crop), 5 year old plants of Quercus ilex L. (evergreen sclerophyll tree), Pistacia terebinthus L. (deciduous sclerophyll shrub), and Celtis australis L.(deciduous mesophyte tree) grown in large pots. Measurements included combined leaf gas exchange (LI-6400) and fluorescence (PAM-2000) under saturating light [Flexas et al., 1998]. After daily irrigation, the plants were subjected to progressive drought stress. Measurements of Fo and Fm (after acclimation to a dark room in the morning) and 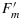 and Ft at full sunlight were taken every other day for 3 weeks.
and Ft at full sunlight were taken every other day for 3 weeks.
4.4. Maize Data Set
In August 2013, as a part of a field measurement campaign supporting the collaborative NASA/U.S. Department of Agriculture (USDA) project “Spectral Bio-Indicators of Ecosystem Photosynthetic Efficiency II: Synthesis and Integration” (PI Dr. E. Middleton), we collected simultaneously leaf gas exchange parameters and active fluorescence light and CO2 response curves on maize (Zea mays, L.) at the irrigated Replicated Nitrogen (N) research plots of the Optimizing Production inputs for Economic and Environmental Enhancement (OPE3) site, USDA Beltsville Agricultural Research Center, Beltsville, MD. At OPE3, adapted maize hybrids are planted in 0.76 m rows on the predominately loamy sand soils and grown under four fertilizer rates (0, 50, 100, and 150% of the recommended rates for these soils), following locally optimized management practices [Daughtry, 2001]. Irrigation timing and amounts are determined using soil moisture sensors and adjusted to ensure the prevention of drought stress, providing a compact site ideally suited for the study of the effects of nitrogen on photosynthetic function and the associated vegetation spectral properties. Leaf gas exchange (assimilated net photosynthetic CO2) and light and CO2 response curves were collected, following standard procedures [LI-COR Biosciences Inc., 2004] on two consecutive days, from three plants representative of each N treatment (n = 12), measuring fully expanded and illuminated leaf (third from the top), using a portable photosynthesis system LI-6400, outfitted with a leaf chamber fluorometer with 2 cm2 measuring aperture [LI-COR Biosciences Inc., 2004]. Leaf temperature was maintained at 25°C. Dark adapted fluorescence measurements and gas exchange parameters were collected before sunrise (at approximately 4:30 A.M.). Light response curves (assimilation rate as function of light level) were collected by ranging incident PAR levels between 0 and 1800 μmol m2s−1, acclimating at each level and maintaining CO2 level slightly above the ambient at 420 ppm. CO2 assimilation responses (assimilation rate as function of intercellular CO2 concentration) were measured ranging CO2 level from 75 to 1500 ppm, acclimating at each level and maintaining incident PAR level at 1600 μmol m−2s−1.
5. Results
The cotton data set included 160 separate measurements of photosynthetic rate and PAM fluorescence. These were a series of response curves to light, temperature, and CO2 concentration that spanned a range of temperatures from 12 to 40°C, 10 to 600 ppm intercellular CO2, and 0 to 2500 μmol m−2s−1PAR flux. Some experiments were conducted in low (2%) oxygen and others in air. ΦP was calculated from fluorescence measurements according to the equation of Genty et al. [1989] and from the gas exchange measurements using equation (11). Figure 2a shows a plot of ΦP obtained by gas exchange and fluorescence. We also used the data to calibrate the photosynthesis model of Collatz et al. [1991]. Simulated and measured rates of photosynthesis are compared in Figure 2b. The model can also be used to simulate ΦP, and these are compared with the measured values in Figure 2c. These simulations used the default parameter for C3 crops given in Sellers et al. [1996] except that Vcmo was increased from 100 to 157 μmol m−2s−1 and the upper temperature limit parameter (Thi) was increased from 308 to 320°K. Our goal is now to extend this model to simulate ΦF.
Figure 2.
Cotton data of (a) photochemical yield ΦP from gas exchange versus ΦP from PAM, (b) modeled [Collatz et al., 1991] versus measured photosynthesis, and (c) modeled versus measured (from gas exchange) ΦP.
As a first step, we plot the observed values of ΦF versus ΦP (Figure 3) to look for any systematic correlations between the two associated with light levels, CO2 concentration or temperature. While the relationship between ΦF and ΦP is clearly nonlinear, there is no systematic difference whether changes in ΦF are associated with variation in CO2 or light. However, ΦF is systematically lower at higher temperatures. The effects of temperature were examined by inspecting the values of Fo and Fm at different temperatures in the cotton and tobacco data (Figure 4). The measurements show a strong decrease of Fm and a weak decrease of Fo when temperature exceeded 26°C. A potential temperature sensitivity of 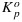 or KF alone cannot explain these features. Fm is independent of
or KF alone cannot explain these features. Fm is independent of 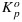 , while a temperature sensitivity of KF would have resulted in nearly equal sensitivity of Fo and Fm to temperature. We attribute the sensitivity to KD, since this can explain the temperature sensitivity of both Fo and Fm. A simple temperature correction of KD = max (0.03T + 0.0773,0.87) by means of linear regression above 26°C was sufficient to explain the variations in Fo and Fm. KD also declined at low temperature (10°C in the tobacco data set), but we did not consider the low-temperature values due to the limited number of data points.
, while a temperature sensitivity of KF would have resulted in nearly equal sensitivity of Fo and Fm to temperature. We attribute the sensitivity to KD, since this can explain the temperature sensitivity of both Fo and Fm. A simple temperature correction of KD = max (0.03T + 0.0773,0.87) by means of linear regression above 26°C was sufficient to explain the variations in Fo and Fm. KD also declined at low temperature (10°C in the tobacco data set), but we did not consider the low-temperature values due to the limited number of data points.
Figure 3.

The data and model results of the cotton experiment presented as 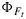 versus ΦP, with different symbols for driving variables. The lines are computed from the empirical KN(x) with temperature correction for 25°C (solid line) and 35°C (dashed line).
versus ΦP, with different symbols for driving variables. The lines are computed from the empirical KN(x) with temperature correction for 25°C (solid line) and 35°C (dashed line).
Figure 4.
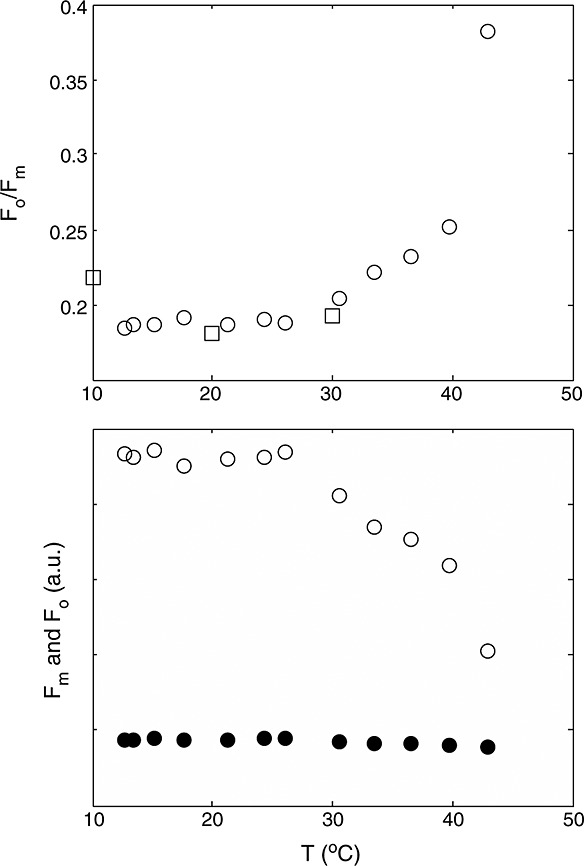
(top) Measurements of Fo/Fm at different temperatures for the cotton experiment (circles) and the tobacco experiment (squares). (bottom) Fm (open symbols) and Fo (closed symbols) at different temperature for the cotton experiment. Note that the values are relative, and the unit on the y axis is arbitrary
The decrease of Fm with temperature is in agreement with observations of Pospisil et al. [1998], who observed a decrease of Fm over a much larger temperature range in a Barley (Hordeum vulgare) leaf. However, they also observed a progressive increase of Fo starting at 30°C until Fm and Fo collapsed at 50°C. This indicates a decline of 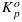 , which we did not observe in the cotton data over the examined temperature range.
, which we did not observe in the cotton data over the examined temperature range.
6. Model for KN
For the cotton data of nondark adapted leaves, we used a constant KF of 0.05 and the temperature corrected KD to calculate KP and KN (equations (8) and (9)). The relative light saturation x was calculated as follows:
| (18) |
A close relationship between the relative light saturation x and KN was found for the cotton experiment, valid for wide ranges of CO2 concentration and light intensity. Figure 5 shows the two rate coefficients, KP and KN, and KP+KN, versus x for this data set. Note that KP can be considered a dependent variable since ΦP and KN are specified. The dashed line in Figure 5 (top) is the theoretical relationship between KP and xif KN were always zero, as in a situation in which NPQ is blocked with an inhibitor Demmig-Adams [1990], making the leaf more sensitive to photoinhibition [Bilger and Björkman, 1990].
Figure 5.

(top to bottom) Rate coefficients KP and KN versus relative light saturation of photosynthesis x, calculated from active fluorescence measurements of for cotton leaves exposed to varying irradiance, varying CO2 concentration, and varying temperature. Open symbols refer to low light conditions (Q < 800μmol m−2 s−2), crosses to high-temperature data (T > 35°C), and closed symbols to all other data. The solid line is an empirical model fit, and the dotted line is the theoretical value for KP if KN were always zero.
The data of Figure 5 suggest that the relation between x and the rate coefficients can be separated into three parts. At low values of x (<0.2), most of the adjustment of ΦF and ΦP is done by KP, i.e., reduction of photosystems, and KN remains low. At intermediate values (0.2 < x < 0.6), there is a phase where KP stabilizes and most of the adjustment is taken by increasing KN. At the highest values of x (>0.6), the slack is taken up again by decreasing KP. High values of x denote either high irradiance, low-atmospheric CO2 concentration, or high temperature (all these data are plotted together). All data appear to follow the same curve, regardless of which of the driving variables was responsible for the changes in x (excess light, low CO2 concentration, or suboptimal temperatures). Figure 5 (middle), KP is relatively stable, and thus, variations in the ratio KP:KF are small. The values in this region correspond to relatively high irradiance: The filled symbols in Figure 5 represent only those data for which 800 < Q < 1800μmol m−2s−2 (high light), 14 < T < 35°C (intermediate temperatures). In those conditions, nonphotochemical quenching dominates, and photochemical yield correlates positively with fluorescence yield.
The relationship between x and KN was modeled with a curve with three coefficients fitted to the data (solid line in Figure 5), using all data where leaf temperature was between 14 and 35°C:
| (19) |
where 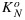 , α, and β are fitting parameters. The form of this equation was chosen to obtain
, α, and β are fitting parameters. The form of this equation was chosen to obtain 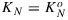 for x = 1 and KN=0 for x = 0 and values in between these extremes for 0 < x < 1. Fitting by means of minimization of the mean square difference between measured and modeled KN resulted in
for x = 1 and KN=0 for x = 0 and values in between these extremes for 0 < x < 1. Fitting by means of minimization of the mean square difference between measured and modeled KN resulted in 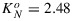 , α = 2.83, and β = 0.114.
, α = 2.83, and β = 0.114.
Data of the other experiments C3 species were plotted in the same way (rate coefficients versus x) in Figure 6. Interestingly, light and CO2 response curves of the tobacco experiment were similar to those of the cotton experiment despite having very different photosynthetic capacities. Apparently, the approach of scaling the quenching response to the x factor can accommodate differences in photosynthetic rate. Interestingly, data for the C4 plant maize followed a similar pattern to cotton and tobacco (Figure 7). There was no apparent difference in the KN versus x relation for leaves from different nitrogen fertilization treatments, despite having nearly 50% differences in carboxylation capacity at optimum temperature, Vcmo. On the other hand, data of the drought experiment, where measurements were taken outdoors on several drought-adapted plants at similar light intensity, deviated from the other observations at higher values of x. Instead of a curve with KN reaching a maximum around 2.5, KN continues to increase with increasing x to about 5. Apparently, NPQ traps a larger portion of excited states under sustained drought conditions. Consequently, the fraction of closed photosystems at a given value of x is smaller (and KP is higher) than in the experiments without water limitation (cotton, maize, and tobacco). We note that the cotton, maize, and tobacco plants had little or no previous exposure to stress and may not be representative of vegetation in natural environments. The values for the drought experiment were sufficiently different from the other experiments to justify a separate fit of equation (19) through the KN versus x data, with coefficients 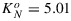 , α = 1.93, and β = 10.
, α = 1.93, and β = 10.
Figure 6.
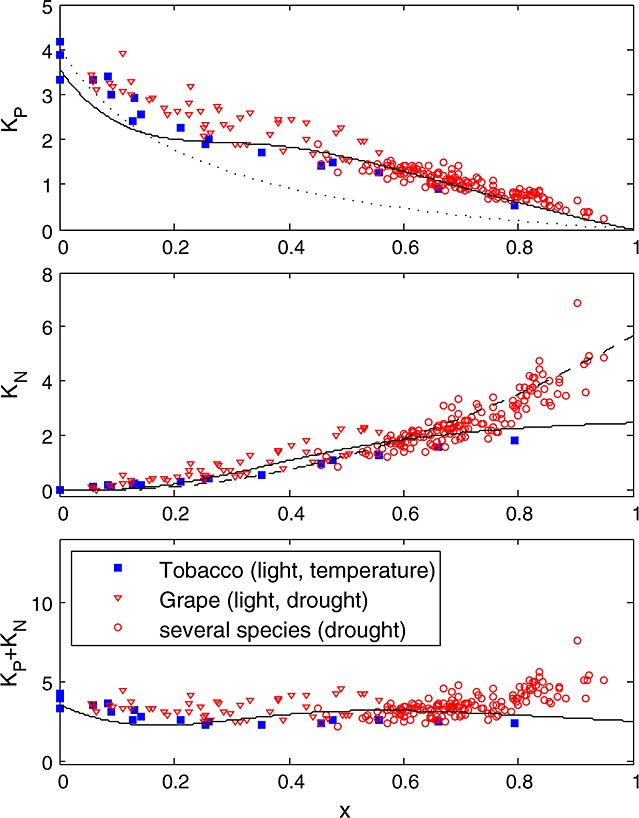
Similar to Figure 5 but for the other experiments: (1) tobacco leaves under different temperature and illumination and (2) grape and other C3 species subject to a drought experiment under full sunlight. The solid line represents the empirical fit of the cotton experiment, and the dashed line is calibrated to the drought experiment data.
Figure 7.
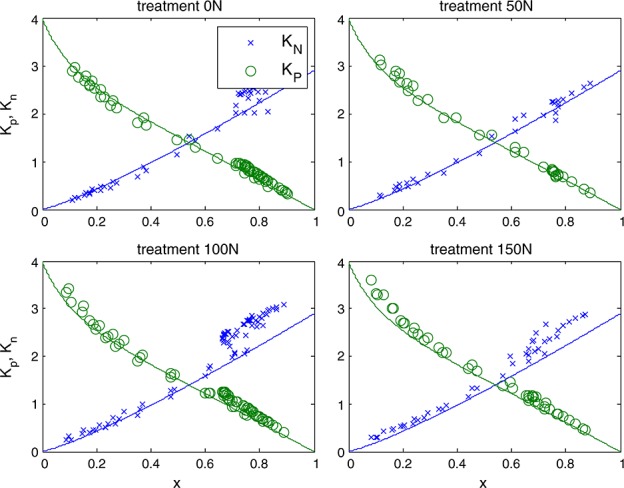
Responses of KP (green) and KN for four different nitrogen treatments in maize (symbols). The lines represent the empirical fit for the cotton experiment.
We are now in a position to link this paramaterization with the photosynthesis model. As shown Figure 2c, ΦP simulated with the carbon model agrees well with the corresponding observations. Similar results were obtained with tobacco and using the C4 model of Collatz et al. [1992]. Thus, we may evaluate the parameter x that corresponds to any model calculation of photosynthesis from the ratio 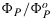 calculated in the solution to the carbon model. It is important that the two yields used to evaluate x are consistent such that x→0 in the limit as PAR →0. KN can then be evaluated using equation (19) and used in equation (13) to solve for
calculated in the solution to the carbon model. It is important that the two yields used to evaluate x are consistent such that x→0 in the limit as PAR →0. KN can then be evaluated using equation (19) and used in equation (13) to solve for  which in turn is used in equation (17) to solve for our target,
which in turn is used in equation (17) to solve for our target, 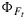 . Note that the
. Note that the 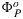 used in equation (17) should be from the fluorescence rather than from the carbon model.
used in equation (17) should be from the fluorescence rather than from the carbon model.
Figure 8 shows measured versus modeled photosynthesis A, 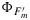 , and
, and 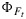 after fitting the model of Collatz et al. [1991] to the cotton and the tobacco and the model of Collatz et al. [1992] to the maize data. Also shown in this figure is the product of
after fitting the model of Collatz et al. [1991] to the cotton and the tobacco and the model of Collatz et al. [1992] to the maize data. Also shown in this figure is the product of 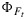 and the flux of absorbed PAR, JaPAR (estimated assuming that JaPAR=0.9·Q/2 where 0.9 is the absorptance and Q is the incident flux). This is an approximation for the fluorescence flux emitted by the leaf JF. In each case the model was calibrated to the respective data sets (e.g., all cotton points), and the same parameter set was used to simulate the group of observations. The model reproduces the photosynthesis and maximum fluorescence
and the flux of absorbed PAR, JaPAR (estimated assuming that JaPAR=0.9·Q/2 where 0.9 is the absorptance and Q is the incident flux). This is an approximation for the fluorescence flux emitted by the leaf JF. In each case the model was calibrated to the respective data sets (e.g., all cotton points), and the same parameter set was used to simulate the group of observations. The model reproduces the photosynthesis and maximum fluorescence 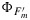 reasonably well. However, the simulations of the fluorescence yield
reasonably well. However, the simulations of the fluorescence yield 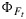 are poorly correlated. In part, this is due to the very small variation (±25%) in
are poorly correlated. In part, this is due to the very small variation (±25%) in 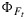 observed in the experiment and to errors in measurement of these small differences. It should also be noted that other factors such as photoinhibition [Demmig-Adams and Adams III, 1996] or chloroplast movement [Brugnoli and Bjorkman, 1992] may also cause changes in the apparent
observed in the experiment and to errors in measurement of these small differences. It should also be noted that other factors such as photoinhibition [Demmig-Adams and Adams III, 1996] or chloroplast movement [Brugnoli and Bjorkman, 1992] may also cause changes in the apparent 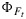 . We did not control for these.
. We did not control for these.
Figure 8.
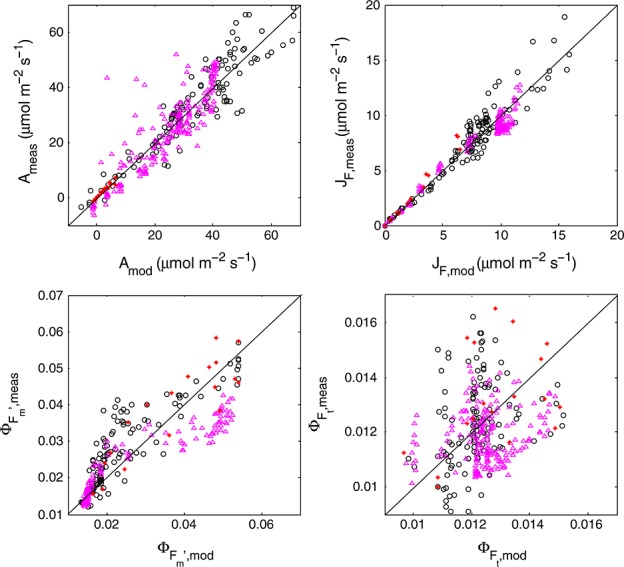
Modeled versus measured photosynthesis A, fluorescence flux 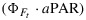 , steady state fluorescence yield
, steady state fluorescence yield 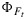 , and maximum fluorescence yield
, and maximum fluorescence yield 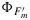 (clockwise). Circles refer to cotton, triangles to maize, and stars to tobacco.
(clockwise). Circles refer to cotton, triangles to maize, and stars to tobacco.
Despite the poor overall performance of the model to reproduce 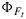 , mainly due to its low variability, simulated versus modeled responses of cotton to environmental drivers light, CO2, and temperature compare well with observations (Figure 9). Of particular interest is the sensitivity to temperature, as illustrated in Figure 9. The model did not capture the temperature sensitivity of photosynthesis well, especially at the lower and higher temperatures, where it overestimates photosynthesis, and hence x. It appears that this is primarily due to calibration errors of the photosynthesis model and fluorescence modeling may be useful to identify and correct problems with model calibration.
, mainly due to its low variability, simulated versus modeled responses of cotton to environmental drivers light, CO2, and temperature compare well with observations (Figure 9). Of particular interest is the sensitivity to temperature, as illustrated in Figure 9. The model did not capture the temperature sensitivity of photosynthesis well, especially at the lower and higher temperatures, where it overestimates photosynthesis, and hence x. It appears that this is primarily due to calibration errors of the photosynthesis model and fluorescence modeling may be useful to identify and correct problems with model calibration.
Figure 9.
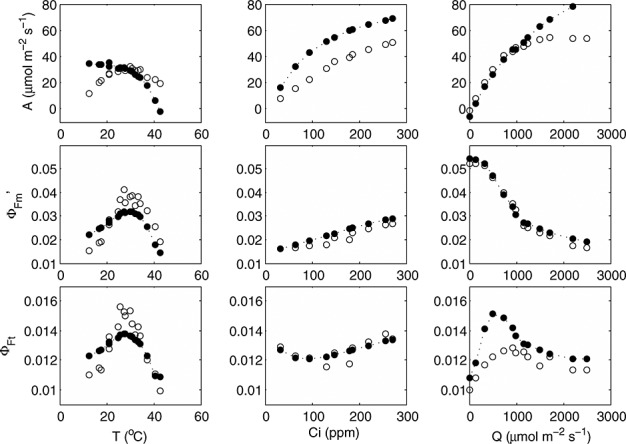
Measured (open symbols) and modeled (closed symbols) responses of photosynthesis, maximum fluorescence yield, and steady state fluorescence yield of selected cotton leaves to temperature, leaf boundary layer CO2 concentration, and irradiance.
If we consider Figure 8 again, we can observe that contrary to 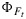 , the fluorescence flux JF is reproduced well. The reason is the small range in
, the fluorescence flux JF is reproduced well. The reason is the small range in 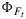 and the dominant effect that incident light flux has on JF. The dominance of irradiance on JF is further illustrated in Figure 10, showing a selection of modeled and “measured” JF as
and the dominant effect that incident light flux has on JF. The dominance of irradiance on JF is further illustrated in Figure 10, showing a selection of modeled and “measured” JF as  versus the CO2 flux from gas exchange for the cotton data. The selection consists of a light response and a CO2 response curve. The light response shows the combined effect of variations in JaPAR and the yields, whereas the CO2 response is only affected by variations in the yields (JaPAR was constant). With irradiance as the driving variable, we notice a large range of fluorescence flux, continuing to increase even after JA saturates. The variations in fluorescence flux are much smaller when CO2 is the driving variable. In that case, all variation of the fluorescence flux originates from the fluorescence yield, while aPAR was constant. In either case, the simulations tracked the observations well.
versus the CO2 flux from gas exchange for the cotton data. The selection consists of a light response and a CO2 response curve. The light response shows the combined effect of variations in JaPAR and the yields, whereas the CO2 response is only affected by variations in the yields (JaPAR was constant). With irradiance as the driving variable, we notice a large range of fluorescence flux, continuing to increase even after JA saturates. The variations in fluorescence flux are much smaller when CO2 is the driving variable. In that case, all variation of the fluorescence flux originates from the fluorescence yield, while aPAR was constant. In either case, the simulations tracked the observations well.
Figure 10.
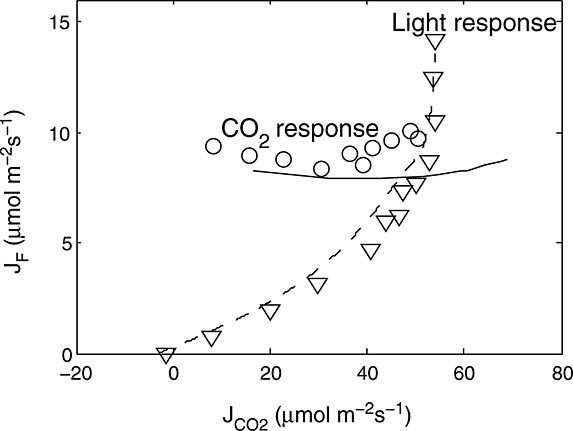
Selection of the cotton data for one light response curve (triangles) and one CO2 response curve at an incident PAR of 1400 μmol m−2 s−1 (circles), with CO2 gas exchange flux on the horizontal axis and fluorescence flux JP=ΦP·aPAR/2 from PAM data on the vertical axis. The lines are model results (cotton parameters for KN(x)) after coupling the PAM fluorescence model to the model of Collatz et al. [1991].
7. Discussion
We have developed an extension of a conventional photosynthesis model to simulate fluorescence. We used an empirical approach to relate NPQ to a factor, x, that expresses the extent to which the actual rate of electron transport is reduced relative to the potential rate. This relationship is similar whether variation is driven by manipulation of light, CO2, and carboxylation capacity. Here we used the photosynthesis models of Collatz et al. [1991] for C3 and Collatz et al. [1992] for C4 vegetation, but this approach could be used by any model based on the assumptions of Farquhar et al. [1980]. A one-by-one sensitivity analysis of this combined fluorescence-photosynthesis model revealed that aPAR and the carboxylation capacity Vcmo are main contributors to variations in fluorescence yield and that their contributions are comparable in magnitude (Figure 11). Temperature affects the dark reactions of photosynthesis [Weis and Berry, 1987b], with an additional effect of KD being temperature dependent. Stomatal effects mediated by the relative humidity appear to have a relatively small effect on fluorescence yield, except at low relative humidity.
Figure 11.
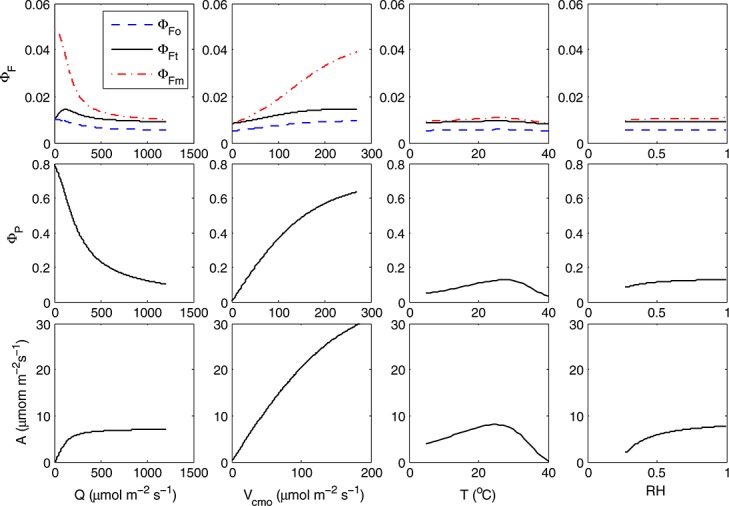
One-by-one sensitivity analysis of the modeled yields (fluorescence and photochemistry) and photosynthesis of a “standard” leaf to four input variables. The sensitivity was calculated for drought relation between x and KN. The parameters of the standard leaf were leaf boundary [CO2] = 380 ppm, aPAR = 1000μmol m−2s−1, leaf temperature T = 20°C, relative humidity RH = 70%, Vcmo=30μmol m−2 s−1, and Ball-Berry stomatal conductance parameter m = 8.
In Figure 12 we show how changes in fluorescence yield associated with changes in Vcmo, which might occur during drought or senescence, correspond to changes in the fluorescence intensity, JF. For this figure drought parameters for KN versus x were used. Changing Vcmo affects the value of irradiance at which the peak of the fluorescence yield occurs (Figure 12, top left). The peak occurs at the transition from light limited to light-saturated photosynthesis, where neither light nor CO2 is in deficit. The fluorescence yield thus peaks at a Vcmo-dependent irradiance, but the fluorescence flux continuously rises with irradiance (Figure 12, bottom left). The rise in intensity is initially steep, but it flattens after the peak of fluorescence yield. Hence, the transition point between light limitation and light saturation can be derived from the change in slope between the fluorescence flux and irradiance. The photochemical yield (Figure 12, top right) decreases strongly with irradiance, as the rate of CO2 uptake begins to saturate (Figure 12, bottom right).
Figure 12.
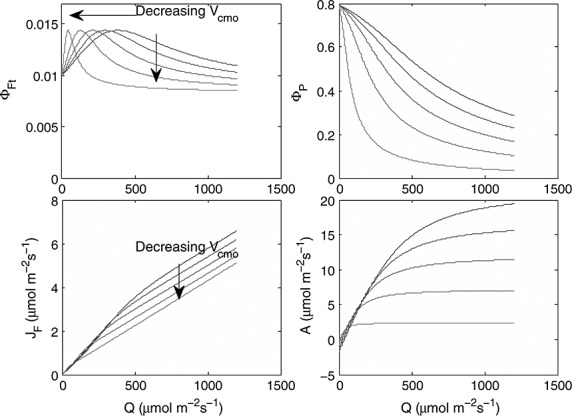
(top left) Modeled fluorescence yield ΦFt (top right)photochemical yield ΦP, (bottom left) photosynthesis A, and (bottom right) fluorescence flux JF, as functions of irradiance for the following values of maximum carboxylation capacity Vcmo: 10 (light gray), 30, 50, 70, and 90 (black) μmol m−2 s−1. The drought relation between x and KN was used.
A clearly different response between the light, CO2, and fertilization experiments on one hand, and the drought experiment on the other hand, prevents us from presenting a deterministic model for KN for all cases. The differences in KN values at high x between the two model fits have a number of implications for the sensitivity of the model and for the interpretation of fluorescence yields, as illustrated in Figure 13. When the parameters of the cotton data are used, then KN levels off and 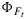 increases at the highest values of x (stressed conditions). This is illustrated in Figure 13 (right), where the yields were modeled using the cotton KN(x) parameterization as a function of irradiance. The steady state yield first increases, then decreases, and finally increases with irradiance. In the drought experiment, values of ΦF continue to decrease with irradiance (Figure 13, left), and the lowest fluorescence yields indicate stress.
increases at the highest values of x (stressed conditions). This is illustrated in Figure 13 (right), where the yields were modeled using the cotton KN(x) parameterization as a function of irradiance. The steady state yield first increases, then decreases, and finally increases with irradiance. In the drought experiment, values of ΦF continue to decrease with irradiance (Figure 13, left), and the lowest fluorescence yields indicate stress.
Figure 13.

Modeled responses of 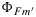 ,
, 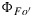 , and ΦF to irradiance, (left) using the drought parameters for KN(x) and (right) using the cotton parameters for KN(x).
, and ΦF to irradiance, (left) using the drought parameters for KN(x) and (right) using the cotton parameters for KN(x).
The mechanisms of NPQ and their regulation are still an area of active research (for reviews see Ruban et al. [2012] and Zaks et al. [2013]). We speculate that the shape of the x-KN relationship is affected by xanthophyll pool sizes as influenced by adaptation to weather conditions. A practical approach would be to relate 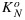 to the concentration of pigments that are capable of NPQ [Lavergne and Trissl, 1995; Oxborough and Baker, 2000]. As noted by Zaks et al. [2013], a high zeaxanthin concentration is necessary but not sufficient for nonphotochemical quenching. To study this further, active fluorescence measurements should be combined with concurrent spectrometry, while tapping into earlier studies that showed a photochemical reflectance index correlating with xanthophyll pigment conversions [Gamon et al., 1990].
to the concentration of pigments that are capable of NPQ [Lavergne and Trissl, 1995; Oxborough and Baker, 2000]. As noted by Zaks et al. [2013], a high zeaxanthin concentration is necessary but not sufficient for nonphotochemical quenching. To study this further, active fluorescence measurements should be combined with concurrent spectrometry, while tapping into earlier studies that showed a photochemical reflectance index correlating with xanthophyll pigment conversions [Gamon et al., 1990].
The analysis presented here have been made for the leaf level. We did not present any canopy level analyses here, although we have implemented the model the 'Soil Canopy Observation of Photosynthesis and Energy fluxes (SCOPE) model, [van der Tol et al., 2009b]. In the canopy, leaf illumination is variable among leaves, and the relationship after aggregating over all leaves may differ from what we presented here. In addition, the emitted fluorescence flux is scattered and reabsorbed within the canopy, thus reducing the observed SIF below the emitted flux of all leaves together. We expect, however, that some features of the leaf level photosynthesis-SIF relationship remain because any observation from the top of canopy will be dominated by the top and most illuminated leaves. First, that NPQ is the main driver of variations in ΦP and 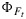 and that the two yields are positively related during daytime. Variations in canopy measurements of SIF, after normalization by estimates of the absorbed PAR, may be related to drought or temperature stress. Second, the variations in
and that the two yields are positively related during daytime. Variations in canopy measurements of SIF, after normalization by estimates of the absorbed PAR, may be related to drought or temperature stress. Second, the variations in 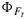 are small compared to those in ΦP (Figure 3). In spatial SIF data (airborne and satellite data) over terrain of mixed vegetation, variations in photosynthetically active leaf area (green leaf area index) will most likely dominate the variations in SIF, since these variations may be much larger than the variations in
are small compared to those in ΦP (Figure 3). In spatial SIF data (airborne and satellite data) over terrain of mixed vegetation, variations in photosynthetically active leaf area (green leaf area index) will most likely dominate the variations in SIF, since these variations may be much larger than the variations in 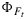 that we observed here.
that we observed here.
8. Conclusion
The fluorescence yield of leaves is strongly influenced by the development of nonphotochemical quenching (NPQ). This (and not fluorescence) is the predominant mechanism for dissipation of excess excitation energy. In fact, fluorescence yield typically remains nearly constant or declines as a result of increased NPQ when leaves experience over excitation. We introduce a factor x that indicates the relative extent that photochemistry of photosystem II is restricted by the limited capacity for CO2 fixation, and we show that there is a strong empirical relationship between the rate constant for nonphotochemical quenching, KN, and x. While this relationship may differ with species and history, it is easily characterized with PAM fluorescence measurements. The other important determinant of fluorescence yield, KP, is captive to the level of KN and the permitted rate of electron transport under light saturation or stress due to strong limitations on photosynthesis by other factors than light. The empirical fits of KN versus x can be used in combination with a photosynthesis model to estimate leaf level fluorescence yield as a function of environmental forcing and photosynthetic capacity. Estimation of the flux of leaf level solar-induced fluorescence (SIF) from the predicted fluorescence yields (Figure 12) shows that SIF will be proportional to photosynthetic rate under conditions where light is limiting. When light is in excess or stress develops, there is a reduction in the fluorescence yield and the slope of the dependence of SIF on light intensity declines. This is the basis for inversions to obtain Vcmo [Zhang et al., 2014]. With increasing stress or reductions in Vcmo at constant light (as would occur with repeated Sun-synchronous satellite observations), SIF would be observed to decrease. The extent of this decrease may depend on the severity and type of stress.
Acknowledgments
We are grateful to Jaume Flexas for providing data on the drought experiments and to A. Moersch for collecting the tobacco data. The comments of two reviewers, the Associate Editor, and Ari Kornfeld helped to greatly improve this paper. We acknowledge the support and participation of E. Middleton and M. P. Cendrero-Mateo for the collection of maize (Zea mays, L.) leaf measurements and the collaborative NASA/USDA research effort “Spectral Bio-Indicators of Ecosystem Photosynthetic Efficiency II: Synthesis and Integration” (PI E. Middleton) and NASA's Terrestrial Ecology program, which enabled the collection. This study was initiated at a workshop supported by the Keck Institute for Space Studies. The research was in part funded by a grant from the Dutch User Support Programme Space Research (ALW-GO/13-32).
References
- Bilger W, Björkman O. Role of the xanthophyll cycle in photoprotection elucidated by measurements of light-induced absorbance changes, fluorescence and photosynthesis in leaves of Hedera canariensis. Photosynth. Res. 1990;25(3):173–185. doi: 10.1007/BF00033159. [DOI] [PubMed] [Google Scholar]
- Bilger W, Schreiber U, Bock M. Determination of the quantum efficiency of photosystem II and of non-photochemical quenching of chlorophyll fluorescence in the field. Oecologia. 1995;102(4):425–432. doi: 10.1007/BF00341354. [DOI] [PubMed] [Google Scholar]
- Björkman O, Demmig B. Photon yield of O2 evolution and chlorophyll fluorescence characteristics at 77 K among vascular plants of diverse origins. Planta. 1987;170(4):489–504. doi: 10.1007/BF00402983. [DOI] [PubMed] [Google Scholar]
- Brugnoli E, Bjorkman O. Chloroplast movements in leaves: Influence on chlorophyll fluorescence and measurements of light-induced absorbance changes related to Δph and zeaxanthin formation. Photosynth. Res. 1992;32(1):23–35. doi: 10.1007/BF00028795. doi: 10.1007/BF00028795. [DOI] [PubMed] [Google Scholar]
- Butler WL. Energy distribution in the photochemical apparatus of photosynthesis. Ann. Rev. Plant Physiol. 1978;29(1):345–378. [Google Scholar]
- Collatz G, Ball J, Grivet C, Berry JA. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. Forest Meteorol. 1991;54(2–4):107–136. doi: 10.1016/0168-1923(91)90002-8. [Google Scholar]
- Collatz G, Ribas-Carbo M, Berry J. Coupled photosynthesis-stomatal conductance model for leaves of C4 plants. Funct. Plant Biol. 1992;19(5):519–538. [Google Scholar]
- Daughtry CS. Discriminating crop residues from soil by shortwave infrared reflectance. Agron. J. 2001;93(1):125–131. [Google Scholar]
- Demmig-Adams B. Carotenoids and photoprotection in plants: A role for the xanthophyll zeaxanthin. Biochim. Biophys. Acta, Bioenerg. 1990;1020(1):1–24. [Google Scholar]
- Demmig-Adams B, Adams III WW. The role of xanthophyll cycle carotenoids in the protection of photosynthesis. Trends Plant Sci. 1996;1(1):21–26. [Google Scholar]
- Farquhar G, Caemmerer Svv, Berry J. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta. 1980;149(1):78–90. doi: 10.1007/BF00386231. [DOI] [PubMed] [Google Scholar]
- Fleming GR, Schlau-Cohen GS, Amarnath K, Zaks J. Design principles of photosynthetic light-harvesting. Faraday Discuss. 2012;155:27–41. doi: 10.1039/c1fd00078k. [DOI] [PubMed] [Google Scholar]
- Flexas J, Escalona J, Medrano H. Down-regulation of photosynthesis by drought under field conditions in grapevine leaves. Funct. Plant Biol. 1998;25(8):893–900. [Google Scholar]
- Flexas J, Escalona JM, Evain S, Gulías J, Moya I, Osmond CB, Medrano H. Steady-state chlorophyll fluorescence (Fs) measurements as a tool to follow variations of net CO2 assimilation and stomatal conductance during water-stress in C3 plants. Physiol. Plant. 2002;114(2):231–240. doi: 10.1034/j.1399-3054.2002.1140209.x. [DOI] [PubMed] [Google Scholar]
- Franck F, Juneau P, Popovic R. Resolution of the Photosystem I and Photosystem II contributions to chlorophyll fluorescence of intact leaves at room temperature. Biochim. Biophys. Acta, Bioenerg. 2002;1556(2):239–246. doi: 10.1016/s0005-2728(02)00366-3. [DOI] [PubMed] [Google Scholar]
- Frankenberg C, et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011;38:L17706. doi: 10.1029/2011GL048738. [Google Scholar]
- Gamon J, Field C, Bilger W, Björkman O, Fredeen A, Peñuelas J. Remote sensing of the xanthophyll cycle and chlorophyll fluorescence in sunflower leaves and canopies. Oecologia. 1990;85(1):1–7. doi: 10.1007/BF00317336. [DOI] [PubMed] [Google Scholar]
- Genty B, Briantais J-M, Baker NR. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta, Bioenerg. 1989;990(1):87–92. doi: 10.1016/S0304-4165(89)80016-9. [Google Scholar]
- Gilmore AM. Mechanistic aspects of xanthophyll cycle-dependent photoprotection in higher plant chloroplasts and leaves. Physiol. Plant. 1997;99(1):197–209. [Google Scholar]
- Guanter L, Alonso L, Gómez-Chova L, Amorós-López J, Vila J, Moreno J. Estimation of solar-induced vegetation fluorescence from space measurements. Geophys. Res. Lett. 2007;34:L08401. doi: 10.1029/2007GL029289. [Google Scholar]
- Hildner R, Brinks D, Nieder JB, Cogdell RJ, van Hulst NF. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Science. 2013;340(6139):1448–1451. doi: 10.1126/science.1235820. doi: 10.1126/science.1235820. [DOI] [PubMed] [Google Scholar]
- Joiner J, Yoshida Y, Vasilkov AP, Yoshida Y, Corp LA, Middleton EM. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences. 2011;8(3):637–651. doi: 10.5194/bg-8-637-2011. [Google Scholar]
- Kitajima M, Butler W. Quenching of chlorophyll fluorescence and primary photochemistry in chloroplasts by dibromothymoquinone. Biochim. Biophys. Acta, Bioenerg. 1975;376(1):105–115. doi: 10.1016/0005-2728(75)90209-1. doi: 10.1016/0005-2728(75)90209-1. [DOI] [PubMed] [Google Scholar]
- Lavergne J, Trissl H-W. Theory of fluorescence induction in photosystem II: Derivation of analytical expressions in a model including exciton-radical-pair equilibrium and restricted energy transfer between photosynthetic units. Biophys. J. 1995;68(6):2474–2492. doi: 10.1016/S0006-3495(95)80429-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LI-COR Biosciences Inc. Using the LI-6400 Portable Photosynthesis System, Version 5. Tech. Rep. 9806-122. 2004:LI-COR Biosciences Inc., Lincoln, Nebr. [Google Scholar]
- Loriaux S, Avenson T, Welles J, McDermitt D, Eckles R, Riensche B, Genty B. Closing in on maximum yield of chlorophyll fluorescence using a single multiphase flash of sub-saturating intensity. Plant Cell Environ. 2013;36(10):1755–1770. doi: 10.1111/pce.12115. [DOI] [PubMed] [Google Scholar]
- Markgraf T, Berry J. Current Research in Photosynthesis. Netherlands: Springer; 1990. Measurement of photochemical and non-photochemical quenching: Correction for turnover of PS2 during steady-state photosynthesis; pp. 3073–3076. [Google Scholar]
- Maxwell K, Johnson G. Chlorophyll fluorescence—A practical guide. J. Exp. Bot. 2000;51(345):1–10. doi: 10.1093/jxb/51.345.659. [DOI] [PubMed] [Google Scholar]
- Mazzoni M, Meroni M, Fortunato C, Colombo R, Verhoef W. Retrieval of maize canopy fluorescence and reflectance by spectral fitting in the O2-A absorption band. Remote Sens. Environ. 2012;124:72–82. [Google Scholar]
- Meroni M, Rossini M, Guanter L, Alonso L, Rascher U, Colombo R, Moreno J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009;113(10):2037–2051. doi: 10.1016/j.rse.2009.05.003. [Google Scholar]
- Mohseni M, Rebentrost P, Lloyd S, Aspuru-Guzik A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008;129(174,106) doi: 10.1063/1.3002335. doi: 10.1063/1.3002335. [DOI] [PubMed] [Google Scholar]
- Moya I, Camenen L, Evain S, Goulas Y, Cerovic Z, Latouche G, Flexas J, Ounis A. A new instrument for passive remote sensing: 1. Measurements of sunlight-induced chlorophyll fluorescence. Remote Sens. Environ. 2004;91(2):186–197. doi: 10.1016/j.rse.2004.02.012. [Google Scholar]
- Oxborough K, Baker NR. An evaluation of the potential triggers of photoinactivation of photosystem II in the context of a Stern-Volmer model for downregulation and the reversible radical pair equilibrium model. Philos. Trans. R. Soc. B. 2000;355(1402):1489–1498. doi: 10.1098/rstb.2000.0709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papageorgiou GC, et al. Chlorophyll a Fluorescence: A Signature of Photosynthesis. Vol. 19. Netherlands: Springer; 2004. [Google Scholar]
- Porcar-Castell A, Tyystjärvi E, Atherton J, van der Tol C, Flexas J, Pfündel EE, Moreno J, Frankenberg C, Berry JA. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014;65:4065–4095. doi: 10.1093/jxb/eru191. doi: 10.1093/jxb/eru191. [DOI] [PubMed] [Google Scholar]
- Pospisil P, Skotnica J, Naus J. Low and high temperature dependence of minimum F0 and maximum Fm chlorophyll fluorescence in vivo. Biochim. Biophys. Acta, Bioenerg. 1998;1363(2):95–99. doi: 10.1016/s0005-2728(97)00095-9. [DOI] [PubMed] [Google Scholar]
- Rebentrost P, M. Mohseni, A. Aspuru-Guzik Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. B. 2009;113(29):9942–9947. doi: 10.1021/jp901724d. doi: 10.1021/jp901724d. [DOI] [PubMed] [Google Scholar]
- Ruban AV, Johnson MP, Duffy CD. The photoprotective molecular switch in the photosystem II antenna. Biochim. Biophys. Acta, Bioenerg. 2012;1817(1):167–181. doi: 10.1016/j.bbabio.2011.04.007. [DOI] [PubMed] [Google Scholar]
- Schreiber U, Schliwa U, Bilger W. Continuous recording of photochemical and non-photochemical chlorophyll fluorescence quenching with a new type of modulation fluorometer. Photosynth. Res. 1986;10(1–2):51–62. doi: 10.1007/BF00024185. [DOI] [PubMed] [Google Scholar]
- Sellers P, Randall D, Collatz G, Berry J, Field C, Dazlich D, Zhang C, Collelo G, Bounoua L. A revised land surface parameterization (SiB2) for atmospheric GCMSs. Part I: Model formulation. J. Clim. 1996;9(4):676–705. [Google Scholar]
- van der Tol C, Verhoef W, Rosema A. A model for chlorophyll fluorescence and photosynthesis at leaf scale. Agric. Forest Meteorol. 2009a;149(1):96–105. [Google Scholar]
- van der Tol C, Verhoef W, Timmermans J, Verhoef A, Su Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences. 2009b;6(12):3109–3129. doi: 10.5194/bg-6-3109-2009. [Google Scholar]
- Weis E, Berry JA. Quantum efficiency of photosystem II in relation to energy-dependent quenching of chlorophyll fluorescence. Biochim. Biophys. Acta, Bioenerg. 1987a;894(2):198–208. doi: 10.1016/0005-2728(87)90190-3. [Google Scholar]
- Weis E, Berry JA. Plants and high temperature stress. Symp. Soc. Exp. Biol. 1987b;42:329–346. [PubMed] [Google Scholar]
- Woodrow I, Berry J. Enzymatic regulation of photosynthetic CO2 fixation in C-3 plants. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1988;39:533–594. doi: 10.1146/annurev.arplant.39.1.533. [Google Scholar]
- Zaks J, Amarnath K, Sylak-Glassman EJ, Fleming GR. Models and measurements of energy-dependent quenching. Photosynt. Research. 2013;116(2-3):389–409. doi: 10.1007/s11120-013-9857-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarco-Tejada P, Catalina A, González M, Martín P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ. 2013;136:247–258. doi: 10.1016/j.rse.2013.05.011. [Google Scholar]
- Zhang Y, Guanter L, Berry JA, Joiner J, Tol C, Huete A, Gitelson A, Voigt M, Köhler P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Global Change Biol. 2014;20(12):3727–3742. doi: 10.1111/gcb.12664. [DOI] [PubMed] [Google Scholar]


