Combining One-Sample Confidence Procedures for Inference in the Two-Sample Case

Summary

We present a simple general method for combining two one-sample confidence procedures to obtain inferences in the two-sample problem. Some applications give striking connections to established methods; for example, combining exact binomial confidence procedures gives new confidence intervals on the difference or ratio of proportions that match inferences using Fisher’s exact test, and numeric studies show the associated confidence intervals bound the type I error rate. Combining exact one-sample Poisson confidence procedures recreates standard confidence intervals on the ratio, and introduces new ones for the difference. Combining confidence procedures associated with one-sample t-tests recreates the Behrens-Fisher intervals. Other applications provide new confidence intervals with fewer assumptions than previously needed. For example, the method creates new confidence intervals on the difference in medians that do not require shift and continuity assumptions. We create a new confidence interval for the difference between two survival distributions at a fixed time point when there is independent censoring by combining the recently developed beta product confidence procedure for each single sample. The resulting interval is designed to guarantee coverage regardless of sample size or censoring distribution, and produces equivalent inferences to Fisher’s exact test when there is no censoring. We show theoretically that when combining intervals asymptotically equivalent to normal intervals, our method has asymptotically accurate coverage. Importantly, all situations studied suggest guaranteed nominal coverage for our new interval whenever the original confidence procedures themselves guarantee coverage.

1. Introduction

We propose a simple procedure to create a confidence interval (CI) for certain functions (e.g., the difference or the ratio) of two scalar parameters from each of two independent samples. The procedure only requires nested confidence intervals from the independent samples and certain monotonicity constraints on the function, and can be applied quite generally. We call our new CIs “melded confidence intervals” since they meld together the CIs from each of the two-samples. In this paper we focus on melded CIs that are created from two one-sample CIs with guaranteed nominal coverage, and we conjecture that the resulting CIs themselves guarantee coverage. This conjecture is supported by simulated, numerical, and mathematical results.

The melded CI method is closely related to methods that have expanded or modified fiducial inference yet focus on frequentist properties, such as confidence structures (Balch, 2012), generalized fiducial inference (Hannig, 2009), inferential models (Martin and Liu, 2013), or confidence distributions (Xie and Singh, 2013). The melded CIs are much simpler to describe than the first three methods mentioned, and, unlike confidence distributions, can be applied to small sample discrete problems.

Fiducial inference is no longer part of mainstream statistics (for more background see Pedersen, 1978; Zabell, 1992; Hannig, 2009); nevertheless, it will be helpful to briefly describe some examples of fiducial inference and some of its shortcomings to show how the melded CIs relate to it and avoid those shortcomings. Unlike frequentist inference where parameters are fixed, or Bayesian inference where parameters are random, fiducial inference is not clearly in either camp, and hence has been the source of much confusion. Fiducial inference is a way of conditioning on the data and getting a distribution on the parameter without using a prior distribution. For example, if x is an observation drawn from a normal distribution with mean µ and variance 1 (i.e., N (µ, 1)), then the corresponding fiducial distribution for µ is N (x, 1). The middle 95% of that fiducial distribution is the usual 95% confidence interval for µ. The problem is that the fiducial distribution cannot be used to get confidence intervals on non-monotonic transformations of the parameter. For example, using the fiducial distribution for µ of N (x, 1) as above, the corresponding distribution for µ² is a non-central chi square. A fiducial approach to creating in a one-sided 95% lower confidence limit for µ² is to take the 5% percentile of that non-central chi square distribution, but this does not work well; when µ = 0.1, the coverage is only about 66% (see Pedersen, 1978, p. 153-155). Another complication is that for discrete data such as a binomial observation, there are two fiducial distributions associated with the parameter, one can be used for obtaining the lower confidence limit and one for the upper limit (Stevens, 1950).

The melded CI approach is similar to the fiducial approach in that without using priors we associate probability distributions with parameters after conditioning on the data. But those probability distributions are only tools used to obtain the melded CIs and need not be interpreted as fiducial probabilities; all statistical theory in this paper is firmly frequentist. The melded CI approach avoids the problems of fiducial inference two ways. First, we create distributions for parameters using only nested (defined in Section 2) one-sample confidence intervals, whose theory is well developed and understood. This seamlessly creates either one distribution (e.g., in the normal case) or two distributions (e.g., in the binomial case) as needed. Second, we limit the application to functions of the parameters that meet some monotonicity constraints, so that when the one-sample CIs have guaranteed coverage, the resulting melded CIs appear to also have guaranteed coverage.

Besides motivating some classical CIs and creating new CIs for these canonical examples, the melded CI method is a very general tool that can easily be used in essentially any complex two-sample inference setting, as long as there is an established approach for computing confidence intervals for a single sample. As an example of a new CI consider the difference in medians. Existing methods require continuity or shift assumptions (the Hodges and Lehmann (1963) intervals) or large samples (the nonparametric bootstrap). A melded CI for this situation inverts the sign test, and requires none of those assumptions. Simulations show that, unlike the Hodges and Lehmann (1963) intervals or nonparametric bootstrap intervals, the melded confidence intervals retain nominal coverage in all cases studied including discrete cases, non-shift cases, and small sample cases.

Here is an outline of the paper. First, we define the procedure in Section 2. Then, we motivate the melded CIs for a simple example in Section 3, giving intuition for why it appears to retain the type I error rate. Section 4 gives more general mathematical results. The heart of the paper shows the applications, with connections to well known tests for simple cases and new tests and confidence intervals for less simple cases. In Sections 5, 6, and 7, we discuss the melded CIs applied to the normal, binomial, and Poisson problems, respectively. In Section 8 we study a nonparametric melded CI for the difference in medians. In Section 9 we explore the application to the difference in survival distributions. In Section 10 we discuss the relationship with the confidence distribution approach, and we end with a short discussion.

2. The Melded Confidence Interval Procedure

Suppose we have two independent samples, where for the ith sample, x_i is the data vector, and X_i is the associated random variable whose distribution depends on a scalar parameter θ_i and possibly other nuisance parameters. Let the nested 100q% one-sided lower and upper confidence limits for θ_i be L_θi (x_i, q) and U_θi (x_i, q), respectively. By nested we mean that if q₁ < q₂ then L_θi (x_i, q₂) ⩽ L_θi (x_i, q₁) and U_θi (x_i, q₁) ⩽ U_θi (x_i, q₂). We limit our application to functions of the parameters, written g(θ₁, θ₂), that are, loosely speaking, decreasing in θ₁ among all allowable values of θ₂ and increasing in θ₂ among all allowable values of θ₁ (see Supplementary Material Section A for a precise statement of the monotonicity constraints). We consider three examples for g(·, ·) in this paper: the difference, g(θ₁, θ₂) = θ₂ − θ₁; the ratio, g(θ₁, θ₂) = θ₂/θ₁, which can be used if the parameter space for θ_i is θ_i ⩾ 0 for i = 1, 2; and the odds ratio, g(θ₁, θ₂) = {θ₂(1 − θ₁)} {θ₁(1 − θ₂)}, which can be used if the the parameter space for θ_i is 0 ⩽ θ_i ⩽ 1 for i = 1, 2. Note this is a crucial restriction because the coverage properties of the method may not hold if the monotonicity constraints on g are violated (see Section 10). Let x = [x₁, x₂]. Then the 100(1 − α)% lower and upper one-sided melded confidence limits for β = g(θ₁, θ₂) are

$$L_{\beta }(\text{x},1-\alpha )=\text{the}\alpha \text{th}\text{quantile}\text{of}g\{U_{{\theta }_1}({\text{x}}_1,A),L_{{\theta }_2}({\text{x}}_2,B)\},$$ (1)

and

$$U_{\beta }(\text{x},1-\alpha )=\text{the}(1-\alpha )\text{th}\text{quantile}\text{of}g\{L_{{\theta }_1}({\text{x}}_1,A),U_{{\theta }_2}({\text{x}}_2,B)\},$$ (2)

where here and throughout the paper, A and B are independent and uniform random variables. The melded CIs can be calculated by Monte Carlo simulation or numeric integration. For the examples in this paper, we used numeric integration. See Section 6 for a worked example.

We can invert the confidence intervals to give p-values associated with the corresponding series of hypothesis tests. For example, p_L(x, β₀) = inf {p : L_β (x, 1 − p) > β₀} is the corresponding p-value for testing the null hypothesis H₀ : g(θ₁, θ₂) ⩽ β₀. The p-values have a simple form when g(θ₁, θ₂) = β₀ implies θ₁ = θ₂ (see Web Appendix B):

$$p_L(\text{x},{\beta }_0)=P_{A,B}\left[L_{{\theta }_2}({\text{x}}_2,B)⩽U_{{\theta }_1}({\text{x}}_1,A)\right],$$ (3)

and, for testing H₀ : g(θ₁, θ₂) ⩾ β₀,

$$p_U(\text{x},{\beta }_0)=P_{A,B}[U_{{\theta }_2}({\text{x}}_2,B)⩾L_{{\theta }_1}({\text{x}}_1,A)].$$ (4)

3. Motivation

We motivate melded confidence intervals using the example of calculating the upper 64% one-sided confidence limit for the difference in two proportions, β = θ₂ − θ₁. We use the 64% confidence interval because the graphs will be easier to interpret, but the ideas are analogous for more standard levels. Suppose we observe x₁ = 4 out of n₁ = 11 positive responses in group 1 and x₂ = 13 out of n₂ = 24 in group 2. Then the difference in sample proportions is 13/24 − 4/11 = 0.542 − 0.364 = 0.178. A very simple 64% confidence interval has upper limit, U_β ([4, 13], 0.64) = U_θ2 (13, 0.8) − L_θ1 (4, 0.8) = 0.644 − 0.217 = 0.427, where U_θ2 and L_θ1 are one-sided Clopper-Pearson limits.

This CI is at least level 0.64, because by the nestedness property of the CIs for the θ_i we can write,

$$\begin{array}{cc}\hfill P[{\theta }_2-{\theta }_1⩽U_{{\theta }_2}(X_2,0.8)-L_{{\theta }_1}(X_1,0.8)]& ⩾P\left[\{{\theta }_2⩽U_{{\theta }_2}(X_2,0.8)\}\text{and}\{L_{{\theta }_1}(X_1,0.8)⩽{\theta }_1\}\right]\hfill \\ \hfill & =P[{\theta }_2⩽U_{{\theta }_2}(X_2,0.8)]P[L_{{\theta }_1}(X_1,0.8)⩽{\theta }_1]\hfill \\ \hfill & ⩾\left(0.8\right)\left(0.8\right)=0.64.\hfill \end{array}$$

This CI for β is illustrated in the upper quadrants of Figure 1. The level curve θ₂−θ₁ = U_β ([4, 13], 0.64) = 0.427 is represented by the dotted lines, and the gray areas represent the set, {θ₂ ⩽ U_θ2 (13, 0.8) and L_θ1 (4, 0.8) ⩽ θ₁}. The left graph is represented in the (θ₁ ×θ₂)-space with the corresponding lower limit levels (a) provided on the top, and the upper limit levels (b) provided on the right. The right graph is represented in the (a × b)-space with the corresponding θ values displayed on the left and bottom. The area of the gray rectangle in the right graph is 0.64 representing the nominal level.

Figure 1.

Plots of simple 64% upper one-sided confidence limits for θ₂ − θ₁ with sample proportions ${\widehat{\theta }}_1=4∕11$ and ${\widehat{\theta }}_2=13∕24$. Top graphs depict U_θ2 (0.8) − L_θ1 (0.8). The bottom graphs depict the CI constructed by combining two rectangles. The left graphs are plotted in the θ₁ vs θ₂ space with the associated levels for the lower limit levels (a) given on the top and the upper limit levels (b) given on the right. The right graphs are plotted on the a vs b space with the θ₁ and θ₂ axes adjusted accordingly. The dotted lines represent the level curve θ₂ − θ₁ = 0.427 (top) or 0.396 (bottom), the upper one-sided confidence limit for θ₂ − θ₁, and the points represent the sample proportions. The right gray areas are 0.64, and pictorially represent the nominal level.

To obtain a lower U_β value, we can combine two gray rectangles as depicted in the lower graphs of Figure 1. Let U_β (x, 0.64) = max_i {U_θ2 (x₂, b_i) − L_θ1 (x₁, a_i)}, where 0 < a₁ < a₂ < 1 and 1 > b₁ > b₂ > 0. For U_β in this form, the coverage is at least q_nom = a₁b₁ + a₂b₂ − a₁b₂ (that is, the area of the gray regions in the right bottom graph). A formal statement of this is given in Theorem 1 (Section 4). For the lower graphs of Figure 1 we use a₁ = 0.6, a₂ = 0.8, b₁ = 0.9 and b₂ = 0.5, so that q_nom = 0.64. For this confidence limit, U_β = 0.396, which is smaller than the value of 0.427 of the upper graphs. Notice the lighter rectangles in the bottom quadrants of Figure 1 do not touch the dotted line at the corner, so there is room for improvement. That is, if we extend the lighter rectangle to the left, we can reduce the height of the darker rectangle; we can then shift the level curve θ₂ − θ₁ = 0.396 to the “southeast” (i.e., θ₂ − θ₁ = c, where c < 0.396), producing a narrower confidence interval.

We can continue adding more rectangles, but in a smarter way such that the corners of the rectangles touch the dotted line at the U_β value. For example, suppose we posit a value for U_β and values for 0 = a₀ < a₁ < a₂ < a₃ < · · · < a_k . Then as long as U_β is not too small or the a_i values are not too close to 0 or 1, we can solve for the b_i values such that U_β = U_θ2 (x₂, b_i) − L_θ1 (x₁, a_i). The nominal level, q_nom, is the gray area in the right panels of Figure 2. Theorem 1 in Section 4 shows that $q_{nom}={\sum }_{i=1}^k(a_i{b}_i-a_{i-1}{b}_i)$, and that the CIs achieve at least that nominal level of coverage. In Figure 2 we do this by positing U_β values of 0.30. For the top graphs we use 9 rectangles and get q_nom = 0.606, which is less than our target of 0.64. But if we increase the number of rectangles to 98 (bottom graphs), we get q_nom = 0.654 > 0.64.

Figure 2.

Plots of 64% upper one-sided confidence limits for θ₂ − θ₁ with sample proportions ${\widehat{\theta }}_1=4∕11$ and ${\widehat{\theta }}_2=13∕24$. Top graphs depict use 9 rectangles (a = 0.1, 0.2, … , 0.9), while the bottom graphs use 98 rectangles (a = 0.02, 0.03, .04, … , 0.99). The associated b values are chosen so that U_θ2 (b) − L_θ1 (a) equals 0.30. The right gray areas represent the nominal level and are 0.606 (top) and 0.654 (bottom). As with Figure 1, the left graphs are plotted in the θ₁ vs θ₂ space with the associated levels for the lower limit levels (a) given on the top and the on the upper limit levels (b) given on the right. The right graphs are plotted on the a vs b space with the θ₁ and θ₂ axes adjusted accordingly. The dotted lines represent the upper one-sided confidence limit for θ₂ − θ₁ and the points represent the sample proportions.

The panel in the lower right of Figure 2 shows that there is now little room for improvement, since there is not much white space below and to the right of the dotted line, and 0.654 is close to the nominal level of 0.64. The melded CIs are equivalent to finding the dotted line, and its corresponding U_β , such that the area under the dotted curve on the a vs b plot is exactly 0.64. For this example, this value is U_β = 0.292, much improved over the original 0.427. We next provide these statements in a more general way (i.e., allowing other functions besides the difference, and not just the binomial case), but there are essentially no new conceptual ideas needed for applying the method more generally.

4. Some General Theorems

We now gather the motivating ideas into two general theorems and propose another about power. The theorems are for the one-sided upper interval; the one-sided lower is analogous and is not presented.

Theorem 1

Define g(·, ·) with monotonicity constraints as in Section 2. Let 0 = a₀ < a₁ < a₂ < · · · < a_k < 1, and 1 > b₁ > b₂ > · · · > b_k > 0, and $q_{nom}={\sum }_{i=1}^k(a_i-a_{i-1})b_i$, and $u\left(\text{X, a, b}\right)=\text{max}\{g(s,t):L_{{\theta }_1}({\text{X}}_1,a_i)⩽sandt⩽U_{{\theta }_2}({\text{X}}_2,b_i),fori=1,\dots ,k\}$.

Then

$$P_{\text{x}}[g({\theta }_1,{\theta }_2)⩽u\left(\text{X, a b}\right)]⩾q_{nom}.$$ (5)

The theorem is proven in Web Appendix C

We relate this theorem to the melded CIs by the following.

Theorem 2

For each data vector, x, the value U_β (x, q) of equation 2 gives the infimum value of u (x, a, b) such that q_nom ⩾ q over all possible vectors a and b as defined in Theorem 1.

The theorem is proven in Web Appendix D

Theorems 1 and 2 suggest that the melded CIs guarantee coverage when each of the single sample CIs guarantee coverage. That conjecture has not been rigorously proven. Although Theorem 1 holds for any fixed a and b, the values of a and b that give the infimum value of u (x, a, b) in Theorem 2 depend on x. So to rigorously show guaranteed coverage, we need to show an inequality analogous to expression 5, except allowing a and b to depend on X. Despite this lack of rigor, in every example studied in the paper, the evidence fully supports the conjecture.

For any confidence interval or series of hypothesis tests, we want not just guaranteed coverage and controlled type I error rates, but tight CIs and powerful tests. To show that the melded CIs are a good strategy in this respect, we turn to the case when each of the individual CIs that are melded together are asymptotically equivalent to standard normal theory confidence intervals.

Theorem 3

Let $L_{{\theta }_i}^Z({\text{X}}_i,1-q)=U_{{\theta }_i}^Z({\text{X}}_i,q)={\widehat{\theta }}_i\left({\text{X}}_i\right)+\frac{{\widehat{\sigma }}_i\left({\text{X}}_i\right)}{\sqrt{n_i}}{\Phi }^{-1}\left(q\right)$ be asymptotically normal, i.e., $\sqrt{n_i}\left\{{\widehat{\theta }}_i\left({\text{X}}_i\right)-{\theta }_i\right\}\to N(0,{\sigma }_i^2)$, and assume that ${\widehat{\theta }}_1,{\widehat{\theta }}_2,{\widehat{\sigma }}_{1}and{\widehat{\sigma }}_2$ converge almost surely to θ₁, θ₂, σ₁, and σ₂, respectively. Suppose that

$$\begin{array}{cc}\hfill & \sqrt{n_i}\{L_{{\theta }_i}({\text{X}}_i,1-\alpha )-L_{{\theta }_i}^Z({\text{X}}_i,1-\alpha )\}\stackrel{a.s.}{\to }0\text{and}\hfill \\ \hfill & \sqrt{n_i}\{U_{{\theta }_i}({\text{X}}_i,1-\alpha )-U_{{\theta }_i}^Z({\text{X}}_i,1-\alpha )\}\stackrel{a.s.}{\to }0.\hfill \end{array}$$

If g has continuous partial derivatives, then the melded CIs using L_θi and U_θi have asymptotically accurate coverage probabilities and are asymptotically equivalent to applying the delta method on the function $g({\widehat{\theta }}_1,{\widehat{\theta }}_2)$; i.e., treating $g({\widehat{\theta }}_1,{\widehat{\theta }}_2)$ as asymptotically normal with mean g(θ₁, θ₂) and variance

$${\left(\frac{\partial g(s,t)}{\partial s}{\mid \phantom{\mid }}_{s={\theta }_1,t={\theta }_2}\right)}^2\left(\frac{{\sigma }_1^2}{n_1}\right)+{\left(\frac{\partial g(s,t)}{\partial s}{\mid \phantom{\mid }}_{s={\theta }_1,t={\theta }_2}\right)}^2\left(\frac{{\sigma }_2^2}{n_1}\right).$$

We can apply Theorem 3 to situations for which the one-sample intervals are asymptotically normal, such as the binomial case of Section 5. For a proof of the theorem and how it applies to the binomial case, see Web Appendix E.

5. Normal Case

Let X_i = [Y_i1, … , Y_ini ] be independently distributed $N({\theta }_i,{\sigma }_i^2)$ for i = 1, 2. Let ${\stackrel{‒}{y}}_i$ and $s_i^2$ be the usual sample mean and unbiased variance estimate from the ith group. Consider first the case with known variances. Then $L_{{\theta }_i}({\text{x}}_i,q)={\stackrel{‒}{y}}_i-\frac{{\sigma }_i}{\sqrt{n_i}}{\Phi }^{-1}\left(q\right)$. Thus, $L_{{\theta }_i}({\text{x}}_i,A)~N\left({\stackrel{‒}{y}}_i,\frac{{\sigma }_i^2}{n_i}\right)$ and $U_{{\theta }_i}({\text{x}}_i,A)~N\left({\stackrel{‒}{y}}_i,\frac{{\sigma }_i^2}{n_i}\right)$ as well. When g(θ₁, θ₂) = θ₂ − θ₁ then $N\left({\stackrel{‒}{y}}_2-{\stackrel{‒}{y}}_1,\frac{{\sigma }_1^2}{n_i}+\frac{{\sigma }_2^2}{n^2}\right)$ and $U_{\beta }({\text{x}}_{\beta },1-\alpha )={\stackrel{‒}{y}}_2-{\stackrel{‒}{y}}_1+{\Phi }^{-1}(1-\alpha )\sqrt{\frac{{\sigma }_2^1}{n_1}+\frac{{\sigma }_2^2}{n_2}}$, which are equivalent to the CIs that match the uniformly most powerful (UMP) one-sided tests (see e.g., Lehmann and Romano, 2005, p. 90).

Now suppose the ${\sigma }_i^2$ are unknown and not assumed equal. Then the usual one-sample t− based confidence intervals at levels a and b give,

$$L_{{\theta }_1}({\text{x}}_1,a)={\stackrel{‒}{y}}_1-\frac{s_1}{\sqrt{n_1}}{t}_{n_1-1}^{-1}\left(a\right)\text{and}{U}_{{\theta }_2}({\text{x}}_2,b)={\stackrel{‒}{y}}_2+\frac{s_2}{\sqrt{n_2}}{t}_{n_2-1}^{-1}\left(b\right)$$ (6)

where $t_d^{-1}$ is the qth quantile of a central t-distribution with d degrees of freedom. By the probability integral transform and with A and B uniform, $T_1=t_{n_1-1}^{-1}\left(A\right)\text{and}{T}_2=t_{n_2-1}^{-1}\left(B\right)$ are t random variables. Then the 100(1 − 2a) melded CI for θ₂ − θ₁ is the ath and (1 − a)th quantiles of g (L_θ1 (x₁, A), U_θ2 (x₂, B)). This is equivalent to the Behrens-Fisher interval (Fisher, 1935). Thus, a test based on that interval would give significance whenever the Behrens-Fisher solution declared the two means significantly different. The coverage of the Behrens-Fisher interval is generally not exactly equal its nominal value, but is thought to be conservative. Robinson (1976) conjectured and supported through extensive calculations that the test based on the Behrens-Fisher solution retains the type I error rate. As far as we are aware (see also Lehmann and Romano, 2005, p. 415), the first proof of this retention of the type I error rate was Balch (2012), which used Dempster-Shafer evidence theory (see e.g., Yager and Liu, 2008) and his newly developed confidence structures. (Note: the rigor of Balch’s proof may be similar to the relationship of Theorem 1 and 2 to our conjecture, because the A in Balch’s Confidence-Mapping Lemma would typically depend on the data, and this is not explicitly accounted for in Balch’s proof.) Theorem 1 and 2 of this paper provide additional support for this claim.

6. Binomial Case

Suppose X_i ~ Binomial(n_i, θ_i). Then using the usual exact (i.e., guaranteed coverage for all values of θ_i, but possibly conservative for many values of θ_i) one-sided intervals for a binomial (Clopper and Pearson, 1934), we have L_θi (x_i, A) ~ Beta(x_i, n_i − x_i + 1) and U_θi (x_i, B) ~ Beta(x_i + 1, n_i − x_i), where A and B are uniform, and for notational convenience we extend the definition of the beta distribution to include point mass distributions at the limits, so Beta(0, j) is a point mass at 0 and Beta(i, 0) is a point mass at 1 for i, j > 0. We can obtain new exact confidence intervals for the difference: θ₂ − θ₁, the ratio: θ₂/θ₁, or the odds ratio: {θ₂(1 − θ₁)} / {θ₁(1 − θ₂)} by choosing the appropriate g.

We illustrate the calculations for the data in Section 3 and the difference, g(θ₁, θ₂) = θ₂ −θ₁, but using a more conventional confidence limit of 95%. Recall that ${\widehat{\theta }}_1=4∕11\text{and}{\widehat{\theta }}_2=13∕24$. First, we run the Monte Carlo calculation, with m = 10⁶ replications. For the lower limit, we use the k^th largest (k = 0.025m) out of m pseudo-random samples of T_L2 − T_{U 1}, where T_L2 ~ Beta(13, 12) and T_{U 1} ~ Beta(5, 7), giving −0.2322. Similarly, for the upper limit we use the (m − k + 1)^th (see Efron and Tibshirani, 1993, p. 160) largest out of m pseudo-random samples of T_{U 2} − T_L1, where T_{U 2} ~ Beta(14, 11) and T_L1 ~ Beta(4, 8), giving 0.5263. The one-sided p-values are the proportion of the T_L2 that are less than T_{U 1}, giving p_L(0) = 0.2703, and the proportion of the T_{U 2} that are greater than T_L1, giving p_U (0) = 0.9114. Alternatively, we could use the numeric integration calculation. Using the relationship between one-sided p-values and confidence limits,

$$p_L\left({\beta }_0\right)=P_{A,B}[L_{{\theta }_2}\left(B\right)-U_{{\theta }_1}⩽{\beta }_0]=P[T_{L2}⩽{\beta }_0+T_{U1}]={\int }_0^1{F}_{L2}(t+{\beta }_0)f_{U1}\left(t\right)dt,$$

where F_L2 is the cumulative distribution of T_L2, and f_{U 1} is the density function of T_{U 1}. Then using a root solving function, we find the value of β₀ such that p_L(β₀) = 0.025, giving −0.2321. Analogously, we solve p_U (β₀) = 0.975 for β₀ using numeric integration to get 0.5262. Using numeric integration, the one-sided p-values for testing β₀ = 0 are p_L(0) = 0.2706 and p_U (0) = 0.9110, giving a two-sided p-value of 2p_L(0) = 0.541.

Note that the associated p-values for testing the one-sided equality of the θ_i (i.e., p_L(0) and p_U (0) for the difference, or generally equations 3 or 4) are equivalent to the one-sided p-values using Fisher’s exact test. This equivalence has been shown in the context of the Bayesian analysis of a 2 × 2 table by Altham (1969). Because of this equivalence the type I error rate is bounded at the nominal level when testing one-sided tests that θ₁ ⩽ θ₂ or θ₁ ⩾ θ₂.

In order to test the coverage, we performed extensive numerical calculations. For any fixed n₁ and n₂ we calculated all the possible melded upper 95% confidence limits. Then, using those upper limits, we calculated the coverage for all (101)² values of θ₁ and θ₂ in {0, 1/100, 2/100, … , 1}. We repeated this calculation for all n₁, n₂ ∈ {1, 2, … , 100}. We repeated these steps for the differences, ratios, and odds ratios. We found that the coverage was always at least 95%. Because of the symmetrical nature of the problem, this implies 95% coverage for the lower limits as well. Thus, it appears that these melded confidence intervals guarantee coverage.

This problem is the widely studied 2 × 2 table with one margin (namely, the sample sizes) fixed. There is no consensus on the best inferential method for this situation. Some argue that conditioning is merited (Yates, 1984, see discussion), but others argue that the unconditional test is preferred because it is generally more powerful in this case (Lydersen et al., 2009). An issue is that if you fix the significance level, then the discreteness of the conditional distribution will typically make the conditional inferences less powerful than the unconditional ones. Some argue for conditioning by noting that fixing the significance level is not needed or scientific (Upton, 1992), or that we condition on the closely related Poisson problems without controversy (Little, 1989). If we remove the discreteness problem by the impractical use of randomization, then a conditional test, the randomized version of Fisher’s exact test, is the uniformly most powerful unbiased test (see Lehmann and Romano, 2005, p.127).

Since our melded confidence limits match the one-sided Fisher’s exact test as mentioned above, the melded confidence limits allow conditional-like inferences for the difference and ratio, whereas previously they have only been available in practice for the odds ratio. Additionally, the melded CIs are much faster to calculate than the unconditional intervals because the unconditional intervals require searching over the space of the nuisance parameter (see e.g., Chan and Zhang, 1999).

7. Poisson Case

Suppose X_i ~ Poisson(n_iθ_i) for i = 1, 2, where the mean n_iθ_i is the rate, θ_i, times the time at risk, n_i. Suppose we are interested in testing $H_0:g({\theta }_1,{\theta }_2)=\frac{{\theta }_2}{{\theta }_2}⩽r$. As with the binomial case, the UMPU test is a randomized one, and practically, we use a non-randomized version of it. In this practical test, we condition on X₁ + X₂; then when θ₂ = rθ₁ we have X₁ | X₁ + X₂ ~ Binomial $\left(X_1+X_2,\frac{n_1}{n_1+r{n}_2}\right)$ (see e.g., Lehmann and Romano, 2005). We reject when X₁ is large and the p-value is

$$p_b(x_1,x_2)=\sum _{i=x_1}^{x_1+x_2}\left(\begin{array}{c}\hfill x_1+x_2\hfill \\ \hfill i\hfill \end{array}\right){\left(\frac{n_1}{n_1+r{n}_2}\right)}^i{\left(1-\frac{n_1}{n_1+r{n}_2}\right)}^{x_1+x_2-i}.$$

We show in Web Appendix F that p_b is equivalent to the melded p-value based on the standard one-sample exact Poisson intervals (Garwood, 1936).

The advantage of the melded intervals is that we may get intervals for the difference in the θ_i. The difference may be more important for measuring public health implications of interventions, since it can be translated into how many lives are affected (see e.g., Chan and Wang, 2009). For example, halving the relative risk from a baseline disease rate of 2% is very different from a public health perspective than if the baseline rate is 20%. Conversely, changing the risk by decreasing the rate of a disease by 1% affects a similar number of people regardless of whether the baseline risk is 2% or 20%. As with the binomial case, the unconditional exact method is much more difficult to calculate because one needs to search over the nuisance parameter space. There are approximate and quasiexact methods available (Chan and Wang, 2009), but no conditional exact method. Because of Theorems 1 and 2, we suspect that the melded CIs retain nominal coverage, and they are easy to calculate. Full exploration of that option and the comparison with the best competitor is left to future work.

8. Difference in Medians

Several methods have been proposed for CIs on the difference in medians from two-samples for non-censored responses. First, assuming that the two distributions represent continuous responses and differ only by a location shift, then the method of Hodges and Lehmann (1963) provides CIs on the difference in medians that guarantee coverage. However, the Hodges-Lehmann CIs can have far less than nominal coverage if either assumption does not hold, as will be shown. Second, the nonparametric bootstrap is valid asymptotically and does not require the shift assumption (Efron and Tibshirani, 1993). Other asymptotic methods require the continuity assumption and allow different types of censoring and will not be discussed further (Su and Wei, 1993; Kosorok, 1999). We create melded CIs for this situation, using single sample CIs derived by inverting the sign test (see e.g., Slud et al., 1984). In Web Appendix G, we derive the lower (equation 15) and upper (equation 16) one-sided confidence limit functions that guarantee coverage even for discrete distributions. These one-sample CI functions may return either −∞ (for the lower limit) or ∞ (for the upper limit), and the melded CI may give (−∞, ∞) if the sample size is too small. For example, in the continuous case with equal sample sizes in the two groups, we need at least 7 in each group to get finite 95% CIs. This is more restrictive than the Hodges-Lehmann procedure, which requires at least 4 in each group for that situation to get finite 95% CIs.

We compare the melded CIs to the Hodges-Lehman CIs and nonparametric percentile bootstrap CIs that uses 2000 replications. We simulate five scenarios, with 10,000 data sets for each scenario with n_i = 20 or n_i = 100 in each sample. Let F_i be the distributions for group i, i = 1, 2, and let N (µ, σ²) denote a normal distribution with mean µ and variance σ². The five scenarios are:

Normals: null case, F₁ = F₂ = N (0, 1);

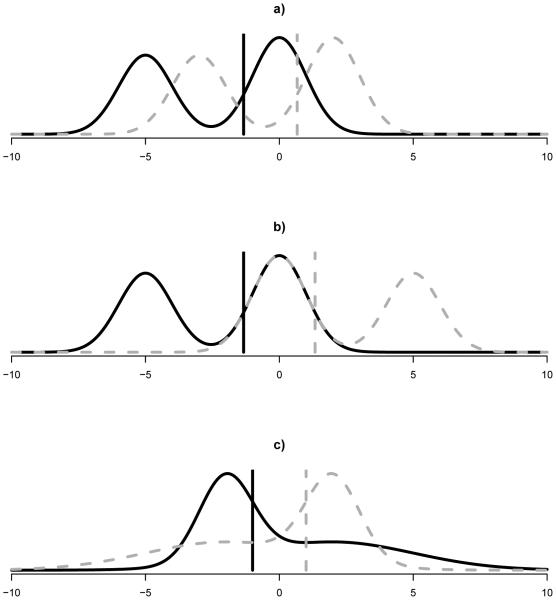
Figure 3a: shift case, F₁ = 0.55 · N (0, 1) + 0.45 · N (−5, 1) (median=−1.335) and F₂ = 0.55 ·

Figure 3.

Mixture of Normal Distributions for median simulations. Sample 1 is black solid, sample 2 is gray dotted, vertical lines are medians.

N (2, 1) + 0.45 · N (−3, 1) (median=0.665);

Figure 3b: asymmetric continuous case 1, F₁ = 0.55 · N (0, 1) + 0.45 · N (−5, 1) (median=−1.335) and F₂ = 0.55 · N (0, 1) + 0.45 · N (5, 1) (median=1.335);

Figure 3c: asymmetric continuous case 2, F₁ = 0.5 · N (−2, 1) + 0.5 · N (2, 9) (median= −1.000) and F₂ = 0.5 · N (−2, 9) + 0.5 · N (2, 1) (median=1.000);

Poissons: discrete and asymmetric case, F₁ is Poisson with mean 2.6 (median=2), and F₂ is Poisson with mean 2.7 (median=3).

The simulation results are given in Table 1. When the continuous and shift assumptions are met (Normals and Figure 3a), the Hodges-Lehman CIs have coverage near the nominal 95%, while in the other cases where those assumptions are not met, the Hodges-Lehmann CI has poor coverage that becomes worse as the sample size increases. In those latter cases, because the assumptions do not hold, the Hodges-Lehmann CIs on the shift are not measuring the difference in medians, and applying the method in those scenarios would lead to incorrect confidence intervals. The bootstrap does reasonably well in most situations, but does not appear to have proper coverage for Figure 3b (when n_i = 20 per group) and the Poissons case (even when n_i = 100). Generally, the melded CIs have wider CIs than the Hodges-Lehmann and the bootstrap CIs, but this wideness ensures simulated coverage of at least the nominal level for all scenarios studied. Thus, if the priority is guaranteed coverage regardless of sample size or distributional assumptions, then the melded CIs are recommended.

Table 1.

Simulated Coverage for nominal 95% confidence intervals for difference in medians. The five scenarios are described in the text, but briefly: Normals is a null case with both groups standard normal, Figures 3a - 3c are mixtures of normals denoting a shift (Figure 3a) or asymmetric mixtures (Figures 3b and 3c), and Poissons are Poisson with means 2.6 and 2.7. Bolded values are significantly less than the nominal 95%.

Description	n per group	Percent Coverage H-L	Percent Coverage Bootstrap	Percent Coverage Melded	Ratio of Median CI Lengths (Melded/H-L)	Ratio of Median CI Lengths (Melded/Bootstrap)
Normals	20	95.1	96.7	99.2	1.51	1.27
	100	95.1	96.4	97.6	1.35	1.09
Figure 3a	20	94.9	96.4	99.0	2.44	1.20
	100	95.2	96.6	97.8	4.18	1.09
Figure 3b	20	47.4	92.4	97.5	2.31	1.20
	100	0.6	95.0	96.7	3.69	1.09
Figure 3c	20	74.7	95.7	98.8	1.42	1.26
	100	17.0	95.8	97.3	1.08	1.10
Poissons	20	87.5	90.3	100.0	2.50	2.00
	100	57.0	91.8	100.0	4.00	2.00

9. Inferences Between Survival Distributions at a Fixed Time for Right Censored Data

The logrank test or weighted logrank tests are popular for testing for differences in survival distributions because of their good power under proportional hazards models or accelerated failure time (AFT) models (see e.g., Kalbfleisch and Prentice, 2002, Chapter 7). In some situations those models do not fit the data well. For example, an aggressive new treatment may lead to substantial mortality immediately after initiation, but can increase survival compared to the standard treatment if the patient survives the first few weeks of treatment (see e.g., Figure 4c). In this case the AFT models do not fit, and a more useful and relevant test is a difference comparison in survival after a fixed amount of time, for example, 1 year after randomization to treatment. Another example is plotted in Figure 4a. Suppose 30% of individuals have a serious version of a disease and die within the first year, while the other 70% have a less serious version and survive longer. Suppose a new treatment prolongs the life of those with the serious version for a short period (less than a year) but does not change that of the others. The logrank test may show significance for the new treatment, but the new treatment is not really curing patients for the long term. A better test may be to test for significant differences at one year.

Figure 4.

Survival Distributions for Simulations, control arm is dotted gray, treatment arm is solid black. The survival distributions are compared at time 1.0.

Klein et al. (2007) studied several two-sample tests for comparing survival estimates at a fixed time. They concluded that the test based on the normal approximation on the complementary log log (CLL) transformation of the Kaplan-Meier survival estimator, estimating the variance for each sample with Greenwood’s formula and the delta method (see equation 3 of that paper) was generally the best at retaining the Type I error rate. We call this the CLL test, and it can fail to retain the type I error rate with small samples and/or heavy censoring. Further, the CLL test cannot be used if the Kaplan-Meier estimator for either one of the groups is equal to 0 or 1 at the fixed test time.

Thus, if we are interested in comparing survival at a fixed time in a small sample case with heavy censoring, the CLL may not be a good test, especially if a conservative procedure is desired, such as in a regulatory setting. As an alternative, we can use the melded confidence intervals based on the beta product confidence procedure (BPCP) for each survival distribution (Fay et al., 2013). The BPCP was designed to guarantee central coverage for survival at a fixed point, and bounds the type I error rate in situations where alternative CIs (including the bootstrap) fail to do so. Thus, the BPCP is a good choice when guaranteed coverage is important with small samples. Further, it has no requirement that the Kaplan-Meier estimators for each sample be between 0 and 1. Using the method of moments implementation of the BPCP, we can create the random variables associated with the BPCP limits using beta distributions. Because the BPCP reduces to the Clooper-Pearson intervals when there is no censoring, the melded confidence limits in this case reduce to the Fisher’s exact test when testing the equality of the survival distributions (see Section 6).

For the simulations, we model the failure times of the two groups as mixture distributions. We consider 4 different pairs of mixture distributions, with survival distributions given by Figure 4, each with either moderate or heavy censoring. We let the number in each group (n_i) be 50 or 100. We simulate 10,000 data sets per condition. Details of the simulation are given in Web Appendix H.

The results are given in Table 2. We divide up the missed coverage into low (test arm has lower survival than control arm) and high (test has higher survival). We use 95% confidence limits so we expect 2.5% error for each side at the nominal level. Data sets with the CLL tests undefined (due to the Kaplan-Meier from either group being equal to 0 or 1 when time is 1) were considered non-rejections in the table. With heavy censoring for model b, there is 33.8% undefined. In most other cases with n_i = 50 there is 2 to 4% undefined. So this is a major practical disadvantage in a clinical trial, where the primary test should be specified in advance. The coverage under null hypotheses (models a and b) can be very inflated with heavy censoring, with upper error about 10% instead of the nominal 2.5%.

Table 2.

Simulated Percent that Reject S₀(1) = S₁(1) at the one-sided 2.5% level. Survival models a and b are null models so simulated percent should be 2.5%, and bolded values for those models are significantly larger than 2.5% (at the two-sided 0.05 level). Models described by Figure 4 and Web Appendix H.

ni	Model	Censoring	meld low	meld high	CLL low	CLL high	CLL, % Undefined
50	a	moderate	0.28	0.43	2.69	2.12	0.00
50	a	heavy	0.01	0.00	2.07	9.97	3.34
50	b	moderate	0.23	0.68	1.78	2.50	2.13
50	b	heavy	0.00	0.19	0.00	9.64	34.92
50	c	moderate	0.00	51.78	0.00	83.31	0.11
50	c	heavy	0.00	0.68	0.00	58.56	6.71
50	d	moderate	0.00	99.96	0.00	97.94	2.06
50	d	heavy	0.00	41.07	0.00	92.15	4.67
100	a	moderate	0.63	0.76	2.94	2.56	0.00
100	a	heavy	0.01	0.04	3.01	7.04	0.51
100	b	moderate	0.51	0.78	2.74	2.51	0.08
100	b	heavy	0.00	0.29	0.05	5.20	19.81
100	c	moderate	0.00	93.58	0.00	98.47	0.00
100	c	heavy	0.00	6.85	0.00	86.08	3.19
100	d	moderate	0.00	100.00	0.00	99.96	0.04
100	d	heavy	0.00	84.47	0.00	97.97	0.87

The melded CI method estimated type I error rate is substantially smaller than the nominal type I error rate in all cases simulated. This leads to reduced power compared to the CLL (see model c). This is because with heavy censoring there are very few observations at risk at time=1, so that in each arm the BPCP confidence limits can get very conservative, and conservativeness of the CI associated with each arm naturally propagates to conservativeness of the melded CIs. Conversely, the anti-conservativeness of the CIs based on the asymptotic normal approximation of the complementary log-log transformation in this heavy censoring situation leads to the anti-conservativeness of the CLL tests.

This is only a preliminary assessment of how the melded confidence interval performs. It appears to be a promising approach when a conservative test is required, although it clearly has low power for some parameters we considered. This may reflect the fact that inference at a fixed time point is fraught with difficulty when there is considerable censoring. Finally, note that because the beta product confidence procedure on the survival distribution may be inverted to get one-sample confidence intervals on the median with right censoring (see Fay et al., 2013, Section 6.1), we can use this procedure to get melded CIs for the difference in medians with right censoring. This once again illustrates the flexibility of the melded confidence interval approach.

10. Connections to the Confidence Distribution Method

The confidence distribution (CD) is a frequentist distributional estimator of a parameter. For example, consider the case where we have an exact one-sided CI for continuous data, where the coverage associated with the one-sided upper confidence limit, U_θi (X_i, q), is q for all q ∈ (0, 1). In this case T_Ui ≡ U_θi (x_i, A) is a CD random variable, and its cumulative distribution function at t is H_U (x_i, t) ≡ $U_{{\theta }_i}^{-1}$(x_i, t). We call H_U (x_i, ·) the CD. It can be used similarly to other distribution estimators like the bootstrap or the posterior distribution. For example, the middle 100q% of the distribution is a 100q% central confidence interval for any q. This application is circular, since we derive the CD from the CI process, then use the CD to get back the CIs. The modern definition of a CD avoids the circular reasoning by defining a CD as a function having two properties: (i) for each x_i, H(x_i, t) is a cumulative distribution for T_i, and (ii) at the true value θ_i, H(X_i, θ_i) is uniform. Importantly, the CD has other uses besides estimating CIs, like estimating the parameter itself or combining information on a parameter from independent samples (see Xie and Singh, 2013; Yang et al., 2014). The latter application is similar to what the melded CI for the continuous case does, it takes the CD random variable for θ₁ and melds it with the CD random variable for θ₂ to create a CD-like random variable for β that is used to create a CI for β.

For the continuous case with exact CIs, we could have equivalently defined the CD random variable as T_Li ≡ L_θ (x_i, 1 − A) with distribution H_Li(x_i, t) = 1 − $L_{{\theta }_i}^{-1}$(x_i, t), since H_U (x_i, t) = H_L(x_i, t) ≡ H(x_i, t) so that T_Ui = T_Li ≡ T_i. Unfortunately, applying the CD method to discrete data is not straightforward because for CIs with guaranteed coverage we generally have H_U (x_i, t) ≠ H_L(x_i, t) and there is not one clear distribution to define as the CD. Further, for discrete data H(X_i, θ_i) cannot be a uniform distribution.

The melded CIs are one way to generalize the CD approach to handle two-sample discrete small sample situations (for another approximate way see Hannig and Xie, 2012). We can generalize by defining the upper and lower CDs as H_U (x_i, t) and H_L(x_i, t), respectively, representing the cumulative distributions of T_Ui and T_Li evaluated at t. For each x_i, the upper and lower CDs are each a cumulative distribution, and at the true value of $\theta ,H_U({\text{X}}_i,\theta )\stackrel{sto}{⩽}A\stackrel{sto}{⩽}{H}_L({\text{X}}_i,\theta )$, where A is a uniform random variable, and $Y_1\stackrel{sto}{⩽}{Y}_2$ implies $Pr[Y_1⩽t]⩾Pr[Y_2⩽t]$ for all t. When we create the upper melded confidence limit for g(θ₁, θ₂), we use the lower CD for θ₁ and the upper CD for θ₂ in g(·, ·) to lead to more conservative coverage.

To ensure valid confidence intervals from CDs on functions of parameters in the continuous case, we require monotonicity (see Xie and Singh, 2013, p.14). In a similar way, for melded CIs we require g(θ₁, θ₂) to meet the monotonicity constraints (see Web Appendix A). If g(·, ·) does not meet these monotonicity constraints, then the resulting interval may not guarantee coverage. For example, the ratio of two parameters is not monotonic in the denominator if the parameter in the numerator is non-zero and the denominator crosses zero. For the ratio of normals, if one performs the melded confidence interval method despite the assumption violation on g(·, ·), then an anonymous reviewer of this paper has shown that the coverage can be either conservative or anti-conservative (see also Xie and Singh, 2013, example 6).

11. Discussion

We have proposed a simple confidence interval procedure for inferences in the two-sample problem. Our melded CI can be interpreted as a generalization of the confidence distribution approach. We take frequentist distributional estimators of single-sample parameters and combine them using a monotonic function to create two-sample confidence intervals that appear to guarantee coverage. Although we are unable to rigorously prove that the melded CI method controls error rates (see discussion after Theorem 2 in Section 4), several lines of additional argument suggest that it does. The first is the remarkable fact that it reproduces accepted tests and intervals in many settings examined (binomial, normal, Poisson, Behrens-Fisher problem). Second, extensive numerical calculations in the binomial case and further simulations in two other situations (difference in medians and difference in survival distributions) failed to find any situation where the melded CIs had less than nominal coverage.

In addition to reproducing some well-accepted tests and confidence intervals, the melding method has yielded new intervals. For example, in the binomial case, it gives confidence intervals for the relative risk and risk difference that match the inferences from Fisher’s exact test. Previously, such intervals were readily available only for the odds ratio. Thus, the new CI for the risk difference could be used as the primary analysis in the regulatory setting where risk difference is traditionally used, such as a new antibiotic is being compared to an existing one in a non-inferiority trial. The melded CI method is so general, it can easily generate a two-sample procedure in any setting where there is a one-sample procedure that guarantees coverage, as illustrated in the methods presented in Sections 8 and 9. We briefly mention two more possible applications. Consider a randomized clinical trial measuring the effect of treatment compared to placebo, and suppose there is an accepted confidence procedure for that treatment effect. If one wants to determine if there is a difference in treatment effects between two subgroups (say between men and women), then the melded CI approach can answer that question. Next consider two trials that measure vaccine efficacy for two different vaccines both designed to protect against the same disease. Each trial estimates vaccine efficacy by comparing the ratio of infection rates of the vaccinated to the unvaccinated. If the trials are done on similar populations and both use the same control vaccine, a comparison of the two vaccine efficacies can be done using melded CIs. So we see that the potential for developing useful new two-sample tests and intervals from exact one-sample procedures makes the melded confidence interval approach an appealing addition to the applied statistician’s toolkit.

12. Supplementary Materials and Software

Web Appendices referenced in Sections 2,4,7,8, 9, and 10 are available with this paper at the Biometrics website on Wiley Online Library. Additionally, the R scripts used in the simulations are available at the Biometrics website on Wiley Online Library. Two R packages, exact2×2 and bpcp, are available on CRAN (http://cran.r-project.org/) and have functions to calculate the binomial melded CIs (binomMeld.test in exact2×2), the difference in medians melded CIs (mdiffmedian.test in bpcp), and the difference in survival distribution melded CIs (bpcp2samp in bpcp).