Regional Annular Geometry in Patients with Mitral Regurgitation: Implications for Annuloplasty Ring Selection

Abstract

Background

The saddle shape of the normal mitral annulus has been quantitatively described by several groups. There is strong evidence that this shape is important to valve function. A more complete understanding of regional annular geometry in diseased valves may provide a more educated approach to annuloplasty ring selection and design. We hypothesized that mitral annular shape is markedly distorted in patients with diseased valves.

Methods

Real-time 3-dimensional echocardiography was performed in patients with normal mitral valves (n=20), ischemic mitral regurgitation (IMR, n=10) and myxomatous mitral regurgitation (MMR, n=20). Thirty-six annular points were defined to generate a 3D model of the annulus. Regional annular parameters were measured from these renderings. Left ventricular inner diameter (LVIDd) was obtained from 2D echocardiographic images.

Results

Annular geometry was significantly different between the three groups. The annuli were larger in the MMR and the IMR groups. The annular enlargement was greater and more pervasive in the MMR. Both diseases were associated with annular flattening though the regional distribution of that flattening was different between groups. LVIDd was increased in both groups. However, relative to the LVIDd, the annulus was disproportionately dilated in the MMR group.

Conclusion

Patients with MMR and IMR have enlarged and flattened annuli. In the case of MMR, annular distortions may be the driving factor leading to valve incompetence. These data suggest that the goal of annuloplasty should be the restoration of normal annular saddle shape and that the use of flexible, partial and flat rings may be ill advised.

Introduction

Levine first reported the three dimensional (3D) saddle shape of the mitral valve annulus in 1987 [1]. For 15 years the finding received little attention until our group described the influence of annular saddle shape on leaflet stress [2, 3]. Since that time we have continued to refine the description of regional mitral annular geometry using 3D echocardiography [4–7]. This information has, to some extent, been useful in guiding annuloplasty ring selection as well as annuloplasty ring design [8–12].

Despite the increasing understanding of the normal annulus, very little has been reported regarding the shape of pathologic valves. Lack of understanding of diseased annuli still hinders annuloplasty ring selection for mitral repair. Many surgeons prefer the use of flexible rings or bands with the idea that such devices preserve annular shape. We hypothesize that regional annular geometry in the two most common forms of mitral valve disease, myxomatous degeneration and ischemic mitral regurgitation, is profoundly abnormal. Therefore, the goal of annuloplasty should be restoration of normal annular systolic saddle shape and not shape preservation.

Patients and Methods

Patients

Intraoperative transesophageal real-time 3D echocardiography (3DE) was performed for 20 patients with myxomatous mitral degeneration (MMR group), 10 patients with ischemic mitral regurgitation (IMR group) and 20 patients with normal mitral valves who were undergoing non-mitral valve cardiac surgery (normal group). Full volume data sets of the annulus were acquired with an iE-33 platform (Philips Medical, Andover, MA) equipped with a X7-2t TEE matrix-array transducer. In the MMR group, 19 patients had posterior leaflet prolapse, and one patient had bi-leaflet prolapse. All patients underwent implantation of an annuloplasty device (complete rigid ring = 15, partial flexible band = 5). Leaflet pathology was addressed using one or combination of the following techniques: triangular resection (n=15), quadrangular resection/ sliding plasty (n=2), leaflet inversion/plication (n=3), chordal transfer or neochord implantation (n=3). All IMR patients had coronary artery disease and discrete LV wall motion abnormality (Inferior = 6, anterolateral = 4). Six patients had significant leaflet restriction. Nine of ten valves were repaired and one valve had to be replaced. Normal patients had no evidence of mitral valvular abnormality. The research protocol was approved by the University of Pennsylvania School of Medicine Institutional Review Board.

Image Segmentation

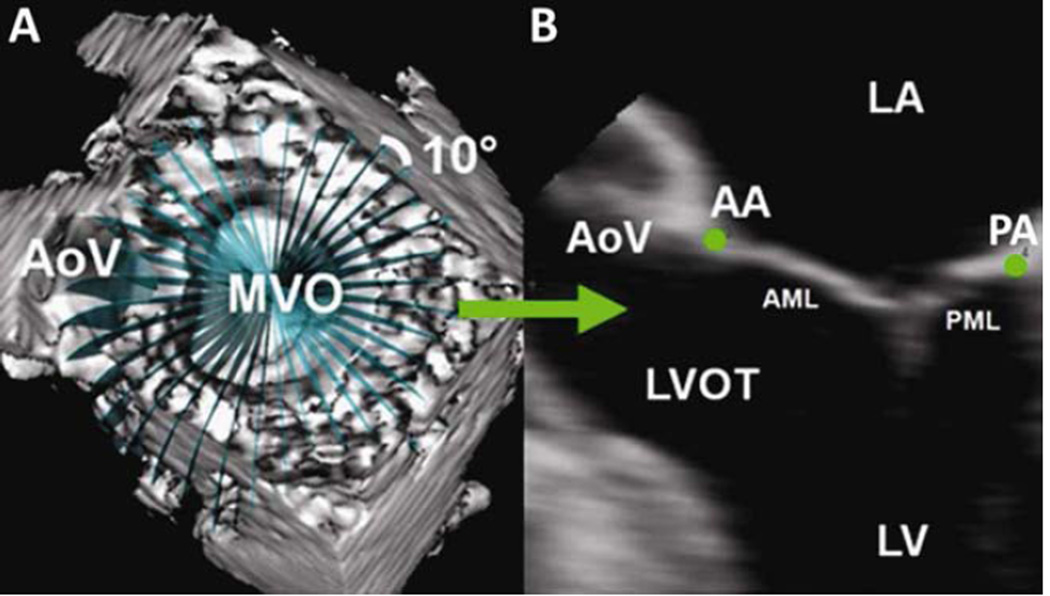
Annular analysis was performed at midsystole as previously described [6]. Each data set was exported to Echo-View 5.4 (TomTec Imaging, Munich, Germany) for image analysis. Two annular points were interactively marked in 18 cross-sectional planes separated by 10 degrees around the annular circumference (Figure 1). Anterior and posterior commissures (AC, PC) were defined at the junction between the anterior and posterior leaflets. The X, Y, Z coordinates were exported from TomTec to Matlab software (The Mathworks, Natick, MA) to perform quantitative reconstruction.

Figure 1. Technique for Annular Segmentation.

Panel A: 3D echocardiographic volume containing the mitral valve with cross-sectional planes at 10° increments; Panel B: Representative 2D cross-section with green dots representing the selected annular points. AA: anterior mitral annulus; AML: anterior mitral leaflet; AoV: aortic valve; LA: left atrium; LV: left ventricle; LVOT: left ventricular outflow tract; MVO: mitral valve orifice; PA: posterior mitral annulus; PML: posterior mitral leaflet

Annular Analysis

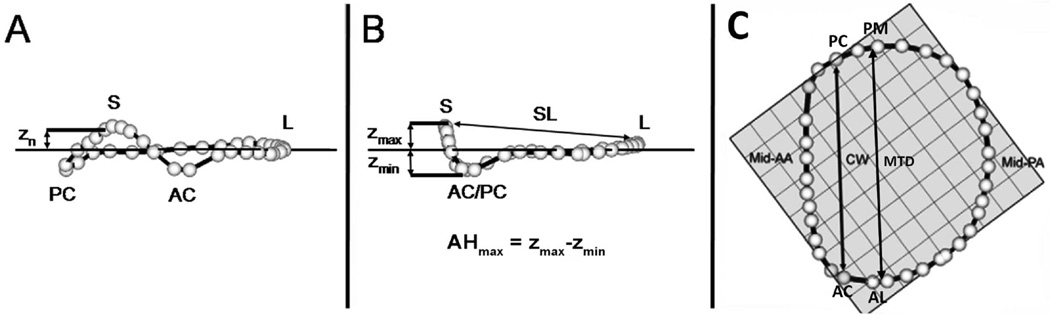
The annulus was reconstructed by interpolation at 1° intervals around the annular circumference. The annular model was rotated such that the valve orifice plane was aligned with the x-y plane. Under these geometric conditions, the z coordinate (z_n) of each annular point was equal to its distance to the plane of the mitral valve (Figure 2a). Regional AH for each data point (AH_n) was then defined as z_n - z_min, where z_min was the lowest point on the mitral annulus. Maximal AH (AH_max) was defined as z_max -z_min, where z_max was the highest point on the mitral annulus.

Figure 2. Annular landmarks.

Oblique (A) Intercommissural (B) and Transvalvular (C) views of a 3D annular model depicting the 36 annular data points (white spheres). Panel A: calculation of annular height at a given annular point (Z_n). Panel B: determination of maximum Annular Height (AH_max) and septolateral diameter (SL). Panel C: determination of intercommissural width (CW) and the mitral transverse diameter (MTD). AA = Anterior annulus, AC = Anterior commissure, AL = Anterolateral Annulus, L= Lateral annulus, PA = Posterior annulus, PC = Posterior commissure, PM= Posteromedial annulus, S = Septum, Z_max = Maximumheight, Z_min = Minimum height. The least squares plane is depicted by a horizontal line in panel A, B and the check boxes in panel C.

Several anatomic landmarks were identified (Figure 2 a,b,c). The septum (S) was identified as the anterior horn of the annulus at the aortic valve, corresponding to z_max. AC and PC co-ordinates were superimposed on to the annulus rendering to divide the annulus into anterior and posterior portion. The lateral annulus (L) was located at the middle of the posterior annulus circumference. Finally, with the annular model rotated such that the commissures were aligned on a plane of constant x, the anterolateral and posteromedial (AL and PM) annular points are the locations of maximal and minimal y-value.

Septolateral (SL) diameter was defined as the distance separating data points S and L. Commissural Width (CW) was defined as the distance between commissures. Mitral transverse diameter (MTD) was defined as the distance separating AL and PM. Mitral annular area (MAA) was defined as the area enclosed by the 2D projection of an annular data set onto its corresponding least squares plane. Total mitral annular circumference and the lengths of the anterior and posterior annuli (LAA, LPA) were calculated.

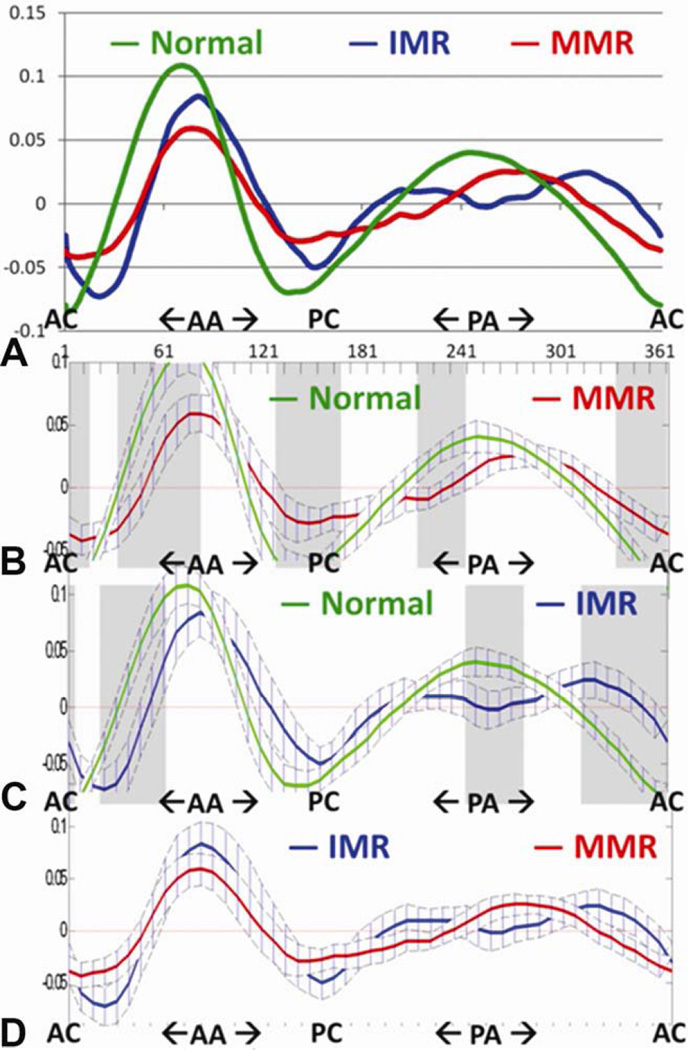
As previously described [2, 4], we define the parameter AH_maxCWR = AH_max/CW *100% to quantify global annular nonplanarity. To facilitate the comparison of regional annular nonplanarity between subjects we define regional AH_nCWR = AH_n/CW *100%. The Cartesian coordinates for each point in a given annular model were converted to cylindrical coordinates (r, Θ, z), and the data set was translated in the z direction and rotated around the MV axis (Θ direction) so that the anterior commissure was located at Θ = 0, and the center of mass of each annulus was located at z=0. Values of AH_n for each point in a given data set were then recalculated in this fixed frame of reference. AH_nCWR was plotted as a function of rotational position (Θ) on the mitral annulus for each data set (Figure 3).

Figure 3.

Panel A depicts mean annular height normalized to commissural width (AHCWR) plotted as a function of rotational position around the annulus for each group. The three curves are different in overall shape from each other (p<0.001 by functional ANOVA). The areas where they differ are indicated by the shaded gray bars. (Panel B): Normal vs myxomatous (MMR): Significant differences (p<0.05) at positions 1–15, 30–85, 125–165, 210–240, 330–360. (Panel C): Normal vs. ischemic (IMR): Significant differences (p<0.05) at positions 1–5, 20–60, 240–275, 310–360. (Panel D): IMR vs MMR: No significant difference at any individual position. AA = anterior annulus, AC = Anterior commissure, PA= posterior annulus, PC = Posterior commissure

Creation of Hybrid annular models

The center of gravity of all the annular models within each group were translated to the origin and aligned such that the sum of least square planes coincided with the XY plane. The annuli are rotated such that both commissures for each valve lay on a plane of constant X value (different for each annulus). Radial distance was calculated from the origin to the projection of each annular point on the XY plane. Annular height was calculated as previously described. The radial distance and annular height were interpolated as a function of rotational position on the annulus by repeating this process at 1° interval around the annulus. A mean radial distance and annular height was calculated by averaging these parameters at each rotational position for all annuli within the group. The annular points such obtained were then re-converted to XYZ co-ordinates and rendered in 3D space to generate the hybrid annulus.

Left Ventricle internal dimension and annular ratio

Left Ventricular (LV) internal dimension in diastole (LVIDd) was obtained from 2D-echocardiography images obtained at the same intraoperative exam. To assess degree of annular dilation relative to LV dilation, ratio of annular parameter (MAA, MAC, CW, MTD, SL) to LVIDd was calculated for the IMR and MMR group, and normalized to the normal group.

Statistical Analysis

Regional parameters were compared using pair wise student t-test. Rotational height curves were compared using functional ANOVA.

Results

Patient characteristics

There was no difference in severity of MR in the IMR and the MMR group. The ejection fraction in the IMR group was significantly depressed as compared to the normal and the MMR group (Table 1).

Table 1.

Patient Demographics

	Normal (n=20)	MMR (n=20)	IMR (n=10)
Age	64.7 ± 15.8	58.3 ± 9.3	67.4 ± 11.3 a
Ejection Fraction (%)	60.6 ± 12.4	58.9 ± 9.1	26.5 ± 17.2 a,b
Mitral regurgitation grade	0.6 ± 0.4	3.6 ± 0.6 c	3.3 ± 0.8 b

Mean ± SD

^a= p<0.05 IMR vs. MMR

^b= p<0.05 Normal vs. IMR

^c= p<0.05 Normal vs. MMR

Annular size and shape

Annular parameters are summarized in Table 2. MAA is increased in both the IMR and the MMR group as compared to normal group, however interesting differences are noted between the IMR and the MMR group. First, only the septolateral diameter is enlarged in the IMR group, but the intercommissural diameter is similar to the normal group. In the MMR group both the septolateral and the intercommissural diameters are increased, resulting in significantly larger annular area, not only when compared to the normal group, but also when compared to the IMR group. Secondly, both the anterior and posterior annular circumference is increased in the MMR group. Only the posterior annular circumference is increased in the IMR group.

Table 2.

Annular Parameters

	Normal (n=20)	MMR (n=20)	IMR (n=10)
Annular height (mm)	7.18 ± 1.65	6.0 ± 1.14 a	7.6 ± 1.8 b
Commissural width (mm)	31.44 ± 3.45	44.50 ± 6.00 a	33.0 ± 3.6 b
Annular height:   Commissural width   ratio	22.90 ± 5.06	12.90 ± 3.65 a	23.2 ± 5.9 b
Septolateral dimension   (mm)	28.62 ± 3.29	37.39 ± 6.05 a	34.6 ± 5.0 c
Maximum transverse   diameter (mm)	34.55 ± 4.00	45.25 ± 6.15 a	38.9 ± 3.0 b,c
Mitral annular area (mm2)	784.49 ± 159.34	1344.47 ± 367.68 a	1067.7 ± 178.5 b,c
Anterior circumference (mm)	39.44 ± 5.18	61.17 ± 9.59 a	41.1 ± 5.0 b
Posterior circumference   (mm)	63.01 ± 9.06	72.81 ± 11.83 a	81.6 ± 7.4 b,c
Total circumference (mm)	102.45 ± 10.80	133.98 ± 17.84 a	122.8 ± 9.4 c

Mean ± SD

^a= p<0.05 Normal vs. MMR

^b= p<0.05 IMR vs. MMR

^c= p<0.05 IMR vs. MMR

The abnormal shape of the annulus in the MMR and the IMR groups is illustrated by the analysis of regional annular height (Figure 3). Regions of annular flattening are prominent in both disease process but more diffuse in the cases of MMR. The MMR annuli are flatten most prominently at the “anterior horn” near the junction of the A1 and A2 regions. Additionally the MMR annuli are flatter at both commisures and the junction of the P2–P3 segments. The IMR annuli are flatten at the AC, A1 region as well as the mid segment of P2 and all of P3.

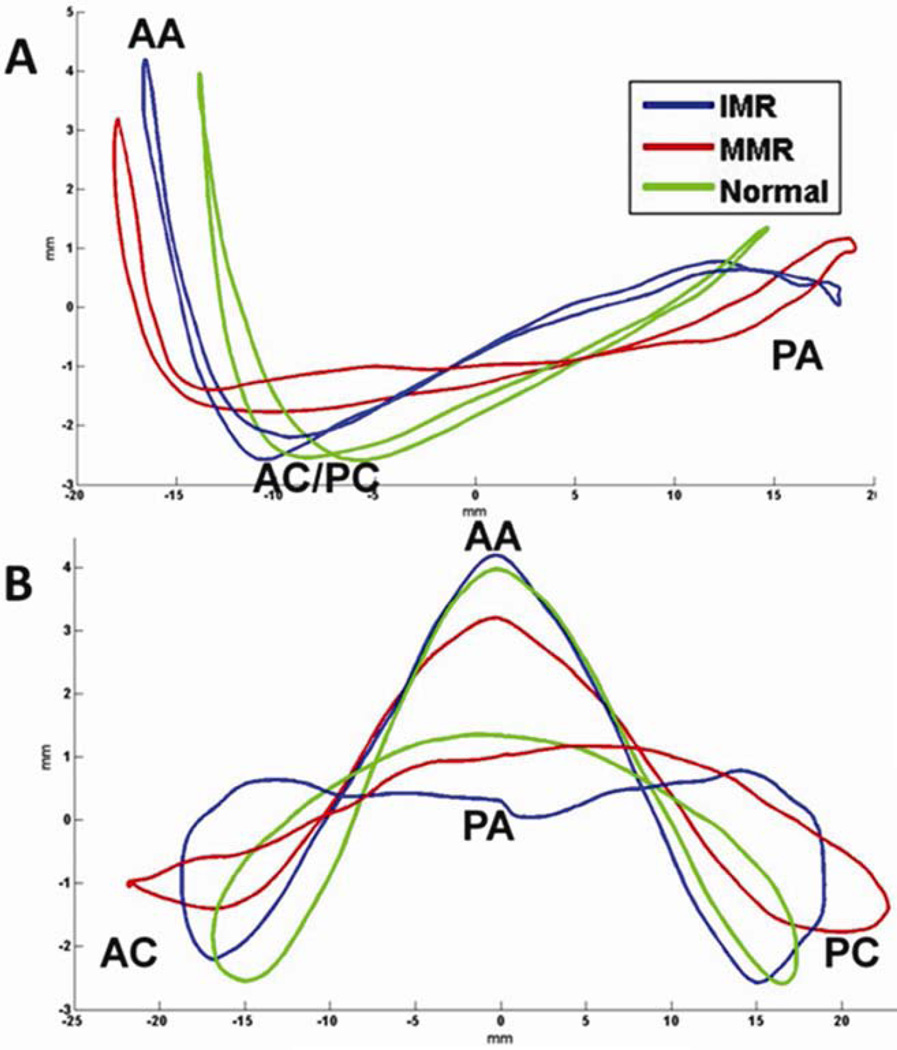
AH_max and AH_maxCWR were markedly reduced in the MMR patients when compared to normal. Interestingly these global assessments of annular nonplanarity were not significantly different from normal in the IMR group. This finding underscores the value of the regional assessment of mitral annular nonplanarity in assessing the geometrical distortions of pathologic valves. If only the global parameters had been assessed the conclusion of this study would have been completely different. These annular distortions are also evident in the hybrid annular models as illustrated in Figure 4.

Figure 4.

Transcommissural (Panel A) and anteroposterior (Panel B) views of hybrid annular models for the normal, ischemic mitral regurgitation (IMR), and myxomatous mitral regurgitation (MMR) groups. AA= Anterior annulus, AC = Anterior commissure, PA = posterior annulus, PC = Posterior commissure

LV- Annular size relationship

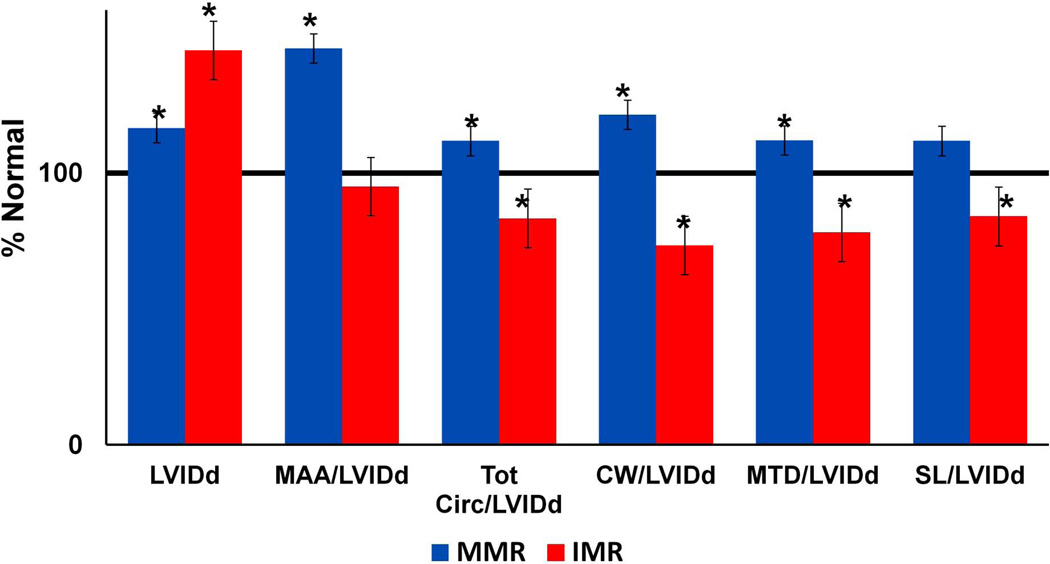
Compared to the normal group, diastolic left ventricular internal dimension (LVIDd) was increased in both the IMR and the MMR group. However, the degree of annular enlargement relative to the LVIDd was significantly higher in the MMR group as compared to the normal group. On the contrary, in the IMR group the ratio of annular size to LV size was less compared to normal values (Figure 5) indicating the LV had undergone a greater degree of dilatation.

Figure 5.

Left ventricle diameter (LVIDd) and ratio of left ventricle diameter to various annular size parameters for the ischemic (IMR) and the myxomatous (MMR) groups are depicted as a percent of the normal group measurements (horizontal black line). Error bars = standard error.

Comment

When taken together the reported annular and LV distortions shed light on the pathogenesis of both diseases. In cases of IMR the annulus is dilated to a lesser degree relative to the LV when compared to normal. The annulus also undergoes significant regional flattening. In the IMR group the annular distortions (enlargement and flattening) were more pronounced along the posterior portion of the annulus. These findings are consistent with what is known about the pathogenesis of IMR. That is, a regional infarct produces regional LV distortion which subsequentenly causes regional annular distortions and leaflet tethering which results in MR [8,13–15].

In MMR patients, the annular enlargement and flattening are both greater and more pervasive when compared to the IMR group. The annular enlargement is also out of proportion to the LV enlargement, suggesting the annular distortions occur prior to and independent of the ventricular enlargement. It raises the possibility that the MMR annuli are congenitally enlarged and flat, and these annular distortions maybe the primary cause of the MMR. Annular flattening and enlargement has been shown to decrease leaflet curvature resulting in increased leaflet stress [2, 3, 16] and strain [17, 18], which in MMR annuli over time, may cause myxomatous tissue degeneration, chordal rupture and MR. A recent study by Lee et.al. supports this theory [19]. Using similar 3D echocardiographic techniques this group evaluated patients with normal valves, mitral valve prolapse with varying degrees of MR as well as patients with MR and no leaflet prolapse. They found that annular flattening in MMR patients had a strong association with progressive leaflet billowing, chordal rupture and MR. In their study patients with AH_maxCWR of < 15% were 7 times more likely to have chordal rupture and MR.

The work by Lee et. al. is also very interesting in that its mean measurements for most annular parameters in all groups (normal, MMR and IMR) are within millimeters (for some parameters fractions of millimeters) of the measurements reported in this study. The two studies taken together bear strongly on annuloplasty ring selection.

For almost 45 years there has been little consensus regarding the most appropriate annuloplasty ring design. Early on the major debate was whether the ring should be rigid [20, 21] or flexible [22, 23]. As more centers became experienced with repair, the debate expanded to include the relative efficacy of complete [24, 25] vs. partial rings [26, 27]. During the early 2000s, the concept of disease specific annuloplasty briefly became vogue [28, 29]. Despite all the conjecture and opinion there was no quantitative support for the use of any device over another. In 2002 our group was the first to propose the efficacy of saddle shape annuloplasty in reducing leaflet stress and potentially increasing repair durability [2]. Other groups have expanded our work to demonstrate that saddle shape preservation decreases leaflet [16, 17] and annular strain [13, 30] as well as increasing leaflet coaptation [31].

Our results and the results of Lee et. al. indicate that in cases of MMR and IMR the annulus is significantly abnormal. This finding argues against the use of flexible and partial rings which were conceived to maintain “normal” annular geometry and function. In these disease processes there is no normal geometry to maintain. The goal of annuloplasty is to restore not maintain annular geometry.

Even more profoundly, the results of the two studies argue strongly against the use of flat annuloplasty rings. If it is true that an AH_maxCWR of less than 15% predesposes to leaflet billowing, chordal rupture and MR what does forcing an annulus to an AHCWR of 0% with a flat annuloplasty ring do to the potential for further tissue degeneration after repair?

This question becomes even more compelling in light of the growing body of evidence indicating that mitral valve repair durability is far less robust than initially reported. Longer term follow-up has revealed that between 10% and 16% of patients undergoing mitral repair for MMR will require reoperation for severe MR within 10 years [32– 34]. Even more concerning are the reports of an unexpectedly high incidence of recurrent moderate MR after repair. Several studies from experienced centers indicate that the recurrence of 2+ or greater MR is between 2% and 4% per year [35–37]. A significant number of these failures result from chordal, leaflet and suture line disruption, suggesting mechanical stress and strain to be the cause [38].

The proposed efficacy of saddle shape annuloplasty on mitral valve repair durability is speculative but compelling in light of a growing body of work by our group and others that supports the positive influence of annular saddle shape on valve stress/strain profiles and leaflet coaptation.

Table 3.

Annular dilation relative to the left ventricular dilation

	Normal (n=20)	MMR (n=20)	IMR (n=10)
Left Ventricular diastolic diameter   (LVIDd) (cm)	4.86 ± 0.61	5.66 ± 0.71 a	7.05 ± 1.11 b,c
Mitral annular area/LVIDd	1.63 ± 0.37	2.38 ± 0.58 a	1.55 ± 0.42 c
Mitral annular circumference/LVIDd	2.14 ± 0.35	2.39 ± 0.35 a	1.78 ± 0.34 b,c
Commisural width/LVIDd	0.65 ± 0.09	0.79 ± 0.12 a	0.48 ± 0.10 b,c
Maximum transverse diameter/LVIDd	0.72 ± 0.12	0.81 ± 0.12 a	0.56 ± 0.10 b,c
Septolateral dimension/LVID	0.60 ± 0.10	0.67 ± 0.12	0.50 ± 0.12b,c

Mean ± SD

^a= p<0.05 Normal vs. MMR,

^b= p<0.05 Normal vs. IMR,

^c= p<0.05 IMR vs. MMR

Abbreviations and Acronyms

AC

Anterior Commissure

AH

Annular Height

AHCWR

Annular height: Commissural width ratio

CW

Commissural width

IMR

Ischemic mitral regurgitation

L

Lateral annulus

LAA

Length of anterior annulus

LPA

Length of posterior annulus

LVIDd

Left ventricle inner diameter (diastolic)

MAA

Mitral annular area

MMR

Myxomatous mitral regurgitation

MTD

Maximum transverse diameter

PC

Posterior commissure

PM

Posteromedial annulus

S

Septum

SL

Septolateral dimension