Integrative and regularized principal component analysis of multiple sources of data

Abstract

Integration of data of disparate types has become increasingly important to enhancing the power for new discoveries by combining complementary strengths of multiple types of data. One application is to uncover tumor subtypes in human cancer research, in which multiple types of genomic data are integrated, including gene expression, DNA copy number and DNA methylation data. In spite of their successes, existing approaches based on joint latent variable models require stringent distributional assumptions and may suffer from unbalanced scales (or units) of different types of data and non-scalability of the corresponding algorithms. In this paper, we propose an alternative based on integrative and regularized principal component analysis, which is distribution-free, computationally efficient, and robust against unbalanced scales. The new method performs dimension reduction simultaneously on multiple types of data, seeking data-adaptive sparsity and scaling. As a result, in addition to feature selection for each type of data, integrative clustering is achieved. Numerically, the proposed method compares favorably against its competitors in terms of accuracy (in identifying hidden clusters), computational efficiency, and robustness against unbalanced scales. In particular, compared to a popular method, the new method was competitive in identifying tumor subtypes associated with distinct patient survival patterns when applied to a combined analysis of DNA copy number, mRNA expression and DNA methylation data in a glioblastoma multiforme study.

1. Introduction

Advances of high-throughput microarray and next-generation sequencing technologies make it possible to simultaneously measure a broad range of genome-wide alterations, such as gene expression, DNA copy numbers and DNA methylation levels in tumor samplES [1]. It is known that these genome-wide alterations are related to tumorigenesis and treatment response in a complex way [2]. As a result, integrative analysis of these alterations may lead to greater power in detecting tumor subtypes with important biological therapeutic differences [3, 4], as opposed to separate analysis on each data type, followed by a manual or ad hoc integration; this point has been observed in many studies [4, 5, 6, 7, 8].

Several integrative analysis methods have been proposed in a framework of joint probability modeling, among which a popular one is iCluster [4], based on Gaussian latent variable models related to principal components analysis [9]. For these methods, model parameters are estimated by the expectation-maximization (EM) algorithm [10] for likelihood inference. One advantage of iCluster is its simultaneous dimension reduction across all data types; that is, it projects all types of data into a common low-dimensional subspace, then clustering analysis is performed for integration. Despite the recent developments of iCluster [6, 7, 11], issues remain with respect to high computational demand and unbalanced scales with different types of data; here unbalanced scales refer to unequal units across data types. First, the EM algorithm is computationally inefficient and suffers from numerical difficulties for high-dimensional data. Second, unbalanced scales among multiple types of data may result in domination of some data type in a larger scale over other data types, which may hamper the goal of integrative analysis. Third, a distributional assumption is difficult to check and may not be met in practice, leading to poor model fitting and results.

To tackle these issues, we propose an alternative, which is computationally efficient, robust against unbalanced scales, and distribution-free. It is based on a novel implementation of integrative and regularized principle component analysis, called irPCA in what follows. It is based on regularized low rank matrix approximations to multiple types of data. To achieve robustness against unbalanced scales, effective regularization to achieve both sparsity and automatic scaling on each data type is applied. Specifically, we propose a regularized sum-of-squares criterion for multiple types of data, seeking a common set of principal components across all data types while regularizing the components’ loadings, called integrative loadings, through imposing the elastic net penalty [12], in which the L₁ and ridge penalties regularize sparsity and scaling respectively. As a result, irPCA yields both simultaneous dimension reduction across all the data types and separate feature selection and scaling for each data type; that is, it simultaneously projects all types of data to a common low-dimensional subspace, as well as regularizes each type of data to achieve separate feature selection and scaling. Interestingly, the proposed method can be efficiently implemented through the regularized low rank matrix approximation method proposed for a single type of data [13].

Besides many integrative methods that focus on clustering or dimension reduction, there also exist some ones based on joint decomposition of multiple data matrices for multi-dimensional pattern discovery. They include some generalization of matrix decomposition techniques, such as non-negative matrix factorization (NMF) [14], and partial least squares regression (PLS) [15] from one or two data types to more than two data types [16, 17, 18, 19]. Although they may not be all designed for sample clustering or dimension reduction, their main ideas on data integration are relevant and enlightening.

This article is organized as follows. The Methods section introduces the proposed method, followed by the Results section, including some simulation studies and a glioblastoma multiforme (GBM) study, in which the proposed method enables de novo discovery of three GBM subtypes associated with hierarchical survival outcomes. The Discussion section summarizes the main advantages and conclusions of the proposed method.

2. METHODS

2.1. irPCA

There is a large body of literature on principal component analysis (PCA, [20]), which seeks linear projections of the original data to a lower dimensional space while capturing major variability of the original data. A class of its variants, called sparse PCA, have been proposed to seek sparsity by setting small nonzero coefficients to zero. Jolliffe [21] considered various rotation techniques to identify sparse loading vectors in the subspace given by PCA, and Cadima and Jolliffe [22] proposed a thresholding rule to set small components of PCA loadings to be zero. Recently, sparse PCA has been obtained by regularizing or penalizing the number of non-zero loadings, including the SCoTLASS method [23] that maximizes the Rayleigh quotient of a covariance matrix based on the L₁-penalty [24]; Zou et al. [25] took a regression approach with the L₁-penalty; other approaches include [13], [26], [27].

Our method is inspired by regularized principal component analysis (rPCA) of [13], where the main idea is to regularize component loadings in singular value decomposition (rSVD). In this paper, to integrate multiple types of data, we propose an integrative and regularized principal analysis (irPCA). More specifically, let X = [X⁽¹⁾, ···, X^(S)] denote an n × (p⁽¹⁾ + ··· + p^(S)) pooled data matrix, where each X^(s); s ∈ {1, ···, S}, is one specific type of data. For a given X, we estimate an n-vector u = (u₁, ···, u_n)^T with ${\sum }_{i=1}^n{u}_i=0$ and || u ||₂= 1 and a (p⁽¹⁾ + ··· + p^(S))-vector v = (v^(1)T, ···, v^(S)T)^T minimizing a regularized sum-of-squares criterion

$$C(\mathbf{u},\mathbf{v})=\sum _{s=1}^S{\Vert {\mathbf{X}}^{(s)}-\mathbf{u}{\mathbf{v}}^{(s)T}\Vert }_F^2+\sum _{s=1}^S{P}^{(s)}({\mathbf{v}}^{(s)}),$$ (1)

where ||·||_F denotes the Frobenius norm and $P^{(s)}({\mathbf{v}}^{(s)})=2{\lambda }^{(s)}{\Vert {\mathbf{v}}^{(s)}\Vert }_1+{\alpha }^{(s)}{\Vert {\mathbf{v}}^{(s)}\Vert }_2^2$ is an elastic net penalty [12].

Next we develop an iterative algorithm to minimize (1).

Algorithm 1

Inputs: an n×(p⁽¹⁾ + ··· + p^(S)) data matrix X = [X⁽¹⁾, ···, X^(S)] and the tuning parameters λ^(s) > 0, α^(s) > 0, s ∈ {1, ···, S}.

Outputs: an n-vector û with || û ||₂= 1 and a (p⁽¹⁾ + ··· + p^(S))-vector v̂ = (v̂^(1)T, ···, v̂^(S)T)^T.

1. Initialize: apply the standard SVD to X: X = UDV^T, where U is an n × n matrix, V is a ${\sum }_{s=1}^S{p}^{(s)}\times {\sum }_{s=1}^S{p}^{(s)}$ matrix and D is an $n\times {\sum }_{s=1}^S{p}^{(s)}$ diagonal matrix with non-negative singular values on the diagonal. Then, obtain the best rank-one approximation of X as duv^T, where u and v are the first columns of U and V respectively and d is the first singular value of X on the diagonal of D. Set u_old = u.

2. Update:

   1. for each s ∈ {1, ···, S}, ${\mathbf{v}}_{\mathit{new}}^{(s)}=h^{(s)}({\mathbf{X}}^{(s)T}{\mathbf{u}}_{\mathit{old}})$ with

      $$h^{(s)}(·)=\frac{{(\mid ·\mid -{\lambda }^{(s)})}_{+}}{1+{\alpha }^{(s)}}\text{sign}(·)$$

      applied componentwise (from formula (6) of [12]), where (| · | − λ^(s))₊sign(·) is the soft-thresholding function with (·)₊ = max(·, 0) and sign(·) denoting the sign function;

   2. u_new = Xv_new/ || Xv_new ||₂ with ${\mathbf{v}}_{\mathit{new}}={({\mathbf{v}}_{\mathit{new}}^{(1)T},\cdots ,{\mathbf{v}}_{\mathit{new}}^{(S)T})}^T$.

3. Replace u_old and { ${\mathbf{v}}_{\mathit{old}}^{(s)}$, s ∈ {1, ···, S}} by u_new and { ${\mathbf{v}}_{\mathit{new}}^{(s)}$, s ∈ {1, ···, S}} respectively, then repeat Step (2) until convergence.

4. Obtain the final u_new as û and the final v_new as v̂ = (v̂^(1)T, ···, v̂^(S)T)^T.

Note that here the goal of the elastic net penalty P^(s)(v^(s)) is to seek a sparse solution v^(s) and to adjust the scales of v^(s) for each data type separately. To be specific, let g^(s)(·) = (| · | − λ^(s))₊sign(·) and then in Step 2(b) of Algorithm 1 we have that ${\mathbf{v}}_{\mathit{new}}={(\frac{g^{(1)}{({\mathbf{X}}^{(1)T}{\mathbf{u}}_{\mathit{old}})}^T}{1+{\alpha }^{(1)}},\cdots ,\frac{g^{(S)}{({\mathbf{X}}^{(S)T}{\mathbf{u}}_{\mathit{old}})}^T}{1+{\alpha }^{(S)}})}^T$, where g^(s)(·), s ∈ {1, ···, S}, are used to seek a sparse solution v_new, while 1+α^(s), s ∈ {1, ···, S}, are used to adjust the scales of different data types to avoid that u_new is dominated by some of the data types with larger scales.

The above iterative procedure obtains vectors u and v^(s) for s ∈ {1, ···, S}, which are viewed as the first integrative principal component and the corresponding integrative regularized component loading vectors respectively. Subsequent principal components and regularized loading vectors can be sequentially obtained via rank-one approximation of residual matrices, which is summarized as follows.

Algorithm 2. (irPCA)

Inputs: an n × (p⁽¹⁾ + ··· + p^(S)) data matrix X = [X⁽¹⁾, ···, X^(S)], the tuning parameters λ^(s) > 0, α^(s) > 0, s ∈ {1, ···, S} and the number of integrative principal components M.

Outputs: an n × M matrix Û_M with the mth column û_m with || û_m ||₂= 1, m ∈ {1, ···, M}, denoting the mth integrative principal component and a (p⁽¹⁾ + ··· + p^(S)) × M matrix ${\widehat{\mathbf{V}}}_M={({\widehat{\mathbf{V}}}_M^{(1)T},\cdots ,{\widehat{\mathbf{V}}}_M^{(S)T})}^T$ with the mth column ${\widehat{\mathbf{v}}}_m={({\widehat{\mathbf{v}}}_m^{(1)T},\cdots ,{\widehat{\mathbf{v}}}_m^{(S)T})}^T$ denoting the mth integrative regularized component loading vector.

1. Let ${\mathbf{X}}_{(1)}^{(s)}={\mathbf{X}}^{(s)}$ for each s ∈ {1, ···, S} and ${\mathbf{X}}_{(1)}=[{\mathbf{X}}_{(1)}^{(1)},\cdots ,{\mathbf{X}}_1^{(S)}]$. For m = 1, ···, M, sequentially perform the following steps:

   1. Apply Algorithm 1 to X_(m) with the tuning parameters λ^(s) > 0, α^(s) > 0, s ∈ {1, ···, S}, which yields û_m and ${\widehat{\mathbf{v}}}_m={({\widehat{\mathbf{v}}}_m^{(1)T},\cdots ,{\widehat{\mathbf{v}}}_m^{(S)T})}^T$.

   2. Compute the residual matrix ${\mathbf{X}}_{m+1}^{(s)}={\mathbf{X}}_{(m)}^{(s)}-{\widehat{d}}^{(s)}{\widehat{\mathbf{u}}}_m{\widehat{\mathbf{v}}}_m^{(s)T}$ with d̂^(s) = 1+α^(s) for each s ∈ {1, ···, S} and let ${\mathbf{X}}_{(m+1)}=[{\mathbf{X}}_{(m+1)}^{(1)},\cdots ,{\mathbf{X}}_{(m+1)}^{(S)}]$.

2. Let Û_M = [û₁, ···, û_M] be the first M integrative principal components, and let V̂_M = [v̂₁, ···, v̂_M] be the first M integrative regularized loading vectors.

Note that Algorithm 1 is a generalization of Algorithm 1 of [13] to integrate multiple types of data. The key here is the application of data type-specific thresholding rules h^(s)(·) to achieve data type-specific feature selection, which is necessary for multiple types of data as in iCluster in [4]. Differing from other methods, an innovation here is the use of the elastic net penalty [12], not the L₁ penalty, to achieve both feature selection and scaling.

2.2. Convergence

We now present some technical lemmas, based on which we establish the convergence of Algorithm 1.

Lemma 1

For fixed v^(s), s ∈ {1, ···, S}, the n-vector u that minimizes (1) and satisfies ||u||₂ = 1 is û = Xv/ || Xv ||₂, where v = (v^(1)T, ···, v^(S)T)^T.

Lemma 2

For fixed u, the vectors v^(s), s ∈ {1, ···, S}, that minimizes (1) are v̂^(s) = h^(s)(X^(s)Tu); s ∈ {1, ···, S}, where $h^{(s)}(·)=\frac{{(\mid ·\mid -{\lambda }^{(s)})}_{+}}{1+{\alpha }^{(s)}}\text{sign}(·)$ is applied componentwise.

Lemma 3

û and v̂ = (v̂^(1)T, ···, v̂^(S)T)^T minimizes (1) with ||u||₂ = 1, if and only if v̂ minimizes

$$-2{\Vert \mathbf{Xv}\Vert }_2+{\Vert \mathbf{v}\Vert }_2^2+\sum _{s=1}^S{P}^{(s)}({\mathbf{v}}^{(s)})$$

and û = Xv̂/||Xv̂||₂.

Theorem 1

Algorithm 1 converges and the final solution satisfies the KKT optimality condition [28].

The proofs of all the lemmas and propositions are in Appendix.

2.3. Tuning

Next we propose a cross-validation method to choose the tuning parameters in Algorithm 2, which is modified from a criterion [29] that was designed for the K-means clustering [30]. Moreover, we use the cluster reproducibility index proposed by [4] to define a prediction strength.

For a given data matrix X = [X⁽¹⁾, ···, X^(S)] and a given number of clusters K ∈ 𝒦, let ℳ × Λ × A be a set of of tuning parameters, where ℳ and 𝒦 are sets of positive integers corresponding to the candidate numbers of integrative principal components and clusters respectively, Λ ⊆ ℝ^S is the candidate set of λ and A ⊆ (ℝ⁺)^S is the candidate set of α. For each i ∈ {1, ···, n}, let X_i be the ith row of X. Our cross-validation method proceeds as follows. First, permute the sample index set V = {1, ···, n} of X randomly, then partition the permuted sample index set into two roughly equal parts. Second, randomly select one part as the test set V^te and form the test data matrix X^te with rows from {X_i: i ∈ V^te}, and the remaining one as the training set V^tr to form the training data matrix X^tr with rows from {X_j : j ∈ V^tr}. For each (M, λ, α) ∈ ℳ × Λ × A with λ = (λ⁽¹⁾, ···, λ^(S))^T and α = (α⁽¹⁾, ···, α^(S))^T, apply Algorithm 2 to X^tr and X^te separately, and then obtain ${\widehat{\mathbf{U}}}_M^{tr}=({\widehat{\mathbf{u}}}_1^{tr},\cdots ,{\widehat{\mathbf{u}}}_M^{tr}),{\widehat{\mathbf{U}}}_M^{te}=({\widehat{\mathbf{u}}}_1^{te},\cdots ,{\widehat{\mathbf{u}}}_M^{te})$. Third, assign the rows of ${\widehat{\mathbf{U}}}_M^{tr}$ and ${\widehat{\mathbf{U}}}_M^{te}$ into K clusters through a specific clustering method, such as the K-means clustering or spectral clustering [31], then let l_tr and l_te be the corresponding clustering assignments. Fourth, assign rows of ${\widehat{\mathbf{U}}}_M^{te}$ into K clusters according to l_tr; that is, assign each row of ${\widehat{\mathbf{U}}}_M^{te}$ into the closest cluster of ${\widehat{\mathbf{U}}}_M^{tr}$ defined by l_tr in terms of the Euclidean distance, and let l_te|tr denote the corresponding clustering assignment. Note that here the distance between a sample and a cluster is the minimum distance between the sample and each sample in the cluster. Finally, compute the adjusted Rand index [32] between l_te|tr and l_te as the prediction strength. Repeat the above process for a specified number of times, say T, with random permutation of the index set for each time, and choose (M̂, λ̂, α̂) ∈ ℳ × Λ × A with the highest average prediction strength.

Then, for each K ∈ 𝒦, we obtain the clustering assignment l(K) based on (M̂, λ̂, α̂), and then select K̂ ∈ 𝒦 with the highest Silhouette index [33] as the best estimate of the number of clusters, based on which we get the final estimate of the clustering assignment, say l(K̂).

3. Results

3.1. Simulation studies

This section demonstrates advantages of the proposed method over iCluster [4], naive integration by principle component analysis (PCA NI) [20], and several methods applicable to two types of data, such as partial least squares regression (PLS) [34], co-inertia analysis (CIA) [35] and canonical correlation analysis (CCA) [36], in terms of clustering accuracy, computational efficiency and robustness to unbalanced scales. Since the main purpose of this paper is for integrative analysis of multiple types of data, not limited to only two types of data, we excluded comparisons with several existing sparse (or regularized) versions of the methods for two types of data [15, 37, 38]. Additionally we did not compare the proposed method with the new version of iCluster, iCluster+ [6], because all the numerical examples involve continuous data that do not require the use of iCluster+.

3.1.1. Simulation set-ups

We build up five numerical examples based on those in [4, 7]. In these examples, for each type of data, clustering information is associated with a small number of functional variants (viewed as features), based on which one cluster can be distinguished from the other two, while the other two are still inseparable.

Case 1.1

We simulate n = 150 samples from three clusters, {1, ···, 50}, {51, ···, 100} and {101, ···, 150}, corresponding to clusters 1–3 respectively. Let S = 2, p⁽¹⁾ = p⁽²⁾ = 500. For s = 1, ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(\mu ,1)$ for i ∈ {1, ···, 50} and j ∈ {1, ···, 10}; ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(1,1)$ for i ∈ {51, ···, 100} and j ∈ {101, ···, 110}; ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(1,1)$ for the rest. For s = 2, ${\mathbf{X}}_{ij}^{(2)}=0.5{\mathbf{X}}_{ij}^{(1)}+{\epsilon }_{ij}$ where ε_ij ~ 𝒩 (0, 1) for i ∈ {1, ···, 50} and j ∈ {1, ···, 10}; ${\mathbf{X}}_{ij}^{(2)}~\mathcal{N}(\mu ,1)$ for i ∈ {101, ···, 150} and j ∈ {101, ···, 110}; and ${\mathbf{X}}_{ij}^{(2)}~\mathcal{N}(0,1)$ for the rest. Let μ = 1.5 and X = [X⁽¹⁾, X⁽²⁾].

In Case 1.1, the two types of data are correlated in the first 10 dimensions. In addition, for each data type, there are two groups of features, {1, ···, 10} and {101, ···, 110}, distinguishing one cluster from the other two.

Case 1.2 and Case 1.3 are similar to Case 1.1, except setting X = [X⁽¹⁾, 10X⁽²⁾] and X = [X⁽¹⁾, exp(X⁽²⁾)] respectively. These two examples are variations of Case 1.1 so that we can investigate the performance of an integrative clustering method in situations of unbalanced scales or non-Gaussian distributions among different data types. Note that to alleviate the problem of unbalanced scales, a simple approach is to standardize each column for each type of data to a common scale, which however may not completely solve the problem and lead to poor clustering performance, which will be studied in the Results section in detail.

Case 2 is also similar to Case 1.1, except setting μ = 3 and p⁽¹⁾ = p⁽²⁾ = 50, 000. We use this example to investigate computational efficiency of the proposed method in a high dimensional situation, in which most of the existing integrative clustering methods are computationally infeasible, e.g. due to an impractical requirement of too large computer memory space.

Case 3

We simulate n = 200 samples from four clusters, {1, ···, 50}, {51, ···, 100}, {101, ···, 150} and {151, ···, 200}, corresponding to clusters 1–4 respectively. Let S = 3, p⁽¹⁾ = p⁽²⁾ = p⁽³⁾ = 500. For s = 1, ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(\mu ,1)$ for i ∈ {1, ···, 50} and j ∈ {1, ···, 10}; ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(1,1)$ for i ∈ {51, ···, 100} and j ∈ {101, ···, 110}; ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(1,1)$ for i ∈ {101, ···, 150} and j ∈ {201, ···, 210}; ${\mathbf{X}}_{ij}^{(1)}~\mathcal{N}(0,1)$ for the rest. For s = 2, ${\mathbf{X}}_{ij}^{(2)}=0.5{\mathbf{X}}_{ij}^{(1)}+{\epsilon }_{ij}$ where ε_ij ~ 𝒩 (0, 1) for i ∈ {1, ···, 50} and j ∈ {1, ···, 10}; ${\mathbf{X}}_{ij}^{(2)}~\mathcal{N}(\mu ,1)$ for i ∈ {51, ···, 100} and j ∈ {101, ···, 110}; ${\mathbf{X}}_{ij}^{(2)}~\mathcal{N}(1,1)$ for i ∈ {101, ···, 150} and j ∈ {201, ···, 210}; ${\mathbf{X}}_{ij}^{(2)}~\mathcal{N}(0,1)$ for the rest. For s = 3, ${\mathbf{X}}_{ij}^{(3)}=0.5{\mathbf{X}}_{ij}^{(1)}+{\epsilon }_{ij}^{\prime }$ where ${\epsilon }_{ij}^{\prime }~\mathcal{N}(0,1)$ for i ∈ {1, ···, 50} and j ∈ {1, ···, 10}; ${\mathbf{X}}_{ij}^{(3)}~\mathcal{N}(\mu ,1)$ for i ∈ {101, ···, 150} and j ∈ {101, ···, 110}; ${\mathbf{X}}_{ij}^{(3)}~\mathcal{N}(1,1)$ for i ∈ {151, ···, 200} and j ∈ {201, ···, 210}; ${\mathbf{X}}_{ij}^{(3)}~\mathcal{N}(0,1)$ for the rest. Let μ = 1.5 and X = [X⁽¹⁾, X⁽²⁾, X⁽³⁾].

Case 3 is designed to investigate performance of the methods for more than two types of data. In such a situation, many methods that are designed specifically for two data types, such as PLS, CIA and CCA, cannot be directly used unless further modifications are implemented. As a result, for this case we only compare the proposed method with iCluster and PCA NI.

3.1.2. Simulation results

Simulation results for the five examples are summarized in Table 1 and Figures 1 and 2. Specifically, Table 1 shows the Rand index and adjusted Rand index values between a method’s estimated cluster assignment and the true one for each case, measuring the accuracy of an integrative clustering. Figure 1 illustrates the performance of dimension reduction for each method. Figures 2 demonstrates the feature selection performance of a method by showing the integrative loadings for each case, where in each panel the (m, s)-th entry is the integrative loading ${\widehat{v}}_m^{(s)}$ for m ∈ {1, ···, M} and s ∈ {1, ···, S}. Here “iCluster” denotes the method proposed by [4] with an L₁ penalty. To guard against confounding of different choices of the number of clusters or number of integrative principal components, here we fix the numbers of clusters at K = 3 for Cases 1.1, 1.2, 1.3 and 2, and at K = 4 for Case 3. Then let the number of integrative principal components M = K − 1, which is in agreement with the number of latent variables in iCluster. For the tuning parameter λ, we use a two-fold cross-validation for irPCA with |Λ| = 8^S, while for iCluster we let |Λ| = 8 for S = 2 and |Λ| = 35 for S = 3, which is the default setting for the tuning procedure in the R package “iCluster”. In addition, for the tuning parameter α, generally we let α^(s) = 0 for each s ∈ {1, ···, S} whenever any type of data cannot be dominated by another one. Therefore, we only use the cross-validation procedure to select α from A with |A| = 4^S for Cases 1.2 and 1.3, while letting α ^(s) = 0, s ∈ {1, ···, S}, for the rest cases. To gain an insight into computing cost, Table 1 reports the CPU time used for all the cases. Note that all the experiments were run on a PC with a single processor Intel(R) Core(TM) i7 CPU @ 3.40GHz (16G Memory), except that iCluster was run on four processors for parallel computation.

Table 1.

Sample means (SD in parentheses) of Rand index (Rand) and adjusted Rand index (aRand) between the clustering assignment by each method and the true assignment, as well as the running time (RT), for the five cases based on 100 simulations. Note ‘- -’ denotes that based on the current computer setting the corresponding method is not available due to excessive memory demand.

Case	n, p	Method	Rand	aRand	RT (min)
1.1	n = 150 p(1) = p(2) = 500	irPCA	.992 (.007)	.982 (.016)	.206 (.074)
		iCluster	.987 (.010)	.971 (.024)	24.03 (2.801)
		PCA NI	.923 (.024)	.826 (.056)	.004 (.001)
		PLS	.762 (.063)	.464 (.143)	.027 (.008)
		CIA	.888 (.030)	.746 (.069)	.008 (.002)
		CCA	.954 (.065)	.896 (.147)	.007 (.001)
1.2	n = 150 p(1) = p(2) = 500	irPCA	.970 (.067)	.934 (.150)	1.886 (.204)
		iCluster	.801 (.070)	.557 (.152)	25.92 (.484)
		PCA NI	.732 (.027)	.398 (.060)	.004 (.000)
		PLS	.762 (.063)	.464 (.143)	.024 (.005)
		CIA	.888 (.030)	.746 (.069)	.007 (.001)
		CCA	.900 (.054)	.775 (.124)	.006 (.001)
1.3	n = 150 p(1) = p(2) = 500	irPCA	.833 (.147)	.670 (.257)	1.616 (.180)
		iCluster	.689 (.127)	.375 (.170)	26.18 (.376)
		PCA NI	.570 (.123)	.243 (.150)	.003 (.001)
		PLS	.709 (.044)	.347 (.097)	.018 (.001)
		CIA	.725 (.071)	.456 (.119)	.006 (.000)
		CCA	.796 (.071)	.566 (.138)	.005 (.000)
2	n = 150 p(1) = p(2) = 50, 000	irPCA	1 (0)	1 (0)	12.29 (.449)
		iCluster	- -	- -	- -
		PCA NI	.625 (.030)	.157 (.068)	1.002 (.010)
		PLS	- -	- -	- -
		CIA	- -	- -	- -
		CCA	.556 (.006)	.002 (.013)	.556 (.006)
3	n = 200 p(1) = p(2) = p(3) = 500	irPCA	.979 (.037)	.944 (.100)	2.902 (.374)
		iCluster	.973 (.046)	.928 (.046)	325.0 (51.49)
		PCA NI	.952 (.018)	.871 (.048)	.012 (.001)

Figure 1.

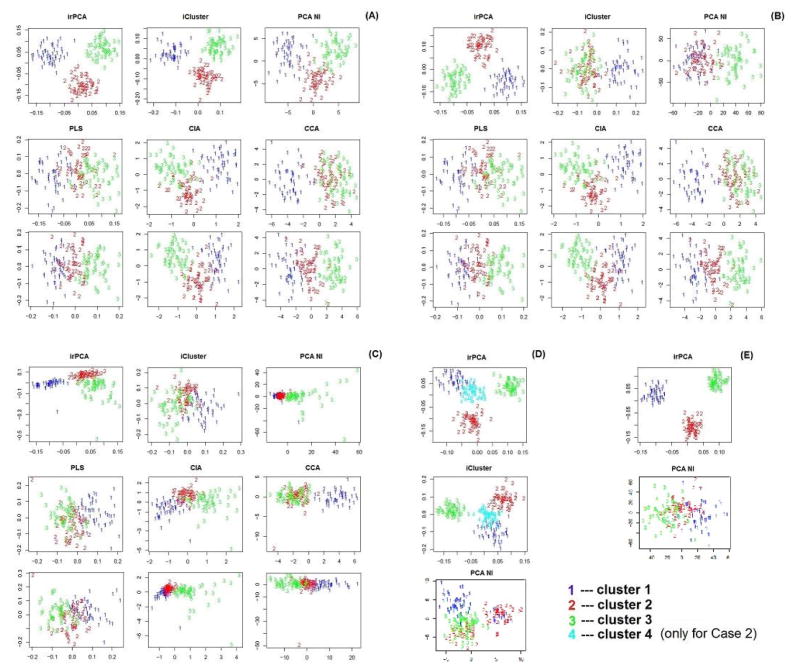
Scatter plots of the observations in the first two dimensions after dimension reduction by each method for a representative dataset in each simulation case. Panels A–E correspond to Cases 1.1–1.3, Case 3 and Case 2 respectively.

Figure 2.

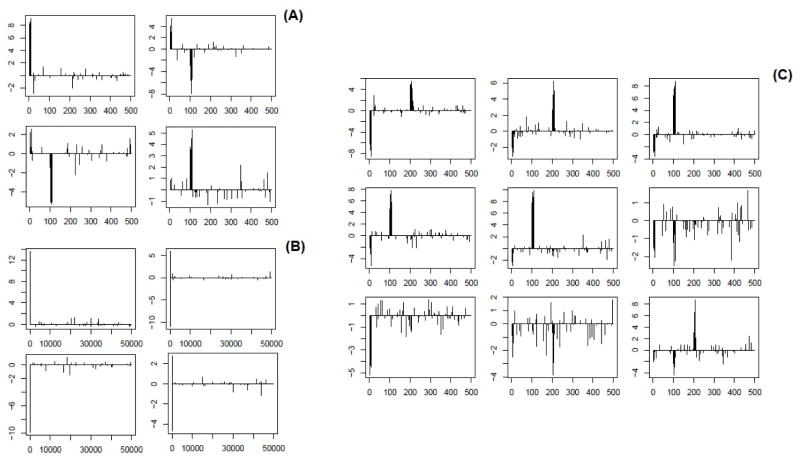
The values of integrative loadings ${\widehat{v}}_m^{(s)}$ versus m ∈ {1, ···, M} for s ∈ {1, ···, S} for a representative dataset in simulation Cases 1.1 (panel A), 2 (B) and 3 (C) respectively.

Below we discuss the results for each case in details. For Case 1.1, as indicated by Table 1, irPCA and iCluster outperform their competitors in terms of accuracy of clustering, measured by the Rand index and adjusted Rand index. This example was first studied in [4] to demonstrate an advantages of iCluster over naive integration by PCA or separate PCA for each type of data. Since the scales of the two types of data are almost identical to each other, as well as both follow Gaussian distributions, this example is ideal for iCluster. Panel (A) of Figure 1 indicates that irPCA and iCluster make the three clusters much more separable than their competitors. Panel (A) of Figure 2 illustrates that the functional variants {1, ···, 10} and {101, ···, 110} are correctly sought out with high absolute loading values by irPCA, while loading values for most of the nonfunctional variants are correctly forced to be 0.

Next, the results of Cases 1.2 and 1.3 suggest that iCluster as well as naive integration may fail for data with unbalanced scales. As shown in Table 1, irPCA outperforms its competitors, partly due to the poor dimension reduction performance by its competitors. From panels (B) and (C) of Figure 1, we see that the three clusters become more or less inseparable after dimension reduction for all the methods, among which irPCA is much more robust than its competitors.

In Case 2, we investigate the performance of these methods by increasing the dimension of each data type to 50,000. In this situation, iCluster, PLS and CIA are not applicable due to their impractical requirement of computer memory space. Among the other methods, irPCA always correctly identifies the true clusters (see panel (E) of Figure 1) and successfully selects the features {1, ···, 10} and {101, ···, 110} (see panel (B) of Figure 2), while PCA NI and CCA have extremely poor clustering results as shown in Table 1.

By Case 3 we examine the clustering performance of irPCA with more than two types of data. From Table 1 and panel (D) of Figure 1, we see that irPCA performs as well as iCluster, almost perfectly identifying the true clusters. In addition, as shown in panel (C) of Figure 2, it successfully selects the features {1, ···, 10}, {101, ···, 110} and {201, ···, 210}.

Finally, as shown in Table 1, we investigate computational efficiency of these methods. PCA, PLS, CIA and CCA run much faster than irPCA and iCluster, however, with poor clustering performance. iCluster works well when the scales of different types of data are balanced, however it is much more time-consuming even when multiple cores were used. This drawback becomes much more obvious when the dimension and S increase.

These numerical results suggest that irPCA is more robust than iCluster in the presence of unbalanced scales among different types of data. Importantly, ir-PCA is much faster than iCluster, making it more competitive for high-throughput genomic data.

3.1.3. Further simulations

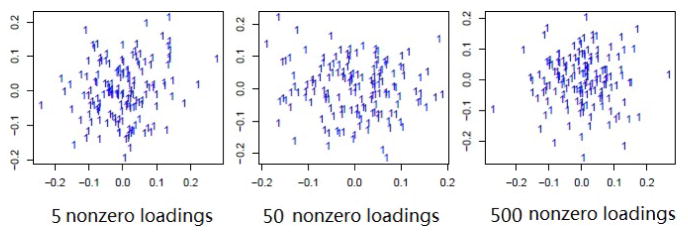
Next, we study Case 4 to investigate the performance of irPCA in the null case: there is only 1 cluster in both data types and no features define the cluster. In Case 4, we simulate n = 150 samples with S = 2, p⁽¹⁾ = p⁽²⁾ = 500 from only one cluster, where ${\mathbf{X}}_{ij}^{(s)}~\mathcal{N}(0,1)$ for each i, j and s. Specifically, we fix the number of nonzero integrative loading values for both data types as 5, 50, 500 respectively, and plot the first two dimensions after dimension reduction for a typicla dataset in Figure 3. As shown in Figure 3, it seems that all the observations belong to only one cluster no matter how many nonzero integrative loading values are used.

Figure 3.

Scatter plots of the observations in the first two dimensions after dimension reduction by irPCA for a representative dataset in simulation Case 4, where 5, 50 and 500 nonzero integrative loadings are used respectively.

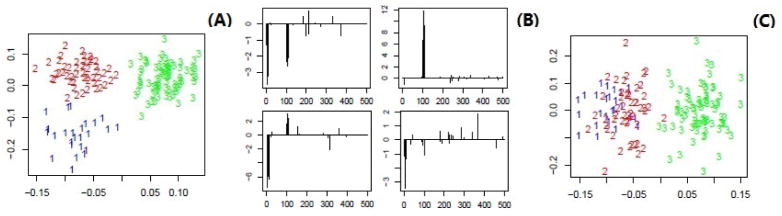
We study Case 5 to investigate the performance of irPCA in a situation with unbalanced numbers of individuals in multiple clusters. Case 5 is similar to Case 1.1 except that the numbers of individuals in the three clusters are unbalanced with values of 25, 50 and 75 respectively. Figure 4 suggests that, after dimension reduction by irPCA, the presence of three clusters is clear (Penal A); the proposed method give large integrative loading values on those features that define the clusters (Penal B). Note that in this case, data standardization is not suitable for clustering and data integration, suggested by Penal C of Figure 4 and the 3rd row of Table 2. Table 2 shows that the proposed method performs much better than iCluster in terms of identifying the true clusters, no matter whether the true number of clusters is known or not in advance.

Figure 4.

Results of irPCA for a respresentative dataset in simulation Case 5: (A) scatter plot of the observations in the first two dimensions after dimension reduction; (B) the values of the first two integrative loadings for both data types; (C) scatter plot of the observations in the first two dimensions after dimension reduction by applying irPCA to the standardized dataset.

Table 2.

Sample means (SD in parentheses) of Rand index (Rand) and adjusted Rand index (aRand) between the clustering assignment by each method and the true assignment, as well as the estimated number of clusters, based on 100 simulations. T denotes the number of cross-validation runs in the tuning part of irPCA; ‘Stand.’ denotes that the multiple types of data are standardized before an integrative analysis.

Case	n, p	Method	Rand	aRand	K̂
5	n = 150 p(1) = p(2) = 500	irPCA (K = 3, T = 1)	.976 (.047)	.949 (.101)	3 (0)
		irPCA (K = 3, T = 1, Stand.)	.905 (.126)	.797 (.272)	3 (0)
		irPCA (K = 3, T = 5)	.988 (.012)	.974 (.027)	3 (0)
		irPCA (K ∈ {2, ···, 5}, T = 1)	.966 (.057)	.925 (.130)	3.2 (.5)
		irPCA (K ∈ {2, ···, 5}, T = 5)	.969 (.046)	.932 (.103)	3.1 (.4)
		iCluster (K = 3)	.901 (.064)	.790 (.140)	3 (0)
1.1	ibid	irPCA (K = 3, T = 1, Stand.)	.866 (.136)	.698 (.306)	3 (0)
		irPCA (K ∈ {2, ···, 5}, T = 1)	.963 (.044)	.913 (.108)	3.4 (.6)
		irPCA (K ∈ {2, ···, 5}, T = 5)	.981 (.029)	.955 (.073)	3.1 (.4)

Moreover, Table 2 suggests that the proposed method performs well in correctly determining the number of clusters using the Silhouette index [33] for Cases 5 and 1.1. It also suggests that the proposed method is likely to perform better in identifying the true clusters when the fold number T of cross-validation is increased.

3.2. Application on a GBM study

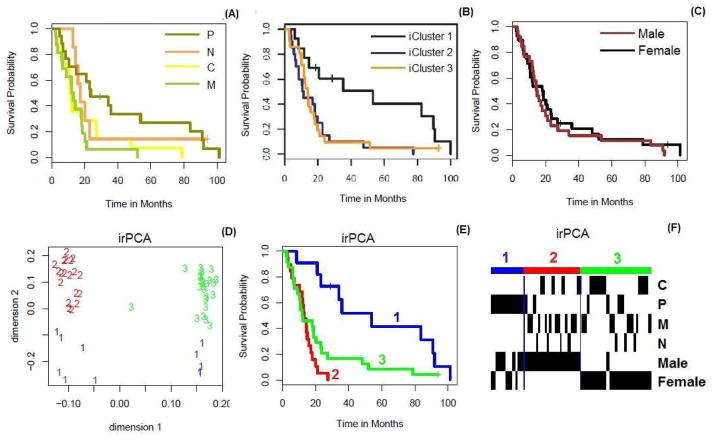
We consider a glioblastoma multiforme (GBM) dataset generated by TCGA [39] and available in the R package “iCluster”. Based on only 1,740 most variable expression levels, four distinct GBM subtypes, Proneural (P), Neural (N), Classical (C) and Mesenchymal (M), were identified [39]. The Kaplan-Meier (K-M) estimates [40] of the survival functions for the four GBM subtypes (see panel (A) of Figure 5) show that the survival probability of the Proneural subtype is higher than those of the other three subtypes, while the differences in survival among the latter three subtypes are small. Integrative analysis of gene expression data and other data may help identify subtypes with more distinguished survival outcomes. [11] performed an integrative analysis by iCluster, combining the use of DNA copy number, methylation and mRNA expression in the GBM data. They divided 55 GBM patients into three integrative clusters (iClusters 1, 2 and 3). From panel (B) of Figure 5 (originally plotted in Figure 6 of [11]), we see that iCluster 1 is associated with higher survival, while both iClusters 2 and 3 are associated with lower and similar survival. In addition, from panel (C) of Figure 5, there is nearly no survival difference between male group and female group.

Figure 5.

(A–C) K-M plots according to the gene expression subtypes (Proneural (P), Neural (N), Classical (C) and Mesenchymal (M)) of GBM, genders, clusters of iCluster, respectively. (D–F) Dimension reduction results of irPCA, K-M plot according to clusters of irPCA and associations among gene expression subtypes, genders and clusters of irPCA.

To test performance of the proposed method and to compare with iCluster, we use the same dataset of the 55 GBM patients studied in [11], in which three types of data, DNA copy numbers, mRNA expression and methylation data, are combined. Based on the result of dimension reduction by irPCA (see panel (D) of Figure 5), we divide the patients into three clusters according to the cross-validation procedure. From panels (E) and (F) of Figure 5, we see that cluster 1 (labeled in blue) is associated with the highest survival, which mainly includes the Proneural (P) subtype; cluster 2 (labeled in red) is associated with lowest survival, and the survival of cluster 3 is intermediate between those of the other two clusters. In contrast to the three clusters identified by iCluster [11] (p-value: 0.0025), the three clusters uncovered by the proposed method (p-value: 0.0004) can be better distinguished from each other with different survival curves and with a more significant p-value by the Logrank test [41].

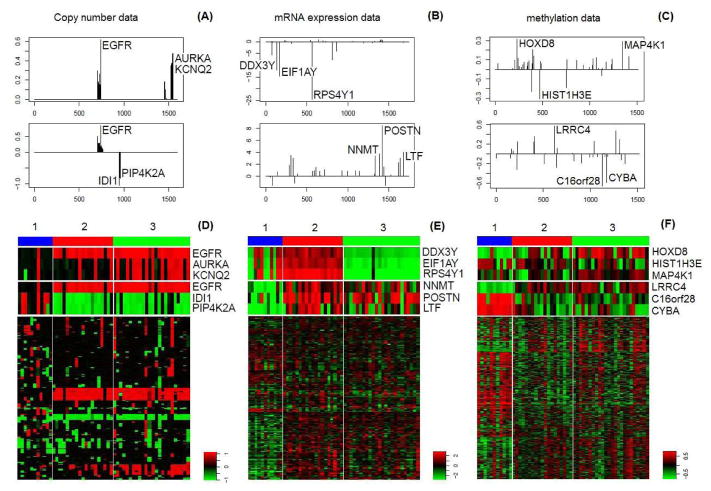
To investigate the performance of feature selection, we examine some candidate functional genes (viewed as features) selected by the proposed method, based on which integrative clusters are formed. Specifically, the candidate functional genes are picked out among the genes with non-zero loading values, where a gene is regarded as more important for integrative clustering whenever it has a larger absolute loading value. As shown in panels (A–C) of Figure 6, the top three genes identified are EGFR, AURKA and KCNQ2 based on the first loading vector of the DNA copy number data, genes DDX3Y, EIF1AY and RPS4Y1 based on that of the mRNA expression data, and genes HOXD8, HIST1H3E and MAP4K1 based on that of the DNA methylation data. From the heatmaps of these genes in panels (D–F) of Figure 6, we see that these genes distinguish cluster 2 from cluster 3, which is also implied by the first principal component in panel (D) of Figure 5. Among these selected genes, EGFR is a common oncogene in GBM, promoting growth and survival of cancer cells [42]. AURKA plays important roles in cell cycle regulation, and its inhibition has been suggested to serve as a novel therapeutic approach for GBM [43], while KCNQ2 has the same copy number value as AURKA and both are located nearby in chromosome 20q13. In addition, from the t-test results [44], DDX3Y, EIF1AY and RPS4Y1 are top genes differentially expressed between the two genders. As for HOXD8, HIST1H3E and MAP4K1, only HOXD8 contributes to distinguishing cluster 1 from the others. As studied in [45], HOXD8 is differentially hypermethylated between short-term survivors and long-term survivors among the GBM patients, which is in agreement with our analysis of survival outcomes for the three clusters.

Figure 6.

(A–C) are plots of the first two integrative loadings of the DNA copy number data, the mRNA expression data and the methylation data respectively, where in each plot the top three genes are marked. (D–F) are heatmaps of the DNA copy number data, the mRNA expression data and the methylation data of the 55 GBM patients from TCGA respectively, where the columns (tumors) are arranged by clusters identified by irPCA. In particular, for each data type the heatmaps of the top three genes of the first two integrative loadings are plotted to explore relationships between these genes and the identified clusters.

Based on the second loading vector for each data type, we identify the top three genes EGFR, IDI1 and PIP4K2A, NNMT, POSTN and LTF, and LRRC4, C16orf28 and CYBA, respectively, as shown in Figure 6(A–C). The corresponding heatmap shows that these genes clearly distinguish cluster 1 from the others; see also panel (D) of Figure 5. Among these genes, EGFR is identified for the second time, illustrating its importance. As mentioned in [46], EGFR amplification and overexpression are a striking feature of GBM, but are rare in low-grade gliomas, suggesting a key role of aberrant EGFR signaling in the pathogenesis of GBM. Interestingly, this point is concordant with our results in that clusters 2 and 3 are associated with frequent EGFR amplifications and shorter survival, while cluster 1 contains rare EGFR amplifications with longer survival. Another important gene identified is NNMT, which has been found in several kinds of tumors, including glioblastoma and hepatocellular carcinoma. As mentioned in the hepatocellular carcinoma study of [47], stratification of patients based on tumor NNMT mRNA levels revealed that the patients who expressed higher NNMT mRNA levels tended to have a shorter survival time. Our results also suggest that higher NNMT mRNA expression is correlated with an adverse patient survival outcome. In particular, cluster 1 is associated with low NNMT expression and high survival, in contrast to high NNMT expression and low survival for clusters 2 and 3. In addition, as suggested by [48], POSTN mRNA expression was significantly associated with survival in the TCGA database: lower expression of POSTN was correlated with significantly decreased survival and shorter time to disease progression. This is in agreement with our survival analysis results. Next, for DNA methylation, as suggested by [49], LRRC4 might act as a novel candidate for tumor suppressor for GBM, and methylation-mediated inactivation of LRRC4 was viewed as a potential biomarker and therapeutic target. Interestingly, this point is consistent with hypomethylation of LRRC4 in cluster 1 with long patient survival.

In view of the known fact that the genes DDX3Y, EIF1AY and RPS4Y1, identified here based on the first integrative loading vector for the mRNA expression data, are differentially expressed between the two genders, below we explore the relationship between the identified subtypes/clusters and gender. The Kaplan-Meier estimates of the survival curves for the male and female GBM patients were close; see panel (C) of Figure 5. Furthermore, another study with more patients found that the male GBM patients had longer survival than that of the female patients [50]. However, here we have obtained seemingly contradictory results: as shown in panels (E) and (F) of Figure 5, while cluster 2 is all composed of male patients and cluster 3 largely of female patients (except one ambiguous case), cluster 2 shows surprisingly lower survival. This novel and interesting discovery by our proposed method can be explained by the status of EGFR: the relative survival outcome of male GBM patients versus female GBM patients, all with EGFR amplifications, may be reversed as compared to that of the general patient population; that is, male patients with EGFR amplifications may have much worse survival outcomes.

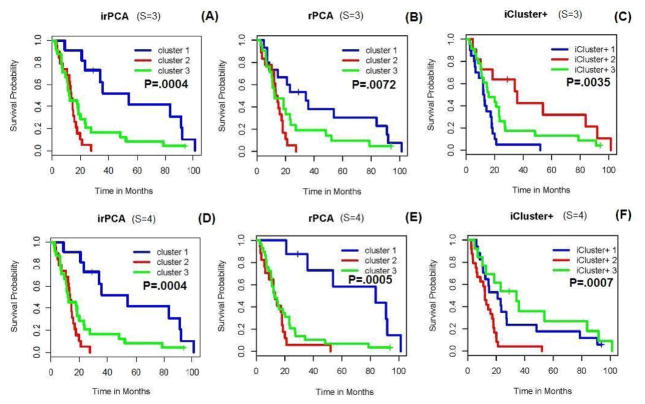
We also compared the performance of the proposed method with naive integration via rPCA [13] and with iCluster+ [6] for the above three types of data (S = 3) with or without the mutation data X⁽⁴⁾ with p⁽⁴⁾ = 306 (S = 4). The results are shown in Figure 7, where the performance of irPCA with either S = 3 or S = 4 gave the most separated survival curves as well as the smallest p-value of a Logrank test. In addition, from the corresponding results of running time shown in Table 3, we see that irPCA is more computationally efficient than iCluster+.

Figure 7.

K-M plots for irPCA, rPCA (naive integration) and iCluster+ with S = 3 and S = 4 respectively, where P denotes the p-value of the Mantel-Haenszel test and S = 4 means that the mutation data X⁽⁴⁾ is added.

Table 3.

Running time (in minutes) of each application of irPCA, rPCA and iCluster+ to the GBM data with S = 3 and S = 4 respectively.

	irPCA	rPCA	iCluster+
S = 3	12.67	.34	59.65
S = 4	81.82	.43	451.60

4. Discussion

We have introduced a novel framework of integrative analysis via regularized principal component analysis, named irPCA, to simultaneously incorporate information from multiple types of data. Specifically, we seek common principal components across all data types while regularizing PC loadings for each data type separately. The proposed approach is simple, distribution-free, robust in terms of unbalanced scales and rather computationally efficient as compared to existing approaches based on joint latent variable models. The proposed method achieves simultaneous dimension reduction, feature selection and data type-specific scale regularization. Although the proposed method is built on regularized PCA for single type of data, there are some key innovations. The most important perhaps is the use of the elastic net penalty, instead of the more commonly used L₁ penalty. The elastic net penalty not only produces a sparse model as does the L₁ penalty, but also achieves data type-specific scale regularization to battle unbalanced scales across multiple types of data. Importantly, this advantage is specific to integrative analysis. In fact, in sparse PCA proposed by [13], using elastic net penalty is identical to using the L₁: in Step 2(b) of Algorithm 1 with S = 1, u_new = Xv_new/ ||Xv_new||₂ is invariant to α⁽¹⁾ due to the standardization of Xv_new.

As suggested by the simulated and real data examples, our proposed method compares favorably against its main competitors with respect to computational efficiency and accuracy in identifying latent clusters, and is more robust to unbalanced scales of multiple types of data and to skewed data distributions. In particular, when applied to the data with 55 GBM patients, our proposed method discovers three novel clusters as three GBM subtypes: the first one is mainly characterized by rare EGFR amplifications and associated with high survival, the second one is composed of male patients with EGFR amplifications and associated with extremely low survival, and the third one is composed of female patients with EGFR amplifications and associated with intermediate survival. Compared to previous results, the three subtypes uncovered by our method show more significantly different survival patterns. These advantages establish the proposed method as a promising candidate for integrative clustering analysis of multiple types (or sources) of high-dimensional data.

The R code for irPCA is available at http://www.biostat.umn.edu/~weip/prog.html.

Appendix

Proof of Lemma 1

This lemma can be proved by using Lemma 1 of [13] and the following equations:

$$\sum _{s=1}^S{\Vert {\mathbf{X}}^{(s)}-\mathbf{u}{\mathbf{v}}^{(s)T}\Vert }_F^2=\sum _{s=1}^S\sum _{i=1}^n\sum _{j=1}^{p^{(s)}}{({\mathbf{X}}_{ij}^{(s)}-{\mathbf{u}}_i{\mathbf{v}}_j^{(s)})}^2={\Vert \mathbf{X}-\mathbf{uv}\Vert }_F^2.$$

Proof of Lemma 2

Because C(u, v) in (1) can be written as

$$\sum _{s=1}^S\sum _{j=1}^{p^{(s)}}\{\sum _{i=1}^n{({\mathbf{X}}_{ij}^{(s)}-{\mathbf{u}}_i{\mathbf{v}}_j^{(s)})}^2+P^{(s)}({\mathbf{v}}_j^{(s)})\},$$

we can optimize over individual components of v^(s) for each s ∈ {1, …, S} separately. In fact, for each s ∈ {1, …, S} and each j ∈ {1, …, p^(s)}, we have that

$$\sum _{i=1}^n{({\mathbf{X}}_{ij}^{(s)}-{\mathbf{u}}_i{\mathbf{v}}_j^{(s)})}^2+P^{(s)}({\mathbf{v}}_j^{(s)})={\mathbf{v}}_j^{(s)2}-2{({\mathbf{X}}^{(s)T}\mathbf{u})}_j{\mathbf{v}}_j^{(s)}+P^{(s)}({\mathbf{v}}_j^{(s)})+\mathit{Const}.$$

Then from Lemma 2 of [13], we can get the formulas of the vector v̂ = (v̂^(1)T, …, v̂^(S)T)^T that minimizes (1) for fixed u given the elastic net penalty.

Proof of Lemma 3

The minimization of (1) is equivalent to that of

$$\sum _{s=1}^S\{-2{\mathbf{v}}^{(s)T}{\mathbf{X}}^{(s)T}\mathbf{u}+{\Vert \mathbf{u}\Vert }_2^2{\Vert {\mathbf{v}}^{(s)}\Vert }_2^2+P^{(s)}({\mathbf{v}}^{(s)})\},$$

because

$$\sum _{s=1}^S{\Vert {\mathbf{X}}^{(s)}-\mathbf{u}{\mathbf{v}}^{(s)T}\Vert }_F^2=\sum _{s=1}^S\{\text{tr}({\mathbf{X}}^{(s)T}{\mathbf{X}}^{(s)})-2{\mathbf{v}}^{(s)T}{\mathbf{X}}^{(s)T}\mathbf{u}+{\Vert \mathbf{u}\Vert }_2^2{\Vert {\mathbf{v}}^{(s)}\Vert }_2^2\}.$$

Combining Lemma 1, the desired result follows.

Proof of Theorem 1

Since C(u_new, u_new) ≥ C(u_old, u_new) ≥ C(u_old, u_old), C(u_new, u_new) is monotonically decreasing for iterations of Algorithm 1. Since C(u_new, u_new) is obviously bounded below, the convergency is proved.

Following the standard theory of constrained optimization, we introduce the Lagrangian multipliers γ and construct the Lagrangian function

$$C_L(\mathbf{u},\mathbf{v},\gamma )=C(\mathbf{u},\mathbf{v})+\gamma ({\mathbf{u}}^T\mathbf{u}-1).$$

Letting $\frac{\partial C_L}{\partial \gamma }=0,\frac{\partial C_L}{\partial \mathbf{u}}=0$ and $\frac{\partial C_L}{\partial \mathbf{v}}=0$, we obtain $\mathbf{u}=\frac{\mathbf{Xv}}{{\Vert \mathbf{Xv}\Vert }_2}$ and ${\sum }_{s=1}^S\{-2{\mathbf{X}}^{(s)T}\mathbf{u}+2{\mathbf{v}}^{(s)}+\frac{\partial P^{(s)}({\mathbf{v}}^{(s)})}{\partial {\mathbf{v}}^{(s)}}\}=0$. When Algorithm 1 converges, we get C(u_new, v_new) = C(u_old, v_old). From Lemma 1 and Lemma 2, we have that u_new = u_old and v_new = v_old. Combining these with the updating steps of Algorithm 1, the desired result follows.

Below we will investigate statistical properties of the proposed method. Let ${\mathbf{X}}_M^{(s)}={\mathbf{X}}^{(s)}{\widehat{\mathbf{V}}}_M^{(s)}{({\widehat{\mathbf{V}}}_M^{(s)T}{\widehat{\mathbf{V}}}_M^{(s)})}^{-1}{\widehat{\mathbf{V}}}_M^{(s)T}$ for each s ∈ {1, · · ·, S}. As in [13], we define the total variance explained by the first M integrative principal components as ${\sum }_{s=1}^S\text{tr}({\mathbf{X}}_M^{(s)T}{\mathbf{X}}_M^{(s)})$, and the total variance in the data matrix X = [X⁽¹⁾, · · ·, X^(S)] as ${\sum }_{s=1}^S\text{tr}({\mathbf{X}}^{(s)T}{\mathbf{X}}^{(s)})$. As suggested by Proposition 1, the total variance explained by the integrative principal components increases as additional integrative regularized loading vectors are added, and is bounded above by the total variance in the data matrix X.

Proposition 1

The following inequalities hold for the total variance explained by the first M integrative principal components:

$$\begin{array}{l}\sum _{s=1}^S\text{tr}({\mathbf{X}}_M^{(s)T}{\mathbf{X}}_M^{(s)})\le \sum _{s=1}^S\text{tr}({\mathbf{X}}_{M+1}^{(s)T}{\mathbf{X}}_{M+1}^{(s)})\\ \le \sum _{s=1}^S\text{tr}({\mathbf{X}}^{(s)T}{\mathbf{X}}^{(s)}).\end{array}$$

This proposition is directly obtained by using Theorem 1 of [13].

Proposition 2

The integrative regularized loading vectors ${\widehat{\mathbf{v}}}_m^{(s)}$, m ∈ {1, · · ·, M}, s ∈ {1, · · ·, S}, obtained by Algorithm 2 and the corresponding total variance ${\sum }_{s=1}^S\text{tr}({\mathbf{X}}_M^{(s)T}{\mathbf{X}}_M^{(s)})$ depend on X only through X^TX.

Proof of Proposition 2

First, from Lemma 3 we see that ${\{{\widehat{\mathbf{v}}}_1^{(s)}\}}_{s=1}^S$ depends on X through ${\{{\mathbf{X}}^{(s)T}{\mathbf{X}}^{(s)}\}}_{s=1}^S$ and then furthermore through X^TX. For each s ∈ {1, …, S}, simple calculation yields

$${\mathbf{X}}_{(1)}^T{\mathbf{X}}_{(1)}={\mathbf{X}}^T\mathbf{X}-\frac{{\stackrel{\sim }{\mathbf{v}}}_1{\stackrel{\sim }{\mathbf{v}}}_1^T{\mathbf{X}}^T\mathbf{X}}{{\Vert \mathbf{X}{\stackrel{\sim }{\mathbf{v}}}_1\Vert }_2}-\frac{{\mathbf{X}}^T\mathbf{X}{\stackrel{\sim }{\mathbf{v}}}_1{\stackrel{\sim }{\mathbf{v}}}_1^T}{{\Vert \mathbf{X}{\stackrel{\sim }{\mathbf{v}}}_1\Vert }_2}+\frac{{\stackrel{\sim }{\mathbf{v}}}_1{\stackrel{\sim }{\mathbf{v}}}_1^T{\mathbf{X}}^T\mathbf{X}{\stackrel{\sim }{\mathbf{v}}}_1{\stackrel{\sim }{\mathbf{v}}}_1^T}{{\Vert \mathbf{X}{\stackrel{\sim }{\mathbf{v}}}_1\Vert }_2},$$

where ${\stackrel{\sim }{\mathbf{v}}}_1={({\widehat{d}}^{(1)}{\widehat{\mathbf{v}}}_1^{(1)T},\cdots ,{\widehat{d}}^{(S)}{\widehat{\mathbf{v}}}_1^{(S)T})}^T$. This indicates that ${\mathbf{X}}_{(1)}^T{\mathbf{X}}_{(1)}$ also depends on X through X^TX.

We assume that for k = m (m < M) we have that ${\{{\widehat{\mathbf{v}}}_k^{(s)}\}}_{s=1}^S$ and ${\mathbf{X}}_{(k)}^T{\mathbf{X}}_{(k)}$ depend on X through X^TX. Next, we consider the case for k = m + 1. Because for each s ∈ {1, …, S}, we have that

$${\mathbf{X}}_{(m+1)}^T{\mathbf{X}}_{(m+1)}={\mathbf{X}}_{(m)}^T{\mathbf{X}}_{(m)}+\frac{{\stackrel{\sim }{\mathbf{v}}}_m{\stackrel{\sim }{\mathbf{v}}}_m^T{\mathbf{X}}_{(m)}^T{\mathbf{X}}_{(m)}{\stackrel{\sim }{\mathbf{v}}}_m{\stackrel{\sim }{\mathbf{v}}}_m^T}{{\Vert {\mathbf{X}}_{(m)}{\stackrel{\sim }{\mathbf{v}}}_m\Vert }_2}-\frac{{\mathbf{X}}_{(m)}^T{\mathbf{X}}_{(m)}{\stackrel{\sim }{\mathbf{v}}}_m{\stackrel{\sim }{\mathbf{v}}}_m^T}{{\Vert {\mathbf{X}}_{(m)}{\stackrel{\sim }{\mathbf{v}}}_m\Vert }_2}-\frac{{\stackrel{\sim }{\mathbf{v}}}_m{\stackrel{\sim }{\mathbf{v}}}_m^T{\mathbf{X}}_{(m)}^T{\mathbf{X}}_{(m)}}{{\Vert {\mathbf{X}}_{(m)}{\stackrel{\sim }{\mathbf{v}}}_m\Vert }_2},$$

where where ${\stackrel{\sim }{\mathbf{v}}}_m={({\widehat{d}}^{(1)}{\widehat{\mathbf{v}}}_m^{(1)T},\cdots ,{\widehat{d}}^{(S)}{\widehat{\mathbf{v}}}_m^{(S)T})}^T$. This indicates that ${\mathbf{X}}_{(m+1)}^T{\mathbf{X}}_{(m+1)}$ also depends on X through X^TX. From the assumption for k = m and Lemma 3, we see that ${\{{\widehat{\mathbf{v}}}_{m+1}^{(s)}\}}_{s=1}^S$ depends on X only through X^TX. As a result, we obtain that ${\{{\widehat{\mathbf{v}}}_1^{(s)}\}}_{s=1}^S,\dots ,{\{{\widehat{\mathbf{v}}}_M^{(s)}\}}_{s=1}^S$ depend on X only through X^TX.

For each s ∈ {1, …, S}, let ${\mathbf{X}}_M^{(s)}={\mathbf{X}}^{(s)}{\mathbf{H}}_M^{(s)}$, and from Theorem A.3 of [13] we have that $\text{tr}({\mathbf{X}}_M^{(s)T}{\mathbf{X}}_M^{(s)})=\text{tr}({\mathbf{X}}^{(s)T}{\mathbf{X}}^{(s)}{\mathbf{H}}_M^{(s)})$. Form Proposition 1, we know that ${\{{\mathbf{H}}_M^{(s)}\}}_{s=1}^S$ depends on X only through X^TX, based on which we obtain the desired result.