Scalable High Performance Image Registration Framework by Unsupervised Deep Feature Representations Learning

Abstract

Feature selection is a critical step in deformable image registration. In particular, selecting the most discriminative features that accurately and concisely describe complex morphological patterns in image patches improves correspondence detection, which in turn improves image registration accuracy. Furthermore, since more and more imaging modalities are being invented to better identify morphological changes in medical imaging data,, the development of deformable image registration method that scales well to new image modalities or new image applications with little to no human intervention would have a significant impact on the medical image analysis community. To address these concerns, a learning-based image registration framework is proposed that uses deep learning to discover compact and highly discriminative features upon observed imaging data. Specifically, the proposed feature selection method uses a convolutional stacked auto-encoder to identify intrinsic deep feature representations in image patches. Since deep learning is an unsupervised learning method, no ground truth label knowledge is required. This makes the proposed feature selection method more flexible to new imaging modalities since feature representations can be directly learned from the observed imaging data in a very short amount of time. Using the LONI and ADNI imaging datasets, image registration performance was compared to two existing state-of-the-art deformable image registration methods that use handcrafted features. To demonstrate the scalability of the proposed image registration framework image registration experiments were conducted on 7.0-tesla brain MR images. In all experiments, the results showed the new image registration framework consistently demonstrated more accurate registration results when compared to state-of-the-art.

I. INTRODUCTION

Deformable image registration is very important to neuroscience and clinical studies for normalizing individual subjects to the reference space [1–5]. In deformable image registration, it is critical to establish accurate anatomical correspondences between two medical images. Typically, a patch-based correspondence detection approach is often used, where a patch is a fixed-size symmetric neighborhood of pixel intensity values centered a point in the image. And if two different patches, from two different images, show similar morphological patterns, the two points (at each patch center) are considered to be well corresponded. Therefore, to improve correspondence detection, the problem becomes the one related to feature selection, i.e., how to consistently select a set of highly discriminative features that can accurately, and concisely, capture the morphological pattern presented in the image patch.

Intensity-based feature selection methods are widely used in medical image registration [6–11], however, two image patches that show similar, or even the same, distribution of intensity values do not guarantee the two points are corresponded from an anatomical point of view [4, 12–14]. Handcrafted features, such as geometric moment invariants [15] or Gabor filters [16], are also widely used by many state-of-the-art image registration methods [4, 11, 13, 14, 17]. In general, the major pitfall of using handcrafted features is that the developed model tends to be very ad-hoc. That is, the model is only intended to recognize image patches specific to an image modality or a certain imaging application [18].

Supervised learning-based methods have been proposed to select the best set of features from a large feature pool that may include plenty of redundant handcrafted features [18–24]. However, for this approach, the ground-truth data with known correspondences across the set of training images is required. Because human experts are typically needed to generate ground-truth data, it is well known that obtaining this type of data can be a very laborious and subjective process. In many cases, ground-truth data is simply not available, and even if it does exist, the size of the training population may be very small, which may dramatically affect the accuracy of the registration method. In general, image registration methods that use supervised learning for feature selection [18, 19] are biased by the registration uncertainty due to the lack of ground truth.

Because deformable image registration is very specific to the input data, it typically takes months, or even years, to develop a new image registration method that has acceptable performance for a new imaging modality or new imaging application. The conventional way of selecting features, including the development of a similarity measurement, requires expert knowledge that is directly related to modality and application. For instance, it is not straightforward to apply the same feature selection methods specifically designed for 1.5-tesla T1 weighted MR image to 7.0-tesla T1 weighted MR images due to the significantly high signal-to-noise ratio in the 7.0-tesla data [25]. Meanwhile, handcrafted features are expensive because manually intensive efforts are required to tune the model for a particular medical image registration application. With the rapid progression of imaging technologies, more and more new modalities are emerging with potentials in disease diagnosis and treatment. Thus the need for a general image registration framework that can quickly be deployed to new modalities and new applications is highly desirable.

To overcome the limitations mentioned above, unsupervised learning-based feature selection methods require further investigation. Because of the complexity of the data, conventional unsupervised approaches that use simple linear models, such as PCA and ICA [26, 27], are typically not suitable because they are unable to preserve the highly nonlinear relationships when projected to the low-dimensional space. More advanced methods, such as ISOMAP [28], kernel SVM [29, 30], locally linear embedding (LLE) [31, 32], and sparse coding [33], can learn the non-linear embedding directly from the observed data within a single layer of projection. However, since the learned features are found using only a single layer, or a shallow model [34], the selected features may lack high-level perception knowledge (e.g., shape and context information), and may not be suitable for correspondence detection.

Recently, unsupervised deep learning feature selection techniques have been successfully applied to solve many difficult computer vision problems [30, 34–42]. The general concept behind deep learning is to learn hierarchical feature representations by inferring simple representations first and then progressively build up more complex ones from the previous level. Compared with the shallow models, a deep learning architecture can encode multi-level information from simple to complex. Thus, for image registration, deep learning is very promising because it: (1) is an unsupervised learning approach that does not require ground truth, (2) uses a hierarchical deep architecture to infer complex non-linear relationships, (3) is completely data-driven and not based on handcrafted feature selection, and (4) can quickly and efficiently compute the hierarchical feature representation for any image patch in the testing data given the trained hierarchical deep architecture (or network).

In this paper, we propose to learn the hierarchical feature representations directly from the observed medical images by using unsupervised deep learning paradigm. Specifically, we introduce a stacked auto-encoder (SAE) [34, 37, 38, 42] with convolutional network architecture [41, 43] into our unsupervised learning framework. The inputs to train the convolutional SAE are the 3D image patches. Generally speaking, our learning-based framework consists of two components, i.e., the encoder and decoder networks. On one hand, the multi-layer encoder network is used to transfer the high-dimension 3D image patches into the low-dimension feature representations, where a single auto-encoder is the building block to learn non-linear and high-order correlations between two feature representation layers. On the other hand, the decoder network is used to recover 3D image patches from the learned low-dimensional feature representations, acting as feedback to refine the inferences in the encoder network. Since the size of 3D image patches can be as large as ∼10⁴, it is very computational intensive to directly use a SAE to learn useful features in each layer. To overcome this problem, we use a convolutional network [41] to efficiently learn the translational invariant feature representations [41, 44] such that the learned features are shared among all image points in a certain region. Finally, we present a general framework to fast develop high performance image registration method by allowing the learned feature representations to steer the correspondence detection between two images.

The main contributions of this paper are two-fold: First, in order to accurately recognize complex morphological patterns in 3D medical image patches, a deep learning feature selection method is proposed. The benefits of using deep learning for feature selection are: (1) does not require manually labeled ground-truth data (that typically is a laborious, subjective, and error-prone process) so it does not suffer from the same limitations as those found in the supervised methods, and (2) offers a hierarchical learning paradigm to learn not only low-level but also high-level features that are more flexible than conventional handcrafted features, or even the best features found by the existing supervised learning-based feature selection methods. Second, since all existing state-of-the-art image registration frameworks use supervised learning or handcrafted feature selection methods, they generally do not scale well to the new data. However, because the proposed deep learning feature selection method does not suffer from these limitations, the proposed image registration framework can be quickly deployed to perform deformable image registration on new image modalities or new imaging applications with little to even no human intervention. This work is the extension of our previous work in [45], where we further refine the registration performance by using more advanced convolutional SAE, comprehensively evaluate the registration results w.r.t. current state-of-the-art registration methods, and show the potential of our learning-based registration framework in rapid development of new image registration method on brand new 7.0-tesla MR images.

To assess the performance of the proposed registration framework, we evaluate its registration performance on the conventional 1.5-tesla MR brain images (i.e., the elderly brains from ADNI dataset and the young brains from LONI dataset [46]) that show the proposed registration framework achieves much better performance than the existing state-of-the-art registration methods with handcrafted features. We also demonstrate the scalability of the proposed registration framework on 7.0-tesla MR brain images, where we rapidly develop an accurate image registration method for this new modality with satisfactory registration results.

The remaining sections are organized as follows: In Section 2 we first present the deep learning approach for extracting intrinsic feature representations and our new learning-based registration framework. In Section 3 we evaluate the performance of the proposed registration framework, and in Section 4 we provide a brief conclusion

II. Method

Because the input feature space defined by a 3D image patch is typically very large, likely to contain redundant and spurious information, and have small translation differences, the proposed method addresses these issues by implementing a convolutional stacked autoencoder (SAE) network. In general, the goal of the convolutional SAE to reduce this high dimension feature space to some lower dimension representation defined by a set of intrinsic basis functions that are robust to redundant and spurious data artifacts and invariant to translation differences. Using the learned convolutional SAE each input high dimension feature vector is efficiently transformed into a small set of coefficients (i.e. intrinsic feature representation) that well describes the morphological pattern presented in the 3D image patch

A. Naive Methods for Intrinsic Feature Representations

K-means [47] and Gaussian mixture model (GMM) [48] are the two well-known clustering methods that are based upon linear learning models. In particular, given a set of training data X_L×M, where L is the dimension of the data and M is the number of samples, the clustering methods learn K centroids such that each sample can be assigned to the closest centroid. Suppose the observed feature vectors (e.g. image intensity patches) form a feature space and the appropriate K centroids in the high-dimension feature space are known. A typical pipeline is to define a function f: ℛ^L→ ℛ^K that map the observed L-dimension feature vector to a K-dimension feature vector (K < L) [49]. For instance, we could first calculate the affiliations for each observed feature vector (w.r.t. to the K centroids) and then use such affiliations as morphological signatures to represent each key point in the feature space. However, the limitation of K-means and GMM is that the number of centroids is required to be very large as the input dimension grows [42]. Thus, these clustering methods may not be applicable in learning the intrinsic representations for high-dimension medical images.

PCA [50] is one of the most commonly used methods for dimension reduction. PCA extracts a set of basis vectors from the observed data, which maximize the data variance of the projected subspace (spanned by the basis vectors). The basis vectors are obtained by calculating the eigenvectors of the covariance matrix of the input data. Given the observed data X = [x₁,…,x_m,…,x_M], the following steps are sequentially applied in the training stage: (1) calculate the mean by $\widehat{x}=\frac{1}{M}{\sum }_{m=1}^M{x}_m$; (2) compute the eigenvectors E = [e_j]_j=1,…L for the covariance matrix $\frac{1}{M-1}\overline{X}{\overline{X}}^T$, where X̄ = [x_m – x̂]_m=1,…,M and E are sorted in the decreasing order of eigenvalues; (3) determine the first Q largest eigenvalues such that ${{\sum }_{j=1}^Q({\lambda }_j)}^2>f_Q{{\sum }_{j=1}^L({\lambda }_j)}^2$, where f_Q defines the proportion of the remaining energy. In the end, each training data x_m can be approximately reconstructed as x_m = x̂ + E_Qb, where E_Q contains the first Q largest eigenvectors of E and $b=E_Q^T(x-\widehat{x})$. In the testing stage, give the new testing data x_new, its low-dimensional feature representation can be obtained by $b_{\mathit{\text{new}}}=E_Q^T(x_{\mathit{\text{new}}}-\widehat{x})$. This classic approach for finding low-dimension representations has achieved many successes in medical image analysis area [51, 52]. However, PCA is only an orthogonal linear transform and is not optimal for finding structures with highly non-Gaussian distributions. As we show in the experiment section, such feature representations learned by PCA can hardly assist image registration to establish more accurate correspondences in feature matching.

Since there are huge variations of anatomical structures across individual medical images, the above unsupervised learning methods have limitations in finding the intrinsic feature representations [30, 35, 53]. In the following, we present the new unsupervised deep learning paradigm to infer the intrinsic feature representations from a set of observed 3D image patches

B. Learn Intrinsic Feature Representations by Unsupervised Deep Learning

Introduction of Auto-Encoder

Auto-Encoder (AE) is one typical neural network and structurally defined by three sequential layers: the input layer, the hidden layer, and the output layer. Here, the goal of AE is to learn the latent feature representations from the 3D image patches collected from medical images. Let D and L denote, respectively, the dimensions of hidden representations and input patches. Given an input image patch x_m ∈ℛ^L(m = 1,…,M), AE maps it to be an activation vector $h_m={[h_m(j)]}_{j=1,\dots ,D}^T\in {ℛ}^D$, by h_m = f(Wx_m+b₁), where the weight matrix W ∈ ℛ^D×L and the bias vector b₁ ∈ ℛ^D are the encoder parameters. Here, f is the logistic sigmoid function f (a) = 1/(1 + exp(–a)). It is worth noting that h_m is considered as the representation vector of the particular input training patch x_m via AE. Next, the representation h_m from the hidden layer is decoded to a vector y_m ∈ ℛ^L, which approximately reconstructs the input image patch vector x by another deterministic mapping y_m = f(W^Th_m + b₂) ≈ x_m, where the bias vector b₂ ∈ ℛ^L is the decoder parameters. Therefore, the energy function in AE can be formulated as:

$$\{W,b_1,b_2\}=\underset{W,b_1,b_2}{\text{arg min}}{\sum }_{m=1}^M{\Vert f(W^T(f(W{x}_m+b_1)))+b_2-x_m\Vert }_2^2.$$ (1)

The sparsity constraint upon the hidden nodes in the network usually leads to more interpretable features. Specifically, we regard each hidden node h_m(j) as being “active” if the value of h_m(j) is close to 1 or “inactive” if the degree is close to 0. Thus, the sparsity constraint requires most of the hidden nodes to remain “inactive” for each training patch x_m. Specifically, the Kullback-Leibler divergence [37, 40, 42] is used to impose the sparsity constraint to each hidden node by enforcing the average activation degree over the whole training data, i.e., ${\widehat{\rho }}_j=\frac{1}{M}{\sum }_{m=1}^M{h}_m(j)$, to be close to a very small value ρ (here, ρ is set to 0.001 in the experiments):

$$\mathit{\text{KL}}(\rho \Vert {\widehat{\rho }}_j)=\rho \text{log}\frac{\rho }{{\widehat{\rho }}_j}+(1-\rho )\text{log}\frac{1-\rho }{1-{\widehat{\rho }}_j}.$$ (2)

Then, the overall energy function of AE with sparsity constraint is defined as:

$$\{W,b_1,b_2\}=\underset{W,b_1,b_2}{\text{arg min}}{\sum }_{m=1}^M{\Vert f(W^T(f(W{x}_m+b_1)))+b_2-x_m\Vert }_2^2+\beta {\sum }_{j=1}^D\mathit{\text{KL}}(\rho \Vert {\widehat{\rho }}_j),$$ (3)

where β controls the strength of sparsity penalty term. Typical gradient based back-propagation algorithm can be used for training single AE [34, 35].

Stacked Auto-Encoder

A single AE is limited in what it can present, since the model is shallow in learning. As shown in Fig. 1(a), a set of training image patches are sampled from brain MR images, each sized at 15 × 15 (For demonstration, we use 2D patches as examples). We set the number of hidden nodes to be 100 in this single AE. The learned basis feature representations are shown in Fig. 1(d), where a 2D slice represents part of 3D filter. Most of them look like Gabor filters that can detect edges in different orientations. The reconstructed image patches are shown in Fig. 1(b). It is obvious that many details have been lost after the reconstruction from low-dimension representations, as the bright regions displayed in Fig. 1(c).

Fig. 1.

The reconstructed image patches by single Auto-Encoder (b) and Stacked Auto-Encoder (e). The bright and dark colors indicate large and small reconstruction errors, respectively.

The power of deep learning emerges when several AEs are stacked to form a Stacked Auto-Encoder (SAE), where each AE becomes a building block in the deep learning model. In order to train SAE, a greedy layer-wise learning approach [36, 37] is used to train a single AE. Specifically, three steps are need to train an SAE, i.e., (1) pre-training, (2) unrolling, and (3) fine-tuning [38]. In the pre-training step, we train the 1^st AE with all image patches as the input. Then, we train the 2^nd AE by using the activations h⁽¹⁾ of the 1^st AE (pink circles in Fig. 2) as the input. In this way, each layer of features captures strong, high-order correlations based on outputs from the layer below. This layer-by-layer learning can be repeated for many times. After pre-training, we build a deep learning network by stacking the AE in each layer, with the higher layer AE nested within the lower layer AE. Fig. 2 shows a SAE consisting of 2-layer stacked AEs. Since the layer-by-layer pre-training procedure provides very good initialization for the multi-level network, we can efficiently use the gradient-based optimization method (such as L-BFGS or Conjugate Gradient [54]) to further refine the SAE parameters in the fine-tuning stage. Due to the deep and hierarchical nature of the network structure, a SAE can discover highly non-linear and complex feature representations for patches in medical images. As shown in Fig. 1(e) and (f), the patch reconstruction performance by SAE becomes much better than using a single AE, where the SAE consists of only 2 layers and the numbers of hidden nodes in each layer are 255 and 100, respectively. It is worth noting that the reconstruction errors in Fig. 1(c) and (f) are in the same range, where bright and dark colors indicate large and small reconstruction errors, respectively.

Fig. 2.

The hierarchical architecture of Stacked Auto-Encoder (SAE).

Convolutional SAE network

Due to complex nature of medical images, learning the latent feature representations in medical data by employing deep learning is much more difficult than similar applications in computer vision and machine learning areas. In particular, the dimension of input training patch is often very high. For example, the intensity vector of a 21 × 21 × 21 3D image patch has 9,261 elements. Thus, the training of SAE network becomes very challenging. To alleviate this issue, we resort to using convolutional technique to construct the SAE network.

As shown in Fig. 3, the input to the convolutional SAE network is the large image patch 𝒫_v with patch size L_v. To make it simple, here, we explain the convolutional SAE network with 2D image patch as example. Since the dimension of the image patch 𝒫_v is too large, we let a L_w × L_w (L_w < L_v) sliding window 𝒫_w (red box in Fig. 2) go through the entire big image patch 𝒫_v, thus obtaining (L_v – L_w + 1) × (L_v – L_w + 1) small image patches. Eventually, we use these small image patches 𝒫_w to train the auto-encoder in each layer, instead of the entire big image patch 𝒫_v. Given the parameters of network (weight matrix W and bias vector b₁ and b₂), we can compute (L_v – L_w + 1) × (L_v – L_w + 1) activation vectors, where we use the red dots in Fig. 3 to denote the activation vectors in a 3 × 3 neighborhood. Then max pooling is used to shrink the representations by a factor of C in each direction (horizontal or vertical). The right part of Fig. 3 demonstrates the 3 × 3 max pooling procedure (C = 3). Specifically, we compute the representative activation vector among these 9 activation vectors in the 3 × 3 neighborhood by choosing the maximum absolute value for each vector element. Thus, the number of activation vector significantly reduces to $\frac{L_v-L_w+1}{C}\times \frac{L_v-L_w+1}{C}$. Since we apply the maximum operation, shrinking the representation with max pooling allows high-level representation to be invariant to small translations of the input image patches and reduce the computational burden. This translation invariant advantage is very useful in establishing anatomical correspondences between two images, as we will demonstrate in our experiments.

Fig. 3.

The 3×3 max pooling procedure in convolutional network.

Sample the image patches

Typically, one brain MR image, with 1 × 1 × 1mm³ spatial resolution, has over 8 million voxels in the brain volume. Obviously, there would be too many image patches to train the deep learning network, not to say that we extract the image patches across a set of training images. Therefore, adaptive sampling strategy is necessary to secure not only using an enough number of image patches but also selecting the most representative image patches to learn the latent feature representations for the entire training set.

To this end, there are two criteria for sampling image patches: 1) In a local view, the selected image patches should locate at distinctive regions in the image, such as sulcal roots and gyral crowns in MR brain images, since they are relatively easy to identify their correspondences; 2) In a global view, the selected image patches should cover the entire brain volume, while the density of sampled points could be low in the uniform regions and high in the context-rich regions. To meet these criteria, we use the importance sampling strategy [11] to hierarchically sample the image patches. Specifically, we smooth and normalize the gradient magnitude values over the whole image domain of each training image. Then, we use the obtained values as the importance degree (or probability) of each voxel to be sampled for deep learning. Note that, although more sophisticated method [55] could be used here for guiding sample selection, we use a simple gradient guided strategy since it is computationally fast. Based on this importance (probability) map, a set of image patches can be sampled via Monte Carlo simulation in each image. Fig. 4(a) shows the non-uniform sampling based on the importance (probability) map in learning the intrinsic feature representations for MR brain images. It can be observed from Fig. 4 that the sampled image patches (with the center point of each sampled patch denoted by the red dot in Fig. 4(b)) are more concentrated at the context-rich (or edge-rich) regions, where the values of importance (or probability) are high.

Fig. 4.

The importance map and the sampled image patches (denoted by the red dots) for deep learning. The color bar indicates the varying importance values for individual voxels.

C. Learning-based Registration Framework Using Learned Feature Representations

After training the convolutional SAE upon a large amount of 3D image patches, it is efficient to obtain the low-dimensional feature representations (blue circles in Fig. 2) by simple matrix multiplication and addition in each encoder layer. Our implementation is developed based on the deep learning software freely available at University of Toronto (http://deeplearning.cs.toronto.edu/codes). Such low-dimensional feature representation, regarded as the morphological signature, allows each point to accurately identify the correspondence during image registration as demonstrated above.

Since the convolutional SAE can directly learn the feature representations from the observed data, the learning procedure is completely free of the limitation of requiring ground-truth data. Thus, it is straightforward to learn optimal feature representations for specific dataset, with little or even no human intervention. Thanks to the state-of-the-art deformation mechanisms developed in many registration methods, we propose a learning-based registration framework by replacing with the learned feature representations and still inheriting the existing deformation mechanism to derive the deformation pathway. In general, deformable image registration methods can be categorized into two types: intensity-based (typical example: Demons [10, 56]) and feature-based (typical example: HAMMER [4, 14, 57]) approaches . In the following, we show how to improve the state-of-the-art registration methods by integrating the feature representations via deep learning.

Multi-Channel Demons With Deep Feature Representation

Many image registration methods, e.g., Demons [10, 56], use the gradient-based optimization approach to iteratively estimate the deformation fields. To utilize multiple image information, such as multi-modality images, multi-channel Demons was proposed by allowing one channel carrying one information source [58–60]. Therefore, it is straightforward to deploy multi-channel Demons, by regarding all elements of the learned feature representations as the multi-channel information. In each iteration, the update vector field is computed independently for each channel and then averaged to update the deformation field, until the overall feature difference across channels reaches local minima.

HAMMER with Deep Feature Representation

HAMMER registration algorithm (with its ITK-based source code available at http://www.nitrc.org/projects/hammerwml) is a typical feature-based deformable registration for MR brain images. Generally, we can replace the handcrafted attribute vectors (i.e., the low-order statistics in multi-resolution histograms) in the feature-based HAMMER registration method [14, 61] with the learned feature representations by the convolutional SAE. Next, we follow the hierarchical deformation optimization mechanism in HAMMER to estimate the deformation pathway between two images. Specifically, we alternate the following 5 steps until the image registration converges:

1. For each image, we follow the importance sampling strategy explained in Section B to select a small number of key points in both images. Since the key points usually locate the distinct regions in the image, as shown in Fig. 4(b), they can establish the correspondences more reliably than other points. Thus, we allow these key points to steer the estimation of entire deform pathway.

2. For each key point, we identify its anatomical correspondence by matching the learned deep feature representations [4, 57]. Here, we use normalized cross correlation as the similarity measurement between the feature representation vectors of the two different points under comparison.

3. Given the correspondence established on key points, we can interpolate the dense deformation field by using thin-plate splines [62].

4. Relax the selection criterion in Step (1) to allow more key points taking part in the correspondence detection until all image points are used as key points.

III. Experiments

Here we evaluate deformable image registration performance of the proposed image registration framework that uses deep learning for feature selection. For comparison, we set diffeomorphic Demons and HAMMER as the baselines for intensity-based and feature-based registration methods, respectively. Then, we extend the diffeomorphic Demons from a single channel (i.e., image intensity) to multi-channel Demons by adapting the learned feature representations via deep learning to multiple channels, which is denoted by M+DP. Similarly, we modify HAMMER to use the feature representations learned via deep learning, and denote the respective method as H+DP. Since PCA is widely used for unsupervised learning, we apply PCA to infer the latent low-dimensional feature representations for our images. After integrating such low-dimensional feature representations by PCA into multi-channel Demons and HAMMER, we can obtain other two new registration methods, denoted as M+PCA and H+PCA, respectively.

A. Experiments on ADNI Dataset

In this experiment, we randomly select 66 MR images from the ADNI dataset (http://adni.loni.ucla.edu/), where 40 images are used to learn feature representations and another 26 images are used for testing image registration. The preprocessing steps include skull removal [63], bias correction [64], and intensity normalization [65]. For each training image, we sample around 7,000 image patches, where the patch size is set to 21×21×21. In the following experiment, we follow the practical guide in [66] to train the deep learning network. Specifically, the convolutional SAE consists of 8 layers (stacked with 4 AEs). We only apply the max pooling in the lowest layer with the pooling factor C = 3. From the lowest to the highest level, the numbers of hidden nodes in each stacked AE are 512, 512, 256, and 128, respectively. Thus, the dimension is 128 after deep learning algorithm is applied. To keep the similar dimension of learned features by PCA, we set the portion of remaining energy f_Q to 0.7 in this experiment. To avoid overfitting, we divide the whole training samples into mini-batches, each consisting of 100 samples. During training, we monitor the progress of learning and adjust the learning rate by inspecting the reconstruction errors. The sparsity target value ρ̂_j in Eq. 2 is set to 0.01.

Advantages of Feature Representations Learned by Deep Learning Network

The power of feature representations learned by deep learning is demonstrated in Fig. 5. A typical image registration result for the elderly brain images is shown in the top of Fig. 5, where the deformed subject image (Fig. 5 (c)) is far from well registered with the template image (Fig. 5(a)), especially for ventricles. Obviously, it is very difficult to learn meaning features given the inaccurate correspondences derived from imperfect image registration, as suffered by many supervised learning methods.

Fig. 5.

The similarity maps of identifying the correspondence for the red-crossed point in the template (a) w.r.t. the subject (b) by handcraft features (d–e) and the learned features by unsupervised deep learning (f). The registered subject image is shown in (c). It is clear that the in-accurate registration results might undermine the supervised feature representation learning that highly relies on the correspondences across all training images.

The performance of our learned features is shown in Fig. 5(f). For a template point (indicated by the red cross in Fig. 5(a)), we can successfully find its corresponding point in the subject image, whose ventricle is significantly larger. Each point in Fig. 5(f) indicate its likelihood of being selected as correspondence in the respective location. According to the color bar shown in Fig. 5, it is easy to locate the correspondence of the red-cross template point in the subject image domain, since the high correspondence probabilities are densely distributed right at the corresponding location and then quickly fade away. Other handcrafted features either detect too many non-corresponding points (when using the entire intensity patch as the feature vector as shown in Fig. 5(d)) or have too low responses and thus miss the correspondence (when using SIFT features as shown in Fig. 5(e)). In general, our method reveals the least confusing correspondence information for the subject point under consideration, and implies the best correspondence detection performance that eventually improve the registration accuracy as follows.

Evaluation of Registration Performance

In image registration, one image is selected as the template and the other 25 images are considered as subject images. Before deploying deformable image registration, FLIRT in FSL package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) is used to linearly align all subject images to the template image. After that, we apply 6 registration methods, i.e., diffeomorphic Demons (simply named as Demons below), M+PCA, M+DP, HAMMER, H+PCA, and H+DP, to normalize those 25 subject images to the template image space, respectively. To quantitatively evaluate the registration accuracy, we first use FAST in FSL package to segment each image into white matter (WM), gray matter (GM), and cerebral-spinal fluid (CSF). After that, we use our in-house tools to label the ventricle (VN) from the CSF segmentation. Here, we use these segmentation results to evaluate the registration accuracy by comparing the Dice ratio of tissue overlap degrees between template and each registered subject image. Specifically, the Dice ratio is defined as:

$$D(R_A,R_B)=\frac{2|R_A\cap R_B|}{\left|R_A\right|+\left|R_B\right|},$$ (4)

where R_A and R_B denote two ROIs (Regions of Interest) and | • | stands for the volume of the region. The Dice ratios on WM, GM, and VN by 6 registration methods are shown in Table I. It is clear that (1) the registration methods integrated with the feature representations by deep learning consistently outperform the counterpart baseline methods and also the methods using PCA-based feature representations only; (2) H+DP achieves the highest registration accuracy with almost 2.5% improvement in overall Dice ratio against the baseline HAMMER registration method. Since ADNI provides the hippocampus labeling for the template and all 25 subject images, we can further evaluate the Dice overlap ratio on hippocampus. The mean and the standard deviation of the Dice ratios on hippocampus by 6 registration methods are (72.2±3.1)% by Demons, (72.3±2.9)% by M+PCA, (72.5±2.8)% by M+DP, (75.5±2.9)% by HAMMER, (75.6±2.5)% by H+PCA, and (76.8±2.2)% by H+DP, respectively. Compared to the baseline methods, M+DP and H+DP obtain 0.3% and 1.3% improvements in terms of Dice ratios, respectively, where H+DP achieves significant improvement on all WM, GM, CSF tissue overlap ratios under paired t-test (p < 0.05), as indicated by ‘*’ in Table I. Particularly, the reason of the less improvement by M+DP compared to H+DP might be related with the high number of channels (128 channels) used in M+DP, compared with only less than 10 channels used in [58–60].

TABLE I.

The dice ratios of WM, GM, and VN on ADNI dataset (unit: %)

Method	WM	GM	VN	Overall
Demons	85.7	76.0	90.2	84.0
M+PCA	85.5	76.6	90.2	84.1
M+DP	85.8	76.5	90.9	84.4
HAMMER	85.4	75.5	91.5	84.1
H+PCA	86.5	76.9	91.7	85.0
H+DP	88.1*	78.6*	93.0*	86.6

B. Experiments on LONI Dataset

In this experiment, we use the LONI LPBA40 dataset [67] which consists of 40 brain images, each with 56 manually labeled ROIs. We use the first 20 images for learning the latent feature representations and another 20 images for testing the registration performance. The preprocessing procedures include bias correction, intensity normalization and linear registration by FLIRT, which are the same with Section 3.1. For each training image, we sample around 9,000 image patches, where the patch size is again set to 21 × 21 × 21. Other parameters in training convolutional SAE are also the same with Section 3.1. Therefore, the dimension of feature representations after deep learning is 128. To keep the similar dimension of learned features by PCA, we set f_Q to 0.65 in this experiment.

One of the 20 testing images is selected as the template and we apply 6 registration methods to register the rest of 19 testing images to the selected template. The averaged Dice ratio in each ROI by 6 registration methods is shown in Fig. 6. The overall Dice ratios across all 56 ROIs by 6 registration methods are provided in Table 3. Again, H+DP achieves the largest improvement (2.5%) over the baseline HAMMER registration method. Specifically, we perform the paired t-test between H+DP and all other 5 registration methods, respectively. The results indicate that H+DP has the statistically significant improvement over all other 5 registration methods in 28 out of 54 ROIs (designated by the red stars in Fig. 6).

Fig. 6.

The Dice ratios of 56 ROIs on LONI dataset by 6 registration methods.

TABLE III.

The Average computational time on all datasets (unit: minute)

Method	ADNI	LONI	7.0-tesla
Demons	3.0	3.0	16.0
M+PCA	125.0	122.0	260.0
M+DP	125.0	121.0	265.0
HAMMER	15.6	12.6	34.6
H+PCA	106.0	98.0	170.0
H+DP	105.0	98.0	168.0

C. Experiments on 7.0-Tesla MR Image Dataset

In the previous experiments, we have demonstrated the power of learned feature representations by deep learning in terms of the improved registration accuracy, represented by overlap ratio of structures. As we mentioned early, another attractive advantage of deep learning is that we can rapidly learn the intrinsic feature representations for the new imaging modality. In this section, we apply the convolutional SAE to 7.0-tesla MR brain images. The learned feature representations are then integrated with HAMMER, and thus we develop a specific registration method for 7.0-tesla MR brain images.

The advent of 7.0-tesla MR imaging technology [68] enables the achievement of high signal-to-noise ratio (SNR) as well as the dramatically increased tissue contrast compared to the 1.5- or 3.0-tesla MR image. A typical 7.0-tesla MR brain image (with the image spatial resolution 0.35 × 0.35 × 0.35mm³) is shown in Fig. 7(b), along with a similar slice from a 1.5-tesla scanner (with the resolution of 1 × 1 × lmm³) in Fig. 7(a) for comparison. As demonstrated in [69], 7.0-tesla MR image can reveal the brains’ architecture with resolution equivalent to that obtained from thin slices in vitro. Thus, researchers are able to observe clearly the fine brain structures in µm unit, which was only possible with in vitro imaging in the past. Without doubt, 7.0-tesla MR imaging technique has the high potential to be the standard in discovering morphological patterns of human brain in the near future.

Fig. 7.

Large structural difference around hippocampus between 1.5-tesla (a) and 7.0-tesla (b) MR images. The 1.5-tesla image is enlarged w.r.t. the image resolution of the 7.0-tesla image for convenience of visual comparison. .

Unfortunately, all existing state-of-the-art deformable registration methods, developed for 1.5-tesla or 3.0-tesla MR images, do not work well for the 7.0-tesla MR images, mainly because 1) severe intensity inhomogeneity issue in 7.0-tesla MR images, and 2) much richer texture information than that in 1.5-tesla or 3.0-MR tesla images, as displayed in Fig. 7(b).

Overall 20 7.0-tesla MR images acquired by the method in [68] were used in this experiment, where 10 are used for training by deep learning and another 10 images used for testing the registration performance. We randomly select one image as the template. For the 7.0-tesla scanner (Magnetom, Siemens), an optimized multichannel radiofrequency (RF) coil and a 3D fast low-angle shot (Spoiled FLASH) sequence were utilized, with TR=50ms, TE=25ms, flip angle 10°, pixel band width 30Hz/pixel, field of view (FOV) 200mm, matrix size 512 × 576 × 60, 3/4 partial Fourier, and number of average (NEX) 1. The image resolution of the acquired images is isotropic, e.g., 0.35 × 0.35 × 0.35mm³. The hippocampi were manually segmented by neurologist [68]. All images were pre-processed by the following steps: 1) manual skull removal; 2) inhomogeneity correction using N4 bias correction [64]; 3) intensity normalization for making image contrast and luminance consistent across all subjects [65]; 4) affine registration to the selected template by FSL.

For each training image, we sample around 9,000 image patches, where the patch size is set to 27×27×27. The convolutional SAE consists of 10 layers (stacked with 5 AEs). We only apply the max pooling in the lowest layer with the pooling factor C = 3. From low level to high level, the numbers of hidden nodes in each stacked AE are 1024, 512, 512, 256, and 128, respectively. Thus, the dimension of feature representations after deep learning is still 128. In order to achieve the best registration performance, we integrate the learned feature representations trained from 7.0-tesla MR images with the HAMMER registration method.

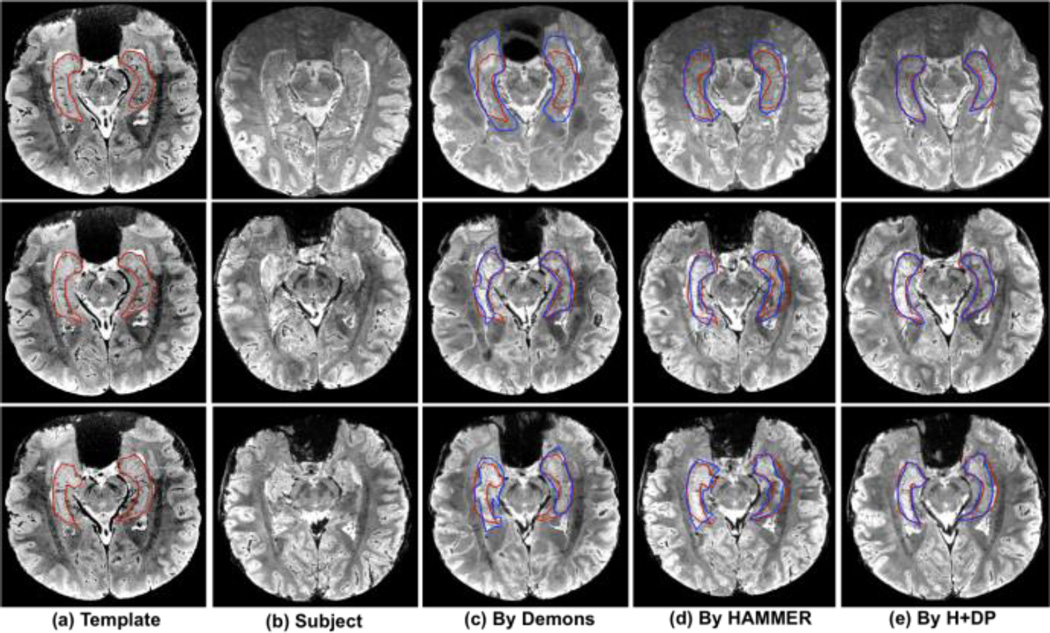
Several typical registration results on 7.0-tesla MR images are displayed in Fig. 8, where the template and subject images are shown in Fig. 8(a) and (b), respectively. Here, we compare the registration results with diffeomorphic Demons (Fig. 8(c)) and HAMMER (Fig. 8(d)). The registration results by H+DP, i.e., integrating the learned feature representations by deep learning with HAMMER, are display in Fig. 8(e), where the manually labeled hippocampus on template image and the deformed subject’s hippocampus by different registration methods are shown by red and blue contours, respectively. Through visual inspection (the overlap of red and blue contours), the registration result by H+DP is much better than both diffeomorphic Demons and HAMMER. Diffeomorphic Demons registration method fails to register 7T image, as shown in Fig. 8 (c), since it is simply driven by image intensities which suffer from image noise and inhomogeneity in 7T images. In addition, due to huge difference of image characteristics between 7T and 3T images, the hand-crafted features optimized for 3T image also do not work well for 7T images in the feature-based HAMMER registration method either, as shown in Fig. 8(d).

Fig. 8.

Typical registration results on 7.0-tesla MR brain images by Demons, HAMMER, and H+DP, respectively. Three rows represent three different slices in the template, subject, and registered subjects.

Since we have the manually labeled hippocampus for template and all subject images, we can further quantitatively measure the registration accuracy. The mean and standard deviation of Dice ratios on hippocampus are (53.5 ± 4.9)% by diffeomorphic Demons, (64.9 ± 3.1)% by HAMMER, and (75.3 ± 1.2)% by H+DP, respectively. Obviously, H+DP achieves a significant improvement on registration accuracy. This experiment demonstrates that (1) the latent feature representations inferred by deep learning can well describe the local image characteristics; (2) we can rapidly develop image registration for the new medical imaging modalities by using deep learning framework to learn the intrinsic feature representations; and (3) the whole learning-based framework is fully adaptive to learn the image data and reusable to various medical imaging applications.

IV. Discussion

A. The Generality of Learned Feature Representations

Recall that we have obtained the feature representations by deep learning on the ADNI dataset in Section III.A. It is interesting to evaluate the generality of deep learning by applying the learned feature representations from the ADNI dataset (which mostly contains elderly brain images) to register the images in the LONI dataset (i.e., containing young brain images). Fig. 9 shows the Dice ratio in each ROI in the LONI dataset by using (1) the baseline HAMMER registration method (in blue), (2) H+DP-LONI (in red) where we use the learned feature representations from LONI dataset and integrate with HAMMER, (3) H+DP-ADNI (in green) where we use the learned feature representations from ADNI dataset and integrate with HAMMER. It is apparent that the registration performance by H+DP-ADNI is comparable to H+DP-LONI, where the average improvements over the baseline HAMMER registration method are 1.99% by H+DP-ADNI and 2.55% by H+DP-LONI, respectively. Under paired t-est (p < 0.05), we find that H+DP-LONI has 28 ROIs with significant improvement (as indicated by red ‘*’ in Fig. 9), while H+DP-ADNI has 18 ROIs with significant improvement (as indicated by the green ‘*’ in Fig. 9). This indicates that the learned feature representations by the convolutional SAE network are general, although the appearances of two datasets are quite different (i.e., due to aging).

Fig. 9.

The Dice ratios of 56 ROIs in LONI dataset by HAMMER (blue), H+DP-LONI (red), and H+DP-ADNI (green), respectively. Note, H+DP-LONI denotes for the HAMMER registration integrating with the feature representations learned directly from LONI dataset, while H+DP-ADNI stands for applying HAMMER registration on LONI dataset but using the feature representations learned from ADNI dataset, respectively.

On the other hand, we use the learned feature representations from the LONI dataset to evaluate the registratoin performance on ADNI dataset. Table II shows the tissue overlap ratios by the baseline HAMMER registration method, H+DP-ADNI (learning features from ADNI dataset), and H+DP-LONI (learning features from LONI dataset). Red ‘*’ indicates significat improment over HAMMER under paired t-est with p < 0.05. It is clear that the feature representations learned from LONI dataset is reusable to ADNI dataset as well, and the registration performance is comparable to the case of directly learning feature reprsentations from the same dataset.

TABLE II.

The dice ratios of WM, GM, amp VN on ADNI dataset (unit: %)

Method	WM	GM	VN	Overall
HAMMER	85.4	75.5	91.5	84.1
H+DP-ADNI	88.1*	78.6*	93.0*	86.6
H+DP-LONI	87.7*	78.3	92.8	86.2

B. Computational Time

Table III shows the computational times for all registration methods on ADNI, LONI, and 7.0-tesla datasets. The computation environment is DELL workstation with 8 CPU cores and 16G memory. Multi-thread technique is used in the implementation for each method. Compare to the baseline methods, the additional computational cost mainly comes from the I/O of feature vectors on each image point and also the feature matching procedure, due to high feature dimension.

C. Comparison with Other State-of-the-Art Registration Methods

As we mentioned early, it is not practical to use supervised leaning approaches to find the best feature representations due to the lack of ground truth anatomical correspondences. In our previous work [18, 19], we have to assume the correspondences established by a certain image registration method as the ground truth which makes the selection of best features not optimal at each point. The average registration error is 0.72mm on the 100 simulated brain images [70], by calculating the voxelwise difference between the estimated and the ground-truth deformations. We apply our H+DP method to the same simulated dataset and find that the registration error can be reduced to 0.62mm, which shows the advantage of unsupervised learning of features for guiding registration.

In [3], 14 deformable image registration methods are comprehensively evaluated on various datasets including the LONI data. The best registration method could achieve 71.85 ± 9.59% as reported in [3]. Our H+DP improves the overlap ratio from 70.47 ± 10.73% (by HAMMER) to 71.91 ± 9.57%, which is slightly better than the top-ranked registration method in [3].

D. Comparison with Other Feature Learning Methods

There are many unsupervised feature extraction/learning approaches. Here, we further evaluate the power of shallow models (such as PCA and k-means) and our deep learning model. For k-means, we cluster the pre-observed image patches into 128 centers (same as the reduced dimension by PCA) in the feature space. For each new image patch, the membership (i.e., patch-wise distance) to each center forms the feature vector. Table IV shows the registration accuracy on ADNI dataset after integrating the learned feature representations by PCA (H+PCA), k-means (H+KMEAN), and deep learning (H+DP). It can be seen that the registration performance by H+KMEANS is slightly worse than H+PCA. But, as shallow models, both of these PCA and k-means models perform worse than H+DP that use the deep learning model to obtain hierarchical feature.

TABLE IV.

The dice ratios of WM, GM, and VN on ADNI dataset (unit: %)

Method	WM	GM	VN	Overall
H+PCA	86.5	76.9	91.7	85.0
H+KMEAN	86.4	76.9	91.6	85.0
H+DP	88.1	78.6	93.0	86.6

V. Conclusion

A new deformable image registration framework is developed that uses deep learning for feature selection. Specifically, an unsupervised deep learning feature selection framework is proposed that implements a convolutional-stacked auto-encoder network (SAE) to identify the intrinsic features in 3D image patches. Using the LONI and ADNI brain datasets, the image registration performance was compared to two existing state-of-the-art deformable image registration frameworks that use handcrafted features. The results showed the new image registration framework consistently demonstrated better Dice ratio scores when compared to state-of-the-art. We contribute these increases in performance to our proposed feature selection framework. In short, because the trained deep learning network selected features that more accurately capture the complex morphological patterns in the image patches, this resulted in better anatomical correspondences, which ultimately improved image registration performance.

To demonstrate the scalability of the proposed registration framework, image registration experiments were also conducted on 7.0-tesla brain MR images. Likewise, the results showed the new image registration framework consistently demonstrated better Dice ratio scores when compared to state-of-the-art. Unlike those existing image registration frameworks, the deep learning architecture was quickly developed, trained using no ground-truth data, and still showed superior registration performance. This experiment demonstrates how the proposed feature selection framework can be quickly used to perform image registration on the new imaging modalities.