Abstract
Objective
Acoustic radiation force (ARF)-based approaches to measure tissue elasticity require transmission of a focused high-energy acoustic pulse from a stationary ultrasound probe and ultrasound-based tracking of the resulting tissue displacements to obtain stiffness images or shear wave speed estimates. The method has established benefits in biomedical applications such as tumor detection and tissue fibrosis staging. One limitation, however, is the dependence on applied probe pressure, which is difficult to control manually and prohibits standardization of quantitative measurements. To overcome this limitation, we built a robot prototype that controls probe contact forces for shear wave speed quantification.
Methods
The robot was evaluated with controlled force increments applied to a tissue-mimicking phantom and in vivo abdominal tissue from three human volunteers.
Results
The root-mean-square error between the desired and measured forces was 0.07 N in the phantom and higher for the fatty layer of in vivo abdominal tissue. The mean shear wave speeds increased from 3.7 to 4.5 m/s in the phantom and 1.0 to 3.0 m/s in the in vivo fat for compressive forces ranging from 2.5 to 30 N. The standard deviation of shear wave speeds obtained with the robotic approach were low in most cases (< 0.2 m/s) and comparable to that obtained with a semiquantitative landmark-based method.
Conclusion
Results are promising for the introduction of robotic systems to control the applied probe pressure for ARF-based measurements of tissue elasticity.
Significance
This approach has potential benefits in longitudinal studies of disease progression, comparative studies between patients, and large-scale multidimensional elasticity imaging.
Index Terms: ARFI, medical robotics, probe contact force, probe pressure, shear wave speed quantification
I. Introduction
Acoustic radiation force (ARF)-based elasticity imaging enables remote visualization and quantification of tissue stiffness. It is beneficial in medical applications such as breast cancer detection [1], [2], prostate cancer detection [3], [4], and liver fibrosis staging [5]. The technique is also useful for intraoperative guidance and monitoring of radio frequency ablation surgeries of the liver [6], [7] or heart [8], [9] as the mechanical properties of ablated regions differ when compared to healthy tissue.
Achieved by transmitting focused high-energy acoustic pulses to generate radiation force in tissue, the resulting ARF-based tissue displacements are tracked using ultrasound data acquired with a stationary probe [10], [11]. There are two general classes of ARF-based elasticity imaging derived from transient tissue responses. ARF impulse imaging tracks on-axis displacements in the region of excitation to produce an image of relative tissue stiffness, whereas ARF-based shear wave imaging tracks off-axis tissue displacements at known distances from the region of excitation and can be used to quantitatively report the propagation speed of transverse waves [12]. The quantitative approach relates the tracked tissue displacements to the stiffness of the interrogated tissue, as the square of the shear wave velocity is proportional to the elastic modulus of the tissue, assuming that the tissue is locally homogenous, linear, elastic, and isotropic [12]–[15].
Previous work demonstrates that the quality and utility of ARF-based elasticity measurements depend on the applied probe pressure when organs are located near the skin surface and, therefore, subjected to compressive forces from the ultrasound probe. Examples include the breast [16]–[18] and transplanted kidneys [19]. To demonstrate the effects of probe compression in quantitative ARF-based elasticity imaging, Syversveen et al. [19] utilized a mechanical lever that rotated about a fulcrum with known weights applied at fixed distances along the lever. This approach is reasonable for laboratory experiments but not convenient for translation to the clinic. Barr and Zhang [18] describe a semiquantitative method that can be used clinically and relies on landmarks in an ultrasound image to indirectly control the probe pressure for breast imaging. However, suitable landmarks may not always be available in other organs. Our previous work [20] takes a robotic approach demonstrating that a force-controlled robot has the potential to improve ARF-based measurements of tissue elasticity by providing consistent probe compression with less than 2% variability in probe-induced strain measurements.
We envision that further development and testing of the robotic approach has potential benefits in three clinical scenarios. First, for measurements that depend on the probe pressure, it is currently difficult to compare two elasticity measurements from the same patient acquired on different days. These types of longitudinal studies are desirable for monitoring disease progression in a single patient. The second scenario is comparative studies between patients. If probe pressure can be controlled, the disease progression in one patient could potentially be used as a predictor for future patients with similar symptoms, thereby enabling more personalized treatment plans to halt, hinder, and/or delay disease progression. Third, large-scale three-dimensional (3-D) elasticity imaging is more readily conceivable with a robotic approach, as it is currently difficult to combine two elasticity images from adjacent regions of the same patient, given expected discontinuities caused by limited control over the applied probe pressure.
Although force-controlled robots have previously been built to assist with carotid artery imaging [21], [22], reconstructive surgery [23], automated assessment of Duchenne muscular dystrophy [24], [25], and remote diagnoses in telemedicine applications [26], [27], to the best of our knowledge, no force-controlled robots currently exist for ARF-based ultrasound applications. The existing force-controlled robots for other ultrasound applications utilized maximum probe contact forces ranging from 2.0 to 20 N [21], [23]–[25], [27], and the required force varied depending on the clinical task and organ being imaged.
An independent study measured a combination of forces caused by gripping and moving the ultrasound probe and applying pressure to enhance image quality, with forces as large as 270 N for obese patients [28], [29]. Obese patients are known to produce poorer images due to acoustic clutter, as quantified in a previous study correlating clutter magnitude and body mass index (BMI) [30]. The increased forces for these obese patients are likely caused by the increased probe pressure required to displace subcutaneous fat, decrease the probe distance to the target organ, and thereby improve image quality [31] (i.e., reduce acoustic clutter). This logic is consistent with sonographers who demonstrated typical and peak contact forces of 11.6–21.4 and 15.6–64.9 N, respectively, for abdominal scans [32]. Additional abdominal scan studies reported mean and max forces of 9.8 and 22 N, respectively, for obese patients (BMI > 25) [33], 7.5 and 17.3 N, respectively, for normal weight patients (BMI = 18.5–25) [33], and 7.0 and 27.3 N, respectively, along the probe axis for all patients (BMIs not reported) [34]. Thus, any robot that applies ultrasound probe contact forces up to these previously reported values is clinically relevant.
This paper demonstrates the feasibility of using a robot to control the applied probe contact force up to 30 N during ARF-based measurements of tissue elasticity. The robot was built in our laboratory and its accuracy was previously tested in phantom, ex vivo, and in vivo canine data [20], [35], [36]. In this paper, we extend previous measurements to in vivo human data and couple the robotic system (with a force sensor resolution of approximately 0.06 N) to an ultrasound system configured to measure shear wave speeds. Although both qualitative and quantitative measurements of tissue elasticity are expected to benefit from this robotic approach, the focus of this paper is quantitative elasticity imaging.
II. Methods and Materials
A. Robotic System
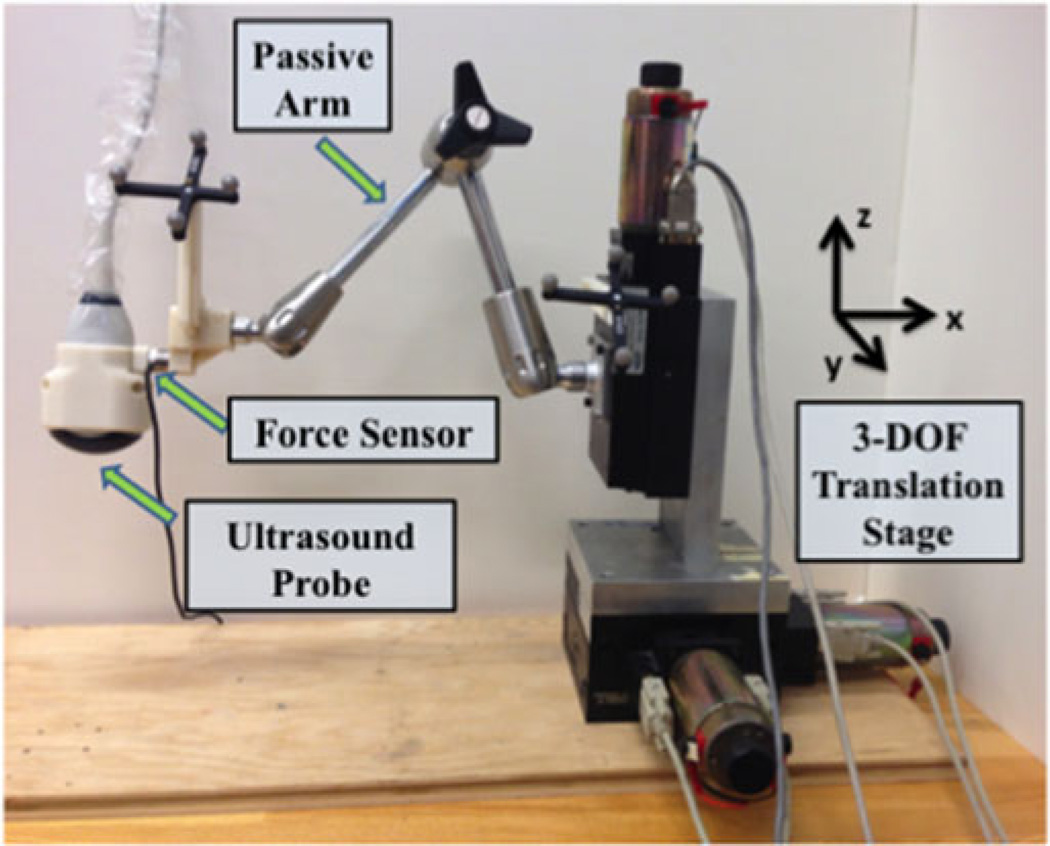
The custom-built robot (see Fig. 1) consisted of a 3-degree-of-freedom (DOF) encoded translation stage (New England Affiliated Technologies, Lawrence, Massachusetts), an articulated passive arm (Model 3.510-G51, Fisso, Zurich, Switzerland), and a six-axis force/torque sensor (Nano25, ATI Industrial Automation, Apex, NC) mounted between the passive arm and ultrasound probe to measure probe-tissue contact forces. The end effector of the robot was the ultrasound probe used to visualize a target of interest.
Fig. 1.
Components of the custom-built robotic system include a 3 DOF translation stage, a passive arm, and a force sensor mounted between the passive arm and ultrasound probe holder.
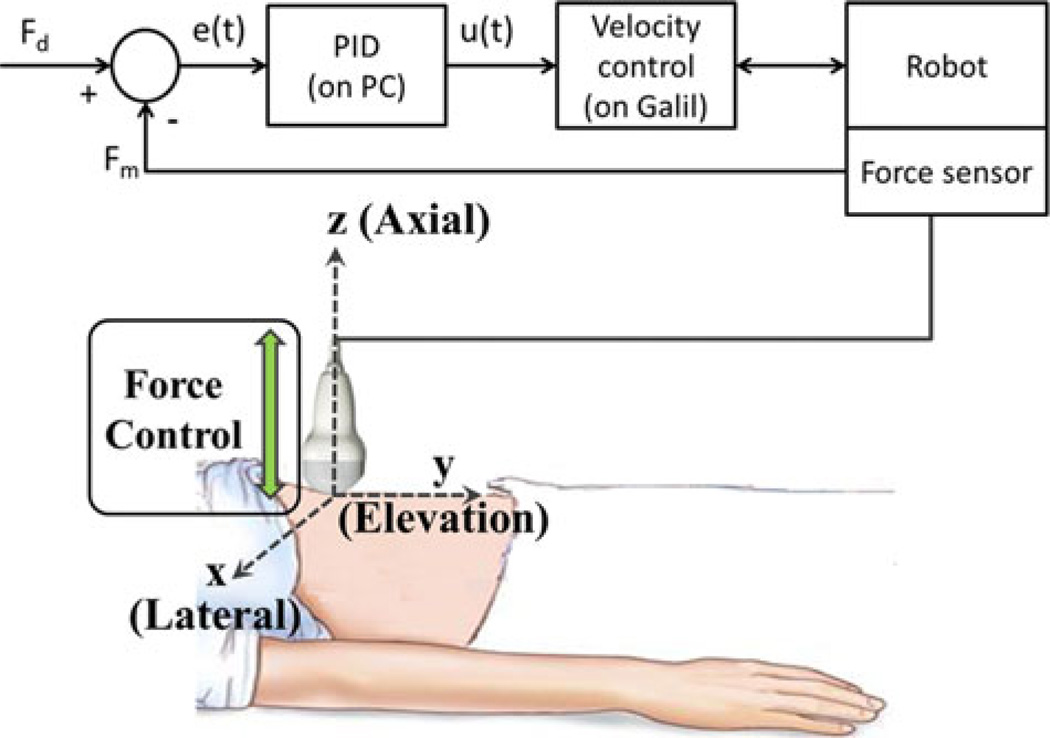
A proportional-integral-derivative (PID) controller was implemented on a personal computer to control probe forces along the axial dimension, which is normal to the face of the probe (i.e., the z direction in Fig. 2). The force error as a function of time e(t) is described by the following equation:
| (1) |
where Fd is the desired force and Fm is the measured force. This force error was converted to a velocity input u(t) for the Galil robot controller (Rocklin, CA) as follows:
| (2) |
where Kp, Ki, and Kd represent the constant tuning parameters of the proportional, integral, and derivative terms, respectively, of the PID controller. Note that we used a discrete formulation of (2) (i.e., differences and summation rather than differentiation and integration, respectively), as described by the following equations:
| (3) |
| (4) |
| (5) |
where n is the discrete time and A[n] is an accumulator that is initialized to 0 at n = 0. A block diagram of this system is shown in Fig. 2.
Fig. 2.
Block diagram and schematic of the robotic system under force control (PID = proportional-integral-derivative controller; PC = personal computer).
B. Imaging Equipment
The imaging equipment included a Siemens (Issaquah, WA) S2000 scanner with the Virtual Touch software package installed [37]. This package was utilized to measure shear wave speeds within a selected region of interest (ROI). As a brief summary, the package enables application of an axial acoustic push pulse located lateral to the chosen ROI. Shear waves are then generated that travel through the ROI, perpendicular to the acoustic push direction. As the shear wavefront travels, the generated displacements are detectable using ultrasound tracking beams, which are continuously transmitted until the passing shear wavefront is identified. The shear wave speed is quantified by observing the shear wavefront at several locations within the ROI and correlating these locations with the elapsed time. In general, shear wave speeds increase with tissue stiffness.
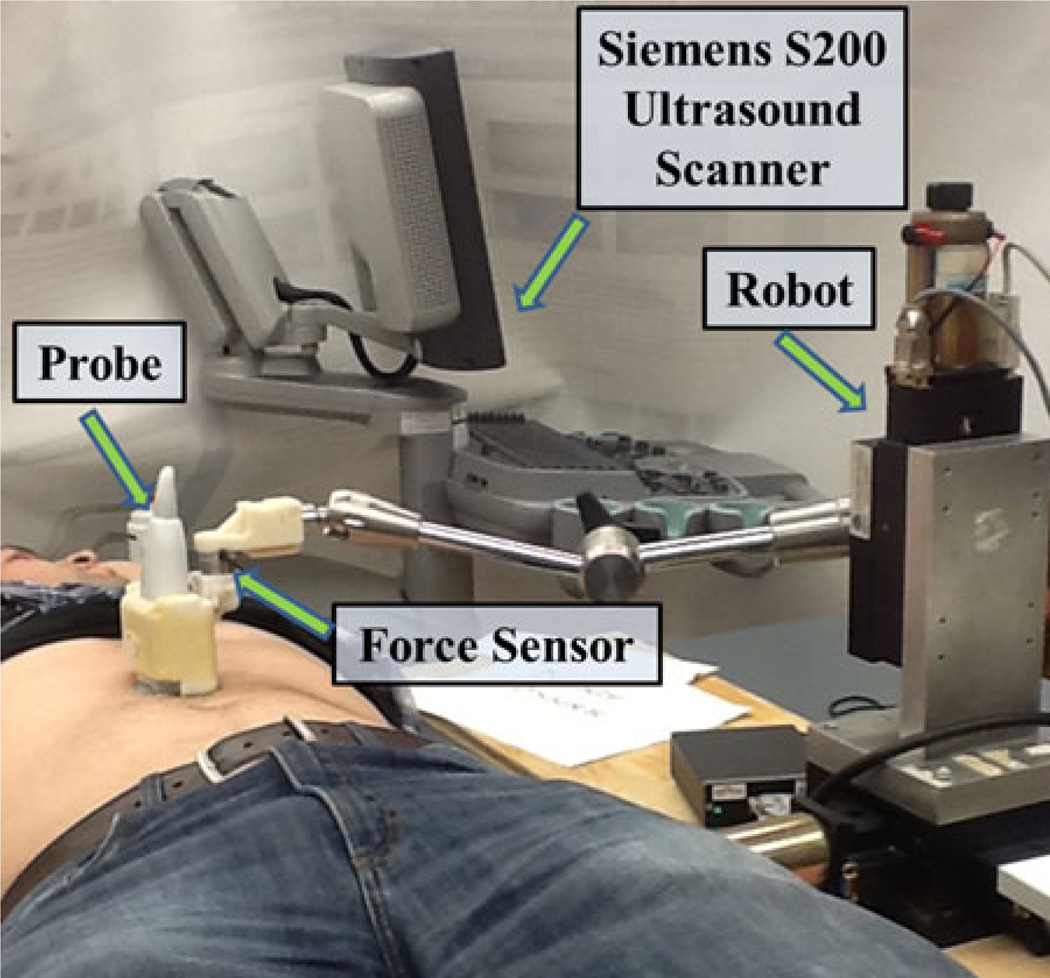
A Siemens 4C1 probe was utilized to measure shear wave speeds in phantom experiments. A higher frequency Siemens 9L4 probe was utilized to measure shear wave speeds in the abdominal fat of three male volunteers, as demonstrated in Fig. 3. The human shear wave imaging studies were approved by the Duke University Institutional Review Board.
Fig. 3.
In vivo experimental setup showing placement of the ultrasound probe used to visualize the abdominal fat of one volunteer.
C. Phantom Fabrication
The phantom fabrication process was a modified version of previously reported methods [38], [39]. Our nonlinear phantom was composed of 250-bloom A-type gelatin (19 g), agar (0.93 g), deionized water (285 mL), graphite (17 g), ethanol (30.3 mL), and 3% formaldehyde diluted with water (3.2 mL). The deionized water was poured into a beaker with a magnetic stirrer, and the agar and gelatin powder were slowly added as the solution was stirred, resulting in approximately 0.3% agar concentration by weight. This concentration was empirically determined, as phantoms with ≤0.2% agar concentration had poor structural integrity, while phantoms with >0.3% agar concentration were too stiff when subjected to compressive forces.
After the gelatin and agar were visibly dissolved, the beaker was covered with plastic wrap and heated to 80 °C for 1 h. Graphite was then mixed into the solution for acoustic scattering [38], and ethanol was added to obtain shear wave propagation speeds close to those of human tissue [40]. The beaker was then placed in a cold water bath until the solution cooled to 60 °C, then placed in a vacuum chamber for 15 min at approximately −20 mmHg pressure. The diluted formaldehyde was then added to increase cross linking among collagen fibers [38], and the entire solution was poured into its prepared mold. The solution-filled mold was then spun about its central axis for approximately 24 h to ensure homogenous distribution of the graphite while casting.
We later learned that this fabrication process produced an unintentional cyst-like void in the phantom, likely formed while casting. This void was approximately 1.1 times stiffer than its surroundings (derived from the ratio of shear wave speed measurements) and shaped like a torus. This structure produced two circular cyst-like cross sections in the ultrasound B-mode images, each approximately 2–3 cm in diameter. We leveraged these cyst-like voids in this study to ensure that the shear wave ROI was placed in the same relative position with each shear wave speed measurement. These voids are otherwise not expected to affect the shear wave speed measurements as they were located distal to the shear wave ROI.
After casting, the phantom was placed in a cylindrical glass jar filled with mineral oil to keep the phantom neutrally buoyant and lubricated, ensuring that it maintains its shape and does not desiccate. The shape of the phantom can be approximated as a conical frustum with top and base circles that are 6.34 and 7.50 cm in diameter, respectively. The height of the frustum was approximately 6.3 cm.
D. Validation Experiments
We investigated two types of motion previously determined to affect the consistency of robotic force control (and hence potentially affect the consistency of shear wave speed measurements) [20].
1) Cyclic Motion
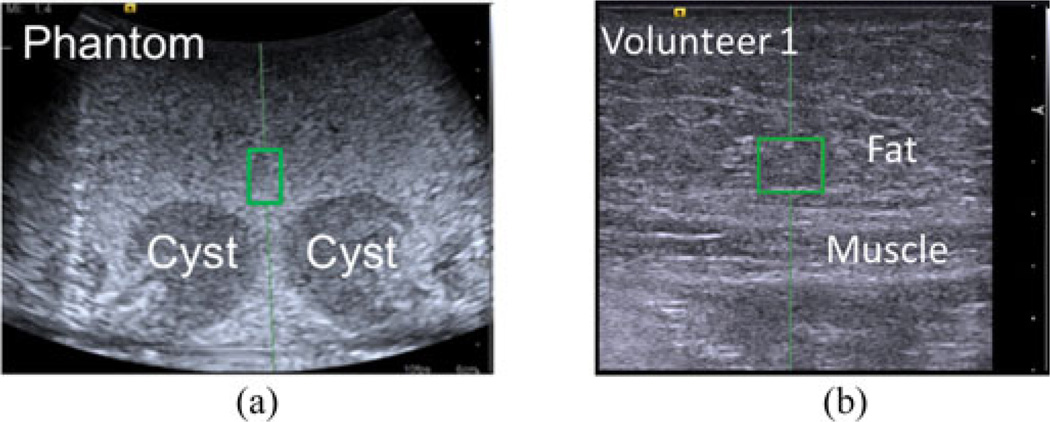
The first experiment investigated cyclic motion, where the applied probe pressure was incrementally adjusted without losing contact with the image target. The phantom described in Section II-C was utilized to study this type of motion. The applied probe contact force was adjusted from 5 to 30 N then returned to 5 N in 5 N (or −5 N) increments. These forces are within the range used clinically, with the higher forces representing those used for obese and difficult-to-image patients [28] to reduce the presence of acoustic clutter [30]. Shear wave speed measurements were obtained with each force increment, with the ROI consistently placed above and between the two visible cyst-like structures in the phantom, as indicated by the green rectangle in Fig. 4(a). The depth of the center of this ROI ranged 2–2.6 cm, depending on the location of the structures as the phantom was compressed. One steady-state reading of the measured force under force control was saved with each increment. This experiment was performed three times.
Fig. 4.
Screenshots from the ultrasound system with green rectangles demonstrating the location of shear wave speed ROIs in all images of the (a) phantom (relative to the two cyst-like structures) and (b) abdominal fat (relative to the fat-muscle boundary). The image depths were 6 and 3.5 cm, respectively, with the dots on the right of each image separated by 5 mm each to indicate the scale.
The above study was repeated in three male volunteers, where the shear wave ROI was consistently placed in the fat layer located directly above the abdominal muscles, as shown in Fig. 4(b). The depth of the center of this ROI ranged 1.3–1.6 cm for Volunteer 1, 0.5–1.4 cm for Volunteer 2, and 1.2–1.4 cm for Volunteer 3, depending on the location of the fat-muscle boundary as the fat was compressed. This region was chosen to investigate the variability in shear wave speeds as a result of fat compression for comparison to that of the female breast, which is composed of up to 56% fat [41]. This fatty component experiences the greatest rate of change of shear wave speeds over a large range of compressive forces, when compared to other tissues [18].
Each volunteer was positioned supine on a gurney and the robot was fixed on a separate cart (as shown in Fig. 3). The wheels of the gurney and cart were locked to ensure no lateral motion. The applied probe force was incrementally adjusted from 2.5 to 30 N then incrementally returned to 2.5 N. The increment size was 2.5 N from 2.5 to 10 N and 5 N, otherwise. The volunteers inhaled and held their breath at the start of each new acquisition for each force increment and were asked to remain still during the acquisitions. The time to complete one cycle was approximately 4–5 min. Three cycles were completed for Volunteers 2 and 3, and two cycles were completed for Volunteer 1 to minimize the overall scan time, particularly when considering the time required to scan this volunteer during the second experiment described in Section II-D2.
The strain in the fat region of the abdomen was measured by using the ultrasound B-mode images to calculate the thickness of the fat layer at the start of each cycle (2.5 N) and at the maximum compressive force (30 N). The difference in these thickness values for each cycle was divided by the initial thickness value at 2.5 N compressive force to derive strain estimates.
Our initial goal was to achieve at least 25% average strain in the fat region, similar to the strain reported for high compression breast imaging [18], while using the same range of force values for all volunteers. Although we were unable to meet this goal, as reported in Table I, we limited the maximum applied force to 30 N to avoid volunteer discomfort. In addition, this force generally corresponded with the 12 cm range of motion limit of our translation stage. This large range of motion was required because abdominal fat is relatively unconstrained. Less probe displacement would likely be required if the probe compressed the tissue against a rigid structure such as the chest wall in breast imaging. However, abdominal organ translation occurs in addition to fat compression [35]. The abdominal fat is also displaced during compression because it is not constrained to motion only in the axial direction, indicating that greater forces are required to achieve minimal strain in the axial direction.
TABLE I.
Average Strain in Abdominal Fat Layer Measured Using Ultrasound B-Mode Images From the Cyclic Motion Experiments
| Volunteer # | Average Fat Thickness (mm) |
Average Strain | |
|---|---|---|---|
| at 5 N | at 30 N | ||
| 1 | 20.0 | 17.8 | 11% |
| 2 | 14.3 | 11.0 | 22% |
| 3 | 16.5 | 15.2 | 8% |
2) Repeated Measurements Under a Single Breathhold
In addition to the cyclic motion experiment, repeated shear wave speed measurements were acquired under robotic force control, while each volunteer held his breath. The maximum number of acquisitions for each breathhold was 10 for Volunteers 2 and 3 and 4 or 5 for Volunteer 1 (based on the maximum time limit that this volunteer was comfortable holding his breath). The time duration of each breathhold was approximately 30–50 s, and the probe lost tissue contact between breathholds. The applied force ranged 2.5–25 N for this experiment. Volunteer 1 completed a total of nine breathholds (three for each force of 5, 15, and 25 N), Volunteer 2 completed three breathholds (one for each force of 2.5, 15, and 25 N), and Volunteer 3 completed one breathhold at a force of 5 N. The number of breathholds for each volunteer decreased over time due to increasing system failures of the imaging equipment after multiple shear wave speed acquisitions.
III. Results
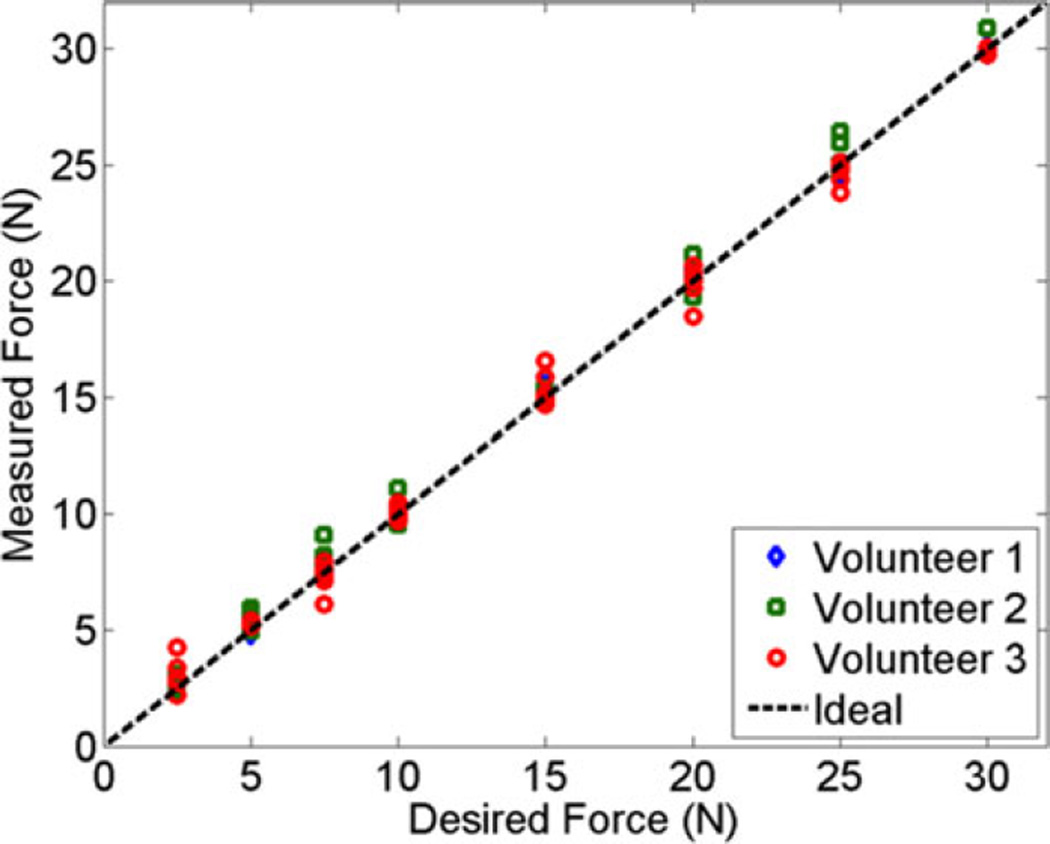
The desired force [Fd in (1)] was compared to the measured force [Fm in (1)] for the cyclic motion experiment, as represented in Fig. 5. The diagonal line indicates the ideal 1:1 relationship between these two variables. Results demonstrate that the force was controlled with root-mean-square (RMS) errors of 0.35, 0.56, and 0.60 N for Volunteers 1, 2, and 3, respectively, compared to 0.07 N for the phantom (not shown). We expect higher RMS errors for the volunteers compared to the phantom because of the dynamic in vivo environment (e.g., pulsating vessels, involuntary muscle motion).
Fig. 5.
Comparison of the desired force [Fd in (1)] to the measured force [Fm in (1)] for the cyclic motion experiment. The dashed line indicates the ideal relationship between these two parameters.
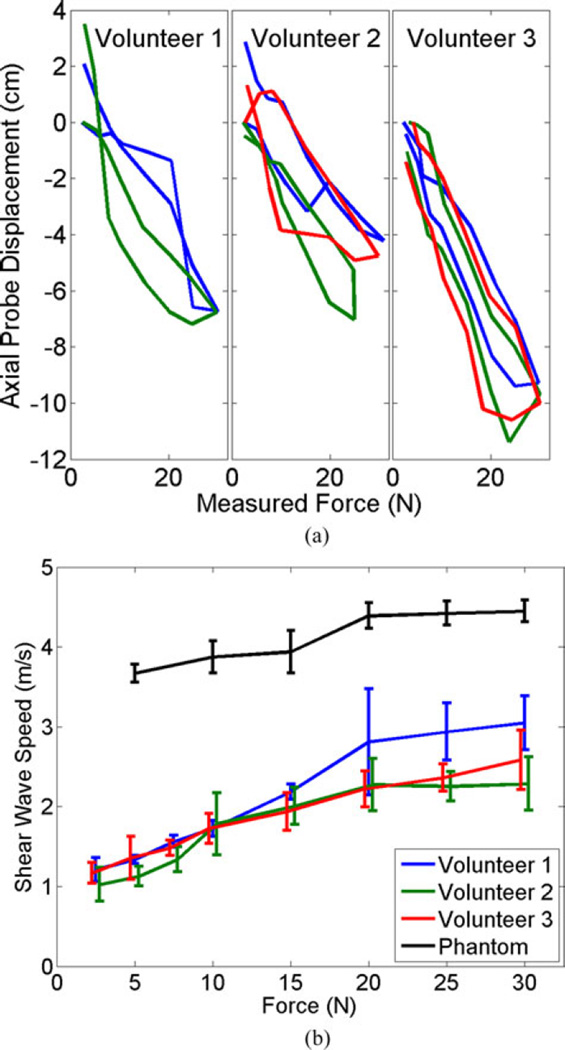
The trajectory of the robotic end effector for the cyclic motion experiment is shown in Fig. 6(a) for the three volunteers. A probe displacement of 0 cm indicates the start of each new cycle, with each cycle differentiated by color. There appears to be a force–displacement hysteresis for each cycle due to tissue nonlinearities. However, the values for this hysteresis were generally not repeatable. Strain measurements corresponding to the results shown in Fig. 6(a) are reported in Table I.
Fig. 6.
(a) Force–displacement profiles of the robot end effector (i.e., the ultrasound probe) for each volunteer, which demonstrates a hysteresis due to tissue nonlinearities. Each color represents a different cycle. (b) Mean shear wave speed as a function of the desired force. Error bars indicate ± one standard deviation with those of Volunteers 2 and 3 slightly offset, to avoid overlap.
Fig. 6(b) demonstrates that the shear wave speed generally increased with an increase in the desired force, indicating increased tissue stiffness. Although force–displacement hystereses were observed for each cycle in these experiments, there was no apparent hysteresis in the shear wave speed measurements, thus all measurements for the same desired force were averaged. The results for the phantom and Volunteers 2 and 3 show the mean ± one standard deviation of six measurements when the desired force was ≤ 25 N and three measurements at the peak of the cyclic motion (i.e., desired force of 30N). The results for Volunteer 1, who had one less cycle than Volunteers 2 and 3, show the mean ± one standard deviation of four and two measurements when the desired force was ≤25 and 30 N, respectively.
The maximum excursion for Volunteer 3 in Fig. 6(a) is up to 4 cm greater than that of Volunteers 1 and 2. However, in Fig. 6(b), the mean shear wave speeds for Volunteer 3 are similar to those of Volunteers 1 and 2 for low and medium forces, respectively, and between those of Volunteers 1 and 2 for the highest forces investigated. In addition, the values of the shear wave speeds at 30 N do not correlate with the measured strain in the abdominal fat region (see Table I). For example, at 30 N force, the interrogated fat region for Volunteer 2 experiences the most strain but the lowest shear wave speed, when compared to the other volunteers.
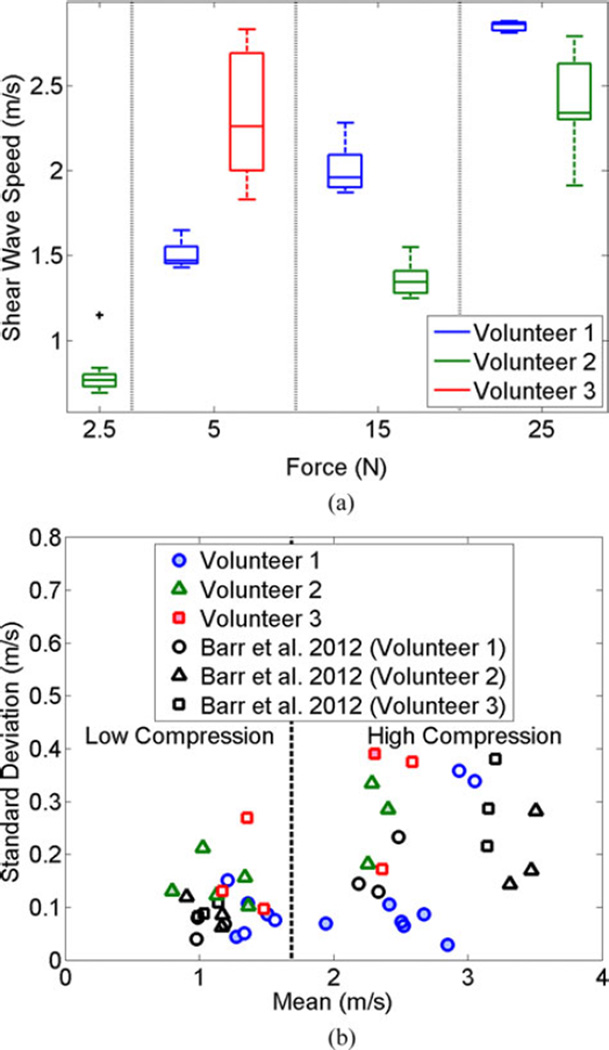
Fig. 7(a) illustrates the variability of shear wave speed measurements for each volunteer after repeated measurements during a single breathhold. The results are shown as box-whisker plots, where the horizontal lines indicate the median of five measurements for Volunteer 1 and 10 measurements for Volunteers 2 and 3 for each force investigated, the top and bottom of each box show the interquartile range (75th and 25th percentiles, respectively), and the lines extending from the boxes (i.e., the whiskers) show the maximum and minimum values. There is one outlier (+ symbol, Volunteer 2 at 2.5 N), defined as any value greater than 1.5 times the interquartile range. Shear wave speeds generally increased with increasing force, and Volunteer 1 generally exhibited similar shear wave speed magnitudes to those observed during the cyclic motion experiment (see Fig. 6). The result for Volunteer 3 had the greatest variability.
Fig. 7.
(a) Box-whisker plots showing the variability of shear wave speed measurements under robotic force control during breathhold. There is one outlier (+ symbol), defined as any value greater than 1.5 times the interquartile range. (b) Variability of our shear wave speed measurements acquired with cyclic motion (unfilled colored shapes) and a single breath hold (filled colored shapes) was compared to that of Barr and Zhang [18] who use a landmark-based approach to control tissue compression. The data are separated into two compression states (i.e., high and low) based on the external data [18], although not consistent for all instances of the data acquired with our robot.
We compared our results to those of Barr and Zhang [18] who described a landmark-based method to standardize the shear wave speed measurements in the breast and quantified results based on the mean and standard deviation from three volunteers under two compression states (i.e., low and high). The low compression state corresponds to 0% (i.e., minimal) strain, while the high compression state corresponds to 25% strain. To enable comparisons of the variability of shear wave speed measurements from the different approaches, our data are plotted alongside this analogous external data in Fig. 7(b).
Each filled colored data point in Fig. 7(b) represents the mean and standard deviation of 4–5 shear wave speed measurements from Volunteer 1 and 10 shear wave speed measurements from Volunteers 2 and 3. The five unfilled colored data points for each volunteer show results from the cyclic motion experiment at 2.5, 5, 7.5, 25, and 30 N (representing low and high compression, over a 5 N force range each). The external data (black unfilled shapes) is similarly separated based on the results of three different volunteers [18], where each data point for each volunteer represents the mean and standard deviation of 10 shear wave speeds obtained by a single sonographer. These external data points were used to create the vertical line separating the compression states, which we defined as the midpoint between the largest and smallest values in the low and high compression states, respectively (i.e., 1.69 m/s). This definition does not hold true for the robot-related data from Volunteers 2 and 3 obtained under a single breathhold at forces of 15 and 5 N, respectively (filled colored shapes), which is also evident from Fig. 7(a). However, the definition is consistent for all of the robot-related data acquired with the cyclic motion (unfilled colored shapes) and all data from Volunteer 1 (filled and unfilled colored circles).
Although the data were taken from two different imaging targets (breast fat and abdominal fat), the standard deviations from the three studies represented in Fig. 7(b) are similar.
IV. Discussion
We successfully implemented a force-controlled robot to investigate the consistency of shear wave speed measurements that vary with the applied force. The RMS errors between the desired and measured forces were sufficiently low, indicating that this control method is viable to achieve standardization of ultrasound-based elasticity measurements and images. The potential for standardization encompasses quantitative estimates like shear wave speeds as well as qualitative images that display relative tissue stiffness.
Two considerations when deciding to clinically implement a robotic system for elasticity imaging include ease of probe manipulation and cost. To address the first concern, the robot can be programmed to enable similar maneuverability to a free-hand approach with cooperative control, as described in our previous publications [36], [42]. With cooperative control, the robot and operator share control of the ultrasound probe via a force sensor that determines the direction of external forces applied (representative of the direction that the operator intends to move the probe). After sensing this direction, the robot helps the operator to arrive at the final destination by applying a velocity that is proportional to the direction of the applied force [36]. Regarding cost considerations, our robot is a small fraction of the cost of an ultrasound machine with an elastography package like Virtual Touch installed. Cost can also be reduced with a 1-DOF load cell that outputs force readings with or without a robot. Without the robot, the sonographer would manually adjust the applied force, enabling standardization by associating a numeric force value with the amount of probe compression applied. In addition, once such a system is present in the clinic, it would not be limited to standardizing elasticity measurements, as there are other applications that would benefit (e.g., carotid artery imaging [21], [22], reconstructive surgery [23], and Duchenne muscular dystrophy assessment [25]).
As seen in Fig. 6(a) and (b), placing the ultrasound probe at similar distances from an initial position neither indicates similar probe contact forces (consistent with results from multiple abdominal targets in our previous in vivo canine experiment [35]), nor ensures repeatable shear wave speeds for different patients. Similarly, applying the same tissue strain does not produce similar compressive forces and vice versa (see Table I). The lack of correlations among these parameters are likely due to the nonlinear relationship between force and displacement in biological tissues.
The standard deviations were low (i.e., <0.2 m/s) in most cases with the robotic approach, as observed in Fig. 7(b) for relatively high and low compression states, which indicates that repeating the same force on the same region of a single patient has the potential to yield similar shear wave speeds. However, with no uniquely identifiable structures in the abdominal fat layer, it is unclear if the same region is interrogated whenever the probe is lifted and replaced, which could contribute to the lack of repeatable shear wave speeds for Volunteer 1 in Fig. 6, as well as for Volunteers 2 and 3 when comparing shear wave speed values from the two experiments. Potential variations in abdominal muscle contraction during each measurement might also be a contributing factor to the lack of repeatable shear wave speeds.
We originally hypothesized that cyclic motion would alter shear wave speed estimates due to the force–displacement hysteresis observed in ex vivo bovine liver and in vivo canine prostates [20], but the results in Figs. 6(b) and 7 suggest otherwise (although similar force-displacement hystereses were observed for the three volunteers). These results indicate that similarities among the applied force are sufficient to reproduce shear wave speeds (regardless of the force-displacement hysteresis).
There are two primary factors that contribute to variability with the proposed force-controlled robot. The first is the large variability of shear wave speed measurements, particularly evident when imaging the same relative region of the tissue mimicking phantom [see Fig. 6(b)]. This variability is commonly attributed to jitter in the ultrasound-based displacement estimates [39], [43] and more recently thought to be caused by speckle-induced bias (i.e., preferential tracking of bright or constructively interfering speckle within an ultrasound tracking beam) [44]. The second potential source of error is the response time of the robot [determined by the tuning parameters in (2)], which was not adjusted to account for the high-frequency cardiovascular induced motion of abdominal organs [45]. However, if the robotic system were adjusted to account for this motion, the ultrasound probe would be less stationary during the shear wave speed measurements, which is not ideal.
Given that the variability of ultrasound-based elasticity measurements has the potential to be improved with the ongoing development of novel transducer hardware [12], [46], robotic systems with lower RMS force errors would be additionally beneficial in the future. However, for the current implementation, robotic force control is not considered to be a primary contributing factor to the shear wave speed variability because the RMS force error was ≤0.6 N, which should have caused ≤2% RMS error at the 5 N contact force for Volunteer 3 with repeated measurements under a single breathhold (see Fig. 7). The RMS error did not vary with an increase in the applied force, as shown in Fig. 5, which additionally indicates that the magnitude of this error is independent of the desired force. User subjectivity is another source of variability when implementing a free-hand approach to measuring tissue elasticity [18]. Hence, eliminating this subjectivity with a robot is one of the most beneficial contributions of the proposed technology.
Our comparison to external data [18] has several limitations in addition to comparing the nonlinear fat response from two different locations in the body. In the external study, three sonographers measured the shear wave speed of the central portion of fat lobules using minimal compression and 25% compression (determined by measuring distance from the chest wall, similar to the image-based method for measuring the tissue strains reported in Table I). The shear wave speed measurements were performed ten times for each patient and each compression state, and the ultrasound probe was removed from the breast between each measurement. This external study differs from the two experiments described in Section II, which acquired 4–10 repeated measurements under a single breathhold with sustained probe contact [see Fig. 7(a)] and 15 measurements under multiple breathholds as the probe was translated with sustained probe contact during a single cycle and removed between cycles (see Fig. 6). It is also difficult to make direct comparisons because a force sensor was not used to determine the corresponding force values for the two compression states investigated in the external study (e.g., minimal and maximum compression could have been <2.5 N and >30 N, respectively).
Despite the differences in study design, the primary conclusion of the study comparison—i.e., similar standard deviations for the landmark-based and robot-based approaches [see Fig. 7(b)]—is not affected. Therefore, a robotic approach appears to be more advantageous than a semiquantitative landmark based approach, particularly in cases where suitable landmarks are not available. The robotic approach is additionally more beneficial when high compressive forces are required, considering the lack of correlation among tissue displacement measurements, strain, and shear wave speeds when comparing results from different volunteers. High compressive forces are potentially relevant for standardizing shear wave speed measurements from the left lobe of the liver [47], considering the previously reported forces required for abdominal imaging [32]–[34].
V. Conclusion
To the authors’ knowledge, this paper is the first to implement a force-controlled robot for ultrasonic ARF-based measurements of tissue elasticity. The robot has promise for standardization with comparable performance to a landmark-based method, thus it is particularly advantageous in imaging applications where suitable landmarks may not be available. It is also advantageous when large compressive forces are required. To this end, results support the introduction of commercially available robots to control the applied force for ARF-based elasticity measurements in three primary clinical scenarios: 1) longitudinal studies of the same patient, 2) comparative studies between patients, and 3) large-scale 3-D elasticity imaging. This paper additionally opens the door for the introduction of novel clinical applications of ARF-based elasticity imaging that are historically unexplored or underreported in the literature due to the significant dependence on the applied probe pressure (e.g., dermatological applications that stage skin cancers).
Acknowledgments
The authors thank N. Liu for phantom fabrication.
This work was supported by the UNCF/Merck and Ford Foundation Postdoctoral Fellowships. The work of M. A. Lediju Bell was additionally supported by NIH Grant K99-EB018994.
Contributor Information
Muyinatu A. Lediju Bell, Department of Computer Science, Johns Hopkins University, Baltimore, MD 21218 USA (mledijubell@jhu.edu).
Shalki Kumar, Department of Biomedical Engineering, Duke University..
Kuo Lily, Department of Biomedical Engineering, Duke University..
H. Tutkun Sen, Department of Computer Science, Johns Hopkins University..
Iulian Iordachita, Department of Mechanical Engineering, Johns Hopkins University..
Peter Kazanzides, Department of Computer Science, Johns Hopkins University..
References
- 1.Meng W, et al. Preliminary results of acoustic radiation force impulse (ARFI) ultrasound imaging of breast lesions. Ultrasound Med. Biol. 2011;37(9):1436–1443. doi: 10.1016/j.ultrasmedbio.2011.05.022. [DOI] [PubMed] [Google Scholar]
- 2.Tozaki M, et al. Preliminary study of ultrasonographic tissue quantification of the breast using the acoustic radiation force impulse (ARFI) technology. Eur. J. Radiol. 2011;80(2):e182–e187. doi: 10.1016/j.ejrad.2011.05.020. [DOI] [PubMed] [Google Scholar]
- 3.Cochlin DL, et al. Elastography in the detection of prostatic cancer. Clin. Radiol. 2002;57(11):1014–1020. doi: 10.1053/crad.2002.0989. [DOI] [PubMed] [Google Scholar]
- 4.Salomon G, et al. Evaluation of prostate cancer detection with ultrasound real-time elastography: A comparison with step section pathological analysis after radical prostatectomy. Eur. Urol. 2008;54(6):1354–1362. doi: 10.1016/j.eururo.2008.02.035. [DOI] [PubMed] [Google Scholar]
- 5.Fierbinteanu-Braticevici C, et al. Acoustic radiation force imaging sonoelastography for noninvasive staging of liver fibrosis. World J. Gastroenterol. 2009;15(44):5525–5532. doi: 10.3748/wjg.15.5525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fahey B, et al. Liver ablation guidance with acoustic radiation force impulse imaging: Challenges and opportunities. Phys. Med. Biol. 2006;51(15):3785–3808. doi: 10.1088/0031-9155/51/15/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kwon H-J, et al. Acoustic radiation force impulse elastography for hepatocellular carcinoma-associated radiofrequency ablation. World J. Gastroenterol. 2011;17(14):1874–1878. doi: 10.3748/wjg.v17.i14.1874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fahey BJ, et al. Acoustic radiation force impulse imaging of myocardial radiofrequency ablation: Initial in vivo results. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2005 Apr;52(4):631–641. doi: 10.1109/tuffc.2005.1428046. [DOI] [PubMed] [Google Scholar]
- 9.Hsu SJ, et al. In vivo assessment of myocardial stiffness with acoustic radiation force impulse imaging. Ultrasound Med. Biol. 2007;33(11):1706–1719. doi: 10.1016/j.ultrasmedbio.2007.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nightingale K, et al. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med. Biol. 2002;28(2):227–235. doi: 10.1016/s0301-5629(01)00499-9. [DOI] [PubMed] [Google Scholar]
- 11.Nightingale K. Acoustic radiation force impulse (ARFI) imaging: A review. Current Med. Imag. Rev. 2011;7(4):328–339. doi: 10.2174/157340511798038657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Doherty JR, et al. Acoustic radiation force elasticity imaging in diagnostic ultrasound. IEEE Trans. Ultrason., Ferroelectr. Freq. Control. 2013 Apr;60(4):685–701. doi: 10.1109/TUFFC.2013.2617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nightingale K, et al. Shear-wave generation using acoustic radiation force: In vivo and ex vivo results. Ultrasound Med. Biol. 2003;29(12):1715–1723. doi: 10.1016/j.ultrasmedbio.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 14.Sarvazyan AP, et al. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 1998;24(9):1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- 15.Bercof J, et al. Ultrafast imaging of beamformed shear waves induced by the acoustic radiation force. Application to transient elastography. Proc. IEEE Ultrason. Symp. 2002;2:1899–1902. [Google Scholar]
- 16.Balleyguier C, et al. Breast elasticity: Principles, technique, results: an update and overview of commercially available software. Eur. J. Radiol. 2012;82:427–434. doi: 10.1016/j.ejrad.2012.03.001. [DOI] [PubMed] [Google Scholar]
- 17.Barr RG. Shear wave imaging of the breast still on the learning curve. J. Ultrasound Med. 2012;31(3):347–350. doi: 10.7863/jum.2012.31.3.347. [DOI] [PubMed] [Google Scholar]
- 18.Barr RG, Zhang Z. Effects of precompression on elasticity imaging of the breast. J. Ultrasound Med. 2012;31(6):895–902. doi: 10.7863/jum.2012.31.6.895. [DOI] [PubMed] [Google Scholar]
- 19.Syversveen T, et al. Tissue elasticity estimated by acoustic radiation force impulse quantification depends on the applied transducer force: An experimental study in kidney transplant patients. Eur. Radiol. 2012;22(10):2130–2137. doi: 10.1007/s00330-012-2476-4. [DOI] [PubMed] [Google Scholar]
- 20.Lediju Bell MA, et al. Force-controlled ultrasound robot for consistent tissue pre-loading: Implications for acoustic radiation force elasticity imaging; Proc. IEEE RAS EMBS 5th Int. Conf. Biomed. Robot. Biomechatron; 2014. pp. 259–264. [Google Scholar]
- 21.Zhu W-H, et al. Motion/force/image control of a diagnostic ultrasound robot. Proc. IEEE Int. Conf. Robot. Autom. 2000;2:1580–1585. [Google Scholar]
- 22.Abolmaesumi P, et al. Image-guided control of a robot for medical ultrasound. IEEE Trans. Robot. Autom. 2002 Feb;18(1):11–23. [Google Scholar]
- 23.Pierrot F, et al. Hippocrate: A safe robot arm for medical applications with force feedback. Med. Image Anal. 1999;3(3):285–300. doi: 10.1016/s1361-8415(99)80025-5. [DOI] [PubMed] [Google Scholar]
- 24.Gilbertson MW, Anthony BW. Ergonomic control strategies for a handheld force-controlled ultrasound probe; Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst; 2012. pp. 1284–1291. [Google Scholar]
- 25.Koppaka S, et al. Assessing duchenne muscular dystrophy with force-controlled ultrasound; Proc. IEEE 11th Int. Symp. Biomed. Imag; 2014. pp. 694–697. [Google Scholar]
- 26.Masuda K, et al. Three dimensional motion mechanism of ultrasound probe and its application for tele-echography system. Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2001;2:1112–1116. [Google Scholar]
- 27.Delgorge C, et al. A tele-operated mobile ultrasound scanner using a light-weight robot. IEEE Trans. Inform. Technol. Biomed. 2005 Mar;9(1):50–58. doi: 10.1109/titb.2004.840062. [DOI] [PubMed] [Google Scholar]
- 28.Village J, Trask C. Ergonomic analysis of postural and muscular loads to diagnostic sonographers. Int. J. Ind. Ergonom. 2007;37(9):781–789. [Google Scholar]
- 29.Rousseau T, et al. Practice guidelines for prevention of musculoskeletal disorders in obstetric sonography. J. Ultrasound Med. 2013;32(1):157–164. doi: 10.7863/jum.2013.32.1.157. [DOI] [PubMed] [Google Scholar]
- 30.Lediju MA, et al. Quantitative assessment of the magnitude, impact and spatial extent of ultrasonic clutter. Ultrasonic Imag. 2008;30(3):151–168. doi: 10.1177/016173460803000302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Uppot RN. Impact of obesity on radiology. Radiol. Clin. North Am. 2007;45(2):231–246. doi: 10.1016/j.rcl.2007.03.001. [DOI] [PubMed] [Google Scholar]
- 32.Habes DJ, Baron S. Health hazard evaluation report 99-0093-2749. Nat. Inst. Occupational Safety Health, Cincinnati, OH, USA, Tech. Rep. HETA-99-0093-2749. 1999 [Google Scholar]
- 33.Dhyani M, et al. Precise quantification of sonographic forces: A first step toward reducing ergonomic injury. presented at the American Inst. Ultrasound Medicine; Apr. 2014; Las Vegas, NV, USA. [Google Scholar]
- 34.Gilbertson MW, Anthony BW. An ergonomic, instrumented ultrasound probe for 6-axis force/torque measurement; Proc. IEEE 35th Annu. Int. Conf. Eng. Med. Biol. Soc; 2013. pp. 140–143. [DOI] [PubMed] [Google Scholar]
- 35.Lediju Bell MA, et al. In vivo reproducibility of robotic probe placement for a novel ultrasound-guided radiation therapy system. J. Med. Imag. 2014;1(2) doi: 10.1117/1.JMI.1.2.025001. pp. 025001-1-025001-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sen HT, et al. A cooperatively controlled robot for ultrasound monitoring of radiation therapy; Proc. IEEE/RSJ Int. Conf. Intell. Robot. Syst; 2013. pp. 3071–3076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lazebnik RS. Tissue strain analytics: Virtual touch tissue imaging and quantification. Malvern, PA, USA: Siemens Medical Solutions USA; 2008. [Google Scholar]
- 38.Hall TJ, et al. Phantom materials for elastography. IEEE Trans. Ultrason., Ferroelectr. Freq. Control. 1997 Nov;44(6):1355–1365. [Google Scholar]
- 39.Nguyen MM, et al. Development of oil-in-gelatin phantoms for viscoelasticity measurement in ultrasound shear wave elastography. Ultrasound Med. Biol. 2014;40(1):168–176. doi: 10.1016/j.ultrasmedbio.2013.08.020. [DOI] [PubMed] [Google Scholar]
- 40.Martin K, Spinks D. Measurement of the speed of sound in ethanol/water mixtures. Ultrasound Med. Biol. 2001;27(2):289–291. doi: 10.1016/s0301-5629(00)00331-8. [DOI] [PubMed] [Google Scholar]
- 41.Vandeweyer E, Hertens D. Quantification of glands and fat in breast tissue: An experimental determination. Ann. Anatomy-Anatomischer Anzeiger. 2002;184(2):181–184. doi: 10.1016/S0940-9602(02)80016-4. [DOI] [PubMed] [Google Scholar]
- 42.Sen HT, et al. System integration and preliminary in-vivo experiments of a robot for ultrasound guidance and monitoring during radiotherapy; Proc. IEEE Int. Conf. Adv. Robot; 2015. pp. 53–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Walker W, Trahey G. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Trans. Ultrason., Ferroelectr. Freq. Control. 1995 Mar;42(2):301–308. [Google Scholar]
- 44.Elegbe EC, McAleavey SA. Single tracking location methods suppress speckle noise in shear wave velocity estimation. Ultrasonic Imag. 2013;35(2):109–125. doi: 10.1177/0161734612474159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lediju Bell MA, et al. In vivo liver tracking with a high volume rate 4d ultrasound scanner and a 2d matrix array probe. Phys. Med. Biol. 2012;57(5):1359–1374. doi: 10.1088/0031-9155/57/5/1359. [DOI] [PubMed] [Google Scholar]
- 46.Dhanaliwala AH, et al. Assessing and improving acoustic radiation force image quality using a 1.5-d transducer design. IEEE Trans. Ultrason., Ferroelectr. Freq. Control. 2012 Jul.59(7):1602–1608. doi: 10.1109/TUFFC.2012.2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Porra L, et al. The effect of applied transducer force on acoustic radiation force impulse quantification within the left lobe of the liver. Australas. J. Ultrasound Med. 2015;18(3):100–106. doi: 10.1002/j.2205-0140.2015.tb00208.x. [DOI] [PMC free article] [PubMed] [Google Scholar]