Calibration and seasonal adjustment for matched case-control studies of vitamin D and cancer

Abstract

Vitamin D measurements are influenced by seasonal variation and specific assay used. Motivated by multi-center studies of associations of vitamin D with cancer, we formulated an analytic framework for matched case-control data that accounts for seasonal variation and calibrates to a reference assay. Calibration data were obtained from controls sampled within decile strata of the uncalibrated vitamin D values. Seasonal sine-cosine series were fit to control data. Practical findings included: (1) Failure to adjust for season and calibrate increased variance, bias and mean square error. (2) Analysis of continuous vitamin D requires a variance adjustment for variation in the calibration estimate. An advantage of the continuous linear risk model is that results are independent of the reference date for seasonal adjustment. (3) For categorical risk models, procedures based on categorizing the seasonally adjusted and calibrated vitamin D have near nominal operating characteristics; estimates of log odds ratios are not robust to choice of seasonal reference date, however. Thus public health recommendations based on categories of vitamin D should also define the time of year to which they refer. This work supports the use of simple methods for calibration and seasonal adjustment and is informing analytic approaches for the multi-center Vitamin D Pooling Project for Breast and Colorectal Cancer.

1. Introduction

Measurements of 25-hydroxyvitamin D, which we call vitamin D, are influenced by seasonal variation and assay calibration. Vitamin D blood concentrations increase in response to sun exposure, inducing seasonal changes. These factors need to be taken into account in the analysis of matched case-control studies to associate vitamin D with disease risk. Although previous case-control analyses have used sine-cosine series to account for seasonal variation [1, 2], as we do, we have not found studies that allow for both calibration and seasonal adjustment. In this paper we present a framework for such analyses. This framework, and parameters based on real studies, underlie our simulations to evaluate the performance of various procedures to estimate log odds ratios.

This work was motivated by collaboration on the Vitamin D Pooling Project of Breast and Colorectal Cancer (hereafter Vitamin D Pooling Project), which includes 21 cohort studies in North America, Europe and Asia. Because vitamin D is stable in stored frozen blood samples, such samples can be used to study associations with cancers that develop years later. Vitamin D was measured in previously stored blood from incident breast or colon cancer cases in these cohorts and from their matched controls. In some studies, the controls were tightly matched to cases on date of blood draw, but not in all studies. Moreover, different assays were used in various studies. Hence calibration against a reference laboratory was required to put measurements from various studies on a common scale. In each study, reference laboratory measurements were obtained from 29 control bloods, selected by stratified random sampling within strata defined by deciles of the uncalibrated control vitamin D measurements. To control for effects of seasonal variation in within-study comparisons of cases and controls, study-specific seasonal adjustment was required. The intent of using calibration and study-specific seasonal adjustment is to transform the original data so that every measurement, regardless of when it was drawn and regardless of study assay, could be thought of as having been measured on the same reference date by the reference laboratory.

This work has several novel features. It provides a statistical framework to accommodate both calibration and seasonal adjustment. Using this framework, we assess procedures for inference on log odds ratios, both for continuous and categorical vitamin D risk models, in realistic simulations based on data from the Vitamin D Pooling Project. Finally, we identify practical recommendations for analysis and interpretation to inform the work of the Vitamin D Pooling Project. In particular our analyses show: (1) failure to adjust for calibration and seasonal trend can inflate variance, bias and mean square error of estimated vitamin D effects; (2) simple analytic methods can be recommended for continuous and for categorical risk models (and perform even better than a theoretically appealing normal model for categorical risk); (3) with the stratified sampling design for calibration samples, there is surprisingly little increase in the variance of log odds ratio estimates from calibration and seasonal adjustment; and (4) unlike continuous vitamin D risk models, categorical models are not robust to the choice of reference date for seasonal adjustment. This finding implies that public heath recommendations for desirable vitamin D levels may need to be season-specific.

Section 2 describes models and statistical methods. Section 3 describes simulation studies in which the logit of disease risk is linear or categorical in vitamin D. Section 4 presents analyses of data from three nested case-control studies, and Section 5 has concluding remarks. Technical results are given in an Appendix and additional methods, simulations and examples are given in Supplementary Information.

2. Methods

2.1. Motivating data

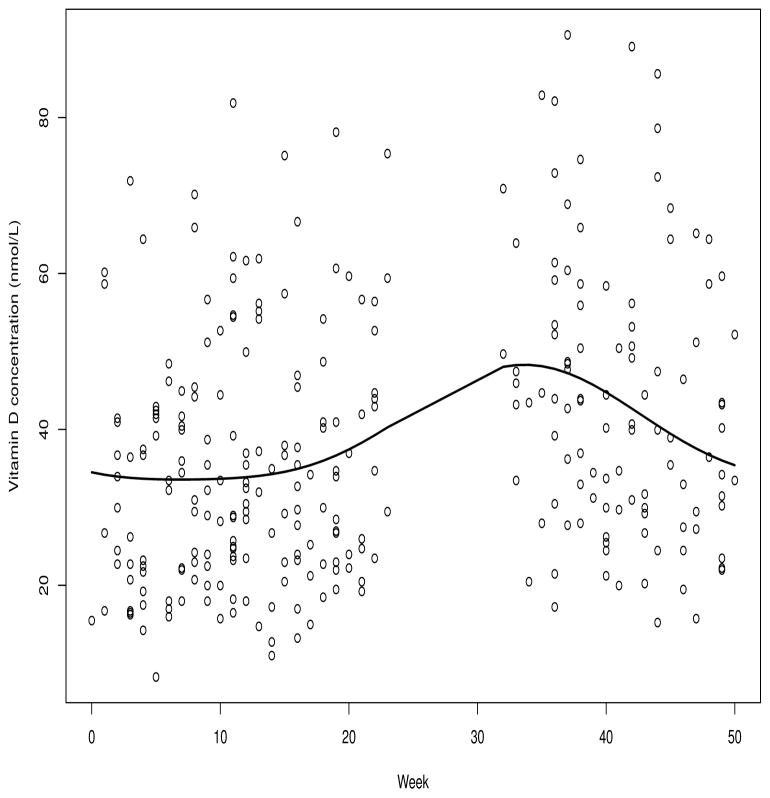
We base our simulations (Section 3) on two typical data sets, one a nested case-control study of colorectal cancer from the Alpha-Tocopherol, Beta-Carotene Cancer Prevention Study [3], hereafter ATBC, and the second a nested case-control study of breast cancer from the Prostate, Lung, Colorectal and Ovarian Cancer Screening Trial or PLCO [4]. We use only data from controls from these studies as the basis of our simulations, and we specify the exposure effects. Figure 1 depicts vitamin D measurements in ATBC controls as a function of week the blood sample was drawn ranging from week 1 (January 1 to January 7) to week 52. The solid line represents a sine/cosine series fit to these data, described fully in Section 2.3. No samples were collected between weeks 24 and 32. The maximum value of the fitted curve is at week 35 (the third week in September) and the fitted values at the beginning and end of the year agree, as would make sense because they represent the same time of year. Another plot of this type is given for the PLCO data as Web Figure 1. In addition to the vitamin D measurements that are available from the study-specific laboratory on all subjects, we have calibration measurements from a reference laboratory on a sample of 29 controls, selected as described in Section 2.4.

Figure 1.

Seasonal trends in vitamin D measurements in controls from the Alpha-Tocopherol, Beta-Carotene study.

We also estimated disease associations with vitamin D from cases and controls in three studies, ATBC (see Table V), and two studies of breast cancer, the New York University Women’s Health Study (NYUWHS) (Web Table X) and the Cancer Prevention Study II Nutrition Cohort (CPSII) (Web Table XI).

Descriptive data for these four cohorts are in Web Table I.

2.2. Statistical framework for calibration and seasonal trend models

The following notation is for a single study. Let w(t) = ς(t) + w be the true value of the study-specific (or “local”) assay for an individual measured at week t, where ς(t) is the seasonal trend in the population and w ~ Normal(0, τ²) represents the deviation of the individual’s value from the trend. The observed local assay value is W(t) = w(t) + u_W, where u_W ~ Normal(0, σ_WW) represents measurement error. We assumed a linear calibration curve because the regression of reference vitamin D measurements against local laboratory measurements was usually linear in Vitamin D Pooling Project studies, and in those few instances where a quadratic component was detected, differences in predictions between the linear and quadratic models were small. Under linear calibration, we denote the true value for the reference laboratory as x(t) = a + bw(t), where a and b represent the true calibration intercept and slope. The observed reference laboratory measurement would be X(t) = x(t) + u_X, where u_X ~ Normal(0, σ_XX) is measurement error. Assuming that (w, u_W, u_X)^T are trivariate normal with cov(w, u_X) = cov(w, u_W) = 0 and cov(u_X, u_W) = σ_XW, it follows that the observable variables {W(t), X(t)}^T are bivariate normal with means {ς(t), a + bς(t)}^T and covariance matrix

$$\mathbf{\sum }=\left(\begin{array}{ll}{\tau }^2+{\sigma }_{WW}\hfill & b{\tau }^2+{\sigma }_{XW}\hfill \\ b{\tau }^2+{\sigma }_{XW}\hfill & b^2{\tau }^2+{\sigma }_{XX}\hfill \end{array}\right).$$

Hence the regression of X(t) on W(t) is

$$\begin{array}{l}E\{X(t)\mid W(t)\}=a+b\varsigma (t)+(b{\tau }^2+{\sigma }_{XW}){({\tau }^2+{\sigma }_{WW})}^{-1}\{W(t)-\varsigma (t)\}\\ =a+\varsigma (t)\{b-(b{\tau }^2+{\sigma }_{XW}){({\tau }^2+{\sigma }_{WW})}^{-1}\}+(b{\tau }^2+{\sigma }_{XW}){({\tau }^2+{\sigma }_{WW})}^{-1}W(t).\end{array}$$ (1)

If we assume that σ_XW = 0, as is reasonable because measurements in the local and reference laboratories on the same sample are usually performed in different locations and/or times, the regression reduces to

$$E\{X(t)\mid W(t)\}=E\{x(t)\mid W(t)\}=a+b\varsigma (t)+b{\kappa }_W\{W(t)-\varsigma (t)\},$$ (2)

where κ_W = τ²(τ² + σ_WW)⁻¹ is an attenuation factor (or intraclass correlation) from measurement error in W(t). Local assay values W(t) are available on all samples, whereas reference laboratory values X(t) are available only on a sample of controls, as described in Section 2.4. We assume σ_XX and σ_WW are known from reliability studies in which the same sample is repeatedly analyzed on different days in the reference and local laboratories. Data from the studies in the Vitamin D Pooling Project indicate that (σ_XX)^1/2 and (σ_WW)^1/2 each ranged from 0.5 to 9 nmol/L, with most values in the range 2–4. To estimate τ² and hence κ_W, we subtracted σ_WW from the empirical variance of {W(t) − ς̂(t)} in controls, where ς̂(t) is the estimated periodic trend in W(t). Because τ² was much larger than σ_WW, results were little changed in sensitivity analyses as σ_XX and σ_WW ranged from 4 to 36. In Section 2.3 we describe how we fit the trend.

2.3. Fitting the trend

We used data on W(t) from controls to estimate the seasonal trend ς(t) by fitting the model

$$W(t)=\varsigma (t)+\epsilon ;$$ (3)

$$\varsigma (t)={\gamma }_0+{\gamma }_{1}sin(2\pi t/52)+{\gamma }_{2}cos(2\pi t/52)+{\gamma }_{3}sin(4\pi t/52)+{\gamma }_{4}cos(4\pi t/52),$$ (4)

where ε ~ Normal(0, σ²) is independent of ς(t), and t is in weeks. Such periodic series have been studied previously, e.g. [5], and shown to fit vitamin D data as an outcome variable with t in days [6] and as an exposure in case-control analyses with t in months [1, 2]. Those vitamin D analyses used only the first three terms in equation (4), but we found that five terms were needed to fit the data well in each of the 21 Vitamin D Pooling Project studies. Figure 1 shows the fit to data from the controls in the ATBC colorectal case-control study. This approach has the advantages only five degrees of freedom are used to fit the trend, which has little impact on the variance of risk estimates (see Web Appendices A.5 and A.6), and the trend gives similar values on December 31 as on January 1, as is desirable. When we tried other more flexible fitting methods, such as splines with many knots or LOESS regression, the trends were not necessarily equal at the beginning and end of the year, and the variance of estimates of vitamin D effects were inflated, as previously noted [7]. Controls were used for fitting seasonal trends because, for low-incidence diseases like breast or colorectal cancer, controls are representative of the general population (see the rare disease assumption in Web Appendix A.1). Matching controls to cases on cancer risk factors such as age changes the age distribution in controls, but would not alter the seasonal vitamin D pattern in controls appreciably unless this were strongly associated with age.

2.4. Estimating the calibration parameters (a, b)

The Vitamin D Pooling Project included calibration samples from controls within each study. For each study, the control values of W(t) were grouped into deciles, and from each decile, three controls were selected at random. (In fact, 29 controls were usually selected this way, rather than 30, but for the simulations below, we selected 3 from each decile). Blood samples from the selected controls were then sent to the reference laboratory for measurement of X(t). Thus the {X(t), W(t)} pairs are a stratified random sample with strata defined by deciles of W(t).

We considered three estimates of the calibration parameters a and b.

• Estimates â₁ and b̂₁ are obtained from simple linear regression of X(t) on W(t) in the calibration data. These quantities are not consistent for a and b, in view of equation (2).

• From equation (2), a somewhat more refined estimate (â₂, b̂₂)^T is obtained by regressing X(t) on κ̂_W {W(t) − ς̂(t)}.

• The most justifiable estimate, in view of equation (2), is (â₃, b̂₃)^T, which is obtained by regressing X(t) on ς̂(t)(1 − κ̂_W) + κ̂_W W(t). For κ̂_W equal 1, this procedure reduces to the regression of X(t) on W(t).

We evaluated each of these approaches in simulations.

2.5. Risk models and estimators

2.5.1. Continuous risk models

For modeling continuous vitamin D, we assumed that the logit of the disease risk is

$$\text{logit}\{\text{pr}(Y=1)\}={\alpha }_0+{\alpha }_1{x}_0,$$ (5)

where x₀ ≡ x(t₀) = a + bw(t₀) is the value that the true reference laboratory would have produced if it had been measured on the reference date t₀ instead of the date t. Each matched case-control pair makes the following contribution to the conditional likelihood:

$$exp\{{\alpha }_1(x_{0,\mathit{case}}-x_{0,\mathit{control}})\}/[exp\{{\alpha }_1(x_{0,\mathit{case}}-x_{0,\mathit{control}})\}+1].$$ (6)

However, we only get to observe W(t), not x₀. One approach is to replace x₀ by its conditional expectation given W(t) in equation (2), which we estimate by

$${\widehat{x}}_0=\widehat{a}+\widehat{b}\widehat{\varsigma }(t_0)+\widehat{b}{\widehat{\kappa }}_W\{W(t)-\widehat{\varsigma }(t)\}=\widehat{a}+\widehat{b}\{\widehat{\varsigma }(t_0)-{\widehat{\kappa }}_W\widehat{\varsigma }(t)\}+\widehat{b}{\widehat{\kappa }}_{W}W(t).$$ (7)

The estimates ς̂(·), â and b̂ are described in Sections 2.3 and 2.4. Then (7) leads to the estimated difference

$${\widehat{x}}_{0,\mathit{case}}-{\widehat{x}}_{0,\mathit{control}}=\widehat{b}{\widehat{\kappa }}_W\{W(t_{\text{case}})-W(t_{\text{cont}})-\widehat{\varsigma }(t_{\text{case}})+\widehat{\varsigma }(t_{\text{cont}})\}.$$ (8)

Under the rare disease assumption, and using equation (8), if one substitutes {W(t_case) − W(t_cont) − ς̂(t_case) + ς̂(t_cont)} for (x_0,case − x_0,control) in equation (6) and maximizes the conditional likelihood with respect to α₁, one obtains the estimate ${\widehat{\alpha }}_1^{\ast }$ of ${\alpha }_1^{\ast }={\alpha }_{1}b{\kappa }_W$. Thus, we estimate α₁ by ${\widehat{\alpha }}_1={\widehat{\alpha }}_1^{\ast }/(\widehat{b}{\widehat{\kappa }}_W)$.

The asymptotic behavior of α̂₁ is derived in Web Appendix A.6. A simple estimate of its variance is obtained as follows. First, estimate the variance of ${\widehat{\alpha }}_1^{\ast }$ by the inverse of the Hessian of the conditional loglikelihood, and call this $\widehat{V}\text{ar}({\widehat{\alpha }}_1^{\ast })$. Then, by the delta method, α̂₁ has approximate variance estimate $\widehat{V}\text{ar}({\widehat{\alpha }}_1)={(\widehat{b}{\widehat{\kappa }}_W)}^{-2}\widehat{V}\text{ar}({\widehat{\alpha }}_1^{\ast })+{({\widehat{\alpha }}_1^{\ast }/{\widehat{b}}^2{\widehat{\kappa }}_W)}^2\widehat{V}\text{ar}(b)$ where V̂ar(b̂) is estimated from the regressions in Section 2.4. In this calculation we use the fact that ${\widehat{\alpha }}_1^{\ast }$ and b̂ are independent, and we assume that the variation from estimates of trend and κ̂_W is numerically negligible (see Web Appendix A.6). Some intuition is obtained by considering the ATBC example. Even if the case and control had t_case = t_cont, Var[{W(t_case) − W(t_cont)}] ≥ 2τ² = 2 × 240.9 = 481.8, which greatly exceeds the variance of the difference in trend estimates. For example, Var{ς̂(39/52) − ς̂(1/52)}=10.9, which is much smaller than 481.8. Likewise, the standard error of κ̂_W was .0066 in simulations, implying small variation about κ_W = 0.9377 with σ_WW = 16.

Importantly, none of these calculations depend on the calibration intercept a. The seasonal adjustment in equation (8) vanishes if the case and control are matched on date of blood draw, so that t_case = t_cont. Also, the seasonal adjustment in (8) does not depend on the reference date, t₀. Ignoring calibration and measurement error in W(t) is equivalent to using ${\widehat{\alpha }}_1^{\ast }$ instead of α̂₁.

2.5.2. Categorized risk models

For categorical vitamin D we assume

$$\text{logit}\{P(Y=1)\}=\mu +\sum _{i=1}^{5}I(c_{i-1}\le x_0<c_i){\beta }_i,$$ (9)

where c₀ = 0 and β₁ = 0. For 1:1 nested case-control matching, the corresponding conditional likelihood contribution from a case-control pair is

$$exp\{{\mathit{\beta }}^T{C}_1(x_0)\}/[exp\{{\mathit{\beta }}^T{C}_1(x_0)\}+exp\{{\mathit{\beta }}^T{C}_0(x_0)\}],$$ (10)

where C_ℓ(x) is a 5 × 1 vector of indicators in (9) for cases (ℓ = 1) and controls (ℓ = 0) and β is the corresponding vector of log odds ratios, β_i. A linear trend risk model sets β_i = (i − 1)β, where β is the log odds increase in risk per exposure category increase. The contribution to the likelihood for the linear model is equation (10) with (i − 1)β replacing β^T C_ℓ(x₀). The cut-points c_i could be externally defined levels, such as those given by the Institute of Medicine for vitamin D [8]. They could also be study-wide quantiles of vitamin D estimated from controls from all participating studies. In the simulations below, they were quintiles of x₀ values among controls from the particular study on which the simulations were based. In particular, we set x₀ = a + b{W(t) − ς̂(t) + ς̂(t₀} where W(t) and ς̂(·) were from controls from that study.

If x₀ were known, we could estimate β or β by maximizing the product of conditional likelihoods (10) with respect to β or β and obtain model-based estimates of their covariance from the Hessian of the log-likelihood. With x̂₀ defined in (7), we proceeded by substituting x̂₀ for x₀ in equation (10) and by estimating covariances from the Hessian as if x₀ were known. We investigated the operating characteristics of this approach in simulations.

Although the preceding estimation procedures are easy to describe and implement, they do not take full advantage of the assumed normal distributions, nor do they acknowledge the uncertainty in assigning risk category based on x̂₀ instead of x₀. Given a, b, ς(·) and W(t), x₀ ~ Normal[a + bς(t₀) + bκ_W {W(t) − ς(t)}, η² ≡ b²σ_WW κ_W]. Hence

$$\text{pr}\{x_0\text{in}\text{category}i\mid W(t)\}\equiv E\{I(c_{i-1}\le x_0<c_i)\mid a,b,\varsigma (·),W(t)\}=\mathrm{\Phi }(z_i)-\mathrm{\Phi }(z_{i-1}),$$ (11)

where z_i = [c_i − a − bς(t₀) − bκ_W {W(t) − ς(t)}]/η and Φ(·) is the standard normal distribution function. For a rare disease, the conditional likelihood corresponding to a matched case-control set is shown in Appendix A.1 to be

$$\frac{{\displaystyle \sum _{i=1}^5}exp({\beta }_i)\text{pr}\{x_{0,\mathit{case}}\text{in}\text{category}i\mid W(t_{\text{case}})\}}{{\displaystyle \sum _{i=1}^5}exp({\beta }_i)\text{pr}\{x_{0,\mathit{case}}\text{in}\text{category}i\mid W(t_{\text{case}})\}+{\displaystyle \sum _{i=1}^5}exp({\beta }_i)\text{pr}\{x_{0,\mathit{control}}\text{in}\text{category}i\mid W(t_{\text{cont}})\}}.$$ (12)

The product of such terms over case-control pairs can be maximized with respect to β in the general model or β (the the per category log odds ratio) in the linear trend model to obtain estimates and their model-based estimated covariance. We substituted estimates ς̂(·), â and b̂ to compute pr{x₀ in i|W(t)} in equation (11). A more precise analysis might maximize the average likelihood over the distribution of ς̂(·), â and b̂. A numerical approach would be to draw repeated samples of ς̂(·), â and b̂ to compute an average likelihood and maximize this quantity, but we have not pursued it because unreported simulations indicated that substitution of ς̂(·), â and b̂ yields similar operating characteristics as using the exact quantities ς(·), a and b.

3. Simulations

3.1. Simulation Setup

In this section we describe methods to simulate realistic case-control samples based on controls from the colorectal cancer case-control study in ATBC. We also used these methods for simulations based on the breast cancer case-cohort study in PLCO. We describe the analytic procedures for continuous and categorical risk models.

Data from the controls were used to estimate the distribution of times of blood draw, the trend ς(t), and τ². In particular we estimated τ² = 240.89 assuming σ_WW = 16. The estimated coefficients in the seasonal trend equation (4) were 39.425, −5.837, −4.485, 1.440, and −0.444, respectively.

We generated 10,000 case-control studies based on the original ATBC data. For each simulated study we generated a large (N = 50,000) source population as follows. First draw a date t of blood by sampling with replacement from the dates in the original controls. Then generate w(t) = ς(t) + w by sampling from w ~ Normal(0, τ²). Set x₀ = a + bw(t₀) = a + b{ς(t₀) + w} and generate the disease status indicator Y from equation (5) for continuous vitamin D and from equation (9) for categorical vitamin D. Generate the observed local vitamin D measurement from W(t) = w(t) + u_W by drawing from u_W ~ Normal(0, σ_WW), where σ_WW is assumed known, and independently generate reference laboratory measurements X(t) = x(t) + u_X = a + bw(t) + u_X by drawing from u_X ~ Normal(0, σ_XX) with σ_XX known. Implicitly we are assuming σ_XW = 0. At this stage we have N triples {Y, W(t), X(t)}^T.

To obtain the case-control data we randomly selected n triples from among the triples with Y = 1 (cases) and n triples from among those with Y = 0 (controls). However, we observed X(t) only in the calibration sample, which is obtained by arranging the W(t) values of controls into decile groups and selecting three controls at random from among the controls in each decile group. For these 30 controls, which we call the calibration sample, we observed {Y, W(t), X(t)}^T, but in all other cases and controls we only observed {Y, W(t)}^T. These triplets and doublets constituted the case-control data available for analysis. The effects of matching variables on risk cancel from the conditional logistic likelihood. We assumed that the matching variables have no effect on risk in these simulations, since there are no matching effects in equations (5) and (9). Hence we randomly matched cases with controls to obtain n pairs, regardless of season.

Analysis of each such simulated data set for continuous vitamin D proceeded as follows. First obtain ς̂(t) by fitting equation (3) to the n control values of W(t). Next estimate τ² by subtracting σ_WW from the variance of W(t) − ς̂(t) in controls. Use τ̂ ² and the assumed known value σ_WW to calculate κ̂_W. Let ${\widehat{\alpha }}_1^{\ast }$ be the estimate obtained from conditional logistic regression using the residuals {W(t) − ς̂(t)}. We described three estimates of (a, b)^T in Section 2.4, and used these results to produce three estimates of α₁, namely, ${\widehat{\alpha }}_1={\widehat{\alpha }}_1^{\ast }/\widehat{b}{\widehat{\kappa }}_W$, with b̂ being b̂₁, b̂₂ or b̂₃. We also present estimates from conditional logistic regression with raw values W(t), and with only seasonally adjusted values, {W(t) − ς̂(t)}. Finally we present an estimate based on calibration only that is obtained by dividing the estimate from the raw values, W(t), by b̂₁κ̂_W. All these estimates were compared to estimates obtained by inserting the true values x₀ from the case and matched control into the conditional logistic regression. None of these estimates depends on a standard reference date, t₀.

For categorical vitamin D, values of Y were generated from equation (9) based on quintiles of x₀ from the study on which the simulation was based, as described in section 2.5.2. A benchmark analysis used the perfect categories in equation (10) based on the true x₀, which is unknown in practice. We also categorized the raw values W(t) without seasonal adjustment or calibration for use in equation (10), as well as the seasonally adjusted but not calibrated values, W(t) − ς̂(t) + ς̂(t₀) and the calibrated but not seasonally adjusted values â₁ + b̂₁W(t). Two more principled estimates x̂₀ were used for categorization in equation (10). We call them x̂₀₁ = â₁ + b̂₁ς̂(t₀) + b̂₁κ̂_W {W(t) − ς̂(t)} and x̂₀₃ = â₃ + b̂₃ς̂(t₀) + b̂₃ς̂_W {W(t) − ς̂(t)}. A final estimate of log odds ratios, called the “normal model” estimate, was based on equations (11) and (12) with â₃ + b̂₃ς̂(t₀) + b̂₃κ̂_W{W(t) − ς̂(t)} and η̂ = b̂₃(σ_WW κ̂_W)^1/2 substituted for corresponding parameters to compute z_i.

3.2. Analysis of continuous vitamin D

In this section we compare procedures with calibration and/or seasonal adjustment for analyzing continuous vitamin D. Table 1 contains comparisons for the various estimators of slope under the null hypothesis α₁ = 0. The logistic intercept was μ = −4. The parameters were chosen to provide a severe test of the various procedures. In particular there were only n = 100 case-control pairs; larger numbers of n make it easier to estimate trends and reduce small sample bias in estimators. The values a = 5 and b = 1.4 represent more severe miscalibration of the local assay than found in most Vitamin D Pooling Project studies. The estimated measurement error variances σ_XX = σ_WW = 16 are representative of values found in replication studies. All the estimates (even those based on the true values x₀) were very slightly upwardly biased, with most bias values near 4 × 10 ⁻⁵, but biases were about twice this high in analyses of the true (but unknown) x₀ values, of raw vitamin D data, and of calibrated data without seasonal adjustment. All the biases were small, however, in comparison to the empirical estimates of the standard error of the estimates; see the column headed SE(α̂₁). The squared ratios of empirical standard error to the empirical standard error for the true data x₀ (see column headed “Var ratio”) were near 1.1 for each of the methods that adjusted both for seasonality and calibration, were 0.964 for the method based on calibration only, 1.912 for the method that adjusted for season only, and 1.665 for the raw data. Thus, there was about a 10% efficiency loss, measured as a variance ratio, for the methods that adjust for season and calibration. The corresponding ratios of mean square errors were almost identical to the variance ratios, because the bias was negligible. All procedures yielded coverage near the nominal 95% level. However, with 10,000 simulations, the 95% confidence interval is approximately equal to the estimated coverage plus or minus 0.43%. Hence some of the coverage rates are statistically significantly less than 95%, although only very slightly less than nominal. This probably reflects the fact that the ratios of the empirical estimates from simulations of the standard error of α̂₁ to the average model-based estimates of standard error range from 1.028 to 1.053 (see the column headed “SE ratio”). For example, if the ratio of the true SE error to the estimated SE is 1.04, the coverage of the nominal 95% confidence interval at the null hypothesis would be Φ(1.96/1.04) − Φ(−1.96/1.04) = 0.9405, where Φ is the stanadard normal distribution function. Although the model-based variance estimates allow for variability in estimates of calibration parameters, they do not take variability in estimation of the trend into account. With n = 200 case-control pairs, this problem disappeared, as shown in Web Table II, where all coverages were within 0.43% of the nominal 95%. With the larger samples, the efficiency loss from calibration and seasonal adjustment was again about 10% (Web Table II).

Table 1.

Simulation performance of procedures for conditional logistic regression (CLR) analysis of continuous vitamin D based on data from the Alpha-Tocopherol, Beta-Carotene Study at the null hypothesis α₁ = 0, with n = 100 case-control pairs.

n	α1	a	b	σWW	Bias of α̂1	CI%	SE (α̂1)	SE ratio	Var ratio	MSE ratio
100	0	5	1.4	16	x 105		x 102
Exposure x measured without error					7.24	94.51	.687	1.032	1.000	1.000
Calibration/season: estimate (â1, b̂1) by regressing X(t) on W(t)					3.82	94.51	.723	1.053	1.108	1.108
Calibration/season: estimate (â2, b̂2) by regressing X(t) on κ̂W {W(t) − ς̂ (t)}					4.31	94.90	.725	1.050	1.114	1.114
Calibration/season: estimate (â3, b̂3) by regressing X(t) on ς̂(t)(1 − κ̂W) + κ̂W W(t), see (2)					3.87	94.51	.731	1.053	1.130	1.130
Raw data					9.14	95.13	.886	1.028	1.665	1.664
Seasonal adjustment only					4.39	94.39	.950	1.052	1.912	1.912
Calibration only					7.65	95.28	.675	1.029	0.964	0.965

n is the number of case-control pairs; a is the calibration curve intercept; b is the calibration curve slope; CI% is the estimated coverage of a 95% nominal confidence interval for α₁; α₁ is the log odds ratio increase per increase in vitamin D by one standard deviation (τ = 15.5206); σ_XX = σ_WW are measurement error variances; “SE” is the empirical estimate of standard error based on simulations; “SE ratio” is the ratio of the empirical SE estimate to the mean model-based estimate of standard error; “Var ratio” is the square of the ratio of the empirical SE for an estimator to the empirical SE of the estimate based on known exposure; “MSE’ ratio” is the ratio of the mean square error from a given procedure to that based on known exposure; “Calibration only using (â₁, b̂₁)”is defined in Section 2.5.1.

In summary, under the null hypothesis, all procedures had nominal coverage for n = 200 and very near nominal coverage for n = 100. The efficiency loss from calibration and seasonal adjustment was about 10%, compared to the ideal situation with known x₀, but the loss in efficiency was much greater for procedures that do not calibrate the local assay data.

Table 2 contains comparisons under the alternative α₁ = −0.04466, which corresponds to a halving of risk for an increase in vitamin D of τ = 15.52 nmol/L, which is the estimated standard deviation of w in the ATBC data. The coverages of all procedures that adjust for season and calibration were within 0.43% of the nominal 95% level and therefore did not deviate statistically significantly from it. Analyses of the raw vitamin D data, data that are seasonally adjusted but not calibrated, and data that are calibrated but not seasonally adjusted led to coverage significantly below nominal levels. Such coverages are even smaller with n = 200 case-control pairs (Web Table III). Biases from failure to calibrate contributed importantly to the mean squared error ratios (Table 2 and Web Table III). With n = 100, all the procedures that adjusted for seasonality and calibration had comparatively small bias and losses in efficiency compared to analysis with known x₀, with variance ratios ranging from 1.112 to 1.192 (Table 2). With n = 200, the variance ratios ranged from 1.207 to 1.385 (Web Table III).

Table 2.

Simulation performance of procedures for conditional logistic regression (CLR) analysis of continuous vitamin D based on data from the Alpha-Tocopherol, Beta-Carotene Study at the alternative hypothesis α₁ = −0.04466, with n = 100 case-control pairs.

n	α1	a	b	σWW	Bias of α̂1	CI%	SE (α̂1)	SE ratio	Var ratio	MSE ratio
100	−.04466	5	1.4	16	x 103		x 102
Exposure x measured without error					−173	95.11	1.028	1.052	1.000	1.000
Calibration/season: estimate (â1, b̂1) by regressing X(t) on W(t)					−153	95.06	1.084	1.061	1.112	1.103
Calibration/season: estimate (â2, b̂2) by regressing X(t) on κ̂W {W(t) − ς̂ (t)}					−163	95.43	1.122	1.030	1.192	1.184
Calibration/season: estimate (â3, b̂3) by regressing X(t) on ς̂(t)(1 − κ̂W) + κ̂W W(t), see (2)					−199	95.11	1.099	1.065	1.143	1.148
Raw data					−1042	92.06	1.254	1.044	1.489	2.447
Seasonal adjustment only					−1607	83.92	1.374	1.060	1.786	4.113
Calibration only					276	90.76	.991	1.048	.929	.974

Here, CI% represents the actual coverage of a 95% nominal confidence interval. Also, α₁ is the log odds ratio per increase in vitamin D by one standard deviation (τ = 15.5206); α_XX = α_WW are measurement error variances. “SE” is the empirical estimate of standard error based on simulations. “SE ratio” is the ratio of the empirical SE estimate to the mean model-based estimate of standard error. “Var ratio” is the square of the ratio of the empirical SE for an estimator to the empirical SE of the estimate based on known exposure. “MSE ratio” is the ratio of the mean square error from a given procedure to that based on known exposure.

Unreported simulations indicated similar results when σ_WW was misspecified as 36 when the true value was 16 and for other values of the calibration parameters.

These simulations suggest that simple procedures that adjust for seasonality and calibration will perform well in practice. In particular the deattenuated estimates ${\widehat{\alpha }}_1={\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_1{\widehat{\kappa }}_W$ and ${\widehat{\alpha }}_1={\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_3{\widehat{\kappa }}_W$ had favorable bias and efficiency characteristics.

3.3. Analysis of categorical vitamin D

Recall that for j = 1, 2, 3, x̂_0j = â_j + b̂_jς̂(t₀) + b̂_jκ̂_W W(t) − ς̂(t)}, and β is the log odds per category increase.

The cutpoints used to generate the relative risks from equation (9) were the quintiles of the control values x₀ for t₀ = 39 in ATBC, namely 49.6, 58.7, 70.8 and 86.9 nmol/L (see section 2.5.2). The intercept was μ = −4. Table 3 summarizes performance under the null hypothesis with n = 100 cases and matched controls. As for the continuous vitamin D analyses, we assumed realistic estimates of measurement error, σ_XX = σ_WW = 16 and substantial mis-calibration with intercept a = 5 and b = 1.4. In Tables 3 and 4, the labels “CLR using (10) with x̂₀₁” and “CLR using (10) with x̂₀₃” denote procedures that substitute the calibrated and seasonally adjusted estimates of x₀, namely x̂₀₁ and x̂₀₃, into the conditional likelihood equation (10). The “Normal model” procedure used equations (11) and (12). These three procedures that adjust for season and calibration had near nominal coverage for β₂, β₅, and β (Table 3) as well as for the log odds β₃ and β₄ (not shown). Adjustment for calibration alone yielded near nominal coverage. Coverage for β₅ was above nominal levels for analyses of raw values and for seasonal adjustment only. Large bias was seen for seasonal adjustment alone for β and β₅. Standard errors for $\widehat{{\beta }_5}$ and β̂ were larger for the raw data analysis and for seasonal adjustment alone than for CLR using (10) with x̂₀₁ or x̂₀₃. The mean square error ratios (compared to the analysis with perfect x₀ data) indicated poor performance for raw data and seasonal adjustment only. For estimating β₂, the normal model had higher mean square error than CLR using (10) with x̂₀₁ or x̂₀₃, primarily because it had larger standard error. The higher variability of β̂₂ from the normal model is not the result of estimating trend parameters, calibration parameters, or κ_W, as shown in unreported simulations using known values for these parameters. Similar results were obtained with n = 200 cases and controls (Web Table IV), except that subnominal coverage of β₂ was found for the raw data and seasonal adjustment only. These results were obtained with the reference date t₀ = 39 weeks. Similar results were obtained with t₀ = 1, in which quintiles were re-estimated to correspond to the new reference date (unreported data). Results were little affected if the variances for measurement error were mistakenly set at σ_XX = σ_WW = 36, when in fact σ_XX = σ_WW = 16 (unreported data).

Table 3.

Simulation performance of procedures for conditional logistic regression (CLR) analysis of categorical vitamin D based on data from the Alpha-Tocopherol, Beta-Carotene Study at the null hypothesis β_i = (i − 1)β = 0, with n = 100 case-control pairs.

	Coverage(%)			Bias x 102			SE			MSE ratio
	β2	β5	β	β2	β5	β	β2	β5	β	β2	β5	β
Category measured without error	95.32	94.93	95.14	−1.031	−665	−.024	.588	.493	.106	1	1	1
CLR using (10) with x̂01 defined using (â1, b̂1)	94.95	95.10	94.98	−10.6	−5.39	−.687	.631	.522	.111	1.285	1.133	1.352
CLR using (10) with x̂03 defined using (â3, b̂3)	95.16	95.20	95.01	−9.11	−1.38	−.379	.562	.505	.109	1.013	1.047	1.067
Normal model using (11)–(12)	94.74	95.63	95.11	−17.8	−1.76	−.337	1.071	.583	.114	3.684	1.398	1.168
Raw data	95.78	100	95.96	.444	−.219	−.096	.461	1.592	.199	.682	10.4	3.510
Seasonal adjustment only	95.76	100	95.27	−2.74	31.5	2.178	.391	2.073	.157	.807	18.1	10.9
Calibration only using (â1, b̂1)	95.65	95.92	95.32	.692	−.849	−.104	1.067	.492	.113	.762	.996	.915

Simulation performance of procedures for conditional logistic regression (CLR) analysis of categorical vitamin D based on data from the Alpha-Tocopherol, Beta-Carotene Study at the null hypothesis β_i = (i − 1)β = 0, with n = 100 cases and controls. Here, (â₁, b̂₁) and (â₃, b̂₃) are different calibration parameter estimates as described in Section 2 and in Table 1. Here a = 5 and b = 1.4 are the calibration curve intercept and slope; σ_XX = σ_WW = 16 are measurement error variances. “SE” is the empirical estimate of standard error based on simulations. “MSE ratio” is the ratio of the mean square error from a given procedure to that based on known exposure. β₂, β₅, and β are respectively the log odds ratios corresponding to the second quintile group, fifth quintile group, and per quintile category increase (trend). The reference date was t₀ = 39/52 (week 39). The 20^th, 40^th, 60^th and 80^th percentiles of control measurements adjusted to t₀ were 49.61, 58.73, 70.80 and 86.89 nmol/L respectively.

Table 4.

Simulation performance of procedures for conditional logistic regression (CLR) analysis of categorical vitamin D based on data from the Alpha-Tocopherol, Beta-Carotene Study at the alternative hypothesis β_i = (i − 1)β, with β = −0.25log(2) = −0.17329 and with n = 100 case-control pairs.

	Coverage(%)			Bias x 102			SE			MSE ratio
	β2	β5	β	β2	β5	β	β2	β5	β	β2	β5	β
Category measured without error	95.63	95.20	95.33	−.921	−3.60	−.347	.524	.507	.107	1	1	1
CLR using (10) with x̂01 defined using (â1, b̂1)	94.95	95.10	94.98	−2.76	−1.21	−.083	.595	.522	.111	1.282	1.075	.965
CLR using (10) with x̂03 defined using (â3, b̂3)	94.97	94.95	95.29	−5.47	2.55	.528	.533	.505	.109	1.032	1.041	0.977
Normal model using (11)–(12)	94.75	95.33	95.45	−16.0	2.95	−.337	1.014	.599	.114	3.727	1.396	1.080
Raw data	94.86	100	95.64	−18.4	53.3	−4.02	.492	1.518	.226	1.901	10.0	26.2
Seasonal adjustment only	94.49	100	94.90	−18.3	67.2	−1.06	.406	2.014	.173	2.230	17.5	37.5
Calibration only using (â1, b̂1)	95.48	94.66	94.04	−4.94	8.05	−.506	.477	.534	.105	.847	1.131	1.364

Here, (â₁, b̂₁) and (â₃, b̂₃) are different calibration parameter estimates as described in Section 2 and in Table 1. Here a = 5 and b = 1.4 are the calibration curve intercept and slope; σ_XX = σ_WW = 16 are measurement error variances. “SE” is the empirical estimate of standard error based on simulations. “MSE ratio” is the ratio of the mean square error from a given procedure to that based on known exposure. β₂, β₅, and β are respectively the log odds ratios corresponding to the second quintile group, fifth quintile group, and per quintile category increase (trend). The reference date was t₀ = 39/52 (week 39). The 20^th, 40^th, 60^th and 80^th percentiles of control measurements adjusted to t₀ were 49.61, 58.73, 70.80 and 86.89 nmol/L respectively.

Under the alternative β_i = (i − 1)β, with β = − 0.25log(2) = − 0.17329, similar results were found. With n = 100 cases and controls (Table 4), the coverage was near the nominal 95% level except for some analyses with raw data and with seasonal adjustment only. Bias was comparatively large for analysis of the raw data, seasonal adjustment only, and the normal model. Standard errors were comparatively large for the normal model. The mean square error ratios were large for raw data analysis, seasonal adjustment only, and the normal model for β̂₂. Similar results were found for n = 200 cases and controls (Web Table V). Results were little affected by misspecifying σ_XX = σ_WW = 36, when in fact σ_XX = σ_WW = 16 (unreported data).

Additional simulations based on PLCO data support these findings for continuous and categorical analyses and are in the Supplementary Information, Web Tables VI,VII,VIII and IX.

To summarize, CLR using (10) with x̂₀₁ and CLR using (10) with x̂₀₃ outperformed other procedures. CLR using (10) with x̂₀₃ usually had smaller MSE than CLR using (10) with x̂₀₁, however, not only under the null hypothesis (Table 3 and Web Tables IV and VIII), but also under the alternative (Table 4 and Web Tables V and IX). Thus we recommend CLR using (10) with x̂₀₃.

4. Examples of Analyses of Three Studies

We present analyses for the colorectal case-control study in ATBC [3] and for two case-control studies of breast cancer, the New York University Women’s Health Study (NYUWHS) [9] and a study from the Cancer Prevention Study II (CPSII) Nutrition Cohort [10]. Table 5 presents categorical analyses for the ATBC data compared to Institute of Medicine cut-points (< 30, [30,50), [50,75), ≥ 75 nmol/L), as well as analyses of continuous vitamin D as a linear effect. The categories correspond respectively to vitamin D deficiency, probable insufficiency, adequacy, and no increased benefit. The ATBC study included 146 colorectal cancer cases and 290 matched controls. Estimates τ̂, â₁, b̂₁, and estimates of the seasonal trend parameters are in the footnote to Table V. Conditional likelihoods (6), (10), and (12) were modified to accomodate varying numbers of matched controls per case. We analyzed the data with two different reference dates for seasonal adjustment to assess the robustness of the conclusions. With week 39 as the reference date, the preferred analyses of the categorical data based on CLR using (10) with x̂₀₃ indicated a strong protective effect of increased vitamin D with a statistically significant odds ratio exp(−1.97)=0.139 for the highest category (≥ 75 nmol/L). Indeed, the log odds ratios for all categories above the reference category (<30 nmol/L) were statistically significantly less than 0; the categorical trend with odds per category increase of exp(−.175)=0.839 was not statistically significant. Analyses based on CLR using (10) with x̂₀₁ were not stable because only 6 cases and 2 controls were categorized below 30 nmol/L. Note that analyses without any adjustment, with seasonal adjustment alone and with calibration alone also indicated protective trends, but the parameter estimates were smaller and usually not statistically significantly different from 0 in the absence of seasonal adjustment. The continuous trend analysis, which does not depend on a reference date, indicated a statistically significant protective odds ratio of exp(−.143)=0.866 per 10 nmol/L increase in vitamin D concentration. When these data were reanalyzed using week 1 as the reference date, the magnitudes of the protective effects in categorical analyses were smaller, but the qualitative conclusion of a significant protective effect remained unchanged. For example, the estimated protective odds ratio for vitamin D ≥75 nmol/L was exp(−1.25)=0.287, instead of the previous 0.139. Analyses based on a linear trend in continuous vitamin D were unchanged.

Table 5.

Log odds ratios for the ATBC Colorectal Cancer Study with Institute of Medicine cut-points and seasonal adjustment to week 39 and to week 1.

Log odds ratio estimates (with standard errors)
	Adjusted for season and calibration			No adjustment (Raw)	Season only	Calibration only
Reference week 39
	CLR using (10) with x̂01	CLR using (10) with x̂03	Normal model
Q2	−10.9(78.2)	−1.81*(.684)	−4.53*(1.16)	.138(.237)	−.749*(.276)	−.653*(.302)
Q3	−10.8(78.2)	−1.54*(.674)	−3.89*(1.05)	−.510(.331)	−.950*(.331)	−.572(.330)
Q4	−11.1(78.2)	−1.97*(.712)	−4.46*(1.11)	−.603(.671)	−1.20*(.572)	−1.36*(.431)
CAT	−.219(.142)	−.175(.137)	−.308*(.148)	−.177(.133)	−.418*(.144)	−.334*(.126)
	${\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_1{\widehat{\kappa }}_W$	${\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_3{\widehat{\kappa }}_W$
CONT	−.143* (.061)	−.143* (.061)		−.168* (.070)	−.171* (.070)	−.140* (.061)
Reference week 1
	CLR using (10) with x̂01	CLR using (10) with x̂03	Normal model
Q2	−.583*(.278)	−.300(.249)	−.415(.330)	.138(.237)	.166(.233)	−.653*(.302)
Q3	−.586(.305)	−.457(.304)	−.399(.342)	−.510(.331)	−.303(.334)	−.573(.330)
Q4	−1.53*(.505)	−1.25*(.526)	−1.29*(.570)	−.603(.671)	−.223(.846)	−1.36*(.431)
CAT	−.366*(.127)	−.311*(.125)	−.300*(.133)	−.117(.133)	−.074(.139)	−.334*(.126)
	${\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_1{\widehat{\kappa }}_W$	${\widehat{\alpha }}_1^{\ast }/{\widehat{b}}_3{\widehat{\kappa }}_W$
CONT	−.143* (.061)	−.143* (.061)		−.168* (.070)	−.171* (.070)	−.140* (.061)

Standard errors are in parentheses. Asterisk * indicates P < 0.05. “NORMAL” indicates the normal model procedure in equations (11) and (12). “CLR using (10) with x̂₀₁” and “CLR using (10) with x̂₀₃” denote procedures that substitute those calibrated and seasonally adjusted estimates of x₀ into the conditional logistic likelihood (10). The quantities Q₂, Q₃ and Q₄ denote log odds ratios for categories 2, 3, and 4 compared to category 1. “CAT” indicates the log odds per category increase in a trend model with scores 0,1,2 and 3. “CONT” refers to the continuous trend model with the trend parameter being the log odds per 10 nmol/L increase in vitamin D. Estimates of (τ, a, b, γ₀, γ₁, γ₂, γ₃, γ₄) from the ATBC data were (15.52, 3.86, 1.20, 39.43, −5.84, −4.49, 1.44, −0.444).

Categorical analyses of the NYUWHS breast cancer data (893 cases, 1642 controls) with a reference date of week 39 suggested a slight favorable effect from increasing vitamin D levels, in line with the analysis based on a linear trend in continuous vitamin D(Web Table 10). Reanalysis with week 1 as the reference date yielded similar small favorable categorical effects that were not statistically significant. Analyses of continuous vitamin D were unchanged.

We performed similar analyses for breast cancer data from CPSII (515 cases, 515 controls) (Web Table 11). With week 39 as the reference date, categorical analyses suggested a slight protective effect of increasing vitamin D, whereas the continuous analysis indicated a slight adverse effect. None of these effects were statistically significant, however. With week 1 as the reference date, categorical effects were less protective. However, all these estimates were consistent with the null hypothesis of no vitamin D effect.

These examples illustrate that for externally selected cut-points, such as the Institute of Medicine guidelines, estimates of category-specific log odds ratios are affected by the choice of reference date for seasonal adjustment, unlike analyses of a continuous linear trend.

5. Discussion

We presented a framework for seasonal adjustment and calibration of matched case-control data and used this framework to evaluate analytic procedures for continuous and catetorical vitamin D risk models. We evaluated the procedures though simulations based on the Vitamin D Pooling Project data. Several practical conclusions and recommendations follow from this work. 1. Adjustment for calibration and seasonal trends yields more nearly nominal coverage of confidence intervals, less bias, smaller variance and reduced mean square error than unadjusted analyses. 2. Simple procedures are available to adjust for calibration and seasonal trend. 3. For calibration samples obtained by stratified random sampling, as in the Vitamin D Pooling Project, there is surprisingly little inflation in the variance of estimates of vitamin D effects, even with only 30 calibration measurements. 4. Estimates for the logit of risk for continuous vitamin D are independent of a reference date for seasonal adjustment. In contrast, estimates for a categorical risk model depend on the reference date. Thus public health recommendations based on vitamin D categories may need to be season-specific. We elaborate on some of these points.

Simple procedures are available for seasonal adjustment and calibration to estimate the slope, α₁, of a linear trend in vitamin D on the the logit of risk. First one estimates the slope ${\alpha }_1^{\ast }$ by using seasonally detrended values {W(t) − ς̂(t)} in place of vitamin D measurements in conditional logistic regression. Then one deattenuates and corrects for calibration by setting ${\widehat{\alpha }}_1={\widehat{\alpha }}_1^{\ast }/\widehat{b_3}{\widehat{\kappa }}_W$. Our methods do not adjust variances for estimating seasonal trend parameters. Nonetheless, even with n = 100 cases and controls, estimating the 5 seasonal trend parameters had little impact on the coverage of confidence intervals for α₁, and with n = 200, there was no evidence of impact. In Web Appendix A.6 we justify this result asymptotically. There is some loss of efficiency in estimating α₁ from estimating the calibration curve, but the additional variance is accounted for in constructing confidence intervals (see Section 2.5.1).

For categorical data, conditional logistic regression (10) with the estimate x̂₀₃ can be recommended. In this procedure, the calibration estimates obtained by regressing X(t) on ς̂(t)(1 − κ̂_W) + κ̂_W W(t) are used, together with the seasonal trend estimate, to compute x̂₀₃ from equation (7). Then x̂₀₃ is categorized as if it were x₀, and the analysis proceeds using standard conditional logistic regression. No special calculations were used to accommodate variation from estimating seasonal trend or calibration parameters. This procedure with x̂₀₁ in place of x̂₀₃ worked nearly as well, but is less theoretically justified because it does not take seasonal adjustment and κ̂_W into account (see equation 2) and usually has larger mean square error. For κ̂_W = 1, however, the two procedures are equivalent. The normal model method has theoretical appeal but tended to yield more variable estimates of log odds parameters, especially β₂. This loss of efficiency seems inherent in the likelihood based on equation (12). Unreported simulations show that even if the parameters a, b, and κ_W are known, the normal model method yields more variable estimates than the procedures that use x̂₀₁ or x̂₀₃ in equation (10).

The sine-cosine series in equation (4) fit the data well, required only 5 parameters, and forced the estimated trend to be periodic. Flexible procedures such as Loess, do not yield periodic trends, are more sensitive to gaps in the data, and can require many parameters, leading to increased variance of estimates of vitamin D effects [7].

We assumed normal distributions in our analytical framework (Section 2.2). More work is needed to assess the performance of our recommended procedures for other distributions.

An important practical issue was brought out by the examples in Section 4. The Institute of Medicine guidelines for categories of vitamin D levels do not specify the time of year the blood sample was drawn. In the examples, vitamin D levels fluctuated by about 16 nmol/L between the highest values, which occurred in September-October, and the lowest values, which occurred in January-April. Thus a person might be categorized in the highest Institute of Medicine category in September, but lower in February. The intent of seasonal adjustment is to transform each person’s vitamin D value to the value that person would have had if measured on a common reference date, such as week 39 or week 1. This improves comparability between cases and controls, especially in studies without matching on date of blood draw. The odds ratios depend on the choice of reference date (Appendix A.2). Thus one should specify the reference date used for categorical analyses applied to fixed cut-points. If, instead of using externally determined cut-points such as the Institute of Medicine categories, one standardizes the control data to {W(t) − ς̂(t) + ς̂(t₀)} and chooses study-specific cut-points as percentiles of the standardized control data, then the categorical analysis is much less sensitive to choice of reference date, t₀, as indicated by unreported simulations. Analysis of continuous vitamin D as a linear trend is not affected by choice of reference date.

An alternative to picking a particular reference date, t₀, is to average the seasonal estimate ς̂(t₀) over the 52 weeks of the year. Because integrated sinusoidal terms vanish over the year, this is equivalent to replacing ς̂(t₀) by γ̂₀, the estimated intercept in equation (4). The resulting log odds estimates for Q₂, Q₃, and Q₄ for the data in Table (5) from equation (10) with x̂₀₃ were −1.176, −1.160 and −1.582, and are intermediate between the values shown in Table (5) for reference weeks t₀=39 (high vitamin D levels) and t₀=1 (low vitamin D levels).

To summarize, simple methods for calibration and seasonal adjustment yield reliable inference for matched case-control data on vitamin D, with only modest loss of statistical efficiency, compared to analyses with perfectly known vitamin D. These findings are informing analytic approaches for the Vitamin D Pooling Project.

Appendices

A.1. Justification for the Normal Model Equation (12)

Let the categories be (C₁, …, C₅), and write the risk model (9) as

$$\text{pr}(Y=1\mid x)=H(\sum _{j=1}^{5}I(x\in C_j){\beta }_j)=\sum _{j=1}^{5}H({\beta }_j)I(x\in C_j),$$

where H(u) = {1 + exp(−u)}⁻¹ is the logistic function. Assuming that Y is conditionally independent of W(t) given that x is in category c,

$$\text{pr}\{Y=1\mid W(t)\}=\sum _{j=1}^{5}H({\beta }_j)\text{pr}\{x\in C_j\mid W(t)\}.$$

Consider the matched pairs problem, with the matching effect α_i belonging to the i^th matched pair, with responses (Y_i1, Y_i2) and predictors (x_i1, x_i2) and {W_i1(t), W_i2(t)}. We have that

$$\begin{array}{l}\text{pr}(Y_{ik}=1\mid x_{ik})=\sum _{j=1}^{5}H({\alpha }_i+{\beta }_j)I(x_{ik}\in C_j);\\ \text{pr}\{Y_{ik}=1\mid W_{ik}(t)\}=\sum _{j=1}^{5}H({\alpha }_i+{\beta }_j)\text{pr}\{x_{ik}\in C_j\mid W_{ik}(t)\}.\end{array}$$

Under the rare disease approximation H(α_i + β_j) ≈ exp(α_i + β_j), it follows that

$$\begin{array}{l}\text{pr}\{Y_{i1}=1,Y_{i2}=0\mid W_{i1}(t),W_{i2}(t),Y_{i1}+Y_{i2}=1\}\\ \approx \frac{{\sum }_{j=1}^{5}exp({\beta }_j)\text{pr}\{(x_{i1}\in C_j\mid W_{i1}(t))\}}{{\sum }_{j=1}^{5}exp({\beta }_j)\text{pr}\{(x_{i1}\in C_j\mid W_{i1}(t))\}+{\sum }_{j=1}^{5}exp({\beta }_j)\text{pr}\{x_{i2}\in C_j\mid W_{i2}(t)\}},\end{array}$$

which equals equation (12).

A.2. Impact of Seasonal Trend Adjustment, Mis-calibration, and Variation in Cut-Points on Categorical Odds Ratios

If fixed cut-points are used to define categories of exposure, then changing the cut-points, changing the reference date for seasonal adjustment, or mis-calibration will induce bias in odds ratios with respect to the original model.

Changing the cut-points

For simplicity we assume only two categories, but the arguments extend to multiple categories. We assume initially that the true exposure at reference date t₀, namely x₀ = x + ς(t₀) is known (no measurement error and no mis-calibration). Suppose that x₀ > c defines the high risk group and x₀ ≤ c the low risk group. Let p₁ be the risk of disease in the high-risk group and p₀ be the risk of disease in the low-risk group. The odds ratio is OR = {p₁/(1 − p₁)}/{p₀/(1 − p₀)}. Now suppose we choose another cut-point c^*. Let F be the distribution of x₀ in the population and f be the density of x₀. Suppose that the risk in the population is given by the model

$$P(x_0,Y=1)=f(x_0)\{p_{1}I(x_0>c)+p_{0}I(x_0\le c)\},$$ (A.1)

where Y = 1 indicates diseased. The portion in curly brackets is a special case of equation (9) of the paper. If we use a new cut-point, c^*, and assume c^* > c,

$$\begin{array}{l}O{R}^{\ast }=\{P(x_0>c^{\ast },Y=1)/P(x_0>c^{\ast },Y=0)\}/\{P(x_0\le c^{\ast },Y=1)/P(x_0\le c^{\ast },Y=0)\}\\ =\frac{[\{P(x_0\le c,Y=0)+P(c<x_0\le c^{\ast },Y=0)\}\{1-F(c^{\ast })\}{p}_1/\{1-F(c^{\ast })\}(1-p_1)]}{\{P(x_0\le c,Y=1)+P(c<x_0\le c^{\ast },Y=1)\}}\\ =\frac{[\{1-F(c^{\ast })\}{p}_1/\{1-F(c^{\ast })\}(1-p_1)]}{[\{F(c)p_0+\{F(c^{\ast })-F(c)\}{p}_1)]/[F(c)(1-p_0)+\{F(c^{\ast })-F(c)\}(1-p_1)]}\\ =\frac{[p_1/(1-p_1)]}{[\{F(c)p_0+\{F(c^{\ast })-F(c)\}{p}_1)]/[F(c)(1-p_0)+\{F(c^{\ast })-F(c)\}(1-p_1)]}.\end{array}$$ (A.2)

For example, if F is a standard normal distribution, c = 0, p₁ = .05 and p₀ = 0.01, then OR=5.21. If, instead, c^* = 1.645, the 95^th percentile of F, then

$$O{R}^{\ast }=(.05/.95)/(0.5\times 0.01+.45\times 0.05/0.5\times .99+.45x.95)=.05263/.0298=1.765,$$

which is severely downwardly biased. Thus, changing the cut-point changes the odds ratios if equation (A.1) is the correct model. A similar argument can be used to compute OR^* if c^* ≤ c (see equation A.3).

Seasonal adjustment

Suppose we chose a different date for seasonal adjustment, $t_0^{\ast }$. This would lead to $x_0^{\ast }=x+\varsigma (t_0^{\ast })>c$, which is equivalent to $x_0>c-\varsigma (t_0^{\ast })+\varsigma (t_0)\equiv c^{\ast }$. Thus, assuming the model based on t₀ is correct, we can compute the bias from using $t_0^{\ast }$ by substituting c^* in equation (A.2), provided c^* > c. If c^* ≤ c,

$$\begin{array}{l}O{R}^{\ast }=\{P(x_0>c^{\ast },Y=1)/P(x_0>c^{\ast },Y=0)\}/\{P(x_0\le c^{\ast },Y=1)/P(x_0\le c^{\ast },Y=0)\}\\ =\frac{\{P(c^{\ast }<x_0\le c,Y=1)+P(c<x_0,Y=1)\}/\{P(c^{\ast }<x_0\le c,Y=0)+P(c<x_0,Y=0)\}}{\{P(x_0\le c^{\ast },Y=1)\}/\{P(x_0\le c^{\ast },Y=0)\}}\\ =\frac{[\{F(c)-F(c^{\ast })\}{p}_0+\{1-F(c)\}{p}_1]/[\{F(c)-F(c^{\ast })\}(1-p_0)+\{1-F(c)\}(1-p_1)]}{\{p_0/(1-p_0)\}}.\end{array}$$ (A.3)

Mis-calibration

Suppose we use a mis-calibrated variable z₀ = a + bx₀ instead of x₀ but retain the cut-point c for x₀. Then, if b > 0, the event z > c is equivalent to x₀ > (c − a)/b ≡ c^*. Hence the biased OR^* can be computed from equation (A.2) or (A.3) according as c^* > c or c^* ≤ c. If b < 0, then z > c is equivalent to x₀ < (c − a)/|b| ≡ c^*. If c^* < c and F is continuous at cut-points, then OR^* can be calculated from

$$\begin{array}{l}O{R}^{\ast }=\{P(x_0<c^{\ast },Y=1)/P(x_0<c^{\ast },Y=0)\}/\{P(x_0\ge c^{\ast },Y=1)/P(x_0\ge c^{\ast },Y=0)\}\\ =\frac{F(c^{\ast })p_0/F(c^{\ast })(1-p_0)}{\{P(x_0\ge c,Y=1)+P(c^{\ast }\le x_0<c,Y=1)\}/\{P(x_0\ge c,Y=0)+P(c^{\ast }\le x_0<c,Y=0)\}}\\ =\frac{[\{1-F(c^{\ast })\}{p}_1/\{1-F(c^{\ast })\}(1-p_1)]}{[\{F(c)p_0+\{F(c^{\ast })-F(c)\}{p}_1)]/[F(c)(1-p_0)+\{F(c^{\ast })-F(c)\}(1-p_1)]}\\ =\frac{[p_0/(1-p_0)]}{[\{1-F(c)\}{p}_1+\{F(c)-F(c^{\ast })\}{p}_0)]/[\{1-F(c)\}(1-p_1)+\{F(c)-F(c^{\ast })\}(1-p_0)]}.\end{array}$$ (A.4)

If c^* ≥ c,

$$\begin{array}{l}O{R}^{\ast }=\{P(x_0<c^{\ast },Y=1)/P(x_0<c^{\ast },Y=0)\}/\{P(x_0\ge c^{\ast },Y=1)/P(x_0\ge c^{\ast },Y=0)\}\\ =\frac{\{P(x_0<c,Y=1)+P(c\le x_0<c^{\ast },Y=1)\}/\{P(x_0<c,Y=0)+P(c\le x_0<c^{\ast },Y=0)\}}{P(x_0\ge c^{\ast },Y=1)/\{P(x_0\ge c^{\ast },Y=0)}\\ =\frac{[F(c)p_0+\{F(c^{\ast })-F(c)\}{p}_1]/[\{F(c)\}(1-p_0)+\{F(c^{\ast })-F(c)\}(1-p_1)]}{p_1/(1-p_1)}.\end{array}$$ (A.5)

Mis-calibration and seasonal adjustment

If $z_0^{\ast }=a+{bx}_0^{\ast }=a+b\{x+\varsigma (t_0^{\ast })\}=a+b\{x_0-\varsigma (t_0)+\varsigma (t_0^{\ast })\}$, then $z_0^{\ast }>c$ is equivalent to $x_0>\{(c-a)/b\}+\varsigma (t_0)-\varsigma (t_0^{\ast })\equiv c^{\ast }$ provided b > 0. Hence OR^* can be computed from (A.2) or (A.3) according as c^* > c or c^* ≤ c. If b < 0, the condition is $x_0<\{(c-a)/\mid b\mid \}+\varsigma (t_0)-\varsigma (t_0^{\ast })\equiv c^{\ast }$. Then OR^* can be computed from (A.4) or (A.5) according as c^* < c or c^* ≥ c.

Summary

These calculations indicate that for categorical analyses the definition of the odds ratio of interest depends on the reference date for seasonal adjustment. They also indicate that mis-calibration will affect the categorical odds ratio.