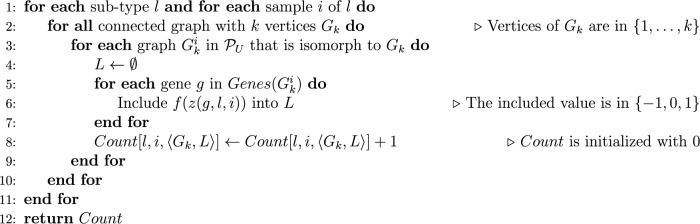A New Approach for Identification of Cancer-related Pathways using Protein Networks and Genomic Data

Abstract

Cancer cells have anomalous development and proliferation due to disturbances in their control systems. The study of the behavior of cellular control system requires high-throughput dynamical data. Unfortunately, this type of data is not largely available. This fact motivates the main issue of this article: how to use static omics data and available biological knowledge to get new information about the elements of the control system in cancer cells. Two important measures to access the state of the cellular control system are the gene expression profile and the signaling pathways. This article uses a combination of these two static omics data to gain insights on the states of a cancer cell. To extract information from this kind of data, a statistical computational model was formalized and implemented. In order to exemplify the application of some aspects of the developed conceptual framework, we verified the hypothesis that different types of cancer cells have different disturbed signaling pathways. To this end, we developed a method that recovers small protein networks, called motifs, which are differentially represented in some subtypes of breast cancer. These differentially represented motifs are enriched with specific gene ontologies as well as with new putative cancer genes.

Introduction

Cancer cells have anomalous development and proliferation due to disturbances in their control systems. To increase the knowledge about these phenomena, some quantitative models and experimental studies have been proposed either in an abstract theoretical perspective^1,2 or in some particular case studies.^3,4 The cell control systems are constituted by the integration of a gene system and signaling pathways that regulate gene expression and metabolic pathways. The signaling pathways are composed of a biochemical network that has a hierarchical modular structure, that is, many complex networks are decomposed in simpler ones, the modules or motifs.⁵

A very informative data for studying such complex phenomena would be dynamical data evaluated through time series of omics measurements taken from a single cell or from a set of synchronized cells. Unfortunately, this kind of data is not largely available. This fact motivates the main issue of this article: how to use static omics data and available biological knowledge to get new information about the elements of the control dynamics of cancer cells.

Two important measures to access the state of the cell control system are the gene expression profile and the signaling pathways (ie, control signals built primarily from protein–protein interaction [PPI]). Tumor biopsies data from large cohorts of patients are abundant (eg, the one from The Cancer Genome Atlas) and allow the assessment of gene expressions, which are important to evaluate the impact of genetic heterogeneity in the control systems. This information may be relevant, for example, to distinguish the control systems’ behavior in different types of cancer or in different stages of a given cancer type. Another available data that has some structural information about the cell control system dynamics is the human PPI network.

This article uses a combination of two static omics data: the human PPI network⁶ and the transcript expression measurements taken from breast cancer tissues⁷ to model the states of a cancer cell. The integration of biological networks and gene expression data is not new. Several reports have addressed the combined use of both types of data using different approaches.^8–14 For each type of cancer, this integrated approach results in a subgraph of the human PPI graph, labeled with relative (with respect to the normal tissue) transcript expression values associated to each protein. This labeled PPI graph connects the problem of extracting information about cancer cell dynamics from static omics data and complementary biological knowledge to the formal approach of probabilistic graph models, such as gene expression network¹⁵ and motif network analysis.¹⁶ This network analysis models the phenomena of different kinds by the same abstract model, a graph. It takes abstract graph structure measures, which depend on nodes and arcs, and interprets them in the context of the phenomena studied. The labeled subgraphs under this study will be called as motifs.

To exemplify the application of some aspects of the developed conceptual framework, we will verify the hypothesis that different subtypes of breast cancer have different representation of motifs. This article proposes an analytical method, which integrates PPI networks and differential tissue transcript expression data to identify motifs (ie, small subgraphs) of disturbed signaling pathways and measure the distribution of the observed state of these motifs in breast cancer subtypes. Motifs showing a differential representation in the subtypes are then analyzed, and new cancer genes are proposed.

Following this section, the “Materials and methods” section presents the methods used to extract, analyze, and model the data. The description of the data includes their source, semantics, and preparation. The “Model of analysis” section presents the mathematical description of the operators used to identify the motifs, estimate the motif distributions, and recognize the characteristic motifs of each cancer subtype. In the following “Results” section, the analysis outputs are given, including identification of motifs, characteristics of motif recognition, data enrichment of the motifs recognized, analysis of motifs internal connections for annotation of new cancer proteins, and corresponding enrichment. The article is ended with the discussion of potential applications of the technique presented here and other similar techniques for learning about the structure of the cellular control system and the disturbed subsystems.

Materials and Methods

Data source

In this subsection, we describe the TGA expression data, the PPI data and the enrichment technique.

TCGA data

The TCGA expression data were retrieved from the cBio portal. A z-score threshold was used to classify the genes as upregulated (z-score >3) or downregulated (z-score <−3). Moreover, to improve the number of available data, both RNA-Seq and microarray experiments were combined. For samples with both types of data, only microarray data were used. This data were acquired using the CGDS-R function, available at cBio.¹⁷ Datasets were all from the same release (January 2015). TCGA clinical data were downloaded from the TCGA public site (http://tcgs-data.nci.nih.gov/tcga/tcgaDownload.jsp). The breast cancer samples were stratified using the molecular signatures described in Refs. ¹⁸ and ¹⁹.

PPI data

The human PPI network was obtained from the STRING database, which includes both known and predicted PPIs.²⁰ For each association, a confidence score is calculated based on the evidence collected from different data types. Here, we selected interactions with score 700 or 900 from experimental or in silico evidences, respectively.

Enrichment data

The protein datasets derived from the analyzed motifs were submitted to clusterProfiler package, a enrichment tool provided by the R platform.²¹ All enrichments were carried out against the Kyoto Encyclopedia of Genes and Genomes (KEGG) database,²² with an adjusted (using the BH method) P-value cutoff equal to 0.05.

Model of analysis

In this subsection, we describe the computational methods developed in this article. First, we introduce some concepts and definitions. Second, we describe the adopted strategy for the motif identification. Finally, we present our methodology to assess the frequencies of the motifs that were obtained in the identification step.

Definitions

A graph is an ordered pair of sets $(\mathcal{V},ℰ)$. The elements of $\mathcal{V}$ are called vertices, while $ℰ$ is a set of pairwise elements of $\mathcal{V}$; the elements of $ℰ$ are called edges. We can now define a PPI network as a graph.

Definition 2.1. A PPI network graph ${\mathcal{P}}_{\mathrm{U}}$ is a graph $(\mathcal{V},ℰ)$ where each vertex is identified by one protein, and each edge represents a potential interaction between proteins.

A subgraph is a graph $G=({\mathcal{V}}^{\prime },{ℰ}^{\prime })$ such that ${\mathcal{V}}^{\prime }\subseteq \mathcal{V}$, ${ℰ}^{\prime }\subseteq ℰ$ and $H=(\mathcal{V},ℰ)$ are also a graph; in this case, we say G is a sub-graph of H. We assume that there is a bijection between the expressed gene set and the protein set. Hence, we can make the following definition.

Definition 2.2. Given a subgraph G of ${\mathcal{P}}_{\mathrm{U}}$, Genes(G) is an ordered list of genes associated to the vertices of G.

In this work, gene expression information is gathered from cancer tissue subtypes. For each subtype, several samples were collected. For each subtype and each sample, the expression levels of a given gene are given by its z-score, which is a real number.

Definition 2.3. Given a gene g, z(g,l,i) is the z-score of g for the ith sample of subtype l.

Let the elements of the set {−1,0,1} be denoted as labels. The labels −1, 0, and 1 are also known as suppressed, normal, and overexpressed, respectively. We define f: ℝ → {−1,0,1} as a function that takes values from z-scores to labels.

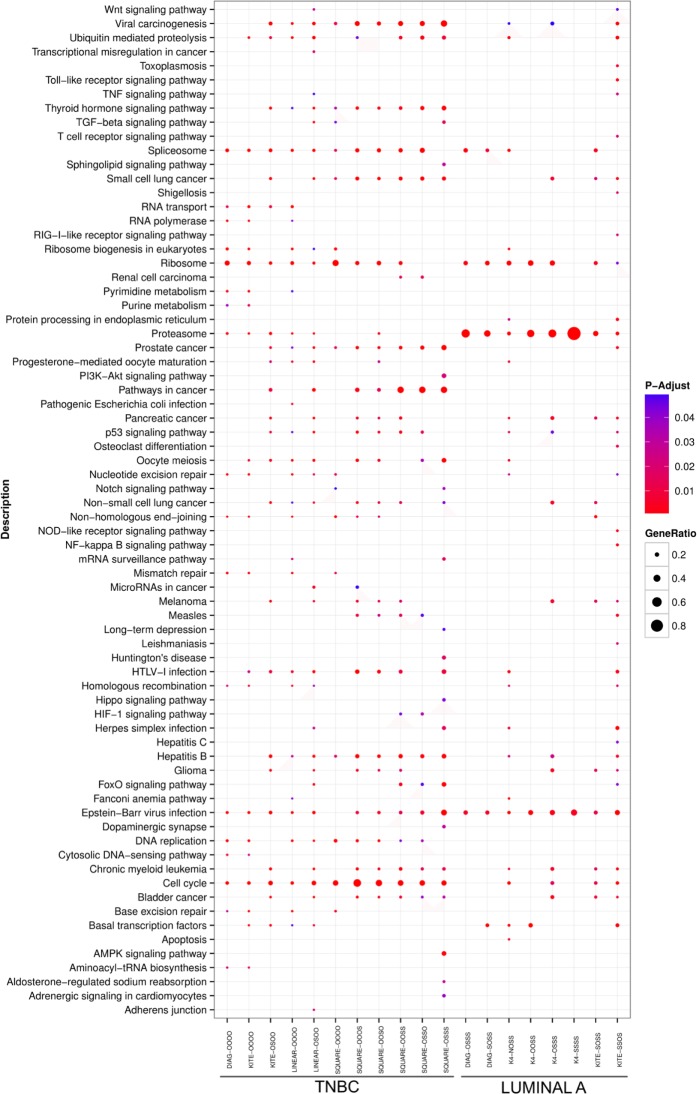
Now, let G be a graph with at least two vertices. We say that G is connected if for every pair 〈u,v〉 of vertices of G there is a set of edges ${\cup }_{1\le i<n}\left\{\left\{u_i,u_{i+1}\right\}\right\}$ such that v₁ = u and v_n = v. In this work, we are interested in sets of graphs that are connected and have the same number of vertices. In Figure 1, we give examples of connected graphs with four vertices.

Figure 1.

Connected graphs with four vertices.

Let G and H be two graphs. We say that G is isomorph to H if there is a bijection b between the vertices sets of G and H such that two vertices u and v of G are adjacent (ie, both are present in the same edge of G) if and only if the vertices b(u) and b(v) of H are adjacent.

With the definitions presented so far, we can now introduce the concept of motif used in this article.

Definition 2.4. A motif 〈G,L〉 is composed by a connected graph G and an ordered list of labels L such that there is a bijection between vertices in G and labels in L.

In Figure 2, we present an example of motif. Finally, let ${ℳ}_1=\langle G_1,L_1\rangle$ and ${ℳ}_2=\langle G_2,L_2\rangle$ be two motifs. We say that ${ℳ}_1$ is symmetric to ${ℳ}_2$ if there is a bijection b between the vertice sets of G₁ and G₂ such that: (i) two vertices u and v of G₁ are adjacent if and only if the vertices b(u) and b(v) of G₂ are adjacent (ie, G₁ is isomorph to G₂) and (ii) for each vertex v of G₁, its label in L₁ is equal to the label of b(v) in L₂.

Figure 2.

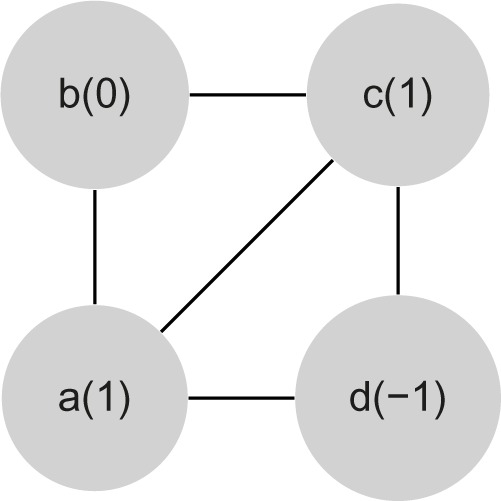
Example of a motif 〈G,L〉 with vertices {a,b,c,d} and L = 〈+1,0,+1,−1〉.

Based on these definitions, we developed algorithms for motif identification that will be explained in the next section.

Motif identification

In this section, we present two algorithms for motif identification, which is, for a given set of motifs, the search and counting of their occurrences in the PPI network graph, cancer tissue subtypes, and their respective samples. The first algorithm is a basic search and count algorithm, which is described in a higher level, that is, we show only the general steps to perform the motif identification. The second algorithm is a modification of the basic search and count algorithm for connected graphs with four vertices, which we further explored in this work with computational experiments.

The basic search and count algorithm

The basic search and count algorithm receives as input a set of cancer tissue subtypes and their respective set of samples, an integer k ≥ 2 and a PPI network graph ${\mathcal{P}}_{\mathrm{U}}$. It returns a table Count, which stores, for each subtype and each sample, the number of observations of the motif 〈G_k,L〉, where G_k is a connected graph with k vertices and L is an ordered set of labels associated to the vertices of G_k. The pseudocode of this algorithm is presented in Figure 3.

Figure 3.

Pseudocode of the basic search and count algorithm.

In this basic search and count algorithm, we assume that the counting issues that might arise due to symmetries between motifs are solved through an appropriate implementation of the for loops in the lines 2–10, 3–9, and 5–7. In the following, we show an implementation of this algorithm for connected graphs with four vertices; this implementation includes a way to circumvent these counting issues.

An algorithm for connected graphs with four vertices

The general strategy of this algorithm is, for each vertex in the PPI network graph ${\mathcal{P}}_{\mathrm{U}}$, to explore its adjacent vertices (and also some vertices adjacent to adjacent vertices) and store all connected subgraphs with four vertices found during that procedure. For each search initiated in a vertex v, the exploration is constrained to vertices smaller than v. Hence, we assume that there is a strict total order relation in the set of vertices of ${\mathcal{P}}_{\mathrm{U}}$, as in the graph depicted in Figure 4.

Figure 4.

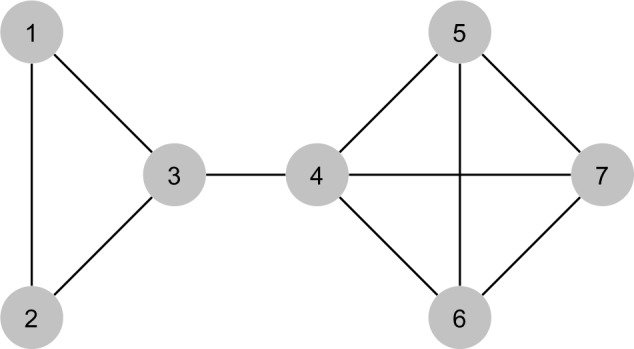
Example of PPI network graph ${\mathcal{P}}_{\mathrm{U}}$.

We start the description of this algorithm by a recursive function to identify the connected subgraphs of four vertices in a PPI network graph ${\mathcal{P}}_{\mathrm{U}}$. To this end, we first introduce an additional concept: let G be a graph and X be a subset of vertices of G. G[X] is a subgraph of G induced by X if G[X] is a sub-graph of G such that for every pair of vertices u and v of G[X], {u,v} is an edge of G[X] if and only if {u,v} is an edge of G.

The IDENTIFY-SUBGRAPHS function receives a PPI network graph ${\mathcal{P}}_{\mathrm{U}}$ and a vertex v of ${\mathcal{P}}_{\mathrm{U}}$, and includes into a given set G all connected subgraphs of four vertices in ${\mathcal{P}}_{\mathrm{U}}$ that can be found in an exploration starting in v. In an initial call of this function, X is set as {v}, and k = 3. The pseudocode of this function is shown in Figure 5.

Figure 5.

Pseudocode of a recursive function to identify the subgraphs from a PPI network graph.

In Table 1, we show a simulation of the IDENTIFY-SUBGRAPHS function for an exploration of the PPI network graph depicted in Figure 4 that starts in vertex 7. The main algorithm receives as input a set of cancer tissue subtypes and their respective set of samples and a PPI network graph ${\mathcal{P}}_{\mathrm{U}}$. It returns a table Count which stores, for each subtype and each sample, the number of observations of the motif 〈G′,L′〉, where G′ is a connected graph with four vertices and L′ is an ordered set of labels associated with the vertices of G′. The pseudocode of this algorithm is presented in Figure 6.

Table 1.

Simulation of the IDENTIFY-SUBGRAPHS function.

#CALL	G (ONLY THE VERTEX SETS OF THE GRAPHS ARE SHOWN)	X	V	K
1	Ø	{7}	7	3
2	{{7, 6, 5, 4}}	{7}	7	2
3	{{7, 6, 5, 4}}	{7, 6, 5}	6	1
4	{{7, 6, 5, 4}}	{7, 6, 5}	5	1
5	{{7, 6, 5, 4}}	{7, 6, 4}	6	1
6	{{7, 6, 5, 4}}	{7, 6, 4}	4	1
7	{{7, 6, 5, 4}, {7, 6, 4, 3}}	{7, 5, 4}	5	1
8	{{7, 6, 5, 4}, {7, 6, 4, 3}}	{7, 5, 4}	4	1
9	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7}	7	1
10	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 6}	6	2
11	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 6}	6	1
12	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 6, 5}	5	1
13	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 6, 4}	4	1
14	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 5}	5	2
15	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 5}	5	1
16	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 5, 4}	4	1
17	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 4}	4	2
18	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 4}	4	1
19	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}}	{7, 4, 3}	3	1
**	{{7, 6, 5, 4}, {7, 6, 4, 3}, {7, 5, 4, 3}, {7, 4, 3, 2}, {7, 4, 3, 1}}	–	–	–

Notes: Each row contains the input values of a call of the function; the first row is the initial call, while the remaining rows are the recursive calls in the sequential order they are executed. For all calls of the function, the PPI network graph ${\mathcal{P}}_{\mathrm{U}}$ is the one depicted in Figure 4.

^**After the execution of the 19th and last recursive call.

Figure 6.

Pseudocode of a search and count algorithm for connected graphs with four vertices.

In the pseudocode shown in Figure 6, the function EXTRACT-TOPOLOGY called in line 11 avoids two motifs that are symmetric to each other of being counted separately. Once for connected graphs with four vertices, there are a few possible configurations when the graph isomorphism is taken into account. Figure 1 shows the six equivalent classes defined by all isomorphisms; we treated each case directly through a table that maps different pairs 〈G₁,L₁〉, …, 〈G_n,L_n〉 into a unique motif 〈G′,L′〉. For instance, each of the two motifs shown in Figure 7A and B is mapped to the motif depicted in Figure 7C.

Figure 7.

A procedure to avoid two motifs that are symmetric to each other of being counted separately. At each figure, vertices names and their associated labels are, respectively, outside parentheses and between parentheses. The motifs of (A) and (B) are symmetric to each other, and the EXTRACT-TOPOLOGY function maps them to the same unique motif (C).

Motif frequency analysis

In this section, we describe the methodology of the analysis of the motif statistics produced using the algorithms presented in the previous section (ie, the data stored in the Count table). The adopted strategy involves the use of the Shannon entropy to assess motifs whose number of occurrences was concentrated in one or more subtypes.

Let $\mathbb{M}$ be the space of motifs, ℒ be the collection of subtypes, and n_l be the number of samples of the subtype l. For each motif $ℳ$ in $\mathbb{M}$, the entropy of among the subtypes in is described by the following equation:

$$H(ℳ)=-{\displaystyle \sum _{l\in ℒ}{P}_{ℳ}}(l)\log P_{ℳ}(l),$$ (1)

where ${\mathcal{P}}_{ℳ}$(·) is the probability distribution function for the motif $ℳ$ among the subtypes in ℒ; this function is defined as follows:

$$P_{ℳ}(l)=\frac{{\displaystyle \sum {}_{1\le n\le nl}Count[l,n,ℳ]}}{{\displaystyle \sum {}_{m\in L}}{\displaystyle \sum {}_{1\le n\le n_m}Count[m,n,ℳ]}},$$ (2)

for all l in ℒ.

Results

The PPI graph used for this work has 7335 nodes, with degrees (ie, number of connections) varying from 1 to 3090 (for the protein UBC), with an average degree of 8. It is important to emphasize that present-day human PPI networks are still incomplete with a high rate of false negatives. We deal with this problem by using mass concentration analysis of relevant motifs. The breast cancer subtypes considered are presented in Table 2.

Table 2.

Number of samples in each breast cancer subtype.

SUBTYPE	SAMPLES
Triple negative	100
Luminal A	393
Luminal B	100
Her 2 enhanced	30

Motif identification

In the following, a motif is just a subgraph where a vertex is associated with any protein with a given label. Consequently, the number of different motifs is 6 × 3⁴ = 486, since there are six topologies (Fig. 1) and three possible labels for each vertex.

As expected, the vast majority of motifs have labels L = 〈0,0,0,0〉, indicating that all proteins have no differential expression compared to a normal cell in that respective sample. Their count is over 95 times the number of occurrences of any other labeled motif in a given subtype. In order to reduce the search space, we removed these motifs from further analysis.

In the following, for the sake of simplicity, we use the letters s, n, and o to indicate the expression levels −1 (suppressed), 0 (normal), and 1 (overexpressed), respectively.

Differential motifs

The counting algorithm of the “Motif identification” section and Expression (2) provide an estimate of motif distribution among breast cancer subtypes. Using Shannon’s entropy (Expression (1)), we identified the motifs that are more represented in each breast cancer subtype.

With four subtypes, the maximum entropy is −4 × 0.25 log₂ 0.25 = 2, representing an uniform distribution. Table 3 shows all the motifs with entropy lesser than one, indicating a concentration of occurrences in one or two subtypes. We are interested in those that are strongly represented in one subtype and have a small relative number of occurrences in others.

Table 3.

Entropy of motifs and distribution among subtypes.

MOTIF	ENTROPY	TRIPLE NEG	LUMINAL A	LUMINAL B	HER2E
K4-osss	0.3667	0.0392	0.9436	0.0166	0.0006
Diag-soss	0.4474	0.0840	0.9130	0.0018	0.0011
K4-ooss	0.5592	0.1184	0.8780	0.0001	0.0035
Square-ooss	0.5614	0.8711	0.1282	0.0003	0.0003
Diag-osss	0.5661	0.0912	0.8919	0.0162	0.0007
Star-ooos	0.6463	0.8699	0.1121	0.0038	0.0141
Linear-oooo	0.6516	0.8549	0.1369	0.0044	0.0039
Square-osso	0.7082	0.8116	0.1874	0.0005	0.0005
Square-oooo	0.7268	0.8252	0.1642	0.0001	0.0106
Kite-soss	0.7296	0.1611	0.8273	0.0107	0.0009
Kite-oooo	0.7428	0.8236	0.1652	0.0044	0.0068
Diag-oooo	0.7969	0.8123	0.1704	0.0102	0.0071
Square-ooos	0.7990	0.7718	0.2252	0.0002	0.0028
Square-ooso	0.8021	0.8236	0.1487	0.0224	0.0053
Kite-osoo	0.8198	0.8137	0.1601	0.0044	0.0219
Linear-osoo	0.8541	0.7807	0.2040	0.0072	0.0081
Square-osss	0.8756	0.7134	0.2855	0.0005	0.0005
K4-ssss	0.8865	0.1755	0.7880	0.0365	0.0000
Kite-ssos	0.8937	0.2093	0.7675	0.0230	0.0003
K4-noss	0.8968	0.1034	0.8107	0.0845	0.0011
Star-ssso	0.9696	0.3358	0.6584	0.0057	0.0001
Star-ssss	0.9991	0.5525	0.4469	0.0003	0.0003

For instance, the first motif in Table 3, K4-osss (topology K4 and expression levels 〈+1,−1,−1,−1〉) is clearly much more represented in the subtype luminal A. The same applies to Diag-soss and K4-ooss. Square-ooss is more represented in the subtype triple negative.

Enrichment of differential motifs with specific ontologies in breast cancer subtypes

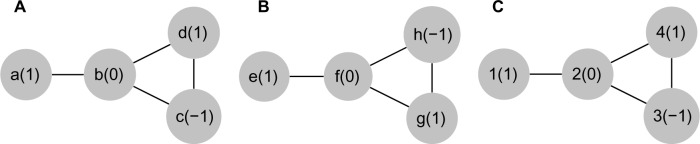
The differential motifs identified in Table 3 were further analyzed in terms of the composition of proteins in the PPI subgraph constructed for each breast tumor subtype. From the samples of each breast cancer subtype, we took the union of all instances of a motif, obtaining a set of proteins. These nonredundant lists (one for each subtype) were then evaluated regarding the enrichment of ontologies from the KEGG.²² A total of 27 and 12 KEGG categories were exclusively present in TNBC and luminal A, respectively (Fig. 8). For luminal A, Kite-ssos was the most enriched motif in the KEGG categories as shown in Figure 8, while for TNBC, Linear-osoo was the most enriched motif.

Figure 8.

KEGG enrichment analysis. The dotchart shows the enrichment analysis performed by using clusterProfiler. All motifs selected by Shannon entropy method are represented at the X-axis, while in the Y-axis, all the enriched KEGG pathways with P-value ≤ 0.05 are listed. The adjusted P-values are sorted from less (blue) to more (red) significant. Furthermore, the dot size is based on gene ratio, which is the observed number of genes in the experimental set within the respective KEGG pathway.

Interestingly, most of the KEGG categories found exclusively in TNBC are involved with tumorigenesis, including transcription misregulation in cancer, renal cell carcinoma, PI3K-AKT signaling pathway, pathways in cancer, mismatch repair, base excision repair, and microRNAs in cancer. This strongly suggests that our method is capable to identify motifs whose nodes are related to tumorigenesis. Furthermore, this also shows that the motifs identified by our methods belong to pathways related to cancer.

Use of motifs to complement the annotation of cancer pathways

One of the most complete annotations of cancer-related pathways is provided by the KEGG database. Its pathways in cancer entry have been widely used as a comprehensive landmark for a systemic view of cancer genes and proteins.

As mentioned earlier, the data in Figure 8 strongly support the view that the motifs identified by our method belong to cancer-related pathways. It is, thus, reasonable to speculate that the set of proteins belonging to our motifs might harbor new putative cancer genes. To evaluate this possibility, we first selected all instances of the motifs that contained at least one node from KEGG’s pathways in cancer entry. Among these instances, half (51%) contained only one node from that respective KEGG entry. Instances with two, three, and four nodes from the KEGG entry corresponded roughly to 33%, 14%, and 2% of all instances, respectively. There was no difference between the breast cancer subtypes regarding the above distribution. Next, we select all other proteins belonging to the same motifs but not belonging to the KEGG’s pathways in cancer. Proteins classified as overexpressed or underexpressed were separately ranked based on their frequency in the motifs.

The top candidates are listed in Table 4. Using the S-score method, recently developed by some of us,²³ we estimated that 52% of the genes listed in Table 4 (54 out of 103 genes) are cancer genes for breast tumor. One interesting protein that our method classifies as potentially oncogenic for triple negative is PSMB4, a subunit of the 26S proteasome that has been classified as a driver oncogene for several types of tumors.²⁴ Another interesting protein found by our method is YEATS2, a component of a histone acetyltransferase complex. YEATS2 has been found to be recurrently altered in chondrosarcoma tumors.²⁵

Table 4.

The ranked proteins associated with pathway in cancer.

PROTEIN	SUPPRESSED (S)				OVER-EXPRESSED (O)
	TNBC	LMNA	LMNB	HER2	TNBC	LMNA	LMNB	HER2
HSF1	0	0	0	0	0.74	0.89	0.72	0.77
RANGRF	0.51	0.46	00.87	0.78	0	0	0	0
ORAOV1	0	0	0	0	0.44	0.89	0.73	0.5
ERBB2IP	0.72	0.36	0.09	0.19	0	0.01	0.01	0
NDUFB9	0	0	0	0	0.92	0.92	0.83	0.86
IFNAR1	0.25	0.1	0	0	0.38	0.21	0	0.89
FBP1	0.83	0.34	0	0.45	0	0	0	0
SRSF12	0	0	0	0	0.85	0.15	0	0
UQCRB	0 0	0 0	0	0.37	0.86	0	0.58	0.67
TOPORS	0.26	0.58	0.36	0.51	0.08	0.02	0.04	0.21
ZNF706	0	0.05	0	0	0.69	0.85	0.74	0.69
RPL19	0.12	0.13	0	0	0	0.13	0.85	0.9
GOLGA1	0.64	0.32	0	0.79	0	0	0.42	0
FLII	0	0.58	0.43	0.35	0	0	0.22	0.35
MRPL53	0.72	0	0	0.66	0	0.27	0	0
NADK2	0	0.13	0	0.83	0	0.25	0.5	0
TCAP	0	0	0	0	0	0.34	0.97	0.96
NUP50	0.13	0.59	0	0	0.13	0	0.42	0.32
NMT1	0	0.34	0.62	0.89	0.26	0.4	0.12	0
MGMT	0.35	0.59	0.82	0.7	0	0	0	0
USP32	0.17	0	0	0.32	0	0.73	0.89	0.32
GATA3	0.87	0.38	0	0.67	0	0	0	0
PTRH2	0	0.05	0	0	0.34	0.75	0.9	0.83
ORMDL3	0	0	0	0	0	0.42	0.95	0.99
PHB	0	0	0	0	0	0.63	0.86	0.89
KAT7	0	0.01	0	0	0.01	0.49	0.9	0.59
FOXA1	0.81	0.47	0	0.42	0	0.02	0.05	0
GRB7	0	0	0	0	0.01	0.37	0.92	0.94
ATMIN	0.33	0.54	0.83	0	0.22	0.05	0	0
ELP3	0.88	0.55	0.86	0.86	0	0.15	0	0
TBCE	0	0	0	0	0.9	0.92	0.88	0.96
VPS72	0	0	0	0	0.83	0.67	0.5	0.86
MRPL27	0.37	0.05	0	0	0	0.59	0.81	0.89
MSL1	0	0	0	0	0	0.12	0.84	0.96
PABPC1	0	0	0	0	0.84	0.67	0.77	0.9
ATP5L	0.39	0.51	0.75	0.84	0	0	0	0
NHP2L1	0.3	0.7	0	0.29	0.1	0	0	0.29
MED7	0.78	0.44	0.05	0	0	0	0	0
MED4	0.36	0.47	0.82	0.6	0.12	0	0	0
YEATS2	0	0	0	0	0.86	0.25	0	0.43
KANSL1	0.2	0.1	0.61	0.82	0	0	0	0
FAM175A	0	0.14	0	0.8	0	0	0	0
RAD21	0	0	0	0	0.83	0.9	0.83	0.93
MRPL10	0.52	0.07	0.38	0.89	0	0.57	0.49	0
MRPL13	0	0	0	0.11	0.77	0.91	0.94	0.85
MED30	0	0	0	0	0.85	0.61	0.06	0.32
POLR2K	0	0	0	0	0.79	0.85	0.82	0.75
TUBGCP3	0	0.09	0.76	0.31	0.8	0.26	0	0.31
DNAJC3	0	0	0.76	0.37	0.07	0.21	0.01	0.02
UBE2Z	0.26	0.26	0	0.13	0	0.46	0.92	0.67
ANKRA2	0.77	0.44	0.37	0.44	0	0	0	0
01/08/02	0	0	0	0	0.86	0.63	0.52	0.83
MCPH1	0.25	0.71	0.61	0.47	0.15	0.01	0.01	0
TNFRSF10B	0.18	0.65	0.22	0	0.18	0	0	0
KRT4	0	0	0	0	0.54	0	0	0.95
CDC6	0	0	0	0	0	0.15	0.88	0.89
VPS45	0	0	0	0	0.38	0.53	0.91	0.43
INTS10	0.09	0.71	0.64	0.37	0.46	0.03	0	0
FBX025	0.49	0.68	0.74	0.82	0.18	0.04	0	0
DDX19A	0	0.63	0	0	0.16	0	0	0
KLHL12	0.15	0	0	0	0	0.6	0.89	0.75
RPS25	0.24	0.57	0.89	0.46	0	0.06	0	0
RABIF	0	0	0	0	0.8	0.85	0.93	0.89
FAM96B	0.4	1	0.75	0.33	0	0	0	0.33
VPS4A	0.13	0.57	0.85	0.22	0	0	0	0.22
MAEA	0.35	0.23	0.77	0.34	0.21	0	0	0
EZH1	0.16	0.13	0.29	0.83	0	0.13	0	0
RI0K1	0	0	0	0	0.84	0.26	0.22	0.36
LRRFIP1	0.83	0.17	0	0	0	0.08	0	0
SKIV2L2	0.73	0.36	0.29	0	0.07	0.18	0	0
MED1	0.09	0.24	0.07	0.08	0.3	0.31	0.89	0.87
PSMB4	0	0	0	0	0.91	0.51	0.62	0.35
FYCOl	0.85	0.33	0	0.82	0	0	0	0
DCAF13	0	0	0	0	0.81	0.87	0.83	0.73
CAMLG	0.76	0.12	0	0.7	0	0.16	0	0
PEX14	0.2	0	0.75	0	0	0	0	0
YWHAZ	0	0	0	0	0.76	0.87	0.74	0.77
NSMCE4A	0	0	0	0.78	0.29	0.39	0	0
ELAC2	0	0.59	0.54	0	0	0	0	0
CDK12	0	0	0	0	0	0.17	0.88	0.96
TLX1	0	0	0	0	0.78	0.25	0.34	0.88
TGOLN2	0.41	0	0	0.79	0	0	0.75	0
CNOT7	0.42	0.74	0.74	0.62	0.21	0.04	0	0
ATP5G2	0.82	0.2	0	0.62	0	0	0	0
COPA	0	0	0	0	0.69	0.78	0.91	0.51
CLASP2	0	0	0	0.79	0	0.2	0.2	0
CLASP1	0.29	0.1	0.51	0.82	0	0.1	0	0
HEATR1	0.04	0.12	0	0	0.86	0.59	0.77	0.67
INTS9	0.55	0.62	0.71	0.62	0	0	0.09	0
SNF8	0.22	0.11	0	0	0	0.54	0.94	0.84
KRIT1	0.18	0.31	0.77	0	0.18	0.31	0	0
DEDD	0	0	0	0	0.88	0.7	0.75	0.8
DUSP12	0	0	0	0	0.55	0.69	1	0.38
LACTB2	0	0	0	0.33	0.7	0.85	0.44	0.33
EX0C4	0.23	0	0.87	0	0	0.24	0	0
HSPA14	0	0.04	0	0	0.83	0.51	0.26	0.58
TINF2	0.72	0.14	0	0.66	0	0	0	0
RPA1	0	0.4	0.77	0.51	0.14	0	0	0
BBS4	0.74	0.25	0	0	0	0.12	0	0
SCRIB	0	0	0	0	0.5	0.9	0.42	0.54
DYNC1I1	0	0	0	0	0.83	0.3	0	0
ACTL6A	0	0	0	0	0.83	0.47	0.49	0.83
ATP6V1C1	0	0	0	0	0.34	0.86	0.74	0.4

Notes: The normalized values were calculated based on absolute frequency of each type expression label in each subtype. For a given protein, the sum of the counts N, O, and S was used to normalize S and 0.

Abbreviations: TNBC, triple negative; LMNA, luminal A; LMNB, luminal B; HER2, Her2 enriched.

In the list of underexpressed proteins, the transcription factor GATA3 was identified by our method as important in triple negative, and several reports have linked alterations in GATA3 with different aspect of breast tumor biology.²⁶ The data presented in Table 4 strongly suggest that our method is able to identify known and new cancer genes.

Discussion

The method presented in this study identifies the recurrent four-node motifs in the human PPI network superimposed with expression data from breast cancer patients from the TCGA project. The PPI graph permits to assess regions of the four-dimensional gene expression space and, based on gene vector distribution, recognize the differential gene vectors. The S-score method corroborated that most of the genes found are oncogenes for breast cancer tumor. Furthermore, up to a reasonable noise level in the PPI network, our method is quite robust, since we have considerable amount of data for the estimation of this kind of distribution (ie, the ones with very high mass concentration). Although breast cancer data were used here, the method can be used for any type of tumor, assuming that there are the corresponding gene expression data. Besides generating a representation map of such motifs in a cohort of breast cancer patients, the method allowed us to gain significant biological insights and identify potential new cancer proteins. Both pieces of information extracted by the method are relevant to increase our understanding of the structure and dynamics of the cancer cell control system. The identification of new cancer proteins tends to progressively complete the architecture of the signal network of cancer cells. Changes in the cancer cell architecture are usually associated with dynamics alterations. The distribution of motifs may allow the investigation of cell control system architecture transformations, which imply in increasing or decreasing the control disturbances in different generations of cancer cells. The effect of such alterations on the cell control systems should be associated with several phenotypes, including cancer malignancy. Thus, under this point of view, methodologies of the kind presented in this article may contribute to the discovery of relevant new knowledge about cancer cell control systems.