A modified exponential behavioral economic demand model to better describe consumption data

Abstract

Behavioral economic demand analyses that quantify the relationship between the consumption of a commodity and its price have proven useful in studying the reinforcing efficacy of many commodities, including drugs of abuse. An exponential equation proposed by Hursh and Silberberg (2008) has proven useful in quantifying the dissociable components of demand intensity and demand elasticity, but is limited as an analysis technique by the inability to correctly analyze consumption values of zero. Here, we examine an exponentiated version of this equation that retains all the beneficial features of the original Hursh and Silberberg equation, but can accommodate consumption values of zero and improves its fit to the data. In Experiment 1, we compared the modified equation to the unmodified equation under different treatments zero values in cigarette consumption data collected online from 272 participants. We found that the unmodified equation produces different results depending on how zeros are treated, while the exponentiated version incorporates zeros into the analysis, accounts for more variance, and is better able to estimate actual unconstrained consumption as reported by participants. In Experiment 2, we simulated 1000 datasets with demand parameters known a priori and compared the equation fits. Results indicate that the exponentiated equation was better able to replicate the true values from which the test data were simulated. In conclusion, an exponentiated version of the Hursh and Silberberg equation provides better fits to the data, is able to fit all consumption values including zero, and more accurately produces true parameter values.

General Introduction

Behavioral economic demand analyses describe the relationship between the price (including monetary cost and/or effort) of a commodity and the amount of that commodity that is consumed. Such analyses have been successful in quantifying the reinforcing efficacy of commodities including drugs of abuse, and have been shown to be related to other markers of addiction (Bickel, Johnson, Koffarnus, MacKillop, & Murphy, 2014; MacKillop & Murphy, 2007). Hursh and Silberberg (2008) proposed a now widely used equation (Equation 6 in the source paper) to be fitted to consumption data across a range of prices:

$${log}_{10}Q={log}_{10}{Q}_0+k(e^{-\alpha Q_{0}C}-1)$$ (1)

where Q is consumption of a given commodity at price C, Q₀ is derived consumption as price approaches zero, α is demand elasticity, and k is the span of the function in log₁₀ units. This equation has a number of attractive features for the analysis of behavioral economic demand data, and has become widely used as a result. It allows for the independent measure of demand intensity (Q₀) and demand elasticity (α) for inferential and descriptive statistics. Generally, this equation also describes demand data well and accounts for a high proportion of the variance of consumption data across a variety of contexts, procedures, and species (Hursh & Silberberg, 2008; Koffarnus, Hall, & Winger, 2012; Koffarnus, Wilson, & Bickel, 2015; Roma, Kaminski, Spiga, Ator, & Hursh, 2010). Demand intensity is often assessed in hypothetical purchase task data without curve fitting by asking participants their level of consumption without cost or other constraints. Outside of hypothetical purchase task assessments, however, unconstrained consumption data is often unavailable and must be estimated from the available data. Demand elasticity can be assessed on a point-to-point basis without curve fitting, but these analyses are highly sensitive to outliers in the data and do not provide a single measure of overall demand elasticity. Furthermore, nonlinear regression models allow for the inclusion of all consumption data in statistical models, accounting for within-subject variability and consistency in any statistical conclusions that are made.

The treatment of zero consumption values is one issue that has arisen in our own and others' research (e.g., Galuska, Banna, Willse, Yahyavi-Firouz-Abadi, & See, 2011; Koffarnus et al., 2012; Koffarnus et al., 2015; MacKillop et al., 2012; Yu, Liu, Collins, Vincent, & Epstein, 2014). Fitting Equation 1 necessitates log-transforming consumption values, as represented by the log Q on the left side of the function. Since values of zero cannot be represented on a logarithmic scale, researchers tend to approach the issue of zero consumption values in one of three ways, each of which presents one or more problems for the analysis and interpretation of data (see also Yu et al., 2014). We note that our intent is not to single out specific researchers as handling this problem inadequately; instead, we are highlighting the fact that an ideal solution to this problem has not been identified.

The first approach is to simply omit the zeros from analysis and fit the curve to just the nonzero consumption values (e.g., Koffarnus et al., 2012). This approach has the advantage of only using measured consumption values, but is not ideal because the zero consumption values are legitimate data that should not be lost. Additionally, omitting zeros is not appropriate for group statistical models because an “average” containing only nonzero consumption values will necessarily be larger than the true average that incorporates all values.

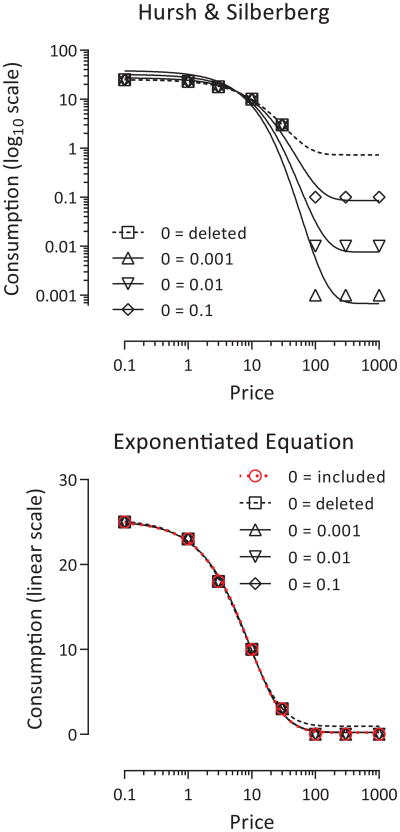
The second approach is to replace the zero consumption values with small, nonzero values such as 0.1 or 0.01 (e.g., Galuska et al., 2011; MacKillop et al., 2012). This approach has the advantage of retaining a value at each price, but can have a large effect on the resulting curve fits. Because Equation 1 relies on log-transformed consumption values, seemingly small differences in the specific nonzero value chosen can have a disproportionately large effect on the resulting curve fit and estimate of elasticity and/or demand intensity. On a logarithmic scale, the difference between 0.1 and 0.01 is the same size as the difference between 10 and 100. In the top panel of Figure 1, we have illustrated the impact of the specific nonzero value chosen with some hypothetical, but typical consumption data that closely approximate Equation 1 and contain five nonzero consumption values followed by three zero consumption values across eight prices. If the data are fit with the zeros omitted, the dashed line results. If the zeros are replaced with either 0.001, 0.01, or 0.1, drastically different curve fits result.

Figure 1.

Hypothetical data illustrating the advantage of exponentiating the Hursh and Silberberg equation. Due to the necessary step of log-transforming consumption data when using the Hursh and Silberberg equation, consumption values of zero cannot be fit as-is. Depending on how these zeros are treated, very different curve fits result (top panel). The exponentiated equation uses non-transformed consumption values and can incorporate consumption values of zero without issue and is also less sensitive to small differences in consumption at high prices (bottom panel). Note that the x axes and the y axis of the top panel are on a log₁₀ scale while the y axis of the bottom panel is a linear scale.

The third approach to addressing consumption values of zero that we have used recently (e.g., Koffarnus et al., 2015) is to restrict the analyses to group models when a large number of zeros reside in the consumption data. Group models that are based on mean data can accurately represent the average consumption of a group including zeros, but are also not ideal because parameters from individual participants are not obtainable using this approach and it also doesn't fully account for between-subject variability in the data.

In the present paper, we will test a modified version of Equation 1 first proposed by Yu et al. (2014) that avoids the problem of omitting or replacing zeros all together because it is able to incorporate unaltered zeros into the curve fits. This formula is simply an exponentiated version of Equation 1:

$$Q=Q_0\ast {10}^{k(e^{-\alpha Q_{0}C}-1)}$$ (2)

where both sizes are raised to the power of 10. Raising the left side of the equation to the power of 10 allows the untransformed consumption values to be fit. The right side of the equation is unaltered in form other than also being raised to the power of 10 (the log₁₀ Q₀ in the right side of Equation 1 reduces to Q₀ when raised to the power of 10). The bottom panel of Figure 1 displays the same hypothetical data as the top panel fitted by Equation 2. Use of Equation 2 not only fits unaltered demand functions with zero values, but also yields fits that are nearly identical to those when zeros are either deleted or replaced with small, nonzero values of 0.001, 0.01, or 0.1. Note that deleting or replacing nonzero values serves no purpose with the exponentiated equation, but these are shown here for comparison purposes.

In the present paper, we will show that these general patterns hold for empirical data we have collected (Experiment 1) as well as for a large amount of simulated data where the true demand elasticity and intensity values are known a priori (Experiment 2). We will also show that, compared to Equation 1, Equation 2 provides better fits to both experimental and simulated and provides measures of demand elasticity and intensity that are equivalent in interpretation and scale.

Experiment 1. Model Test with Empirical Data

In Experiment 1, we compare the performance of Equations 1 and 2 to characterize cigarette consumption data from an internet-based, hypothetical purchase task. These data were chosen as a basis for model comparison because they exemplify the issues with zero consumption values discussed above. They were collected from a purchase task with prices meant to be appropriate for a wide variety of commodities, and therefore contained many zero consumption values at prices far above what is typical for cigarettes.

Method

Participants

Participants were recruited from Amazon Mechanical Turk (www.mturk.com), an online crowdsourcing service. Out of those participants completing a large health survey, those participants (n = 289) who endorsed cigarettes as their preferred drug of abuse were selected for inclusion in the current analyses. Participants who did not vary their consumption as a function of price (n = 14, most of these put 0 at all prices) and those who with an unrealistically large number of cigarettes (≥1000 in a 24-hr period) for at least one price (n = 3) were excluded, leaving a final sample of 272. Participants had an average age of 36.1 (SD = 11.0), smoked a median of 10-19 cigarettes per day, were 50.5% female, and were 76.5% Caucasian.

Procedures

As part of a larger battery of assessments, participants completed a hypothetical cigarette purchase task. They were asked to indicate how many cigarettes they would purchase and consume in a single day if the price per cigarette was $0.00 (free), $0.10, $1.00, $3.00, $10.00, $30.00, $100.00, $300.00, and $1000.00.

Data analyses

Individual subject data at all prices except $0.00 were fit in GraphPad Prism 6.05 (La Jolla, CA, USA). With Equation 2, all consumption values were fit without removing or altering any consumption data, including datasets containing one or more zeros. With Equation 1, consumption values of zero were deleted or replaced with 0.1, 0.01, and 0.001. To enable direct comparisons of Q₀ and α values, the k parameter was set to a common value across all analyses. Since k represents the span of the data in log₁₀ units, k was determined by subtracting the log₁₀-transformed average consumption at the highest price ($1000.00) from the log₁₀-transformed average consumption at the lowest price used in curve fitting ($0.10). This constant k value used for all analyses was 3.096. This left Q₀ and α as free parameters, which were computed for each participant across each equation and zero replacement condition. Instances in which R² values were less than 0 (indicating a fit worse than a horizontal line; Motulsky & Christopoulos, 2004), or when Prism was unable to converge on specific parameter values were categorized as a “poor fit”. Data series with fewer than three consumption values after zeros were deleted were unable to be fit and also excluded from further analyses, which only occurred in the Hursh & Silberberg equation analyses with zeros deleted. We also conducted analyses on these data with 4 or 5 set as the minimum number of points. Spearman correlations and model two linear regression lines (Deming, 1943) were also calculated in Prism to compare the derived Q₀ parameters to the consumption at $0.00, as these values should be comparable. For a general discussion of nonlinear regression techniques, see Motulsky and Christopoulos (2004).

The Q₀, α, and goodness-of-fit (R²) values were compared across conditions in IBM SPSS Statistics 22 (Armonk, NY, USA). Q₀ and α were transformed to log₁₀ values and R² values were transformed to a logit scale before inferential statistics were computed so each would more closely approximate a normal distribution. Parameters from each of the five model fit conditions (zeroes deleted or replaced with 0.1, 0.01, or 0.001 in Equation 1; zeroes included in Equation 2;) were compared with a generalized linear model using generalized estimating equations (Liang & Zeger, 1986) to control for missing data (i.e., parameters from poor fits, as defined above) and within-subject correlations across repeated analyses. Post hoc tests with Bonferroni-corrected p values were used to compare specific analysis conditions and Cohen's d_z effect sizes (Cohen, 1992) were calculated comparing the estimated marginal means (± SD) from the generalized linear models.

Results

Mean (±SD) and the proportion of zero consumption values at each price are displayed in Table 1. The exponentiated equation and the Hursh and Silberberg equation with four different treatments of the zeros yielded fitted regression parameters that varied wildly (Figure 2). Fitted demand elasticity (α) values were significantly different across conditions [Figure 2, top left panel; χ²(4) = 4359, p < .001]. Post hoc tests showed that α values from the exponentiated equation and the Hursh and Silberberg equation with zeros deleted were not statistically different and associated with an effect size below the cutoff for a ‘small’ effect (Table 2), but each of the zero replacements in the Hursh and Silberberg equation produced α values different from both these and larger effect sizes (Table 2).

Table 1.

Summarized consumption data from each experiment by price.

	Price
	$0.10	$1	$3	$10	$30	$100	$300	$1000
Experiment 1: Empirical
Mean consumption	18.32	12.47	8.61	3.88	1.06	0.14	0.03	0.01
Standard deviation	12.02	10.52	8.64	6.82	4.43	0.96	0.21	0.15
Proportion of zeros	0.0%	5.1%	15.8%	48.5%	84.6%	96.0%	97.8%	98.9%
Experiment 2: Simulated
Mean consumption	18.74	11.39	6.97	3.37	1.38	0.28	0.05	0.01
Standard deviation	14.50	10.11	7.47	4.63	2.53	1.20	0.52	0.12
Proportion of zeros	0.8%	7.0%	16.1%	33.5%	49.0%	87.4%	97.7%	99.7%

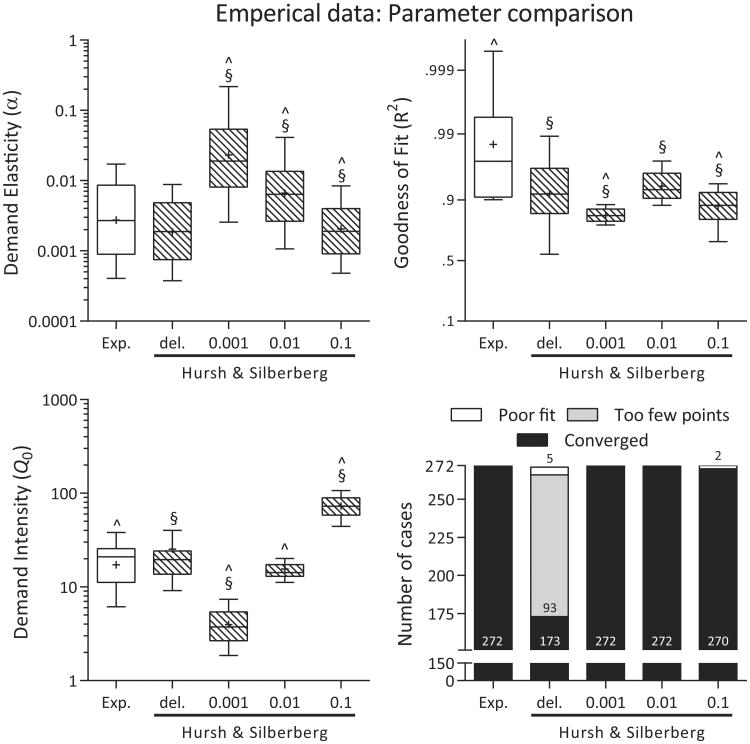
Figure 2.

Comparison of best-fit α (top left) and Q₀ (bottom left) parameter values on log₁₀ scales for the empirical consumption data from the exponentiated equation and the Hursh and Silberberg equation with zeros either deleted or replaced by 0.001, 0.01, or 0.1. Goodness of fit R² values (top right, logit scale) and the number of cases fit by each equation version (bottom right) are also shown. The bars in the box and whisker plots are at the median, the boxes extend to the 25^th and 75^th percentiles, the whiskers extend to the 10^th and 90^th percentiles, and the + sign indicates the mean. Note: ∧ Significantly different from the Hursh & Silberberg with zeros deleted condition. §Significantly different from the exponentiated equation. Exp. = Exponentiated equation. del. = deleted.

Table 2.

Empirical data (Experiment 1) Cohen's d_z effect sizes for demand elasticity (α) and demand intensity (Q₀) among the test conditions.

	Hursh & Silberberg equation zero condition
	deleted	0.001	0.01	0.1
α
Hursh & Silberberg: zeros deleted	-	1.57	0.87	0.42
Exponentiated equation	0.17	2.17	1.03	0.31
Q0
Hursh & Silberberg: zeros deleted	-	0.86	0.27	0.51
Exponentiated equation	0.14	1.49	0.14	1.54

Demand intensity (Q₀) values were also significantly different across conditions [χ²(4) = 3519, p < .001], and post hoc test showed that the exponentiated equation and the Hursh and Silberberg equation with zeros deleted were significantly different from one another (Figure 2, bottom left panel), but associated with an effect size below the cutoff for a ‘small’ effect (Table 2). Despite similar medians, this difference appears to be due to a small number of large Q₀ estimates with the Hursh and Silberberg equation, resulting in a positively skewed distribution (note that the mean is above the median in Figure 1). Q₀ values from the Hursh and Silberberg equation with zero replacement were different from the exponentiated equation and the Hursh and Silberberg equation with zeros deleted in all cases except the exponentiated equation was not statistically different from the Hursh and Silberberg equation with zeros replaced by 0.01.

Goodness of fit values were different across conditions [χ²(4) = 1000, p < .001], with the exponentiated equation resulting in higher R² values than each of the versions of the Hursh and Silberberg equation (Figure 2, top right panel). The versions of the Hursh and Silberberg equation with zeros omitted or replaced by 0.01 resulted in higher R² values than if zeros were replaced by 0.1 or 0.001. Many of the participants had data that could not be fit by the Hursh and Silberberg model with zeros deleted due to an inadequate number of data points (n = 93) or poor model fits (n = 5), while nearly all of the data was fit by the other functions (Figure 2, bottom right panel).

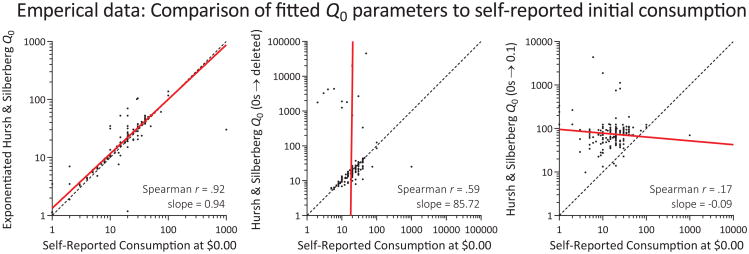
Ideally, the fitted Q₀ parameters should closely resemble the consumption at a price of $0.00. To test how well this was the case for each version of the demand equation tested, we used Spearman correlations to compare the fitted Q₀ parameters from each equation condition to empirical free-price consumption (Figure 3). Q₀ values from the exponentiated equation closely approximated free-price consumption (r = .92, p < .001), while the correlations from the Hursh and Silberberg equation with zeros omitted (r = .59, p < .001) or replaced by 0.001 (r = .48, p < .001), 0.01 (r = .68, p < .001), or 0.1 (r = .17, p = .006) were significantly lower (ps< .001 comparing exponentiated correlation with each of the others), indicating these functions provided fits that more poorly approximated the participant's self-reported consumption at $0.00. The lower correlation in the zeros omitted condition did not seem to be affected by data series with an especially low number of points, as correlations with series containing at least 4 (r = .56, p < .001) or 5 (r = .22, p = .2) points were not improved. The regression line slope from the exponentiated equation was 0.94, further indicating a close match between empirical and derived consumption values. Regression lines from the Hursh and Silberberg equation with zeros omitted (85.72) or replaced by 0.001 (1.24), 0.01 (0.36), and 0.1 (-0.09) were far from 1.0, often due to the presence of a population of fitted parameters that were wildly inaccurate (see Figure 3).

Figure 3.

Correlations between self-reported consumption if the price were free and the derived consumption when free (Q₀) from the exponentiated equation (left), Hursh and Silberberg equation with zeros deleted (center), and Hursh and Silberberg equation with each zero replaced by 0.1 (right). The exponentiated equation was most accurate at estimated the self-reported initial consumption. Note the log-log axes.

Experiment 2: Model Test with Simulated Data

In Experiment 2, we simulated consumption data so the actual Q₀ and α value in each case would be known, therefore giving us a reference by which to judge the adequacy of each model fit for deriving this true value.

Method

Simulation Procedure

Data were simulated to approximate the consumption data from Experiment 1 by randomly selecting 1000 log₁₀(Q₀) and 1000 log₁₀(α) values from a normal distributions with means and standard deviations for the values from the fits of the exponentiated equation in Experiment 1. For each of the 1000 cases, consumption amounts at each of the nonzero prices from the hypothetical purchase task in Experiment 1 were sampled from a normal distribution with a mean at the value determined by the Hursh and Silberberg equation for the Q₀ and α values for that case and a standard deviation equal to the mean standard deviation of residuals from the curve fits from Experiment 1, adjusted by the difference in standard deviation of consumption values across the prices in the actual consumption data in Experiment 1. Residuals from the exponentiated equation were used for the simulation since these were on the same scale as the source data (i.e., not resulting from log-transformed data). Resulting consumption values were then rounded to the nearest integer to mimic consumption data on an actual purchase task. These simulations were conducted in Microsoft Excel 2013 (Redmond, WA, USA).

Data Analyses

Simulated purchase task data were fit to Equation 1 with the same four zero replacement techniques and to Equation 2 with zeros included in GraphPad Prism 6.05. Best-fit regression parameters were compared in IBM SPSS Statistics 22 as they were in Experiment 1, but with the addition of the true simulated values as another level of the independent variable in the model. Spearman correlations and model two linear regression lines were also calculated in Prism to compare the derived Q₀ and α parameters to the true values for these parameters from the simulation runs. Consumption data from Experiment 1 and Experiment 2 were compared in SPSS Statistics 22 with a generalized linear mixed model with Price and Experiment as main effects and a Price by Experiment interaction.

Results

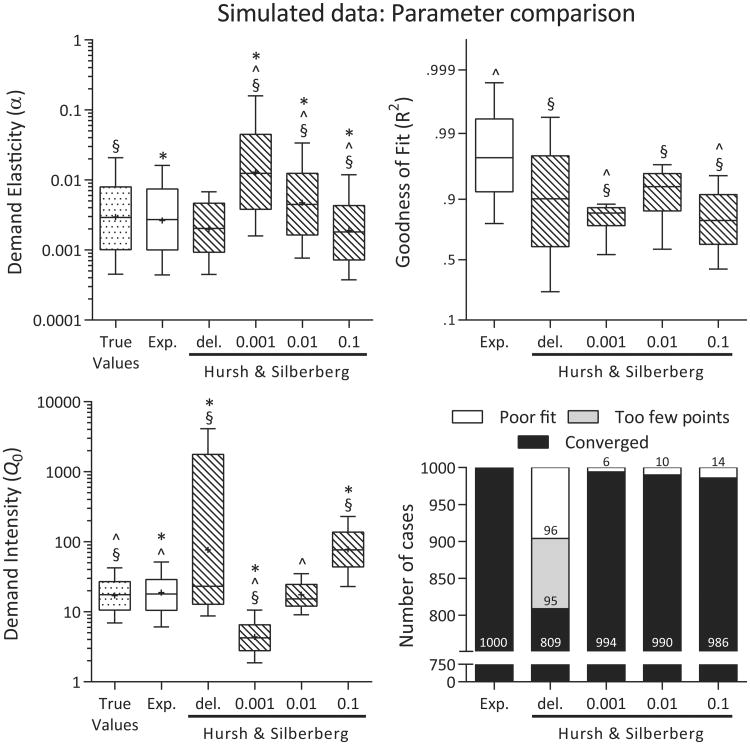
Mean (±SD) and the proportion of zero consumption values at each price for the simulated data are displayed in Table 1. Consumption values from Experiments 1 and 2 did not differ significantly (i.e., Experiment main effect of F(1,10172) = 1.65, p = .2; Price by Experiment interaction of F(1,10172) = 2.10, p = .1). Figure 4 depicts the parameter estimates from Equation 1 with the four different treatments of the zeros and Equation 2. Fitted demand elasticity (α) values were significantly different across conditions [Figure 4, top left panel; χ²(5) = 6160, p < .001]. Post hoc tests showed that α values from the exponentiated equation and true values differed significantly from one another, although this difference was associated with an effect size that was under 0.2, the convention for a ‘small’ effect (Table 3; Cohen, 1992). Each of the zero replacements produced α values different from the zeros omitted condition, the exponentiated equation, and the true values (Figure 4) with effect sizes ranging from 0.38 to over 1.0 (Table 3).

Figure 4.

Comparison of the true values from the simulation runs to the best-fit α (top left) and Q₀ (bottom left) parameter values on log₁₀ scales for the simulated consumption data from the exponentiated equation and the Hursh and Silberberg equation with zeros either deleted or replaced by 0.001, 0.01, or 0.1. Goodness of fit R² values (top right, logit scale) and the number of cases fit by each equation version (bottom right) are also shown for the fitted parameter estimates. The bars in the box and whisker plots are at the median, the boxes extend to the 25^th and 75^th percentiles, the whiskers extend to the 10^th and 90^th percentiles, and the + indicates the mean. Note: * Significantly different from the true values. ∧ Significantly different from the Hursh & Silberberg with zeros deleted condition. §Significantly different from the exponentiated equation. Exp. = Exponentiated equation. del. = deleted.

Table 3.

Simulated data (Experiment 2) Cohen's d_z effect sizes for demand elasticity (α) and demand intensity (Q₀) among the test conditions.

	Exponentiated equation	Hursh & Silberberg equation zero condition
		deleted	0.001	0.01	0.1
α
Hursh & Silberberg: zeros deleted	-	-	1.06	0.43	0.38
Exponentiated equation	-	0.03	1.65	0.69	0.39
True values	0.17	0.10	1.49	0.53	0.48
Q0
Hursh & Silberberg: zeros deleted	-	-	0.94	0.02	0.04
Exponentiated equation	-	0.49	1.24	0.08	1.11
True values	0.11	0.50	1.38	0.02	1.31

Demand intensity (Q₀) values were also significantly different across conditions [χ²(5) = 5068, p < .001], with post hoc tests showing that true values, exponentiated equation, and the Hursh and Silberberg equation with zeros deleted all differed significantly from one another (Figure 4, bottom left panel). Of these, the exponentiated equation provided Q₀ estimates near to the true values, a difference that was under the criteria for a ‘small’ effect (Table 3). The values from the Hursh and Silberberg equation with zero replacement again were highly dependent on the specific value chosen to replace zero, with the 0.001 and 0.1 producing the most errant results in this case.

Goodness of fit values were different across conditions [χ²(5) = 5619, p < .001], with the exponentiated equation resulting in higher R² values than each of the versions of the Hursh and Silberberg equation (Figure 4, top right panel). The version of the Hursh and Silberberg equation with zeros omitted or replaced by 0.01 resulted in higher R² values than if zeros were replaced by 0.1 or 0.001. Of the 1000 simulated data sets, all 1000 were fit by the exponentiated equation (Figure 4, bottom right). The Hursh and Silberberg equation with zeros deleted was able to fit just over 80% of the data series, with the remainder split between those containing too few points and those poorly fit by the function. The Hursh and Silberberg equation with zero replacement fit nearly all of the data series across the three replacement values.

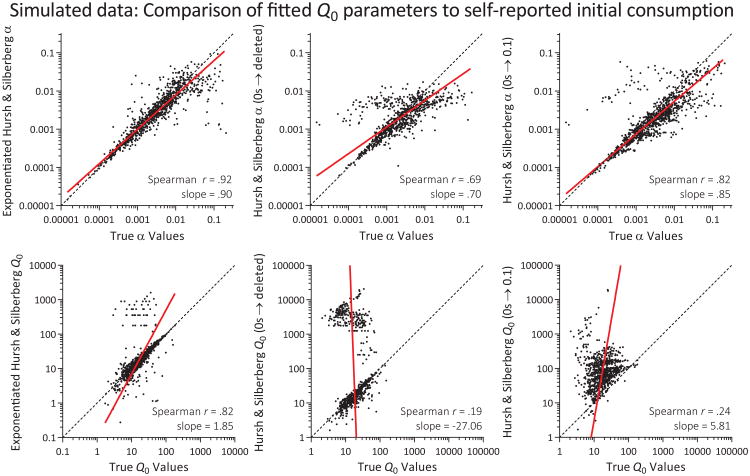
With these simulated data, the actual Q₀ and α values are known for each data series, allowing us to compare the fitted parameters to their true values (see Figure 5). Fitted α values from the exponentiated equation correlated significantly more highly (ps < .001 comparing exponentiated correlation with each of the others) with the true values (r = .92, p < .001, slope = 0.90) than those from the Hursh and Silberberg equation with zeros deleted (r = .69, p < .001, slope = 0.70) or replaced by 0.001 (r = .84, p < .001, slope = 1.15), 0.01 (r = .84, p < .001, slope = 0.97), or 0.1 (r = .82, p < .001, slope = 0.85). The α correlation in the zeros deleted condition did not seem to be affected by data series with an especially low number of points, as correlations with series containing at least 4 (r = .62, p < .001) or 5 (r = .54, p < .001) points were not improved. Fitted Q₀ values from the exponentiated equation were also highly correlated with the true values (r = .82, p < .001), and correlations were significantly lower (ps < .001 comparing exponentiated correlation with each of the others) than those from the Hursh and Silberberg equation with zeros deleted (r = .19, p < .001) or replaced by 0.001 (r = .27, p < .001), 0.01 (r = .50, p < .001), or 0.1 (r = .24, p < .001). The Q₀ correlation in the zeros deleted condition also did not seem to be affected by data series with an especially low number of points, as correlations with series containing at least 4 (r = .13, p = .001) or 5 (r = -.04, p = .5) points were not improved. The regression line slopes in most of the conditions were influenced by a number of poorly estimated values, leading to slopes that differed substantially from 1.0. The exponentiated equation regression had a slope of 1.85 and the Hursh and Silberberg equation regressions had slopes of -27.06 with zeros deleted, but closer to 1.0 when zeros were replaced by 0.001 (2.47), 0.01 (1.17), and 0.1 (5.81).

Figure 5.

Correlations between the true α (top panels) and Q₀ (bottom panels) parameter values from the simulation runs and the best-fit parameter values for the exponentiated equation (left panels), Hursh and Silberberg equation with zeros deleted (center panels), and Hursh and Silberberg equation with each zero replaced by 0.1 (right panels). The exponentiated equation was most accurate at estimating the true values. Note the log-log axes.

General Discussion

Experiment 1 results showed that the exponentiated version (Equation 2) of the Hursh and Silberberg equation with zeros included was able to fit more of the datasets and accounted for a greater proportion of the variance than the original Hursh and Silberberg equation (Figure 2). The exponentiated equation provided a more favorable result than replacing the zeros with nonzero values in the original Hursh and Silberberg equation, which altered the resulting fitted parameters. The exponentiated equation provided fits most comparable to the original Hursh and Silberberg equation with zeros removed, but was still superior in estimating participants' self-reported consumption at the $0.00 price (Figure 2). The analyses of the simulated data of Experiment 2 confirmed the results of Experiment 1, and also allowed us to compare the fitted parameter values from each version of the equation with the true values that were used to generate each data series (Figure 3). These comparisons showed that the exponentiated equation more closely reproduced the true values (Figure 4), and was the only equation to reproduce these true values with effect sizes that did not meet even the criteria for ‘small’ as defined by Cohen (1992) for both fitted parameters (Table 3).

The primary benefit of this exponentiated equation is that it allows for the inclusion of consumption values of zero without replacing them with nonzero values that could affect the curve fit. In many purchase task experiments, higher unit prices result in many participants indicating they would not consume any of the commodity. As these zero consumption values are no less valid or sincere than a nonzero value reported by the participant, they should be represented accurately in the statistical analyses. As noted previously (Yu et al., 2014), by exponentiating the Hursh and Silberberg equation and fitting the untransformed consumption values, all values can be fit including zeros. This would be a substantial benefit by itself for the reasons discussed in the introduction of this paper and in Yu et al. (2014), but the exponentiated equation also accounts for more of the variance than the original Hursh and Silberberg equation and more accurately approximates the actual initial consumption and demand elasticity. The exponentiated equation is also easy to use since it does not require transforming any of the raw data, allowing both consumption and price values to be entered in the same units in which they are measured.

An additional benefit of the exponentiated equation is that the fitted Q₀ and α parameters are on the same scale and interpreted identically to those obtained from the unmodified Hursh and Silberberg equation. This allows researchers who currently use the Hursh and Silberberg equation to seamlessly transition to this modified equation. This also means that existing descriptive statistics that use these values can still be calculated. For example, Hursh and Roma (2013) describe an equation to calculate P_max, or the price that supports maximum expenditure, using the Q₀, α, and k values from Equation 1. These same fitted parameter values from Equation 2 can still be used to calculate P_max.

In the Hursh and Silberberg (2008) demand equation and in the exponentiated version, the parameter k represents the range of the function from highest to lowest consumption in log₁₀ units. For simplicity in analysis and interpreting of Q₀ and α values, this parameter is often set to a constant value across conditions or subjects. Researchers have taken the approach of selecting a k value a priori that seems appropriate (e.g., McClure, Vandrey, Johnson, & Stitzer, 2013) or fitting a common k to all the data and then using this for all analyses (e.g., Koffarnus et al., 2012; Koffarnus et al., 2015; Koffarnus & Woods, 2013). We have favored the second approach in the past as it allows for the k that is appropriate for the data at hand. In the present analyses, we did not want to use one version of the equation to determine a common k value to avoid biasing subsequent fits to the equation from which it was derived. We therefore chose to set k to the actual span of the mean data from the lowest price to the highest price for the present analyses.

A limitation of these experiments is that they were based on a single dataset collected online with cigarette smokers endorsing a range of smoking behavior from light (less than 10 per day) to heavy (greater than 30 per day). We chose this dataset as the basis for these analyses because it had characteristics that presented analytical challenges. Specifically, the prices assessed were drawn from a list of prices meant to be appropriate for a wide range of commodities and therefore were somewhat higher than prices that would be more typical of a cigarette purchase task. This resulted in relatively few nonzero values for many participants on which to base curve fitting efforts. These data pose more analytical problems than most demand data, and is not meant to be representative in that regard. It was chosen because it exemplifies and is representative of those data where reasonable estimates of demand intensity and elasticity cannot be obtained with the Hursh and Silberberg equation due to the presence of consumption values of zero. Data from other purchase tasks or from non-hypothetical demand experiments may fare differently with this exponentiated equation, but we do not expect this to be case, as this exponentiated function has the same underlying shape in relation to the data as the original Hursh and Silberberg equation and the Hursh and Silberberg equation has been shown to describe demand data from a wide variety of contexts very well.

In conclusion, an exponentiated version (Equation 2) of the Hursh and Silberberg equation provides better fits to the data, is able to fit all consumption values including zero, more accurately estimates participants' self-reported initial consumption, and more accurately reproduces true parameter values from which simulated data are generated.