Six Degrees of Auditory Spatial Separation

Abstract

The location of a sound is derived computationally from acoustical cues rather than being inherent in the topography of the input signal, as in vision. Since Lord Rayleigh, the descriptions of that representation have swung between “labeled line” and “opponent process” models. Employing a simple variant of a two-point separation judgment using concurrent speech sounds, we found that spatial discrimination thresholds changed nonmonotonically as a function of the overall separation. Rather than increasing with separation, spatial discrimination thresholds first declined as two-point separation increased before reaching a turning point and increasing thereafter with further separation. This “dipper” function, with a minimum at 6 ° of separation, was seen for regions around the midline as well as for more lateral regions (30 and 45 °). The discrimination thresholds for the binaural localization cues were linear over the same range, so these cannot explain the shape of these functions. These data and a simple computational model indicate that the perception of auditory space involves a local code or multichannel mapping emerging subsequent to the binaural cue coding.

INTRODUCTION

Hearing and vision both provide information about remote events in the environment which is often integrated to enhance spatial perception (Pouget et al. 2002). Vision is fundamentally a spatial sense built on a reflected image of the world (Wandell et al. 2005), and visual space is related to the relative position of the eye. By contrast, the sensory receptors of the ear encode frequency so that space must be computed from binaural and monaural acoustical cues at the ears (Blauert 1997; Carlile et al. 2005) and is dependent on the relative position of the head. Despite considerable progress, some fundamental questions remain: in particular, (i) how the binaural cues are encoded (see Grothe et al. 2010; Ashida and Carr 2011); (ii) the way in which auditory space is represented, particularly at cortical levels (King and Middlebrooks 2010; Middlebrooks and Bremen 2013); and (iii) how audio-visual spatial information is so efficiently combined particularly given the different coordinate systems of the receptors. Understanding the higher-level architecture of the auditory spatial representation is key to understanding this efficient sensory convergence.

In vision, spatial representations are often modeled as a mosaic of receptive fields interacting through lateral connections which serve to sharpen spatial tuning and enhance responses to stimuli (Tolhurst and Barfield 1978). Auditory spatial tuning in the midbrain (e.g., Palmer and King 1982) suggests a similar model (Knudsen et al. 1977), but this is not consistent with the lack of a similar cortical representation (King and Middlebrooks 2010). An earlier psychoacoustic study (Carlile et al. 2001), however, suggested that, at a perceptual level, auditory spatial processing might also be based on a mosaic of multiple interacting channels. To complicate matters, there is also evidence that binaural cue processing, at least around the midline, may be computed from the output of a two-channel (e.g., McAlpine et al. 2001) or three-channel (Dingle et al. 2010) opponent process, encoding left and right (and possibly center) locations. This is in contrast to the previously proposed “labeled line” code for processing the interaural time difference cue (Ashida and Carr 2011). A combination of codes, however, also has some theoretical and empirical support (Harper and McAlpine 2004).

Taking a very different approach, we used concurrent auditory stimuli in a simple two-point discrimination test where we measured subjects’ JNDs for changes in the spatial separation of the two sounds. Two broadband speech tokens (male /da/, female /ee/) were selected so that, when played concurrently, they would clearly segregate into two distinct auditory objects that were easily and separably localizable. This expectation is based on numerous lines of evidence. First, speech spectra, compared to noise sources, are spectro-temporally sparse so that, with only two concurrent speech sources, each frequency/time segment is likely to be dominated by only one of the tokens so that there will be minimal energetic interference between the talker tokens (reviewed in Darwin 2008). Secondly, the difference in fundamental frequencies, the harmonic structure of each token, and the differences in onset time all combine to ensure that the spectral components would be appropriately grouped to each token (e.g., Darwin 1981, reviewed in Darwin 2008). The computation of the spatial location of each token has been shown to be dependent on the spatial cues present in the grouped components (Woods and Colburn 1992; Hill and Darwin 1996). Consistent with this, the lack of spatial interactions between two concurrent speech stimuli has been shown previously (Simpson et al. 2006; Kopco et al. 2010). Changes in the localization accuracy of a single word of the order of only 1 ° in RMS error are reported when second masker word is presented concurrently (although greater interference is demonstrated for larger numbers (3–6) of concurrent talkers).

We reasoned that, for a multichannel model of auditory space, if two auditory stimuli were closely spaced they would activate the same spatial channel and thresholds for discriminating two simultaneous points would be high. Following well-established models of channel interactions in vision (Levi et al. 1990; Legge and Foley 1980), we expected that if separation between the two sources were increased, the discrimination threshold would first decrease until the separation between the stimuli equaled the width of the underlying spatial channels, beyond which, for acoustic reasons (see below), thresholds would then rise monotonically. In other words, such a model predicts a U-shaped or “dipper” function. By contrast, models based on a left-right opponent process predict a linear rather than nonmonotonic increase in discrimination threshold for all increases in separation, with highest sensitivity around the midline where the cue rate functions are steepest (see McAlpine et al. 2001; Grothe et al. 2010). Importantly, the multichannel model would predict that the dipper function would also occur if the concurrent stimuli were moved to eccentric locations (e.g., both located in the left hemisphere).

To preview the results, we found a nonmonotonic dipper pattern of thresholds which repeated at each eccentricity tested (0, 30, and 45 °), indicating the presence of multiple spatial channels for judgments of spatial separation. We also measured threshold sensitivity to the binaural localization cues which were monotonic over a comparable range of offsets and therefore suggesting that any multichannel mapping of space emerges after binaural encoding.

Methods

Participants

For the separation discrimination experiments, seven subjects (six male, one female; mean 22, range 21–23 years) were recruited. Six were naive listeners, and one was an author of this article. One subject provided very erratic responses indicating an inability to complete the task as instructed and was excluded from the study (see also below). In the ITD discrimination experiment, there were six participants (four male; mean 23 (21–25) years), and in the ILD discrimination experiment, there were seven subjects (four male; mean 23 (21–25) years), four of which had participated in the free-field and ITD discrimination task, two were authors. Standard audiometry confirmed that all had normal hearing. Informed consent was provided, and experiments were approved by the Human Research Ethics Committee of the University of Sydney.

Separation Discrimination Experiments

Stimuli and Apparatus

The auditory stimuli used were word tokens /da/ (male talker) and /ee/ (female talker) of duration 160 ms, sampled at 48 kHz and were presented concurrently with a 50 ms offset to the /ee/ token. The stimuli were selected to ensure strong perceptual segregation based on harmonicity and offset and to ensure minimal interaction between the location cues associated with the grouped spectral components (see “INTRODUCTION” section, and in particular Darwin 2008, for a review)—the /da/ token had a strong fundamental and a broad spectral peak from 0.2 to 1 kHz while the /ee/ token was strongly harmonic with partials extending up above 4 kHz, and both tokens contained energy out to at least 10 kHz. Pilot studies demonstrated that subjects were able to accurately localize each stimulus when presented individually.

The /da/ speech token was always and only presented from one of a horizontal array of five fixed VIFA OT19NC00 loud speakers (5 ° separation) centered on the frontal midline, at a comfortable listening level (65 dB SPL) corrected for each speaker’s frequency response. The /ee/ token was always and only played from a sixth loud speaker mounted on a robotic arm which enabled stimulation from anywhere on the audio-visual horizon. The roving speaker was vertically displaced by 1 ° to ensure a clear line of transmission when in the vicinity of the fixed horizontal array. The experiment was controlled via Matlab (Mathworks), and an RME FireFace 400 was used for stimulus delivery.

The experiment was conducted in a darkened, anechoic chamber of size 3 m × 3 m × 3 m, with participants seated and resting their heads on a chin-rest. The subject was seated on a platform adjusted so that the loudspeakers were located on the audio-visual horizon, 1 m from the center of the head. A head tracker (Polhemus Fastrak) ensured that participants did not move during trials; otherwise, the trial was restarted.

Design and Procedure

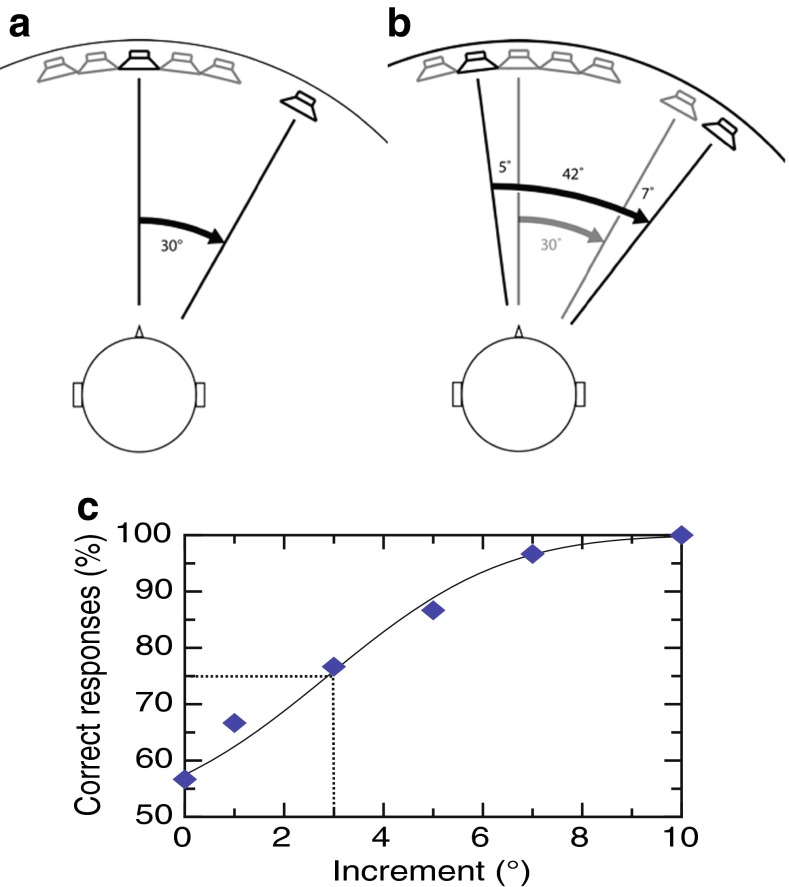
In this task, the discrimination of spatial perception was measured for different “base separations” (or “pedestals” 0, 3, 6, 12, 30, and 45 °). A two-interval, 2AFC design was used (Fig. 1) so that in the control interval, two sounds were separated at one base separation (Fig. 1A) and in the test interval (Fig. 1B) the spatial separation increased by a variable increment. Participants reported, by button press, which interval contained the largest spatial separation. A constant stimulus paradigm used separation increments of 0, 1, 3, 5, 7, and 10 ° for base intervals of 0, 3, 6, and 12 °, and separation increments of 0, 3, 6, 9, 12, and 15 ° for base intervals of 30 and 45 °. Both endpoints of the angular separation were varied such that neither the left or right endpoint of the two intervals (control and test) was ever in the same location in any one trial ensuring a response to the perceived angular separation rather than simply a shift in location of either speech token. For base intervals of 0, 3, 6, and 12 °, locations for the /da/ token were randomly chosen from three values (−2.5, 0, or 2.5 °) and for base intervals 30 and 45 ° locations were chosen from −5, 0, or 5 °. For the locations of −2.5 and 2.5 °, amplitude panning between adjacent loudspeakers was used. Where the resulting threshold separation was greater than the total variation of the endpoints, then a subject may have been able to use a simple shift in location strategy to judge the larger separation. As this would have only worked for a few % of the total trials, this would have been an unreliable strategy and produced relatively flat psychometric functions (c.f. Fig. 1C). The poor performance of the one subject not included in the analysis (see above) may have resulted from the adoption of such a strategy.

FIG. 1.

A, B Schematic of the experimental setup for the anterior field, as viewed from directly above the listener. A fixed array of five speakers, each separated by 5 °, and a single speaker attached to a movable robotic arm (black outer circle) are located in front of the participant. In each interval, participants are concurrently presented two spatially separated sounds. Participants reported the interval that contained the wider spatial separation. A An example standard interval: /da/ is presented at 0 ° using the middle speaker in the array and /ee/ 30 ° to the right of the midline using the speaker on the movable arm. This produces a spatial separation of 30 °, the base separation in this trial. Active speakers and their sound direction lines are in black and inactive speakers are in gray. B An example test interval: /da/ is presented 5 ° to the left of the midline using a fixed speaker and /ee/ is presented 37 ° to the right of the midline using the speaker on the movable arm. This results in a spatial separation of 42 °, which corresponds to an increment of 12 ° on the base separation of 30 °. The gray lines show the spatial separation in the previous interval. The left and right endpoints were varied across trials and neither was ever in the same location, preventing participants reporting a change in the location of one of the tokens. C Data from a representative subject for a single base separation in the free-field task. The percentage of correct responses is plotted as a function of the increment presented, with each point representing the average of 18 trials. The line shows the best-fitting cumulative Gaussian function from which thresholds are calculated. The dotted lines show the increment corresponding to 75 % correct performance.

Initial training blocks were given to familiarize participants with the task. For each base interval, participants completed five sessions and in each session the six separation increments were presented six times in random order (180 trials in total) with no feedback as to accuracy. Each base separation was tested in separate blocks which were counterbalanced against learning effects. Testing was only carried out for the right hemifield; however, in pilot experiments, two participants also completed the task for leftward-directed separations and showed no significant differences between hemifields.

ITD and ILD Discrimination Experiments

Stimuli and Apparatus

The word token /ee/ was filtered with the frequency response of the loudspeaker before headphone presentation (BeyerDynamics DT990 PRO) to ensure consistency with the free-field testing. The binaural cue was applied producing a left lateralized percept, and JNDs were measured for different binaural offsets corresponding to the free-field different base intervals. The experiment was conducted in sound-attenuated booth using Matlab and the RME interface as before.

For ITD discrimination, the individualized ITD offsets were calculated from each participant’s head diameter according to Kuhn (1977). For ILD discrimination, the ILDs were calculated using the head-related transfer functions (HRTFs) of one of the subjects in the study. The dB RMS amplitude of the /ee/ token filtered by the impulse response measured at each ear (band passed 300 Hz to 16 kHz) was used to estimate the ILD at each base separation location in the free-field study. The overall binaural level was held constant.

Design and Procedure

In the first of three presentation intervals, the /ee/ stimulus was presented at a standard binaural offset (pedestal value) followed by an incremental variation in the binaural cue followed again by the standard. Subjects indicated whether the lateralized image moved to the right or the left relative to the standard interval. For ITD, test increments were 10, 20, 30, 40, 60, and 100 μs and for ILD offsets were 0, 0.5, 1.0, 2.0, and 3.0 dB.

For each binaural offset, subjects completed four sessions, each comprising six repeats of each increment in random order (total of 180 trials). Participants were given training trials to familiarize themselves with the task and given feedback on accuracy after each trial.

Data Analysis

The percentage correct responses were plotted as a function of the increment appropriate for each experiment, and a constrained maximum likelihood estimation technique (Wichmann and Hill 2001) was used to fit a cumulative Gaussian psychometric function. The increment thresholds were taken at the 75 % correct position on the psychometric function, an example of which is shown in Figure 1C.

RESULTS

Spatial Separation Thresholds for the Anterior Field

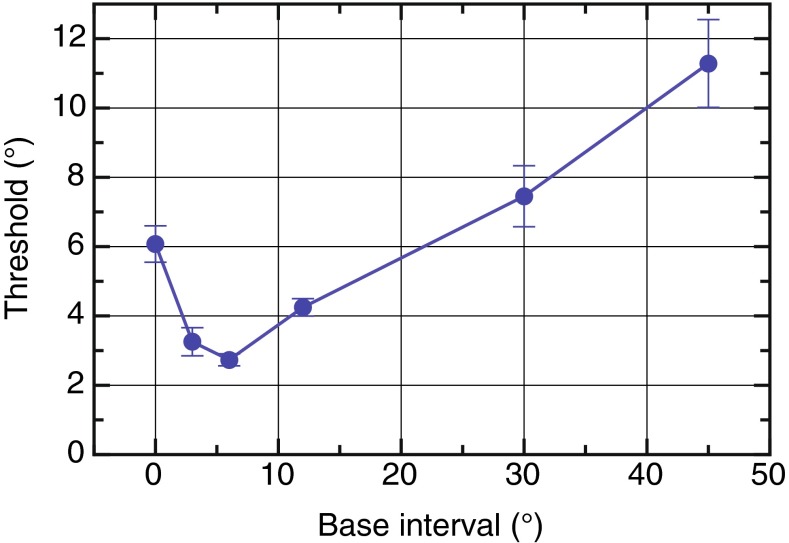
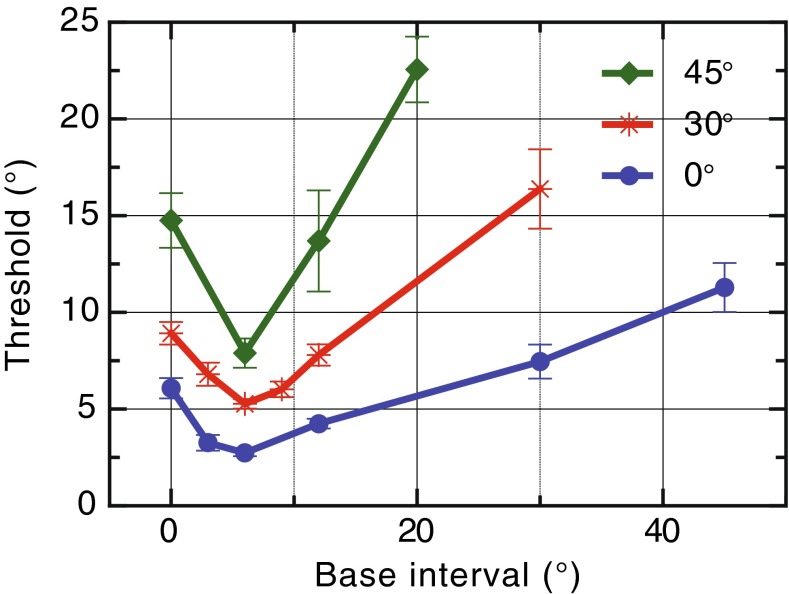
We measured increment thresholds in a spatial separation task for sounds located at different locations on the frontal audio-visual horizon. Subjects heard two distinct but concurrent sounds separated by a “base” interval of 0, 3, 6, 12, 30, and 45 ° in one interval, while in the other interval, this separation was varied incrementally using the method of constant stimuli. In a 2AFC task, subjects indicated which interval contained the wider spatial separation (Fig. 1A, B) from which the increment thresholds or just noticeable differences (JNDs) were calculated (Fig. 1C). When the two stimuli were collocated (0 ° base interval) at the midline, the mean JND was 6.1 ° (Fig. 2). As the base separation increased, JNDs initially declined to a minimum of 2.7 ° for a base separation of 6 ° before progressively increasing for larger spatial intervals up to 11 ° JND at 45 ° base separation (Fig. 2).

FIG. 2.

Overall mean increment discrimination thresholds in the free-field task as a function of the base interval.

It is common for JND variations to follow Weber’s law, where sensitivities increase linearly with the magnitude of the signal; however, the initial decline in JNDs followed by the rise found here was a consistent and striking pattern across all subjects. A repeated-measures ANOVA was performed with base separation as a within-subject variable. This showed a significant effect of base separation on the thresholds (F(5,25) = 31.8, p < 0.001, with Huynh-Feldt correction). There were significant linear (F(1,5) = 21.3, p = 0.006) and quadratic trends (F(1,5) = 131.2, p < 0.001). Pairwise comparisons (Bonferroni corrected) were made between all base intervals and, most critically, the threshold at 6 ° was significantly lower than at 0, 12, 30, and 45 ° (p = 0.022, p = 0.04, p = 0.011, and p = 0.004, respectively).

Difference Thresholds for Binaural Cues

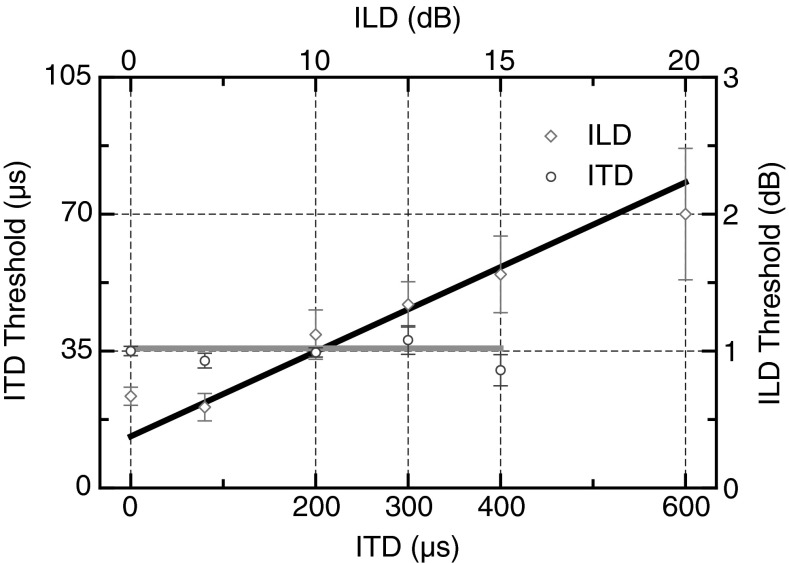
In order to examine the contribution of the binaural cues, we measured the sensitivity thresholds to changes in interaural level (ILD) and time differences (ITD) (Fig. 3). JNDs were measured at different ILD and ITD offsets chosen to correspond to the lateral locations in the previous task (ITD offset 0–400 μs; ILD offset 0–20 dB). In an interesting dissociation, JNDs for ITD varied little as a function of ITD magnitude (Fig. 3; open circles and light gray line) while JNDs for ILD increased linearly with ILD magnitude (Fig. 3; open diamonds and solid line). Confirming the trends evident in Figure 3, a within-subjects ANOVA comparing JNDs over the ITD range demonstrated no significant difference in JNDs over the ITD range (F(4,24) = 0.73, p = 0.6). A within-subjects ANOVA comparing JNDs over the ILD range found a significant effect (ANOVA, F(5,30) = 5.7, p = 0.029 with Huynh-Feldt correction) with a significant linear trend (F(1,6) = 6.8 p = 0.04) as threshold increased with ILD offset.

FIG. 3.

Overall mean increment discrimination thresholds for the single-source ITD and ILD tasks as a function of the baseline ITD or ILD offset. All error bars are ±1 SEM.

Spatial Separation Thresholds for Lateral Regions of Space

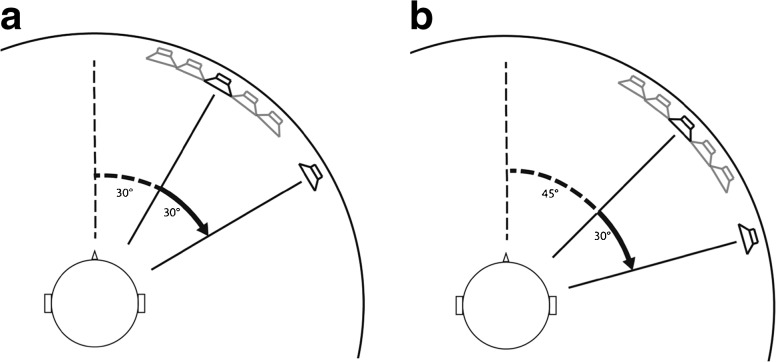
The JNDs plotted in Figure 2 show a dip for a spatial interval around 6 ° rather than rising monotonically as a function of the spatial interval, as Weber’s law predicts. This sort of nonlinear response function has been referred to previously as a dipper function, particularly related to observations in visual spatial tasks and has often been interpreted in terms of spatial channels (e.g., Levi et al. 1990). This is not consistent with the previously published opponent-process accounts of perceived auditory space which would predict the highest sensitivity around the midline where there is optimal location information and monotonically rising thresholds as the spatial interval expands laterally (McAlpine et al. 2001). We note however that for locations around the midline, depending on the shape of the opponent channel sensitivity functions, shallow dipper functions could be generated. Furthermore, a three-channel model with a spatially restricted center channel (Dingle et al. 2010, 2012) might also produce such a function. By contrast, a “multiple spatial channels” perceptual model makes the additional prediction that the dipper function seen in Figure 2 should be replicated at various lateral locations. To test this hypothesis, we rotated the speaker array such that the spatial interval began at an eccentricity of either 30 or 45 ° to the right of the midline and extended laterally (Fig. 4A, B).

FIG. 4.

A, B Schematic of the experimental setup for eccentric regions of space. A The fixed array is located 30 ° to the right of the midline. B The fixed array is located 45 ° to the right of the midline.

The results from the 30 to 45 ° eccentricity conditions are presented in Figure 5, overlaid with the data from the 0 ° condition, and reveals clear dipper functions at each of the more lateral locations. For the 30 ° condition, an ANOVA showed a significant effect of base separation (F(5,25) = 23.6, p < 0.001, with Huynh-Feldt correction). This showed a significant linear (F(1,5) = 23.5, p = 0.005) and quadratic trend (F(1,5) = 37.9, p = 0.002). Pairwise comparisons (Bonferroni corrected) between all base intervals were performed. Most importantly, the thresholds at 6 and 9 ° were significantly lower than at 0 ° (p = 0.05 and p = 0.02) and 30 ° (p = 0.03 and p = 0.03). For the 45 ° condition, an ANOVA showed a significant effect of base separation (F(3,15) = 32.9, p < 0.001, with Huynh-Feldt correction) and a significant linear (F(1,5) = 55.6, p = 0.001) and quadratic (F(1,5) = 98.7, p < 0.001) trends. Pairwise comparisons (Bonferroni corrected) between all base intervals were performed. Likewise, the threshold at 6 ° was significantly lower than at 0 ° (p = 0.02) and 20 ° (p = 0.001).

FIG. 5.

Overall mean increment thresholds as a function of the base separation for each of the eccentric conditions.

All eccentricity conditions in Figure 2C show a rising JND once the spatial base separation exceeded 6 °. Linear fits were applied to these data points. For the 0 ° degree condition, the best-fitting slope was 0.21, while the slope increased for the more lateral conditions: for the 30 ° condition, the slope was 0.4 and for the 45 ° condition, the slope was 1.0.

Modeling Free-Field Spatial Separation Discrimination

As far as we are aware, there are no acoustical cue-based models available to explain the nonmonotonicity in the localization responses found here, and none that can describe the results at different eccentricities. Perceptual models, however, have been successfully used to describe such psychophysical dipper functions in other domains, including spatial vision and time perception in audition (see for, e.g., Legge and Foley 1980; Burr et al. 2009) although their interpretation is still open to some debate (e.g., Solomon 2009). In order to create a perceptual model for the concurrent localization of two sound sources, we build on our earlier work that successfully modeled sensitivity to a single target, as a Gaussian-like activation spreading across an array of channels (Carlile et al. 2001). In the situation with two sound sources then, each will elicit its own response and the capacity to discriminate their individual locations can be modeled by the interactions of the two Gaussians. As illustrated in Figure 6A, when the two concurrent stimuli are collocated their individual responses will also overlap (green solid and blue dashed lines), and their combined response will be the arithmetic sum of the two (sharp magenta peak). Increasing the spatial separation between the sound sources reduces the amplitude while broadening the width of the summed peak (Fig. 6B).

FIG. 6.

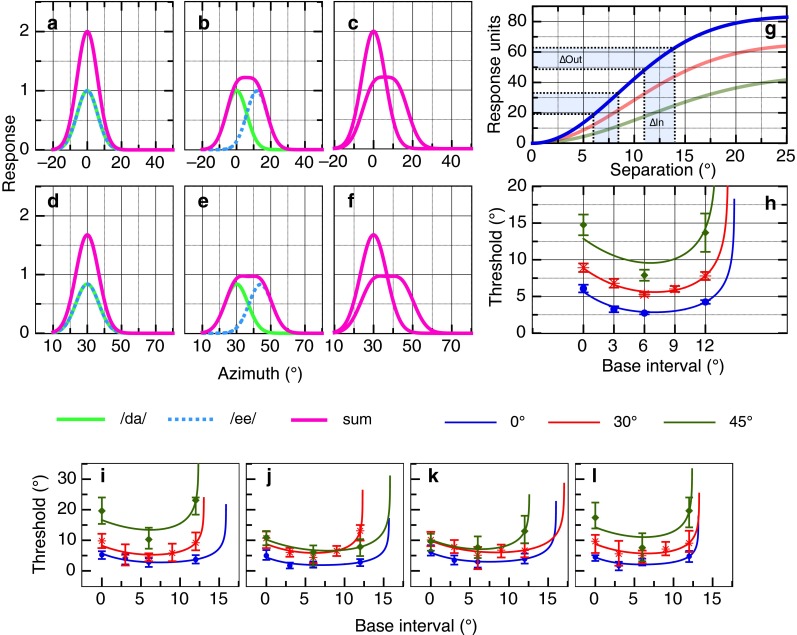
Proposed model for free-field spatial separation discrimination. A Two collocated responses (blue and green) located at lateral offset of 0 ° each of magnitude 1, the sum forms a single peak of amplitude 2.0 (magenta line). B Two spatially separated responses (blue and green); the summed response forms a flattened peak (magenta line). C The summed Gaussian responses taken from A and B. D Two collocated responses located at a lateral offset of 30 ° as in A but each with a magnitude of 0.8. E Two spatially separated responses as in B. F The summed Gaussians taken from D and E. The effect of the gain (attenuation) factor for more eccentric location can be seen by the reduction in amplitude of the responses D–F, with the summed response reaching a maximum of 1.6. G The summed Gaussian responses (magenta lines) in C are subtracted from each other, and the sum of the square of this difference is taken across all azimuth values. This produces a sigmoidal pattern of accelerating nonlinearity followed by compressive nonlinearity (blue curve). The red curve shows this computation for F and the green curve for an eccentricity of 45 ° (summed Gaussians not illustrated). H Measured thresholds and predictions from the model. Thresholds were simulated by assuming correct discrimination requires a constant change in response output from the functions shown in (G—e.g., blue shading). I–L Predicted and measured thresholds for four participants who completed all three lateral offset conditions. All error bars are 95 % confidence intervals. See text for further details.

The relationship between the summed peak and the separation of the underlying sources (in this case localization sensitivity as described by Gaussian distributions) has been the subject of much study and modeling effort (see Burr et al. 2009), since it characterizes the underlying perceptual transducer function. Here, given that subjects were required to compare the separation of two separate sources at various spatial intervals, we modeled their responses in a similar manner. Hence, at each spatial interval (denoted by the X-axis in Fig. 6G), the sum of squared difference between the response in the separated (Fig. 6B, magenta) and collocated conditions (Fig. 6A magenta) was calculated. Such interactions can be described by a sigmoidal transducer function containing both an accelerating and decelerating nonlinearity. Figure 6G shows the results of this calculation, plotting the transducer functions for each eccentricity (blue 0 °; red 30 °; green 45 °). Our choice to use sum of squared difference was motivated by simplicity and robustness (see Burr et al. 2009), other metrics such as the ratio of the distance between the peaks in the sum and its overall width can also be used without loss of generality.

The slope of the transducer describes the observed behavioral results where the steepest part corresponds to maximum behavioral sensitivity, leading to the “dip” in threshold. The corollary being that higher thresholds are due to the shallow regions of the transducer curve. A certain level of activation from the transducer output (∆Out) is required for detection, which after some experimentation, we fixed at 20 % of the total response. As illustrated in Figure 6G (highlighted area), the corresponding ∆In is then the perceptual threshold. Here, we showed the derivation of thresholds for base intervals of 6 and 11 ° for eccentricity of 0 °. Importantly, the steep slope of the transducer at separation around 6 ° will lead to correspondingly lower perceptual thresholds, whereas the shallow slope at larger separations (>6 °) or small separations (<6 °) will lead to correspondingly higher perceptual thresholds, completing the “U-shape” in Figure 6H.

Two other factors were incorporated to better model localization at different eccentricities. Firstly, the reduction in localization precision of the binaural cues at increasingly eccentric locations were modeled with a gain factor (e.g., Mills 1958; see also “DISCUSSION” section), allowing for a variation in the amplitude of the individual Gaussian responses in the model. This is illustrated by comparing Figure 6A with D—the amplitude of each of the responses in Figure 6A is 1 with a sum of 2, while the amplitude of the responses in Figure 6D is 0.8, resulting in a sum of 1.6. The gain factor was a free variable in the fitting procedure, and its final value was compared with changes in the precision of localization performance measured as a function of eccentricity in previous studies. Second, the width of the putative channels in this model is described by the width of the underlying Gaussian functions. This parameter was also allowed to vary in the fitting.

A nonlinear constrained minimization of the sum of squared error function was used to fit the model to both the mean group data (Fig. 6H) and to the individual data (Fig. 6I–L). For the group data, the best-fitting parameters at each of the three lateral location conditions were azimuth 0 °, 1.0 (gain factor) and 5.90 ° (Gaussian width); azimuth 30 °, 0.71 and 6.85 °; and azimuth 45 °, 0.56 and 7.79 °. These gain factors show a decrease that mirrors the decreased localization performance with eccentricity (Mills 1958; Grantham et al. 2003; Carlile et al. 1997). The modeled JND functions for the group mean JNDs as well the data from the four individual subjects (Fig. 6I–J) show a close agreement between the model and observed data.

A feature typically seen in dipper functions is that the base separation producing the minimum JND is similar to the JND at a base separation of zero. This pattern was confirmed for JNDs measured in the 0 ° eccentricity condition. The introduction of the gain feature not only successfully predicts dipper functions with minima near 6 ° regardless of the eccentricity of the interval but also captures the upward shift in JNDs as eccentricity increases (Fig. 6H).

Summary of Findings in Spatial Coordinates

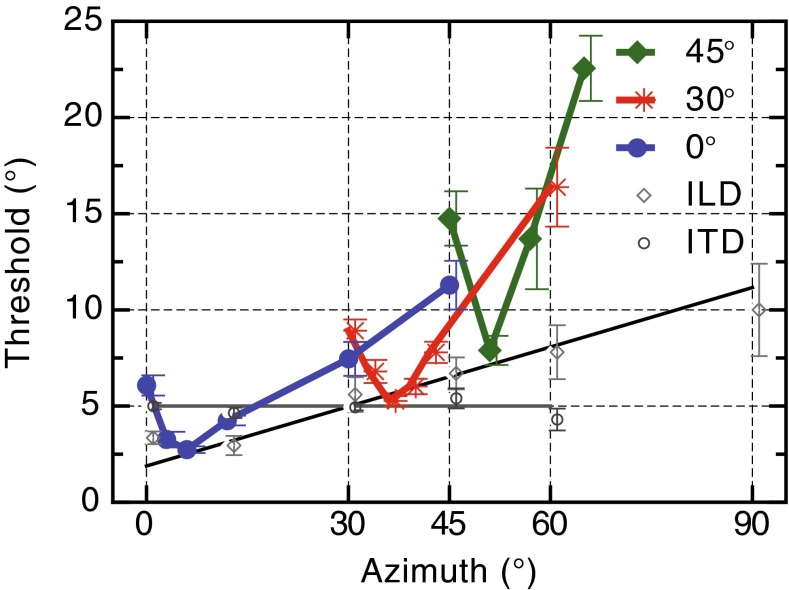
The data for all experiments in this study have been overlaid in Figure 7 to allow easy comparison of spatial-interval discrimination and ITD/ILD localization as a function of eccentricity. The JNDs for the binaural cues have been converted to equivalent degrees threshold. Two important features of these data warrant comment. First, the vertical location of each dipper function rises systematically with increasing eccentricity and the functions become steeper, both likely reflecting the poorer precision of the localization cues for the more eccentric locations (see “DISCUSSION” section). Second, by overlaying the ITD and ILD thresholds, we see that the best threshold in each dipper function is determined by the JND for ILD (the minima of the three dipper functions all touch the best-fitting line through the ILD data) rather than by JNDs for ITD, which appear to have little relationship to performance at any lateral location. This latter result is somewhat surprising given some previous studies have emphasized the role of ITDs in sound localization particularly under the sort of anechoic conditions used in this study (Wightman and Kistler 1992; Macpherson and Middlebrooks 2002). Later work has demonstrated, however, that the weighting of ILD and ITD cues is a more complex function of stimulus characteristics such as spectrum, interaural coherence, and onset characteristics (e.g., Stecker 2013; Stecker et al. 2013). Our use of two concurrent stimuli, however, may have acted to decorrelate to some extent, the timing information at each ear, making the extraction of ITD cues for each stimulus unreliable (see Lee et al. 2009; Rakerd and Hartmann 2010, but see also Schwartz et al. 2012) and causing a down-weighting of the ITD cue relative to the ILD cue. This would be consistent with recent models of optimal cue integration in a variety of sensory systems which embody a Bayesian or “Kalman filter” approach to optimize fusion of multiple cues that may vary in reliability (Ley et al. 2009; Wozny and Shams 2011).

FIG. 7.

Overall mean increment thresholds for the free-field and binaural cue tasks as a function of eccentricity in degrees azimuth from the midline. The increment thresholds for the binaural cues have been converted to an equivalent threshold in degrees. All error bars are ±1 SEM.

DISCUSSION

We have shown that increment thresholds for spatial intervals defined by two auditory speech tokens demonstrated a nonmonotonic dipper function when plotted as a function of interval magnitude. This pattern was observed for locations about the midline as well as at eccentricities of 30 and 45 °. The monotonic pattern of JNDs for the ILD and ITD cues measured in our subjects are consistent with previous studies (see below) and cannot account for the nonmonotonic JNDs for spatial interval discrimination. A simple perceptual model, however, based on a sigmoidal transducer explains the data well. The replication of the dipper function at various eccentricities and the linear pattern in the JNDs of the binaural cues, suggest that the perceptual representation of auditory space involves a multichannel mapping or local code which emerges subsequent to the encoding of binaural cues. The intriguing possibility considered below is that this is operating at the level of perceptual objects rather than cue features and may emerge as late as the multisensory representation.

Before focusing on the dipper component of this function, it is useful to consider how the JNDs overall and the linear portion in particular, reflect the acoustic cues upon which they are based. For a source on the midline, ear symmetry means that the ITD is around 0 μs and varies with eccentricity as a sine function (Kuhn 1977). Consequently, for small location changes around the midline, ITDs vary at a much faster rate than for the same variations around the interaural axis. The same argument holds generally for ILD, although it is slightly more complicated as peak monaural transmission depends on the pinna acoustic axis (Middlebrooks et al. 1989) and reflection and diffraction about the head (Shaw 1974). Likewise, the rate of location-dependent spectral filtering by the outer ear is greater around the midline compared to the interaural axis (Carlile and Pralong 1994).

The linear rising region of a dipper function is often observed as following Weber’s law where the JNDs rise in proportion to the base quantity (e.g., Foley 1994). The increase in JNDs in our experiment, however, likely reflects the decrease in cue precision for more lateral locations rather than reduced discrimination reflecting cue magnitude per se (Fig. 3). Such an argument has also been applied to explain the decreased accuracy for single-source localization reported for more lateral locations (Divenyi and Oliver 1989; Carlile et al. 1997) and an associated increase in the minimum audible angle (MAA: Mills 1958). If viewed as increasing spatial noise, this explanation is also consistent with the increased variability in JNDs observed here for increasingly more lateral offsets. Likewise, the overall increase in JNDs from 0 ° out to the 45 ° condition also likely reflects this decreased spatial resolution. This was captured in our model using a decrease in the transducer gain, requiring a larger spatial interval to produce a threshold dip in the summed output. Significantly, the model converged on gains at each eccentricity that match well the decreases in localization performance reported previously (Mills 1958; Perrott 1984; Grantham et al. 2003).

One very important feature of the JND functions for single source ITD and ILD is that neither binaural cue exhibited a dipper function (Fig. 3). The ITD JNDs were stable at around 30–35 μs regardless of base ITD and although slightly more than those calculated from low-frequency pure-tone MAAs (Mills 1958), agree closely with data obtained using click stimuli which are similarly impulsive and spectrally dense compared to our stimuli (Hafter and Demaio 1975). By comparison, the ILD JNDs clearly increased with ILD magnitude (Fig. 3) and are comparable to those previously reported by Yost and Dye (1988) out to the maximum offset they tested (15 dB ILD) and slightly higher at lower offsets than those reported by Hafter et al. (1977). Again, these changes in binaural sensitivity cannot by themselves explain the magnitude of the increases in MAA as a function of eccentricity which must then also reflect the spatial variation in the acoustic cues.

Whether the JND function is flat (as in ITD) or monotonically rising (as in ILD), the important point is, however, that neither demonstrates a dipper function. This is significant because it makes it very unlikely that the encoding of binaural cues themselves is responsible for the dipper function we observe for spatial interval discrimination. As binaural cues are encoded early in auditory processing, this indicates that the dipper function arises from computational processes subsequent to the stage of binaural cue encoding.

While the rising portion of the dipper function can be accounted for by the decreasing spatial precision of the underlying spatial cues, the nonmonotonic (dipper) portion might possibly be explained by location-based changes in the interactions between different components in the two speech tokens. While the data we report here cannot directly rule out this possibility, we do not favor this interpretation. In detection and intelligibility experiments, when two speech stimuli can be easily segregated on the basis of nonspatial differences, there is little spatial release from masking. This suggests that the grouping of the spectral components is sufficiently complete based on the nonspatial attributes that spatial differences are irrelevant. If this were commutative, then it would be unlikely that the relative magnitudes of the spatial cues would affect the grouping of the spectral components to each speech object and thereby change the computed locations of the speech tokens.

In contrast to the approach taken here, early psychophysical studies of auditory spatial resolution measured the MAA between sequential stimuli (e.g., Mills 1958; Hartmann and Rakerd 1989; Chandler and Grantham 1992). Uniformly, the MAA was smallest at the midline and increased for more eccentric locations. On the one hand, this variation supports an opponent process model as maximum sensitivity should occur at the midline where the encoding rate functions are steepest. On the other hand, such a result could also reflect decreasing spatial resolution of the cues from the midline. In the current study, we used two concurrent broadband speech stimuli. One other study of concurrent MAA (Perrott 1984) employed two low-frequency pure tones separated by ΔF = 20 % and reported thresholds of around 10 ° for midline locations that remained fairly constant out to 55 ° eccentricity. Divenyi and Oliver (1989) reported that the concurrent MAA (∼25 ° for AM modulated tones) was about twice as large as the sequential MAA around the midline and doubled for locations at 80 ° azimuth. In our midline condition, we observe JNDs as small as ∼3 ° which was probably due to the spectral and temporal complexity of the speech tokens compared to the relatively simple spectral stimuli in the previous studies. At the sound level of presentation, our speech tokens had audible energy up to at least 10 kHz providing a wide range of binaural and monaural cues (see also Divenyi and Oliver 1989). Interestingly, Perrott’s study (Perrott 1984) compared a range of spatial intervals but found no evidence of a dipper function probably because his base separation spacing was too large (0, 25, 45, 55, and 67 °).

Recordings from primary auditory cortex have demonstrated a remarkable difference in the spatial responses to concurrent stimuli compared to single stimuli. The majority of single-unit studies using single sound sources describe spatial receptive fields that are very large, often covering the contralateral hemisphere of space and the data are broadly consistent with an opponent process (reviewed in King and Middlebrooks 2010). Such studies have generally combined simple stimuli (such a broadband noise and or varied individual location cue parameters) with spike rate as the dependent variable. The picture appears to be very different using multiple, concurrent complex stimuli and various information-based approaches to analyze single-unit responses. For instance, in the avian field-L (homologue of the auditory cortex), song identification is strongly modulated by the relative location of a concurrent masker (Maddox et al. 2012). At a population level, the resulting spatial unmasking of the target approaches what can be demonstrated behaviorally (Best et al. 2005). Similarly, in the anesthetized cat, Middlebrooks and Breman found an order of magnitude improvement in spatial selectivity using two concurrent but interleaved streams of rhythmic stimuli (Middlebrooks and Bremen 2013). Spatial separation of only 8 ° was required for individual neurons to become entrained to one of the two streams and human subjects performed well on the same task at this separation (Middlebrooks and Onsan 2012). This spatial separation compares well with the maximum performance we observed here at around 6 ° for our nonstreaming, concurrent stimulus task.

Best et al. (2004) reported spatial discrimination and localization of two concurrent broadband noise stimuli in human subjects when they were separated by as little as 15 ° for locations around the midline. Threshold separations also increased for more eccentric locations. Using a maximum likelihood decoder model of neuronal responses, this response pattern could be modeled using the recording of the inferior colliculus neurons of the awake rabbit (Day and Delgutte 2013). Their data suggested that interaural coherence plays a key role at both high and low frequencies as a potential means for “glimpsing” the localization cues to concurrent stimuli (see also Faller and Merimaa 2004; Stellmack et al. 2010). The spectro-temporal sparsity of any concurrent stimuli allows such glimpsing. Best et al. used two broadband noise sources that may have reduced the opportunity for glimpses leading to slightly larger discrimination thresholds than reported here for our more sparse speech tokens.

Here, we found that when concurrent stimuli were increasingly further apart, the increment thresholds (JNDs) followed a nonmonotonic or dipper function. Dipper functions were first reported in audition (Pfafflin and Mathews 1962; Raab et al. 1963; Hanna et al. 1986); however, most of the models for dipper functions have been for visual tasks including contrast (e.g., Foley and Legge 1981), blur (e.g., Watt and Morgan 1983), and motion (e.g., Simpson and Finsten 1995). One rare exception is a recent study showing that discrimination of auditory duration follows a dipper function (Burr et al. 2009). Perceptual models like the dipper model proposed here are not necessarily based on what is known about the underlying biological processes. Nonetheless, in addition to providing a high-level description of perceptual performance, inferences about lower-level function can still be made. For instance, dipper functions for psychophysical tasks dependent on energy transduction (e.g., sound intensity, luminance) are easily understood in terms of a nonlinear energy transducer. For dimensions such as spatial separation, the underlying mechanisms are not as obvious, although dipper functions are reported for nonenergetic visual dimensions such as orientation (Morgan et al. 2008) and spatial interval (Levi et al. 1990).

Together, the data and modeling strongly support the idea of a channel-based representation of auditory space that emerges downstream of the early processing stages encoding binaural cues. Moreover, the location of the dip on the function provides an insight into the spatial resolution of the underlying process. With a base separation of 0 ° separation (i.e., collocated), the responses to the two sounds fall within the same processing channel. At 6 ° separation, threshold-level performance is possible as identifiable responses from different processing channels become available. This suggests that 6 ° is an important resolution limit for auditory spatial processing, and one that appears quite constant out to an eccentricity of 45 °—the limit of our testing. Although no such dipper functions were observed in the binaural data, importantly, our data do not exclude the possibility that the individual binaural cues are encoded using an opponent process. Indeed, physiological evidence suggests such a strategy occurs in early binaural processing (reviews Grothe et al. 2010; Ashida and Carr 2011). The current data do suggest, however, that binaural information is then integrated with monaural cues, and possibly other sensory-motor information, to form a channel-based representation of auditory space.

The downstream representation of auditory space we suggest need not be a topographical representation as in the superior colliculus. Indeed, the available cortical and imaging data indicates it is not (King and Middlebrooks 2010; Ahveninen et al. 2014) and could be based instead on a logical representation of space operating as a network of neural interconnections. The temporally complex and integrative nature of auditory cortical processing (Walker et al. 2011; Bizley and Cohen 2013) and the need to integrate nonauditory cues (e.g., Goossens and van Opstal 1999) suggests that auditory space and the objects within it will ultimately depend on diverse inputs. Importantly, our stimuli were two spectro-temporally complex stimuli chosen so that their various components would strongly bind to one of two perceptual objects. Similarly, in the work in avian field-L discussed above, spatial modulation of song identity was the dependent variable (Maddox et al. 2012). In the cat, it was the preferential tuning to one of two concurrent streams of rhythmic stimuli that was modulated by their relative location (Middlebrooks and Bremen 2013). These sorts of stimuli are better described as perceptual objects or streams rather than as the sum of the many physical parameters of the acoustic sources.

Finally, we conjecture that there would be significant advantages to representing space through the logical relationships of “object locations” rather than at the level of cues or features. First, objects provide a basis for attentional selection and the heightened processing to accompany it (Bregman 1990; Griffiths and Warren 2004; Shinn-Cunningham 2008). A mosaic of spatial channels would provide the basis for steering spatial attention, a process thought to operate at the level of perceptual objects rather than individual cues (e.g., Shinn-Cunningham 2008; Ding and Simon 2012). Second, a channel-based spatial map at the level of auditory object representation would facilitate the challenge of integrating auditory information with visual object representations in “mid-level vision,” downstream of the early retinotopic stages where visual features are represented. Audio-visual binding at the level of object representation would obviate the need to convert audition’s head coordinates to vision’s retinal coordinates on a feature by feature basis. In a recent audiovisual experiment using a very similar two-point spatial discrimination task, we found an almost identical dipper function to that reported here, even though one point was a sound source and the other a light source (Orchard-Mills et al. 2013). This finding cannot be accounted for by interactions at a parameter level, as their spatial locations were defined by completely different cues, and therefore corroborates the notion of spatial interactions at the level of object representation.

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.