Microfluidic Emulation of Mechanical Circulatory Support Device Shear-Mediated Platelet Activation

Abstract

Thrombosis of ventricular assist devices (VADs) compromises their performance, with associated risks of systemic embolization, stroke, pump stop and possible death. Anti-thrombotic (AT) drugs, utilized to limit thrombosis, are largely dosed empirically, with limited testing of their efficacy. Further, such testing, if performed, typically examines efficacy under static conditions, which is not reflective of actual shear-mediated flow. Here we adopted our previously developed Device Thrombogenicity Emulation methodology to design microfluidic platforms able to emulate representative shear stress profiles of mechanical circulatory support (MCS) devices. Our long-term goal is to utilize these systems for point-of-care (POC) personalized testing of AT efficacy under specific, individual shear profiles. First, we designed different types of microfluidic channels able to replicate sample shear stress patterns observed in MCS devices. Second, we explored the flexibility of microfluidic technology in generating dynamic shear stress profiles by modulating the geometrical features of the channels. Finally, we designed microfluidic channel systems able to emulate the shear stress profiles of two commercial VADs. From CFD analyses, the VAD-emulating microfluidic systems were able to replicate the main characteristics of the shear stress waveforms of the macroscale VADs (i.e. shear stress peaks and duration). Our results establish the basis for development of a lab-on-chip POC system able to perform device-specific and patient-specific platelet activation state assays.

1. INTRODUCTION

Mechanical circulatory support (MCS) devices have emerged as a major advance in the management of patients with advanced heart failure (Stewart et al. 2012). Despite their clinical success, MCS devices unfortunately are plagued by device-related thrombosis (Mehra et al 2014), often resulting in reduced function, recurrent heart failure, systemic emboli, possible stroke, potential pump stop and even death. To prevent thrombosis, MCS-implanted patients rely on the use of a combination of anti-thrombotic agents (e.g. aspirin, dipyridamole, clopidrogel) to limit platelet activation resulting from passage through the device (Eckman and Ranjit 2012, Von Ruden et al 2012). Despite the use of these drugs, thrombosis has persisted as a clinical problem (Starling et al 2014). A weakness of the present pharmacologic strategy is the fact that administered drugs are typically monitored only in the peri-operative period, during hospitalization and immediately thereafter. Drug monitoring in the out-of-hospital home environment is still not a common practice, with few systems available for routine point-of-care or home-based monitoring of platelet function (Mani et al 2014). More often, drug monitoring is performed with laboratory-based devices, e.g. light-based aggregometry or PFA-100. These assays largely examine biochemical endpoints of platelet activation, studied under static conditions or constant shear conditions, and are not reflective of the actual dynamic shear and flow that occurs in a given MCS device, particularly as to the shear stress levels and dose to which platelets are exposed.

Shear forces are a major means of activation of platelets, as platelets pass through small dimensions and unusual geometries at high speed in MCS systems. Our laboratories have characterized many blood-contacting systems, including MCS devices, and have described the overall shear stress history and dose as a probability density function (PDF) of a scalar value, termed Stress Accumulation (SA), that takes into account the shear stress levels and exposure time acting on individual platelets. A PDF is device-specific and can be seen as its "thrombogenic footprint", representing a means of calculating the net shear exposure history of a large population of platelets passing through the device.

Device Thrombogenicity Emulation (DTE) as a methodology allows one to subject platelets to realistic shear stress profiles obtained from complex computational fluid dynamics (CFD) analyses performed within realistic geometries of cardiac devices (Xenos et al 2010, Alemu et al 2010). The flow path in the device is modeled and platelets are tracked in order to detect individual platelet trajectories that may drive them beyond the activation threshold. For this purpose, cumulative stress, i.e. the SA, is calculated along multiple flow trajectories (thousands of simulated platelet trajectories) and collapsed into PDFs. Extreme cases of platelet stress loading trajectories, termed as “hotspot” or “flight” trajectories, can be extracted from the PDF and reproduced in vitro for actual exposure of platelets via a novel lab system - a Hemodynamic Shearing Device (HSD) (Nobili et al 2008). The HSD consists of a programmable high-torque servo motor-controller system (Baldor Electric Company, AR) that propels the platelet sample in a modified cone-Couette viscometer with the capability of exposing platelets to highly-controlled dynamic, uniform shear stress waveforms (Xenos et al 2010). The HSD-treated platelet sample is then assayed for platelet activation via the Platelet Activation State (PAS) assay (Jesty and Bluestein 1999) developed by our group, which measures the rate of thrombin generation as a surrogate validated biomarker. While initially developed to analyze mechanical heart valves (Xenos et al 2010, Alemu et al 2010), the DTE methodology has been utilized to evaluate and optimize MCS devices, such as ventricular assist devices (VADs) (Girdhar et al 2012). Herein, we hypothesized that the individual shear and flow characteristics of a given VAD, i.e. defined hotspot trajectories, may be emulated in a microfluidic channel system. As such, creating a "Device-Specific" VAD microfluidic facsimile would ultimately allow development of a small, point-of-care, lab-on-a chip system that may be utilized readily at the bedside to assess the adequacy of anti-thrombotic drug efficacy. We envision a point-of care system made of polydimethylsiloxane (PDMS), through standard soft lithography (Whitesides 2006).

As such, the overall goal of the present study was to investigate the feasibility of designing microfluidic emulators capable of replicating MCS fluid dynamics in terms of dynamic shear stress history patterns. Here we generate the PDFs of two VADs in actual clinical use. Using these PDFs we translate and replicate specific component shear stress peaks into fluid microchannel geometries. We then examine the flexibility of this microfluidic approach via changing channel design features in order to modulate shear stress curves. Finally, we design two different microfluidic platforms to emulate the shear stress history defined by the device specific PDFs of two commercial VADs.

2. METHODS AND MATERIALS

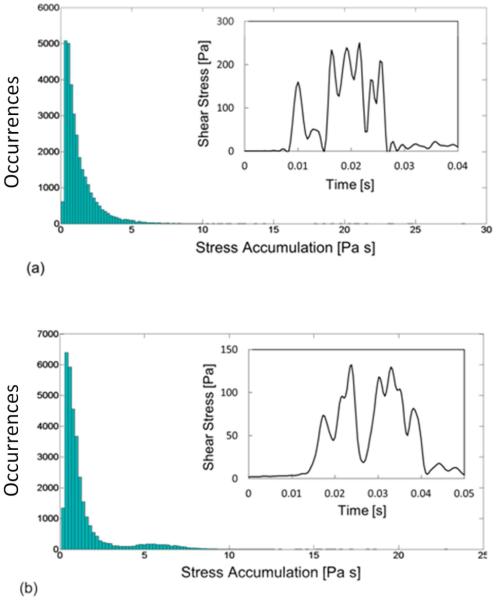
The essence of the present approach is to modulate the geometry of microfluidic channels in order to generate shear stress history patterns that replicate MCS device shear patterns. In particular, two commercial VADs, the HeartAssist5 (HA5, MicroMed Technology Inc., Houston, TX, USA) and HeartMateII (HMII, Thoratec Corportation, Pleasanton, CA, USA) VADs, were studied. The PDFs of the two VADs studied in the work of Chiu et al (2014) are reported in Fig.1, together with representative shear stress waveforms that were identified. The PDF is depicted as histogram bars in which the occurrences of SA along all the simulated particle trajectories are reported.

FIG. 1.

PDF of the SA of HeartAssist5 (a) and HeartMateII (b) VADs and representative shear stress waveforms extracted from the 90^th percentile of the PDFs. The histograms of PDF and shear stress waveforms were reproduced by data provided by (Chiu et al. 2014).

The shear stress waveforms of the two VADs were characterized by the superimposition of stress peaks ranging from 60 to 250 Pa, for an overall duration of 10-20 ms (with durations of each peak varying from 3 to 6 ms). These data were the starting point for the design of the microfluidic platforms.

2.1 Microfluidic model design

2.1.1 Design of microfluidic stress-generating templates

As a first step, a sample shear stress waveform with a triangular shape was considered, featuring a baseline shear stress value lower than 20 Pa, a peak shear stress of 130 Pa and duration of 4 ms. This sample waveform was chosen as a template pattern, characterized by typical values of shear stress and exposure time observed in MCS devices. The goal of this step was to test the feasibility of using microfluidic devices to replicate typical features of shear stress waveforms experienced by blood platelets in actual MCS devices.

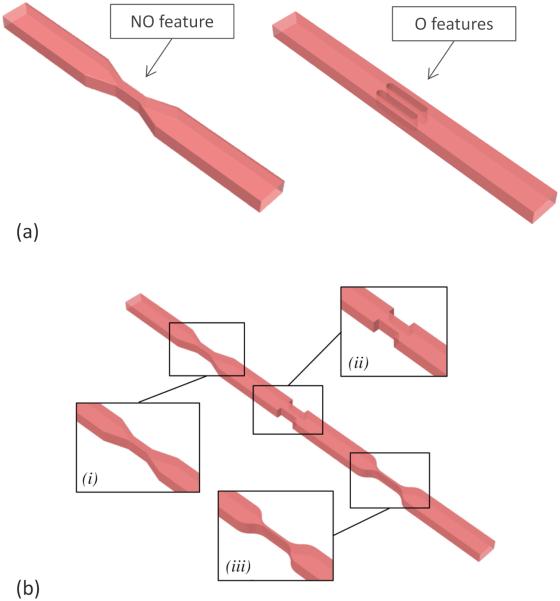
To this end, two microfluidic layout configurations were designed at different scale-sizes, corresponding to the opposing limits of attainable geometries with standard photo-lithography: a first configuration (M1) with a rectangular reference channel cross-section of 50 μm × 25 μm (width × height) and a second configuration (M2) with a reference channel cross-section of 500 μm × 200 μm (width × height). As in most microfluidic applications, the heights of features in each configuration were maintained constant, achieving the desired levels of shear stress by either modulating the width of the channel (non-obstructive, NO, Fig. 2, top panel) or inserting obstacles along the channel (obstructive, O, Fig. 2, top panel). In both cases, the peak shear stress was obtained by decreasing the flow area with respect to the reference section of the channel.

FIG. 2.

a) Example of non-obstructive (left) and obstructive (right) geometries. b) Geometries investigated in 2.1.2. Subpanels show the enlarged view of the three different kinds of narrowing: i) angled, ii) sharp and sudden, and iii) smoothed. The dimensions of the model in the figure are not reported in the actual scale in order to show the general pattern of the stress generating features.

For the M1 configuration, the obstructive model (M1_O2) was obtained by inserting two oval-shape obstacles along the channel, while for the M2 configuration, either one and three obstacles were designed (obtaining M2_O1 and M2_O3 models). The dimensions of the obstacles were determined in order to obtain the same peak shear stress values as in the corresponding NO geometry, at the same flow rate. The dimensions of the designed models are summarized in Table 1.

TABLE 1.

Dimensions of the models designed in II.A.1: width (W) of the reference cross-section, height (h) and length (L) of the channel; width (W_feat) and length (L_feat) of the stress-generating features. W_feat refers to the width of the narrowed section in NO models and to the width of each obstacle in O models

	M1_NO	M1_O2	M2_NO	M2_O1	M2_O3
N. of obstacles	-	2	-	1	3
W (μm)	50	50	500	500	500
h (μm)	25	25	200	200	200
L (mm)	2.1	2.9	17.1	20.7	15.3
Wfeat (μm)	12	15	84	370	113
Lfeat (mm)	0.9	1.35	8.1	9.4	6.3

2.1.2 Achieving different shear stress levels

As a second step of our approach, we tested how the levels and waveforms of shear stress in the microfluidic devices can be modulated, by varying the shapes and dimensions of the shear stress-generating features.

To this end, a further NO model was designed, characterized by 3 different NO stress-generating features (M1_3SGF) as shown in Fig. 2, bottom panel: the NO feature described in the first designing step (subpanel i), an abrupt contraction followed by a sudden expansion (subpanel ii), and a smoothed narrowing feature without sharp corners (subpanel iii). The features were sized in order to generate shear stress peaks differing by three orders of magnitude (160, 80 and 1000 Pa, respectively).

2.1.3 Design of microfluidic devices to replicate commercial VADs

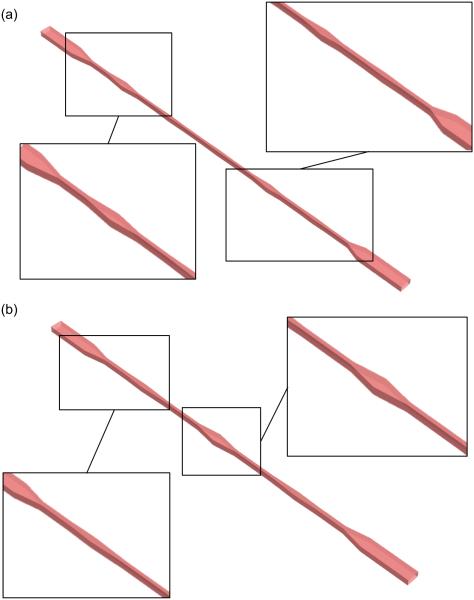
Finally, we considered two commercial VADs: the HMII and the HA5 axial flow pumps. These devices have recently been studied through CFD analyses by Chiu and colleagues (Chiu et al 2014), who used a discrete phase model to extract shear stress waveforms along platelet trajectories. Here, two microfluidic devices, termed the HMII_microfluidic and the HA5_microfluidic (Fig. 3), were designed in order to replicate the critical shear stress waveforms extracted by Chiu and colleagues (corresponding to the 90^th percentile of the stress accumulation distribution of each VAD). The original shear stress waveforms were described as a series of triangular shaped shear stress patterns that were replicated by a corresponding series of stress-generating features in the emulating microchannels. A reference channel cross-section of intermediate size (50 μm × 120 μm) and a NO configuration was chosen in both cases.

FIG. 3.

Microfluidic units emulating the shear stress waveforms corresponding to the 90th percentile of SA of HMII (a) and HA5 (b) VADs with enlarged views of the channel features. The dimensions of the model in the figure are not reported in the actual scale in order to show the general pattern of the stress generating features.

2. 2 Computational Fluid Dynamic analyses

The flow fields in all the described microdevices were analyzed through CFD using the commercial finite volume solver ANSYS Fluent^® (Ansys Inc., USA), following the approach proposed by Pelosi and co-authors (2014). NO models were discretized with hexaedral structured grids, while obstructive models and M1_3SGF model were discretized with hexahedral unstrucured grids, due to the higher complexity of their fluid domains. The element size of each model was based on a previous sensitivity analysis in which the minimum number of elements in the channel cross-section required for convergence below 4% of the shear stress profile was determined. The sensitivity analysis lead to a minimum number of elements in the channel cross-section of 15.

The fluid phase, representing a solution of gel-filtered platelets (GFP) was modeled as an incompressible and Newtonian fluid with rheological properties of a serum-like medium: a density of 1000 kg/m3 and a dynamic viscosity of 0.001 Pa s. The choice of simulating GFP was adopted with the aim of replicating the currently used in vitro conditions tested in the HSD device for measuring shear-induced activation by means of the PAS assay. Indeed, in the present study the DTE approach was taken as a reference for the development of the microfluidic emulator devices. A SIMPLE method was used for pressure-velocity coupling and a second order upwind scheme was chosen for the discretization of the momentum equation. A constant uniform velocity and zero pressure were imposed as boundary conditions at the inlet and the outlet of the fluid domain, respectively. Velocities of 11.6 cm/s and 57 cm/s were assigned at the inlet of the M1 and M2 models, respectively, and a velocity of 10 cm/s was imposed in the two VAD emulating microchannels. In all the simulations the maximum Reynolds number was well below the limit of the transition flow regime. The lowest peak Reynolds number was 7 in model M1_NO, while the highest was close to 400 in model M2_NO. The peak Reynolds number refer to the values in the shear stress generating features where the velocities are higher than in the baseline part of the channels.

The steady-state velocity and pressure fields were first computed through a steady flow simulation. Once convergence was reached, a transient simulation was run in which a discrete phase, modeled as buoyant spherical particles, was injected from a cross-section downstream of the inlet surface. The discrete phase was assigned characteristics of human platelets, with a diameter of 3 μm and the density of water, 998 Kg/m³.

The particle tracking approach available in Fluent^® (Ansys Inc., USA) was used. According to this approach, the trajectories of a population of particles flowing in a fluid domain are computed by solving the momentum equation for the particle in a Lagrangian reference frame. The equation normalized with respect to the particle mass has the following expression:

$$\frac{d{\overrightarrow{u}}_p}{dt}=F_D(\overrightarrow{u}-{\overrightarrow{u}}_p)+g\frac{{\rho }_p-\rho }{{\rho }_p}$$ (1)

where $\overrightarrow{u}$ and ${\overrightarrow{u}}_p$ refer to the fluid and particle velocity, respectively; ρ and ρ_p to their density; and F_D is a drag coefficient that depends on both the discrete and the continuous phase, and is expressed as

$$F_D=\frac{18\mu }{{\rho }_p{d}_p^2}\frac{C_{D}R{e}_p}{24}$$ (2)

where Re_p is the particle Reynolds number, computed as

$$R{e}_p=\frac{{\rho }_p{d}_p\mid {\overrightarrow{u}}_p-\overrightarrow{u}\mid }{\mu }$$ (3)

and C_D is a coefficient calculated according to the spherical drag law

$$C_D=a_1+\frac{a_2}{Re}+\frac{a_3}{R{e}^2}$$ (4)

where a₁, a₂ and a₃ are constant values that apply over several ranges of Re_p (Morsi and Alexander 1972).

In this work lift forces were not included in the equation of motion of the particles. This choice was made according to preliminary numerical simulations in which the contribution of lift forces was quantified and evaluated to be negligible in the models simulated in the present study.

According to the discrete phase approach particles are not explicitly modeled within the discretized fluid domain of the continuous phase and the effect of the continuous phase on the particles is subsumed into drag force contributions. This approach is based on the assumption that the particulate phase is sufficiently diluted and occupies a small volume fraction (less than 10%) of the fluid domain. In the present work, the dilution of platelets used in the DTE approach to quantify the shear-related platelet activation by means of the PAS assay was replicated. The PAS assay requires a concentration of the platelet sample of 20×10³ platelets/μl, which corresponds to a volume fraction of 0.03%, supporting the use of the discrete phase approach in these models. Despite the approximation of neglecting the explicit presence of the particles in the discretized fluid domain, the discrete phase model allows to take into account the contribution of mass flow that the particles transfer to the continuous phase, through a fully-coupled approach. The fully-coupled approach is implemented in Fluent by adding a source of momentum to the Navier-Stokes equation of the fluid which is proportional to the mass of particles entering a grid cell of the fluid domain and their velocity, as in the following equation:

$$F_p={\Sigma }_{i=1}^{N_p}\left[F_D(u_{pi}-u)\right]{\stackrel{.}{m}}_{pi}\Delta t$$ (5)

where N_p is the number of particles entering the cell of the fluid domain, u_pi is the particle velocity, ${\stackrel{.}{m}}_{pi}$ its mass flow rate and △t is the time step of the simulation.

Particles were injected in the fluid domain according to the following seeding strategy: with the aim of obtaining probabilistic distribution of shear stress waveforms along platelet trajectories, a population of about 700 platelets was injected from a cross-section downstream of the inlet surface in each model. The injections were distributed in time in order to replicate a dilution of 20×10³ platelets/μl. Moreover, the spatial distribution of platelets was assigned following the velocity distribution of the flow field on the injection surface in order to replicate the fact that trajectories characterized by higher velocities will be followed by a larger population of platelets. In the computational models particle-particle interactions were neglected since this approximation is justified by the condition of high dilution of the particulate phase already satisfied, while particle-wall interactions were treated as elastic collisions: a particle impacting the wall is reflected by retaining the same amount of normal and tangential momentum (with respect to the wall) before the impact.

The discretization step for the advancement in time of the solution was set to 0.1 ms and for each model the simulation was run until all the particles escaped the fluid domain.

At each time step, the stress tensor acting on a particle was assumed equal to the stress tensor in the fluid where the particle center of mass is located. In order to condense the complex stress tensor instantaneously associated to each particle in a scalar quantity, an effective measurement of shear stress was derived: as described in previous computational study (Apel et al 2001, Alemu and Bluestein 2007), the so-called scalar stress was computed from the fluid stress tensor τ_ij, as in (5)

$$\sigma =\frac{1}{\sqrt{3}}\sqrt{{\tau }_{11}^2+{\tau }_{22}^2+{\tau }_{33}^2-{\tau }_{11}{\tau }_{22}-{\tau }_{11}{\tau }_{33}-{\tau }_{22}{\tau }_{33}+3({\tau }_{12}^2+{\tau }_{13}^2+{\tau }_{23}^2)}$$ (5)

Particle trajectories were extracted from the discrete phase simulations. Moreover, the scalar stress along each trajectory and at each time step was also exported: from each simulated model, N dynamic scalar stress waveforms were obtained (where N is the number of simulated particles in the domain). The linear stress accumulation (SA) of each trajectory was computed as

$$SA={\int }_0^T\sigma \left(s\right)ds$$ (6)

thus obtaining a stochastic distribution of SA in each microfluidic model. Indeed, the probability density function (PDF) of SA can be seen as the synthetic description of its flow-related thrombogenic potential, and was used to identify representative shear stress waveforms of the microfluidic VAD emulator channels.

The geometry of each model was designed according to preliminary analytical formulae and then optimized through the CFD analyses. A semi-automatic algorithm was implemented allowing to optimize channel geometrical parameters (widths and lengths of the shear stress-generating features) based on the discrepancy between descriptive parameters of the shear stress waveforms along platelet trajectories in the microfluidic channels and the reference shear stress waveform to be replicated.

3. RESULTS

3.1 Design of microfluidic stress-generating templates

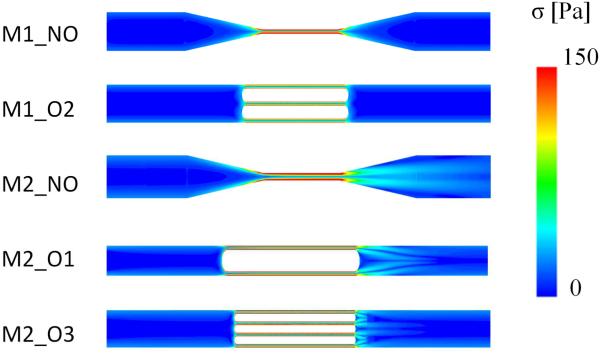
In Fig. 4, the contours of the scalar stress in the mean longitudinal plane of the models designed in 2.1.1 are shown. The scalar stress levels in the stress generating features show a similar trend, even though differences were observed in terms of maximum scalar stress, as reported in Table 2 where the maximum scalar stress values and the pressure drop across the models are reported. Maximum values of scalar stress range from 305 (model M2_NO) to 332 Pa (model M1_O1).

FIG. 4.

Contours of scalar stress in the mean longitudinal plane of the stress generating features in the models designed in 2.1.1. The models are not in their actual scale dimensions in order to allow comparison between different models.

TABLE 2.

Maximum scalar stress (σ_max) values and pressure drop levels (ΔP) in all the models simulated.

	M1_NO	M1_O2	M2_NO	M2_O1	M2_O3
σmax (Pa)	317	330	325	305	303
ΔP (atm)	0.24	0.90	0.29	0.70	1.1

In general, higher pressure drops were observed in obstructive models independently of the maximum scalar stress reported.

In M2 models, flow trails could be observed downstream of the stress-generating feature, unlike models M1_NO and M1_O2, where a symmetric stress distribution was obtained across the stress-generating feature. The latter was characterized by predominant viscous flow and the narrowing of the channel did not lead to any flow disturbances. On the contrary, the flow regime was different for configuration M2_NO, where the flow rate was 300 fold higher than in M1_NO.

In order to compare results obtained from the particle tracking simulations, distributions of parameters extracted from platelet trajectories were compared. In all the models, the median value of the shear stress in the baseline part of the channel was below 10 Pa and no trajectories reported scalar stress values reaching 20 Pa, which is in agreement with the desired baseline values. In Table 3,the distributions of peak scalar stress and exposure time along particle trajectories are reported, both expressed as 10^th, 50^th, and 90^th percentile values.

TABLE 3.

10^th, median (50^th percentile) and 90^th percentiles of σ_peak and T_peak along particle trajectories.

	M1_NO	M1_O2	M2_NO	M2_O1	M2_O3
10th percentile of σpeak (Pa)	54	65	55	61	54
50th percentile of σpeak (Pa)	132	128	132	128	130
90th percentile of σpeak (Pa)	215	236	204	238	214
10th percentile of Tpeak (ms)	3.5	3.2	2.9	2.8	3.1
50th percentile of Tpeak (ms)	4.2	4.0	4.1	4.0	3.9
90th percentile of Tpeak (ms)	8.4	7.7	10	9.4	7.8

In general, symmetrical distributions were obtained in terms of scalar stress values which has lower and higher percentiles almost equidistant from the median value (50th percentile). On the contrary the distributions of exposure time along trajectories are non symmetrical with the median values located in the bottom part of the distribution and a long tail extending towards higher values. However, in all the models a large fraction of trajectories (70% of the total) falls in a range between 0.8 and 1.2 of the median values, which means that a large population of platelets would experience similar exposure times.

For this reason, as a result of the design optimization phase, all the models were set to have the same median values of peak scalar stress and exposure time. In particular, the median values of the distributions were chosen as representative parameters to describe the shear stress patterns generated by the microchannels. From this point of view, the models replicated the template shear stress patterns chosen in the designing phase, with peak scalar stress and exposure time close to the objective values: the desired template shear stress waveform was then considered achieved in terms of representative statistical values of peak scalar stress (130 Pa) and duration (4 ms), suggesting the potential use of microfluidics in performing HSD-like shear-controlled experiments. Furthermore, the distributions of the shear stress waveform parameters showed similar trends demonstrating that similar shear stress patterns experienced by platelets can be replicated in different microfluidic devices. Although similar results were obtained with NO and O features in terms of generated shear stress waveforms, NO channels have the advantage – given the aspect ratios of obstacles considered here - of being easier to accurately fabricate through soft lithography.

3. 2 Achieving different shear stress levels

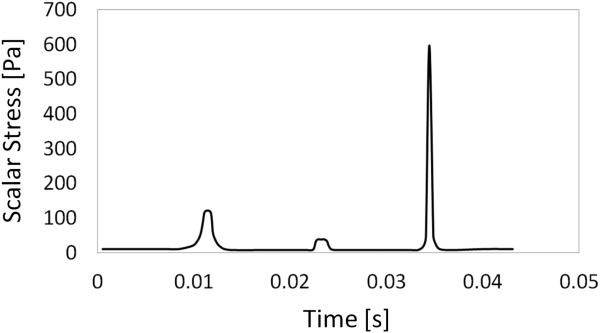
The maximum scalar stress levels in the three stress-generating features of M1_3SGF model were 317 Pa, 110 Pa, and 920 Pa, respectively, following the ranges set in the designing phase. This result demonstrated how it could be possible to span very large ranges of shear stress within a single microfluidic device. A similar result could be observed from the transient discrete phase simulation. As an example, the scalar stress along a representative particle trajectory reporting median values of peak shear stresses is shown in Fig. 5.

FIG. 5.

Scalar stress along a particle flowing in M1_3SGF, corresponding to the 90th percentile of SA.

3. 3 Microfluidic devices to replicate commercial VADs

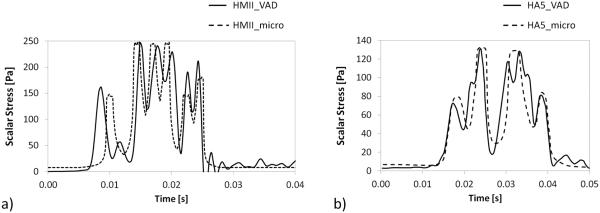
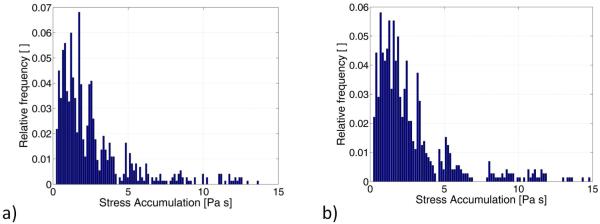
As a third step, two microfluidic models (Fig. 3) were designed in order to replicate significant scalar stress trajectories computed in a previous study (Chiu et al 2014) for two commercial VADs: the HMII and the HA5 devices. In Fig. 6 the PDF of SA of the HMII and HA5 microfluidic channels are shown: as observed, in both the models the SA spans a wide range of values. However, the distribution is characterized by a long tail that extends towards higher values and the fraction of particles experiencing higher levels of SA (in the region above the 50^th percentile of the distribution) is more dispersed and non-uniform. For this reason the trajectories falling in this part of the distribution were considered to be less representative of the shear-induced thrombogenic potential of the microfluidic channel. On the contrary the region of the distribution ranging from the 10^th percentile to the median values is more uniform. Thus, in this work trajectories characterized by levels of SA values in this range of the PDF were identified as the representative trajectories of the microfluidic devices. Those representative trajectories are reported in Fig. 7 and compared to the VAD waveforms obtained at the macroscale (Chiu et al. 2014).

FIG. 6.

PDF of SA distribution obtained in the (a) HMII and (b) HA5 microfluidic models.

FIG. 7.

Comparison between the scalar stress waveforms corresponding to the 90th percentile of SA distribution obtained in the (a) HMII and (b) HA5 VAD simulations at the macroscale (Chiu et al. 2014) and in the corresponding microfluidic simulations.

Although schematic, the microfluidic platforms succeeded in capturing the main features of the scalar stress waveforms experienced by blood platelets at the macroscale, in terms of both peak of scalar stress values and exposure time. The pressure drop across the two channels was 4.9 atm and 2.3 atm in model HMII and HA5, respectively.

4. DISCUSSION

In the present work, we demonstrate the feasibility of using PDMS microfluidic platforms to replicate VAD-specific shear stress history patterns The high resolution achievable with soft lithography allowed the design of microfluidic devices in which shear stress levels could be finely controlled, thus representing the basis for a technique well-suited to design lab-on-chip shear-mediated platelet activity assays.

Recently, microfluidic devices have been developed to test platelet function under flow. Platelet adhesion on collagen-coated glass surfaces was investigated by detecting platelet cytosolic Ca²⁺ influx using fluorescence microscopy in microfluidic channels perfused at physiological arterial shear rate (Zijp et al, 2014). Similar studies were carried out by Gutierrez and colleagues (2008) who detected platelet adhesion to glass surfaces coated with extracellular matrix proteins under flow by labeling platelet dense granules with a fluorescence dye. Li and Diamond (2014) developed a microfluidic device allowing to test the effect of different anti-platelet drugs on a single platform under physiological and constant venous shear rate, by monitoring the fluorescence intensity of platelets labeled with anti-human CD61 antibody. Li and co-authors (2012) proposed a microfluidic PDMS-based device to monitor platelet aggregation at different shear rates in microfluidic channels with a modeled stenosis. An optical system measuring the transmitted light across the channels was developed allowing monitoring of the formation of platelet thrombus inside the channels. In a more recent paper (Li et al. 2014), the same device was used to test the effect of anti-platelet drugs at different shear rates. These studies showed the potential use of microfluidics to test and investigate platelet behaviour under flow. However, the analyses were performed under constant shear rate. To the best of our knowledge, no previous studies in the literature made use of microfluidic technology to develop systems for testing platelets under dynamic and controlled shear stress patterns, demonstrated to have a strong influence in triggering platelet activation (Girdhar and Bluestein, 2008).

PDMS microfluidic platforms have significant advantages as they are transparent, gas permeable, chemically inert; the bulk material cost is low and fabrication may be carried out under normal laboratory conditions, without the need for expensive clean room facilities (Friend and Yeo 2010). PDMS-based microfluidic systems allow multiple experiments or tests to be performed in parallel on a small footprint. Furthermore, the high surface-to-volume ratio dramatically reduces reaction times and allows for very precise fluid handling. Nevertheless, in the design of microfluidic systems, some constraints inherent to soft lithographic techniques have to be considered. First, high resolution photomasks printed on low-cost transparencies allow for lateral resolutions up to 5 μm. Chrome masks are required beyond this limit, despite a price increase of several orders of magnitude. Second, the height of microfabricated features (e.g. fluidic channels) is limited by the ability to uniformly deposit photoresist on silicon wafers. Spin coating yields thicknesses in the range 1-200 μm when using standard SU-8 resins, presenting limits on maximum dimensions of attainable features. Third, a maximum aspect ratio of silicon/photoresist master features is generally set to 20, although aspect ratios (ARs) larger than 50 can be achieved at the expense of process repeatability (Liu et al 2015). However, due to the low elastic modulus of PDMS, when features having AR higher than 10 or lower than 0.1 are realized, pairing and sagging effects can compromise the designed geometry (Xia and Whitesides 1998). Fourth, plasma sealing is watertight and irreversible, and can withstand, reasonably, hydraulic pressures as high as 5-10 atm, depending on the channel dimensions and the effective sealing area.

The use of microfluidics also allows for a high flexibility, as demonstrated by the simulation of M1_3SGF model. The designed microchannel is able to span several orders of magnitude of shear stress levels, up to values approaching 1000 Pa, which is not attainable with the traditional HSD. As reported, high pressure drop levels were obtained in the microfluidic emulator channels (HMII and HA5 microfluidic models). This would limit the possible number of repetitive units on a single platform to one or two elements on single platforms, since the bonding between the PDMS and the glass slide would reasonably withstand maximum pressure head of about 5 atm. Proper experimental approaches should be adopted in order to increase the number of passages of the fluid sample through the microfluidic units, as for example a system of two synchronized syringe pumps allowing the sample to flow alternatively in the two directions.

Despite the promising results, the modeling strategy that was adopted in this work has some limitations. In particular, an assumption was made in order to compute shear stresses acting on platelets that were assumed to be equal to the shear stress in the fluid field where the center of mass of each platelet is located. A more accurate description of shear stress on the platelet surface would require more sophisticated fluid-structure interaction approaches in which platelets would be explicitly modeled in the discretized fluid domain, resulting in the need for a refined fluid mesh around particles and leading to heavier computational models, especially in cases in which a large number of particles are modeled in relatively large fluid domains. This approach would not be suited to our models in which the platelet size (3 μm diameter) is much smaller than the channel dimensions which have lengths that vary from a minimum of 2 mm to a maximum of 20 mm, approximately. In the last decades, the Lattice-Boltzmann method (LBM) has emerged as an alternative to standard CFD methods. According to the LBM the fluid is treated as a distribution of fictitious particles on a fixed regular grid which determines macroscopic properties of the flow field, while evolving over time through processes of streaming and collisions between particles (Chen et al. 1992). In general the LBM method performs better compared to standard CFD methods in terms of computational efficiency and scalability. In a recent work, the LBM has been used by Wu and colleagues (Wu et al. 2011) to compute platelet trajectories in microfluidic channels. Although the advantage of this method in providing a more accurate description of the interaction between the continuous and discrete phases, this approach would still be too computationally expensive for our models where large number of particles are tracked. In fact, in the work published by Wu and collaborators, a total number of 40 particles was simulated in each model and furthermore, particles characterized by longer residence time were not included in order to limit the simulation duration. Based on these considerations, the discrete phase model implemented in Fluent has been considered more appropriate to the present study in which the aim is to implement a numerical approach that allows to describe on a statistical basis the behaviour of a representative population of platelets flowing in microfluidic channels. Moreover, the approach is intended to represent a designing tool to optimize the microfluidic channel design, thus requiring additional iterative runs to be accomplished.

With the envisioned utilization of the PAS assay (Jesty and Bluestein 1999, Jesty et al 2003) to quantify shear-mediated platelet activation of the microchannel, the system must allow the collection of 10 μl of GFP. After a desired number of passages through the device, 10 μl of activated sample will be collected and assayed spectrophotometrically for generated thrombin using a thrombin-specific substrate, normalizing the results with respect to positive and blank control samples. From this perspective, the priming volume of the microchip should be increased by extending the connecting channels to the pumps in order to guarantee the collection of at least 10 μl of fluid needed to perform a single PAS assay. Assuming a chip consisting of 1 single repetition of the HMII_microfluidic unit (characterized by a priming volume of about 62 nl), at a flow rate of 36 μl/min, around 17 s would be necessary to flow the 10 μl sample volume in one direction. In order to replicate 100 passages through the device, the test would take approximately 30 min to be performed. A further decrease of testing time could be obtained by reducing the sample volume needed with an ad hoc modification of the standard PAS assay.

The possibility of adopting strategies to enhance mixing of platelets must also be considered, as the low flow regime attainable in microfluidic systems strongly limits particles and species mixing. A contemplated approach might include the introduction of bas-relief structures on the top of the channel, as proposed by Stroock and co-authors (2002). Such structures generate local convective phenomena enhancing mixing of the fluid particulate sample, which would be of value to assure uniform activation levels over the population of platelets assayed.

We have demonstrated the feasibility of downscaling HSD-like experiments on a microfluidic level. This study serves as a proof-of-concept and is intended to set the basis for the future development of a Lab-on-a-Chip system able to perform device-specific and patient-specific platelet activity state assays. Validation of the microfluidic platforms through comparison with test-cases performed on standard laboratory systems (i.e. HSD) is currently ongoing.

In order to develop a fully functional point-of-care (POC) device, some additional critical points need to be addressed. First, in this preliminary study GFP was simulated in the microfluidic channels. This choice was done with the aim of replicating the in vitro conditions tested in the HSD to quantify the shear-induced activation by means of the PAS assay. The possibility of using whole blood should also be considered since this would ultimately represent a more suitable approach for a POC device. However in case of whole blood the assumption of highly dilution of the particulate sample and of absence of particle interactions could not be fully satisfied and more sofisticated discrete phase models should be implemented in order to account for these effects. Second, issues arising from interfacing the microfluidic device to the patient must be considered. Filling of the chip with patient blood must be achieved in a manner that minimizes the air-blood interface, which could potentially affect platelet function. An ad hoc connection between the chip and the pumping system should be studied in order to minimize the dead volume of the assembled system. Finally, as highlighted, downscaling and on-chip integration of the assay for platelet activation quantification is vital to advance the system for POC diagnostic use.

The approach that we described could be also applied to other clinical scenarios. As an example, the POC device could be designed to emulate hemodynamics in patient-specific disease conditions. To this end, CFD analyses on patient-specific anatomies (e.g. aortic stenosis or obstructive coronary artery disease) could be utilized to design a “personalized” microfluidic platform for analysis of the efficacy of individual patients anti-thrombotic therapy, under the actual dynamic conditions of their own specific flow altering anatomy.

5. CONCLUSIONS

In the present study the use of microfluidic technologies to design platforms for shear-controlled assays on blood under dynamic conditions has been studied through CFD analyses: a range of types and scale-sized microfluidic geometries were analyzed. Moreover, a CFD-based approach to design microfluidic platforms for emulation of the shear-induced thrombogenic potential of MCS devices has been presented. Test cases on two commercial VADs were investigated to demonstrate the feasibility of this approach. Research activities are now focusing on fabrication and experimental validation of microfluidic VAD-emulating prototypes. Development of an effective, accurate, personalized and user-friendly POC system will enhance the safety and effectiveness of MCS systems and reduce thrombotic risk.

Abbreviations

AR

Aspect Ratio

CFD

Computational Fluid Dynamics

DTE

Device Thrombogenicity Emulator

HA5

Heart Assist 5

HMII

HeartMate II

HSD

Hemodynamic Shearing Device

MCS

Mechanical Circulatory Support

NO

Non-obstructive

O

Obstructive

PAS

Platelet Activation State

PDF

Probability Density Function

PDMS

Polydimethylsiloxane

POC

Point-of-Care

SA

Stress Accumulation

VAD

Ventricular Assist Device