Sex Speeds Adaptation by Altering the Dynamics of Molecular Evolution

Abstract

Sex and recombination are pervasive throughout nature despite their substantial costs¹. Understanding the evolutionary forces that maintain these phenomena is a central challenge in biology^2,3. One longstanding hypothesis argues that sex is beneficial because recombination speeds adaptation⁴. Theory has proposed a number of distinct population genetic mechanisms that could underlie this advantage. For example, sex can promote the fixation of beneficial mutations either by alleviating interference competition (the Fisher-Muller effect)^5,6 or by separating them from deleterious load (the ruby in the rubbish effect)^7,8. Previous experiments confirm that sex can increase the rate of adaptation^9–17, but these studies did not observe the evolutionary dynamics that drive this effect at the genomic level. Here, we present the first comparison between the sequence-level dynamics of adaptation in experimental sexual and asexual populations, which allows us to identify the specific mechanisms by which sex speeds adaptation. We find that sex alters the molecular signatures of evolution by changing the spectrum of mutations that fix, and confirm theoretical predictions that it does so by alleviating clonal interference. We also show that substantially deleterious mutations hitchhike to fixation in adapting asexual populations. In contrast, recombination prevents such mutations from fixing. Our results demonstrate that sex both speeds adaptation and alters its molecular signature by allowing natural selection to more efficiently sort beneficial from deleterious mutations.

The vast majority of species engage in some form of sex or genetic exchange¹. Yet the evolutionary forces that make sex widespread in nature remain incompletely understood. In principle, asexual reproduction should be more efficient: it avoids the costs of mating and allows individuals to pass all (rather than half) of their genetic material to their offspring. Extensive theoretical work has sought to understand why sex is pervasive despite these substantial costs^2,3.

One potential evolutionary advantage of sex is that recombination can speed adaptation⁴. Several distinct mechanisms could drive this effect. For example, recombination can relieve clonal interference, bringing together beneficial mutations that arise on different genetic backgrounds and would otherwise compete^5,6,18–20. Sex can also rescue beneficial mutations from deleterious backgrounds^7,8. Recent empirical work suggests that such interference effects are widespread in adapting asexual microbial^21,22 and viral populations²³, and may also be common in higher eukaryotes²⁴. Thus the role of recombination in speeding adaptation may be broadly important in the evolution and maintenance of sexual reproduction.

Several laboratory evolution experiments have confirmed that sex can indeed increase the rate of adaptation^9–17. By analyzing how the strength of this effect depends on population size^13,14 and other parameters^9–12, these studies sought to quantify the relative importance of various potential advantages of sex. However, previous studies have been limited almost exclusively to phenotypic measurements. Hence they have been unable to observe how recombination alters evolutionary dynamics at the sequence level. This has made it difficult to connect phenotypic observations of the advantages or disadvantages of sex to their underlying molecular causes.

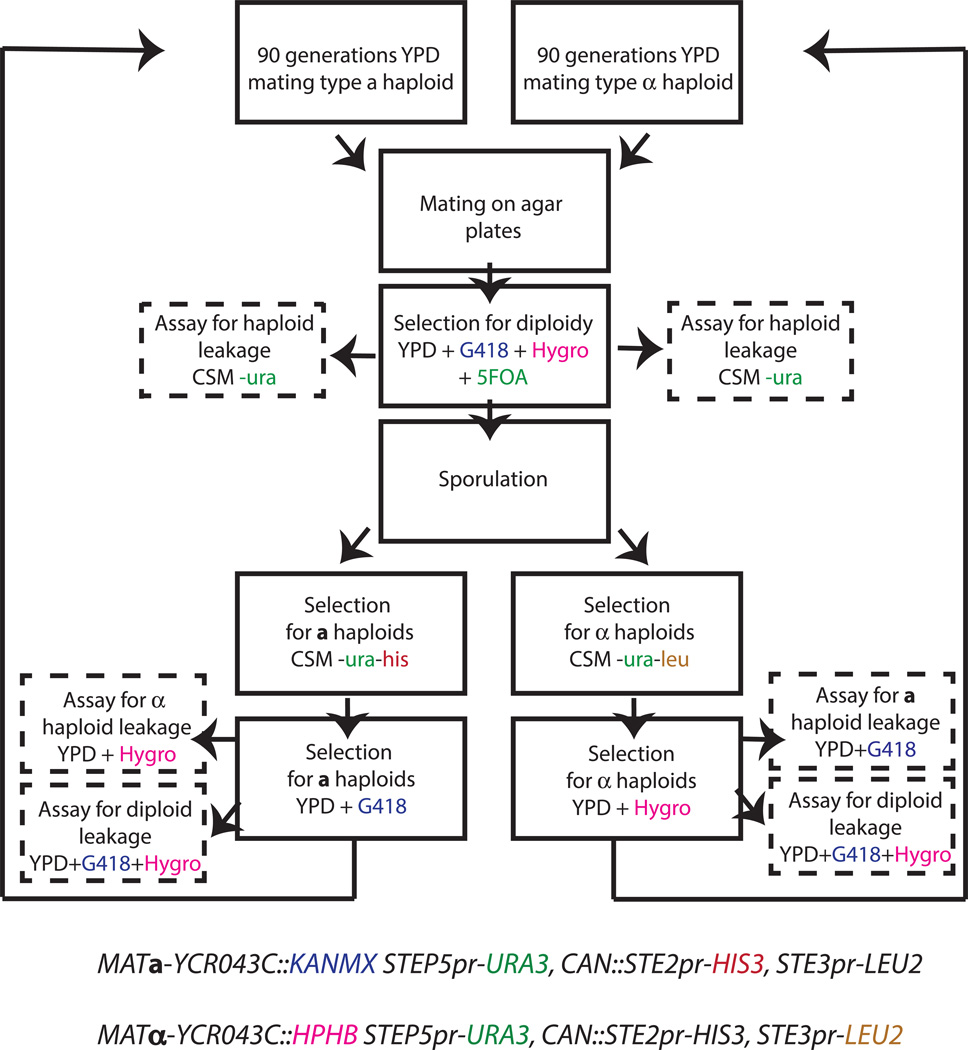
Here, we describe the first comparison of the dynamics of genome sequence evolution in sexual and asexual populations. We use experimental evolution of S. cerevisiae as a model system. As in earlier studies^11,12, we incorporate recombination by interspersing asexual mitotic growth (with mating type a and α subpopulations propagated separately) with discrete “sexual cycles” of mating followed by sporulation (Methods). Sexual cycles pose a key technical challenge: it is difficult to ensure that most of the population sporulates and mates without inbreeding. To overcome this obstacle, we developed a genetic system involving two drug markers, one tightly linked to each mating locus, combined with haploid-specific and mating type-specific nutrient markers (Extended Data Figure 1). This enables us to force outcrossing by selecting separately for haploid a and α cells after sporulation and for diploids after mating. We verified that leakage of mitotically dividing cells through each cycle is minimal (<0.1%), and that sexual cycles do not introduce bottlenecks compared to the effective population size (Methods, Extended Data Table 1). This system allows us to control the rate of outcrossing, and hence isolate the effects of recombination from ancillary features of the experimental protocol.

Using this approach, we evolved six replicate sexual populations and twelve asexual controls (each consisting of a single type a or α population). Each population was founded from a single clone and propagated at an effective population size of ~10⁵ cells (Methods). We induced sex every 90 generations. During sexual cycles, we ensured that selection pressures in sexual and asexual lines were as equivalent as possible (without inducing mating or sporulation in asexuals; Methods). We verified that any differences between these treatments do not lead to differential adaptation to sexual cycles (or asexual control conditions) by measuring how sexual and asexual lines adapted to both conditions (Extended Data Figure 2). We also confirmed that these conditions do not lead to different mutation rates (Extended Data Table 2). We note that each sexual line consists of a mating type a and type α subpopulation, while asexual lines consist of a single type a or α population, creating a potential difference in effective population size. To verify that this does not affect our conclusions, we evolved a parallel set of asexual control lines, each consisting of two type a subpopulations mixed at 90-generation intervals (analogous to sexual lines but without recombination). We confirmed that these lines adapt at the same rate as asexual lines consisting of a single subpopulation each (Methods; Extended Data Figure 3).

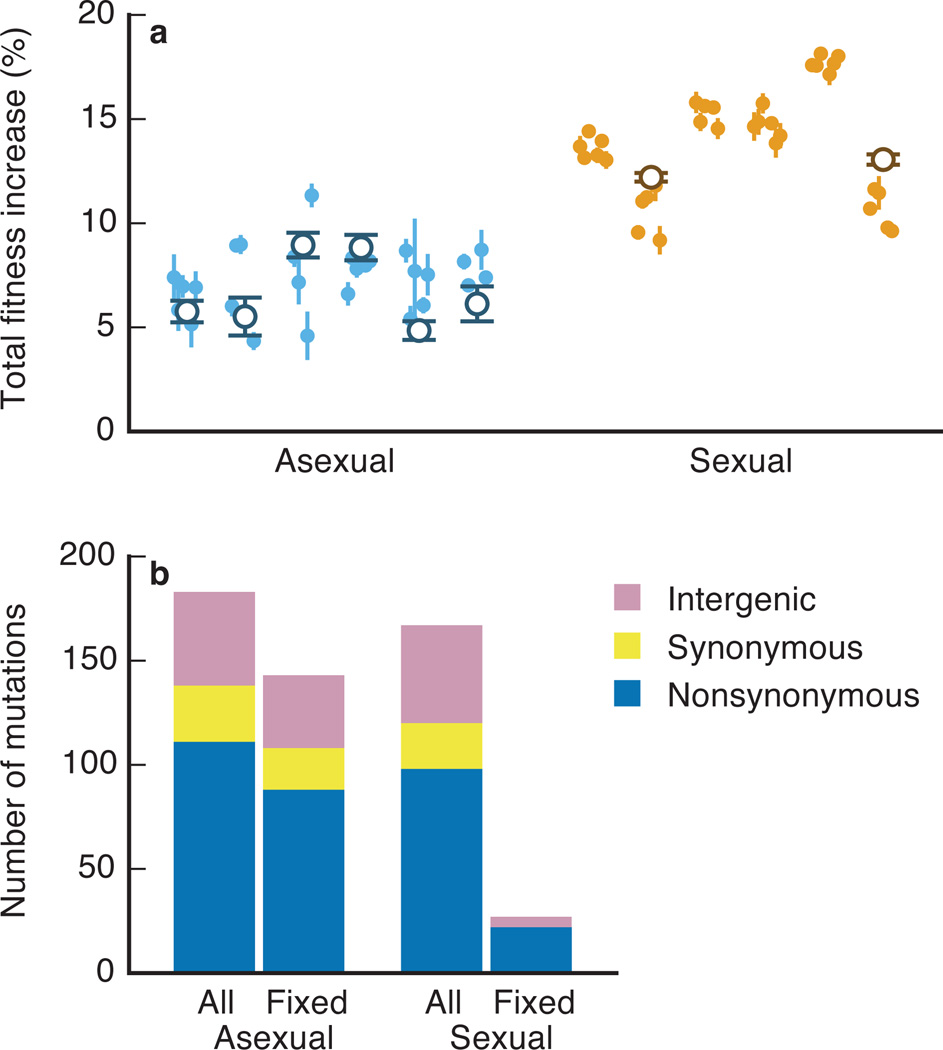
After ~1000 generations of adaptation, including 11 sexual cycles, we measured the fitness of multiple clones isolated from each population (Methods; note one sexual population ended at generation 900 due to technical failures during evolution). We also measured the fitness of whole-population samples, except in four sexual populations where the spontaneous evolution of frequency-dependent interactions make population fitness undefined (we describe this frequency dependence below). Both clone (Mann-Whitney U, P<0.001) and whole-population (two-sided t-test, P<0.001) fitness data show that sexual populations adapted significantly faster than asexual controls (Figure 1a).

Figure 1. The rate and molecular signatures of adaptation.

a, Total fitness increase over ~1000 generations of adaptation in asexual (blue) and sexual (orange) populations. Open circles represent the mean fitness of the population (for type a populations without frequency dependence); solid points represent the fitness of individual clones (mean of five replicate fitness assays, error bars ±s.e.m.). b, Classification of observed and fixed mutations in sequenced lines.

To reveal the molecular mechanisms underlying faster adaptation in sexual populations, we turned to whole-genome sequencing. We sequenced whole-population samples every 90 generations in four sexual and four asexual populations. We identified segregating mutations and tracked their frequencies through time (Methods). We detected an average of 44 de novo mutations per population (Extended Data Table 3, Supplementary Data 1). We emphasize that these results represent a subset of all mutations in our populations. Most importantly, we focus on SNPs and small indels; we cannot call certain more complex types of mutations (e.g. large indels and chromosomal rearrangements) from whole-population data. To estimate the impact of these complex mutations, we sequenced eight total clones isolated from two sexual and two asexual populations, identifying no aneuplodies and only a small number (~2.5 per population) of duplications and deletions of at most 65kb (half in transposable elements; Methods, Extended Data Figure 4, Extended Data Table 4). Since we cannot track them in whole-population data, we neglect these events in our analysis.

We find that sex alters the molecular signatures of adaptation. We observe similar proportions of synonymous, nonsynonymous, and intergenic mutations segregating in sexual and asexual lines (Figure 1b). Consistent with earlier work²¹, in asexual populations these types of mutations are roughly equally likely to fix, conditional on reaching observable frequency (Figure 1b, Extended Data Table 3). This indicates that natural selection cannot efficiently distinguish between their effects. In contrast, fewer mutations fix in sexual populations, and these mutations are overwhelmingly nonsynonymous. These observations suggest that sex improves the efficiency of selection, so that only beneficial mutations fix.

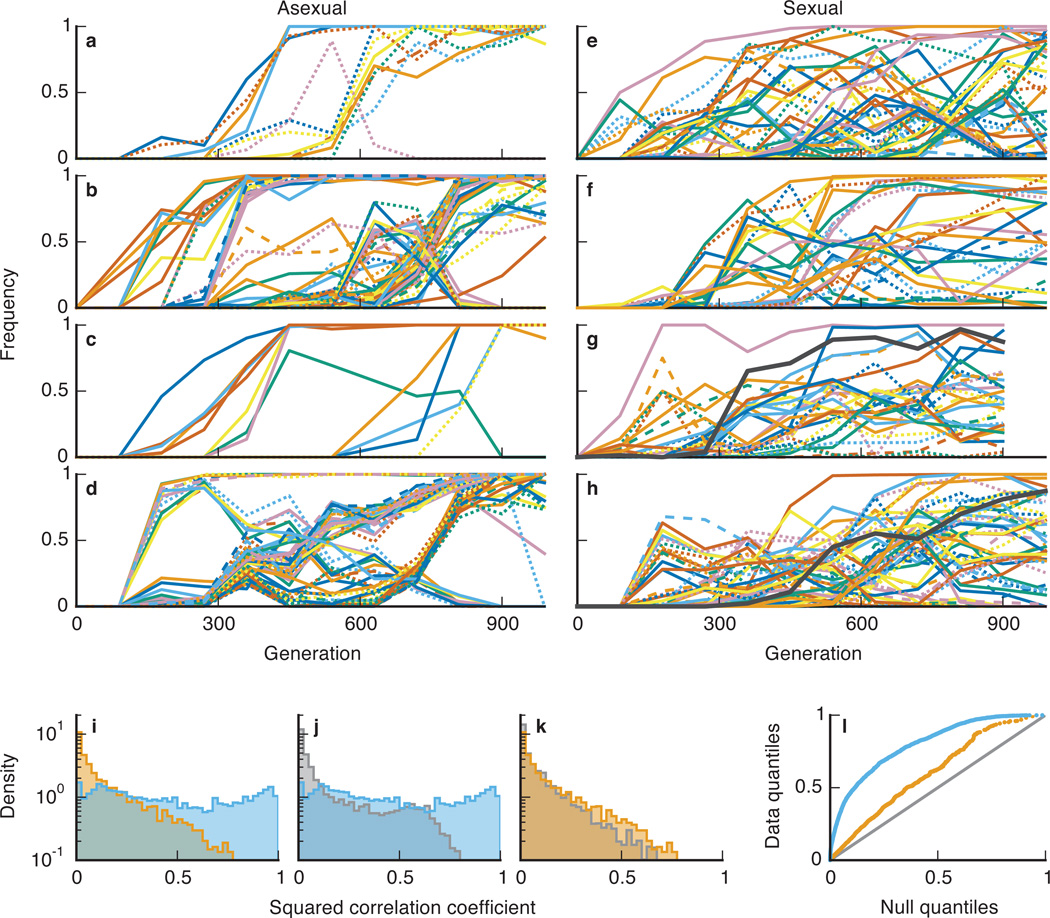
To investigate how sex improves the efficiency of selection, we analyzed the dynamics of adaptation. As in earlier studies^21,22, asexual populations exhibit signatures of hitchhiking and clonal interference (Figure 2a–d). Groups of functionally unrelated mutations, linked within the same genetic background, change in frequency together as clonal cohorts. The outcomes of evolution are determined by competition between these cohorts. In contrast, sexual populations are not characterized by cohorts of linked mutations (Figure 2e–h). Instead, the dynamics of each mutation is largely independent of other variation in the population. In these populations, mutations that occur on different backgrounds fix independently, while others briefly hitchhike to moderate frequencies where they persist or are eliminated from the population.

Figure 2. Fates of spontaneously arising mutations.

a–h, The frequencies of all identified de novo mutations through ~1000 generations in four asexual populations (a–d) and four sexual populations (e–h). Solid lines are nonsynonymous mutations; dashed are synonymous; dotted are intergenic. Black trajectories represent mutations in ERG3 subject to balancing selection. i, Distribution of correlations in frequency changes among pairs of trajectories in asexual (blue) and sexual (orange) populations. j,k, Comparison between these correlations and an empirical null distribution (gray) in asexual (j) and sexual (k) populations. l, Quantile-quantile plot summarizing deviations from null expectations (gray) in asexual (blue) and sexual (orange) populations.

We quantified these differences in dynamics by calculating the correlations in frequency changes between mutations (Methods). This measures how linked or independent the fates of these mutations are (e.g. linked mutations within clonal cohorts are strongly correlated). As expected, we find stronger correlations in asexual populations (K-S test, P<10⁻⁶, Figure 2i). We also compared the correlations within each population to a null distribution of correlations between trajectories in different populations (Methods). Both sexual and asexual populations exhibit stronger correlations than the null expectation (K-S test, P<10⁻⁶, Figure 2j,k), but the deviation is stronger in asexuals (Figure 2l).

These differences in the dynamics and molecular signatures of adaptation suggest that recombination makes natural selection more efficient at fixing beneficial mutations and purging neutral or deleterious hitchhikers, as argued by earlier studies⁹. For example, in asexual populations some cohorts that initially increase in frequency are later driven to extinction (Figure 2a–d), consistent with earlier work²¹. This indicates that adaptation in asexuals is limited by competition between cohorts that drives some beneficial mutations extinct. To analyze the efficiency of selection more directly, we measured fitness effects of individual mutations using two methods. First, we used a sequencing-based fitness assay. Specifically, we crossed an evolved clone from each sequenced population to its ancestor, generating a bulk segregant pool in which each mutation is present in many genetic backgrounds. We propagated this pool for 70 generations, sequenced at four time points, and tracked the frequency of each mutation to measure its fitness effect averaged across backgrounds (Methods). Second, we selected four genes that were mutated in both an asexual and sexual population, reconstructed each in a corresponding ancestral or evolved clone, and measured their fitness effects (Methods).

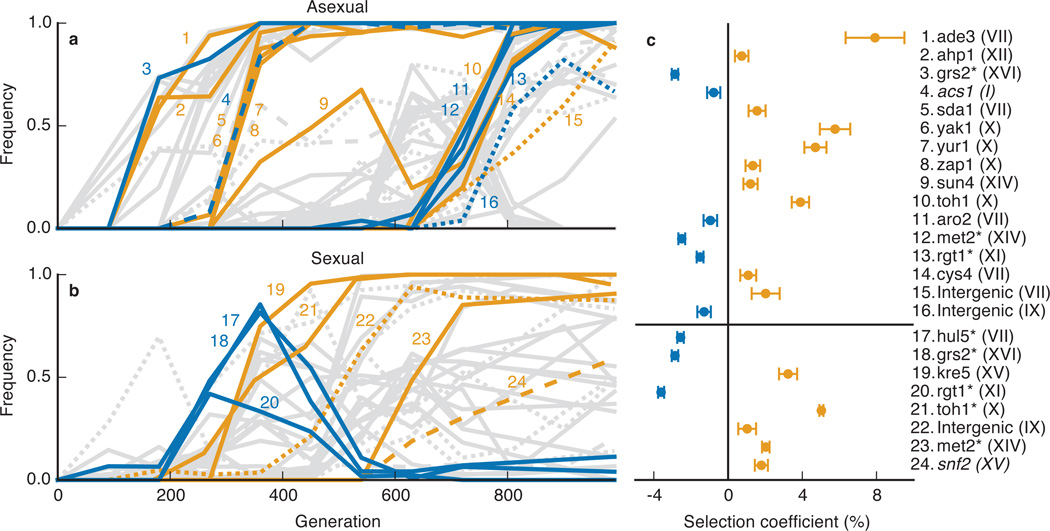
As expected, we find that each clonal cohort that fixes in an asexual population contains at least one beneficial mutation. However, we also find that significantly deleterious mutations hitchhike to fixation (Figure 3a,c). Recent theory has argued that the fixation of strongly deleterious mutations can be common in adapting asexual populations^25,26. Our results provide the first direct experimental support for this hypothesis. In contrast, recombination decouples hitchhiking mutations from their initial background, and we identify no deleterious mutations that fix in sexual populations (Figure 3b,c). The potential for sex to purge deleterious mutations in non-adapting populations has been extensively studied²⁷ (e.g. in work on Muller’s ratchet). Our experiments show that this effect is important even in adapting populations, confirming recent theory^28,29.

Figure 3. Fitness effects of individual mutations.

a, b, Mutation trajectories in an asexual (a) and sexual (b) line. Orange mutations are significantly beneficial; blue are deleterious; gray are unmeasured or consistent with neutrality. Several mutations were present in the founding population and hence omitted from Figures 1 and 2. c, Identities and fitness effects of significantly beneficial or deleterious mutations (chromosome number in parenthesis). Asterisks indicate fitness effects measured from reconstructions (mean of six replicate fitness assays, error bars ±s.e.m.); other fitnesses are from sequencing-based assay (error bars ±s.e. of regression coefficient; Methods). Italicized mutations are synonymous.

Our genetic reconstructions also highlight the potential importance of epistasis. For example, we identified a mutation in MET2 which fixed in a sexual population despite being deleterious in the ancestral background. However, further reconstructions showed that this mutation is beneficial in an evolved background, an example of sign epistasis (Methods). We cannot rule out the possibility of similar epistatic effects involving other mutations; this represents a limitation of the analysis in Figure 3.

Four sexual populations spontaneously evolved an “adherent” phenotype which stably coexists with the wild-type. In earlier work³⁰, we showed that this adherent type arises due to a loss-of-function mutation in the ergosterol pathway, which is maintained by balancing selection. Sequencing two of these populations revealed distinct mutations in ERG3 which persist at intermediate frequencies (Figure 2g,h). Despite the stable coexistence of these two phenotypes, our sequence data demonstrates that other mutations recombine between types before sweeping through the entire population. In combination with our fitness data, these results show that sex speeds adaptation despite the action of balancing selection at the ERG3 locus. Our earlier work shows that this stable polymorphism can also occur in asexual populations, but much less commonly³⁰, possibly due to clonal interference limiting the initial spread of ergosterol mutants. Further work is required to fully characterize how interactions between sex and balancing selection affect the evolutionary dynamics and long-term stability of this phenotypic diversification.

Together, our results show that sex increases the rate of adaptation both by combining beneficial mutations into the same background and by separating deleterious mutations from advantageous backgrounds that would otherwise drive them to fixation. In other words, sex makes natural selection more efficient at sorting beneficial from deleterious mutations. This alters the rate and molecular signatures of adaptation. These benefits persist even when balancing selection maintains phenotypic polymorphism within the population. Future studies are needed to fully understand the consequences of this interplay between sex and balancing selection, and to investigate how epistasis interacts with recombination to alter the dynamics of sequence evolution. By combining precise control of the sexual cycle with whole-population timecourse sequencing, this experimental system offers the potential to understand how these factors affect the rate, molecular outcomes, and repeatability of adaptation.

METHODS

Genotype and Strain Construction

The strains used in this study are derived from the base strains JYL1129 and JYL1130, haploid W303 yeast strains with genotypes MATa, STE5pr-URA3, ade2-1, his3Δ::3xHA, leu2Δ::3xHA, trp1-1, can1::STE2pr-HIS3 STE3pr-LEU2 and MATα STE5pr-URA3 ade2-1 his3Δ::3xHA, leu2Δ::3xHA, trp1-1, can1::STE2pr-HIS3 STE3pr-LEU2 respectively (generously provided by Jun-Yi Leu). Note these strains contain nutrient markers driven by promoters that are specific to haploid cells (STE5pr-URA3) and either mating type a (STE2pr-HIS3) or mating type α (STE3pr-LEU2)³¹. We identified a likely nonfunctional ORF (YCR043C) as an ideal target for insertion of mating type specific drug resistance markers close to the MAT locus. We amplified flanking regions from genomic DNA obtained from the YCR043C deletion mutant of the S. cerevisiae whole genome deletion collection³² using primers KANampFw and KANampRv (Supplementary Data 2) and integrated this product at the YCR043C locus of JYL1129 to generate strain MJM64. We then amplified the HPHB gene from plasmid pJHK137 (provided by John Koschwanez) using primers HYGampFw and HYGampRv (Supplementary Data 2) and integrated at the YCR043C locus of JYL1130 to generate strain MJM36.

Evolution experiment

We founded 12 mating type a lines using strain MJM64 and 12 mating type α lines using strain MJM36. Each of our 6 sexual populations consists of one specific pair of these MATa and MATα lines. The other 6 MATa and 6 MATα lines were designated as asexual controls (a total of 12 asexual controls). Between sexual cycles, we propagated these lines at 30°C in unshaken round bottom 96 well plates containing 128µl of YPD with daily 1:2¹⁰ dilutions using a Biomek FX liquid handling robot (Beckman Coulter, California). Pairs of MATa and MATα lines that represent a single sexual population were propagated independently in this mitotic phase. As previously described³³, this protocol results in approximately 10 generations per day and an effective population size of N_e~10⁵. Aliquots from generation 30 of each 90 generation cycle were mixed with glycerol to 25% and kept at −80°C for long-term storage.

After each 90 generations of asexual propagation, we initiated sexual cycles in the sexual populations. In each sexual cycle, we mixed and mated each pair of MATa and MATα lines, sporulated the resulting six diploid populations, isolated a and α subpopulations, and used these to initiate another 90 generations of mitotic growth (Extended Data Figure 1). To mate our lines we mixed a and α haploids, spotted onto YPD plates, and then incubated at 30°C. After 5 hours, cells were scraped from the plate, resuspended in PBS buffer solution and then plated on YPD agar containing Hygromycin (300µg/mL) and G418 (200µg/ml) to select for diploids. For sporulation, 10µl of saturated diploid culture was inoculated into 1ml of Yeast Peptone Acetate (YEPA) liquid media for incubation on a roller drum at room temperature. After 12–15 hours, cells were pelleted, resuspended in 1ml of 1M KOAc and then incubated at room temperature with agitation in a roller drum. After three days, the presence of spores was confirmed by microscope. We then pelleted and resuspended cells in Zymolase solution (Zymo research, Irvine, CA, 0.4U/µl) in order to digest spore walls and eliminate the majority of unmated diploids. In order to ensure that only mated and sporulated individuals survived this treatment, the zymolase lysate was divided, with one half plated onto defined amino acid dropout media CSM (-uracil, -leucine) to select for α haploids, and the other half plated onto CSM (-uracil, -histidine) to select for a haploids. After 24hrs of growth at 30°C, the lawn of cells was washed from plates and diluted into liquid CSM ( -uracil, -leucine) or CSM (-uracil, -histidine) and propagated for 24hrs. We used a dilution series to estimate the population size of this lawn, to confirm that this procedure does not lead to a population size bottleneck compared to the effective population size. Cultures were checked for diploids by plating a sample on YPD containing G418 and Hygromycin to quantify the number of unsporulated diploids that survive haploid selection. We found that diploid leakage was never more than 0.1% (see Extended Data Table 1 for details). These cultures were diluted into YPD and propagated for 90 generations before the sexual cycle was repeated. Asexual control populations were maintained in the same conditions as sexuals wherever possible, with the exception of sporulation, during which time these populations were kept at 17°C without dilution or agitation.

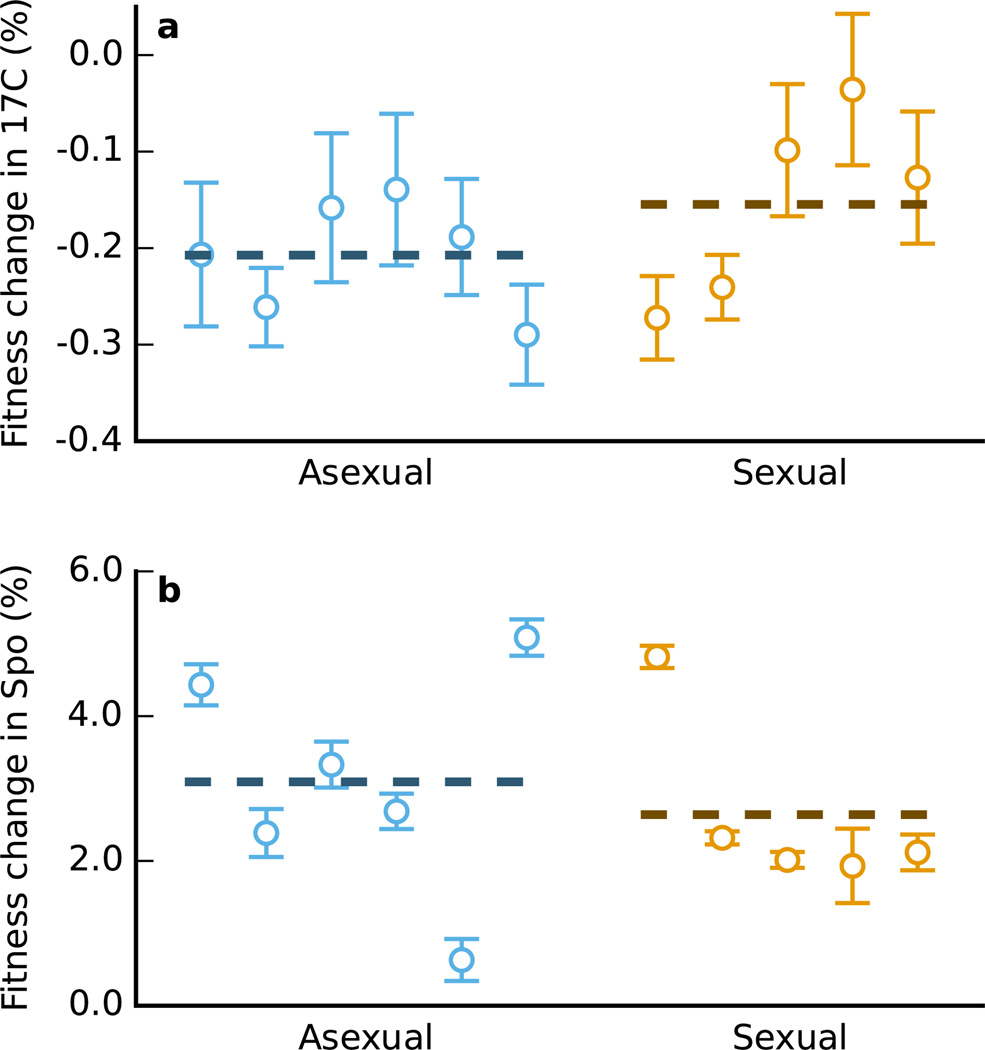
In principle, sexual and asexual populations could adapt differentially to the conditions specific to the sexual and asexual treatments. To test whether this effect could drive any differences between sexual and asexual lines, we measured the relative fitness of all evolved lines compared to the ancestor in both the sporulation and the 17°C treatment conditions. Specifically, we acclimatized six replicates of each evolved strain to YPD for 24h and then mixed each with a fluorescently marked ancestral strain in equal proportions. We subjected three of these replicate populations of each evolved strain to the 17°C treatment (plates were sealed and incubated at 17°C for 4 days) and the other three to the sporulation treatment (1 day incubation in YEPA liquid media, followed by 3 days in 1M KOAc at room temperature). We used flow cytometry (Fortessa, BD Biosciences, San Jose, CA) to measure the ratio of the two competing types immediately after mixing and again immediately after the four day treatment, counting approximately 20,000 cells for each measurement. We found that both sexual and asexual evolved lines performed better than the ancestor in 17°C treatment and worse in the sporulation treatment (Extended Data Figure 2). However, the effects of the sporulation and 17°C treatments do not vary systematically between evolved sexual and asexual populations (two-sided t-test, P=0.5 and P=0.8 respectively), and averaged over a 90 generation cycle any differences are small compared to the gains in fitness attained during adaptation to YPD. Thus there is no evidence that adaptation to sporulation or 17°C plays any role in our results.

We also tested whether conditions specific to the asexual treatment (4 days at 17°C without dilution) or the sexual treatment (four days of sporulation without dilution) caused variation in the number of mutations that occur in sexual and asexual lines. We assayed mutation rate by counting the number of spontaneous 5’FOA resistant mutants that arose in independent cultures of the ancestral W303 strain. Specifically, we propagated 54 populations in a microwell plate containing 128µl YPD. After one dilution cycle, we plated 18 of these cultures on agar plates containing SC-uracil supplemented with 1g.ml⁻¹ 5’ FOA (Sigma/Aldrich), and we counted the number of 5’FOA resistant mutants in each culture. Of the remaining 36 cultures, we incubated 18 for 4 days at 17°C in a microplate, and put 18 through our sporulation cycle (1 day in YEPA and 3 days in 1ml of KOAc). We then plated both sets of cultures on selective media and counted the total number of mutants in each (Extended Data Table 2). We then calculated the number of mutations per culture (m) using the Ma-Sandri-Sarkar maximum likelihood method³⁴. We found no difference in the numbers of mutations across all three data sets, suggesting that most mutations occurred primarily during growth in YPD, and not during incubation at 17°C or during sporulation culture conditions.

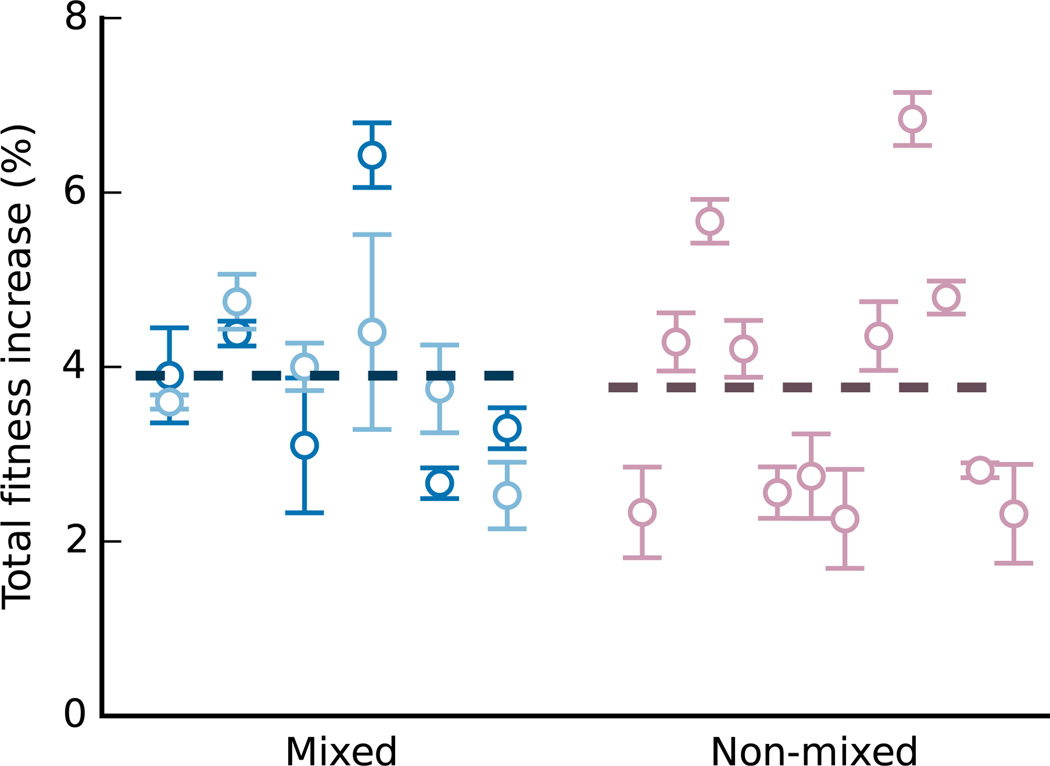
We note that each sexual population consists of a mating type a and a mating type α subpopulation, while each asexual population consists of a single type a or type α line. Although sexual populations were bottlenecked to the same total size as the asexuals during each sexual cycle, this difference means there is a potential difference in effective population size between treatments. To test whether this difference can explain the more rapid adaptation in sexual populations, we evolved an alternate set of 6 asexual control populations for 990 generations. Each of these alternate asexual controls consisted of one specific pair of MATa lines (i.e. two MATa subpopulations per asexual population). We propagated these subpopulations separately between sexual cycles. Every 90 generations, we mixed the two subpopulations (exactly analogous to the sexual lines but without recombination) and then divided them for another 90 generations of separate propagation. Simultaneously, we evolved 12 additional asexual control lines propagated in the same manner but without mixing every 90 generations. After 990 generations of evolution, we measured the fitness of all evolved populations. We find these mixed and unmixed asexual controls adapt at the same rate (Extended Data Figure 3, two-sided t-test, P=0.8). Thus this difference in treatments is not responsible for the faster adaptation in sexual populations.

Fitness assays

Fitness assays were carried out as described previously³³. Briefly, fitness was measured by competing test clones or populations against an ancestral reference strain containing an mCitrine fluorescent marker inserted at the HIS3 locus³⁵. Because this reference strain would mate with MATα lines, all population fitness assays were carried out on MATa subpopulations. After strains had acclimatized to YPD media for 24hrs, competing strains were mixed in equal proportions and propagated by diluting 1:2¹⁰ every 24hrs. We used flow cytometry (Fortessa, BD Biosciences, San Jose, CA) to measure the ratio of the two competing types after one and three days (approximately 10 generations and 30 generations respectively), counting approximately 20,000 cells for each measurement. We confirmed the appropriateness of each t-test conducted using this fitness data with an F-test.

Sequencing and variant calling

Glycerol stocks of populations to be sequenced were defrosted and 10µl inoculated into 3ml of YPD and incubated without shaking at 30°C for 16hrs (MATa and MATα subpopulations of each sexual line were sequenced separately). Genomic DNA was prepared from these cultures using the Yeastar Genomic DNA kit (Zymo Research, Irvine CA). Library preparations were prepared using the Nextera kit, using a protocol we previously described³⁶. Libraries were sequenced to an approximate depth of 40-fold coverage using an Illumina HiSeq 2500 (Illumina Inc., San Diego, CA).

We aligned Illumina reads from all samples (after trimming Nextera adaptor sequences) to a SNP/Indel corrected W303 reference genome²¹ using bowtie2 v2.1.0³⁷. Next, we marked duplicate reads with Picard v1.44. We generated a list of candidate SNPs and Indels by applying GATK’s UnifiedGenotyper v2.3 to all timepoints in each population at once³⁸. In order to find low-frequency variants, we set the minimum phred-scaled confidence threshold for GATK to call a mutation to 4.0. For each candidate mutation, we extracted the allele depth supporting the reference and alternate allele from the resulting VCF file and calculated mutation frequencies for each timepoint. We excluded potential mutations if there was less than 10× average coverage across all timepoints or if GATK called two or more alternate alleles at that site. We required that a mutation be supported by at least ten total reads and that it reach a frequency of 0.1 in two or more timepoints of the population in which it was called.

To refine our list of candidate mutations, we took advantage of our timecourse sequencing and multiple replicate lines. The frequency of a real mutation should be correlated across timepoints, while errors should be uncorrelated. We thus excluded candidate mutations whose frequency trajectories were uncorrelated (lag-1 autocorrelation less than 0.2). Also, it is unlikely that the same basepair substitution will arise independently in replicate populations. Thus, for each candidate mutation, we estimated the site-specific error rate by calculating the frequency of the alternate allele outside of the population in which the mutation was called. We then excluded candidates with an estimated error rate above 0.05. We also calculated the probability of detecting at least the observed number of alternate alleles in the focal population, assuming a binomial error model (given the observed coverage and estimated error rate). We excluded candidates where this probability exceeded 10⁻⁵. We also detected several mutations that were present in the founding stock and thus in multiple replicate populations. We marked these mutations and excluded them from our counts of de novo mutations and from Figure 2. After carrying out this procedure in the MATa and MATα subpopulations of each sexual line separately, we combined called mutations from both subpopulations and averaged the mutation frequencies to generate the whole-population trajectories in Figure 2; data on each subpopulation separately is available in Supplementary Data 1.

We annotated each called mutation using a SNP/Indel corrected GFF file and determined its effect on amino acid sequence. We also screened for complex mutations: pairs of mutations that were within 1kb of one another and followed the same trajectory. We discovered 7 complex mutations, all within 41 bases of one another. We determined the net effect of each complex mutation and considered them to be single mutations in our analysis.

We note that it is not possible to determine the fraction of mutations that we detect with our variant-calling method. For example, sequencing depth fundamentally limits our ability to detect rare mutations. We do not attempt to call mutations that never reach ~10% frequency because our 40-fold coverage gives no resolution below that level; our results thus represent only mutations that reach substantial frequency. We are also limited to the set of mutations that can be identified by GATK, mainly SNPs and small insertions and deletions (but see below for an analysis of larger-scale mutations from clone sequence data). These limitations apply equally to our sexual and asexual populations.

Correlations between frequency trajectories

Clonal interference is expected to generate correlations between the frequency trajectories of mutations that segregate at the same time. Two mutations in the same genetic background should increase or decrease together, while mutations on different backgrounds will tend to move in opposite directions. For each mutation trajectory, we calculated the change in frequency between each sequenced timepoint. We then computed the correlation coefficient between changes in the same time interval for every pair of mutations in the same population. We excluded pairs of mutations that did not segregate at the same time (i.e. pairs whose frequencies were never between 0.05 and 0.95 in the same timepoint). Because large positive and large negative correlation coefficients are both evidence of interference effects, we compared the distributions of squared correlation coefficients (R-squared) in asexual and sexual populations (Figure 2i–l).

The dynamics of natural selection will introduce such correlations even among unlinked mutations by constraining the shapes of frequency trajectories. For example, two simultaneous but genetically unlinked selective sweeps will each follow a similar sigmoidal trajectory and thus be strongly correlated with one another. We controlled for this effect by repeating the above calculations with all pairs of mutations segregating in different populations of the same reproductive type. The R-squared values from this procedure comprise two empirical null distributions (sexual and asexual) for mutations that are certain to be independent of one another (Figure 2j–l).

Detection of large deletions and copy-number variants

Our primary variant-calling pipeline can only detect substitutions, insertions, and deletions affecting ~3bp or less. To estimate the prevalence of larger-scale mutations in our populations, we implemented an alternative pipeline to detect large deletions and copy-number variants based on coverage depth as a function of genome position. Coverage depth in whole-population samples is difficult to interpret because it convolves individual copy-number with population variation. For example, a fixed duplication and a four-fold amplification present in half the population would generate identical coverage data in a whole-population sample. To avoid this problem, we sequenced eight total clones isolated from the final timepoints of two sexual and two asexual populations to an average depth per clone of 50–80×.

After aligning reads to the reference as described above, we tabulated coverage depth in 100 basepair windows as the number of mapped reads whose start positions fall within each window. These windows vary naturally in coverage depth due to pre-existing duplications, PCR artifacts, and properties of the alignment algorithm. Therefore, to generate a baseline expectation, we calculated coverage in the same windows for all of the generation-0 and generation-90 population samples. Added together, these data yield 564 reads in the median window. We thus calculated the expected relative coverage in each window by dividing its total coverage in the generation-0 and generation-90 samples by 564. For each clone, we then multiplied this expected relative coverage by the median coverage per window in that clone to get the expected coverage in each window.

We next looked for windows in which the observed coverage depth deviated from its expectation. This is complicated by the fact that random noise is introduced by the sequencing and alignment process. Because the coverage depth is generated by a counting process, the noise variance scales with the expected coverage. We therefore applied a variance-stabilizing Anscombe transform³⁹ to standardize the noise across windows with different expectations. First, we modeled the variance as v(m) ∝ m+m² / r, where m is the expected coverage in a window, v is the mean squared deviation from that expectation, and r is a parameter fit to the data by a linear regression of v/m by m (we find a best-fit value r ≈ 440). This variance function, which is characteristic of negative-binomial counting noise, leads to an Anscombe transformation $A(k)=\text{arcsinh}\left[\sqrt{\frac{k+c}{r-2c}}\right]$, where k is the observed coverage and c = 3/8 following the recommendation of Ref. 39 for negative-binomial data. The transformed data is approximately normally distributed with mean A(m) and constant variance.

Deletions and amplifications larger than our 100bp window size should generate spatially-correlated signals in our data, while the variance-stabilized noise will be largely uncorrelated between adjacent windows. To take advantage of this, we performed a “wavelet denoising” procedure, a standard signal-processing method for separating spatially-correlated signals from white noise⁴⁰, which has been used previously⁴¹ in similar analyses of biological sequence data. Specifically, we applied a discrete wavelet transform with the Haar basis, using the Python package PyWavelets, to our variance-stabilized and mean-centered data. We then performed noise reduction by replacing each wavelet coefficient a_i with a thresholded coefficient a_i*, according to the formula a_i^* = sign(a_i)max[0,|a_i|−t], where the threshold value t was set to three standard deviations of the variance-stabilized data.

After noise reduction, we inverted the wavelet and Anscombe transforms to get a smoothed estimate of the ratio of observed to expected coverage as a function of position (Extended Data Figure 4). By visual inspection, we identified ten regions exhibiting strong signals of amplification or deletion in at least one clone (Extended Data Table 4). Of these, two regions (an rDNA-rich segment of chromosome XII and the segment of chromosome VIII containing CUP1-1 and CUP1-2) appear to have undergone amplification in multiple independent populations. Both of these regions are known to exhibit copy-number variation across S. cerevisiae strains^42,43. Of the remaining regions, five contain Ty elements.

Genetic dissection and reconstructions

To probe their fitness effects, we reconstructed mutations from evolved strains in the mating type a ancestral genetic background, MATa, ura3Δ::NATMX, ade2-1, his3Δ::3xHA, leu2Δ::3xHA, trp1-1, CAN1. First, DNA fragments containing URA3 and HPHB were amplified from plasmid pJHK137 using primers containing 40 nucleotides of homology to sequence on each side of the target nucleotide (see Supplementary Data 2 for primer sequences). The mating type a ancestor was transformed with the resulting PCR product, resulting in Hygromycin resistant URA⁺ strains. These mutants were in turn transformed with an 80bp double stranded oligonucleotide centered on the mutant allele (see Supplementary Data 2). We plated on 5’FOA to select for the replacement of the URA3 genes with the mutant allele, and confirmed replacement by replica plating on YPD+Hygromycin. Correct genotypes were confirmed by Sanger sequencing.

We found one example of a mutation in MET2 which had a strong deleterious effect when introduced into the ancestral genetic background, despite fixing in a sexual population. We also found that this mutation had no significant effect in the sequencing fitness assay. To investigate whether epistasis could be responsible for these observations, we sought to measure the effect of this met2 mutation in the evolved background from the sexual population in which it fixed. In order to use our URA3-HPHB strategy, we first replaced the STE5pr::URA3 locus in the evolved clone with a NATMX marker, resulting in ura3Δ::NATMX (primers in Supplementary Data 2). We confirmed that this manipulation did not affect fitness. We then used this strain as the basis to reintroduce the wildtype MET2 allele. The resulting difference in fitness between the evolved sexual clone and reconstructed wildtype was used to calculate the fitness effect for the met2 allele shown in Figure 3c.

Sequencing-based fitness assay

In order to measure the fitness effects of mutations in evolved populations, we sampled a single evolved clone from generation 990 of each of the sequenced asexual populations and from generation 630 of each of the sequenced sexual populations. We backcrossed each of these clones with its corresponding ancestor. This resulted in diploids heterozygous for all mutant sites that were present in each original clone. We bulk sporulated each of these diploids to generate a large number of recombinant haploids with different combinations of wild type and mutant alleles. Each of these populations of haploids was then propagated in YPD liquid medium in the same conditions used during mitotic propagation in the evolution experiment. We sampled each population after 10, 30, 50 and 70 generations, prepared genomic DNA, and sequenced to measure the frequencies of each mutation over time. We estimated the fitness effect of each mutation (Figure 3; Supplementary Data 1) from the coverage depth supporting the mutant and ancestral alleles as a function of time (binomial regression with a logistic link function, coefficients and standard errors calculated using the glm function in R).

Extended Data

Extended Data Figure 1. Genetic system and experimental protocol for evolution of sexual populations.

Genotypes of the two haploid mating types are indicated at bottom, with selectable markers that are expressed in each strain indicated in color. Steps in our experimental protocols involving these markers are indicated in the corresponding color. STE5pr is a haploid-specific promoter and STE2pr and STE3pr are a and α-specific promoters respectively, so haploid a cells express URA3 and HIS3, while haploid α cells express URA3 and LEU2. The drug resistance markers KANMX and HPHB, tightly linked to the a and α mating locus respectively, are constitutively expressed. URA3 is counterselectable; it is not expressed in diploids, rendering them resistant to 5’ FOA.

Extended Data Figure 2. Adaptation to 17°C and sporulation conditions.

a, b, Relative fitness of evolved asexual (blue) and sexual (orange) populations over four days in 17°C (a) and sporulation conditions (b). Fitness changes are reported averaged over a complete experimental cycle (90 generations; mean of three replicate fitness assays, error bars ±s.e.m.). Mean fitness differences between asexual and sexual evolved strains are not significant in either the 17°C (two-sided t-test, P=0.5) or sporulation (two-sided t-test, P=0.8) treatment.

Extended Data Figure 3. Adaptation in mixed and non-mixed asexual populations.

Fitness increases after 990 generations of evolution in mixed (blue) and non-mixed (pink) alternative asexual control populations (mean of four replicate fitness measurements, error bars ±s.e.m.). Each non-mixed line was maintained independently. Subpopulations from mixed populations were mixed in pairs every 90 generations; each pair is indicated by a corresponding light and dark circle.

Extended Data Figure 4. Read-depth variation analysis of sequenced clones.

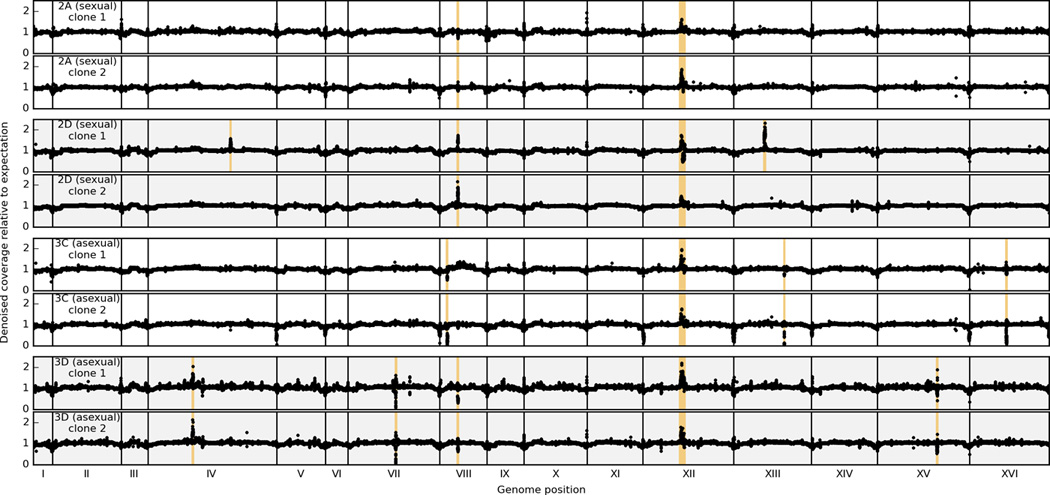
Denoised, normalized coverage in 100bp windows along the genome (Methods). Each panel represents a clone isolated from one of 4 independent populations. Pairs of clones from the same population are adjacent and indicated by the population label on the left. Regions containing putative amplifications and deletions (Extended Data Table 4) are highlighted in orange.

Extended Data Table 1. Leakage of diploids through the sexual cycle.

Fraction (×10⁴) of diploid leakage observed in each sexual population after sporulation, immediately prior to the 90 generation asexual cycle.

Generation
Population	0	90	180	270	390	450	540	630	720	810	990
2A	<0.1	<0.1	0.8	<0.1	0.7	<0.1	0.7	0.1	0.6	0.4	0.9
2B	<0.1	<0.1	0.9	0.2	0.2	<0.1	2.4	0.1	0.9	0.9	<0.1
2C	<0.1	<0.1	1.0	<0.1	<0.1	<0.1	2.0	0.1	0.2	0.2	<0.1
2D	<0.1	<0.1	4.0	0.4	<0.1	<0.1	1.7	0.3	0.1	0.5	<0.1
2E	<0.1	<0.1	2.0	<0.1	0.6	<0.1	2.1	0.5	0.4	05.	<0.1
2F	<0.1	<0.1	3.0	0.1	0.8	<0.1	0.8	0.1	0.1	0.1	<0.1
5A	<0.1	6.0	<0.1	0.1	<0.1	<0.1	<0.1	<0.1	0.2	<0.1	0.5
5B	<0.1	3.0	<0.1	0.6	<0.1	<0.1	1.1	<0.1	<0.1	<0.1	1.1
5C	<0.1	4.5	<0.1	0.5	<0.1	<0.1	0.6	<0.1	<0.1	<0.1	0.8
5D	<0.1	<0.1	<0.1	1.7	<0.1	<0.1	0.4	<0.1	0.4	<0.1	0.3
5E	<0.1	6.0	<0.1	0.4	<0.1	<0.1	0.2	<0.1	<0.1	0.1	0.4
5F	<0.1	4.5	<0.1	0.1	<0.1	<0.1	0.1	<0.1	<0.1	<0.1	0.1

Extended Data Table 2. Mutation frequency in YPD, sporulation and 17°C treatments.

Colony counts of 5’FOA resistant mutants are listed for each treatment. The number of mutations per culture (m) was calculated from the colony counts shown using the Ma-Sandri-Sarkar maximum likelihood method.

Culture	YPD	YPD+Spo	YPD+17°C
1	1	9	0
2	3	0	18
3	11	1	10
4	7	5	12
5	0	0	34
6	9	15	15
7	9	10	2
8	2	2	1
9	6	2	9
10	3	8	23
11	10	1	0
12	1	4	6
13	2	11	6
14	4	12	1
15	1	9	2
16	9	12	12
17	14	21	1
18	3	2	9
m	3.2	3.2	3.3

Extended Data Table 3. Classification of observed mutations.

The total number of mutations observed and fixed in the four sequenced asexual populations and four sequenced sexual populations. We classified mutations as fixed if they attain a frequency greater than 0.8 at the final sequenced timepoint. The percentage of mutations that were fixed in a given class is shown in parentheses next to the number of fixed mutations.

		All	Nonsyn	Syn	Intergenic
Asexual	All	183	111	27	45
	Fixed	143 (78%)	88 (79%)	20 (74%)	35 (78%)
Sexual	All	167	58	22	47
	Fixed	27 (16%)	22 (22%)	0 (0%)	5 (11%)

Extended Data Table 4. Larger-scale mutations.

Summary of mutations identified by read depth variation analysis of sequenced clones. We report the approximate start and end position of each mutation along with the specific functional elements affected by each event.

Chromosome	Start(kb)	End (kb)	Clones	Annotation
ChrIV	525	545	3D-1, 3D-2	ENA5, ENA2, ENA1
ChrIV	975	990	2D-1	Ty
ChrVII	560	575	3D-1, 3D-2	Ty
ChrVIII	80	95	3C-1, 3C-2	Ty
ChrVIII	205	220	2A-1, 2A-2, 2D-1, 2D-2, 3D-1, 3D-2	CUP-1, CUP-2
ChrXII	435	500	2A-1, 2A-2, 2D-1, 2D-2, 3C-1, 3C-2, 3D-1, 3D-2	rDNA
ChrXIII	355	375	2D-1	NUP116, CSM3, ERB1
ChrXIII	595	605	3C-1, 3C-2	ALD3, ALD2
ChrXV	700	715	3D-1, 3D-2	Ty
ChrXVI	430	445	3C-1, 3C-2	Ty