Echolocating bats use future-target information for optimal foraging

Significance

This study shows how an animal dynamically and rationally controls its sensing and navigates to capture multiple prey items. To perform this study, we extracted sonar attention and flight attention of foraging wild bats from both empirical data and mathematical modeling. We show that the bats directed their sonar and flight attention toward not only an immediate prey but also the next prey. In addition, numerical simulation shows a possibility that the bats select suitable flight paths for the consecutive capture. Hence, wild echolocating bats plan their flight paths by distributing their attention among multiple prey items, which means that the bats do not forage in a hit-or-miss fashion but rather spatially anticipate their future targets for optimum routing.

Abstract

When seeing or listening to an object, we aim our attention toward it. While capturing prey, many animal species focus their visual or acoustic attention toward the prey. However, for multiple prey items, the direction and timing of attention for effective foraging remain unknown. In this study, we adopted both experimental and mathematical methodology with microphone-array measurements and mathematical modeling analysis to quantify the attention of echolocating bats that were repeatedly capturing airborne insects in the field. Here we show that bats select rational flight paths to consecutively capture multiple prey items. Microphone-array measurements showed that bats direct their sonar attention not only to the immediate prey but also to the next prey. In addition, we found that a bat’s attention in terms of its flight also aims toward the next prey even when approaching the immediate prey. Numerical simulations revealed a possibility that bats shift their flight attention to control suitable flight paths for consecutive capture. When a bat only aims its flight attention toward its immediate prey, it rarely succeeds in capturing the next prey. These findings indicate that bats gain increased benefit by distributing their attention among multiple targets and planning the future flight path based on additional information of the next prey. These experimental and mathematical studies allowed us to observe the process of decision making by bats during their natural flight dynamics.

Selectively focusing attention on a particular target allows us to effectively extract information (1–4). Animals spatially focus their attention toward prey for suitable foraging (5, 6). During prey pursuit, most animals direct their visual attention toward it [e.g., tiger beetle (7), dragonfly (8), and falcon (9)]. Specifically, for example, dragonflies maintain a prey item at a constant retinal position during approaching it so that they steer an interception flight path (interception strategy) (10). However, for multiple prey items, the direction and timing of attention for effective foraging remain unknown.

Echolocating bats actively emit sonar signals to obtain surrounding information and adaptively change the characteristics of the emissions depending on the situation (11). Therefore, their attention in terms of the sonar (sonar attention) is characterized as the direction to which bats emit their sonar beams (12–14). When echolocating bats approach an airborne insect, the sonar attention directs toward the prey (12, 13). During natural foraging, the sonar attention of bats alternately shifts from their flying direction to the side (15). Additionally the wild bats are capable of capturing two prey items within the short interval of 1 s (16).

We predicted that bats localize multiple prey items by distributing their attention between them and then select an efficient flight path to successively capture the multiple prey. To test this prediction, we developed a mathematical model describing the 3D flight behavior of the Japanese house bat (Pipistrellus abramus) during its foraging of two prey items and then estimated the parameters of the model based on experimental data obtained using microphone-array measurements. Consequently, we quantified the attention in terms of flight (flight attention) of the bats and assessed the rationality of their flight paths based on numerical simulations.

Results

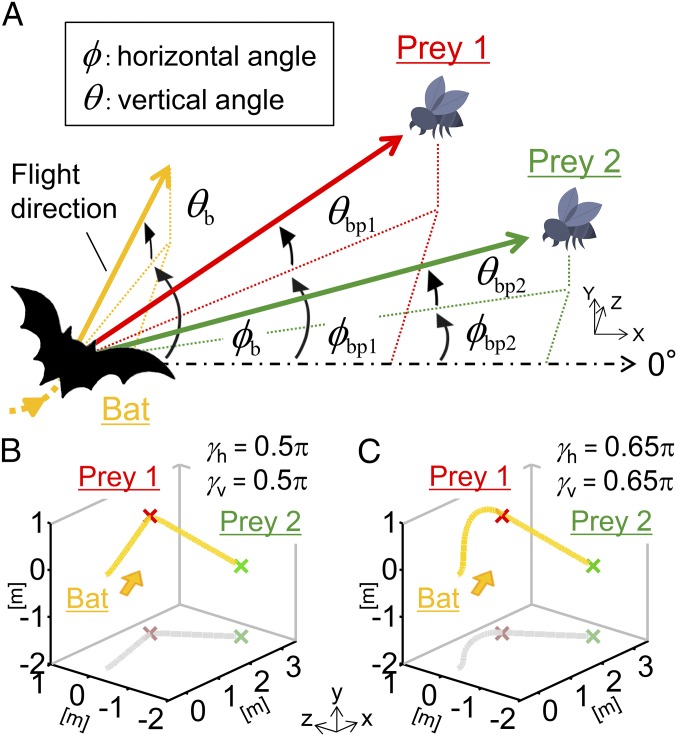
We assume that the bats adjust their flight direction between the two prey items (17) in the horizontal and vertical planes (Fig. 1A). Then, we define the bats’ attention to each prey in terms of their flight (flight attention) as attention parameters α for the immediate prey (prey 1) and β for the next prey (prey 2) in the mathematical model (Materials and Methods). Using this mathematical model, temporal changes in the bats’ attention toward prey items could be extracted based on their flight paths. In addition, to examine the ratio of the flight attention between the two prey items, the arctangent of parameters α and β is defined by γ: namely, γ_h and γ_v represent the arctangents in the horizontal and vertical planes, respectively. For example, when γ_h and γ_v are 0.5π, the bat exhibits a straight-ahead approach to an immediate prey (Fig. 1B) because the attention parameter α (α_h in the horizontal plane and α_v in the vertical plane) is equal to 1, and attention parameter β for the next prey (β_h and β_v) is equal to 0. When γ_h and γ_v are not equal to 0.5π, the approaching path can be considered to be affected by the position of the next prey (Fig. 1C). If the flight attention α (or β) is positive, the bat turns toward prey 1 (or prey 2). If the flight attention α (or β) is negative, the bat turns away from prey 1 (or prey 2).

Fig. 1.

Model of bat’s flight dynamics. (A) Schematic diagram to mathematically model the flight dynamics of a bat approaching two prey items in 3D space. Horizontal and vertical angles are represented by ϕ and θ, respectively. The flight direction of the bat (ϕ_b and θ_b, the yellow arrow) is assumed to be adjusted in the directions leading from the bat to prey 1 (ϕ_bp1 and θ_bp1, the red arrow) and to prey 2 (ϕ_bp2 and θ_bp2, the green arrow). (B and C) Examples of numerical simulations of our mathematical model. When γ_h and γ_v are equal to 0.5π (α_h = α_v = 1, β_h = β_v = 0), the bat exhibits a straight-ahead approach to prey 1 (B). When γ_h and γ_v are 0.65π, the bat takes a circuitous flight path to approach prey 1 and then prey 2 (C). After capturing prey 1, it is assumed that the bat approaches prey 2 in a linear manner (α_h = α_v = 0, β_h = β_v = 1).

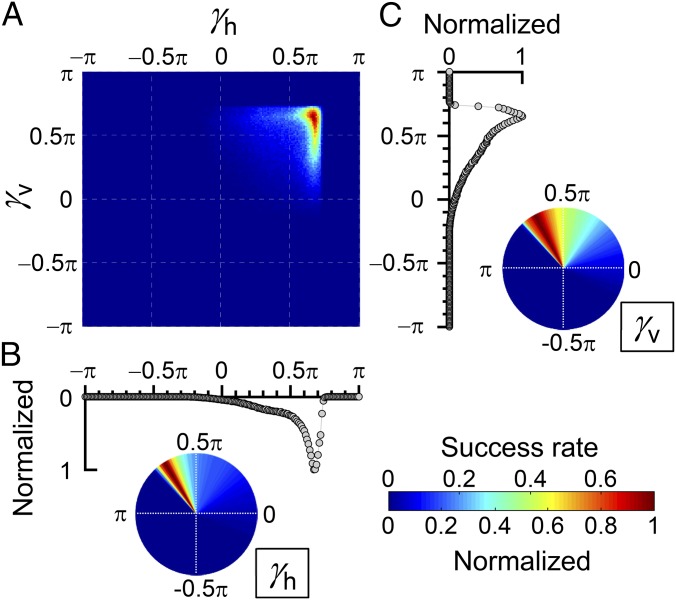
To examine the set of parameters γ_h and γ_v showing an optimal flight path to successively capture both prey items, we conducted numerical simulations (Materials and Methods). The results of the simulations showed that the model bat could catch both prey items with high probability when both γ_h and γ_v narrowly ranged within the second quadrant (0.5π < γ_h < π, 0.5π < γ_v < π) rather than just equaling 0.5π (Fig. 2). The optimal value of the high probability to successively capture was obtained when both γ_h and γ_v ranged from 0.6π to 0.8π. This result indicated that selection of a flight path that is influenced by the positions not only of prey 1 but also of prey 2 increases the likelihood of successively capturing the two prey items. The γ within the second quadrant shows that the flight attention to prey 1 (α) is positive but that to prey 2 (β) is negative.

Fig. 2.

Results of the numerical simulation. (A) The rate of success in consecutively coming close to two targets (i.e., within 10 cm, corresponding to the wing length of the bat) without losing sight of the immediate target (prey 1 and 2 before capturing prey 1 and 2, respectively) as a function of γ_h and γ_v where δ_h and δ_v are both fixed at 0.01. A total of 500 trials were simulated for each parameter set with the 0.01π step. (B and C) Normalized histograms (rectangular and polar coordinates) of (B) γ_h and (C) γ_v for the calculation result (A). Each point on the rectangular histograms was calculated by averaging the success rates and then normalized. The success rate is highest when both γ_h and γ_v exist within the second quadrant.

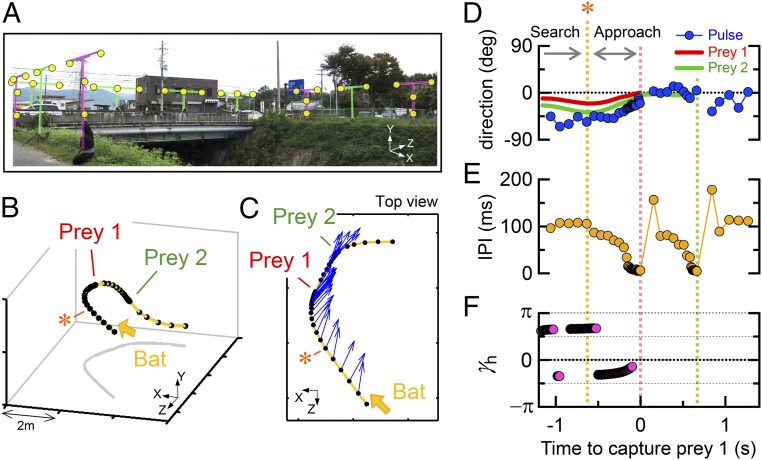
Field measurements were conducted to examine the attention of the bats. We observed 797 prey attacks on 6 recording days. To accurately reconstruct the flight paths of the bats, we selected 70 prey attacks in 35 flight paths (20 short-interval and 15 long-interval consecutive captures) for analysis in this study (Materials and Methods and Table S1). By analyzing sound data obtained using the microphone array system, 3D flight paths and the direction to which bats emit sonar beams could be reconstructed (Fig. 3 A–C and Materials and Methods). When the bats consecutively captured two prey items within short time intervals, sonar attention directed not only toward the immediate prey but also to the next prey before capturing the immediate one (15) (Fig. 3C). During approach to the immediate prey, the bats directed their pulses toward the next prey (Fig. 3D), and immediately after the capture of prey 1, they started to approach the next prey, i.e., to decrease interpulse intervals (Materials and Methods and Fig. 3E). In their flight, we estimated the flight attention of bats using the proposed mathematical model. Because the bats changed their flight paths more actively in the horizontal plane than in the vertical plane, we focused on bat flight dynamics in the horizontal plane. As a result, when they approached the immediate prey, γ_h in Fig. 3F shifted between two regions: namely the region between 0.5π and π (corresponding to the second quadrant in Fig. 2; the flight attention to prey 1 and that to prey 2 are positive and negative, respectively) and the region between −0.5π and 0 (corresponding to the fourth quadrant; the flight attention to prey 1 and that to prey 2 are negative and positive, respectively). This fact suggests that the bat shifted its attention to approach between the immediate prey and the next prey before capturing.

Table S1.

Summary of the bat flight data used in this study

Flight no.	Capture interval* (s)	Pause† after buzz 1 (ms)	Pause after buzz 2 (ms)	Approaching time‡ for prey 1 (s)	Date
Short-interval capture
1	0.58	109	122	0.60	28 October 2011
2	0.64	114	240	0.79	28 October 2011
3	0.66	111	220	0.54	28 October 2011
4	0.67	25	55	0.58	23 October 2010
5	0.67	154	169	0.63	28 October 2011
6	0.79	114	109	0.90	28 October 2011
7	0.81	120	32	0.93	28 October 2011
8	0.88	64	91	0.35	14 October 2013
9	0.89	109	217	0.78	28 October 2011
10	0.91	123	151	0.84	28 October 2011
11	0.91	151	119	0.70	28 October 2011
12	0.94	29	160	0.36	28 October 2011
13	1.02	94	179	0.83	14 October 2013
14	1.03	97	107	0.51	16 October 2014
15	1.06	47	204	0.32	14 October 2013
16	1.10	117	114	0.24	28 October 2011
17	1.10	107	111	0.59	14 October 2013
18	1.12	114	109	0.89	14 October 2013
19	1.19	36	122	0.59	13 October 2010
20	1.49	68	109	0.61	14 October 2013
Long-interval capture
1	3.28	85	108	0.57	23 October 2010
2	3.35	29	112	0.51	14 October 2013
3	3.93	258	84	0.63	23 October 2010
4	3.97	26	85	0.52	23 October 2010
5	4.50	89	31	0.93	23 October 2010
6	4.62	157	168	0.34	9 October 2012
7	5.19	31	89	0.85	13 October 2010
8	5.20	32	120	0.36	28 October 2011
9	5.25	108	223	0.33	23 October 2010
10	5.36	112	107	0.42	14 October 2013
11	5.84	223	180	0.39	23 October 2010
12	6.03	91	68	0.31	14 October 2013
13	6.69	83	89	1.04	23 October 2010
14	8.71	109	70	0.76	14 October 2013
15	9.90	185	102	0.36	23 October 2010

^*The interval between two consecutive captures.

^†The pause duration just after the feeding buzz.

^‡The time period of the approach phase (Materials and Methods).

Fig. 3.

Acoustical measurements in the field. (A) Microphone-array system with 10 units [4 Y-shaped (magenta) and 6 T-shaped arrangements (green)], which together hold 32 microphones (yellow circles). (B) Typical example of a 3D flight path of a bat during consecutive attack of two prey items. Black dots on the flight path (the yellow curve) show the positions where the bat emits sonar sounds. (C) Top view of the flight path and the directions of the bat’s sonar attention (blue arrows). The yellow arrow indicates the flight direction of the bat. (D–F) Changes in the direction of sonar attention (blue markers) relative to the flight direction (D), the interpulse interval (IPI; E), and the ratio of flight attention γ_h estimated from the flight path (F) as a function of time to capture prey 1. The red and green lines in D show the directions from the bat toward prey 1 and 2, respectively. Orange asterisks in each panel indicate the point when the bat started to approach prey 1.

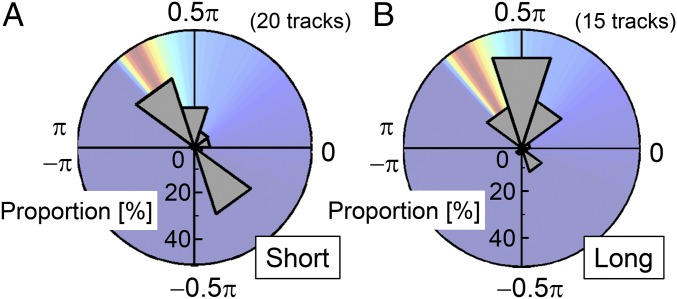
This attention shift between the two prey items was common among successive captures with short time intervals (defined as less than 1.5 s). Therefore, the distribution of γ_h during short-interval successive captures showed bimodal peaks in parts of the second (0.6–0.8π) and fourth quadrants (−0.4 to −0.2π; 20 flight tracks; Fig. 4A). On the other hand, in the case of capture with long time intervals (defined as over 3 s), γ_h was distributed around 0.5π (0.4–0.6π; 15 flight tracks; Fig. 4B), indicating that the bats approached the immediate prey without paying attention to the next prey. This result also means that during long-interval successive captures, bats did not use information about the next prey to determine their path of approach for the immediate prey. As a result, the distribution of γ_h significantly differed between the short and long intervals of the two captures [the Mardia-Watson-Wheeler test, P < 0.005; n = 1,161 (short) and 820 (long)]. Taking these points into account, we conclude that the bats control their flight paths during short-interval successive capture using current information about near future prey items before capturing an immediate prey.

Fig. 4.

Results of parameter estimation. (A and B) Circular histograms of the γ_h distribution during two consecutive captures with short (A) and long (B) time intervals. Data were taken from 20 (A) and 15 (B) reconstructed flight tracks of bats when approaching prey 1. The points to calculate the distributions were 1,161 (A) and 820 (B), respectively. The calculated success rate distribution, which is shown in Fig. 2B, is displayed behind the histogram.

Discussion

The mathematical model demonstrates that bats produce flight patterns by using future prey information based on their flight dynamics, as well as their sonar dynamics; i.e., they are capable of localizing multiple prey items. In addition, one of the two obvious peaks of the estimated γ_h distribution during the short interval successive capture was 0.6–0.8π, corresponding to the optimal value of the probability to successively capture two prey items based on numerical simulations. This result demonstrates that the bats select their flight paths to effectively capture multiple prey items. Such parameter sets suggest that bats take a path in the direction of the next prey just before capturing the immediate prey, so that they can acoustically view both prey items (Fig. 1C). In other words, bats might select their flight paths to keep both prey items within their sonar beam. Our numerical simulations using a fixed parameter set throughout the flight demonstrated that bats cannot successfully capture prey 1 when the flight attention toward prey 2 is positive and that toward prey 1 is negative (i.e., γ_h, and γ_v existed in the fourth quadrant; Fig. 2). On the other hand, bats in the wild varied dynamically their parameter set (flight attention) from moment to moment as they approached multiple prey items (Figs. 3F and 4A). This result implies that the bats actually use a more complex behavioral strategy that has not been assumed by the current mathematical model. Temporal change in the parameters should be considered in a future model to investigate the flight dynamics of bats, as well as more dynamical sonar attention.

Aerial-feeding echolocating bats expend large amounts of energy during foraging efforts. For example, the foraging activity of Myotis lucifugus accounts for two-thirds of total energy expenditure in a day (18). During foraging flights, Macrotus californicus expends energy at a rate ∼14 times faster than its basal metabolic rate (19). To compensate for this high rate of energy expenditure, foraging bats must capture insects as efficiently as possible. The Japanese pipistrelle bat (Pipistrellus abramus) increased its body weight by up to ∼20% during nightly foraging (20). We previously reported that P. abramus are capable of capturing prey every 2–3 s (15, 21). In this study, we have shown that the bats select flight paths to efficiently capture consecutive prey items. Controlling flight paths using the information of the future prey item may allow aerial-feeding bats to rapidly capture many prey insects. This behavior should be an effective foraging technique used by aerial-feeding bats.

Previous studies have intensively examined spatial attention to a particular target (7–14). However, in fact, predators usually capture successive prey items (e.g., aerial-feeding bats) (21). For multiple targets, it is beneficial for bats in the wild to distribute their sonar attention and flight attention among multiple targets and to plan the future flight path based on the next prey for effective foraging. On the other hand, pipistrelle bats in the wild alternately and rapidly shift their sonar attention (15, 22). This fact suggests that bats process echo streams from multiple targets in a time-sharing manner and then select the optimal flight path to capture and hunt a lot of airborne insects. These findings and suggestions originated from the unique capabilities of bats to fly while actively emitting sonar signals. Our mathematical modeling revealed the process of decision making for tracking and capturing targets, and extracting those signals from natural flight dynamics.

Materials and Methods

Mathematical Modeling.

The framework to mathematically model the 3D flight behavior of the bats is shown in Fig. 1A. The model assumes two prey items, because the microphone-array measurement showed that bats sometimes capture two prey items consecutively and rarely capture more than two insects within short time intervals. Bats changed their flight paths much more acrobatically in the horizontal plane than in the vertical plane during natural foraging (15, 16). Thus, we separately model flight dynamics in the horizontal and vertical planes as follows:

$$\frac{d{\phi }_{\mathrm{b}}\left(t\right)}{dt}=\frac{1}{{\delta }_{\mathrm{h}}}\left\{{\alpha }_{\mathrm{h}}\sin \left[{\phi }_{\mathrm{bp1}}\left(t\right)-{\phi }_{\text{b}}\left(t\right)\right]+{\beta }_{\text{h}}\sin \left[{\phi }_{\text{bp}2}\left(t\right)-{\phi }_{\text{b}}\left(t\right)\right]\right\},$$ [1]

$$\frac{d{\theta }_{\text{b}}\left(t\right)}{dt}=\frac{1}{{\delta }_{\text{v}}}\left\{{\alpha }_{\text{v}}\sin \left[{\theta }_{\text{bp}1}\left(t\right)-{\theta }_{\text{b}}\left(t\right)\right]+{\beta }_{\text{v}}\sin \left[{\theta }_{\text{bp}2}\left(t\right)-{\theta }_{\text{b}}\left(t\right)\right]\right\},$$ [2]

where δ_h and δ_v represent positive weighting factors [i.e., the rapidity of bat motion control on ϕ_b(t) and θ_b(t), respectively], and α (namely, α_h or α_v) is the minimization of the angular difference between the bat’s own flight direction [ϕ_b(t), θ_b(t)] and the direction to prey 1 [ϕ_bp1(t), θ_bp1(t)] (similar for β to prey 2) (17). Therefore, we define α and β as bat’s flight attention to prey 1 (α_h, α_v) and 2 (β_h, β_v), respectively. In this model, the bat controls its flight path from moment to moment depending on current information about the location of each of the two targets. The sinusoidal function allows the bat to turn to the directions of prey 1 and 2, regardless of its position (when α_h, β_h, α_v, and β_v are all positive; namely, positive flight attention) (17). For example, when an insect is located on the left side of a bat in the horizontal plane, the bat approaches the insect by turning in a counter clockwise direction. To analyze the ratio of the flight attention between prey 1 and 2, we constrain these parameters as follows:

$${\alpha }_{\text{h}}^2+{\beta }_{\text{h}}^2=1,$$ [3]

$${\alpha }_{\text{v}}^2+{\beta }_{\text{v}}^2=1.$$ [4]

Parameters α_h and β_h (α_v and β_v) are described as α_h = sinγ_h and β_h = cosγ_h (α_v = sinγ_v and β_v = cosγ_v), and γ_h (or γ_v) represents the ratio of attention to prey 1 and 2, α_h and β_h (or α_v and β_v). By squaring attention parameters α and β in the constraint equations, the ratio of attention to the two targets with either positive or negative values can be shown by a single parameter (γ) on the unit circle. This constraint allows us to intuitively and easily understand the bat’s flight attention toward both prey items. Positive and negative attention parameters allow us to determine whether bats intend to turn toward or away from a prey item, respectively. For example, when α_h and α_v are both positive, the bat turns in the direction of prey 1 in the horizontal and vertical planes but the distance from the bat to prey 1 does not always decrease. Therefore, these attention parameters are not directly correlated with the distance between the bat and prey.

Numerical Simulation.

We examined which parameter set had a high probability of consecutively capturing two prey items. The sonar beam of the bat was modeled as a circular piston oscillating in an infinite baffle (23, 24) (Fig. S1). A parameter set was defined as a success when the bat closed to capture prey 1 and then prey 2 in sequence. The distance at which the bat was considered to capture prey was within 10 cm from the bat, which corresponds to the wing length of P. abramus (25), without losing the location of the immediate target (inside the bat’s sonar beam). A simulation trial was considered a failure when prey 1 located outside the sonar beam before capture, or when prey 2 located outside the sonar beam after the capture of prey 1. Just after the capture of prey 1, it was assumed that the bat aimed its flight attention only to prey 2 (α = 0, β = 1). When the bat captured prey in reverse order (prey 2 and then prey 1), the trial was not considered a success, because we defined the prey captured first by the real bat as prey 1.

Fig. S1.

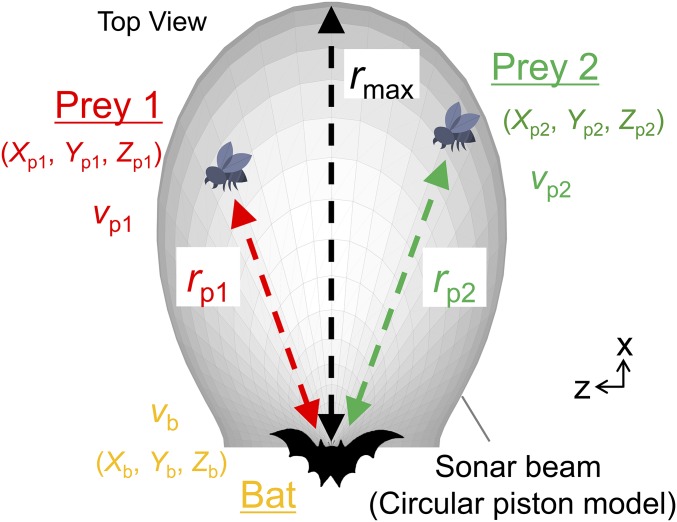
Schematic diagram of the condition for numerical simulations. The initial positions of prey 1 and 2 are randomly distributed inside the sonar beam (the gray portion) modeled as a circular piston oscillating in an infinite baffle. Flight speeds of the bat (v_b) and prey (v_p1, v_p2) are assumed to be 5 and 0 m/s, respectively. When the distances from the bat to prey 1 (r_p1, the red arrow) and to prey 2 (r_p2, the green arrow) become less than 10 cm in sequence, the simulation trial is deemed successful (see Materials and Methods for details).

A total of 500 trials were performed for each parameter set of γ_h and γ_v, ranging from −π to π, respectively with the 0.01π step, and 201 × 201 pairs. For all of the numerical simulations, parameters δ_h and δ_v were both fixed at 0.01, determined from the parameter estimations using experimental data (see below). Each trial was calculated using the fourth-order Runge-Kutta method. The initial position and flight direction of the bat (X_b, Y_b, Z_b) were (0, 0, 0) and the x axis direction, respectively (Fig. S1). The sonar beam was assumed to be directed toward the flight direction of the bat for simplicity. The maximum search range (r_max) was 5 m (16). Initial positions of prey 1 (X_p1, Y_p1, Z_p1) and prey 2 (X_p2, Y_p2, Z_p2) were randomly determined in every trial by the echolocation distances (r_p1 and r_p2) ranging from 1.2 to 5.0 m because bats seem not to listen to their own echoes during their own emissions (i.e., they adjust their pulse duration to avoid overlap between outgoing vocalization and returning echoes) (26, 27). The pulse duration of P. abramus during natural foraging is 7 ms on average (16), which corresponds to a traveling distance of 1.2 m. The −6-dB beam width of the terminal frequency portion of the downward sweep emitted by Japanese house bats was approximately ±50° at 40 kHz (15). Therefore, to set the −6-dB beam width around ±50°, the diameter of the circular piston was defined as 8 mm. The flight speed of the model bat (v_b) was 5 m/s based on the experimental data. Because the target prey items of bats are mainly small hemipterans and dipterans (28), bat flight speed is considered much faster than those of insects. Therefore, we assumed that the flight speed of targets (v_p1 and v_p2) was 0 m/s for simplicity.

Field Measurements.

We recorded flight data for 6 d, namely during a 1-h period before and after sunset on 13 and 23 October 2010, 28 October 2011, 9 October 2012, 14 October 2013, and 16 October 2014 (total, 282 min). For all of the recording days, ∼130 bats appeared at the study site (average 20–30 bats/d). The recording sound data included 797 prey attacks (i.e., the feeding buzzes). To accurately reconstruct the bat flight paths and identify the capture points, we selected prey-capture flights for which the amplitude of sonar sounds was sufficiently high, even at the end of the terminal buzz. Furthermore, we analyzed bats’ continuous flight paths that could be reconstructed without any deficit in the data for consecutive capture flights. As a result, 70 prey attacks (35 truncated 3D flight paths: 20 short-interval and 15 long-interval consecutive captures) were selected for analysis in this study, and the detailed information on the analyzed recording data were shown in Table S1 (note that Table S1 provides the number of flight paths rather than the number of bats because we were unable to exactly identify individual bats across multiple measured flight paths).

The 3D flight path and pulse direction of echolocating Pipistrellus abramus (Vespertilionidae, ∼15 cm wingspan, 5–8 g body mass) (16, 25) in the wild were reconstructed using differences in arrival time and sound pressure between the microphones (Fig. 3A). The theoretical range error of the microphone array system was less than 20 cm, which is almost identical to the wing length of the bats, in the tracking area 24 m long (the x axis) and 22 m wide (the z axis) (15). We confirmed through acoustic calibration tests that the actual maximum range error was less than 10 cm for sound sources within 5 m of the Y-shaped array unit (magenta bars in Fig. 3A). Therefore, the accuracy is sufficient to measure the flight paths of bats. We approximated the position of pulse emissions by bats using the polynomial function [i.e., polynomial approximation for each time series coordinate datum (X, Y, Z) of the calculated sound source]. The flight speed of P. abramus during natural foraging was 9 m/s at a maximum (average, 5 m/s), which is roughly 10 times greater than that of a prey species of the bats (29). At the study site, we also visually observed that dipteran midges took several seconds to fly across an area of a few tens of centimeters.

P. abramus during natural foraging emits long (9–11 ms) shallow-sweeping frequency-modulated (FM) sounds, with energy concentrated in the terminal sweep frequency of the fundamental component around 40 kHz (15, 25). The bat decreases the pulse duration and interpulse interval (IPI) while approaching target prey (16, 30) and slightly extends the constant-frequency (CF) portion of the pulse just before approaching a prey item (16). When the bat successfully captures an insect, it completes the interception with an easily recognized brief burst of sounds emitted at a high rate of about 150 Hz (the “feeding buzz”), followed by a silent interval (the “postbuzz pause”) (31). In this study, the minimum and maximum durations of the postbuzz pause were 25 and 258 ms, respectively (n = 70; Table S1). When the postbuzz pause duration was short, the bats were thought to have failed to capture prey (31). However, it is difficult to strictly conclude whether bats successfully captured prey based only on information about the postbuzz pause because (i) it is technically difficult to observe whether a bat successfully captured one of the small midges at the study site, and (ii) it is reported that the postbuzz pause duration during natural foraging (Myotis daubentonii) does not differ significantly between successful and failed cases of prey capture (31). Furthermore, we confirmed that the distances between the first and second capture positions were too far for the prey (small midges) to move during the observed intercapture intervals. Therefore, even if the bats fail to capture prey, it is highly unlikely that they attacked the same prey item again by the second capture trial just after the unsuccessful first capture. Based on our field measurements using the microphone array system, bats emit the feeding buzz at a distance of a few tens of centimeters (∼30 cm) from prey. Therefore, we assumed that the bats attempted to capture prey and approached within a few tens of centimeters from the prey when the feeding buzz was observed. Therefore, we defined the bat’s 3D position at the end of the feeding buzz as the location of the “capture” (Fig. 3). We defined the direction from the bat to the capturing position as the prey direction (Fig. 3D). We also defined the approach phase as the interval between the extension of CF duration and capture (15, 16). Intervals between two successive captures within 1.5 s and over 3 s were defined as short-interval and long-interval successive captures, respectively. Short-interval captures comprised approximately one-quarter to one-half of successful captures, depending on the day of measurement.

Parameter Estimation.

Our model includes four parameters δ_h, δ_v, γ_h, and γ_v, as shown in Eqs. 1–4. We estimated these parameters using the least-squares method with 3D flight paths that we previously measured, based on the method reported in Aihara et al. (17). The microphone array can determine the positions where bats emit ultrasonic pulses. To precisely analyze changes in the flight attention of bats approaching prey, we interpolated and smoothed each bat’s flight path before the parameter estimation. Using smoothing spline interpolation, the sampling period of the bat’s flight path was decreased from ∼100 (IPI during the search phase) to 8 ms (125 point/s). The time period used in the least-squares analysis to calculate δ_h, δ_v, γ_h, and γ_v for each instant of time was 160 ms (20 points). When the correlation coefficient of the linear regression for the estimation was low (r < 0.4), the estimated parameters were not used. We calculated the distributions of the model parameters using data from the approach phase. We used the position of prey items as the capture point during the approach phase.

The results of vertical parameter estimation for γ_v are shown in Fig. S2. The γ_v during long-interval successive captures mostly appeared within the second quadrant, suggesting that the bats chose flight paths that were affected by the next prey in the vertical plane. This result is because Japanese house bats in the wild usually approach prey with a descending flight pattern in the final stage (16). Thus, the bats often appear to turn away from the next prey in the vertical plane, resulting in apparent negative flight attention to the next prey. Therefore, in this study, results of the γ_v estimation cannot be compared between short and long intervals of two successive captures.

Fig. S2.

Results of parameter estimations for the flight attention in the vertical plane. (A and B) Circular histograms of the γ_v distribution during two consecutive captures at short (A) and long (B) time intervals. Data were taken from 20 (A) and 15 (B) reconstructed flight tracks of bats when approaching prey 1. The numbers of points to calculate the distributions were 1,251 (A) and 829 (B). The calculated success rate distribution shown in Fig. 2C is displayed faintly behind the histogram.

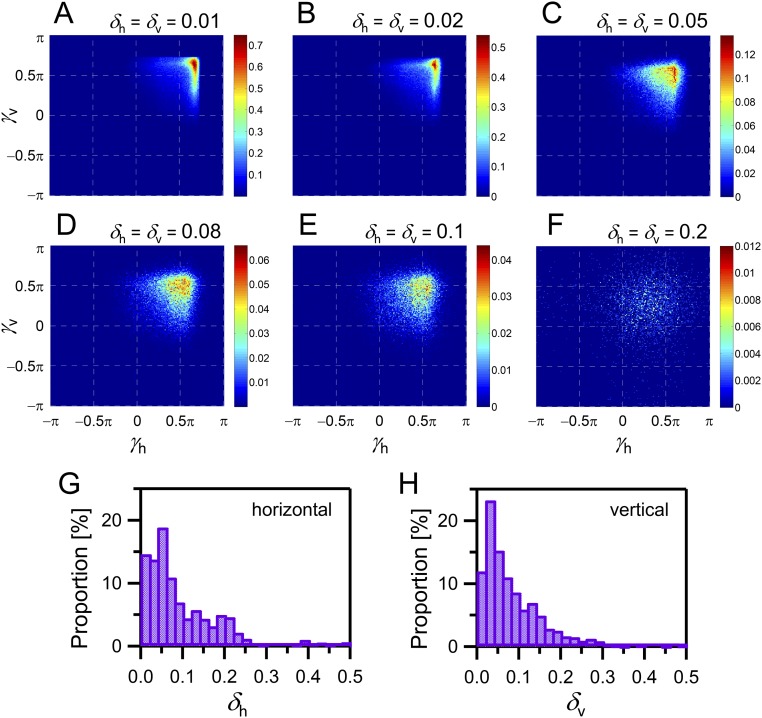
Numerical simulations of other δ_h and δ_v values and distributions of δ_h and δ_v during short-interval consecutive capture estimated using experimental data are shown in Fig. S3 A–F and G and H, respectively. When δ_h and δ_v are more than 0.1 (Fig. S3 E and F), the optimal value does not appear in the second quadrant, but just around 0.5π. However, estimated δ_h and δ_v are well distributed within less than 0.1 (Fig. S3 G and H). Therefore, for the estimated δ_h and δ_v, the optimal values of γ_h and γ_v appears within the second quadrant, i.e., a flight path with attention to the next prey is effective to catch two prey items.

Fig. S3.

Results of the numerical simulations for the other δ_h and δ_v. (A–F) Rates of successful capture of two successively close targets within 10 cm (corresponding to wing length of the bat) without losing sight of the immediate target as functions of γ_h and γ_v [δ_h and δ_v = 0.01 (A), 0.02 (B), 0.05 (C), 0.08 (D), 0.1 (E), and 0.2 (F)]. The color bar at the right of each distribution indicates the success rate of each result. A total of 500 trials were simulated for each parameter set with the 0.01π step. (G and H) Distributions of δ_h (G) and δ_v (H) during the approach phase estimated using experimental data. The numbers of points used to calculate the distributions were 1,161 (G) and 1,251 (H).