Significance
Fast-folding proteins provide a testing ground for theories and simulations of folding at the extreme limit, in particular when it occurs on the timescale of chain diffusion and potentially in the elusive barrier-free limit. Whereas most fast-folding studies probe the reaction near the transition point with limited resolution, we apply hydrogen exchange methods to a microsecond folder, characterizing its energy landscape with amino acid precision under highly stabilizing conditions where barrier-free folding is most probable. Despite folding with τ = 5 μs, we find that the molecule folds and unfolds in a cooperative process matching the properties observed at elevated denaturant concentration, implying that much faster folding rate constants are required to reach the downhill limit.
Keywords: protein folding, hydrogen exchange, cooperative folding, λ repressor, folding pathway
Abstract
The relationship between folding cooperativity and downhill, or barrier-free, folding of proteins under highly stabilizing conditions remains an unresolved topic, especially for proteins such as λ-repressor that fold on the microsecond timescale. Under aqueous conditions where downhill folding is most likely to occur, we measure the stability of multiple H bonds, using hydrogen exchange (HX) in a λYA variant that is suggested to be an incipient downhill folder having an extrapolated folding rate constant of 2 × 105 s−1 and a stability of 7.4 kcal·mol−1 at 298 K. At least one H bond on each of the three largest helices (α1, α3, and α4) breaks during a common unfolding event that reflects global denaturation. The use of HX enables us to both examine folding under highly stabilizing, native-like conditions and probe the pretransition state region for stable species without the need to initiate the folding reaction. The equivalence of the stability determined at zero and high denaturant indicates that any residual denatured state structure minimally affects the stability even under native conditions. Using our ψ analysis method along with mutational ϕ analysis, we find that the three aforementioned helices are all present in the folding transition state. Hence, the free energy surface has a sufficiently high barrier separating the denatured and native states that folding appears cooperative even under extremely stable and fast folding conditions.
The nature of the energy landscape when folding occurs on the microsecond timescale continues to be investigated using both experimental and computational approaches. The 80-residue subdomain of the λ-repressor transcription factor, λ6–85 (1–11), is an appealing system as it contains five α-helices arranged in a nonsymmetric pattern, folds in microseconds, and is nearly a downhill folder (12), a condition where a continuous series of folding events may be characterized. These characteristics along with a folding time that nears the upper limit for current all-atom simulations (13–19) make this protein appropriate for detailed comparisons between experiment and simulations.
The energy landscape of λ6–85 is significantly influenced by its sequence. Oas and coworkers found that the wild type and a faster-folding mutant with two helix-promoting substitutions (λAA with G46A/G48A, Fig. S1A) fold cooperatively (1–4). The transition state ensemble (TSE) characterized using ϕ analysis minimally contains α1 and α4 (3). Kinetic H/D isotope effect measurements in the Sosnick laboratory found that both λ6–85 and λAA fold cooperatively with ∼70% of the H bonds being formed in the TSE, matching the degree of surface buried in the TSE [beta Tanford value (βTanford)] (5).
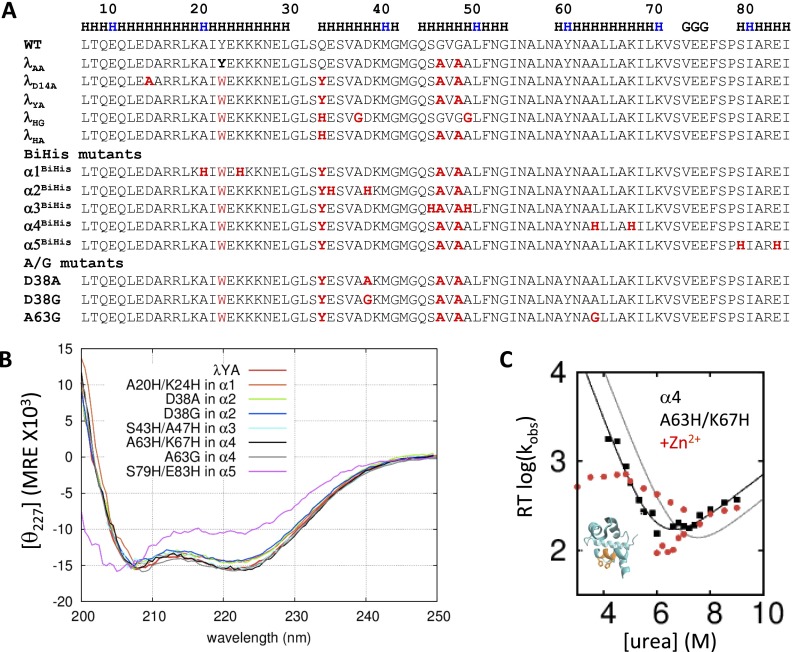
Fig. S1.
Folding properties of λ variants. (A) Sequences of λ-repressor variants. (B) CD spectra of variants. (C) Chevron plot for λYA with biHis site in α4, which did not produce readily interpretable data.
Using nanosecond T-jump and other methods, Gruebele and coworkers proposed that faster-folding and stabilized variants, such as λYA (λAA + Q33Y) and λD14A (λYA + D14A), fold in an incipient or fully downhill manner, especially under highly stable conditions at lower temperatures (6–9). Key signatures of downhill folding are the presence of kinetics that are on the same timescale as the chain dynamics, suggestive of a free energy barrier with near-zero activation energy, and a fast “molecular phase” reflecting the rapid redistribution of species near the top of the barrier after the T-jump that is more pronounced for the faster-folding variants (8). Additional signatures include probe-dependent kinetics (20) and aggregation tendencies (6). Lapidus and coworkers proposed that the λD14A variant folds in a downhill manner based on a combination of microfluidic mixing measurements and probe-dependent melting temperatures (10). Various computational methods, ranging from Gō models to all-atom simulations, have been applied to study the folding of λ6–85 and its variants, yielding mixed agreement with experiment and each other (13–19).
Here, a high-resolution characterization of the landscape and of the TSE of the λYA variant is obtained from a combination of equilibrium native state hydrogen exchange (NSHX) data, along with kinetic studies using both ψ analysis with bi-Histidine (biHis) metal ion binding sites and ϕ analysis at 298 K. The hydrogen exchange (HX) rates and their denaturant dependence provide information on individual H-bond stabilities and the structural fluctuations that lead to their breakage. Another advantage of HX is that measurements can be carried out without denaturant at room temperature, thereby enabling the characterization of folding behavior under highly stabilizing conditions where downhill folding is most likely to occur (7). Furthermore, HX has the ability to characterize stable pretransition state species, if they exist, as the surface is studied under equilibrium conditions.
We find that λYA folds in a manner typical of many proteins with a landscape that does not qualitatively change in destabilizing (urea) or stabilizing (sarcosine) conditions. The protein folds with considerable cooperativity, implying there is a sizable barrier between the native state ensemble (NSE) and the denatured state ensemble (DSE). Three helices (α1, α3, and α4) unfold in the same step, representing the major unfolding event. According to kinetic studies, these three helices are present in the TSE, whereas α2 and α5 fold later, consistent with the HX data. These results are compared with those of previous experimental and computational studies.
Results
Cooperative Folding Behavior.
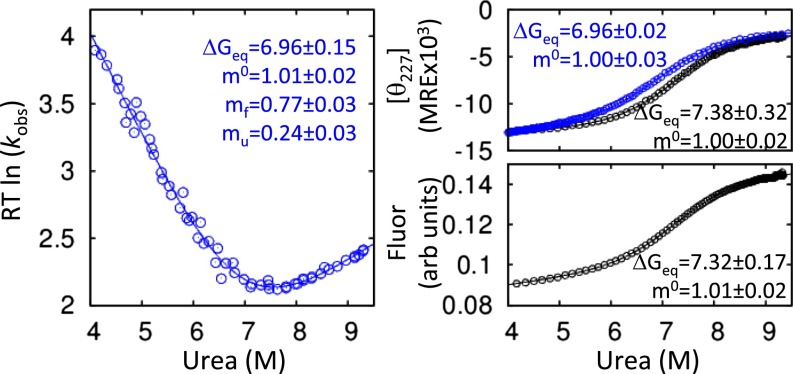
Denaturation with urea at 298 K, monitored with far-UV circular dichroism (CD), fits well to a two-state model having a linear denaturant dependence, ΔGeq = ΔG0eq – m0[urea] (Table S1). The measured values, ΔGeq = 6.96 ± 0.02 kcal·mol−1 and m0 = 1.00 ± 0.02 kcal·mol−1·M−1, closely match their counterparts derived from kinetic measurements using chevron analysis (21–23), ΔGeq = RT ln (kf/ku) = 6.96 ± 0.15 kcal·mol−1 and m0 = 1.01 ± 0.02 kcal·mol−1·M−1 (extrapolated kfwater ∼ 2 × 105 s−1 and βT = 0.76 ± 0.03, Fig. 1), where R is the gas constant, and T is the absolute temperature. The agreement between equilibrium and kinetic data indicates that all of the free energy and surface burial are accounted for in the observed kinetic phase. This finding is a generally accepted demonstration that folding is well approximated by a double-well energy surface with a single barrier and that no species with appreciable population exists before the millisecond observation window (21–23).
Table S1.
ΔG, m value from CD, chevron, fluorescence, and HX
| Experiment | Location | Buffer, H2O/D2O | ΔGfit, kcal·mol−1 | ΔGHX,0Mmeasure, kcal·mol−1 | m, kcal·mol−1·M−1 |
| Kinetic (chevron) | Global | 100/0 | 6.96 ± 0.15 | — | 1.01 ± 0.02 |
| CD | Global | 100/0 | 6.96 ± 0.02 | — | 1.00 ± 0.02 |
| CD | Global | 20/80 | 7.38 ± 0.32 | — | 1.00 ± 0.02 |
| Fluorescence | Global | 20/80 | 7.32 ± 0.17 | 1.01 ± 0.02 | |
| HX | R16 (α1) | 20/80 | 7.67 ± 0.08 | 7.12 ± 0.03 | 0.82 ± 0.04 |
| L18 (α1) | 7.74 ± 0.13 | 7.17 ± 0.08 | 0.98 ± 0.06 | ||
| A20 (α1) | 8.22 ± 0.12 | 7.34 ± 0.04 | 1.05 ± 0.13 | ||
| I21 (α1) | 7.44 ± 0.18 | 7.58 ± 0.01 | 1.04 ± 0.08 | ||
| N27 (α1) | 8.81 ± 0.14 | 9.00 ± 0.17 | 1.05 ± 0.08 | ||
| F51 (α3) | 7.43 ± 0.07 | 7.26 ± 0.06 | 0.99 ± 0.06 | ||
| N52 (α3) | 7.41 ± 0.06 | 7.26 ± 0.04 | 0.79 ± 0.07 | ||
| A62 (α4) | 7.64 ± 0.12 | 6.86 ± 0.02 | 0.90 ± 0.08 | ||
| L65 (α4) | 7.65 ± 0.20 | 7.79 ± 0.02 | 1.07 ± 0.10 | ||
| K67 (α4) | 7.93 ± 0.10 | 7.27 ± 0.03 | 1.02 ± 0.03 | ||
| I68 (α4) | 8.18 ± 0.23 | 7.44 ± 0.02 | 1.14 ± 0.10 | ||
| V71 (α4) | 7.27 ± 0.10 | 6.97 ± 0.02 | 0.97 ± 0.05 |
Fig. 1.
Folding behavior of λYA. Chevron plot of folding and unfolding rate constants using tryptophan fluorescence (Left) and chemical denaturation monitored using fluorescence and CD (Right), obtained in 100% H2O (blue) and 80% D2O (black, as used in HX measurements). Units for ΔG and m are kcal·mol−1 and kcal·mol−1·M−1, respectively.
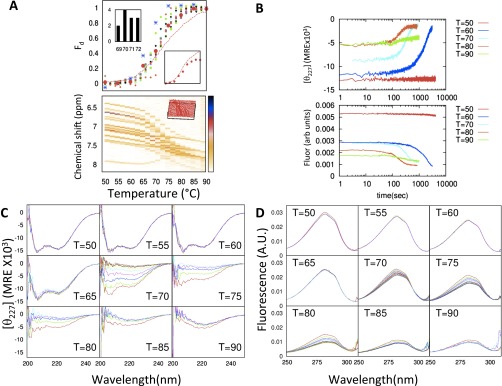
Thermal denaturation is more complicated, in part due to aggregation (SI Text and Fig. S2). Rapid CD and fluorescence measurements before aggregation suggest thermal denaturation is adequately described as proceeding through a single transition, consistent with Ma and Gruebele’s findings (20). Whereas two-state, barrier-limited folding behavior near the thermal or urea-induced melting transition is possible even for downhill folders (24), the major issue under investigation is whether the cooperativity persists even under highly stabilizing conditions, which we will determine using HX.
Fig. S2.
λYA aggregation at high temperature. (A, Upper) Population fraction of the denatured state during temperature melting measured by CD (red line is with aggregation and red circles are after removing aggregation effect) and fluorescence (blue), and 1D NMR chemical shifts of hydrogens in aromatic residues. Upper Left Inset shows distribution of Tm for 1D NMR data, and Lower Right Inset shows raw data for CD. (A, Lower) One-dimensional NMR chemical shifts of hydrogens in aromatic residues from T = 50 °C to T = 90 °C with 2 °C increment. (B) The CD and fluorescence data at T = 323–363 K show a decrease in signal, suggesting that λYA aggregates at high temperature. (C and D) Corresponding CD (C) and fluorescence (D) spectra at different times, separated by ∼1 min.
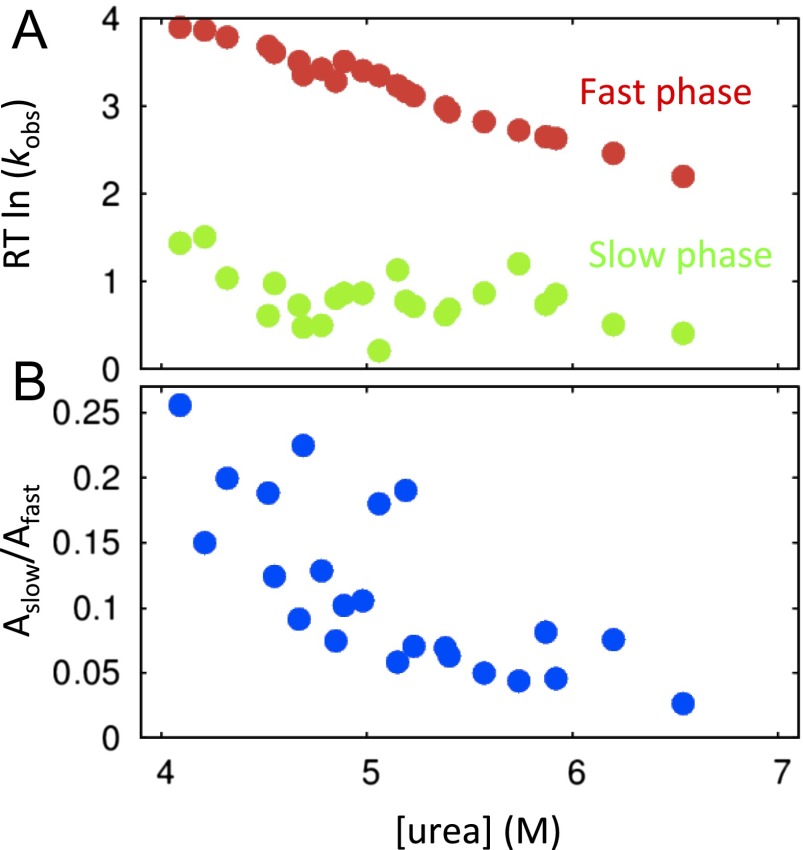
Whereas the major folding phase satisfies a two-state folding model, we do note that a minor (5–20%) slow refolding phase of ∼2–10 s−1 is observed for λYA, which persists beyond 6 M urea with little to no denaturant dependence (Fig. S3). This phase may be due to a subpopulation folding along a parallel pathway (25) that accumulates due to a misfolding event (26, 27), e.g., potentially the rearrangement of α2 or α5. Prigozhin and Gruebele (11) proposed the presence of a trapped intermediate containing nonnative β structure based on similar results and as observed in some simulations (18). Interestingly, this minor phase is not observed in the biHis and A/G variants used to characterize the TSE. Because we are interested in the major folding pathway (and the minor phase is absent in the various mutants), we focus on properties of the major phase.
Fig. S3.
(A) Rates and (B) amplitudes of the slow and fast folding phases of λYA.
HX Studies.
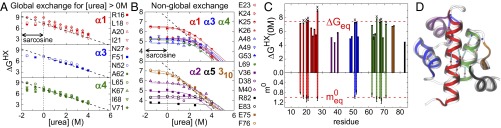
A detailed characterization of the folding landscape is obtained using NSHX/NMR measurements in 0–4 M urea and in 0.5 M and 1 M sarcosine, a stabilizing osmolyte (ΔΔG1M sarcCD = 1.5 kcal·mol−1, Tables S1 and S2). The analysis of HX data assumes that amide protons (NH) exist in states that are either exchange competent (open) or incompetent (closed) (28). The observed HX rate (kex) depends on the rates of opening (kop) and closing (kcl) and the intrinsic exchange from the open state (kchem) according to . Values for kchem are calculated from peptide studies (29). Often kcl >> kchem (including our experiments where kfold = kcl > 5kchem), and kex reduces to the “EX2” limit; i.e., , where Kop = kop/kcl is the equilibrium constant, and the free energy of exchange, ΔGHX = RT ln Kop.
Table S2.
ΔGHX at different urea and sarcosine concentrations
| Sarcosine | Urea | ||||||||||
| Site | 1 M | 0.5 M | 0 M | 0.5 M | 1 M | 1.5 M | 2.0 M | 2.5 M | 3.0 M | 3.5 M | 4.0 M |
| Global exchanging protons | |||||||||||
| R16 (α1) | 7.16(6) | 7.03(5) | 7.12(3) | 6.83(3) | 6.56(4) | 6.18(2) | 5.93(2) | 5.56(1) | 5.30(3) | 4.79(7) | 4.29(2) |
| L18 (α1) | 7.50(4) | 7.30(5) | 7.17(8) | 6.75(4) | 6.96(10) | 6.03(2) | 5.74(3) | 5.22(2) | 4.78(2) | 4.39(5) | 3.77(3) |
| A20 (α1) | 7.34(4) | 7.29(5) | 7.02(3) | 6.38(1) | 5.69(3) | 5.04(2) | |||||
| I21 (α1) | 8.32(2) | 7.58(1) | 6.01(1) | 5.94(1) | 5.10(3) | 5.13(3) | 4.42(2) | 3.79(6) | 3.25(2) | ||
| N27 (α1) | 9.02(7) | 9.04(9) | 9.00(17) | 7.91(8) | 7.76(2) | 7.04(10) | 6.51(8) | 6.35(11) | 5.68(9) | 5.40(5) | 4.47(2) |
| F51 (α3) | 7.48(3) | 7.05(4) | 7.26(6) | 6.80(1) | 6.30(3) | 5.75(2) | 5.29(3) | 5.12(1) | 4.42(1) | 3.99(8) | 3.43(4) |
| N52 (α3) | 7.48(11) | 7.26(4) | 6.70(3) | 6.53(1) | 6.10(4) | 5.86(4) | 5.55(3) | 4.98(1) | |||
| A62 (α4) | 6.93(6) | 6.61(2) | 6.86(2) | 6.57(5) | 6.30(3) | 5.93(1) | 5.76(3) | 5.52(2) | 5.00(2) | 3.93(2) | |
| L65 (α4) | 8.73(5) | 7.79(2) | 7.24(4) | 6.08(2) | 5.53(2) | 5.44(1) | 5.32(3) | 4.60(3) | 3.87(4) | 3.46(4) | |
| K67 (α4) | 7.49(8) | 7.31(7) | 7.27(3) | 7.07(2) | 6.72(3) | 6.25(2) | 5.78(3) | 5.47(3) | 4.88(2) | 3.80(5) | |
| I68 (α4) | 7.74(15) | 7.71(8) | 7.44(2) | 6.69(4) | 6.48(3) | 5.82(2) | 5.52(3) | 4.70(3) | 4.01(7) | 3.64(6) | |
| V71 (α4) | 9.04(10) | 7.91(6) | 6.97(3) | 6.65(2) | 6.46(5) | 5.69(3) | 5.19(4) | 5.06(2) | 4.39(4) | 3.90(2) | 3.32(3) |
| Nonglobal exchanging protons | |||||||||||
| E23 (α1) | 6.56(2) | 6.40(3) | 6.46(5) | 6.35(2) | 5.98(2) | 5.73(5) | 4.72(2) | 3.43(2) | |||
| K24 (α1) | 5.36(1) | 5.31(1) | 5.31(2) | 5.35(3) | 5.44(3) | 5.00(3) | 5.08(5) | 4.87(3) | 4.43(2) | 4.30(4) | 3.51(2) |
| K25 (α1) | 6.47(1) | 6.44(2) | 6.27(3) | 6.35(2) | 6.15(5) | 5.86(4) | 5.57(2) | 5.21(1) | 4.22(4) | ||
| K26 (α1) | 5.44(2) | 5.33(1) | 5.45(4) | 5.36(3) | 5.16(5) | 4.89(2) | 4.87(3) | 5.22(3) | 4.35(1) | 3.37(3) | |
| V36 (α2) | 5.02(1) | 4.88(1) | 5.10(1) | 4.88(3) | 4.76(2) | 4.51(1) | 4.54(2) | 4.36(2) | 4.02(2) | ||
| D38 (α2) | 4.27(7) | 4.28(4) | 4.34(3) | 4.38(2) | 4.18(1) | 3.97(2) | 4.30(1) | 4.12(3) | 3.59(1) | ||
| M40 (α2) | 5.98(1) | 5.82(3) | 5.82(3) | 5.73(1) | 5.69(1) | 5.37(1) | 5.21(4) | 5.11(6) | 4.71(2) | 4.68(8) | 3.79(3) |
| A48 (α3) | 5.01(2) | 4.82(3) | 4.91(2) | 4.88(1) | 4.74(3) | 4.56(2) | 4.69(3) | 4.37(2) | |||
| A49 (α3) | 5.21(2) | 5.53(4) | 5.24(2) | 5.09(3) | 5.45(4) | 5.28(3) | 5.34(1) | 5.05(3) | 4.68(3) | 4.59(3) | 3.83(2) |
| G53 (α3) | 5.36(2) | 5.21(1) | 5.19(1) | 5.17(5) | 5.10(5) | 4.95(4) | 4.95(1) | 4.67(1) | |||
| L69 (α4) | 5.26(4) | 5.23(1) | 5.04(1) | 4.86(5) | 4.64(3) | 4.72(2) | 4.02(2) | ||||
| E75 (310) | 7.01(5) | 6.77(4) | 6.70(1) | 6.49(3) | 6.05(4) | 5.77(1) | 5.51(2) | 5.34(1) | 4.70(2) | 4.27(3) | 3.59(2) |
| F76 (310) | 7.11(4) | 7.01(1) | 6.79(2) | 6.61(2) | 6.34(2) | 5.85(3) | 4.98(2) | 4.36(1) | |||
| R82 (α5) | 3.79(5) | 3.77(3) | 3.65(1) | 3.52(3) | 3.61(3) | ||||||
| E83 (α5) | 4.34(3) | 4.45(5) | 4.43(2) | 4.36(3) | 4.41(2) | 4.28(2) | 3.87(3) | ||||
Values in parentheses represent SEs of the fitting and derived parameters; e.g., 7.16(6) = 7.16 ± 0.06.
The use of denaturants enables the quantification of the amount of accessible surface area (ASA) present in the various conformational states that are exchange competent, i.e., an open state. Denaturants stabilize states with more exposed area (30) and thus provide a quantitative measure of exposure (28). Residue-specific mHX values reflect the size of the opening event for each NH undergoing HX and depend upon whether exchange occurs in a near native state, the DSE, or an intermediate state, i.e., local, global, and subglobal openings, respectively (28, 31). In a local event, mHX is near zero, implying that HX occurs from the NSE via a small-scale perturbation that exposes little additional surface area. Sites that require complete unfolding exchange with global properties, ΔGHX = ΔGglobal and mHX = m0. The third class, subglobal exchange, is more often found in larger proteins and occurs when residues in one or more pieces of secondary structure, or “foldons,” collectively exchange with ΔGHX < ΔGglobal and 0 < mHX < mglobal. These openings represent intermediate states that can provide information on the folding pathway. In the case of apparent two-state folding reactions, these species lie on the native side of the major barrier.
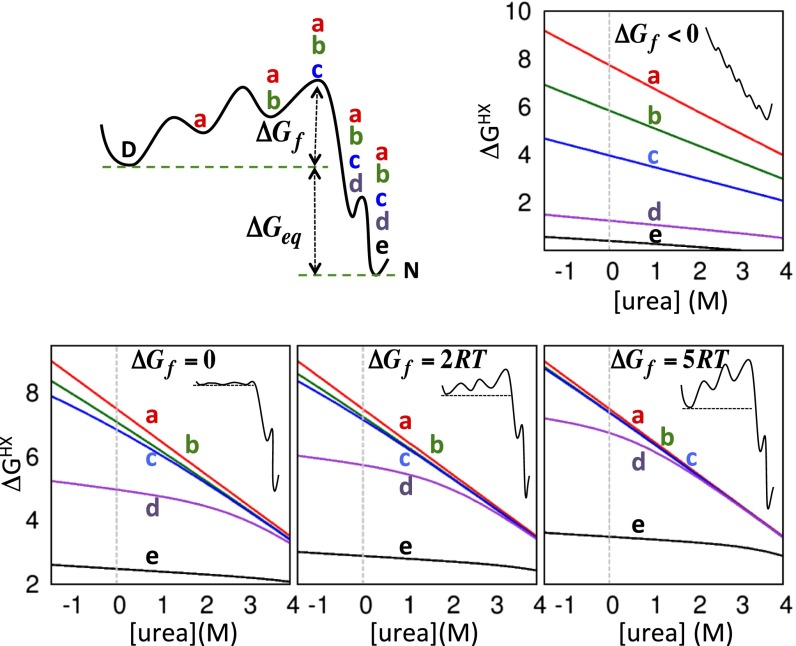
Whereas some residues may predominantly exchange via only one of the three classes of openings, other residues may exchange from two or all three classes to varying degrees that depend on the relative values of ΔGglobal, ΔGlocal, and ΔGsubglobal. For example, increasing the denaturant concentration preferentially promotes the global unfolding event such that exchange may first occur through a local event but merge with the global “isotherm” at higher denaturant concentrations, [denaturant]switch ∼ (ΔGglobal – ΔGlocal)/m0 (32). More complex behavior can occur if all three classes contribute, which results in the merging of three isotherms. Alternatively, a continuum of states suggestive of a downhill folding landscape would result in a continuous spread in ΔGiHX and mHX values over the entire protein (Fig. 2).
Fig. 2.
Free energy surface (Upper Left) and predicted HX patterns for four barrier heights: <0 RT, 0 RT, 2 RT, and 5 RT. The indicated mHX values are the fitted slopes from 0 to 4 M urea for the isotherms associated with the various states. The set of states located between the DSE-TSE and the set between the TSE-NSE are assumed to possess free energy differences and m values that are uniformly spaced within each set. Insets depict the energy surface for each condition.
HX rates were obtained using 1H-15N heteronuclear single-quantum correlation (HSQC) spectra for fully-H λYA in 80% D2O at 298 K, pDread 5.8 ∼ 7.5, a condition where the protein is 0.4 kcal·mol−1 more stable than in 100% H2O (Table S1). The urea and sarcosine data are combined using a conversion factor murea/msarc = −1.5 (33), providing points for apparent [urea] of −0.75 M and −1.5 M.
HX data for nine residues on α1, α3, and α4 can be fitted allowing for only a global unfolding process from 0 M to 4 M urea. The HX data for three residues on α1 and α4 (I21, L65, and V71) track with the global unfolding even in −1.5 M urea (1 M sarcosine). To fit the combined urea/sarcosine data for the other six residues, a local unfolding process is added with ΔGlocal ∼ 7 kcal·mol−1 and ΔGglobal ≥ 7.3 kcal·mol−1 with mHX ≤ 1.0 kcal·mol−1·M−1 (Fig. 3). These values match the equilibrium values of ΔG0eq = 7.3–7.4 kcal·mol−1 and m0 = 1.0 kcal·mol−1·M−1 obtained in the same solvent condition. The results indicate that the most stable sites on α1, α3, and α4 exchange via global unfolding and preclude the presence of a stable intermediate having one or more of these helices unfolded.
Fig. 3.
Denaturant dependence of HX. (A and B) Data are fitted using a model allowing for global and local unfolding processes except for M40 and E75 where additional subglobal processes are allowed (dashed-dotted lines). The denaturant dependence of the equilibrium global stability from Fig. 1 is shown as a black dashed line. (C) Fitted values for ΔGHX in zero denaturant are shown along with the m values for sites in A that exchange via the global unfolding process. Sites not requiring a local unfolding process to fit the data down to 0 M urea are highlighted with an “x.” Units for ΔG and m are kcal·mol−1 and kcal·mol−1·M−1, respectively. (D) The locations of associated H bonds are highlighted with a cyan solid line. N27 amide does not have an H bond in PDB structure and best candidate H-bond partners for N27 are highlighted with blue dashed lines.
One site, N27, has a slightly higher stability than the global exchanging sites, ΔΔGHX ∼ 0.5–1 kcal·mol−1, yet exhibits the same global urea dependence. The N27 amide proton is located in a distorted region at the C terminus of α1 and lacks an obvious H-bond partner (Fig. 3D). This superprotection could be due to an inaccurate estimate of its kchem. Alternatively, this proton may be partially buried or participating in an H bond that is formed 50–80% of the time in an otherwise unfolded chain. The persistence of the superprotection out to 4 M urea necessitates that any possible burial or H-bond stability in the DSE be denaturant independent. As this requirement seems unlikely, we believe instead that kchem is inaccurately estimated for this residue.
The remaining observable HX data for the five α-helices and the 310 helix can be fitted with a model containing both global and local unfolding processes with ΔGlocal < 7 kcal·mol−1. Of these residues, two on the 310 helix (E75, F76), have the highest stability with |ΔGglobal − ΔGlocal| ∼ 1 kcal·mol−1 below the global value.
The fit of the data for M40 in α2 can be slightly improved by allowing for a subglobal unfolding process with ΔGsub = 5.8 kcal·mol−1 and msub = 0.15 kcal·mol−1·M−1. The kinetic value mu = 0.24 kcal·mol−1·M−1, obtained from the chevron analysis (Fig. 1), reflects the surface exposed going from the NSE to the TSE. Because msub < mu, the possible intermediate reflected by the subglobal opening must exist between the TSE and the NSE. This finding is consistent with the kinetic data described below and the other HX data. The three observable NHs on α2 exchange with ΔGHX = 4.3–5.9 kcal·mol−1 whereas the two NHs on α5 exchange with ΔGHX = 3.6–4.4 kcal·mol−1. This difference, in conjunction with equilibrium mutation studies (34), suggests that α5 folds after α2, although α5 just may be more dynamic in the NSE. Regardless, the significant HX protection found in α5 indicates that it is folded at least 99.9% of the time.
The TSE and Folding Pathway.
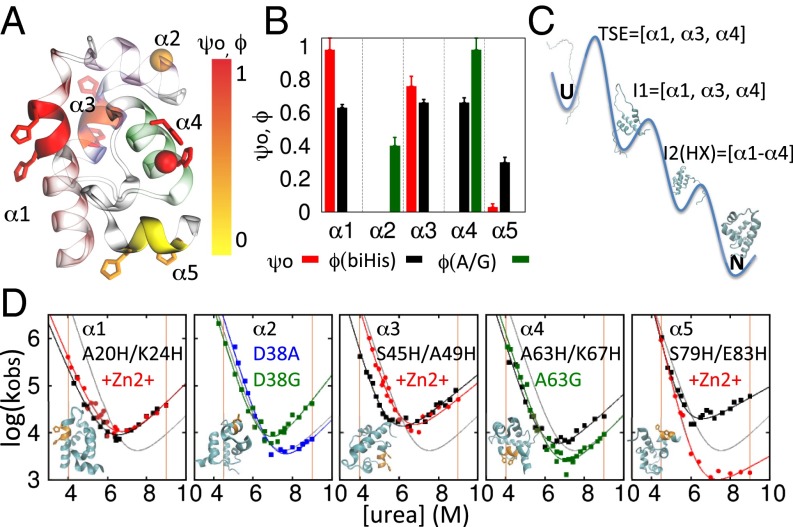
We applied a combination of ψ and ϕ analyses to characterize the TSE. To conduct ψ analysis, five biHis sites were individually introduced into the five helices of λYA (biHis1–biHis5, Fig. 4 and Table S3). The addition of zinc or nickel ions, which coordinate the pair of histidines, alters the protein’s stability and activation free energy for folding (ΔΔGeq and ΔΔGf, respectively) due to differences in binding constants KDSE, KN, and KTSE (35–37). The ion-induced changes in ΔΔGeq and ΔΔGf are used to define the ψ value, a parameter analogous to the mutational ϕ value, with ψ being the instantaneous change in ΔΔGf relative to ΔΔGeq,
| [1] |
Any potential artifacts related to metal ion binding are alleviated by evaluating ψ in the limit of zero perturbation, ψ0. The value of ψ0 reflects the intrinsic degree of contact formation in the TSE in the absence of metal ions. ψ0 values of zero and unity indicate that the binding affinity of the biHis site in the TSE is the same as found in the DSE and NSE, respectively. These two behaviors are interpreted as the biHis site being absent or native-like in the TSE, respectively. A fractional ψ0 indicates that the biHis site either is native-like in a subpopulation of the TSE or contains nonnative binding affinity (e.g., a distorted site with less favorable binding geometry or a flexible site that must be restricted before ion binding) or some combination thereof (35, 38–42) (SI Materials and Methods). Mutational ϕbiHis values also are calculated for each biHis site, using double-mutant data (in the absence of metal ions) with the wild-type protein data serving as the reference point.
Fig. 4.
ψ, ϕ analysis. (A) The ψ0, ϕ values are mapped onto the protein structure by coloring the biHis side chains and ribbon according to the associated ϕbiHis and ψ0 values, respectively. The D38 and A63 Cα atoms are denoted with colored spheres according to their ϕA→G values. (B) Measured ψ, ϕ values. (C) Proposed folding pathway. The 310 helix is not shown for simplicity and lack of information; HX measurements are consistent with it forming before α2. (D) Chevron plots. Shown are biHis mutant data without (black) and with 1 mM Zn2+ (red) and glycine (green) and alanine (blue) variants; orange vertical lines designate the [urea] at which ΔΔGf and ΔΔGu are used for the ψ calculation, obtained by simultaneously folding and unfolding data (SI Materials and Methods).
Table S3.
Chevron analysis in λYA
| Location | Mutation | ψ0 | ϕbiHis, ϕ | ΔΔGeqZn2+ | ΔΔGmuteq | m0 | m0Zn2+ | βT = mf/mo | βTZn2+ |
| WT(λYA) | — | — | — | 0 | 1.01 ± 0.02 | — | 0.76 ± 0.03 | — | |
| α1 | A20H/K24H (biHis1) | 0.98 ± 0.28 | 0.63 ± 0.02 | 0.15 ± 0.06 | −1.21 ± 0.05 | 1.01 ± 0.02 | 0.85 ± 0.03 | 0.79 ± 0.02 | 0.71 ± 0.04 |
| α2 | D38A | — | ND | — | 0.21 ± 0.05 | 1.05 ± 0.02 | — | 0.77 ± 0.03 | — |
| D38G | — | 0.20 ± 0.09 | — | −0.55 ± 0.09 | 1.11 ± 0.04 | — | 0.71 ± 0.04 | — | |
| A38G | 0.40 ± 0.05 | −0.74 ± 0.06 | 1.12 ± 0.03 | 0.75 ± 0.03 | |||||
| α3 | S45H/A49H (biHis3) | 0.76 ± 0.06 | 0.55 ± 0.02 | 0.66 ± 0.06 | −1.29 ± 0.04 | 1.02 ± 0.02 | 1.07 ± 0.04 | 0.78 ± 0.02 | 0.81 ± 0.05 |
| α4 | A63H/K67H (biHis4) | — | 0.66 ± 0.03 | — | −0.90 ± 0.05 | 1.02 ± 0.02 | — | 0.77 ± 0.02 | — |
| A63G | — | 0.98 ± 0.07 | — | −0.43 ± 0.05 | 1.03 ± 0.02 | — | 0.75 ± 0.02 | — | |
| α5 | S79H/E83H (biHis5) | 0.03 ± 0.02 | 0.30 ± 0.03 | 0.94 ± 0.07 | 0.79 ± 0.05 | 1.03 ± 0.02 | 1.19 ± 0.05 | 0.79 ± 0.02 | 0.88 ± 0.06 |
The CD spectra of the biHis variants are very similar to those for λYA except for biHis5, the variant with the biHis site on α5 (Fig. S1B). Its spectrum suggests that α5 may be unfolded before the addition of metal ions. The refolding fluorescence signal for biHis2 was too small to measure, whereas for biHis4, the addition of cations did not produce a readily interpretable shift in the chevron plot (Fig. S1C). To compensate, we measured ϕAla→Gly to probe for the presence of α2 and α4 helices in the TSE. This application of ϕ analysis using helix promoting/disrupting substitutions at solvent-exposed positions avoids many of the factors that typically confound the interpretation of ϕ values (38) and has proved consistent with ψ analysis (43, 44). We also calculated ϕbiHis to further probe the presence of α2 and α4 in the TSE.
The combination of ψ and ϕ data indicates that the TSE contains α1, α3, and α4 but likely lacks the two smaller helices (Fig. 4). Specifically, we obtain ψ0bH1 = 0.98 ± 0.28 and ψ0bH3 = 0.76 ± 0.06 whereas ψ0bH5 = 0.03 ± 0.02. The corresponding ϕbiHis values for α1, α3, and α5 are 0.63 ± 0.02, 0.55 ± 0.02, and 0.30 ± 0.03, respectively. The site on α4 yields ϕbiHis = 0.66 ± 0.03, whereas the A/G pairs in α2 and α4 produce ϕA38G = 0.40 ± 0.05 and ϕA63G = 0.98 ± 0.07. The intermediate ϕA38G value is challenging to interpret; it could reflect fractional helix formation or the loss of some backbone entropy due to the chain becoming constrained upon the folding of the flanking helices α1 and α3.
Regardless, our identification of the presence of α1, α3, and α4 as the major constituents in the TSE is consistent with the HX data as they are the same three helices that unfold in the global unfolding process. The folding cooperativity of these three helices identified by HX precludes the presence of a stable intermediate having one or more of these helices unfolded. Rigorously, local unfolding events do not provide pathway information. However, the possible subglobal opening for α2 along with lower stability of sites in α5 suggests that α2 folds before α5 (Fig. 4).
HX Pattern for Cooperative and Downhill Folding.
To assist in the interpretation of the data, we model the HX pattern for a landscape with barrier heights of ΔGf = 0 RT, 2 RT, and 5 RT (Fig. 2). The model has five sequential states (other than the DSE), with each folding event representing the formation of an additional helix. The folding order of the first three helices is unknown so that their order is left ambiguous (labeled a–c in Fig. 2) whereas the HX data suggest α2 folds before α5. The state containing helices a–c is the TSE with βT = 0.75, in accord with the chevron data.
For a barrier height of 5 RT, the HX isotherms for helices a–c display global or near global behavior, whereas the helix d isotherm is notably lower and flatter. With decreasing barrier height, the three highest isotherms diverge. The observed HX data are noticeably closer to those of the models with higher barriers. The addition of alternative pathways or more states would only accentuate the difference with the observed data by increasing the number of states from which HX could occur and further separate the highest three isotherms from the global isotherm. Although the experimental data cannot identify the barrier height, this model illustrates that the folding reaction must overcome a significant barrier to be consistent with the observed HX pattern.
SI Text
SI Materials and Methods
Proteins.
The sequence of λYA was taken from PDB 3KZ3 (6), was cloned into pet21 expression vector with a His6-tag and protein expression tag, and was expressed in Escherichia coli BL21 (DE3). Codon Plus cells (Stratagene, Agilent Technologies) were grown in LB at 37 °C until OD600nm = 0.8. Protein expression was induced with 1 mM IPTG and incubated at 37 °C for another 4 h. Cells were pelleted by centrifugation at 4,400 × g for 10 min at 18 °C and stored at −80 °C.
The His6-tagged λYA protein was purified by immobilized metal ion affinity chromatography. The His6-tag was removed by using the Tobacco Etch Virus protease. The protein was purified using cation exchange chromatography (SP HiTrap column; GE Healthcare) with a salt gradient for elution at pH 5.3 in 50 mM sodium acetate buffer. The salts were removed from the protein eluate by dialysis in 20 mM ammonium bicarbonate, pH 7.78. The purity of the protein was verified by SDS/PAGE and its identity was confirmed using an Agilent 6224 time-of-flight mass spectrometer analyzed with MassHunter version B06.00.
Hydrogen Exchange Measurements.
HX was initiated by buffer exchange from H2O to a final condition of 80% D2O/20% H2O, 50 mM sodium phosphate, using Sephedex G-15 columns (0.1–0.2 mM protein, 1 mM sodium azide). Proton levels were measured with a Bruker AVANCE III console at 500 MHz, using SOFAST-HMQC and HSQC pulse sequences (63). HX rate constants were obtained by fitting the normalized peak volumes to single exponential equations; i.e.,
| [S1a] |
| [S1b] |
where V(0) is the initial peak volume; represents the average normalized volumes of 7–10 peaks that are fully exchanged at each time t; and a, b, and k are fitting parameters. ΔGHX are reported for all peaks for which 0.6 < a < 1.0 and 0.1 < b < 0.3.
Urea concentrations were determined by refractive index. The pDread was corrected by +0.32 according to the D2O fraction. Final urea concentrations for pDread were 0 M/6.6, 0.5 M/6.62, 1.0 M/6.28, 1.5 M/6.65, 2.0 M/6.42, 3.0 M/6.16, 3.5 M/6.87, and 4.0 M/6.79. For sarcosine the final conditions were 0.5 M/7.90 and 6.37 and 1 M/7.70 and 6.22. Intrinsic exchange rates were corrected for urea concentration according to refs. 65 and 66. No correction was made for the addition of sarcosine, consistent with the local unfolding processes maintaining a constant ΔG across all concentrations of urea and sarcosine (Fig. 3B).
Circular Dichroism and Fluorescence.
Equilibrium denaturation was monitored with a Jasco J-715 CD spectrometer in a 1-cm path length cuvette at a protein concentration of 2 μM and 50 mM sodium phosphate buffer, pH = 7.0, by CD at 227 ± 5 nm and total fluorescence at λexcite = 280; fluorescence at λemission was measured downstream of a 310-nm cutoff filter. The urea-dependent CD and fluorescence data were fitted with a two-state equilibrium,
| [S2] |
where a and c are the baseline values and b and d are the baseline linear slopes for the NSE and DSE, respectively.
Kinetics and Equilibrium Studies.
Kinetic data were collected at 10–20 μM protein concentration in 50 mM Hepes, pH 7.5, at 298 K, using a Bio-Logic SFM-4000 stopped-flow apparatus connected to a PTI A101 arc lamp.
Data Analysis.
The kinetic data were analyzed using “chevron analysis” for the denaturant dependence of folding rate constants, where ΔGeq, ΔGf, and ΔGu are linearly dependent on denaturant concentration
| [S3a] |
| [S3b] |
| [S3c] |
where R is the universal gas constant, and T is the absolute temperature. The dependences on denaturant concentration, i.e., the m values, report on the degree of surface area burial during the folding process. Equilibrium values of m0 were calculated from the kinetic measurements according to ΔGeq = ΔGf − ΔGu and m0 = mu + mf.
ψ Analysis.
ψ analysis uses engineered biHis sites to probe the fraction of native metal ion binding energy realized in the TSE. The kinetic response as a function of metal ion concentration quantifies the degree to which the biHis site is present in the TSE (see refs. 35 and 37 for detailed treatment). In a manner analogous to the ϕ analysis performed using point mutations, the kinetic response due to metal-induced binding can be obtained from the denaturant dependence of folding rates (chevron analysis) in the limits of zero and high metal ion concentrations or by measuring the metal ion dependence of the folding and unfolding rates for strongly folding (4–5 M urea) and unfolding conditions (9–10 M urea), respectively (“Leffler analysis”). To obtain ψ0, the data are fitted using the equation relating the changes in activation energy and stability; i.e.,
| [S4] |
When side chain substitution or metal binding affects only the unfolding rate ku and not the free energy of the TSE relative to the unfolded state, the sites probed by the biHis mutations are absent in the TSE, and the corresponding ϕ or ψ vanishes. Conversely, when the perturbation affects only the folding rate, kf, the structure probed is likely to be native-like in the TSE, and the associated ϕ or ψ value is unity. When both the folding and unfolding arms shift, the ϕ or ψ value is a fractional quantity whose origin can be challenging to discern in both methods. Fractional ϕ may arise either because of partial structure formation in the TSE or because of the presence of multiple, distinct TSE structures. A fractional ψ value indicates that the biHis site either is native-like in a subfraction of the TSE or has nonnative binding affinity in the entire TSE (e.g., a distorted site with less favorable binding geometry or a flexible site that must be restricted before ion binding) or some combination thereof. In the limit of homogenous TSEs with nonnative binding affinities, ΔΔGeq and ΔΔGf become
| [S5a] |
| [S5b] |
where KDSE, KN, and KTSE are the cation-binding disassociation constants of the denatured state ensemble, the native state, and the TSE, respectively.
To minimize extrapolation errors, folding and unfolding denaturant concentrations xf and xu are chosen in the linear regions of the folding and unfolding arms of the chevron, respectively, typically 4–4.5 M and 9–10 M urea. Given an appropriate selection of xf and xu (and hence appropriate characterization of ΔΔGf and ΔΔGu), ψ0 values are determined from a simultaneous fit to the vanishing and high-Zn2+ chevrons, with ψ0 included as one of the fitting parameters and using nonlinear least-squares algorithms implemented in the Origin software package (OriginLab). Specifically, we simultaneously fitted both chevrons, using
| [S6a] |
| [S6b] |
| [S6c] |
where ΔΔGeq and ΔΔGf are set to 0 for the no metal chevron, and in the high metal chevron, the functional form of ΔΔGf(ψ0, ΔΔGeq) in Eq. S4 is applied.
Modeling HX Patterns.
We constructed a simple folding landscape with six states: D (zero helices), one helix, two helices, three helices, four helices, and N (all five helices). The state with three helices is taken to be the TSE and further assumed to bury 75% of the surface area to match the βT value (i.e., the mf/m0 from the chevron plot). The free energy of each state is uniformly spaced from D to the TSE and from the TSE to N. The height of the folding barrier increases with denaturant by mf·[urea] (i.e., ΔGT-D([urea]) = ΔGT-D + mf·[urea]) and stability decreases by m0·[urea] (i.e., ΔGD-N([urea]) = ΔGD-N − m0·[urea]) according to the values from the experimental chevron plot (ΔGD-N = 7.5 kcal·mol−1, mf = 0.75 kcal·mol−1·M−1, m0 = 1.0 kcal·mol−1·M−1). ΔGHX for a site i on each helix can be expressed in a straightforward manner; i.e.,
| [S7] |
Discussion
The HX, kinetic, and equilibrium data indicate that the λYA variant folds cooperatively, which is well approximated by a double-well energy landscape that is typical of many globular proteins. Folding is cooperative even under highly stabilizing conditions where the (extrapolated) folding rate constant is extremely fast, (5 μs)−1. Our HX data indicate that the last major unfolding barrier reflects the concerted unfolding of α1, α3, and α4. Kinetic data using ψ and ϕ analysis indicate that folding events occur in the reverse order, with the three helices forming early, being present in the TSE. A possible subglobal opening was measured for α2, suggesting that this helix folds after the TSE, consistent with the apparent two-state folding behavior and the mutational data.
λYA has been suggested to be an incipient downhill folder (6). Ma and Gruebele (20) observed probe-dependent kinetics for its major folding phase. λYA shares some properties of λD14A, a protein suggested to be a downhill folder (6, 10), including an initial 2-μs signal change. This phase is proposed to be a molecular phase resulting from the fast redistribution of molecules residing at the top of the barrier immediately following the T-jump, in part justified by the phase being more pronounced in the faster-folding variants. Alternatively, this phase, which is observed upon a shift to unfolding conditions, could be reporting on a redistribution of states in the native energy well rather than states near the top of the major barrier. These events could include helical fraying or even the unfolding of α2 or α5. Despite the better agreement between the HX data and models of cooperative folding (Fig. 2), it is difficult to rule out a small fraction of molecules existing near the TSE on an incipient downhill landscape for λYA.
We previously investigated the possibility of downhill folding for the cross-linked GCN4-p2 coiled coil (45) and similarly inferred that folding remains barrier limited using HX even though kf = (5 μs)−1 and ΔGeq = 6 kcal·mol−1 at 313 K. These two HX studies on fast-folding proteins indicate that significant barriers remain even in the absence of denaturants and that the prefactor (kattempt) used to estimate barrier heights (46), , must be faster than (5 μs)−1.
TSE Structure.
In our previous studies of kinetic H/D isotope effects on λAA, we obtained ϕH/D = 73 ± 4%, which is interpreted as three-quarters of the helical H bonds are formed in its TSE (5). This magnitude is the same as the βT value and the percentage of λYA’s H bonds contained within the three helices present in the TSE. Our results also are largely consistent with those of Burton et al. (3) for λ6–85, where the seven ϕA/G values measured on α12sites, α2, α3, α42sites, and α5 have ϕA/G = 0.5/1.0, 0.2, 0.3, 0.8/1.2, and 0.6, respectively. Only one of two A/G sites on α1 and on α4 has a highly exposed Cβ, a desirable feature for probing helix formation independent of tertiary contacts. These positions produce large ϕ values in agreement with our identification of these two helices as members of the TSE (ϕA20G = 1.0 and ϕA63G = 0.8).
The high ψ and ϕ values in α1, α3, and α4 point to a TSE with limited conformational diversity. However, we are hesitant to entirely rule out the presence of α2 (or the 310 helix) in the TSE, in part, as we observed a nonzero ϕ value in α2 (ϕA38G = 0.4 ± 0.1). Furthermore, excluding α2 from the TSE requires that all of the H bonds in α1, α3, and α4 be present in the TSE to satisfy the H/D isotope effect data (5). This possibility seems unlikely especially as α1 is 20 residues long with a poorly packed amino terminus that is possibly frayed in the TSE. Hence, we suspect other portions of the protein could be partially structured in the TSE in a native or nonnative manner and contribute to the 74% H-bond formation inferred from our prior isotope effect measurements (5).
In recent folding studies of λYA, Prigozhin et al. (47) compared the fluorescence quenching of W22 on α1 by Y32 on α2 with two new W-Y pairs on α1–α3 and α3–α2. The kf for the α1–α3 construct is slower by up to 20% than the other pairs, suggesting that the contacts involving α2 form earlier. We find, however, that the TSE largely lacks α2. It is possible that the quenching signals do not require that α2 be folded. Alternatively, the changes in rates could be viewed from the perspective of ϕ analysis where rate differences reflect energetic perturbations to the TSE. This view suggests that α1–α3 contacts are the most significant, consistent with our finding of a TSE that contains α1, α3, and α4.
The present study produces a picture of an extensive TSE, as observed for six other proteins studied using ψ (36, 37, 41, 48–50). Their TSEs adopt a high fraction of the native topology, defined using the relative contact order (RCO) parameter, RCOTSE ∼ 0.7·RCON. A TSE model composed only of the contacts between α1, α3, and α4 follows this trend, yielding an RCOTSE ∼ 0.85·RCON, further supporting this relationship and the well-known correlation between kf and RCO (51).
Residual Structure.
The importance of residual structure elicits diverse views. Both the stability and the m-value determined by HX for λYA even in 1-M sarcosine match those determined by equilibrium denaturation at high [urea]. This equivalence implies that residual structure has no (additional) thermodynamic effect in the absence of denaturant and the level of surface exposure in the DSE is the same in zero- and high-urea concentrations.
For a denatured analog of λAA, Chugha et al. (52) measured a CD222 nm = −4,500 deg·cm2·dmol−1. This level is equivalent to ∼13–15% helical content. By comparison, a helix-coil theory based on primary sequence (53) predicts an average helicity of 19% for λYA, most of which is concentrated in α1 and α4. These two helices have a stretch of 12 or 11 residues with an average helical probability of 66% or 30%, respectively. The remaining helices have minimal helicity (<5%), including α3, which is present in the TSE. There is no obvious correlation between intrinsic helicity and a higher ΔGHX, indicating that residual helicity, if present, affords no measurable HX protection.
Evidence of a thermodynamically equivalent DSE under stabilizing and denaturing conditions can be found for many other proteins. We found that the HX-determined stabilities and m values match those derived from global denaturation measurements for ubiquitin (54), a coiled coil (45), and protein G (32). In addition, Huyghues-Despointes et al. (55) observed that the stability in water obtained from HX data agrees with values determined by traditional chemical and thermal denaturation studies for 19 of 20 proteins. This equivalence indicates that the two methods probe the same folding transition to a DSE that is devoid of stable H bonds. Moreover, data from small-angle X-ray scattering imply that the dimensions in the DSE of many [but not all (56, 57)] small proteins remain unchanged upon shifting to a lower level of denaturant (32, 58–60). Furthermore, most [but not all (61)] small proteins satisfy the two-state chevron criterion, sometimes even down to 0 M denaturant (21, 22), indicating that the DSE remains highly solvated under native conditions for many proteins.
Comparison with Other Simulations.
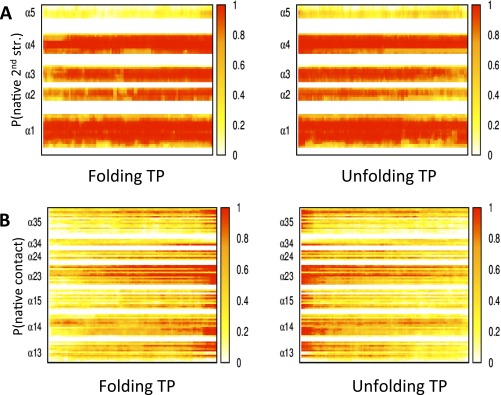
Previous simulations on λ repressor and variants used a variety of methodologies from all-atom molecular dynamics (MD) simulations to coarse-grain models (13–19, 62) (Fig. S4 and Table S4). Some all-atom simulations produce a DSE that is overly collapsed with a considerable amount of helix formation, in contrast with experimental data, as discussed in Residual Structure. Hence, it is challenging to identify the folding order; in these cases, folding is ranked by when the entire helix becomes folded.
Fig. S4.
Transition path analysis of DESRES trajectories of λD14A. (A and B) The probability of native (A) secondary structure for each helix and (B) side chain contacts for the folding and unfolding transition paths (TPs). The average TPs of the trajectories are obtained by averaging the 14 folding TPs and the 16 unfolding TPs after normalizing the reaction coordinate of each TP to begin and finish at 0 and 1, respectively, according to protocols given in ref. 36. More trajectory analysis of λD14A can be found in ref. 32.
Table S4.
Simulations and helix formation during simulation
| Research group | Method | protein | TSE, when possible | Folding pathway |
| Shoemaker et al. (15) | Go-like, 1 bead per residue | λWT | α1–α4 | (α1–α4) ⇒ +α5 |
| Allen et al.(16) | Go-like, 1 bead per residue | λWT | All helices present in DSE at 70+% | (α1–α4) ⇒ +α5 or (α1, α2, α4) ⇒ +α3 ⇒ +α5 |
| Pogorelov and Luthey-Schulten (62) | All-atom MD (CHARMM) with Go-like potential | λWT | (α1, α2, α4) ⇒ +α5 ⇒ +α3 | |
| λYA | (α1, α2, α4) ⇒ +α3 ⇒ +α5 | |||
| Adhikari et al. (13, 14) | TerItFix (MCSA), Cβ level chain | λD14A | α1, α3, α4 | (α1, α3, α4) ⇒ +α2 ⇒ +α5 |
| Bowman et al. (18) | MSM with all-atom MD (AMBER03) | λD14A | P1/2 and later structures have variable β and α content† | (α1, α4) ⇒ +(α2, α3) ⇒ α5 |
| Lindorff-Larsen et al. (19) | All-atom MD (CHARMM22*) | λD14A | TSE contains 94% secondary structure and α5 less than α1–α4 | (α1, α4) ⇒ +(α2, α3) ⇒ α5 or (α1–α4) ⇒ +α5‡ |
| Liu et al. (17) | All-atom MD (CHARMM22+CMAP) | λHG | (α1–α3) ⇒ +(α4, α5) |
Most, but not all, simulations (17) predict that α1 and α4 fold first, in good agreement with our data. These two helices are the longest, have the highest intrinsic helicity, and provide a suitable scaffold for the folding of α2 and α3. A Gō model, however, describes the folding of α2 and α3 as effectively commensurate with α1 and α4 (15). The C-terminal helix, α5, tends to fold last and to fluctuate in the native state.
Some of the variability in the folding order of α2 and α3 may be due to minor sequence differences. Our TerItFix algorithm that is based on the principle of sequential stabilization (13, 14) predicts a folding pathway for λD14A that is in agreement with the experimental data for λYA. However, using slightly different protocols for passing information to the next round of trajectories switches the order of helix formation between α2 and α3. This switch suggests that, at least computationally, the relative folding order of α2 and α3 is sensitive to small energetic differences and may be sequence dependent.
Conclusion
The cooperative folding behavior observed for λYA is consistent with an energy surface containing a single major energy barrier. Prior simulations generally support the experimental findings regarding the order of helix formation with nearly all studies identifying α1 and α4 as the first to fold. However, simulations typically describe the DSE as highly compact and highly structured in contrast to experimental data where any possible residual structure is thermodynamically silent and affords little, if any, HX protection. We have also observed cooperative folding for λYA, which also folds with an extrapolated time constant, τ = 5 μs, implying that much faster folding-rate constants are required to achieve the downhill limit.
Materials and Methods
The sequence of λYA was taken from Protein Data Bank (PDB) 3KZ3 (6) and cloned into a pet21 expression vector with a His6-tag and an expression tag with a TEV cleavage site for tag removal. See SI Materials and Methods for additional details.
HX was initiated by buffer exchange from H2O to a final condition of 80% D2O/20% H2O, 50 mM sodium phosphate, using sephedex G-15 spin columns (0.1–0.2 mM protein, 1 mM sodium azide). Proton levels were measured with a Bruker AVANCE III console at 500 MHz, using SOFAST-HMQC (heteronuclear multiple-quantum correlation spectroscopy) (63) and HSQC pulse sequences.
Equilibrium denaturation was monitored with a Jasco J-715 CD spectrometer in a 1-cm path length cuvette at a protein concentration of 2 μM and 50 mM sodium phosphate buffer at pH 7.0 by CD at 227 ± 5 nm and fluorescence at λexcite = 280; fluorescence was measured downstream of a 310-nm cutoff filter. Kinetic measurements were obtained using a Bio-Logic SFM-400, -4000 stopped-flow instrument integrated with a PTI light source to monitor tryptophan fluorescence at λexcite = 285 nm. ψ0 values were determined from a simultaneous fit to the vanishing and high Zn2+ chevrons, with ψ0 included as one of the fitting parameters and using nonlinear least-squares algorithms implemented in the Origin software package (OriginLab).
Thermal Denaturation and Aggregation
Chemical denaturation of λ variants reported here and in past studies (1) indicate that the process is cooperative. The results for thermal denaturation, however, are more complicated in part due to protein aggregation. Huang and Oas (1) observed coincident thermal denaturation profiles when tracking far-UV CD and 1D 1H NMR signals for the four aromatic residues. However, they also observed irreversible aggregation (30% upon cooling), suggesting that aggregation can be an issue for any λ6–85 variant regardless of whether folding is cooperative or downhill. They also noted that monitoring denaturation by NMR has an advantage in that resonances of aggregates are significantly line-broadened and do not affect the position of the resonances associated with monomeric species, thereby enabling a more accurate quantification of thermal denaturation. The Gruebele and Lapidus groups conducted thermal denaturation measurements for a variety of λ6–85 variants and observed probe-dependent melting in some, but not all, mutants (e.g., λYA) (20), typically with a ΔTm = TmCD – Tmfl ∼ 5–10 K (6, 7, 10, 47, 64).
Thermal denaturation of λYA was initially found to be probe dependent with TmCD > Tm1H-NMR > Tmfl (Fig. S2A). However, we observe time-dependent aggregation, and the slope of the fluorescence baseline is steeper than the unfolding transition itself. As observed in previous studies (6), the CD and fluorescence signals change on a timescale of minutes due to aggregation that affects the apparent Tm. To reduce the unwanted aggregation, we rapidly dilute proteins from room temperature into buffer preequilibrated at temperatures spanning the transition region (323–353 K). Additionally, we measure CD levels within the first minute before aggregation (Fig. S2). The revised Tm is 343 K, or 2 K lower than the Tm obtained from traditional (hours long) thermal denaturation measurements, and, more importantly, Tm now lies within the range of Tm obtained from aromatic NMR peaks (342–345 K). Similarly, the fluorescence-monitored Tm is 341 K when the data are analyzed using the revised protocol. The latter are only slightly lower than the CD and NMR values. Overall, we find thermal denaturation of λYA to be adequately described as proceeding through a single transition, as observed for the denaturant-induced transition and consistent with Ma and Gruebele’s (20) findings of a single Tm between 344 K and 345 K, using fluorescence, CD, and IR.
Acknowledgments
We thank M. Gruebele, G. Bowman, and members of our groups for useful comments. Trajectories for λ repressor were kindly provided by D. E. Shaw Research. This work was supported by National Institutes of Health Research Grant R01 GM055694 and by the NSF (CHE-1363012). W.Y. was supported in part by National Creative Research Initiatives (Center for Proteome Biophysics) of the National Research Foundation, Korea (Grant 2011-0000041).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1522500113/-/DCSupplemental.
References
- 1.Huang GS, Oas TG. Structure and stability of monomeric lambda repressor: NMR evidence for two-state folding. Biochemistry. 1995;34(12):3884–3892. doi: 10.1021/bi00012a003. [DOI] [PubMed] [Google Scholar]
- 2.Ghaemmaghami S, Word JM, Burton RE, Richardson JS, Oas TG. Folding kinetics of a fluorescent variant of monomeric lambda repressor. Biochemistry. 1998;37(25):9179–9185. doi: 10.1021/bi980356b. [DOI] [PubMed] [Google Scholar]
- 3.Burton RE, Huang GS, Daugherty MA, Calderone TL, Oas TG. The energy landscape of a fast-folding protein mapped by Ala-->Gly substitutions. Nat Struct Biol. 1997;4(4):305–310. doi: 10.1038/nsb0497-305. [DOI] [PubMed] [Google Scholar]
- 4.Burton RE, Huang GS, Daugherty MA, Fullbright PW, Oas TG. Microsecond protein folding through a compact transition state. J Mol Biol. 1996;263(2):311–322. doi: 10.1006/jmbi.1996.0577. [DOI] [PubMed] [Google Scholar]
- 5.Krantz BA, et al. Understanding protein hydrogen bond formation with kinetic H/D amide isotope effects. Nat Struct Biol. 2002;9(6):458–463. doi: 10.1038/nsb794. [DOI] [PubMed] [Google Scholar]
- 6.Liu F, Gao YG, Gruebele M. A survey of lambda repressor fragments from two-state to downhill folding. J Mol Biol. 2010;397(3):789–798. doi: 10.1016/j.jmb.2010.01.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang WY, Gruebele M. Folding lambda-repressor at its speed limit. Biophys J. 2004;87(1):596–608. doi: 10.1529/biophysj.103.039040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu F, Gruebele M. Tuning lambda6-85 towards downhill folding at its melting temperature. J Mol Biol. 2007;370(3):574–584. doi: 10.1016/j.jmb.2007.04.036. [DOI] [PubMed] [Google Scholar]
- 9.Yang WY, Gruebele M. Folding at the speed limit. Nature. 2003;423(6936):193–197. doi: 10.1038/nature01609. [DOI] [PubMed] [Google Scholar]
- 10.DeCamp SJ, Naganathan AN, Waldauer SA, Bakajin O, Lapidus LJ. Direct observation of downhill folding of lambda-repressor in a microfluidic mixer. Biophys J. 2009;97(6):1772–1777. doi: 10.1016/j.bpj.2009.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Prigozhin MB, Gruebele M. The fast and the slow: Folding and trapping of λ6-85. J Am Chem Soc. 2011;133(48):19338–19341. doi: 10.1021/ja209073z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gelman H, Gruebele M. Fast protein folding kinetics. Q Rev Biophys. 2014;47(2):95–142. doi: 10.1017/S003358351400002X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Adhikari AN, Freed KF, Sosnick TR. Simplified protein models: Predicting folding pathways and structure using amino acid sequences. Phys Rev Lett. 2013;111(2):028103. doi: 10.1103/PhysRevLett.111.028103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Adhikari AN, Freed KF, Sosnick TR. De novo prediction of protein folding pathways and structure using the principle of sequential stabilization. Proc Natl Acad Sci USA. 2012;109(43):17442–17447. doi: 10.1073/pnas.1209000109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shoemaker BA, Wang J, Wolynes PG. Exploring structures in protein folding funnels with free energy functionals: The transition state ensemble. J Mol Biol. 1999;287(3):675–694. doi: 10.1006/jmbi.1999.2613. [DOI] [PubMed] [Google Scholar]
- 16.Allen LR, Krivov SV, Paci E. Analysis of the free-energy surface of proteins from reversible folding simulations. PLoS Comput Biol. 2009;5(7):e1000428. doi: 10.1371/journal.pcbi.1000428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu Y, Strümpfer J, Freddolino PL, Gruebele M, Schulten K. Structural characterization of λ-repressor folding from all-atom molecular dynamics simulations. J Phys Chem Lett. 2012;3(9):1117–1123. doi: 10.1021/jz300017c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bowman GR, Voelz VA, Pande VS. Atomistic folding simulations of the five-helix bundle protein λ(6−85) J Am Chem Soc. 2011;133(4):664–667. doi: 10.1021/ja106936n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334(6055):517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 20.Ma H, Gruebele M. Kinetics are probe-dependent during downhill folding of an engineered lambda6-85 protein. Proc Natl Acad Sci USA. 2005;102(7):2283–2287. doi: 10.1073/pnas.0409270102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jackson SE, Fersht AR. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry. 1991;30(43):10428–10435. doi: 10.1021/bi00107a010. [DOI] [PubMed] [Google Scholar]
- 22.Krantz BA, Mayne L, Rumbley J, Englander SW, Sosnick TR. Fast and slow intermediate accumulation and the initial barrier mechanism in protein folding. J Mol Biol. 2002;324(2):359–371. doi: 10.1016/s0022-2836(02)01029-x. [DOI] [PubMed] [Google Scholar]
- 23.Jackson SE. How do small single-domain proteins fold? Fold Des. 1998;3(4):R81–R91. doi: 10.1016/S1359-0278(98)00033-9. [DOI] [PubMed] [Google Scholar]
- 24.Kim SJ, Matsumura Y, Dumont C, Kihara H, Gruebele M. Slowing down downhill folding: A three-probe study. Biophys J. 2009;97(1):295–302. doi: 10.1016/j.bpj.2009.04.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kiefhaber T. Kinetic traps in lysozyme folding. Proc Natl Acad Sci USA. 1995;92(20):9029–9033. doi: 10.1073/pnas.92.20.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sosnick TR, Mayne L, Hiller R, Englander SW. The barriers in protein folding. Nat Struct Biol. 1994;1(3):149–156. doi: 10.1038/nsb0394-149. [DOI] [PubMed] [Google Scholar]
- 27.Krishna MM, Englander SW. A unified mechanism for protein folding: Predetermined pathways with optional errors. Protein Sci. 2007;16(3):449–464. doi: 10.1110/ps.062655907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Englander SW, Mayne L, Bai Y, Sosnick TR. Hydrogen exchange: The modern legacy of Linderstrøm-Lang. Protein Sci. 1997;6(5):1101–1109. doi: 10.1002/pro.5560060517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bai Y, Milne JS, Mayne L, Englander SW. Primary structure effects on peptide group hydrogen exchange. Proteins. 1993;17(1):75–86. doi: 10.1002/prot.340170110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Auton M, Holthauzen LM, Bolen DW. Anatomy of energetic changes accompanying urea-induced protein denaturation. Proc Natl Acad Sci USA. 2007;104(39):15317–15322. doi: 10.1073/pnas.0706251104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Englander SW, Sosnick TR, Englander JJ, Mayne L. Mechanisms and uses of hydrogen exchange. Curr Opin Struct Biol. 1996;6(1):18–23. doi: 10.1016/s0959-440x(96)80090-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Skinner JJ, et al. Benchmarking all-atom simulations using hydrogen exchange. Proc Natl Acad Sci USA. 2014;111(45):15975–15980. doi: 10.1073/pnas.1404213111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Auton M, Rösgen J, Sinev M, Holthauzen LM, Bolen DW. Osmolyte effects on protein stability and solubility: A balancing act between backbone and side-chains. Biophys Chem. 2011;159(1):90–99. doi: 10.1016/j.bpc.2011.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Larios E, Pitera JW, Swope WC, Gruebele M. Correlation of early orientational ordering of engineered λ6–85 structure with kinetics and thermodynamics. Chem Phys. 2006;323(1):45–53. [Google Scholar]
- 35.Sosnick TR, Krantz BA, Dothager RS, Baxa M. Characterizing the protein folding transition state using psi analysis. Chem Rev. 2006;106(5):1862–1876. doi: 10.1021/cr040431q. [DOI] [PubMed] [Google Scholar]
- 36.Baxa MC, et al. Even with nonnative interactions, the updated folding transition states of the homologs Proteins G & L are extensive and similar. Proc Natl Acad Sci USA. 2015;112(27):8302–8307. doi: 10.1073/pnas.1503613112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pandit AD, Jha A, Freed KF, Sosnick TR. Small proteins fold through transition states with native-like topologies. J Mol Biol. 2006;361(4):755–770. doi: 10.1016/j.jmb.2006.06.041. [DOI] [PubMed] [Google Scholar]
- 38.Sosnick TR, Dothager RS, Krantz BA. Differences in the folding transition state of ubiquitin indicated by phi and psi analyses. Proc Natl Acad Sci USA. 2004;101(50):17377–17382. doi: 10.1073/pnas.0407683101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fersht AR. φ value versus ψ analysis. Proc Natl Acad Sci USA. 2004;101(50):17327–17328. doi: 10.1073/pnas.0407863101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bodenreider C, Kiefhaber T. Interpretation of protein folding psi values. J Mol Biol. 2005;351(2):393–401. doi: 10.1016/j.jmb.2005.05.062. [DOI] [PubMed] [Google Scholar]
- 41.Krantz BA, Dothager RS, Sosnick TR. Discerning the structure and energy of multiple transition states in protein folding using psi-analysis. J Mol Biol. 2004;337(2):463–475. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 42.Krantz BA, Dothager RS, Sosnick TR. Discerning the structure and energy of multiple transition states in protein folding using psi-analysis. J Mol Biol. 2004;337(2):463–475, and erratum (2005) 347(5):1103. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 43.Moran LB, Schneider JP, Kentsis A, Reddy GA, Sosnick TR. Transition state heterogeneity in GCN4 coiled coil folding studied by using multisite mutations and crosslinking. Proc Natl Acad Sci USA. 1999;96(19):10699–10704. doi: 10.1073/pnas.96.19.10699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Krantz BA, Sosnick TR. Engineered metal binding sites map the heterogeneous folding landscape of a coiled coil. Nat Struct Biol. 2001;8(12):1042–1047. doi: 10.1038/nsb723. [DOI] [PubMed] [Google Scholar]
- 45.Meisner WK, Sosnick TR. Barrier-limited, microsecond folding of a stable protein measured with hydrogen exchange: Implications for downhill folding. Proc Natl Acad Sci USA. 2004;101(44):15639–15644. doi: 10.1073/pnas.0404895101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 47.Prigozhin MB, Chao SH, Sukenik S, Pogorelov TV, Gruebele M. Mapping fast protein folding with multiple-site fluorescent probes. Proc Natl Acad Sci USA. 2015;112(26):7966–7971. doi: 10.1073/pnas.1422683112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yoo TY, et al. The folding transition state of protein L is extensive with nonnative interactions (and not small and polarized) J Mol Biol. 2012;420(3):220–234. doi: 10.1016/j.jmb.2012.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sosnick TR, Barrick D. The folding of single domain proteins--Have we reached a consensus? Curr Opin Struct Biol. 2011;21(1):12–24. doi: 10.1016/j.sbi.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Baxa MC, Freed KF, Sosnick TR. Psi-constrained simulations of protein folding transition states: Implications for calculating. J Mol Biol. 2009;386(4):920–928. doi: 10.1016/j.jmb.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Plaxco KW, Simons KT, Baker D. Contact order, transition state placement and the refolding rates of single domain proteins. J Mol Biol. 1998;277(4):985–994. doi: 10.1006/jmbi.1998.1645. [DOI] [PubMed] [Google Scholar]
- 52.Chugha P, Sage HJ, Oas TG. Methionine oxidation of monomeric lambda repressor: The denatured state ensemble under nondenaturing conditions. Protein Sci. 2006;15(3):533–542. doi: 10.1110/ps.051856406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lacroix E, Viguera AR, Serrano L. Elucidating the folding problem of alpha-helices: Local motifs, long-range electrostatics, ionic-strength dependence and prediction of NMR parameters. J Mol Biol. 1998;284(1):173–191. doi: 10.1006/jmbi.1998.2145. [DOI] [PubMed] [Google Scholar]
- 54.Zheng Z, Sosnick TR. Protein vivisection reveals elusive intermediates in folding. J Mol Biol. 2010;397(3):777–788. doi: 10.1016/j.jmb.2010.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Huyghues-Despointes BMP, Scholtz JM, Pace CN. Protein conformational stabilities can be determined from hydrogen exchange rates. Nat Struct Biol. 1999;6(10):910–912. doi: 10.1038/13273. [DOI] [PubMed] [Google Scholar]
- 56.Kimura T, et al. Specific collapse followed by slow hydrogen-bond formation of beta-sheet in the folding of single-chain monellin. Proc Natl Acad Sci USA. 2005;102(8):2748–2753. doi: 10.1073/pnas.0407982102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Luan B, Lyle N, Pappu RV, Raleigh DP. Denatured state ensembles with the same radii of gyration can form significantly different long-range contacts. Biochemistry. 2014;53(1):39–47. doi: 10.1021/bi4008337. [DOI] [PubMed] [Google Scholar]
- 58.Yoo TY, et al. Small-angle X-ray scattering and single-molecule FRET spectroscopy produce highly divergent views of the low-denaturant unfolded state. J Mol Biol. 2012;418(3–4):226–236. doi: 10.1016/j.jmb.2012.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jacob J, Dothager RS, Thiyagarajan P, Sosnick TR. Fully reduced ribonuclease A does not expand at high denaturant concentration or temperature. J Mol Biol. 2007;367(3):609–615. doi: 10.1016/j.jmb.2007.01.012. [DOI] [PubMed] [Google Scholar]
- 60.Jacob J, Krantz B, Dothager RS, Thiyagarajan P, Sosnick TR. Early collapse is not an obligate step in protein folding. J Mol Biol. 2004;338(2):369–382. doi: 10.1016/j.jmb.2004.02.065. [DOI] [PubMed] [Google Scholar]
- 61.Religa TL, Markson JS, Mayor U, Freund SM, Fersht AR. Solution structure of a protein denatured state and folding intermediate. Nature. 2005;437(7061):1053–1056. doi: 10.1038/nature04054. [DOI] [PubMed] [Google Scholar]
- 62.Pogorelov TV, Luthey-Schulten Z. Variations in the fast folding rates of the lambda-repressor: A hybrid molecular dynamics study. Biophys J. 2004;87(1):207–214. doi: 10.1529/biophysj.104.042861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Schanda P, Kupce E, Brutscher B. SOFAST-HMQC experiments for recording two-dimensional heteronuclear correlation spectra of proteins within a few seconds. J Biomol NMR. 2005;33(4):199–211. doi: 10.1007/s10858-005-4425-x. [DOI] [PubMed] [Google Scholar]
- 64.Prigozhin MB, et al. Misplaced helix slows down ultrafast pressure-jump protein folding. Proc Natl Acad Sci USA. 2013;110(20):8087–8092. doi: 10.1073/pnas.1219163110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Loftus D, Gbenle GO, Kim PS, Baldwin RL. Effects of denaturants on amide proton exchange rates: A test for structure in protein fragments and folding intermediates. Biochemistry. 1986;25(6):1428–1436. doi: 10.1021/bi00354a036. [DOI] [PubMed] [Google Scholar]
- 66.Lim WK, Rösgen J, Englander SW. Urea, but not guanidinium, destabilizes proteins by forming hydrogen bonds to the peptide group. Proc Natl Acad Sci USA. 2009;106(8):2595–2600. doi: 10.1073/pnas.0812588106. [DOI] [PMC free article] [PubMed] [Google Scholar]