Emergent ultra–long-range interactions between active particles in hybrid active–inactive systems

Significance

Particle–particle interactions determine the state of a system. Control over the range and magnitude of such interactions is critical for science and technology. Here, we show that active particles experience an emergent ultra–long-range attractive interaction in the presence of a passive medium. The range and magnitude of this interaction are controlled by the elasticity of the medium and the activity of the particles. For the conditions studied here, we have found the range to be as large as 20 particle diameters, which is much larger than the typical interaction range between colloids. This interaction may open up new routes of control between active objects in passive environments and help us to understand the emergent interactions in nonequilibrium (biological) systems.

Abstract

Particle–particle interactions determine the state of a system. Control over the range of such interactions as well as their magnitude has been an active area of research for decades due to the fundamental challenges it poses in science and technology. Very recently, effective interactions between active particles have gathered much attention as they can lead to out-of-equilibrium cooperative states such as flocking. Inspired by nature, where active living cells coexist with lifeless objects and structures, here we study the effective interactions that appear in systems composed of active and passive mixtures of colloids. Our systems are 2D colloidal monolayers composed primarily of passive (inactive) colloids, and a very small fraction of active (spinning) ferromagnetic colloids. We find an emergent ultra–long-range attractive interaction induced by the activity of the spinning particles and mediated by the elasticity of the passive medium. Interestingly, the appearance of such interaction depends on the spinning protocol and has a minimum actuation timescale below which no attraction is observed. Overall, these results clearly show that, in the presence of elastic components, active particles can interact across very long distances without any chemical modification of the environment. Such a mechanism might potentially be important for some biological systems and can be harnessed for newer developments in synthetic active soft materials.

Active-matter systems have received much interest due to their emergent nonequilibrium phase and collective dynamical behavior. This interest is well founded as some of the most ubiquitous and important biological systems or processes can exhibit such emergent nonequilibrium behavior, which is perhaps most recognizable in macroscopic examples ranging from schools of aquatic organisms like rays or fish (1–3), herds of livestock (4), flocks of birds (5–7), and even a mosh pit at a heavy metal concert (8). Active-matter systems are additionally unique in that such phenomena spans multiple length scales from meter to nanometer. At these smaller length scales, it is clear that such dynamical adaptation and phase separation are necessary to perform many vital biological processes. Dense crowds of cells move collectively through tissue during development and in many of the immune response processes, i.e., wound healing (9). Sea urchin sperm cells have been found to phase separate and organize into arrays of vortices when the density of spermatozoa is large enough (10). In fact, a myriad of biological systems, and experimental systems with biological components, have reported swarming (11–13), flocking (6, 14, 15), spiraling (13, 16), and many more nonequilibrium steady states (17, 18). It is clear that, in all these systems, a combination of the activity, shape of the active agents, and the environment lead to effective out-of-equilibrium interactions that determine their steady states. These active-matter systems have been particularly attractive for theoretical studies as there are relatively few artificial systems that can mimic these active-matter systems, in addition to a wide range of parameter space that can be explored. Simulations have been able to capture a wide range of collective dynamical behavior and spontaneous phase separation in these nonequilibrium systems (19–22).

Although most experimental and simulation studies have focused on systems composed of purely active components (23), here we investigate a hybrid system composed of active and passive components. This hybrid active–passive system serves as an excellent model for collective motion in complex, crowded biological environments where active units must move through or past nonmotile cells or tissues. Such a model system could potentially help to explain collective motion and phase separation observed in bacterial biofilms (24) and cells migrating through tissue interfaces or within tissues and cell sheets (25–29). In the past, there have been very few studies investigating hybrid active–passive systems and almost all of them are simulation or theoretical studies. Interestingly, these studies have reported nonequilibrium phase segregation in systems of motile and nonmotile rods (21), passive spheres and active rods (22), active and passive agents (15, 29), and active and passive hard spheres (30). Attempts to observe similar behavior in experimental artificial model systems have proved to be a more difficult task, presumably due to the fact that other interactions are present in such systems compared with the relatively simple models that theory and simulation have considered. Despite this, there are many systems, both experimental and theoretical, that show an emergent attraction between active agents in mixtures of active and passive populations and subsequent phase separation. Nevertheless, the origin of this nonequilibrium phase segregation is not well understood. Here, we clearly show that two active spinning particles in a dense monolayer of passive colloids attract, and such attraction can be felt at extremely long distances. This range is much longer than the magnetic dipole–dipole interaction and tunable via the activity and kinetics of the system. The origin of such long-range attraction is due to the elasticity of the monolayer. Our results, thus, provide much-needed understanding of the emergent interactions in synthetic mixed active systems and can help distinguish what biological interactions can be due to purely physical phenomena and which interactions require presumably physical and biological/biochemical stimuli.

Results and Discussion

Spinner Aggregation in Hybrid Active–Passive Systems.

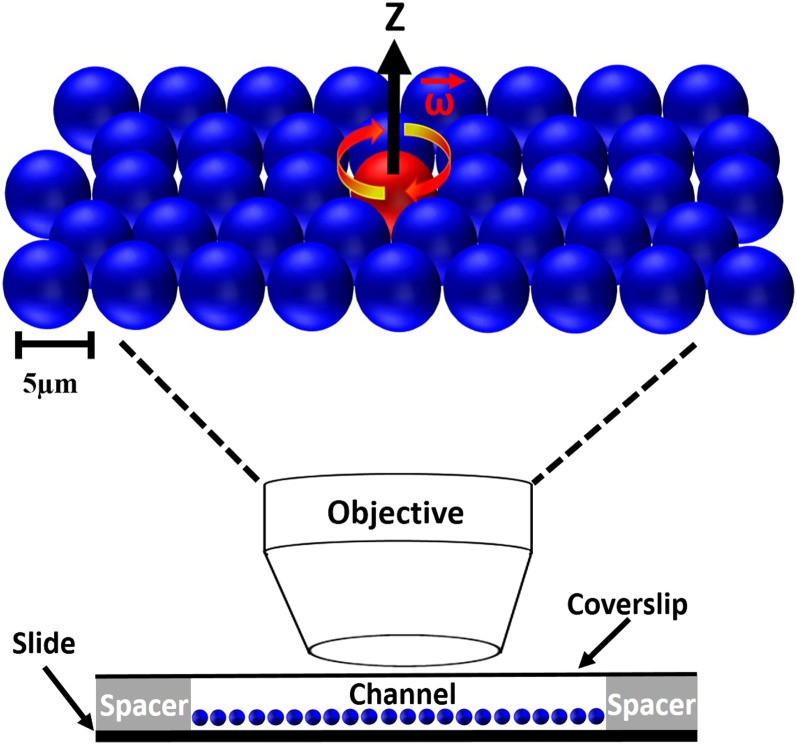
These hybrid systems are composed of a mixture of active and passive particles in water. The active particles are ferromagnetic colloids composed of a polystyrene core and an outer shell composed of CrO₂ and polystyrene. The passive particles are purely polystyrene. We use a dilute solution of active particles, ≈2 μg/mL, to study two-body interactions between active particles. This concentration is kept fixed unless otherwise noted. We impart activity to the ferromagnetic particles by rotating an external magnetic field around the axis perpendicular to the monolayer plane; this causes the active particles to spin in place, henceforth referred to as “spinners.” The experiments are conducted in small channels [22 mm (length) $\times$ 3 mm (width) $\times$ 300 μm (height)], which are made between a slide and a coverslip. After the particle solution is injected into the channel, the channel is sealed with epoxy. Before applying the rotating magnetic field, the particles are allowed to sediment for ∼10 min (see SI Appendix for more details); this allows for the formation of a dense colloidal monolayer on the substrate, as shown in Fig. 1.

Fig. 1.

Schematic representation of hybrid active–passive system. A mixture of passive polystyrene particles (blue spheres) and active ferromagnetic particles (red spheres) is inserted into a small channel that is then sealed with epoxy. Visualization is accomplished using a microscope in bright-field mode. Active particles are rotated at an angular frequency, ω, in the x–y plane in a dense monolayer of passive particles. The active and inactive particles are both 5 μm in diameter.

To study pairwise interactions between spinners, we control both the density of passive particles and the activity of the spinners, the latter of which is regulated by changing the frequency of rotation of the magnetic field, ω, which is shown schematically in Fig. 1. The magnitude of the field is maintained constant at 5 mT, which is large enough to ensure alignment of the rotational frequency of the ferromagnetic particles with the rotational frequency of the field. As a reference system, we investigate the interaction between two spinners in the absence of a passive medium (i.e., no passive particles; see Movie S1). First, we identify isolated pairs of spinners separated by different initial distances and magnetically actuate them by rotating the magnetic field at an angular frequency ω of 5 Hz. Then, we track the time evolution of the distance between the identified spinner pairs, R. The trajectories, normalized by the diameter of the particles, D, are shown in Fig. 2A.

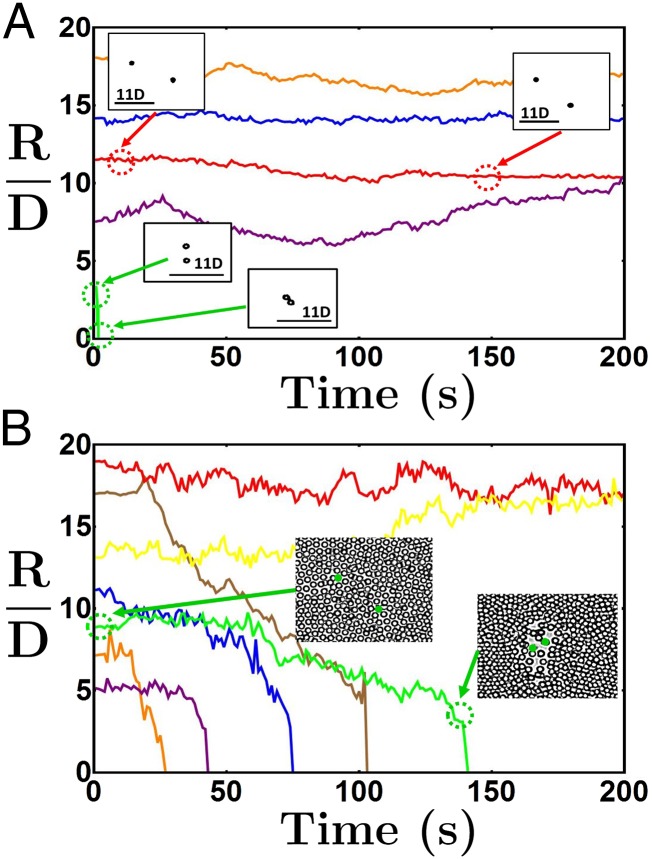
Fig. 2.

(A) Time evolution of the normalized distance $R/D$ between two active spinning particles in the absence of a passive colloidal monolayer. (B) Time evolution of the normalized distance between two spinners in a dense colloidal monolayer of ${\varphi }_A\sim 0.7$. In both cases, the frequency of rotation is ω = 5 Hz. The snapshots correspond to selected configurations along the trajectories at the time indicated by the arrows.

We observe that spinners initially separated by distances larger than $R/D>4$ do not interact, and thus the distance between them remains almost constant, as shown by the red trajectory and the experimental snapshots in Fig. 2A. These trajectories exhibit minor fluctuations, most likely due to the fluid flows generated by other spinners in the channel. When spinners are initially positioned closer than $R/D\approx 4$, they attract very rapidly and form a dimer, as seen in the green trajectory of Fig. 2A. This attraction is due to the magnetic dipole–dipole interaction, yet it becomes quite small above the threshold of $R/D>4$ as the force decays as $1/R^4$.

The interaction between spinners embedded in a dense passive media is of a different nature. We observe that spinners embedded within a dense monolayer of passive polystyrene particles at an area fraction ${\varphi }_A\sim 0.7$ attract (see Movie S2); however, the range of the interaction is dramatically increased, and spinners initially separated up to $17D$ apart are still able to attract. (This corresponds to an extremely small average density of the order of 1 active particle per 4,000 passive particles. In this limit, it is almost impossible to image all the active neighbors that might affect the interactions observed.) Interestingly, the trajectories for spinners that exhibit an attractive interaction are characterized by two distinct regimes: (i) at smaller distances, 4D or less, the slope of the trajectory is extremely steep, as the dominant attractive force in this regime is controlled by the magnetic dipole–dipole interaction; (ii) at distances larger than 4D, the slope is much smaller and close to 0 for certain periods of time, which indicates that the dominant attractive interaction in this regime is of a different nature than a magnetic dipole–dipole interaction. In fact, within the time frame of the experiments, the force is both stochastic and attractive.

To gain a deeper insight into the nature of the interaction between spinners embedded in passive mediums, we carry out numerical simulations using a coarse-grained model of this system. Specifically, we perform Lattice–Boltzmann simulations for a fluid of density, ρ = 1, and kinematic viscosity, ν = 1/6, coupled to a molecular-dynamics simulation for the colloidal particles (31). We explicitly solve the fluid field generated by the spinners by means of the fluctuating Lattice–Boltzmann equation (32), with $k_{\mathrm{B}}T$ = 0.00002. We then obtain the forces exerted by the fluid on the colloidal particles, represented by hard solid objects, and enforcing no-slip boundary conditions at their surfaces, we integrate the time evolution of the system. For this model, which neglects the dipole–dipole interaction between ferromagnetic particles, we observe that spinners suspended in a viscous fluid repel each other, whereas spinners embedded in passive monolayers attract each other (SI Appendix) (33). In the simulations, we observe only the stochastic attractive regime (ii), indicating that the monolayer of passive particles is responsible for the attraction, and that the strong short-range attraction is due to the magnetic dipole–dipole interaction present in the experiments.

Regarding the fluid flows, one spinner suspended in a viscous fluid generates a rotational flow around the axis of rotation, i.e., z. At Reynolds number (Re) zero, this is the only contribution to the fluid field; however, at small but finite Re, inertial effects produce the so-called secondary flows (34). As a consequence, the fluid is pulled in toward the poles and expelled from the equator (SI Appendix, Fig. S29). These secondary flows cause one spinner to repel other spinners or neighboring passive particles, and thus the formation of the corona (33).

Spinner–Spinner Interaction Mediated by Elasticity of Passive Monolayer and Angular Rotation Frequency.

To understand the attractive interaction between spinners in a passive monolayer, we need to understand how the activity of the spinners modifies the passive monolayer. Under the actuation of the rotating magnetic field, the spinners rotate in place and generate a rotational flow and secondary flows as previously mentioned. In the purely active system, these flows produce small perturbations on the positions of neighboring spinners, which may lead to a fast attraction between two spinners separated by distances of about 4D due to the strong magnetic dipole–dipole interaction. In the presence of a passive monolayer, the rotational flow generated by the spinner rotates the surrounding passive particles. Therefore, spinners embedded in a dense passive medium rotate the first shell of passive particles around them as a consequence of the momentum transferred through the fluid. In addition, the secondary flows generated by the spinners push the first shell of passive particles away from the spinners, creating a region that is devoid of passive particles, as shown in Fig. 3A (e.g., ${\varphi }_A\sim 0.7$). We denote this region as the corona. The creation of the corona is similar to shear banding phenomena (35) and implies an effective hydrodynamic repulsive interaction between the spinners and the passive particles that leads to a weak but noticeable compression of the monolayer. The size and angular velocity of the corona depend on both the passive monolayer area fraction and the rotational frequency of the magnetic field (SI Appendix, Figs. S21 and S22). Upon actuation of a magnetic field, the spinners begin to degrade or erode the passive monolayer that initially separates the pair of spinners. We refer to this region of passive particles between the spinners as the bridge. The degradation or erosion of the bridge is a slow and stochastic, but nevertheless steady, process resulting in an effective attractive interaction between the spinners. The fact that the bridge is degraded to a greater extent than the other regions of the monolayer is related to the activity-induced elastic stresses imposed on the monolayer. To prove directly the importance of elasticity in this system, we measure the range of the attractive interaction between spinners in passive monolayers with area fractions ranging from ${\varphi }_A$ = 0 to 0.8.

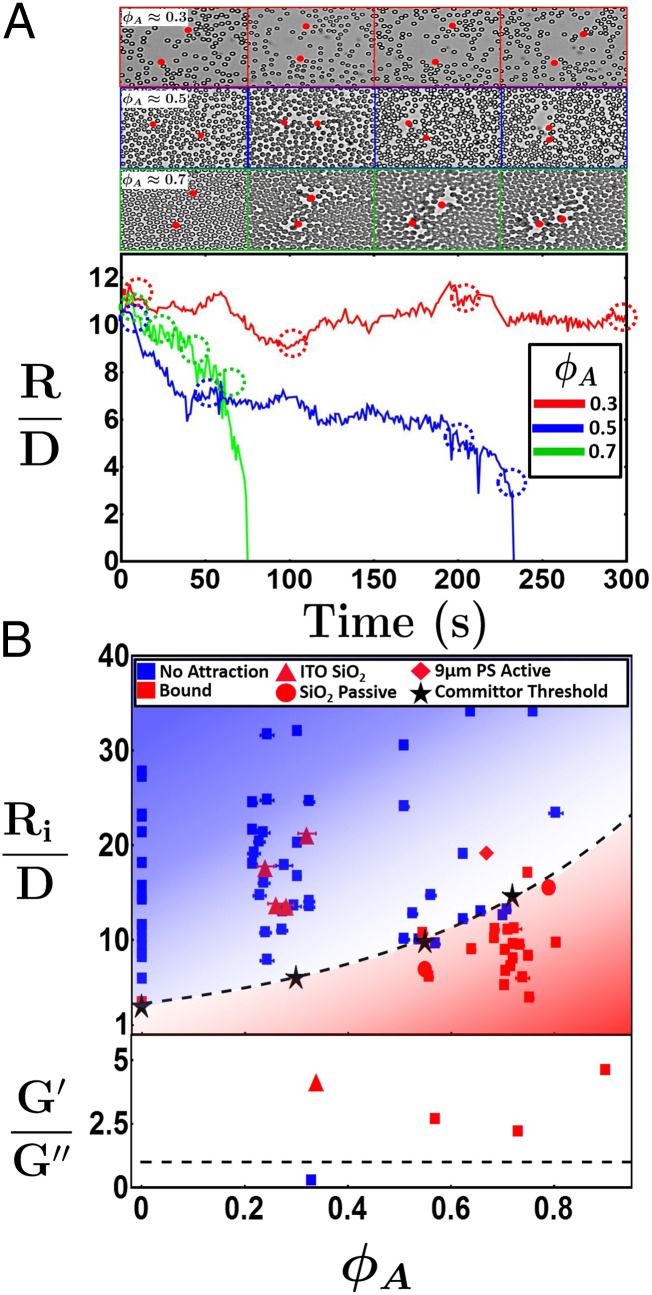
Fig. 3.

(A) Experimental snapshots of the active spinners in passive mediums with area fractions ${\varphi }_A$ = 0.3 (red), 0.5 (blue), and 0.7 (green), and their corresponding distance trajectories. (B) The range of the interaction as a function of the area fraction of passive monolayer computed for actuation periods of 5 min. The different symbols represent the following: (i) no attraction (blue symbols) and (ii) bound (red symbols). The threshold committor probability is represented by black stars and fitted by the dashed black line. Square symbols indicate experiments using ferromagnetic polystyrene active particles and polystyrene passive particles, both 5 μm in diameter. The ratio of G′ to G″ was calculated, at experimental times of about 5 min, for various packing fractions of ${\varphi }_A$. The dashed line indicates a value of 1, which delineates mediums that behave elastically and viscous.

From the experiments at different monolayer area fractions, we built a “range diagram,” presented in Fig. 3B together with the ratio between the storage modulus, G′, and the loss modulus, G″ at very long experimental times (5 min). These mechanical properties are calculated by particle tracking passive microrheology of purely passive monolayers at different area fractions (see SI Appendix for details). The range, $R_i/D$, corresponds to the initial distance between a pair of spinners, and the results are cataloged as (i) no attraction or (ii) bound. The state i of no attraction implies that there is no observable attraction found within the experimental timescale (in and all future discussions set to 5 min per spinner pair). State ii is the bound state, and it means that the spinners have formed a dimer within the experimental time protocol. We observe that only the larger area fractions, ${\varphi }_A\ge 0.5$, increase the range of the interaction with respect to the reference system (i.e., spinners in the absence of passive particles, ${\varphi }_A=0$), as shown in Fig. 3B. The long-range attraction in this system emerges when the ratio between the storage and loss modulus, G′/G″, becomes larger than 1, which implies the solid-like character of the monolayer, as shown in the bottom panel of Fig. 3B. Thus, the long-range interaction between spinners is mediated by the activity-induced elastic stresses imposed on the monolayer. In fact, we observe even longer ranged interactions between spinners if embedded in monolayers of passive particles interacting through a strong repulsive potential (red triangles in Fig. 3B). We achieve this repulsive interaction between the passive particles in the monolayer by using silica beads, 3 μm in diameter, that are polarized by an externally applied potential of 2.5 V between the top and bottom surfaces of the channel, built using indium tin oxide-coated glass slides. These passive matrices present a more pronounced solid-like character, which allows the spinners to interact at distances up to 20D apart at much smaller area fractions, $\varphi \approx 0.3$ (see Movie S3).

To provide a more quantitative analysis concerning the range of the attractive interaction between spinners embedded in passive mediums, we perform a “committor-like analysis” of the trajectories presented in SI Appendix, Fig. S8. Committor analyses have been used to identify transition states in protein folding, vesicle fusion, and gold nanoparticle insertion (36–39). A similar analysis can be used in this hybrid active–passive system to analyze the transition between the (i) no attraction and (ii) bound states, and thus identify the threshold of this emergent spinner–spinner interaction. As a consequence of the mechanical properties of the passive matrix, an average interaction potential between active particles emerges, similar to how a depletion force or potential emerges between two colloids upon introduction of depletants. In this system, we can define two stable energy basins: (i) no attraction and (ii) bound, schematically depicted in SI Appendix, Fig. S23, and we can compute the committor probability, P, between these two states. The committor probability is assigned a value of 0 for state i and a value of 1 for state ii, with intermediate values occurring between these two basins. To calculate the committor probability as a function of the interspinner distance, all spinner trajectories for passive monolayer area fractions ${\varphi }_A=$ 0–0.8 were binned in time intervals of 5, 10, and 20 s. If the interspinner distance decreases between time intervals, a committor probability of $P=1$ is assigned for that interspinner distance. If the distance increases between time intervals, the committor probability at that interspinner distance is assigned a value of $P=0$. This procedure is repeated for all spinner trajectories to calculate the average committor probability as a function of interspinner distance. We define the committor threshold, or equivalently the interaction threshold, as the interspinner distance at which the committor probability $P\approx 0.5$. This interspinner distance corresponds to the point where the spinner pair is equally likely to move into state (i) no attraction or state (ii) bound, as indicated by black star symbols in Fig. 3B. This committor threshold would be analogous to a transitions state of activated processes.

We study other systems composed of mixtures of spheres of different sizes at 5 Hz to ensure the emergent attraction between spinners is indeed ubiquitous and not unique to the particular system previously described. The same long-range emergent spinner attraction is observed when using larger active particles, 9-μm diameter, in a dense passive medium of 5-μm passive polystyrene particles (red diamond in Fig. 3B). Systems composed of 5-μm active ferromagnetic polystyrene particles in a dense monolayer of 3-μm passive silica particles shows attraction up to $20D$. Note that we always normalize by the diameter of the passive particles. Furthermore any interaction between the particles and the substrate serves to inhibit any emergent attractive interaction between spinners (see Movie S4).

The elastic stresses, as well as the kinetics of the monolayer, also depend on the frequency of rotation. Therefore, we study the spinner–spinner interaction as a function of the angular frequency of the spinners in monolayers of ${\varphi }_A=0.7\pm 0.1$. We identify pairs of spinners at initial distances ranging from 3 to 40D, and then actuate the magnetic field for a period of 5 min at frequencies of ω = 0.5, 1.0, 3.0, and 5.0 Hz. For comparison, this is also done in the absence of a passive medium to show that there is no long-range interaction between spinners in this case regardless of the frequency at which the magnetic field is actuated. The range diagram for both of these scenarios is shown in Fig. 4.

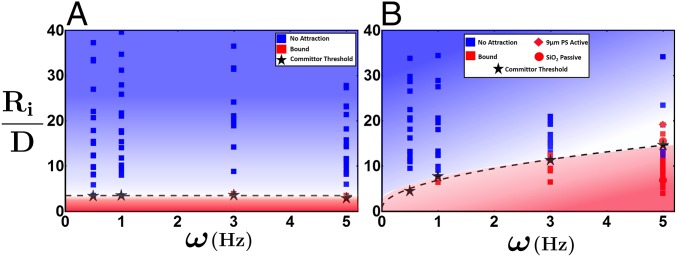
Fig. 4.

(A) Range of the interaction ($R_i/D$) in the pure active system as a function of the angular frequency of the spinners. The spinners show essentially no long-range attractive behavior. Spinners only form dimers when they are initially placed closer than $R_i/D<4D$, where magnetic interactions dominate. (B) Range of the interaction ($R_i/D$) between spinners embedded in a dense colloidal monolayer of ${\varphi }_A=0.7\pm 0.1$ for different angular frequencies. The spinners show extremely long-range attraction at distances up to $17D$ as frequency increases.

In the case of no passive particles, the system has a threshold interaction range on the order of 4D. In contrast, in the case where a dense passive monolayer is present, we find a much longer range of attraction, up to 17D. Interestingly, the range rapidly decreases below a frequency of 1 Hz. At this point, the spinners are unable to stress the monolayer (or form a corona; SI Appendix, Fig. S21), and we believe that the rate at which the system can dissipate energy is faster than the rate of energy input. As the frequency is increased, part of the energy is stored in deformations of the monolayer that can only be released by cooperative particle motions, such as yielding events (33).

Loading and Yielding of the Monolayer.

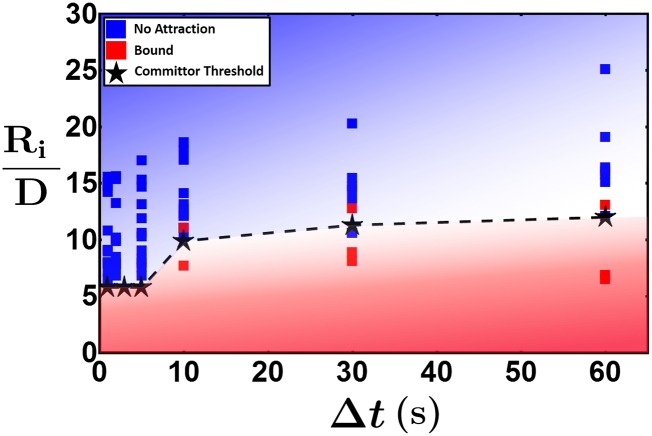
In the previous sections, we have shown that the activity of the spinners and the elasticity of the monolayer determine the range of the interaction between spinners. The activity of the spinners produces the rotation of the neighboring particles, which in turn increase the mobility of the surrounding particles. However, the mobility of the passive particles in the monolayer follows activated dynamics (40), which have a characteristic timescale associated. To detect the minimum timescale associated with the activity necessary to observe the emergent long-range interaction, we modify the nonequilibrium actuation protocol. In particular, we use a protocol in which the spinner rotation, clockwise or counterclockwise, is alternated every period $\mathrm{\Delta }t$ until the 5-min actuation time is reached. The angular frequency is set to 5 Hz for both spinner rotational directions. We observe no attraction between spinners for loading times, $\mathrm{\Delta }t$, lower than 10 s, as shown in Fig. 5.

Fig. 5.

Range diagram for an alternating protocol in which the spinners are rotated in alternating directions, first for a period $\mathrm{\Delta }t$ in a counterclockwise direction and afterward in a clockwise direction for another $\mathrm{\Delta }t$. This process is repeated for 5 min. Notice the lack of long-range attraction until the spinners are rotated continuously in the same direction for more than $\mathrm{\Delta }$t = 10 s. The area fraction of the monolayer is ${\varphi }_A=0.7\pm 0.1$ for all experiments.

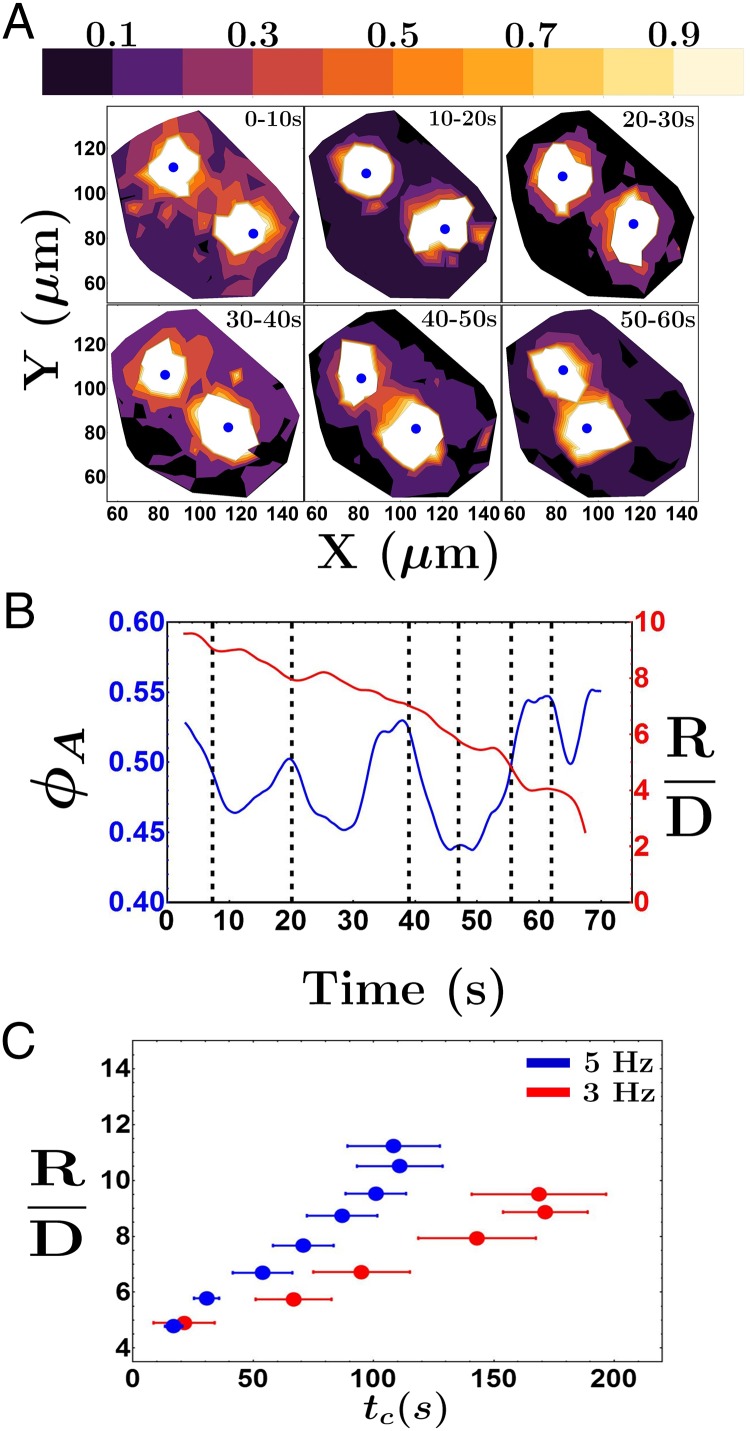
This implies that there is indeed a characteristic monolayer rearrangement timescale under stress, and that the level of stress must be constant on the monolayer before it yields. These yielding events can be easily detected by measuring the velocity of the passive particles. The mobility of the passive particles located in the bridge is low during the initial loading process, whereas, when the system yields, groups of passive particles move; this becomes apparent from the areas of high mobility in contour maps of the spatial velocity of the passive particles as shown in Fig. 6A. In this time series, we do not use the alternating protocol, but it is evident that the system undergoes repeated cycles of high and low mobility in the area between both spinners. The characteristic time between these events is also in the range of 10–20 s. In addition, the area fraction in the bridge decreases momentarily when the system yields, as shown in Fig. 6B. The time evolution of the density of passive particles in the bridge increases and decreases in agreement with periods of loading and yielding, respectively. The dynamics of attraction seems to be highly correlated with this temporal evolution of the area fraction. In particular, one can clearly see that, around t = 55 s, the density rises when the relative motion between the spinners becomes slower. It is important to highlight that all of the timescales associated with the microscopic rearrangement of the monolayer are consistent with the 10-s minimum timescale found for attraction. In particular, it is clear that the shear stresses in the bridge region are higher because of the imposed flow conditions, i.e., the direction of the flow reverses on opposite sides of the bridge. In the other regions, the stresses decay more slowly. Although in equilibrium one would naturally see an equilibration of the system, here the energy to move the particles is coming mostly from the activity of the spinners. Imploring a quasiequilibrium approximation, this would imply a locally higher free energy per passive particle as now one needs to include elastic terms in the free energy. Moreover, taking a look at longer timescales, this system clearly follows activated dynamics. To show this, we evaluate the average time required for spinners to bind or time to contact, $t_c$, as a function of interspinner distance for two different frequencies, 3 and 5 Hz, as shown in Fig. 6C. The average time to contact decreases with the separation distance between the spinners; however, the slope of that curve increases with frequency, or similarly with the activity of the spinners. As the frequency increases, the amount of stress exerted on the system by the spinners increases. The mobility of the passive particles increases as well, and the time required for the spinners to bind decreases. Thus, the spinners’ activity controls both the strength as well as the kinetics of this emergent interaction.

Fig. 6.

(A) Spatial velocity contour map of the passive particles averaged over 10-s intervals. The positions of the spinners are marked by blue dots. The first shell of passive particles around the spinners, as well as the spinners, have the largest mobility. The bridge region appears to alternate between periods where the mobility of the particles in the bridge is enhanced, corresponding to yielding events in the bridge, and periods where the particles appear somewhat arrested, corresponding to the compression of the bridge. (B) Time evolution of the distance between spinners normalized by the diameter of the spinners (red line). The area fraction of the passive particles located in the bride (blue line). The black dotted lines indicate the time at which a line of passive particles was removed from the bridge. The fluctuation in the density of the passive particles in the bridge corresponds to periodic compression of the bridge, where the density increases, and shearing and yielding of the bridge, when the packing fraction decreases. (C) Time to contact, $t_c$, measured at different distances for rotational frequencies of 3 and 5 Hz. The bars represent the range of spinner $t_c$ measured at different interspinner distances.

In summary, we have developed an artificial nonequilibrium hybrid active–passive matter system to study interactions between active units in passive matrices. An ultra–long-range attractive interaction between the active components, spinners, emerges when the spinners are actuated in these dense passive mediums. This attractive interaction between spinners depends on the monolayer area fraction and the angular frequency of the rotating magnetic field. The area fraction of the monolayer determines the mechanical properties of the passive matrix, whereas the angular frequency controls the activity of the spinners. We find that the long-range attractive interaction between spinners is mediated by the mechanical properties of the medium and the ability of the active agents to erode the passive medium. This interaction emerges when the passive medium behaves elastically and disappears when the medium behaves as a viscous fluid. In the presence of a solid-like media, the activity of the spinners increases the stress on the system, thereby increasing the range of the interaction between them. We also find a characteristic minimum actuation timescale below which the spinners are unable to stress the monolayer as the system dissipates energy faster than the rate of energy input. For actuation periods longer than this characteristic time period, the medium is not able to dissipate energy fast enough and the monolayer dissipates the stored energy via yielding events. These results have far reaching implications: (i) activity in a dense monolayer yields ultra–long-range interactions due to elastic stresses. This physical mechanism could be used for communication in synthetic or biological systems without the need for chemical sensing (27). (ii) This elastically induced interaction can be modulated and can be applied to many different systems to control their out-of-equilibrium states. (iii) This particular phenomenon could offer insight into wear and erosion at the microscopic scale, as the attraction is due to the erosion of the bridge which occurs through avalanches of passive particles that reconfigure the monolayer.