Abstract
First- to fifth-grade mathematics and word reading achievement were assessed for children with mathematical learning disability (MLD, n = 16), persistent low achievement (LA, n = 29), and typical achievement (n = 132). Intelligence, working memory, processing speed, and in-class attention were assessed in 2 or more grades, and mathematical cognition was assessed with experimental tasks in all grades. The MLD group was characterized by low school-entry mathematics achievement and poor word reading skills. The former was mediated by poor fluency in processing or accessing quantities associated with small sets of objects and corresponding Arabic numerals, whereas the latter was mediated by slow automatized naming of letters and numbers. Both the MLD and LA groups showed slow across-grade growth in mathematics achievement. Group differences in growth were mediated by deficits or delays in fluency of number processing, the ability to retrieve basic facts from long-term memory and to decompose numbers to aid in problem solving, and by the central executive component of working memory and in-class attention.
Keywords: learning disability, mathematics, mathematical cognition, reading, achievement growth
As with literacy in the 20th century, numeracy will be needed for everyday living in the 21st: Individuals who do not acquire basic competencies in mathematics before leaving high school will be disadvantaged in the workforce of the 21st century and in their ability to function in many now routine day-to-day activities. The associated competencies include basic arithmetic, measurement, and simple algebraic skills, with large-scale studies of representative samples of adults suggesting that as many as 1 in 4 of them have not mastered the mathematics expected of a sixth grader, making them functionally innumerate (Every Child a Chance Trust, 2009). Considerable progress has been made in terms of identifying the mathematical deficits and the underlying cognitive mechanisms of children at risk of innumeracy in adulthood. These include the approximately 7% (ranging from 4% to 14%, depending on classification methods) of students who are identified as having a learning disability in mathematics (MLD; Barbaresi, Katusic, Colligan, Weaver, & Jacobsen 2005; Lewis, Hitch, & Walker, 1994; Shalev, Manor, & Gross-Tsur, 2005), and another 10% of students who will experience mild but persistent learning difficulties (Berch & Mazzocco, 2007), hereafter, low achieving (LA). These groups represent more of a continuum (below) than distinct categories, but more important they capture the population of children at high risk for long-term difficulties in occupational and everyday activities that require basic mathematical knowledge.
In terms of mathematics achievement patterns, children with MLD score at or below the 10th percentile in most grades, whereas LA children typically score between the 11th and 25th percentile. The mathematical deficits and delays of these students have been well documented in single-grade, cross-sectional, and short-term longitudinal studies (Cawley & Miller, 1989; Cawley, Parmar, Foley, Salmon, & Roy, 2001; Geary, 1990; Geary, Hoard, Byrd-Craven, & Desoto, 2004; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Goldman, Pellegrino, & Mertz, 1988; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan, Hanich, & Kaplan, 2003a; Jordan & Montani, 1997; Murphy, Mazzocco, Hanich, & Early, 2007). The majority of the latter studies have focused on specific arithmetical competencies (Ostad, 1997, 1999) or on the relation between kindergarten and first-grade competence in number, counting, and arithmetic and mathematics achievement 1 to 3 years later (Geary, Bailey, & Hoard, 2009; Landerl, Bevan, & Butterworth, 2004; Locuniak & Jordan, 2008; Mazzocco & Thompson, 2005). Studies of the mechanisms (e.g., working memory) contributing to these mathematical deficits have generally been short term and largely focused on the early elementary years (Bull, Espy, & Wiebe, 2008; Geary, Hoard, Nugent, & Byrd-Craven, 2008; Passolunghi, Mammarella, & Altoe`, 2008; H. L. Swanson, Jerman, & Zheng, 2008). In a comprehensive 3-year longitudinal study of elementary school children’s arithmetic skills, Andersson (2008, 2010) demonstrated persistent deficits associated with MLD (e.g., in retrieving arithmetic facts) that could not be attributed to their below average working memory, confirming earlier studies (Garnett & Fleischner, 1983; Geary, 1990; Goldman et al., 1988).
In the context of a first- to fifth-grade prospective study of mathematics achievement, our first goal was to chart the start points and 5-year growth trajectories of key numerical and arithmetical competencies of children with MLD and their LA peers relative to typically achieving (TA) children. Our second goal was to determine the extent to which these competencies and their growth mediate group differences in school entry mathematics achievement and 5-year achievement growth. To isolate the numerical and arithmetic deficits specific to group differences in mathematics achievement, we assessed whether the same or different predictors emerged for word reading achievement and controlled for the contributions of general cognitive abilities that influence learning in many if not all academic areas. A further control was provided by teacher assessments of students’ in-class attention. The study contributes to our understanding of the sources of mathematical learning disability and deficits by providing one of the longest prospective studies of these children. It is one of the few studies that has combined multiyear assessments of numerical and arithmetic cognition, general cognitive abilities, and in-class attention in order to isolate deficits specific to poor mathematics learning.
General Cognitive Abilities
General cognitive abilities include intelligence, working memory, and processing speed that in some combination affect learning in many academic domains, including mathematics. Their measurement is thus critical for identifying more specific mathematical cognition deficits that contribute to the poor achievement of children with MLD and their LA peers. Measures of these abilities tend to be moderately to strongly correlated with one another—the source of which is vigorously debated (Ackerman, Beier, & Boyle, 2005; Conway, Cowan, Bunting, Therriault, & Minkoff, 2002)— but each appears to assess some unique competencies (Carroll, 1993). Although the importance of these general abilities for predicting mathematics achievement and performance on mathematical cognition measures has been established, the majority of these studies have not simultaneously assessed all of them and most of those that have assessed all three general abilities have not done so longitudinally (but see Andersson, 2010).
Performance on measures of intelligence and working memory may be correlated, in part, because they both require attentional and inhibitory control (Engle, Tuholski, Laughlin, & Conway, 1999), but these mechanisms appear to be more important for the central executive than for intelligence. Performance on measures of intelligence, in contrast, is much more dependent on the ability to think logically and systematically (Embretson, 1995) and is particularly important for understanding new ideas and dealing with complex, nuanced domains, including mathematics. In a study of more than 70,000 students, Deary, Strand, Smith, and Fernandes (2007) found that intelligence assessed at age 11 years explained nearly 60% of the variation on national mathematics tests at age 16 years. Other studies have confirmed the importance of intelligence for mathematics achievement, above and beyond the influence of motivational factors, such as self-efficacy (e.g., Chamorro-Premuzic, Harlaar, Greven, & Plomin, 2010).
Working memory represents the ability to hold an idea or piece of information in mind while simultaneously engaging in other mental processes. At the core is the central executive, which is expressed as attention-driven control of active information in two representational systems (Baddeley & Hitch, 1974; Cowan, 1995). These are a language-based phonological loop (Baddeley, Gathercole, & Papagno, 1998) and a visuospatial sketch pad (Logie, 1995). The relation between performance on measures of these components of working memory and mathematics achievement tests and on specific mathematical cognition tasks (below) is well established (Andersson, 2008; DeStefano & LeFevre, 2004; Geary et al., 2007; H. L. Swanson & Sachse-Lee, 2001), with some but not all of these studies simultaneously controlling for intelligence (Geary et al., 2008; McLean & Hitch, 1999).
Whether assessed concurrently or 1 or more years earlier, the higher the capacity of the central executive, the better the performance on measures of mathematics achievement and cognition (Bull et al., 2008; Mazzocco & Kover, 2007; Passolunghi, Vercelloni, & Schadee, 2007; Toll, Van der Ven, Kroesbergen, & Van Luit, 2011; Van der Ven, Kroesbergen, Boom, & Leseman, 2011). The importance of the phonological loop and visuospatial sketch pad varies with the complexity and content of the mathematics being assessed (Bull et al., 2008; Geary et al., 2007). The phonological loop appears to be important for processes that involve the articulation of numbers, as in counting (Krajewski & Schneider, 2009), and may be related to arithmetic fact retrieval (Chong & Siegel, 2008; Geary, 1993). The visuospatial sketch pad appears to support learning and performance in a broader number of mathematical domains, such as word problems (Geary, Saults, Liu, & Hoard, 2000; H. L. Swanson et al., 2008).
Whatever the underlying source of the correlations among measures of processing speed, intelligence, and working memory, processing speed may contribute to mathematics achievement and to the development of specific mathematical competencies, independent of the influence of working memory (Bull & Johnston, 1997) and intelligence (Taub, Floyd, Keith, & McGrew, 2008). The key point is that simultaneous control of intelligence, working memory, and processing speed is necessary for isolating the specific mathematical cognition deficits that contribute to the low start points and slow achievement growth of groups of MLD and LA children.
Mathematical Cognition
Relative to TA children, children with MLD have severe and persistent deficits in the ability to develop long-term memory representations of basic arithmetic facts or retrieve them once they are learned (Andersson, 2010; Chan & Ho, 2010; Geary, 1993; Jordan et al., 2003a; Jordan, Hanich, & Kaplan, 2003b; Russell & Ginsburg, 1984). It is not that these children cannot remember any facts. Rather, they remember fewer of them and when they do retrieve they commit more errors and especially more atypical errors, such as 5 × 4 = 40; a more common error is 24 (Geary, 1990; Jordan et al., 2003a; Mazzocco, Devlin, & McKenney, 2008). These children also have delays in the development of procedures for solving arithmetic problems. Many of these children eventually learn basic procedures but are one to several years behind their TA peers; the magnitude of this deficit and the extent of the delay appear to vary with the complexity (e.g., number of steps) of the procedure (Andersson, 2010). The retrieval and procedural competencies of LA children are between those of children with MLD and TA children. Although LA children may not fully close the achievement gap, their competencies become more similar to TA children than to children with MLD across grades (Chong & Siegel, 2008; Mazzocco et al., 2008).
Although there are fewer studies, the associated results suggest that children with MLD and, to a lesser extent, their LA peers may have deficits in the potentially inherent systems that represent small exact magnitudes (≤4), approximate magnitudes of larger quantities, or in mapping Arabic numerals and other mathematical notations, such as the number line, onto these representational systems (Butterworth, 2005; Geary et al., 2008; Holloway & Ansari, 2009; Koontz & Berch, 1996; Landerl et al., 2004). It is not currently known if these number representation or mapping deficits contribute to these children’s fact retrieval deficit and procedural delays.
We used three tasks to assess retrieval, procedural, and number processing development. The first is the addition strategy assessment, which involves a trial-by-trial categorization of how children solve simple (e.g., 4 + 3) and more complex (e.g., 17 + 6) problems and provides information on retrieval and procedural competence. First graders often use counting to solve such problems, sometimes with (finger-counting strategy) and sometimes without (verbal counting strategy) using their fingers (Siegler & Shrager, 1984). The min and sum procedures are two common ways that children count (Groen & Parkman, 1972). Min counting involves stating the larger valued addend and then counting a number of times equal to the value of the smaller one. Both addends are counted, starting from one, with the sum procedure; the less common max procedure involves stating the smaller addend and counting the larger one. Counting results in the development of long-term memory representations of basic facts, which then support the use of memory-based processes (Siegler & Shrager, 1984); specifically, direct retrieval of arithmetic facts and decomposition (e.g., 6 + 7 is solved by retrieving the answer to 6 + 6 and then adding 1).
The Number Sets Test was one of two number measures used in this study. It assesses the speed with which children process and add sets of objects and Arabic numerals to match a target number (e.g., whether ‘•• 3’ = ‘5’). Using signal detection methods, Geary et al. (2009) demonstrated that a sensitivity measure, d-prime, is correlated with mathematics but not reading achievement above and beyond the influence of general cognitive abilities. The processes underlying this sensitivity are not yet known and may include a combination of basic numerical processes and representations, which have been the focus of intense study and debate (De Smedt, Verschaffel, & Ghesquière, 2009; Holloway & Ansari, 2008; Iuculano, Moro, & Butterworth, 2010; Iuculano, Tang, Hall, & Butterworth, 2008; Piazza et al., 2010; Rousselle & Noël, 2007). The possibilities include low acuity in the brain and cognitive systems for representing exact small quantities or approximate larger ones, resulting in poor discrimination of collections of objects or symbolic representation of quantities when the magnitudes are similar (e.g., ‘8 vs. 9’; Koontz & Berch, 1996; Piazza et al., 2010; Price, Holloway, Räsänen, Vesterinen, & Ansari, 2007); poor mapping of Arabic numerals onto the underlying representation of magnitude (De Smedt & Gilmore, 2011; Iuculano et al., 2010; Landerl & Kölle, 2009; Rousselle & Noël, 2007); or numerosity coding (Butterworth, 2010). The latter refers to a poor understanding of cardinal value and the idea that numbers are composed of sets of smaller magnitude numbers (Butterworth, 2010; Geary et al., 2004).
The second assessment was a number line task (Siegler & Opfer, 2003). As with processing of simple numerals and magnitudes of collections of items, the mechanisms that support children’s learning of the mathematical number line are debated (Feigenson, Dehaene, & Spelke, 2004; Núñez, 2009). One view is that children use the system for representing approximate magnitudes to understand the magnitude of numerals on the line. In this view, children are predicted to place numerals on number lines in a way that conforms to the natural logarithm (nl) of these numbers; nl is thought to represent acuity in distinguishing magnitudes such that differences between smaller ones are more distinct (e.g., 2 from 3) than differences between larger ones (e.g., 19 from 20; Feigenson et al., 2004; Gallistel & Gelman, 1992). Whatever the underlying representational system, the key for academic mathematics is the insight that the distance between two consecutive whole numbers is the same, regardless of position on the line (i.e., the line is linear). Indeed, accuracy in making linear placements on number lines is predictive of later mathematics achievement (Booth & Siegler, 2006).
Current Study
As noted, the central goals were to document the first- to fifth-grade start points and growth trajectories in number processing, arithmetic fact retrieval, and arithmetic procedural competencies of groups of MLD, LA, and TA children and to determine how differences in these competences contribute to group differences in mathematics school-entry start point and achievement growth through fifth grade, while simultaneously controlling for general cognitive abilities and in-class attention. As detailed below, we used several clustering and growth curve procedures applied to mathematics achievements scores in an attempt to identify MLD and LA groups. The results, however, indicated the key mathematics start point and growth variables were distributed as a single group; that is, distinct MLD and LA groups did not emerge. This result is theoretically important, as it suggests children with MLD and their LA peers are part of the normal distribution of mathematical competence but with different cutpoints for group categorization (Murphy et al., 2007). Knowing that children in MLD and LA groups in this literature may come from lower ends of a single normal distribution, however, is not useful for the development of eligibility criteria for special education programs and associated remedial interventions, nor is it useful for integrating the current findings with the extant literature on MLD. We thus sought to create MLD and LA groups that would allow for this integration and provide guidelines for use in educational settings.
Based on previous studies that have identified start point and growth as critical and potentially independent aspects of mathematical development (Duncan et al., 2007; Fuchs, Geary, Compton, Fuchs, & Hamlett, 2010; Geary, in press; Jordan, Kaplan, Oláh, & Locuniak, 2006; Jordan, Kaplan, Ramineni, & Locuniak, 2009), growth curve analyses were used to identify groups of children with low start point (i.e., low mathematics scores in kindergarten) and slow growth; average start point and slow growth; and, average start point and average growth. The mean mathematics achievement scores of these groups (below) were consistent with those found for MLD, LA, and TA groups, respectively, in previous studies (e.g., Murphy et al., 2007). Moreover, the word reading achievement of the MLD and LA groups was consistent with previous contrasts of groups of children with combined MLD and poor reading achievement and children with MLD only (e.g., Andersson, 2010; Geary et al., 2000; Hanich et al., 2001). In other words, the groups of children identified with the procedure used here show achievement patterns consistent with those of similarly named groups in this literature.
Method
Participants
All kindergarten children from 12 elementary schools that serve families from a wide range of socioeconomic backgrounds were invited to participate. Parental consent and child assent were received for 37% (n = 311) of these children, and 288 of them completed the first year of testing. The mathematics curriculum when the children began the study was Investigations in Number, Data, and Space (Russell, Tierney, Mokros, & Economopoulos, 1999), and most continued with this curriculum throughout the grades analyzed here.
Of the 288 children, 249 remained in the study through the end of fourth grade (86% retention). Thirteen children were then dropped because their mathematics achievement was in the average range (part of the control sample) and they had moved at some point during the study and thus assessments were costly, and nine dropped between fourth and fifth grade. The remaining 227 children were invited to continue with the second 5-year phase of the study, and 192 consented. Parental consent for administration of the first-grade working memory battery (added after the initial consent to enter the study was obtained) had been obtained for 185 of the 192. Of these children, eight had missing data on one or more measures (e.g., due to experimental error, inattention during testing) over the 5 years covered by this study. The net result was complete mathematics and reading achievement scores, first- and fifth-grade working memory assessments, and first- to fifth-grade mathematical cognition data, inclusive, for 177 of children. These children composed the current sample. During fifth grade, 22 children who scored below the 30th percentile on the state mathematics assessment in fourth grade and were thus considered at risk were added to the overall study. They began in fifth grade and are not included in the current analyses.
We used measures of verbal and nonverbal IQ in the analyses (below) but also have an estimated full-scale IQ based on national norms (Wechsler, 1999). For the retained sample, full-scale IQ was average (M = 102, SD = 14), as were their first-grade (based on national norms; Wechsler, 2001) standard scores for mathematics (M = 94, SD = 13) and reading (M = 108, SD = 16). There are, of course, ways to estimate missing values assuming the data were lost randomly (e.g., Luke, 2004), but because the children who dropped from the study or had missing data for other reasons had lower full-scale IQ scores (M = 94, SD = 14) than the retained sample, the random assumption was not met. Thus, we elected to not estimate missing data. Despite this limitation, the retained sample is in the average range with respect to national norms and a substantial range of scores is maintained for these tests; intelligence (74 to 149), mathematics (minimum range of 3rd to 99th national percentile ranking per grade), and reading (minimum range of 3rd to 99th national percentile ranking per grade).
To identify groups of MLD and LA children, we analyzed raw kindergarten to fifth-grade mathematics achievement scores in R (Ihaka & Gentleman, 1996) using model-based clustering (Mclust; Fraley & Raftery, 2002, 2005, 2006). The Mclust method identifies the best fitting solution, based on the Bayesian information criterion (a preferred criterion for choosing among solutions; Nylund, Asparouhov, & Muthén, 2007), for 1–9 class solutions with various parameterizations of the covariance matrix for each number of classes (spherical, diagonal, and ellipsoidal distributions; equal and variable class volumes; equal and variable class shapes; and equal and variable orientations). However, the Mclust procedure indicated that a one-class solution was the best fit, failing to identify distinct groups of MLD and LA children as noted above.
To generate start point and growth variables, we ran a free curve slope intercept model in Mplus Version 5.21 (Muthén & Muthén, 1998–2007). This model assessed the “intercept,” which can be interpreted as each participant’s level, independent of the growth trajectory, at the point at which level and trajectory are closest to orthogonal (Wood, 2010). The results yielded intercept (start point) and slope (growth) estimates that were not highly correlated (r = .29, p < .001); based on the slope loadings (0.53, 1.06, 1.89, 2.61, 3.58, and 4.51 for kindergarten through fifth grade), the point at which the intercept was assessed (i.e., where trajectory and level are closest to being orthogonal) occurs just before our kindergarten assessment. Slope and intercept scores from this model were entered into Mclust, which again indicated that a one-class solution was the best fit. We then used the 25th percentile for these variables as cutoffs to identify children with a low start point and slow growth (n = 16, six boys); average start point and slow growth (n = 29, eight boys); and average start point and average growth (n = 132, 68 boys). Based on mean mathematics achievement scores (below), the first and second groups were consistent with patterns associated with MLD and LA, respectively, whereas the final group served as a TA control.
To obtain a power of 0.80, the effect size for contrasts of the MLD and TA groups would need to be at least 0.67 for one-tailed tests and 0.76 for two-tailed tests, with corresponding values of 0.51 and 0.58, respectively, for the LA and TA contrasts (Cohen, 1988). Nearly all of the key effects (below) exceeded these values, indicating adequate power for these contrasts. The values for the MLD and LA contrasts were 0.78 (one-tailed) and 0.90 (two-tailed) and many but not all of the effects (below) exceeded these values, indicating nonsignificant contrasts of these two groups need to be interpreted with caution.
The mean ages at the time of the first-grade mathematical cognition assessment varied between 80 (SD = 3) and 82 (4) months and differed significantly across groups (p < .05), but not practically. The racial composition of the TA and LA groups did not differ (χ2 = 1.36, p > .50); White (80%, and 82%, respectively), Asian (5%, 4%), Black (5%, 4%), and mixed race (5%, 4%), with the parents of the remaining children identifying them as Native American, Pacific Islander, or unknown. The racial composition of the MLD group differed from that of the two other groups (χ2 = 37.91, p < .0002); White (36%), Black (14%), and more than one race (50%). We did not have information on parental socioeconomic status, but we did have information on the percentage of children eligible for free or reduced price lunches at the 12 schools from which the initial sample was drawn. More children in the MLD group than the LA or TA groups started in schools with a higher percentage of free or reduced price lunches, but the group differences were not significant (M = 41%, 35%, 31%, respectively, p > .25).
Standardized Measures
Intelligence
The children were administered the Raven’s Coloured Progressive Matrices (CPM; Raven, Court, & Raven, 1993), a nontimed test that is considered to be an excellent measure of fluid intelligence, and the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). The CPM scores were standardized based on the 287 children who were administered the test (M = 100, SD = 15), and the WASI standard scores were converted to the same metric. The Vocabulary subtest was used as a measure of verbal IQ, and the mean of the CPM and Matrix Reasoning tests was used as a measure of nonverbal IQ.
Achievement
Mathematics and reading achievement were assessed with the Numerical Operations and Word Reading subtests from the Wechsler Individual Achievement Test–II: Abbreviated (Wechsler, 2001), respectively. The easier Numerical Operations items assess number discrimination, rote counting, number production, and basic addition and subtraction. More difficult items include multidigit addition and subtraction, multiplication and division, and rational number problems solved with pencil and paper. The easier Word Reading items require matching and identifying letters, rhyming, beginning and ending sounds, and phoneme blending. The more difficult items assess accuracy of reading increasingly difficult words.
Mathematical Tasks
Addition strategy choices
Fourteen simple addition problems and six more complex problems were horizontally presented, one at a time, at the center of a computer monitor. The simple problems consisted of the integers 2 through 9, with the constraint that the same two integers (e.g., 2 + 2) were never used in the same problem; ½ of the problems summed to 10 or less, and the smaller valued addend appeared in the first position for ½ of the problems. The complex items were 16 + 7, 3 + 18, 9 + 15, 17 + 4, 6 + 19, and 14 + 8.
The child was asked to solve each problem (without pencil and paper) as quickly as possible without making too many mistakes. It was emphasized that the child could use whatever strategy was easiest to get the answer and was instructed to speak the answer into a microphone that was interfaced with the computer, which in turn recorded reaction time (RT) from onset of problem presentation to microphone activation. After each problem was solved, the child was asked to describe how he or she had got the answer. Based on the child’s description and the experimenter’s observations, the trial was classified based on problem-solving strategy; the four most common were counting fingers, verbal counting, retrieval, and decomposition. Counting trials were further classified as min, sum, or max. The combination of experimenter observation and child reports immediately after each problem is solved has proven to be a useful measure of children’s strategy choices (Geary, 1990; Siegler, 1987). The validity of this information is supported by RT patterns; finger-counting trials have the longest RTs, followed respectively by verbal counting, decomposition, and direct retrieval (e.g., Geary, Hoard, & Bailey, 2011; Siegler, 1987).
Four summary variables, two for simple problems and two for complex ones, were created to represent children’s competence in solving addition problems. The first variable represented the extent to which memory-based processes were used in problem solving. When the children correctly used memory-based strategies, they directly retrieved the answer 62% of the time and used decomposition 38% of the time. The memory-based strategy for complex problems was decomposition, as direct retrieval was uncommon. The second, procedural competence variable was coded such that high scores represented frequent and accurate use of the min procedure, whether or not the children used their fingers, and low scores represented frequent counting errors: (2 × frequency of min counts) + (frequency of sum counts) – (total frequency of counting errors). For children who used counting on only a subset of problems, scores were adjusted based on the percentage of counting trials. The maximum scores were 28 and 12, respectively, for simple and complex addition.
Number sets
Two types of stimuli are used: objects (e.g., stars) in a half-inch square and an Arabic numeral (18-pt font) in a half-inch square. Stimuli are joined in domino-like rectangles with different combinations of objects and numerals. These dominos are presented in lines of five across a page. The last two lines of the page show three 3-square dominos. Target sums (5 or 9) are shown in large font at the top the page. On each page, 18 items match the target; 12 are larger than the target; six are smaller than the target; and six contain 0 or an empty square.
The tester begins by explaining two items matching a target sum of 4 and then uses the target sum of 3 for practice. The measure is then administered. The child is told to move across each line of the page from left to right without skipping any; to “circle any groups that can be put together to make the top number, 5 (9)”; and to “work as fast as you can without making many mistakes.” The child has 60 s per page for the target 5 and 90 s per page for the target 9. Time limits were chosen to avoid ceiling effects and to assess fluent recognition and manipulation of quantities. Performance was consistent across target number and item content (e.g., whether the rectangle included Arabic numerals or shapes) and thus combined to create an overall frequency of hits (alpha, α = .88), correct rejections (α = .85), misses (α = .70), and false alarms (α = .90; Geary et al., 2007). The variable used here was based on the d-prime measure; specifically, (hits – false alarms) × (maximum RT/actual RT). The maximums, as noted, were 120 and 180 s for targets of 5 and 9, respectively. Thus, the scores of children who completed the test in less than the maximum time were adjusted upward. The adjustment was made because nearly all children completed the test in more than the maximum time when they were younger (Geary et al., 2009), but some of them completed the test in less time in later grades. The adjustment enabled us to maintain the sensitivity of the test, despite faster processing times across grades.
Number line estimation
A series of twenty-four 25-cm number lines containing a blank line with two endpoints (0 and 100) was presented, one at a time, to the child with a target number (e.g., 45) in a large font printed above the line. The child’s task was to mark the line where the target number should lie (Siegler & Booth, 2004); a pencil-and-paper version was used in first grade and a computerized version, where the child used the mouse to mark the line, was used thereafter. Siegler and Opfer (2003) used group-level median placements fitted to linear and ln models to make inferences about the modal representation children were using to make the placements; for individual difference analyses, they used an accuracy measure. Accuracy is defined as the absolute difference between the child’s placement and the correct position of the number. For the number 45, placements of 35 and 55 produce difference scores of 10. The overall score is the mean of these differences across trials. An alternative approach is to classify whether the child used a linear or ln representation to make the placement on a trial by trial basis (Geary et al., 2007, 2008). This is a useful approach in earlier grades, when such variation is common, but is not as useful in later grades, when most children appear to rely on a linear representation for most trials, albeit individual differences in accuracy remain.
Working Memory and Processing Speed
The Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) consists of nine subtests that assess the central executive, phonological loop, and visuospatial sketch pad. All of the subtests have six items at each span level. Across subtests, the span levels range from one to six to one to nine. Passing four items at one level moves the child to the next. At each span level, the number of items (e.g., words) to be remembered is increased by one. Failing three items at one span level terminates the subtest. Working memory spans for the central executive, phonological loop, and visuospatial sketch pad are the mean span scores for the corresponding subtests.
Central executive
The central executive was assessed with three dual-task subtests. Listening Recall requires the child to determine if a sentence is true or false and then recall the last word in a series of sentences. Counting Recall requires the child to count a set of 4, 5, 6, or 7 dots on a card and then to recall the number of counted dots at the end of a series of cards. Backward Digit Recall is a standard-format backward digit span.
Phonological loop
Digit Recall, Word List Recall, and Nonword List Recall are standard span tasks with differing content stimuli; the child’s task is to repeat words spoken by the experimenter in the same order as presented by the experimenter. In the Word List Matching task, a series of words, beginning with two words and adding one word at each successive level, is presented to the child. The same words, but possibly in a different order, are then presented again, and the child’s task is to determine if the second list is in the same or different order than the first list.
Visuospatial sketch pad
Block Recall is another span task, but the stimuli consist of a board with nine raised blocks in what appears to the child as a “random” arrangement. The blocks have numbers on one side that can only be seen from the experimenter’s perspective. The experimenter taps a block (or series of blocks), and the child’s task is to duplicate the tapping in the same order as presented by the experimenter. In the Mazes Memory task, the child is presented a maze with more than one solution and a picture of an identical maze with a path drawn for one solution. The picture is removed and the child’s task is to duplicate in the path in the response booklet. At each level, the mazes get larger by one wall.
Processing speed
Two rapid automatized naming (RAN) tasks assessed processing speed (Denckla & Rudel, 1976; Mazzocco & Myers, 2003). Although the RAN does not assess all of the multiple components of processing speed (Carroll, 1993), it does assess the educationally relevant facility of serially encoding arrays of visual stimuli, as with words and multidigit Arabic numerals (Wolf, Bowers, & Biddle, 2000). The child is presented with five letters or numbers to first determine if the child can read the stimuli correctly. After these practice items, the child is presented with a 5 × 10 matrix of incidences of these same letters or numbers and is asked to name them as quickly as possible without making any mistakes. RT is measured via a stopwatch. RTs for letter and number naming were highly correlated in each grade (rs = .75 to .84, p < .0001), and thus we used their mean.
In-Class Attention
The Strength and Weaknesses of ADHD-Symptoms and Normal-Behavior (SWAN) measure of in-class attention was used (J. M. Swanson et al., 2008). The measure includes items that assess attentional deficits and hyperactivity but the scores are normally distributed, based on the behavior of a typical child in the classroom. The nine item (e.g., “Gives close attention to detail and avoids careless mistakes”) measure was distributed to the children’s second-, third-, and fourth-grade teachers, who were asked to rate the behavior of the child relative to other children of the same age on a 1 (far below) to 7 (far above) scale. Scores across grades were highly correlated (rs = .70 to .77), and thus we used their mean (α = .88). If the child had only one or two scores these were used, and if no scores were available (16% of the sample) then the corresponding group mean was used.
Procedure
Assessments
The CPM and WASI were administered in the spring of kindergarten and first grade, respectively, and the achievement tests were administered every spring beginning in kindergarten. The mathematical cognition and RAN tasks were administered in the fall of first grade to fifth grade, inclusive. The only exception was the number line task, which was administered in the fall of first grade but in the spring of second to fifth grade, inclusive, to reduce fall assessment times. The majority of children were tested in a quiet location at their school site and occasionally on the university campus or in a mobile testing van. Testing in the van occurred for children who had moved out of the school district or to a nonparticipating school and for administration of the WMTB-C (e.g., on the weekend or after school). The WMTB-C was administered in first (mean age = 84 months, SD = 6) and fifth (M = 128 months, SD = 5) grades. The mathematical cognition and achievement assessments required between 20 and 40 minutes and the WMTB-C required about 60 minutes per assessment.
Analyses
In some cases, standard statistical procedures were used, but the primary focus was on group differences in start point and rate of first- to fifth-grade change in achievement scores, in processing speed, and on the mathematical cognition variables. Therefore, multilevel modeling was used (i.e., PROC MIXED). Linear and quadratic (grade2) slopes for grade and intercept values were random effects. The intercept values estimate the mean raw scores in first grade (coded 0), and the grade variables represent rate of change from first to fifth grade; second, third, fourth, and fifth grades were coded 1 to 4, respectively. The TA children were the contrast group for the initial analyses, and then models were rerun to provide a contrast of the MLD and LA groups. The repetitive procedure allowed us to obtain pairwise contrasts for intercept and slope values.
Results
The variables used in our analyses are summarized in Table 1, and the results are presented in three sections. The first addresses the goal of documenting group differences in start point and growth for the mathematical cognition variables. Group differences in achievement start point and growth, as well as general cognitive abilities and in-class attention, are described in the second section, and the third addresses the goal of identifying mediators of group differences in mathematics achievement start point and growth.
Table 1.
Summary of Measures
| Variable | Task | Coding |
|---|---|---|
| Mathematical cognition | ||
| Number sets fluency | Number sets | Hits minus false alarms, adjusted for reaction time (RT) |
| Number line error | Number line | Mean of absolute difference between correct placement and child’s actual placement |
| Simple addition retrieval | Addition strategy choice | The number of simple problems correctly solved (out of 14) with direct retrieval or decomposition |
| Simple addition procedural competence | Addition strategy choice | Sophistication and accuracy of counting procedures used for problem solving |
| Complex addition decomposition | Addition strategy choice | The number of complex problems (out of 6) correctly solved with decomposition |
| Complex addition procedural competence | Addition strategy choice | Sophistication and accuracy of counting procedures used for problem solving |
| General cognitive and in-class attention | ||
| Verbal intelligence | Vocabulary subtest of WASI (Wechsler, 1999) | Standard scores from national norms (M= 100, SD= 15) |
| Nonverbal intelligence | Matrix Reasoning subtest of WASI (Wechsler, 1999); CPM (Raven et al., 1993) | Mean of scores from national WAIS norms and standardized CPM scores (M= 100, SD= 15) |
| Central executive | WMTB-C (Pickering & Gathercole, 2001) | The mean of subtest span scores for first and fifth grade |
| Phonological loop | WMTB-C (Pickering & Gathercole, 2001) | The mean of subtest span scores for first and fifth grade |
| Visuospatial sketch pad | WMTB-C (Pickering & Gathercole, 2001) | The mean of subtest span scores for first and fifth grade |
| Processing speed | Rapid Automatized Naming (Denckla & Rudel, 1976) | The mean of number naming and letter naming RTs for first to fifth grade, inclusive |
| In-class attention | SWAN (J. M. Swanson et al., 2008) | Mean teacher ratings across second to fourth grade, inclusive |
Note. WASI = Wechsler Abbreviated Scale of Intelligence; CPM = Raven’s Coloured Progressive Matrices; WMTB-C = Working Memory Test Battery for Children; SWAN = Strength and Weaknesses of ADHD-Symptoms and Normal-Behavior.
Growth in Mathematical Cognition
Number sets
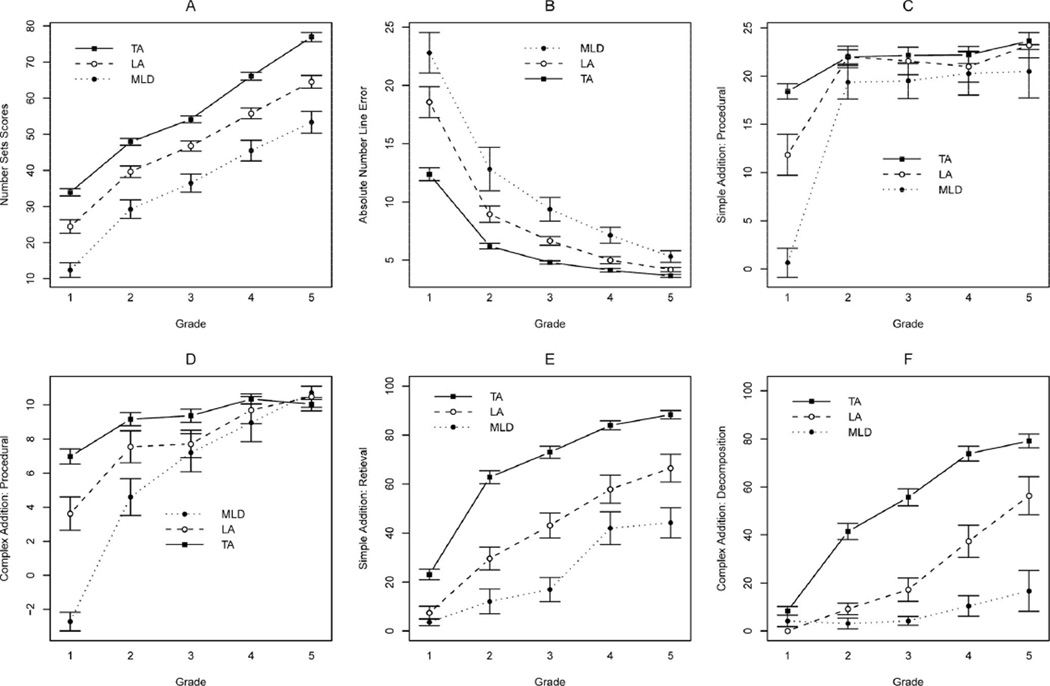
The gist is significant group differences are evident at the beginning of first grade. The children in the MLD and LA groups showed some catch-up to their TA peers from first to second grade, but growth was essentially parallel across groups after that point. The pattern is shown in Figure 1 (Panel A) and the corresponding mixed model results in Table 2. The intercept value is the estimate of the TA children’s first-grade score, and the intercept on MLD and LA are the intercept differences comparing these groups with the TA group, respectively (ps < .0001, d = 2.21, 0.88, respectively, for first-grade scores). The linear slope variable estimates average linear grade-to-grade change for the TA group, whereas the quadratic slope variable estimates the acceleration or deceleration in the rate of change across grades. As shown in Table 2, the TA children’s scores increased an average of 10.58 points from one grade to the next, with no significant acceleration or deceleration.
Figure 1.
Number sets scores (Panel A) and absolute errors for number line (Panel B). Procedural competence scores for simple (Panel C) and complex (Panel D) addition. Maximum scores of 28 and 12 would be received if the verbal and finger-counting strategies were always executed without error and with application of the min procedure. Percentage of the 14 simple addition problems that was correctly solved using retrieval or decomposition (Panel E) and percentage of the six complex addition problems that was correctly solved using decomposition (Panel F). Brackets are standard errors. Plotted using the Sciplot package in R (Morales, 2010). MLD = mathematical learning disability; LA = low achieving; TA = typically achieving.
Table 2.
Mixed Model Results for Growth and Group Membership Effects for Mathematical Cognition Tasks
| Estimate | Number sets fluency |
Number line error |
Simple addition procedure |
Complex addition procedure |
Simple addition retrieval |
Complex addition decomposition |
|---|---|---|---|---|---|---|
| Intercept | 34.89* | 11.87* | 18.91* | 7.11* | 3.63* | 0.42* |
| Linear slope (grade) | 10.58* | −5.42* | 2.33* | 1.93* | 4.87* | 1.80* |
| Quadratic slope (grade2) | −0.04 | 0.87* | −0.31 | −0.30* | −0.68* | −0.24* |
| Intercept on MLD | −21.42* | 10.24* | − 16.17* | −9.32* | −3.29* | −0.40 |
| Intercept on LA | −9.49* | 5.94* | −5.62* | −3.12* | −2.53* | −0.46* |
| Slope on MLD | 3.87* | −3.64* | 12.13* | 4.61* | −3.55* | − 1.76* |
| Slope on LA | 2.20 | −3.06* | 4.43* | 0.93 | − 1.79* | − 1.56* |
| Quadratic slope on MLD | − 1.12* | 0.38 | −2.28* | −0.55a | 0.73* | 0.26* |
| Quadratic slope on LA | −0.75* | 0.44* | −0.83 | −0.02 | 0.42* | 0.35* |
| Variance intercept | 85.45* | 32.58* | 6.11 | 6.67* | 6.94* | 0.16 |
| Variance grade | 8.35 | 15.55* | 2.86 | 0.61 | 4.15* | 1.81* |
| Variance quadratic grade | 0.38 | 0.40* | 0.07 | 0 | 0.23* | 0.12* |
Note. MLD = mathematical learning disability; LA = low achieving.
p = .057.
p < .05.
The positive linear slope on MLD and LA effects indicate that the average rate of change for these groups was higher than that of the TA children, but the negative quadratic contrasts indicate the rate of catching up decelerated across grades. In fact, examination of Figure 1 (Panel A) suggests that most of the catch-up occurred between first and second grade, and a mixed model including only Grades 2 to 5, inclusive, confirmed no significant linear or quadratic slope on MLD or LA effects (ps > .15). The contrast of the MLD and LA groups confirmed the significant intercept difference (p < .0005), but the linear and quadratic slope on MLD effects were not significant (ps > .25), indicating parallel across-grade changes for these two groups.
Number line
The gist is that group differences are evident at the beginning of first grade but the gap between the TA and LA groups closed by the end of fifth grade. The magnitude of the gap between the TA and MLD groups narrowed by about a third across grades but nonetheless remained significant at the end of fifth grade. The pattern is shown in Figure 1 (Panel B), and the corresponding mixed model results can be seen in Table 2. In first grade (intercept), the TA group had smaller errors than the MLD (d = 1.55) and LA (d = 0.92) groups, but the significant linear slope on MLD and LA effects indicate catch-up after this; the quadratic effects reflect more catch-up between first and second grade than in later grades. The contrast of the MLD and LA groups confirmed the significant intercept difference (p < .05), but the linear and quadratic slope on MLD effects were not significant (ps > .50), indicating parallel across-grade change.
Comparison of pairwise means (honestly significant difference test) revealed that the advantage of the TA children over the LA children was significant in first (d = 0.97) through fourth (d = 0.60) grade, inclusive (ps < .05), but not fifth (p > .05). The TA children maintained a significant advantage over their MLD peers in all grades (ps < .05), but the gap decreased in magnitude from first (d = 1.55) to fifth (d = 0.97) grade. In contrast, a consistent gap between the MLD and LA groups was evident across first (d = 0.59) to fifth (d = 0.78) grade.
Addition procedural competence
The gist is that significant group differences in procedural competence are evident in first grade, but the gap closed by the beginning of second grade for simple problems and third grade for more complex ones. Procedural competence scores for simple and complex addition are shown in Figure 1 (Panel C, Panel D, respectively), and the corresponding mixed model results are shown in Table 2. The TA children started first grade with higher scores than children in the MLD and LA groups for both simple (ps < .002, d = 2.20, 0.64, respectively) and complex (ps < .002, d = 2.66, 1.69) addition. The significant linear grade on MLD and LA effects confirmed catch-up for simple addition, and pairwise contrasts (HSD) revealed no significant group differences from second to fifth grade (ps > .05), inclusive. The same pattern emerged for complex addition, except that the LA group closed the gap with the TA group by second grade and the MLD group by third. The contrasts of the MLD and LA groups confirmed significant intercept differences (ps < .0001, d = 1.21) and a significant linear slope on MLD effect (ps < .02) reflected the convergence of group means; pairwise comparisons revealed the MLD and LA groups did not differ after first grade (ps > .05).
Addition retrieval and decomposition
Substantial group differences in frequency of correct retrieval of simple addition facts were evident at the beginning of first grade. The advantage of the TA children over their LA peers widened from first to second grade, followed by a narrowing of the gap that nonetheless remained significant in fifth grade. In comparison to children with MLD, TA children started first grade with a substantial advantage in use of correct retrieval and widened this advantage across grades. The children with MLD and their LA peers began first grade with similarly low knowledge of addition facts, but the LA children showed more consistent growth and established an advantage over the children with MLD by the beginning of third grade. Few of the children in any of the groups used decomposition at the beginning of first grade, but the TA children showed rapid, steady growth through fifth grade. A corresponding growth spurt started 2 years later for LA children, but the children with MLD showed little growth from first to fifth grade.
The percentage of simple addition problems correctly solved with direct retrieval or decomposition is shown in Figure 1 (Panel E), and the mixed model results are shown in Table 2; the analyses were based on raw scores, not percentages. For simple addition, the TA group started with an advantage over the MLD (d = 1.3) and LA (d = 0.84) groups. All of the groups improved across grades, but the negative linear slope on MLD and LA effects indicate that the advantage of the TA children widened. The quadratic slope effect (− 0.68) indicates that the rate of the TA children’s across-grade improvement slowed and the quadratic slope on LA effect indicates the same, but with a less dramatic change in the across-grade slope (i.e., −.68 + .42 = −.26). The quadratic slope on MLD effect (i.e., −.68 + .73 = .05) indicates the rate of change tended to accelerate across grades, but the effect was not significant (p > .10); in other words, the across-group contrasts were significantly different but the quadratic slope effect was not significantly different from 0 for the MLD group.
Pairwise comparisons confirmed the TA advantage over the MLD and LA groups in all grades. Relative to first grade, the gap between the TA and MLD groups increased from 1.3 to 2.0 SDs, whereas the gap between the TA and LA group decreased from 0.84 to 0.45 SDs. An advantage for the LA group over the MLD group emerged in third grade and remained through fifth (ps < .05, d = 1.07, 0.54, 0.82, respectively).
As shown in Figure 2 (Panel F), first graders rarely used decomposition to solve complex addition problems. The significant intercept effect in the last column of Table 2 indicates the TA children used decomposition to correctly solve 0.42 of the six complex problems, on average. The negative intercept on MLD and LA effects indicates that children in these groups almost never used decomposition in first grade; for example, the estimate for the MLD children is 0.02 problems (i.e., 0.42 – 0.40), on average. The linear and quadratic slope effects indicate the TA children’s use of decomposition increased significantly across grades and that this rate of improvement decelerated across grades. The pattern is clearly shown in Figure 1, with substantial gains from first to second grade and continuing but less dramatic grade-to-grade changes thereafter. The significant negative linear slope on MLD and LA effects reflects less average grade-to-grade increase in the correct use of decomposition relative to that for the TA children. However, this trend is qualified by the significant quadratic slope on LA effect, specifically suggesting the LA children began to catch up with the TA children.
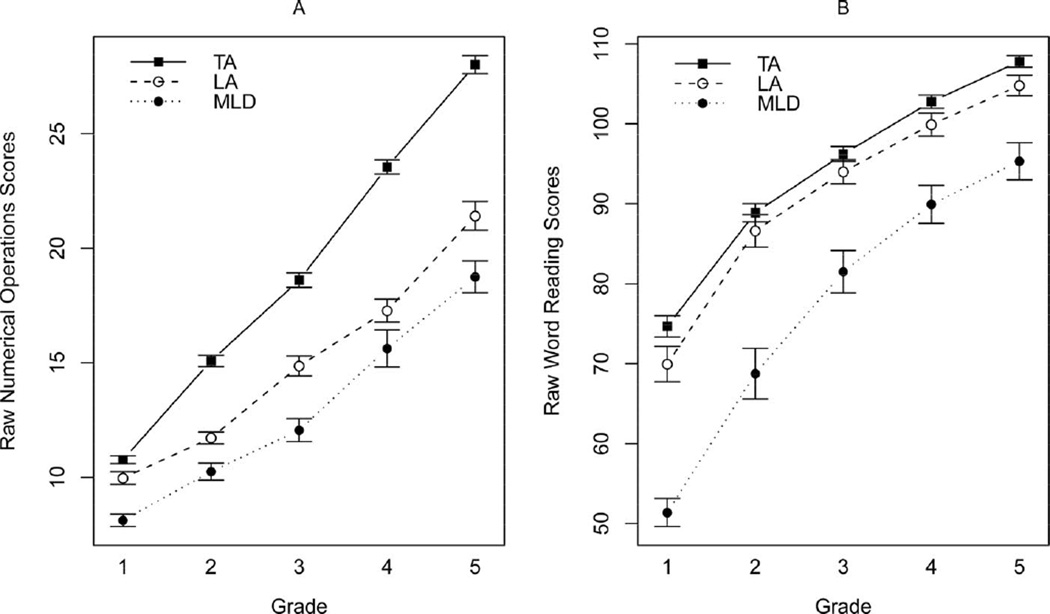
Figure 2.
Raw Numerical Operations (Panel A) and Word Reading (Panel B) scores. Brackets are standard errors. Plotted using the Sciplot package in R (Morales, 2010). MLD = mathematical learning disability; LA = low achieving; TA = typically achieving.
Indeed, the pattern in Figure 2 (Panel F) suggests similar grade-to-grade increases in use of decomposition for the TA and LA children after first grade. A mixed model that only estimated change from second to fifth grade, inclusive, revealed a nonsignificant linear slope on LA effect (p > .10) and a trend for a positive quadratic slope on LA effect (p = .067). That is, the linear increases were similar across the TA and LA groups, and there was a trend for the slope for the LA group to increase across grades relative to that of the TA group. The pattern for the MLD children is more complex, as their use of decomposition did not differ from 0 until third grade and then increased slightly thereafter; this is reflected in the significant quadratic slope on MLD effect.
In any case, pairwise comparisons indicated that the TA children correctly used decomposition to solve complex addition problems more often than their LA and MLD peers from second to fifth grades (ps < .05), inclusive. Their advantage over the LA children decreased from second (d = 1.22) to fifth (d = 0.61) grade and increased over the children with MLD (d = 1.64, 1.90 for second and fifth grade, respectively). Pairwise differences across the LA and MLD groups were significant for fourth (d = 1.02) and fifth (d = 1.03) grade (ps < .05).
Group Differences in Achievement, General Cognitive Ability, and In-Class Attention
The just described group differences in start point and growth on the mathematical cognition tasks identify potential mediators of the group differences in mathematics achievement start point and growth described below. In this section, we turn our attention to group differences in intelligence, working memory, processing speed, and in-class attention to identify other potential mediators of group differences in mathematics achievement.
Achievement
The first- to fifth-grade Numerical Operations and Word Reading scores shown in Table 3 are national percentiles (Wechsler, 2001), and the corresponding raw scores are shown in Figure 2 (Panel A, Panel B, respectively); pairwise contrasts (honestly significant difference test) are shown as subscripts in Table 3. Consistent with the earlier described classification procedure, the MLD group had a significantly lower intercept than the TA group and a more shallow linear slope (p < .0001); there was a significant quadratic slope effect (p < .05), but this did not differ across groups. The intercept differences across the TA and LA groups were small but significant (p < .05), and the slope effect was more substantive (p < .0001). By design, the intercepts differed significantly across the MLD and LA groups (p < .005) but the slopes did not (p > .50).
Table 3.
Intelligence and Achievement Scores
| Grade |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First |
Second |
Third |
Fourth |
Fifth |
|||||||||
| Group | N | Verbal IQ | Nonverbal IQ | WR | NO | WR | NO | WR | NO | WR | NO | WR | NO |
| MLD | 16 | 90a (13) | 95a (25) | 23a (14) | 10a (7) | 26a (24) | 10a (10) | 30a (19) | 7a (7) | 31a (17) | 10a (12) | 31a (18) | 8a (8) |
| LA | 29 | 99a (15) | 98ab (11) | 61b (25) | 28b (20) | 65b (24) | 19a (13) | 56b (20) | 19b (13) | 54b (21) | 14a (11) | 54b (20) | 19a (14) |
| TA | 132 | 106b (14) | 104b (10) | 68b (28) | 40b (25) | 68b (26) | 49b (28) | 62 (24) | 48c (27) | 62b (23) | 53b (26) | 63b (22) | 57b (26) |
Note. Group means with different subscripts differ significantly (p< .05) when using the honestly significant difference test. Parenthetical values are standard deviations. MLD = mathematical learning disability; LA = low achieving; TA = typically achieving; WR = Word Reading; NO = Numerical Operations.
Word reading scores are also plotted in Figure 1 (Panel B), and associated analyses confirmed the TA and LA groups did not differ on intercept values or for linear or quadratic slopes (ps > .10). Both groups had significantly higher intercepts than the MLD group (ps < .0001). The linear (estimate = 5.5, p < .005) and quadratic (estimate = −0.7, p = .053) slope effects contrasting the TA and MLD groups were significant. In combination, they indicate that the latter group showed some catch-up with the former group and that the rate of catch-up declined across grades. The linear slope contrast across the LA and MLD group also suggested some catch-up, but the effect was only a trend (p = .092); the quadratic contrast of these groups was not significant (p > .50).
Intelligence
The TA children had higher verbal IQ scores than the children in the two other groups (ps < .05; honestly significant difference test), who in turn did not differ (see Table 3). The TA children also had a higher mean nonverbal score than the children with MLD, but no other group contrasts were significant.
Working memory
Across groups, mean span scores increased substantially from first to fifth grade for the phonological loop (d = 1.08), visuospatial sketch pad (d = 1.90), and central executive (d = 1.66; see Table 4). A mixed analysis of variance yielded significant effects for group, F(2, 174) = 43.10; year, F(1, 174) = 637.31; and component, F(2, 348) = 184.04 (ps < .0001). There was a trend for the group by year interaction (p = .065), and the group by component and year by component interactions were significant (ps < .01), as was the three-way, F(4, 348) = 5.57, p < .0002. The latter emerged because first-grade phonological spans were higher than visuospatial spans for the LA and TA groups (ps <.01) and marginally so for the MLD group (p < .01), as contrasted with nonsignificant differences in fifth grade for the LA group (ps > .25) and a reversal of this pattern for the TA group (p < .01).
Table 4.
Mean Working Memory Spans
| First-grade working memory spans |
Fifth-grade working memory spans |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phonological loop |
Visuospatial sketch pad |
Central executive |
Phonological loop |
Visuospatial sketch pad |
Central Executive |
|||||||
| Group | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD |
| MLD | 2.3a | 0.7 | 2.0a | 0.6 | 1.4a | 0.4 | 3.6a | 0.5 | 3.3a | 0.8 | 2.3a | 0.4 |
| LA | 3.4b | 0.6 | 2.6b | 0.6 | 1.9b | 0.5 | 3.9b | 0.6 | 3.8a | 0.8 | 2.9b | 0.4 |
| TA | 3.4b | 0.5 | 2.9c | 0.5 | 2.3c | 0.5 | 4.0b | 0.6 | 4.4b | 0.7 | 3.2c | 0.5 |
Note. Group means with different subscripts differ significantly (p< .05) when using the honestly significant difference test. MLD = mathematical learning disability; LA = low achieving; TA = typically achieving.
The significances of the group-level contrasts (honestly significant difference test) are indicated by subscripts for the corresponding mean scores in Table 4. With the exception of the visuospatial sketch pad in fifth grade, the spans for the MLD group were lower than those of the LA group in both grades (ds = 0.55 to 1.50). The LA and TA groups had comparable phonological loop spans in both grades, but the TA group had advantages on the visuospatial sketch pad (d = 0.55, 0.80, for first and fifth grade, respectively) and central executive (d = 0.80, 0.67) in both grades. The advantage of the TA group over the MLD group was significant for all components of working memory in both grades (ds = 0.73 to 2.00).
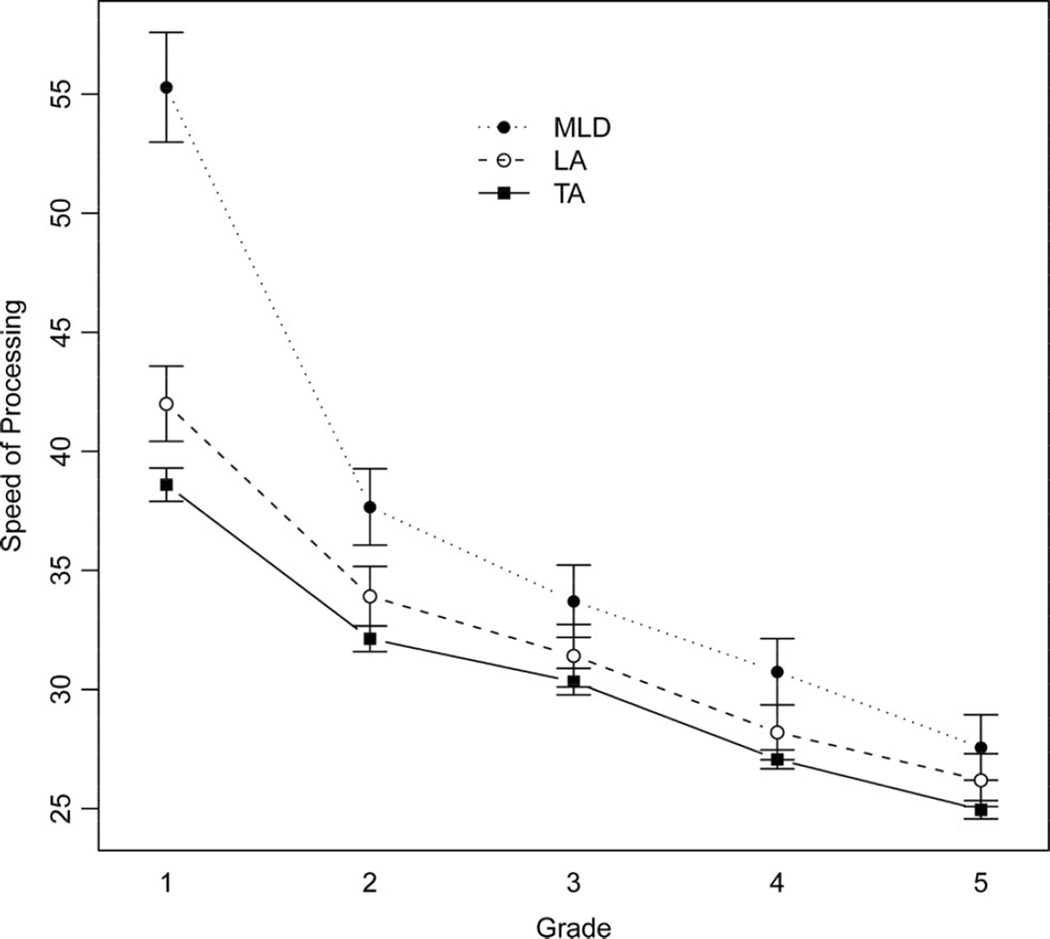
Processing speed
Mean RAN RTs are plotted in Figure 3. The mixed models confirmed the TA group had a lower intercept (faster start point RTs) than the MLD and LA groups, but the linear and quadratic slope effects on MLD were significant (ps < .0001) and reflected across-grade catch-up. There was a trend for a linear slope on LA effect (p = .07), also indicating catch-up. The contrast of the LA and MLD groups confirmed a significant intercept on MLD effect and significant linear and quadrate slope effects on MLD (ps < .001); the advantage of the LA group disappeared across grades. Pairwise comparisons of means revealed no differences between the LA and TA groups in any grade (ps > .05); the TA group had an advantage over the MLD group in first (d = 1.88), second (d = 1.0), and fourth (d = 0.73) grades.
Figure 3.
Mean letter and number naming reaction times. Brackets are standard errors. Plotted using the Sciplot package in R (Morales, 2010). MLD = mathematical learning disability; LA = low achieving; TA = typically achieving.
Based on the potential number-processing deficits of children with MLD and their LA peers a follow-up repeated-measures analysis of variance was conducted, with type (i.e., number vs. letter) and grade as within-subjects factors and group as a between-subjects factor. Group differences in processing speed were confirmed, but the type by group (p > .50) and grade by type by group (p > .50) interactions were not significant, indicating the group differences in processing speed were not specific to numbers.
In-class attention
The groups differed significantly on the SWAN measure, F(2, 174) = 30.67, p < .0001. The TA group (M = 5.20, SD = 1.02) had higher scores than the MLD (M = 3.43, SD = 0.79, d = 1.96) and LA (M = 4.07, SD = 1.03, d = 1.01) groups (honestly significant difference test, ps < .05), who in turn did not differ.
Mediational Analyses
The mediational analyses focused on the sources of the group differences in mathematics achievement start point (intercept) and growth (slope). To do this, we contrasted the intercept difference for Numerical Operations comparing the TA and MLD groups and the slope difference comparing the TA group with a combined MLD/LA group. The procedures followed Baron and Kenny (1986), using Sobel’s (1988) test. If the hypothesized mediational effect is significant and reduces the group contrast to nonsignificance (p > .05) then full mediation is implied; partial mediation is implied if the group contrast remains significant.
First, a stepwise regression was used to identify the best potential set of mediators for the intercept and slope variables. Because the former estimates mathematical achievement at the beginning of schooling, potential mediators were restricted to tasks that were administered in kindergarten and first grade and that showed significant differences across the TA and MLD groups. The corresponding variables included the number sets scores, number line error, simple addition retrieval, procedural competence for simple and complex addition, verbal and nonverbal IQ, the three components of working memory, and RAN RT. These variables were also used to predict kindergarten Word Reading scores. These scores were chosen because they are the closest to the estimated intercept point for Numerical Operations and provide a means of determining if the predictors are unique to beginning mathematics. Potential predictors of the Numerical Operations slope variable included these variables as well as slope measures for simple addition retrieval and complex addition decomposition (estimated with the same free curve slope intercept models used for Numerical Operations), in-class attention, and fifth-grade working memory scores. We did not run a Word Reading contrast for the Numerical Operations slope because the Word Reading differences across the MLD and TA groups narrowed across grades, not widened as with Numerical Operations.
A set of three predictors emerged for the Numerical Operations intercept scores, F(3, 173) = 38.80, p < .0001, R2 = .40; in order of selection, number sets scores (β = .40, t = 4.92, p < .0001), complex addition decomposition (β = .20, t = 2.76, p < .01), and simple addition retrieval (β = .15, t = 2.19, p < .05). A different set of predictors emerged for Word Reading scores, F(5, 171) = 32.75, p < .0001, R2 = .49; RAN RT (β = −.33, t = −5.02, p < .0001); nonverbal IQ (β = .22, t = 3.54, p < .0005); phonological loop (β = .15, t = 2.13, p < .05); central executive (β = .16, t = 2.22, p < .05); and verbal IQ (β = .13, t = 1.98, p < .05). A set of five predictors emerged for the Numerical Operations slope scores, F(5, 171) = 46.63, p < .0001, R2 = .58; number sets scores (β = .14, t = 2.03, p < .05); in-class attention (β = .23, t = 3.76, p < .0005); simple addition retrieval (β = .30, t = 5.11, p < .0001); first-grade central executive (β = .24, t = 3.70, p < .0005); and the slope variable estimated for complex addition decomposition (β = .17, t = 2.85, p < .005).
These potential mediators were first tested sequentially and independently. The sequence followed the order of selection from the stepwise regression. If the first variable fully mediated the group difference, the procedure was stopped. Otherwise, the procedure continued until a full mediator was found or it was determined that no single variable fully mediated the group difference. In this situation, all of the potential mediators were assessed simultaneously.
Numerical operations intercept
The first variable tested, number sets scores, emerged as a full mediator (z = 5.91, p < .0001) of the intercept difference across the TA and MLD groups. As a contrast, RAN RT emerged as a full mediator (z = 3.65, p < .0005) of the group difference in Word Reading scores. Number sets scores and RAN RT scores were significantly correlated (r = − .51, p< .0001), but the relation between the former variable and Numerical Operations intercept scores remained significant after controlling for RAN RTs; the magnitude of the relation between numbers sets scores and Numerical Operations intercept scores did not change significantly (p > .10) when comparing estimates before (β = .67, t = 9.97) to after (β = .58, t = 7.48) controlling for RAN RTs. The strength of relation between RAN RT and Word Reading scores declined (p < .05) comparing estimates before (β = −.58, t = −8.22) to after (β = −.44, t = −5.51) controlling for number sets scores, but the latter relation remained highly significant (p < .0001).
Numerical operations slope
Each of the five predictors emerged as a partial mediator of the group difference (MLD/LA vs. TA; zs > 3.87, ps < .0001), and the group contrast remained significant (t = 6.84, p < .001), with the simultaneous control of all five predictors. However, before control of these partial mediators, 49% of the variance in Numerical Operations slope scores was explained by the group contrast, as compared to 9% after control, a significant reduction (t = 14.41, p < .0001).
Discussion
Our first goal was to determine the start points and 5-year growth trajectories for groups of MLD and LA children, as contrasted with their TA peers, on several key mathematical competencies. Our second goal was to determine if group differences in start point and growth in these competencies contributed to group differences in mathematical achievement above and beyond the influence of general cognitive abilities and in-class attention. We flesh out the results with respect to these goals, following brief discussion of classification issues.
Classification of MLD and LA Children
Our failure to find distinct MLD and LA groups with the cluster and growth curve analyses suggests the children composing these groups are part of the normal distribution of mathematics achievement. Nevertheless, selection for special education or related interventions must be based on selection criteria, whether or not the chosen students form qualitatively distinct groups. The study of the deficits and delays of these children and how to remediate them is also facilitated by using specific cut points, albeit these are necessarily arbitrary. In this literature, children with MLD tend to have grade-to-grade mathematics achievement scores at or below the 10th national percentile (Jordan et al., 2003b; Jordan & Montani, 1997; Murphy et al., 2007), and this was the case with our MLD sample. The low start point of this group confirms the importance of basic school-entry quantitative competencies (Duncan et al., 2007; Jordan et al., 2009). The current results indicate the factors underlying their low start point and their slow growth overlap but are not identical, and they also indicate that their slow growth is related to several specific mathematical-cognition deficits and delays and not to across-the-board deficits (below). Our results also confirm that children with MLD are typically poor readers (Geary, 1993; Jordan et al., 2003b), and we extend this literature with the finding that their low entry-level word reading ability is mediated by a different mechanism (speed of retrieving letters and numbers from long-term memory; Denckla & Rudel, 1976) than their low entry-level mathematics achievement.
Low achieving children often have average intelligence and reading ability but nevertheless persistently score below the 25th percentile on mathematics achievement tests (Jordan et al., 2003b; Murphy et al., 2007), and this was again the case with our sample. Our LA group was characterized by typical entry-level mathematics achievement but grade-to-grade growth that paralleled that of their MLD peers. In terms of identification for special education or other interventions, our findings and those of related studies (Locuniak & Jordan, 2008) suggest that children at risk for MLD are in the lower quartile of basic quantitative competencies in kindergarten, but, at this time, identification of LA children will require documentation of two or more years of below average growth in mathematics achievement after school entry.
Start Point and Growth in Mathematical Competencies
The most extensively studied mathematical competencies of children with MLD and their LA peers are their difficulties in committing basic arithmetic facts to long-term memory or retrieving these facts once they have been learned (Andersson, 2010; Cawley et al., 2001; Chan & Ho, 2010; Geary, 1993; Jordan et al., 2003a; Ostad, 1997, 1999) and their use of developmentally immature procedures for solving these problems (Chong & Siegel, 2008; Geary et al., 2004). The current study confirms these findings and documents their developmental trajectories across the elementary school years. Butterworth and colleagues (Butterworth, 2005; Landerl et al., 2004), in contrast, have argued that the core deficit can be traced to difficulty in accessing representations of numerical magnitude (but see Butterworth, 2010). Our results address this hypothesis as well.
Retrieval deficits
The retrieval deficits of our children with MLD do not appear to be as severe as those documented by Jordan et al. (2003a), whose sample showed little to no growth in their ability to retrieve facts across second and third grade, but they were substantive. The retrieval deficit of our children with MLD was characterized by very slow growth, relative to their TA and LA peers, especially through third grade. Although there was growth in the ability to retrieve basic facts, the children with MLD did not catch up with their TA peers, and their trajectory suggests that they will not do so, as found by Andersson (2010) for up through sixth grade and Ostad (1997) through seventh. The retrieval start point for our LA group was similar to that of the children with MLD, but their growth trajectory was similar to that of TA children from second grade forward. Nevertheless, their performance in fifth grade was comparable to that of TA second graders.
We caution that, despite normal growth from second grade forward, these results do not mean LA children cannot have retrieval deficits or, if they do, that it is more of a developmental delay. Indeed, the poor retrievers in Jordan et al.’s (2003a) study had mathematics achievement scores somewhat higher than those of our LA group but had been identified using a forced retrieval task (i.e., the children were instructed to remember only the answers to simple addition and subtraction problems). With the use of this task, Jordan et al. and others (Geary et al., 2011) have identified a subgroup of LA children with retrieval deficits that appear to be as trenchant as or more so than those of children with MLD. The combined studies suggest many LA children identified based on mathematics achievement tests can learn basic facts nearly as well as their TA peers, although they may be delayed in doing so, but a subgroup of them may have more persistent deficits that are only identifiable using Jordan’s forced retrieval task (Jordan et al., 2003a; Jordan & Montani, 1997).
In any event, the LA children’s third-to-fifth grade improvement in their ability to solve simple problems with direct retrieval was complemented by an increase in the use of decomposition to solve complex problems, consistent with reliance on memory retrieval for use of both of these strategies. Our data, however, do not speak to the source of this improved performance. One possibility is developmental change in the mechanisms that support memory formation and retrieval (Cho, Ryali, Geary, & Menon, 2011; Rivera, Reiss, Eckert, & Menon, 2005), but brain imaging studies will be needed to explore this possibility. Although the retrieval competencies of the children with MLD were slowly improving, these did not result in a parallel increase in the use of decomposition. The children with MLD may not have a firm conceptual understanding of how to decompose numbers to aid in their problem solving, as suggested by Geary et al. (2004) and Butterworth (2010), but again this hypothesis remains to be directly confirmed.
Procedural delays
The early deficits of the MLD and LA groups in the accurate use of the min counting procedure to solve simple and complex problems are clearly a developmental delay, 1 year for simple problems and 1 to 2 years for slightly more complex ones. The pattern confirms Geary’s (1993) prediction, and our 5-year assessment extends the results of other empirical studies (Chong & Siegel, 2008; Geary et al., 2004). Equally important, the sharp increase in procedural skills contrasts with slow retrieval growth and suggests that different mechanisms underlie the development of these competencies.
We note, however, that our procedural competence variables assess only one type of procedure. Studies that have assessed competence in solving more complex problems, as in use of trading to solve multidigit problems (e.g., 64 – 19 = ?), have revealed that children with MLD commit more procedural errors than their TA peers, but it is not clear if these are developmental delays or more persistent deficits (Andersson, 2010; Raghubar et al., 2009). Either way, this is not the final word, as critical related competencies, including children’s conceptual understanding of the base-10 system and their ability to solve fractions, are only beginning to be studied. Available evidence suggests substantive deficits for children with MLD and many of their LA peers (Andersson, 2010; Chan & Ho, 2010; Mazzocco & Devlin, 2008).
Number deficits
Children with MLD are sometimes described as having a poor number sense (Gersten, Jordan, & Flojo, 2005), although precise definition and measurement of this concept have eluded the field (see Berch, 2005) and debate continues regarding the underlying mechanisms (e.g., Butterworth, 2010; Iuculano et al., 2008; Núñez, 2009). Among the proposed component skills are fast implicit recognition of numerical relations (e.g., that 9 > 5, 52 > 39) and fluent manipulation, mapping, and integration of these relations to meet current task demands (Butterworth, 2005). On the basis of performance of TA children and children with dyscalculia (identified based on low performance on a timed arithmetic test) on tasks that assess very basic number competencies, Landerl et al. (2004) suggested “understanding of numerosity, and a poor capacity to recognize and discriminate small numerosities . . . may prevent dyscalculics developing the normal meanings for numerical expressions and lead to their difficulties in learning and retaining information regarding numbers” (p. 122).
Although more complex than the tasks used by Landerl et al. (2004), the number sets variable falls under the number sense umbrella, as scores are likely to be based on the speed and accuracy of accessing the quantities of small sets of objects and Arabic numerals and combining them to match a target quantity. The ability to map Arabic numerals onto corresponding quantities may be a related critical skill (Rousselle & Noël, 2007). Geary et al. (2009) demonstrated that performance on this task was predictive of mathematics but not reading achievement above and beyond the influence of general cognitive abilities. This finding and the task demands of test items suggest individual differences on this measure are driven in part by variation in very basic number-related abilities, but at this time the specific nature of these abilities is not fully known. Number line tasks are sometimes included as a number sense measure, because they involve an understanding of relative magnitude and require a mapping of magnitudes onto the line (Berch, 2005), although this too is debated (Núñez, 2009).
Our finding for the Number Sets Test suggests that the MLD and LA groups are at below average and very low ends of the normal distribution of some aspects of number sense, respectively. The results may be consistent with Landerl et al.’s (2004) hypothesis that one core deficit associated with poor mathematics achievement is slow access to representations of numerical magnitude, but this conclusion is tentative until the suite of component processes underlying performance on the test is better understood. Whatever the processes, the children in MLD and LA groups showed growth in these competencies but no indication of catching up to the TA children. Their slow growth and lack of catch-up stand in clear contrast to their developing procedural competencies, suggesting again different underlying mechanisms and a persistent disadvantage on basic “number sense” measures (De Smedt et al., 2009; Holloway & Ansari, 2008; Iuculano et al., 2008; Piazza et al., 2010; Rousselle & Noël, 2007). Whether poor access to numerosities or slow manipulation of them contributes to their fact retrieval deficit, as hypothesized by Butterworth (2005), cannot be directly determined with this study. Whatever the underlying mechanisms, performance on the number sets task is important, as it mediated the mathematics achievement start point difference across the TA and MLD groups and contributed to the slow mathematics achievement growth of the LA and MLD groups.
The developmental pattern was somewhat different for the number line task. Rather than show parallel development across grades, the LA children slowly caught up with their TA peers by the end of fifth grade. The children with MLD narrowed the gap by fifth grade but had not completely closed it. Because we used the same 0 to 100 number line in all five grades, we do not know if a gap would reemerge if the number line where expanded to 0 to 1000 (Booth & Siegler, 2006; Siegler & Opfer, 2003). We suspect it will and will test this hypothesis in follow-up assessments. For now, we can conclude that children with MLD are substantially delayed in the ability to map quantities associated with Arabic numerals onto the mathematical number line. To the extent that development of competence with the number line is dependent on the system for representing approximate magnitudes, our results are consistent with those of Piazza et al. (2010), who found a 5-year delay in the development of the acuity of the approximate number system in children with dyscalculia. Whatever the source of this developmental delay, it may differ to some extent from the source of their relatively poor number sets fluency scores. Definitive conclusions must await studies that assess the relation between performance on our two number tasks and tasks that assess very basic number competencies (Koontz & Berch, 1996; Landerl et al., 2004).
Sources of Achievement Deficits
School-entry performance on the mathematical cognition tasks contributed to individual and group differences for Numerical Operations start point and growth trajectory, as found by Jordan et al. (2009; see also Fuchs et al., 2010). Our results extend theirs by demonstrating these early mathematical cognition competencies are important above and beyond the contributions of general cognitive learning abilities, remain important throughout the elementary school years, and are largely unrelated to word reading ability. More precisely, the mathematical achievement deficits of the children with MLD and their LA peers cannot be attributed to the general cognitive abilities assessed in this study, with two exceptions, the central executive component of working memory and in-class attention. These exceptions replicate previous findings and thus will not be considered further (Andersson, 2010; Bull et al., 2008; Fuchs et al., 2006; Mazzocco & Kover, 2007; Passolunghi et al., 2007; H. L. Swanson & Sachse-Lee, 2001). The contributions here are with the isolation of the specific quantitative competencies that predicted group differences in mathematics achievement start point and achievement growth above and beyond more general factors.
The mediation analyses revealed that the low start point of the children with MLD was fully mediated by poor scores on the Number Sets Test. The implication is that some combination of poor access to representations of quantities associated with small sets and Arabic numerals, deficits in the mechanisms that enable children to map numerals to quantities, or poor ability to add these representations is a core deficit of children with MLD and a deficit that should be addressed in kindergarten. The mediation analyses indicated slow mathematics achievement growth was related to performance on the Number Sets Test and to poor addition fact retrieval and infrequent use of decomposition, as well as to the central executive and in-class attention. Addressing low start point might involve specific instruction on basic quantitative competencies, especially on understanding numbers and the relations among them. This would include knowing the number word and Arabic numeral symbols for numbers, the magnitudes they represent, and fluency in translating between these representations. Addressing slow growth will likely require several simultaneous types of remedial intervention, specifically, instruction on specific mathematical competencies (Gersten et al., 2008), building working memory (Diamond, Barnett, Thomas, & Munro, 2007), and improving on-task behavior in the classroom (e.g., Glynn, Thomas, & Shee, 1973).
Summary and Limitations
Other than that for in-class attention, we did not have measures of more nuanced in-class behavior or instructional information or intrapersonal measures of mathematical self-efficacy or anxiety. This limits the breadth of our conclusions. The exclusion of the 110 children with some missing data is another limitation, although if anything our effects might have been larger with their inclusion, given that their ability scores were lower than those of the sample we analyzed. The Numerical Operations Test assesses basic computational abilities and not mathematical reasoning and problem solving (e.g., word problems), although these types of tests are highly correlated (rs > 0.7; Wechsler, 1992). In any case, we are currently administering problem-solving measures and will present results in a follow-up analysis. Despite these limitations, the study provides one of the longest and most comprehensive studies of MLD and LA groups to date and documents the growth trajectories of key mathematical competencies and the relation between these and group differences in mathematics achievement start point and grade-to-grade growth.
Acknowledgments
David C. Geary acknowledges support from the Eunice Kennedy Shriver National Institute of Child Health and Human Development Grants R01 HD38283 and R37 HD045914. We thank Jennifer Byrd-Craven, Rachel Christensen, Caitlin Cole, Linda Coutts, Mike Coutts, Patricia Hoard, Rehab Mojid, Cy Nadler, Chatty Numtee, Robyn Tenney, Jonathan Thacker, Leah Thomas, Jasmine Tilghman, Erin Twellman, Jessica Wallace, and Katie Waller for help on various aspects of the project.
References
- Ackerman PL, Beier ME, Boyle MO. Working memory and intelligence: The same or different constructs? Psychological Bulletin. 2005;131:30–60. doi: 10.1037/0033-2909.131.1.30. [DOI] [PubMed] [Google Scholar]
- Andersson U. Mathematical competencies in children with different types of learning difficulties. Journal of Educational Psychology. 2008;100:48–66. [Google Scholar]
- Andersson U. Skill development in different components of arithmetic and basic cognitive functions: Findings from a 3-year longitudinal study of children with different types of learning difficulties. Journal of Educational Psychology. 2010;102:115–134. [Google Scholar]
- Baddeley A, Gathercole S, Papagno C. The phonological loop as a language learning device. Psychological Review. 1998;105:158–173. doi: 10.1037/0033-295x.105.1.158. [DOI] [PubMed] [Google Scholar]
- Baddeley AD, Hitch GJ. Working memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 8. New York, NY: Academic Press; 1974. pp. 47–90. [Google Scholar]
- Barbaresi WJ, Katusic SK, Colligan RC, Weaver AL, Jacobsen SJ. Math learning disorder: Incidence in a population-based birth cohort, 1976–82, Rochester, Minn. Ambulatory Pediatrics. 2005;5:281–289. doi: 10.1367/A04-209R.1. [DOI] [PubMed] [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Berch DB. Making sense of number sense: Implications for children with mathematical disabilities. Journal of Learning Disabilities. 2005;38:333–339. doi: 10.1177/00222194050380040901. [DOI] [PubMed] [Google Scholar]
- Berch DB, Mazzocco MMM, editors. Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. Baltimore, MD: Brookes; 2007. [Google Scholar]
- Booth JL, Siegler RS. Developmental and individual differences in pure numerical estimation. Developmental Psychology. 2006;42:189–201. doi: 10.1037/0012-1649.41.6.189. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functions in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology. 2008;33:205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R, Johnston RS. Children’s arithmetical difficulties: Contributions from processing speed, item identification, and short-term memory. Journal of Experimental Child Psychology. 1997;65:1–24. doi: 10.1006/jecp.1996.2358. [DOI] [PubMed] [Google Scholar]
- Butterworth B. Developmental dyscalculia. In: Campbell JID, editor. Handbook of mathematical cognition. New York, NY: Psychology Press; 2005. pp. 455–467. [Google Scholar]
- Butterworth B. Foundational numerical capacities and the origins of dyscalculia. Trends in Cognitive Sciences. 2010;14:534–541. doi: 10.1016/j.tics.2010.09.007. [DOI] [PubMed] [Google Scholar]
- Carroll JB. Human cognitive abilities: A survey of factor-analytic studies. New York, NY: Cambridge University Press; 1993. [Google Scholar]
- Cawley JF, Miller JH. Cross-sectional comparisons of the mathematical performance of children with learning disabilities: Are we on the right track toward comprehensive programming? Journal of Learning Disabilities. 1989;22:250–254. doi: 10.1177/002221948902200409. [DOI] [PubMed] [Google Scholar]
- Cawley JF, Parmar R, Foley TE, Salmon S, Roy S. Arithmetic performance of students: Implications for standards and programming. Exceptional Children. 2001;67:311–328. [Google Scholar]
- Chamorro-Premuzic T, Harlaar N, Greven CU, Plomin R. More than just IQ: A longitudinal examination of self-perceived abilities as predictors of academic performance in a large sample of UK twins. Intelligence. 2010;38:385–392. doi: 10.1016/j.intell.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan BM, Ho CS. The cognitive profile of Chinese children with mathematics difficulties. Journal of Experimental Child Psychology. 2010;107:260–279. doi: 10.1016/j.jecp.2010.04.016. [DOI] [PubMed] [Google Scholar]
- Cho S, Ryali S, Geary DC, Menon V. How do you solve 7 + 8? Decoding brain activity patterns associated with counting and retrieval strategies. Developmental Science. 2011;14:989–1001. doi: 10.1111/j.1467-7687.2011.01055.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong SL, Siegel LS. Stability of computational deficits in math learning disability from second through fifth grades. Developmental Neuropsychology. 2008;33:300–317. doi: 10.1080/87565640801982387. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Conway ARA, Cowan N, Bunting MF, Therriault DJ, Minkoff SRB. A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence. 2002;30:163–183. [Google Scholar]
- Cowan N. Attention and memory: An integrated framework. New York, NY: Oxford University Press; 1995. [Google Scholar]
- Deary IJ, Strand S, Smith P, Fernandes C. Intelligence and educational achievement. Intelligence. 2007;35:13–21. [Google Scholar]
- Denckla MB, Rudel R. Rapid automatized naming (RAN): Dyslexia differentiated from other learning disabilities. Neuropsychologia. 1976;14:471–479. doi: 10.1016/0028-3932(76)90075-0. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Gilmore CK. Defective number module or impaired access? Numerical magnitude processing in first graders with mathematical difficulties. Journal of Experimental Child Psychology. 2011;108:278–292. doi: 10.1016/j.jecp.2010.09.003. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquière P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103:469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- DeStefano D, LeFevre J-A. The role of working memory in mental arithmetic. European Journal of Cognitive Psychology. 2004;16:353–386. [Google Scholar]
- Diamond A, Barnett S, Thomas J, Munro S. Preschool program improves cognitive control. Science. 2007 Nov 30;318:1387–1388. doi: 10.1126/science.1151148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Japel C. School readiness and later achievement. Developmental Psychology. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Embretson SE. The role of working memory capacity and general control processes in intelligence. Intelligence. 1995;20:169–189. [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, Conway ARA. Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General. 1999;128:309–331. doi: 10.1037//0096-3445.128.3.309. [DOI] [PubMed] [Google Scholar]
- Every Child a Chance Trust. The long-term costs of numeracy difficulties. 2009 Retrieved from http://www.everychildachancetrust.org.
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association. 2002;97:611–631. [Google Scholar]
- Fraley C, Raftery AE. Bayesian regularization for normal mixture estimation and model-based clustering (Tech. Rep. No. 486) Seattle: Department of Statistics, University of Washington; 2005. [Google Scholar]
- Fraley C, Raftery AE. MCLUST version 3 for R: Normal mixture modeling and model-based clustering (Tech. Rep. No. 504) Seattle: Department of Statistics, University of Washington; 2006. [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Powell SR, Seethaler PM, Capizzi AM, Fletcher JM. The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology. 2006;98:29–43. [Google Scholar]
- Fuchs LS, Geary DC, Compton DL, Fuchs D, Hamlett CL. The contributions of numerosity and domain-general abilities for school readiness. Child Development. 2010;81:1520–1533. doi: 10.1111/j.1467-8624.2010.01489.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Garnett K, Fleischner JE. Automatization and basic fact performance of normal and learning disabled children. Learning Disability Quarterly. 1983;6:223–230. [Google Scholar]
- Geary DC. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology. 1990;49:363–383. doi: 10.1016/0022-0965(90)90065-g. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Cognitive predictors of individual differences in achievement growth in mathematics: A five-year longitudinal study. Developmental Psychology. doi: 10.1037/a0025510. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Bailey DH, Hoard MK. Predicting mathematical achievement and mathematical learning disability with a simple screening tool: The Number Sets Test. Journal of Psychoeducational Assessment. 2009;27:265–279. doi: 10.1177/0734282908330592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Bailey DH. Fact retrieval deficits in low achieving children and children with mathematical learning disability. Journal of Learning Disabilities. 2011 doi: 10.1177/0022219410392046. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Desoto M. Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology. 2004;88:121–151. doi: 10.1016/j.jecp.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, Byrd-Craven J. Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology. 2008;33:277–299. doi: 10.1080/87565640801982361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Saults SJ, Liu F, Hoard MK. Sex differences in spatial cognition, computational fluency, and arithmetical reasoning. Journal of Experimental Child Psychology. 2000;77:337–353. doi: 10.1006/jecp.2000.2594. [DOI] [PubMed] [Google Scholar]
- Gersten R, Ferrini-Mundy J, Benbow C, Clements DH, Loveless T, Williams V, Banfield M. National Mathematics Advisory Panel, Reports of the task groups and subcommittees. Washington, DC: United States Department of Education; 2008. Report of the Task Group on Instructional Practices. 6-i-6-224. [Google Scholar]
- Gersten R, Jordan NC, Flojo JR. Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities. 2005;38:293–304. doi: 10.1177/00222194050380040301. [DOI] [PubMed] [Google Scholar]
- Glynn EL, Thomas JD, Shee SM. Behavioral self-control of on-task behaviors in an elementary classroom. Journal of Applied Behavior Analysis. 1973;6:105–113. doi: 10.1901/jaba.1973.6-105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman SR, Pellegrino JW, Mertz DL. Extended practice of basic addition facts: Strategy changes in learning disabled students. Cognition and Instruction. 1988;5:223–265. [Google Scholar]
- Groen GJ, Parkman JM. A chronometric analysis of simple addition. Psychological Review. 1972;79:329–343. [Google Scholar]
- Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology. 2001;93:615–626. [Google Scholar]
- Holloway ID, Ansari D. Domain-specific and domain-general changes in children’s development of number comparison. Developmental Science. 2008;11:644–649. doi: 10.1111/j.1467-7687.2008.00712.x. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s mathematical achievement. Journal of Experimental Child Psychology. 2009;103:17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Ihaka R, Gentleman R. R: A language for data analysis and graphics. Journal of Computational and Graphical Statistics. 1996;5:299–314. [Google Scholar]
- Iuculano T, Moro R, Butterworth B. Updating working memory and arithmetical attainment in school. Learning and Individual Differences. 2010 Advance online publication. [Google Scholar]
- Iuculano T, Tang J, Hall CWB, Butterworth B. Core information processing deficits in developmental dyscalculia and low numeracy. Developmental Science. 2008;11:669–680. doi: 10.1111/j.1467-7687.2008.00716.x. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. Arithmetic fact mastery in young children: A longitudinal investigation. Journal of Experimental Child Psychology. 2003a;85:103–119. doi: 10.1016/s0022-0965(03)00032-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. A longitudinal study of mathematical competencies of children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties. Child Development. 2003b;74:834–850. doi: 10.1111/1467-8624.00571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Oláh LN, Locuniak MN. Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Development. 2006;77:153–175. doi: 10.1111/j.1467-8624.2006.00862.x. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology. 2009;45:850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Montani TO. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997;30:624–634. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
- Koontz KL, Berch DB. Identifying simple numerical stimuli: Processing inefficiencies exhibited by arithmetic learning disabled children. Mathematical Cognition. 1996;2:1–23. [Google Scholar]
- Krajewski K, Schneider W. Exploring the impact of phonological awareness, visual-spatial working memory, and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year longitudinal study. Journal of Experimental Child Psychology. 2009;103:516–531. doi: 10.1016/j.jecp.2009.03.009. [DOI] [PubMed] [Google Scholar]
- Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9-year-old students. Cognition. 2004;93:99–125. doi: 10.1016/j.cognition.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Landerl K, Kölle C. Typical and atypical development of basic numerical skills in elementary school. Journal of Experimental Child Psychology. 2009;103:546–565. doi: 10.1016/j.jecp.2008.12.006. [DOI] [PubMed] [Google Scholar]
- Lewis C, Hitch GJ, Walker P. The prevalence of specific arithmetic difficulties and specific reading difficulties in 9-year-old to 10-year-old boys and girls. Journal of Child Psychology and Psychiatry. 1994;35:283–292. doi: 10.1111/j.1469-7610.1994.tb01162.x. [DOI] [PubMed] [Google Scholar]
- Locuniak MN, Jordan NC. Using kindergarten number sense to predict calculation fluency in second grade. Journal of Learning Disabilities. 2008;41:451–459. doi: 10.1177/0022219408321126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logie RH. Visuo-spatial working memory. Hove, England: Erlbaum; 1995. [Google Scholar]
- Luke DA. Multilevel modeling. Thousand Oaks, CA: Sage; 2004. [Google Scholar]
- Mazzocco MMM, Devlin KT. Parts and “holes”: Gaps in rational number sense in children with vs. without mathematical learning disability. Developmental Science. 2008;11:681–691. doi: 10.1111/j.1467-7687.2008.00717.x. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Devlin KT, McKenney SJ. Is it a fact? Timed arithmetic performance of children with mathematical learning disabilities (MLD) varies as a function of how MLD is defined. Developmental Neuropsychology. 2008;33:318–344. doi: 10.1080/87565640801982403. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Kover ST. A longitudinal assessment of executive function skills and their association with math performance. Child Neuropsychology. 2007;13:18–45. doi: 10.1080/09297040600611346. [DOI] [PubMed] [Google Scholar]
- Mazzocco MMM, Myers G. Complexities in identifying and defining mathematics learning disability in the primary school-age years. Annals of Dyslexia. 2003;53:218–253. doi: 10.1007/s11881-003-0011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MMM, Thompson RE. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice. 2005;20:142–155. doi: 10.1111/j.1540-5826.2005.00129.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean JF, Hitch GJ. Working memory impairments in children with specific arithmetic learning difficulties. Journal of Experimental Child Psychology. 1999;74:240–260. doi: 10.1006/jecp.1999.2516. [DOI] [PubMed] [Google Scholar]
- Morales M. The sciplot package: Scientific graphing functions for factorial designs [Computer software] 2010 Available from cran.r-project.org/web/packages/sciplot/index.html.
- Murphy MM, Mazzocco MMM, Hanich LB, Early MC. Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. Journal of Learning Disabilities. 2007;40:458–478. doi: 10.1177/00222194070400050901. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 5th. Los Angeles, CA: Author; 1998–2007. [Google Scholar]
- Núñez R. Numbers and arithmetic: Neither hardwired nor out there. Biological Theory. 2009;4:68–83. [Google Scholar]
- Nylund KL, Asparouhov T, Muthen B. Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural Equation Modeling. 2007;14:535–569. [Google Scholar]
- Ostad SA. Developmental differences in addition strategies: A comparison of mathematically disabled and mathematically normal children. British Journal of Educational Psychology. 1997;67:345–357. doi: 10.1111/j.2044-8279.1997.tb01249.x. [DOI] [PubMed] [Google Scholar]
- Ostad SA. Developmental progression of subtraction strategies: A comparison of mathematically normal and mathematically disabled children. European Journal of Special Needs Education. 1999;14:21–36. [Google Scholar]
- Passolunghi MC, Mammarella IC, Altoe` G. Cognitive abilities as precursors of the early acquisition of mathematical skills during first through second grades. Developmental Neuropsychology. 2008;33:229–250. doi: 10.1080/87565640801982320. [DOI] [PubMed] [Google Scholar]
- Passolunghi MC, Vercelloni B, Schadee H. The precursors of mathematics learning: Working memory, phonological ability and numerical competence. Cognitive Development. 2007;22:165–184. [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, Zorzi M. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116:33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children (WMTB-C) manual. London, England: Psychological Corporation; 2001. [Google Scholar]
- Price GR, Holloway I, Raäsänen P, Vesterinen M, Ansari D. Impaired parietal magnitude processing in developmental dyscalculia. Current Biology. 2007;17:R1042–R1043. doi: 10.1016/j.cub.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Raghubar K, Cirino P, Barnes M, Ewing-Cobbs L, Fletcher J, Fuchs L. Errors in multi-digit arithmetic and behavioral inattention in children with math difficulties. Journal of Learning Disabilities. 2009;42:356–371. doi: 10.1177/0022219409335211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raven JC, Court JH, Raven J. Manual for Raven’s Progressive Matrices and Vocabulary Scales. London, England: Lewis; 1993. [Google Scholar]
- Rivera SM, Reiss AL, Eckert MA, Menon V. Developmental changes in mental arithmetic: Evidence for increased functional specialization in the left inferior parietal cortex. Cerebral Cortex. 2005;15:1779–1790. doi: 10.1093/cercor/bhi055. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Noël M-P. Basic numerical skills in children with mathematical learning disabilities: A comparison of symbolic vs. non-symbolic number magnitude processing. Cognition. 2007;102:361–395. doi: 10.1016/j.cognition.2006.01.005. [DOI] [PubMed] [Google Scholar]
- Russell RL, Ginsburg HP. Cognitive analysis of children’s mathematical difficulties. Cognition and Instruction. 1984;1:217–244. [Google Scholar]
- Russell SJ, Tierney C, Mokros J, Economopoulos K. Investigations in number, data, and space. Glenview, IL: Pearson Scott Foresman; 1999. [Google Scholar]
- Shalev RS, Manor O, Gross-Tsur V. Developmental dyscalculia: A prospective six-year follow-up. Developmental Medicine & Child Neurology. 2005;47:121–125. doi: 10.1017/s0012162205000216. [DOI] [PubMed] [Google Scholar]
- Siegler RS. The perils of averaging data over strategies: An example from children’s addition. Journal of Experimental Psychology: General. 1987;116:250–264. [Google Scholar]
- Siegler RS, Booth JL. Development of numerical estimation in young children. Child Development. 2004;75:428–444. doi: 10.1111/j.1467-8624.2004.00684.x. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Opfer J. The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science. 2003;14:237–243. doi: 10.1111/1467-9280.02438. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Shrager J. Strategy choice in addition and subtraction: How do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Hillsdale, NJ: Erlbaum; 1984. pp. 229–293. [Google Scholar]
- Sobel ME. Direct and indirect effect in linear structural equation models. In: Long JS, editor. Common problems/proper solutions: Avoiding error in quantitative research. Beverly Hills, CA: Sage; 1988. pp. 46–64. [Google Scholar]
- Swanson HL, Jerman O, Zheng X. Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology. 2008;100:343–379. [Google Scholar]
- Swanson HL, Sachse-Lee C. Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important. Journal of Experimental Child Psychology. 2001;79:294–321. doi: 10.1006/jecp.2000.2587. [DOI] [PubMed] [Google Scholar]
- Swanson JM, Schuck S, Mann M, Carlson C, Hartman K, Sergeant J, McCleary R. Categorical and dimensional definitions and evaluations of symptoms of ADHD: The SNAP and the SWAN rating scales. 2008 Retrieved from http://www.aifaonlus.it/index. [PMC free article] [PubMed]
- Taub GE, Floyd RG, Keith TZ, McGrew KS. Effects of general and broad cognitive abilities on mathematics achievement. School Psychology Quarterly. 2008;23:187–198. [Google Scholar]
- Toll SWM, Van der Ven SHG, Kroesbergen EH, Van Luit JEH. Executive functions as predictors of math learning. Journal of Learning Disabilities. 2011 doi: 10.1177/0022219410387302. Advance online publication. [DOI] [PubMed] [Google Scholar]
- Van der Ven SHG, Kroesbergen EH, Boom J, Leseman The development of executive functions and early mathematical skills: A longitudinal approach. British Journal of Educational Psychology. 2011 doi: 10.1111/j.2044-8279.2011.02035.x. Advance online publication. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test. San Antonio, TX: Psychological Corporation; 1992. [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test–II: Abbreviated. San Antonio, TX: Psychological Corporation; 2001. [Google Scholar]
- Wolf M, Bowers PG, Biddle K. Naming-speed processes, timing, and reading: A conceptual review. Journal of Learning Disabilities. 2000;33:387–407. doi: 10.1177/002221940003300409. [DOI] [PubMed] [Google Scholar]
- Wood PK. Developmental models for children’s temperament: Alternatives to chronometric polynomial curves. Infant and Child Development. 2010;20:194–212. [Google Scholar]