Parallel Excitation for B-Field Insensitive Fat-Saturation Preparation

Abstract

Multichannel transmission has the potential to improve many aspects of MRI through a new paradigm in excitation. In this study, multichannel transmission is used to address the effects that variations in B₀ homogeneity have on fat-saturation preparation through the use of the frequency, phase, and amplitude degrees of freedom afforded by independent transmission channels. B₁ homogeneity is intrinsically included via use of coil sensitivities in calculations. A new method, parallel excitation for B-field insensitive fat-saturation preparation, can achieve fat saturation in 89% of voxels with M_z ≤ 0.1 in the presence of ±4 ppm B₀ variation, where traditional CHESS methods achieve only 40% in the same conditions. While there has been much progress to apply multichannel transmission at high field strengths, particular focus is given here to application of these methods at 1.5 T.

The problematic effects of B₀ and B₁ inhomogeneity are encountered daily in clinical MR imaging. B₀ inhomogeneity results in spatially varying off-resonance, which influences both spectral content and accumulated phase within tissue magnetization. Common image manifestations of B₀ inhomogeneity include incomplete fat saturation, off-resonance banding in TrueFISP images, blurring in spiral imaging, and geometric distortions in echo planar imaging. Variations in the B₁ field result in nonuniform tip angles, which introduce spatially dependent contrast and also reduce the efficacy of saturation and inversion preparation.

Recently, there has been increased scientific effort devoted to the potential application of arrays of transmission coils (1,2). Examples include SAR reduction and improvement of B₁ homogeneity and transmission efficiency (3–6), particularly for high field strengths (B₀ ≥ 3 T). Multiple methods have been developed for using optimized amplitudes and phases of the exciting elements (5,7) or using optimized multidimensional radiofrequency (RF) pulses (8–12). With few notable exceptions (13–15), there has been little work directed toward applying parallel transmission to the more common clinical field strength of 1.5 T. Yet shown here, there is at least one problem at low field strengths which can benefit from transmission multichannel transmission array. What is more, only a few works have begun to probe the intrinsic potential of excitation of these devices without multidimensional pulses (14,16).

The hypothesis of this work is that if one could uniquely define the frequency, phase, and amplitude in each voxel of our imaging volume, such that any location can be uniformly excited at its local resonant frequency and with phase of our choosing, many problems related to off-resonance can be reduced or eliminated. Transmission with a standard, homogenous volume coil generates a B₁ field with frequency, bandwidth, and phase determined by the time varying RF amplitude and has limited ability to create excitation profiles that vary spatially. Such control and many appropriate applications have been shown using multidimensional pulses, which usually increase excitation time. On the other hand, parallel transmission can exhibit spatially varying excitation that matches certain slowly varying off-resonance patterns. While we believe parallel transmission in some form can correct many manifestations of B₀ inhomogeneity, we specifically address the common clinical problem of fat saturation.

Fat-saturation preparation or fat/water separation methods are common techniques used to improve contrast in clinical images. Fat appears hyperintense in fast spin echo sequences (17) or short echo time gradient echo images, and can suffer from misregistration and ghosting artifacts. Many of the simplest fat/water separation schemes, such as CHESS (18,19) or SECSI (20), binomial and spatial/spectral pulses (10,21–23), and two-point Dixon (24–26) are relatively fast but cannot compensate for variations in B₀ caused by magnetic susceptibility of tissues, differences at tissue interfaces (e.g., water/air), limited shim compensation, or intrinsic fringe fields. Methods that are insensitive to field inhomogeneities, such as IDEAL (27,28), multidimensional pulses (10,26,27), and inversion-recovery fat suppression methods (29,30) typically have increased acquisition times due to the need to collect additional calibration information or longer spin preparation. In practice, there is still a need for a fast fat suppression method which is insensitive to field inhomogeneities.

In this work, we demonstrate a simple and robust method that uses a parallel transmission array to enhance the effective B₀ and B₁ homogeneity and apply this freedom to improve fat suppression. This method, called Parallel excitAtion for B-field insensitive fat Saturation preparaTion (PABST), reduces the effects of off-resonance on fat saturation by tailoring the frequency of each channel to its local, mean B₀ field. The method does not increase excitation or imaging time and is not ‘‘multidimensional’’ in the traditional definition of gradient modulation during RF application to cover a field of excitation. PABST exploits the inherent ability of a transmission array to easily encode frequency, phase, and amplitude as a function of position, as determined by the spatial location and sensitivity profile of a local excitation channel, to influence the B₁ field during the normal RF application window without gradient activity. It can function with only minor increase in calibration time and does not necessarily require coil sensitivity or frequency maps.

While problems such as nonuniform fat saturation are worse at higher fields, they are widespread at 1.5 T. For this reason, we have adapted our recently developed oncoil current-mode class-D (CMCD) parallel transmitter (31,32) for use in a conventional 1.5 T system for all experimental work shown here. After the description of the general theory of the method, we show the performance of the concept in both simulation and phantom experiments.

THEORY

PABST

Our proposal is that CHESS-type fat-saturation preparation, where we desire all fat spins within a sample to be excited to 90° and subsequently spoiled by gradients, can be improved in the presence of B₀ and B₁ inhomogeneity by instructing each channel to play a narrow-band fat-selective excitation pulse with a frequency centered at the average resonance frequency of spins in the vicinity of the channel. Frequency calibration of a channel is determined through a simple, frequency calibration experiment, or through the use of coil sensitivity data and a frequency map. Assuming that the spatial variation in B₀ is small with respect to the dimensions of a particular coil, such that all of the fat spins (and none of the water) within the coil’s sensitivity lie within the narrow bandwidth of the frequency selective pulse, fat spins will be preferentially excited without deleterious water excitation, though the global inhomogeneity can be quite large.

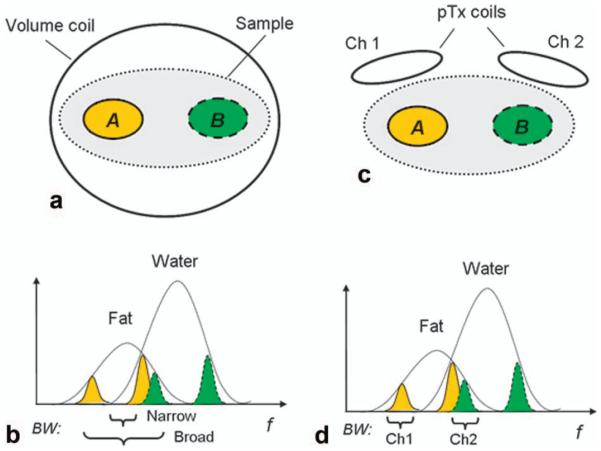
To illustrate this, consider the schematic of a simple situation shown in Fig. 1. Here, the sample has a mean Larmor frequency ω₀. Owing to variations in B₀, we can identify two regions within the sample, A and B (Fig. 1a), that have mean resonant frequencies ω_A and ω_B, respectively, which differ from ω₀. Let us assume the spectrum appears as in Fig. 1b, where the B₀ variation is around 4 ppm, such that the water component of region A overlaps the fat component of region B. If we try to saturate fat within the entire sample (e.g., with a volume coil) using the pulse with narrow bandwidth fat-saturation pulse in Fig. 1b, we will fail to effectively saturate fat in either region A or region B. If the bandwidth of the pulse is broadened to cover the entire fat spectrum, it will also cause unwanted saturation of the water signal within region B.

FIG. 1.

An illustration comparing fat saturation with a single channel to potential improvement with a multichannel technique. A single-channel volume coil (a) has only the ability to define a narrow or broad bandwidth to address spectral broadening (b), and is liable to suffer from incomplete fat excitation or unwanted water saturation, due to spectral overlap. Two independent transmit coils (c) can improve this situation by addressing the smaller bandwidth (d) of a select region, improving fat saturation without water saturation. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In PABST, we replace the volume coil with two surface transmit coils, channel 1 and channel 2 (Fig. 1c), located near regions A and B, respectively. Each surface coil will play out a narrow band fat-saturation pulse centered at the mean Larmor frequency of the nearby tissues, i.e., channel 1 is centered at ω_A and channel 2 at ω_B. The narrow bandwidth of the two pulses (Fig. 1d) is sufficient to include the broadened fat spectra in their respective regions. While the bandwidth of channel 2’s pulse still overlaps the frequency of water spins in region A, if channel 2 is sufficiently far away from region A that its sensitivity is low it will thus have a small effect on excitation of water spins in that area, but will still properly saturate fat spins in region B.

The primary difficulty in PABST is determining the optimal frequencies and amplitudes of the pulses to be played out in each channel of the array. Here, we will describe our realization of PABST through a series of successive optimizations. First, the frequency of each channel is determined through spectral analysis. Second, optimized amplitudes are found to impose a uniform 90° pulse for all fat spins within the sample. We will show how these steps can be performed with and without the explicit knowledge of coil sensitivities and a frequency map, with the expectation that better results can be obtained with coil sensitivity information.

Frequency Calibration of Each Transmission Channel

If we assume that the sensitivity of each channel is relatively confined in space and that the variations in B₀ are smaller than the variation in sensitivity for each channel, an appropriate frequency for each transmission channel can be estimated through spectral analysis of a simple non-selective FID or spin echo experiment. This data can be acquired by sequentially using each element of the transmission array for a non-selective excitation and receiving with all available coils. The resulting spectrum will be inherently weighted by proton density and the coil sensitivity profile of the coil and by extension the resonant frequency of those protons near the coil. The ability to resolve fat and water components in this spectrum is sufficient to meet the condition of small variation of B₀ across a coil’s sensitivity. This spectral information is then used to define the center frequency for fat-saturation preparation pulses from that coil.

Alternatively, if transmit coil sensitivities and a frequency map are available, the local frequency can be calculated using a standard optimization framework. This enables the selection of a frequency more representative of a coil’s region of highest sensitivity or to weight a user-defined region of interest. While many options are available to derive the per-coil frequency assignments with this information, in this study, we used both a least-squares optimization routine and iterative minimization that provided the minimum residual fat signal over the entire sample.

Amplitude Calibration of Each Transmission Channel

If each channel in the parallel array is considered individually, as a surface coil, we will clearly have a nonuniform excitation profile, and fat could only be maximally suppressed along a contour where the magnitude and duration of B₁ place spins completely in the transverse plane. To achieve uniform saturation of fat across the entire sample, it will be necessary for many coils to act in conjunction to create a volumetric excitation. In this case, we must examine how multiple coils with different excitation frequencies interact to affect the spins in an intermediate location where their fields interfere.

A general solution for the superposition field of many RF sources with time varying amplitudes A(t), frequencies exp(jωt), and spatial weights C(x), can be found through frequency analysis. Under the small tip angle approximation, the spectrum of B₁(x,f) in a sample with N transmission coils, where the superposition field is given by

$$B_1\text{sup}(\mathbf{x},t)=\sum _{n=1}^N{C}_n\left(\mathbf{x}\right)A_n\left(t\right){\text{e}}^{j{\omega }_{n}t}$$ [1]

can be found by Fourier analysis

$$B_1(\mathbf{x},f)=𝔍\left(B_{1,\text{sup}}(\mathbf{x},t)\right)=\sum _{n=1}^N{C}_n\left(\mathbf{x}\right)𝔍\left(A_n\left(t\right){\mathrm{e}}^{j{\omega }_n}t\right)$$ [2]

Thus, the combined spectrum is merely the mean of the individual channel spectra weighted by the coil sensitivity at the particular spatial position denoted by x. In the high tip regime, the spectrum can be found through full Bloch simulation or SLR pulse design. A key observation is that if we assume small, smooth variations in B₀ and smooth coil sensitivities, the superposition field will also vary smoothly across the sample. Thus, the average excitation frequency will tend to mimic the trends of the off-resonance variations. This holds true regardless of the number of channels available, though more channels will conceivably be capable of addressing more severe B₀ variations.

While this concept will provide the frequency for each coil, in general the resulting tip angle of the superposition field will be different (typically lower) than a simple on-resonance case. Here, we present two methods for calculating corrected amplitudes.

For simple coil geometries where we can define an “array center,” where the magnitude of the individual coil sensitivities are approximately equal, one solution is to restore the tip angle at the center of the array to 90° by adjusting the B₁ amplitude of all channels by the same amount. Calculation for this correction is straight-forward and requires only a standard tip angle calibration from the array. As an example, consider a cylindrical transmit array, where the magnitude of each channel’s sensitivity at the center is the same. In this case, we can perform two excitations: one with the standard homogeneous pulse and another with the frequency optimized pulse. The B₁ correction factor can then be calculated by dividing the resulting flip angles at the center of the array. This solution corrects the flip angle at the center, but the solution is not necessarily optimized for the entire volume.

A more general and robust solution that makes no assumptions about the coil configuration exists but requires the individual coil sensitivities. This second method uses a least-squares optimization to find unique amplitudes for each transmit channel. While potentially more complicated, this method is more powerful, because it considers the relative off-resonance of a channel, the coil sensitivity profiles, and user-definable locations of maximum fat suppression and minimum water suppression. Beginning with Eq. 2 above, we now allow the B₁ amplitudes to be unique for each channel. We introduce a magnitude term for each channel, A_n, by making the substitution A_n (t) → A_n a (t), where a(t) represents an amplitude modulation envelope that is the same for all channels. In this case, the superposition B₁ field becomes

$$B_1(\mathbf{x},f)=𝔍\left(B_{1\text{sup}}(\mathbf{x},t)\right)=\sum _{n=1}^N{A}_n{C}_n\left(\mathbf{x}\right)𝔍\left(a\left(t\right){\mathrm{e}}^{j{\omega }_{n}t}\right)$$ [3]

The optimized values A_n that give a homogeneous 90° flip angle for fat frequencies can calculated using a least-squares optimization by, for example, applying a pseudoinverse of the spatial and temporal sensitivity matrix to a user-defined set of tip angles and locations. The locations can be chosen to be uniformly distributed throughout the field of view (FOV) or can be concentrated near an organ of interest. In addition, one can simultaneously solve for a 90° flip angle for spins at the frequency of fat and a flip of 0° for spins at the water frequency to reduce unwanted water saturation by including the chemical shift in the exp(jω_nt) term.

An interesting point here is that the fit is N coils to M pixels, where M >> N if all pixels are taken into account, the problem is underdetermined. However, under the assumption that B₀ varies slowly across the sample we expect the excitation to be similar for adjacent voxels, such that rather simple regularization schemes can yield acceptable results.

MATERIALS AND METHODS

As demonstration of PABST for improved uniformity and efficacy of fat saturation with simultaneous reduction in water saturation, we have performed a Bloch simulation in 1D of the illustration shown in Fig. 1). First, traditional fat saturation is simulated with uniform B₁ field, which would be generated by a volume coil (Fig. 2). A linear gradient is imposed across the sample, from −5 ppm to +5 ppm, to create smoothly varying, inhomogeneous B₀. This range is sufficient to disrupt the uniformity of traditional fat-saturation methods. Selective excitation is done with a 10-ms-long CHESS pulse, centered at the frequency of fat, −3.5 ppm, and with a 2 ppm bandwidth. The amplitude has been chosen to provide a 90° tip angle for spins on-resonance.

FIG. 2.

a: Coil sensitivities B1 magnitude of single-channel volume coil and magnitude profiles of two independent transmit channels. Position is expressed in terms of the linear off-resonance. The results of saturation on a 1D sample, for the (b) single-channel volume coil, (c) two adjacent coils playing an unmodified CHESS pulse, and (d) a pulse with optimized frequency. The two coil setup with optimized frequencies yields saturation over a broader range without the unwanted saturation band of water spins in the single-channel case. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In a second 1D simulation, the volume coil is replaced with two adjacent surface coils whose dimensions are chosen such that they span ~2 ppm of the inhomogeneity to satisfy the small variation assumption (Fig. 2a). The position of channel 1 corresponds to a mean off-resonance of −1 ppm, whereas the mean off-resonance at channel 2 is +1 ppm. Two cases are described: one, where each coil plays the same pulse as used by the volume coil, and second, where the center frequency has been calculated as the sensitivity weighted mean of the variation, which would be obtained from a nonselective FID experiment. The phase of each RF source is chosen to yield constructive interference in the center of the pulse, and the amplitude is increased slightly to retain a 90° tip at the center.

To demonstrate a more general situation using a multichannel volume array, simulations of this technique were performed in 2D, with a simulation phantom shown in Fig. 3. A baseline image is formed with an eight-rung homogenous volume coil with 70-cm diameter playing a 10-ms CHESS pulse. The improvement to fat saturation with PABST was simulated for a cylindrical, 70-cm diameter, eight-channel transmission array in the presence of a linear, x-oriented, ±4 ppm variation of B₀ across a 50-cm circular FOV. The frequency of each channel is calculated as a linear density and sensitivity weighted average (as would be collected from the spectrum of an FID). We simulate PABST using the two amplitude correction methods (single amplitude correction applied to all coils and coil-by-coil correction) described above. All pixels within the phantom were used when calculating optimized amplitudes in Eq. 3, and the target excitation profile was chosen to be 90° tip for fat frequencies and 0° for water frequencies. To compare the results of the least-squares approximation methods to brute-force minimization, a fourth simulation was performed that simultaneously solved the frequency and amplitudes of each channel by iteratively minimizing the cost function ∑_pixels |M_z,fat| + |1 − M_z,water|. A FLASH image (α = 10°, pulse repetition time = 20, echo time = 5) was constructed for these four situations to demonstrate postsaturation contrast. The cumulative sum of a histogram displaying the number of pixels in the FOV as a function of their residual longitudinal magnetization, M_z, following the saturation were determined for both fat and water as an estimate of the uniformity of saturation.

FIG. 3.

Simulated FLASH images following saturation preparation. a: Traditional CHESS played on single-channel volume coil. PABST with FID tuned frequency for (b) equal amplitude correction on all channels and (c) amplitudes least-squares optimized for each channel. d: Result of simultaneously solving for frequency and amplitude of each channel using iterative minimization and Bloch simulation. A noticeable improvement in uniformity and accuracy of saturation is made with increasingly sophisticated amplitude adjustments. Also, note the absence of water saturation (indicated by arrow, a) when using PABST.

The effect of exceeding the small variation across a coil is tested by imposing linear off-resonance with maxima of ± 2, ± 4, and ± 6 ppm across a fixed FOV, such that as the total off-resonance increases, the variation across one channel becomes greater. The same simulation phantom and coil dimensions used in Fig. 3 were used here, though channel counts of 1, 4, 8, 12, 16, and 32 channels were tested. In all cases, the frequency was determined from an FID, and amplitude of each channel was found individually by the least-squares method, using all pixels within the phantom for the fitting. The total number of pixels with |M_z| < 0.1 for each channel count is shown as a measure of saturation efficacy versus off-resonance, where M_z = 0 would represent a perfect saturation preparation pulse.

The PABST method was implemented on a Siemens Espree (Siemens AG, Erlangen, Germany) using a fourchannel transmission array based on the on-coil CMCD amplifier with a controlled current source for excitation (31,32). The transmission channels consisted of 7.5 × 15 cm² rectangular coils with concentric shield (33), arrayed in cylindrical fashion on a 23-cm diameter former. The array was driven by a Tektronix DTG5078 digital timing generator, which generates the required amplitude and carrier signals required for the CMCD elements. These signals were calculated using a sigma–delta encoding scheme and were transmitted into the room on separate fiber-optic cables. A cylindrical phantom was constructed to mimic that used in the simulation (Fig. 3) by suspending a number of balloons filled with water doped with copper sulfate (~1–2 g/L, for T₁ times ranging from 100 to 300 ms) in canola oil. Receiving was performed by wrapping the Siemens body array coil around the phantom. Here, baseline images were acquired using the array excited in the homogenous mode with optimized shims. A 5-ms hard pulse was used for fat saturation, due to limited memory of the data-timing generator that did not allow long, amplitude modulated pulses. Five milliseconds was chosen because it exhibits a null the cost function at ±200 Hz and thus could best demonstrate the frequency selectiveness of PABST. The frequency of each channel was determined through individual excitation and capture of the FID, and the amplitude correction method based on the flip angle in the center of the phantom was used. As signal levels varied between the images, distorting a possible calculation of the mean saturation level, we present the standard deviation of ROIs chosen to cover the majority of the fat and water areas.

RESULTS

Figure 2b demonstrates the 1D simulation results for fat-saturation preparation using a volume coil. We can see that all fat spins within the ~1 ppm bandwidth of the saturation pulse, centered at 0 ppm, are excited into the transverse plane, whereas spins outside the bandwidth are unchanged and would contribute fully in a subsequent imaging experiment. In addition, water spins located in the region where their Larmor frequency is −3.5 ppm are on-resonance with the pulse, resulting in a broad saturation band at this location.

Figure 2c shows the saturation results from two independent transmit channels playing pulses identical to the volume coil. The lack of coil sensitivity in the region of −3.5 ppm has reduced water saturation, but the uniformity of fat saturation is not improved compared to the volume coil case. In Fig. 2d, the center frequency of each channel has been tuned to their local, mean B₀ field and amplitudes renormalized to produce the same level of excitation as the previous cases. Here, fat spins have been saturated over a broader region, which corresponds to ~3 ppm in bandwidth. The region between the coils, despite being at the edge of the saturation bandwidth for either pulse, experiences a cumulative saturation effect from the combined coils resulting in a final M_z near zero. Unwanted saturation of water has been reduced from complete saturation of an entire band to mild saturation in the vicinities of the coils.

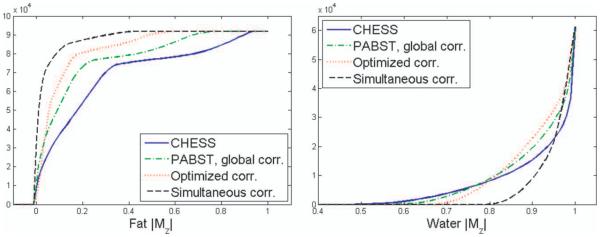
Figure 3 displays simulated FLASH images with fat-saturation preparation using a traditional CHESS pulse (Fig. 3a), the PABST method with a eight-channel array for FID determined frequencies with the two amplitude correction methods derived from Eq. 3 (Fig. 3b,c). Simultaneous solution of frequency and amplitude is shown in Fig. 3d. PABST yields better saturation for more pixels with less water saturation, as can be seen in the qualitatively better contrast. This can be seen numerically in the cumulative sum plots (Fig. 4). Perfect fat saturation, where all fat is excited to 90°, would have a step function at |M_z/M₀| = 0. Following the CHESS excitation, only 40% of fat pixels exhibit |M_z| < 0.1, while PABST with exhibited 57% and 71% saturation for the correction methods corresponding to Fig. 3b,c, respectively. The simultaneous solution of angle and frequency shows excellent performance, with a full 89% of fat spins having |M_z/M₀| < 0.1. Water suppression is similarly improved with PABST, with 63% of water having |M_z/M₀| > 0.9 for CHESS excitation, while PABST shows 68%, 75%, and 85% for the corrections of Fig. 3b–d, respectively.

FIG. 4.

Cumulative sum of the magnitude of M_z for water and fat following saturation preparation for the cases in Fig. 3. Ideal fat saturation would exhibit a step function at 0.0: the increased steepness and rapid approach to 100% saturation demonstrates the improvement with the PABST method. Water saturation is arguably better, with fewer pixels exhibiting more saturation in excess of 50%. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The effect of increasing off-resonance and channel count is displayed in Fig. 5. Fat-saturation efficacy decreases as off-resonance increases, particularly for low channel counts where the approximation of small B₀ variation across a coil is violated. Also of interest is the diminished benefit of high channel counts for severe off-resonance, as we can see that the curves for 12 or more channels lay on top of one another for the cases tested. Further, higher channel counts yield slightly poorer results at the highest off-resonance tested, which may be the result of poorer interpolation between channels.

FIG. 5.

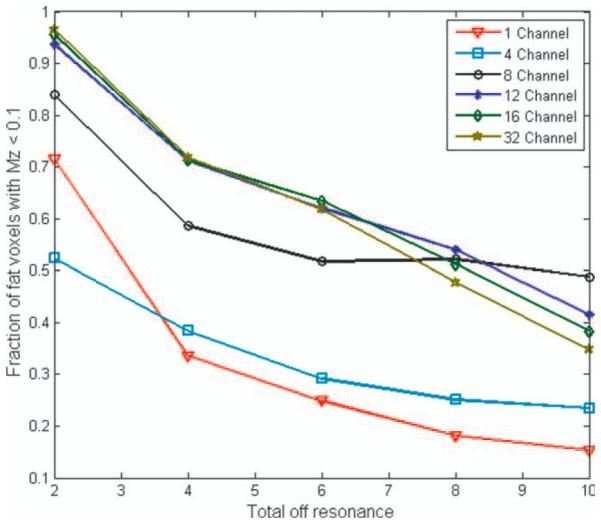
PABST saturation levels versus total off-resonance (in ppm) for a constant FOV with six different arrays. Plots display the fraction of fat pixels with M_z < 0.1 following PABST pulses optimized for the different coils. Little gain is seen for channel counts greater than 12. At extremely high off-resonance (8 and 10 ppm), the PABST method is able to effectively saturate over three times more fat than a single-channel transmitter. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The results of imaging with the four-channel CMCD array can be seen in Fig. 6. We see that, as opposed to the well-shimmed case (Fig. 6a), in a badly distorted B₀ shim (Fig. 6b) the simple fat-saturation pulse fails, yielding poor fat saturation left and right sides of the phantom and some water saturation on the right side. However, using PABST significantly improves the saturation (Fig. 6c), almost restoring it contrast similar to the case in Fig. 6a. We see some residual water saturation in the lower right, along with some remaining fat signal on the left and lower right. ROI analysis shows a standard deviation of 16.1 (arbitrary signal level units) for the baseline image with uniform shim, 43.8 for the corrupted shim with standard CHESS, and 17.9 for the PABST corrected image, indicating that PABST has similar residual fat signal as a IDEAL shimming case. Regions of water signal level showed 26.7, 45.7, and 24.3 for the same situations, respectively.

FIG. 6.

Imaging results using the PABST technique and a four-channel CMCD transmission array. The baseline image in a uniform B₀ field (a), the effect of a the same CHESS pulse in (a) when the y shim has been corrupted to induce roughly ± 4 ppm off-resonance, and (b) the result of applying the PABST frequency calibration and global amplitude correction. Again, note the reduction of water saturation (indicated by an arrow) and recovery of fat/water contrast in image (c), despite the severe off-resonance.

DISCUSSION

B₀ variation or off-resonance results in poor fat saturation when spectral broadening across the sample exceeds the narrow bandwidth of the chemically selective excitation pulse. By tuning the individual channels in a multichannel transmit array to the local mean sample Larmor frequency, each channel will effectively tip the nearby fat spins, and the broadened saturation bandwidth of the entire sample is achieved through the superposition of the frequency spectrum of the many channels in the transmit array. Here, we have shown that the PABST method is both simple and effective in increasing the performance of fat saturation in the presence of B₀ variations. This technique assumes that the variations are slow across the sample and small with respect to coil size and excitation bandwidth. This assumption implies that all spins within a coil’s sensitivity pattern lie within the bandwidth of that element’s excitation pulse. The stringency of this assumption will depend heavily on the frequency content of the RF pulse. All the pulses used in simulation had gaussian envelopes, and thus, their spectra were also gaussian. The slow decay of the spectrum can be beneficial in situations where the variation of B₀ is on the order of the bandwidth/size relationship. In contrast, a sinc shaped pulse, with its associated rectangular spectrum, will have no effect on spins outside of its bandwidth and may prove very difficult to reconcile with typical coil sensitivity profiles.

The assumption of slow B₀ variations across the sample is necessary for the uniformity of fat saturation throughout the entire sample. Equation 3 describes how the RF superposition interpolates between coils by weighing the frequency of the many channels by their amplitude. More uniform excitation is achieved as this weighted interpolation more closely matches the underlying B₀ variation. If B₀ fluctuates dramatically between coils, the individual coils will be unable to effectively excite spins in their intermediate regions. In extreme situations, it seems that it would be desirable to have very high channel counts, such that the linear interpolation is generally applicable.

All of the off-resonant fields for the fat-saturation experiments were modeled as linear variations in B₀. While this is admittedly contrived (as such a problem could be trivially fixed through a linear shim), it simply and effectively demonstrates the situation where channel count is sufficiently high that the variation between coils can be assumed linear. We note that there are some forms of off-resonance to which a cylindrical coil has no sensitivity and will not perform any better than a standard volume coil. An example is off-resonance that has a form x² + y², which matches the symmetry of the transmitter. In this situation, each channel would see the same spectrum and thus would transmit at the same frequency, making the excitation very similar to that of a single-channel coil. However, our experience shows that many types of off-resonance profiles are not as symmetrical and thus could potentially be corrected using a PABST-like approach.

The results for fat saturation show appreciable improvement in fat saturation and decreased water saturation. The points of most obvious failure are located at the extremes of the off-resonance (in our example, the left and right of the images). This is attributable to defining the frequency by the simple FID method, where a better solution could be obtained with frequencies more heavily weighted by the coil sensitivities. Preliminary studies show that using a spin echo instead of FID to measure the channel frequencies (which is equivalent to weighting a frequency map by the square of the coil sensitivities because of the two pulses) yields frequencies that are often within 10% of those found by the iterative solution shown in Fig. 3d. Another potential optimization is to customize the bandwidth of any particular channel to reflect the spectrum attained by the FID frequency calibration, potentially narrowing its frequency width to reduce its long-range effects on water saturation or biasing the spectrum to assist a neighboring coil.

When applying the optimized amplitude correction method, the selection of pixels for use in the least squares fit is critical for the efficacy of the resulting fat saturation, as this selection determines the effective B₁ uniformity. To maintain good conditioning in the fit when a limited number of channels are available, it is best to select pixels that reflect the character of the off-resonance. For general-use, one could define a number of pixels distributed uniformly across the FOV, and if more accurate results are needed in a specific ROI, allow the user to select those pixels. There is considerable benefit to be had from knowledge of a frequency map and coil sensitivities for advanced calibration and simultaneous solution of frequency and amplitude, as shown in the dramatic improvements seen in Fig. 3c,d. However, obtaining this information could also be time consuming and prone to errors, and the iterative solution can be slow to compute due to full Bloch simulations.

However, calibration routines such as those needed in PABST can be substantially reduced, if the transmitter is constructed with load-insensitive sources such as the CMCD amplifier. As current is directly proportional to the generated B₁ field, one only needs to perform a one-time calibration with the CMCD to determine the scale factor between the applied current and generated B₁ field. Additionally, as the load-dependent coil-tissue interactions are not generally a problem at 1.5 T, these sensitivities can be calibrated infrequently and stored for use in all subjects (34). We believe developments such as this will be the key to future parallel transmission concepts.

CONCLUSIONS

We have presented methods that utilize the inherent degrees of a freedom in a parallel transmitter to improve B₀ and B₁ homogeneity within the confines of usual slice selective and chemically selective pulses, with demonstration of significantly improved fat-saturation preparation. In PABST, a traditional CHESS excitation was enhanced by calibrating the frequency of each channel in a multichannel transmitter to its local, mean resonant frequency, which increases the uniformity of fat saturation throughout a volume, as confirmed in simulation and phantom experiments. This method does not increase the RF pulse duration and can function with as little information as a channel frequency adjustment and homogenous tip angle calibration, and does not require coil sensitivity or frequency maps. We believe this technique will complement the previously developed multidimensional and phase optimized methods. The general concept of correcting for inhomogeneities in B₀ with inhomogeneous B₁ from a parallel transmission system is applicable to a broad range of problems beyond the fat-saturation application presented here and provides an entirely new justification for parallel transmission at normal clinical field strengths.