Probability Distributome: A Web Computational Infrastructure for Exploring the Properties, Interrelations, and Applications of Probability Distributions

Abstract

Probability distributions are useful for modeling, simulation, analysis, and inference on varieties of natural processes and physical phenomena. There are uncountably many probability distributions. However, a few dozen families of distributions are commonly defined and are frequently used in practice for problem solving, experimental applications, and theoretical studies. In this paper, we present a new computational and graphical infrastructure, the Distributome, which facilitates the discovery, exploration and application of diverse spectra of probability distributions. The extensible Distributome infrastructure provides interfaces for (human and machine) traversal, search, and navigation of all common probability distributions. It also enables distribution modeling, applications, investigation of inter-distribution relations, as well as their analytical representations and computational utilization. The entire Distributome framework is designed and implemented as an open-source, community-built, and Internet-accessible infrastructure. It is portable, extensible and compatible with HTML5 and Web2.0 standards (http://Distributome.org).

We demonstrate two types of applications of the probability Distributome resources: computational research and science education. The Distributome tools may be employed to address five complementary computational modeling applications (simulation, data-analysis and inference, model-fitting, examination of the analytical, mathematical and computational properties of specific probability distributions, and exploration of the inter-distributional relations). Many high school and college science, technology, engineering and mathematics (STEM) courses may be enriched by the use of modern pedagogical approaches and technology-enhanced methods. The Distributome resources provide enhancements for blended STEM education by improving student motivation, augmenting the classical curriculum with interactive webapps, and overhauling the learning assessment protocols.

I. Introduction

Probability distributions are rich objects that enable the mathematical representation, algorithmic modeling, computational processing and scientific inference of diverse types of natural phenomena.

Figure 1 illustrates the main 3 components of the decision making process: specific natural phenomenon, model development and quantitative analysis. Probability distributions are critical in quantifying these decision-making components, identifying the process characteristics, validating model assumptions, generating algorithmic approximations, and provide the foundation of the quantitative (typically statistical) inference regarding the natural process.

Figure 1.

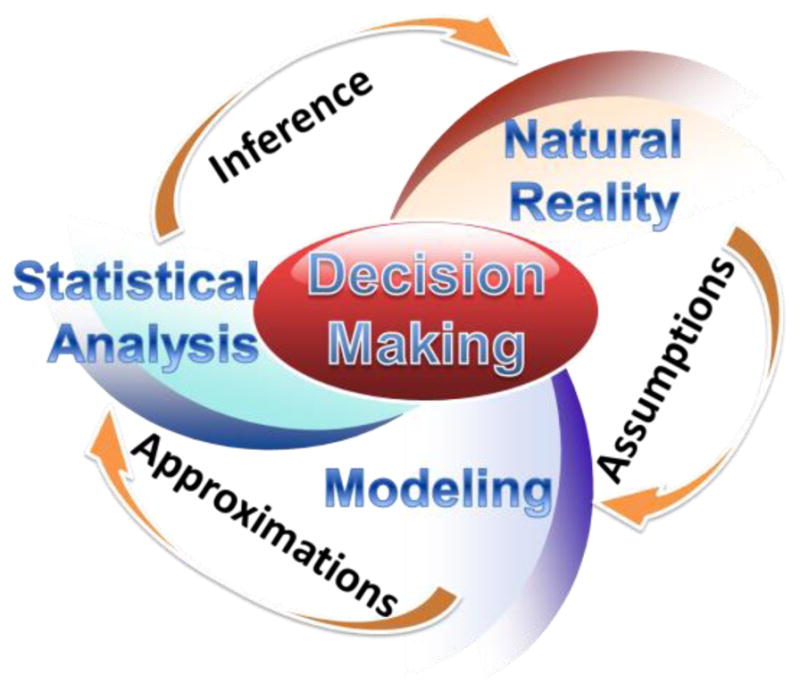
Components of the decision making process – observable natural processes, modeling approaches, and analytic tools, and the corresponding model assumptions, algorithmic approximations, and scientific inference.

There are numerous powerful examples of using probability distributions to study observable biomedical, social, financial or engineering processes. For example, Poisson distribution, which is completely understood and computationally tractable, may be used as a model of bacteria counts [1], studies of viral infections [2], scattering of particles in nuclear experiments [3] (e.g., Positron Emission Tomography [4]), software reliability assessment [5], and so on. Probability distributions enable computational simulations that play a key role in understanding the important characteristics, exploring the intrinsic properties and enabling the data-driven decision making in various scientific fields [6–8]. In finance, investors may observe the time-course of each stock in a specific portfolio. The optimal investment strategy may be obtained if an investor knows the (joint) probability distribution of the price fluctuations for the entire portfolio, or if one can accurately estimate the (marginal) probability distributions of individual stock prices [9–11]. In practice, however, the (marginal and joint) stock distributions are never known exactly. Partial prior information about the stock (or portfolio) may frequently include the stock’s variability, range, mean value, etc. Together with other information about the company and their products, knowing such relevant prior statistics should be valuable in the process of selecting an optimal investment approach.

The aim of this article is to provide the means to traverse, discover and explore the large and complex universe of (univariate) probability distributions. This space includes an abundant collection of probability distributions that may be used for various modeling, comparison, and computational tasks. Probability distribution modeling is common in a number of other social [12], biological [13], physical [14], medical [15] and environmental [16, 17] applications.

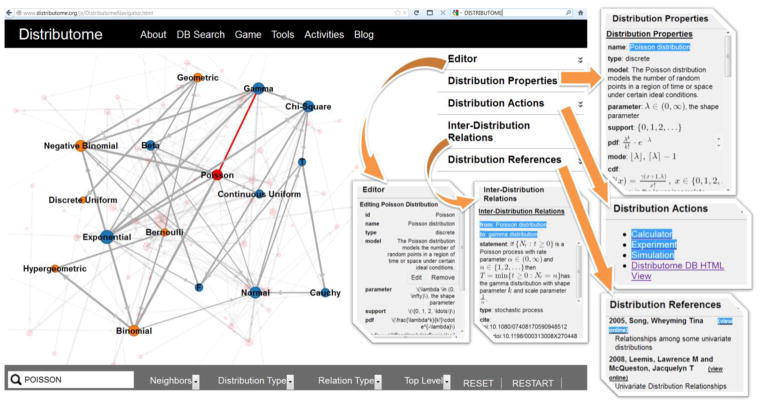
The Distributome infrastructure is developed by a multi-institutional effort involving the Virtual Laboratories in Probability and Statistics [18], the Statistics Online Computational Resource [19], and the Consortium for the Advancement of Undergraduate Statistics Education [20]. It enables computational utilization of over 70 different univariate distributions, graphical exploration of their inter-distribution relations, and facilitates the comparison of their properties. The Distributome infrastructure is open-source, portable, freely available to the entire community (www.Distributome.org), and its content is compiled collectively by the entire community. Figure 2 shows the Probability Distributome Navigator, which is a graphical user interface enabling exploration and editing the Distributome meta-data.

Figure 2.

The Distributome Navigator provides an interactive web-based interface for traversal, search and exploration of the properties of distributions, as nodes, and their interrelations, as edges in the graph. The Navigator graphical interface is mobile device compatible, software platform agnostic and runs directly in the browser. User can keyword search for distributions, properties or relations, or navigate the graph with the mouse. The top-right corner accordion panels may be expanded to show or edit the appropriate meta data (distribution properties, invoke distribution actions, inter-distributional relations, and scientific publications).

Probability distributions

A probability distribution is a function describing (1) the likelihood that a certain random event will take place, or (2) the chance that a random variable is bound in a certain range. Each distribution is defined by a probability density function (PDF). The PDF is non-negative and must integrate to one over its support, which is the outcome space of the process that the PDF is associated with [21]. Naturally, there are discrete and continuous probability distributions, as random events may range over finite, countable or continuous spaces. For example, the outcomes of rolling a pair of hexagonal dice may be represented by the (discrete) sum of the two dice, which is in the range 2, 3, 4, …, 12. On the other hand, observing time of arrival or the wavelength of a distant light source generates a continuous process with an underlying continuous probability distribution.

All physical processes and natural phenomena (including the atomic clock) generate observations or measurements that contain some intrinsic and/or extrinsic errors [22, 23]. Thus, it is better to describe the behavior of processes using probabilistic models (e.g., probability distributions) rather than deterministic ones (e.g., using elliptic equations). Exact values provided by deterministic models are good for calculations, but are often inadequate for describing random quantities. On the other hand, appropriate probability distribution models may contain the complete description of specific random processes, and they may also increase the model computational complexity [24, 25].

Diversity of distribution families

Some families of distributions are labeled and analytically described [26]. These include distributions that are discrete, continuous, mixtures, joint, marginal, well-defined, or random [27]. In reality, there are uncountably many families of probability distributions [28]. At first glance, this fact may be discouraging since we could never even label, let alone describe analytically, all observable or plausible processes. At the same time, two things bring hope in our ability to study all plausible natural phenomena. Both of these are related to our clever representation of the (uncountable) field of the real numbers using significantly fewer (countably many) rational and transcendental numbers [29]. The first tool for understanding the universe of distributions using only countably many of them comes from various limiting results (e.g., central limit theorem [7]). Such distribution-limiting properties provide the means of obtaining pathways between different distributions [30]. To use the analogy of the field of real numbers, we understand approximation of (transcendental) real numbers by rationals. The second advancement that allows us to scale our knowledge of the few to many distributions is based on our ability to study relations between pairs of distributions [31].

Closure properties of distributions

There are a number of distribution properties that can be defined to help us identify the distributions of functions of independent and identically distributed measurements or observations [32]. Such properties cover a wide spectrum, from linear transformations of a single random quantity to products of random quantities of a family of distributions (possibly with different distribution parameters), which capture closures of distribution family with respect to different functions. The following ten distribution properties are most useful in identifying and relating distributions and are included as descriptors for each distribution included in the Distributome.

1. Convolution: The convolution property guarantees that the sum of independent and identically distributed (iid) quantities from one specific distribution has a distribution from the same distribution family (possibly with different parameters).

   Example, for Poisson distribution, if X_i ~ Poisson (λ_i), then ${\sum }_{i=1}^n{X}_i~\mathit{Poisson}\left({\sum }_{i=1}^n{\lambda }_i\right)$.

2. Inverse: The inverse distribution property indicates that the distribution of the reciprocal (inverse) of a random quantity is of the same distribution family as the original quantity (possibly with different distribution parameters).

   Example, for Cauchy distribution, if X ~ Cauchy, then $\frac{1}{X}~\mathit{Cauchy}$.

3. Scaling: This property implies that the distribution of a multiplication (scaling) of a random quantity by a real-value will have a distribution of the same family.

   Example, for Gamma distribution, if X ~ Γ(κ,θ) and t>0, then Y= t× X ~ Γ(κ,t×θ).

4. Linear Combination: This distribution property ensures that a linear combination of random (independent) quantities from one specific distribution has a distribution of the same distribution family. The linear combination property implies the convolution and scaling properties.

   Example, if $X_i~\mathit{Normal}({\mu }_i,{\sigma }_i^2)$ are independent and {a_i|1≤i≤n} are constants, then ${\sum }_{i=1}^n{a}_i{X}_i~\mathit{Normal}\left({\sum }_{i=1}^n{a}_i\times {\mu }_i,{\sum }_{i=1}^n{a}_i^2\times {\sigma }_i^2\right)$.

5. Minimum: The minimum distribution property yields that the smallest of n iid random quantities from a specific distribution has a distribution of the same family.

   Example, for Geometric distribution, if X_i ~ Geometric (p_i), where {0≤p_i≤1|1≤i≤n}, then $\underset{1\le i\le n}{min}\left\{X_i\right\} \sim \mathit{\text{Geometric}} \left(1-\prod _{i=1}^n(1-p_i)\right)$.

6. Maximum: Analogously, the maximum distribution property indicates that the largest of n iid random quantities from a specific distribution has a distribution of the same family.

   Example, for Bernoulli distribution, if X_i ~ Bernoulli (p_i), where {0≤p_i≤1|1≤i≤n}, then $\underset{1\le i\le n}{max}{X}_i\sim \mathit{\text{Bernoulli}}\left(1-\prod _{i=1}^n(1-p_i)\right)$.

7. Product: This distribution property ensures that a product of random (independent) quantities from one specific distribution has a distribution of the same distribution family.

   Example, if $X_i~\mathit{LogNormal}({\mu }_i,{\sigma }_i^2)$, then ${\prod }_{i=1}^n{X}_i~\mathit{LogNormal}\left({\sum }_{i=1}^n{\mu }_i,{\sum }_{i=1}^n{\sigma }_i^2\right)$.

8. Conditional Residual: This property insures that the conditional distribution of a random quantity whose support is limited from the left (within the support of the original distribution) has a distribution of the same family.

   Example, for Uniform distribution, if X ~ Uniform (a,b), and a≤m≤b then the random quantity whose support is limited from the left, Y, also has Uniform distribution, i.e., Y={X|X≥m}~ Uniform (m,b).

9. Memoryless: The memoryless distribution property assures the equality of the conditional and unconditional distribution of a random quantity. This property is a special case of the Conditional Residual property.

   For instance, for Exponential distribution, if X ~ Exp(λ), then P(X> x_o + t|X > x_o) = P(X > t). In other words, the (conditional) probability of having to wait x_o + t = 20 minutes to observe the first arrival—given that the first arrival has not yet happened after x_o = 5 minutes—is the same as the (unconditional) probability that we need to wait more than t = 15 minutes for the first arrival.

   Note that among the continuous distributions, the exponential distribution family is the only one that possesses the memoryless property and the geometric family is the only memoryless probability distribution among the discrete distributions [33].

10. Simulate: This property guarantees that the inverse cumulative distribution may be expressed in analytical closed form, which indicates that sampling or simulation from this distribution is as trivial as sampling from Uniform(0,1).

    Example, for U-quadratic distribution, if X ~ UQuadratic(0,1), then $F_X^{-1}(u)=\frac{1+\sqrt[3]{2u-1}}{2}$ and if U~Uniform(0,1), then $F_X^{-1}(U)$ will be U-quadratic distributed.

    Note that the “simulate” property only implies that the inverse cumulative distribution may be expressed in analytical closed form. There are many alternative methods to simulate (or generate random samples) from a specific probability distribution [34–36].

Relationships between probability distributions

Identifying the relationships between different distributions is useful for two reasons. First, knowledge of these relations allows us to determine the underlying distributions of various functions (e.g., linear combinations, reciprocals, powers, exponentials, etc.) defined on one or more independent random quantities whose marginal distributions are known (at least approximately). For instance, different radioactive isotopes have different exponential rates of decay [37, 38]. Suppose we use a Geiger counter to measure the rate of decay of a mixture of isotopes. Then the distribution of the total sum of clicks (or arrivals) is known to be Exponential with a parameter equal to the sum of the exponential parameters of the distributions modeling each isotope in the mixture. Thus, for any 0≤ n< N < ∞, we know exactly the probability of recording more than n but less than N clicks in a given time period.

The second reason for studying the relationships between distributions is to understand the limiting behaviors of distributions [30]. Again using our radioactive isotope example, the distribution of the total number of Geiger counter clicks will approach Normal—with a mean and variance equal to the total sum of exponential parameters—as the total sum of parameters increases. This theoretical knowledge is used routinely in positron emission tomography imaging [39] and has many other scientific applications.

The core types of distribution relations may be summarized [32] as follows:

• Special case relations indicate that one distribution may be directly obtained from another one by specifying some of its parameters. Special case relations also encapsulate standard form distributions where the distribution’s location and scale parameters are 0 and 1, respectively. An example of a special case distribution pair is the Chi-square distribution and the Gamma distribution $\left({\chi }^2(n)\leftrightarrow \mathrm{\Gamma }\left(\frac{n}{2},2\right)\right)$.

• Transformation relations arise when transforming random quantities from one distribution, using some transform function, generates a new random quantity of known distribution. For example, Normal and Log-Normal distributions are related via a logarithmic transformation.

• Asymptotic (Limiting) relationships indicate that the probability distribution of one process converges to another known distribution as some of the parameters of the initial distribution tend to some singular values (e.g., ∞). For instance, hyper-geometric(N,m,n) distribution tends to Binomial(n,p) distribution as the hyper-geometric parameters N and m increase proportionately.

• Bayesian relation indicates that the parameters of one of the distributions are obtained via a Bayesian relation from the second distribution [32]. Examples of Bayesian-type relations include Poisson(μ) → Gamma-Poisson(α,β), where the Poisson mean parameter is μ~Gamma(α,β), and Binomial(n,p) → Beta-Binomial(α,β,n), where the distribution of the Binomial success probability is p~Beta(α,β).

• The Distributome infrastructure captures these distribution properties and inter-distributional relations. Of course, there may be other process characteristics of relations between distributions that may not be currently included in the Distributome. For instance, there is a special relationship between the U~Uniform(0,1) distribution and any other continuous distribution with a well-defined inverse cumulative distribution function, $F_X^{-1}(U)$. As the inverse CDF has the distribution of X; step-wise transformations between several distributions may be concatenated to obtain new relations. The Distributome framework allows such extensions to the various distribution properties and interrelations to be easily included, managed and disseminated for community-based exploration and validation.

II. The Probability Distributome

The Probability Distributome infrastructure is focused on special distributions that are important enough to be labeled uniquely (i.e., named). They are important because they arise in diverse and interesting applications, have a certain level of mathematical elegance, and are related to one-another in interesting ways. This infrastructure emphasizes the properties and relations of special distributions. For example, properties that completely determine the distribution include probability density function, moments, distribution function, quantile function, and the generating function. For positively-supported distributions, other properties describing the distributions include reliability function and failure rate function. Additional meta-data included in the Distributome database include generating functions (e.g., probability generating function, moment generating function, characteristic function), sequences of moments (e.g., raw, central, factorial), special moments (e.g., mean, variance, skewness, kurtosis, entropy), and special quantiles (e.g., 1^st quartile, median, 3^rd quartile).

Infrastructure

The core Probability Distributome infrastructure consists of a backend server, database of meta-data, a computational JavaScript library, and a collection of HTML5 webapps wrapping the library functionality, hardware resources and user interfaces. The Distributome server is a Linux server, 50.63.42.1 (MySQL, PHP5, WordPress3.4), which is available via HTTP/HTTPS protocols (www.Distributome.org). We have developed an extensible JavaScript computational library that includes a number of tools (http://www.distributome.org/tools.html), webapps with graphical interfaces (e.g., http://distributome.org/V3) and webservices (e.g., www.distributome.org/js/DistributomeDBSearch.xml.php?debug=true&s=poisson+AND+Lorentz).

The Distributome database is stored as XML (www.distributome.org/V3/data/Distributome.xml), which is based on a predefined XSD schema (www.distributome.org/js/Distributome.xsd) and utilizes BibTeX (http://www.distributome.org/V3/data/Distributome.bib) for managing citations. The Meta-data may be parsed on-demand by JavaScript/HTML5 (e.g., http://distributome.org/V3/Distributome.xml.html). The XML data contains the distribution properties and the inter-distributional relations meta-data. The BibTeX file includes TeX/LaTeX based citation bibliography. As LaTeX syntax is used to store all mathematical expressions in the Distributome database, we use MathJax (http://mathjax.org) JavaScript to parse these formulas and symbols and HTML5-render the content dynamically on the page at load time.

The Distributome Navigator (http://www.distributome.org/V3) provides the main (human) interface to the Distributome database. It allows the traversal, search and exploration of the universe of distributions (as nodes) and their relations (as edges in the graph), as demonstrated in Figure 2. The open-source D3 library (http://d3js.org) is used to generate scale-vector graphics (SVG) of the dynamic Distributome Navigator. The Distributome preferences (www.distributome.org/V3/data/Distributome.xml.pref) may be used to specify alternative ontological classifications of the probability distributions as level hierarchies of objects. Different types of distributions (nodes) or relations (edges) may be highlighted using the appropriate controls in the webapp. Once a distribution or a relation is selected, the accordion panels in the top-right corner show the relative properties and provide access to tools for using the chosen object. The Distributome Editor allows users to modify the meta-data, add additional objects or properties, and submit these for review and potential inclusion in the master Distributome database. Community engagement in the validation, expansion and support of the Distributome meta-data is critical for the success and long-term sustainability of the project. The distribution tools associated with each node in the graph provide dynamic access to calculators, simulators or virtual experiments for each selected distribution. We have significantly tested the HTML5/JavaScript distribution calculators against Mathematica® [40], R [41, 42] and SOCR [43] computational libraries.

In addition to the human graphical user interface, the Distributome framework provides a machine-interface (API) to the core database. This API enables external programs and services to automatically harvest and process Distributome data and resources. The Distributome meta-data validator (www.distributome.org/js/Distributome.xml.html) and the Search service (e.g., www.distributome.org/js/DistributomeDBSearch.xml.php?debug=true&s=poisson+AND+Lorentz) provide examples of this machine interface. Each of the Distributome components (from the backend server to the database, interfaces and learning modules) are designed to be integrated, HTML5-complient, extensible, portable and user-friendly.

Utilization

The two fundamental use-cases of the Distributome infrastructure include research applications and science, technology, engineering and mathematics (STEM) education.

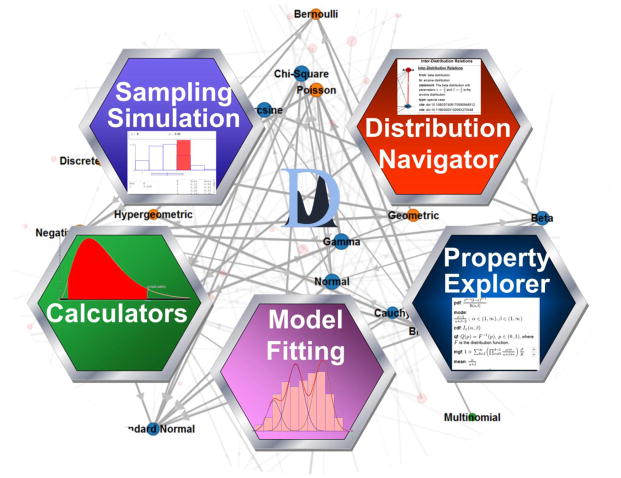
There are at least five types of research applications of probability distributions and their interrelations (Figure 3). The first application uses probability distributions for simulations [44, 45]. This application allows generation of random samples from specified probability distribution and enables the modeling of diverse natural processes. For example, Monte Carlo simulations [46] use probability density functions to generate random sets of values which may be used to estimate process parameters, study the process properties, and investigate process rare events in biomedical [47, 48] and physics [49] applications.

Figure 3.

Core Distributome applications (clockwise starting at the top-left) – sampling and simulation, inter-distribution relations navigator, distribution properties explorer, model fitting tools, and distribution calculators.

The second direction of using model probability distributions is for data analysis [50, 51] and Bayesian inference [52, 53]. In empirical Bayesian inference, the likelihood function [54]—L(x|θ)—may be specified as an analytical model by one concrete distribution, but the (prior) parameter distribution of θ may be a different distribution. In these situations, Bayesian inference allows us to estimate (or at least approximate) the process probability distribution from the properties of the given prior distribution and the likelihood function. For instance, the Beta-binomial is a Binomial distribution where the probability of success (p) is not constant, but instead is a random variable following a beta distribution. The third application of the Distributome is in terms of fitting distribution models to specific datasets. The fourth application is to explore the analytical, mathematical and computational properties of specific probability distributions. Such knowledge enables studies of efficient function representation and theoretical process characterization. The fifth application of probability distributions is for the exploration of the inter-distributional relations like special cases, limiting properties, transformations, etc.

As a concrete application demonstrating the need, utilization and unique features of the Distributome infrastructure, consider biomedical studies that generate enormous amounts of data (e.g., imaging, molecular sequence analysis, and clinical trials). Suppose a researcher has collected data to study obesity (e.g., calorie intake/expenditure, age, gender) and needs to make inference about the underlying biophysical process that generated the data (e.g., identify if there are gender effects on calorie expenditure). For instance, there may be a research hypothesis about a treatment-effect (e.g., metabolic activity as measured by the subject’s calorie circulation) on a specific phenotypic trait (e.g., gender) that needs to be tested, validated or disproved. In many experiments and observational studies, the exact distribution of the underlying physical process is unknown and its parameters may be uncertain. Using the Distributome framework, investigators may specify some of the known characteristics of the process (e.g., center, spread, shape, symmetry, etc.) and use the Distributome infrastructure to identify potential candidate distribution models. Then researchers can fit the selected distribution models to the observed data, assess the model quality, re-fit models as needed, and finally complete the inference to address the initial research hypotheses using the Distributome-derived (analytical) model (rather than solely relying on the empirically observed or discrete sample).

Many K-12 and college STEM classes discuss the concepts of probability modeling and statistical data analysis. According to the U.S. Department of Education National Center for Education Statistics’ 2007–08 National Postsecondary Student Aid Study (http://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=200801), the number of students enrolled in college-level engineering, mathematics, biomedical and computer science classes exceeds 1,000,000, 110,000, 606,000, 702,000 students a year, respectively (in the U.S. alone). Virtually all of these courses could benefit from modern pedagogical approaches and technology-enhanced methods for improving student motivation, augmenting the classical curriculum with interactive webapps and overhauling the student assessment protocols. The Distributome resources provide such enhancements for blended instruction of probability, statistics and applied modeling courses. Many high schools and AP training programs offer STEM classes covering probability theory that enroll millions of students each year.

III. Applications

Distributome Game

The number and complexity of the different kinds of natural processes significantly exceed the finite number of well-described probability distribution models. One can gain intuition about the varieties of different processes and the characteristics of different probability distributions by interactively exploring their properties using the Distributome calculators, simulators and experiments (www.distributome.org/tools.html). The Probability Distributome Game Webapp (http://www.distributome.org/V3/DistributomeGame.html) enables this exploration of natural phenomena and models as an interactive game of matching pairs of processes and distributions.

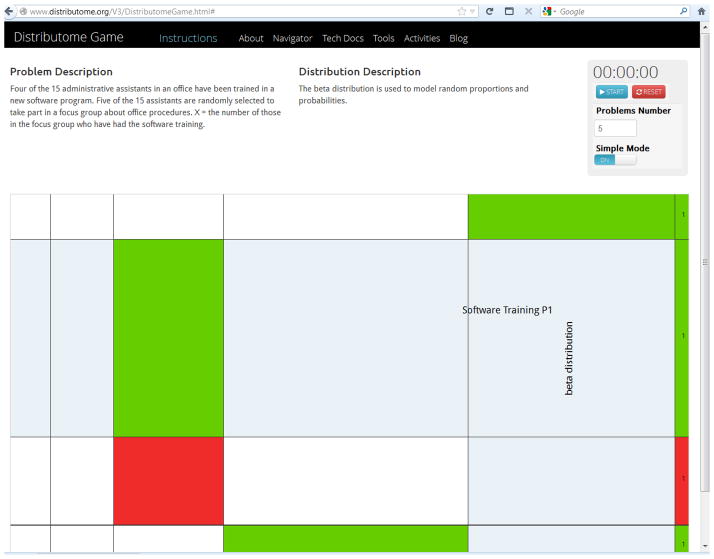
The goal of the Distributome Game is to correctly identify the correspondences between pairs of processes (represented as problems) and probability distributions (represented as models). A Cartesian plane represents the game-board where rows and columns show problems/processes and distribution models, respectively. As the mouse moves over the Cartesian grid, the zoom-function automatically expands the Cartesian space around the mouse location. The rows and columns of the matching Problem-Distribution pairs corresponding for the current location are dynamically highlighted. To find one or more distribution(s) that may represent good model(s) for the process described in the problem, the user navigates the space using the mouse. Clicking on a cell in this 2D Cartesian plane makes a selection and highlights the chosen matching problem-distribution pair. Correct or incorrect matches are indicated by green and red cell background coloring, respectively. Clicking on a highlighted cell provides access to the appropriate Distributome tools for the selected distribution and optional hints for solving the problem.

Figure 4 illustrates the main Game interface, which is constantly evolving to enhance the user gaming experience and improve the learning process. Players may reduce the number of rows to include, say, 20 randomly picked problems from the problems database. Then using the Start, Pause, Stop and Reset controls, players can time and compare their performances (e.g., best times and score ranking). Scores could also represent the number of guesses until all problems are correctly identified, subject to the number of hints requested + 10*(#of seconds used). Low (good) or high (poor) scores would be indicative of the players’ conceptual probability knowledge. We are also working on improving the search/navigation functionality so users can quickly find and tag a distribution, a problem, or a problem-distribution pair. There are several alternative Distributome games (http://www.distributome.org/V3/DistributomeGames.html) that challenge users to match sample-histograms and density curves or to test their ability to remember and recall the shape and form of various distributions. These games include a number of user-specifications defining different expertise levels:

Figure 4.

The Distributome Game is a game-interface where players aim to quickly identify the correspondences between pairs of processes (represented as problems) and probability distributions (as models). The Cartesian plane represents the game-board where rows and columns show problems/processes and distribution models, respectively. Correct and incorrect matches are green and red colored. Various optional hints and help mechanisms are provided for the players. Green and red cells indicate correct and incorrect pairing of the problems and model distributions, respectively. The last column indicated the number of guesses for each problem.

1. Beginners (distribution descriptions are available and only have columns for the distributions used in the round of play)

2. Intermediate players (no distribution descriptions and only have columns for distributions used in the round of play)

3. Advanced players (no distribution descriptions and have columns for all distributions at level under use)

Learning Activities

Modern STEM education emphasizes learning modules that integrate concepts, data, applications and assessment [55, 56]. We have developed a collection of interactive learning activities (http://distributome.org/blog/?cat=4) that merge probability concepts with scientific applications, provide access to available data and facilitate student evaluation. Below are two examples of probability learning activities that demonstrate an integrated approach to enhancing probability education and statistical literacy using Distributome resources. There are additional activities online http://distributome.org/blog/?cat=4. In each of these examples on the website, a fundamental concept in probability theory is used to motivate a case study where real data may be collected and used to obtain quantitative estimates of parameters of interest. The calculations may be accomplished using Distributome tools, which also provide hints and solutions as well as enabling learning assessment (i.e., self-assessment for students, or formal instructor evaluation of students’ learning).

Distributome Colorblindness Activity

Can you correctly identify the number shown in Figure 5? This Distributome Activity illustrates an application of probability theory to study Daltonism (i.e., colorblindness), which is typically a non-dominant or recessive genetic disorder that results from an abnormality on the X chromosome [57, 58]. The condition is thus rarer in women, since a woman would need to have the abnormality on both of her X chromosomes in order to be colorblind (i.e., abnormality on one X chromosome is essentially independent of having it on the other).

Figure 5.

Distributome Colorblindness activity focuses on the estimation of the probability of female colorblindness using data for males.

The goal of this activity is to demonstrate an efficient protocol of estimating the probability that a randomly chosen male may be colorblind. Suppose that p is the probability that a randomly selected “man” is colorblind. The following steps address the process of estimating the probability that a random woman is colorblind:

• 100 men are selected at random. What is the distribution of X_m = the number of these men that are colorblind? X_m ~ Binomial(100,p).

• 100 women are selected at random. What is the distribution of X_f = the number of these women that are colorblind? The chance that an individual woman is colorblind is p². Thus, X_f ~ Binomial(100,p²).

• To estimate the probability that a randomly selected woman is colorblind, you might use the proportion of colorblind women in a sample of n women. What is the variance of this estimator? As X_f ~ Binomial(n,p²), the $\mathit{Var}\left(\frac{X_f}{n}\right)\equiv \frac{p^2(1-p^2)}{n}$.

• Alternatively, to estimate the probability that a randomly selected woman is colorblind, you might use the square of the proportion of colorblind men in a sample of n men. The explanation of this fact is based on the variance of this estimator. The moment generating function can be used to find the fourth moment about the origin. We want to estimate p² and $\frac{X_m}{n}$ estimates p, so it makes sense to use ${\left(\frac{X_m}{n}\right)}^2$ as the estimator (in fact it will be the maximum likelihood estimate [54]). We have $\mathit{Var}{\left(\frac{X_m}{n}\right)}^2=\frac{1}{n^4}\left[E(X_m^4)-{(E(X_m^2))}^2\right]$. If q = 1 − p we can compute the fourth moment about the origin of a binomial process E(X⁴) = np(q − 6pq² + 7npq − 11np²q + 6n²p²q + n³p³) and the second moment E(X²) = np(q + np). Thus, $\mathit{Var}{\left(\frac{X_m}{n}\right)}^2=\frac{1}{n^3}[pq+6(n-1)p^2{q}^2+4n(n-1)p^{3}q]$.

• For large samples, is it better to use a sample of men or a sample of women to estimate the probability that a randomly selected female is colorblind? Normal approximation is valid for both cases and comparing their variances may yield clues to which approach may generate more stable estimates. For large n, the ratio of the variances for the male and female estimates is $\frac{\mathit{Var}\left(\frac{X_f}{n}\right)}{\mathit{Var}\left[{\left(\frac{X_m}{n}\right)}^2\right]}~\frac{p^2(1-p^2)}{4p^{3}q}=\frac{1+p}{4p}$. When this ratio is greater than 1, the estimator based on the sample of men will be better (as the male variance would be less than the variance estimate for female). Since this happens for any $p<\frac{1}{3}$, which is clearly the case for colorblindness, it is better to use a sample of men to estimate the probability that a random woman is colorblind.

In practice, it may difficult to obtain reliable parameter estimates when the event at hand is very rare (as with colorblindness in women). Using an appropriate probability model improves the reliability of the likelihood estimates that quantify the chance of colorblindness in men or women.

Homicides Trend Activity

A Columbus Dispatch newspaper story on Friday ,January 1, 2010 discussed a drop in the number of homicides in the city the previous year. The title of the article was “Homicides take big drop in city: Trend also being seen nationally, but why is a mystery.” The story began with:

The number of homicides in Columbus dropped 25 percent last year after spiking in 2008. As of last night, the city was expected to close out 2009 with 83 homicides, 27 fewer than in 2008, according to records kept by police and The Dispatch. In 2007, 79 people were slain in Columbus. “I don’t know that there’s one reason for homicides going up or down,” said Lt. David Watkins, supervisor of the Police Division’s homicide unit.

Why one year do we have 130, and then the next year we have 80?

“You just can’t explain it,” Sgt. Dana Norman said. He supervises the third-shift squad that investigated 44 of last year’s homicides, which occurred at a rate of 11.1 for every 100,000 people in Columbus, based on recent population estimates.

A table appearing with the article showed that there were 568 homicides in the previous 6 years. Sargent Norman’s statement that “You just can’t explain it” presents an intriguing probability question: Is it possible that natural random fluctuation might be a good explanation? Let us consider probability models for the number of observed crimes and how they might fluctuate to see if the data mentioned in the article is unusual.

If homicides are rare events that might be independently perpetrated by individuals in a large population, what distribution would approximately describe the number of murders in a year? A reasonable model would be the Poisson distribution (i.e., since the mean is quite large, a normal model with equal mean and variance would be an alternative approximation).

Suppose the expected annual number of homicides in the city is denoted by λ and that the number of homicides is independent from year to year. The article notes that 2008 saw a “spike” in the number of homicides and that it was the highest number in the last six years. If nothing is going on except random fluctuations, we want to know if observing 27 fewer homicides in 2009 after the peak year is unusual (peak here meaning the highest in the last 6 years).

Using the Distributome Poisson simulator, we can find an appropriate model and examine the distribution of the change in the number of homicides one would expect to see following a peak of a six-year stretch. The main question is “Does the 27-murder drop seem unusual?” To get started, we will need to:

1. Find an estimate of λ to use in your simulations, and

2. Examine groups of 7 years of simulated homicide data and isolate those cases that satisfy the conditions of the problem.

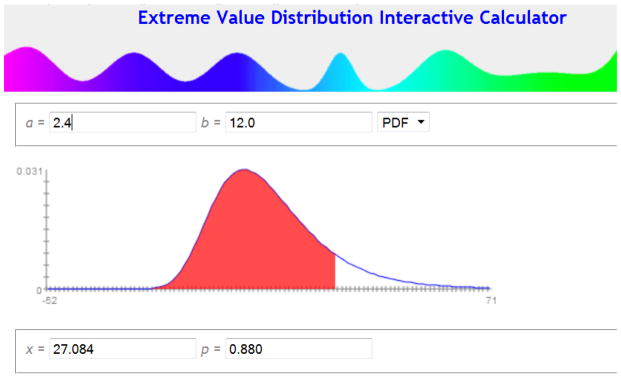
There were 568 homicides in the preceding six years, so a reasonable estimate of λ would be $\lambda =\frac{568}{6}=82.67$. We can use the Distributome Poisson simulator to generate a simulated sample of 100,000 sets of six independent Poisson variables (total of 600,000 simulations). Then we can empirically find the distribution of the maximum (of these sets of 6 Poisson(λ=82.67) observations), which will be Extreme-Value Type I distribution [59, 60] with probability density decaying in the upper tail as an exponential function. We aim to make inference on the difference between this maximum and another independent Poisson(λ=82.67) variable. We are looking for the distribution of this difference, specifically the likelihood of this difference to exceed 27. This probability can be computed to be about 0.12, or about 12% of the time (Figure 6) these values are computed using the Distributome Extreme-Value Distribution (EVD) calculator based on these parameter settings EVD(a=2.4, b=12.0). Thus, the drop of homicides in Columbus would not be particularly unusual when nothing is happening but regular random fluctuations. When viewing a random process over time, it is the extremes that make the headlines; so the probability models we should use to answer the question “What is unusual?” should be probability models about extremes.

Figure 6.

The Distributome Extreme-Value distribution calculator is used to estimate the likelihood of the event of observing fewer than 27 homicides in Columbus, Ohio in a given year.

IV. Discussion

Different types of representations, classifications and orderings of probability distributions have been previously proposed [32, 61]. Most of these efforts attempt to label ontologically the observed patterns and characteristics of probability distributions. Pearson proposed a systematic classification of the common continuous distributions using differential equations [62]. Maximum entropy-based classification of distributions employs information theory to explore the associations and relations between process information content, magnitude, invariance, symmetry and measurement scale [63].

Currently, there is no unique probability distribution classification ontology that satisfies the needs of different disciplines and which is also appropriate for all scientific applications. Our approach is based on identifying a 3-tier hierarchy of probability distributions based in their general use in practical studies. Although there are not very many utilities to navigate, explore or computationally utilize the diverse spectra of probability distributions, some previous efforts are worth noting. The Wolfram Univariate Probability Distribution Explorer is one of these (http://blog.wolfram.com/2013/02/01/the-ultimate-univariate-probability-distribution-explorer/). It relies on a backend Mathematica® server to provide remote clients with a browser-embedded interface to distribution properties, density and cumulative function plots, entropies, hazard functions for a large number of distributions included in the Mathematica® library. Another example is the dynamic PDF-based Univariate Distribution Relationships chart (www.math.wm.edu/~leemis/chart/UDR/UDR.html) [32]. It includes a collection of about 75 probability discrete and continuous distributions and allows mouse-driven exploration of the PDF chart. The open-encyclopedia, Wikipedia, includes perhaps the most complete, reliable and integrated textural description of probability distributions (https://en.wikipedia.org/wiki/Probability_distribution) [64, 65]. Other static diagrams of distribution relationships exist that illustrate the affinities between different univatiate distributions, e.g., www.johndcook.com/blog/distribution_chart. Lastly, the R statistical computing package provides the most elaborate open-source compilation of probability distribution calculators (http://www.r-project.org) [41, 66].

The probability Distributome infrastructure offers several advantages based on its open-source design, crowd-based development model, and portable and dynamic HTML5 architecture. It provides a unique interactive explorer for distribution navigation, exploration and computation. The Distributome navigator enables dynamic travelling through the universe of probability distributions, which supports customizable views of the hierarchy of classes of probability distributions on any internet-connected device (including mobile phones and tables). The Distributome explorer facilitates phrase and graphical search, discovery and examination of intrinsic probability distribution properties and inter-distributional relations. Finally, the Distributome framework provides game-based learning experiences and supports five complementary use-cases for computational utilization of probability distributions (sampling and simulation, data analysis and inference, probability model-fitting, investigation of the analytical, mathematical and computational properties of specific probability distributions, and exploration of the inter-distributional relations).

The entire Distributome source-code is LGPL-licensed and is available online at http://Distributome.googlecode.com (as well as at, https://github.com/distributome). The community can also use the Distributome Editor (www.distributome.org/V3) to expand, revise, modify and branch the current probability Distributome meta-data. The technical documentation page (www.distributome.org/docs.html) and the Distributome blog (www.distributome.org/blog) provide all details about the approach, functionality, challenges, progress, and future developments of the probability Distributome project. The Distributome website includes a web-form that collects, aggregates and manages user feedback, recommendations and requests (http://distributome.org/survey.html). All user feedback and ideas are welcome.