An updated perspective on the role of environmental autocorrelation in animal populations

Abstract

Ecological theory predicts that the presence of temporal autocorrelation in environments can considerably affect population extinction risk. However, empirical estimates of autocorrelation values in animal populations have not decoupled intrinsic growth and density feedback processes from environmental autocorrelation. In this study we first discuss how the autocorrelation present in environmental covariates can be reduced through nonlinear interactions or by interactions with multiple limiting resources. We then estimated the degree of environmental autocorrelation present in the Global Population Dynamics Database using a robust, model-based approach. Our empirical results indicate that time series of animal populations are affected by low levels of environmental autocorrelation, a result consistent with predictions from our theoretical models. Claims supporting the importance of autocorrelated environments have been largely based on indirect empirical measures and theoretical models seldom anchored in realistic assumptions. It is likely that a more nuanced understanding of the effects of autocorrelated environments is necessary to reconcile our conclusions with previous theory. We anticipate that our findings and other recent results will lead to improvements in understanding how to incorporate fluctuating environments into population risk assessments.

1 Introduction

Biologists have long understood that stochastic factors influence population growth through both intrinsic and extrinsic processes (Goodman, 1987; Hilfinger and Paulsson, 2011). How these processes are articulated mathematically can strongly influence extinction risk assessments. Therefore mathematical representations of the forces affecting risk need to accurately reflect the processes driving population variability.

Environmental variability is a practical way to account for the emergent effects of biotic and abiotic interactions in single species population dynamics models when detailed information on extrinsic covariates is not available (Dennis and Costantino, 1988). For sufficiently large populations, environmental variance is considered to be the primary contributor to population variability (Lande, 1993). It is often assumed that the factors driving environmental variation converge to a normal distribution following the central limit theorem (Lewontin and Cohen, 1969). This model formulation assumes that the processes driving variability are independent through time; however, many ecological and environmental time series are characterized by strong temporal dependencies where the assumption of independence may not hold. This means that the environment at the current time can be forecast as a function of the state at the earlier times (Shumway and Stoffer, 2006).

A number of theoretical studies have shown that environmental autocorrelation, that is an environment that fluctuates on longer time-scales than a single reproductive cycle, can have important consequences on population persistence (Roughgarden, 1975; Mode and Jacobson, 1987; Rotenberg, 1987; Caswell and Cohen, 1995; Cohen, 1995; Ripa and Lundberg, 1996; Kaitala et al, 1997; Petchey et al, 1997; Morales, 1999; Cuddington and Yodzis, 1999; Heino and Sabadell, 2003; Holt et al, 2003; Wichmann et al, 2003; Roy et al, 2005; Wichmann et al, 2005; Tuljapurkar and Haridas, 2006; Schwager et al, 2006; Ruokolainen et al, 2007; Kamenev et al, 2008; Lögdberg and Wennergren, 2012). However, most studies that have empirically estimated the degree of autocorrelation present in population abundances have been unable to directly link this autocorrelation to environmental covariates (Pimm and Redfearn, 1988; Cyr, 1997; Swanson, 1998; Miramontes and Rohani, 1998; Petchey, 2000; Inchausti and Halley, 2001, 2002; Halley and Inchausti, 2004) or have found that the link between environmental covariates and population growth is weak (Knape and de Valpine, 2010; Garcia-Carreras and Reuman, 2011). Because of the potential importance that theoretical investigations have placed on environmental autocorrelation for applications such as population viability analysis, empirically determining how animal population growth is affected by autocorrelated environmental covariates is crucial.

To analyze the role that environmental autocorrelation models have in population risk assessment we first looked at how population dynamics interact with autocorrelated environmental variables in a simulation study. This provided a baseline expectation for the behavior of real populations embedded in autocorrelated environments. We then estimated the environmental autocorrelation present in a broad range of taxa using a large number of time series from the Global Population Dynamics Database (GPDD) (NERC, 2010), decomposing the intrinsic autocorrelation generated by population processes from environmental autocorrelation. Many of the concepts presented in this work have been explored previously to some degree, however, here we integrate these ideas to provide a foundation for theoretical expectations and to better understand empirical estimates of environmental autocorrelation in animal populations. Taken together, our results raise questions regarding the importance of autocorrelated environmental variation in population dynamics and provide an updated perspective on how to think about the influence of the environment on extinction risk predictions.

We begin the introduction with a brief account of stochastic population models, showing how these models can be used to integrate population growth processes with autocorrelated environmental variability. Then past work on the impact of autocorrelated environments on animal populations is briefly summarized and we define a number of key concepts. Finally, we introduce environmental tracking models which describe how changes in the environment drive changes in population growth.

1.1 Stochastic population models

Time series of abundances are often modeled using discrete-time density dependent recursive equations. This is due both to the discrete nature of reproduction and life history structure in many species and to the discrete nature of the sampling process. Two commonly used forms of density-dependence are the discrete Gompertz and Ricker models. The Gompertz model has been widely used in ecology to detect density dependence in animal populations (Morris, 1959; Sibly et al, 2007; Ziebarth et al, 2010). It has also been the basis for the development of measurement error models (Dennis et al, 2006) and for analysis of density dependence in large datasets (Sibly et al, 2007; Abbott et al, 2009; Knape and de Valpine, 2010; Ziebarth et al, 2010; Knape and de Valpine, 2011). The Ricker model was originally derived by William Ricker (1954) emerging from a cannibalistic interaction between adults and juveniles in a population. There have been a number of other derivations (Royama, 1992; Geritz and Kisdi, 2004; Bräannström and Sumpter, 2005) linking a variety of mechanistic interpretations to this model. Variations of the Ricker model have been used in many past studies examining the theoretical properties of environmental autocorrelation (Petchey et al, 1997; Morales, 1999; Cuddington and Yodzis, 1999; Heino and Sabadell, 2003; Ruokolainen et al, 2007) and in studies examining properties of density dependence (Sibly et al, 2005).

The Gompertz model is given by

$$N\left(t\right)=N(t-1)\exp [a+b\ln \left(N(t-1)\right)+E\left(t\right)],$$ (1)

and the Ricker model is

$$N\left(t\right)=N(t-1)\exp [a+bN(t-1)+E\left(t\right)].$$ (2)

Here N(t) is the abundance metric at time t, a is the maximum per capita rate of increase, b is the strength of density dependence, and the E(t) is the environmental perturbation which is usually assumed to affect the rate of increase and is therefore typically modeled as independent and identically distributed (iid) draws from a normal distribution with mean 0 and where σ² is the environmental variance in the per capita growth rate (Ferguson and Ponciano, 2015). We have not included the effects of demographic stochasticity in the variance model E(t). Demographic factors can generate variation in births and deaths even in a constant environment, though this is often considered only for populations with low abundances that may be at risk of extinction (Shaffer, 1987; Lande, 1993). The per capita growth rate, defined as R(t) = ln (N(t)/N(t – 1)), is a commonly used transformation that turns the nonlinear stochastic models such as equation 2 into a standard linear model.

One approach to modeling the emergent effects of environmental interactions on a population is to relax the assumption that realizations of the stochastic environment, E(t) in equations 1 and 2, are iid. Suitably specified autocorrelation models have been proposed to account for effects due to complex environmental processes, species interactions, and measurement error that is not otherwise captured by single-species models. Theoretical evidence generally predicts that autocorrelated environments have important population-level impacts; however, as discussed below the empirical evidence supporting the importance of these population-level impacts is much more tentative.

1.2 Autocorrelation models

Autocovariance is a measure of how strongly a signal covaries with itself at multiple time lags. For the k^th lag in the time series X this is written as Cov(X(t), X(t – k)). The autocorrelation function is the normalized quantity, Corr(X(t), X(t – k)) = Cov(X(t), X(t – k))/σ_tσ_t–k, where σ is the standard deviation (Shumway and Stoffer, 2006). Both autocovariance and autocorrelation are functions of the lag, k, and are generally expected to go to zero with increasing lag.

The simplest example of an autocorrelation model is the autoregressive lag 1 (AR(1)) model. The AR(1) has found wide use in statistical time series modeling (Shumway and Stoffer, 2006). It is given by

$$E\left(t\right)=\varphi E(t-1)+W\left(t\right),$$ (3)

where W(t) is a normal distribution with mean equal to zero and variance given by σ², and ϕ controls the degree of autocorrelation of the current observation on the previous observation. Alternative error models that incorporate long-memory processes are discussed in Appendix D.

An additional autocorrelation model of interest is the moving average lag 1 (MA(1)) model, which can be interpreted as stochastic influences from either measurement error terms (Dennis et al. 2006) or intraspecific and interspecific interactions (Royama, 1981; Abbott et al, 2009; Ferguson and Ponciano, 2014). The MA(1) model is given by

$$E\left(t\right)=W\left(t\right)+\theta W(t-1),$$ (4)

where the W(t)'s are drawn from a normal distribution with mean equal to zero and variance given by σ². As opposed to AR(1) processes, in which the autocorrelation is in the process, the MA(1) model has autocorrelation introduced in the random shock, distributing the effect of variance perturbations from previous time lags onto the current observation. The AR(1) and MA(1) models can be applied simultaneously through the ARMA(1,1) model (Appendix B). In addition, an important connection between AR and MA processes exists as any causal, invertible ARMA process can be written as an MA or AR process of infinite order (Shumway and Stoffer, 2006).

Not specifying an accurate autocorrelation model can lead to confounding estimates of environmental autocorrelation with measurement error (Akçakaya et al, 2003). When independent estimates of measurement error are not available, state space methods can be used to estimate measurement error (de Valpine and Hastings, 2002). For the Gompertz model the state-space approach reduces to an MA(1) error structure (Dennis et al, 2006). Thus, the ARMA(1,1) error process accounts for the impact of environmental autocorrelation along with measurement error.

One of the underlying assumptions behind using AR models to capture the effects of population-environmental interactions is that there are no feedbacks between the environmental conditions driving population fluctuations and the population. Interactions with feedbacks can generate similar environmental autocorrelation patterns though with added complexity. For example, consider observing the dynamics of a single population that is interacting with another unobserved population. The dynamics of the observed population approximated around a point can be approximated as a Gompertz model with an ARMA(1,1) environmental error process (Abbott et al, 2009). Under this scenario, the sign and magnitude of the AR component depends on the signs of the interspecific interaction and on relative magnitude of intraspecific to the interspecific interactions (Ferguson and Ponciano, 2014).

1.3 Impacts of environmental autocorrelation in animal populations

Population abundances are inherently autocorrelated because abundances in the next year are dependent on the previous year through intrinsic processes such as birth and survival. Environmental processes that drive population fluctuations may operate at longer timescales than the population reproductive process. When specific covariates cannot be linked to this variability the environmental variance, E(t), may be best modeled with some autocorrelation (Roughgarden, 1975). Examples of extrinsic conditions that can drive population change and may also exhibit temporal autocorrelation are rainfall (Dennis and Otten, 2000; Taper and Gogan, 2002) and temperature (Savage et al, 2004), or demography and ecological factors such as interspecific interactions (Royama, 1977; Abbott et al, 2009; Ferguson and Ponciano, 2014). Because understanding the potential impact of autocorrelated environments on population dynamics requires untangling interactions between multiple autocorrelated random variables, we provide a summary of these terms in Table 1.

Table 1.

Glossary of terms related to environmental autocorrelation in animal populations.

Term (abbr.)	Definition
Environmental variance in the per capita growth rate	Var(E(t))	The variance of population abundances due to environmental fluctuations.
Intrinsic population autocorrelation	Corr (N(t), N(t – k)|E(t))	This is the autocorrelation present in the population abundances induced only by growth and density feedback processes.
Population environmental autocorrelation (PEA)	Corr (E(t), E(t – k))	Autocorrelation in the population environmental variance may arise when population growth is affected by autocorrelated environmental covariates.
Total population autocorrelation (TPA)	Corr (N(t), N(t – k))	The total autocorrelation present in the population abundances. This can be a mixture of intrinsic and environmental processes.
Environmental covariate autocorrelation	Corr (C(t), C(t – k))	Autocorrelation in an environmental covariate, C(t).
Environmental tracking		Environmental tracking is the degree to which changes in the per capita growth rate reflect changes in environmental covariates.
Environmental filter		These models map covariate values (C(t)) to environmental perturbations (E(t)).
Stochastic Leibig's Law of the Minimum (SLLM)		A sampling process where the limiting factor for each year is the minimum observed environmental covariate value for that year from the set of all limiting environmental factors.

The intrinsic population autocorrelation is defined as the temporal correlation in abundances (per capita growth rate) in a constant environment. For the abundances (per capita growth rate) this can be denoted as Corr(N(t), N(t – k)|E(t)) (Corr(R(t), R(t – k)|E(t))), where E(t) is population abundance at time t and the notation indicates we have conditioned the stochastic growth process to occur in a constant environment, E(t). This intrinsic autocorrelation is generally assumed to be positive due to the nature of growth processes but complex deterministic dynamics may also generate negative autocorrelation (Cohen, 1995). Extrinsic processes that generate population environmental autocorrelation (PEA) are denoted as Corr(E(t), E(t–k)). These are also often assumed to be positively autocorrelated, though some ecological processes may generate negative values.

The total population autocorrelation (TPA) is a measure of the total autocorrelation observed in population abundances though it is oftentimes measured in the per capita growth rate as well. For the abundances (per capita growth rate) this can be written as Corr(E(t), E(t – k)) (Corr(R(t), R(t – k))). As noted in previous work (Sugihara, 1995; Kaitala et al, 1997; Ranta et al, 2000), the autocorrelation measured at the ophtpulation level is influenced by the intrinsic processes of growth and density feedback as well as by autocorrelation generated through extrinsic processes. This effect is nicely illustrated in Figure 1 of Garcia-Carreras and Reuman (2011). Different combinations of the intrisic population autocorrelation and PEA can generate identical TPA values so previous work examining only the TPA does not provide information on the relative contributions of PEA to the observed population dynamics. Although most previous work has focused on the direct impacts an autocorrelated environment has on population dynamics, the process of translating environmental conditions into population growth is often characterized by complex relationships that may influence the strength of PEA.

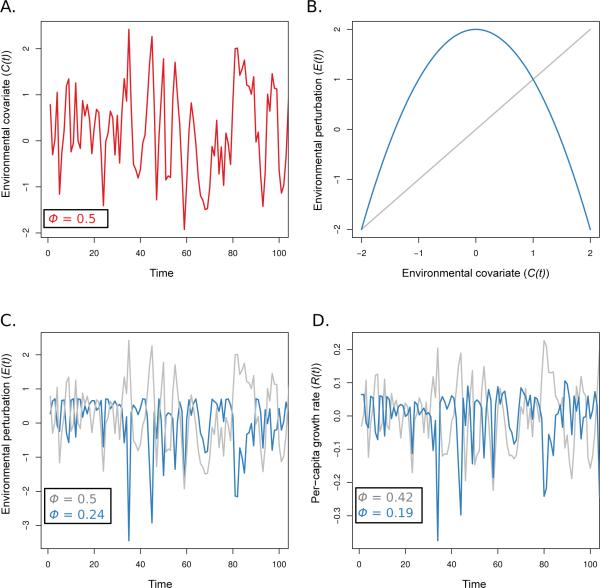
Fig. 1.

An illustration of how environmental filters can transform the autocorrelation in environmental covariates and the resulting effect on population dynamics. Panel A shows a time series of an environmental covariate, C(t), with lag one autocorrelation ϕ = 0.5. Panel B shows the tracking model, which describes the perturbation, E(t), on the per capita growth rate for different values of the environmental covariate. We illustrate a linear tracking model (grey) and a unimodal tracking model (blue). Panel C illustrates the resulting perturbation, E(t), once the covariate, C(t), passes through the filter. This resulting time series has some population environmental autocorrelation (PEA) that is a result of this transformation. Finally the environmental perturbations affect the population growth process and the total population autocorrelation (TPA) in panel D. The per capita growth rate, R(t), in the Ricker model (parameter values: a = 0.10, b = –0.0010, σ = 0.10) displays a lag one autocorrelation value that is a function the environmental signal, E(t), and the effects of density dependence.

Starting with an observation at time t of the environmental covariate, C(t), we define the covariate autocorrelation as defined as Corr(C(t), C(t – k)). This environmental covariate is linked to stochastic perturbations of the population growth, E(t), though an environmental filter that defines the relationship between C(t) and population growth. When there is a linear transformation between C(t) and E(t) the PEA will be equal to the autocorrelation in the environmental covariate. However, when the mapping between C(t) and E(t) is nonlinear this correspondence may be disrupted. We discuss several potentially common filters in the next section.

The incorporation of high levels of PEA into population projections has been shown to lead to large differences in extinction risk predictions, as reviewed by Ruokolainen et al (2009). PEA coupled with under-compensatory density dependence tends to increase extinction risk due to the increased probability of having a series of bad years in autocorrelated environments. Overcompensatory population dynamics in autocorrelated environments will tend to decrease extinction risk due to the reduced probability of having a single extreme event occur in some time period (Schwager et al, 2006). In general, the effects on population extinction are dependent on both the underlying dynamics and on the magnitude of PEA. These results suggest that accurately assessing species extinction risk using population dynamics models requires estimating both the form of density dependence and the degree of PEA present in a population.

Previous studies that have attempted to empirically quantify levels of autocorrelation in animal population time series have typically looked at the TPA, the overall autocorrelation present in population abundances (Pimm and Redfearn, 1988; Cyr, 1997; Miramontes and Rohani, 1998; Inchausti and Halley, 2001, 2002; Halley and Inchausti, 2004). Because past studies of TPA have not decomposed environmental variability from density dependent processes, it is not known how much of the observed TPA signal is contributed by the intrinsic population autocorrelation relative to the PEA, though both are thought to occur in most animal populations (Ariño and Pimm, 1995). Furthermore, these studies have generally failed to link estimated TPA to specific environmental covariates despite suggestions that species depending on autocorrelated environmental covariates should display PEA.

Several recent empirical studies that have attempted to determine whether population growth directly tracks specific environmental covariates. Knape and de Valpine (2010) incorporated weather and climatic index data as covariates into a large number animal time series models and showed that environmental covariates can improve model predictions. However, these improvements were often marginal when corrected for model overfitting. A similar study by (Garcia-Carreras and Reuman, 2011) also examined a number of climatic variables and animal time series, their results suggest that the autocorrelation in mean summer temperature is weakly correlated (r = 0.312) with the TPA in populations from the GPDD. The results of these studies suggest that the average coupling between any one climatic variable and population growth will be weak. However, both studies point out the important caveat that most populations will be affected by multiple environmental factors that may not be directly measured by convenient summary statistics available for global analyses. The theoretical body of literature has little to say on how the effects of multiple autocorrelated environmental factors might combine to drive extinction risk.

We are also aware of four microcosm experiments that have examined the role of autocorrelated environments on population dynamics. The first study (Petchey, 2000) found no significant effects of the environmental autocorrelation on the resulting TPA, contrary to theoretical predictions. However, populations in positively autocorrelated environments did tend to be more correlated to the environmental state than populations in uncorrelated environments, an effect that while statistically significant was weak. The author points out that the tracking ability of experimental Colpidium populations relies on long periods of very high temperatures, during which the population growth was strongly correlated to the environment while at other temperatures this correlation was weak. A second study (Gonzalez and Holt, 2002) found that average population abundances in autocorrelated environments were higher than in uncorrelated environments, as predicted by theory. The other prediction tested, that populations in autocorrelated environments display greater variability, was supported in one of the two experimental treatments. In addition, this study was with open populations that allowed migration between subpopulations, potentially leading to stronger responses to environmental conditions than growth processes due to the potential for rapid migration in response to current conditions. Another microcosm experiment (Laakso et al, 2003b) found that population abundances and temperature were more strongly correlated when temperature was positively autocorrelated, supporting theoretical predictions. A culling experiment (Pike et al, 2004) was suggestive of autocorrelated mortality effects on extinction times for one of two experimental treatments, partially supporting theoretical predictions.

These experimental results suggest that although it may be possible for populations to be strongly coupled to the environment, often this relationship does not hold even in relatively simple experimental systems. Taken together, past empirical and experimental studies suggest that assuming a direct, linear relationship between correlation in environments and the resulting PEA is likely an oversimplification and that more biologically plausible models of environmental autocorrelation are needed to be empirically useful under natural conditions. In order to complement theoretical work to date, we assess whether linear models of environmental autocorrelation are sufficient to accurately estimate density dependence and autocorrelated environmental variability using animal abundance time series.

1.4 Environmental tracking models

Environmental tracking models call into question the implicit assumption that the autocorrelation in environmental factors will translate directly into population environmental autocorrelation (PEA) and thus affect the total population autocorrelation (TPA). Nonlinear growth responses to environmental conditions and phenotypic plasticity define the ecological niche, a central concept in ecology (Holt, 2009). These responses can affect the way that animals track environmental conditions, which in turn can lead to PEA values that are much different than the autocorrelation present in environmental covariates (Laakso et al, 2001).

Nonlinear responses to the environmental state can alter an autocorrelated environmental variable so that the PEA differs from the original autocorrelation in an environmental covariate (Laakso et al, 2001, 2003a; Ruokolainen and McCann, 2013). Figure 1 is a heurisitic illustration of the steps required to transform a changing environmental state into population growth. This multi-step process begins by passing the environmental covariate signal (Figure 1A) through a nonlinear filter (Figure 1B). The resulting transformed fluctuations drive perturbations in the per capita growth rate (Figure 1C). Finally, the TPA is measured on the resulting time series (Figure 1D). The resulting autocorrelation in the per capita growth is affected by the nonlinear filter selectively dampening extreme oscillations in the environment.

In addition to previously studied nonlinear tracking models we propose a stochastic version of Liebig's law of the minimum (SLLM) (Hooker, 1917; Farrior et al, 2013) (Table 1). This may reduce the PEA for populations that are limited by multiple limiting resources by changing the limiting resource each year, breaking the autocorrelation that would be present in a single limiting resource. The model assumes that the limiting environmental factor for each year is one of several resources, each of which may be autocorrelated with itself but is uncorrelated to the other limiting resources. Sampling from these different resources may serve to disrupt the autocorrelation present in any one of the environmental covariates and reduce the overall PEA.

A third process that has been shown to disrupt the influence of autocorrelation in environmental covariates on PEA is demographic stochasticity. The presence of demographic stochasticity leads to the addition of white noise to the total population variance, potentially reducing the overall importance of PEA at low abundances (van de Pol et al, 2011). Although demographic stochasticity is at work to some degree in all populations, our analysis is primarily focused on long-term studies of stable populations that are likely to have relatively low amounts of demographic stochasticity.

Single-species time series without environmental covariate data are not sufficient to estimate environmental filters, therefore, we provide estimates of PEA values in the GPDD and use those estimates as a lens to indirectly determine how well standard assumptions about how autocorrelated environments effect populations hold up. We explored the impacts of the nonlinear and SLLM tracking models on the observed PEA in animal populations with a simulation study.

2 Methods

2.1 Effects of environmental tracking models

We used simulations to explore the impacts of environmental filters on covariates with autocorrelation, then estimated the population environmental autocorrelation (PEA) in the GPDD. Although we cannnot estimate environmental filters directly from abundance time series, the simulation work provides a baseline to compare what we estimate in the GPDD to what would be expected by a linear environmental filter.

In order to assess the effects nonlinear tracking models have in transforming environmental covariates with autocorrelation into PEA, we simulated the impact of several forms of population responses to environmental variation on time series generated from an AR(1) model. Various functions that have been used when modeling species responses to environmental covariates. Two of the most common functions are the power and the logistic (or S-shape) transformations. The power function is often justified as a niche model of environmental suitability because at even powers the function results in one optimal response along an environmental axis. A squared power can be viewed as a second order approximation to functions describing a unimodal response of populations to an environmental factor. Such responses include the temperature response of fitness in ectothermic species (Huey and Stevenson, 1979; Amarasekare and Savage, 2012). Cubic and other odd functions are more rarely observed in ecological systems but can be used to incorporate the effects of skewness into a model (Austin, 2007) or to approximate an environmentally-driven allee affect such that low levels of an environmental resource correspond to negative growth while high values correspond to positive growth. Quartic powers can approximate truncated fitness responses where the fitness is near optimal over some finite range, then drops off outside this range (Huey and Stevenson, 1979; Kearney et al, 2008). The logistic function is often used to model the response of survival to an environmental variable (Jonzén et al, 2010). Although the logistic function can also be a power function of the environment, we limit our analysis to logistic transforms of linear environments.

To determine the effect of these transformations we simulated an environmental covariate, C(t), as an AR(1) process (equation (3)) with mean equal to 0 and variance equal to 1. Data were generated using the arima.sim function in R (R Development Core Team, 2012) and were rescaled to variance 1 by rescaling all observations by $\sqrt{1-{\varphi }^2}$ (Shumway and Stoffer, 2006). For each series the autocorrelation in an environmental covariate, given by ϕ in (3), was set to one of 30 equally space values in the interval [–0.9, 0.9]. We drew a time series of length 10⁶ from each level of autocorrelation. We then transformed C(t) into E(t) using the power transform, E(t) = –C(t)^η , and the logistic transform, $E\left(t\right)=\frac{e^{\zeta C\left(t\right)}}{1+e^{\zeta C\left(t\right)}}$. The value η was varied between the integer values 1 to 4 and ζ was set to be 1, 5, 10, or 20. We transformed C(t) into E(t) for all values of η, and or ζ. The PEA, ϕ^′, was estimated by regressing the series on its previous state E(t) = ϕ^′E(t–1)+W(t), where W(t) was iid normally distributed with mean zero and estimated variance.

The effect of the stochastic Leibig's law of the minimum (SLLM) on the overall PEA was also determined by using another simulation procedure. First, we assumed that a number (n) of time series with autocorrelation are determinants of per capita growth rate. Then we simulated these n time series using an AR(1) process with mean 0, variance 1, and of length 10⁶. Data were generated using the arima.sim function in R (R Development Core Team, 2012) were rescaled to variance 1 by rescaling all observations by $\sqrt{1-{\varphi }^2}$ (Shumway and Stoffer, 2006). We took the minimum value from the n realizations at each time step, so that E(t) = min{X₁(t), X₂(t), . . . , X_n(t)}, where E(t) is the environmental variance in the per capita growth rate.

We examined two scenarios for the SLLM. In the first, we let all the X_i's have the same degree of autocorrelation, we then applied the SLLM to construct the new E(t). In the second scenario, we fixed the autocorrelation for n–1 of these series at 0.5, a level hypothesized to be a reasonable default for environmental processes (Halley and Inchausti, 2004). The remaining covariate time series had an autocorrelation level that was incrementally varied. In all simulations we incrementally varied the autocorrelation in the interval [–0.9, 0.9], by steps of 0.1 for a total of 20 values. We then estimated the PEA, ϕ^′, by regressing the SLLM series on its previous state E(t) = ϕ^′E(t – 1) + W(t), where the W(t) are iid normally distributed with mean zero and estimated variance. We repeated the simulation for n = 2, 3, 4, and 5 limiting environmental factors. These two scenarios examine the potential of SLLM to disrupt autocorrelation among similar environmental covariates, and the potential of SLLM to affect the PEA when a single series is less than or greater than the other covariates.

2.2 Joint estimation of density dependence and the autocorrelation structure for the GPDD

We examined the degree of environmental autocorrelation in the GPDD by jointly estimating growth and density dependence (contributing to the intrinsic population autocorrelation) as well as the autocorrelation in the environmental variance (the PEA). Our curated dataset consisted of 445 high quality time series from the approximately 5000 available datasets in the GPDD (NERC, 2010). In order to include a dataset from the GPDD we required at least 15 observations in the time series, the qualitative GPDD reliability rating must have been 4 or 5 (out of a maximum rating of 5), and the data must not have been constant over the first three years. In addition, we only allowed datasets where sampling units indicated nonharvest indices, as harvests may not reflect true population abundances. All data was transformed by adding 1 to all observations in order to remove any 0's. We tested the effects of this data transformation by analyzing a subset of the 445 datasets where there were no zero counts, but fewer datasets (166) were available for this analysis. We report the unique GPDD identification numbers for the series chosen in Appendix A.

The ability to accurately estimate the PEA in density dependent models was determined using a model structural adequacy analysis (Taper et al, 2008). This allowed us to determine how well simple density dependence models could estimate the PEA arising from a more complex model. Because previous work has shown that both measurement error (Lindén and Knape, 2009) and model structure (Jonzén and Lundberg, 2002; Lindén et al, 2013) can affect the estimation of the environmental autocorrelation we explored the impacts of these factors on the estimation process of the PEA estimator, $\widehat{\varphi }$.

We began by fitting a population dynamics model to each of the 445 GPDD time series included in our study to obtain parameters for simulating new datasets. This fitting procedure was performed for density dependence lags of 0 (density independent) through 3 with the Gompertz model of density dependence and with an ARMA(1,1) error structure to decompose estimates of PEA and measurement error. A new dataset was then generated using each of the fitted model's parameters except the AR(1) component, ϕ in equation (3), was set to one of the values (0.0, 0.225, 0.45, 0.675, 0.9). These generated data had the same parameters, sample size, and were initialized at the same initial population abundance as the original dataset. For each of the generated datasets, we fit a set of candidate models of lags 0 to 3 with an ARMA(1,1) error term. We then compared the estimator bias and mean squared error in the case where we selected the best lag model using AICc versus the case where we simply use the lag-1 density dependence model regardless of the generating model.

Based on the results of this simulation study we were able to determine the best method for estimating the PEA in the GPDD time series in terms of the estimator bias and mean squared error. We then were able to apply this procedure to the GPDD and also use the estimated bias in the AR(1) parameter to perform a bias correction procedure. In order to determine whether there were underlying patterns in the distribution of PEA estimates we tested a number of covariates associated with the GPDD to determine if they could explain estimated PEA values. These methods and results are fully described in Appendix C.

Finally, bias in our estimates of the PEA may arise if the source of environmental variation is perturbations to the carrying capacity, rather than the maximum per capita rate of increase as we assumed. We conducted a simulation study to determine whether this source of bias is negligible or not, presented in Appendix D.

3 Results

3.1 Effects of environmental tracking models

We found that the magnitude of population environmental autocorrelation (PEA) was reduced from the original autocorrelation in environmental covariates by the nonlinear environmental tracking models (Figure 2). This decrease in magnitude has not been described in the literature to the best of our knowledge. Previous work that has explored the impact of tracking models on PEA has found that they can also affect the magnitude of the variance, skew, and kurtosis in the resulting PEA (Laakso et al, 2001). Although this can have potentially important impacts on predictions of extinction dynamics (Laakso et al, 2003a, 2004) we were solely concerned with the ability of tracking models to modify the strength of autocorrelation in environmental covariates.

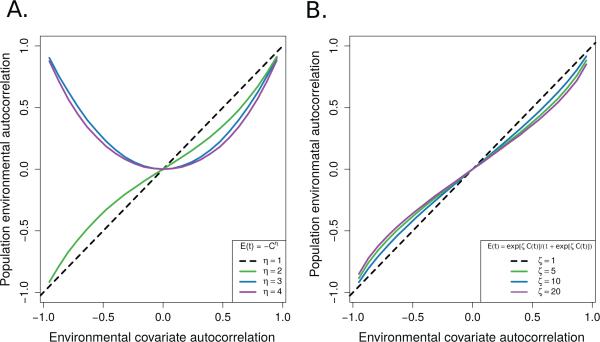
Fig. 2.

The effect of two different nonlinear interactions on an autocorrelated time series, C(t). The dashed black line is the autocorrelation estimated in the untransformed environmental covariate, while the colored lines are the population environmental autocorrelation (PEA) values in E(t) for different transformations. Panel A corresponds to power transforms of the form E(t) = –C(t)^η. Panel B corresponds to the logistic function, $E\left(t\right)=\frac{e^{\zeta C\left(t\right)}}{1+e^{\zeta C\left(t\right)}}$. All estimations were made using an AR(1) model.

The degree of the autocorrelation dampening when translating autocorrelated covariates into PEA with nonlinear tracking models depended on the relationship between the population and the environmental variable. However, power and threshold functions both tended to reduce the PEA relative to the original covariate, with the greatest dampening effect coming from even-powered, symmetric niche models (Figure 2). Asymmetric models such as the power model with odd coefficients and the logistic model had less impact on the original covariate autocorrelation than the symmetric models, due to the ability of symmetric models to cause changes in the sign of the covariate autocorrelation. Symmetric tracking models had weak effects on higher levels of autocorrelation than at moderate values, as these series correspond to populations that spend more consecutive time on the edges of their environmental tolerances where the curvatur eof the tracking model is less. These results suggest that the dampening of autocorrelation in covariates is a ubiquitous phenomenon but may often depend on whether a population is near the limits of its niche tolerance or not. For populations in marginal environments where the tracking model is centered on the tails of the niche model, rather than the center, a linear tracking model may be a reasonable approximation.

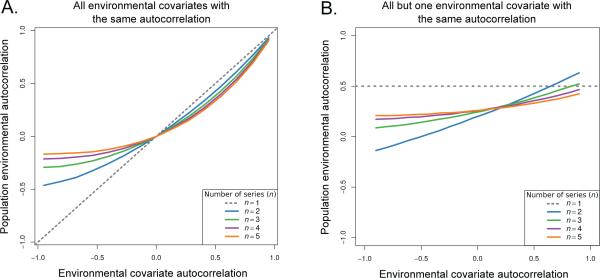
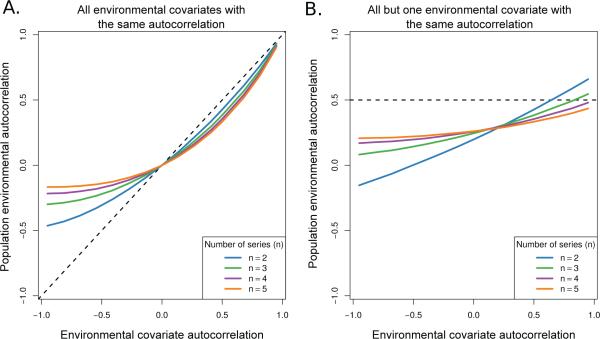
Applying the stochastic Leibig's law of the minimum (SLLM) also led to reductions in the PEA by breaking the dependency present in long runs from any one of the time series (Figure 3). In both simulation experiments dampening due to the SLLM was stronger on negative values of autocorrelation, due to oscillatory behavior in this parameter regime that leads to frequent changes in the minimum limiting environmental factor. With equal and positive autocorrelation in all the environmental covariates (Figure 3A) the degree of dampening was less but still potentially significant, for example when there were 5 time series all with autocorrelation values of 0.5 the resulting PEA was 0.33. For the case when the autocorrelation of a single environmental covariate was varied and the remaining series were set to the plausible general values of 0.5, the general trend was to reduce the PEA, though very high values in one environmental covariate combined with few limiting factors can lead to values greater than 0.5 (Figure 3B). Overall, these results suggest that both the number of environmental covariates limiting population growth and the distribution of autocorrelation in those covariates will have potentially important consequences on the PEA.

Fig. 3.

Two applications of the SLLM to a number, n, of autocorrelated time-series. In both panels the x-axis denotes the autocorrelation in the environmental covariate while y-axis is the population environmental autocorrelation (PEA) that affects the per capita growth rate once the SLLM has been applied. In panel A all n covariates have the same autocorrelation. In panel B, n – 1 of the covariates have an autocorrelation of 0.5, while the remaining covariate has the autocorrelation value given on the x-axis. In both panels the dashed line denotes the covariate's autocorrelation, for comparison. The overall effect of the SLLM depends on the number of environmental covariates, n, that limit the population. In general the SLLM tends to reduce the magnitude of the PEA relative to what is expected from a single limiting factor. However, as shown in the right panel the effect can increase the PEA if a single limiting environmental factor has a high enough autocorrelation. All estimations were made using an AR(1) model.

In these simulations we only tested the impacts of environmental processes without direct feedbacks to the population. Previous work has identified that interactions with feedbacks can often be approximated by more complex ARMA autocorrelation structures that are additive extensions of the AR(1) process used here. Therefore, we expcet that our conclusions will generalize to interactions with feedbacks as long as ARMA models are appropriate approximations to those feedbacks.

3.2 GPDD estimates

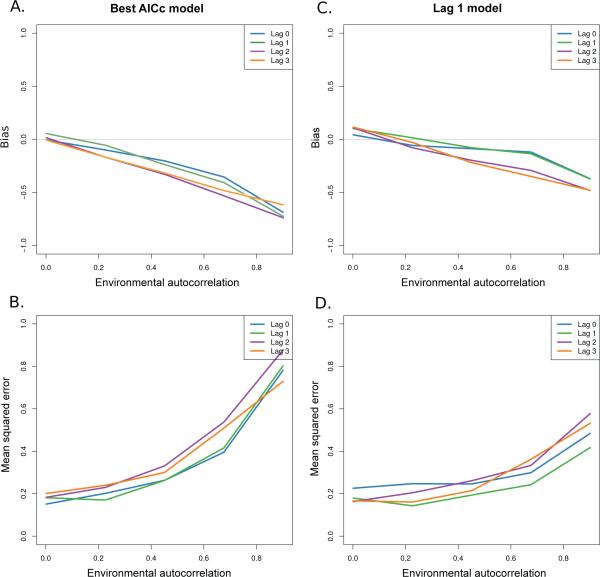
Our simulation study indicated that estimations of the population environmental autocorrelation (PEA) depend on the model form and error structure used, consistent with previous work (Jonzén and Lundberg, 2002; Lindén and Knape, 2009; Lindén et al, 2013; Fowler and Ruokolainen, 2013). Bias in estimates of $\widehat{\varphi }$ tended to be negative at moderate to high values (Figure 4A, 4C), and slightly positive when using the lag-1 model at low values (Figure 4C). The magnitude of bias and the mean squared error in the estimates using the lag-1 model tended to be less than when performing model selection at moderate to high autocorrelation values and over all lags. This suggests that the model selection procedure introduced estimation error through model uncertainty (Figure 4). Finally, we found that both the AR component and MA component were necessary in order to decompose the effects of PEA and measurement error.

Fig. 4.

Bias and mean squared error (MSE) in the estimated environmental autocorrelation, $\widehat{\varphi }$ for data generated from a given lag with the Gompertz model with an ARMA(1,1) error structure. A) The estimated bias when performing model selection using AICc, B) the corresponding estimated mean squared error in $\widehat{\varphi }$. C) The estimated bias present when using estimates from the lag-1 model, and D) the corresponding estimated mean squared error in $\widehat{\varphi }$ estimator.

Based on the lag-1 estimates we tested whether the degree of bias could be estimated as a linear function of the true environmental autocorrelation (Figure 4C). We found that a linear model was better than a model with constant intercept (ΔAICc = 34.3), suggesting that a bias correction term could be implemented. Including model lag did not lead to improvements in model performance (ΔAICc = 0.21) suggesting that the true dimension of the generating model will not significantly affect our correction. Our estimated bias was, $\widehat{\varphi }-\varphi =0.10-0.54\varphi$. Then the bias correction is estimated as,

$${\widehat{\varphi }}_{\text{Corrected}}=\frac{\widehat{\varphi }-0.1}{0.46}.$$

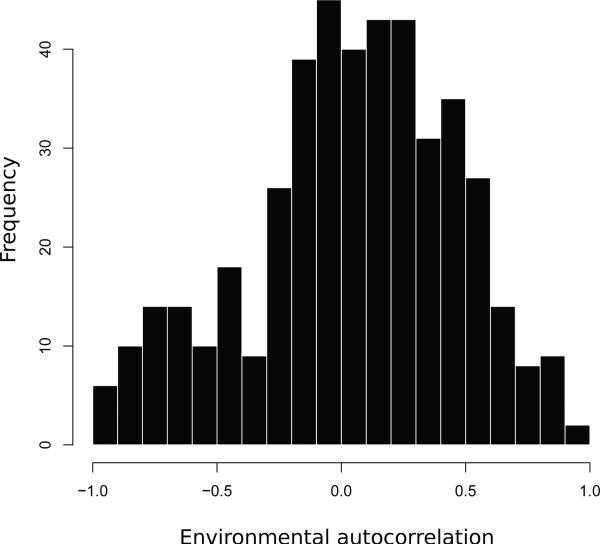
We provide a set of different PEA estimators for our analysis of the GPDD, including both the raw estimates of PEA, $\widehat{\varphi }$, and bias corrected PEA estimates, ${\widehat{\varphi }}_{\text{Corrected}}$, (Table 2). When testing between Gompertz, Ricker, and density independent models we found an estimate of $\widehat{\varphi }=0.08$ and ${\widehat{\varphi }}_{\text{Corrected}}=-0.03$. Not including datasets with observed zeros changed the PEA estimate to $\widehat{\varphi }=0.07$ and ${\widehat{\varphi }}_{\text{Corrected}}=-0.06$, suggesting that adding one to all observations had little effect on these estimates. When selecting between the Gompertz and density independent models we found a median PEA estimate in the GPDD of $\widehat{\varphi }=0.08$ and ${\widehat{\varphi }}_{\text{Corrected}}=-0.05$ while when selecting between the Ricker and density independent models we estimated $\widehat{\varphi }=0.06$ and ${\widehat{\varphi }}_{\text{Corrected}}=-0.10$ (Table 2). In all cases estimates were near zero and 86% of the raw estimates and 73% of the bias corrected estimates were below 0.5, a level that has been hypothesized as a reasonable default for the PEA (Halley and Inchausti, 2004).

Table 2.

Summary statistics and sample size for distributions of PEA estimated under different models and with different data sets. Estimates are given as the raw estimator with the bias corrected estimator in parentheses. The density dependence column reports the forms of density dependence considered in the model set. “No +1 transform” means that all datasets with zeros were excluded from the analysis. For all model analyses density independent models were also included. All models included an MA(1) term to account for measurement error.

Density dependence	Autocorrelation model	Sample size	Median $\widehat{\varphi }$	SD $\widehat{\varphi }$
Gompertz & Ricker	ARMA(1,1)	445	0.08 (−0.03)	0.42 (0.90)
Gompertz & Ricker (no +1 transform)	ARMA(1,1)	168	0.07 (−0.06)	0.42 (0.91)
Gompertz	ARMA(1,1)	445	0.08 (−0.05)	0.42 (0.90)
Ricker	ARMA(1,1)	445	0.06 (−0.10)	0.42 (0.91)

We tested a number of potential covariates to determine if they could explain variability in our estimates of PEA, however we found no important explanatory variables (methods and results in Appendix C). Our diagnostic tests were suggestive that estimates of PEA tended to decrease with sample size and that specialist species may be subject to different levels of PEA than generalists, consistent with predictions from the SLLM. However, these effects were also not statistically significant (Appendix C).

Finally, we examined the impact of PEA arising through environmental variation in the carrying capacity, rather than the maximum per capita rate of increase, using a simulation study. Our results (Appendix E) suggest that this is not a source of significant estimation bias of the PEA, though at very high levels of variability in the carrying capacity the magnitude of the estimated PEA may be slightly lower than the actual PEA. More details on the method and results are provided in Appendix E

4 Discussion

Here we have shown that decoupling population dynamics from the environmental variance in the per capita growth rate is necessary to provide interpretable population environmental autocorrelation (PEA) estimates. Previous estimates of total population autocorrelation (TPA) (Pimm and Redfearn, 1988; Cyr, 1997; Miramontes and Rohani, 1998; Swanson, 1998; Inchausti and Halley, 2001, 2002; Halley and Inchausti, 2004) have not decomposed the TPA into its basic components, and therefore provide an ambiguous guide to the levels of PEA present in populations. When external and internal sources of TPA are teased apart using process-based statistical methods evidence for low levels of PEA emerges. Median levels of autocorrelation were not in the range that previous studies have identified as significantly affecting population extinction risk, typically PEA values greater than 0.5 (Petchey et al, 1997; Cuddington and Yodzis, 1999; Schwager et al, 2006), though this threshold can be lower depending on model assumptions (e.g., Ripa and Lundberg, 1996). We emphasize that these results are not evidence that environmental changes do not strongly affect population dynamics. Instead, they indicate that the population environmental variance does not exhibit the high autocorrelation levels we would expect from a linear interaction between high-levels of autocorrelation in environmental covariates and the per capita growth rate.

There is reason to expect that a decoupling of covariate autocorrelation and the PEA is a general phenomenon. Evolution should act to flatten the norm of reaction to environmental perturbations leading to hump-shaped responses to environmental conditions. Mutations that improve the performance of conditions other than most frequent will be selected for if they don't diminish the performance of the individual under the most frequent condition. This will be true even when the mutation has deleterious pleiotropic effects under even rarer conditions. Thus, evolution should lead to a mesa like norm of reaction where individuals are largely indifferent to small variation in environmental covariates but are disproportionately vulnerable to rare extreme events, decoupling environmental variation from covariate autocorrelation.

Our study provides a reasonable biological mechanism describing the lack of PEA in the GPDD. Nonlinear interactions can reduce the ability of an animal population to track environmental covariates and dampen the autocorrelation perceived by the population. Because single-species time series data are not sufficient to determine the causes of these low autocorrelation in the GPDD we cannot precisely identify the mechanisms involved. However, it is not unreasonable to think that one or more of our proposed environmental filters are operating in most animal populations. As a result, an imperfect translation of covariate autocorrelation into PEA may be quite common and recent empirical results are beginning to support this viewpoint (Knape and de Valpine, 2010; Garcia-Carreras and Reuman, 2011; van de Pol et al, 2011; Engen et al, 2013).

Despite the converging lines of evidence in observational studies there is conflicting experimental evidence demonstrating that autocorrelated environments can affect population dynamics (Petchey, 2000; Gonzalez and Holt, 2002; Laakso et al, 2003b; Pike et al, 2004). Reconciling the body of experimental evidence with our model predictions is crucial for understanding when autocorrelated environments can affect population persistence. Our study proposes the nonlinear response of populations to environmental conditions must be considered in the resolution of these viewpoints (Petchey, 2000). Our models predict that populations in environments near the limits of their ecological niche are more likely to exhibit stronger environmental tracking behavior and therefore display higher PEA values. Future work may make progress by examining the impact of autocorrelated environments over environmental gradients. Because populations at the edge of their range are also often at lower abundance it may be that autocorrelated environments have important implications on persistence for these populations and on species distributions.

At first glance the potentially weak relationship between environmental covariates and population abundance suggested by our results is at odds with the view that populations can be strongly regulated by density independent factors (Andrewartha and Birch, 1954). In their classic study on the pest species, Thrips imaginis, Davidson and Andrewartha (1948) found that environmental variables could be used to explained over 80% in the annual variance in peak log densities. However, their investigation into daily fluctuations of variability showed that environmental effects could only explain 10% of the variation not due to population growth processes. The use of yearly peak log abundances is likely to be more sensitive to fluctuations under nonlinear environmental tracking because populations will often have disproportionately stronger responses to environmental covariates as conditions deviate farther from the average. This also highlights the potential difficulties of detecting the impact of environmental covariates when using relatively sparsely sampled time series data. Our modeling approach assumes that generations are either overlapping or non-overlapping with a generation time equal to the sampling period. For populations not following these assumptions our model estimates may not correspond to the interpretations presented here. For example, when generations are non-overlapping and much longer than the sampling period we expect that the long times between reproductive events will be accounted for by higher order lags in the AR model, potentially confounding the estimated PEA with other effects.

We did not consider more complex life histories in our analysis although theory has suggested that PEA may have significant effects on the per capita growth rate of age- and stage-structured populations (Tuljapurkar, 1982; Tuljapurkar and Haridas, 2006). However, recent work has found that the presence of autocorrelation in a temperature dependent, stage-structured model of Eurasian oystercatchers (Haematopus ostralegus) only weakly affected population extinction risk primarily due to nonlinear interactions between demographic rates and environmental covariates that led to poor environmental tracking (van de Pol et al, 2011) and estimates in four other age-structured populations were found to be quite small (Engen et al, 2013). These results provide an empirical example that coupling real life-history complexity to nonlinear environmental responses leads to reductions in the influence of autocorrelated environments. It is likely that in many species differing ecological and climate covariates typically limit specific life stages through mechanisms such as ontogenetic shifts and other complex life histories that may serve to buffer populations against autocorrelated environments (Ratikainen et al, 2008).

The mechanisms that link animal populations to their environment are undoubtedly more complex than the tracking models used here. Yet, our work shows that simple, tractable models can be used to reveal the stochastic properties of population-environment interactions. In the face of long term climatic change it is important to be able to make informed predictions for management and conservation purposes. In our view understanding how fluctuations in the environment translate into animal population growth is an important step towards better predictions of population abundances that account for environmental changes.

Fig. 5.

Histogram of 445 estimated population environmental autocorrelation (PEA) values from the GPDD.

Appendix A: Curating the GPDD

We chose a high quality subset of the over 5000 GPDD datasets using the following criteria: there must have been at least 15 observations in the time series, the qualitative GPDD reliability rating must have been 4 or 5 (out of a maximum rating of 5), and the data must not have been constant over the first three years. In addition, we only allowed datasets where sampling units indicated nonharvest indices, as harvests may not reflect true population abundances. All data was transformed by adding 1 to all observations, in order to remove any 0's. We tested the effects of this data transformation by analyzing a subset of the 445 datasets where this transformation was not applied, but fewer datasets (166) were available for this analysis. The MainID's of the GPDD datasets used in our analysis were: 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 56 57 58 59 60 61 62 63 64 65 66 67 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1172 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1211 1213 1248 1250 1254 1261 1268 1272 1275 1276 1347 2770 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781 2787 2789 2791 2798 2800 2802 2805 2810 2815 2829 2833 2840 2842 2844 2852 2857 2867 2869 2879 2887 2891 2901 2903 2905 2915 2917 2922 2926 2935 2937 2939 2958 2960 2962 2974 2976 2986 2991 3001 3003 3017 3021 3028 3030 3037 3043 3045 3051 3056 3059 3068 3070 3072 3084 3092 3108 3110 3112 3118 3123 3127 3133 3135 3139 3144 3157 3159 3161 3170 3177 3182 3190 3214 3216 3218 3223 3225 3233 3237 3249 3251 3253 3260 3263 3265 3268 3275 3283 3295 3297 3306 3312 3316 3323 3330 3356 3358 3360 3372 3378 3382 3393 3395 3406 3426 3428 3430 3437 3442 3445 3455 3466 3468 3470 3477 3480 3482 3484 3489 3496 3508 3521 3533 3535 3539 3546 3557 3559 3567 3575 3577 3583 3585 3592 3623 3625 3627 3639 3641 3650 3664 3666 3673 3676 3678 3680 3683 3688 3693 3706 3708 3716 3718 3723 3726 3739 3741 3757 3774 3776 3784 3787 3795 3797 3799 3811 3814 3825 3827 3829 3838 3840 3849 3853 3864 3866 3876 3882 5019 5020 6057 6104 6105 6106 6107 6108 6109 6110 6111 6112 6113 6114 6115 6116 6117 6118 6119 6120 6121 6122 6123 6124 6125 6126 6127 6128 6129 6130 6131 6132 6133 6134 6135 6136 6137 6138 6139 6140 6141 6142 6143 6592 6728 6729 6730 6731 6732 6733 6734 6735 6736 6737 6738 6739 6740 6741 6742 6743 6744 6745 6788 6789 6790 6791 6792 6793 6794 6795 6796 6797 6798 6799 6800 6801 6802 6803 6804 6805 6806 6807 6808 6809 6810 6811 6812 6813 6814 6815 6816 6817 6818 6819 6820 6821 6822 6823 6824 6825 6826 6827 6828 6829 6830 6831 6832 6833 6834 6835 6836 6837 6838 6839 6840 6841 6842 6843 6844 6845 6846 6847 6848 6849 6850 6851 6852 6853 6854 6855 6856 6857 6858 6859 6860 6861 6862 7065 9191 9192 9193 9245 9246 9247 9248 9249 9279 9280 9302 9338 9339 9340 9341 9342 9343 9344 9345 9346 9347 9348 9365 9391 9393 9425 9517 9518 9519 9536 9542 9684 9833 9834 9911

Appendix B: Parameter estimation and model selection

Parameter estimation

Parameter estimation was performed using both maximum likelihood (ML) and restricted maximum likelihood (ReML) methods. We used one-step predictions to fit population dynamics models with PEA using abundance data from the GPDD. AICc was used to perform model selection from among the candidate models using the model's ML estimates. However, our reported values of $\widehat{\varphi }$ used ReML parameter estimates from the best AICc models. ReML estimation has been shown to perform better than traditional ML when estimating variance components, but is not valid for model selection using information criterion (Staples et al, 2004). ML and ReML estimations were performed using the generalized least squares (gls) function from the NLME package in the R software environment (Pinheiro et al, 2011; R Development Core Team, 2012). We assumed a multivariate normal distribution for the observed per capita growth rate, ln $\left(\frac{N\left(t\right)}{N(t-1)}\right)$, where the mean vector was given by the predicted per capita growth rate for the corresponding form of density dependence. The covariance matrix was given by σ²R, where the correlation matrix, R, was given by the correlation structure for the appropriate ARMA(1,1) model used. For k observations of the per capita growth rate, the ARMA(1,1) correlation structure with AR(1) parameter ϕ and MA(1) parameter θ is given by

$$\mathbf{R}=\frac{(1+\theta \varphi )(\theta +\varphi )}{1+2\theta \varphi +{\theta }^2}\left[\begin{array}{cccc}1\hfill & {\varphi }^0\hfill & \dots \hfill & {\varphi }^{k-2}\hfill \\ {\varphi }^0\hfill & 1\hfill & \dots \hfill & {\varphi }^{k-3}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ {\varphi }^{k-2}\hfill & {\varphi }^{k-3}\hfill & \dots \hfill & 1\hfill \end{array}\right],$$ (B1)

where the AR(1) model corresponds to a special case where θ = 0. For example, the log-likelihood for the Gompertz lag 1 density dependence model was then given by,

$$\ln \left(L\right)=-\frac{k\ln \left(2\pi \right)}{2}-\frac{k\ln \mid {\sigma }^2\mathbf{R}\mid }{2}-\frac{1}{2{\sigma }^2}{\left(\ln \left(\frac{N\left(t\right)}{N(t-1)}\right)-a+b\ln \left(N(t-1)\right)\right)}^T{\mathbf{R}}^{-1}\left(\ln \left(\frac{N\left(t\right)}{N(t-1)}\right)-a+b\ln \left(N(t-1)\right)\right).$$ (B2)

Appendix C: Covariate analysis

We tested the explanatory power of a suite of covariates, available in the GPDD, on $\widehat{\varphi }$. We explored whether environmental factors, species information, and data quality metrics could explain variation in $\widehat{\varphi }$. Specifically, we tested whether time series length, latitude and longitude of the data collection location, GPDD reliability index, and sampling frequency were significant predictors of $\widehat{\varphi }$ at the α = 0.10 level. We ran an additional regression looking at species taxa as predictors of $\widehat{\varphi }$ at the α = 0.10 level. We also tested whether species status as specialists or generalists could explain variation in $\widehat{\varphi }$. We used definitions from Murdoch et al (2002) to determine specialist/generalist status in 48 time of the GPDD series. We predicted that generalists, with potentially more trophic interactions would have lower levels of PEA than specialists who may have fewer, but stronger, trophic interactions consistent with our results from the SLLM model in the main text.

Results

Our exploratory regression analysis on $\widehat{\varphi }$ was used to determine whether covariates could explain results from our analysis. We used the arctanh transformation on $\widehat{\varphi }$, defined by $Z=\text{arctan}\left(\widehat{\varphi }\right)$, in order to satisfy the assumption of normally distributed residuals. We performed a test on all sampling units reported in the GPDD. We found that only the Breeding females category was a statistically significantly predictor (t-test, p-value = 0.0293), though when using the Bonferonni correction for multiple tests this is no longer a significant predictor. The two species in this category were Tringa nebulariaxyxy and Melospiza melodia. We also examined whether sample size and GPDD reliability index influenced estimates. We found that $\widehat{\varphi }$ tended to decrease with increases in sample size and the reliability index, though these effects were not statistically significant.

Status as specialist ($\widehat{\varphi }=0.11$) or generalist ($\widehat{\varphi }=0.03$) was not found to be a significant explanatory value of $\widehat{\varphi }$ at the α = 0.1 level (p-value=0.44). However the results were consistent with our predictions with the specialist having slightly higher mean levels of autocorrelation, consistent with predictions from the SLLM.

Appendix D: Alternative error models

Past work has formulated autocorrelation models several di erent ways. Here, we discuss the differences in two alternative model formulations of temporally autocorrelated processes and contrast their properties to methods used by past studies examining the TPA.

A potentially important distinction in autocorrelated time series models is between long- and short-memory processes. Short-memory processes have autocorrelation functions that decay exponentially to 0 as k → ∞ (e.g., exp(–ϕk)), while long-memory processes have autocorrelation functions that converge to 0 according to slow-decaying power-law functions as k → ∞ (e.g., k^–β) (Shumway and Stoffer, 2006). Thus, though both processes may have the same degree of autocorrelation and go to 0, short-memory processes go to 0 faster than long-memory models. Short-memory models depend only on recent realizations of the process while long-memory models exhibit autocorrelation over many past realizations of the process. The relevance of this distinction is that incorporating PEA in long- and short-term memory models with the same degree of autocorrelation can lead to different predictions about species persistence in otherwise identical models (Cuddington and Yodzis, 1999; Fowler and Ruokolainen, 2013). These findings suggests that distinguishing between long- and short-memory PEA may have practical implications for population modeling.

While it is often convenient to think of population abundances as functions of time, previous discussions of long-memory processes in the ecological literature have often used the frequency domain representation of time series (Halley, 1996; Cuddington and Yodzis, 1999; Vasseur and Yodzis, 2004). This approach decomposes a time dependent signal into an infinite sum of sine waves with different frequencies through the Fourier transform. The transformation calculates the amplitude for each sine wave, giving the relative contribution of that frequency to the original series. This frequency representation can then be used as a convenient diagnostic tool when determining the appropriateness of a particular time dependent model (Box et al, 2011).

The power spectral density function, denoted as S(f), gives the distribution of the frequencies f present in a time series. The most commonly used long-memory process is the inverse power law model (1/f model) (Johnson, 1925). For this model the spectral density function is given by

$$S\left(f\right)=\text{constant}∕f^{\beta },$$ (D1)

where β controls the degree of autocorrelation. The 1/f model has also been proposed several times as a general model of environmental variation for population dynamics due to its apparent ubiquity in natural phenomena (Montroll and Shlesinger, 1982; Bak et al, 1987; Halley, 1996). The mathematical representation of the autocorrelation in a time series model and the function S(f) are transforms of each other and thus are mathematically equivalent.

Long-memory models are typically investigated within the framework of frequency domain methods while short memory processes are usually studied using traditional time domain tools, which tend to be more convenient for model estimation. We used the fractionally differenced model (FDM) to model time series with long-memory. In the FDM, the current state of the autocorrelated process is given as the sum of all the past contributions to the process and an independent random shock (Hosking, 1981). Autocorrelation is controlled by a single coeffcient, d, which determines the relative contributions of all past states. The mathematical representation of the model is

$$E\left(t\right)=\sum _{k=1}^{\infty }\frac{-\Gamma (k-d)}{\Gamma (k+1)\Gamma (-d)}E(t-k)+W\left(t\right),$$ (D2)

where E(t) is the state of a process at time t, Γ(x) is a gamma function, d is the fractional differencing parameter where –0.5 < d < 0.5, and W(t) is a normal distribution with mean equal to zero and variance of σ². In this model, the state at the current time step depends on all previous time lags through an infinite series representation, leading to the long-memory property. The differencing degree d controls the degree of autocorrelation and corresponds approximately to β/2 in the 1/f model (Hosking, 1981). Thus, the FDM and the 1/f model are approximately equivalent for –1 < β < 1.

Because previous methods have often used frequency domain approaches we determined whether estimates of the total population autocorrelation (TPA) made to the GPDD dataset using an AR(1) model would be different from previous studies that were based on the estimated spectral exponent, a long-memory model used in several past studies of TPA (Pimm and Redfearn, 1988; Inchausti and Halley, 2001). We were also interested in whether the FDM model would be more consistent with the long-memory process that is spectral exponent than the AR(1) model. We first estimated the spectral exponent by fitting a linear regression to the Fourier transform of the log-transformed abundances in our GPDD dataset consistent with previous methods. The transform was calculated with the fft function in the R software environment (R Development Core Team, 2012). The frequency amplitude of the transformed time series, S(f), was then fit to a model of the form, ln(S(f)) = a – βln(f, where f is the observed sampling frequency of the time series signal, is the spectral exponent, and a is an intercept term. We also estimated the FDM and AR(1) coefficients in equations (D2) and (3) using the arfima package in R (Veenstra, 2012) from the log-transformed abundance time series in order to compare them to $\widehat{\beta }$.

We evaluated the consistency of the AR(1) model and the FDM with $\widehat{\beta }$ by regressing each models autocorrelation estimates (ϕ in equation (3) and d in equation (D2)) against $\widehat{\beta }$ using standard major axis linear regression due to the higher variance in estimates of β. For the AR(1) model we fit, $\widehat{\beta }∕2=a_{\varphi }+b_{\varphi }\widehat{\varphi }+W$, and for the FDM model we fit $\widehat{\beta }∕2=a_d+b_d\widehat{d}+W$, where W was a random variable assumed to be iid Normally distributed. Consistency with the 1/f^β model was determined by whether the confidence intervals of the intercept parameters (a) contained 0 and the intervals of the slope parameters (b) contained 1. This comparative method was used rather than directly performing model selection on AR(1) and FDM models of PEA due to the inability for information theoretic methods to reliably distinguish between long- and short-memory models (Wagenmakers et al, 2004). We also determined if the properties of the data sets used here were consistent with previous studies on the GPDD by comparing our estimates of the TPA in our GPDD datasets using the 1/f model to previous estimates of TPA in the GPDD (e.g., Inchausti and Halley, 2001).

Results

We found levels of the spectral exponent with our dataset, $\widehat{\beta }=0.94$ that were similar to previous estimates of $\widehat{\beta }=1.02$ (Inchausti and Halley, 2002), indicating that the data set used here is comparable to previous work on the GPDD. We also compared autocorrelation estimates from both the AR(1) and FDM error processes to $\widehat{\beta }$ in order to determine model consistency with previous estimates from the GPDD. In the comparison of the AR(1) and to 1/f noise we did not include estimates that indicated nonstationary time series, which led to 387 data sets in the analysis. In the comparison of the FDM model and 1/f model this same criterion led to 244 data sets being included in the analysis. For the AR(1) model, we found an intercept value of ${\widehat{a}}_{\varphi }=-0.0.072$, 95% CI= (-0.101, -0.045) and slope of ${\widehat{b}}_{\varphi }=1.18$, 95% CI=(1.109, 1.26). For the FDM model, we found an intercept value of ${\widehat{a}}_d=0.075$, 95% CI=(0.069, 0.081), and slope of ${\widehat{b}}_d=0.086$, 95% CI=(0.78, 0.95). These results indicate that there may be bias in both models with regards to comparisons with the spectral exponent. However, the AR(1) model does make estimates that are broadly consistent with the spectral exponent, an interesting result. Despite the important differences in the properties of the spectral density of the AR(1) and the spectral exponent, our results suggest that parameter estimation using the AR(1) model is comparable to estimates that would be obtained with a long-memory process population environmental autocorrelation (PEA) model.

Appendix E: PEA in the carrying capacity

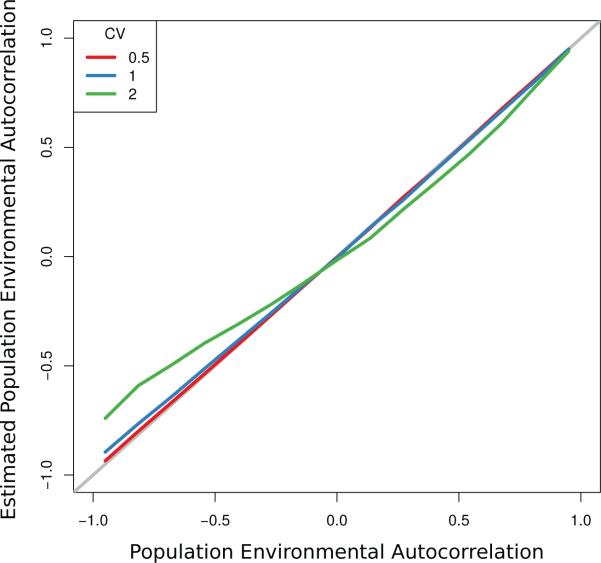
We performed a simulation analysis in order to determine if our analysis would provide biased estimates when the PEA occurs in the carrying capacity rather the maximum per capita rate of increase. The carrying capacity in the lag 1 Ricker model, given by K = a/b in equation 2, was assumed to be an AR(1) random variable. We set a = ln(1.5) and E[K] = 100 for all simulations. We tested 15 different autocorrelation levels evenly spaced in the interval [–0.95, 0.95] over 3 different levels of variability in K, where variation was measured used the coefficient of variation (standard deviation of K divided by the mean). The CV values we tested were 0.5, 1, and 2. For values of the CV higher than 2 we found that some values of our simulated K became negative and were therefore unrealistic. For each combination of autocorrelation and CV value we estimated the autocorrelation from a time series with length of 10⁵ following the methods of the main text that assume that the variation occurs in the intrinsic growth rate.

We found that estimation error was negligible at the low CV levels of 0.5 and 1 (Figure E1). At CV= 2 there was estimation bias at very low negative levels of the autocorrelation but the bias was low for positive levels of autocorrelation. Overall we found that the influence of this kind of model specification to be low, suggesting that our results are not biased by the way that the environmental variation enters into the population dynamics. These results are not too surprising as variation in the carrying capacity is often difficult to distinguish from variation in the maximum per capita rate of increase with differences emerging primarily at very low or very high abundances (Ferguson, unpublished results).

Fig. E1.

The impact on estimated PEA when the PEA arises in the population carrying capacity but the error model is in the intrinsic rate of reproduction. The degree of estimation error increases as a function of the coeffcient of variation (CV) in the carrying capacity and is larger for negative values of the PEA.

Appendix F: Spectral mimicry

In the main text we used the known distributional form of stationary AR time series to ensure that the simulated time series had identical properties except for the degree of autocorrelation. Although this allowed us to control all the statistical moments, alternative methods, such as spectral mimicry, exist that allow the generation of time series using the same realization of the generated data with only the degree of autocorrelation changing. We used this method to check if our approach properly accounted for changes in statistical properties with autocorrelation.

Spectral mimicry (Cohen et al, 1999) can vary the autocorrelation in the same realization of a stochastic process, thereby controlling for the effects of not scaling of process variance with autocorrelation or other unintended mismatches that may arise between simulated series. The method works by first generating a series from a stochastic model such as a standard normal distribution. In order to turn this iid stochastic process into an autocorrelated one, a new reference series with the desired degree of autocorrelation is generated. The original process is then reordered such that it's sequence of order statistics matches the reference series. This reordered version has the same realized values as the original process, however, the autocorrelation is equal to the reference series. Because the new series has the same values as the original series, just in a different order, the statistical properties of the ensemble must be equivalent.

We reproduced Figures 2 and 3 using datasets generated with spectral mimicry in order to confirm that our method of generating autocorrelated data did not lead to any differences between time series other than the degree of autocorrelation. The reproduced figures (Figures F1 and F2) show no differences with the figures in the main text (Figures 2 and 3).

Fig. F1.

The effect of two different nonlinear interactions on an autocorrelated time series, C(t), when data is generated using the spectral mimicry method. The dashed black line is the autocorrelation in the untransformed environmental covariate, while the colored lines are the population environmental autocorrelation (PEA) values in E(t) for different transformations. Panel A corresponds to power transforms of the form E(t) = –C(t)^η . Panel B corresponds to the logistic function, $E\left(t\right)=\frac{e^{\zeta C\left(t\right)}}{1+e^{\zeta C\left(t\right)}}$.

Fig. F2.

Two applications of the SLLM to a number, n, of autocorrelated time-series. In both panels the x-axis denotes the autocorrelation in the environmental covariate while y-axis is the population environmental autocorrelation (PEA) that affects the per capita growth rate once the SLLM has been applied. In panel A all n covariates have the same autocorrelation. In panel B, n – 1 of the covariates have an autocorrelation of 0.5, while the remaining covariate has the autocorrelation value given on the x-axis. In both panels the dashed line denotes the covariate's autocorrelation, for comparison. The overall effect of the SLLM depends on the number of environmental covariates, n, that limit the population. In general the SLLM tends to reduce the magnitude of the PEA relative to what is expected from a single limiting factor. However, as shown in the right panel the effect can increase the PEA if a single limiting environmental factor has a high enough autocorrelation.