Multi-armed Bandit Models for the Optimal Design of Clinical Trials: Benefits and Challenges

Abstract

Multi-armed bandit problems (MABPs) are a special type of optimal control problem well suited to model resource allocation under uncertainty in a wide variety of contexts. Since the first publication of the optimal solution of the classic MABP by a dynamic index rule, the bandit literature quickly diversified and emerged as an active research topic. Across this literature, the use of bandit models to optimally design clinical trials became a typical motivating application, yet little of the resulting theory has ever been used in the actual design and analysis of clinical trials. To this end, we review two MABP decision-theoretic approaches to the optimal allocation of treatments in a clinical trial: the infinite-horizon Bayesian Bernoulli MABP and the finite-horizon variant. These models possess distinct theoretical properties and lead to separate allocation rules in a clinical trial design context. We evaluate their performance compared to other allocation rules, including fixed randomization. Our results indicate that bandit approaches offer significant advantages, in terms of assigning more patients to better treatments, and severe limitations, in terms of their resulting statistical power. We propose a novel bandit-based patient allocation rule that overcomes the issue of low power, thus removing a potential barrier for their use in practice.

1. INTRODUCTION

Randomized controlled trials have become the gold-standard approach in clinical research over the last 60 years. Fixing the probability of being assigned to each arm for its duration, it removes (asymptotically) any systematic differences between patients on different arms with respect to all known or unknown confounders. The frequentist operating characteristics of the standard approach (e.g., the type-I error rate and power) are well understood, and the size of the trial can easily be chosen in advance to fix these at any level the practitioner desires. However, while it is important for a clinical trial to be adequately powered to detect a significant difference at its conclusion, the well-being of patients during the study itself must not be forgotten.

MABPs are an idealized mathematical decision framework for deciding how to optimally allocate a resource among a number of competing uses, given that such allocation is to be done sequentially and under randomly evolving conditions. In its simplest version, the resource is work which can further be devoted to only one use at a time. The uses are treated as independent “projects” with a binary outcome which develop following Markov rules. Their roots can be traced back to work produced by Thompson (1933), which was later continued and developed in Robbins (1952), Bellman (1956), and finally Gittins and Jones (1974). Although their scope is much more general, the most common scenario chosen to motivate this methodology is that of a clinical trial which has the aim of balancing two separate goals:

• To correctly identify the best treatment (exploration or learning).

• To treat patients as effectively as possible during the trial (exploitation or earning).

One might think that these two goals are naturally complementary, but this is not the case. Correctly identifying the best treatment requires some patients to be assigned to all treatments, and therefore the former acts to limit the latter.

Despite this apparent near-perfect fit between a real-world problem and a mathematical theory, the MABP has yet to be applied to an actual clinical trial. Such a state of affairs was pointed out early on by Peter Armitage in a paper reflecting upon the use in practice of theoretical models to derive optimal solutions for problems in clinical trials:

Either the theoreticians have got hold of the wrong problem, or the practising triallists have shown a culpable lack of awareness of relevant theoretical developments, or both. In any case, the situation does not reflect particularly well on the statistical community (Armitage, 1985, page 15).

A very similar picture is described two decades later in Palmer (2002) when discussing and advocating for the use of “learn-as-you-go” designs as a means of alleviating many problems faced by those involved with clinical trials today. More recently, Don Berry—a leading proponent of the use of Bayesian methods to develop innovative adaptive clinical trials—also highlighted the resistance to the use of bandit theoretical results:

But if you want to actually use the result then people will attack your assumptions. Bandit problems are good examples. An explicit assumption is the goal to treat patients effectively, in the trial as well as out. That is controversial (…) (Stangl, Inoue and Irony, 2012).

In view of this, a broad goal of this article is to contribute to setting the ground for change by reviewing a concrete area of theoretical bandit results, in order to facilitate their application in practice. The layout of the paper is as follows: In Section 2 we first recount the basic elements of the Bayesian Bernoulli MABP. In Section 3 we focus on the infinite-horizon case, presenting its solution in terms of an index rule—whose optimality was first proved by Gittins and Jones over 30 years ago. In Section 4 we review the finite horizon variant by reformulating it as an equivalent infinite-horizon restless MABP, which further provides a means to compute the index rule for the original problem. In Section 5 we compare, via simulation, the performance of the MABP approaches to existing methods of response adaptive allocation (including standard randomization) in several clinical trial settings. These results motivate the proposal of a composite method, that combines bandit-based allocation for the experimental treatment arms with standard randomization for the control arm. We conclude in Section 6 with a discussion of the existing barriers to the implementation of bandit-based rules for the design of clinical trials and point to future research.

2. THE BAYESIAN BERNOULLI MULTI-ARMED BANDIT PROBLEM

The Bayesian Bernoulli K-armed bandit problem corresponds to a MABP in which only one arm can be worked on at a time t , and work on arm k = 1, …, K represents drawing a sample observation from a Bernoulli population Y_k,t with unknown parameter p_k, “earning” the observed value y_k,t as a reward (i.e., either 0 or 1). In a clinical trial context, each arm represents a treatment with an unknown success rate. The Bayesian feature is introduced by letting each parameter p_k have a Beta prior with parameters s_k,0 and f_k,0 such that $(s_{k,0},f_{k,0})\in {\mathbb{N}}_{+}^2$ before the first sample observation is drawn (i.e., at t = 0). After having observed $S_{k,t}=s_{k,t}$ successes and $F_{k,t}=f_{k,t}$ failures, with $\left(S_{k,t},F_{k,t}\right)\in {\mathbb{N}}_0^2$ for any t ≥ 1, the posterior density is a Beta distribution with parameters $\left(s_{k,0}+s_{k,t},f_{k,0}+f_{k,t}\right).$

Formally, the Bernoulli Bayesian MABP is defined by letting each arm k be a discrete-time Markov Control Process (MCP) with the following elements:

• (a)The state space: ${𝕏}_{k,t}=\{(s_{k,0}+S_{k,t},f_{k,0}+F_{k,t})\in {\mathbb{N}}_{+}^2:S_{k,t}+F_{k,t}\le t,\hspace{0.17em}\text{for}\hspace{0.17em}t=0,1,\mathrm{\dots },T\}$ which represents all the possible two-dimensional vectors of information on the unknown parameter p_k at time t . We denote the available information on treatment k at time t as x_k,t = (s_k,0 + S_k,t, f_k,0 + F_k,t) and the initial prior as x_k,0 = (s_k,0, f_k,0). In a clinical trial context, the random vector (S_k,t, F_k,t) represents the number of successful and unsuccessful patient outcomes (e.g., response to treatment, remission of tumor, etc.).
• (b)The action set $𝔸$_k is a binary set representing the action of drawing a sample observation from population k at time t (a_k,t = 1) or not (a_k,t = 0). In a clinical context, the action variable stands for the choice of assigning patient t to treatment arm k or not.
• (c)
  The Markovian transition law P_k(x_k,t+1|x_k,t, a_k) describing the evolution of the information state variable in population k from time t to t + 1 is given by

  $${\mathbf{\text{x}}}_{k,t+1}=\{\begin{array}{c}\begin{array}{l}(s_{k,0}+s_{k,t}+1,f_{k,0}+f_{k,t}),\\ \text{if}\hspace{0.17em}{a}_{k,t}=1\end{array}\\ \text{w}.\text{p}.\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}},\\ \begin{array}{l}(s_{k,0}+s_{k,t},f_{k,0}+f_{k,t}+1),\\ \text{if}\hspace{0.17em}{a}_{k,t}=1\end{array}\\ \begin{array}{l}\text{w}.\text{p}.\frac{f_{k,0}+f_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}},\\ {\mathbf{\text{x}}}_{k,t},\\ \text{if}\hspace{0.17em}{a}_{k,t}=0\hspace{0.17em}\text{w}.\text{p}.1,\end{array}\end{array}$$ (2.1)

  for any x_k,t ∈ $𝕏$_k,t and where w.p. stands for “with probability.”
• (d)
  The expected rewards and resource consumption functions are

  $$\begin{array}{l}ℛ\left({\mathbf{\text{x}}}_{k,t},a_{k,t}\right)=\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}{a}_{k,t},\\ \mathcal{C}\left({\mathbf{\text{x}}}_{k,t},a_{k,t}\right)=a_{k,t},\end{array}$$ (2.2)

  for t = 0, 1, …, T − 1, where, in accordance to (2.1), a reward (i.e., a treatment success) in arm k arises only if that arm is worked on and with a probability given by the posterior predictive mean of p_k at time t and resource consumption is restricted by the fact that (at most) one treatment can be allocated to every patient in the trial, that is, ${\displaystyle {\Sigma }_{k=1}^K{a}_{k,t}\le 1}$ for all t.

A rule is required to operate the resulting MCP, indicating which action to take for each of the K arms, for every possible combination of information states and at every time t, until the final horizon T. Such a rule forms a sequence of actions {a_k,t }, which depends on the information available up to time t, that is, on {x_k,t}, and it is known as a policy within the Markov Decision Processes literature. To complete the specification of this multi-armed bandit model as an optimal control model, the problem’s objective function must be selected. Given an objective function and a time horizon, a multi-armed bandit optimal control problem is mathematically summarized as the problem of finding a feasible policy, π, in ∏ (the set of all the feasible policies given the resource constraint) that optimizes the selected performance objective.

The performance objective in the Bayesian Bernoulli MABP is to maximize the Expected Total Discounted (ETD) number of successes after T observations, letting 0 ≤ d < 1 be the discount factor. Then, the corresponding bandit optimization problem is to find a discount-optimal policy such that

$$\begin{array}{l}{V}_D^{*}({\widetilde{\mathbf{\text{x}}}}_0)=\underset{\pi \in \prod }{\max }{E}^{\pi }\left[{\displaystyle \sum _{t=0}^{T-1}{\displaystyle \sum _{k=1}^K{d}^t}\frac{s_{k,0}+S_{k,t}}{s_{k,0}+f_{k,0}+S_{k,t}+F_{k,t}}}.a_{k,t}|{\tilde{\mathbf{x}}}_0={({\text{x}}_{k,0})}_{k=1}^K\right],\end{array}$$ (2.3)

where ${\widetilde{\mathbf{\text{x}}}}_0$ is the initial joint state, E^π [⋅] denotes expectation under policy π and transition probability rule (2.1), $V_D^{*}({\widetilde{\mathbf{\text{x}}}}_0)$ is the optimal expected total discounted value function conditional on the initial joint state being equal to ${\widetilde{\mathbf{\text{x}}}}_0$ (for any possible joint initial state), and where, given the resource constraint, the family of admissible feasible policies Π contains the sampling rules π for which it holds that ${\displaystyle {\Sigma }_{k=1}^K{a}_{k,t}\le 1}$ for all t.

A generic MABP formally consists of K discrete-time MCPs with their elements defined in more generality, that is, (a) the state space: a Borel space, (b) the binary action set, (c) the Markovian transition law: a stochastic kernel on the state space given each action and (d) a reward function and a work consumption function: two measurable functions. As before, the MABP is to find a policy that optimizes a given performance criterion, for example, it maximizes the ETD net rewards.

Robbins (1952) proposed an alternative version of the Bayesian Bernoulli MABP problem by considering the average regret after allocating T sample observations [for a large T and for any given and unknown ${(p_k)}_{k=1}^K]$. For the Bayesian Bernoulli MABP, the total regret ρ is defined as

$$\begin{array}{c}\rho =T\hspace{0.17em}\underset{k}{\max }\{p_k\}-E^{\pi }\left[{\displaystyle \sum _{t=0}^{T-1}{\displaystyle \sum _{k=1}^K\hspace{0.17em}{a}_{k,t}{Y}_{k,t}}}\right]\\ {\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}(p_k)}_{k=1}^K.\end{array}$$ (2.4)

A form of asymptotic optimality can be defined for sampling rules π in terms of (2.4) if it holds that for any ${(p_k)}_{k=1}^K$, ${\lim }_{T\to \infty }\frac{\rho }{T}=0$. A necessary condition for a rule to attain this property is to sample each of the K populations infinitely often, that is, to continue to sample from (possibly) suboptimal arms for every t < ∞. In other words, asymptotically optimal rules have a strictly positive probability of allocating a patient to every arm at any point of the trial. Of course, within the set of asymptotically optimal policies secondary criteria may be defined and considered (see, e.g., Lai and Robbins, 1985). As it will be illustrated in Section 5, objectives in terms of (2.3) or (2.4) give rise to sampling rules with distinct statistical properties. Asymptotically optimal rules, that is, in terms of (2.4), maximize the learning about the best treatment, provided it exists, while the rules that are optimal in terms of (2.3) maximize the mean number of total successes in the trial.

3. THE INFINITE-HORIZON CASE: A CLASSIC MABP

We now review the solution giving the optimal policy to optimization problem (2.3) in the infinite-horizon setting by letting T = ∞. In general, as MABPs are a special class of MCPs, the traditional technique to address them is via a dynamic programming (DP) approach. Thus, the solution to (2.3), according to Bellman’s principle of optimality (Bellman, 1952), is such that for every t = 0, 1, … the following DP equation holds:

$$\begin{array}{l}{V}_D^{*}({\mathbf{\text{x}}}_{1,t},\mathrm{\dots },{\mathbf{\text{x}}}_{K,t})=\underset{k}{\max }\{\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}+d(\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}\hspace{0.17em}·V_D^{*}({\mathbf{\text{x}}}_{1,t},{\mathbf{\text{x}}}_{k,t}+{\mathbf{\text{e}}}_1,\dots ,{\mathbf{\text{x}}}_{K,t})+\frac{f_{k,0+}{f}_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}·V_D^{*}({\mathbf{\text{x}}}_{1,t},{\mathbf{\text{x}}}_{k,t}+{\mathbf{\text{e}}}_2,\mathrm{\dots },{\mathbf{\text{x}}}_{K,t}))\},\end{array}$$ (3.1)

where e₁, e₂ respectively denote the unit vectors (1, 0) and (0, 1). Under the assumptions defining the Bayesian Bernoulli MABP, the theory for discounted MCPs ensures the existence of an optimal solution to (3.1) and also the monotone convergence of the value functions $V_D^{*}({\widetilde{\mathbf{\text{x}}}}_t)$. Therefore, equation (3.1) can be approximately solved iteratively using a backward induction algorithm.

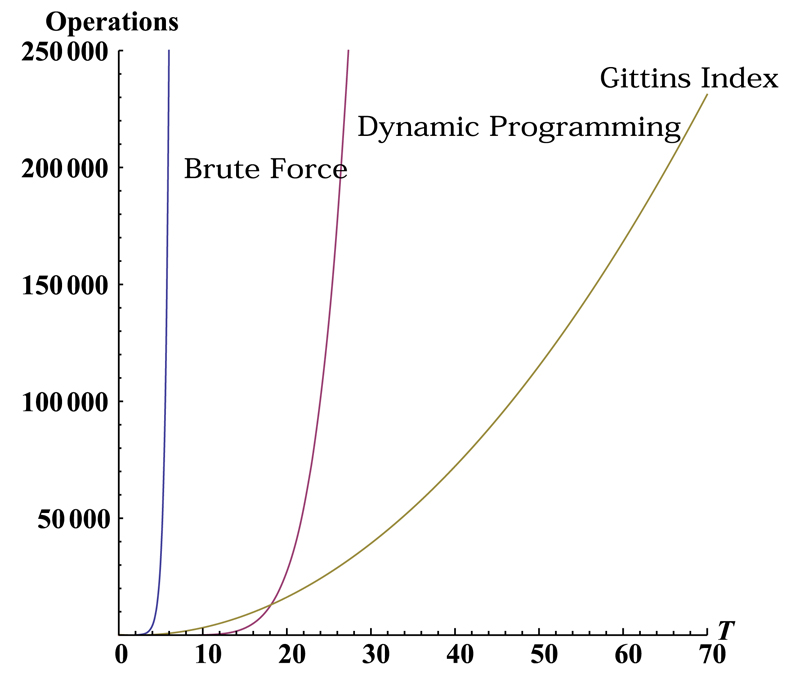
Unfortunately, as shown in Figure 1, such a DP technique suffers from a severe computational burden, which is particularly well illustrated in the classic MABP where the size of the state space grows with the truncation horizon T. To illustrate this fact, consider the case of K treatments with an initial uniform prior distribution (i.e., $s_{k,0}=f_{k,0}=1\hspace{0.17em}\forall k$) and truncation horizon to initialize the algorithm equal to T. The total number of individual calculations [i.e., the number of successive evaluations of $V_D^{*}({\mathbf{\text{x}}}_{\text{1,}t},\dots ,{\mathbf{\text{x}}}_{K,t})]$ required to find an approximate optimal solution by means of the DP algorithm equals $\frac{(T-1)!}{(2K)!(T-2K-1)!}$. The precision of such an approximation depends on d, for example, if d ≤ 0.9 values to four-figure accuracy are calculated for T ≥ 100. Therefore, considering the problem with K = 3 and d = 0.9 (and hence T ≥ 100) makes the intractability of the problem’s optimal policy become evident. (For a more detailed discussion see the Appendix.)

FIG. 1.

The number of individual computations for an approximation to the optimal rule in a particular instance of the Bayesian Bernoulli MABP as a function of T with K = 3 and d = 0.9 for the Brute force, DP and Gittins index approaches.

3.1. The Gittins Index Theorem

The computational cost of the DP algorithm to solve equation (3.1) is significantly smaller than the cost of a complete enumeration the set of feasible policies ∏ (i.e., the brute force strategy), yet it is still not enough to make the solution of the problem applicable for most real world scenarios, with more than 2 treatment arms. For this reason the problem gained the reputation of being extremely hard to solve soon after being formulated for the first time, becoming a paradigmatic problem to describe the exploration versus exploitation dilemma characteristic of any data-based learning process.

Such a state of affairs explains why the solution first obtained by Gittins and Jones (1974) constitutes such a landmark event in the bandit literature. The Index theorem states that if problem P is an infinite-horizon MABP with each of its K composing MCPs having (1) a finite action set $𝔸$_k, (2) a finite or infinite numerable state space $𝕏$_k, (3) a Markovian transition law under the passive action a_k,t = 0 (i.e., the passive dynamics) such that

$$\begin{array}{l}{P}_k\left(x_k^{\prime }|x_k,0\right)=P_k\left\{X_{k,t+1}=x_k^{\prime }|X_{k,t}=x_k,a_{k,t}=0\right\}\\ =1_{\left\{x_{k^{\prime }}=x_k\right\},}\end{array}$$ (3.2)

for any $x_k,x_k^{\prime }\in {𝕏}_k,{\text{where 1}}_{\text{{}{x}_{k^{\prime }}\text{=}{x}_k\text{}}}$ is an indicator variable for the event that the state variable value at time $t+1:x_{k^{\prime }}$ equals the state variable value of state t : x_k, and (4) the set of feasible polices П contains all polices π such that for all t

$${\displaystyle \sum _{k=1}^K{a}_{k,t}\le 1,}$$ (3.3)

then there exists a real-valued index function $\mathcal{G}\left(x_{k,t}\right)$, which recovers the optimal solution to such a MABP when the objective function is defined under a ETD criterion, as in (2.3). Such a function is defined as follows:

$${\mathcal{G}}_k(x_{k,t})=\underset{\tau \ge 1}{\sup }\frac{E_{X_{k,t}=x_{k,t}}{\displaystyle {\sum }_{i=0}^{\tau -1}ℛ}\left(X_{k,t+i},1\right)d^i}{E_{X_{k,t}=x_{k,t}}{\displaystyle {\sum }_{i=0}^{\tau -1}\mathcal{C}\left(X_{k,t+i},1\right)d^i}},$$ (3.4)

where the expectation is computed with respect to the corresponding Markovian (active) transition law $P_k(x_k^{\prime }|x_k,1)$, and τ is a stopping time. Specifically, the optimal policy π* for problem P is to work on the bandit process with the highest index value, breaking ties randomly. Note that the stopping time τ is past-measurable, that is, it is based on the information available at each decision stage only. Observe also that the index is defined as the ratio of the ETD reward up to τ active steps to the ETD cost up to τ active steps.

MABPs whose dynamics are restricted as in (3.2) (namely, those in which passive projects remain frozen in their states) are referred to in the specialized literature as classic MABPs and the name Gittins index is used for the function (3.4). The Index theorem’s significant impact derives from the possibility of using such a result to break the curse of dimensionality by decomposing the optimal solution to a K -armed MABP in terms of its independent parts, which are remarkably more tractable than the original problem as shown in Figure 1. The number of individual calculations required to solve problem (3.1) using the Index theorem is of order $\frac{1}{2}(T-1)(T-2)$, which no longer explodes with the truncation horizon T. Further, it is completely independent of K, which means that a single index table suffices for all possible trials, therefore reducing the computing requirements appreciably. (For more details, see the Appendix.)

Such computational savings are particularly well illustrated in the Bayesian Bernoulli MABP where the Gittins index (3.4) is given by

$${\mathcal{G}}_k\left({\mathbf{\text{x}}}_{k,t}\right)=\underset{\tau \ge 1}{\sup }\frac{E.{\displaystyle {\sum }_{i=0}^{\tau -1}\frac{s_{k,0}+S_{k,t+i}}{s_{k,0}+f_{k,0}+S_{k,t+i}+F_{k,t+i}}{d}^i}}{E.{\displaystyle {\sum }_{i=0}^{\tau -1}{d}^i}},$$ (3.5)

where $E.{=E}_{{\mathbf{\text{x}}}_{k,t=(s_{k,0}+s_{k,t},f_{k,0}+f_{k,t})}}.$

Calculations of the indices (3.5) have been reported in brief tables as in Gittins (1979) and Robinson (1982). Improvements to the efficiency of this computing the index have since been proposed by Katehakis and Veinott (1985), Katehakis and Derman (1986). Moreover, since the publication of Gittins’ first proof of the optimality result of the index policy for a classic MABP in Gittins and Jones (1974), there have been alternative proofs, each offering complementary insights and interpretations. Among them, the proofs by Whittle (1980), Varaiya, Walrand and Buyukkoc (1985), Weber (1992) and Bertsimas and Niño-Mora (1996) stand out.

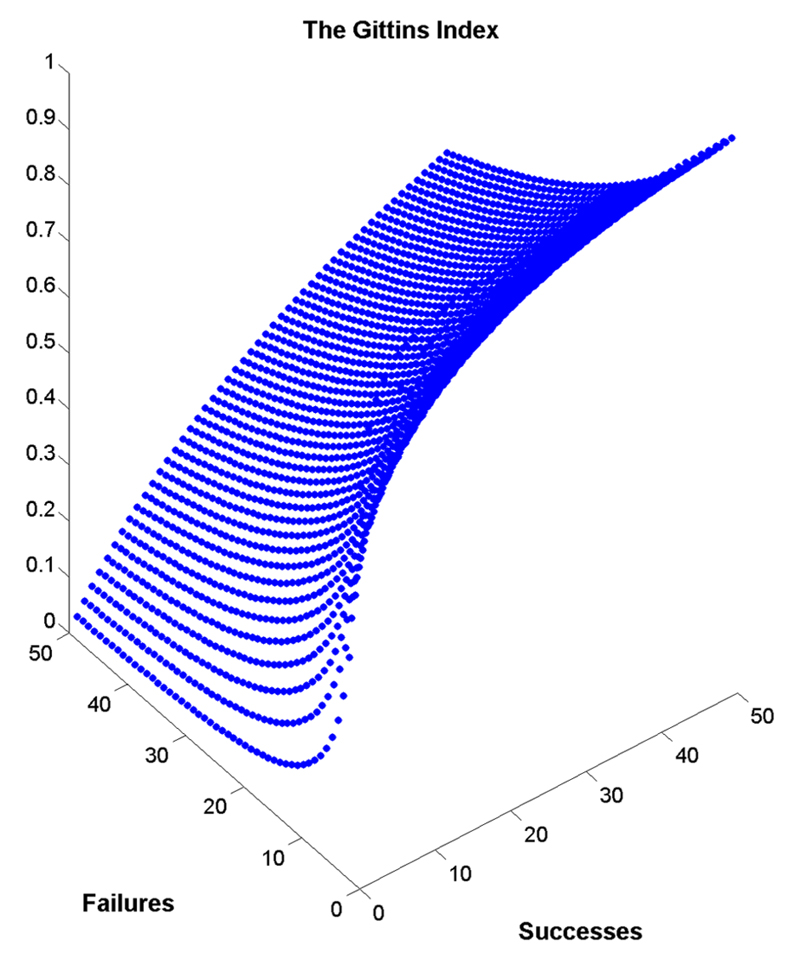
To elaborate a little more on the use of the Gittins index for solving a K -armed Bayesian Bernoulli MABP in a clinical trial context, we have included some values of the Gittins index in Table 1 and Figure 2. These values correspond to a particular instance in which the initial prior for every arm is uniform, the discount factor is d = 0.99, the index precision is of 4 digits and we have truncated the search of the best stopping time to T = 750. The choice of d = 0.99 is a widely used value in the related bandit literature. In our example, since 0.99⁷⁵⁰ < 10⁻³, patients treated after this time yield an almost zero expected discounted reward and are hence ignored.

Table 1.

The (approximate) Gittins index values for an information vector of s₀ + s_t successes and f₀ + f_t failures, where d = 0.99 and T is truncated at T = 750

f/s	1	2	3	4	5	6
1	0.8699	0.9102	0.9285	0.9395	0.9470	0.9525
2	0.7005	0.7844	0.8268	0.8533	0.8719	0.8857
3	0.5671	$\underset{¯}{\underset{¯}{0.6726}}$	0.7308	0.7696	0.7973	0.8184
4	0.4701	0.5806	0.6490	0.6952	0.7295	0.7561
5	0.3969	0.5093	0.5798	0.6311	0.6697	0.6998
6	0.3415	0.4509	0.5225	0.5756	0.6172	$\underset{¯}{\underset{¯}{0.6504}}$

FIG. 2.

The (approximate) Gittins index values for an information vector of s₀+s_t successes and f₀+f_t failures, where d = 0.99 and T is truncated at T = 750.

The Gittins index policy assigns a number to every treatment (from an extended version of Table 1) based on the values of s_k,t and f_k,t observed, and then prioritizes sampling the one with the highest value. Thus, provided that we adjust for each treatment prior, the same table can be used for making the allocation decision of all treatments in a trial. Furthermore, the number of treatments need not be prespecified in advance and new treatments may be seamlessly introduced part way through the trial as well (see Whittle, 1981). To give a concrete example, suppose that all treatments start with a common uniform prior, then all initial states are equal to x_k,0 = (1, 1) with a corresponding Gittins index value of 0.8699 for all of them. Yet, if a treatment k has a beta prior with parameters (1, 2) and another treatment k′ has a prior with parameters (2, 1), their respective initial states are x_k,0 = (1, 2) and ${\mathbf{\text{x}}}_{k^{\prime },0}=(2,1)$, and their associated index values respectively are 0.7005, 0.9102. The same reasoning applies for the case in which priors combine with data so as to have x_k,1 = (1, 2) and ${\mathbf{\text{x}}}_{k^{\prime },1}=(2,1)$.

The underlined values in Table 1 describe situations in which the learning element plays a key role. Consider two treatments with the same posterior mean of success 2/4 = 4/8 = 1/2. According to the indices denoted by the single line, the treatment with the smallest number of observations is preferred: 0.7844 > 0.6952. Moreover, consider the case in which the posterior means of success suggest the superiority of one over the other: 2/5 = 0.4 < 6/12 = 0.5, yet their indices denoted by the double-underline suggest the opposite, 0.6726 > 0.6504, again prioritizing the least observed population.

Gittins and Wang (1992) define the learning component of the index as the difference between the index value and the expected immediate reward, which for the general Bayesian Bernoulli MABP is given by $\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}$. This posterior probability is the current belief that a treatment k is successful and it can be used for making patient allocation decisions in a myopic way, that is, exploiting the available information without taking into account the possible future learning. Consider, for instance, the case where x_k,0 = (1, 1) for all k. In that case, the learning component before making any treatment allocation decision is thus (0.8699 − 0.5) = 0.3699. As the number of observations of a bandit increases, the learning part of the indices decreases.

4. THE FINITE HORIZON CASE: A RESTLESS MABP

Of course, clinical trials are not run with infinite resources or patients. Rather, one usually attempts to recruit the minimum number of patients to achieve a pre-determined power. Thus, we now consider the optimization problem defined in (2.3) for a finite value of T . Indeed, a solution could in theory be obtained via DP, but it is impractical in large-scale scenarios for reasons already stated. Moreover, the Index theorem does not apply to this case, thus, the Gittins index function as defined for the infinite-horizon variant does not exist (Berry and Fristedt, 1985). In the infinite-horizon problem, at any t there is always an infinite number of possible sample observations to be drawn from any of the populations. This is no longer the case in a finite-horizon problem, and the value of a sampling history (s_k,t, f_k,t) is not the same when the sampling process is about to start than when it is about to end. The finite-horizon problem analysis is thus more complex, because these transient effects must be considered for the characterization of the optimal policy. In what follows we summarize how to derive an index function analogous to Gittins’ rule for the finite-horizon Bayesian Bernoulli MABP based on an equivalent reformulation of it as an infinite-horizon Restless MABP, as it was done in Niño-Mora (2005). In the equivalent model the information state is augmented, adding the number of remaining sample observations that can be drawn from the K populations. Hence, the MCP has the following modified elements:

• (a)An augmented state space ${\widehat{\mathbb{X}}}_k$ given by the union of the set ${\mathbb{X}}_{k,t}\times \mathbb{T}$, where $\mathbb{T}=\{0,1,\dots ,T\}$, and an absorbing state {E}, representing the end of the sampling process. Thus, ${\widehat{\mathbf{\text{x}}}}_{k,t}=({\mathbf{\text{x}}}_{k,t},T-t)$ is a three-dimensional vector combining the information on the treatment (prior and observed) and the number of remaining patients to allocate until the end of the trial.
• (b)The same as in Section 2.
• (c)
  A transition law $P_k({\widehat{\mathbf{\text{x}}}}_{k,t+1}|{\widehat{\mathbf{\text{x}}}}_{k,t},a_k)$ for every ${\widehat{\mathbf{\text{x}}}}_{k,t}$ such that 0 ≤ t ≤ T − 1:

  $$\begin{array}{l}{\widehat{\mathbf{\text{x}}}}_{k,t+1}=\{\begin{array}{l}\text{if}\hspace{0.17em}{a}_{k,t}=1:\\ (s_{k,0}\text{+}{s}_{k,t}\text{+}1,f_{k,0}+f_{k,t},T-(t+1)),\\ \text{w}.\text{p}.\frac{s_{k,t}+s_{k,0}}{s_{k,t}+f_{k,t}+s_{k,0+}{f}_{k,0}},\\ (s_{k,0}+s_{k,t},f_{k,0}+f_{k,t}+1,T-(t+1)),\\ \text{w}.\text{p}.\frac{f_{k,t}+f_{k,0}}{s_{k,t}+f_{k,t}+s_{k,0}+f_{k,0}},\\ \text{if}\hspace{0.17em}{a}_{k,t}=0({\mathbf{\text{x}}}_{k,t},T-(t+1)),\\ \text{w}.\text{p}.1,\end{array}\end{array}$$ (4.1)

  ${\widehat{\mathbf{\text{x}}}}_{k,T}$ and E under both actions, lead to E with probability one.
• (d)The one-period expected rewards and resource consumption functions are defined as in (2.2) for t = 0, 1, …, T − 1, while the states E and ${\widehat{\mathbf{\text{x}}}}_{k,T}$ both yield 0 reward and work consumption.

The objective in the resulting bandit optimization problem is also to find a discount-optimal policy that maximizes the ETD rewards.

4.1. Restless MABPs and the Whittle Index

In this equivalent version the horizon is infinite (a fiction introduced by forcing every arm of the MABP to remain in state E after the period T ), nonetheless, the Index theorem does not apply to it because its dynamics do not fulfil condition (3.2). The inclusion of the number of remaining observations to allocate as a state variable causes inactive arms to evolve regardless of the selected action, and this particular feature makes the augmented MABP restless.

In the seminal work by Whittle (1988), this particular extension to the MABP dynamics was first proposed and the name restless was introduced to refer to this class of problems. Whittle deployed a Lagrangian relaxation and decomposition approach to derive an index function, analogous to the one Gittins had proposed to solve the classic case, which has become known as the Whittle index.

One of the main implications of Whittle’s work is the realization that the existence of such an index function is not guaranteed for every restless MABP. Moreover, even in those cases in which it exists, the index rule does not necessarily recover the optimal solution to the original MABP (as it does in the classic case), being thus a heuristic rule. Whittle further conjectured that the index policy for the restless variant enjoys a form of asymptotic optimality (in terms of the ETD rewards achieved), a property later established by Weber and Weiss (1990) under certain conditions. Typically, the resulting heuristic has been found to be nearly optimal in various models.

4.2. Indexability of Finite-Horizon Classic MABP

In general, establishing the existence of an index function for a restless MABP (i.e., showing its indexability) and computing it is a tedious task. In some cases, the sufficient indexability conditions (SIC) introduced by Niño-Mora (2001) can be applied for both purposes.

The restless bandit reformulation of finite-horizon classic MABPs, as defined in Section 2, is always indexable. Such a property can either be shown by means of the SIC approach or simply using the seminal result in Bellman (1956), by which the monotonicity of the optimal policies can be ensured, allowing to focus attention on a nested family of stopping times.

Moreover, the fact that in this restless MABP reformulation the part of the augmented state that continues to evolve under a_k,t = 0, that is, T − t , does so in the exact same way that under a_k,t = 1 allows computation of the Whittle index as a modified version of the Gittins index, in which the search of the optimal stopping time in (3.4) is truncated to be less than or equal to the number of remaining observations to allocate (at each decision period) (see Proposition 3.1 in Niño-Mora, 2011). Hence, the Whittle index for the finite-horizon Bayesian Bernoulli MABP is

$$\begin{array}{l}{W}_k({\widehat{\mathbf{\text{x}}}}_{k,t})=\underset{1\le \tau \le T-t}{\sup }\frac{E_{{\widehat{\mathbf{\text{X}}}}_{k,t}={\widehat{\mathbf{\text{x}}}}_{k,t}}{\displaystyle {\sum }_{i=0}^{\tau -1}ℛ({\widehat{\mathbf{\text{X}}}}_{k,t+i},1)d^i}}{E_{{\widehat{\mathbf{\text{X}}}}_{k,t}={\widehat{\mathbf{\text{x}}}}_{k,t}}{\displaystyle {\sum }_{i=0}^{\tau -1}\mathcal{C}({\widehat{\mathbf{\text{X}}}}_{k,t+i},1)}{d}^i},\\ \text{for}\hspace{0.17em}{\widehat{\mathbf{\text{x}}}}_{k,t}\in {\widehat{\mathbf{\text{X}}}}_k\backslash \{E,{\widehat{\mathbf{\text{x}}}}_{k,T}\},\end{array}$$ (4.2)

where the expectation is computed with respect to the corresponding Markovian (active) transition law $P_k({\widehat{\mathbf{\text{x}}}}_{k,t+1}|{\widehat{\mathbf{\text{x}}}}_{k,t},1)$ and τ is a stopping time.

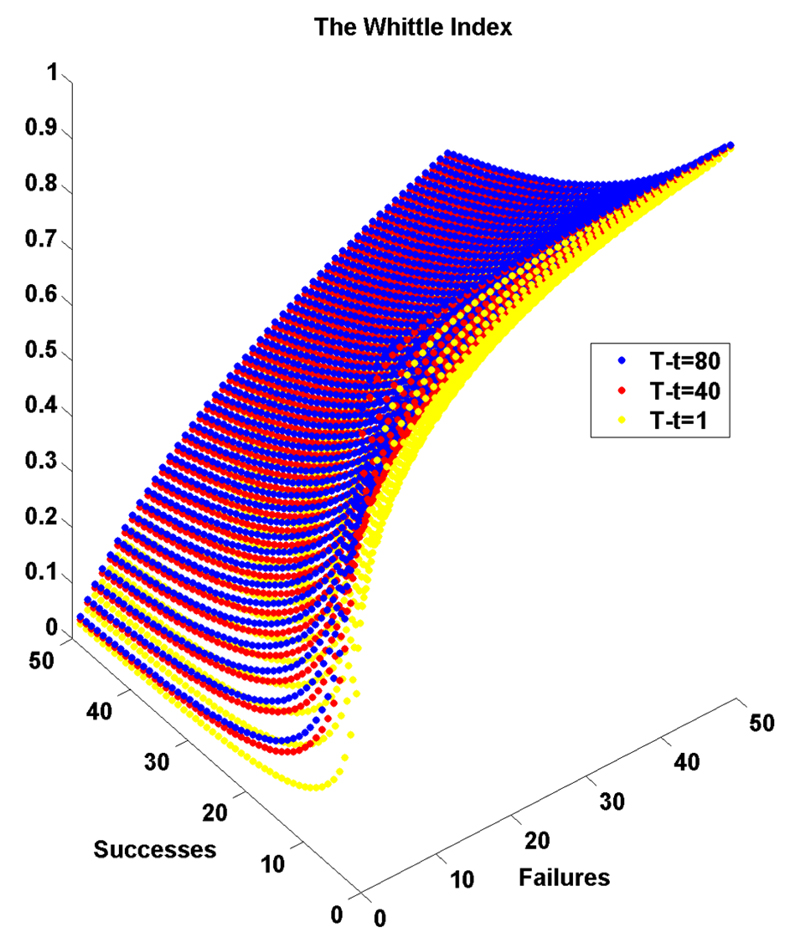
Table 2, Table 3 and Table 4 include some values of the Whittle indices for instances in which, as before, the initial prior is uniform for all the arms and the index precision is of 4 digits, but the discount factor is d = 1, the sampling horizon is set to be T = 180, and the number of remaining observations is respectively allowed to be T − t = 80, T − t = 40 and T − t = 1. Again, the Whittle index rule assigns a number from these tables to every treatment, based on the values of s_k,0 + s_k,t and f_k,0 + f_k,t and on the number of remaining periods T − t , and then prioritizes sampling the one with the highest value.

Table 2.

The Whittle index values for an information vector of s₀ + s_t successes and f₀ + f_t failures, T − t = 80, d = 1 and where the size of the trial is T = 180

f/s	1	2	3	4	5	6
1	0.8558	0.9002	0.9204	0.9326	0.9409	0.9471
2	0.6803	0.7689	0.8140	0.8423	0.8621	0.8769
3	0.5463	$\underset{¯}{\underset{¯}{0.6552}}$	0.7158	0.7565	0.7855	0.8077
4	0.4503	0.5630	0.6335	0.6812	0.7167	0.7444
5	0.3786	0.4923	0.5642	0.6169	0.6565	0.6876
6	0.3247	0.4348	0.5073	0.6040	0.6040	$\underset{¯}{\underset{¯}{0.6380}}$

Table 3.

The Whittle index at T − t = 40

f/s	1	2	3	4	5	6
1	0.8107	0.8698	0.8969	0.9132	0.9244	0.9326
2	0.6199	0.7239	0.7778	0.8120	0.8360	0.8539
3	0.4877	$\underset{¯}{\underset{¯}{0.6067}}$	0.6753	0.7214	0.7546	0.7802
4	0.3955	0.5157	0.5920	0.6447	0.6837	0.7147
5	0.3297	0.4476	0.5231	0.5802	0.6233	0.6573
6	0.2805	0.3929	0.4690	0.5254	0.571	$\underset{¯}{\underset{¯}{0.6075}}$

Table 4.

The Whittle index at T − t = 1

f/s	1	2	3	4	5	6
1	0.5000	0.6667	0.7500	0.8000	0.8333	0.8571
2	0.3333	0.5000	0.6000	0.6667	0.7143	0.7500
3	0.2500	$\underset{¯}{\underset{¯}{0.4000}}$	0.5000	0.5714	0.6250	0.6667
4	0.2000	0.3333	0.4286	0.5000	0.5556	0.6000
5	0.1667	0.2857	0.3750	0.4444	0.5000	0.5455
6	0.1429	0.2500	0.3333	0.4000	0.4545	$\underset{¯}{\underset{¯}{0.5000}}$

It follows from the above tables that the learning element of this index decreases as T − t decreases. In the limit, when T − t = 1 the Whittle index is exactly the posterior mean of success (which corresponds to the myopic allocation rule that results from using current belief as an index). On the contrary, as T − t → ∞, the Whittle index tends to approximate the Gittins index. Hence, for a given information vector, the relative importance of exploring (or learning) vs. exploiting (or being myopic) varies significantly over time in a finite-horizon problem as opposed to the infinite-horizon case in which this balance remains constant in time depending solely on the sampling history. Notice that the computational cost of a single Whittle index table is, at most, the same as for a Gittins index one; however, solving a finite horizon MABP using the Whittle rule has significantly higher computational cost than the infinite-horizon case, because the Whittle indices must be computed at every time point t.

This evolution of the learning vs. earning trade-off is depicted graphically in Figure 3 and causes the decisions in each of the highlighted situations of Table 1 to change over time when considered for a finite-horizon problem. In Table 2 with T − t = 80 both decisions coincide with the ones described for Table 1, while in Table 3, in which T − t = 40, the decision for the second example has changed, and in Table 4, in which T − t = 1, the decisions in both cases are different.

FIG. 3.

The (approximate) Whittle index values for an information vector of s₀ + s_t successes and f₀ + f_t failures, plotted for T − t ∈ {1, 40, 80} with d = 1 and T = 180.

5. SIMULATION STUDY

In this section we evaluate the performance of a range of patient allocation rules in a clinical trial context, including the bandit-based solutions of Section 3 and Section 4. We focus on the following: statistical power (1 − β); type-I error rate (α); expected proportion of patients in the trial assigned to the best treatment (p*); expected number of patient successes (ENS); and, for the two-arm case, bias in the maximum likelihood estimate of treatment effect associated with each decision rule. Specifically, we investigate the following patient allocation procedures:

• Fixed Randomized design (FR): uses an equal, fixed probability to allocate patients to each arm throughout the trial.

• Current Belief (CB): allocates each patient to the treatment with the highest mean posterior probability of success.

• Thompson Sampling (TS): randomizes each patient to a treatment k with a probability that is proportional to the posterior probability that treatment k is the best given the data. In the simulations we shall use the allocation probabilities defined as

  $$\begin{array}{l}{\pi }_{k,t}=P\left(a_{k,t}=1|{\mathbf{\text{x}}}_{k,t}\right)\\ =\frac{{P\left({\max }_i\hspace{0.17em}{p}_i=p_k{|\mathbf{\text{x}}}_{k,t}\right)}^c}{{\displaystyle {\sum }_{k=1}^K{P\left({\max }_i\hspace{0.17em}{p}_i=p_k{|\mathbf{\text{x}}}_{k,t}\right)}^c}},\end{array}$$ (5.1)

  where c is a tuning parameter defined as $\frac{t}{2T},$ and t and T are the current and maximum sample size respectively. See, for example, Thall and Wathen (2007).

• Gittins index (GI) and Whittle index (WI): respectively use the corresponding index functions defined by formulae (3.5) and (4.2).

• Upper Confidence Bound index (UCB): developed by Auer, Cesa-Bianchi and Fischer (2002), takes into account not only the posterior mean but also its variability by allocating the next patient to the treatment with the highest value of an index, calculated as follows: $\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}+\sqrt{\frac{2\log t}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}.}$

Semi-Randomized (Asymptotically Optimal) Bandit Approaches. In addition, we consider a randomized class of index-based bandit patient allocation procedures based on a simple modification first suggested in Bather (1981). The key idea is to add small perturbations to the index value corresponding to the observed data at each stage, obtaining a new set of indices in which the (deterministic) index-based part captures the importance of the exploitation based on the accumulated information and the (random) perturbation part captures the learning element. Formally, these rules are defined as follows:

$$\begin{array}{l}I\left(s_{k,0}+s_{k,t},f_{k,0}+f_{k,t}\right)+Z_t*\lambda \left(s_{k,0}+s_{k,t}+f_{k,t}+f_{k,0}\right),\end{array}$$ (5.2)

where $I\left(s_{k,0}+s_{k,t},f_{k,0}+f_{k,t}\right)$ is the index value associated to the prior and observed data on arm k by time t , Z_t is an i.i.d. positive and unbounded random variable, and $\lambda \left(s_{k,0}+s_{k,t}+f_{k,t}+f_{k,0}\right)$ is a sequence of strictly positive constants tending to 0 as $s_{k,0}+s_{k,t}+f_{k,t}+f_{k,0}$ tends to ∞. The interest in this class of rules is due to their asymptotic optimality, that is, property (2.4) discussed in Section 2, specifically on assessing how their performance compares to the index rules that are optimal (or nearly optimal) in terms of the ETD objective (2.3). Notice that rules defined by (5.2) have a decreasing, though strictly positive, probability of allocating patients to every arm at any point of the trial. In other words, rules (5.2) are such that most of the patients are allocated sequentially to the current best arm (according to the criteria given by the index value), while some patients are allocated all the other of the treatment arms.

For the simulations included in this paper we let Z_t(K) be an exponential random variable with parameter $\frac{1}{K};\lambda \left(s_{k,0}+s_{k,t}+f_{k,t}+f_{k,0}\right)=\frac{K}{s_{k,0}+s_{k,t}+f_{k,t}+f_{k,0}}$ and define two additional approaches:

• Randomized Belief index (RBI) design: makes the sampling decisions between the populations based on an index computed setting $I\left(s_{k,0}+s_{k,t},f_{k,t}+f_{k,0}\right)=\frac{s_{k,0}+s_{k,t}}{s_{k,0}+f_{k,0}+s_{k,t}+f_{k,t}}$ in (5.2).

• Randomized Gittins index (RGI) design: first suggested in Glazebrook (1980), makes the sampling decisions between the populations based on the index computed setting $I\left(s_{k,0}+s_{k,t},f_{k,t}+f_{k,0}\right)=\mathcal{G}\left(s_{k,0}+s_{k,t},f_{k,t}+f_{k,0}\right)$ in (5.2)

For every design, ties are broken at random and in every simulated scenario we let ${\mathbf{\text{x}}}_{k,0}=\left(s_{k,0},f_{k,0}\right)=\left(1,1\right)$ for all k.

Design Scenarios. We implement all of the above methods in several K-arm trial design settings. In each case, trials are made up of K −1 experimental treatments and one control treatment. The control group (and its associated quantities) is always denoted by the subscript 0 and the experimental treatment groups by 1, …, K − 1. We first consider the case K = 2. To compare the two treatments, we consider the following hypothesis: H₀ : p₀ ≥ p₁, with the type-I error rate calculated at p₀ = p₁ = 0.3 and the power to reject H₀ calculated at H₁ : p₀ = 0.3; p₁ = 0.5. We set the size of the trial to be T = 148 to ensure that FR will attain at least 80% power when rejecting H₀ with a one-sided 5% type-I error rate. We then evaluate the performances of these designs by simulating 10⁴ repetitions of the trials under each hypothesis and comparing the resulting operating characteristics of the trials. Hypothesis testing is performed using a normal cutoff value (when appropriate) and using an adjusted Fisher’s exact test for comparing two binomial distributions, where the adjustment chooses the cutoff value to achieve a 5% type-I error.

For the K -arm design settings we shall consider the following hypothesis: H₀ : p₀ ≥ p_i for i = 1, …, K −1 with the family-wise error rate calculated at p₀ = p₁ = ⋯ = p_K−1 = 0.3. We use the Bonferroni correction method to account for multiple testing and therefore ensure that the family-wise error rate is less than or equal to 5%, that is, all hypotheses whose p-values p_k are such that $p_k<\frac{\alpha }{K-1}$ are rejected. Additionally, when there are multiple experimental treatments, we shall define the statistical power as the probability of the trial ending with the conclusion that a truly effective treatment is effective.

5.1. Two-Arm Trial Setting Simulations

Table 5 shows the results for K = 2 under both hypotheses and for each proposed allocation rule. The randomized and semi-randomized response-adaptive procedures (i.e., TS, UCB, RBI and RGI) exhibit a slightly inferior power level than a FR design; however, they have an advantage in terms of ENS over a FR design. On the other hand, the three deterministic index-based approaches (i.e., CB, WI and GI) have the best performance in terms of ENS, yet result in power values which are far below the required values. In the most extreme case, for the CB and WI rules, the power is approximately 3.5 times smaller than with a FR design.

Table 5.

Comparison of different two-arm trial designs of size T = 148. F_a: Fisher's adjusted test; α: type-I error; 1 − β: power; p*: expected proportion of patients in the trial assigned to the best treatment; ENS: expected number of patient successes; UB: upper bound

	Crit. value	H0 : p0 = p1 = 0.3			H1 : p0 = 0.3, p1 = 0.5
		α	p* (s.e.)	ENS (s.e.)	1− β	p* (s.e.)	ENS (s.e.)
FR	1.645	0.052	0.500 (0.04)	44.34 (5.62)	0.809	0.501 (0.04)	59.17 (6.03)
TS	1.645	0.066	0.499 (0.10)	44.39 (5.58)	0.795	0.685 (0.09)	64.85 (6.62)
UCB	1.645	0.062	0.499 (0.10)	44.30 (5.60)	0.799	0.721 (0.07)	66.03 (6.54)
RBI	1.645	0.067	0.502 (0.14)	44.40 (5.57)	0.763	0.737 (0.07)	66.43 (6.54)
RGI	1.645	0.063	0.500 (0.11)	44.40 (5.61)	0.785	0.705 (0.07)	65.46 (6.40)
CB	Fa	0.046	0.528 (0.44)	44.34 (5.55)	0.228	0.782 (0.35)	67.75 (12.0)
WI	Fa	0.048	0.499 (0.35)	44.37 (5.59)	0.282	0.878 (0.18)	70.73 (8.16)
GI	Fa	0.053	0.501 (0.26)	44.41 (5.58)	0.364	0.862 (0.11)	70.21 (7.11)
UB				44.40 (0.00)		1	74.00 (0.00)

Adaptive rules have their power reduced because they induce correlation among treatment assignments; however, for the deterministic index policies this effect is the most severe because they permanently skew treatment allocation toward a treatment as soon as one exhibits a certain advantage over the other arms.

To illustrate the above point, let n₀ and n₁ be the number of patients allocated to treatment 0 and 1 respectively, then for the results in Table 5 it holds that E^CB(n₀) = 31.60, E^CB(n₁) = 116.40, E^WI(n₀) = 16.49, E^WI(n₁) = 131.51 and E^GI(n₀) = 19.06, E^GI(n₁) = 128.94. Moreover, this implies that the required “superiority” does not need to be a statistically significant difference of the size included in the alternative hypothesis as suggested by the following values: $E_k^{\text{CB}}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.1437;0.4208],$$V_k^{\text{CB}}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.1528;0.1831],$$E_k^{\text{WI}}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.1976;0.4860],$$V_k^{WI}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.1470;0.08875],$$E_k^{\text{GI}}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.2283;0.4959]$ and $V_k^{\text{GI}}(\mathbf{\text{s}}/\mathbf{\text{n}})=[0.1271;0.0538]$.

The results in Table 5 illustrate the natural tension between the two opposing goals of maximizing the statistical power to detect significant treatment effects (using FR) and maximizing the health of the patients in the trial (using GI). The optimality property inherent in the GI design produces an average gain in successfully treated patients of 11 (an improvement of 18.62% over the FR design). This is only 4 fewer patients on average than the theoretical upper bound (calculated as T × p₁ = 74) achievable if all patients were assigned to the best treatment from the start. It is worth noting that the asymptotically optimal index approaches [w.r.t. (2.4)] improve on the statistical power of the index designs (around 76%–78% for a 5% type-I error rate) at the expense of attaining an inferior value of ENS (around 5 fewer successes on average compared to the bandit-based rules). Yet, these rules significantly improve on the value of ENS attained by a FR design, naturally striking a better balance in the patient health/power trade-off.

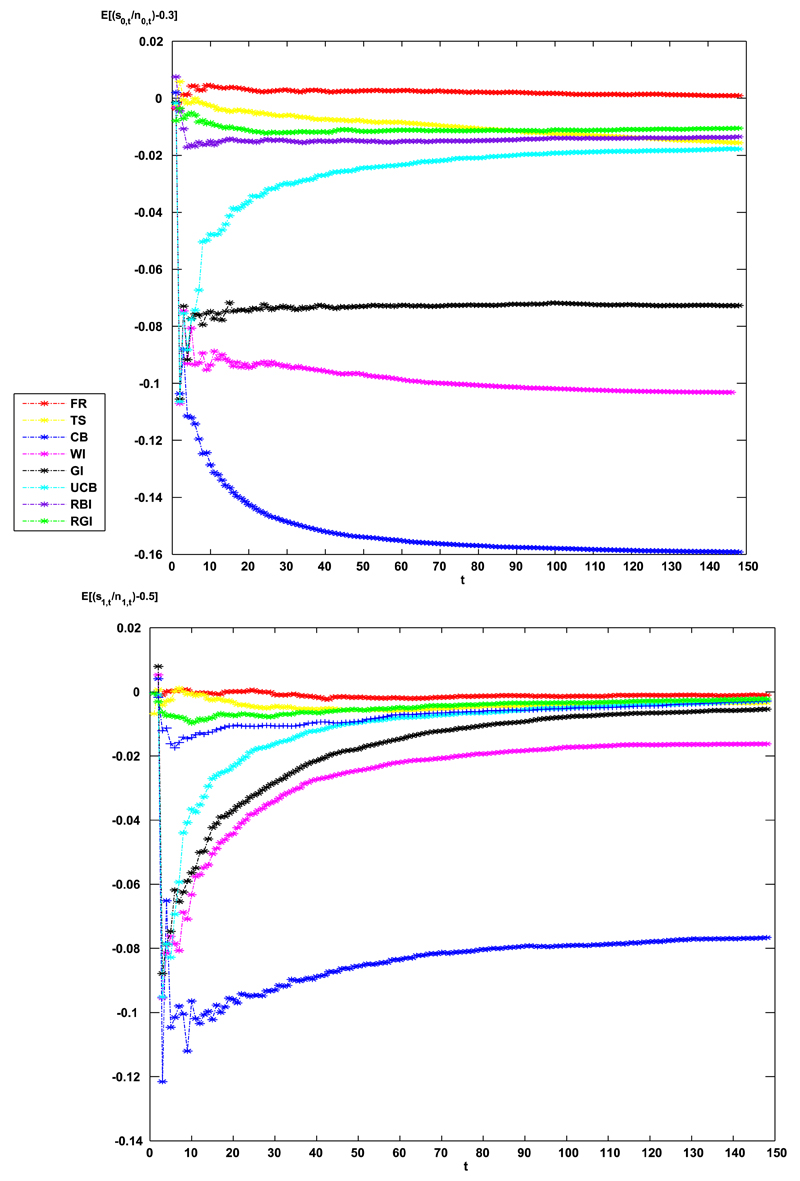
From Table 5 one can see that the three index-based rules significantly improve on the average number of successes in the trial by increasing the allocation toward the superior treatment based on the observed data. This acts to reduce the power to detect significant treatment effect. Another factor at play is bias: index-based rules induce a negative bias in the treatment effect estimates of each arm, the magnitude of this bias is largest for inferior treatments (for which less patients are assigned to than superior treatments). When the control is inferior to the experimental treatment, this induces a positive bias in the estimated benefit of the experimental treatment over the control. This is shown in Figure 4. A heuristic explanation for this is as follows. The index-based rules select a “superior” treatment before the trial is over based on the accumulated data. This implies that if a treatment performs worse than its true average, that is, worse for a certain number of consecutive patients, then the treatment will not be assigned further patients. The treatment’s estimate then has no chance to regress up toward the true value. Conversely, if a treatment performs better than its true average, the index-based rules all assign further patients to receive it, and its estimate then has the scope to regress down toward its true value. This negative bias of the unselected arms is observed for all dynamic allocation rules, and is the most extreme for the CB method.

FIG. 4.

Top: The bias in the control treatment estimate as a function of the number of allocated patients under H₁. Bottom: The bias in the experimental treatment estimate under H₁.

The final observation refers to the fact that although all the index-based rules fail to achieve the required level of power to detect the true superior treatment, they tend to correctly skew patient allocation toward the best treatment within the trial, when it exists. For the simulation reported in Table 5 we have computed the probability that each rule makes the wrong choice (i.e., stops allocating patients to the experimental treatment). These values are as follows: 0.1730, 0.0307, 0.0035 for the CB, WI and GI methods respectively.

5.2. Multi-Arm Trial Setting

We now present results for a K = 4 setting. First, we consider the case of a trial with T = 423 patients. As before, we set the size of the trial to ensure that a FR design results in at least 80% power to detect an effective treatment for a family-wise error rate of less than 5%. Results for this case are depicted in Table 6. The Whittle index approach is omitted because for T roughly larger than 150 its performance is near identical to that attained by the Gittins index but with a significantly higher computational cost.

Table 6.

Comparison of different four-arm trial designs of size T = 423. F_a: Fisher's adjusted test; α: family-wise type-I error; 1 − β: power; p*: expected proportion of patients in the trial assigned to the best treatment; ENS: expected number of patient successes; UB: upper bound

	Crit. value	H0 : p0 = pi = 0.3 for i = 1, …, 3			H1 : p0 = pi = 0.3, i = 1, 2, p3 = 0.5
		α	p* (s.e.)	ENS (s.e.)	(1 − β)	p* (s.e.)	ENS (s.e.)
FR	2.128	0.047	0.250 (0.02)	126.86 (9.41)	0.814	0.250 (0.02)	148.03 (9.77)
TS	2.128	0.056	0.251 (0.07)	126.93 (9.47)	0.884	0.529 (0.09)	172.15 (13.0)
UCB	2.128	0.055	0.251 (0.06)	126.97 (9.41)	0.877	0.526 (0.07)	171.70 (11.9)
RBI	2.128	0.049	0.250 (0.03)	126.77 (9.40)	0.846	0.368 (0.04)	158.34 (10.4)
RGI	2.128	0.046	0.250 (0.03)	126.80 (9.36)	0.847	0.358 (0.03)	157.26 (10.3)
CB	Fa	0.047	0.269 (0.39)	126.89 (9.61)	0.213	0.677 (0.41)	184.87 (36.8)
GI	Fa	0.048	0.248 (0.18)	126.68 (9.40)	0.428	0.831 (0.10)	198.25 (13.7)
CG	2.128	0.034	0.250 (0.02)	127.16 (9.46)	0.925	0.640 (0.08)	182.10 (12.3)
UB				126.90 (0.00)		1	211.50 (0.00)

In this setting, the randomized and semi-randomized adaptive rules (i.e., TS, UCB, RBI, RGI) exhibit an advantage over a FR both in the achieved power and in ENS. The reason for that is that these rules continue to allocate patients to all arms while they skew allocation to the best performing arm, hence, ensuring that by the end of the design the control arm will have a similar number of observations than with FR while the best arm will have a larger number. Among these rules, TS and UCB exhibit the best balance between power-ENS which achieve the 80% power increasing ENS in approximately 23 over a FR design. The deterministic index-based rules CB and GI increase this advantage in ENS over a FR design by roughly 36 and 50, respectively. However, a severe reduction is again observed in the power values of these designs. On the other hand, the probability that each of these rules makes a wrong choice (i.e., it does not skew the allocation toward the best experimental treatment) is 0.2691 and 0.0051, respectively, for the CB and GI.

5.3. The Controlled Gittins Index Approach

To overcome the severe loss of statistical power of the Gittins index, we introduce, for the multi-arm trial setting only, a composite design in which the allocation to the control treatment is done in such a way that one in every K patients is allocated to the control group while the allocation of the remaining patients among the experimental treatments is done using the Gittins index rule. We refer to this design as the controlled Gittins (CG) approach.

Based on the simulation results, CG manages to solve the trade-off quite successfully, in the sense that it achieves more than 80% power, while it achieves a mean number of successes very close to the one achieved by the CB rule and with a third of the variability that CB exhibits in expected number of patient successes.

5.4. Multi-Arm Trial in a Rare Disease Setting

Finally, we imagine a rare disease setting, where the number of patients in the trial is a high proportion of all patients with the condition, but is not enough to guarantee reasonable power to detect a treatment effect of a meaningful size. In such a context, the idea of prioritizing patient benefit over hypothesis testing is likely to raise less controversy than in a common disease context (Wang and Arnold, 2002). We therefore simulate a four-arm trial as before but where the size of the trial is T = 80. Given that the size of the trial implies a very small number of observations per arm, Table 7 only includes the results of the tests using Fisher’s exact test and Fisher’s adjusted exact test (in this case, adjusted to attain the same type-I error as the other methods). Also, to make the scenario more general, we have considered that under the alternative hypothesis the parameters are such that H₁ : p_k = 0.3 + 0.1 × k, k = 0, 1, 2, 3.

Table 7.

Comparison of different four-arm trial designs of size T = 80. F: Fisher; α: type-I error; 1 − β: power; p* : expected proportion of patients in the trial assigned to the best treatment; ENS: expected number of patient successes; UB: upper bound

	Crit. value	H0 : p0 = pi = 0.3 for i = 1, …, 3			H1 : pk = 0.3 + 0.1 × k, k = 0, 1, 2, 3
		α	p* (s.e.)	ENS (s.e.)	(1 − β)	p* (s.e.)	ENS (s.e.)
FR	F	0.019	0.251 (0.04)	24.01 (4.07)	0.300	0.250 (0.04)	35.99 (4.41)
TS	F	0.013	0.250 (0.07)	24.01 (4.15)	0.246	0.338 (0.08)	38.34 (4.68)
UCB	F	0.011	0.252 (0.06)	24.00 (4.12)	0.218	0.362 (0.08)	38.84 (4.71)
RBI	F	0.018	0.250 (0.03)	23.97 (4.06)	0.295	0.268 (0.03)	36.52 (4.41)
RGI	F	0.017	0.250 (0.02)	24.07 (4.07)	0.298	0.265 (0.03)	36.45 (4.36)
CB	Fa	0.017	0.270 (0.30)	23.98 (4.08)	0.056	0.419 (0.38)	40.92 (6.89)
WI	Fa	0.015	0.258 (0.22)	23.00 (4.14)	0.101	0.537 (0.31)	42.65 (6.02)
GI	Fa	0.000	0.251 (0.13)	23.97 (4.11)	0.002	0.492 (0.21)	41.60 (5.44)
CG	Fa	0.015	0.253 (0.13)	24.04 (4.13)	0.349	0.393 (0.16)	38.29 (4.82)
UB				24.00 (0.00)		1	48.00 (0.00)

The FR approach exhibits a 30% power and attains an ENS value of 36. Table 7 shows the results attained for each of the designs considered. Under the alternative hypotheses, the GI and WI designs achieve an ENS gain over the FR design of 6 patients. Again, the CG rule exhibits an advantage over FR both in the achieved power and in the ENS (which in the case of this small population equals the advantage achieved by TS or UCB). Its ENS is less than 10 below the theoretical upper bound of 48. An important feature to highlight is that the Whittle rule does not significantly differ from the Gittins rule as it could be expected, given the trial (and hence its horizon) is small. These results illustrate how the GI and WI start skewing patient allocation toward the best arm (when it exists) earlier than other adaptive designs, therefore explaining their advantage in terms of p* for small T over all of them.

6. DISCUSSION

Multi-armed bandit problems have emerged as the archetypal model for approaching learning problems while addressing the dilemma of exploration versus exploitation. Although it has long been used as the motivating example, they have yet to find any real application in clinical trials. After reviewing the theory of the Bernoulli MABP approach, and the Gittins and Whittle indices in particular, we have attempted to illustrate their utility compared to other methods of patient allocation in several multi-arm clinical trial contexts.

Our results in Section 5 show that the Gittins and Whittle index-based allocation methods perform extremely well when judged solely on patient outcomes, compared to the traditional fixed randomization approach. The two indexes have distinct theoretical properties, yet in our simulations any differences in their performances were negligible, with both designs being close to each other and the best possible scenario in terms of patient benefit. Since it only needs to be calculated once before the trial starts, the Gittins index may naturally be preferred.

The Gittins index, therefore, represents an extremely simple—yet near optimal—rule for allocating patients to treatments within the finite horizon of a real clinical trial. Furthermore, since the index is independent of the number of treatments, it can seamlessly incorporate the addition of new arms in a trial, by balancing the need to learn about the new treatment with the need to exploit existing knowledge on others. The issue of adding treatment arms is present in today’s cutting-edge clinical trials. For example, this facet has been built into the I-SPY 2 trial investigating tumour-specific treatments for breast cancer from the start (Barker et al., 2009). It is also now being considered in the multi-arm multi-stage STAMPEDE trial into treatments for prostate cancer as an unplanned protocol amendment, due to a new agent becoming available (Sydes et al., 2009; Wason et al., 2012).

Gittins indices and analogous optimality results have been derived for endpoints other than binary. Therefore, the analysis and conclusions of this work naturally extend to the multinomial distribution (Glazebrook, 1978), normally distributed processes with known variance (Jones, 1970) and with unknown variance (Jones, 1975), and exponentially distributed populations (Do Amaral, 1985; Gittins, Glazebrook and Weber, 2011).

Unfortunately, the frequentist properties of designs that utilize index-based rules can certainly be questioned; both the Gittins and Whittle index approaches required an adjustment of the Fisher’s exact test in order to attain type-I error control, produced biased estimates and, most importantly, had very low power to detect a treatment difference at the end of the trial. Since this latter issue greatly reduces their practical appeal, we proposed a simple modification that acted to stabilize the numbers of patients allocated to the control arm. This greatly increased their power while seemingly avoiding any unwanted type-I error inflation above the nominal level. This principle is not without precedence, indeed, Trippa et al. (2012) have recently proposed a Bayesian adaptive design in the oncology setting for which protecting the control group allocation is also an integral part. Further research is needed to see whether statistical tests can be developed for bandit-based designs with well-controlled type-I error rates and also if bias-adjusted estimation is possible.

There are of course other obvious limitations to the use of index-based approaches in practice. A patient’s response to treatment needs to be known before the next patient is recruited, since the subsequent allocation decision depends on it. This will only be true in a small number of clinical contexts, for example, in early phase trials where the outcome is quick to evaluate or for trials where the recruitment rate may be slow (e.g., some rare disease settings). MABPs rely on this simplifying assumption for the sake of ensuring both tractability and optimality, and can not claim these special properties without making additional assumptions (see, e.g., Caro and Yoo, 2010). It would be interesting to see, however, if index-based approaches could be successfully applied in the more general settings where patient outcomes are observed in groups at a finite number of interim analyses, such as in a multi-arm multi-stage trial (Magirr, Jaki and Whitehead, 2012; Wason and Jaki, 2012). Further research is needed to address this question.

A different limitation to the use of bandit strategies is found in the fact that the approach leads to deterministic strategies. Randomization naturally protects designs against many possible sources of bias, for example, patient drift unbalancing treatment arms (Tang et al., 2010) or unscrupulous trial sponsors cherry-picking patients (FDA, 2006). Of course, while these are serious concerns, they could also be leveled at any other deterministic allocation rule, such as play-the-winner. Further research is needed to introduce randomization to bandit strategies and also to determine some general conditions under which arms are selected or dropped when using the index rules.

Further supporting materials for this paper, including programs to calculate extended tables of the Gittins and Whittle indexes, can be found at http://www.mrc-bsu.cam.ac.uk/software/miscellaneous-software/.

APPENDIX: INDEX COMPUTATION

There is a vast literature on the efficient computation of the Gittins indices. In Beale (1979), Varaiya, Walrand and Buyukkoc (1985) and Chen and Katehakis (1986), among others, algorithms for computing the Gittins indices for the infinite-horizon classic MABP with a finite state space are provided. The computational cost for all of them (in terms of its running time as a function of the number of states N) is N³ + $𝒪$(N²). The algorithm for computing the Gittins indices in such a case achieving the lowest time complexity, 2/3N³ + $𝒪$(N²), was provided by Niño-Mora (2007). For MABP with an infinite state space, such as the Bayesian Bernoulli MABP in Section 3, the indices can be computed using any of the above algorithms but confining attention to some finite set of states, which will eventually determine the precision of their calculation. For the finite-horizon classic MABP, as reviewed in Section 4, an efficient exact computation method based on a recursive adaptive-greedy algorithm is provided in Niño-Mora (2011).

In what follows we examine in more detail the so-called calibration method for the approximate index computation in the Bayesian Bernoulli MABP, both for the infinite- (Gittins index) and finite-horizon case (Whittle index). There are many reasons for focusing on this approach, not least because it was the algorithm used for computing the values presented in this paper. It also sheds light on the interpretation of the resulting index values, by connecting the Gittins index approach to the work in Bellman (1956), and has long been the preferred computational method.

The Calibration Method

Bellman (1956) studied an infinite random sampling problem involving two binomial distributions: one with a known success rate and the other one with an unknown rate but with a Beta prior. Bellman’s key contribution was to show that the solution to the problem of determining the sequence of choices that maximize the ETD number of successes exists, is unique and, moreover, is expressible in terms of an index function which depends only on the total observed number of successes s and failures f of the unknown process.

Gittins and Jones (1974) used that result and showed that the optimal rule for an infinite-horizon MABP can also be expressed in terms of an index function for each of the K Bernoulli populations and based on their observed sampling histories (s, f ). Such an index function is given by the value p ∈ [0, 1] for which the decision maker is indifferent between sampling the next observation from a population with known success rate p or from an unknown one with an expected success rate $\frac{s}{s+f}$. The calibration method uses DP to approximate the Gittins index values based on this idea, as explained in Gittins and Jones (1979), and it can be adapted to compute the finite-horizon counterpart, as explained in Berry and Fristedt (1985), Chapter 5.

Specifically, this index computation method solves, for a grid of p values (the size of which determines the accuracy of the resulting index values approximations), the following DP problem:

$$\begin{array}{l}{V}_{D,t}^{*}(s,f,p)=max\left\{p\frac{1-d^{T-t}}{1-d},\frac{s}{s+f}(1+d{V}_{D,(t+1)}^{*}(s+1,f,p))+\frac{f}{s+f}(d{V}_{D,(t+1)}^{*}(s,f+1,p))\right\},t=0,\dots ,T-2,\\ V_{D,T-1}^{*}(s,f,p)=max\left\{p,\frac{s}{s+f}\right\}.\end{array}$$ (A.1)

For the infinite-horizon problem and with 0 ≤ d < 1, the convergence result allows for the omission of the subscript t in the optimal value functions in (A.1), letting the reward associated to the known arm be $\frac{p}{(1-d)}$. For obtaining a reasonably good initial approximation of the optimal value function, the terminal condition on $V_{D,T-1}^{*}(s,f,p)$ is solved for some values of s and f such that s + f = T − 1, and for a large T and then a backward induction algorithm is applied to yield an approximate value for $V_{D,0}^{*}(s,f,p)$. For a fixed p the total number of arithmetic operations to solve (A.1) is 1/2(T − 1)(T − 2), which, as stated in Section 3.1, no longer grows exponentially in the horizon of truncation T (nor does it grow in the number of arms of the MABP).

For the finite-horizon variant, the terminal condition is not used for approximating the initial point of the backward-induction algorithm and the solution, but for computing the optimal value function exactly. The resulting number of operations to compute the Whittle index is basically the same as for the Gittins index, yet the total computational cost is significantly higher given that the Whittle indices must be computed and stored for every possible t ≤ T − 1 and (s, f ). However, notice that an important advantage of the Whittle index over the Gittins index is that the discount factor d = 1 can be explicitly considered for the former directly adopting an Expected Total objective function, by replacing the term $\frac{1-d^{T-t}}{1-d}$ by T − t , using the fact that

$$\underset{d\to 1}{\lim }\frac{1-d^{T-t}}{1-d}={\displaystyle \sum _{i=0}^{T-t-1}{d}^i.}$$