Abstract
Standing surface acoustic waves (SSAW) are commonly used in microfluidics to manipulate cells and other micro/nano particles. However, except for a simple one-dimensional (1D) harmonic standing waves (HSW) model, a practical model that can predict particle behaviour in SSAW microfluidics is still lacking. Herein, we established a two-dimensional (2D) SSAW microfluidic model based on the basic theory in acoustophoresis and our previous modelling strategy to predict the acoustophoresis of microparticles in SSAW microfluidics. This 2D SSAW microfluidic model considers the effects of boundary vibrations, channel materials, and channel dimensions on the acoustic propagation; as an experimental validation, the acoustophoresis of microparticles under continuous flow through narrow channels made of PDMS and silicon was studied. The experimentally observed motion of the microparticles matched well with the numerical predictions, while the 1D HSW model failed to predict many of the experimental observations. Particularly, the 1D HSW model cannot account for particle aggregation on the sidewall in PDMS channels, which is well explained by our 2D SSAW microfluidic model. Our model can be used for device design and optimization in SSAW microfluidics.
Graphical abstract
We numerically and experimentally investigate the acoustophoresis of microparticles in standing surface acoustic wave microfluidic devices.

Introduction
The ability to manipulate micro-sized objects is of critical importance in a variety of biophysical, biochemical, and biomedical applications.1–4 In the past decade, magnetic, hydrodynamic, electrokinetic, and acoustic methods have all been applied to successfully manipulate micro-objects and fluids.5–11 Each method is associated with characteristic advantages and disadvantages. In particular, standing surface acoustic waves (SSAW)-based microfluidic techniques have become increasingly popular due to their advantages of label-free operation, excellent biocompatibility, compact size, and easy integration with other microfluidic units.1–3,12,13 SSAW microfluidic techniques have been applied to manipulate micro-sized objects in many applications, including separating,1,14–19 focusing,15,20 sorting,21,22 patterning,23–25 culturing,24,26,27 and enriching cells28,29.
Regardless of application, SSAW-based manipulation devices share similar working principles. Once SSAW is formed on the surface of a substrate, a wave-form distribution of displacement nodes and anti-nodes, as well as pressure nodes and anti-nodes, is created.2,24 When a fluid, like water, is in contact with the surface where SSAW is formed, a portion of the vibration energy leaks into the fluid yielding a longitudinal wave and forming pressure nodes and anti-nodes in the fluid domain. Micro-sized objects suspended in the fluid can move towards these nodes or anti-nodes, depending on the contrast in density and acoustic compressibility between the particles and the fluid. The movement of particles towards pressure nodes or anti-nodes is the underlying mechanism used to manipulate particles in all SSAW-based manipulation devices. Therefore, in order to manipulate micro-sized objects in a highly precise, controllable manner, the distribution of pressure nodes or anti-nodes inside the channel needs to be well predicted.
Until now, except for SSAW-driven droplets in channel-less open space,30 the analysis and design of the pressure distribution inside SSAW microfluidic devices has been guided by a 1D harmonic standing waves (HSW) model.1,14–17,24,27,31,32 In the 1D HSW model, the pressure nodes and anti-nodes are evenly distributed with a distance of a half wavelength (λ/2) between adjacent pressure nodes or anti-nodes. However, the actual acoustic pressure distribution inside the channel can be significantly different from that predicted by a 1D HSW model: first, the real pressure distribution is three-dimensional (3D) rather than 1D; second, the longitudinal waves caused by SSAW leaking into the fluid domain have a propagation direction, which is not parallel to the surface of the substrate; third, channel walls do cause some reflection of acoustic energy due to a mismatch in acoustic impedances between the channel material and the working fluid. When the channel width is narrow, the wall reflection of acoustic wave propagation is especially noticeable, and the acoustic field inside the channel will be very different from that predicted by a conventional 1D HSW model. Due to the above-mentioned factors, there are many circumstances where the 1D HSW model cannot be used to accurately predict particle trajectories; therefore, the 1D HSW model is of limited value when attempting to design and optimize SSAW microfluidic devices. In this regard, it is highly desirable to establish an accurate representation of the acoustic pressure distribution originating from SSAW inside the microfluidic channel.
Besides the 1D HSW model, numerical and analytic methods have been used to find the acoustic field, acoustic radiation force, and acoustic streaming in bulk acoustic wave (BAW)-based resonator33–38 and surface acoustic wave (SAW)-driven droplets.30,39,40 The basic theory used in these cases is a perturbation theory in which the governing equations, namely conservation of mass, momentum, and energy of the fluid, are re-written as an asymptotic expansion based on a smallness parameter.41–43 The solution of the resulting first-order problem yields the identification of the harmonic component of the motion, whereas the solution of the second-order equations identify the streaming motion. Some of our previous work44 numerically studied the acoustic field, acoustic radiation force, and acoustic streaming in a confined SSAW-driven fluid domain using this approach. Here, we present a simplified numerical model to determine the acoustic field actuated by SSAW in microfluidic devices. Our two-dimensional (2D) SSAW microfluidic model considers the effects of boundary vibrations, channel materials, and channel dimensions on the acoustic propagation and acoustophoresis. In addition to the numerical study, this article presents experimental studies on microparticle acoustophoresis aiming at validating the effectiveness of the model. The numerical model was established based on the Helmholtz equation for damped waves. By giving certain boundary conditions to model both the reflection of acoustic waves by the microfluidic channel walls and the vibrations of the channel walls themselves, the acoustic pressure, radiation force potential, and acoustic radiation force distributions inside the narrow channels (with width of λ/2 and λ) made of polydimethylsiloxane (PDMS) and silicon were found. Meanwhile, the traces of microparticles (such as polystyrene beads and PDMS beads) in such channels under continuous flow mode were obtained experimentally. Excellent agreement between the experimental results and the particle trajectories predicted by the numerical model indicate that our 2D SSAW microfluidic model is reliable and can be used to predict microparticle acoustophoresis in SSAW microfluidic devices.
Theory and numerical model
As shown in Fig. 1 (a, b, d, and e), in typical SSAW microfluidic devices, the microchannel is bonded on a piezoelectric substrate and aligned with the interdigitated transducers (IDTs). When RF signals are applied to the IDTs, two SAWs are excited and propagate like two plane waves, with nearly uniform amplitude along the longitudinal direction of the microchannel (y), in opposite directions (x) on the surface to form SSAW. Since the SSAW is nearly uniform along the longitudinal direction of the channel, 2D modelling of the device cross-section can be used to simplify the analysis. Furthermore, as dimensions of the channel walls are generally much larger than those of the fluid domain, the channel walls are not included in the model, and their physical effects on the acoustic field in the fluid domain are modelled via specific boundary conditions. An additional simplification that is typically adopted is the fact that the mutual effects of the fluid-substrate interaction are neglected. The surface displacement can be modelled as consisting of two leaky SAWs, which are generated when travelling SAWs meet with fluid.45 Once the surface displacements are determined, this vibration can be used to generate corresponding acceleration boundary conditions, which are responsible for actuating the acoustophoresis in the fluid domain. Adopting this strategy, a simplified 2D SSAW microfluidic model is established that pertains only to the fluid domain (Fig. 1c and Fig. 1f). The governing equation for the acoustic field in the fluid domain is the well-known lossy Helmholtz equation.42 By assuming a harmonic time dependence of the acoustic field (p(r,t)=p(r,t)eiωt), the lossy Helmholtz equation can be written as,42
| (1) |
where p, ρf, cf, ω, β, μ, and i indicate the acoustic pressure, density of fluid, acoustic phase velocity of fluid, angular velocity, fluid viscosity ratio, fluid dynamic viscosity, and imaginary unit, respectively. When the fluid is compressible, an equation of state relates the pressure and density fields. We adopt the following linear relationship: , where ρ is small density variation. Then, the acoustic field p and v (acoustic particle velocity) are coupled via the momentum balance equation in fluid:
| (2) |
For the flow regimes of interest in our application, it is physically reasonable to neglect the terms in Eq. (2) that have the velocity gradients. In this case, Eq. (2) can be simplified to
| (3) |
To account for viscosity effects, Eq. (3) is modified as follows:
| (4) |
Fig. 1.
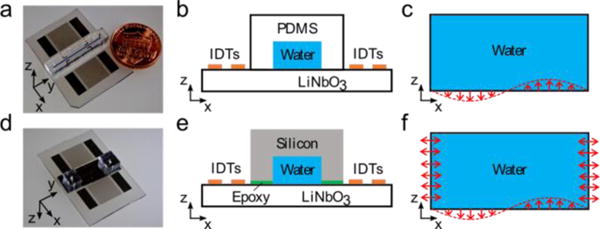
(a) Photograph of a SSAW microfluidic device mounted with PDMS channel. (b) Schematic of x-z plane of device shown in (a). (c) Modelled fluid domain shown in (b), with actuation boundary at bottom. (d) Photograph of an inverted SSAW microfluidic device mounted with silicon channel. (e) Schematic of x-z plane of device shown in (d). (f) Modelled fluid domain shown in (e), with actuations both at the bottom and the sidewalls.
The above equation allows us to compute the velocity field corresponding to a given pressure solution of Eq. (1). The latter can be solved by selecting appropriate boundary conditions. The lower boundary at the interface between the piezoelectric substrate and the fluid domain is actuated by the SSAW. These are formed by two leaky Rayleigh SAW, with oscillations both parallel and perpendicular to the surface, which decay along the propagating paths. Here, the decay is ignored due to the narrow width of the fluid domain. As only the perpendicular oscillation can generate compressible acoustic waves and radiate into the fluid domain, the parallel component of leaky Rayleigh SAW is not considered either. Thus we model the harmonic actuation at the lower boundary by prescribing the normal component of boundary acceleration, as this condition can be easily translated into a normal “flux” boundary condition for the pressure:
| (5a) |
| (5b) |
where A0, ks, w0, and n correspond to the amplitude of leaky SAW displacement, wave number of leaky SAW, channel width, and boundary normal vector, respectively. In Eq. (5), the accelerations aPN and aAN represent the boundary conditions given for the cases when pressure node (displacement node) and pressure anti-node (displacement anti-node) of the SSAW is located in the middle of the channel. For devices using PDMS channel, a lossy-wall condition42 is given to model partial acoustic losses when a radiation wave propagates from the fluid domain into the PDMS through the side and top walls. Here, the effect of wave reflection from the PDMS/air interface on the inner fluid domain is eliminated due to high viscoelasticity and wave absorption of PDMS. This condition is often given in the following form:
| (6) |
where ρw and cw are the density and sound speed of the wall material. Unlike the PDMS channel, which is bonded directly to the substrate, the silicon channel is bonded on the substrate via a UV-epoxy in our experiments. For the silicon channel, waves propagate through the epoxy and excite the solid channel with both shear and longitudinal waves. The displacement amplitude in a silicon channel can be greater than in a PDMS channel. Thus, the sidewalls of the silicon channel can vibrate as well.42 The actuation boundaries for the fluid domain confined by the silicon channel include the sidewalls. The acceleration induced by the vibration of the sidewalls is given by
| (7) |
where the sign ± is used to represent in phase and counter phase oscillations of the sidewalls. The top wall in Fig. 1f is modelled as a hard wall boundary for simplicity and motivated by the fact that stiff silicon has been used as the channel wall, as opposed to soft PDMS. As a result, the normal component of the fluid velocity at this wall is taken to be equal to zero. Then, using Eq. (4), such a condition can be re-expressed using the pressure gradient as follows:
| (8) |
After obtaining the acoustic fields p and v from the 2D model, the time-averaged radiation force potential in the domain and acoustic radiation force on a single spherical particle can be determined by adopting the theory of Gor’kov.28 Here, the acoustic radiation force can be considered as the time-average contact force between the fluid and the particle over a cycle of oscillation, i.e., the radiation-pressure forces acting on the particle in a sound wave. This yields46
| (9a) |
| (9b) |
with , and f2=2(ρp−ρf)/(2ρp+ρf). U is the so-called radiation force potential. In Eq. (9), V0 is the particle volume; ρp and cp are the density and sound speed of the particle, respectively; Re is the real part of a complex value, and the asterisk indicates complex conjugation.
The problem formulated above has been solved for 2D cases using the finite element software package COMSOL multiphysics 4.3a. The module “Pressure Acoustics" was used to numerically solve the equations by using a frequency domain study type. A mesh-independence test has been conducted. To ensure accuracy, a uniform mapped mesh with size of 1 μm × 1 μm for each element was employed. Particle-tracing simulations were carried out in COMSOL Multiphysics 4.3a by the module called “Particle Tracing for Fluidic Flow.” These simulations were conducted to predict the particle motion in the lateral direction (x-z plane) under the action of the acoustic radiation force and the Stokes drag force created when particles move relative to the fluid. Physical properties of the fluid and parameters used in the numerical study are given in Table 1 listed in the electronic supplementary information (ESI).
Table 1.
Comparison between the 1D HSW and 2D SSAW microfluidic models on prediction of microparticle acoustophoresis in PDMS channel. PN: pressure node; AN: pressure antinode.
| Channel width | 170 μm | 340 μm | ||||||
|---|---|---|---|---|---|---|---|---|
| SSAW actuation | PNa1 centred | ANa2 centred | PNa1 centred | ANa1 centred | ||||
| Bead type | PSa3 | PDMS | PS | PDMS | PS | PDMS | PS | PDMS |
| 1D HSW | Na4 | N | Y | N | Y | Y | N | Y |
| 2D SSAW | Ya5 | Y | Y | Y | Y | Y | Y | Y |
PN: Pressure node (Displacement node of SSAW) at the middle
AN: Pressure antinode (Displacement anti-node of SSAW) at the middle
PS: Polystyrene beads
N indicates disagreement
Y indicates agreement
Materials and methods
Device fabrication
Two types of SSAW microfluidic devices made of PDMS (Fig. 1a) and silicon (Fig. 1b) were used in our experiments. Each device had a LiNbO3 piezoelectric substrate (Y+128° X-propagation, Red Optronics, USA) with IDTs on its surface. One pair of IDTs with uniform electrode widths (75 μm) and spacing gaps (75 μm) were placed parallel to each other, and perpendicular to the X crystal axis on the LiNbO3 substrate. Thus, the wavelength of SAW is 300 μm, and the associated frequency to excite the SAW is 12.883 MHz in our experiments. The IDTs, composed of two metal layers (Cr/Au, 50 Å/500 Å), were patterned and deposited on the substrate by a photolithography process and an e-beam evaporation process1,24,29 successively. A lift-off process was followed to give final form of the IDTs, containing 30 pairs of electrodes in each set. PDMS channels (Fig. 1a) were fabricated by a standard soft-lithography and mould-replica procedures. The channels were designed with two different widths (170 μm and 340 μm) and the same height (60 μm). Silicon channels (Fig. 1d) with the same dimensions as the PDMS channels were fabricated by deep reactive-ion etching (DRIE) on a silicon wafer. For the PDMS device, the channel was carefully aligned with the markers on the substrate under a microscope and bonded on the substrate after surface activation on both the channel and the substrate in an oxygen plasma cleaner (Harrick Plasma Inc., Ithaca, NY, USA). The assembly of the device with a silicon channel required additional steps. Firstly, two holes for the inlet and outlet were drilled through the substrate after the fabrication of the IDTs. The silicon channel was then aligned and bonded at the top of the substrate via UV-epoxy (NOA 60, Norland Optical Adhesives, Cranbury, NJ, USA) following the method proposed by Langelier et al.47 Finally, two small PDMS blocks with through holes were aligned with the drilled holes in the substrate, and bonded at the bottom of the substrate by the same bonding method used for the device with PDMS channel. Detailed procedures for fabrication of the devices can be found in Fig. S1 of the ESI.
Preparation of microparticles
Polystyrene and PDMS microparticles were used in the experiments. The diameter of polystyrene beads (Polysciences, Inc., Warrington, PA, USA) is 10.11 μm. PDMS beads were prepared by following a protocol proposed by Johnson et al.48 A one-gram mixture (Sylgard 184, Dow Corning Inc., Freeland, MI, USA) of prepolymer and curing agent at a 10:1 weight ratio was added into 1 % (w/w) SDS solution. The mixture was sonicated for 20 min to form emulsion by a mixer (Genemate, BioExpress, UT, USA). Subsequently, the emulsion was incubated at 65°C for 60 min, and left at ambient conditions for 12 hr to permit curing.
Experimental method
The devices with the PDMS channel were mounted on the stage of an inverted microscope (TE2000U, Nikon, Japan) to visualize the motion of particles inside the channel. The devices using the silicon channel were placed upside down on an upright microscope (Eclipse LV-100, Nikon, Japan) to observe the motion of particles in a reflection mode due to the opaque nature of the silicon channel. Particle suspensions were injected into the microchannel using a syringe pump (neMESYS, Cetoni GmbH, Germany) at a flow rate of 10 μL/min. To excite the SSAW, AC signals, produced by a RF signal generator (E4422B, Agilent, USA), were applied to the two sets of IDTs on the substrate after amplification by a power amplifier (100A250A, Amplifier Research, USA). The frequency of the AC signals was set to 12.883 MHz to generate SAW with a wavelength of 300 μm. The motion of the particles was recorded by a CCD camera (CoolSNAP HQ2, Photometrics, USA). The trajectories of the particles were illustrated by stacking frames of recorded videos using software package ImageJ.
Results
The following results present numerical and experimental results pertaining to the acoustic field and the acoustic radiation force in narrow (λ/2 and λ in width) microfluidic channels under continuous flow. The dependence of microparticle acoustophoresis on the channel dimensions, material, and vibration is also discussed.
Microparticle acoustophoresis in PDMS channels
For the PDMS channel, the acoustic field and corresponding acoustic radiation force in the fluid domain were first simulated with 2D simulations (presented in section of theory and numerical model). Fig. 2b and Fig. 2e show the field of radiation force potential for polystyrene beads and PDMS beads in a PDMS channel with a width of 170 μm when the displacement node of the SSAW is located at the midpoint of the bottom boundary. The acoustic radiation force, pointing from high radiation force potential area (red colour) to the area with lower radiation force potential (blue colour), are also indicated. Particle trajectories and final positions of polystyrene (Fig. 2c) and PDMS (Fig. 2f) beads are demonstrated in the PDMS channel as well. It can be seen that polystyrene beads move to the middle plane of the channel and along the sidewalls. However, PDMS beads are focused at only two positions within the channel.
Fig. 2.
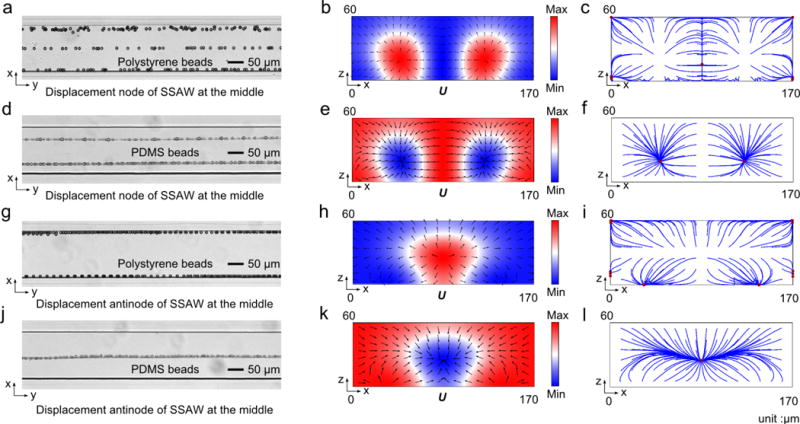
Microparticle acoustophoresis in PDMS channels with a width of 170 μm. (a)–(c), Particle traces and numerical results for polystyrene beads when the displacement node is located in the middle of the channel. (d)–(f), Particle traces and numerical results for PDMS beads when the displacement node is located in the middle of the channel. (g)–(i), Particle traces and numerical results for polystyrene beads when the displacement antinode is located in the middle of the channel. (j)–(l), Particle traces and numerical results for PDMS beads when the displacement antinode is located in the middle of the channel. (a), (d), (g), and (j), experimental particle traces in the x-y plane under the mentioned conditions (a, g: polystyrene beads; d, j: PDMS beads). (b), (e), (h), and (k), Numerical results of radiation force potential and acoustic radiation forces in the x-z plane for the mentioned cases (b, h: polystyrene beads; e, k: PDMS beads). (c), (f), (i), and (l), Numerical results of bead trajectories and final locations in the x-z plane for the mentioned cases (c, i: polystyrene beads; f, l: PDMS beads).
Experiments were also conducted by using the device with PDMS channels to validate our model. The trajectories of polystyrene (Fig. 2a) and PDMS (Fig. 2d) beads are shown in x-y plane when SSAW was on, where a continuous flow moved along y direction. Polystyrene beads (Fig. 2a) move along three lines in which two lines are located near the sidewalls and one aligned at the middle. PDMS beads (Fig. 2d) left two traces symmetrically distributed about the middle of the channel. Both of the experimental results agree well with the predictions from simulations shown in Fig. 2c and Fig. 2f. We also investigated microparticle acoustophoresis in the small PDMS channel when the displacement antinode of the SSAW was located at the midpoint of the bottom boundary. The fields of radiation force potential and the acoustic radiation force for polystyrene and PDMS beads are shown in Fig. 2h and Fig. 2k, respectively. The corresponding particle trajectories and final positions are given in Fig. 2i and Fig. 2l. In this case, the polystyrene beads flowed close to the sidewalls and showed two traces. The PDMS beads were focused at the middle of the channel.
Microparticle acoustophoresis in wider PDMS channels was also investigated. The numerical and experimental results are listed in Fig. 3 in a similar manner to Fig. 2. Fig. 3a and Fig. 3d are the experimental particle traces of polystyrene and PDMS beads in the x-y plane, respectively, when aPN is applied at the bottom. The corresponding numerical results are listed to the right. Seen from these results, the polystyrene beads move to the middle plane and the sidewalls while PDMS beads leave two traces in the channel when the SSAW was on. When aAN is applied at the bottom, experimentally, polystyrene and PDMS beads leave five and three traces in x-y plane, respectively, as shown in Fig. 3g and Fig. 3j. The relevant numerical results are listed in Fig. 3h, 3i, 3k, and 3l. All of the experimental results agree with the numerical predictions well except the one shown in Fig. 3j, where only three clear traces were found corresponding to the five predicted particle streams. It seems that the two traces symmetrically distributed about the middle plane were missing. Actually, there were some PDMS beads flowing around the central line (shown in Fig. 3j). The possible reason for the missing traces is that the acoustic radiation force in the middle region is not large enough to focus the PDMS beads and form the two additional traces.
Fig. 3.
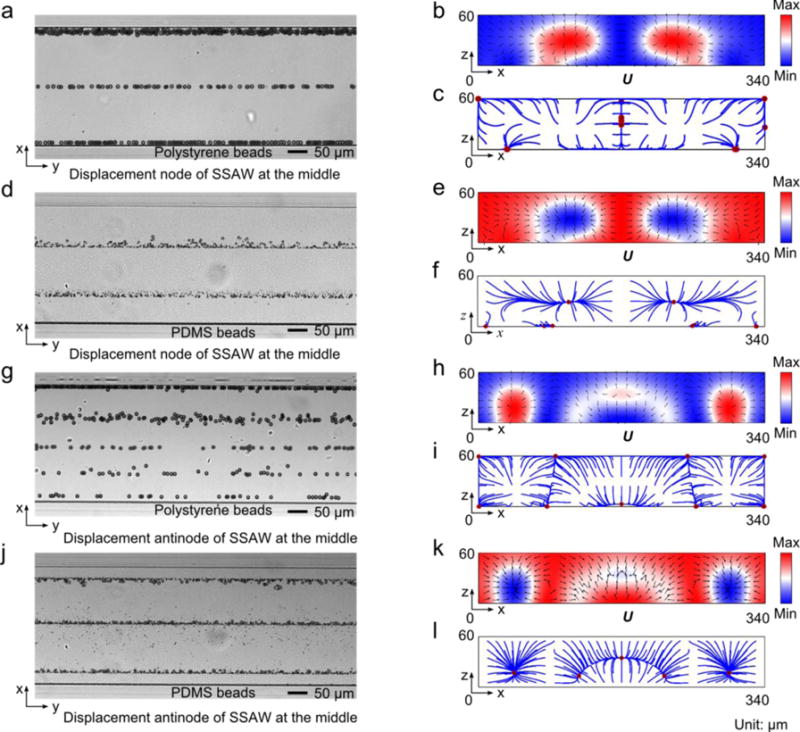
Microparticle acoustophoresis in PDMS channels with a width of 340 μm. (a)–(c), Particle traces and numerical results for polystyrene beads when the displacement node is located in the middle of the channel. (d)–(f), Particle traces and numerical results for PDMS beads when the displacement node is located in the middle of the channel. (g)–(i), Particle traces and numerical results for polystyrene beads when the displacement antinode is located in the middle of the channel. (j)–(l), Particle traces and numerical results for PDMS beads when the displacement antinode is located in the middle of the channel. (a), (d), (g), and (j), Experimental particle traces in the x-y plane under the mentioned conditions (a, g: polystyrene beads; d, j: PDMS beads). (b), (e), (h), and (k), Numerical results of radiation force potential and acoustic radiation forces in the x-z plane for the mentioned cases (b, h: polystyrene beads; e, k: PDMS beads). (c), (f), (i), and (l), Numerical results of bead trajectories and final locations in the x-z plane for the mentioned cases (c, i: polystyrene beads; f, l: PDMS beads).
Microparticle acoustophoresis in silicon channels
To investigate the effect of channel material, microparticle acoustophoresis induced by SSAW inside silicon channels was studied. The radiation force potential and particle trajectories for polystyrene (Fig. 4c) and PDMS (Fig. 4f) beads were also simulated, in which the boundary condition aPN was given at the bottom of a silicon channel with a width of 170 μm. Results show that polystyrene beads are pushed to three locations seen from the x-y plane, one in the middle plane and the rest symmetrically positing away from the sidewalls in the channel. PDMS beads are driven to the top wall (two regions) and the bottom corners. More similar simulations with the boundary condition aAN at the bottom can be found in Fig. S2 and Fig. S3 (ESI).
Fig. 4.
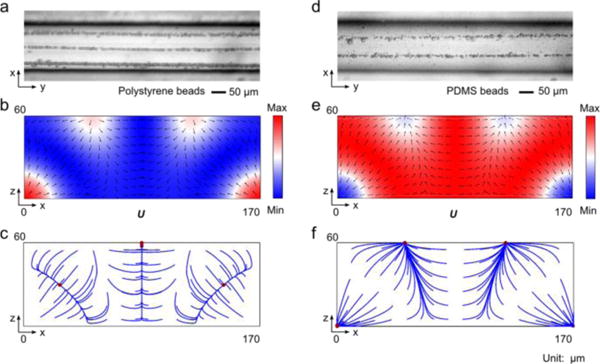
Microparticle acoustophoresis in silicon channels with a width of 170 μm. (a)–(c), Particle traces and numerical results for polystyrene beads. (d)–(f), Particle traces and numerical results for PDMS beads. (a) and (d), Experimental particle traces in the x-y plane (a: polystyrene beads; d: PDMS beads). (b) and (e), Numerical results of radiation force potential and acoustic radiation forces in the x-z plane (b: polystryrene beads; e: PDMS beads). (c) and (f), Numerical results of bead trajectories and final locations in the x-z plane (c: polystyrene beads; f: PDMS beads).
The particle traces of polystyrene (Fig. 4a) and PDMS (Fig. 4b) beads inside silicon channels with a width of 170 μm confirmed the numerical predictions for polystyrene beads. For PDMS beads, only two clear traces were observed in the experiment (Fig. 4b). Two factors may account for the missing two traces at the corners. First, it is difficult to image objects well near the channel sidewalls in reflection mode, especially when the planes of focus for the particles on the top and at the corners are different. Second, the portion of PDMS beads that would move to the corners is much smaller than the one that can be focused on the top wall. Besides the trivial discrepancies, the experiments match well with our simulation results.
Microparticle acoustophoresis in wider silicon channels (width: 340 μm) has been investigated as well. According to the numerical results shown in Fig. 5, polystyrene beads are patterned at six positions inside the channel, while PDMS beads are pushed to different locations on the wall and can form roughly seven traces from the bottom view (x-y plane). These numerical results agree with the experimental observations, which show six traces for polystyrene beads and five traces for PDMS beads (the two near the sidewalls were missing due to the same reasons causing the missing traces in the smaller silicon channel). Based on the experimental and numerical results (shown in Fig. 4 and Fig. 5), we can find that the sidewalls, rather than the bottom boundary, are the main actuation boundaries. For this kind of actuation, a half-wavelength resonance can be generated. According to f=ncf/2w0, the nth resonance mode at the applied frequency of 12.883 MHz is three for the small silicon channel (width: 170 μm), and six for the wider silicon channel. Therefore, three and six pressure nodes can be formed in the narrow and wide silicon channels, respectively. The corresponding number of pressure antinodes are four and seven, respectively. These resonance modes explain the particle traces observed in experiments very well.
Fig. 5.
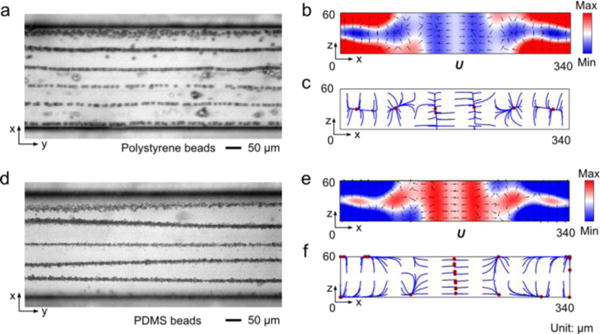
Microparticle acoustophoresis in silicon channels with a width of 340 μm. (a)–(c), Particle traces and numerical results for polystyrene beads. (d)–(f), Particle traces and numerical results for PDMS beads. (a) and (d), Experimental particle traces in the x-y plane (a: polystyrene beads; d: PDMS beads). (b) and (e), Numerical results of radiation force potential and acoustic radiation forces in the x-z plane (b: polystyrene beads; e: PDMS beads). (c) and (f), Numerical results of bead trajectories and final locations in the x-z plane (c: polystyrene beads; f: PDMS beads)
Discussion
Comparison between the 1D HSW model and the 2D SSAW microfluidic model
The 1D HSW model predicts that the pressure nodes and antinodes are evenly distributed with a distance of a half wavelength. According to the 1D HSW model, polystyrene beads move away from pressure antinodes to pressure nodes; while PDMS beads moves from pressure nodes to pressure antinodes. We found that the 1D HSW model fails to predict the particle focusing locations in PDMS-based microfluidic channels under several conditions, while our 2D SSAW microfluidic model remains effective among all examples we tested (summarized in Table 1).
In the PDMS channel with a width of 170 μm, the 1D HSW model predicts that there should be one pressure node and two pressure antinodes when the pressure node is located in the middle of the channel. As a result, the 1D HSW model predicts that polystyrene beads could leave three traces along the channel: one in the middle and two along the sidewalls; and PDMS beads were predicted to form two streamlines, each 10 μm away from the channel wall. This prediction does not match the experimental results shown in Fig. 2d. The actual traces of PDMS beads are about 40 μm away from the sidewall. When the pressure antinode is located in the middle of the channel, the number of pressure nodes and antinodes are two and one, respectively. Based on the 1D HSW model, polystyrene beads move to the pressure nodes which are 10 μm away from the sidewall. PDMS beads should be focused both at the pressure antinode in the middle and be pushed to the sidewall by the forces from the pressure nodes, locating 10 μm away the sidewall. The prediction for polystyrene beads agrees with the experimental traces shown in Fig. 2g, while the one for PDMS beads does not match the experimental results shown in Fig. 2h.
In a wider PDMS channel (in width of 340 μm) with the pressure node at its middle, the 1D HSW model predicted the formation of three pressure nodes and two pressure antinodes. It was predicted that polystyrene and PDMS beads would form three and two lines in the continuous flow inside the channel, respectively, which agrees with the experimental results shown in Fig. 3a and Fig. 3d. When the pressure antinode is located in the middle of the wider channel, the 1D HSW model predicts that two pressure nodes and three pressure antinodes (one in the middle and the other two are 20 μm away from the sidewalls) will form in the channel. The resulting number of traces for polystyrene and PDMS beads should be four (two attached on the wall because of the two pressure antinodes 20 μm away from the sidewalls) and three, respectively. The prediction for the motion of PDMS beads agrees with the experimental results shown in Fig. 3j. However, the actual motion of polystyrene beads (Fig. 3g) is far away from the prediction of the 1D HSW model. There are five lines left in the channel, including one at the middle where a pressure antinode is supposed to be. The fact that polystyrene beads are located at the pressure antinode is in direct conflict with the 1D HSW model, which states that polystyrene particles move away from the pressure antinode.
Regarding all the given results, the 1D HSW model is not reliable to predict the microparticle acoustophoresis in narrow channels made of PDMS. By contrast, our 2D SSAW microfluidic model, which is validated by the experimental results, can accurately analyse the microparticle acoustophoresis in such channels.
“Wall-effect” at channel/fluid interface
The failure of the 1D HSW model in predicting particle trajectories in the narrow (width of λ/2 and λ) PDMS channels is due to the mismatch in acoustic impedances between the fluid and the channel material. The SSAW along the bottom boundary induces longitudinal waves that propagate into the fluid in direction nearly perpendicular to the surface, and successively into the channel wall and ambient air. For fluid confined by an infinite perfectly-matched material, the acoustic pressure distribution in the direction parallel to the surface will coincide with the displacement distribution of the SSAW vibration at the bottom. The distribution of pressure nodes and antinodes can be predicted by the vibration of the SSAW, and the 1D HSW model can work well for this ideal case. However, in actual situations, the acoustic impedance of the channel material, like PDMS, does not match with that of the fluid. Acoustic reflection occurs at the PDMS/fluid interface, as well as the PDMS/air interface. These acoustic reflections can affect the acoustic field inside the fluid domain, and make the locations of pressure nodes and antinodes different from displacement nodes and antinodes on the bottom, particularly when the channel is narrow and short. The 1D HSW model is not applicable in these situations. It should be noted that the PDMS/air interface is eliminated in the model reported here. Thus, the acoustic reflection occurring at this interface is not considered. This is a simplification strategy for the purpose of modelling. A reason for this treatment is that PDMS is a viscoelastic material in which acoustic damping and acoustic attenuation is strong. We can use the idealized lossy-wall boundary condition to eliminate this effect in the model. On the other hand, the acoustic reflection that occurs at this interface can potentially affect the acoustic field in the fluid, especially when the PDMS layer is thin. This may be the reason for that some particle locations predicted by the numerical model (located at the bottom of the channel shown in Fig. 2i, Fig. 3c, and Fig. 3f) were not found in experiments.
The small contrast of acoustic impedance at the interface of channel/fluid leads to interesting phenomena of particle aggregation along the PDMS channel wall, named the “wall-effect” here. Fig. 2 and Fig. 3 demonstrated that polystyrene beads were pushed to the sidewalls for all cases due to the low acoustic impedance of PDMS comparing to that of water. The radiation force potential for polystyrene beads near the sidewalls is lower than the other regions. As a result, the acoustic radiation force acting on polystyrene beads points towards the wall for all cases. The wall-effect needs to be considered and well controlled in microparticle manipulations, such as focusing and separation, especially for manipulations of microparticles in high concentrations. However, microparticle aggregation along the sidewalls is rarely reported in SAW-driven microparticle manipulations. The reason may be that, when particle concentrations are low, or particles are initially distributed far away from the sidewalls due to inertial effect, it is possible that very few particles are located close enough to the sidewalls as the SSAW is turned on.
Hard materials (e.g., silicon), which have higher acoustic impedance than the fluid confined in the channel and induce larger contrast in acoustic impedance between channel and fluid, can be a potential material to overcome the wall-effect. Fig. 4 and Fig. 5 showed that the radiation force potential for polystyrene beads near the corners of the silicon channel is higher than the surrounding region. This is due to the strong acoustic reflection occurred there. The acoustic radiation force near the sidewalls points into the fluid domain, and expels the polystyrene beads away from the sidewall. In short, the acoustic properties of the channel material can affect the acoustic fields and microparticle acoustophoresis inside the channel. The wall-effect should not be ignored in microparticle acoustophoresis.
Conclusion
In this study, a 2D SSAW microfluidic model was established to investigate microparticle acoustophoresis in SSAW-based microfluidic devices under continuous flow. This model considered the actuation of SSAW and proper boundary conditions to mimic the acoustic propagation at the channel wall. The acoustophoretic microparticle motion in narrow channels (in width of 1/2 λ and λ) was numerically studied based on the 2D SSAW microfluidic model. Experiments were also conducted to study the acoustophoretic motion of polystyrene and PDMS beads in channels made of PDMS and silicon, respectively. By comparing the numerical and experimental results, we found that the predictions from the 2D SSAW microfluidic model agree with the experimental results well, while the typically used 1D HSW model is unable to explain all of the experimental observations. Meanwhile, the effect of channel material on the acoustic field and microparticle acoustophoresis was discussed based on the numerical and experimental results. We found that microparticles with positive acoustic contrast factor will most likely aggregate along the sidewalls of PDMS channels for all cases due to low acoustic impedance of PDMS. On the other hand, the channels made of silicon can strongly reflect impinging acoustic waves and expel the microparticles away from the sidewall. In summary, the simple, effective 2D SSAW microfluidic model presented in this article can be a powerful tool for designing and optimizing SSAW-based microfluidic devices.
Supplementary Material
Acknowledgments
This research was supported by National Institutes of Health (1 R01 GM112048-01A1 and 1R33EB019785-01), National Science Foundation (CBET-1438126 and IDBR-1455658), and the Penn State Center for Nanoscale Science (MRSEC) under grant DMR-1420620. Components of this work were conducted at the Penn State node of the NSF-funded National Nanotechnology Infrastructure Network (NNIN) and Microscopy and Cytometry Facility. The authors also acknowledge the Research Computing and Cyber infrastructure Unit of Information Technology Services at The Pennsylvania State University for providing advanced computing resources and services that have contributed to the research results reported in this paper.
References
- 1.Shi J, Huang H, Stratton Z, Huang Y, Huang TJ. Lab Chip. 2009;9:3354–3359. doi: 10.1039/b915113c. [DOI] [PubMed] [Google Scholar]
- 2.Ding X, Lin SCS, Kiraly B, Yue H, Li S, Chiang IK, Shi J, Benkovic SJ, Huang TJ. Proc Natl Acad Sci U S A. 2012;109:11105–11109. doi: 10.1073/pnas.1209288109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Petersson F, Aberg L, Swärd-Nilsson AM, Laurell T. Anal Chem. 2007;79:5117–5123. doi: 10.1021/ac070444e. [DOI] [PubMed] [Google Scholar]
- 4.Gossett DR, Weaver WM, Mach AJ, Hur SC, Tse HTK, Lee W, Amini H, Di Carlo D. Anal Bioanal Chem. 2010;397:3249–3267. doi: 10.1007/s00216-010-3721-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lenshof A, Laurell T. Chem Soc Rev. 2010;39:1203–1217. doi: 10.1039/b915999c. [DOI] [PubMed] [Google Scholar]
- 6.Friend J, Yeo LY. Rev Mod Phys. 2011;83:647–704. [Google Scholar]
- 7.Muller PB, Rossi M, Marín ÁG, Barnkob R, Augustsson P, Laurell T, Kähler CJ, Bruus H. Phys Rev E. 2013;88:023006. doi: 10.1103/PhysRevE.88.023006. [DOI] [PubMed] [Google Scholar]
- 8.Fan LL, He XK, Han Y, Du L, Zhao L, Zhe J. Biomicrofluidics. 2014;8:024108. doi: 10.1063/1.4870253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Huang PH, Nama N, Mao Z, Li P, Rufo J, Chen Y, Xie Y, Wei CH, Wang L, Huang TJ. Lab Chip. 2014;14:4319–4323. doi: 10.1039/c4lc00806e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xie Y, Ahmed D, Lapsley MI, Lin SCS, Nawaz AA, Wang L, Huang TJ. Anal Chem. 2012;84:7495–7501. doi: 10.1021/ac301590y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang PH, Xie Y, Ahmed D, Rufo J, Nama N, Chen Y, Chan CY, Huang TJ. Lab Chip. 2013;13:3847–3852. doi: 10.1039/c3lc50568e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lenshof A, Magnusson C, Laurell T. Lab Chip. 2012;12:1210–1223. doi: 10.1039/c2lc21256k. [DOI] [PubMed] [Google Scholar]
- 13.Ding X, Li P, Lin SCS, Stratton ZS, Nama N, Guo F, Slotcavage D, Mao X, Shi J, Costanzo F, Huang TJ. Lab Chip. 2013;13:3626–3649. doi: 10.1039/c3lc50361e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ai Y, Sanders CK, Marrone BL. Anal Chem. 2013;85:9126–9134. doi: 10.1021/ac4017715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guldiken R, Jo MC, Gallant ND, Demirci U, Zhe J. Sensors (Basel) 2012;12:905–922. doi: 10.3390/s120100905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jo MC, Guldiken R. Sensors Actuators A Phys. 2012;187:22–28. [Google Scholar]
- 17.Nam J, Lee Y, Shin S. Microfluid Nanofluidics. 2011;11:317–326. [Google Scholar]
- 18.Nam J, Lim H, Kim D, Shin S. Lab Chip. 2011;11:3361–3364. doi: 10.1039/c1lc20346k. [DOI] [PubMed] [Google Scholar]
- 19.Li P, Mao Z, Peng Z, Zhou L, Chen Y, Huang PH, Truica CI, Drabick JJ, El-Deiry WS, Dao M, Suresh S, Huang TJ. Proc Natl Acad Sci U S A. 2015;112:4970–4975. doi: 10.1073/pnas.1504484112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shi J, Mao X, Ahmed D, Colletti A, Huang TJ. Lab Chip. 2008;8:221–223. doi: 10.1039/b716321e. [DOI] [PubMed] [Google Scholar]
- 21.Ding X, Lin SCS, Lapsley MI, Li S, Guo X, Chan CY, Chiang IK, Wang L, McCoy JP, Huang TJ. Lab Chip. 2012;12:4228–4231. doi: 10.1039/c2lc40751e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li S, Ding X, Guo F, Chen Y, Lapsley MI, Lin SCS, Wang L, McCoy JP, Cameron CE, Huang TJ. Anal Chem. 2013;85:5468–5474. doi: 10.1021/ac400548d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guo F, Zhou W, Li P, Mao Z, Yennawar NH, French JB, Huang TJ. Small. 2015;11:2733–2737. doi: 10.1002/smll.201403262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shi J, Ahmed D, Mao X, Lin SCS, Lawit A, Huang TJ. Lab Chip. 2009;9:2890–2895. doi: 10.1039/b910595f. [DOI] [PubMed] [Google Scholar]
- 25.Guo F, Li P, French JB, Mao Z, Zhao H, Li S, Nama N, Fick JR, Benkovic SJ, Huang TJ. Proc Natl Acad Sci U S A. 2015;112:43–48. doi: 10.1073/pnas.1422068112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li S, Guo F, Chen Y, Ding X, Li P, Wang L, Cameron CE, Huang TJ. Anal Chem. 2014;86:9853–9859. doi: 10.1021/ac502453z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wood CD, Evans SD, Cunningham JE, O’Rorke R, Wälti C, Davies AG. Appl Phys Lett. 2008;92:044104. [Google Scholar]
- 28.Chen Y, Li P, Huang PH, Xie Y, Mai JD, Wang L, Nguyen NT, Huang TJ. Lab Chip. 2014;14:626–645. doi: 10.1039/c3lc90136j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chen Y, Li S, Gu Y, Li P, Ding X, Wang L, McCoy JP, Levine SJ, Huang TJ. Lab Chip. 2014;14:924–930. doi: 10.1039/c3lc51001h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yeo LY, Friend JR. Biomicrofluidics. 2009;3:12002. doi: 10.1063/1.3056040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nam J, Lim H, Kim C, Yoon Kang J, Shin S. Biomicrofluidics. 2012;6:24120–2412010. doi: 10.1063/1.4718719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tran SBQ, Marmottant P, Thibault P. Appl Phys Lett. 2012;101:114103. [Google Scholar]
- 33.Bruus H. Lab Chip. 2012;12:1014–1021. doi: 10.1039/c2lc21068a. [DOI] [PubMed] [Google Scholar]
- 34.Muller PB, Barnkob R, Jensen MJH, Bruus H. Lab Chip. 2012;12:4617–4627. doi: 10.1039/c2lc40612h. [DOI] [PubMed] [Google Scholar]
- 35.Muller PB, Bruus H. Procedia IUTAM. 2014;10:410–415. [Google Scholar]
- 36.Barnkob R, Augustsson P, Laurell T, Bruus H. Phys Rev E. 2012;86:056307. doi: 10.1103/PhysRevE.86.056307. [DOI] [PubMed] [Google Scholar]
- 37.Settnes M, Bruus H. Phys Rev E. 2012;85:016327. doi: 10.1103/PhysRevE.85.016327. [DOI] [PubMed] [Google Scholar]
- 38.Muller PB, Bruus H. Phys Rev E. 2014;90:043016. doi: 10.1103/PhysRevE.90.043016. [DOI] [PubMed] [Google Scholar]
- 39.Shilton R, Tan MK, Yeo LY, Friend JR. J Appl Phys. 2008;104:014910. [Google Scholar]
- 40.Alghane M, Chen BX, Fu YQ, Li Y, Desmulliez MPY, Mohammed MI, Walton AJ. Phys Rev E. 2012;86:056304. doi: 10.1103/PhysRevE.86.056304. [DOI] [PubMed] [Google Scholar]
- 41.Nyborg WL. Acoustic streaming. Academic Press; New York: 1965. [Google Scholar]
- 42.Bruus H. Lab Chip. 2012;12:20–28. doi: 10.1039/c1lc20770a. [DOI] [PubMed] [Google Scholar]
- 43.Friend J, Yeo LY. Rev Mod Phys. 2011;83:647–704. [Google Scholar]
- 44.Nama N, Barnkob R, Mao Z, Kähler CJ, Costanzo F, Huang TJ. Lab Chip. 2015;15:2700–2709. doi: 10.1039/c5lc00231a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Viktorov AI. Rayleigh and Lamb Waves Physical Theory and Applications. Plenum press; New York: 1967. [Google Scholar]
- 46.Gorkov LP. Sov Physics-Doklady. 1962;6:773–775. [Google Scholar]
- 47.Langelier SM, Yeo LY, Friend J. Lab Chip. 2012;12:2970–2976. doi: 10.1039/c2lc40085e. [DOI] [PubMed] [Google Scholar]
- 48.Johnson LM, Gao L, Shields CW, IV, Smith M, Efimenko K, Cushing K, Genzer J, López GP. J Nanobiotechnology. 2013;11:22. doi: 10.1186/1477-3155-11-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


