The Sensitivity of Non-Uniform Sampling NMR

Abstract

Many information rich multi-dimensional experiments in nuclear magnetic resonance spectroscopy can benefit from a signal-to-noise ratio (SNR) enhancement up to about two-fold if a decaying signal in an indirect dimension is sampled with nonconsecutive increments, termed non-uniform sampling (NUS). This work provides formal theoretical results and applications to resolve major questions on the scope of the NUS enhancement. First, we introduce the NUS Sensitivity Theorem, that any decreasing sampling density applied to any exponentially decaying signal always results in higher sensitivity (SNR per square root of measurement time) than uniform sampling (US). Several cases will illustrate this theorem, and show that even conservative applications of NUS improve sensitivity by useful amounts. Next, we turn to a serious limitation of uniform sampling: the SNR by US decreases for extending evolution times, and thus total experimental times, beyond 1.26 T₂ (T₂ = signal decay constant). Thus SNR and resolution cannot be simultaneously improved by extending US beyond 1.26 T₂. We find that NUS can eliminate this constraint, and introduce the Matched NUS SNR Theorem: an exponential sampling density matched to the signal decay always improves the SNR with additional evolution time. Though proved for a specific case, broader classes of NUS densities also improve SNR with evolution time. Applications of these theoretical results are given for a soluble plant natural product and a solid tripeptide (u-¹³C,¹⁵N-MLF). These formal results clearly demonstrate the inadequacies of applying US to decaying signals in indirect nD-NMR dimensions, supporting broader adoption of NUS.

Graphical Abstract

Introduction

A growing practice for acquiring data in indirect evolution periods in NMR spectroscopy is non-uniform sampling (NUS), which often means acquiring data points (samples) in the time domain in non-consecutive time increments.^1,2 Traditionally, indirect evolution periods are recorded with equally spaced time increments, termed uniform sampling (US). Uniform sampling is paired with the Fourier Transform to obtain frequency domain signals, whereas NUS data can be treated with a number of robust non-Fourier algorithms for estimating frequency spectra.³ Given that resolution is inversely proportional to evolution time, achieving long evolution times beyond T₂ is desirable in many applications of nD-NMR. Each sample in the indirect time dimension of nD-NMR is a specific time increment that is acquired as a one-dimensional (1D) experiment, with a certain number of transients for coherence selection. Uniform sampling must employ many incremented 1D-NMR experiments to reach evolution times that achieve needed resolution along the indirectly detected frequency axes. When recording decaying signals by US, it is a concern that long experiment times are devoted to samples that negligibly add to the signal-to-noise ratio (T₂ < t < 1.26 T₂) or which decrease SNR (t > 1.26 T₂).^4–6 In these cases, SNR is harmed by US in order to achieve resolution. For this reason, certain nD-NMR spectra may be out of reach for mass-restricted samples such as natural products and biosolids.^7,8 Improved signal-to-noise ratios in NMR spectra have been achieved through cryogenic probe circuitry, micro-coil probe heads, and dynamic nuclear polarization, but the fundamental SNR limitations on uniform sampling remain.

Sculpting the acquisition to the signal envelope improves signal levels relative to noise.^1,9–11 Weighted non-uniform sampling (NUS) is the practice of acquiring a signal in proportion to its envelope (i.e. more data obtained where the signal is stronger) and yields SNR enhancements versus uniform sampling (US) for decaying signals.^1,7,12,13 Here, non-uniform sampling is implemented by choosing a weighting function to predetermine a list of samples (a sampling schedule) selected from the uniform grid, acquiring the same number of transients per sample, and specifying more samples where the signal has its highest intensity.¹ The SNR enhancement obtained by NUS is analytically solved and under user control,^7,12 although current NMR data acquisition software does not include facilities to compute this enhancement. Briefly, the NUS-based enhancement for sampling decaying signals can be understood in two parts. First, NUS eliminates many samples from evolution times after 1.26 T₂, where T₂ is the signal decay constant. Since all samples after 1.26 T₂ decrease the SNR of the raw data,⁶ the SNR is improved when samples after 1.26 T₂ are eliminated. Second, the experimental time saved by not acquiring certain samples is used to acquire more transients across the weighted sampling schedule. In this report, NUS means the samples are selected from the Nyquist grid and are each acquired with the same number of transients, but NUS has been further generalized with respect to sample phases,¹⁴ while a strategy of acquiring different numbers of transients on the uniform grid¹⁰ has been revisited.^15,16

Uniform sampling is governed by the Nyquist Theorem, which guarantees that signals in a certain frequency window will be correctly detected for a corresponding time interval between the acquired samples. Further, when US is paired with the Fourier transform, Parseval’s Theorem guarantees that the frequency and time domain data have equal power or, stated informally, that the frequency domain signal produced by the FFT is a lossless representation of the uniformly acquired time domain data. Even as NUS is seeing wider adoption for acquiring the indirect dimensions of nD-NMR spectra, there is less theoretical support for the performance of nD-NMR by NUS compared to the formal results on US FT-NMR.

Bandwidth^17,18 and power^19–21 have been described previously for NUS. The frequency bandwidth of NUS is complicated and is not governed by Nyquist, but a great deal is known about the relative advantages of choosing the non-uniform points off the Nyquist grid¹⁷ or on the Nyquist grid.¹⁸ In either case, the concern is to minimize aliasing effects within the spectral window. These aliasing effects are reduced whenever the greatest common divisor (GCD) of the sample intervals is also reduced. For off-grid NUS, there is the possibility to dramatically increase the bandwidth if the precision of the sample times is very small.¹⁷ However on-grid NUS is a much more widespread practice, where the GCD is usually just the inverse of the Nyquist frequency, meaning that the Nyquist frequency is treated as an upper bound on the NUS bandwidth. It has been demonstrated for on-grid NUS that when the NUS schedules are not too sparse, but instead contain several dense tracts, then NUS yields a bandwidth closely approximated by Nyquist, and better bandwidth is obtained by choosing the NUS schedule from an oversampled Nyquist grid.¹⁸

Also, linearity has been investigated for some reconstruction algorithms including maximum entropy reconstruction (MaxEnt). For example a maximum entropy interpolation regime (MINT) shows high linearity,⁷ while MaxEnt is extremely useful in the non-linear regime.^19,22 Specifically, the MINT regime is useful when amplitudes need to be quantified or line shapes preserved, whereas the Bayesian regime where MaxEnt is non-linear is statistically robust. Whereas the bandwidth of NUS appears to depend most strongly on the choice of samples, the degree of linearity obtained by NUS is seen to depend on both the sampling schedule and the method of spectral estimation, suggesting that it may be difficult to characterize power conservation based only on the NUS schedule alone. Although NUS-MaxEnt is employed here, there are a number of non-traditional approaches to nD-NMR and subsequent spectral estimation, which are recently reviewed.²³ A few highlights of recent developments include time resolved nD-NMR using NUS combined with multi-way decomposition,²⁴ and new efficient algorithms for l1-norm regularization.²⁵ In addition, compressed sensing,^26,27 and soft thresholding,^28,29 are finding wider use in biomolecular applications, while unsymmetrical covariance has shown high promise in unraveling natural products spectra.^30,31

This report characterizes the signal-to-noise ratio (SNR) in the time domain, a strategy which has been shown to have high utility because it avoids the problems attending nonlinearity of most non-Fourier methods for estimating the spectrum.^4,6 Time domain calculations assuming continuous functions for the signal and sampling density are convenient for describing NUS. In general, a great deal of time domain analytic results can be obtained with formal theory.^4,6 Specifically, it has been shown for time-domain NUS SNR calculations that theoretical predictions based on continuous functions correspond well to calculations and experiments using discrete NUS schedules, as long as the discrete NUS schedule follows its prescribed density reasonably closely.¹² Additionally, the time domain SNR describes fundamental properties of the non-uniform samples themselves, prior to and independent of any and all subsequent data manipulations and transforms. Indeed, it is useful from this point on to distinguish the signal-to-noise ratio of the raw data prior to post-acquisition manipulations as the intrinsic SNR, or iSNR.³² Any improvement in the iSNR of the acquired time domain data is then available to subsequent spectral reconstruction techniques, regardless of whether they are linear or not. Since a variety of computational techniques can be used to increase the apparent SNR starting from the iSNR, we recognize that the iSNR is a fundamental constraint on detecting a peak, and thus a peak is intrinsically more detectable if its iSNR is improved. The importance of improving iSNR is embodied in hardware advances such as DNP and cryogenically cooled probes whose sole effect is to improve the iSNR of the time domain data, which of course lead to improved peak detection. Non-uniform sampling a decaying signal following a weighting function increases the iSNR, and the NUS iSNR enhancements that have been measured using a linear transform, maximum entropy interpolation, agree closely with theoretical predictions of NUS iSNR enhancements in the time domain.⁷

We report here two theorems that govern the iSNR of non-uniform sampling applied to decaying signals. First, it is shown that NUS always has greater iSNR than US in the same experimental time, and thus greater sensitivity, when using any decreasing NUS density. This is a very broad rule, which we term the NUS Sensitivity Theorem. Next, we address a question that has been overlooked to date: given that uniform sampling has an iSNR maximum at an evolution time of about 1.26 T₂,^4,6 are there similar maxima for NUS that could guide experimentalists in designing NUS experiments? A perhaps surprising finding follows: we prove in a second theorem that, for matched exponential NUS, the iSNR is always increasing with evolution time and has no maximum. Although proved for the narrow case of matched exponential NUS, we employ a simple graphical strategy to verify that many useful NUS densities have this property of a positive iSNR slope at all evolution times. We term this second result the Matched NUS SNR Theorem; it has a remarkable interpretation: given that increasing evolution time increases the ability to resolve signals, any NUS density with increasing iSNR at all times has the distinction of simultaneously increasing iSNR and resolution with additional evolution time, a statement that is not true for uniform sampling. With these stronger theoretical insights on the fundamental properties of raw NUS data, wider adoption of weighted NUS for detecting decaying signals in indirect dimensions of nD-NMR is merited.

Theoretical Results

(i) Theorems for the Sensitivity and SNR of Non-Uniform Sampling

As noted above, the intrinsic SNR (iSNR) of the raw data prior to post-acquisition manipulations is distinguished from the apparent SNR of data following manipulations such as apodization, linear prediction, etc.³² Once the receiver is turned off, the iSNR is fixed. Although spectra can be produced with apparent SNR greater than the iSNR, the apparent SNR is constrained by the original signal. If a power conserving transform, such as the Fourier transform, is used as the sole post-acquisition operation on the data, then the iSNR is equal in the time and frequency domains. The SNR of non-Fourier reconstructed spectra may not be a valid metric,³³ but the time domain iSNR is (i) a processing-independent metric of signal strength relative to noise, and (ii) not subject to folding artifacts, which are viewed as sampling noise.^18,34 We will see shortly that iSNR is also independent of the implementation of NUS, so that it is a general metric for describing NUS. The method of spectrum analysis used to convert time-domain data into frequency-domain spectra also impacts the sensitivity, and with the emergence and importance of nonlinear non-Fourier methods for dealing with NUS data, this is a nontrivial problem. Focusing on iSNR allows us to isolate these impacts from the impact of the amount of signal captured by a sampling strategy. This report analyzes and compares solely the iSNR of uniform and non-uniform sampling, but some results here could apply also to the apparent SNR.

An exponentially decaying signal with an arbitrary positive T₂ value is assumed in all further analysis. It is convenient to take the signal to be at zero frequency so that it is described only by its decay, S(t) = e^−t/T₂ = e^−tR₂, where R₂ =1/T₂, and normally one considers the net decay T₂*. The time domain iSNR is the ratio of the integral of the signal envelope to the square root of the signal evolution time.^4,6,22,35 For US, the dependence of the iSNR on evolution time is^4,6

$$i\text{SNR}(t)\propto \frac{1-e^{-t{R}_2}}{R_2\sqrt{t}}.$$ (1)

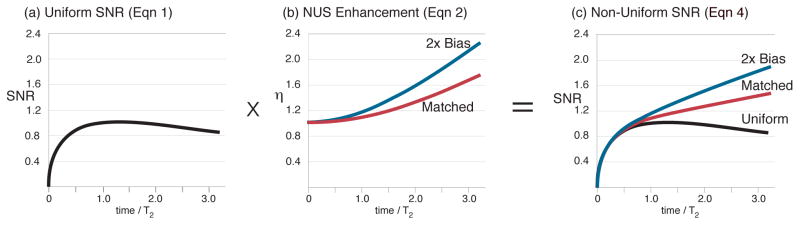
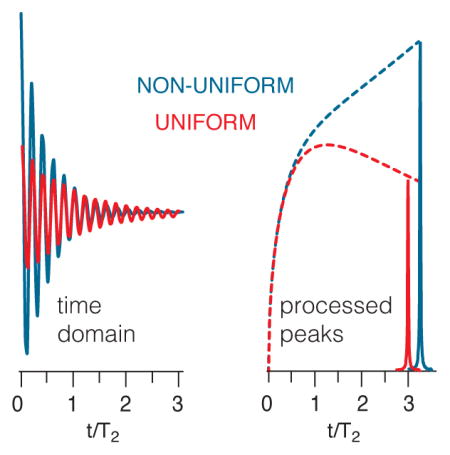
For a power conserving transform such as the Fourier transform, the definition of SNR in the time domain is equivalent to the familiar definition of SNR in the frequency domain as the ratio of the peak height, S(ω), to the rms noise. Briefly, the square root of the signal evolution time is proportional to the rms noise in the frequency domain, and the integral of the signal envelope is the peak height when employing the power conserving Fourier transform.^4,6 Recalling that sensitivity is the SNR per square root of experimental time,³⁶ the terms SNR and sensitivity are interchangeable when comparing experiments that consume equal times. Equation (1) has several implications for uniform sampling.^1,4 The maximum SNR occurs for t_max ~ 1.26 T₂ (Figure 1A), which falls short of the ~3T₂ evolution time needed to obtain optimal resolution (Figure S.1 and citations therein). Thus, US can improve either SNR (t < 1.26 T₂) or resolution (t~3 T₂), each at the expense of the other.

Figure 1.

(a–b) Deriving the iSNR of matched and 2X-biased exponential NUS per Eqs. 1–4. (c) The iSNR increases monotonically, has no maximum, and is always greater than US. Figures scaled so US to 1.26 T₂ has iSNR=1.

Some further notation follows next. Non-uniform sampling an exponentially decaying signal using an exponential density of samples will be termed exponential NUS. Matched exponential NUS means the decay constant of the NUS probability density (T_SMP) equals that of the signal (T₂). Biased NUS takes more samples at early signal evolution times than matched NUS, meaning T_SMP < T₂ in the case of exponential NUS. Exponential and Gaussian sampling densities are straightforward to modify for biased NUS. For example, we often treat the case of a sampling density with a decay rate that is twice that of matched NUS, and call this case two-fold biased NUS (Figure 1bc). Next we briefly review prior results (Eqs. 1–6).

Non-uniform samples are chosen according to a probability density, h(t), a function which prescribes the likelihood that a sample will be recorded at a given evolution time, t. To guarantee that uniform and non-uniform sampling consume identical experimental times, their sampling densities must have equal areas. Setting uniform sampling to have a constant probability density of 1, and letting h(t) be the NUS density, then¹²

$$\chi \left(t_{max}\right)=\frac{t_{max}}{{\int }_0^{t_{max}}h(t)dt}$$ (2)

is the scaling factor which guarantees that NUS and US use equal total experiment times. For matched exponential NUS,

$${\chi }_{\text{match-exp}}=\frac{{\alpha }_{max}}{1-e^{-{\alpha }_{max}}},$$ (3)

where the total signal evolution t_max can be parameterized as α_max = t_max/T₂. Taking S(t) = e^−t/T₂ as the signal envelope, the uniform signal is scaled by unity, while the NUS signal is χh(t)S(t). In other words, χ describes a simple experimental protocol in NUS which can be illustrated by example: suppose a uniform acquisition employs 2 transients for each of 512 incremented evolution times; then a NUS schedule which selects one quarter of these would employ 8 transients for each of the 128 samples selected from the original Nyquist grid.

Notice that these and all subsequent results depend only on the probability density h(t), regardless of how the experimenter implements h(t). The sampling density h(t) could be realized by different numbers of transients on a uniform grid, by selecting samples non-uniformly from a uniform grid or off-grid, by random phase methods, and by a combination of these approaches. Consider also that different randomly generated lists of samples could all closely conform to a given h(t). In other words, all of the results in this manuscript for the iSNR are sampling-independent, meaning they apply to any method of acquiring data following a weighting function h(t).

If NUS and US acquisitions use the same experimental time, they must employ the same number of transients and therefore have the same noise, which means that it is only necessary to compare the amount of signal recorded by NUS and US to determine iSNR enhancements. The NUS-based iSNR enhancement is obtained as the ratio of the non-uniform and uniform signal areas,

$$\eta =\frac{\chi \left(t_{max}\right){\int }_0^{t_{max}}h(t)e^{-t/T_2}dt}{T_2\left(1-e^{-\alpha }\right)}=\frac{\alpha }{\left(1-e^{-\alpha }\right)}\frac{{\int }_0^{t_{max}}h(t)e^{-t/T_2}dt}{{\int }_0^{t_{max}}h(t)dt},$$ (4)

which is general for any sampling density h(t).⁷ For exponential NUS, equation (4) becomes

$${\eta }_{exp}=\frac{\chi \left(1-e^{-\alpha ((T_2/T_{\mathit{SMP}})+1)}\right)}{\left(T_2/T_{\mathit{SMP}}+1\right)\left(1-e^{-\alpha }\right)}.$$ (5)

For matched exponential NUS, the enhancement is

$${\eta }_{\text{match-exp}}=\frac{\chi \left(1-e^{-2\alpha }\right)}{2\left(1-e^{-\alpha }\right)}=\frac{\alpha }{2}\frac{\left(1+e^{-\alpha }\right)}{\left(1-e^{-\alpha }\right)}.$$ (6)

The iSNR enhancements (η) for matched and two-fold biased exponential NUS relative to uniform sampling in the same total experimental time are illustrated in Figure 1b, and can approach or slightly exceed a factor of two, respectively.¹² Theory and linear reconstructions of experimental NUS data show close agreement, and also that improving the iSNR by NUS enables detecting new peaks.^7,12,37 Further, applying NUS in multiple indirect dimensions compounds the iSNR enhancements up to about four-fold.^7,37 The key conditions for realizing an NUS-based iSNR enhancement are that the signal must have a decreasing amplitude envelope, and the NUS must follow a probability density that favors the signal envelope. It is not possible to obtain NUS-based iSNR enhancements for constant-time evolution periods or by random (i.e. unweighted) sampling.¹²

Equations 1–6 have been reported,^12,20 and visual inspection suggests that the enhancement for matched exponential NUS represented in Figure 1b appears to always be greater than one. Could NUS ever decrease the iSNR relative to US in the same time? This question can be answered very generally, that a NUS-based iSNR enhancement is always greater than one for any non-constant sampling density applied to any exponentially decaying signal (Appendix A1). A function h(t) defined on an interval is called nonincreasing if h(t₁) ≥ h(t₂) for any points t₁ < t₂ in the interval.

Theorem I (NUS Sensitivity Theorem). Assume h(t) is a positive, nonincreasing function on some interval 0 ≤ t < A, where A ≤ ∞. For any positive T₂ and 0 < t_max < A, the time domain iSNR enhancement (Eq. 4) satisfies

$$\eta =\frac{\alpha }{\left(1-e^{-\alpha }\right)}\frac{{\int }_0^{t_{max}}h(t)e^{-t/T_2}dt}{{\int }_0^{t_{max}}h(t)dt}\ge 1,$$ (A1)

where α = t_max/T₂, and equality holds if and only if h(t) is constant for 0 < t < t_max.

Since Theorem 1 treats the iSNR of NUS and uniform experiments using equal experimental times, it therefore assures that the use of any decreasing sampling density results in greater sensitivity than uniform sampling. As one practical example, it can be appreciated from Figure 1b that the sensitivity advantage for exponential NUS is negligible for short evolution times but is nontrivial for times beyond T₂, which will be seen to be a theme for other NUS densities as well. The enhancements for several other sampling densities will be computed in the next section to demonstrate the broad applicability of Theorem 1 to a variety of decreasing sampling densities.

Theorem 1 applies to both continuous and discontinuous NUS densities such as step functions, which have been used to good effect in prior work.⁷ Notice also that Theorem 1 establishes that equal sensitivity for US and NUS holds only if the NUS density is constant, which would be the case for a random non-uniform sampling density. A special case of constant sampling density is a comparison of 2D-HSQC spectra obtained with different spectral windows, for which iSNR is not changed. (Figure S.1,¹²).

Another key question has yet to be considered: how does the iSNR of NUS depend on the evolution time? In other words, by analogy to the 1.26 T₂ iSNR maximum for uniform sampling, is there also an iSNR maximum in the time evolution of NUS? To learn the iSNR of exponential NUS (Figure 1c), the iSNR of uniform sampling (Eq. 1, Figure 1a) is scaled by the NUS-based enhancement (Eq. 5, Figure 1b), giving

$$i{\text{SNR}}_{exp}\propto \frac{T_2\sqrt{t}}{(T_2+T_{\text{SMP}})}\frac{(1-e^{-\alpha ((T_2/T_{\text{SMP}})+1)})}{(1-e^{-\alpha T_2/T_{\text{SMP}}})}.$$ (7a)

For matched NUS, T₂=T_SMP, a simpler form emerges:

$$i{\text{SNR}}_{\text{match-exp}}\propto \frac{(1+e^{-\alpha })\sqrt{t}}{2}.$$ (7b)

Inspection of Figure 1c suggests that the iSNR by NUS is always increasing with evolution time; in other words there appears to be no time that gives a maximum iSNR in matched or biased (e.g. T₂/T_SMP = 2) NUS. Confirming our visual inspection of the NUS curves in Figure 1c, it can be proved that Equation (7b) is always increasing with evolution time (Appendix A2):

Theorem 2 (Matched NUS SNR Theorem): The iSNR of matched exponential NUS (Equation 7b) always has a positive slope for an arbitrary, positive T₂ and positive evolution time t_max.

Although Theorem 2 is proved for the case of matched exponential NUS, it is appreciated by inspection of Figure 1c for example, that any biased (T_SMP < T₂) exponential NUS density also has the property of a positive iSNR slope for all times. Specifically, it will be shown empirically that the iSNR has a positive slope at all times for exponential densities for which T_SMP/T₂ > 1.35, encompassing a broad class of useful NUS densities. Some decreasing NUS densities do not improve iSNR slope for all times, so Theorem 2 may not be stated for all decreasing NUS densities. Analytic expressions for the iSNR of several other NUS densities will be given and evaluated visually to verify that the conclusions of Theorem 2 do hold for other large classes of useful sampling densities. Since uniform sampling has a decreasing iSNR beyond 1.26 T₂, Theorem 2 is certainly not true for uniform sampling. An important restatement of Theorem 2 is possible,

Matched exponential NUS simultaneously improves resolution and iSNR if increased experimental time is used to span longer evolution times of a decaying signal.

Acquiring samples at longer evolution times non-uniformly will introduce more constraints on distinguishing closely spaced signals and will improve resolution.³² While resolution is inversely proportional to evolution time for US, there is not an analytic rule to describe by how much the resolution improves with NUS evolution time. Empirically, matched NUS has been shown to yield resolution comparable to uniform sampling when they span the same evolution period and when the degree of data reduction is on the order of a third to a fourth of the US samples.^7,12,32 On the other hand, strongly biased NUS (e.g.T₂/T_SMP ≥2), does not yield the same resolution as uniform sampling over the same evolution time and the increase in signal resolution with evolution time by biased NUS is complex and needs more investigation.^7,8,32

Theorem 2 can only be stated with respect to the iSNR. Sensitivity does not have a positive slope with evolution time by NUS or US. Recall that sensitivity is SNR per square root of experimental time. Evolution time is directly proportional to experimental time, so that the intrinsic sensitivity of NUS is obtained by dividing equation 7b by the square root of time, giving

$${\text{Sensitivity}}_{\text{match-exp}}\propto (1+e^{-\alpha }),$$ (7c)

where the factor of 2 is dropped since this is already a proportionality, and it is seen that equation 7c is clearly a decreasing function with evolution time. Sensitivity also decreases with evolution time for US (equation 1 divided by the square root of time),

$${\text{Sensitivity}}_{\text{uniform}}\propto \frac{1}{t}(1-e^{-\alpha }),$$ (8)

where it can be recognized that sensitivity by matched exponential NUS decreases at a slower rate than the decrease in sensitivity by uniform sampling.

In principle, the signal is continuously sampled following the NUS probability density, however signals are sampled discretely, and an NUS schedule is a list of the time domain samples in which more are acquired where the probability density is greater. The close correspondence between discrete and continuous treatments is further demonstrated by sensitivity results reported using discrete treatments which include confirming well known results such as the 1.26 T₂ limit.³⁸ Prior work has shown that the degree to which a discrete NUS schedule conforms to the desired density influences if the theoretical NUS enhancement is realized, that significant iSNR enhancements are obtained even when NUS schedules follow an exponential sampling density coarsely, and that typical and conservative applications of NUS closely approach the theoretical predictions for the iSNR enhancement.^7,12 In other words, the properties of Theorem 2 therefore apply to diverse discrete implementations of NUS.

It is technically correct that, as illustrated in Figure 1c, an arbitrary iSNR improvement by NUS versus US occurs for evolution times beyond πT₂, but two cases need to be clarified. First, if all signals have similar relaxation rates, the high NUS enhancements for t_max≫πT₂ derive from eliminating samples containing only noise (>πT₂) and replacing them with samples containing signal (<πT₂), an unfair comparison to US. When T₂ values are uniform, sampling beyond πT₂ by US or NUS is not justified. A second case is if signals have a distribution of T₂ values. Then an exponential NUS density at the average of the T₂ values causes the enhancements of the faster and slower decaying signals to be closer to the enhancement for the T_2,avg value. For example, large enhancements are not realized for faster decaying signals (t_max≫πT_2,fast,) since the NUS density favors the slower T_2,avg. When T₂ varies over an order of magnitude, a narrow range of enhancements is observed.³⁹

We tested Eqs. 7a–7b by performing simulations in which a noise FID received injected signals corresponding to non-uniformly distributed transients on a uniform grid, having the same sampling density as NUS,¹⁰ but treatable by the power-conserving fast-Fourier transform (FFT). The FFT of matched (Eq. 7b) and two-fold biased (Eq. 7a) exponential sampling confirms theoretically predicted NUS signal intensities.(Figure 2). Again, equations 7a–b and Figure 2 are presented so that increasing evolution time entails greater overall experimental time. Taking an experiment from 1T₂ to 3T₂ will significantly improve resolution but will also require threefold more experiment time, which would harm iSNR by US, but is seen to increase iSNR by NUS. The strong positive slope of the NUS iSNR peak intensities in Figure 2 confirms Theorem 2.

Figure 2.

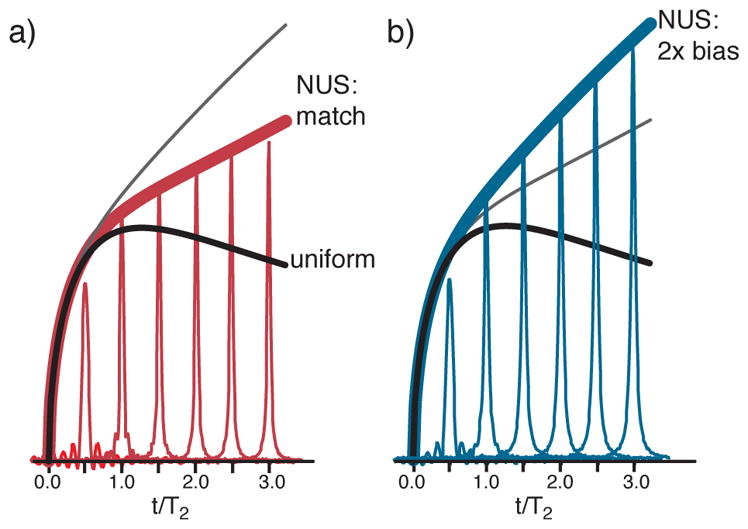
The iSNR of exponential NUS (Eqs. 4–7, Figure 1c) is tested by applying the FFT to a synthetic signal that has non-uniform intensity on the uniform grid injected in to a real noise FID¹: the resulting peaks are shown for (a) matched (red) NUS and (b) two-fold biased (blue) NUS. These simulated peaks are superimposed on the solid lines that illustrate the formal theoretical predictions given by Eq. 7a for matched(red) and two-fold biased (blue) NUS. The black line corresponds to the iSNR of US (Eq. 1).

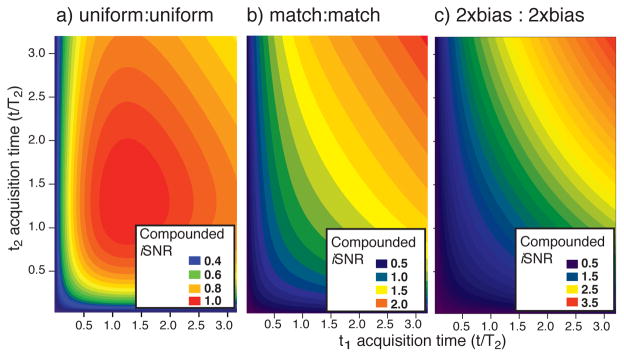
For further experimental confirmation, recently reported data³² also provide an example of how NUS iSNR enhancements are governed by Eqs. 7ab, included here in the supporting information (Figure S2). Compounding the NUS-based iSNR enhancement (equation 5) in multiple dimensions yields enhancements on the order of three- to fourfold, which was experimentally observed in biosolids applications.⁷ By analogy, the direct calculation of iSNR in Eqn. 7a can be compounded for two NUS dimensions (Figure 3), to help illustrate how iSNR depends on time in two indirect evolution periods. First, recall that the highest obtainable iSNR by US is achieved if each evolution period is sampled to 1.26 T₂ and that iSNR by US decreases for longer evolution times (e.g. the US curve in Figure 2). Thus, when employing US in two indirect evolution periods, the iSNR after 1.3T₂ now decreases at a compounded rate (Figure 3a, obtained compounding the US curve in Figure 2). In contrast, iSNR by NUS increases at a compounded rate for longer evolution times in multiple dimensions (Figure 3bc).

Figure 3.

Representative contour plots delineate the achievable iSNR in nD-NMR when (a) US is applied in each of two indirect dimensions and (b–c) NUS is applied in each of two indirect dimensions as a function of acquisition time. Notice the rather steeply decreasing iSNR when both indirect dimensions are sampled by US. In contrast panel (b) shows the iSNR when a matched exponential sampling bias is applied in each indirect dimension, and panel (c) shows the iSNR for employing 2x exponentially biased NUS in each indirect dimension. Values are scaled such that uniform acquisition to 1.26 T₂ in both indirect dimensions has a iSNR of 1.

Finally, it should be stressed that Theorems 1 and 2 apply equally to on-grid NUS, non-uniform transients on the uniform grid (eg Figure 2),^10,15,16 off-grid NUS, hypercomplex NUS,¹⁴ and other implementations that may yet arise.

(ii) Analyses of other Sampling Densities

A survey of the iSNR performance of several NUS densities follows, placing each in context with Theorems 1 and 2. These are sinusoidal, Gaussian, linear and cosine weighted NUS. Graphical inspection is particularly useful in recognizing how the properties of these NUS densities relate to Theorems 1 and 2.

Sinusoidal NUS Density

The portion of the sine between π and 3π/2 has recently been investigated as an alternative to the matched exponential NUS density, where it was found to have a nearly identical iSNR enhancement to that of matched exponential NUS, while also yielding improved constraints on line shapes.³² The iSNR of this sinusoid will be analyzed by equations 2, and 4. The sampling density prior to normalizing its area versus uniform sampling is

$$h(\text{sinusoid},t)=1-sin\left(\frac{t}{\pi T_2}\frac{\pi }{2}\right)=1-sin\left(\frac{t}{2T_2}\right),$$ (8a)

which spans an acquisition time of πT₂. Equation 2 is employed to find the scaling factor that normalizes the sinusoidal density to have the same area as the uniform density,

$$\chi (\text{sine})=\frac{t_{max}}{{\int }_0^{t_{max}}(1-sin(\frac{t}{2T_2}))dt}=\frac{\alpha }{\alpha +2[cos(\frac{\alpha }{2})-1]},$$ (8b)

where α = t_max/T₂, and the resulting density is illustrated in Figure 4a. Now the iSNR enhancement for sinusoidal NUS is determined,

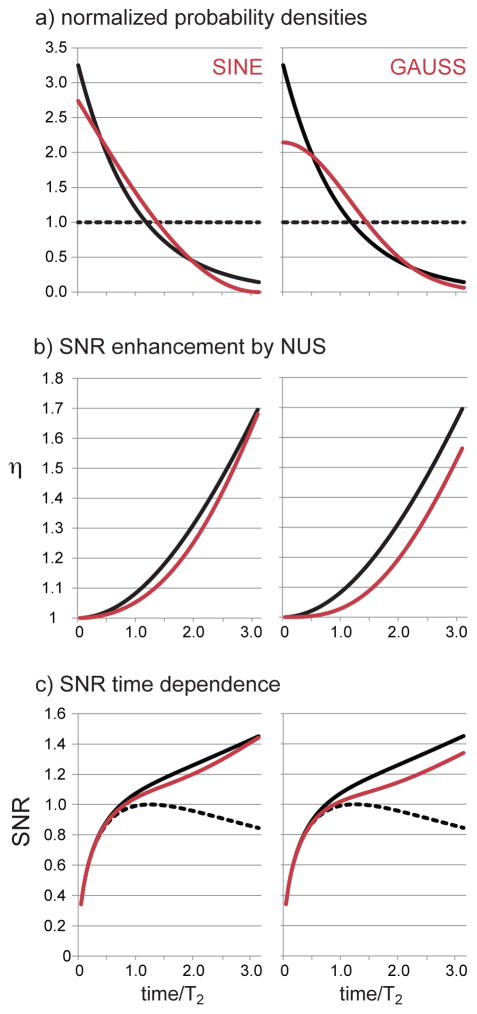
Figure 4.

NUS probability densities following a sinusoid and a Gaussian are analyzed following the same procedure as illustrated for exponential sampling in Figure 1. In all panels, the behavior of matched exponential NUS is given by the solid black line for comparison, while uniform sampling is described by the dashed black line. In (a) the sinusoid and matched exponential densities have been normalized to have the same area as uniform sampling; the value of χ is given by equation 8b or 9b. In (b) the iSNR NUS enhancements over US given by equations 8c or 9c are illustrated. In (c) the direct iSNR is obtained by multiplying the enhancement in equation 8c (sinusoid) or 9c (Gaussian) by the iSNR of uniform sampling in equation 1.

$$\eta (\text{sine})=\frac{\chi (\text{sine}){\int }_0^{t_{max}}(1-sin(\frac{t}{2T_2}))e^{-t/T_2}dt}{T_2(1-e^{-t/T_2})},$$

which yields

$$\eta (\text{sine},t)=\chi (\text{sine})-\frac{\chi (\text{sine})\times (2-4e^{-\alpha }(sin\frac{\alpha }{2}+\frac{1}{2}cos\frac{\alpha }{2}))}{5(1-e^{-\alpha })},$$ (8c)

and is illustrated in Figure 4b. To calculate the iSNR for the sinusoidal NUS, Eq. 8c is multiplied by Eq. 1, and the result is illustrated in Figure 4c. As we could expect from observing the close agreement between the sinusoidal and matched exponential densities in Figure 4a, their respective iSNR values are very similar to each other. However the sinusoidal density does include more samples beyond 1T₂ than a matched exponential density, yielding slightly improved line shapes in spectra obtained by MaxEnt processing.³² Inspection of Figure 4b illustrates Theorem 1 for the sinusoid, that the enhancement is always greater than 1. Theorem 2 was proved for the specific case of matched exponential NUS, but inspection of Figure 4c shows that the iSNR using the sinusoidal NUS density also always has a positive slope with evolution time sinusoid.

Gaussian NUS Density

Let the NUS time domain weighting be

$$h(\mathit{gauss},t)=e^{\raisebox{1ex}{$-t^2$}\!\left/ \!\raisebox{-1ex}{$2{\sigma }^2$}\right.},$$ (9a)

where σ is a constant to be determined. Consider the Fourier Transform of equation 9a,

$$h(\nu )=\frac{1}{\theta \sqrt{2\pi }}{e}^{\raisebox{1ex}{$-{\nu }^2$}\!\left/ \!\raisebox{-1ex}{$2{\theta }^2$}\right.},$$

where $\theta \equiv \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2\pi \sigma $}\right.$ and the line width is $2\theta \sqrt{2ln2}$. In order for Gaussian NUS to be ‘matched’, the frequency domain line width (full width at half maximum) of the Gaussian NUS density must equal the line width of the signal decay, which is 1/πT₂. One then finds that ‘matched Gaussian’ NUS is obtained when ${\sigma }^2=2T_2^{2}ln2$ is employed in Equation 9a. For an evolution time t_max, find the scaling factor according to Equation 2:

$$\chi \left(\text{Match-Gauss}\right)=\frac{t_{max}}{{\int }_0^{t_{max}}{e}^{\raisebox{1ex}{$-t^2$}\!\left/ \!\raisebox{-1ex}{$4T_2^{2}ln2$}\right.}dt}=\frac{t_{max}}{T_2\sqrt{\pi ln2}\times \mathit{erf}(\alpha /2\sqrt{ln2})},$$ (9b)

where, again, α = t_max/T₂ is convenient for parameterizing the evolution time. Next compute the iSNR enhancement using Equation 4 and inserting the scaling factor just obtained for matched-guassian NUS in Equation 4:

$$\eta (\text{Match-Gauss})=\frac{\chi (\text{Match-Gauss}){\int }_0^{t_{max}}{e}^{-t^2/4T_2^{2}ln2}{e}^{-t/T_2}dt}{T_2(1-e^{-t/T_2})}.$$

After completing the square in the exponent, the integral for the iSNR enhancement of matched Gaussion NUS simplifies to

$$\eta (\text{Match-Gauss})=\frac{2\alpha }{\mathit{erf}\left(\frac{\alpha }{2\sqrt{ln2}}\right)}\frac{\mathit{erf}\left(\frac{\alpha +2ln2}{2\sqrt{ln2}}\right)-\mathit{erf}\left(\sqrt{ln2}\right)}{(1-e^{-\alpha })}.$$ (9c)

Similar to the sinusoid, the Gaussian density also acquires more samples after 1T₂ than matched exponential NUS. The Gaussian density is a decreasing function and so the enhancement for Gaussian NUS must always be greater than 1 according to Theorem 1, which can be appreciated by inspection of Figure 4b. Finally, the iSNR is seen from Figure 4c to always increase with evolution time.

Linear NUS Density

A linearly decreasing sampling density is also capable of placing more emphasis on sampling early portions of the exponential signal. As will be seen, the linear density does not emphasize early evolution times as much as the matched exponential, sinusoidal and matched Gaussian densities. So the linear density is a very conservative choice for implementing NUS. Prior to normalization, the density is

$$h(t)=1-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\pi T_2$}\right.,$$ (10a)

which continues the practice herein to consider sampling densities spanning πT₂. The normalization factor computed from equation 2 is

$$\chi (\text{linear})=\frac{t_{max}}{{\int }_0^{t_{max}}\left(1-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\pi T_2$}\right.\right)dt}=\frac{1}{1-\frac{\alpha }{2\pi }},$$ (10b)

where the linear density is seen to specify much greater sampling beyond 1xT₂ than matched exponential NUS. The iSNR enhancement by linearly weighted NUS is

$$\eta =\frac{\chi (\text{sine}){\int }_0^{t_{max}}\left(1-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\pi T_2$}\right.\right)dt}{T_2(1-e^{-\alpha })}=\frac{(1-e^{-\alpha })-\frac{1}{\pi }(1-(\alpha +1)e^{-\alpha })}{(1-e^{-\alpha })(1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2\pi $}\right.)}.$$ (10c)

One can see by inspection of the figures that the linear density not only includes more sampling density after 1T₂ than any of the densities in Figure 4, it also restores more samples after 2T₂ than the sinusoid, Gaussian and matched-exponential. Figure 5b illustrates that the enhancement is still always greater than 1 as required by Theorem 1, but Figure 5c shows that the iSNR grows at a much slower rate than the densities in Figure 4.

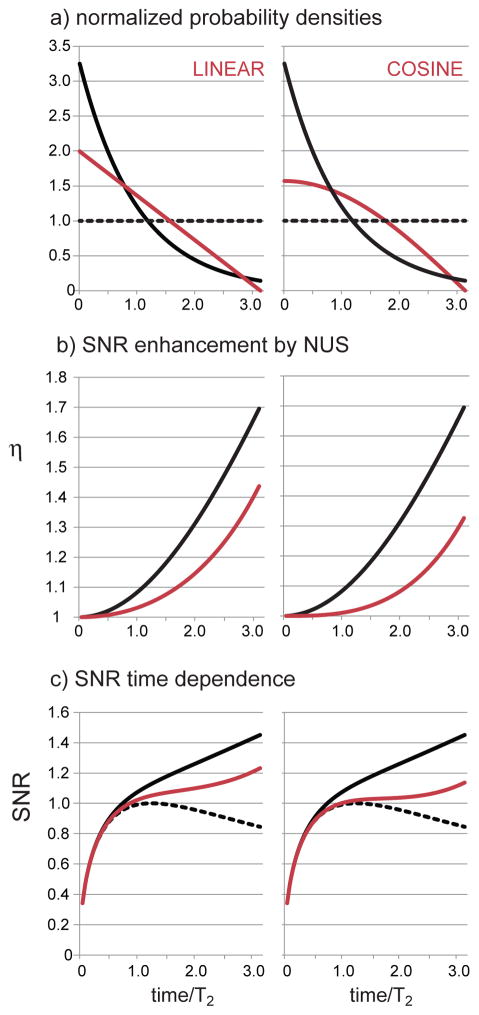
Figure 5.

NUS probability densities following a line and a cosine are analyzed following the same procedure as illustrated for exponential sampling in Figure 1. In all panels, the behavior of matched exponential NUS is given by the solid black line for comparison, while uniform sampling is described by the dashed black line. In (a) the linear and cosine densities have been normalized to have the same area as uniform sampling; the value of χ is given by equation 10b or 11b. In (b) the iSNR NUS enhancements over US as given by equations 10c or 11c are illustrated. In (c) the direct iSNR is obtained by multiplying the enhancement in equation 10c (sinusoid) or 11c (Gaussian) by the iSNR of uniform sampling in equation 1.

Cosine NUS density

An even more conservative NUS approach is a probability density weighted according to the 0-π/2 portion of the cosine function. The cosine density will only weakly bias the early portion of the signal, and will retain even more samples beyond 1×T₂ than the linear density. Following the recipe that has been illustrated for the cases above, we first define the cosine density over the time period πT₂, prior to normalizing it against uniform sampling, as

$$h\left(\text{cosine},t\right)=cos\left(\frac{t}{\pi T_2}\frac{\pi }{2}\right)=cos\left(\frac{t}{2T_2}\right).$$ (11a)

The normalizing factor for this cosine density is

$$\chi \left(\text{cosine}\right)=\frac{t_{max}}{{\int }_0^{t_{max}}cos\left(\frac{t}{2T_2}\right)dt}=\frac{\alpha }{2sin\frac{\alpha }{2}},$$ (11b)

leading to the iSNR enhancement for cosine weighted NUS as

$$\eta =\frac{\alpha }{10\text{sin}\left(\frac{\alpha }{2}\right)(1-e^{-\alpha })}\left(4+2sin\frac{\alpha }{2}{e}^{-\alpha }-4cos\left(\frac{\alpha }{2}\right)e^{-\alpha }\right).$$ (11c)

As NUS densities more closely resemble uniform sampling, it is to be expected that their iSNR enhancements will decrease further, as seen here with the cosine density. Still, the cosine density is a decreasing function, and so Equation 11c is governed by Theorem 1. Indeed, inspection of Figure 5b confirms that all enhancements are greater than 1.

By graphical inspection, it has been seen for the other densities considered above that they all exhibit an iSNR with a positive slope for all evolution times. However the cosine density is interesting because, as shown in Figure 5c, its iSNR is approximately constant for a broad range of evolution times (about 1T₂ – 2.5T₂). So the cosine density may not have the properties of Theorem 2.

(iii) Scope of Theorem 2

The properties of the cosine density illustrate that it is possible to choose very conservative NUS densities which may not have increasing iSNR with evolution time (Figure 5). Whereas Theorem 1 applies broadly to any sampling density that is nonincreasing, Theorem 2 has a narrower scope, which should be characterized further. We return to the exponential and Gaussian sampling densities, since it is straightforward to modify them to sample more densely at early or later times.

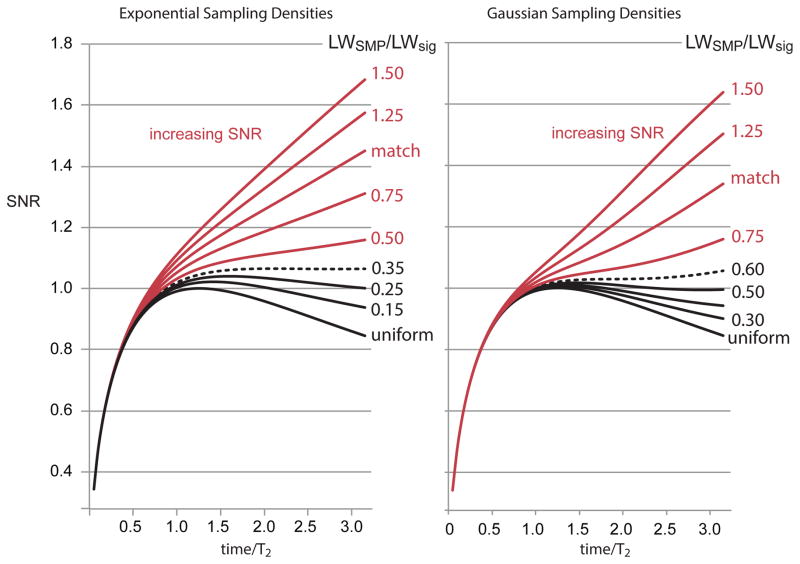
It is useful to introduce the ratio of the line width of the sampling density to the line width of the signal, or LW_SMP/LW_sig. As explained in the prior sections, we say that the NUS exponential or Gaussian density is ‘matched’ if LW_SMP=LW_sig. If we choose to bias the NUS to acquire more data at earlier times relative to matched NUS, then we are specifying LW_SMP > LW_sig. For example, the case of LW_SMP/LW_sig=2 is often referred to informally as 2X biased NUS, and can result in iSNR enhancements over two-fold.^7,12 The time dependence of the iSNR for different LW_SMP/LW_sig ratios is obtained by equations 2, 4 and 7, as illustrated in Figure X6. It is seen through inspection that the exponential NUS density will have a positive iSNR slope at all times if LW_SMP/LW_sig > ~0.35, while the Gaussian NUS density will deliver positive iSNR slopes at all times for LW_SMP/LW_sig > ~0.60 (Figure 6). Matched exponential and Gaussian NUS (e.g. LW_SMP/LW_sig ~ 1.0) are already viewed as rather conservative on the basis of extensive experimentation. The NUS densities illustrated with black lines in Figure 6 have negative iSNR slopes, similar to uniform sampling, but correspond to situations that are unlikely to be used in NUS practice. Indeed, it would be straightforward to modify NUS acquisition software to advise users on whether they are in the positive or negative iSNR slope regimes.

Figure 6.

The time dependence of the iSNR is computed for several different cases of exponential and Gaussian NUS applied to an exponentially decaying signal. All cases resulting in a positive iSNR slope with evolution time are colored red, showing that broad classes of even very conservative NUS densities possess this critical property. Notice also that all of the exponential and Gaussian densities have iSNR greater than uniform sampling, as required by Theorem 1.

Experimental Results

We tested the theoretical results and simulations of the prior section first with 2D HSQC spectra of a plant-derived natural product that has ¹³C line widths ca. 3.7 Hz (T₂*~86 ms, 25°C, DMSO). The ¹³C dimension must span 265 ms (~3.1 T_2, Figure S.1) to obtain this line width. First, the potential to use NUS to improve the spectra for an evolution time spanning 1.3 T₂ is considered in Figure 7. Comparing Figure 7b and 7c, there is only a slight gain in spectral quality from applying matched exponential NUS to a maximum evolution time of 1.3 T₂. Some improvement results from using two-fold biased NUS (Figure 7a and 7c) at 1.3 T₂. The data in Figure 7 are adjusted such that the uniformly sampled data, processed by FFT, is at the limit of detection for most peaks, by mis-setting the proton pulse width. It has been a concern that the use of spectral reconstruction methods could be misleading as they improve the apparent SNR.³³ Yet Figure 7 clearly shows that neither the slight improvement in iSNR by NUS nor the use of MaxEnt can significantly change the detectability of peaks when evolution times span about 1.3 T₂, although two-fold biased NUS does show some slight improvement in signal detection. In contrast, substantial enhancements are observed by NUS when the evolution time spans about 3T₂. In Figure 8, uniform and exponential NUS data are compared for a maximum evolution time of about 3T₂, where significant improvements by NUS are realized. Both ¹H and ¹³C cross-sections verify the significant gains. Importantly, contrasting Figure 7–8 leads to the realization that the improvement illustrated in Figure 8 must owe to changing the iSNR of the raw data by NUS, and not to the use of MaxEnt. Indeed, these experiments used conditions in which the MaxEnt reconstruction approaches linear behavior, so that the ¹³C cross-sections show close agreement with theoretical predictions (Figure 8, top). The agreement between the ¹³C cross-sections and the theory is not exact since the peak heights have uncertainty from the high level of noise, and also because the reconstruction by MaxEnt was not perfectly linear. In the next section, results from the formally linearized protocol for maximum entropy, termed MINT,²⁰ will also be shown.

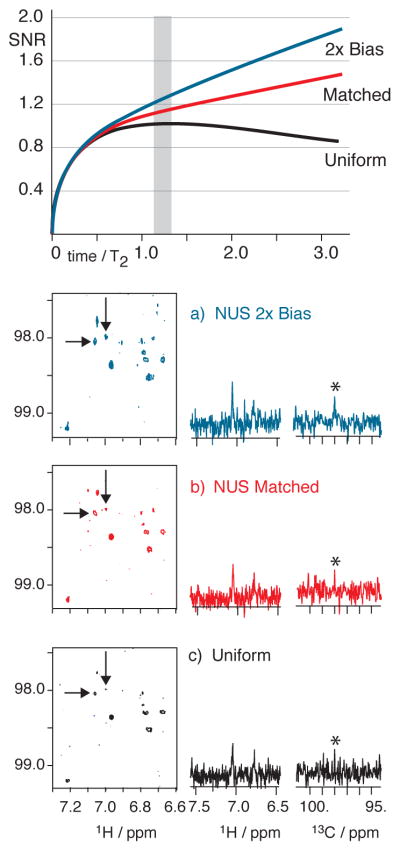
Figure 7.

¹H(¹³C) HSQC spectra of 9 mg natural product spanning an evolution time of about 1.3 T₂. Very little improvement occurs for either matched or two-fold biased NUS as seen in panels (a–c): 3 hrs each, NUS selecting 160 of 640 uniform samples. (US: 4 transients per sample; NUS:16 per sample). Contour levels are consistent in (a–c). All NUS spectra processed by MaxEnt. The iSNR in (a–c) was adjusted by mis-setting pulse lengths so that signals by US would be at the limit of detectability; thus the very slight improvement in the ability to distinguish signals by NUS reflects the small iSNR improvement by NUS for evolution times spanning 1.3 T₂. (shaded vertical bar)

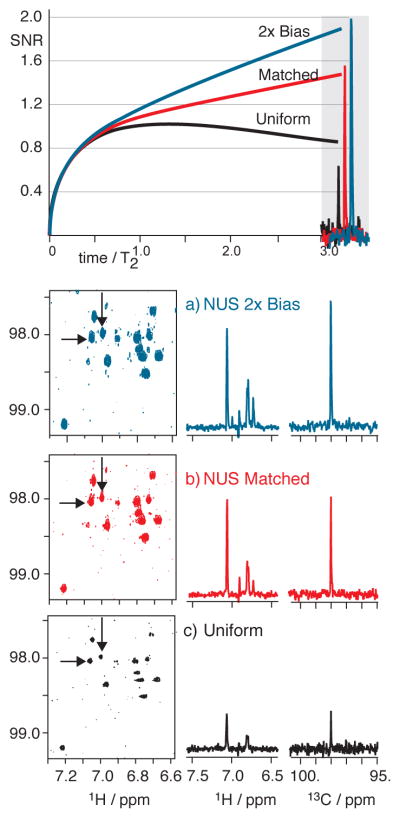
Figure 8.

¹H(¹³C) HSQC spectra of 9 mg natural product spanning an evolution time of about 3 T₂. Significant improvements in signal levels occur for matched or two-fold biased NUS as seen in panels (a–c): 9 hrs each, NUS selecting 400 of 1600 uniform samples. (US: 4 transients per sample; NUS:16 per sample). Contour levels are consistent in (a–c) so that as peaks grow in intensity from (a) to (c) the base of the peak rises above the noise, but the lines are not broadening. Inspection of the ¹³C cross-sections shows that line widths are not significantly changed from (a) to (c). The ¹³C cross-sections are overlaid at approximately the 3 T₂ evolution period to show close correspondence to theoretical predictions.

Contrasting NUS evolution to 1.3T₂ and 3T₂ in Figure 7–8 confirms both key theorems developed herein. We see that, following Theorem 1, all exponential NUS cases resulted in greater SNR than uniform sampling. Next, following Theorem 2, the positive iSNR slope with evolution time is illustrated by recognizing the much larger NUS-based enhancements were realized for 3 T₂ than for 1.3 T₂. MaxEnt processing is not responsible for the trends observed here: consider that the improved spectral quality of the biased versus matched NUS (e.g. Figure 8ab) must owe to higher iSNR in the time domain of the biased NUS data since both were processed with identical maximum entropy reconstruction (MaxEnt) parameters. That is, MaxEnt is not responsible for iSNR enhancements.³³

We also examined 2D ¹³C-¹³C homonuclear correlation spectroscopy of biological systems under magic angle spinning (MAS), posing unique challenges: i) high dynamic range with signal intensities spanning over two orders of magnitude; ii) a spread of T₂* values over an order of magnitude from 1–30 ms in the same sample (even longer T₂* values with fast-MAS methods). The latter mandates sampling to long t₁ evolution times to attain high resolution, particularly in large protein assemblies exhibiting narrow lines.³⁹ Indeed, NUS is ideally suited to these conditions, and conservative NUS schemes paired with MINT processing produce high-quality artifact-free spectra with sensitivity gains consistent with theory.^7,39 In the U-¹³C,¹⁵N-MLF tripeptide the average T₂* relaxation time is 3 ms, and the longest is ca. 10.8 ms (methyl Cδ of met).

The average T₂* is very short: to avoid truncation artifacts and achieve highest resolution, one should sample up to πT₂* of the slowest-decaying signal (31.4 ms). Sampling to 6.4 ms (2x the average T₂*) results in truncation artifacts in the indirect dimension of both US and NUS data by MINT, and moderate iSNR gains ca. 1.3 fold (Figure 9ab, Table 1). Similar findings result for sampling to 9.6 ms (Table 1) Yet, sampling to 31.4 ms gives truncation-artifact-free spectra in US and NUS datasets, and yields greater iSNR enhancements of 1.7–2 fold (Figure 9cd, Table 1).

Figure 9.

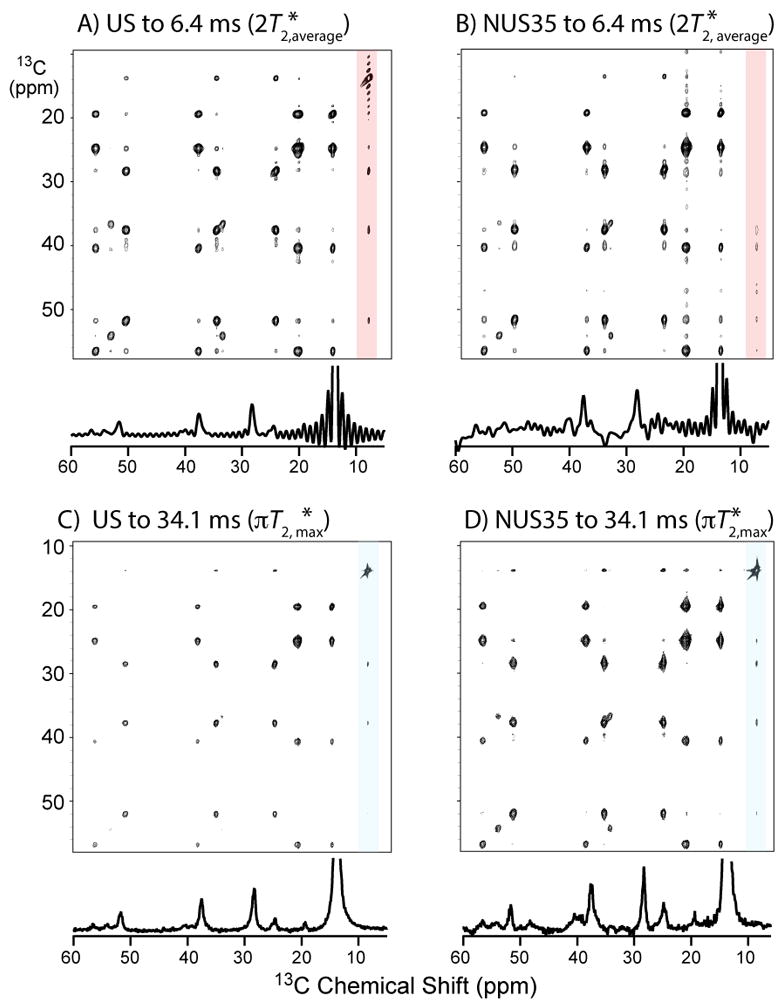
2D ¹³C-¹³C DARR⁴⁰ 14.1 T spectra of U-¹³C,¹⁵N-MLF at full spectral width.(Table 1) (A) US/MINT to 6.4 ms in f₁ (2x the average T₂*), (B) NUS35/MINT to 6.4 ms in f₁, (C) US/MINT to 34.1 ms in f₁ (π x longest T₂*), (D) NUS35/MINT to 34.1 ms in f₁. Peaks enhanced more for the 34.1 ms data (same contour levels. For US: 2000x1024 complex, 4 scans per t₁ step, equally spaced by dwell time (33.33 ms) to 6.4, 9.6, or 34.1 ms. For NUS: 2000x512 complex, 8 scans per t₁ step; 512 t₁ samples followed exponential densities of 35 Hz (T₂* of slowest decaying signal; NUS35), 100 Hz (average T₂*; NUS100), or 300 Hz (NUS300) to final samples of 6.4, 9.6, or 31.4 ms.

Table 1.

Measured NUS iSNR enhancements (η) and average line widths (LW) depend on evolution time.

Experiment	Evolution (ms)*	η (vs. US)	LW (Hz)
US	6.4		128
NUS 35 Hz	6.4	1.32	133
NUS 100 Hz	6.4	1.36	139
NUS 300 Hz	6.4	1.47	166
US	9.6		108
NUS 35 Hz	9.6	1.28	114
NUS 100 Hz	9.6	1.31	122
NUS 300 Hz	9.6	1.67	141
US	31.4		101
NUS 35 Hz	31.4	1.69	107
NUS 100 Hz	31.4	2.10	107

^*(6.4 ms =2T_2,avg, 9.6 ms=3T_2,avg, 31.4 ms=πT_2,max)

The experimentally observed enhancements depend on the maximum evolution time and sampling bias, consistent with the analytic expressions shown in this (Eq. 7ab) and our earlier reports (Eqs. 1–6).^7,12 The US and NUS (50% retained samples) experiments used equal total times, and the NUS followed 35 Hz, 100 Hz, and 300 Hz exponential decays to test different biases (Table 1). The line widths also depend on the maximum evolution time and sampling bias when evolution times are insufficient to overcome the truncation artifacts. (Table 1, example given in Figure S3)

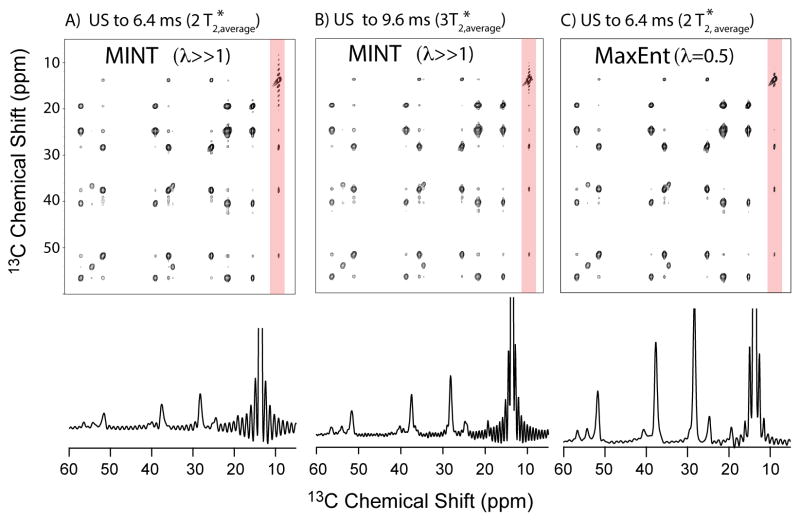
Maximum entropy interpolation (MINT) is a protocol for achieving linear maximum entropy reconstructions of spectra from non-uniformly sampled time domain data.⁷ Maximum entropy reconstruction has long been noted for its insensitivity to truncation artifacts,²¹ however the linearity of MINT forces spectral reconstructions to closely approximate the behavior of the Fourier Transform, and truncation artifacts arise from applying MINT to severely truncated NUS data as in Figure 9. We further illustrate this concept by contrasting MINT with the more common use of maximum entropy reconstruction in a non-linear regime in Figure 10 (Figure 10a reproduces Figure 10a to facilitate comparisons), and illustrates the application of MINT to a uniformly sampled indirection dimension of ¹³C-¹³C correlation spectra in the solid phase, and when the maximum evolution time is just 6.4 ms. Strong truncation wiggles are observed for MINT conditions, achieved by setting the parameter lambda (λ) to very large values in order to force extremely close agreement between mock and experimental time domain samples. Significant truncation wiggles are also observed for MINT processing of uniform data sampled to 9.6 ms (Figure 10b). In contrast Figure 10c illustrates the common application of MaxEnt in which λ is set to intermediate values which deliver high fidelity reconstructions, but which are no longer linear.²¹ Truncation artifacts are reduced significantly in Figure 10c, but peak intensities have changed and are no longer linear.

Figure 10.

Comparison of MINT versus traditional non-linear MaxEnt for 2D ¹³C-¹³C DARR spectroscopy in MLF (see main text, Figure 4). Figure 9A reproduces Figure 8A. MINT conditions (50% NUS with λ ≫1) result in truncation wiggles for truncated signals, however MaxEnt conditions (λ = 0.5) exhibit significant nonlinearity while also strongly suppressing truncation artifacts, as has been widely described.²¹

Conclusion

Recording the indirect dimensions of nD-NMR by weighted non-uniform sampling is rigorously shown with new theorems to have benefits with respect to the intrinsic SNR and sensitivity of the detected signals. First, and a particularly broad result, any weighting of NUS which has a decreasing probability density always has greater sensitivity than US for recording decaying signals in indirect evolution periods. Both conservative and aggressive NUS densities yield useful sensitivity improvements. Next, the iSNR is shown to always increase with evolution time for matched exponential NUS, while many other useful sampling densities have this property as well, bearing the critical implication that iSNR and resolution are simultaneously improved with additional evolution time. The results presented here are (i) intrinsic properties of the raw NUS data, prior to any signal manipulation and processing, and (ii) applicable to all NUS protocols (off-grid, on-grid, weighted transients, hypercomplex, etc.) that acquire data following a sampling density. These theorems, with broad applicability, assure the performance of widely used approaches to NUS, and it is hoped this work will stimulate its broader adoption.

Appendix I

Theorem I (NUS Sensitivity Theorem)

Assume h(t) is a positive, nonincreasing function on some interval 0 ≤t < A, where A ≤∞. For any positive T₂ and 0 < t_max < A, the time domain iSNR enhancement (Eq. 4) satisfies

$$\eta =\frac{\alpha }{\left(1-e^{-\alpha }\right)}\frac{{\int }_0^{t_{max}}h(t)e^{-t/T_2}dt}{{\int }_0^{t_{max}}h(t)dt}\ge 1,$$ (A1)

where α = t_max/T₂, and equality holds in Eqn. (A1) if and only if h(t) is constant for 0 < t < t_max.

Proof

We will prove Eqn. (A1) with strict inequality in the case that is most broadly used in experimentation, namely where h(t) is positive, continuous, and strictly decreasing on the [0,A). Let v = t/T₂ and so dt=T₂dv. Also set k(v) = h(T₂v). The inequality to be proved becomes

$$\eta =\frac{\alpha }{\left(1-e^{-\alpha }\right)}\frac{{\int }_0^{\alpha }k(v)e^{-v}dv}{{\int }_0^{\alpha }k(v)dv}>1,$$ (A2)

where 0 < α < A/T₂. The denominators in Eq. A2 are positive, so the inequality to be proved is

$${\int }_0^{\alpha }k(v)e^{-v}dv>\frac{1-e^{-\alpha }}{\alpha }{\int }_0^{\alpha }k(v)dv,$$ (A3)

or F(α) > 0 where

$$F(\alpha )={\int }_0^{\alpha }k(v)e^{-v}dv-\left(\frac{1-e^{-\alpha }}{\alpha }\right){\int }_0^{\alpha }k(v)dv>0.$$

Notice F(0) = 0, and so Eq. A3 will be proved if F′(a) > 0, or

$$\frac{d}{d\alpha }{\int }_0^{\alpha }k(v)e^{-v}dv>\frac{d}{d\alpha }\left(\frac{1-e^{-\alpha }}{\alpha }{\int }_0^{\alpha }k(v)dv\right),$$ (A4)

for all 0 < α < A/T₂. By the Fundamental Theorem of Calculus, the inequality of A4 becomes

$$\begin{array}{l}k(\alpha )e^{-\alpha }>{\left(\frac{1-e^{-\alpha }}{\alpha }\right)}^{\prime }{\int }_0^{\alpha }k(v)dv+\left(\frac{1-e^{-\alpha }}{\alpha }\right)k(\alpha ),\text{or}\\ k(\alpha )\left(e^{-\alpha }-\frac{1-e^{-\alpha }}{\alpha }\right)>{\left(\frac{1-e^{-\alpha }}{\alpha }\right)}^{\prime }{\int }_0^{\alpha }k(v)dv.\end{array}$$ (A5)

Notice that

$${\left(\frac{1-e^{-\alpha }}{\alpha }\right)}^{\prime }=\frac{\alpha e^{-\alpha }-(1-e^{-\alpha })}{{\alpha }^2}=\frac{1}{\alpha }\left(e^{-\alpha }-\frac{1-e^{-\alpha }}{\alpha }\right),$$ (A6)

so that Eq. A5 becomes

$$k(\alpha )\left(e^{-\alpha }-\frac{1-e^{-\alpha }}{\alpha }\right)>\frac{1}{\alpha }\left(e^{-\alpha }-\frac{1-e^{-\alpha }}{{\alpha }^2}\right){\int }_0^{\alpha }k(v)dv.$$ (A7)

Although the common factor in Eq. A6 can be cancelled, it should be recognized that it is negative:

$$e^{-\alpha }-\frac{1-e^{-\alpha }}{\alpha }<0.$$

Thus the direction of the inequality in Eq. A7 must be changed when performing the cancellation, yielding the following expression that needs to be proved:

$$k(\alpha )<\frac{1}{\alpha }{\int }_0^{\alpha }k(v)dv.$$ (A8)

By the Mean Value Theorem, there exists an α₁ in [0,α] such that

$${\int }_0^{\alpha }k(v)dv=(\alpha -0)k({\alpha }_1),$$

where α₁ ≠ α because k(v) is strictly decreasing. Since then α₁ < α, we have k(α₁)>k(α), and then

$${\int }_0^{\alpha }k(v)dv=\alpha k({\alpha }_1)>\alpha k(\alpha ),$$ (A9)

which proves the inequality of Eq. (A8).

The complete case of Eqn. (A1) for any nonincreasing function can be obtained from the special case proved above by an approximation argument. The main step for the last assertion of the theorem is to show that equality in Eqn. (A1) holds only for constant h(t). A complete proof is provided in the Supplementary Information(S5).

Appendix 2

Theorem 2 (Matched NUS SNR Theorem)

The iSNR of matched exponential NUS (Equation 7b) always has a positive slope for an arbitrary, positive T₂ and positive evolution time t_max.

Proof

It is necessary to show that the derivative of equation 7b is positive for t > 0,

$$\frac{dt}{dt}{\mathit{SNR}}_{exp-\text{match}}=\frac{d}{dt}\left(\frac{\sqrt{t}}{2}\left(1+e^{-t/T_2}\right)\right)>0.$$ (A10)

One finds

$$\frac{d}{dt}{\mathit{SNR}}_{exp-\text{match}}=\frac{1}{4\sqrt{t}}\left(1+e^{-t/T_2}\left(1-\frac{2t}{T_2}\right)\right),$$ (A11)

where the sign of the derivative is positive if

$$w(\alpha )=1+e^{\alpha }\left(1-2\alpha \right)>0,$$ (A12)

where α=t/T₂. Equation A12 is always positive for α > 0, which can be seen as follows. The issue in determining if equation A12 is always positive is that (1–2α) can be negative for physically meaningful values of α. A formal min/max calculation on Eq. A12 is straightforward, and will establish the existence of a positive minimum for equation A12. A more succinct approach is also possible. Notice first that w(0) = 2 and lim_α→∞w(α) = 1. To understand the behavior of w(α) for 0 < α < ∞ examine the slope of w(α),

$$w^{\prime }(\alpha )=-e^{-\alpha }\left(1-2\alpha \right)+e^{-\alpha }\left(-2\right)=e^{-\alpha }\left(2\alpha -3\right).$$ (A13)

Equation A13 shows a minimum at α=3/2, where the slope is negative for 0 < α < 3/2, and is positive for 3/2 < α, establishing α=3/2 as a minimum in w(α). We see that

$$w(3/2)=0.5537\dots ,$$

and so w(t) is always equal or greater than this value and therefore always positive.