Photoacoustic elastography

Abstract

Elastography can noninvasively map the elasticity distribution in biological tissue, which can potentially be used to reveal disease conditions. In this paper, we have demonstrated photoacoustic elastography by using a linear-array photoacoustic computed tomography system. The feasibility of photoacoustic elastography was first demonstrated by imaging the strains of single-layer and bilayer gelatin phantoms with various stiffness values. The measured strains agreed well with the theoretical values, with an average error of less than 5.2%. Next, in vivo photoacoustic elastography was demonstrated on a mouse leg, where the fat and muscle distribution was mapped based on the elasticity contrast. We confirmed the photoacoustic elastography results by ultrasound elastography performed simultaneously.

Elastic properties of biological tissues can reflect pathological conditions [1–2]. Elastography, an imaging technique that is typically implemented using existing medical imaging techniques, can map the elasticity distribution in biological tissue [3]. Elastography was first performed using ultrasound imaging in 1991 [4]. Later, elastography was implemented using magnetic resonance imaging, namely magnetic resonance elastography, at the whole body level with a spatial resolution of ~1–3 mm [5]. Elastography was also implemented in optical coherence tomography (OCT), which has greatly improved the spatial resolution to ~1–10 μm, but OCT has limited imaging depth (~1 mm in the skin) due to the strong optical scattering in biological tissue [6].

Photoacoustic (PA) tomography (PAT) is a hybrid imaging technique that combines rich optical absorption contrast and high ultrasonic spatial resolution [7]. PAT has proven capable of imaging anatomical, functional, molecular, and metabolic information of biological tissue [8–11]. There have been several photoacoustic studies on measuring the elastic properties of biological tissue. In one study, the viscoelasticity of biological tissues was imaged by photoacoustic technique, but the elasticity could not be measured because the detected photoacoustic signal phase delay was related to the viscosity-elasticity ratio instead of the elasticity alone [12–13]. In a second study, the volume-averaged Young’s modulus of soft tissue was measured by a photoacoustic sensing technique, which, however, possessed no spatial resolution [14]. Yet another study introduced speckles in photoacoustic images for sample displacement estimation, but demonstrated the concept only with simulation data [15]. So far, elastography has not been successfully implemented using photoacoustic imaging. Here, we demonstrate photoacoustic elastography, capable of high-resolution strain imaging of biological tissue based on the contrast of Young’s modulus. Implemented using photoacoustic computed tomography (PACT), photoacoustic elastography can map the mechanical contrast in biological tissue while maintaining high spatial resolution and excellent penetration depth.

The photoacoustic elastography was developed based on a linear-array PACT system [16], which is capable of high-resolution imaging of the elasticity distribution in tissue in vivo. A 10 ns pulsed laser beam at 680 nm was used for photoacoustic excitation with a 20 Hz pulse repetition rate. Light was first coupled into a fiber bundle. The fiber bundle was then split into two rectangular light bars mounted on each side of a linear ultrasonic transducer array (LZ250, VisualSonics Inc., 21 MHz center frequency, 256 elements), which detected the generated photoacoustic waves. Photoacoustic signals were sampled at 84 MHz. For each laser pulse, one quarter of the 256 ultrasonic array elements were used for detecting PA signals. Acquired with four laser pulses, the full data set was used to reconstruct a cross-sectional PA image, yielding a frame rate of 5 Hz. The spatial resolutions of the PACT system were 119 μm in the lateral direction, 86 μm in the axial direction, and 1.2 mm in the elevational direction [17].

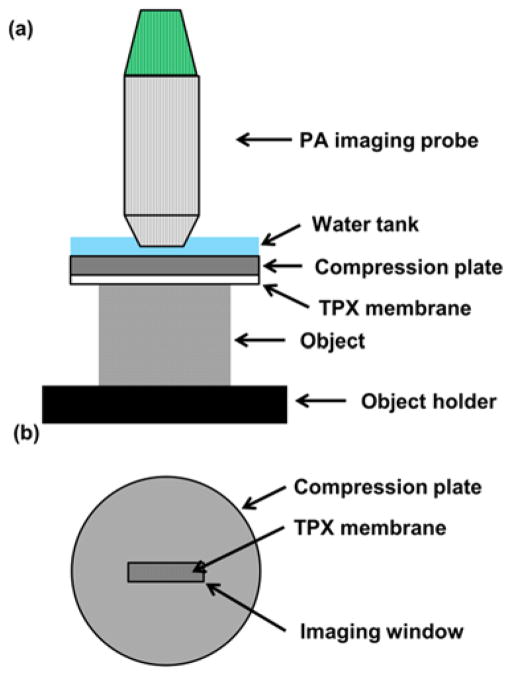
In our photoacoustic elastography system, an aluminum compression plate larger than the object exerted a small axial compressive force on the object [Fig. 1(a)]. An imaging window slightly larger than the ultrasonic transducer probe was opened at the center of the compression plate [Fig. 1(b)]. A piece of fully stretched polymethylpentene (TPX) plastic membrane was attached to the bottom of the compression plate to provide uniform and uniaxial force to the object while passing the illumination laser beam. Ultrasound gel was used for acoustic coupling between the compression plate and the object, without changing the elasticity of the gelatin phantoms. Ultrasound gel is also convenient for in vivo animal imaging and potential clinical applications. For acoustic coupling between the probe and the compression plate, water was chosen as the medium. The compression plate was adjusted by a manual translation stage to provide precise compression to the object against a rigid object holder. The total displacement of the object surface was read from the translation stage. The object and the object holder were placed on a high-precision digital weighing scale (S200, Ohaus). The compression stress applied to the object was calculated from the difference in the scale readings before and after compression:

$$\sigma =\frac{g(m_a-m_b)}{A}.$$ (1)

Fig. 1.

Schematic of the photoacoustic elastography system. (a) Side view of the photoacoustic elastography system. (b) Top view of the compression plate with the imaging window at the center.

Here, σ is the compression stress, g is the acceleration of gravity, m_a and m_b are the scale readings before and after compression, and A is the area on which the compression force is applied.

To demonstrate quantitative elasticity measurement, photoacoustic elastography was first used to image four homogeneous gelatin phantoms with respective gelatin concentration of 40, 60, 80, and 100 g/L. To provide absorption contrast for photoacoustic imaging, 50 μm microspheres were mixed in the gelatin phantoms at a concentration of ~5 microspheres per mm³. Each gelatin phantom was imaged with the photoacoustic elastography system before and after compression with an external stress of 53 Pa [Figs. 2(a) and (b)]. The maximum surface displacement in the experiments was 120 μm, and the maximum strain was 4%, which was considered to be within the linear strain response regime of the phantom [18]. Time-resolved A-line signals before and after compression were cross-correlated to calculate the axial displacement due to compression [19], generating a cross-sectional map of displacements after compression [Fig. 2(c)]. Here, short-window cross-correlation between corresponding A-lines was computed. We slid a 90-μm-wide window along the A-lines acquired before and after compression, and computed the cross-correlations to find the displacement between the A-lines at each window position. Displacements were then averaged among the microspheres at each depth [Fig. 2(d)]. The slope of the linear fitting of the displacements versus depths—i.e., the magnitude of the average gradient of the displacement—quantified the average strain of each gelatin phantom. The same data processing was performed on 20 measurements, 5 each for four gelatin phantoms [Fig. 2(e)]. The measured strains were then fitted by the model below [18]:

$$\epsilon =\frac{\sigma }{K}\frac{1}{C^2}.$$ (2)

Fig. 2.

Strain measurement on single-layer gelatin phantoms by photoacoustic elastography. (a–b) Cross-sectional PA images of a gelatin phantom (40 g/L gelatin concentration) mixed with 50 μm microspheres acquired (a) before and (b) after compression. (c) Displacement image obtained from (a) and (b). (d) Average displacement versus the depth. The strain of the phantom was estimated as the slope of the linear fitting. (e) Measured strains of gelatin phantoms with 4%, 6%, 8%, and 10% concentration in weight. The data was fitted to a quadratic model that describes the relationship between the strain and the gelatin concentration [Equation. (2)].

Here, ε is the strain of the gelatin phantom, σ is the stress applied to the phantom, K is a constant factor, and C is the gelatin concentration. Note K is affected by the equilibrium temperature, the temperature and duration of the gelatin mixing process, and the molecular weight of gelatin.

Photoacoustic elastography was then used to image a bilayer gelatin phantom with different gelatin concentrations in each layer. The top layer had a gelatin concentration of 50 g/L and a thickness of 2.5 mm.³ The bottom layer had a gelatin concentration of 100 g/L and a thickness of 2.0 mm. Again, 50 μm microspheres were mixed in the gelatin phantom at the concentration of 5 microspheres per mm³. The bilayer phantom was imaged by the photoacoustic elastography system before and after compression with a stress of 98 Pa [Fig. 3(a) and (b)]. A displacement image was generated using the same method as above [Fig. 3(c)]. Displacements of the microspheres were averaged at each depth, and fitted by a linear function for each layer [Fig. 3(d)]. The slopes of the two linear fittings reflect the strains in the two layers. The strain ratio between the two layers is 4.0 ± 0.2, which agrees with the theoretical value of 4.

Fig. 3.

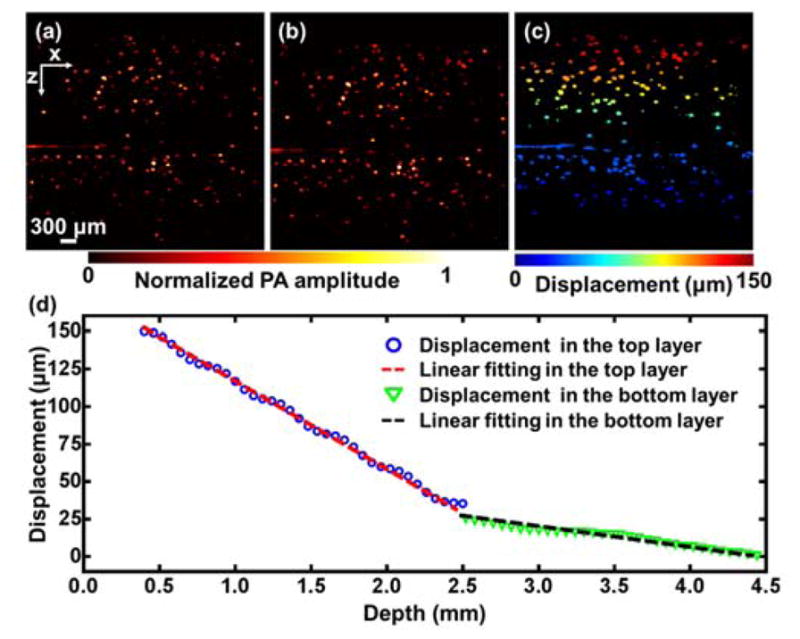
Strain measurement of a bilayer gelatin phantom by photoacoustic elastography. (a–b) PA images of a bilayer gelatin phantom mixed with 50 μm microspheres acquired (a) before and (b) after compression. (c) Displacement image obtained from (a) and (b). (d) Average displacement versus depth. The data was fitted by a linear function for each layer.

A mouse leg was then imaged in vivo by photoacoustic elastography. All experimental animal procedures were carried out in conformity with laboratory animal protocols approved by the Animal Studies Committee at Washington University in St. Louis. The mouse leg was imaged before and after applying an external compression force of 12 mN [Figs. 4(a) and (b)]. A displacement image was obtained by cross-correlating the PA images before and after compression, using the image pixels with PA signal amplitudes above the noise level. A raw strain image was then obtained by numerically differentiating the axial displacements, assuming that the applied stress was uniaxial [Fig. 4(c)]. The raw strain image was then superimposed on the structural PA image [Fig. 4(e)]. The regions of tissue with larger strains were softer than regions with smaller strains, and thus were thought to have more fat. The photoacoustic elastography was validated by ultrasound elastography using the same linear-array imaging probe, which showed a similar distribution of strains [Figs. 4(d) and (f)]. In ultrasound elastography, structural ultrasound images were acquired simultaneously with structural photoacoustic images before and after the compression. The displacement and strain images in the ultrasound elastography were computed using the same data processing method as in the photoacoustic elastography. The average strains over the entire cross-sectional image were 0.84 ± 0.49% in photoacoustic elastography and 0.82 ± 0.29% in ultrasound elastography. Here it is worth noting that there were differences between the strain distribution measured by photoacoustic elastography and ultrasound elastography. Although both methods measured the elastic property of the tissue, they were based on different contrast mechanisms. Within each resolution voxel (~119 μm by 86 μm by 1.2 mm) of the strain image, optical-absorption-based photoacoustic elastography measured the integrated elasticity of the tissue only through the displacement of the vasculature, while acoustic-scattering-based ultrasound elastography mapped the integrated elasticity through the displacement of more tissue components, including vasculature, muscle fibers, and fat. Under compression, there may be more relative displacements between vasculature and other tissue components in the soft regions, resulting in higher strain values than those in ultrasound elastography. Another possible reason for the discrepancy between the measured strain images is the different number of useful pixels in photoacoustic and ultrasound elastography images. Lacking speckles and imaging only the blood vasculature, photoacoustic elastography has fewer useful pixels than ultrasound elastography, resulting in fewer effective pixels for interpolation, especially in the tissue region with less blood.

Figure 4.

Photoacoustic elastography of a mouse leg in vivo. (a–b) PA images of a mouse leg in vivo before and after compression. (c) A strain image of the mouse leg obtained by photoacoustic elastography in vivo. (d) A strain image of the mouse leg obtained by ultrasound elastography in vivo. (e) The strain image of the mouse leg obtained by photoacoustic elastography superimposed on the structural PA image. (d) The strain image of the mouse leg obtained by ultrasound elastography on the structural ultrasound image.

Compared to previous studies, our photoacoustic elastography technique based on a linear-array photoacoustic computed tomography has the following distinctive features [12–15]. First, photoacoustic elastography maps the Young’s modulus of biological tissue, but previous photoacoustic viscoelasticity studies are based on the contrast of the viscosity-elasticity ratio [12–13]. Second, photoacoustic elastography is able to provide cross-sectional strain images of biological tissue with high axial resolution, while viscosity-elasticity ratio measurement has no axial resolution [12–13]. Third, photoacoustic viscoelasticity imaging is based on an intensity-modulated continuous-wave laser excitation, yielding a much lower signal to noise ratio than that in photoacoustic elastography using a pulsed laser excitation [20]. Fourth, photoacoustic elastography is implemented on a commercial linear-array-based photoacoustic computed tomography system, which can measure other biological parameters including vasculature density, tumor volume, oxygen saturation of hemoglobin, and blood flow velocity [16–17, 21].

In summary, we have demonstrated photoacoustic elastography on gelatin phantoms and in vivo. Lacking speckles, photoacoustic elastography can still measure tissue displacements using optical absorption contrast provided by abundant endogenous biomolecules, especially hemoglobin in red blood cells [22]. Photoacoustic elastography has a 100% relative sensitivity to optical absorption contrast, which means a given percentage change in the optical absorption coefficient yields the same percentage change in the PA signal amplitude. Photoacoustic elastography is well suited for mapping the elastic properties of diseased tissues with highly vascularized structures, such as carcinoma and glioblastoma [23]. At longer wavelengths where water and lipids have relatively strong absorption, photoacoustic elastography can potentially map the elastic properties of tissues by using water and lipids as the contrast [24–25].

We would like to point out that the motivation of this work is not to prove that photoacoustic elastography is superior to ultrasound elastography. Instead, the major motivation is to demonstrate the feasibility of elasticity measurement by using PAT as an independent device: Not all the photoacoustic imaging systems have the capability of ultrasound transmission, and thus ultrasound elastography is not always available. Photoacoustic elastography can be implemented on existing photoacoustic imaging systems, as an additional function, to provide more comprehensive information about the tissue’s mechanical and functional information.

Further, photoacoustic tomography can potentially measure elasticity concurrently with other functional parameters, including the oxygen saturation of hemoglobin, which may provide more comprehensive information for disease diagnosis and treatment evaluation [26]. Noninvasive imaging of elasticity distribution expands the functionality of photoacoustic tomography and is expected to find potential applications in clinical practice, such as cancer detection and arterial plaque assessment. To advance the current photoacoustic elastography technique for clinical applications, several challenges remain to be solved. One challenge is to apply normal uniform compression force in vivo. A special compression mechanism needs to be developed for curved tissue surface. Another challenge is to achieve three dimensional volumetric strain imaging. To achieve this, the current linear-array photoacoustic probe can be linearly scanned orthogonally.