Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Apr 11;138(17):5685–5692. doi: 10.1021/jacs.6b02151

Π Band Dispersion along Conjugated Organic Nanowires Synthesized on a Metal Oxide Semiconductor

Guillaume Vasseur †,‡,*, Mikel Abadia †, Luis A Miccio †,‡, Jens Brede †,‡,*, Aran Garcia-Lekue ‡,§, Dimas G de Oteyza †,‡,§, Celia Rogero †,‡, Jorge Lobo-Checa †,∥,⊥, J Enrique Ortega †,‡,#
PMCID: PMC4858753  PMID: 27115554

Abstract

graphic file with name ja-2016-02151e_0005.jpg

Surface-confined dehalogenation reactions are versatile bottom-up approaches for the synthesis of carbon-based nanostructures with predefined chemical properties. However, for devices generally requiring low-conductivity substrates, potential applications are so far severely hampered by the necessity of a metallic surface to catalyze the reactions. In this work we report the synthesis of ordered arrays of poly(p-phenylene) chains on the surface of semiconducting TiO2(110) via a dehalogenative homocoupling of 4,4″-dibromoterphenyl precursors. The supramolecular phase is clearly distinguished from the polymeric one using low-energy electron diffraction and scanning tunneling microscopy as the substrate temperature used for deposition is varied. X-ray photoelectron spectroscopy of C 1s and Br 3d core levels traces the temperature of the onset of dehalogenation to around 475 K. Moreover, angle-resolved photoemission spectroscopy and tight-binding calculations identify a highly dispersive band characteristic of a substantial overlap between the precursor’s π states along the polymer, considered as the fingerprint of a successful polymerization. Thus, these results establish the first spectroscopic evidence that atomically precise carbon-based nanostructures can readily be synthesized on top of a transition-metal oxide surface, opening the prospect for the bottom-up production of novel molecule–semiconductor devices.

Introduction

The chemical versatility as well as relative abundance of carbon-based molecules makes them promising candidates for integration into next-generation devices such as molecular machines,1,2 organic field-effect transistors,3−5 or light-emitting diodes.6,7 However, technological applications require controllable, scalable, and cost-efficient techniques before implementation into industrially manufactured devices becomes available. Toward this end, the exploitation of self-assembly of organic nanostructures on surfaces is one of the major challenges in the field of nanotechnologies.8−11 In this respect, the surface-confined Ullmann reaction is a powerful bottom-up approach that exploits covalent bonding of halogenated precursors on top of metallic substrates.12−14 The covalently bonded nanostructures exhibit superior thermal and mechanical stability, as well as improved charge transport properties that are mandatory in the field of electronics.15,16 In addition, both the geometry and electronic properties, including the band gap, can be tailored by a judicious choice of monomers.17−20 To date, a wide variety of these structures have been reported, including well-defined clusters,21 one-dimensional wires,22−24 two-dimensional networks,25−27 and a large panel of width-controlled graphene nanoribbons (GNRs).28−31 However, practical applications are so far limited by the use of a metallic substrate, requisite to catalyze the reaction. Further processing is thus required to transfer the synthesized structures onto device-ready semiconductor surfaces which enable back-gating and minimize leak currents as well as substrate hybridization effects.32 Recent experiments performed by local probe techniques indicate that the synthesis of covalently bonded nanostructures on insulator surfaces,33−35 transition-metal oxides,36,37 and also passivated semiconductors38 may be feasible, but in particular the electronic properties of the synthesized structures have not been established yet.

Toward this end, photoemission spectroscopy is known as a powerful technique to investigate electronic states in self-assembled organic layers on surfaces. It is commonly used to probe the energies of molecular levels, thereby allowing tracing such properties as molecule–substrate interactions39 or changes in the molecular chemical composition.40 Moreover, the angular dependence of the photoemission intensity contains rich information about orbital topologies.41 Using inverse Fourier transformation, these orbitals can be recovered,42 including their phase which is supposed to be lost during the photoemission process.43 Band dispersions were also reported for molecular layers and crystals as the signature of weak electronic coupling mediated either directly by intermolecular interations44 or indirectly by the substrate.45 Direct evidence of conjugation associated with covalent bonding was reported for bottom-up-synthesized carbonaceous materials such as 2D covalent networks46 and graphene nanorribons.47 More recently, the complete valence band structure of poly(p-phenylene) (PPP) has been measured both on Cu(110)48 and on Au(788).49 We note that the long-range ordering and uniaxial alignment, requisite for angle-resolved photoemission measurements of one-dimensional systems, is frequently achieved by exploiting inherently anisotropic substrates such as high-index surfaces.47,49,50

Herein we report the first spectroscopic study of ordered arrays of PPP chains directly synthesized on top of a titanium dioxide surface. The growth of 4,4″-dibromoterphenyl (DBTP) precursors is followed by low-energy electron diffraction (LEED), scanning tunneling microscopy (STM), and X-ray photoemission spectroscopy (XPS) as a function of the substrate temperature. LEED and STM clearly resolve two distinct and well-ordered structural phases with a transition temperature between the phases of about 475 K. This structural transition coincides with a shift of both C 1s and Br 3d core levels, as observed in XPS. Similar shifts are often considered as the fingerprint of the dehalogenation of precursors. Successful polymerization is established by angle-resolved photoemission (ARPES), resolving the transition from a single, well-defined highest occupied molecular orbital (HOMO), corresponding to a supramolecular phase, to a continuous valence band dispersion associated with the PPP polymer.

Results and Discussion

Structural Characterization

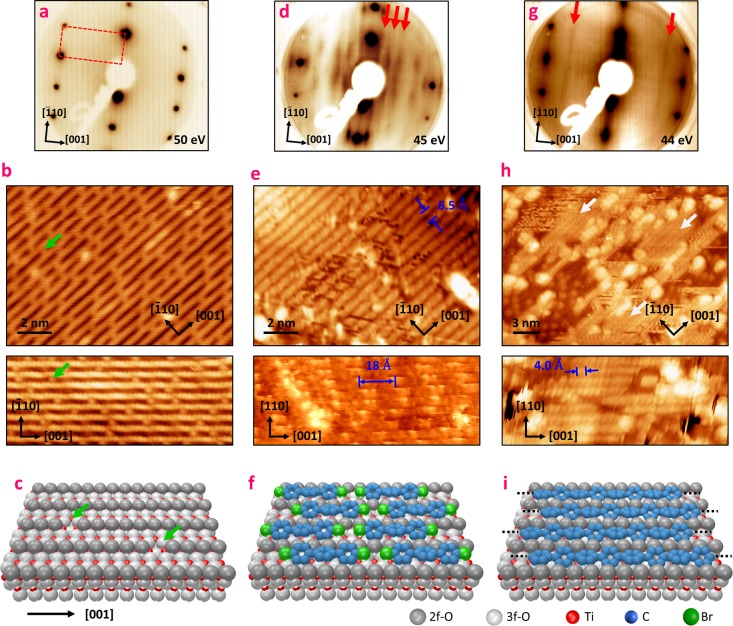
The rutile-TiO2(110) 1 × 1 substrate (Figure 1a–c) consists mainly of alternating rows of 5-fold-coordinated titanium (5f-Ti) and 2-fold- or 3-fold-coordinated oxygen atoms (2f-O/3f-O), running along the [001] direction.51 Due to its rectangular unit cell (2.95 × 6.49 Å), the surface is characterized in LEED by an anisotropic pattern, presented in Figure 1a. This inherent anisotropy is further enhanced by the 2f-O atoms protruding out of the surface plane, framing quasi-one-dimensional trenches of 5-fold-coordinated 5f-Ti atoms as depicted in the model in Figure 1c. The STM image (Figure 1b) of the surface is, at the given tunneling conditions, dominated by electronic rather than geometrical effects; hence, bright rows are assigned to 5f-Ti atoms and dark spaces in between to 2f-O atoms.52 Moreover, after reduction of the crystal by several sputtering and annealing cycles, the surface exhibits defects, in particular oxygen vacancies (Ovs, green arrows in Figure 1b,c), which are known to be involved in several catalytic properties of titanium dioxide such as water dissociation.53

Figure 1.

Figure 1

Open in a new tab

Structural characterization of supramolecular and polymeric phases. LEED patterns (a, d, g), room temperature STM images (b, e, h), and ball models (c, f, i) associated with the clean rutile-TiO2(110) substrate (a–c), the supramolecular layer (d–f), and the polymeric layer (g–i). (d) and (e) were measured after saturation of the surface with DBTP deposited at room temperature, (g) was measured after saturation with the substrate held at 575 K, and (h) was measured after semisaturation with the surface held at 575 K. For clarity, hydrogen atoms have been omitted in the ball models. In (b) and (c), green arrows indicate some oxygen vacancies. The white arrows in (h) indicate the polymeric chains.

Upon evaporation of DBTP on top of the surface held at room temperature (RT), several additional stripes, highlighted by red arrows in Figure 1d, appear in the LEED image. The separation between these stripes indicates a superperiodicity along the [001] direction of 2.1 ± 0.2 nm. With saturation of the surface (see Figure S1, Supporting Information), the STM images exhibit well-defined rows running along the [001] direction (Figure 1e). The distance between these rows is 6.5 ± 0.1 Å, equal to the lattice parameter of the clean substrate in the [1̅10] direction. Higher resolution data (Figure 1e, bottom, and Figure S2) have revealed an intrachain superperiodicity of 1.8 ± 0.2 nm along the [001] axis, close to the value deduced in LEED. Furthermore, we no longer observe the characteristic O vacancies. All these considerations strongly suggest a one-dimensional arrangement of the DBTP molecules into supramolecular chains, as schematically depicted in Figure 1e. This model can readily be rationalized considering density functional theory (DFT) calculations of the free-standing molecules (Figures S3 and S4 and Note 1, Supporting Information). Geometry optimization leads to a molecule’s length (Br to Br) of about 15.2 Å. Considering two molecules facing each other along their main axis, the Van der Waals interactions stabilize the intermolecular Br–Br distance at around 3.8 Å. Therefore, the periodicity of a one-dimensional DBTP supramolecular chain is about 1.9 nm, in agreement with the values experimentally deduced from LEED and STM. Note that, in this model, the lack of a phase relation between two adjacent chains explains the apparition of a striped pattern instead of well-defined diffraction spots in LEED (Figure S5 and Note 2, Supporting Information).

Postannealing the sample prepared at room temperature leads to a clear transition characterized in LEED by the rapid disappearance of the supramolecular features around 470 K (Figure S7, Supporting Information). Only the characteristic spots of the substrate remain, and no signature of any ordered molecular layer is observed in LEED. However, STM images (Figure S8) show some short chainlike features oriented along the [001] direction and a multitude of disordered protrusions. While it is appealing to attribute the chainlike features to polymerized molecules,33−37 this assignment remains ambiguous without further characterization. To improve the overall order of the surface, we proceeded to evaporate the precursors on the surface kept at 575 K. This procedure leads to the appearance of two well-defined stripes in LEED images, indicated by red arrows in Figure 1g. The corresponding lattice parameter along the [001] direction is about 4.2 ± 0.2 Å. This value matches the theoretical inter-phenyl distance of 4.23 Å obtained by DFT for a PPP chain,54 as well as that of 4.4 Å measured experimentally on Cu(110).55 STM images of a nonsaturated layer (Figure S1) reveal several chains running along the [001] direction, marked by white arrows in Figure 1h (see also Figure S8b). In this case, the bare TiO2 surface is also readily identified by the familiar striped pattern and the characteristic defects. In the [1̅10] direction, surface and molecular chains show the same perpendicular spacing of 6.5 ± 0.2 Å as the bare substrate and the supramolecular layer. An intrachain periodicity of 4.0 ± 0.3 Å is deduced from high-resolution STM images, which is in complete agreement with the formation of PPP chains running along oxygen rows, as depicted in Figure 1i. Once again, the lack of a phase relation between two adjacent polymers is responsible for the striped pattern observed in LEED (Figure S6). However, we note that, up to now, for both supramolecular and polymeric phases, it has not been possible to determine with accuracy the absolute positions of the chains with respect to the substrate.

Chemical Characterization

XPS analysis is intensively used to follow the evolution of core levels in several chemical reactions that occur on top of surfaces.56−58 Especially on metals, the Ullmann coupling was recently studied both theoretically14 and experimentally,59,60 revealing an organometallic intermediate that appears close to room temperature on copper and silver substrates. In our case, both C 1s and Br 3d core levels were followed as a function of the sample temperature, to characterize the chemical process of the reaction on titanium dioxide.

First, DBTP was evaporated on the sample kept at low temperature (LT, 80 K) to characterize a multilayer of intact (nondebrominated) molecules (Figure 2a, bottom). In the Br 3d region, two contributions associated with Br 3d3/2 and Br 3d5/2 are resolved with binding energies (BEs) of 70.6 and 71.6 eV, respectively. Likewise, the spectrum in the C 1s region is fitted by two contributions at 284.7 and 285.3 eV, respectively associated with the active and hydrogen-passivated carbon atoms, in agreement with the literature.14,59,60 After 1 monolayer (ML) deposition at room temperature, both of the C 1s and Br 3d features remain globally unchanged compared to LT multilayers, and no significant shifts were observed (Figure 2a, middle). This result suggests that the molecules are still intact on the surface, in agreement with the model proposed in Figure 1f. However, for high-temperature depositions, a substantial shift of both Br 3d and C 1s core levels, respectively by 1.4 and 0.2 eV toward lower BE, are observed. The shift of the Br 3d doublet is attributed to the scission of the C–Br bond and the formation of Br–Ti species. Its magnitude of 1.4 eV is comparable to the theoretically predicted value of 1.6–1.9 eV core level shift on noble-metal surfaces.14 The evolution of the carbon line shape is in agreement with the formation of a polymeric phase, i.e., a C–C homocoupling of the dehalogenated precursors.59

Figure 2.

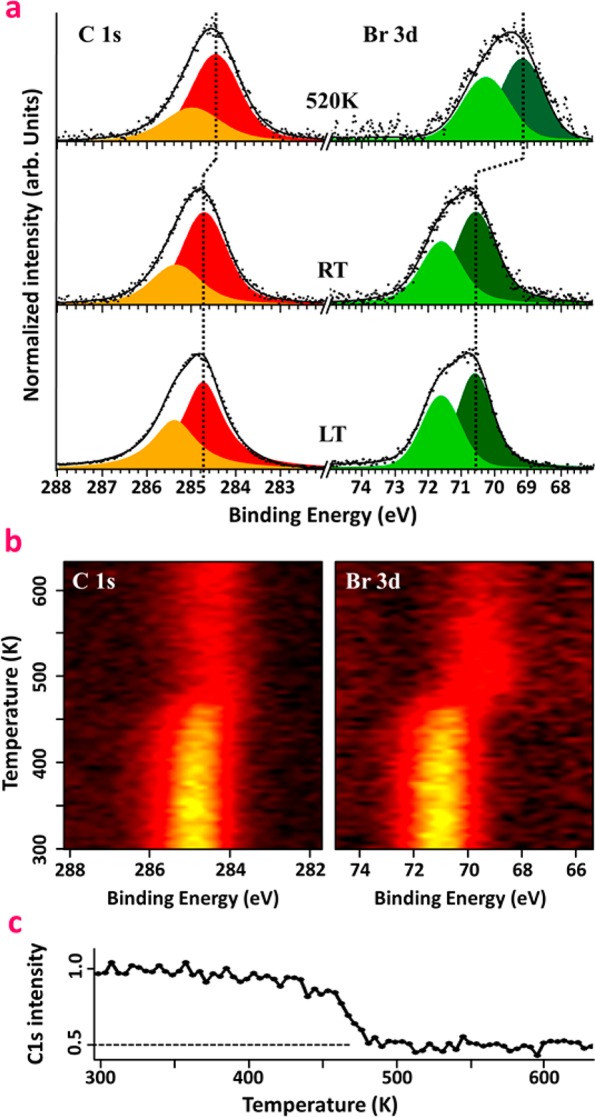
Figure 2

Open in a new tab

X-ray photoemission spectroscopy: (a) C 1s and Br 3d core level spectra measured after a multilayer deposition of DBTP with the sample kept at 80 K (bottom), after 1 ML deposition at RT (middle), and after 1 ML deposition at 520 K (top); (b) evolution of C 1s and Br 3d core levels as a function of temperature, measured after deposition of 1 ML at RT; (c) evolution of the integrated C 1s signal as a function of temperature, extracted from (b).

A precise determination of the activation temperature for the high-temperature (HT) phase formation is obtained by following the XPS spectra during the annealing process of a sample prepared initially at RT (Figure 2b). The line shape of the C 1s and Br 3d core levels remains unchanged until 450 K. Then a clear shift accompanied by a substantial loss in photoemission intensity takes place within 50 K until about 500 K. The obtained energy shifts are identical to those discussed above, but the reduction in intensity is about 50% throughout the transition as depicted in Figure 2c. This overall decline is distinct from previous experiments reported on metals suggesting that, due to the weakly interacting nature of the molecular precursor on the substrate, a large part of the molecules are desorbed during the annealing process. Since the intensity decrease coincides with the onset of the core level shifts, we can conclude that the activation energy of C–Br scission on TiO2 is on the same order as the binding energy of DBPT molecules in the RT phase. Then, by increasing the temperature past 575 K, bromine is gradually desorbed from the surface. We notice that XPS data of a postannealed RT phase and a HT-deposited phase are indistinguishable within our experimental resolution; i.e., dehalogenation and C–C coupling occur in both cases, even if the global order is improved after a high-temperature deposition (Figure S8, Supporting Information). Furthermore, we exclude the possibility that the clusters observed with STM after polymerization are due to Br atoms remaining on the surface since these features are visible also in STM data taken on samples that showed no trace of the Br 3d core level in XPS after annealing at higher temperature.

In summary, the XPS characterization shows all characteristic features of a dehalogenation reaction. However, in contrast to noble-metal-catalyzed reactions reported previously, a substantial loss of molecular precursors due to desorption from the surface is observed.

Electronic Properties

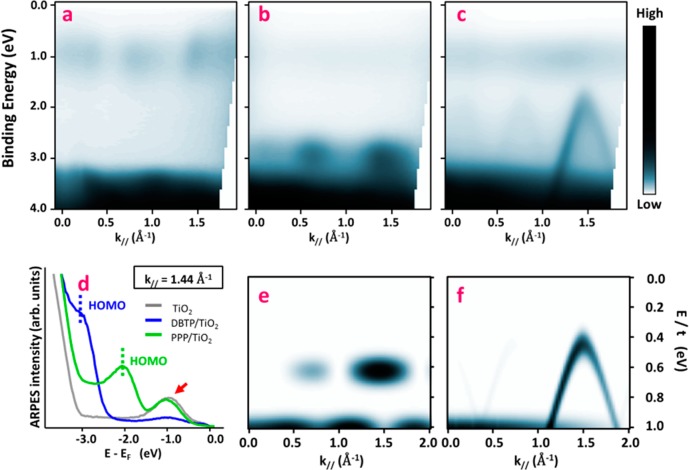
The structural and chemical characterization of the RT and HT phases offers compelling evidence for the polymerization reaction. However, measurement of electronic dispersion throughout the formed PPP oligomers is still lacking. In many ways the band structure of the polymer is its key property and may be considered as its defining fingerprint. In particular, a large precursor’s orbital overlap associated with covalent bonding induces generally highly dispersive bands,47 while a small dispersion is rather a sign of weak interactions.44,48 To probe the electronic levels in the different structural and chemical phases, we directly mapped the electron dispersion with ARPES along the [001] direction, parallel to the oxygen rows. Incident photons are p-polarized, with an energy of 21.22 eV. The comparison between measurements of the pristine substrate with the RT and HT molecular layers enables us to determine the features originating from molecules.

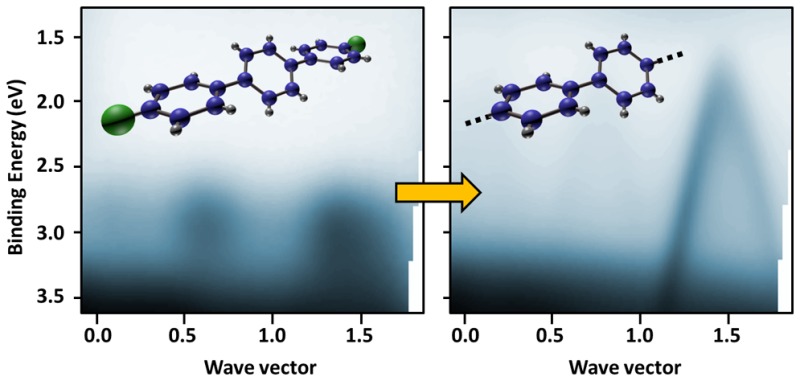
The clean substrate (Figure 3a,d, gray trace in (d)) is characterized by broad features appearing between 3.3 and 9 eV below the Fermi energy, which correspond to the valence bulk bands (bVBs) with a predominantly O2p character.61 The ARPES map also shows a characteristic defect state (DS) close to 1 eV, indicated in Figure 3d by the red arrow. The origin of this feature is still under debate and has been assigned both to O vacancies62 and to interstitial Ti atoms.63 After deposition of 1 ML of DBTP at room temperature, a well-defined molecular state appears just over the bVB, around −2.9 eV, as depicted in Figure 3b,d (blue trace in (d)). Such levels have already been evidenced for a large variety of organic molecules on metallic surfaces39,42 and are usually associated with their π HOMO state. The photoemission intensity of this feature is modulated along the [001] direction, with two maxima appearing at 0.6 and 1.4 Å–1. This spectral weight distribution, already observed for similar molecules such as sexiphenyl,42,44 is intrinsically related to the topology of the HOMO state and its Fourier transform.41−44 Thus, the main contribution at 1.4 Å–1 is directly related to the inter-phenyl distance (4.4 Å), while that at 0.6 Å–1 is due to the natural twisted conformation of the molecule64 (see also Figure S3, Supporting Information). Furthermore, a strong suppression of the defect state is also observed and will be discussed in the following section. Then depositing DBTP at high temperature leads to the complete disappearance of the single molecular level, replacing it by a strongly dispersive band, as presented in Figure 3c,d (green trace in (d)). The top of the band is located at −2.06 eV, shifted toward the Fermi energy by 0.9 eV when compared to the supramolecular phase. This shift is fully compatible with the HOMO/LUMO (lowest unoccupied molecular orbital) gap reduction expected for the formation of covalent C–C bonds between the dehalogenated precursors.46 The band apex is reached at 1.45 Å–1, in agreement with the polymer periodicity of 4.2 ± 0.2 Å deduced by LEED. From the parabolic fit, we determine an effective mass of −0.17m0, with m0 being the free electron mass. Another important quantity is the group velocity, which reaches a value of 9.2 × 105 m·s–1 in the linear part of the band, around −1 eV below the maximum. Such characteristics are in perfect agreement with previous works reported on PPP oligomers,48,49 reflecting the large overlap between the precursor’s molecular orbitals, and are more generally expected for graphene-based materials such as nanoribbons.47

Figure 3.

Figure 3

Open in a new tab

Angle-resolved photoemission spectroscopy: (a–c) experimental raw ARPES intensity maps acquired on the pristine surface (a), after 1 ML DBTP deposition at room temperature (b), and after 1 ML deposition with the sample kept at 575 K (c); (d) energy dispersion curves taken at k∥ = 1.44 Å–1 from the three previous maps; (e, f) theoretical ARPES intensity distributions calculated within a tight-binding model for a terphenyl molecule (e) and an infinite poly(p-phenylene) chain (f). The energy scale (E) is normalized by the resonance integral (t) between the pz orbitals of two neighboring carbon atoms.

A simple tight-binding (TB) model allows us to qualitatively reproduce the main characteristics of the supramolecular and polymeric features observed in ARPES. The theoretical signature of the HOMO of a terphenyl molecule is depicted in Figure 3e. The state is characterized by two maxima appearing at 0.6 and 1.4 Å –1, in agreement with experimental observations. Considering an infinite polymer chain, we observe that the discrete molecular states transform into a dispersive band, as depicted in Figure 3f. For an inter-phenyl distance of 4.4 Å, the top of this band is found at 1.43 Å –1. Quantitatively, considering a resonance integral (t) between the two pz orbitals of neighboring C atoms equal to 2.7 eV (expected for graphene-like materials65), these calculations lead to an effective mass of −0.14m0, close to that deduced experimentally. Therefore, we consider the observed band as the spectroscopic fingerprint of a successful polymerization of DBPT molecules into an ordered array of long PPP chains.

Evolution of the Defect Peak in ARPES

ARPES also provides important information about the mechanism responsible for the dehalogenation reaction occurring on titanium dioxide. As stated previously, for the clean surface, the reduction of the substrate by sputtering/annealing cycles generates defects, leading to an excess of charge that originates the Ti 3d DS, which is visible in photoemission around 1.0 eV below the Fermi energy (red arrow in Figure 3d). After RT deposition, this peak almost vanishes, but is fully recovered for the polymeric phase. In a recent study, Kolmer et al. demonstrated on the (011) surface that the reaction is catalyzed by hydroxyl groups.37 However, our STM images of the clean surface suggest only a negligible amount of hydroxyl groups prior to molecule deposition.66 Although a small amount of hydroxyl groups may be created during thermal evaporation of DBTP onto the surface, a temperature of more than 575 K during molecule deposition for the polymerized HT phase is sufficient to induce diffusion of H from the surface hydroxyl groups into the bulk of TiO2(110).67 Detailed information on the rates of surface hydroxyl group annihilation and creation are thus necessary to draw conclusions about their role in the present polymerization reaction, but other factors appear to play a role as well. In particular, the observed attenuation of the DS peak in our ARPES data was shown previously to not be related to the formation of OH groups.63 Moreover, several other studies reported that the DS is preserved after thin-layer depositions of different organic molecules68 such as phthalocyanines69 or perylenetetracarboxylic dianhydride.70 Thus, a direct screening of the DS by an organic layer seems very unlikely. Therefore, another interpretation of the ARPES data is the direct interaction of halogen atoms with Ovs, leading to the disappearance of the DS. A similar effect was observed previously for chlorine deposited71 on TiO2(110). However, in the present case a question arises about whether the quenching of the DS is due to a minute amount of Br atoms that were directly evaporated from the molecular source or whether Br-terminated molecules are interacting directly with the DS. Unfortunately, the resolution of our laboratory XPS source does not allow deciding between these two scenarios. Nonetheless, we can conclude that upon heating the sample during polymerization of DBTP a re-evaporation of Br correlates with the restoration of the DS.

Conclusion

Here, we have presented a spectroscopic study of an in situ polymerization of DBTP precursors into ordered arrays of poly(p-phenylene) nanowires on top of the TiO2(110) surface. The signatures of the DBTP supramolecular assembly as well as PPP oligomers were characterized by LEED, STM, XPS, ARPES, and TB calculations. In particular, LEED and STM data resolved long organic wires perfectly aligned along the oxygen rows in the [001] crystal direction. Collecting temperature dependent XPS spectra, we have traced the C–Br bond scission temperature of the DBPT precursors which is accompanied by the onset of the polymerization process to 475 ± 25 K. Angle-resolved photoemission spectroscopy was used to map a strongly dispersive π-conjugated band upon formation of long PPP chains. Analysis of the data has revealed an effective mass of −0.17m0 at the top of the valence band as well as a group velocity of up to 9.2 × 105 m/s in the linear part of the dispersion. The latter reflects the large orbital overlap originating from covalent coupling of the precursors and generally expected for conjugated systems. Therefore, the presented on-surface bottom-up synthesis opens up the prospect of the fabrication of an atomically controlled nanostructure, such as graphene nanoribbons, on top of transition-metal oxides. This paves a new pathway toward the integration of these structures into multifunctional electronic devices that will take advantage of both molecular and substrate properties.

Methods

Experiments were carried out in ultra-high-vacuum (UHV) systems at a base pressure of 10–10 mbar. Commercial TiO2(110) single crystals (Cyrstek) were prepared by repeated cycles of sputtering (Ar+, 1 keV) and annealing (900 K). While still considered as a semiconductor,72 optical inspection of the crystals revealed a dark blue color indicating a certain degree of reduction of the TiO2 bulk. 4,4″-Dibromoterphenyl molecules (Sigma-Aldrich) were initially degassed thoroughly for several hours/days by heating the source to temperatures slightly below 350 K under UHV conditions and subsequently sublimed using a Knudsen cell heated to about 375 K, to obtain a rate close to 0.33 ML/min. For both RT and HT depositions, the sample saturates at 1 ML, leading to a self-limited growth (Figure S1, Supporting Information).

Scanning tunneling microscopy

was carried out at RT using either an Omicron VT-STM or a SPECS Aarhus scanning tunneling micrscope. STM images were recorded at constant tunneling current (30 pA) and constant bias voltage (applied to the sample) between 1.8 and 2.5 V.

XPS

experiments were performed using a Phoibos photoelectron spectrometer equipped with an Al Kα X-ray source (16 mA, 12.5 kV) as the incident photon radiation. The overall resolution of the instrument is approximately 0.9 eV. During the temperature-dependent measurement the temperature was increased at a rate of 1.7 K/min.

Photoemission

measurements were performed using a Phoibos 150 SPECS high-resolution hemispherical electron analyzer. The sample was cooled to 150 K. He I (hν = 21.2 eV) radiation was provided by a high-intensity UVS-300 SPECS discharge lamp coupled to a TMM-302 SPECS monochromator.

Theoretical ARPES intensity

distributions were obtained by taking the square modulus of the Fourier transform of the molecular orbitals calculated for both terphenyl and long PPP chains within the tight-binding model, according to the method presented in refs (41) and (42).

Acknowledgments

This work was supported by the Spanish Ministry of Economy (Grant No. MAT2013-46593-C6-4-P), the Basque Government (Grant No. IT-621-13), and the European Research Council under the EU Horizon 2020 research and innovation program (Grant Agreement No. 635919). We also acknowledge support from the Basque Department of Education, UPV/EHU (Grant No. IT-756-13), the Spanish Ministry of Science and Innovation (Grant No. MAT2013-46593-C6-2-P), and the European Union FP7-ICT Integrated Project PAMS (Contract No. 610446).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b02151.

  • Self-limited growth of supramolecular and polymeric phases, additional STM images of the supramolecular phase, geometry optimization of the DBTP molecule and supramolecular phase, theoretical supramolecular and polymeric LEED patterns, phase transition in LEED, and comparison of postannealed room temperature preparation with high-temperature deposition (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja6b02151_si_001.pdf (1.8MB, pdf)

References

  1. Perera U. G. E.; Ample F.; Kersell H.; Zhang Y.; Vives G.; Echeverria J.; Grisolia M.; Rapenne G.; Joachim C.; Hla S.-W. Nat. Nanotechnol. 2013, 8, 46. 10.1038/nnano.2012.218. [DOI] [PubMed] [Google Scholar]
  2. Chiaravalloti F.; Gross L.; Rieder K.-H.; Stojkovic S. M.; Gourdon A.; Joachim C.; Moresco F. Nat. Mater. 2007, 6, 30. 10.1038/nmat1802. [DOI] [PubMed] [Google Scholar]
  3. Schön J. H.; Meng H.; Bao Z. Nature 2001, 413, 713. 10.1038/35099520. [DOI] [PubMed] [Google Scholar]
  4. Kobayashi S.; Nishikawa T.; Takenobu T.; Mori S.; Shimoda T.; Mitani T.; Shimotani H.; Yoshimoto N.; Ogawa S.; Iwasa Y. Nat. Mater. 2004, 3, 317. 10.1038/nmat1105. [DOI] [PubMed] [Google Scholar]
  5. Schwierz F. Nat. Nanotechnol. 2010, 5, 487. 10.1038/nnano.2010.89. [DOI] [PubMed] [Google Scholar]
  6. Friend R. H.; Gymer R. W.; Holmes A. B.; Burroughes J. H.; Marks R. N.; Taliani C.; Bradley D. D. C.; Santos D. A. D.; Brédas J. L.; Lögdlund M.; Salaneck W. R. Nature 1999, 397, 121. 10.1038/16393. [DOI] [Google Scholar]
  7. Gross M.; Müller D. C.; Nothofer H.-G.; Scherf U.; Neher D.; Bräuchle C.; Meerholz K. Nature 2000, 405, 661. 10.1038/35015037. [DOI] [PubMed] [Google Scholar]
  8. Joachim C.; Gimzewski J. K.; Aviram A. Nature 2000, 408, 541. 10.1038/35046000. [DOI] [PubMed] [Google Scholar]
  9. Barth J. V.; Costantini G.; Kern K. Nature 2005, 437, 671. 10.1038/nature04166. [DOI] [PubMed] [Google Scholar]
  10. Sirringhaus H.; Brown P. J.; Friend R. H.; Nielsen M. M.; Bechgaard K.; Langeveld-Voss B. M. W.; Spiering A. J. H.; Janssen R. a. J.; Meijer E. W.; Herwig P.; de Leeuw D. M. Nature 1999, 401, 685. 10.1038/44359. [DOI] [Google Scholar]
  11. Baringhaus J.; Ruan M.; Edler F.; Tejeda A.; Sicot M.; Taleb-Ibrahimi A.; Li A.-P.; Jiang Z.; Conrad E. H.; Berger C.; Tegenkamp C.; de Heer W. A. Nature 2014, 506, 349. 10.1038/nature12952. [DOI] [PubMed] [Google Scholar]
  12. Ullmann F.; Bielecki J. Ber. Dtsch. Chem. Ges. 1901, 34, 2174. 10.1002/cber.190103402141. [DOI] [Google Scholar]
  13. Hla S.-W.; Bartels L.; Meyer G.; Rieder K.-H. Phys. Rev. Lett. 2000, 85, 2777. 10.1103/PhysRevLett.85.2777. [DOI] [PubMed] [Google Scholar]
  14. Björk J.; Hanke F.; Stafström S. J. Am. Chem. Soc. 2013, 135, 5768. 10.1021/ja400304b. [DOI] [PubMed] [Google Scholar]
  15. Koch M.; Ample F.; Joachim C.; Grill L. Nat. Nanotechnol. 2012, 7, 713. 10.1038/nnano.2012.169. [DOI] [PubMed] [Google Scholar]
  16. Reecht G.; Scheurer F.; Speisser V.; Dappe Y. J.; Mathevet F.; Schull G. Phys. Rev. Lett. 2014, 112, 047403. 10.1103/PhysRevLett.112.047403. [DOI] [PubMed] [Google Scholar]
  17. Grill L.; Dyer M.; Lafferentz L.; Persson M.; Peters M. V.; Hecht S. Nat. Nanotechnol. 2007, 2, 687. 10.1038/nnano.2007.346. [DOI] [PubMed] [Google Scholar]
  18. Lafferentz L.; Eberhardt V.; Dri C.; Africh C.; Comelli G.; Esch F.; Hecht S.; Grill L. Nat. Chem. 2012, 4, 215. 10.1038/nchem.1242. [DOI] [PubMed] [Google Scholar]
  19. Cai J.; Pignedoli C. A.; Talirz L.; Ruffieux P.; Söde H.; Liang L.; Meunier V.; Berger R.; Li R.; Feng X.; Müllen K.; Fasel R. Nat. Nanotechnol. 2014, 9, 896. 10.1038/nnano.2014.184. [DOI] [PubMed] [Google Scholar]
  20. Kawai S.; Saito S.; Osumi S.; Yamaguchi S.; Foster A. S.; Spijker P.; Meyer E. Nat. Commun. 2015, 6, 8098. 10.1038/ncomms9098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hla S.-W.; Meyer G.; Rieder K.-H. ChemPhysChem 2001, 2, 361.. [DOI] [PubMed] [Google Scholar]
  22. Repp J.; Liljeroth P.; Meyer G. Nat. Phys. 2010, 6, 975. 10.1038/nphys1802. [DOI] [Google Scholar]
  23. Reecht G.; Bulou H.; Scheurer F.; Speisser V.; Carrière B.; Mathevet F.; Schull G. Phys. Rev. Lett. 2013, 110, 056802. 10.1103/PhysRevLett.110.056802. [DOI] [PubMed] [Google Scholar]
  24. Wang S.; Wang W.; Lin N. Phys. Rev. Lett. 2011, 106, 206803. 10.1103/PhysRevLett.106.206803. [DOI] [PubMed] [Google Scholar]
  25. Gutzler R.; Walch H.; Eder G.; Kloft S.; Heckl W. M.; Lackinger M. Chem. Commun. 2009, 29, 4456. 10.1039/b906836h. [DOI] [PubMed] [Google Scholar]
  26. Blunt M. O.; Russell J. C.; Champness N. R.; Beton P. H. Chem. Commun. 2010, 46, 7157. 10.1039/c0cc01810d. [DOI] [PubMed] [Google Scholar]
  27. Bieri M.; Treier M.; Cai J.; Aït-Mansour K.; Ruffieux P.; Gröning O.; Gröning P.; Kastler M.; Rieger R.; Feng X.; Müllen K.; Fasel R. Chem. Commun. 2009, 6919. 10.1039/b915190g. [DOI] [PubMed] [Google Scholar]
  28. Basagni A.; Sedona F.; Pignedoli C. A.; Cattelan M.; Nicolas L.; Casarin M.; Sambi M. J. Am. Chem. Soc. 2015, 137, 1802. 10.1021/ja510292b. [DOI] [PubMed] [Google Scholar]
  29. Zhang H.; Lin H.; Sun K.; Chen L.; Zagranyarski Y.; Aghdassi N.; Duhm S.; Li Q.; Zhong D.; Li Y.; Müllen K.; Fuchs H.; Chi L. J. Am. Chem. Soc. 2015, 137, 4022. 10.1021/ja511995r. [DOI] [PubMed] [Google Scholar]
  30. Cai J.; Ruffieux P.; Jaafar R.; Bieri M.; Braun T.; Blankenburg S.; Muoth M.; Seitsonen A. P.; Saleh M.; Feng X.; Müllen K.; Fasel R. Nature 2010, 466, 470. 10.1038/nature09211. [DOI] [PubMed] [Google Scholar]
  31. Chen Y.-C.; de Oteyza D. G.; Pedramrazi Z.; Chen C.; Fischer F. R.; Crommie M. F. ACS Nano 2013, 7, 6123. 10.1021/nn401948e. [DOI] [PubMed] [Google Scholar]
  32. Bennett P. B.; Pedramrazi Z.; Madani A.; Chen Y.-C.; de Oteyza D. G.; Chen C.; Fischer F. R.; Crommie M. F.; Bokor J. Appl. Phys. Lett. 2013, 103, 253114. 10.1063/1.4855116. [DOI] [Google Scholar]
  33. Bombis C.; Ample F.; Lafferentz L.; Yu H.; Hecht S.; Joachim C.; Grill L. Angew. Chem., Int. Ed. 2009, 48, 9966. 10.1002/anie.200904645. [DOI] [PubMed] [Google Scholar]
  34. Kittelmann M.; Rahe P.; Nimmrich M.; Hauke C. M.; Gourdon A.; Kühnle A. ACS Nano 2011, 5, 8420. 10.1021/nn2033192. [DOI] [PubMed] [Google Scholar]
  35. Kittelmann M.; Nimmrich M.; Lindner R.; Gourdon A.; Kühnle A. ACS Nano 2013, 7, 5614. 10.1021/nn402018w. [DOI] [PubMed] [Google Scholar]
  36. Kolmer M.; Ahmad Zebari A. A.; Prauzner-Bechcicki J. S.; Piskorz W.; Zasada F.; Godlewski S.; Such B.; Sojka Z.; Szymonski M. Angew. Chem., Int. Ed. 2013, 52, 10300. 10.1002/anie.201303657. [DOI] [PubMed] [Google Scholar]
  37. Kolmer M.; Zuzak R.; Zebari A. A. A.; Godlewski S.; Prauzner-Bechcicki J. S.; Piskorz W.; Zasada F.; Sojka Z.; Bléger D.; Hecht S.; Szymonski M. Chem. Commun. 2015, 51, 11276. 10.1039/C5CC02989A. [DOI] [PubMed] [Google Scholar]
  38. Olszowski P.; Zapotoczny B.; Prauzner-Bechcicki J. S.; Vilas-Varela M.; Pérez D.; Guitián E.; Peña D.; Szymonski M. J. Phys. Chem. C 2015, 119, 27478. 10.1021/acs.jpcc.5b08883. [DOI] [Google Scholar]
  39. Heimel G.; Duhm S.; Salzmann I.; Gerlach A.; Strozecka A.; Niederhausen J.; Bürker C.; Hosokai T.; Fernandez-Torrente I.; Schulze G.; Winkler S.; Wilke A.; Schlesinger R.; Frisch J.; Bröker B.; Vollmer A.; Detlefs B.; Pflaum J.; Kera S.; Franke K. J.; Ueno N.; Pascual J. I.; Schreiber F.; Koch N. Nat. Chem. 2013, 5, 187. 10.1038/nchem.1572. [DOI] [PubMed] [Google Scholar]
  40. Borghetti P.; Santo G. D.; Castellarin-Cudia C.; Fanetti M.; Sangaletti L.; Magnano E.; Bondino F.; Goldoni A. J. Chem. Phys. 2013, 138, 144702. 10.1063/1.4798934. [DOI] [PubMed] [Google Scholar]
  41. Ziroff J.; Forster F.; Schöll A.; Puschnig P.; Reinert F. Phys. Rev. Lett. 2010, 104, 233004. 10.1103/PhysRevLett.104.233004. [DOI] [PubMed] [Google Scholar]
  42. Puschnig P.; Berkebile S.; Fleming A. J.; Koller G.; Emtsev K.; Seyller T.; Riley J. D.; Ambrosch-Draxl C.; Netzer F. P.; Ramsey M. G. Science 2009, 326, 702. 10.1126/science.1176105. [DOI] [PubMed] [Google Scholar]
  43. Lüftner D.; Ules T.; Reinisch E. M.; Koller G.; Soubatch S.; Tautz F. S.; Ramsey M. G.; Puschnig P. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 605. 10.1073/pnas.1315716110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Koller G.; Berkebile S.; Oehzelt M.; Puschnig P.; Ambrosch-Draxl C.; Netzer F. P.; Ramsey M. G. Science 2007, 317, 351. 10.1126/science.1143239. [DOI] [PubMed] [Google Scholar]
  45. Wießner M.; Ziroff J.; Forster F.; Arita M.; Shimada K.; Puschnig P.; Schöll A.; Reinert F. Nat. Commun. 2013, 4, 1514. 10.1038/ncomms2522. [DOI] [PubMed] [Google Scholar]
  46. Cardenas L.; Gutzler R.; Lipton-Duffin J.; Fu C.; Brusso J. L.; Dinca L. E.; Vondráček M.; Fagot-Revurat Y.; Malterre D.; Rosei F.; Perepichka D. F. Chem. Sci. 2013, 4, 3263. 10.1039/c3sc50800e. [DOI] [Google Scholar]
  47. Ruffieux P.; Cai J.; Plumb N. C.; Patthey L.; Prezzi D.; Ferretti A.; Molinari E.; Feng X.; Müllen K.; Pignedoli C. A.; Fasel R. ACS Nano 2012, 6, 6930. 10.1021/nn3021376. [DOI] [PubMed] [Google Scholar]
  48. Vasseur G.; Fagot-Revurat Y.; Sicot M.; Kierren B.; Moreau L.; Malterre D.; Cardenas L.; Galeotti G.; Lipton-Duffin J.; Rosei F.; Di Giovannantonio M.; Contini G.; Le Fèvre P.; Bertran F.; Liang L.; Meunier V.; Perepichka D. F. Nat. Commun. 2016, 7, 10235. 10.1038/ncomms10235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Basagni A.; Vasseur G.; Pignedoli C. A.; Vilas-Varela M.; Peña D.; Nicolas L.; Vitali L.; Lobo-Checa J.; de Oteyza D. G.; Sedona F.; Casarin M.; Ortega J. E.; Sambi M. ACS Nano 2016, 10, 2644. 10.1021/acsnano.5b07683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Linden S.; Zhong D.; Timmer A.; Aghdassi N.; Franke J. H.; Zhang H.; Feng X.; Müllen K.; Fuchs H.; Chi L.; Zacharias H. Phys. Rev. Lett. 2012, 108, 216801. 10.1103/PhysRevLett.108.216801. [DOI] [PubMed] [Google Scholar]
  51. Diebold U. Surf. Sci. Rep. 2003, 48, 53. 10.1016/S0167-5729(02)00100-0. [DOI] [Google Scholar]
  52. Sánchez-Sánchez C.; González C.; Jelinek P.; Méndez J.; de Andres P. L.; Martín-Gago J. A.; López M. F. Nanotechnology 2010, 21, 405702. 10.1088/0957-4484/21/40/405702. [DOI] [PubMed] [Google Scholar]
  53. Pang C. L.; Lindsay R.; Thornton G. Chem. Soc. Rev. 2008, 37, 2328. 10.1039/b719085a. [DOI] [PubMed] [Google Scholar]
  54. Ambrosch-Draxl C.; Majewski J. A.; Vogl P.; Leising G. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 9668. 10.1103/PhysRevB.51.9668. [DOI] [PubMed] [Google Scholar]
  55. Lipton-Duffin J. A.; Ivasenko O.; Perepichka D. F.; Rosei F. Small 2009, 5, 592. 10.1002/smll.200801943. [DOI] [PubMed] [Google Scholar]
  56. Arado O. D.; Mönig H.; Franke J.-H.; Timmer A.; Held P. A.; Studer A.; Fuchs H. Chem. Commun. 2015, 51, 4887. 10.1039/C4CC09634G. [DOI] [PubMed] [Google Scholar]
  57. Abadía M.; González-Moreno R.; Sarasola A.; Otero-Irurueta G.; Verdini A.; Floreano L.; Garcia-Lekue A.; Rogero C. J. Phys. Chem. C 2014, 118, 29704. 10.1021/jp505802h. [DOI] [Google Scholar]
  58. Kanuru V. K.; Kyriakou G.; Beaumont S. K.; Papageorgiou A. C.; Watson D. J.; Lambert R. M. J. Am. Chem. Soc. 2010, 132, 8081. 10.1021/ja1011542. [DOI] [PubMed] [Google Scholar]
  59. Di Giovannantonio M.; El Garah M.; Lipton-Duffin J.; Meunier V.; Cardenas L.; Fagot Revurat Y.; Cossaro A.; Verdini A.; Perepichka D. F.; Rosei F.; Contini G. ACS Nano 2013, 7, 8190. 10.1021/nn4035684. [DOI] [PubMed] [Google Scholar]
  60. Gutzler R.; Cardenas L.; Lipton-Duffin J.; El Garah M.; Dinca L. E.; Szakacs C. E.; Fu C.; Gallagher M.; Vondráček M.; Rybachuk M.; Perepichka D. F.; Rosei F. Nanoscale 2014, 6, 2660. 10.1039/c3nr05710k. [DOI] [PubMed] [Google Scholar]
  61. Scanlon D. O.; Dunnill C. W.; Buckeridge J.; Shevlin S. A.; Logsdail A. J.; Woodley S. M.; Catlow C. R. A.; Powell M. J.; Palgrave R. G.; Parkin I. P.; Watson G. W.; Keal T. W.; Sherwood P.; Walsh A.; Sokol A. A. Nat. Mater. 2013, 12, 798. 10.1038/nmat3697. [DOI] [PubMed] [Google Scholar]
  62. Yim C. M.; Pang C. L.; Thornton G. Phys. Rev. Lett. 2010, 104, 036806. 10.1103/PhysRevLett.104.036806. [DOI] [PubMed] [Google Scholar]
  63. Wendt S.; Sprunger P. T.; Lira E.; Madsen G. K. H.; Li Z.; Hansen J. O.; Matthiesen J.; Blekinge-Rasmussen A.; Lægsgaard E.; Hammer B.; Besenbacher F. Science 2008, 320, 1755. 10.1126/science.1159846. [DOI] [PubMed] [Google Scholar]
  64. Reinisch E. M.; Ules T.; Puschnig P.; Berkebile S.; Ostler M.; Seyller T.; Ramsey M. G.; Koller G. New J. Phys. 2014, 16, 023011. 10.1088/1367-2630/16/2/023011. [DOI] [Google Scholar]
  65. Son Y.-W.; Cohen M. L.; Louie S. G. Phys. Rev. Lett. 2006, 97, 216803. 10.1103/PhysRevLett.97.216803. [DOI] [PubMed] [Google Scholar]
  66. Cui X.; Wang Z.; Tan S.; Wang B.; Yang J.; Hou J. G. J. Phys. Chem. C 2009, 113, 13204. 10.1021/jp901657u. [DOI] [Google Scholar]
  67. Yin X.-L.; Calatayud M.; Qiu H.; Wang Y.; Birkner A.; Minot C.; Wöll Ch. ChemPhysChem 2008, 9, 253–256. 10.1002/cphc.200700612. [DOI] [PubMed] [Google Scholar]
  68. Otero-Irurueta G.; Martínez J. I.; Lovat G.; Lanzilotto V.; Méndez J.; López M. F.; Floreano L.; Martín-Gago J. A. J. Phys. Chem. C 2015, 119, 7809. 10.1021/acs.jpcc.5b00851. [DOI] [Google Scholar]
  69. Palmgren P.; Nilson K.; Yu S.; Hennies F.; Angot T.; Layet J.-M.; Le Lay G.; Göthelid M. J. Phys. Chem. C 2008, 112, 5972. 10.1021/jp711311s. [DOI] [Google Scholar]
  70. Cao L.; Wang Y.; Zhong J.; Han Y.; Zhang W.; Yu X.; Xu F.; Qi D.-C.; Wee A. T. S. J. Phys. Chem. C 2011, 115, 24880. 10.1021/jp2083924. [DOI] [Google Scholar]
  71. Hebenstreit E. L. D.; Hebenstreit W.; Geisler H.; Ventrice C. A. Jr.; Hite D. A.; Sprunger P. T.; Diebold U. Surf. Sci. 2002, 505, 336. 10.1016/S0039-6028(02)01385-7. [DOI] [Google Scholar]
  72. Klusek Z.; Pierzgalski S.; Datta S. Appl. Surf. Sci. 2004, 221, 120. 10.1016/S0169-4332(03)00877-8. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja6b02151_si_001.pdf (1.8MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES