Abstract
The distribution of mutational effects on fitness is central to evolutionary genetics. Typical univariate distributions, however, cannot model the effects of multiple mutations at the same site, so we introduce a model in which mutations at the same site have correlated fitness effects. To infer the strength of that correlation, we developed a diffusion approximation to the triallelic frequency spectrum, which we applied to data from Drosophila melanogaster. We found a moderate positive correlation between the fitness effects of nonsynonymous mutations at the same codon, suggesting that both mutation identity and location are important for determining fitness effects in proteins. We validated our approach by comparing it to biochemical mutational scanning experiments, finding strong quantitative agreement, even between different organisms. We also found that the correlation of mutational fitness effects was not affected by protein solvent exposure or structural disorder. Together, our results suggest that the correlation of fitness effects at the same site is a previously overlooked yet fundamental property of protein evolution.
Keywords: diffusion approximation, distribution of fitness effects, Drosophila melanogaster, nonsynonymous mutations, triallelic sites
MUTATIONS create genetic variation within populations, some of which causes differential fitness among individuals upon which natural selection operates. The effects of mutations on fitness range from strongly deleterious to strongly beneficial, and the distribution of fitness effects (DFE) is key for many problems in genetics, from the evolution of sex (Barton and Charlesworth 1998) to the architecture of human disease (Di Rienzo 2006). For protein-coding regions, there are generally many strongly deleterious or lethal mutations, a similar number of moderately deleterious or nearly neutral mutations, and a small number of beneficial mutations (Eyre-Walker and Keightley 2007). The DFE may be determined experimentally through direct measurements of mutation fitness effects in clonal populations of viruses, bacteria, or yeast (Wloch et al. 2001; Sanjuán et al. 2004), and recent studies have provided high-resolution DFEs for single genes (Bank et al. 2014; Firnberg et al. 2014) and for beneficial mutations (Levy et al. 2015). The DFE may also be inferred from comparative (Nielsen and Yang 2003; Tamuri et al. 2012) or population genetic (Williamson et al. 2005; Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008) data, although these approaches have little power for strongly deleterious mutations.
In the typical population genetic approach for estimating the DFE, the population demography is first inferred using a putatively neutral class of mutations, and the DFE for another class of mutations is inferred by modeling the distribution of allele frequencies expected under a model of demography plus selection. Most population genetic inference has focused on biallelic loci, for which the ancestral allele and a single mutant (derived) allele are segregating in the population. When many individuals are sequenced, however, even single-nucleotide loci are often found to be multiallelic, with three or more segregating alleles. Multiallelic loci pose a challenge for modeling selection. To use a typical univariate DFE, one must assume that mutations at the same site all have either equal fitness effects (so that mutation location completely determines fitness) or independent fitness effects (so that mutation identity completely determines fitness). Neither of these assumptions is biologically well founded, suggesting the need for more sophisticated models of fitness effects. Here we introduce a model of correlated fitness effects for mutations at the same site, and we analyze sequence data to infer the strength of that correlation.
Our inference is based on triallelic codons, loci where three mutually nonsynonymous amino acid alleles are segregating in the population (Figure 1A). Interest in triallelic loci has grown recently, because such loci, while typically much less numerous than biallelic loci, are often observed in sequencing studies that sample tens or hundreds of individuals within single populations. For example, Hodgkinson and Eyre-Walker (2010) found in humans a roughly twofold excess of triallelic sites over the expectation under neutral conditions and random distribution of mutations. This led them to suggest an alternate mutational mechanism that could simultaneously generate two unique mutations, although recent population growth and substructure can account for the distribution of observed triallelic variation (Jenkins et al. 2014). Recently, Jenkins, Mueller, and Song (Jenkins and Song 2011; Jenkins et al. 2014) developed a coalescent method to calculate the expected triallelic frequency spectrum under arbitrary single-population demography. They showed that triallelic frequencies are sensitive to demographic history (Jenkins and Song 2011; Jenkins et al. 2014), but their method cannot model selection.
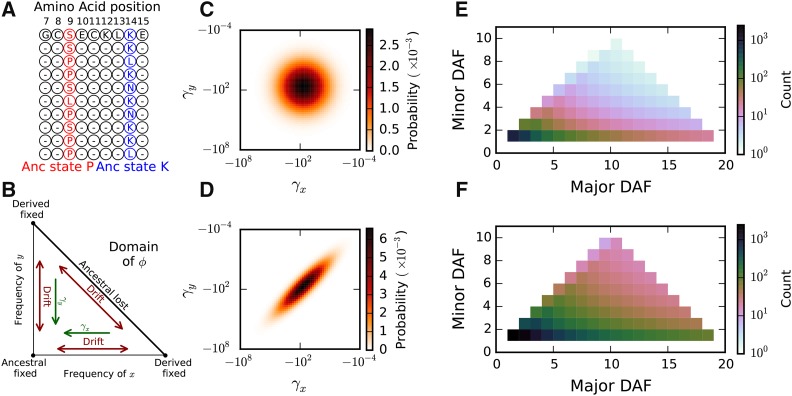
Figure 1.
The triallelic frequency spectrum (TFS). (A) Mutually nonsynonymous triallelic loci in protein-coding regions have three observed segregating amino acid alleles. Here, with 10 sampled chromosomes, at position 9 the major and minor derived alleles, serine (S) and leucine (L), have frequencies 4 and 1, so this site contributes to the (4, 1) bin of the TFS. Similarly, position 14 contributes to the (2, 2) bin. (B) The domain of the triallelic diffusion equation, ϕ, from Equation 5. The corners correspond to fixation of one of the three alleles, and the edges correspond to loss of one of the three alleles. New mutations enter the population along the horizontal and vertical axes, with density dependent on the background biallelic frequency spectrum. Pairs of selection coefficients for the two derived nonsynonymous mutations are sampled from a bivariate DFE, which includes a parameter for correlation between selection coefficients ρ. (C) For an uncorrelated DFE, with the selection coefficients are independent and often dissimilar. (D) For strong correlation, here selection coefficients are typically very similar. (E and F) The correlation coefficient affects the expected frequency spectrum, with stronger correlation (F: ), resulting in a higher proportion of intermediate- to high-frequency derived alleles and more triallelic sites overall relative to weak correlation (E: ).
In this study, we developed a numerical diffusion simulation of expected triallelic allele frequencies for single populations with arbitrary demography and selection at one or both derived alleles. We coupled this simulation to a DFE that models the correlation between fitness effects of the two derived alleles. We applied this approach to infer the correlation coefficient of fitness effects from whole-genome Drosophila melanogaster data, inferring a moderate positive correlation between fitness effects of mutually nonsynonymous mutations in the same codon. To validate our inference, we compared this approach with direct biochemical experiments, finding strong agreement. Finally, we applied our approach to biologically relevant subsets of nonsynonymous mutations to assess how the fitness effects correlation varies among classes of mutations.
Theory and Methods
Here we describe the model for triallelic loci and how we solve the triallelic diffusion equation to obtain the expected sample triallelic frequency spectrum under arbitrary demography and selection. We also describe how to obtain the sample frequency spectrum under an arbitrary univariate or bivariate DFE, which we used in our inference of the correlation coefficient for selection strength at triallelic loci. Finally, we compared our results to correlation coefficients estimated from mutational scanning experiment data, discussed here as well.
Model for triallelic loci
The diffusion approximation we used is based on a triallelic extension to the standard Wright–Fisher (WF) model for allele frequency dynamics, which assumes nonoverlapping generations and random mating. The two derived alleles have selection coefficients, and so their fitnesses relative to the ancestral allele are and If the two derived alleles have frequencies in generation t in a diploid population of size N, then their frequencies in generation are sampled from a trinomial distribution, such that the probability of sampling is
| (1) |
where
and is the trinomial coefficient From here on, we focus on relative allele frequencies and
Most applications of the biallelic WF model assume infinite sites, so each new mutation is unique, and new mutations enter the population at a rate proportional to Here is the population-scaled mutation rate, is the ancestral effective population size, and μ is the per-generation mutation rate. Mutations begin at frequency and are assumed to evolve independently. Given these assumptions, the density function for derived allele frequencies in a population can be approximated by diffusion theory (Kimura 1964), such that the expected total number of alleles with frequency between and is a key result from Poisson random field theory (Sawyer and Hartl 1992). The expected sample allele frequency spectrum F with n samples is then
| (2) |
where is the binomial coefficient. The likelihood of an observed allele frequency spectrum under this model is then a product of Poisson likelihoods for each entry in the spectrum (Sawyer and Hartl 1992).
Whereas new biallelic mutations begin at frequency triallelic loci are created when a novel mutation occurs at a locus that is already biallelic. The new derived allele initially has frequency and the existing derived allele has a frequency drawn from the population distribution of biallelic frequencies in that generation. The net rate at which triallelic loci arise is thus
| (3) |
where is the rate for mutations that hit existing biallelic sites and produce a third allele. Triallelic sites then evolve under the three-locus WF model, and we denote the density function for frequencies of triallelic loci as The triallelic frequency spectrum summarizes sequence data from a sample of individuals by storing the counts of triallelic loci with each set of observed derived allele frequencies (Jenkins et al. 2014) (Figure 1, E and F). The expected triallelic frequency spectrum T with n samples is proportional to the integral of the density function φ against the trinomial sampling distribution:
| (4) |
Because the net triallelic mutation rate is sensitive to mutation rate heterogeneity, in our triallelic analyses we focused on the normalized triallelic frequency spectrum, which does not depend on the overall rate of creation. Similarly, because the order in which the two derived alleles arose is often unknown, we considered only counts of major and minor derived alleles, which have respectively higher or lower sample frequencies (Figure 1). That is, for given major and minor derived allele frequencies i and j, with we collapsed the and counts together into the bin. If in a sample we observe counts of independent triallelic frequencies Poisson Random Field theory shows that the data are Poisson distributed with mean enabling likelihood calculations.
Diffusion approximation to the triallelic frequency spectrum with selection
To obtain the expected sample frequency spectrum for a given model of selection and demography, we numerically solved the corresponding diffusion equation. First described by Kimura (1955, 1956), the triallelic diffusion equation models the evolution of the density function for the expected number of loci in the population with derived allele frequencies such that and (Figure 1B):
| (5) |
Time τ is measured is units of generations, where is the ancestral effective population size. The spatial second-derivative terms account for genetic drift, which is scaled by the relative population size and the mixed derivative term accounts for the covariance in allele frequency changes. The population-scaled selection coefficient is where s is the relative fitness of the derived vs. ancestral allele. Here that selection coefficient must be adjusted to to account for competition between the two segregating derived alleles, dependent on their allele frequencies. For example, if their selection coefficients are roughly equal, they will be effectively neutral when at high frequency. In general,
| (6) |
with a similar expression for
Like the biallelic diffusion method Equation 5 does not account for recurrent mutation, which would tend to increase derived allele frequencies. Recurrent mutation could be accounted for in the first-derivative terms, but at the cost of additional model complexity. If it is common, neglecting recurrent mutation can bias inferences of mutation rate, population size, and selection (Desai and Plotkin 2008; Mathew et al. 2013). Applying our present theory thus requires that the mutation rate be high enough to create a substantial number of triallelic sites for inference, but not so high that a large fraction of biallelic or triallelic sites are affected by recurrent mutation. For most eukaryotes, including humans and Drosophila, mutation rates are low enough that recurrent mutation is negligible in most applications (Desai and Plotkin 2008).
Some analytic results are known for triallelic diffusion (Tier and Keller 1978; Tier 1979; Spencer and Barakat 1992), but we solved Equation 5 numerically. We used a finite-difference method similar to that in (Gutenkunst et al. 2009). To integrate the diffusion equation forward in time, we used operator splitting to separately apply the nonmixed and mixed derivative terms each time step (Supplemental Material, File S1). We integrated the nonmixed terms, using a conservative alternating direction implicit (ADI) finite difference scheme (Chang and Cooper 1970). We integrated the mixed term, using a standard explicit scheme for mixed derivatives. We used uniform grids in x and y with equal grid spacing so that grid points lie directly on the diagonal boundary of the domain, which readily allowed the diagonal boundary to be absorbing. Although these integration schemes worked well in the interior of the domain, application at the diagonal boundary led to an excess of density being lost (File S1 and Figure S1). To avoid this excess loss, we did not apply the ADI and mixed derivative schemes at the closest grid points to the diagonal boundary. Instead, at each time step we calculated the amount of density at each grid point that would fix along the diagonal boundary, and we directly removed that amount from the numerical density function and added it to the boundary.
To inject density into φ for new triallelic loci, at each time step we added density to the first interior rows of grid points based on the expected background biallelic frequency For example, we added to the row of grid points with weight for point proportional to the biallelic population allele density at frequency x. We directly coupled with to track To obtain the expected sample frequency spectrum T from the population frequency spectrum φ, we numerically integrated against the trinomial distribution with sample size n, using Equation 4. Our code implementing these methods is integrated into available at https://bitbucket.org/gutenkunstlab/dadi.
Calculating frequency spectra under a DFE
Given a DFE, the expected sample frequency spectrum can be obtained by integrating over the expected frequency spectrum for each selection coefficient, weighted by the DFE. For biallelic sites, the DFE is a univariate distribution. For triallelic sites, the DFE is a two-dimensional joint distribution, because there are two derived alleles. Moreover, the two marginal distributions are identical, because we assume no knowledge of which allele arose first.
For our primary analysis, we used a lognormal model for the deleterious triallelic DFE (Figure 1, C and D), plus a point mass of positive selection. The lognormal distribution readily generalizes to an arbitrary number of dimensions, and the bivariate lognormal distribution includes a correlation coefficient ρ that characterizes the correlation between selection coefficients. If the selection coefficients of the two derived alleles at a single triallelic locus are independent, whereas if they are equal. For a fixed marginal DFE, as the correlation coefficient ρ increases, more segregating triallelic loci are expected, particularly at moderate and high derived allele frequencies (Figure 1, C–F). We quantified the relative importance of identity and location for protein mutation fitness effects through ρ; low correlation suggests that identity is more important, whereas high correlation suggests that location within the protein is more important.
To numerically integrate over the univariate DFE, we used a logarithmically spaced grid with 2000 grid points ranging from to along with and a point mass of positive selection Biallelic spectra were cached for each resulting in 2001 cached spectra. We assumed that alleles with were effectively lethal and did not contribute to the sample frequency spectrum. We also assumed that alleles with were effectively neutral, and we used the cached spectrum for for contributions from this range of the DFE (Figure S2A).
To integrate over the bivariate DFE we used a logarithmically spaced grid with 50 grid points ranging from to along with and determined by the univariate DFE fit. We cached spectra for each possible pair yielding cached spectra. A pair of selection coefficients could fall into four quadrants, depending on the sign of and The overall frequency spectrum was calculated by summing over the weighted frequency spectra for each quadrant based on the DFE parameters and ρ. The weights were for both for one selection coefficient positive and the other negative, and for both These weights were found by taking the distribution of two point masses (one for positive selection, and one for negative selection, ) and extending it to a bivariate distribution of point masses with correlation coefficient ρ (File S1). To integrate over the continuous distributions with one or both of the selection coefficients negative, we used the trapezoid rule. We approximated as effectively neutral and as effectively lethal (Figure S2B).
Genomic data
We extracted SNPs from phase 3 of the Drosophila Population Genomics Project (DPGP3) population of fruit flies from the Drosophila Genome Nexus Data (Lack et al. 2015). The data we used consist of 197 sequenced genomes from a Zambian population obtained through high-coverage haploid embryo sequencing. This population has high genetic diversity, and it did not experience the out-of-Africa bottleneck or New World admixture that other D. melanogaster populations have experienced (Lack et al. 2015). We used Annovar (Wang et al. 2010) to determine the transcript and codon position of each coding SNP. The ancestral state of each codon was determined using the aligned sequences of D. melanogaster (April 2006, dm3) and D. simulans (droSim1) downloaded from the University of California, Santa Cruz genome database, by assuming that the D. simulans allele was ancestral. We excluded loci with no aligned D. simulans sequence. We downloaded the reference transcript sequences from Ensembl Biomart (Flicek et al. 2014) and used the ancestral states determined by the droSim1 alignment to determine the ancestral codon state.
Inferring the selection correlation coefficient
In our application to D. melanogaster, we used biallelic synonymous data to infer the single-population demographic history and then used nonsynonymous data to infer the parameters of the DFE. Using the unfolded synonymous allele frequency spectrum, we fitted a neutral three-epoch demographic model. This model has two instantaneous size changes, at times and in the past, with constant population sizes, and relative to the ancestral population size. We also included a parameter to account for ancestral state misidentification, which creates an excess of high-frequency derived alleles (Baudry and Depaulis 2003). Specifically, we compared the data not with the expected true unfolded frequency spectrum under the demographic model, but rather with the expected observed unfolded frequency such that where n is the sample size. We chose to include misidentification in our model rather than adjusting the data spectra (Hernandez et al. 2007), because adjusting the data leads to violations of the Poisson random field assumption, most obviously when the adjustment leads to negative entries in the data spectrum. The population-scaled mutation rate was an implicit free parameter. We used the built-in optimization routines in (Gutenkunst et al. 2009) to fit the model to the data. We fixed this demographic model for all future inferences.
The unfolded biallelic nonsynonymous allele frequency spectrum was used to infer the marginal DFE. As described above, we used a lognormal distribution for negative selection combined with a point mass of positive selection. This yielded a total of four parameters, μ and σ for the lognormal portion and and proportion for the point mass. As in the fits for demography using synonymous data, we also included a parameter to model ancestral state misidentification. In this fit, the population-scaled mutation rate was fixed to and we again used ’s optimization routines to fit the DFE to the data.
Finally, we used triallelic data with two mutually nonsynonymous derived codons to infer the correlation coefficient ρ. We fixed the demography to that inferred from the biallelic synonymous data, and we fixed the DFE parameters μ, σ, and to the values inferred from the biallelic nonsynonymous data. This left the correlation coefficient ρ as the only free parameter of the bivariate DFE, and we also included a free parameter to account for ancestral misidentification. Assuming that the two observed derived alleles were equally likely to be the true ancestral allele, we calculated the expected observed triallelic spectrum from the expected true spectrum by We also left the overall population-scaled mutation rate for triallelic loci as an implicit free parameter, so our fit considered only the distribution of triallelic codons among frequency classes, not the overall number of such codons. We did this because the overall number of triallelic codons can be strongly affected by mutation rate heterogeneity, and imperfect modeling of that heterogeneity could bias our results.
We estimated model parameters by maximum composite likelihood. Following the Poisson random field framework, likelihoods of the data D given the model parameters were calculated by assuming that each entry in the observed triallelic frequency spectrum was an independent Poisson random variable with mean (Sawyer and Hartl 1992), where T is the expected triallelic frequency spectrum generated under
| (7) |
Because our SNP data are not actually independent, is not the true likelihood, but rather a composite likelihood. To account for this, we calculated parameter uncertainties for each model fit, using the Godambe information matrix (Coffman et al. 2016), which adjusts the composite-likelihood statistic to account for the effects of linkage. To do so, we generated 1000 bootstrap data sets by dividing the D. melanogaster autosomal genome into 1000 regions of equal length and resampling among these regions.
Tests on simulated data
To generate simulated data for tests of statistical power, we first calculated the expected frequency spectrum under each model considered, using our diffusion method. To generate an observed frequency spectrum with exactly n entries, we generated n multinomial samples of frequencies, weighted by the expected frequency spectrum. To generate an observed frequency spectrum with a given mutation rate θ, we scaled the expected frequency spectrum by θ, treated the bin weights as Poisson random variables, and sampled independently for each bin.
Mutational scanning data
For comparison with our population genetic inference, we considered data from three mutational scanning studies (Roscoe et al. 2013; Firnberg et al. 2014; Starita et al. 2015). Each study assayed a different protein from a different organism, using a different proxy for fitness. In all three experiments, the distribution of fitnesses was bimodal, with peaks of moderately and strongly deleterious mutations, although the relative sizes of these peaks differed markedly between experiments (Figure S3, A–C). To calculate the fitness correlation coefficient, we sampled a pair of mutually nonsynonymous mutations from each site in the protein (excluding mutations without reported fitness) and calculated the Pearson correlation of those fitnesses. The confidence intervals in Table 1 are 2.5% and 97.5% quantiles from 10,000 repetitions of this sampling. To visualize the correlations, we calculated the proportion of mutually nonsynonymous mutation pairs within each possible bin of joint fitness effects (Figure 4B and Figure S3, D–I). Because our population-genetic analysis is not sensitive to strongly deleterious mutations, we focused our analysis on moderately deleterious mutations (shaded regions in Figure S3, A–C, joint distributions in Figure S3, D–F). For details on each data set, see File S1.
Table 1. Fitness effect correlation coefficients for nonsynonymous mutations at the same codon, inferred from population genomic data and biochemical experiments.
| Approach | Data set | ρ | 95% C.I. |
|---|---|---|---|
| Population genomic data | D. melanogaster all | 0.51 | 0.45–0.57 |
| Biochemical experiments | E. coli TEM-1 β-lactamase (Firnberg et al. 2014) | 0.41 | 0.34–0.50 |
| Yeast ubiquitin (Roscoe et al. 2013) | 0.34 | 0.20–0.56 | |
| Human BRCA1 (Starita et al. 2015) | 0.32 | 0.16–0.48 | |
| Population genomic data | 20% most similar amino acids | 0.72 | 0.58–0.85 |
| 20% most dissimilar amino acids | 0.24 | 0.15–0.32 | |
| 20% highest solvent accessibility | 0.54 | 0.43–0.65 | |
| 20% lowest solvent accessibility | 0.50 | 0.37–0.63 | |
| Disordered residues | 0.54 | 0.45–0.62 | |
| Ordered residues | 0.45 | 0.35–0.55 |
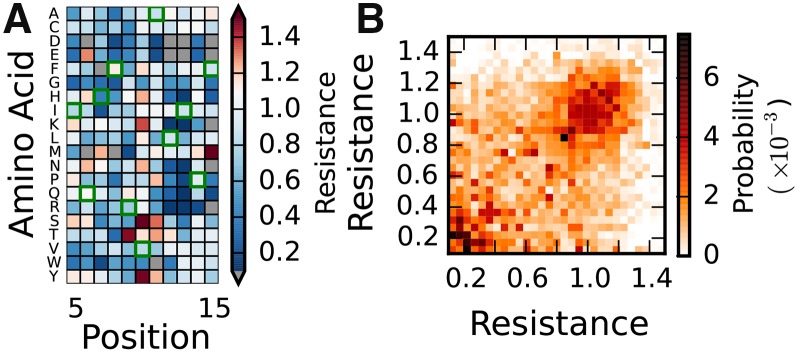
Figure 4.
Mutational scanning data. (A) Partial mutational fitness landscape for E. coli TEM-1 β-lactamase, adapted from Firnberg et al. (2014). For almost all possible single mutants, fitness was assayed as relative antibiotic resistance. Gray entries denote mutations not measured, and green squares highlight the ancestral sequence. (B) Joint distribution of fitnesses for mutually nonsynonymous mutations for TEM-1 β-lactamase, using data from Firnberg et al. (2014). For other data sets in Table 1, see Figure S3.
Data availability
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.
Results and Discussion
We first validated our diffusion approach to calculating the expected triallelic frequency spectrum through comparisons with coalescent simulations including demography (Figure S4) and Wright–Fisher simulations including selection (Figure S5). We then applied our method to genomic data from D. melanogaster to infer the strength of correlation of selection coefficients for nonsynonymous mutations that occur at the same codon in protein-coding regions. We then used simulations to characterize the performance of our approach with varying amounts of data and possible model misspecification. Finally, we compared our results to inferences made from deep mutation scanning experiments and refined our inferences to consider biologically relevant subsets of the data.
Correlation of selection strengths for nonsynonymous mutations at the same site
To estimate the correlation between fitness effects of amino acid-altering mutations, we used 197 Zambian D. melanogaster whole-genome sequences from the DPGP3 (Lack et al. 2015). We chose this population because it has high genetic diversity (and thus many triallelic sites) and a demographic history without admixture from non-sub-Saharan populations (Lack et al. 2015), which allowed us to model the population’s demographic history using a single-population model. Recurrent mutation is expected to be rare in this population, because only of sites are polymorphic, and of the nonsynonymous sites, only are triallelic. As detailed in Theory and Methods, we first inferred demographic history using biallelic synonymous sites. We then inferred the marginal DFE for newly arising nonsynonymous mutations, using that demographic model and the biallelic nonsynonymous data. Finally, we inferred the fitness effects correlation coefficient, using our inferred demography and marginal DFE and the mutually nonsynonymous triallelic loci in the data. For all model fits, we included a parameter to account for ancestral state misidentification, which creates an excess of high-frequency derived alleles (Baudry and Depaulis 2003).
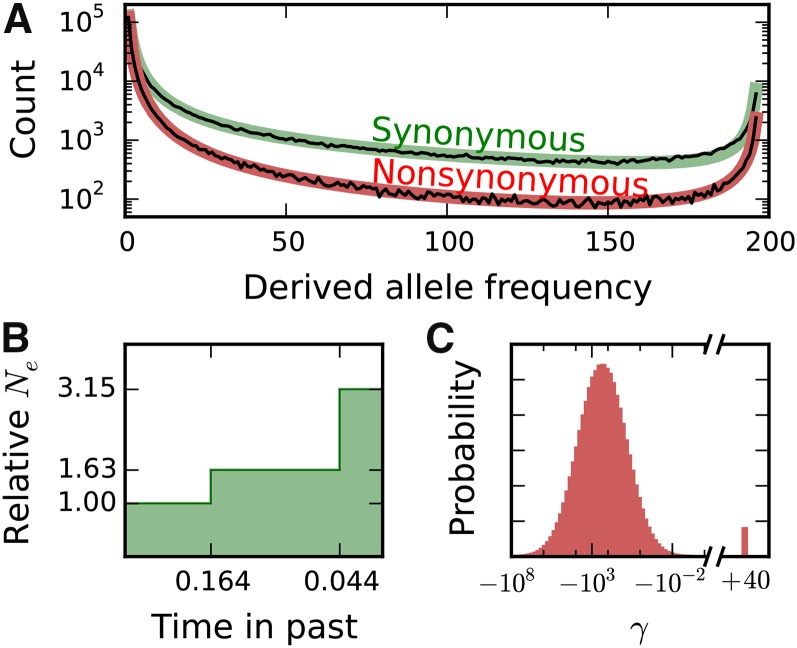
We used (Gutenkunst et al. 2009) to fit a three-epoch population size model to the unfolded biallelic synonymous frequency spectrum (Figure 2, A and B, and Table S1). We fixed this demographic model for all future inferences, and we fitted a univariate DFE to the biallelic nonsynonymous data. For negatively selected sites (), we assumed a lognormal distribution of selection coefficients with mean and variance parameters μ and σ, which has been previously shown to be a good approximation for the biallelic DFE for D. melanogaster (Kousathanas and Keightley 2013). Our DFE also included a point mass modeling a proportion of positively selected sites with scaled selection coefficient Our inferred biallelic DFE (Figure 2C and Table S1) fits the data well (Figure 2A), with just under 1% of new mutations inferred to be beneficial (inferred ). When fitting the DFE to the nonsynonymous data, the parameters for the lognormal portion (negatively selected sites) were tightly constrained, but and were confounded and inversely correlated, as found in other studies (Sella et al. 2009; Schneider et al. 2011). Our inferred proportions of mutations in various selective regimes agreed well with prior work (Table S2).
Figure 2.
Inferences of demographic history and marginal distribution of fitness effects from biallelic data. (A) Biallelic synonymous and nonsynonymous data (thin black lines) and corresponding maximum-likelihood model fits (thick colored lines). Ancestral state misidentification is likely responsible for most of the excess of high-frequency derived alleles, and a parameter to model such misidentification was included in both the synonymous and nonsynonymous models. (B) Inferred demographic model, with two instantaneous population size changes. Time is in units of generations, where is the ancestral effective population size. (C) Inferred distribution of fitness effects, lognormally distributed for negatively selected mutations with a proportion of positively selected mutations.
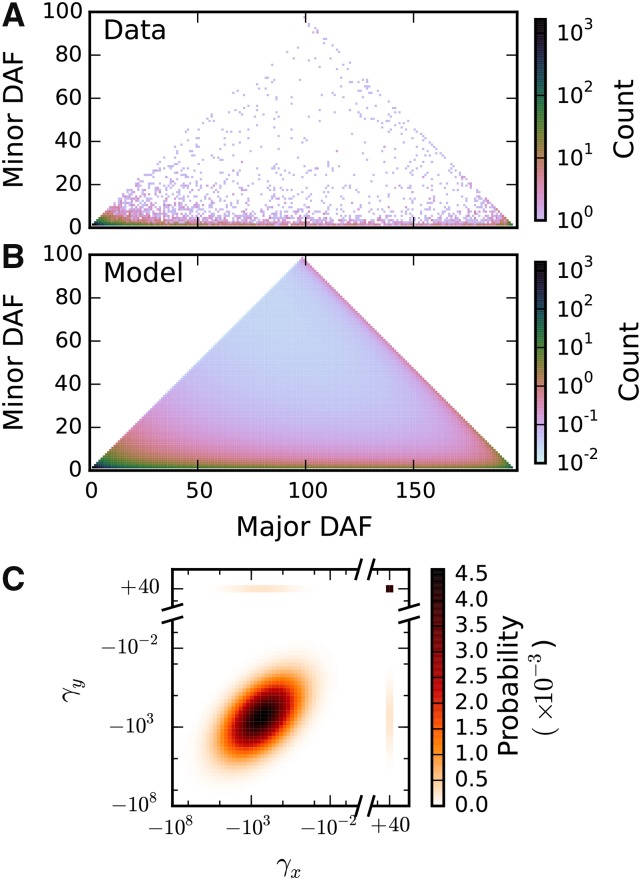
We worked at the codon level to assess the correlation in selection coefficients for nonsynonymous mutations, so a triallelic locus could arise from two mutations at the same nucleotide or at different nucleotides in the same codon. We extended our inferred one-dimensional DFE to two dimensions, fixing the parameters and so that the correlation coefficient ρ was the only free parameter of the bivariate lognormal distribution, along with a single parameter for ancestral misidentification. Fitting to 10,471 mutually nonsynonymous triallelic loci (Figure 3A), we inferred (Figure 3B, Table 1, and Table S1). Selection coefficients for nonsynonymous mutations at the same codon are thus somewhat but not completely correlated, so location and identity play roughly equal roles in determining mutation fitness effects.
Figure 3.
Inference of selection correlation coefficient from triallelic data. (A) The observed triallelic frequency spectrum for mutually nonsynonymous triallelic sites, which contained 10,471 triallelic sites. (B) The best-fit model, optimizing the correlation coefficient ρ and the ancestral misidentification parameters. (C) Joint distribution of selection coefficients from the maximum-likelihood inferred correlation coefficient of Selection coefficients for nonsynonymous mutations at the same site are moderately correlated.
Effects of data quality and model misspecification
Statistical power to infer the selection correlation coefficient varies with the number of observed triallelic loci and the number of sampled individuals. Inference may also be biased by distortions in the observed frequency spectrum due to sequencing error or by misspecification of the demographic or selection model. To assess the sensitivity of our analysis to such effects, we considered both fits to simulated data and alternative fits to the Drosophila data.
There were 10,471 mutually nonsynonymous triallelic codon polymorphisms in the 197 sampled genomes of the Zambian fruit fly data, which yielded a tight confidence interval for the selection correlation coefficient (Table 1). To test the power of our inference for different true values of the underlying correlation coefficient and smaller numbers of sampled individuals or triallelic loci, we fitted simulated data sets, assuming the exact demography and marginal DFE were known. As expected, inferences of the correlation coefficient were unbiased, and power increased with increasing number of observed triallelic loci (Figure S6, A–E). For a constant number of observed triallelic loci, the precision of the inference was insensitive to the number of sampled individuals (Figure S6F), suggesting that capturing rare triallelic variants is not crucial. To infer the correlation coefficient to a similar precision to that in the mutational-scanning studies, >2000 triallelic sites were needed, suggesting that our inference can be carried out only for populations with high genetic diversity. For example, in the 1000 Genomes Project Phase 3 human data (1000 Genomes Project Consortium 2015), among the 216 genomes from the Yoruba population, there were only 658 mutually nonsynonymous triallelic codons for which we were able to determine the ancestral state. Based on our fits to simulated data, we would not have power to accurately infer the correlation coefficient from these data.
Errors in sequencing may distort the observed site frequency spectrum, particularly at low frequencies. To test the sensitivity of our approach to sequencing error, we simulated data under our three-epoch demographic model and DFE, plus an additional model for sequencing error. The model assumed that each sequenced base had probability to be incorrectly identified; that is, with probability ε, for each polymorphic site, an individual’s true derived base was called as ancestral, or an individual’s true ancestral base was called as derived (Johnson and Slatkin 2008). We then refitted parameters for all of our models to both the biallelic and triallelic data simulated under this model. We found that high error rates () biased our inference of the selection correlation coefficient upward (Figure S7). This is likely because, under this model, sequencing error reduces the proportion of alleles observed at low vs. moderate and high frequencies, and higher values of ρ similarly reduce the proportion of alleles expected at low frequency vs. high and moderate frequencies (Figure 1, C–F).
Sequencing errors may bias inference, but the DPGP3 D. melanogaster data we used are high-coverage (30–50) haploid sequences (Lack et al. 2015), so we expect sequencing error was negligible in our inference. In particular, Lack et al. (2015) report error rates on the order per site, below the error rate that caused bias in our simulation study.
To assess the sensitivity of our inferences to the demographic model, we fitted two additional models to the Drosophila data, both simpler than the three-epoch model we focused on. For both models, we fitted the demographic parameters to the synonymous biallelic data, fitted the marginal DFE to the nonsynonymous biallelic data, and finally inferred ρ from the mutually nonsynonymous triallelic data, all as described previously. We first considered a two-epoch demographic model, consisting of a single instantaneous population size change at some time in the past. Using this model resulted in a noticeably poorer fit to the biallelic and triallelic data (Figure S8A and Table S3). The inferred lognormal portion of the marginal DFE was similar to that from the three-epoch model. Under the two-epoch model, however, we inferred more and stronger positive selection, likely because this compensates for the underestimation of high-frequency alleles in the two-epoch model (Figure S8B). This in turn caused the inferred correlation coefficient to be substantially lower (Table S3), likely because a lower correlation coefficient reduces the number of moderate- and high-frequency triallelic loci (Figure 1, C–F), partially compensating for the effect of increased positive selection. We then considered an equilibrium demography, assuming no population size changes. This model fitted the data very poorly (Figure S8A and Table S3), and the marginal DFE and the correlation coefficient we inferred were skewed toward neutrality and a lower ρ (Table S3), because these skews generate more rare variants to account for the deficit produced by this poor demographic model. Together, these analyses suggest that inference of the triallelic DFE is sensitive to misspecification of the demographic model.
In our primary Drosophila analysis, we assumed that the DFE followed a lognormal distribution, because such a distribution fits the biallelic data well and easily generalizes to two or more dimensions. Other analyses of the univariate DFE have, however, used other parametric distributions (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008; Kousathanas and Keightley 2013), particularly the gamma distribution (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007). When we fitted a DFE with a gamma distribution for negatively selected sites and a point mass of positive selection to the bivariate data, we found a poorer fit than that of the lognormal distribution (Table S4). We nevertheless fitted a bivariate extension of the gamma distribution to the triallelic data. A number of bivariate gamma distributions have been defined (reviewed by Yue et al. 2001). We chose one that maintains the univariate gamma distribution when marginalized (Kibble 1941; File S1). When fitted to the Drosophila data, the bivariate gamma distribution yielded with a moderately worse likelihood than that of the bivariate lognormal (Table S4). Note, however, that the bivariate gamma DFE is in terms of the selection coefficient γ, and the lognormal distribution is in terms of so the correlation coefficients are not directly comparable. Given that the lognormal distribution better fits our data and has been previously found to be a good approximation for the D. melanogaster univariate DFE (Kousathanas and Keightley 2013), we prefer the lognormal estimate. This analysis shows, however, that the inferred correlation coefficient is sensitive to the parametric form of the bivariate distribution. Future applications may thus consider other possible forms for the bivariate DFE.
Comparison to experimental mutational scanning studies
Our population genetic approach allowed us to simultaneously study the whole genome, but it is an indirect approach to measuring the selection coefficient correlation. Complementary experimental data come from mutational scanning experiments, which use deep sequencing to simultaneously assay the function of thousands of mutant forms of a protein (Araya and Fowler 2011; Figure 4A). To measure selection coefficient correlations from such data, we sampled pairs of mutually nonsynonymous mutations for each site assayed in the protein and calculated the resulting correlations (Figure 4B and File S1). Because our population genetic inference is insensitive to strongly deleterious mutations, we restricted our analysis to the moderately deleterious mutations found in each experiment (Figure S3). We analyzed proteins from Escherichia coli (Firnberg et al. 2014), Saccharomyces cerevisiae (Roscoe et al. 2013), and humans (Starita et al. 2015) (Table 1). In all three cases these direct biochemical assays yielded a fitness effects correlation in agreement with our population genetic estimate, although the limited number of sites within each experiment yielded large confidence intervals, and experimental noise would tend to systematically bias the experimental correlations downward. These results suggest that the moderate correlation of mutational fitness effects we found in D. melanogaster also holds true for other organisms and proteins.
Selection coefficient correlation for subsets of data
Sites within proteins vary in their evolutionary properties (Halpern and Bruno 1998; Holder et al. 2008), so we asked how the fitness effect correlation coefficient differs among subsets of the D. melanogaster population genomic data. We first tested our expectation that biochemically similar derived amino acids would have more tightly correlated selection coefficients than dissimilar derived amino acids (Yampolsky et al. 2005; Blanquart and Lartillot 2008). We assessed similarity, using the Grantham matrix (Grantham 1974), which scores pairs of amino acids based on similarity of biochemical properties. We then refitted the correlation coefficient and misidentification parameter to the subsets of loci with the top and bottom 20% of similarity scores. We indeed found that highly similar derived amino acids exhibited stronger correlation than dissimilar amino acids (Table 1), validating our approach.
We also assessed the correlation of fitness effects for subsets of amino acids that are buried or exposed, based on solvent accessibility, as well as subsets that are ordered or disordered, because protein structural properties are known to affect the amino acid substitution process (Dimmic et al. 2000). We used SPINE-D (Zhang et al. 2012) to separate sites into the top and bottom 20% of solvent accessibility scores and into disordered and ordered classes. For each subset, we refitted the underlying marginal DFE and then fitted the bivariate DFE to measure the correlation coefficient. As expected (Goldman et al. 1998; Bustamante et al. 2000; Tseng and Liang 2006; Lin et al. 2007), for buried residues with low solvent accessibility and for ordered residues, we inferred DFEs that were more negatively skewed than for residues with high solvent accessibility or that were structurally disordered (Table S5). We found, however, that these structural features did not affect the inferred fitness effects correlation coefficient (Table 1). Together, these results suggest that models of protein evolution that incorporate structural features (Wilke 2012; Arenas et al. 2013) do need to account for differences in the marginal DFE, but not for differences in correlation.
Conclusions
Based on the three-allele Wright–Fisher model with an influx of new mutations, we developed a novel numerical solution to the triallelic diffusion equation that simultaneously models the effects of demography and selection on pairs of derived alleles (Figure 1). Using our method, we inferred, for the first time, the correlation of mutation fitness effects at the same site within proteins from triallelic nonsynonymous SNP data (Figure 3). We found that the correlation coefficient is intermediate between completely uncorrelated and completely correlated. Early mutation–selection models of protein evolution made the unrealistic assumption that the fitness effects of multiple mutations occurring at the same site were identical (Nielsen and Yang 2003). More recent methods estimate selection coefficients for every possible amino acid at every site (Tamuri et al. 2012), but these complex models require a great deal of data (Tamuri et al. 2014). Our model of correlated fitness effects is a useful intermediate-complexity model.
We found strong quantitative agreement between the fitness effects correlation coefficient inferred from our population genomic inference and those from direct biochemical experiments (Figure 4). Moreover, this agreement held across a wide range of model organisms, for genes that vary dramatically in function, and using several measures of fitness, suggesting that this correlation of mutational fitness effects is a fundamental property of protein biology, not species or protein specific. We also refined our analysis to biologically relevant subsets of the data (Table 1). As expected, nonsynonymous pairs of similar derived amino acids show significantly higher correlation of fitness effects than dissimilar pairs. Although solvent accessibility and structural disorder did affect the marginal DFE (Table S5), we did not find a difference in fitness effects correlation among these classes of sites (Table 1). Together, our results suggest that the fitness effects correlation we inferred is a nearly universal property of protein evolution, with important implications for modeling protein evolution.
Acknowledgments
This work was supported by the National Science Foundation (DEB-1146074 to R.N.G.).
Footnotes
Communicating editor: Y. S. Song
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.184812/-/DC1.
Literature Cited
- Araya C. L., Fowler D. M., 2011. Deep mutational scanning: assessing protein function on a massive scale. Trends Biotechnol. 29: 435–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arenas M., Dos Santos H. G., Posada D., Bastolla U., 2013. Protein evolution along phylogenetic histories under structurally constrained substitution models. Bioinformatics 29: 3020–3028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bank C., Hietpas R. T., Wong A., Bolon D. N., Jensen J. D., 2014. A Bayesian MCMC approach to assess the complete distribution of fitness effects of new mutations: uncovering the potential for adaptive walks in challenging environments. Genetics 196: 841–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton N. H., Charlesworth B., 1998. Why sex and recombination? Science 281: 1986–1990. [PubMed] [Google Scholar]
- Baudry E., Depaulis F., 2003. Effect of misoriented sites on neutrality tests with outgroup. Genetics 165: 1619–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanquart S., Lartillot N., 2008. A site- and time-heterogeneous model of amino acid replacement. Mol. Biol. Evol. 25: 842–858. [DOI] [PubMed] [Google Scholar]
- Boyko A. R., Williamson S. H., Indap A. R., Degenhardt J. D., Hernandez R. D., et al. , 2008. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 4: e1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante C. D., Townsend J. P., Hartl D. L., 2000. Solvent accessibility and purifying selection within proteins of Escherichia coli and Salmonella enterica. Mol. Biol. Evol. 17: 301–308. [DOI] [PubMed] [Google Scholar]
- Chang J. S., Cooper G., 1970. A practical difference scheme for Fokker-Planck equations. J. Comput. Phys. 6: 1–16. [Google Scholar]
- Coffman A. J., Hsieh P., Gravel S., Gutenkunst R. N., 2016. Computationally efficient composite likelihood statistics for demographic inference. Mol. Biol. Evol. 33: 591–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai M. M., Plotkin J. B., 2008. The polymorphism frequency spectrum of finitely many sites under selection. Genetics 180: 2175–2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Rienzo A., 2006. Population genetics models of common diseases. Curr. Opin. Genet. Dev. 16: 630–636. [DOI] [PubMed] [Google Scholar]
- Dimmic M. W., Mindell D. P., Goldstein R. A., 2000. Modeling evolution at the protein level using an adjustable amino acid fitness model. Pac. Symp. Biocomput. 29: 18–29. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., Keightley P. D., 2007. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 8: 61061–61068. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., Woolfit M., Phelps T., 2006. The distribution of fitness effects of new deleterious amino acid mutations in humans. Genetics 173: 891–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firnberg E., Labonte J. W., Gray J. J., Ostermeier M., 2014. A comprehensive, high-resolution map of a gene’s fitness landscape. Mol. Biol. Evol. 31: 1581–1592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flicek P., Amode M. R., Barrell D., Beal K., Billis K., et al. , 2014. Ensembl 2014. Nucleic Acids Res. 42: 749–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman N., Thorne J. L., Jones D. T., 1998. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics 149: 445–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R., 1974. Amino acid difference formula to help explain protein evolution. Science 185: 862–864. [DOI] [PubMed] [Google Scholar]
- Gutenkunst R. N., Hernandez R. D., Williamson S. H., Bustamante C. D., 2009. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5: e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern A. L., Bruno W. J., 1998. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol. Biol. Evol. 15: 910–917. [DOI] [PubMed] [Google Scholar]
- Hernandez R. D., Williamson S. H., Bustamante C. D., 2007. Context dependence, ancestral misidentification, and spurious signatures of natural selection. Mol. Biol. Evol. 24: 1792–1800. [DOI] [PubMed] [Google Scholar]
- Hodgkinson A., Eyre-Walker A., 2010. Human triallelic sites: evidence for a new mutational mechanism? Genetics 184: 233–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holder M. T., Zwickl D. J., Dessimoz C., 2008. Evaluating the robustness of phylogenetic methods to among-site variability in substitution processes. Philos Trans. R. Soc B 363: 4013–4021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins P. A., Song Y. S., 2011. The effect of recurrent mutation on the frequency spectrum of a segregating site and the age of an allele. Theor. Popul. Biol. 80: 158–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins P. A., Mueller J. W., Song Y. S., 2014. General triallelic frequency spectrum under demographic models with variable population size. Genetics 196: 295–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson P. L. F., Slatkin M., 2008. Accounting for bias from sequencing error in population genetic estimates. Mol. Biol. Evol. 25: 199–206. [DOI] [PubMed] [Google Scholar]
- Keightley P. D., Eyre-Walker A., 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics 177: 2251–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kibble W. F., 1941. A two-variate gamma type distribution. Sankhya 5: 137–150. [Google Scholar]
- Kimura M., 1955. Random genetic drift in multi-allelic locus. Evolution 9: 419–435. [Google Scholar]
- Kimura M., 1956. Random genetic drift in a tri-allelic locus; exact solution with a continuous model. Biometrics 12: 57–66. [Google Scholar]
- Kimura M., 1964. Diffusion models in population genetics. J. Appl. Probab. 1: 177–232. [Google Scholar]
- Kousathanas A., Keightley P. D., 2013. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics 193: 1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lack J. B., Cardeno C. M., Crepeau M. W., Taylor W., Corbett-Detig R. B., et al. , 2015. The Drosophila Genome Nexus: a population genomic resource of 623 Drosophila melanogaster genomes, including 197 from a single ancestral range population. Genetics 199: 1229–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy S. F., Blundell J. R., Venkataram S., Petrov D. A., Fisher D. S., et al. , 2015. Quantitative evolutionary dynamics using high-resolution lineage tracking. Nature 519: 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y. S., Hsu W. L., Hwang J. K., Li W. H., 2007. Proportion of solvent-exposed amino acids in a protein and rate of protein evolution. Mol. Biol. Evol. 24: 1005–1011. [DOI] [PubMed] [Google Scholar]
- Mathew L. A., Staab P. R., Rose L. E., Metzler D., 2013. Why to account for finite sites in population genetic studies and how to do this with Jaatha 2.0. Ecol. Evol. 3: 3647–3662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Yang Z., 2003. Estimating the distribution of selection coefficients from phylogenetic data with applications to mitochondrial and viral DNA. Mol. Biol. Evol. 20: 1231–1239. [DOI] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium , 2015. A global reference for human genetic variation. Nature 526: 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roscoe B. P., Thayer K. M., Zeldovich K. B., Fushman D., Bolon D. N. A., 2013. Analyses of the effects of all ubiquitin point mutants on yeast growth rate. J. Mol. Biol. 425: 1363–1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R., Moya A., Elena S. F., 2004. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA 101: 8396–8401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer S. A., Hartl D. L., 1992. Population genetics of polymorphism and divergence. Genetics 132: 1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider A., Charlesworth B., Eyre-Walker A., Keightley P. D., 2011. A method for inferring the rate of occurrence and fitness effects of advantageous mutations. Genetics 189: 1427–1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella G., Petrov D. A., Przeworski M., Andolfatto P., 2009. Pervasive natural selection in the Drosophila genome? PLoS Genet. 5: e1000495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer H. G., Barakat R., 1992. Random genetic drift and selection in a triallelic locus: a continuous diffusion model. Math. Biosci. 108: 127–139. [DOI] [PubMed] [Google Scholar]
- Starita L. M., Young D. L., Islam M., Kitzman J. O., Gullingsrud J., et al. , 2015. Massively parallel functional analysis of BRCA1 RING domain variants. Genetics 200: 413–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamuri A. U., dos Reis M., Goldstein R. A., 2012. Estimating the distribution of selection coefficients from phylogenetic data using sitewise mutation-selection models. Genetics 190: 1101–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamuri A. U., Goldman N., dos Reis M., 2014. A penalized-likelihood method to estimate the distribution of selection coefficients from phylogenetic data. Genetics 197: 257–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tier C., 1979. A tri-allelic diffusion model with selection, migration, and mutation. Math. Biosci. 60: 41–60. [Google Scholar]
- Tier C., Keller J. B., 1978. A tri-allelic diffusion model with selection. SIAM J. Appl. Math. 35: 521–535. [Google Scholar]
- Tseng Y. Y., Liang J., 2006. Estimation of amino acid residue substitution rates at local spatial regions and application in protein function inference: a Bayesian Monte Carlo approach. Mol. Biol. Evol. 23: 421–436. [DOI] [PubMed] [Google Scholar]
- Wang K., Li M., Hakonarson H., 2010. ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data. Nucleic Acids Res. 38: 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke C. O., 2012. Bringing molecules back into molecular evolution. PLoS Comput. Biol. 8: 6–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson S. H., Hernandez R., Fledel-alon A., Zhu L., Nielsen R., et al. , 2005. Simultanous inference of selection and population growth from patterns of variation in the human genome. Proc. Natl. Acad. Sci. USA 102: 7882–7887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wloch D. M., Szafraniec K., Borts R. H., Korona R., 2001. Direct estimate of the mutation rate and the distribution of fitness effects in the yeast Saccharomyces cerevisiae. Genetics 159: 441–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yampolsky L. Y., Kondrashov F. A., Kondrashov A. S., 2005. Distribution of the strength of selection against amino acid replacements in human proteins. Hum. Mol. Genet. 14: 3191–3201. [DOI] [PubMed] [Google Scholar]
- Yue S., Ouarda T. B. M. J., Bobée B., 2001. A review of bivariate gamma distributions for hydrological application. J. Hydrol. 246: 1–18. [Google Scholar]
- Zhang T., Faraggi E., Xue B., Dunker A. K., Uversky V. N., et al. , 2012. SPINE-D: accurate prediction of short and long disordered regions by a single neural-network based method. J. Biomol. Struct. Dyn. 29: 799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.