Abstract
The application of supraphysiological temperatures (>40°C) to biological tissues causes changes at the molecular, cellular, and structural level, with corresponding changes in tissue function and in thermal, mechanical and dielectric tissue properties. This is particularly relevant for image-guided thermal treatments (e.g. hyperthermia and thermal ablation) delivering heat via focused ultrasound (FUS), radiofrequency (RF), microwave (MW), or laser energy; temperature induced changes in tissue properties are of relevance in relation to predicting tissue temperature profile, monitoring during treatment, and evaluation of treatment results.
This paper presents a literature survey of temperature dependence of electrical (electrical conductivity, resistivity, permittivity) and thermal tissue properties (thermal conductivity, specific heat, diffusivity). Data of soft tissues (liver, prostate, muscle, kidney, uterus, collagen, myocardium and spleen) for temperatures between 5 to 90°C, and dielectric properties in the frequency range between 460 kHz and 3 GHz are reported. Furthermore, perfusion changes in tumors including carcinomas, sarcomas, rhabdomyosarcoma, adenocarcinoma and ependymoblastoma in response to hyperthmic temperatures up to 46°C are presented. Where appropriate, mathematical models to describe temperature dependence of properties are presented.
The presented data is valuable for mathematical models that predict tissue temperature during thermal therapies (e.g. hyperthermia or thermal ablation), as well as for applications related to prediction and monitoring of temperature induced tissue changes.
I. BACKGROUND
The use of supraphysiological temperatures (greater 40°C) during hyperthermia and thermal ablation therapy is clinically used or investigated to treat a broad range of diseases including cancer, cardiac arrhythmias, Parkinson's disease, joint laxity, hyperopia, hyperplasia, and others. During these thermal therapies, heat is applied to intentionally cause either reversible tissue changes including increase of cellular metabolism, perfusion and oxygenation via hyperthermia (40–45°C), or to irreversibly destroy or modify tissue during ablation treatment (50–110°C) (1–7). Such tissue changes typically depend on both time and temperature, and can affect perfusion, as well as mechanical, electrical and thermal tissue properties.
The electrical tissue properties directly impact absorption of electromagnetic energy that results in heat generation, whereas thermal properties and perfusion affect heat transfer within the tissue; these properties therefore are crucial to pre-clinical and clinical applications that employ electromagnetic energy for heating, as well as for thermal therapies in general. Specific examples include planning and monitoring thermal treatments facilitating radiofrequency (RF), microwave (MW), focused ultrasound (FUS), and laser energy where the goal is to obtain defined temperatures in a targeted tissue region. Recently, FUS combined with magnetic resonance imaging (MRI) has gained interest due to the ability to non-invasively heat tissue, as well as to provide non-invasive monitoring of tissue temperature via MR thermometry (8–12)
Another imaging application where accurate consideration of electrical properties is necessary is electrical impedance tomography (EIT), where images are generated based on differences in electrical tissue properties. While EIT is emerging in pre-clinical applications to detect breast cancer by measuring differences in conductivity of normal and neoplastic tissue (13, 14), recent studies also suggests that EIT is also potentially useful tool for measuring temperatures based on conductivity changes during hyperthermia treatment (15), but this requires accurate information on temperature-dependent changes of electrical tissue conductivity.
Besides clinical and experimental studies, mathematical models have been used to investigate and improve clinical procedures and devices by simulating tissue heating. These models are typically based on solving the appropriate heat-transfer equations; when perfusion is considered, Pennes' Bioheat equation (16) for modeling perfusion is commonly employed. Since thermal and electrical tissue properties significantly vary with the temperature, adequate consideration of tissue properties and their temperature dependence is necessary to achieve accurate results (17–23).
This review presents an extensive review of temperature dependence of electrical and thermal tissue properties, as well as perfusion. All these data are necessary for determining absorption of electromagnetic energy (e.g. RF current or microwaves), to predict heat generated by a particular device or method (electromagnetic or other), as well as for estimating resulting tissue temperature profile.
II. Theoretical modeling of thermal therapies
Mathematical modeling of thermal therapies has been used extensively to predict and optimize clinical treatments and medical devices (19–22, 24–40). Regardless of the method employed to achieve tissue heating, the heat transfer equation has to be solved to model the temperature distribution T (°C) in biological tissues:
| (1) |
where ρ is the density [kg·m−3], C is the specific heat [J·kg−1·K−1], k is the thermal conductivity [W·m−1·K−1], and QP [W·m−3], is the heat loss due to blood perfusion. The most widely used model of tissue perfusion is Pennes' Bioheat Equation (16), where a distributed heat sink term is employed to model perfusion:
| (2) |
Q [W·m−3] is the distributed heat source representing heat energy produced by any heating modality, such as external heat, RF, MW, laser, and FUS energy. However, for RF and MW heating the electro-magnetic equations modeling heat generation depend on temperature-dependent dielectric properties, which will be described in more detail: Heating modalities such as RF and MW facilitate electromagnetic energy to achieve tissue heating. While both heating modalities may be used to apply localized hyperthermia, in clinical routine they are also commonly used during localized ablation treatments with frequencies in the range of 450-500 kHz for RF ablation and in the range 900–3000 MHz for MW ablation. Due to electromagnetic wavelengths greater 100 m and negligible displacement currents, the heat generation during RF follows the simple approach of the electrostatic case (Laplace's equation) (21, 41). The distributed heat source Q (Joule loss, also referred to as external heating term) is given by
| (3) |
where J is the current density [A·m−2], and E is the electric field intensity [V·m−1]. The values of these two vectors are evaluated using Laplace's equation:
| (4) |
where V is the voltage [V] and σ is the electrical conductivity [S·m−1]. By using the quasi-static approach, the values of “direct-current” (DC) voltage calculated from the model correspond to the root mean squared value of the applied RF voltage.
Microwave energy is converted to heat within tissue due to dielectric losses and this requires modeling of wave propagation since MW wavelengths in tissue are in the cm range (33). The simulation of microwave propagation is based on the fundamental electromagnetic equations, well known as Maxwell's equations. The first Maxwell equation describes how conduction current as well as displacement current affect the magnetic field:
| (5) |
where H denotes the magnetic field strength [A·m−1], J the current density [A·m−2], D the electric flux density [A·s·m−2] and the displacement current density [A·m−2]. The second Maxwell equation states that changes in the magnetic field B [V·s·m−2] influence the electric field strength E [V·m−2]:
| (6) |
The third and fourth equations are describing the facts that the magnetic field B is without any source and that the electrical charge ρ [A·s·m−3] is the source for the electric displacement:
| (7) |
We can use further relations between the vectors H, D, B, J, and E, which depend on the tissue properties, i.e. on the permittivity ε [A·s·V−1·m−1], the permeability μ [V·s·A−1·m−1], and the electrical conductivity σ [A·V−1·m−1]. For the modeling of MWA or MW hyperthermia, these material properties have to be known with respect to the different tissue types. After solving the Maxwell's equations described above, the calculated energy from the microwaves serves as heat source Q in the heat transfer equation, which can be modeled as:
| (8) |
| (9) |
Where σ is the dielectric conduction in [S·m−1], and E is the electric field intensity [V·m−1]. When Q is normalized by tissue density, it is referred to as the specific absorption rate (SAR [W/kg], see Equ. 9).
An important factor to achieve realistic models is the use of mathematical functions to describe the temperature dependence of thermal and electrical properties of tissue.
A commonly used approach for modeling the temperature dependence of thermal and electrical properties for temperatures below 100°C is based on linear equations and employs constant temperature coefficients such as:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where σ0 and ε0 are the electrical conductivity and permittivity, and k0, α0 and c0 represent thermal conductivity, diffusivity and specific heat capacity at a reference temperature, k1 is the temperature coefficient and, ΔT [°C] is the temperature differenc to the reference temperature. Note that for some of these properties, a linear approximation is only adequate within a limited temperature range.
III. Temperature Dependence of Electrical Properties
The knowledge of temperature-dependent electrical properties of biological tissues is important to calculate the deposition of electromagnetic energy in a variety of diagnostic procedures and treatments. For example to calculate the electromagnetic field and SAR distribution in tissues subjected to MRI scans, to diagnostically differentiate between normal and pathologic tissue, and for the delivery of heat during MW and RF treatment (22, 23, 42–45).
The heat generation in biological tissues due to dissipation of electromagnetic energy is dependent on dielectric permittivity ε [F·m−1] and conductivity σ [S·m−1]. Sometimes the electrical resistivity [Ohm·m] is reported, which is the inverse of the electrical conductivity. The relative permittivity, also known as dielectric constant, varies with temperature and frequency, and is defined as ratio of electrical energy stored by applied voltage within the medium relative to vacuum. The dielectric properties of materials are completely described the complex relative permittivity ε*, which can be expressed as
| (15) |
where ε′ is the relative permittivity of the material and ε″ is the out of phase loss factor and may be expressed as
| (16) |
where σ represents the ionic conductivity, ε0 is the permittivity of vacuum, and ω is the angular frequency [rad·s−1]. Depending on the nature of the tissue, σ may include a contribution from a frequency-independent ionic conductivity σi. It is important to note, that in many soft tissues, σ both and ε vary with frequency, temperature and water content.
Extensive literature has been around for more than 30 years presenting tabulated dielectric properties of tissues in the frequency range from 10 kHz to 10 GHz around body temperatures (20–40°C) and have been reported by Gabriel et al., Duck et(46) al. and other researchers (42–44, 47–50); however, the temperature dependence of these frequency-dependent dielectric properties in the RF and MW frequency range has only been studied more recently.
Only few data on temperature-dependent dielectric properties are available in the frequency range of RF ablation (450 - 500 kHz). Ryan et al. measured electrical conductivity of brain, muscle, liver and fat at 500 kHz between 40 and 90 °C. They found increase of conductivity with temperature, and irreversible changes above ~60 °C (23). Pop et al. investigated the changes of kidney and fat during heating within a temperature range between 48 and 75°C at 460 kHz. Two separate components, a reversible temperature-dependent component and an irreversible component, were identified (51); this observation was confirmed by a recent study based on MR impedance tomography (52). Similarly, Zurbuchen et al. presented temperature-dependent in-vivo and ex-vivo electric conductivity data at 470 kHz and found conductivity to be increasing up to 80 °C (53). Macchi et al. measured dielectric properties of liver ex-vivo up to 100 °C and found increasing conductivity with temperature; in addition, they found a dependence on heating rate which could be modeled by an Arrhenius relationship (46). McRae et al. measured electrical resistivity from 100 Hz to 40 MHz of skeletal muscle ex-vivo, and mouse tumors ex-vivo and in-vivo, at hyperthermic temperatures between 37 and 50 °C (54–56).
More data is available for frequencies in the MW range. Fu et al. studied frequency-dependent dielectric properties of various tissues including liver, muscle and kidney. Via open-ended coaxial line method properties within the temperature and frequency ranges typically used for MRI-guided focused ultrasound surgery (36–60°C, 42–468 MHz) were measured (57). Stauffer et al. developed equivalent liver-like phantoms based on measurements of in-vivo and ex-vivo human and animal tissues made with a dielectric measurement probe for frequencies from 0.3–3 GHz. Additionally, dielectric properties at 915 MHz for bovine liver tissue were presented for 10 to 90°C more in detail (58). Chin et al. used a coaxial measurement system and studied the changes of dielectric properties in ex-vivo bovine liver and rat prostate during MW heating at 915 MHz for temperatures from 30 to 80°C (59, 60). Key findings include that property changes due to tissue water content were found to be reversible with temperature, while changes due to protein denaturation were found to be permanent. Among others, the temperature dependence of the electrical parameters of human blood was studied by Mohapatra for temperatures between 22 and 40°C at 100 kHz who found an decrease in resistivity (i.e. increase in conductivity) with temperature (61). In a more extensive study by Jaspard et al. dielectric properties of animal and human blood have been investigated via impedance meter and open-ended coaxial probe for the temperature range 25–45°C and frequency range from 1 MHz to 1 GHz (62). Results presented suggest a weak temperature dependence, and a negative temperature coefficient of the relative permittivity. Lazebnik et al. characterized the temperature-dependent dielectric properties of porcine and bovine liver from 0.5 to 20 GHz for temperatures up to 60°C and demonstrated that linear temperature coefficients are inadequate over wide frequency- and temperature ranges (63). They modeled the dielectric properties via temperature-dependent Cole–Cole and second-order polynomial parameters. To investigate the temperature-dependence of dielectric properties of liver, Brace et al. measured the changes in tissue properties during microwave ablation at 915 and 2.45 GHz with temperatures up to 100°C. They found that relative permittivity and conductivity decrease substantially and irreversibly at high temperatures (64). In agreement, Lopresto et al. looked at tissue changes at 2.45 GHz and found a considerable decrease of relative permittivity (about 38%) and electrical conductivity (about 33%) as the temperature increased to over 60°C (65).
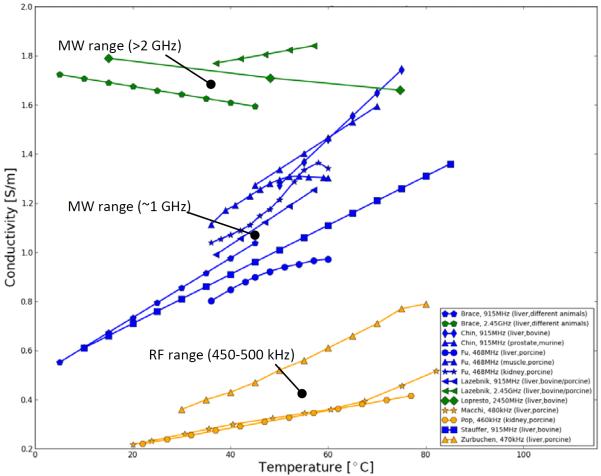
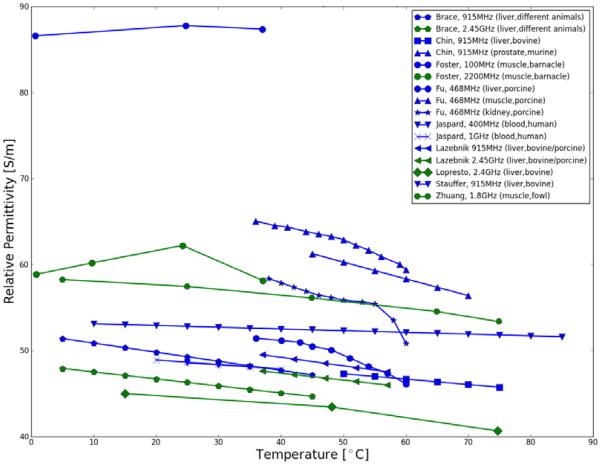
A representative summary of these studies on temperature-dependent dielectric properties (conductivity and permittivity) of biological tissues presently available are plotted in Figure I and comprehensive data is listed in Table I. Data of various tissues is presented; however, most data is available of liver tissue in the temperature range from room temperature (20°C) up to approximately 80°C due to increasing research interests in understanding, evaluating and improving liver cancer treatments via RF and MW ablation. There is evidence in all presented studies that for frequencies below 1 GHz, electrical conductivity of undamaged and unheated tissues increases with temperature. At frequencies around 2.4 GHz there is evidence that the electrical conductivity decreases with temperature as presented by Brace et al. and Lopresto et al. (see Figure 1)
Figure 1.
Electrical conductivity of human and various animal tissues as a function of temperature. Colors are indicating frequencies [yellow: 450-500 kHz (RF), blue: ~1 GHz (low MW), green: >2 GHz (high MW)].
Table 1.
Comprehensive listing of presently available temperature-dependent electrical properties of tissues
| Reference | Frequency [MHz] |
σ [S/m] |
σ Coeff. [%/°C] |
ε [-] |
ε Coeff. [%/°C] |
Tissue type | Temperature range [°C] |
Tissue state |
|---|---|---|---|---|---|---|---|---|
| Brace, 2008 | 915 | 0.94 | 1.29 | 48.00 | −0.22 | liver, different animals | 5–50 | within 48h post-excision |
| Brace, 2008 | 2450 | 1.62 | −0.20 | 45.30 | −0.18 | liver, different animals | 5–50 | within 48h post-excision |
| Chin,2001 | 915 | 1.03 | 1.82 | 48.10 | −0.13 | liver, bovine | 49.8–79.2 | ex-vivo |
| Chin,2004 | 915 | 1.17 | 1.10 | 62.80 | −0.31 | prostate, murine | 45–75 | ex-vivo |
| Duck,1990 | 0.1 | 7.00 | 2.10 | 14000.00 | 1.40 | muscle, canine | 20–40 | ex-vivo |
| Duck,1990 | 0.1 | 1.41 | 0.60 | 6940.00 | 1.20 | liver, human | 20–40 | ex-vivo, 1–2hr post-mortem |
| Duck,1990 | 0.1 | 3.28 | 0.90 | 11200.00 | 0.80 | kidney, human | 20–40 | ex-vivo, 1–2hr post-mortem |
| Duck,1990 | 1.0 | 5.80 | 2.10 | 1900.00 | 2.20 | muscle, pig | 20–40 | in-vivo |
| Duck,1990 | 1.0 | 2.27 | 1.30 | 1970.00 | 1.50 | liver, human | 20–40 | ex-vivo, 1–2hr post-mortem |
| Duck,1990 | 1.0 | 4.93 | 0.80 | 2450.00 | 1.40 | kidney, human | 20–40 | ex-vivo, 1–2hr post-mortem |
| Duck,1990 | 200 | 1 | 1.50 | - | - | muscle | 20–40 | Not specified |
| Duck,1990 | 200 | 2 | 1.80 | 50.00 | 0.20 | liver | 20–40 | Not specified |
| Duck,1990 | 200 | 9 | 2.00 | 10.50 | 0.20 | kidney | 20–40 | Not specified |
| Duck,1990 | 900 | 1 | 1.00 | 57 | −0.20 | muscle | 20–40 | Not specified |
| Duck,1990 | 900 | 2 | 1.40 | 46.50 | −0.20 | liver | 20–40 | Not specified |
| Duck,1990 | 900 | 9 | 1.30 | 22.50 | −0.40 | kidney | 20–40 | Not specified |
| Duck,1990 | 3000 | 1 | 0.30 | 54.00 | −0.10 | muscle | 20–40 | Not specified |
| Foster,1989* | 100 | 1.82 | 2.67 | 87.67 | 0.03 | muscle, barnacle | 5–40 | Not specified |
| Foster,1989* | 2200 | 3.60 | 0.10 | 60.05 | 0.06 | muscle, barnacle | 5–40 | Not specified |
| Fu,2014 | 468 | 0.80 | 1.03 | 51.43 | −0.35 | liver, porcine | 36–60 | within 2hrs post-mortem |
| Fu,2014 | 468 | 0.72 | 2.78 | 60.16 | −0.60 | uterus, porcine | 36–60 | within 2hrs post-mortem |
| Fu,2014 | 468 | 1.11 | 0.92 | 65.03 | −0.30 | muscle, porcine | 36–60 | within 2hrs post-mortem |
| Fu,2014 | 468 | 1.04 | 1.30 | 58.36 | −0.42 | kidney, porcine | 36–60 | within 2hrs post-mortem |
| Fu,2014 | 468 | 1.02 | 0.73 | 58.24 | −0.48 | bladder, porcine | 36–60 | within 2hrs post-mortem |
| Jaspard,2002 | 400 | 0.70 | 1.13 | - | −0.10 | blood, human | 25–45 | within 15min post-mortem |
| Jaspard,2002 | 1000 | 0.70 | 0.98 | - | −0.11 | blood, human | 25–45 | within 15min post-mortem |
| Lazebnik,2006 | 915 | 0.99 | 1.33 | 49.50 | −0.20 | liver bovine/porcine | 37–60 | within 2hrs post-mortem |
| Lazebnik,2006 | 2450 | 1.77 | 0.20 | 47.60 | −0.17 | liver bovine/porcine | 37–60 | within 2hrs post-mortem |
| Lopresto,2012* | 2450 | 1.74 | −0.13 | 43.52 | −0.15 | liver bovine | 15–80 | ex-vivo |
| Macchi,2014 | 0.48 | 0.28 | 1.45 | - | - | liver, porcine | 20–80 | ex-vivo |
| Pop,2003* | 0.46 | 0.27 | 1.30 | 3210.00 | - | kidney, porcine | 22–78 | ~hours post-excision |
| Ryan,1997 | 0.50 | 1.38 | 2.0 | - | - | muscle | 30–60 | ex-vivo |
| Stauffer,2003* | 915 | 0.88 | 1.14 | 52.56 | −0.04 | liver, bovine | 10–90 | within 15min post-excision |
| Zuhang, 2007 | 1800 | - | - | 58.25 | −0.17 | muscle, fowl | 5–85 | >22h post-mortem |
| Zurbuchen,2008* | 0.47 | 0.42 | 2.05 | - | - | liver, porcine | 30–80 | within 8hrs after slaughter |
Sigma and Epsilon were calculated for 37°C; original values were presented temperatures different from 37°C
Additional data are available from food industry research presenting dielectric data of processed tissues including beef, chicken, salmon and comminuted meats at temperatures of 5–80°C (66–72). Zhuang investigated the properties of uncooked meats including fowl muscle for temperatures between 5 and 80°C at 1.8 GHz (73). Data available in literature hints at a slight decrease of dielectric permittivity with increasing temperature for frequencies from approximately 500 MHz to 2.4 GHz.
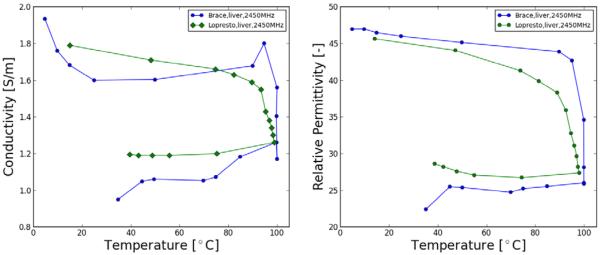
Table 1 presents data and coefficients from literature to calculate temperature-dependent electrical tissue properties, assuming no irreversible components are present. However, the application of temperatures greater 50°C likely causes irreversible changes in the electrical properties as result of dehydration, shutdown of perfusion, and other cellular and molecular changes. Brace et al. and Lopresto et al. demonstrated the irreversible decrease of permittivity and electrical conductivity at 2.45 GHz with high temperatures up to ~100°C (see Figure 3). As already noted, both Pop et al. and Kwon et al. demonstrate similar irreversible changes at RF frequencies above ~60 °C (51, 52); Macchi showed conductivity dependence on rate of heating in addition to temperature (46). These time- and temperature-dependent changes have been modeled by an Arrhenius relationship in several studies (46, 51, 55), which may be preferred in some applications to a simple dependence on temperature alone.
Figure 3.
Relative permittivity and conductivity measurements made at 915 MHz and 2.45 GHz during thermal ablation. Accumulated ablation times noted on each figure to identify temporal variations. Values tended to drop quickly in all cases when temperatures reached 100°C and continued to drop as temperature was maintained and the tissue became more dehydrated (64, 65).
Due to the great difficulty of measuring temperature dependence of electrical tissue properties in-vivo, the presented studies almost exclusively are based on ex-vivo measurement in excised tissues with varying duration between tissue extraction and measurement. Electrical tissue properties change as soon as tissue is removed, and this change is particularly pronounced at frequencies below 500 kHz. Data is available on change of electrical tissue properties of muscle, liver, kidney and spleen after tissue extraction and suggest property changes dependent on carcass temperature and degree of tissue degradation (74–76). Haemmerich et al. measured swine liver resistivity in-vivo and after excision over for 12h to examine the magnitude of resistivity change (77). After 2 h post-mortem, resistivity decreases considerably, by 53% at 10 Hz and by 32% at 1 MHz; factors contributing to this decrease may include increase in extracellular fluid due to loss of membrane integrity post-mortem, that allows continuity between intracellular and extracellular fluid compartments, and lysosomal agents are released within the cell, contributing to cell membrane damage.
At microwave frequencies, dielectric properties are primarily determined by water content and thus less affected by tissue removal than at RF frequencies. O'Rourke et al. characterized the dielectric properties of in-vivo and ex-vivo normal, malignant and cirrhotic human liver tissues from 0.5 to 20 GHz (78). Even though their results were not statistically significant (with the exception of effective conductivity at 915 MHz, where malignant tissue properties are 16% higher than normal) they reported that conductivity of in-vivo normal liver tissue is 16% (915 MHz) to 43% (2.45 GHz) higher than ex-vivo.
IV. Temperature Dependence of Thermal Properties
Heat transport in biological tissues may occur due to conductive, convective or radiative mechanisms (47). These heat transfer mechanisms can be characterized via thermal conduction and heat capacity properties. The thermal conductivity of biological materials describes how well the material conducts heat and may be defined by the amount of heat Q [W·m−3], transmitted due to a temperature gradient. This transmitted heat can be expressed considering steady-state conditions by the Poisson equation
| (17) |
where k [W·m−1·K−1] is the thermal conductivity,▽ is the gradient ator and T [°C] is the temperature. Where steady-state conditions are not adequate, the quantity of thermal diffusivity α [m2·s−1] is used to describe the spatial variation of the temperature T via heat equation
| (18) |
with
| (19) |
where, ρ is density [kg·m−3] and C is the specific heat capacity (J·kg−1·K−1).
It is important for mathematical models of thermal therapies to have accurate values of these thermal properties in order to generate valid results (19, 79). Note that equation (19) shows that the three thermal properties are interrelated, i.e. it is sufficient to report two of these properties for a complete representation of heat transfer characteristics. While most literature available presents data limited to room temperature, the thermal tissue properties vary with temperature (80).
Valvano et al. presented an experimental method via self-heated thermistors and measured thermal conductivity and diffusivity of biomaterials (i.e. tissues) in the temperature range 3 to 45°C (81). Even though they found considerable variations in the thermal properties between tissue types, the temperature coefficients consistently matched the temperature coefficients of water. Bhattachara et al. used a hot-wire technique and based on the principle of transient one-dimensional conduction and measured the thermal conductivity of dead cow liver and sheep collagen as a function of temperature between 25 and 80°C (82). Tissues were found to exhibit irreversible changes in thermal conductivity beyond a threshold which was suggested to be 55 and 90°C for sheep collagen and cow liver, respectively. Similarly, van Gemert measured the thermal conductivity and diffusivity of human aorta and canine arteries in the temperature range of 20 to 90°C, which has relevance for laser angioplasty (83).
Thermal properties of various animal tissues were measured by Liang et al. via custom developed probe which may be used over a temperature range from −40 to 150°C and reported a noticeable influence of tissue water content on the magnitude of the thermal conductivity of tissues (84). In agreement, Bhavaraju et al. reported an experimental technique and results for the thermal conductivity and diffusivity, and density of swine myocardial tissue. A significant dependency of the thermal properties on water content and irreversible tissue changes at temperatures greater 50°C, likely due to denaturing of proteins in the cell structures, was reported (85). To investigate the temperature-dependent thermal properties of porcine liver tissue during RF ablation Guntur et al. presented data from 20 to 90°C. In their study, they found that both heat capacity and thermal conductivity rose with temperature, and found irreversible property changes even after the sample cooled down (86). For a similar temperature range (20–80°C) Choi et al. investigated the correlation of protein denaturation and water loss with the thermal properties of human and porcine liver (87). Key findings in their study include that denaturation and water vaporization correlate negatively with thermal conductivity and that apparent specific heat1 within the samples by up to 20% during heating.
Haemmerich et al. measured the temperature-dependent specific heat of liver tissue from 25 to 85°C which was found to be increasing for temperatures greater 65°C and presumably related to tissue water loss (88, 89). Similar to the dielectric properties, food industry driven research contributed to the understanding of temperature-dependent properties of biomaterials. To design food processing operations and increase process efficiency and product quality, data of various processed meats was presented by Rahman, Mohsenin, Baghe-Khandan et al. and Marcotte et al. (90–93).
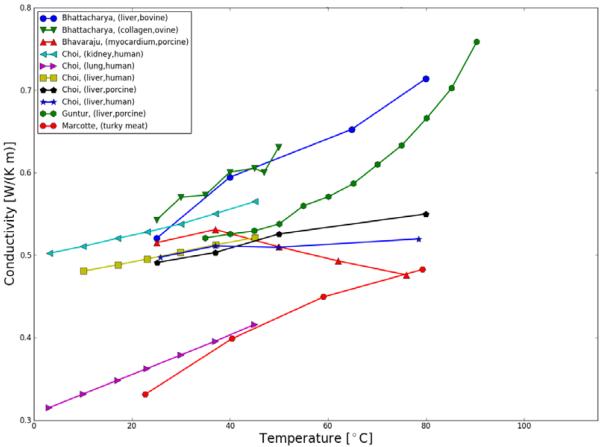
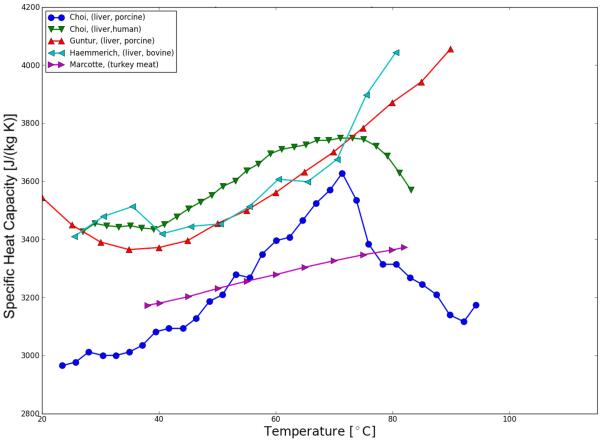
A representative summary of published research on temperature-dependent thermal properties (thermal conductivity, thermal diffusivity and specific heat capacity) of biological tissues presently available are plotted in Figure 4, Figure 5; Table 2 shows a comprehensive listing of available studies. On the data of various tissues presented, the studies are in general agreement that thermal conductivity of tissue increases with temperature within the studies temperature range of 5 to ~90 °C.
Figure 4.
Thermal conductivity of various tissues as a function of temperature.
Figure 5.
Specific heat of various tissues as a function of temperature.
Table 2.
Thermal properties of various tissues from literature
| Reference | k [W/m/K] |
k Coeff. [%/°C] |
α [m2/s] |
alpha Coeff. [%/°C] |
c [W/m/K] |
c Coeff. [%/°C] |
Tissue type | Temperature range [°C] |
Tissue state |
|---|---|---|---|---|---|---|---|---|---|
| Bhattacharya,2003 | 0.563 | 0.626 | - | - | - | - | liver, bovine | 25–80 | ex-vivo |
| Bhattacharya,2003 | 0.582 | 0.559 | - | - | - | - | collagen, ovine | 25–80 | ex-vivo |
| Bhavaraju,1999+ | 0.508 | −0.114 | 1.587E-07 | 0.354 | 3077 | myocardium, porcine | 25–76 | Not specified | |
| Choi,2013 | 0.504 | 0.222 | - | - | 3112* | 0.35* | liver, porcine | 25–80 | > 12–24 h postmortem |
| Choi,2013 | 0.503 | 0.092 | - | - | 3499* | 0.2* | liver, human | 25–80 | > 12–24 h postmortem |
| Choi,2013 | 0.550 | 0.257 | - | - | - | - | kidney, human | 3–45 | Not specified |
| Choi,2013 | 0.396 | 0.603 | - | - | - | - | lung, human | 3–45 | Not specified |
| Choi, 2013 | 0.481 | 0.242 | - | - | - | - | liver, human | 10–45 | Not specified |
| Guntur, 2013 | 0.521 | 0.615 | 1.424E-07 | 0.462 | 3386 | 0.32 | liver, porcine | 35–90 | samples obtained 1hr before experiments |
| Haemmerich, 2006 | - | - | - | - | 3493 | 0.21 | liver, bovine | 25–83 | in vitro, immediately after removal |
| Marcotte, 2008 | 0.373 | 0.780 | - | - | 3167 | 0.15 | turky meat | 20–80 | Not specified |
| Valvano,1985 | 0.493 | 0.120 | 1.474E-07 | 0.339 | 3212 | - | myocardium, human | 3–45 | 1–2 days after biopsy |
| Valvano,1985 | 0.407 | 0.118 | 1.307E-07 | 0.237 | 2967 | . | lung, human | 3–45 | 1–2 days after biopsy |
| Valvano,1985 | 0.469 | 0.116 | 1.412E-07 | 0.255 | 3134 | - | liver, human | 3–45 | 1–2 days after biopsy |
| Valvano,1985 | 0.415 | 0.004 | 1.436E-07 | −0.341 | 2726 | - | adenocarinoma of the breast, human | 3–45 | within 24hrs |
| Valvano,1985 | 0.545 | 0.080 | 1.134E-07 | - | 4533 | - | colon cancer, human | - | within 24hrs |
| Valvano,1985 | 0.540 | 0.204 | 1.482E-07 | 0.371 | 3505 | - | renal medulla,human | 3–45 | 1–2 days after biopsy |
| Valvano,1985 | 0.547 | 0.236 | 1.470E-07 | 0.374 | 3576 | - | renal cortex,human | 3–45 | 1–2 days after biopsy |
| Valvano,1985 | 0.539 | 0.241 | 1.444E-07 | 0.326 | 3592 | - | spleen,human | 3–45 | 1–2 days after biopsy |
c calculated via k/alpha/rho
The values and the coefficient were calculated for the temperature range 20 to 70°C
The presented conductivity and diffusivity were calculated for 37°C; original values were presented temperatures different from 37°C
No data could be found to demonstrate variation of thermal tissue properties in-vivo versus ex-vivo. However, some data is available from food industry studies reporting no significant post-mortem changes in the thermal conductivity of white and dark chicken meat by Sweat et al., who studied the effects of temperature and time post-mortem on the thermal conductivity with a line heat source thermal conductivity probe for the temperature range from 20 to −75°C (94). As several studies suggest that thermal properties are primarily dependent on relative content of constituents (i.e. relative content of water, protein, fat; see Rahman et al. (90)), it is reasonable to assume that cellular changes following tissue extraction have limited impact on thermal properties. However, ex-vivo tissues should be stored in a slightly hypertonic saline buffer to minimize tissue water loss or gain prior to measurement (85).
V. Temperature Dependence of Blood Perfusion
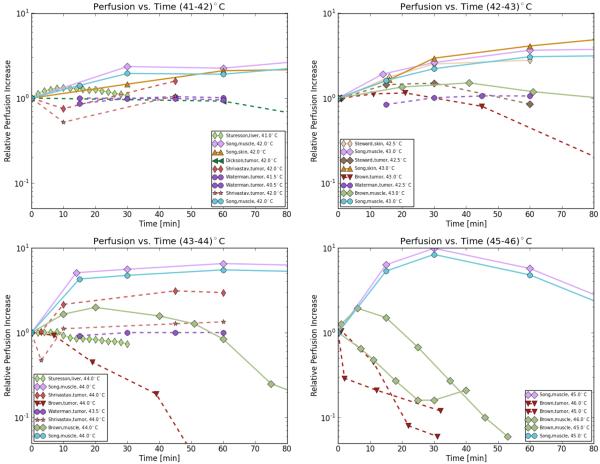
Blood flow strongly affects temperature distribution due to convective heat transfer between the tissue and circulating blood during heating. Several studies have reviewed the effects of hyperthermia on tumors, the microenvironment, and perfusion. Common findings include that the blood flow and response to hyperthermia varies considerably among different tumor types, where both higher and lower perfusion relative to normal tissue has been reported (95–99). Furthermore, even within the same tumor the distribution of vasculature and blood flow is quite heterogeneous (96). Even though tumors of larger size tend to have reduced blood flow, in many tumors, particularly in small tumors, blood flow can be greater than that of surrounding normal tissues at hyperthermia temperature conditions. In general, the ability to increase blood flow in response to hyperthermic temperatures appears to be limited in tumors compared to normal tissues. Thus heat cannot be removed as sufficiently as in normal tissues which may lead to higher temperatures in tumors during heating. This can lead to tumor vascular damage and alter the intratumoral blood flow causing the intratumoral environment to become acidic, hypoxic and nutritionally deprived at temperatures in the upper hyperthermic range (between 41-43°C). Below we summarize first small animal studies, and then the more limited number of studies in large animals and in humans. Bicher et al. studied the effects of microwave hyperthermia and reported a dual effect of hyperthermia on local blood of mouse tumors (99). Tumor temperatures below 41°C increased blood flow, whereas higher temperatures caused a collapse in blood flow. A similar response was seen in normal tissue, but with 43°C as threshold temperature. Specific changes in clearance rate of muscle and KHT tumor in male mice as response to hyperthermic temperatures (43–46°C) have been reported by Brown et al. (100). In agreement with other studies they measured an initial increase in clearance rate (which correlates with perfusion) for all tissues and a higher heat sensitivity (factor two) of the tumor resulting in faster shut down of blood flow compared to normal tissue. Dickson et al. heated animal tumors (Yoshida sarcoma in rats) in a water bath to 42°C and reported a progressive decrease in blood flow for heating times greater than one hour for the tumor tissue while blood flow of normal tissue increased to 4–7 times the resting values. The response of microvasculature to heating between 41 and 45°C was studied by H. Eddy for squamous cell carcinoma in hamsters. At 45°C the response of tumor vasculature to the elevated temperature included early reduction in vessel caliber, vascular stasis and was followed later by infarction and coagulation necrosis (101). Shrivastav et al. investigated the effects of microwave hyperthermia on microcirculation of normal and malignant tissues in rats for temperatures between 39–44°C (102). No significant change of circulation in the normal or malignant tissues for lower temperatures were observed, whereas significant changes in the tissue vascular resistance and blood flow occurred at temperatures > 42°C. After heating for 10 min at 42°C and 3 min at 44°C, the tumor vascular resistance to blood flow doubled, and the relative blood flow significantly decreased while that to the surrounding musculature remained unaltered indicating the tumor vasculature seems more responsive to heat treatment. An interstitial laser Doppler approach was used by Sturesson et al. to measure the increase of liver perfusion in rat liver at temperatures of 41 and 44°C (103). An increase in liver perfusion up to 33% was found at a local tissue temperature of 41°C whereas blood flow decreased continuously during and after heating to 44°C. Van den Berg-Block et al. measured the tumor (undifferentiated Rhabdomyosarcoma BA I 112) vasculature failure in rats for temperatures between 42–43.5°C via stereomicroscope and reported shorter times (about on third) for 50% vascular stoppage at 43.5°C compared to heating to 42°C (104).
While small animal studies suggest tumors to be highly sensitive to hyperthermia with reduction in blood flow or vascular shutdown commencing at 42–43 °C, there is evidence that tumors in large animals, and more importantly human tumors are considerably less sensitive (105–111). Vujaskovic et al. observed a significant increase in perfusion (about 19%) of canine soft tissue sarcomas 24 h after local hyperthermia which was particularly pronounced at temperatures around 44°C (105). Similarly, Milligan et al. investigated blood flow in canine mast cell tumors during and after hyperthermia with temperatures up to 44°C. In contrast to normal tissue, where blood flow increased after 40 minutes of heating by about 5%, the mast cell sarcomas showed little change in estimated blood flow (107). A thermal pulse decay technique was used by Xu and Holmes to investigate blood perfusion rated of canine prostate under normal and hyperthermic (41-43°C) conditions induced by RF and MW heating (112). In agreement with other studies, perfusion increased about 3.5 fold relative to the baseline perfusion when the tissue was heated from body temperature to 41.3°C and increased another 0.5 fold with further heating to 43.1°C. In normal tissues such as canine brain tissue Lyons et al. found a 2-3-fold increase in blood flow rate which occurred gradually throughout the course of heating with temperatures between 42 to 49°C and heating durations ranging between 15 and 45 min (106).
Waterman et al. studied the response of human tumor blood flow to a fractionated course of thermoradiotherapy (15 days) in four superficial human tumors (three adenocarcinomas, one melanoma) during 60 minutes of local hyperthermia (40-44°C) and observed varying decrease in blood flow (50 to 100%) during the course of thermoradiotherapy in all four cases (113). In a later study, Waterman et al. presented the response of blood flow in superficial human tumors (tumor volumes from 18 to 810cm3) during 60 minutes of local hyperthermia (40-44°C) administered via MW approach. The mean blood flow rate was found to be increasing by 10–15% within the first 30 minutes and remained nearly constant afterwards (114). In this study no reduction in blood flow occurred, though data in one tumor suggests that a reduction in perfusion may occur at temperatures above 44°C. Interestingly though, comparison of the tumor size relative to baseline tumor blood flow revealed that larger tumors tend to be perfused less than smaller ones. Van Vulpen et al. presented prostate perfusion data in 18 patients with locally advanced prostate carcinoma treated with a combination of external beam irradiation and regional or interstitial hyperthermia (39.4–53.1°C) (115). Their data revealed that perfusion increased due to hyperthermia with higher perfusion values for interstitial hyperthermia (470% increase) compared with regional hyperthermia (40% increase), which may be explained by higher temperatures during interstitial hyperthermia. No change in perfusion during hyperthermic (up to 44°C) sessions was found in a study by Lagendijk et al.; they showed that perfusion in inoperable breast tumors may both increase and decrease after successful hyperthermia and the average tumor blood flow is not related to tumour volume (116). Overall, studies in human patients suggest no reduction in perfusion at temperatures up to at least 44 °C. Thus, in particular small animal tumor models may not appropriately model blood flow response of human tumors in response to hyperthermia.
A summary of temperature-dependent perfusion of biological tissues presently available are plotted in Figure 6 and a more comprehensive list of data is presented in Table 3.
Figure 6.
Effect of hyperthermic temperatures (41 – 46°C) on blood flow
Table 3.
Effect of hyperthermic (40 – 46°C) temperatures on blood flow
| Autor | Tumor | Temperature/conditions | Blood flow/observations |
|---|---|---|---|
|
| |||
| Ardenne and Reitnauer, 1980 | DS carcinoma (rats) | Total body heat to 39.5°C plus local heat 43°C/100min | inhibition of tumor microcirculation |
|
| |||
| 40–41°C | |||
| Tumor pO2 increased | |||
| Bicher and Vaupel, 1980 | C3H mammary carcinoma, mouse | >41°C | |
| 42.0°C,40min | vascular stasis | ||
|
| |||
| Brown et al. 1992 | SCC-VII,RIF-1,C3H mammary carcinoma, human mammary carcinomas, mouse | 43–46°C/60min | decreased clearance rate, vascular damage followed a 1°C chance eq. change in heating time factor 2 |
| Muscle tissue, mouse | 43–46°C/60min | similar to initial clearance rate | |
|
| |||
| Dickson and carcinomaldenvood, 1980 | Yoshida sarcoma, rat | 42.0°C/1hr | vascular stasis |
|
| |||
| Dudar and Jain, 1984 | VX2 carcinoma, Rabbit | 42.5°C,40min | vascular stasis |
|
| |||
| 43.0°C/30min | vascular stasis | ||
| 43°C2–15min | vaso dilation | ||
| Eddy, 1980 | Squamous cell carcinoma in hamster cheek pouch | 43°C > 15min | mild stasis |
| 45°C/30min | marked stasis | ||
|
| |||
| 40.5°C/40min | no change | ||
| BA1112 rats sarcoma | 42.5°C/40min | dilation and congestion | |
| Emami et al, 1981 | |||
| 44.5°C/40min | hemorrhage and necrosis | ||
| BA-1112 rhabdomyosarcoma, rat | 42.5°C/40min | vascular stasis | |
|
| |||
| 40.0°C/1hr | vascular stasis | ||
| Endrich et al., 1979 | BA-1112 rhabdomyosarcoma, rat | decreased flow and decreased | |
| 41.3°C/1 h | |||
| number of functional capillaries | |||
|
| |||
| >43.0°C/1h | vascular stasis | ||
| Gullino et al., 1978 | Walker 256 rat mammary carcinoma | ||
| 40–42°C/1h | no consistent or predictable change in blood flow or O2 consumption | ||
| Rappaport and Song, 1983 | 13762A carcinoma,rat | 43.5°C/1hr | vascular stasis |
|
| |||
| 42–42.5°C/l h | no change | ||
| Reinhold and Van den Berg-Blok,1981 | BA-1112 rhabdomyosarcoma, rat | 42–42.5°C/2–3h | reduced blood flow and vascular collapse |
| 42.5°C/2.5hr | vascular stasis | ||
|
| |||
| 39°C/45min | unaltered vascular resistance and blood flow | ||
| Shrivastav et al. 1983 | SMT-2A mammary adenocarcinoma, rat | 42°C/45min | |
| increased blood flow | |||
| 45°C/60min | |||
|
| |||
| Song at al., 1980b | SCK carcinoma, mouse | 40.5°C/30min | vascular stasis |
|
| |||
| 43°C/1 h | no change in tumor blood flow | ||
| Song et al., 1980 | Walker 256 carcinoma, rat | ||
| >43.0°C/1hr | vascular stasis | ||
|
| |||
| Song et al., 1984 | RIF-1 tumor, mouse | 42.5°C/1hr | vascular stasis |
|
| |||
| SAFA tumor, mouse | 42.5°C/1hr | ||
| CAMT, mouse | 42.5°C/1hr | ||
| Stewart and Begg, 1983 | vascular stasis | ||
| CANT, mouse | 42.5°C/1hr | ||
| SAF, mouse | 42.5°C/1hr | ||
|
| |||
| 41/30min | increased blood flow | ||
| Sturesson et al., 1999 | Rat liver parenchyma | ||
| 44°C/30min | decreased blood flow | ||
|
| |||
| Sutton,1983 | Ependymoblastana, Mouse | 42.0°C/1hr | vascular stasis |
|
| |||
| 42°C/30min | vascular stasis | ||
| Vaupel et al., 1980 | DA carcinoma in rat kidneys | 39.5°C/> 30min | increased blood flow and O2 consumption |
| 42°C/> 30min | decreased blood flow and O2 consumption | ||
|
| |||
| Waterman et al., 1991 | Superficial human tumors | 40–44°C/60min | blood flow independent of temperature |
VI. Modelling of Temperature Dependence of Tissue Properties
Computer simulations have increasingly been utilized in recent years as assistive tools for thermal treatments and are used as aid for planning, evaluating and optimizing therapies, and to minimize treatment risks preoperatively (20, 23, 28, 29, 32, 33, 37, 117–120). To obtain realistic models of thermal therapies it is important to use adequate mathematical functions to model the temperature dependence of tissue properties, or resort to using interpolation based on tabulated data if necessary.
Trujillo and Berjano reviewed the mathematical functions most commonly used for modeling the temperature dependence of the thermal and electrical conductivities (k and σ) in RFA computational modeling. Using models with constant values or mathematical functions to reflect the temperature dependence of these parameters, and rapid change at temperatures greater 100°C, their findings suggest that the different methods of piecewise modeling temperature dependence of k and σ reported in the literature do not significantly affect the computed thermal lesion diameter following ablation therapies (18). Similarly, Lobo et al. used computer simulation via the Bioheat equation coupled with temperature-dependent solutions for RF electric fields to generate tissue temperature profiles for an internally cooled electrode (121). They demonstrated that thermal conductivity alters the expected heating pattern for electrical conductivity and temperature distribution. Ji and Brace measured the dielectric properties of liver tissue during high-temperature microwave heating and derived a mathematical function of the time-temperature curve for relative permittivity and effective conductivity and compared to simulations with existing linear and static models, and experimental temperatures in liver tissue. They found from these studies that a sigmoidal model of tissue dielectric properties improves prediction of experimental results. To characterize the combined effects of varying perfusion, electrical, as well as thermal conductivity on RF heating, Ahmed et al. simulated RF ablation (30). They demonstrated that while tissue perfusion has the dominant effect on RF heating; suboptimal thermal and electrical conductivity markedly limit successful ablation except in the setting of almost non-existent perfusion for clinically relevant tumor sizes. Beep-Min, et al. developed a finite-element program to simulate the dynamic evolution of coagulation in tissue considering temperature and damage dependence of both the optical properties and blood perfusion rate during laser coagulation (122). A relatively significant overestimation of the temperature rise occurs if the dynamic parameters are ignored. Blood perfusion is temperature and time dependent and depends on the degree of microvascular stasis. The inequality between the normalized blood perfusion and the predicted degree of microvascular stasis found in this study suggests that a first order rate model may be insufficient to model renal blood perfusion response during microwave thermal therapy (123). Schutt et al. and Prakash et al. compared the effect of different microvascular perfusion algorithms on ablation zone dimensions and found that the choice of microvascular perfusion algorithm and base line tissue perfusion have significant effects on final ablation zone dimensions in computer models of thermal ablation (17, 124). It is evident that the choice of modeling the temperature dependence of the electrical as well as thermal and perfusion properties have significant effects on the electrical field and temperature distribution in computer models, respectively (17, 18, 30, 64, 123). Thus, accurate models require the consideration of temperature-dependent properties, and among tissue properties in many cases perfusion and its temperature dependence is often dominating and of primary importance (30, 79, 111, 124).
VII. Summary
In this paper we reviewed temperature-dependent thermal and electrical properties of biological tissues primarily in the supraphysiological temperature regime. In general, when heat is applied, the biophysical properties of biological tissues change. For some properties, the change directly correlates with temperature (e.g. thermal conductivity); for others, a strong irreversible component is observable with complex interaction between temperature and time (e.g. perfusion). The temperature-dependent changes need to be considered to enhance the accuracy of predicting and monitoring pre-clinical and clinical procedures and treatments, where for some properties (e.g. thermal conductivity) simple linear approximations are usually sufficient. The data summarized in this review can be used in models to calculate electromagnetic field and SAR distribution within tissues subjected to MR scans, for planning and optimization of electromagnetic heating with radiofrequency current and microwaves, and in models of other thermal therapies such as laser and focused ultrasound. For some properties (e.g. electrical conductivity at RF frequencies), the tissue state (in-vivo, in situ, ex-vivo with time following tissue extraction) has considerable impact and needs to be considered.
Figure 2.
Electrical permittivity of various animal tissues as a function of temperature. Colors are indicating frequencies (blue: ~1 GHz, green: >2 GHz). Permittivity for frequencies in the RF heating range (450-500 kHz) is not presented; however the electrical permittivity has limited relevance at RF frequencies where conduction current is dominating.
Footnotes
Apparent specific heat relates directly to the differential scanning calorimeter (DSC)-measured enthalpies that capture both sensible and latent heat effects in tissues.
VIII. References
- 1.Brace CL. Radiofrequency and microwave ablation of the liver, lung, kidney, and bone: what are the differences? Curr Probl Diagn Radiol. 2009 May-Jun;38(3):135–43. doi: 10.1067/j.cpradiol.2007.10.001. PubMed PMID: 19298912. Pubmed Central PMCID: 2941203. Epub 2009/03/21. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gazelle GS, Goldberg SN, Solbiati L, Livraghi T. Tumor ablation with radio-frequency energy. Radiology. 2000 Dec;217(3):633–46. doi: 10.1148/radiology.217.3.r00dc26633. PubMed PMID: 11110923. Epub 2000/12/09. eng. [DOI] [PubMed] [Google Scholar]
- 3.Goldberg SN, Gazelle GS, Mueller PR. Thermal ablation therapy for focal malignancy: a unified approach to underlying principles, techniques, and diagnostic imaging guidance. AJR Am J Roentgenol. 2000 Feb;174(2):323–31. doi: 10.2214/ajr.174.2.1740323. PubMed PMID: 10658699. Epub 2000/02/05. eng. [DOI] [PubMed] [Google Scholar]
- 4.Madersbacher S, Kratzik C, Susani M, Marberger M. Tissue ablation in benign prostatic hyperplasia with high intensity focused ultrasound. J Urol. 1994 Dec;152(6 Pt 1):1956–60. doi: 10.1016/s0022-5347(17)32278-4. discussion 60–1. PubMed PMID: 7525992. Epub 1994/12/01. eng. [DOI] [PubMed] [Google Scholar]
- 5.Partanen A, Yarmolenko PS, Viitala A, Appanaboyina S, Haemmerich D, Ranjan A, et al. Mild hyperthermia with magnetic resonance-guided high-intensity focused ultrasound for applications in drug delivery. Int J Hyperthermia. 2012;28(4):320–36. doi: 10.3109/02656736.2012.680173. PubMed PMID: 22621734. Epub 2012/05/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wolf FJ, Grand DJ, Machan JT, Dipetrillo TA, Mayo-Smith WW, Dupuy DE. Microwave ablation of lung malignancies: effectiveness, CT findings, and safety in 50 patients. Radiology. 2008 Jun;247(3):871–9. doi: 10.1148/radiol.2473070996. PubMed PMID: 18372457. Epub 2008/03/29. eng. [DOI] [PubMed] [Google Scholar]
- 7.Falk MH, Issels RD. Hyperthermia in oncology. Int J Hyperthermia. 2001 Jan-Feb;17(1):1–18. doi: 10.1080/02656730150201552. PubMed PMID: 11212876. Epub 2001/02/24. eng. [DOI] [PubMed] [Google Scholar]
- 8.Abdullah B, Subramaniam R, Omar S, Wragg P, Ramli N, Wui A, et al. Magnetic resonance-guided focused ultrasound surgery (MRgFUS) treatment for uterine fibroids. Biomed Imaging Interv J. 2010 Apr-Jun;6(2):e15. doi: 10.2349/biij.6.2.e15. PubMed PMID: 21611036. Pubmed Central PMCID: 3097768. Epub 2011/05/26. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Diederich CJ. Thermal ablation and high-temperature thermal therapy: overview of technology and clinical implementation. Int J Hyperthermia. 2005 Dec;21(8):745–53. doi: 10.1080/02656730500271692. PubMed PMID: 16338857. Epub 2005/12/13. eng. [DOI] [PubMed] [Google Scholar]
- 10.Staruch R, Chopra R, Hynynen K. MRI-Controlled Ultrasound Thermal Therapy. Pulse, IEEE. 2011;2(5):39–47. doi: 10.1109/MPUL.2011.942604. [DOI] [PubMed] [Google Scholar]
- 11.Collins CM, Wang Z. Calculation of radiofrequency electromagnetic fields and their effects in MRI of human subjects. Magn Reson Med. 2011 May;65(5):1470–82. doi: 10.1002/mrm.22845. PubMed PMID: 21381106. Pubmed Central PMCID: 3078983. Epub 2011/03/08. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xin X, Wang D, Han J, Feng Y, Feng Q, Chen W. Numerical optimization of a three-channel radiofrequency coil for open, vertical-field, MR-guided, focused ultrasound surgery using the hybrid method of moment/finite difference time domain method. NMR Biomed. 2012 Jul;25(7):909–16. doi: 10.1002/nbm.1811. PubMed PMID: 22161891. Epub 2011/12/14. eng. [DOI] [PubMed] [Google Scholar]
- 13.Cherepenin V, Karpov A, Korjenevsky A, Kornienko V, Mazaletskaya A, Mazourov D, et al. A 3D electrical impedance tomography (EIT) system for breast cancer detection. Physiol Meas. 2001 Feb;22(1):9–18. doi: 10.1088/0967-3334/22/1/302. PubMed PMID: 11236894. Epub 2001/03/10. eng. [DOI] [PubMed] [Google Scholar]
- 14.Zou Y, Guo Z. A review of electrical impedance techniques for breast cancer detection. Med Eng Phys. 2003 Mar;25(2):79–90. doi: 10.1016/s1350-4533(02)00194-7. PubMed PMID: 12538062. Epub 2003/01/23. eng. [DOI] [PubMed] [Google Scholar]
- 15.Paulsen KD, Moskowitz MJ, Ryan TP, Mitchell SE, Hoopes PJ. Initial in vivo experience with EIT as a thermal estimator during hyperthermia. International Journal of Hyperthermia. 1996;12(5):573–91. doi: 10.3109/02656739609027666. [DOI] [PubMed] [Google Scholar]
- 16.Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol. 1948 Aug;1(2):93–122. doi: 10.1152/jappl.1948.1.2.93. PubMed PMID: 18887578. Epub 1948/08/01. eng. [DOI] [PubMed] [Google Scholar]
- 17.Schutt DJ, Haemmerich D. Effects of variation in perfusion rates and of perfusion models in computational models of radio frequency tumor ablation. Med Phys. 2008 Aug;35(8):3462–70. doi: 10.1118/1.2948388. PubMed PMID: 18777906. Pubmed Central PMCID: 2673648. Epub 2008/09/10. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Trujillo M, Berjano E. Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation. Int J Hyperthermia. 2013 Sep;29(6):590–7. doi: 10.3109/02656736.2013.807438. PubMed PMID: 23841882. Epub 2013/07/12. eng. [DOI] [PubMed] [Google Scholar]
- 19.Tungjitkusolmun S, Woo EJ, Cao H, Tsai JZ, Vorperian VR, Webster JG. Thermal--electrical finite element modelling for radio frequency cardiac ablation: effects of changes in myocardial properties. Med Biol Eng Comput. 2000 Sep;38(5):562–8. doi: 10.1007/BF02345754. PubMed PMID: 11094815. Epub 2000/11/30. eng. [DOI] [PubMed] [Google Scholar]
- 20.Rossmann C, Rattay F, Haemmerich D. Platform for patient-specific finite-element modeling and application for radiofrequency ablation. Visualization, Image Processing and Computation in Biomedicine. 2012;1(1):0. 2012-11-16. [Google Scholar]
- 21.Berjano EJ. Theoretical modeling for radiofrequency ablation: state-of-the-art and challenges for the future. Biomed Eng Online. 2006;5:24. doi: 10.1186/1475-925X-5-24. PubMed PMID: 16620380. Pubmed Central PMCID: 1459161. Epub 2006/04/20. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Van de Kamer JB, Van Wieringen N, De Leeuw AA, Lagendijk JJ. The significance of accurate dielectric tissue data for hyperthermia treatment planning. Int J Hyperthermia. 2001 Mar-Apr;17(2):123–42. doi: 10.1080/02656730150502297. PubMed PMID: 11252357. [DOI] [PubMed] [Google Scholar]
- 23.Ryan TP, Platt RC, Dadd JS, Humphries S. Tissue electrical properties as a function of thermal dose for use in a finite element model. Advances in Heat and Mass Transfer in Biotechnology. 1997;355(167–71) [Google Scholar]
- 24.Gasselhuber A, Dreher MR, Partanen A, Yarmolenko PS, Woods D, Wood BJ, et al. Targeted drug delivery by high intensity focused ultrasound mediated hyperthermia combined with temperature-sensitive liposomes: computational modelling and preliminary in vivovalidation. Int J Hyperthermia. 2012;28(4):337–48. doi: 10.3109/02656736.2012.677930. PubMed PMID: 22621735. Epub 2012/05/25. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gasselhuber A, Dreher MR, Negussie A, Wood BJ, Rattay F, Haemmerich D. Mathematical spatio-temporal model of drug delivery from low temperature sensitive liposomes during radiofrequency tumour ablation. Int J Hyperthermia. 2010;26(5):499–513. doi: 10.3109/02656731003623590. PubMed PMID: 20377363. Pubmed Central PMCID: 2958178. Epub 2010/04/10. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tungjitkusolmun S, Staelin ST, Haemmerich D, Tsai JZ, Webster JG, Lee FT, Jr, et al. Three-Dimensional finite-element analyses for radio-frequency hepatic tumor ablation. IEEE Trans Biomed Eng. 2002 Jan;49(1):3–9. doi: 10.1109/10.972834. PubMed PMID: 11797653. Epub 2002/01/19. eng. [DOI] [PubMed] [Google Scholar]
- 27.Strigel RM, Schutt DJ, Webster JG, Mahvi DM, Haemmerich D. An Electrode Array for Limiting Blood Loss During Liver Resection: Optimization via Mathematical Modeling. Open Biomed Eng J. 2010;4:39–46. doi: 10.2174/1874120701004020039. PubMed PMID: 20309395. Pubmed Central PMCID: 2840609. Epub 2010/03/24. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Paulides MM, Stauffer PR, Neufeld E, Maccarini PF, Kyriakou A, Canters RA, et al. Simulation techniques in hyperthermia treatment planning. Int J Hyperthermia. 2013 Jun;29(4):346–57. doi: 10.3109/02656736.2013.790092. PubMed PMID: 23672453. Pubmed Central PMCID: 3711016. Epub 2013/05/16. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Scott SJ, Salgaonkar V, Prakash P, Burdette EC, Diederich CJ. Interstitial ultrasound ablation of vertebral and paraspinal tumours: Parametric and patient-specific simulations. Int J Hyperthermia. 2014 Jun;30(4):228–44. doi: 10.3109/02656736.2014.915992. PubMed PMID: 25017322. Epub 2014/07/16. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ahmed M, Liu Z, Humphries S, Goldberg SN. Computer modeling of the combined effects of perfusion, electrical conductivity, and thermal conductivity on tissue heating patterns in radiofrequency tumor ablation. Int J Hyperthermia. 2008 Nov;24(7):577–88. doi: 10.1080/02656730802192661. PubMed PMID: 18608580. Epub 2008/07/09. eng. [DOI] [PubMed] [Google Scholar]
- 31.Chiang J, Wang P, Brace CL. Computational modelling of microwave tumour ablations. Int J Hyperthermia. 2013 Jun;29(4):308–17. doi: 10.3109/02656736.2013.799295. PubMed PMID: 23738698. Pubmed Central PMCID: 3768158. Epub 2013/06/07. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schumann C, Rieder C, Bieberstein J, Weihusen A, Zidowitz S, Moltz JH, et al. State of the art in computer-assisted planning, intervention, and assessment of liver-tumor ablation. Crit Rev Biomed Eng. 2010;38(1):31–52. doi: 10.1615/critrevbiomedeng.v38.i1.40. PubMed PMID: 21175402. Epub 2010/12/24. eng. [DOI] [PubMed] [Google Scholar]
- 33.Prakash P. Theoretical modeling for hepatic microwave ablation. Open Biomed Eng J. 2010;4:27–38. doi: 10.2174/1874120701004020027. PubMed PMID: 20309393. Pubmed Central PMCID: 2840585. Epub 2010/03/24. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Panescu D, Whayne JG, Fleischman SD, Mirotznik MS, Swanson DK, Webster JG. Three-dimensional finite element analysis of current density and temperature distributions during radio-frequency ablation. IEEE Trans Biomed Eng. 1995 Sep;42(9):879–90. doi: 10.1109/10.412649. PubMed PMID: 7558062. Epub 1995/09/01. eng. [DOI] [PubMed] [Google Scholar]
- 35.Canney MS, Bailey MR, Crum LA, Khokhlova VA, Sapozhnikov OA. Acoustic characterization of high intensity focused ultrasound fields: A combined measurement and modeling approach. The Journal of the Acoustical Society of America. 2008;124(4):2406–20. doi: 10.1121/1.2967836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Payne S, Flanagan R, Pollari M, Alhonnoro T, Bost C, O'Neill D, et al. Image-based multi-scale modelling and validation of radio-frequency ablation in liver tumours. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2011;369(1954):4233–54. doi: 10.1098/rsta.2011.0240. [DOI] [PubMed] [Google Scholar]
- 37.Strohbehn JW. Temperature distributions from interstitial rf electrode hyperthermia systems: theoretical predictions. Int J Radiat Oncol Biol Phys. 1983 Nov;9(11):1655–67. doi: 10.1016/0360-3016(83)90419-4. PubMed PMID: 6643161. [DOI] [PubMed] [Google Scholar]
- 38.Goharrizi AY, Kwong R, Chopra R. Development of robust/predictive control strategies for image-guided ablative treatments using a minimally invasive ultrasound applicator. Int J Hyperthermia. 2014 Nov;30(7):438–46. doi: 10.3109/02656736.2014.963702. PubMed PMID: 25314227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kok HP, Gellermann J, van den Berg CA, Stauffer PR, Hand JW, Crezee J. Thermal modelling using discrete vasculature for thermal therapy: A review. Int J Hyperthermia. 2013 Jun;29(4):336–45. doi: 10.3109/02656736.2013.801521. PubMed PMID: 23738700. Pubmed Central PMCID: 3684078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fahrenholtz SJ, Stafford RJ, Maier F, Hazle JD, Fuentes D. Generalised polynomial chaos-based uncertainty quantification for planning MRgLITT procedures. Int J Hyperthermia. 2013 Jun;29(4):324–35. doi: 10.3109/02656736.2013.798036. PubMed PMID: 23692295. Pubmed Central PMCID: 3924420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Haemmerich D. Biophysics of radiofrequency ablation. Crit Rev Biomed Eng. 2010;38(1):53–63. doi: 10.1615/critrevbiomedeng.v38.i1.50. PubMed PMID: 21175403. Epub 2010/12/24. eng. [DOI] [PubMed] [Google Scholar]
- 42.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol. 1996 Nov;41(11):2271–93. doi: 10.1088/0031-9155/41/11/003. PubMed PMID: 8938026. Epub 1996/11/01. eng. [DOI] [PubMed] [Google Scholar]
- 43.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol. 1996 Nov;41(11):2251–69. doi: 10.1088/0031-9155/41/11/002. PubMed PMID: 8938025. Epub 1996/11/01. eng. [DOI] [PubMed] [Google Scholar]
- 44.Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues: I. Literature survey. Phys Med Biol. 1996 Nov;41(11):2231–49. doi: 10.1088/0031-9155/41/11/001. PubMed PMID: 8938024. Epub 1996/11/01. eng. [DOI] [PubMed] [Google Scholar]
- 45.Haemmerich D, Schutt DJ, Wright AW, Webster JG, Mahvi DM. Electrical conductivity measurement of excised human metastatic liver tumours before and after thermal ablation. Physiol Meas. 2009 Apr 6;30(5):459–66. doi: 10.1088/0967-3334/30/5/003. PubMed PMID: 19349647. Epub 2009/04/08. Eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Macchi E, Gallati M, Braschi G, Persi E. Dielectric properties of RF heated ex vivo porcine liver tissue at 480 kHz: measurements and simulations. Journal of Physics D: Applied Physics. 2014 epub. [Google Scholar]
- 47.Duck FA. Physical Properties of Tissue. Academic Press; London: 1990. Chapter 6: Electrical Properties of Tissue; pp. 167–223. [Google Scholar]
- 48.Gabriel C, Peyman A, Grant EH. Electrical conductivity of tissue at frequencies below 1 MHz. Phys Med Biol. 2009 Aug 21;54(16):4863–78. doi: 10.1088/0031-9155/54/16/002. PubMed PMID: 19636081. Epub 2009/07/29. eng. [DOI] [PubMed] [Google Scholar]
- 49.Schwan HP. Electrical properties of blood at ultrahigh frequencies. Am J Phys Med. 1953 Jun;32(3):144–52. PubMed PMID: 13058019. Epub 1953/06/01. eng. [PubMed] [Google Scholar]
- 50.Foster KR, Schwan HP. Dielectric properties of tissues and biological materials: a critical review. Crit Rev Biomed Eng. 1989;17(1):25–104. PubMed PMID: 2651001. Epub 1989/01/01. eng. [PubMed] [Google Scholar]
- 51.Pop M, Molckovsky A, Chin L, Kolios MC, Jewett MA, Sherar MD. Changes in dielectric properties at 460 kHz of kidney and fat during heating: importance for radio-frequency thermal therapy. Phys Med Biol. 2003 Aug 7;48(15):2509–25. doi: 10.1088/0031-9155/48/15/317. PubMed PMID: 12953912. Epub 2003/09/05. eng. [DOI] [PubMed] [Google Scholar]
- 52.Kwon OI, Chauhan M, Kim HJ, Jeong WC, Wi H, Oh TI, et al. Fast conductivity imaging in magnetic resonance electrical impedance tomography (MREIT) for RF ablation monitoring. Int J Hyperthermia. 2014 Nov;30(7):447–55. doi: 10.3109/02656736.2014.966337. PubMed PMID: 25329351. [DOI] [PubMed] [Google Scholar]
- 53.Zurbuchen U, Holmer C, Lehmann KS, Stein T, Roggan A, Seifarth C, et al. Determination of the temperature-dependent electric conductivity of liver tissue ex vivo and in vivo: Importance for therapy planning for the radiofrequency ablation of liver tumours. Int J Hyperthermia. 2010 Feb;26(1):26–33. doi: 10.3109/02656730903436442. PubMed PMID: 20100050. Pubmed Central PMCID: AB. Epub 2010/01/27. eng. [DOI] [PubMed] [Google Scholar]
- 54.McRae DA, Esrick MA. The dielectric parameters of excised EMT-6 tumours and their change during hyperthermia. Phys Med Biol. 1992 Nov;37(11):2045–58. doi: 10.1088/0031-9155/37/11/002. PubMed PMID: 1438561. [DOI] [PubMed] [Google Scholar]
- 55.McRae DA, Esrick MA. Changes in electrical impedance of skeletal muscle measured during hyperthermia. Int J Hyperthermia. 1993 Mar-Apr;9(2):247–61. doi: 10.3109/02656739309022538. PubMed PMID: 8468508. [DOI] [PubMed] [Google Scholar]
- 56.McRae DA, Esrick MA, Mueller SC. Non-invasive, in-vivo electrical impedance of EMT-6 tumours during hyperthermia: correlation with morphology and tumour-growth-delay. Int J Hyperthermia. 1997 Jan-Feb;13(1):1–20. doi: 10.3109/02656739709056426. PubMed PMID: 9024923. [DOI] [PubMed] [Google Scholar]
- 57.Fu F, Xin SX, Chen W. Temperature- and frequency-dependent dielectric properties of biological tissues within the temperature and frequency ranges typically used for magnetic resonance imaging-guided focused ultrasound surgery. Int J Hyperthermia. 2014 Feb;30(1):56–65. doi: 10.3109/02656736.2013.868534. PubMed PMID: 24417349. Epub 2014/01/15. eng. [DOI] [PubMed] [Google Scholar]
- 58.Stauffer PR, Rossetto F, Prakash M, Neuman DG, Lee T. Phantom and animal tissues for modelling the electrical properties of human liver. Int J Hyperthermia. 2003 Jan-Feb;19(1):89–101. doi: 10.1080/0265673021000017064. PubMed PMID: 12519714. Epub 2003/01/10. eng. [DOI] [PubMed] [Google Scholar]
- 59.Chin L, Sherar M. Changes in dielectric properties of ex vivo bovine liver at 915 MHz during heating. Phys Med Biol. 2001 Jan;46(1):197–211. doi: 10.1088/0031-9155/46/1/314. PubMed PMID: 11197672. Epub 2001/02/24. eng. [DOI] [PubMed] [Google Scholar]
- 60.Chin L, Sherar M. Changes in the dielectric properties of rat prostate ex vivo at 915 MHz during heating. Int J Hyperthermia. 2004 Aug;20(5):517–27. doi: 10.1080/02656730310001657738. PubMed PMID: 15277024. Epub 2004/07/28. eng. [DOI] [PubMed] [Google Scholar]
- 61.Mohapatra SN, Hill DW. The changes in blood resistivity with haematocrit and temperature. Eur J Intensive Care Med. 1975 Dec;1(4):153–62. doi: 10.1007/BF00624433. [DOI] [PubMed] [Google Scholar]
- 62.Jaspard F, Nadi M. Dielectric properties of blood: an investigation of temperature dependence. Physiol Meas. 2002 Aug;23(3):547–54. doi: 10.1088/0967-3334/23/3/306. PubMed PMID: 12214762. Epub 2002/09/07. eng. [DOI] [PubMed] [Google Scholar]
- 63.Lazebnik M, Converse MC, Booske JH, Hagness SC. Ultrawideband temperature-dependent dielectric properties of animal liver tissue in the microwave frequency range. Phys Med Biol. 2006 Apr 7;51(7):1941–55. doi: 10.1088/0031-9155/51/7/022. PubMed PMID: 16552116. Epub 2006/03/23. eng. [DOI] [PubMed] [Google Scholar]
- 64.Brace CL. Temperature-dependent dielectric properties of liver tissue measured during thermal ablation: toward an improved numerical model. Conf Proc IEEE Eng Med Biol Soc. 2008;2008:230–3. doi: 10.1109/IEMBS.2008.4649132. PubMed PMID: 19162635. Epub 2009/01/24. eng. [DOI] [PubMed] [Google Scholar]
- 65.Lopresto V, Pinto R, Lovisolo GA, Cavagnaro M. Changes in the dielectric properties of ex vivo bovine liver during microwave thermal ablation at 2.45 GHz. Phys Med Biol. 2012 Apr 21;57(8):2309–27. doi: 10.1088/0031-9155/57/8/2309. PubMed PMID: 22460062. Epub 2012/03/31. eng. [DOI] [PubMed] [Google Scholar]
- 66.Tran VN, Stuchly SS. Dielectric properties of beef, beef liver, chicken and salmon at frequencies from 100 to 2500 MHz. J Microw Power Electromagn Energy. 1987;22(1):29–33. doi: 10.1080/08327823.1987.11688003. PubMed PMID: 3598827. Epub 1987/01/01. eng. [DOI] [PubMed] [Google Scholar]
- 67.Zhang H, Cheng S, He L, Zhang A, Zheng Y, Gao D. Determination of Thermal Conductivity of Biomaterials in the Temperature Range 233–313K Using a Tiny Detector Made of a Self-Heated Thermistor. Cell Preservation Technology. 2002;1(2):141–7. [Google Scholar]
- 68.Zhang L, Lyng JG, Brunton N, Morgan D, McKenna B. Dielectric and thermophysical properties of meat batters over a temperature range of 5–85 degrees C. Meat Sci. 2004 Oct;68(2):173–84. doi: 10.1016/j.meatsci.2004.02.009. PubMed PMID: 22062226. Epub 2004/10/01. eng. [DOI] [PubMed] [Google Scholar]
- 69.Darvishi H, Khostaghaza MH, Najafi G. Ohmic heating of pomegranate juice: Electrical conductivity and pH change. Journal of the Saudi Society of Agricultural Sciences. 2013;12(2):101–8. [Google Scholar]
- 70.Jha SN, Narsaiah K, Basediya AL, Sharma R, Jaiswal P, Kumar R, et al. Measurement techniques and application of electrical properties for nondestructive quality evaluation of foods-a review. J Food Sci Technol. 2011 Aug;48(4):387–411. doi: 10.1007/s13197-011-0263-x. PubMed PMID: 23572764. Pubmed Central PMCID: 3551172. Epub 2011/08/01. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Icier F, Ilicali C. Temperature dependent electrical conductivities of fruit purees during ohmic heating. Food Research International. 2005;38(10):1135–42. [Google Scholar]
- 72.Sarang S, Sastry SK, Knipe L. Electrical conductivity of fruits and meats during ohmic heating. Journal of Food Engineering. 2008;87(3):351–6. [Google Scholar]
- 73.Zhuang H, Nelson SO, Trabelsi S, Savage EM. Dielectric properties of uncooked chicken breast muscles from ten to one thousand eight hundred megahertz. Poult Sci. 2007 Nov;86(11):2433–40. doi: 10.3382/ps.2006-00434. PubMed PMID: 17954595. Epub 2007/10/24. eng. [DOI] [PubMed] [Google Scholar]
- 74.Zheng E, Shao S, Webster JG. Impedance of skeletal muscle from 1 Hz to 1 MHz. IEEE Trans Biomed Eng. 1984 Jun;31(6):477–81. doi: 10.1109/TBME.1984.325417. PubMed PMID: 6429032. Epub 1984/06/01. eng. [DOI] [PubMed] [Google Scholar]
- 75.Swatland H. Postmortem changes in electrical capacitance and resistivity of pork. J Anim Sci. 1980;51(5):1108–12. [Google Scholar]
- 76.Surowiec A, Stuchly SS, Swarup A. Radiofrequency dielectric properties of animal tissues as a function of time following death. Phys Med Biol. 1985 Oct;30(10):1131–41. doi: 10.1088/0031-9155/30/10/012. PubMed PMID: 4070369. Epub 1985/10/01. eng. [DOI] [PubMed] [Google Scholar]
- 77.Haemmerich D, Ozkan R, Tungjitkusolmun S, Tsai JZ, Mahvi DM, Staelin ST, et al. Changes in electrical resistivity of swine liver after occlusion and postmortem. Med Biol Eng Comput. 2002 Jan;40(1):29–33. doi: 10.1007/BF02347692. PubMed PMID: 11954705. Epub 2002/04/17. eng. [DOI] [PubMed] [Google Scholar]
- 78.O'Rourke AP, Lazebnik M, Bertram JM, Converse MC, Hagness SC, Webster JG, et al. Dielectric properties of human normal, malignant and cirrhotic liver tissue: in vivo and ex vivo measurements from 0.5 to 20 GHz using a precision open-ended coaxial probe. Phys Med Biol. 2007 Aug 7;52(15):4707–19. doi: 10.1088/0031-9155/52/15/022. PubMed PMID: 17634659. Epub 2007/07/20. eng. [DOI] [PubMed] [Google Scholar]
- 79.Dos Santos I, Haemmerich D, Schutt D, da Rocha AF, Menezes LR. Probabilistic finite element analysis of radiofrequency liver ablation using the unscented transform. Phys Med Biol. 2009 Feb 7;54(3):627–40. doi: 10.1088/0031-9155/54/3/010. PubMed PMID: 19124948. Pubmed Central PMCID: 2730782. Epub 2009/01/07. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Vernon CC, Hand JW, Field SB, Machin D, Whaley JB, van der Zee J, et al. Radiotherapy with or without hyperthermia in the treatment of superficial localized breast cancer: results from five randomized controlled trials. International Collaborative Hyperthermia Group. Int J Radiat Oncol Biol Phys. 1996 Jul 1;35(4):731–44. doi: 10.1016/0360-3016(96)00154-x. PubMed PMID: 8690639. Epub 1996/07/01. eng. [DOI] [PubMed] [Google Scholar]
- 81.Valvano JW, Cochran JR, Diller KR. Thermal conductivity and diffusivity of biomaterials measured with self-heated thermistors. Int J Thermophys. 1985;6(3):301–11. [Google Scholar]
- 82.Bhattacharya A, Mahajan RL. Temperature dependence of thermal conductivity of biological tissues. Physiol Meas. 2003 Aug;24(3):769–83. doi: 10.1088/0967-3334/24/3/312. PubMed PMID: 14509313. Epub 2003/09/26. eng. [DOI] [PubMed] [Google Scholar]
- 83.van Gemert MJ, Welch A, Bonnier JJ, Valvano JW, Yoon G, Rastegar S, editors. Seminars in Interventional Radiology. 1986. Some physical concepts in laser angioplasty. Copyright© 1986 by Thieme Medical Publishers, Inc. [Google Scholar]
- 84.Liang XG, Ge XS, Zhang YP, Wang GJ. A convenient method of measuring the thermal conductivity of biological tissue. Phys Med Biol. 1991;36(12):1599–605. doi: 10.1088/0031-9155/36/12/005. [DOI] [PubMed] [Google Scholar]
- 85.Bhavaraju NC, Valvano JW. Thermophysical properties of swine myocardium. International Journal of Thermophysics. 1999 Mar;20(2):665–76. [Google Scholar]
- 86.Guntur SR, Lee KI, Paeng DG, Coleman AJ, Choi MJ. Temperature-dependent thermal properties of ex vivo liver undergoing thermal ablation. Ultrasound Med Biol. 2013 Oct;39(10):1771–84. doi: 10.1016/j.ultrasmedbio.2013.04.014. PubMed PMID: 23932271. Epub 2013/08/13. eng. [DOI] [PubMed] [Google Scholar]
- 87.Choi J, Morrissey M, Bischof JC. Thermal Processing of Biological Tissue at High Temperatures: Impact of Protein Denaturation and Water Loss on the Thermal Properties of Human and Porcine Liver in the Range 25–80 °C. Journal of Heat Transfer. 2013;135(6):061302. [Google Scholar]
- 88.Haemmerich D, dos Santos I, Schutt D, Webster JG, Mahvi DM. In vitro measurements of temperature–dependent specific heat of liver tissue. Med Eng Phys. 2006;28(2):194–7. doi: 10.1016/j.medengphy.2005.04.020. [DOI] [PubMed] [Google Scholar]
- 89.Haemmerich D, Schutt DJ, dos Santos I, Webster JG, Mahvi DM. Measurement of temperature-dependent specific heat of biological tissues. Physiol Meas. 2005 Feb;26(1):59–67. doi: 10.1088/0967-3334/26/1/006. PubMed PMID: 15742879. [DOI] [PubMed] [Google Scholar]
- 90.Rahman S. Food Properties Handbook. CRC Press; Boca Raton: 1995. [Google Scholar]
- 91.Marcotte M, Taherian AR, Karimi Y. Thermophysical properties of processed meat and poultry products. Journal of Food Engineering. 2008;88(3):315–22. [Google Scholar]
- 92.Baghe-Khandan MS, Okos MR, Sweat VE. The Thermal Conductivity of Beef as Affected by Temperature and Composition Transactions of the ASABE. 1982;24:1118–22. [Google Scholar]
- 93.Mohsenin NN. Thermal Properties of Food and Agricultural Materials. CRC Press; 1980. [Google Scholar]
- 94.Sweat VE, Haugh CG, Stadelman WJ. Thermal conductivity of chicken meat at temperatures between −75 and 20°C. J Food Sci. 1973;38(1):158–60. [Google Scholar]
- 95.Dickson JA, Calderwood SK. Temperature range and selective sensitivity of tumors to hyperthermia: a critical review. Ann N Y Acad Sci. 1980;335:180–205. doi: 10.1111/j.1749-6632.1980.tb50749.x. PubMed PMID: 6931518. Epub 1980/01/01. eng. [DOI] [PubMed] [Google Scholar]
- 96.Song CW. Effect of local hyperthermia on blood flow and microenvironment: a review. Cancer Res. 1984 Oct;44(10 Suppl):4721s–30s. PubMed PMID: 6467226. Epub 1984/10/01. eng. [PubMed] [Google Scholar]
- 97.Dudar TE, Jain RK. Differential response of normal and tumor microcirculation to hyperthermia. Cancer Res. 1984 Feb;44(2):605–12. PubMed PMID: 6692365. Epub 1984/02/01. eng. [PubMed] [Google Scholar]
- 98.Song CW, Choi IB, Nah BS, Sahu SK, Osborn JL. Microvasculature and Perfusion in Normal Tissues and Tumors. In: Seegenschmiedt MH, Fessenden P, Vernon C, editors. Thermoradiotherapy and Thermochemotherapy. Medical Radiology: Springer Berlin Heidelberg; 1995. pp. 139–56. [Google Scholar]
- 99.Bicher HI, Hetzel FW, Sandhu TS, Frinak S, Vaupel P, O'Hara MD, et al. Effects of hyperthermia on normal and tumor microenvironment. Radiology. 1980 Nov;137(2):523–30. doi: 10.1148/radiology.137.2.7433686. PubMed PMID: 7433686. Epub 1980/11/01. eng. [DOI] [PubMed] [Google Scholar]
- 100.Brown SL, Hunt JW, Hill RP. Differential thermal sensitivity of tumour and normal tissue microvascular response during hyperthermia. Int J Hyperthermia. 1992 Jul-Aug;8(4):501–14. doi: 10.3109/02656739209037988. PubMed PMID: 1402130. Pubmed Central PMCID: A. [DOI] [PubMed] [Google Scholar]
- 101.Eddy HA. Alterations in tumor microvasculature during hyperthermia. Radiology. 1980 Nov;137(2):515–21. doi: 10.1148/radiology.137.2.7433685. [DOI] [PubMed] [Google Scholar]
- 102.Shrivastav S, Kaelin WG, Jr., Joines WT, Jirtle RL. Microwave hyperthermia and its effect on tumor blood flow in rats. Cancer Res. 1983 Oct;43(10):4665–9. Pubmed Central PMCID: C. [PubMed] [Google Scholar]
- 103.Sturesson C, Ivarsson K, Andersson-Engels S, Tranberg KG. Changes in local hepatic blood perfusion during interstitial laser-induced thermotherapy of normal rat liver measured by interstitial laser Doppler flowmetry. Lasers in Medical Science. 1999;14(2):143–9. doi: 10.1007/s101030050036. [DOI] [PubMed] [Google Scholar]
- 104.van den Berg-Block AE, Reinhold HS. Time-temperature relationship for hyperthermia induced stoppage of the microcirculation in tumors. Int J Radiat Oncol Biol Phys. 1984 May;10(5):737–40. doi: 10.1016/0360-3016(84)90304-3. [DOI] [PubMed] [Google Scholar]
- 105.Vujaskovic Z, Poulson JM, Gaskin AA, Thrall DE, Page RL, Charles HC, et al. Temperature-dependent changes in physiologic parameters of spontaneous canine soft tissue sarcomas after combined radiotherapy and hyperthermia treatment. Int J Radiat Oncol Biol Phys. 2000 Jan 1;46(1):179–85. doi: 10.1016/s0360-3016(99)00362-4. PubMed PMID: 10656391. Epub 2000/02/03. eng. [DOI] [PubMed] [Google Scholar]
- 106.Lyons BE, Samulski TV, Cox RS, Fessenden P. Heat loss and blood flow during hyperthermia in normal canine brain. I: Empirical study and analysis. Int J Hyperthermia. 1989 Mar-Apr;5(2):225–47. doi: 10.3109/02656738909140450. PubMed PMID: 2926187. Epub 1989/03/01. eng. [DOI] [PubMed] [Google Scholar]
- 107.Milligan AJ, Panjehpour M. Canine normal and tumor tissue estimated blood flow during fractionated hyperthermia. Int J Radiat Oncol Biol Phys. 1985 Sep;11(9):1679–84. doi: 10.1016/0360-3016(85)90221-4. PubMed PMID: 3928546. Epub 1985/09/01. eng. [DOI] [PubMed] [Google Scholar]
- 108.Samulski TV, Fessenden P, Valdagni R, Kapp DS. Correlations of thermal washout rate, steady state temperatures, and tissue type in deep seated recurrent or metastatic tumors. Int J Radiat Oncol Biol Phys. 1987 Jun;13(6):907–16. doi: 10.1016/0360-3016(87)90106-4. PubMed PMID: 3583862. Epub 1987/06/01. eng. [DOI] [PubMed] [Google Scholar]
- 109.Akyurekli D, Gerig LH, Raaphorst GP. Changes in muscle blood flow distribution during hyperthermia. Int J Hyperthermia. 1997 Sep-Oct;13(5):481–96. doi: 10.3109/02656739709023547. PubMed PMID: 9354933. Epub 1997/11/14. eng. [DOI] [PubMed] [Google Scholar]
- 110.Feldmann HJ, Sievers K, Fuller J, Molls M, Lohr E. Evaluation of tumor blood perfusion by dynamic MRI and CT in patients undergoing thermoradiotherapy. Eur J Radiol. 1993 Apr;16(3):224–9. doi: 10.1016/0720-048x(93)90079-3. PubMed PMID: 8508842. Epub 1993/04/01. eng. [DOI] [PubMed] [Google Scholar]
- 111.Guiot C, Madon E, Allegro D, Pianta PG, Baiotto B, Gabriele P. Perfusion and thermal field during hyperthermia. Experimental measurements and modelling in recurrent breast cancer. Phys Med Biol. 1998 Oct;43(10):2831–43. doi: 10.1088/0031-9155/43/10/012. PubMed PMID: 9814521. Epub 1998/11/14. eng. [DOI] [PubMed] [Google Scholar]
- 112.Xu LX, Zhu L, Holmes KR. Blood perfusion measurements in the canine prostate during transurethral hyperthermia. Ann N Y Acad Sci. 1998 Sep 11;858:21–9. doi: 10.1111/j.1749-6632.1998.tb10136.x. [DOI] [PubMed] [Google Scholar]
- 113.Waterman FM, Nerlinger RE, Moylan DJ, 3rd, Leeper DB. Response of human tumor blood flow to local hyperthermia. Int J Radiat Oncol Biol Phys. 1987 Jan;13(1):75–82. doi: 10.1016/0360-3016(87)90263-x. PubMed PMID: 3804819. Epub 1987/01/01. eng. [DOI] [PubMed] [Google Scholar]
- 114.Waterman FM, Tupchong L, Nerlinger RE, Matthews J. Blood flow in human tumors during local hyperthermia. Int J Radiat Oncol Biol Phys. 1991 Jun;20(6):1255–62. doi: 10.1016/0360-3016(91)90236-w. PubMed PMID: 2045300. Epub 1991/06/01. eng. [DOI] [PubMed] [Google Scholar]
- 115.van Vulpen M, Raaymakers BW, de Leeuw AA, van de Kamer JB, van Moorselaar RJ, Hobbelink MG, et al. Prostate perfusion in patients with locally advanced prostate carcinoma treated with different hyperthermia techniques. J Urol. 2002 Oct;168(4 Pt 1):1597–602. doi: 10.1016/S0022-5347(05)64527-2. PubMed PMID: 12352464. Epub 2002/09/28. eng. [DOI] [PubMed] [Google Scholar]
- 116.Lagendijk JJ, Hofman P, Schipper J. Perfusion analyses in advanced breast carcinoma during hyperthermia. Int J Hyperthermia. 1988 Sep-Oct;4(5):479–95. doi: 10.3109/02656738809027693. PubMed PMID: 3292667. Epub 1988/09/01. eng. [DOI] [PubMed] [Google Scholar]
- 117.Keangin P, Wessapan T, Rattanadecho P. Analysis of heat transfer in deformed liver cancer modeling treated using a microwave coaxial antenna. Applied Thermal Engineering. 2011;31(16):3243–54. [Google Scholar]
- 118.Yull Park J, Young Park C, Min Lee J. Estimation of saline-mixed tissue conductivity and ablation lesion size. Comput Biol Med. 2013 Jun;43(5):504–12. doi: 10.1016/j.compbiomed.2013.02.012. PubMed PMID: 23566396. Epub 2013/04/10. eng. [DOI] [PubMed] [Google Scholar]
- 119.Payne S, Flanagan R, Pollari M, Alhonnoro T, Bost C, O'Neill D, et al. Image-based multi-scale modelling and validation of radio-frequency ablation in liver tumours. Philos Trans A Math Phys Eng Sci. 2011 Nov 13;369(1954):4233–54. doi: 10.1098/rsta.2011.0240. PubMed PMID: 21969674. Epub 2011/10/05. eng. [DOI] [PubMed] [Google Scholar]
- 120.Lai YC, Choy YB, Haemmerich D, Vorperian VR, Webster JG. Lesion size estimator of cardiac radiofrequency ablation at different common locations with different tip temperatures. IEEE Trans Biomed Eng. 2004 Oct;51(10):1859–64. doi: 10.1109/TBME.2004.831529. PubMed PMID: 15490835. Epub 2004/10/20. eng. [DOI] [PubMed] [Google Scholar]
- 121.Lobo SM, Liu ZJ, Yu NC, Humphries S, Ahmed M, Cosman ER, et al. RF tumour ablation: computer simulation and mathematical modelling of the effects of electrical and thermal conductivity. Int J Hyperthermia. 2005 May;21(3):199–213. doi: 10.1080/02656730400001108. PubMed PMID: 16019848. Epub 2005/07/16. eng. [DOI] [PubMed] [Google Scholar]
- 122.Beep-Min K, Jacques SL, Rastegar S, Thomsen S, Motamedi M. Nonlinear finite-element analysis of the role of dynamic changes in blood perfusion and optical properties in laser coagulation of tissue. Selected Topics in Quantum Electronics, IEEE Journal of. 1996;2(4):922–33. [Google Scholar]
- 123.He X, McGee S, Coad JE, Schmidlin F, Iaizzo PA, Swanlund DJ, et al. Investigation of the thermal and tissue injury behaviour in microwave thermal therapy using a porcine kidney model. Int J Hyperthermia. 2004 Sep;20(6):567–93. doi: 10.1080/0265673042000209770. PubMed PMID: 15370815. Epub 2004/09/17. eng. [DOI] [PubMed] [Google Scholar]
- 124.Prakash P, Diederich CJ. Considerations for theoretical modelling of thermal ablation with catheter-based ultrasonic sources: Implications for treatment planning, monitoring and control. Int J Hyperthermia. 2012;28(1):69–86. doi: 10.3109/02656736.2011.630337. PubMed PMID: 22235787. Epub 2012/01/13. eng. [DOI] [PMC free article] [PubMed] [Google Scholar]