Tailoring light-matter coupling in semiconductor and hybrid-plasmonic nanowires

Abstract

Understanding interactions between light and matter is central to many fields, providing invaluable insights into the nature of matter. In its own right, a greater understanding of light-matter coupling has allowed for the creation of tailored applications, resulting in a variety of devices such as lasers, switches, sensors, modulators, and detectors. Reduction of optical mode volume is crucial to enhancing light-matter coupling strength, and among solid-state systems, self-assembled semiconductor and hybrid-plasmonic nanowires are amenable to creation of highly-confined optical modes. Following development of unique spectroscopic techniques designed for the nanowire morphology, carefully engineered semiconductor nanowire cavities have recently been tailored to enhance light-matter coupling strength in a manner previously seen in optical microcavities. Much smaller mode volumes in tailored hybrid-plasmonic nanowires have recently allowed for similar breakthroughs, resulting in sub-picosecond excited-state lifetimes and exceptionally high radiative rate enhancement. Here, we review literature on light-matter interactions in semiconductor and hybrid-plasmonic monolithic nanowire optical cavities to highlight recent progress made in tailoring light-matter coupling strengths. Beginning with a discussion of relevant concepts from optical physics, we will discuss how our knowledge of light-matter coupling has evolved with our ability to produce ever-shrinking optical mode volumes, shifting focus from bulk materials to optical microcavities, before moving on to recent results obtained from semiconducting nanowires.

1. Introduction

Understanding, and ultimately, tailoring, the interaction of electromagnetic radiation (light) and matter has historically borne consequences for fields far beyond modern optical physics. An initial understanding birthed spectroscopy, which provided the first insights into basic optical phenomena such as absorption, emission, and scattering of light upon interaction with matter. The development of more sophisticated measurement techniques and the advent of highly engineered material systems led to the uncovering of novel phenomena which could be controlled by materials design. Further advancement in materials science allowed for exploration of these phenomena in nanostructured materials, which has revealed that hallmarks such as enhanced surface-to-volume ratios, photonic, and electronic confinement can significantly alter their behavior with respect to bulk materials. Myriad solid-state photonic applications, which rely on control over these properties, such as novel light sources, amplifiers, detectors, transmission media, switches and modulators, for example, can be engineered to take advantage for improved performance.

Maxwell’s equations and appreciation of electronic band structure are sufficient to describe light-matter interactions in bulk materials, and at dimensions approaching the photon wavelength, cavity effects can alter these properties. Furthermore, enhanced field intensities in fabricated optical microcavities can also induce nonlinear photon-dipole interactions at lower applied power than in bulk materials while the introduction of electronically confined structures can further reduce the validity of continuum treatments, necessitating the need for a more quantum mechanical approach. This convolution of classical and quantum physics can become even more pronounced in self-assembled nanowires, where anisotropic morphologies and improved surface conditions with respect to top-down structures can result in even tighter radial optical confinement while acting as longitudinal or axial waveguides.

Before discussing tailored light matter coupling in monolithic nanowire optical cavities, then, it is important to first review the quasiparticles (e.g., exciton-polaritons), which form at the onset of strong light-matter interaction and recent developments in studying the phenomenon in optical microcavities. Following this, we will move on to the challenges associated with evaluating light-matter interactions in nanowires, development of analysis techniques, and finally progress made towards tailoring such interactions as well as discussion on their potential and early applications. Both semiconductor and semiconductor-metallic hybrid nanowires will be discussed; while this is an area that is rapidly growing and evolving, we believe a topical review discussing these systems can be beneficial to many researchers.

1.1. Exciton-polaritons

Polaritons, bosonic quasiparticles resulting from the coupling between electromagnetic radiation and dipole-carrying excitations, were first conceived by Tolpygo in 1950[1] and observed by Hopfield in 1958,[2] at the time used as a term for quantization of the polarization field created upon interaction between photons and electron-hole pairs (excitons). While the broader definition allows for many types of polaritons named for various light-dipole pairings, including intersubband-polaritons (coupling of light to intersubband electronic levels),[3] phonon-polaritons (coupling of light to optical phonons),[4–6] and Bragg-polaritons (coupling of Bragg modes to excitons),[7, 8] here we will focus largely on the aforementioned exciton-polaritons and interactions between light and surface plasmons known as surface-plasmon polaritons (For an excellent review of exciton-polariton coupling in semiconductors, see [9]. For an introductory discussion of strong light-matter coupling and exciton-polaritons in general, please refer to the work by Klingshirn (Semiconductor Optics, Chapters 5 and 6).[10])

The study of exciton-polaritons in particular began in earnest with the aforementioned first observation in 1958, with the field largely established through a series of works by Hopfield and Thomas published through the late 1950s and 1960s.[2, 11–14] These early studies focused initially on interactions in CdS and improved upon the previous semiclassical theory for light absorption by exciton states, showing that the exciton field plays the role of classical polarization field upon interaction with electromagnetic radiation. At low excitation levels, this results in an absorption feature slightly below the band edge where, due to the substantially larger oscillator strength of excitons than that of free electron and hole recombination, excitons can couple strongly to the light field resulting in quasiparticles of mixed electronic and photonic character. The resulting normal modes are described by the coupled Schrodinger equations for exciton and photon fields, ψ_P,X = ψ_P,X(r,t):[15]

$$\mathrm{i}{\partial }_t\left(\begin{array}{c}{\psi }_{\mathrm{P}}\\ {\psi }_{\mathrm{X}}\end{array}\right)={\widehat{H}}_0\left(\begin{array}{c}{\psi }_{\mathrm{P}}\\ {\psi }_{\mathrm{X}}\end{array}\right)$$ Equation 1.1

$${\widehat{H}}_0=\left(\begin{array}{cc}{\omega }_{\mathrm{P}}(k)-\mathrm{i}{\kappa }_{\mathrm{P}}& {\mathrm{\Omega }}_{\mathrm{R}}/2\\ {\mathrm{\Omega }}_{\mathrm{R}}/2& {\omega }_{\mathrm{X}}-\mathrm{i}{\kappa }_{\mathrm{X}}\end{array}\right)$$ Equation 1.2

where ω_P(k) is the uncoupled photon dispersion, ω_X is the uncoupled exciton dispersion in the absence of spatial dispersion, Ω_R is the vacuum Rabi splitting,[16, 17] and κ_P and κ_X are the photon and exciton decay rates, respectively. These equations establish the basic foundation for coupled exciton and photon fields where Ω_R is governed by both electronic resonances and environment, giving rise to appreciable differences between infinite (bulk) and confined (microcavity) systems.

Early studies establishing the framework of exciton-polariton knowledge largely focused on interactions in “bulk” materials, with the smallest dimensions on the order of microns. Considering exciton Bohr radii are typically on the order of nanometers and relevant photon wavelengths hundreds of nanometers, neither electronic nor photonic confinement were invoked in the discussion. In this “bulk polariton” regime relationships between the parameters used to describe the strength of light-matter coupling in semiconductors are straightforward: the Rabi splitting can be expressed in terms of the experimentally accessible longitudinal-transverse resonance splitting ω_LT: [18, 19]

$${\mathrm{\Omega }}_{\mathrm{R}}=\sqrt{2{\omega }_{\mathrm{T}}{\omega }_{\text{LT}}}$$ Equation 1.3

where ω_T is the transverse resonance frequency. For a system with nonzero Ω_R the eigenstates of Equation 1.1 give rise to “dressed states” of the system, ψ_P,X, known as the upper and lower polaritons. The angular frequency-wavevector dispersion relation for polaritons is then defined implicitly by the so-called “polariton equation”:

$$\frac{c^2{k}^2}{{\omega }^2}=\epsilon (\omega ).$$ Equation 1.4

where ε(ω) is the dielectric function, which itself can be defined in terms of Ω_R.[10]

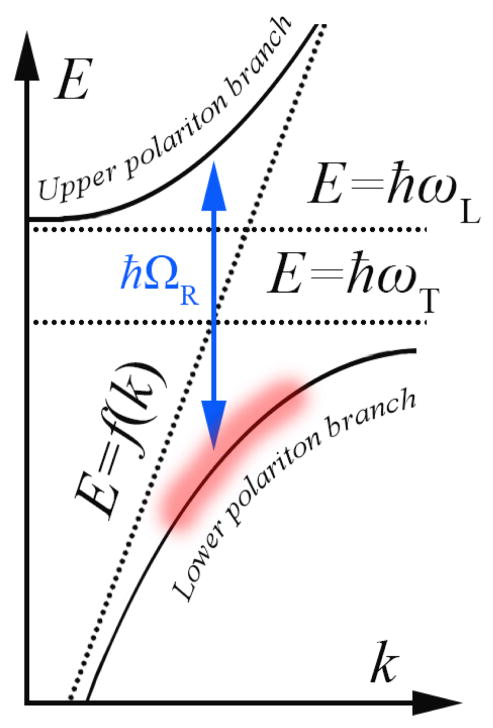
The ultimate result of this coupling is the dispersion relation shown in Figure 1.1, where interaction between photons and excitons produces upper- and lower-polariton branches with the characteristic anti-crossing of width ħΩ_R. Therefore, in systems with stronger light-matter coupling (between excitons and photons), the splitting between the two polariton branches is large.

Figure 1.1.

Schematic energy versus wavevector dispersion for a system of coupled oscillators near resonance. Dotted lines represent photon dispersion (E=f(k)) alongside transverse (E=ħω_T) and longitudinal (E=ħω_L) dipole resonances in an uncoupled system. Anticrossing behavior manifests upon oscillator interaction at Rabi frequency Ω_R, resulting in creation of upper (UPB) and lower (LPB) polariton branches separated by ħΩ_R. Reduced density of available states in the region of high curvature highlighted in red slows polariton relaxation from exciton-like to photon-like states, creating what is known as the polariton thermalization bottleneck regime[20].

The desirable optical properties associated with highly nonlinear dispersions have long inspired research into materials systems with intrinsically strong light-matter coupling, e.g. CdS, and ZnO, but as Ω_R is fixed in bulk materials and damping limits practical access to interesting optical effects on resonance, the practical implications of light-matter coupling in bulk semiconductors remains limited. Vacuum Rabi splitting can be engineered with the introduction of an emitter to a high-finesse microcavity environment, where κ_P is reduced and coupling between light and emitter can increase. The equation for Rabi splitting at a field maximum (anti-node) is then defined more generally by:[19, 21]

$${\mathrm{\Omega }}_{\mathrm{R}}=\sqrt{\frac{e^2}{{\epsilon }_0{\epsilon }_r{m}_0}\frac{nf}{V_m}}$$ Equation 1.5

with relative permittivity ε_r, number of oscillators n, mode volume V_m, and oscillator strength f, a dimensionless quantity which expresses the probability of a given state transition occurring. [18]

Reduced emitter decay rates in ultrahigh Q microcavities have allowed for unambiguous observation of strong coupling in atomic systems since the 1980s [22, 23], but poor cavity finesse long hindered observation of a crossover into this cavity polariton regime in semiconductors. It was not until progress in materials processing allowed for routine creation of vertical cavity surface emitting lasers (VCSELs) with high quality-factor solid-state optical microcavities that Weisbuch et al.[24] were able to observe the same phenomenon in solid-state systems: in the landmark 1992 study, excitons confined to quantum well spacer layers were coupled to cavity photons and exhibited the normal mode splitting in experimental dispersions measured through angle-dependent reflectivity.

Following the work of Weisbuch, Baumberg et al.[25] and Savvidis et al.[26] experimentally demonstrated boson amplification of polaritons induced by stimulated relaxation. Considering low effective masses (on the order of 10⁻⁴ those of the electron rest mass), and therefore long spatial coherence lengths, these results showed that high-temperature Bose-Einstein condensates (BECs), and associated low threshold polariton lasing,[27] would be possible. A polariton BEC was demonstrated shortly thereafter,[28] as were polariton lasing[29, 30] and superfluidity.[31] Demonstration of cavity polaritons persisting to room temperature in GaN[32] and ZnO[33] likewise paved the way for room temperature[34] and electrically-driven polariton lasers.[35] Though missing the past few years of progress, Microcavities by Kavokin et al. contains perhaps the most thorough review of the field through 2007 and is recommended for further reading.[36]

While dielectric microcavities are certainly notable for the observation and manipulation of strong light-matter coupling to semiconductors, however, the mode volumes produced are far from theoretical limits and total device footprints are quite large. Owing to sidewall defects inherent to microfabrication, top-down microcavity pillars suffer significant surface recombination and large exciton dead volumes, extending beyond the Bohr radius due to surface roughness.[37] Mode volumes near ~(λ/n)³ are currently infeasible as a result, limiting the potential to truly maximize light-matter coupling strength in microcavity structures. Reducing mode volumes beyond those achievable in microcavity pillars, into the “nanocavity” regime, requires alternate methodologies entirely.

Dielectric nanocavities were first produced through the use of photonic crystal structures,[38] but top-down fabricated photonic crystal systems can share the same surface quality issues as microcavity pillars, and their footprints are much larger than the active region alone. Self-assembled dielectric structures have the potential to circumvent both issues, however, with pristine surfaces and extremely small footprints. Semiconductor nanowires, in particular, are noteworthy for the ability to function as longitudinal nanocavities at total volumes an order of magnitude smaller than the best microcavities. While Q factors remain low (<1000 in monolithic homogenous nanowires),[39] self-assembly produces pristine sidewalls with significantly reduced surface recombination in comparison to top-down fabricated structures of comparable dimensions. Mode volumes on the order of (λ/n)³ are accessible in the nanowire morphology, and this combined with possible exciton confinement in engineered quantum dots[40] has raised the possibility of tailored strong coupling in solid-state devices in addition to footprints at the physical minimum for purely dielectric structures.

1.2 Surface plasmons and surface plasmon polaritons

Surface plasmons (SPs) are coherent electron oscillations that occur at the interface between metal and dielectric media, given that the permittivity of the metal is negative. SPs can exchange energy with light in a manner analogous to exciton-polaritons, forming strongly coupled quasi-particles known as surface-plasmon polaritions (SPPs) [41]. A key difference between SPPs and exciton-polaritons is that the electronic component of SPPs are surface electrons, thus they only propagate along the metal surface and decay exponentially normal to the surface. This confinement results in extraordinary sensitivity to surface conditions, but in the idealized planar metal-dielectric interface, boundary conditions also mean the SPP dispersion lies to the right (longer wavevectors) of the dielectric light line: as a consequence it is not possible to excite SPPs with conventional illumination from the adjacent dielectric due to insufficient in-plane momentum and requires coupling schemes such as those detailed by Otto [42] and Kretschmann [43]. SPPs may also be excited in the near-field via dipolar emission from light-emitting materials situated within the evanescent field of an SPP excitation in both planar [44–50] and curved metal cavity geometries. [51, 52]

It should be noted that SPPs are a solution to Maxwell’s equations corresponding to propagating modes and differ from localized surface plasmon (LSP) resonances, which dominate the optical response of metallic nanoparticles [53]. LSPs are non-propagating modes, which may be excited in deep-subwavelength nanoparticles, where the interaction between surface electrons and light may be described quasi-statically. Thus, LSPs are not bound to the SPP dispersion relation and may be excited directly by incident light [53]. SP-based optical systems are free from the limitations in scaling-down of their sizes for maintaining functionality, unlike their diffraction-limited dielectric counterparts [54]. The ability to simultaneously transmit information at fiber-optic speeds and at ever-smaller dimensions has motivated researchers to investigate the unique subwavelength properties of SP-based optics or plasmonics such as propagation, confinement, and local field enhancement [55–58] in nanostructured materials.

Pioneering work in applications of plasmonics leveraged extreme sensitivity to surface conditions to develop thin film [59] and electrochemical interface [60] monitoring, gas sensing [61] and biosensing [62]. More recently, the large field enhancements which follow high confinement of light were used to augment the Raman cross section of organic species enabling single-molecule detection [63, 64]. Their enhanced absorption and scattering properties may be used to enhance the efficiencies of solar cells [65]. Even the large local heat dissipated by SPs due to ohmic losses has been harnessed to treat tumors locally rather than globally [66]. Almost all of these applications and many others use SPs passively, in other words, they explore the effect of the environment on SPs (or vice versa) without the presence of a material with electronic resonances spectrally matched to the SP resonance.

Adding yet another level of complexity (and opportunity) is the interface of SPs with gain media or materials that have electronic resonances in the vicinity of the SP resonance; what we may call active plasmonics. It should be noted that “active plasmonics” has also been used to describe systems in which the propagation of SPPs is controlled via passive means, i.e. by changing the dielectric environment [67]. In this manuscript, we use the term “active” to refer to the active media interfaced with the SP oscillation. In a manner similar to the aforementioned quasi-particles such as exciton-polaritons, SPs can interact with excitons in both weak and strong coupling regimes opening the road for SP-based engineering of material optical properties. This emerging field has already found applications such as deep subdiffraction (i.e. truly nanoscopic) lasers [68], spasers [48, 69, 70], efficient light emitters with very short radiative lifetimes [51], and light emission from normally “dark” semiconductors [52]. In the following chapters, we will discuss recent progress in evaluating, analyzing, and applying light-matter coupling in both all-semiconductor and hybrid-semiconductor-plasmonic nanowires.

2. Light-matter coupling in semiconductor nanowires

Semiconducting nanowires have received intense attention [71, 72] recently for their potential use in applications such as sensing,[73, 74] light generation,[75, 76], light detection[77, 78] electronic switching[79] and photovoltaics.[80, 81]. Aside from any physical advantages they may gain from reduced dimensions, they are also of particular interest to the semiconductor industry at large[82–84] because their dimensions are of a technologically relevant scale and inroads have been made towards incorporating them into existing integrated circuit technology.[85, 86] Nanowires can be synthesized via a variety of techniques, including solvothermal,[87–89] template-assisted,[90, 91] and both physical-[92, 93] and chemical-[94, 95] vapor deposition, among others. Typically, nanowires grown via the higher temperature vapor-based techniques result in single-crystalline structures with high yields and consistent physical properties along with superior surface conditions when compared with similar morphologies produced solely through “top-down” methods.

When semiconductor nanowires possessing both high aspect ratios and crystalline quality are desired, the most reliable method is currently the same as that first used by Wagner and Ellis, known as the vapor-liquid-solid (VLS) process,[96] where small metal clusters are deposited on the desired growth substrate, the assembly is heated to melt the clusters, and a gas containing the semiconductor growth material is then introduced to the reaction tube. When this alloy reaches the point of supersaturation, the semiconductor component is expelled at the liquid/substrate interface, resulting in vertical growth of the desired semiconductor nanowire crystal. Variations on growth parameters such as alternating vapor phase reactants to produce branched heterostructures,[95] superlattice structures,[97–100] varying vapor phase pressure to induce radial shell growth,[101] and substrate lattice matching for epitaxial growth,[102] for example, subsequently allow for control over material properties.

Optical properties in particular are significantly altered in the nanowire morphology. Among altered properties relevant to the discussion, anisotropy in absorption and emission as a function of polarization owing to morphology[103] and radial electronic confinement effects[104] are noteworthy, but it is the radial optical confinement effects which arise when diameters approach optical wavelengths which are most pertinent. In this size range, nanowires both inorganic[105–107] and organic[108, 109] can function as cylindrical dielectric waveguides, with many waveguiding properties sufficiently described through solutions to Maxwell’s equations.[110] In noting this, one can leverage knowledge from optical waveguide literature to understand and manipulate a number of optical properties. At diameters approaching the wavelength of light in material, semiconductor nanowires act as single-mode cylindrical waveguides, allowing only the fundamental waveguide (HE₁₁) mode, with a known cross-sectional intensity profile and waveguide dispersion. As will be discussed in Section 2.2, diameters can be tailored to either maximize radial confinement or permit a degree of evanescent wave leaking, allowing for enhanced internal field intensity or increased environmental sensitivity, respectively.

Surfaces of self-assembled nanowires are typically superior to those of top-down fabricated microcavities as-is, and the confinement achievable at smaller nanowire diameters further serves to enhance the range of light-matter interactions achievable. Furthermore, surface passivation has been shown to reduce surface exciton recombination in nanowires to the point where direct free exciton recombination is directly observed,[39] ultimately resulting in ideal crystals with extremely low defect emission.

Considering these factors together, in many cases, nanowires have potential to serve as ideal materials for fundamental research. Their minute dimensions, however, do severely limit the usefulness of traditional characterization techniques in evaluating individual samples, meaning new tools were first required before any analysis could begin. With this in mind, we first review progress in experimental method development, before moving on to results, analysis, and applications. While progress has recently been made in fabrication of coupled nanowire-microcavity systems[111–113] the body of literature on these hybrid structures is still shallow, this review will focus on isolated nanowire structures as a result.

2.1. Experimental methods for obtaining energy vs. wavevector dispersion relations for nanowires

While the scope of potential light-matter interactions described by complex optical dispersion relationships is certainly limited, the wealth of information on material electronic structure, cavity influence, and environment they can provide for a given sample geometry make obtainment of dispersion relationships a high priority in evaluating a new morphology. In evaluating the optical properties of semiconductor microcavities, many of the spectroscopic techniques developed for the purpose of illuminating the optical response of bulk materials were readily adapted to the smaller geometry. White light reflectivity,[24] transmission,[24, 114] and absorption spectra [115] can generally be obtained from planar microcavities with minimal modification to established techniques, while angle-resolved measurements[116] have allowed for direct measurements of optical dispersion near exciton-polariton resonances, constituting a complete set of tools for understanding how light interacts with the structures.

While dispersed ensembles of semiconductor nanowires can provide some information on a given batch, the utility of results is limited when considering the range of diameter, length, and morphology variations possible due to current limitations in synthesis control. Furthermore, the dimensions of individual nanowires render conventional spectroscopic techniques ineffectual. In addition to the added constraints inherent in in-coupling light via microscope objectives,[117] analysis is hindered by the short transmission times involved,[118] as well as the fact that nanowire end facets act as subwavelength apertures, scrambling angular information [119] which could be obtained from a larger sample. Before discussing and dissecting studies into enhanced light-matter coupling in semiconductor nanowires, then, it is important to note that mere evaluation is a significant hurdle.

In regards to evaluating the real part of the optical dispersion relation for individual semiconductor nanowires, two independent studies carried out by van Vugt et al. were instrumental in establishing a practical methodology. The first, carried out on ZnO nanowires, utilized scanning-excitation single-wire photoluminescence spectroscopy to demonstrate the existence of exciton-polaritons in the nanowire morphology[120] in a far-field analogue to techniques earlier pioneered in the near-field through development of the near-field scanning optical microscope (NSOM).[121] A subsequent study, utilized this methodology to place bounds on the upper and lower exciton-polariton branches, ZnO, a II–VI semiconductor previously shown to possess large exciton oscillator strength in macroscopic samples,[122] was shown here to exhibit an enhanced vacuum Rabi splitting (greater than bulk) in the nanowire morphology.

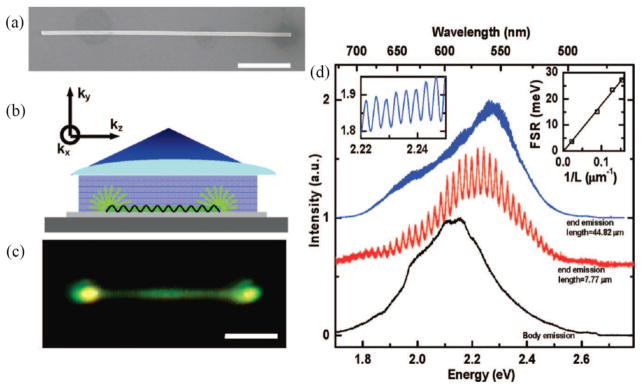
In addition to their utility in extracting vacuum Rabi splitting, the enhancement spectra extracted through scanning-excitation spectroscopy were found to exhibit periodic modulation in the photonic spectral region attributed by van Vugt et al. to Fabry-Pérot resonances running along the nanowire growth axis. While this was not the first claim of Fabry-Pérot observation in individual nanowires,[119] it was the first instance of the authors demonstrating their usefulness in experimentally determining the real part of nanowire E-k dispersion relationships. As shown in Figure 2.1, this nascent analysis continued undergoing development in a subsequent study of ZnSe nanowires.[123] Here, a ZnSe nanowire under diffuse 2.706 eV laser excitation (Figure 2.1b) was shown to exhibit a nonuniform photoluminescence intensity profile along its length, with significantly brighter emission from the nanowire end facets (Figure 2.1c). Spectra from the nanowire body using a position-sensitive photodetector (Figure 2.1d) appear similar to literature spectra for bulk ZnSe, but spectra collected exclusively from nanowire end facets again exhibited periodic modulations in the photonic regime. In measuring an inverse relationship between mode spacing and nanowire length (Figure 2.1d, inset) across multiple nanowires, van Vugt et al. confirmed the source of spectral modulation as the formation of longitudinal Fabry-Pérot resonances (k=k_z, where z is parallel to the nanowire growth axis).

Figure 2.1.

a) Scanning electron microscopy image of a ZnSe nanowire. Scale bar, 2 μm. b) Experimental geometry whereby the nanowire is uniformly excited perpendicular to its long axis. c) Optical image of nanowire photoluminescence under uniform laser illumination. Scale bar, 2 μm. d) Typical emission spectra collected from the middle (lower trace, black) and from the end of a 7.77 μm short nanowire (middle trace, red), and at the end of a 44.82 μm long wire (upper trace, blue), shows Fabry-Pérot modes of the nanowire resonator. A magnification of the upper trace is shown in the left inset. (Right inset) mode spacing at 2.1 eV for nanowires of comparable widths as a function of their reciprocal length, fitted by a least squares linear fit. Reproduced with permission from Nano Letters. Copyright 2009 American Chemical Society[123].

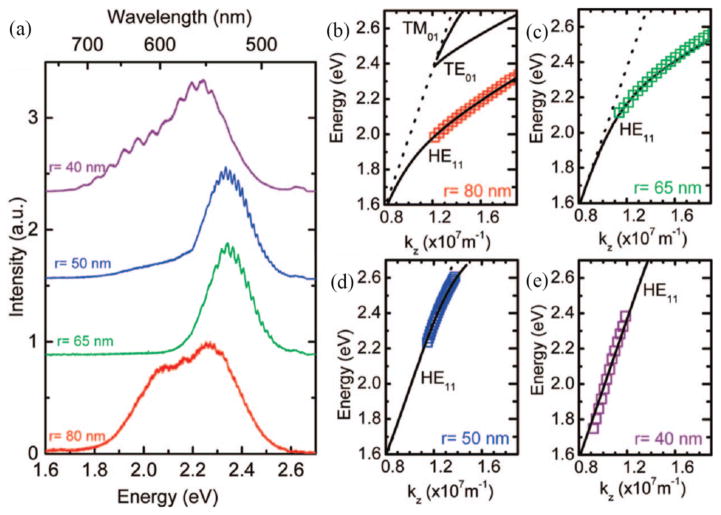
In confirming that end facet emission indeed contains information on Fabry-Pérot resonances, van Vugt et al. uncovered a powerful tool for quantifying light-matter coupling strength. As shown in Figure 2.2, exploiting the fact that Fabry-Pérot resonances occur at integer multiples of nπ/l_z in k-space (where n is an integer and l_z is nanowire length) allows for creation of experimental E-k dispersions for individual nanowires. In solving Maxwell’s equations for a cylindrical dielectric waveguide geometry using a phenomenological expression for ZnSe permittivity, van Vugt et al. calculated bulk ZnSe dispersions against which they could compare their results. Among the findings of this study were evidence of largely evanescent, dispersionless waveguiding in a 80 nm diameter nanowire, as well as altered dispersions and confirmation of significantly reduced group velocity near the exciton-polariton bottleneck.

Figure 2.2.

a) Emission spectra acquired from the end facets of ZnSe nanowires with radii of 75, 65, 50 and 40 nm and lengths of 8.52, 8.02, 33.15 and 14.0 μm respectively, with increasing diameters from top to bottom trace. b–e) Dispersion of the HE₁₁ mode of the nanowires with radii of 75 nm, 65 nm, 50 nm, and 40 nm, respectively. The solid lines are the results of the numerical solutions for the eigenvalue equation of the HE₁₁ mode of a dielectric cylinder using a phenomenological equation for ZnSe permittivity and the dashed line is the dispersion of light in vacuum. In panels d) and e) the mode dispersion overlaps with the dispersion of light in vacuum. Reproduced with permission from Nano Letters. Copyright 2009 American Chemical Society[123].

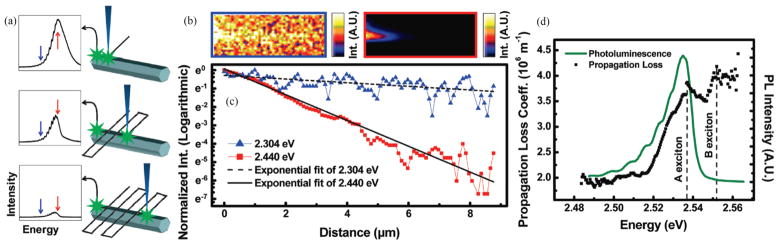
In addition to obtaining the real part of optical dispersion (E-k) relations, evaluation of the imaginary part is necessary for a full understanding of material response, providing precise resonance locations and absorption coefficients. The imaginary response of individual nanowires was first obtained using a similar methodology to that detailed above: using an experimental setup identical to van Vugt et al., Piccione et al.[124] began by assembling VLS-grown CdS nanowires on a SiO₂/Si substrate, cooling the system to 77 K, and centering a position-sensitive detector over a single nanowire end facet. While continuously collecting photoluminescence spectra emitted from the end fact, an exciting laser was scanned down the length of the nanowire body (Figure 2.3a). By then mapping out the obtained spectra spatially and producing an individual spatial map for each emitted wavelength (Figure 2.3b), the decrease of transmitted light intensity as a function of distance from nanowire end facet was obtained. In fitting this relationship to an exponential decay function (Figure 2.3c) and retrieving the decay constant for each wavelength, a spectrum showing propagation loss in individual nanowires as a function of wavelength was obtained.

Figure 2.3.

a) Illustration of a CdS nanowire under focused laser excitation at 300 K. A position-sensitive photodetector collects photoluminescence spectra from the end facet as the laser is scanned along the wire, generating a local light source which propagates inside the nanowire waveguide. b) Spatially resolved excitation images of a 9.7 μm-long, 245 nm-diameter nanowire obtained at energies 2.304 and 2.440 eV (highlighted in blue and red), respectively. Each pixel shows the relative intensity of light detected by the position-sensitive photodetector stationed over the leftmost end facet. c) Normalized intensity vs. distance of the excitation laser from the end facet line profiles extracted from the spatially resolved images in b). Propagation loss coefficients were obtained by fitting each line trace to the form Ae^{−α(z−z₀)}, where α is the propagation loss coefficient, A is the amplitude, and z₀ is fixed at the nanowire end facet. d) Propagation loss spectrum (black) for a 9.0 μm-long, 260 nm-diameter nanowire at liquid nitrogen temperatures, obtained by plotting α as a function of energy. A waveguided photoluminescence spectrum from the same wire is shown in green. Reproduced with permission from Nano Letters. Copyright 2010 American Chemical Society[124].

Though the final propagation loss spectrum (Figure 2.3d) is not identical to a bulk material absorption spectrum due to additional power losses to the substrate, largely adding a broad offset to the obtained results, successful identification of exciton-polariton resonances was still achieved. Considering this limitation and the fact that the bandwidth of the method is ultimately limited to that of the material photoluminescence output, further development of experimental methods is still needed to obtain complete complex dispersions especially related to the upper polariton branch, which is highly damped. Precise positioning of electronic resonances at a given temperature is still invaluable information, however, as will be shown in the following section.

2.2. Tailoring light-matter coupling in semiconductor nanowires

Before gaining the ability to tailor light-matter coupling in nanowires, it is necessary to first have in hand a model which explicitly quantifies its strength, a particularly difficult task in nanowires due to the difficulty in obtaining upper polarition branch dispersions. The cylindrical waveguide approximation used in the earliest studies by van Vugt et al.[123] utilized a phenomenological model for material permittivity, modeling light traveling through the mostly linear “photonic” regime of the real part of the E-k dispersion for CdS. This is useful to some degree, providing a baseline theoretical dispersion to compare with changes near transverse exciton resonances in experimentally obtained spectra. Utilization of phenomenological permittivity, however, ignores the complex interactions between light and matter, which occur near these resonances and ultimately allows only a qualitative observation of enhancement. In order to make the leap to quantitative evaluation, a more realistic material dispersion must be incorporated.

These polaritonic effects on nanowire dispersion were first incorporated in a follow-up study by van Vugt et al.,[125] utilizing an equation for permittivity near two interacting resonances in place of the phenomenological model (Sellmeier equation) to explicitly capture changes near the close-lying A- and B-exciton resonances in CdS:

$$\epsilon (\omega )={\epsilon }_b\left(1+\frac{{\omega }_{BL}^2-{\omega }_{AT}^2}{{\omega }_{BT}^2-{\omega }_{AT}^2}\frac{{\omega }_{AL}^2-{\omega }_{AT}^2}{{\omega }_{AT}^2-{\omega }^2-i\omega {\mathrm{\Gamma }}_A}+\frac{{\omega }_{AL}^2-{\omega }_{BT}^2}{{\omega }_{AT}^2-{\omega }_{BT}^2}\frac{{\omega }_{AL}^2-{\omega }_{AT}^2}{{\omega }_{BT}^2-{\omega }^2-i\omega {\mathrm{\Gamma }}_B}\right)$$ Equation 2.1

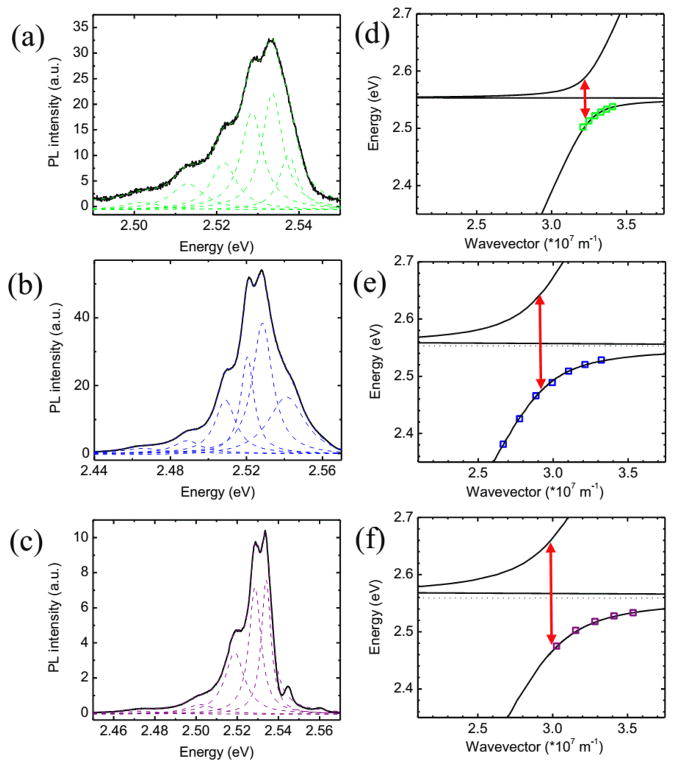
where ε_b is the background dielectric constant, ω_AT and ω_AL are the A-exciton transverse and longitudinal resonance frequencies, ω_BT and ω_BL are the B-exciton transverse and longitudinal resonance frequencies, Γ_A the A–exciton damping and Γ_B the B–exciton damping. In utilizing literature values for the background dielectric constant and damping, only the longitudinal and transverse frequencies remain variable. Utilization of propagation loss spectroscopy provides a precise measurement of the transverse resonance frequencies for a given temperature, leaving only the longitudinal resonance frequencies variable. In leaving the longitudinal resonance as a fitting parameter, van Vugt et al. were then able to extract the longitudinal-transverse splitting, and ultimately vacuum Rabi splitting, for a given experimental nanowire dispersion. With a verified model in hand, theoretical curves were fit to experimental dispersions for nanowires of various lengths and diameters (Figure 2.4), allowing for obtainment of coupling strength (g = Ω_R/2) as a function of nanowire mode volume.[126] Following this measurement, a three-dimensional finite-element model was used to calculate effective mode volumes (V_eff) for each nanowire volume (Figure 2.5), paving the way for an explicit size-dependent study of light-matter coupling.

Figure 2.4.

Photoluminescence spectra of the waveguided emission and size-dependent light-matter coupling strength in CdS nanowires. a), b), c) PL spectra of emission collected at the waveguided (non excited) end facets of nanowires with diameter x length dimensions of a) 260 nm x 7.9 μm, c) 190 nm x 8.1 μm and e) 200 nm x 2.45 μm. The spectra show multiple Fabry-Pérot interference peaks which have been fitted by Lorentzian line shapes to determine the resonance energies. d), e), f) Energy-wavevector dispersion in the z-direction (along nanowire length) for the three wires shown in panels a), c) and e). The square data points indicate the Fabry-Pérot maxima, which have been placed in wavevector space at integer values of π/l_z. The solid lines show the results of numerical calculations for the fundamental HE₁₁ guided mode including light-matter coupling with the CdS B-exciton (dotted horizontal line). Importantly, as is shown by the arrows indicating 2ħg(=ħΩ_R), accurate fits could only be obtained by increasing the longitudinal-transverse splitting ΔE_LT from 1x (bulk value) in panel b) to 4.5x in panel d), and to 6x in panel f). Reproduced with permission from Proceedings of the National Academy of Sciences. Copyright 2011 National Academy of Sciences[126].

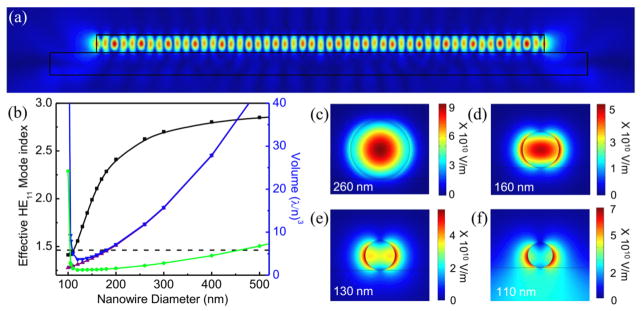
Figure 2.5.

Numerical mode volume calculations of CdS nanowire waveguide cavities. a) Two-dimensional projection of the obtained three-dimensional electric-field distribution |E|² for the HE₁₁ confined mode in a 200 nm wide and 5 μm-long nanowire at λ = 480nm. b) Effective mode index of the fundamental HE₁₁ mode (black line and square symbols, left axis) and effective volume V_eff (blue line and down triangle symbols), V (purple line, up triangle symbols) and V_m (green line, circle symbols) for a wire with a length of 1μm (right axis) as a function of nanowire cavity width. As the nanowire width decreases, the mode volume and the effective mode index decrease until at a width of ~110nm the mode index attains the refractive index of SiO₂ substrate (dashed line), which causes a dramatic increase in effective and mode volumes. c–f) Plots of the normalized electric-field |E|² for nanowire diameters of (c) 260 nm, (d) 160 nm (e) 130 nm and (f) 110 nm, confirm that this increase in V_m is caused by loss of electric field confinement for the smallest cavities, providing a lower limit on the nanowire cavity lateral dimensions for optical confinement. Reproduced with permission from Proceedings of the National Academy of Sciences. Copyright 2011 National Academy of Sciences[126].

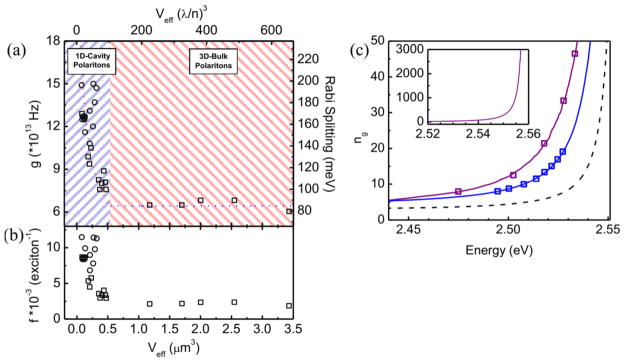
As shown in Figure 2.6a, g remains constant at larger effective mode volumes in accordance with Equation 1.3 for a fixed longitudinal-transverse splitting, matching values previously measured for bulk CdS. Below a threshold V_eff, however, g begins increasing at an appreciable rate inversely proportional to mode volume in a manner analogous with Equation 1.5 with additional consideration for crystal volume (V) dependencies of number of oscillators n, oscillator strength per oscillator f, and effective mode volume:

$$g_{\text{cavity}}=\sqrt{\frac{e^2}{4{\epsilon }_0{\epsilon }_{\mathrm{r}}{m}_0}\frac{n(V)f(V)}{V_{\text{eff}}(V)}}$$ Equation 2.2

Figure 2.6.

The transition from the bulk-polariton to the confined cavity-polariton regime in CdS nanowires. a) Experimental coupling strength, g, vs. mode volume for 28 nanowire waveguides with diameters ranging from 160–575 nm and lengths ranging from 2.45 to 21 μm. For larger mode volumes, the coupling strength remains constant and can be fitted by Equation 2.2 with a constant quotient nf/V_eff (blue line). For smaller mode volumes, the coupling strength g increases by up to 2.4 times the bulk value of CdS. b) In the bulk polariton regime the oscillator strength per oscillator f remains constant whereas in the cavity-polariton regime it peaks due to the increased electric field amplitude and giant oscillator strength effect. c) Group refractive index vs. energy for nanowires with Rabi splitting of 82 meV (bulk, dashed line), 140 meV (blue line), and 200 meV (purple line). The experimentally determined Fabry-Pérot peaks are indicated by squares. Inset: Group refractive index obtained for a wire with 200 meV Rabi splitting that is cut off at the highest observed guided emission for the lower polariton branch (see Figure 2.4e). Reproduced with permission from Proceedings of the National Academy of Sciences. Copyright 2011 National Academy of Sciences[126].

Even accounting for the inverse dependence on V_eff, however, Equation 2.2 fails to return measured values of g at known (bulk) values of f, showing that the oscillator strength per oscillator itself was indeed enhanced (Figure 2.6b). Enhancement in the cavity polariton can be explained through the so-called “giant” oscillator effect,[127] a known phenomenon of oscillator strength enhancement upon coherent dipole formation from overlap of polariton wavefunctions at reduced mode volumes. Further confirmation of enhanced coupling can be found in the substantially reduced relative group velocities inferred from experimental dispersions (Figure 2.6c), a hallmark of the phenomenon in this spectral regime. However, it would be beneficial to observe the superradiance phenomena (enhancement of oscillator strength) via time resolved measurements.

With vacuum Rabi splitting and oscillator strength shown innately tied to nanowire mode volume, it stands to reason that the developments highlighted above have paved the way for applications which benefit from tunable light-matter coupling. Tailored coupling strength in turn means reduced group velocities, which in turn imparts the benefits inherent to slow light.[118] With this in mind, we turn to highlight applications which can benefit from these findings, with an emphasis on all-optical switching in individual semiconductor nanowires.

2.3. All-optical switching in semiconductor nanowires

Aside from providing a solid foundation for further studies of one-dimensional polariton systems, the above research directly benefits the development of numerous applications. Controlled crossing into the cavity polariton regime and formation of coherent oscillators in the solid-state bodes well for low-threshold polaritonic lasing[30] and Bose-Einstein condensation.[28, 128] Additionally one may simply consider the benefits conferred from reduced group velocities: enhanced sensitivity in sensors,[129] optical buffering,[130] quantum optics.[131] Among the various applications which benefit from the above, however, few have the potential for illustrating the utility of light-matter coupling enhancement in nanostructures as all-optical switching.

The condition in which two different output intensities are possible for a given optical input intensity, traditionally described as optical bistability,[132, 133] was first described theoretically and observed experimentally using an absorptive optical nonlinearity by Szoke et al. in 1969.[134] Though the condition manifests in vapors[135] and soft matter,[136] optical bistability in inorganic semiconductors[137] in particular was the subject of intense interest in the 1980s and early 1990s for its potential for use in digital optical computers based upon optically bistable elements.[138] Typically high power requirements of operating bulk optically bistable devices[10] may have stunted development in the subsequent years, but it is important to note that they are not symptomatic of optical bistability itself: rather, a consequence of the necessity for strong optical nonlinearity, which itself benefits from high optical intensities. Even when sufficiently high intensity fields are generated in bulk materials, maximization requires tight focusing, which leads to a shortened light-matter interaction length due to the reduced confocal parameter.[139] Attempts to circumvent these issues thus far have resulted in various integrated solutions, including vertical-cavity optical amplifiers[140] and ring resonators,[141] all of which show promise but require large device footprint.

Within the realm of all-optical device morphologies, then, we argue the nanowire waveguide geometry is an ideal structure for minimizing the input power needed to induce bistability as it both maximizes light confinement in the radial direction and provides an effective light-matter interaction length as long as the nanowire itself. Though dielectric contrast between the waveguide core and its cladding ceases to tightly confine light beneath a certain critical radius r_c where evanescent fields begin to dominate, even the modest contrast between a glass rod (n_core=1.42) and air (n_clad=1) provides maximal fundamental waveguide mode light intensity for diameters well below a micron,[142, 143] and as shown in Figure 2.5, changing the core to CdS (n_core=2.83) results in maximal confinement at diameters on the order of 100 nm.

At sufficient intensity in optically active materials such as CdS, a number of distinct physical mechanisms are known to induce nonlinear interactions between light and medium.[10] Sufficient excitation on an exciton resonance can lead to its disappearance, bleaching the resonance and allowing transmission at a frequency where light was previously absorbed. Similarly, plasma screening effects above the critical carrier Mott density can lead to a shift in the bandgap energy through renormalization, shifting electronic resonances onto previously featureless spectral regions, producing absorption where light was previously transmitted. Temperature-based bandgap shifts can result in similar behavior, and any one of these mechanisms utilized in conjunction with a cavity can result in tailored hysteretic behavior by taking advantage of constructive and destructive interference from closely-spaced cavity resonances. It is this confluence of factors: known enhancement of light-matter coupling, strong radial confinement, multiple potential switching mechanisms, and high cavity Q-factors that allowed Piccione et al. to begin their study on all-optical switching in individual CdS nanowires.[144]

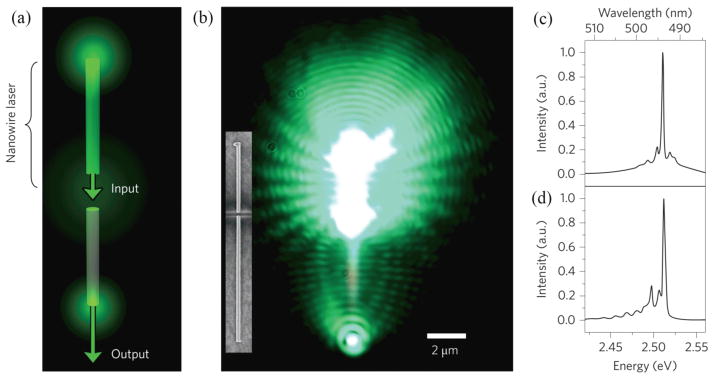
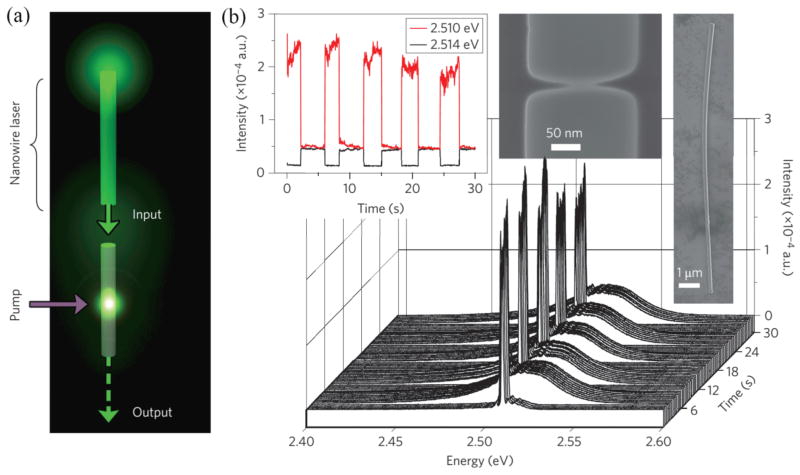
Regardless of likelihood that switching in nanowires was possible, however, a practical experimental framework is necessary before testing can begin. High-intensity, narrow bandwidth probe light in the exciton-polariton bottleneck regime must first be injected into a nanowire with minimal in-coupling losses, nontrivial when considering dispersed nanowires accessed through an objective lie perpendicular to the incident light source. To solve this issue, the authors created an on-chip laser source by cutting dispersed nanowires with a focused Ga ion beam and optically exciting one half to lasing conditions with an external Ti:Sapph laser source (Figure 2.7a and b). The resulting nanowire laser was naturally self-aligned with the other half, resulting in the on-chip laser output traversing the nanometer-scale gap and the length of the other half with minimal loss in intensity (Figure 2.7c and d).

Figure 2.7.

Creation of on-chip laser light sources for optical switching. a) Illustration of the switching device concept with a single CdS nanowire cut in two with a focused Ga ion beam, resulting in two nanowires of identical diameters aligned end-to-end, structurally isolated from one another and separated by a distance of 5 to 500 nm. A Ti:Sapphire laser is used to optically pump the upper portion to lasing conditions; the resultant on-chip laser light emitted by the nanowire is then transmitted through the gap and waveguided to the bottom end facet. b) Optical microscope image of a 10.9 μm long, 205 nm diameter CdS nanowire device at 77 K under the conditions explained in (a). Inset: SEM micrograph of the nanowire device. Scale bar applies to both images. c) and d) Photoluminescence spectra collected using a position-sensitive photodetector positioned at the top (c) and bottom (d) end facets. Note the two spectra are similar and the laser peak at 2.510 eV remains intact. Reproduced with permission from Nature Nanotechnology. Copyright 2012 Nature Publishing Group[144].

With a suitable probe source in hand, Piccione et al. were able to test for all-optical switching by leaving on the nanowire laser probe while periodically applying an external continuous wave pump laser source at 2.706 eV and continuously monitoring the output from the bottom end facet (Figure 2.8a). The stark interaction between 2.706 eV pump and 2.510 eV probe shown in Figure 2.8b is a clear indication of light-matter interactions at work, though the exact pathway is not immediately clear from this figure. In testing the switch mechanism, the authors ruled out the dispersive, absorptive, and induced absorptive bistabilities previously shown by Wegener et al. in CdS platelets,[145] instead identifying the more recently discovered phenomenon of stimulated polariton-polariton scattering[146–148] as the most likely solution. First shown in larger microcavity structures, stimulated polariton scattering occurs when slowly decaying exciton-polaritons in the bottleneck regime at momentum k quickly scatter to a higher-momentum “idler” state at 2k and a lower momentum “signal” state at k~ 0 in the presence of resonant excitation and an existing idler signal to stimulate scattering into the mode. Though the experimental geometry precludes angle-dependent measurements needed to confirm scattering pathways, the authors demonstrated scattering to a lower-momentum state in the presence of an idler, implicating the mechanism made possible only through the bottleneck buildup of polaritons in the strong-coupling regime.

Figure 2.8.

All optical active switching in CdS nanowires. a) Schematic of all-optical switching experimental setup. As in Figure 2.8a, on-chip laser light is generated in the top portion and transmitted across an ion-milled gap. An Ar+ laser is focused on the center of the bottom portion and turned on and off while the position-sensitive photodetector remains fixed on the bottom facet, collecting spectra every 30 ms. b) Cascaded plot of the spectra collected from the bottom facet of a 13.2 μm-long (3.58 μm-long switch portion), 190 nm-diameter nanowire device with a 5 nm gap as a function of time. At t=0 s, only the on-chip laser is on. Ar+ laser is turned on at 3s and turned off at 6s, and this process is repeated. Left inset: Cross-section of the waterfall plot, tracking the laser peak intensities at 2.509 and 2.514 eV. Right inset: SEM micrographs of the nanowire device. Reproduced with permission from Nature Nanotechnology. Copyright 2012 Nature Publishing Group[144].

In developing all-optical switching via stimulated polariton scattering, Piccione et al. demonstrated the potential of nanowires tailored to the cavity polariton regime, and sustained attention for both semiconductor nanowires and polariton physics over the past decade suggests there will be more applications to come. Though the construction of a working NAND gate from multiple switches by Piccione et al. suggests a straightforward path towards all-optical nanowire circuits, as with many nanowire applications, poor control over nanowire placement and orientation prevents further scaling. Applications aside, we now turn our attention to a related materials system currently drawing similar attention, i.e., hybrid-plasmonic nanowires.

3. Light-matter interaction in semiconductor-metal hybrid-plasmonic nanowires

Surface plasmons may be used to deliberately affect the optical properties of matter by interfacing them resonantly with active media, i.e. materials that posses electronic resonances in the same spectral region. Depending on coupling strength, the interaction between SPs (both SPPs and LSPs) and active media results in either strongly coupled SPs and excitons at the metal/semiconductor interface, where the strongly coupled mixed state demonstrates Rabi splittings similar to those of exciton-polaritons in semiconductor quantum wells embedded in microcavities[149, 150] or in a weakly coupled system, where the spontaneous emission rate of the active medium may be significantly modified via the Purcell effect [44–46, 49, 51, 151, 152]

Surface plasmon modes enable the confinement of light at deep subwavelength scales resulting in ultra-small mode volumes, which provide very high electromagnetic energy densities. However, the intrinsic dissipation (Ohmic losses) in metals yields relatively low quality factors (typically < 100) indicating low spectral energy density in nanostructured plasmon cavities [153]. Nevertheless, the emission rate can be tuned over a very wide range due to the ultra-small mode volumes at the price of moderate quality factors. It is the lower values of quality factor that enable broad-band enhancement due to large spectral overlap between cavity SP-resonances and electronic states of the semiconductor.

3.1 Purcell enhancement and semiconductor-metal hybrid nanocavities

Edward Purcell was the first to recognize that spontaneous emission from dipole sources (e.g., electron-hole pair) may be enhanced by tuning cavity resonances to that of an emitter [154]. The spontaneous emission rate enhancement of the emitter, known as the Purcell effect, is given by:

$$\frac{\gamma }{{\gamma }_0}=\frac{3}{2\pi }{\left(\frac{\lambda }{2n}\right)}^3\frac{Q}{V_m}$$ Equation 3.1

where γ and γ₀ are the spontaneous emission rate in the optical cavity and vacuum respectively, and λ, n, Q, and V_m are the vacuum wavelength, refractive index, quality factor and mode volume respectively [155]. Though first developed for radio-frequency operation, growing expertise in nanoscale fabrication has extended the Purcell Effect into the optical regime. In other words, by engineering optical cavities with nanoscale dimensions it is possible to tune their electromagnetic resonances to the nanometer-scale region of the electromagnetic spectrum. There are a number of Purcell-cavity paradigms [17, 156] yet they all depend on optimizing two key classical parameters of electromagnetic modes, the quality factor (Q), which describes the longevity of the cavity modes, and mode volume (V_mode). The Purcell factor is directly proportional to the ratio of the quality factor to mode volume, in other words, to achieve optimal enhancements we require long-lived modes that are also highly confined. Among the highest Purcell factors in all-dielectric cavities observed at optical frequency (1.66 eV), is that of a microdisk whispering gallery mode resonator, with a quality factor of 12,000 and mode volume of ~8(λ/n)³ corresponding to a Purcell factor of ~125 [157].

There has been a substantial amount of work exploring the modified emission properties in active plasmonic systems based on the Purcell effect. Anger et al. have shown a single molecule coupled with a gold nanoparticle strongly can alter emission quantum yield as a function of distance [152], and semiconductor quantum wells in close proximity to planar metal films also exhibited similar enhancement in spontaneous emission by resonant SP coupling [44, 45]. In addition, other plasmonic cavity structures including metal-dielectric-metal slabs and metal holes have been examined to verify the Purcell enhancements in radiative decay processes [158, 159]. On the other hand, plasmonic nanostructures could allow us to control the directionality of light emission as demonstrated by theoretical and experimental studies [50, 160]. Importantly, the plasmonic cavity structures can be utilized to generate nanoscale lasing where the SPs on the metallic cavities are amplified by a resonantly coupled dielectric gain medium. A gold nanoparticle-based laser has been demonstrated where the LSP resonance modes in the gold nanoparticle core are amplified by the optical gain provided by the dye molecules contained in a nano-shell [70]. In addition, Oulton and co-workers have reported a hybrid plasmonic laser consisting of a semiconductor nanowire, an insulator, and a metal substrate [68] (for a review of progress in surface plasmon lasers, see [161]). Here, the strong modal confinement occurs in the insulating gap where Fabry-Pérot hybrid-SPP cavity modes are formed in between the nanowire end facets. For these plasmonic lasers, it is essential that the plasmonic nanostructures are capable of supporting cavity modes at deep subwavelength scales thus optimizing the emission rates to generate nanoscopic laser light.

Metallic nanostructures, interfaced with organic or inorganic emitters, have mostly demonstrated modest Purcell factors (< 100) [44–46, 49, 151, 152]. Only recently, Cho et al. demonstrated that even larger gains in spontaneous emission rates can be extracted by engineering a complete metal-semiconductor core-shell nanowire optical nanocavities, which maximize the Q/V ratio. The ultra-small mode volumes and associated field enhancements obtained by completely wrapping the metal film around a semiconductor nanowire core, led to highly enhanced and non-thermalized spontaneous emission. In addition, these cavities posses interesting electromagnetic properties, where the enhancement is mediated by hybrid nanocavity plasmons resulting in Purcell factors on the order of 10³ [51]. In more recent developments, the spontaneous emission of an organic film interfaced with a silver film and silver nanowire also reported a Purcell factor of ~10³ [162]. Here, we review the work on SPP-induced extremely large Purcell enhancements leading to emission from non-thermalized excitons/free carrier recombination from both direct band-gap [51] and indirect band-gap semiconductor nanowires [52] integrated with surface-plasmon nanocavities.

3.2 Emission from non-thermalized (hot) excitons in direct bandgap semiconductor nanowires coupled with plasmonic nanocavities

With the ability to propagate along the metal surface, one could design subwavelength scale waveguides to interconnect optical components [163] and the modulator to process signals for highly integrated photonic circuits [164]. The strong SPP-based confinement in metallic nanostructures coupled with dielectric gain medium has triggered the development of true nanoscale lasers, which are far beyond the diffraction limit [48, 68, 70]. The light concentration could also be useful for nanoscale resonant antennas to enhance the optical absorption in photodetectors and solar cells [165, 166]. Furthermore, the coupled localized surface plasmon resonances of closely spaced metallic nanostructures (which in essence is a rough metal film) are orders of magnitude larger than their uncoupled counterparts [167] and have resulted in enhancements in the Raman scattering cross-section substantial enough to enable single-molecule detection [63, 64]. By properly designing the plasmonic nanostructures, one could engineer the light-matter interaction to modify optical processes such as excited carrier dynamics and also obtain nonlinear phenomena such as higher harmonic generation [168, 169] potentially giving rise to a variety of novel functional photonic devices.

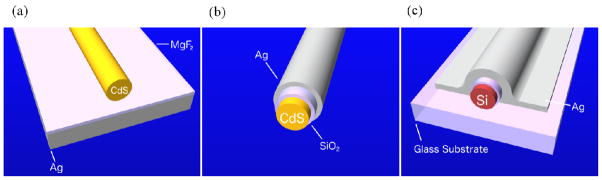
An obstacle in the design of plasmonic nanocavities are the ohmic losses sustained by metals where the local currents formed by collective electron oscillations dissipate heat, yet these may be mitigated by storing the majority of the optical energy within a low-index and insulating dielectric medium interfaced with both the metal and semiconductor [55]. Semiconductor nanowires have been integrated with metal cavities in three different designs, nanowire on flat silver film, core-shell, and the semi-conformal omega-shaped cavity, all of which possess the low index dielectric spacer layer, maintaining the optical confinement while preventing the direct quenching of carriers into the metal (Figure 3.1a–c). Furthermore, these geometries involve the use of lithography-free VLS-grown nanowires, which exhibit high crystalline quality, and smooth interfaces (see section 2), leading to superior optical properties and reduced scattering.

Figure 3.1.

Schematic of semiconductor nanowires integrated with plasmonic cavities in a) nanowire-on-planar metal with a thin dielectric spacer layer, b) core-shell semiconductor-thin insulator-metal, and c) semiconductor-thin insulator-Ω-shaped metal cavity architecture.

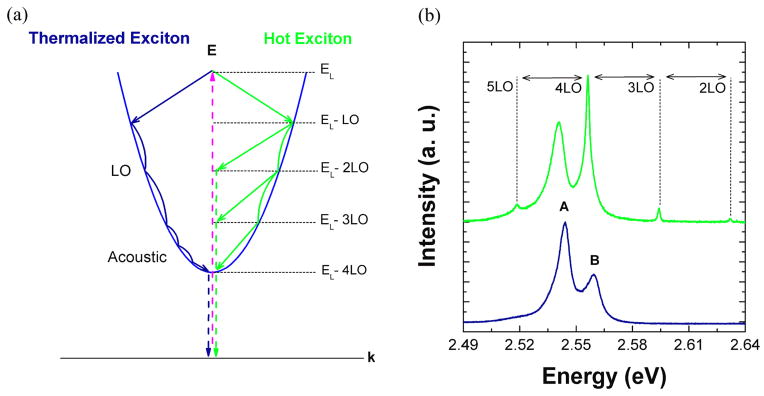
In direct band-gap semiconductors, optical excitation of electrons into the conduction band (and subsequent formation of excitons), is normally followed by rapid relaxation via longitudinal optical (LO) and acoustic phonon scattering into the k~0 state (quasi-equilibrium), which is close to the light-line [170, 171]. At this point the exciton decays radiatively via the emission of a photon. Relaxation to the light line via non-radiative processes involving LO and acoustic phonons is usually much faster (approximately 0.1 ps and 100 ps respectively) than direct radiative recombination (> ns) [172, 173], which results in observation of thermalized emission from k~0 states only. This emission process is illustrated for a thermalized exciton in Figure 3.2a. Spontaneous emission enhancement via the Purcell effect results in increased spontaneous emission of thermalized carriers. The CdS nanowire-silver film system, for example, demonstrated increased emission near the band-edge via a measured Purcell factor of ~10 [68]. On the other hand, if the spontaneous emission enhancement is high enough, for this case >10³, then the radiative recombination timescale becomes comparable and competitive with the relaxation time scale of sub-picoseconds. The fast interaction with LO-phonons now serves to both scatter carriers back to the light-line (k~0) and relax along the electronic branch leading to emission from non-thermalized or “hot”-states separated via LO-phonon multiples (Figure 3.2b). This hot-exciton emission mechanism has been demonstrated experimentally in CdS coupled with a conformally coated (core-shell) insulator (SiO₂) and metal (silver) nanocavity (Figure 3.1b). The photoluminescence spectrum of photonic or bare CdS is dominated by emission from the “A” and “B” free excitons [11]. However, the plasmonic nanowire demonstrates clear sharp peaks above the band gap (~2.65 eV) energy of CdS at 77 K. The sharp peaks are equally spaced at ~38 meV intervals corresponding to the LO-phonon energy in CdS (near k=0), confirming that hot exciton emission during the cooling processes is mediated via coupling with LO phonons (Figure 3.1a) [174].

Figure 3.2.

a) Schematic of exciton generation, relaxation, and emission process for a thermalized exciton (blue curve, left) and non-thermalized (hot)-exciton (green curve, right) in a direct bandgap semiconductor. E_L denotes the laser excitation energy. b) Photoluminescence spectra for a bare CdS nanowire (blue curve, bottom) and plasmonic-core shell CdS nanowire (green curve, top) showing the different exciton emission processes explained in a). Bare CdS nanowire shows emission from thermalized excitons while the plasmonic CdS nanowire cavity shows emission peaks corresponding to non-thermalized excitons. Reproduced with permission from Nature Materials. Copyright 2011 Nature Publishing Group[51].

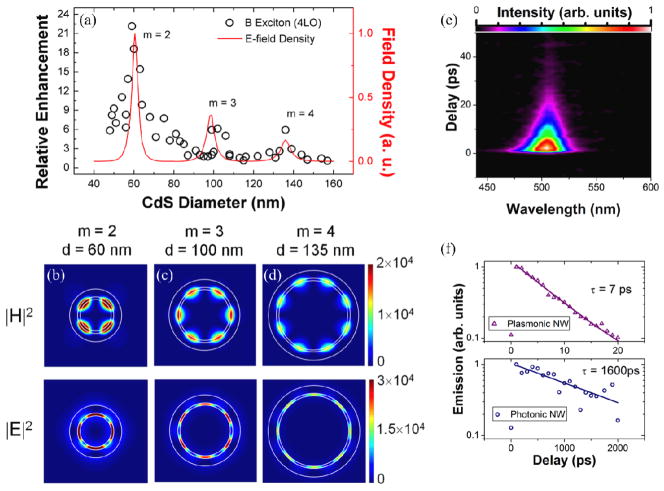
The occurrence of non-thermalized or hot luminescence peaks points to a sharp increase in the radiative rates due to the interaction of excitons with a plasmonic nanocavity in CdS. A plot of the highest intensity peak (when the B-exciton is resonant with a hot exciton peak) as a function of nanowire size reveals an anomalous size dependence in the plasmonic CdS nanowires (Figure 3.3a). There is an overall increase in the relative enhancement of hot exciton emission intensity as the cavity size shrinks. In addition, the monotonic increase is punctuated by peaks at three different nanowire sizes. Finite difference time domain (FDTD) calculations reveal that these peaks correspond to SPP modes that have a marked dependence on the nanowire diameter and wavevector, k, in the angular direction only, and thus are directly analogous to whispering gallery modes in all-dielectric structures, but with substantially higher levels of confinement. Furthermore, the 3 peaks at d=60 nm, 100 nm, and 135 nm correspond to the m = 2^nd, 3^rd, and 4^th order whispering gallery modes, where m denotes the integer number of wavelengths (Figure 3.3b). A near complete transition from thermalized to non-thermalized emission was further confirmed via time-resolved photoluminescence measurements on an ensemble of plasmonic CdS nanowires with substantial polydispersity (Figure 3.3e,f). It should be noted that even though the average nanowire size corresponds to an off-resonance condition (average diameter 140 nm +/− 50 nm) a transition from ~ns to single ps lifetimes was observed, which points to even lower expected lifetimes at the single-resonant nanowire level [51].

Figure 3.3.

a) Size-dependent enhancement of 4-LO hot exciton photoluminescence peak (open circles) in plasmonic CdS nanowires and calculated field intensity per unit area (red curve) as a function of nanowire diameter. (b–d) Simulated magnetic field (|H|²) and electric field (|E|²) intensity profiles, as a function of nanowire diameter for three resonant sizes b) d=60 nm (azimuthal mode number, m = 2) c) d=100 nm (m=3), and d) d=135 nm (m=4) All simulations of cavity modes were performed with Lumerical, a commercial finite difference time domain software package. e) Time-resolved PL spectral map from ensemble of 300–500 nanowires with average diameter 140 ± 50 nm at room temperature (300 K). f) Time-resolved integrated emission intensity for plasmonic (upper) and photonic (lower) nanowires. Solid lines are an exponential fit to the data. Fitting results yield radiative recombination lifetimes of 7 ps and 1600 ps for plasmonic and photonic nanowires respectively and are included next to the fitted curves. Reproduced with permission from Nature Materials. Copyright 2011 Nature Publishing Group[51].

3.3 Hot-carrier dynamics in indirect-band gap semiconductor nanowires coupled with plasmonic nanocavities

Silicon, due to its indirect bandgap, converts excitation energy to heat much more efficiently than light. The electronic dispersion of indirect band-gap semiconductors includes a momentum mismatch between the top of the valence band and the bottom of the conduction band. In Si the top of the valence band maxima is at the Γ-point whereas the bottom of the conduction band is close to the X-point. As a result, radiative recombination of an electron-hole pair requires an additional phonon to bring the carrier from the bottom of the conduction band, back to the light line near k~0, (Figure 3.4a, blue curve). In addition to scattering with a phonon to combine radiatively, carriers in Si experience non-radiative recombination at defect sites due to impurity states [175], free carrier absorption [175], and Auger recombination [176].

Figure 3.4.

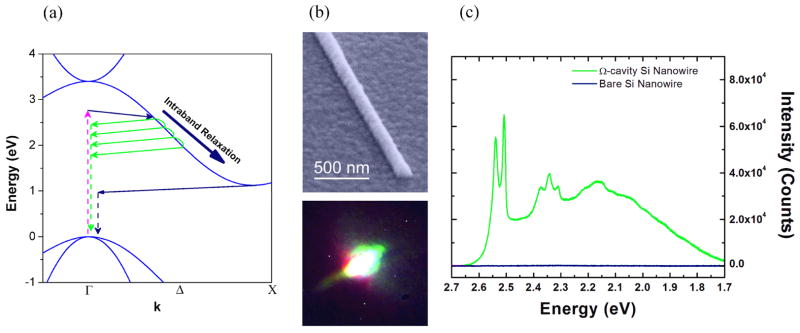
a) Schematic of carrier generation, relaxation and emission in Si for a carrier thermalized to the conduction band minimum (blue curve) and a hot, i.e. non-thermalized, carrier (green curve). b) SEM micrograph of Ω-shaped Si-SiO₂-Ag plasmonic nanocavity (top) and optical image of white light emission from Ω-cavity Si under laser illumination (bottom). c) Photoluminescence spectrum of bare Si (blue curve) and Ω-cavity Si (green curve). Reproduced with permission from Nature Photonics. Copyright 2013 Nature Publishing Group[52].

In Si, carriers excited above the band gap relax to the conduction band minimum quickly via intra-band relaxation on a 0.1–1 ps timescale [177–179]. The radiative recombination lifetime for direct transitions at the Γ-point is reported as ~10 ns [180] thus, from the ratio of radiative rates the quantum yield or luminescence from non-thermalized carriers (i.e. hot PL) is estimated to be ~10⁻⁴ at the Γ-point. Note the quantum yield is even lower for transitions from thermalized carriers near at the bottom of the conduction band (~10⁻⁶), which have the greatest momentum mismatch with the light-line [181]. Stimulation of hot-luminescence is a logical route for efficient light emission from Si, noting the farther carriers relax along the electronic dispersion, the less-likely it is to find a phonon of the appropriate momentum to enable radiative recombination. As in the case of CdS, excited electrons in Si may scatter back to the light-line (and recombine radiatively) if the Purcell enhancement is high enough to make the radiative lifetime comparable with the non-radiative (phonon relaxation) processes. To probe SPP-coupled Si, Si NWs were integrated with plasmonic nanocavities in the “omega”-shape geometry (see section 3.2), i.e. “Ω-cavity Si”. In the case of Si, the competition between hot luminescence and intra-band relaxation processes would lead to broad emission from excited carriers by coupling with various phonon modes as they relax along the electronic branch towards the conduction band minimum (Figure 3.4c. green curve).

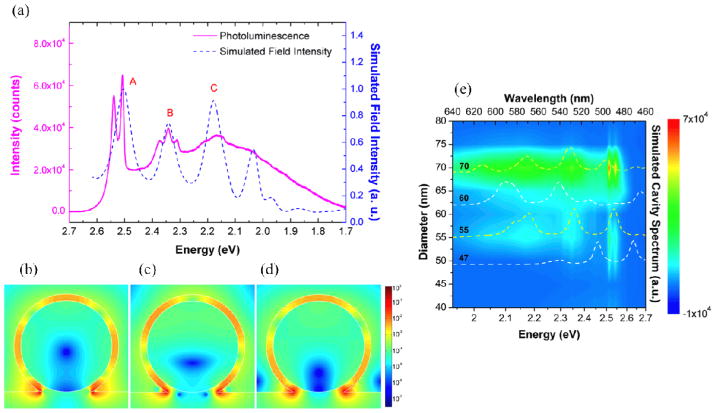
The broad photoluminescence spectrum of Si is closely linked to nanocavity surface plasmon modes at the SiO₂-Ag interface. Figure 3.5a reveals three sub-bands (labeled A–C), which, at the appropriate nanowire size, are resonant with cavity modes sustained in the nanowire cross section (Figure 3.5b). Interestingly, Si emission benefits from the broken symmetry of the Ω-shape, which may sustain modes at half-integer multiples of the surface plasmon wavelength unlike previous work on the CdS core-shell nanocavity which, due to the periodic boundary condition, may only support full integer wavelength multiples [51]. The quantum yield of Ω-cavity Si was estimated to be 1.4%, which represents at least 2 orders of magnitude enhancement over Si without the plasmonic cavity.

Figure 3.5.

a) Photoluminescence spectrum of Ω-cavity Si for a 70 nm (diameter) Si nanowire, which corresponds to a size where efficient emission channels in Si (A–C) are resonant with nanocavity surface plasmon modes (b). b)–d) Plots of electric field intensity (from FDTD simulations) for Ω-cavity Si in (a) at energies corresponding to peaks A–C in photoluminescence spectrum also reported in (a). e) Size dependent plot of photoluminescence spectra of Ω-cavity Si for sizes in the range d=40–80 nm. Simulated cavity spectra are superimposed (dashed curves) for select sizes denoting non-resonant cases (d=47, 70, white curves) and resonant cases (d=55 and d=70 as in (a), (b), yellow curves). Reproduced with permission from Nature Photonics. Copyright 2013 Nature Publishing Group[52].

Size dependent studies further confirmed the role of cavity modes in light emission from Si. Photoluminescence spectra from Si nanowires with a range of diameters (Figure 3.5e) demonstrate that Si emits most efficiently for sizes where the cavity modes are resonant with efficient emission channels, as is the case for the 70 nm-diameter nanowire shown in Figure 3.5b. It is expected that the most efficient emission channels are mediated by phonons with high density of states.

The metal-semiconductor hybrid structures reviewed here (i.e. plasmonic nanowires), represent a new class of integrated semiconductor nanowire structures where the semiconductor nanowire serves as both a source of emitters and an integral part of the optical cavity. The quality factors sustained in these nanocavities are modest compared to their all-dielectric micron-scale counter parts (>10⁴) [17], yet the mode volumes of the hybrid-plasmonic modes are as low as 10⁻⁴ that of free space [51, 52] leading to higher values of Q/V_mode and thus Purcell enhancements. Real applications of these fast emitters will likely require broadband operation at ever-smaller length scales. Plasmonic nanowires meet both of these requirements by relying on low-Q modes to promote broadband emission with optical cavities in the nanoscale regime as opposed to the extremely narrow resonances of the high-Q modes in all-dielectric structures, which require at least micron-scale dimensions and severely limit spectral overlap between the emitter and the cavity mode. This concept was applied to both direct and indirect bandgap materials. In the case of a direct band-gap semiconductor (CdS), hybrid plasmonic whispering gallery modes resulted in a nearly complete transition from thermalized exciton emission to non-thermalized emission from CdS hot-states. In the case of an indirect band-gap semiconductor (Si), hot-emission resulted in a broadband spectrum spanning the entire visible range. In both of these systems, the emission lifetimes are extremely short (picosecond level), which can find applications as efficient active nanophotonic devices, which may be modulated at high frequencies. Finally, the highly enhanced emission in plasmonic nanowires implies an enhanced reciprocal process, i.e. these devices should serve as enhanced optical absorbers, where the plasmonic-nanocavities serve as optical antenna to enhance absorption of incident light. Such a property will find immediate applications in photovoltaics and photodetection and requires further investigation.

4. Conclusion

Self-assembled nanowires occupy an important niche among nanostructures with the ability to bridge nanoscopic to microscopic phenomena through their unique morphology and length scales. With regards to optical properties, superior surface conditions at diameters pushing the diffraction limit have allowed for an exploration of properties inaccessible in microcavities.

Once the difficulties inherent in measuring optical properties of individual nanowires were overcome, evaluation and tailoring of light-matter coupling quickly followed suit. In semiconductor nanowires, it was shown that reduced mode volumes can induce a transition from bulk to cavity exciton-polaritons, allowing for tailored coupling and ultimately, nanophotonic applications such as switches and sensors. In hybrid-plasmonic nanowires, it was shown that plasmon nanocavities can result in sub-picosecond excited-state lifetimes and highly enhanced Purcell factors via whispering gallery surface plasmon polariton modes, enabling broadband absorption tuning and white light emission from bulk silicon. With both, the physics revealed thus far have shown that high-quality nanowires can indeed be used for fundamental photonic research.

The nanowire photonics field is young, but developments in evaluation, analysis, and applications of tailored light-matter coupling are occurring at a quick pace. In concert with advances with nanoscale materials processing that can create novel quantum-confined heterostructures,[101, 182–184] these developments may ultimately result in truly tunable light-matter coupling strengths.