Health, Economic Resources and the Work Decisions of Older Men

Abstract

We specify a dynamic programming model that addresses the interplay among health, financial resources, and the labor market behavior of men late in their working lives. We model health as a latent variable, for which self reported disability status is an indicator, and allow self-reported disability to be endogenous to labor market behavior. We use panel data from the Health and Retirement Study. While we find large impacts of health on behavior, they are substantially smaller than in models that treat self-reports as exogenous. We also simulate the impacts of several potential reforms to the Social Security program.

Introduction

Population aging and other challenges to public and private pension financing highlight the importance of understanding the determinants of retirement behavior. Much of the recent research on the labor force behavior of older workers has focused on the effects of financial incentives such as Social Security and private pensions, generally showing that these incentives have powerful behavioral effects (e.g., Blinder, et al., 1980; Burkhauser and Quinn, 1983; Diamond and Hausman, 1984; Stock and Wise, 1990; Rust and Phelan, 1997; Gruber and Wise, 1999, 2004; Gustman and Steinmeier, 1986, 2000, 2005). Additionally, a substantial amount of research has focused on the effects of the availability of both privately and publicly provided health insurance on retirement behavior (Rust and Phelan, 1997; Gustman and Steinmeier, 1994; Blau and Gilleskie, 2001a, 2006, Forthcoming). At the same time, econometric studies of retirement behavior have provided strong evidence for the importance of health factors (e.g., Quinn, 1977; Gordon and Blinder, 1980; Burkhauser and Quinn, 1983; Diamond and Hausman, 1984; Gustman and Steinmeier, 1986; Quinn et al., 1990; Rust and Phelan, 1997; Bound et al., 1999; Blau and Gilleskie, 2001b). Indeed, in analyses using Census data we found that more than half of men and one third of women who leave the labor force before reaching the Social Security early retirement age of 62 report that health limits their capacity to work (Bound et al., 1997).

However, as several reviews have noted, important questions remain regarding the magnitude of the effect of health on labor market behavior (Chirikos, 1993; Lumsdaine and Mitchell, 1999; Currie and Madrian, 1999). Moreover, except for early work by Quinn (1977) and research focusing specifically on the effects of changes in Social Security Disability Insurance (DI) on the work force attachment of older men (e.g., Parsons, 1980; Halpern and Hausman, 1986; Bound, 1989; Haveman et al., 1991; Bound and Waidmann, 1992, 2002; Kreider 1999a; Kreider and Riphahn, 2000), no one has studied the effect of the availability of financial resources on the relationship between health and retirement. This despite the likelihood that health and financial factors interact in affecting retirement decisions -- that is, deteriorating health will tend to make continued work less attractive, but individuals will tend to retire only if they have sufficient financial resources.

More fundamentally, previous longitudinal retirement research has suffered from limited measures of health, relying heavily on global measures such as self-rated work limitations and self-rated health. There are a number of potential problems with such survey measures: (1) they are discrete, whereas the construct researchers are interested in measuring is presumably continuous; (2) they are presumably error ridden, since not everyone will use the same scale when responding to survey questions; and (3) they are likely to be endogenous to retirement decisions, since it seems plausible that responses to these global questions will be related to labor market status.¹

In this paper we use methods designed to address all three of these problems. We use both the global and the more detailed health measures available on the Health and Retirement Study (HRS) within the context of latent variable models. This approach can be thought of as using the detailed health measures available on the HRS to instrument the global measures. We find that the choice of how we model health is substantively important. To preview our results, our estimates confirm the central role health plays in the early retirement behavior of men. Indeed, we estimate the rate of labor force exit before the age of 62 to be 5 times as great for those in poor health than it is for those in average health. Importantly, however, we found that using the standard (binary) model of health would overstate the magnitude of this effect. At the same time, our simulations suggest that the availability of financial resources also plays an important role in determining behavior. In particular, we find that a large fraction of those who leave the workforce in poor health before the age of 62 apply for DI. Consistent with other estimates in the literature, our estimates imply that the DI application decision is quite sensitive to benefit levels. Even so, our estimates suggest that seemingly dramatic changes to Social Security rules-increasing the normal retirement age or eliminating the early retirement benefit--would have small spill over effects on the DI program. The reason is simple: most men in their 60s are too healthy to qualify for DI.

Similar approaches to modeling health have been used by other researchers in both cross-sectional (Kreider, 1999a) and longitudinal studies (Lindeboom and Kerkhofs, 2004; Disney et al., 2006). However, to our knowledge no one has embedded such modeling into the kind of dynamic programming models that are currently state of the art for modeling retirement behavior. This is the approach that we take in this paper.

For our method to yield valid results, responses to the more detailed measures available on the HRS must be exogenous to labor market behavior. While many researchers have worked with the presumption that the more specific health measures available on the HRS are less susceptible to the kinds of problems we have discussed, these measures may not be completely immune. We discuss evidence below that suggests to us that these measures are, indeed, exogenous. The latent variable model we use is computationally intensive, which may explain why other researchers have continued to use the global health measures available on the HRS. For this reason, it seems important to know whether our model yields answers that are substantially different from those we obtain if we follow the standard practice of simply including discrete health indicators in our behavioral models, and thus we include estimates from both approaches.

Researchers increasingly view retirement as a process rather than a single event (Honig and Hanoch, 1985; Honig, 1985; Quinn et al., 1990; Ruhm, 1990; Quinn and Kozy, 1996; Quinn, 1997, 2000). While poor health induces many individuals to leave the work force altogether, it may induce others to merely change jobs or find ways to accommodate their limitation on their current job. A more general literature on the adaptations that older adults make in response to deteriorating health indicates that ceasing to perform an activity is often the response of last resort (Baltes and Baltes, 1990; Brim, 1988). Before this occurs, older adults will expend increased effort, allow more time, and reduce performance standards in order to perform the activity. However, to date very little research has attempted to model the effect of health on labor force transitions other than retirement.²

As far as we know, with the exception of work in progress by Rust and his colleagues (Rust, Benitez-Silva, Buchinsky 2001), we are the only researchers modeling retirement behavior to distinguish the application for DI benefits from other modes of labor force exit. Doing so seems crucial because: (a) our estimates suggest that, of those in poor health, the number that apply for disability is greater than the number that simply leave the workforce, and (b) the financial incentives involved in the two behaviors are quite different.

In our modeling and estimation to this point we have focused on single men nearing retirement age during the 1990s. We focus on single individuals to avoid the very significant complication arising from trying to model the joint labor supply decisions of married men and women. While, as a result, our sample is not representative of the population, we believe that we can learn a considerable amount by examining the behavior of this group.³

In section 2 we describe our dynamic programming (DP) model and the methods that we use to solve the value functions that are the key inputs into our estimation procedure. In Section 3 we describe the estimation methods we use. In Section 4 we present parameter estimates and simulations which highlight important aspects and implications of our model. Additionally we compare results based on our model to results that simply use self reported work limitations as the measure of health. In Section 5 we conclude.

Model Specification and Solution

Model and Estimation Overview

We model the behavior of males who are working as of a “baseline” time (t=0) which corresponds to the first wave (1992) of the Health and Retirement Study. The basic behavioral model is a dynamic programming model in which individuals take into account that current period decisions may have substantial effects on their future utility. Central to this model is a set of current period utility equations that allows a person to construct the expected lifetime utility, or value, that he will receive from each option that he considers in each year that he makes a decision.

The solution of the value functions and the estimation of the parameters of these “behavioral” equations is complicated by our desire to address two issues. First, those who are working at our baseline time period are a select group of individuals. For example, from the standpoint of understanding the effects of health on behavior, it is possible that the individuals in poor health who are still working at t=0 have unobserved characteristics and preferences regarding work that are on average different from those of individuals who are in poor health at time t=0 but are no longer working. Second, although our model posits that individuals make decisions based on actual health, as mentioned earlier, it is self-reported health that is observed in our data.

We address the former concern by adding a reduced form initial conditions equation that describes whether a person is working at our baseline time period. Following Bound (1991) we address the latter concern by adding a latent health equation that formally describes the relationship between self-reported health, health reporting error, and true health. The presence of these additional equations has several practical implications that increase the difficulty of the solution and estimation of our model. First, in order for the additional equations to serve their purpose, our estimation procedure must allow correlations between certain unobservables that appear in the initial conditions equation, the health equation, and the behavioral equations. Our use of a multivariate normal distribution, which allows these correlations, implies that closed form solutions do not exist for integrals that are needed to compute value functions or for the likelihood contributions that serve as inputs into the Maximum Likelihood algorithm that is used for estimation. Second, our health framework produces a continuous measure of true health that is serially correlated over time, a well-known challenge for researchers employing dynamic, discrete choice estimation methods (Stinebrickner 2000). These issues, when combined with our desire to include unobserved heterogeneity, our use of up to six years of observed choices in addition to the initial condition, and our need to include a non-trivial number of state variables other than health, imply that the computational burden of solving and estimating our model is very high.

In this section we describe the behavioral portion of our model and the methods used to solve value functions given the presence of the serially correlated health variable. This discussion implicitly assumes that the true health of each individual is known at each point that a person makes a decision. In reality, true health is not observed. In Section 3, we describe the modifications that we make to our model to address this issue and the sample selection/initial conditions issue, and we describe the estimation method that we implement to deal with the nonstandard features of our model.

2.1 Choice Set

Each individual has a finite decision horizon beginning at year t=1 (1993) and ending at year t=T.⁴ At each time t, an individual chooses an activity state from a finite set of mutually exclusive alternatives D_t. D_t ⊂ {C, B, N, A} where C is the option of remaining in the person’s career job (defined to be the job that the person held at baseline, t=0), B is the option of accepting a bridge job (defined to be a job other than the job held at baseline), A is the option of leaving the workforce and applying for Disability Insurance, and N is the option of leaving the workforce without applying for Disability Insurance (often referred to hereafter as the “non-work” option). Let d^j(t)=1 if option j is chosen (j=C, B, N, A) at time t and zero otherwise.

At any time t<T, a person can choose any of the options in the set {C, B, N, and A} unless it is ruled out by one or more of the following two assumptions. First, we assume that a person imagines that he will not return to his career job in the future if he leaves his career job in any year t. With respect to this assumption, we allow for both the possibility that a person could leave his career job by choice and the possibility that a person may get exogenously displaced from his career job for a reason such as a plant closing. Notationally, we let L(t) be an indicator of whether a person who is working in a career job at time t-1 gets exogenously displaced before time t. Second, we assume that a person imagines that, if he applies for Disability Insurance and is approved for benefits, he will remain out of the workforce (i.e., he will be in option N) and collect his Disability Insurance payments for the remainder of his life. Notationally, we let DI(t) indicate whether a person has been approved for disability benefits as of time t. A person can apply for Disability Insurance if he is less than the normal retirement age for Social Security Retirement Benefits (65 for most of our sample).⁵ These assumptions imply that sufficient to characterize the choice set D_t is the person’s age at t, the person’s choice at t-1, whether the person becomes displaced from his career job between time t-1 and time t if he was working in his career job at time t-1, and whether the person has been approved for Disability Insurance at any time in the past.

This choice set implies that we do not formally model an individual’s optimal consumption/savings decision. Rather, consistent with much previous research in the dynamic, discrete choice literature we assume that a person consumes all of his “income” in year t.⁶ In Appendix E (available in the NBER working paper version of this paper or by request from the authors) we describe the tradeoff between approximation quality and model “size” that influenced our decision not to expand the choice set to model the consumption/savings decision (and other endogenous decisions). Instead we view pension wealth, non-pension wealth, Social Security earnings, Disability Insurance payments, and other entitlements as sources of income and attempt to make reasonable assumptions about the timing of the income from these sources in cases where the timing is not immediately obvious from institutional details.

Our specification of the opportunity set implies that an individual applying for Social Security Disability benefits will incur financial costs. For the year of application he will forgo all earnings. Further, if his application is rejected, he will not be able to return to his previous job which will tend to represent a loss of income since earnings on bridge jobs are typically lower than earnings in career jobs. These costs vary across the population. Those with little in the way of income outside of earnings will lose a greater proportion of their total income during the year they apply for disability benefits, and, as a result, will suffer a larger loss in utility if utility is not linear in consumption. In addition, those in high paying jobs stand to lose more by applying both because disability benefits are paid on a progressive schedule and because those with high paying jobs are likely to suffer a larger loss if they give up their career job for a bridge job.

2.2 Current Period Reward

The current period reward in any year t, R^j(t), contains all of the benefits and costs associated with alternative j; R^j(t) is the sum of the utility from consumption, $U_{\mathit{cons}}^j(t)$, and the non-pecuniary utility, $U_{np}^j(t)$, that the person receives from option j at time t.

2.2.1 Utility from Consumption, $U_{\mathit{cons}}^j(t)$

Defining Y^j(t) to be the person’s total income net of expenditures on health care if he chooses option j at time t, the individual’s utility from consumption is assumed to be of the form

$$U_{\mathit{cons}}^j(t)=\tau \frac{Y^j{(t)}^{1-\theta }}{1-\theta }\text{for}j\in \{C,B,N,A\}$$ (1)

where θ determines the level of risk aversion and τ (along with parameters in the non-pecuniary utility equation (2) that will be discussed in Section 2.2.2) is used to determine the importance of utility from consumption relative to non-pecuniary utility.

A benefit of the HRS is that it allows us to capture in detail how expenditures on health care and income vary across the possible options j. For option j at time t, Y^j(t) is the sum of income from earnings, Social Security entitlements, defined benefit and defined contribution pension plans, Disability Insurance payments, non-pension wealth, food stamps,⁷ Supplemental Security Income, and other exogenous sources of income (such as veteran benefits) minus expenditures on health care. In Appendix A.2 we discuss in general terms our timing assumptions related to the receipt of income from these sources and later in Section 2.3.2 (and in Appendix A.3) we provide detail about modelling and computation issues related to these sources. At this point it is worth noting that the reason that we can take full advantage of the detail about these incomes sources in the HRS is that, unlike much other work using the types of models employed here, we solve our model separately for each person in our sample.

All incomes are converted to 1992 dollars. The concept of income we use is after tax income. To this end we subtract off from our estimate of gross income both the worker’s share of the payroll tax and a piecewise linear approximation of the individual’s federal income tax obligations.⁸

While the approach we use for modeling the effect of the availability of health insurance is now common in the literature (Rust and Phelan, 1997; French and Jones, 2007; Blau and Gilleskie, 2006), using it implies that we are treating health care utilization as exogenous.⁹ Indeed, the observed difference in out of pocket health care expenditures between those that do and do not have health insurance almost surely represents an underestimate of the value individuals put on the availability of health insurance benefits. In an attempt to mitigate the bias that this underestimation introduces in the estimates of our behavioral equations in Section 2.2.2, we allow the availability of employer provided health insurance benefits to have a direct effect on an individual’s utility.

2.2.2. Non-Pecuniary Utility, $U_{np}^j(t)$

We assume that the nonpecuniary utility $U_{np}^j(t)$ associated with an option j is a linear function of a person’s time t health η_t, an indicator HI^j(t) of whether the person has either private health insurance or medicare at time t if he chooses option j, exogenous observable characteristics of the individual X(t), and a set of other transitory factors (ε_t^j) unobserved by the econometrician (but known to the individual in the current period) that measure the person’s particular circumstances and outlook in year t. In addition, we allow individuals to have unobserved, permanent differences in their preferences for work by including a person-specific, permanent heterogeneity term κ that enters the non-pecuniary utility associated with the work options C and B, i.e., κ^C=κ^B=κ and κ^N= κ^A=0.

$$U_{np}^j(t)={\lambda }_X^{j}X(t)+{\lambda }_{HI}^j{HI}^j(t)+{\kappa }^j+{\lambda }_{\eta }^j{\eta }_t+{\epsilon }_t^j,j\in (C,B,N,A)$$ (2)

Thus, in addition to allowing health to have effects on net income, our model allows decisions to have non-pecuniary costs which depend on a person’s health.¹⁰

We choose N as the base case of our discrete choice model which implies that we normalize the coefficients ${\mathrm{\lambda }}_{\mathrm{X}}^{\mathrm{N}}$ and ${\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{N}}$ to zero and interpret ${\mathrm{\lambda }}_{\mathrm{X}}^{\mathrm{j}}$, j=C,B,A as the effect of X on the utility of option j relative to option N and interpret ${\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{j}}$, j=C,B,A as the effect of η_t on the utility of option j relative to option N. To summarize,

$$R^j(t)=U_{\mathit{cons}}^j(t)+U_{np}^j(t)=\tau \frac{Y^j{(t)}^{1-\theta }}{1-\theta }+{\lambda }_X^{j}X(t)+{\lambda }_{HI}^j{HI}^j(t)+{\kappa }^j+{\lambda }_{\eta }^j{\eta }_t+{\epsilon }_t^j,j\in \{C,B,N,A\}$$ (3)

with ${\mathrm{\lambda }}_{\mathrm{X}}^{\mathrm{N}}=0$ and ${\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{N}}=0$.

2.3 Discounted Expected Utility - Value Functions

2.3.1 Specification of Value Functions

Letting S(t) represent the set of all state variables at time t, the expected present value of lifetime rewards associated with any option j∈{C,B,N,A} that is available at time t can be represented by a standard Bellman equation (Bellman 1957):

$$V_j\left(t,S(t)\right)=R^j\left(S(t)\right)+\beta \left(S(t)\right)·E\left[V\left(t+1,S(t+1)\right)\mid S(t),d^j(t)=1\right]$$ (4)

where V(t+1, S(t+1)) = max{V_k (t+1, S(t+1)): k∈D_t+1(d^j(t) = 1, S(t+1))}.

We have written D_t+1 as a function of d^j(t) and S(t+1) because, as discussed earlier, a person’s choice set at time t+1 depends on the person’s choice at t, the person’s age at time t+1, whether the person becomes displaced from his career job between time t and time t+1 if he was working in his career job at time t, and whether the person has been approved for Disability Insurance at any time in the past.

β is the one period discount factor which varies across people and across time for a particular person. Specifically, we assume that for person i at time t, β depends on a factor β^Common that is common across people and on the probability that person i will be alive at time t+1:

$$\mathrm{\beta }={\mathrm{\beta }}^{\text{Common}}·Pr(\text{Alive}\text{at}\mathrm{t}+1\mid \text{Alive}\text{at}\mathrm{t}).$$¹¹ (5)

We assume that the probability of dying between t and t+1 depends on the respondent’s age and his health at t, η_t. This probability is computed using a discrete-time proportional hazard model. The baseline hazard, which represents the probability of dying at a particular age conditional on not dying before that age, is computed using life table survival probabilities for U.S. men obtained from the Social Security Administration. Health shifts the baseline hazard in a proportional fashion.¹²

2.3.2 State Variables

The set of state variables at time t, S(t), includes all variables that provide information about the set of choices that will be available in the current and future periods, the discount factor, or the utility associated with all choices that may be available in the current and future periods. The information that influences future choices and the discount factor was described in Sections 2.1 and 2.3.1 respectively. In the next two subsections we focus on the state variables that influence either non-pecuniary or pecuniary utility - ${\mathrm{U}}_{\text{np}}^{\mathrm{j}}(\mathrm{t})$ or ${\mathrm{U}}_{\text{cons}}^{\mathrm{j}}(\mathrm{t})$.

State variables that influence non-pecuniary utility

Equation (2), indicates that non-pecuniary utility at time t is determined by X(t), ε(t), κ, η_t, and HI(t) where $\mathrm{\epsilon }(\mathrm{t})\subseteq \{{\mathrm{\epsilon }}_{\mathrm{t}}^{\mathrm{C}},{\mathrm{\epsilon }}_{\mathrm{t}}^{\mathrm{B}},{\mathrm{\epsilon }}_{\mathrm{t}}^{\mathrm{N}},{\mathrm{\epsilon }}_{\mathrm{t}}^{\mathrm{A}}\}$ is the vector of ε’s from all of the current period utility equations that are relevant in time t given a person’s choice set. X which includes, for example, a constant and a person’s educational level, is predetermined and known to the agent and econometrician for all periods. The permanent, person-specific, unobserved heterogeneity value, κ, is known to the individual but is unobserved to the econometrician. We assume that, in the population, κ ~ N(0, σ²_κ) where σ_κ, which determines the importance of unobserved heterogeneity, is a parameter to be estimated. ε(t) is observed by the individual but not by the econometrician at time t. Both the econometrician and individual know the distribution of ε in future periods. We assume that ε_t^j~N(0,1), j=C,B,A,N and that E(ε_t^j, ε_r^k)=0 if j≠k or t≠r.¹³

A person’s health, η, is exogenously determined but correlated across time. We assume that health at time t depends on demographic characteristics in X(t), including a person’s age. Based on evidence in Bound et al. (1999), we assume that the portion of health that remains after removing the effect of X(t) in each period follows an AR(1) process:

$${\mathrm{\eta }}_{\mathrm{t}+1}=\mathrm{\rho }({\mathrm{\eta }}_{\mathrm{t}}-\mathrm{\pi }{\mathrm{X}}_{\mathrm{t}})+\mathrm{\pi }{\mathrm{X}}_{\mathrm{t}+1}+{\mathrm{\xi }}_{\mathrm{t}+1}$$ (6)

where ξ_t+1 ~ N(0, σ²_ξ) ∀ t. Given a current period value of health, both the agent and econometrician can use equation (6) to compute the distribution of health in all future periods. However, while the agent knows his current health, the econometrician observes only a noisy, self-reported health measure. The manner in which we deal with this data problem is an estimation issue which we discuss in detail in Section 3.

Finally, at time t a person’s beliefs about his health insurance status at time t+1, HI(t+1), is determined by the health insurance characteristics of his career job (which we denote HI^C), the health insurance characteristics of his bridge job at time t if he is working in a bridge job at time t (which we denote HI^B(t)), and the person’s age at t+1. We identify the health insurance associated with the career job to be one of three types: HI^C =3 if the insurance plan covers the worker while he is working on his career job and also provides retiree health insurance which covers him after he leaves the job; HI^C =2 if the insurance plan covers the worker while he is working on his career job but does not provide retiree coverage; HI^C =1 if the person has no health insurance on his career job. Primarily for computational reasons, we assume that bridge jobs do not have retiree health insurance. Thus, there are only two possible characterizations for HI^B(t): HI ^B(t) =2 if the insurance plan covers the worker while he is working on his bridge job and HI^B(t)=1 if a person does not work in a bridge job in time t or works in a bridge job that does not have health insurance.

We assume that at time t a person believes he will have health insurance at future time t+1 if any of the following conditions are true: 1). HI^C=3; 2). d^C(t+1)=1 and (HI^C=2 or HI^C=3); 3). d^B(t+1)=1 and HI^B(t)=2; 4). Age(t+1) ≥ 65; or 5) DI(t)=1. The first condition indicates that a person with retiree health insurance on his career job believes that he will always have health insurance. The second condition identifies a person who is still working in a career job which has health insurance. The third condition indicates that a person who has health insurance in a bridge job imagines that he will continue to have health insurance if he remains in a bridge job in the next period. The fourth condition is present because everyone who has turned 65 years of age receives medicare. The last condition shows that, if approved for Disability insurance, individuals begin to receive medicare benefits (after a waiting period).¹⁴ In addition, we assume that a person who is working in a bridge job without health insurance at time t or has chosen an option other than the bridge option at time t believes that there is some probability that the bridge offer he receives in time t+1 will include health insurance. ¹⁵ In addition, we allow any person who has employer provided health insurance at time t but not at time t+1 to buy COBRA insurance at time t+1.¹⁶

Then, to summarize, at time t the state variables that influence non-pecuniary utility are {X(t), ε(t), κ, η_t, HI^C, and HI^B(t)}.

State variables that influence income

Some of the variables that influence non-pecuniary utility also provide information about current and future income levels Y^j, j=C, B, N, A. For example, the specification of the health expenditure equation in Appendix A.3.1 indicates that X(t), η_t, HI^C, HI^B(t), and DI(t) all influence health expenditures at time t.

In addition, some new state variables are needed to represent a person’s information about income. For example, income calculations depend in part on a set of baseline variables, ϐ, that describe everything about a person’s financial situation, previous work history, and earnings potential when the person arrives at t=1. This set of baseline variables describes exogenous sources of income (such as veterans benefits) and also contains information about a person’s wealth at time t=1. In addition, because ϐ contains information about a person’s complete SS earnings history as of time t=1 and the specific details that characterize an individual’s defined benefit and defined contribution pension plans, it also plays an important role in determining the income that would be received from the remaining sources of income described in Section 2.2.1: earnings, the SS and DI systems, and DB and DC pension plans. Below we describe the state variables that are needed (in addition to ϐ) to characterize what a person knows about the income from each of these sources. More detail on modelling and computation issues related to these sources is presented in Appendix A3.

The earnings equations are given in Appendix A.3.2. Earnings in career jobs depend on a fixed effect (which can be viewed as an element of ϐ) and a transitory component ψ^C_t. Earnings in bridge jobs are allowed to vary with a person’s baseline earnings in his career job W^C_O (which is contained in ϐ), a transitory component ψ^B_t, and the age at which a person left his career job. Notationally, we let $\mathrm{\psi }(\mathrm{t})\subset \{{\mathrm{\psi }}_{\mathrm{t}}^{\mathrm{C}},{\mathrm{\psi }}_{\mathrm{t}}^{\mathrm{B}}\}$ be the vector of transitory earnings shocks that are relevant at time t given a person’s choice set. Sufficient for knowing the age at which a person left his career job is the person’s age at baseline (contained in X) and the number of years of experience that the person worked in his career job as of time t (which we refer to as EXC(t)).¹⁷

A person’s SS benefits at some future year t* depend on his 35 highest years of labor earnings, the age when he began receiving SS benefits, and details about any earnings that were received after beginning benefits. Sufficient for providing this information is the person’s earnings history as of time one (which is contained in the baseline characteristics ϐ), and his complete earnings history between time t=1 and time t*-1. Unfortunately, a specification which requires the agent to keep track of a complete earnings history is not tractable since it requires that a person’s entire histories of the ψ^C’s and the ψ^B’s be treated as state variables in the model. Our model is made tractable through an assumption that an individual considers expected future earnings rather than actual future earnings when thinking about future SS benefits.¹⁸ In this case, sufficient for computing the SS benefits that a person will receive in some future year t* is the person’s earnings history as of time t=1 (which is contained in ϐ), the number of years that he will work in his career job after time zero and before time t* (which we denote EXC(t*)), the number of years that he will work in his bridge jobs after time zero and before time t* (EXB(t*)), and a variable which keeps track of all relevant information about what years the person worked after age 62 and before time t* (which we denote SSEX(t*) and describe in more detail in Appendix A.3.3). These three state variables are endogenously determined within the model.¹⁹

As with the SS calculation, we assume that individuals consider expected future earnings when thinking about payments from DB pensions, DC pensions, and the DI system. In this case, a person can compute the DB payment he will receive from his career job at some future time t* if he knows the details of the pension plan and his earnings history as of t=1 (which are both contained in the set of baseline information ϐ) and the year that he left his career job, as described by EXC(t*). With respect to defined contribution plans, future payments will depend on details of the plan, past contributions, and future contributions. We assume that an individual will continue to contribute to the DC plan at his career job at the same rate as he has contributed in the past. In this case, as with DB benefits, sufficient to characterize DC benefits at some future t* is information in ϐ and EXC(t*). Disability Insurance benefits are a part of the Social Security system and, with the exception of differences that arise because DI benefits are not age-restricted, are determined in a manner similar to SS payments. This implies that an individual can compute the DI payment he would receive at some future time t* if he knew the baseline information ϐ, EXC(t*), EXB(t*), and whether he has been approved for benefits as of time t*, DI(t*). We assume that a person who applies for Disability Insurance benefits at some time t is approved for benefits if

$${{\mathrm{A}}_1}^{\text{DI}}+{{\mathrm{A}}_2}^{\text{DI}}{\mathrm{\eta }}_{\mathrm{t}}+{\mathrm{e}}^{\text{DI}}>0$$ (7)

where A₁^DI and A₂^DI are a constant and slope coefficient and e^DI is a random component that is normally distributed.

Then, to summarize, the time t state variables in the model are S(t)={ϐ, X(t), EXC(t), EXB(t), SSEX(t), DI(t), ε(t), ψ(t), L(t), κ, η_t, HI^C, and HI^B(t)}.

2.3.3 Solving value functions

The expected value in equation (4) is a multi-dimensional integral over the stochastic elements of S(t+1) whose realizations are not known at time t given the decision to choose j. For illustration, consider a person who is working in his career job in time t, d^C(t)=1. In this case, the stochastic elements of the state space whose time t+1 realizations are not known are L(t+1), ε(t+1), ψ(t+1), η_t+1, and HI^B(t+1). L(t+1) and HI^B(t+1) are discrete random variables so the expected value involves summing over the probability functions of these variables and integrating over the density functions of the remaining continuous variables.²⁰

Researchers have often relied on convenient distributional assumptions to reduce the burden of evaluating integrals of the type described in the previous paragraph. For example, as shown in Rust (1987) if one specifies the choice specific transitory shocks (i.e., ε(t) in our case) to be iid extreme value, the expected value in equation (4) has a closed form solution conditional on the values of the other state variables.²¹ However, in this application, the Section 2.3.2 normality assumption for ε(t) is driven by practical considerations related to the importance of allowing certain correlations that will be discussed in detail in Section 3. This assumption, along with the equation (6) assumption about the distribution of η_t+1 given η_t and the fact that we wish to avoid functional form assumptions related to earnings by taking advantage of the empirical distribution of ψ, implies that the expected value in equation (6) does not have a closed form solution. In Appendix B (available in the NBER working paper version of this paper or by request from the authors) we describe in detail our method for approximating the integrals involved in this expectation. This method, which draws heavily on Keane and Moffitt (1998) and Stinebrickner (2000), involves a combination of Gaussian quadrature and simulation methods. Of importance from the standpoint of estimation feasibility, the derivatives of the expected value “approximator” are continuous with respect to model parameters.

The recursive formulation of value functions in equation (4) motivates a backwards recursion solution process of the general type that is standard in finite horizon, dynamic, discrete choice models. The most basic property of the algorithm is that in order to solve all necessary value functions at time t, it is necessary to know value functions at time t+1 for each combination of the state variables in S(t+1) that could arise at time t+1. In Appendix B we discuss computational issues that arise when implementing the backwards recursion solution process in our particular application, including the modification that is needed to deal with our continuous, serially correlated health variable. Our approach for dealing with these issues is directly informed by a substantial amount of previous work, including, but not limited to, that of Tauchen and Hussey (1991), Keane and Wolpin (1994, 1997), Rust (1997), and Stinebrickner (2000),

Estimation

Individuals make choices by comparing the values of the various options that are available. Generally speaking, our estimation approach is to choose parameters that maximize the probability of observed choices. However, as discussed at the beginning of Section 2, we would like to address two issues during estimation. First, although our model posits that individuals make decisions based on actual health, it is self-reported health that is observed in our data. Second, the group of individuals that are working at baseline is a select group of individuals. In sections 3.1 and 3.2 we discuss these two issues in turn and then in Section 3.3 and Appendix C (available in the NBER working paper version of this paper or by request from the authors) we describe our Simulated Maximum Likelihood estimation approach.

3.1 Health

Because true health is unobserved, we use a latent variable model to construct an index of health (Bound 1991, Bound et al. 1999). Specifically, we imagine that health in time t is a linear function of exogenous factors (e.g. age and education), X_t; detailed health measures (i.e., physical performance measures), Z_t ; and other unobserved factors ν_t.

$${\mathrm{\eta }}_{\mathrm{t}}=\mathrm{\pi }{\mathrm{X}}_{\mathrm{t}}+\mathrm{\gamma }{\mathrm{Z}}_{\mathrm{t}}+{\mathrm{\nu }}_{\mathrm{t}}$$ (8)

We assume that ν_t is uncorrelated with both X_t and Z_t (this assumption is essentially definitional: ν_t is the part of health that is uncorrelated with X_t and Z_t). While we do not directly observe η_t, we do observe an indicator variable, h_t, of whether a person is work limited. Letting h_t* represent self-reported health at time t, the latent counterpart to h_t, we assume that h_t* is a simple function of η_t and a term reflecting reporting error

$${\mathrm{h}}_{\mathrm{t}}\ast ={\mathrm{\eta }}_{\mathrm{t}}+{\mathrm{\mu }}_{\mathrm{t}}$$ (9)

We assume that μ_t and η_t are uncorrelated. Substituting equation (8) into equation (9), we get

$${\mathrm{h}}_{\mathrm{t}}\ast =\mathrm{\pi }{\mathrm{X}}_{\mathrm{t}}+\mathrm{\gamma }{\mathrm{Z}}_{\mathrm{t}}+[{\mathrm{\nu }}_{\mathrm{t}}+{\mathrm{\mu }}_{\mathrm{t}}].$$ (10)

If ν_t+μ_t is assumed to be normally distributed with a variance that is normalized to be one, equation (10) represents a probit model in which h_t* is greater than zero if the person reports that he is work limited. Estimates that use respondents rating of their own health on a five point scale as our measure of h_t* yield very similar results to those reported here. The relative size of var(ν_t) and var(μ_t) is not important for the estimation of π and γ in equation (10) but is important for other parts of the model because, for example, it is true health (i.e., the portion not including μ_t) that enters the utility equations.

The composite error term in equation (10), ν_t+μ_t, reflects a number of different factors. The ν_t component reflects aspects of health not captured by X_t and Z_t, while the μ_t component reflects reporting errors. These errors reflect differences in reporting behavior across individuals and across time for the same individual. The presence of μ_t introduces a number of biases in our estimates if we were to use h_t* directly when estimating the impact of health on labor market outcomes. If μ_t were completely random, it would represent classical measurement error, which will attenuate the estimated effect of health on labor market outcomes. If, however, people use health as a way to rationalize labor market behavior, then one would expect μ_t to be correlated with labor market status. In this context, the use of global self-reported health measures might well exaggerate the effect of health. This consideration suggests that our specification should allow for the possibility that the reporting error μ_t is correlated with each of the shocks ε_t^C, ε_t^B, ε_t^N, ε_t^A in the behavioral equations. For identification reasons similar to those that require us to set the equation (3) current period utility coefficients ${\lambda }_X^N$ and ${\lambda }_{\eta }^N$ in the base case to zero, we normalize the covariance between the reporting error and the utility unobservable in the base case to be zero (i.e., COV(μ_t, ε_t^N)=0) and estimate the three covariance parameters COV(μ_t, ε_t^j), j=C,B,A.

Essentially, our latent variable model uses the detailed health information available in the HRS (the Z’s) to instrument the potentially endogenous and error-ridden work limitation measure, h_t*. The validity of this approach for estimating the effects of health on labor force withdrawal depends critically on the assumptions that the reports on the detailed health information available in the HRS are exogenous with respect to labor force status. In Bound et al (1998), we test this assumption by comparing the performance of our preferred health model to health models estimated using a sparser and arguably more clearly exogenous set of measures from the HRS and find no evidence that the physical performance measures we are using are endogenous to labor market status. There are a number of reasons we do not simply use the more detailed performance measures directly in our behavioral equations. Among these, the measures reflect only a component of health and our latent variable model substantially reduces the number of parameters we need to estimate. Substituting equation (8) and equation (3) into equation (4) shows that the value functions at time t can be rewritten as

$$V_j\left(t,S(t)\right)=\tau \frac{Y^j{(t)}^{1-\theta }}{1-\theta }+{\lambda }_X^j{X}_t+{\lambda }_{HI}{HI}^j(t)+{\kappa }^j+{\lambda }_{\eta }^j\left[\pi X_t+\gamma Z_t\right]+{\lambda }_{\eta }^j{\nu }_t+{\epsilon }_t^j+\beta \mathrm{E}\left[V\left(t+1,S(t+1)\right)\mid S(t),d^j(t)=1\right],j=C,B,N,A$$ (11)

3.2 Initial Conditions

Although the choices we have been considering are all conditional on a person being employed at time t=0, this group will be a non-random sample of the population of people working at time t=0. To account for this we include in our estimation a reduced form initial conditions equation. In particular, we imagine a latent variable I* that is greater than 0 if the individual is working as of t=0 where

$$\mathrm{I}\ast ={\mathrm{\Pi }}_1{\mathrm{X}}_0+{\mathrm{\Pi }}_2{\mathrm{Z}}_0+{\mathrm{\epsilon }}^{\text{I.}}$$ (12)

We assume that ε^I ~ N(0,1) in which case equation (12) is a probit model.

In this reduced form specification, ε^I captures both the portion of true health at baseline and the portion of preferences for work at baseline that are not captured by observed characteristics (i.e., not captured by demographic characteristics at t=0, X₀, and physical performance measures at t=0, Z₀). The former suggests that ε^I may be correlated with the unobserved portions of health ν_t, t=1,2,.... Equation (6) implies that for t>1, COV(ε^I, ν_t) is a function of COV(ε^I, ν₁) and ρ, and we estimate COV(ε^I, ν₁). The latter suggests that ε^I may be correlated with unobserved preferences to work which influence behavioral decisions in t=1,2,...,T. To allow for this possibility we estimate COV(ε^I, κ), the covariance between the initial conditions equation and the permanent unobserved heterogeneity term.

Credible identification of the covariance between the initial condition and the behavioral equations depends crucially on exclusion restrictions. In particular, some variable or variables must influence the initial condition, but have no direct effect on subsequent behavior. In our case we have assumed that, while health at t=0 affects whether or not one works at t=0, it does not have a direct effect on subsequent behavior after conditioning on health at t=1. We believe this assumption is a natural one. Current health affects current behavior directly by affecting the utility that a person derives from work and also affects behavior through the role that is plays in determining individuals’ expectations about future health. After conditioning on current health, it seems reasonable to believe that the primary avenue through which past health would influence current behavior is that decisions made in the past (which are influenced by past health) have an implication for the set of choices that are available to the person in the current period. In this case, after conditioning on a person’s opportunity set and his current health, it does not seem that past health should have much of a direct impact on behavior. In addition, for this exclusion restriction to be valid, health must be exogenous to retirement and must follow a Markov process. Like much other research in this area, we maintain these assumptions throughout. In earlier work (Bound, Schoenbaum, Stinebrickner and Waidmann, 1999 we found the Markov assumption to be a reasonable one. In current work (Bound and Waidmann, 2007) we test the exogeneity of health to retirement by testing to see if there are identifiable changes in health in response to exogenous retirements. We found no evidence of such changes and concluded that the assumption that health is exogenous to retirement to be a reasonable one.

3.3 The Likelihood Function

Estimation proceeds by evaluating the joint probability of the simultaneous conditions that must be satisfied for a person who is working at our baseline t=0 (i.e., is in our behavioral sample) or is not working at our baseline period t=0 (i.e., is not in our behavioral sample). The set of simultaneous conditions that must hold can be written in terms of the simultaneous equations (10), (11), and (12) that define our model and contain the parameters to be estimated. We describe the likelihood function and the methods we use to compute the likelihood function in Appendix C. The GHK simulator of Geweke (1991), Hajivassiliou (1990), and Keane (1994) is used to evaluate the joint probability of interest. The use of this simulator also suggests a natural way to formally address important missing data issues related to our health variable (Stinebrickner, 1999; Lavy et al., 1998)

Results

4.1 Data

Data for this research come from the Health and Retirement Study (HRS), which contains both the detailed health data necessary to implement our latent variable framework and the the labor force and economic data necessary to accurately model the choice sets faced by individuals. The first wave (wave 1) of the survey was conducted in 1992/93; respondents were re-interviewed in 1994 (wave 2) and at two-year intervals since. The HRS covers a representative national sample of non-institutionalized men and women born between 1931 and 1941 (inclusive), so that respondents in the sample frame were aged 50–62 at the time of the first wave. The estimation of our model uses the public release versions of the first four waves of data, supplemented by confidential matched data from the Social Security Administration giving earnings histories and from employers giving details of private pension plans in which respondents are enrolled. Once we limit ourselves to single men with valid data, we end up with a sample of 328 individuals in our initial conditions sample and 196 (working) individuals in the behavioral sample who contribute a total of 837 person-year observations. More detail about the HRS and the composition of our sample is presented in Appendix A.1.

4.2 Timing of Behavioral Choices and Health

As described in Section 2.1, the decision periods in our model are one year in length. Assumptions are required to map the continuous work histories that can be constructed from the data to a sequence of yearly decision periods, each characterized by a single behavioral decision. A consideration particularly relevant for making these assumptions is that a person’s economic incentives tend to vary with the person’s age. For example, changes in the payment amounts that a person would be eligible to receive from the social security system if he were to retire typically take place on a persons’ birthdays. This motivates our desire to have each yearly period in our model correspond to a birthday year (i.e., the period that a person is a particular age). From a practical standpoint, in order to assign a single behavioral decision to a birthday year it is necessary to choose the point in time during the birthday year at which the behavioral decision will be determined from the data. In order to take into account that a person may not always make decisions immediately after his economic incentives change, we choose the point in time to be close to the end of the birthday year.²² In the typical case where there are zero or one transition during a birthday year, this approach allows the behavioral choice for a particular age to reflect whether a transition has taken place at any time during which the financial incentives related to that age are relevant.

While a person’s activity status can be ascertained at any point during the sample period, a person’s health measures are available only at the HRS interview dates. We map the health information to a decision period using the person’s age at the time of the interview. Given that interviews take place approximately two years apart, this implies that health information is only observed for a subset of the yearly decision periods for which we have determined a behavioral decision. As discussed in Appendix C, we address this issue by integrating over the joint probability of the missing health values as suggested by the missing data literature.

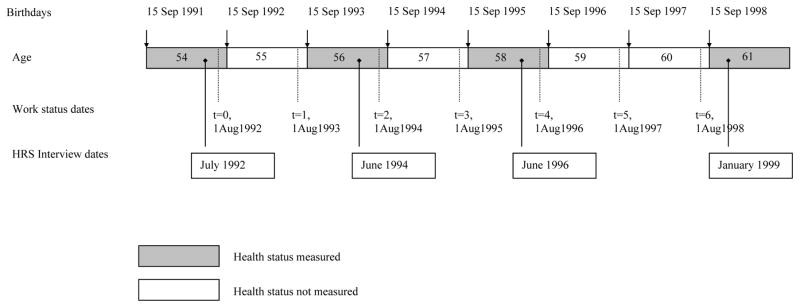
Figure 1 gives an example of how surveys are used to establish timing of health status measurements and job status transitions. For a hypothetical individual born on 15 September 1937, the behavioral year runs from 15 September to 14 September the following year. For such a person, we will measure work status as of 1 August in each year. We set t=0 at the first such point following the baseline interview. In this example, the baseline interview took place in July, 1992, making 1 August 1992 correspond to t=0. For this individual, age at the interview (and at t=0) is 54. Depending on the spacing of the interviews, there may be one, two, or three possible transition points between survey waves. In the case illustrated, behavior at t=1 is defined using the second wave survey conducted in June 1994. Behavior at t=2 and t=3 is defined using the third wave survey from June 1996, and behavior at t=4, 5, and 6 is defined by the fourth wave survey in January 1999. In this example, health status is observed at t=0,2,4 & 7.

Figure 1.

Example timeline for measurement of health and work status

4.3 Descriptive Statistics

We are interested in understanding how the availability of economic resources and health affect economic behavior. Table 1 presents descriptive information on the incomes sources in 1991 for age-eligible men in the HRS. Results are stratified according to whether or not the man was working as of the date of his wave 1 interview and whether or not he identified himself as suffering from health conditions that might limit his capacity for work. The table is limited to those who report no change in employment or disability status between January 1991 and the date of their wave 1 interview. This restriction was imposed to ensure that the incomes reported represent incomes commensurate with the data we use to stratify the sample.

Table 1.

Income Sources at Baseline

Work Status	Not Working		Not Working		Working		Working
Limitation Status	No Limitation		Limited		No Limitation		Limited
N	40		122		377		31
Own
Earnings	15.0%	1,590	3.3%	762	94.2%	33,174	90.3%	20555
Unemployment Insurance	2.5%	40	0.8%	25	5.3%	90	9.7%	333
Worker’s Comp	0.0%	-	2.5%	105	1.9%	53	0.0%	-
Veteran’s Benefits	12.5%	1,831	8.2%	592	3.7%	420	9.7%	1,329
Pensions	40.0%	5,894	13.9%	1,868	2.7%	400	6.5%	365
Annuities	0.0%	-	3.3%	544	0.0%	-	3.2%	258
SSI	7.5%	173	35.2%	1,749	0.0%	-	0.0%	-
Social Security	10.0%	558	37.7%	2,462	0.0%	-	6.5%	646
Welfare	5.0%	85	12.3%	242	0.5%	5	0.0%	-
Total		10,172		8,350		34,141		23,485
Household
Business/Royalties/Trusts	0.0%	-	0.0%	-	9.0%	3,325	9.7%	1,355
Unearned Income	35.0%	488	9.8%	216	35.3%	1,875	41.9%	1,376
Alimony	2.5%	98	0.8%	15	0.3%	3	0.0%	-
Food Stamps	15.0%	185	32.0%	353	1.9%	23	3.2%	108
Total		770		583		5,226		2,839
Total, all sources		10,941		8,933		39,367		26,324

While only 27% of the overall sample report work limitations, more than 75% of those out of work report work limitations. Focusing on those not working, income sources differ substantially depending on the respondent’s self-reported work limitation status. For example, while 40% of the men without work limitations report pension income, less than 14% of those with work limitations report pension income. In contrast, roughly 68% of those with limitations report receiving income from one of the major federal disability programs, Supplemental Security Income (SSI) and Social Security Disability Insurance (DI).²³ Crudely put, Table 1 suggests that men are not likely to leave the labor force before the age of 62 unless they have income sources on which they can rely, but that the composition of the income sources that are used to support an exit from the labor force varies dramatically with health status. Not surprisingly, those who are working and report work limitations have lower incomes than those who are working and do not report work limitations. However these differences may have preceded the work limitation.

Table 2 presents incomes and income sources as of 1991 and 1999 for age-eligible men working as of wave 1, stratified by behavior as of wave 4. Here we see, for example, that while almost 90% of those men who continued to work in their career jobs as of wave 4 (1998) had earnings in 1999, only 70% of those who had changed jobs between wave 1 and wave 4 and only 19% of those who had applied for disability benefits had earnings in 1999. At the median, household incomes rose by 65% between 1991 and 1999 for those that stayed with the same employer. In contrast, the drop in median income for those that retired was about 25%, and for those that applied for disability benefits median income declined by about 7%.

Table 2.

Income Transitions: Percent with each income source and mean among those with any

1992–1998 Choice	Bridge				Career				Apply for DI				Retire
N	63				86				27				77
	1991		1999		1991		1999		1991		1999		1991		1999
	%	mean	%	mean	%	mean	%	mean	%	mean	%	mean	%	mean	%	mean
Own
Earnings	96.8%	$31,469	69.8%	$29,158	98.8%	$29,936	89.5%	$36,200	100.0%	$20,802	18.5%	$2,951	100.0%	$30,293	10.4%	$1,506
Unemployment Ins.	4.8%	106	7.9%	297	8.1%	262	4.7%	127	7.4%	326	0.0%	-	11.7%	182	1.3%	104
Workers’ Comp	1.6%	63	1.6%	14	1.2%	2	2.3%	264	0.0%	-	3.7%	185	2.6%	21	0.0%	-
Veteran’s Benefits	4.8%	629	4.8%	620	4.7%	497	5.8%	710	0.0%	-	0.0%	-	6.5%	979	6.5%	1255
Pensions	1.6%	206	60.3%	7962	4.7%	286	44.2%	2133	0.0%	-	29.6%	1785	3.9%	676	79.2%	15986
Annuities	3.2%	317	3.2%	143	0.0%	-	2.3%	-	3.7%	370	0.0%	-	1.3%	117	5.2%	320
SSI	0.0%	-	1.6%	133	0.0%	-	0.0%	-	3.7%	148	18.5%	655	0.0%	-	2.6%	17
Social Security	1.6%	111	36.5%	3447	1.2%	82	18.6%	1507	0.0%	-	70.4%	6828	1.3%	56	64.9%	5874
Welfare	1.6%	38	0.0%	-	0.0%	-	0.0%	-	3.7%	69	0.0%	-	0.0%	-	1.3%	8
Total Own		$32,940		$41,774		$31,064		$40,940		$21,715		$12,404		$32,323		$25,071
Spouse
Earnings	0.0%	-	11.1%	2333	0.0%	-	14.0%	4360	0.0%	-	11.1%	3963	0.0%	-	20.8%	4983
Unemployment Ins.	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-
Workers’ Comp	0.0%	-	0.0%	-	0.0%	-	1.2%	47	0.0%	-	0.0%	-	0.0%	-	0.0%	-
Veteran’s Benefits	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	3.7%	44	0.0%	-	0.0%	-
Pensions	0.0%	-	4.8%	91	0.0%	-	2.3%	195	0.0%	-	3.7%	281	0.0%	-	7.8%	236
Annuities	0.0%	-	1.6%	105	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	1.3%	-
SSI	0.0%	-	0.0%	-	0.0%	-	2.3%	99	0.0%	-	0.0%	-	0.0%	-	1.3%	-
Social Security	0.0%	-	3.2%	136	0.0%	-	0.0%	-	0.0%	-	7.4%	659	0.0%	-	2.6%	192
Welfare	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-
Total Spouse		-		$2,665		-		$4,701		-		$4,948		-		$5,412
Household
Business	4.8%	249	22.2%	13743	8.1%	1430	14.0%	3079	3.7%	444	11.1%	2169	0.0%	-	3.9%	91
Unearned Income	39.7%	778	61.9%	7679	39.5%	1583	62.8%	5575	11.1%	5850	37.0%	3365	35.1%	1327	62.3%	4485
Alimony	1.6%	16	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-	0.0%	-
Food Stamps	3.2%	4	0.0%	-	0.0%	-	2.3%	26	11.1%	141	29.6%	101	3.9%	35	1.3%	-
Total Household		$1,047		$21,422		$3,013		$8,680		$6,436		$5,626		$1,362		$4,576
Total		$33,988		$65,862		$34,077		$54,322		$28,151		$22,978		$33,686		$35,059
Distribution
25th Percentile		$18,000		$17,432		$15,500		$22,000		$9,000		$6,144		$18,000		$15,320
Median		$30,000		$27,764		$27,400		$45,140		$14,600		$13,560		$34,000		$25,728
75th Percentile		$45,000		$58,460		$48,000		$70,200		$29,000		$26,400		$42,169		$48,872

Note: Columns represent choice in 1998 based on response to the wave 4 survey. All respondents were employed at baseline.

Table 3 shows descriptive statistics for both the behavioral sample (working in 1992) and the group of individuals who are not working. The first column in this table shows that the average age at the last survey for individuals in our behavioral sample is 60.6. Approximately 10% report that they suffer a work limitation. The second column of Table 3 shows that men in our sample who are not working at baseline tend to be slightly older and are approximately three times as likely than those working to report having a work limitation.

Table 3.

Descriptive Statistics

	Working at t=0	Not working at t=0	Of those working at t=0, behavior last observation
			Career	Bridge	Retired	Disability
Age at wave 4	60.6	61.1	59.8	61.1	62.0	59.6
< High School	0.222	0.261	0.243	0.229	0.188	0.267
Some College	0.170	0.183	0.135	0.114	0.208	0.333
College Grad	0.193	0.191	0.243	0.114	0.167	0.200
Work limited at wave 1	0.097	0.296	0.095	0.143	0.083	0.067
Work limited at wave 4	0.188	0.365	0.108	0.057	0.208	0.867
Age 62 or older at wave 4	0.369	0.435	0.243	0.457	0.583	0.133
Normal retirement benefit (assuming no further work)	$12,820	$11,271	$13,136	$12,327	$12,775	$11,711
Eligible for DB pension ever	0.466	0.078	0.419	0.486	0.542	0.333
Eligible for DC pension ever	0.369	0.122	0.405	0.371	0.375	0.267
Expected Career Earnings at last observation	$32,854	$6,048	$33,143	$32,904	$34,700	$23,761
Expected Bridge Earnings at last observation	$13,098	$2,294	$14,647	$12,253	$10,658	$13,793
With no employer health insurance	0.176		0.095	0.314	0.125	0.467
With only current coverage	0.290		0.297	0.286	0.292	0.200
With both current & retiree coverage	0.534		0.608	0.400	0.583	0.333
Median Non-housing wealth	$18,900	$15,000	$20,250	$15,000	$24,000	$8,000
Median Housing wealth	$4,750	-	$250	-	$33,500	$10,000
Fraction Choosing	0.605	0.395	0.430	0.204	0.279	0.087

Recall that the choice data used to identify the behavioral portion of the model come from the activity status of our behavioral sample at approximately yearly intervals. The third through sixth columns of table 3 report descriptive statistics on our behavioral sample broken down by whether they chose C, B, A, or N in the final survey.²⁴ There are several things to note. Those who retire (i.e., choose option N) are more likely to be eligible for a private defined benefit pension and more likely to have reached age 62 by wave 4 than those who did not. What is more, those who retire (N)--and especially those who applied for DI benefits (A)--were no more likely to be in poor health or report a work limitation at their wave 1 interview, but were much more likely to report health problems as of the final survey. These patterns make considerable sense.

A person in our behavioral sample would receive an average of $12,820 in SS benefits at age 65 (based on the contributions made as of the baseline interview) and would receive DI benefits of the same amount if he is approved for the program. On average, the expected career earnings and bridge earnings at the final survey based on estimates of Appendix equations (A.2) and (A.3) are $32,854 and $13,098 respectively.

4.4 Model Estimates and Simulations

The parameters that enter our model are:

1. the parameters of the DI approval equation (7);

2. the parameters π, γ, and σ²_ν from the health equation (8) and the parameters ρ and σ²_ξ from equation (6);

3. the parameters in the earnings equations (A.2 and A.3 in Appendix A);

4. the parameters of the health expenditure equation (A.1 in Appendix A);

5. τ, λ_HI, and { ${\mathrm{\lambda }}_{\mathrm{X}}^{\mathrm{j}},{\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{j}}$:j=C,B,A} from the current period utility equation (3);

6. the parameters Π₁ and Π₂ from the initial conditions equation (12);

7. the standard deviation of unobserved heterogeneity σ_κ;

8. The covariance parameters {COV(μ_t, ε_t^j), j=C,B,A} discussed after equation (10);

9. the covariance parameters {COV(ε^I, ν₁) and COV(ε^I, κ), j=C,B,A} discussed after equation (12);

10. the parameter β^Common from the discount factor equation (6); and

11. the parameter θ from the pecuniary utility function in equation (1).

The identification of the DI approval equation (10) is made difficult in practice by the reality that the DI approval decision is only observed for those who apply for benefits and virtually all DI applicants have poor or fair self-reported health. While our model has features that in theory can address this type of problem, the reality that only a relatively small number of individuals apply for DI during our sample period makes identification difficult in practice. For our structural estimation we set A₁^DI=.08 and A₂^DI=Var(e^DI)=1 in equation (7). The assumption that A₂^DI=Var(e^DI)=1 amounts to assuming that DI award decisions are about as equally reliable indicators of disability status as are the global self-reported measures available in the HRS, which is consistent with the work of Benitez-Silva, Buchinsky and Rust (2006). We chose our estimate of A₁^DI so that the fraction of those that apply for benefits who are awarded them implied by our model matches the fraction in the data, roughly 2/3.

In Appendix D (available in the NBER working paper version of this paper or by request from the authors) we describe the technical/computing steps used to address a very time-intensive estimation problem.²⁵ In part due to the importance of having a likelihood function with certain properties that make estimation feasible and in part as a concession to the size of the computing task we reduced the number of parameters in the model by estimating the parameters of the earnings equations (#3 above with estimates shown in Appendix A.3.2) and health equations (#2 above with estimates shown in Table 4) outside of the behavioral model.²⁶ To estimate the health parameters (# 2 above) using Maximum Likelihood, we specify the likelihood contribution for a person in a way similar to equation (C.7) in Appendix C but we include in the probability expression only the conditions involving aggregate unobservables of the form ν_t+μ_t which are the terms related to self-reported health (i.e., in illustrative equation (C.7) in Appendix C this would involve the first three terms in the intersection, ν₂+μ₂<−πX₂−γZ_2, ν₃+μ₃<−πX₃−γZ₃, ν₅+μ₅>−πX₅−γZ₅). π and γ enter these conditions directly. The remainder of the health parameters (in #2 above) affect the likelihood contribution through their effect on the covariance matrix of the aggregate unobservables. Given the discrete nature of the self-reported health variable, once we make the normalization var(ν_t+μ_t)=1 ∀ t, it is possible to identify the covariance between each pair of aggregate unobservables. In addition, the fact that we observe information about h_t* at multiple times implies that it is possible to separately identify var(ν_t) and var(μ_t). What allows the separate identification is that fact that μ_t has only a transitory effect on measured health, while ν_t has an effect which dies out over time only slowly.

Table 4.

Estimates of Health Equation and Initial Conditions Equation for Baseline Specification

	Health Equation (10)	Initial Conditions Equation (12)
X from equations (10) and (12)
Constant	−.785 (.105)	.134 (.104)
Less than high school education	−.031 (.190)	.108 (.198)
College education	−.203 (.187)	−.155 (.194)
Age	.008 (.019)	−.059 (.022)
Z’s — Respondent reports difficulty with the specified activity.*
Jog one mile	.202 (.077)	.091 (.091)
Walk several blocks	.325 (.106)	−.0622 (.178)
Walk one block	−.244 (.140)	−.080 (.280)
Sit for about 2 hours	.081 (.100)	.003 (.102)
Get up from a chair after sitting long periods	−.024 (.140)	.045 (.137)
Get in and out of bed without help	.107 (.149)	−.131 (.191)
Go up several flights of stairs	.225 (.073)	−.249 (.134)
Go up one flight of stairs	.230 (.123)	−.207 (.218)
Lift or carry weights over 10 lbs	.307 (.105)	.154 (.164)
Stoop, kneel, or crouch	.157 (.086)	.128 (.131)
Pickup a dime from a table	.152 (.116)	.022 (.199)
Reach or extend your arms above shoulder level	.273 (.102)	.270 (.200)
Pull or push large objects like a living room chair	.200 (.105)	−.347 (.181)
ρ	.92 (.155)
var(νt)	.82 (.080)

^*Activities of Daily Living at time health is observed for first column and t=0 for second column. Coded as 1 if the man reports difficulty doing the activity, 0 otherwise.

An additional concern was the difficulty of credibly identifying and estimating β^Common and θ. In response to this concern we take the approach of seeking guidance from recent literature in order to choose reasonable values of these two parameters, and we estimate the thirty-six remaining parameters described above.²⁷ We begin by estimating a “baseline” specification in which β^Common=0.90 and θ =1 which implies that Y^j(t)^1−θ/(1−θ)=ln(Y).²⁸

The first column of Table 5 shows the estimates of the behavioral equations for the baseline specification.²⁹ The estimate of τ indicates that the amount of consumption available from a particular option plays a statistically significant role in the utility that is derived from that option. The estimates in the first column of Table 5 also indicate that health plays a statistically significant role. Given that larger values of health represent worse health, the negative estimates of ${\lambda }_{\eta }^C$ and ${\lambda }_{\eta }^B$ indicate that individuals in bad health get less utility from the work options (relative to the option N) than individuals in better health. The positive estimate of ${\lambda }_{\eta }^A$ indicates that individuals in bad health get higher non-pecuniary benefits from applying for Disability Insurance (relative to the option N) than individuals in better health. In addition, the estimates imply that individuals, especially those in decent health, face a very significant non-pecuniary cost associated with applying for DI benefits.³⁰ Our estimates imply that, over and above the effect of health insurance on disposable income, health insurance has a positive relationship with well-being in the sample, but the estimated effect is quite small and not statistically significant. Among the variance/covariance estimates, most striking is the importance of unobserved heterogeneity; the point estimate (standard error) of the standard deviation σ_κ is 1.423 (.322).

Table 5.

Estimates of Model (behavioral equations and covariance terms)

	Baseline	Traditional model with Binary Health
	Estimate (Std. Error)	Estimate (Std. Error)
Pecuniary Utility
τ	.336 (.060)	.325 (.060)
UnpC(t) Non-Pecuniary Utility Career (C)
Constant	.546 (.338)	.772 (.193)
ληC (Health, η)	−.776 (.397)	−1.590 (.242)
λHI (Has Health Insurance)	.063 (.043)	.131 (.102)
UnpB(t) Non-Pecuniary Utility Bridge (B)
Constant	−.908(.486)	.242 (.197)
ληB (Health, η)	−1.357(.351)	−2.978 (.394)
λHI (Has Health Insurance)	.063 (.043)	.131 (.102)
UnpA(t) Non-Pecuniary Utility DI (A)
Constant	−2.102(.399 )	−3.496 (1.690)
ληA (Health, η)	.851 (.212)	2.900 (1.657)
λHI (Has Health Insurance)	.063 (.043)	.131 (.102)
UnpN(t) Non-Pecuniary Utility Non-Work (N)
Constant	Normalized to zero	Normalized to zero
ληN (Health, η)	Normalized to zero	Normalized to zero
λHI (Has Health Insurance)	.063 (.043)	.129 (.104)
Health Equation	See Table 4	N.A.
Initial Conditions Equation	See Table 4	Not Shown
Covariance Terms
σκ	1.423 (.322)	.824 (.052)
COV(εI, νt)	−.309 (.106)	−.319 (.125)
COV(μt, εtC)	−.191 (.173)	N.A.
COV(μt, εtB)	.216 (.128)	N.A.
COV(εI, κ)	−.784 (.412)	.008 (.255)
Log Likelihood Function Value	−940.033

Although not shown, each non-pecuniary equation also includes two dummy variables characterizing a person’s education level (less than high school and more than high school). The effect of health insurance is constrained to be the same across choices.

In order to quantify the roles that economic resources and health play in determining labor decisions we begin by performing simulations using an “illustrative person.” We construct a person who has a college education and has career earnings, bridge earnings, SS benefits, and potential DI benefits that are close to the average for people in our sample, but has no private pension wealth or other sources of wealth.³¹ We first assume that the illustrative person has true health η₁ at time t=1 that is equal to the average true health of the individuals in our sample. The first column of Table 6 shows simulated choice probabilities at t=1 for an illustrative person at 55, 60, 62, 64, and 65 years of age, respectively. Since the simulated individuals would have been employed at t=0, these simulated probabilities can be thought of as one year labor force exit rates.

Table 6.

Choice Probabilities of Illustrative Person at Different Ages - Baseline

Choice at t=1	A. Average Health	B. Health 1 Std. Dev. Below Average	C. Health 1.5 Std. Dev. Below Average
	AGE=55
Labor Force Exit (N+A)	0.019	0.098	0.195
Non-Work (N)	0.018	0.057	0.084
Apply DI (A)	0.001	0.041	0.111
	AGE=60
Labor Force Exit (N+A)	0.025	0.106	0.198
Non-Work (N)	0.024	0.082	0.127
Apply DI (A)	0.001	0.024	0.071
	AGE=62
Labor Force Exit (N+A)	0.049	0.168	0.269
Non-Work (N)	0.046	0.138	0.209
Apply DI (A)	0.003	0.030	0.060
	AGE=64
Labor Force Exit (N+A)	0.053	0.172	0.279
Non-Work (N)	0.050	0.146	0.207
Apply DI (A)	0.003	0.026	0.072
	AGE=65
Labor Force Exit (N+A)	0.053	0.161	0.254
Non-Work (N)	0.053	0.161	0.254
Apply DI (A)	NA*	NA*	NA*

^*Person cannot apply for Disability Insurance at age 65 or older.

The simulated choice probabilities at age 55 and age 60 are quite similar. At these ages, the illustrative person’s only economic resources if he leaves the workforce come from assistance programs such as the food stamp program. This reality, combined with the fact that being in average health implies that it is not particularly unenjoyable to work and that applying for Disability Insurance is not particularly worthwhile, implies that the person at age 55 and age 60 has a very low probability of leaving the workforce for either the non-work option N (0.02) or for the option of applying for Disability Insurance A (0.001). Evidence regarding the effect of economic resources on behavior can be seen by comparing the choice probabilities at the age of 60 to the choice probabilities at the age of 62 at which time the person becomes eligible for Social Security retirement benefits. The consumption increase in the non-work option (N) causes the probability of choosing this option to increase by a factor of approximately two (from 0.024 to 0.046). The fact that the probability of applying for DI remains extremely small (0.003) for the average health person even when SS benefits become available is evidence of the very strong importance of health in the DI application decision.³² Delaying retirement past the age of 62 increases a person’s Social Security benefits. Comparing simulated choice probabilities between the age of 62 and the ages of 64 and 65 reveals that this increase in Social Security benefits has a relatively small effect on retirement decisions.

The second column of Table 6 shows choice probabilities at different ages for the illustrative person under the assumption that his health at t=1 is one standard deviation below average.³³ As before, the choice probabilities are fairly similar at ages 55 and 60 for this person. However, comparing the choice probabilities for this person at ages 55 and 60 to the choice probabilities for the person in average health at ages 55 and 60 indicates that health has a very important effect on the probability that a person will transition out of the workforce at ages 55 and 60. For example, the total probability of leaving the workforce (N+A) at age 60 is 0.025 for the person in average health and is 0.106 for the below-average health person with the impact of worse health coming from both an increase in the probability of choosing the non-work category (N) and an increase in the probability of applying for DI (A). Comparing these two numbers with the choice probabilities of the individuals in average and below-average health at age 62 indicates that the incentive effect of economic resources depends to some extent on health. At age 62 when SS benefits become available, the total probability of leaving the workforce increases by approximately 0.06 (from 0.106 to 0.168) for the person in below-average health but increases by only approximately 0.02 (from 0.025 to 0.049) for the person in average health.

The third column of Table 6 shows choice probabilities at different ages for the illustrative person under the assumption that his health is 1.5 standard deviations below average. Comparing the results of the second and third columns indicates that, once a person reaches poor health, an incremental worsening of health can have large effects on decisions. When compared to the person who has health 1 standard deviation below average, the person in worse health is at least twice as likely to apply for Disability Insurance at each age and has a probability of leaving work (N+A) that is approximately 10 percentage points higher at each age.

In a previous version of this work (Bound, Stinebrickner and Waidmann 2007), we also examined the robustness of these estimates to the assumptions made about time preferences and risk aversion. In general, varying these parameters produced results that were consistent with the baseline specification.

Does the treatment of health matter? - A comparison to a model trusting self-reported health

Our models deal with the measurement error and endogeneity problems that are potentially present in self-reported, survey health measures. Given that the implementation of the health portions of our models is non-trivial, and, as a result, has implications for the feasibility of estimating other aspects of the decision process, it is valuable to examine the extent to which our findings would differ from a model in which these potential problems were ignored.

To do this, we estimate a new version of our model in which our health framework has been replaced with a treatment of health that is consistent with the standard in the literature. Specifically, in the current period utility equation (2) of our baseline specification we replace our continuous measure of health, η_t, with a binary health variable that is equal to one if the person is in bad health and is equal to zero otherwise. We assume that the person’s self-report of this binary health variable is accurate so that, unlike the continuous health measure that enters our models, the binary health measure that enters this new model is observed directly in the HRS data.³⁴ In order to compute the new value functions of the type in equation (4), we make the standard assumption that a person knows his current period binary health status, and, given this status, knows the probability of each possible health status arising in period t+1. To be consistent with the self-reported health measure that we use to estimate equation (10), we characterize a person to be in bad health if he reports that he has an impairment or health problem that limits the kind or amount of paid work he can do.³⁵

The second column of Table 5 reports the estimates of this “traditional” model. The estimate of τ is similar to the estimate shown in the first column of Table 5 for the baseline specification of our continuous-health model. Consistent with the estimates of ${\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{C}},{\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{B}}$ and ${\mathrm{\lambda }}_{\mathrm{\eta }}^{\mathrm{A}}$ in the continuous-health model, the estimated effects of the binary health variables in the traditional model are statistically significant in each of the current period utility equations. However, the t-statistics associated with the estimated effects of health are non-trivially different between the models. For example, the t-statistic associated with the effect of health in the option C is greater by a factor of more than three in the traditional health model than it is in the baseline specification of our baseline continuous-health model. While these differences in statistical significance raise the possibility that ignoring the measurement and endogeneity issues related to self-reported health may lead to different conclusions about the importance of health, knowing whether this is actually the case cannot be confirmed simply by examining individual coefficients in isolation. Therefore, we take the approach of comparing the health implications of the two models by examining whether simulated choice probabilities from our baseline model are different than simulated choice probabilities from the traditional model.

To do this, we again make use of the illustrative person that was used to produce the simulations in Table 6. For the traditional model there are only two possible health values. In In the first two columns of Table 7 we show choice probabilities at different ages for the illustrative person who reports himself to be in good and bad health, respectively. A comparison of these two columns reveals that changing the self-reported health of the illustrative person from good to bad has very large effects on behavior. For example, the probability that the illustrative person will be out of the workforce at age 60 is .094 if the illustrative person reports being in good health and is .426 if the illustrative person reports being in bad health.

Table 7.

Choice Probabilities of Illustrative Person at Different Ages Using Alternate Models of Health

	Traditional Model w/Binary S-R Health		Continuous Health Model		Continuous Health w/σκ Fixed at Binary Value
	Good Health	Bad Health	Good Health	Bad Health	Good Health	Bad Health
	AGE=55
Labor Force Exit (N+A)	0.079	0.452	0.079	0.244	0.071	0.336
Non-Work (N)	0.068	0.111	0.067	0.096	0.061	0.149
Apply DI (A)	0.011	0.341	0.011	0.148	0.010	0.186
	AGE=60
Labor Force Exit (N+A)	0.094	0.426	0.083	0.245	0.082	0.340
Non-Work (N)	0.088	0.183	0.074	0.140	0.074	0.207
Apply DI (A)	0.006	0.243	0.008	0.105	0.008	0.133
	AGE=62
Labor Force Exit (N+A)	0.159	0.513	0.112	0.293	0.120	0.403
Non-Work (N)	0.147	0.286	0.102	0.191	0.110	0.259
Apply DI (A)	0.012	0.227	0.010	0.101	0.010	0.144
	AGE=64
Labor Force Exit (N+A)	0.115	0.515	0.114	0.303	0.125	0.411
Non-Work (N)	0.107	0.158	0.105	0.190	0.114	0.251
Apply DI (A)	0.008	0.356	0.009	0.113	0.010	0.160
	AGE=65
Labor Force Exit (N+A)	0.091	0.291	0.111	0.274	0.118	0.359
Non-Work (N)	0.091	0.291	0.111	0.274	0.118	0.359
Apply DI (A)	NA*	NA*	NA*	NA*	NA*	NA*

^*person cannot apply for Disability Insurance at age 65 or older.

The goal is to compare the numbers from the traditional model to analogous numbers constructed from our continuous health model. It is not trivial to construct choice probabilities for the illustrative person who reports being in good or bad health in our continuous health model because this model is written in terms of true rather than reported health. To construct these probabilities, we need to account that, in our model, there is a continuum of health values, η, with a distribution that is characterized by equation (8) and that the connection between a particular value of continuous health, η, and the person’s self-reported binary health is provided by equations (9) and (10) which determine the probability that a person with a particular value of η will report himself to be in bad health or good health. Thus to construct the analog to the first two columns, we integrate the choice probabilities that can be constructed for the illustrative person for a particular value of η over the person’s distribution of η, where we weight the choice probabilities in the integral to reflect the probability that a person would report himself to be in bad health given η. The results of this exercise shown in the third column represent the average choice probabilities of the illustrative person over all health scenarios in which he would report good health. Similarly, the results in the fourth column represent the average choice probabilities of the illustrative person over all health scenarios in which he would report bad health.

A pair-wise comparison across the first four columns provides evidence of substantial differences between the traditional model and our model. For example, for the traditional health model, we see the difference between good and bad self-reported health is a .33 difference in the probability of not working at age 60. In our continuous health model, we see a .16 difference in the probability of working at age 60 between a person who reports himself to be in good health and a person who reports himself to be in bad health. Thus, our results suggest that dealing with the potential problems associated with self-reported health is important in this context.

It is not an easy task to pinpoint exactly why these differences exist. Somewhat generically, the difference between the two models arises to a large extent because our continuous health model is able to take into account that reported differences in health should be attributed to both true differences in health and a non-trivial amount of reporting error. More concretely, we find evidence that a large part of the difference between the traditional model and our model operates through differences in the importance of unobserved heterogeneity between the models. Specifically, we find in the last two columns of Table 7 that if we reestimate and resimulate our continuous model holding the standard deviation of heterogeneity, σ_κ, constant at its value from the traditional model, a little more than half of the aforementioned difference between the traditional model and our model disappears. For example, we see that there is now a .26 difference in the probability of working at age 60 between a person who reports himself to be in good health and a person who reports himself to be in bad health. It is necessary to leave a detailed exploration of why substantial differences exist in the importance of heterogeneity between the traditional and continuous models to future work. What we note here is that a stark implication of moving from the traditional model (in which true health is observed exactly) to the continuous model (which recognizes that only the distribution of true health can be observed) is that σ_κ is estimated less precisely. This finding highlights the importance of work such as Kasahara and Shimotsu (2007) that focuses on understanding the identification of finite mixture models in dynamic, discrete choice models.

Potential Changes in Policy

The simulations involving the illustrative person suggest that changes in policy that influence economic resources may have substantial effects on individual behavior and that these effects may vary across people with different health. Here we use our baseline model and our behavioral sample to simulate the effects of several potential changes in policy. Policy 1 examines the effect of removing the option of early SS benefits. Policy 2 examines the effect of a policy that has been implemented - changing the normal retirement age from 65 to 67. Policy 3 examines the impact of removing the Disability Insurance program entirely. Policies 4, 5, and 6 examine, respectively, a 25% reduction in SS benefits, a 25% reduction in DI benefits, and a 25% reduction in both SS and DI benefits.

To quantify the effects of these policy changes, we first perform a baseline simulation in which no policy change has occurred. For each person in our behavioral sample (i.e., those individuals working at time t=0), we condition on the person’s information that is available at time t=0 and simulate a sequence of choices corresponding to the years that a choice is observed for the person in the data.³⁶ We then repeat this process 7200 times for each person in our behavioral sample. The resulting simulations can be used to compute the proportion of individuals that would choose each of the options in the set {C, B, N, A} at particular ages and the proportion that would choose each of the options when all of the ages are pooled. The results are shown in the first column of Table 8.

Table 8.

Policy Simulations - All Health Combined

	Baseline	Policy 1 Remove SS ERB	Policy 2 SS NRA to 67	Policy 3 Eliminate DI	Policy 4 25% Decrease DI Benefits	Policy 5 25% Decrease SS Benefits	Policy 6 25% Decrease DI & SS Benefits
Pooled Ages
LF Exit (N+A)	0.152	0.148	0.151	0.144	0.150	0.150	0.148
Non-Work (N)	0.134	0.128	0.130	0.144	0.135	0.130	0.132
Apply DI (A)	0.019	0.020	0.021	0**	0.015	0.020	0.017
AGE=55
LF Exit (N+A)	0.147	0.147	0.147	0.136	0.145	0.147	0.144
Non-Work (N)	0.123	0.121	0.122	0.136	0.125	0.122	0.123
Apply DI (A)	0.024	0.026	0.025	0**	0.020	0.025	0.021
AGE=60
LF Exit (N+A)	0.154	0.151	0.153	0.149	0.153	0.153	0.151
Non-Work (N)	0.142	0.137	0.140	0.149	0.143	0.140	0.140
Apply DI (A)	0.012	0.014	0.013	0**	0.010	0.013	0.011
AGE=62
LF Exit (N+A)	0.170	0.147	0.163	0.163	0.168	0.162	0.160
Non-Work (N)	0.155	0.132	0.146	0.163	0.156	0.145	0.146
Apply DI (A)	0.015	0.016	0.016	0**	0.012	0.017	0.014
AGE=64
LF Exit (N+A)	0.205	0.183	0.197	0.197	0.204	0.197	0.195
Non-Work (N)	0.176	0.158	0.166	0.197	0.180	0.164	0.167
Apply DI (A)	0.029	0.025	0.031	0**	0.024	0.033	0.028
AGE=65
LF Exit (N+A)	0.220	0.214	0.218	0.216	0.220	0.209	0.208
Non-Work (N)	0.220	0.214	0.181	0.216	0.220	0.209	0.208
Apply DI (A)	0*	0*	0.037	0*	0*	0*	0*

^*Person cannot apply for Disability Insurance at age 65 or older except in Policy 2.

^**Policy involves removing Disability Insurance program.

Policy 1 involves removing all SS benefits before age 65.

Policy 2 involves changing the normal retirement age from 65 to 67.

Policy 3 involves removing the DI program.

Policy 4 involves a 25% decrease in DI benefits without changing SS Retirement benefits.

Policy 5 involves a 25% decrease in SS Retirement benefits without changing DI benefits.

Policy 6 involves ad 25% reduction in both SS Retirement and DI benefits.

The first entries in Column 1 represent the choice proportions that are generated if individual choices at all ages are pooled. ³⁷ Thus, under the baseline specification, our model indicates that individuals will choose the work option (C+B) in 1-.152=.848 of the periods in the pooled decision periods, will choose the non-work option (N) in .134 of the pooled decision periods, and will choose to apply for Disability Insurance (A) in .019 of the pooled decision periods. To get a sense of the fit of our model, recall from Section 4.3 that the actual proportions in the data are, respectively, .830 (C+B), .153 (N), and .018 (A). The remainder of the entries in Column 1 reflect the choice proportions when choices are disaggregated by age (for select ages). We note that, while from an operational standpoint it would be possible to compare these disaggregated simulated proportions to the actual disaggregated proportions in the data, in practice the usefulness of a full comparison of this type is limited due to relatively small sample sizes at individual ages. However, it is certainly worth noting that the general message from such a comparison is that the age gradient in the simulations is substantially less steep than the comparable age gradient in the actual data. For example, while the proportion of men working falls from roughly .89 to .54 between the ages of 55 and 65 in the data, our simulations (using our model which does not allow a person’s age to influence his non-pecuniary utility) show a decrease from .85 to .78 between these ages. Thus, roughly speaking, at least in our model, health and economic resources can explain about 20% of the decline in work between the age of 55 and 65.

For each policy change, the simulation process is repeated after modifying the model appropriately to reflect the change. Column 2 of Table 8 shows the proportions associated with Policy 1 in which no benefits are available from the Social Security system until a person reaches the age of 65. When a person is younger than 62, this policy change influences decisions only through its influence on future income. Because knowledge that Social Security benefits will not be available at the ages of 62–64 tends to reduce the value of each option in a somewhat similar fashion, it is perhaps not surprising that the policy change has little effect before the age of 62. For example, at age 55, the proportion choosing the non-work option (N) is .123 under the baseline simulation and .121 under the policy change. The policy change leads to an increase in work at the age of 62 when the amount of current period consumption that a person receives in the non-work and DI options is reduced relative to the baseline case; at age 62 the proportion choosing the non-work option falls by approximately 15% (from .155 under the baseline simulation to .132 under the policy change). A similar effect (.176 versus .158) is shown in the table for age 64. The policy change leads to little change in the number of DI applicants. Thus, the decrease in the proportion choosing N is accompanied by an increase of similar size in the proportion choosing C or B. At 65 when Social Security benefits become the same in the baseline simulation and policy change simulation, the proportion choosing option N becomes similar under the baseline and policy change (.220 vs. .214).

We also construct the analog to Table 8 for individuals with health that is one standard deviation or more below the average for the sample (hereafter referred to as “bad” health) and for the remaining individuals in our sample (hereafter referred to as individuals in “good” health) and show these proportions in Table 9 and Table 10, respectively.³⁸ Consistent with our illustrative person simulations, we find that individuals in bad health are much less likely to be working in all periods than individuals in good health. Also consistent with our illustrative person simulations, we find some evidence that the effect of this policy change varies with a person’s health. For example, a comparison of the first and second columns of Table 9 reveals that, for individuals in our sample with bad health, the policy causes the proportion choosing N at age 62 to fall by approximately .04 (from .351 under the baseline to .310 under Policy 1), while the proportion applying for DI rises by 0.014. Thus, our model implies that among those in poor health affected by the elimination of early retirement benefits, roughly one third would apply for DI, while two thirds would continue to work. A comparison of the first and second columns of Table 10 reveals that, for individuals in our sample with good health, the policy causes the proportion choosing N at age 62 to fall by approximately .02 (from .137 under the baseline to .116 under Policy 1). For this group, there is essentially no effect of the policy change on the number of men applying for DI.

Table 9.

Policy Simulations - Bad Health (1 standard deviation or more below average)

	Baseline	Policy 1 Remove SS ERB	Policy 2 SS NRA to 67	Policy 3 Eliminate DI	Policy 4 25% Decrease DI Benefits	Policy 5 25% Decrease SS Benefits	Policy 6 25% Decrease DI & SS Benefits
Pooled Ages
LF Exit (N+A)	0.400	0.396	0.399	0.363	0.390	0.399	0.389
Non-Work (N)	0.296	0.283	0.283	0.363	0.307	0.286	0.297
Apply DI (A)	0.104	0.112	0.117	0**	0.084	0.113	0.092
AGE=55
LF Exit (N+A)	0.405	0.406	0.405	0.359	0.393	0.406	0.394
Non-Work (N)	0.277	0.272	0.275	0.359	0.289	0.273	0.285
Apply DI (A)	0.127	0.133	0.130	0**	0.104	0.133	0.109
AGE=60
LF Exit (N+A)	0.384	0.381	0.383	0.366	0.380	0.383	0.377
Non-Work (N)	0.324	0.308	0.317	0.366	0.332	0.315	0.322
Apply DI (A)	0.060	0.074	0.066	0**	0.048	0.068	0.055
AGE=62
LF Exit (N+A)	0.451	0.423	0.444	0.425	0.444	0.444	0.436
Non-Work (N)	0.351	0.310	0.333	0.425	0.367	0.326	0.340
Apply DI (A)	0.100	0.114	0.111	0**	0.078	0.118	0.096
AGE=64
LF Exit (N+A)	0.481	0.455	0.472	0.446	0.473	0.473	0.463
Non-Work (N)	0.301	0.296	0.274	0.446	0.329	0.261	0.290
Apply DI (A)	0.180	0.159	0.198	0**	0.144	0.212	0.173
AGE=65
LF Exit (N+A)	0.474	0.465	0.489	0.457	0.474	0.461	0.456
Non-Work (N)	0.474	0.465	0.307	0.457	0.474	0.461	0.456
Apply DI (A)	0*	0*	0.181	0*	0*	0*	0*

^*person cannot apply for Disability Insurance at age 65 or older except in Policy 2.

^**policy involves removing Disability Insurance program.

Policy 1 involves removing all SS benefits before age 65.

Policy 2 involves changing the normal retirement age from 65 to 67.

Policy 3 involves removing the DI program.

Policy 4 involves a 25% decrease in DI benefits without changing SS Retirement benefits.

Policy 5 involves a 25% decrease in SS Retirement benefits without changing DI benefits.

Policy 6 involves ad 25% reduction in both SS Retirement and DI benefits.

Table 10.

Policy Simulations - Good Health (no worse than 1 standard deviation below average)

	Baseline	Policy 1 Remove SS ERB	Policy 2 SS NRA to 67	Policy 3 Eliminate DI	Policy 4 25% Decrease DI Benefits	Policy 5 25% Decrease SS Benefits	Policy 6 25% Decrease DI & SS Benefits
Pooled Ages
LF Exit (N+A)	0.118	0.113	0.116	0.113	0.117	0.116	0.114
Non-Work (N)	0.111	0.106	0.109	0.113	0.111	0.109	0.108
Apply DI (A)	0.007	0.007	0.007	0**	0.006	0.007	0.006
AGE=55
LF Exit (N+A)	0.103	0.103	0.103	0.098	0.102	0.103	0.102
Non-Work (N)	0.097	0.095	0.096	0.098	0.097	0.096	0.096
Apply DI (A)	0.007	0.007	0.007	0**	0.006	0.007	0.006
AGE=60
LF Exit (N+A)	0.125	0.122	0.123	0.122	0.124	0.123	0.122
Non-Work (N)	0.119	0.115	0.117	0.122	0.119	0.117	0.117
Apply DI (A)	0.006	0.007	0.006	0**	0.005	0.006	0.006
AGE=62
LF Exit (N+A)	0.145	0.123	0.138	0.140	0.144	0.137	0.136
Non-Work (N)	0.137	0.116	0.130	0.140	0.137	0.129	0.129
Apply DI (A)	0.008	0.007	0.008	0**	0.006	0.008	0.007
AGE=64
LF Exit (N+A)	0.171	0.149	0.163	0.166	0.170	0.163	0.161
Non-Work (N)	0.161	0.141	0.152	0.166	0.161	0.151	0.151
Apply DI (A)	0.010	0.008	0.010	0**	0.009	0.011	0.010
AGE=65
LF Exit (N+A)	0.178	0.172	0.208	0.175	0.178	0.167	0.166
Non-Work (N)	0.178	0.172	0.195	0.175	0.178	0.167	0.166
Apply DI (A)	0*	0*	0.013	0*	0*	0.013	0*

^*person cannot apply for Disability Insurance at age 65 or older except in Policy 2.

^**policy involves removing Disability Insurance program.

Policy 1 involves removing all SS benefits before age 65.

Policy 2 involves changing the normal retirement age from 65 to 67.

Policy 3 involves removing the DI program.

Policy 4 involves a 25% decrease in DI benefits without changing SS Retirement benefits.

Policy 5 involves a 25% decrease in SS Retirement benefits without changing DI benefits.

Policy 6 involves ad 25% reduction in both SS Retirement and DI benefits.

The third column in this set of tables (Policy 2) shows the proportions associated with a second policy which influences Social Security benefits in a less drastic way than the first policy. Specifically, the policy change involves increasing the normal retirement age from 65 to 67 and allowing individuals to apply for DI benefits until the age of 67. Under this policy, while individuals still become eligible for Social Security benefits at the age of 62, the amount of the benefits that is received if one retires at age 62 is reduced by 12.5%.³⁹ This change in the normal retirement age is currently being phased in. A comparison of Column 1 and Column 3 of Table 8 reveals that this policy will have relatively small effects on individual decisions. The change has virtually no effect before age 62. At ages 62 and 64, the policy causes a decrease in the proportion choosing the non-work option (N) of one percentage point or approximately seven percent for people in our sample.⁴⁰

The fourth column of Table 8 (Policy 3) shows the proportions associated with a third policy change in which the Disability Insurance program is removed entirely. Comparing the “Pooled Ages” entries in Column 1 to those in Column 4 reveals that, when the DI program is removed, slightly less than half of the individuals who were DI applicants under the baseline simulation choose to work.⁴¹ Evidence about the differential effect of the policy change by health status can be seen in Tables 11B and 11C. The “Pooled Ages” entry in Column 1 of Table 10 shows that, under the baseline simulation, individuals in good health choose to apply for DI benefits (A) in only .007 of the pooled decision years. Thus, removing DI benefits has very little effect on individuals in good health. The “Pooled Ages” entry in Column 1 of Table 9 shows that, under the baseline simulation, individuals in bad health choose to apply for DI (A) benefits in .104 of the pooled decision years. For these individuals, comparing the “Pooled Ages” entries under the baseline (Column 1 of Table 9) to that under Policy 3 (Column 4 of Table 9) shows that the removal of the DI option results in an increase in the proportion choosing N from .296 to .362 and a smaller change in the proportion choosing C+B (from .600 to .637). Thus, to a large extent, the differential impact of this policy change by health status comes from the fact that many individuals in bad health who apply for DI benefits under the baseline remain out of the workforce but no longer receive income from DI benefits when the program is removed.

The last three columns of Tables 8, 9 and 10 report results from simulating what would happen if first just DI benefits, then just Retirement benefits, and then both together were reduced by 25%. Although not shown, the results from simulating what would happen were benefits increased by 25% were very similar. Our estimates suggest that a 25% reduction in DI benefits would reduce applications for DI by a little over 20%.⁴² The effect of reducing Retirement benefits by 25% varies by age. For those who have reached the Social Security early retirement age of 62, there is about a 7% reduction in the fraction of men simply leaving the labor force (N).⁴³ One can also see in this table a clear evidence of interaction effects between the Social Security retirement and Disability Programs; when retirement but not disability benefits are reduced, the application for disability benefits increases, with the reverse being true when disability, but not retirement benefits are reduced.

Conclusion

In this paper, we report estimates of a dynamic programming model that addresses the interplay among health, financial resources, and the labor market behavior of men nearing retirement age. A significant contribution of our work is the use of a latent variable model for health that we believe is robust to concerns about the endogeneity of self-reported health. Our comparison of results obtained using this health model to those obtained using a more traditional measure of health suggest that the manner in which one models health can have a substantial effect on conclusions about the behavioral effects of poor health.

Our estimates imply that individuals in good health are unlikely to retire unless they have generous financial resources available to them. On the other hand, our estimates imply that a man in poor health is quite likely to leave the workforce even when he is not yet eligible for any kind of pension benefits. In fact, our simulations show that a typical individual in poor health is 10 times more likely than a similar person in average health to retire before becoming eligible for pension benefits. These estimates underline the importance that health plays in determining early retirement behavior.

Strikingly, our estimates imply that changes in the Social Security Retirement Program are likely to have quite small effects on applications for the Disability Insurance Program.⁴⁴ We suspect that the reason for this has to do with the fact that those potentially eligible for DI are a quite a distinct population. Our findings have strong predictions about the patterns we might see in the application for DI benefits as the age for normal retirement under Social Security rises over the next decade. Despite the fact that this change will substantially increase the financial rewards associated with receiving DI rather than early retirement benefits, our estimates suggest that the number of individuals over the age of 62 who apply for DI will not rise by much.

Data Appendix

A.1 Overview of Health and Retirement Study and sample composition

The HRS is described in additional detail in Juster and Suzman (1995). The survey covers a representative national sample of non-institutionalized men and women born between 1931 and 1941 (inclusive), so that respondents in the sample frame were aged 50–62 at the time of the first wave. The HRS over-samples Blacks, individuals of Mexican descent, and residents of the state of Florida to permit reliable analysis of these groups. The first wave of HRS was conducted in person in respondents’ homes; the response rate was 82%. The total sample size of the first wave is 12,654 respondents. The second wave of the HRS was conducted by telephone in 1994; the second wave re-interviewed 11,317 of the original respondents, representing 91% of the original sample. The third wave (1996) reinterviewed 10,681 of the original sample, and the fourth (1998) reinterviewed 10,242, representing 86 percent of the original respondents. By 1998, 805 (6.4%) of the original respondents were deceased.

The HRS includes the spouses/partners of the survey population even if they are not themselves in the age range of the sample frame; since respondents out of the sample frame do not constitute a representative sample, they are excluded here. The age-eligible first wave sample consists of 9,824 respondents, of whom 4,522 are men, of whom 733 are not married/partnered. Table A.1 describes the effects of sample exclusions necessary for our analysis. From this group, we exclude 206 respondents who did not have a Social Security earnings history, either because the respondent refused the HRS permission to access their records or because they had no covered earnings between 1951 and 1991. We exclude 31 respondents who claim to have a private pension on their current job, but who have no corresponding record provided by their employers. We then exclude 153 respondents who were not eligible to receive both retirement (old age) and disability payments from the Social Security system if they did not work past 1992 because they lacked the required number of quarters of covered employment. Finally we excluded 15 respondents who had missing data for any of the variables used in our models. These exclusions left 328 respondents who were included in the initial conditions sample. Of these, 132 were not employed (or were self employed) at the date of their wave 1 (1992/93) interview. The remaining 196 respondents make up the “behavioral sample.”

A.2 Timing Issues Related to Income Sources

Given our assumption that an individual consumes all of the income that he receives in the same year, characterizing consumption in a particular year requires that we describe our assumptions related to the timing of the income from a variety of sources. For some sources of income, institutional details imply that the timing of receipt is obvious given the labor supply decisions that a person makes. For example, that defined benefit (DB) pension plans do not typically include an actuarial adjustment for delayed receipt implies that individuals will begin receiving DB pension payments from a particular job as soon as they become eligible for benefits and are no longer working in a job. We assume that DB pension wealth is not accrued in bridge jobs. While this assumption is made largely for computational reasons, the data suggest that it is a reasonable simplifying assumption. Individuals also have little discretion about the timing of income from food stamps, Supplemental Security Income, and other exogenous sources of income. In addition, the receipt of Disability insurance payments starts automatically after one applies and is approved for benefits. We treat defined contribution pension plans analogously to defined benefit pension plans by assuming that benefits from these plans are only accrued on career jobs and that an individual starts receiving benefits as soon as he becomes eligible and is no longer working at his career job.

For Social Security, some individual discretion about the timing of benefits remains given a person’s labor supply choices, and we try to make reasonable assumptions about the timing of benefits. Specifically, we assume that an individual begins receiving Social Security benefits in the first year he is both eligible (i.e, he is 62 years old or older) and not-working. As noted, the choice-set allows individuals who are younger than 70 years of age the flexibility of returning to work after leaving the workforce. If an individual returns to work after beginning to collect benefits, earnings are taxed away and actuarial adjustments are made to future earnings in accordance with the rules of the Social Security system.

Perhaps the most difficult timing issue relates to the manner in which a person spends the wealth that he has accumulated by the beginning of the sample period. Our approach for dealing with wealth takes into account the intuitively appealing notion that individuals who are not working are more likely to use portions of their wealth for consumption. Specifically, we compute the yearly value of a hypothetical annuity that a person could buy at time t=0 given his wealth. In any year for the remainder of his life that the person does not work, he is assumed to consume the annuitized value of his wealth. In any year that the person does work, we assume that the person saves the annuitized amount.¹ This additional savings is used to increase consumption when he retires permanently (i.e., takes a year off at age 70 or older).²

Finally, we assume that health expenditures are paid out of income in the year that they are incurred. However, consistent with the notion that there exists government assistance, we assume that a person’s consumption in a period cannot fall below a minimum level of subsistence.³

A.3. More detailed information related to various sources of income

A.3.1 The health expenditure equation

Following French and Jones (2004), we assume that a person’s health expenditures at time t depends on the person’s health insurance status k, age, and health:

$$ln\text{Expenditures}(\mathrm{t})={{\mathrm{\Lambda }}_1}^{\mathrm{k}}+{\mathrm{\Lambda }}_2(\text{Age-}53)+{\mathrm{\Lambda }}_3{\mathrm{\eta }}_{\mathrm{t}}+{\mathrm{e}}^{\mathrm{k}}$$ (A.1)

where we differentiate between four possible health insurance categories - k∈{ESI (employer sponsored health insurance) only, ESI and Medicare, Medicare only, no coverage}. Λ₁ is a constant which depends on a person’s health insurance status k. Λ₂ and Λ₃ measure the impact of age and health respectively. e is a a random component which is assumed to be normally distributed with a mean of zero and a variance which depends on a person’s health insurance status.

To estimate the model of out-of-pocket health care expenditures, we used the 1996 and 1998 waves of the HRS. The sample we use (n= 4,619) consists of age-eligible men, who had not applied for Disability Insurance, and who did not have Medicaid between 1995 and 1998. Respondents fall into one of four insurance groups: those with employer sponsored health insurance (ESI) and Medicare coverage (n=261), those with ESI but no Medicare (n=2,419), those with Medicare but no ESI (n=527), and those with neither ESI nor Medicare (n=1,412).

The expenditure variable we use includes out-of-pocket payments for medical care provided during the two years between interviews plus any insurance premiums paid by the person. As a result, during estimation we divide the amounts from the expenditure equation by two. Payments included are all those for nursing home and hospital stays, doctor visits, outpatient surgeries, dental visits, prescriptions drugs, and in-home medical care. The expenditure model is estimated using a Tobit method with expenditure censored on the left at the median level of expenditures and on the right at the 99th percentile. The censoring is done, first, for the entire sample and, then, separately by insurance group. Residual variances are allowed to vary across insurance groups but are fixed within them. The estimates of the expenditure model are shown in Table A.2.

To see the effect of insurance group on the distribution of expenditures, in Table A.3 we report hypothetical distributions of expenditure using the Λ₁^k and variance estimates while holding age and health constant. Our predictions imply that a ESI reduces out of pocket expenditures in the upper tail of the distribution, but not at the median. This finding is similar to that of French and Jones (2004), and is consistent with findings from the Medical Expenditure Panel Survey (MEPS) (Olin & Machlin, 2004) that persons with more comprehensive insurance coverage receive substantially more care, and as a result may have significant coinsurance expenses.

A.3.2. The earnings equations

We assume that the log of a person’s real earnings in his career job at time t evolves according to the fixed-effect specification

$$ln(W_t^C)={\alpha }_1^i+{\alpha }_{2}t+{\psi }_t^C\Rightarrow W_t^C=exp({\alpha }_1^i+{\alpha }_{2}t)\text{exp}({\psi }_t^C)$$ (A.2)

where α₁ⁱ is a person-specific fixed-effect that can be estimated given multiple career-job earnings observations in the Health and Retirement Study and ψ^C_t is the stochastic component of career job earnings. The log of a person’s real earnings in his bridge job option is given by

$$ln(W_t^B)={\alpha }_3\text{EXITAGE}+{\alpha }_{4}ln(W_0^C)+{\psi }_t^B\Rightarrow W_t^B=exp[{\alpha }_3\text{EXITAGE}+{\alpha }_{4}ln(W_0^C)]\text{exp}[{\psi }_t^B]$$ (A.3)

where ψ^B_t is the stochastic component of bridge job earnings, and EXITAGE is the age at which a person left his career job. Our specification allows for the possibility that the earnings a person received in his career job at t=0 may contain information more generally about his earnings potential.

We do not make functional form assumptions about the distributions of ${\mathrm{\psi }}_{\mathrm{t}}^{\mathrm{C}}$ and ${\mathrm{\psi }}_{\mathrm{t}}^{\mathrm{B}}$ since our simulation approach described in Section 3 allows us to use the empirical distributions of these random variables.

Earnings in the career job are estimated using Internal Revenue Service (Form W-2) data linked to HRS records. The data cover reported wage and salary income and self-employment income from the years 1980–1991. We estimated the rate of growth in real earnings for the persons in our sample over the period to be 1.93% (s.e.=0.23%) per year. Future real earnings were thus assumed to grow at this rate from the base reported in 1992. Earnings in bridge jobs were estimated using self-reported data from survey year 1994. Sample individuals who reported working in a job different from the one reported in the 1992 survey were included in the estimation sample. Results are show in Table A.4.

A.3.3. Issues related to Social Security Benefits

Recall that the choice set in Section 2.1 allows individuals to leave the workforce and return at a later time. With respect to bridge job information, in reality the actual SS benefit formula implies that a person’s SS benefits would depend on not only the number of years that a person works in a bridge job before t and the wages in those years but also to some extent on the specific ages that the bridge job wages were received. This is the case because earnings that enter the Average Indexed Monthly Earnings (AIME) which determines SS benefit amounts are indexed by year-specific factors (that are different than standard rates of inflation) at ages less than 60 and are not indexed at ages greater than 60. We choose not to use this age information when computing SS benefits because including it in the model is not computationally feasible since it would require that the model contain a set of state variables that characterize the specific ages at which the person worked in bridge jobs (or alternatively state variables that keep track of the years the person was out of the workforce before time t). This assumption does not seem particularly problematic because the age information tends to have a relatively small effect on benefits. The SS benefits that we use in our model are those obtained with the person’s bridge years taking place immediately after a person’s career years.

The SS rules imply that, when recomputing the actuarial adjustment factor, one month is added to the Social Security starting age for each month before the normal retirement age that a person incurs a benefit reduction (including partial reductions) due to work. Thus, the actuarial adjustment factor typically changes when a person returns to work before the normal retirement age (after beginning to collect SS benefits) because a partial benefit reduction occurs in a month for anyone who earns more than the monthly equivalent of approximately $10,000 a year. However, working after the normal retirement age (after beginning to collect SS benefits) only leads to a change in the actuarial adjustment factor if the person incurs a full benefit reduction due to work in a particular month. Thus, the actuarial adjustment factor does not typically change for those working after the normal retirement age (after beginning to collect SS benefits) because, for example, a person with $20,000 in yearly SS benefits would only incur a full benefit reduction in a month if he earned more than the monthly equivalent of approximately $70,000 a year in his bridge job. This implies that the state variable SSEX in Section 2.3.2 keeps track of the number of years that the person is out of the workforce between the age of 62 and his normal retirement age, and, if the person is not out of the workforce in any of these years, SSEX keeps track of the first subsequent age that the person is out of the workforce.

Social security benefits are calculated using SSA data on covered earnings that have been attached to HRS records and self reported data from 1992 using program rules in effect as of 1992. Earnings histories are available for persons in covered employment beginning in 1950. Future earnings are assumed to evolve according to the estimates described above. Individuals who do not give HRS permission to access earnings histories are excluded from the analysis.

A.3.4 Issues related to Defined Benefit Pensions

In order to be eligible for a defined benefit payment from a particular job at time t≥1, a person must have left this job at this point. In this case, whether a payment is received and the amount of the payment depends on a person’s earnings history in that job as of time t and the details of the employer’s pension plan. Much heterogeneity exists in both eligibility ages and payment structures across plans.

For the discussion here it is worthwhile to group the set of jobs that a person holds during his working lifetime as jobs that the person left before t=0 (referred to hereafter as previously held jobs), the job the worker held at t=0 (defined above as a career job), and jobs that the worker begins after t=0 (defined above as bridge jobs). With respect to bridge jobs, for reasons of model tractability we assume that defined benefit pensions are not accumulated in these jobs.⁴ Descriptive work shows that this is a reasonable simplifying assumption. With respect to any previously held job, because the worker has left this job as of t=0, ϐ contains all details of the pension plan and information about the worker’s earnings history at the job that is necessary for the person at t=1 to compute the defined benefit payment he will receive at any t≥1. With respect to the career job, because the worker has not left this job at t=0, in order he must know not only the details of the employer’s pension plan and information about his earnings history at the job that are contained in ϐ but also the endogenously determined number of years that he will remain in his career job and the wages that he will earn in each of these years. Letting EXC(t) denote the years of experience that a person has accumulated in his career job as of time t, the number of years that the person stays in his career job before leaving is EXC(T) and the set of wages relevant to the DB calculation is given by $W_1^C,W_2^C,\dots ,W_{\mathit{EXC}(T)}^C$.⁵ The assumption that an individual considers expected future earnings when thinking about future DB benefits implies that the information in ϐ and EXC(T) is sufficient for the person at t=1 to compute the DB that he will receive in some year in the future.

Values for defined benefit pension income are computed by the HRS Pension Benefit Calculator. In 1992 the HRS asked respondents who were working for the name and address of their current employer as well as their previous employer. Using this information, the HRS contacted the employers to obtain summary plan descriptions. These descriptions, supplemented with data on pension plans maintained by the U. S. Department of Labor were used to produce formulas for the calculation of individual pension benefits based on the individual’s wage history for any given date of retirement. See Curtin et al. (1998) for details on the pension calculator program. For each sample member with a pension plan recorded in the plan database we generated annual pension benefit values for every future age of retirement from the current job beginning in the current year through the year in which the respondent reaches age 70.

A.3.5 Issues related to Defined Contribution Pensions

Defined contribution pensions are treated analogously to defined benefit pensions. To be consistent with our DB assumption regarding bridge jobs, we assume that DC benefits are not accumulated in jobs that begin after t=0. The defined contribution benefits at future time t associated with jobs that ended before t=0 are entirely characterized by information about the total amount of contributions that have been made to the plan and the plan’s age of eligibility that is contained in our baseline financial characteristics ϐ.⁶ With respect to the career job, because the worker has not left this job at t=0, in order for the person at t=0 to compute the DC that he will receive in some year in the future he must know not only information about previous contributions and the plan’s age of eligibility that is contained in ϐ but also the endogenously determined number years he will remain in his career job and how much he will contribute to his DC plan in each of these years. We abstract from the endogeneity of the contribution decision by assuming that each individual continues to contribute the same percentage of his income to the DC plan at his career job in the future as he has in the past. In this case, given the past rate of contribution which is information contained in ϐ, the information needed to compute future DC benefits is very similar to that of the DB case. In particular, in addition to knowing the information in ϐ, the person must know how many years EXC(T) that he will remain in his career job and the wages $W_1^C,W_2^C,\dots ,W_{\mathit{EXC}(T)}^C$ that he will earn in each of these years. The assumption that an individual considers expected future earnings when thinking about future DC benefits implies that the information in ϐ and EXC(T) is sufficient for the person at t=1 to compute the DC that he will receive in some year in the future.

Values for defined contribution pension income are derived as an actuarially fair annuity based on the accumulated value in the DC pension account at the time of retirement from the career job, according to the formula

$$W(a)=\sum _{x=a}^{119}\frac{l_i(x)}{l_i(a)}\frac{A(a)}{{(1+r)}^{x-a}}$$ (A.4)

where W(a) is the accumulated value of the pension fund at age a, l_i(x) is the adjusted (see above) life table probability of survival to age x, A(a) is the annuity payment for an individual who begins receiving it at age a, and r is the (real) interest rate, assumed here to be 3.29%. Pension wealth is self-reported at baseline, and it is assumed to accumulate with annual contributions from either or both employers and employees calculated as percentages of wage and salary income from the career job until retirement. Interest is accrued on these pension assets until they are converted to an annuity.

A.3.6. Non-pension wealth

Our general approach for dealing with wealth is described in Appendix A.2. The HRS respondents are asked to value a wide variety of assets and debts (see Smith, 1995, and Hill, 1993, for details). We calculate the total net value of non-pension sources of wealth available at baseline (1992).

A.4 Survival Probabilities

We calculate health-adjusted survival probabilities at each future age for the purposes of discounting future utility and converting stocks of wealth into annuity income estimates. The relationship between current health and survival is estimated using a discrete time hazard model of mortality and the longitudinal data from the HRS. In particular, for persons who are interviewed (taken as an objective measure of survival) in successive waves, we record the date of each interview, and include in the likelihood function an expression for the probability that the individual survives to that date. For those who die between waves, we include in the likelihood function the cumulative probability that the individual dies sometime in the two-year period following their last interview. The survival function is assumed to be exponential. Thus, the probability of survival from year t-1 to year t is next is

$$S(t)=exp[-exp(X_t^{\prime }\beta )],$$ (A.5)

where single year of age dummies and a health index (the predicted latent variable from an ordered probit estimate of self-assessed health status) are included in X. The probability of surviving from one survey (t-2) to the next (t) is then S(t-1)S(t) and the probability of dying during the interval is just 1 - S(t-1)S(t). Health as of t-2 and age as of t-1 and t are included in the model. The coefficient on the health index was 0.623 (0.071). Our estimate of the coefficient on health in the survival model implies that a one standard deviation increase in the latent health index (worse health) increases the mortality hazard by a factor of 1.86. Using this coefficient estimate and individual values of the latent health index, individual survival probabilities to future ages are increased or decreased relative to the national probabilities obtained from Social Security life tables (SSA, 1995).

A.5 Characterizing a person’s decisions

An individual in the behavioral sample is classified as having applied for disability benefits at time t if he reported applying for Social Security Disability or Supplemental Security Income sometime between the target dates t-1 and t, regardless of his work status as of time t. Among those not classified as disability applicants, those who report that they are doing no work for pay as of time t are classified as “non-workers.” Note that this classification can include respondents who had applied for disability benefits but did so more than a year before time t-1. At each survey, workers are asked if they work for the same employer, named by the interviewer, they reported in the previous wave. If not (or if they reported being self-employed), they are asked the dates at which the previous job ended and the current job began. This information is used to classify individuals as working in a career job or a bridge job. Finally, respondents who either denied working for the employer given in a previous interview or didn’t know if they worked for the same employer were excluded from the behavioral sample. Persons who were working but self-employed at wave 1 were also excluded from the behavioral sample.

Table A.1.

Sample Definition

HRS Age-Eligible Single Men	733
...with a social security earnings history available	527
...with valid pension plan data	496
...who were covered for Social Security retirement and disability	343
...with no missing data (Initial Conditions Sample )	328
...employed as of wave 1(Behavioral Sample )	196

Table A.2.

Estimates of parameters in health expenditure equation

Variable	Common Truncation		Separate Truncation
	Coefficient	Std Error	Coefficient	Std Error
Age-55	0.015	0.008	0.014	0.008
Health	0.335	0.032	0.339	0.032
ESI, Medicare	0.407	0.119	0.382	0.129
ESI, no Medicare	0.214	0.07	0.218	0.068
no ESI, Medicare	0.344	0.099	0.413	0.099
Constant	6.926	0.102	6.926	0.101
Insurance Group	Variance		Variance
ESI, Medicare	1.893		2.042
ESI, no Medicare	1.659		1.682
no ESI, Medicare	1.84		1.632
no ESI, no Medicare	2.392		2.421

Table A.3.

Hypothetical Distribution of Medical Expenditures by Insurance Status

	25th Percentile	Median	75th Percentile
Common Truncation:
ESI, Medicare	$284.86	$715.48	$1,789.05
ESI, no Medicare	$483.76	$602.89	$749.57
no ESI, Medicare	$271.26	$672.50	$1,659.87
no ESI, no Medicare	$168.88	$475.41	$1,331.61
Separate Truncation:
ESI, Medicare	$269.60	$685.78	$1,809.54
ESI, no Medicare	$480.64	$600.81	$746.96
no ESI, Medicare	$307.93	$709.37	$1,688.58
no ESI, no Medicare	$168.94	$466.89	$1,342.89

Table A.4.

Estimates of Parameters in Earnings Equations

	Coefficient	Standard Error
Career Job
Age	0.019	0.002
Constant	8.954	0.108
σu (dispersion of fixed effects)	0.994
σe (dispersion of residuals)	0.396
ρ(fraction of variance due to u)	0.863
n	4923
F test that all ui=0:	F(2142, 2779)=	9.81
Bridge Job
Age left career job	−0.061	0.021
1992 log wage	0.381	0.082
Constant	9.429	1.358
n	230
R2	0.107