EVALUATING RISK-PREDICTION MODELS USING DATA FROM ELECTRONIC HEALTH RECORDS

Abstract

The availability of data from electronic health records facilitates the development and evaluation of risk-prediction models, but estimation of prediction accuracy could be limited by outcome misclassification, which can arise if events are not captured. We evaluate the robustness of prediction accuracy summaries, obtained from receiver operating characteristic curves and risk-reclassification methods, if events are not captured (i.e., “false negatives”). We derive estimators for sensitivity and specificity if misclassification is independent of marker values. In simulation studies, we quantify the potential for bias in prediction accuracy summaries if misclassification depends on marker values. We compare the accuracy of alternative prognostic models for 30-day all-cause hospital readmission among 4548 patients discharged from the University of Pennsylvania Health System with a primary diagnosis of heart failure. Simulation studies indicate that if misclassification depends on marker values, then the estimated accuracy improvement is also biased, but the direction of the bias depends on the direction of the association between markers and the probability of misclassification. In our application, 29% of the 1143 readmitted patients were readmitted to a hospital elsewhere in Pennsylvania, which reduced prediction accuracy. Outcome misclassification can result in erroneous conclusions regarding the accuracy of risk-prediction models.

1. Introduction

Accurate risk prediction is one of the most important determinants of delivering high-quality care to patients, improving the public’s health and reducing health care costs. For example, unplanned hospital readmissions among patients with chronic diseases such as heart failure represent a substantial public health burden and cost [Bueno et al. (2010), Dunlay et al. (2011), Liao, Allen and Whellan (2008), O’Connell (2000)]. To reduce these costs, the Patient Protection and Affordable Care Act established public-reporting guidelines and instituted financial penalties for hospitals with high rates of short-term hospital readmission. Therefore, there is particular interest in developing and evaluating models that predict hospital readmission. Accurate risk-prediction models can be used to stratify patients at the point of care and to inform personalized treatment strategies [Chen et al. (2013)]. Prognostic models have been developed to predict the occurrence of a single readmission 30 days after hospital discharge [Amarasingham et al.(2010), Chin and Goldman (1997), Felker et al. (2004), Krumholz et al. (2000), Philbin and DiSalvo (1999), Yamokoski et al. (2007)], for which evaluation of prediction accuracy has been based on receiver operating characteristic (ROC) curves and risk-reclassification methods [Cook and Ridker (2009), Hanley and McNeil (1982), Pencina et al. (2008)].

As interest in individualized prediction has grown, so too has the availability of large-scale clinical information systems [Lauer (2012)]. A primary goal of the Health Information Technology for Economic and Clinical Health Act is to advance the use of health information technology by providing financial incentives to physicians and hospitals that adopt and demonstrate “meaningful use” of health information technology, particularly electronic health record (EHR) systems. Integrated EHR systems, for which technology capacity is rapidly progressing, provide unprecedented opportunities for medical discovery [Weiskopf and Weng (2013)]. Specifically, EHR systems capture detailed information regarding clinical events and potential risk factors for large and diverse patient populations, and therefore represent a unique resource for the development and evaluation of prediction models.

Analyses based on EHR data should consider the potential for outcome misclassification, which can arise if an EHR system fails to capture clinical events [Burnum (1989), van der Lei (1991)]. For example, misclassification can arise if only severe illnesses are brought to medical attention. In our motivating example, we focus on 30-day hospital readmission. If a patient is readmitted to a hospital outside the catchment area of the discharging hospital’s EHR system, then the patient is incorrectly classified. Previous literature has focused on the impact of outcome misclassification on estimation of exposure-outcome associations. It is well known that outcome misclassification results in biased association estimates [Barron (1977), Magder and Hughes (1997), Neuhaus (1999), Rosner, Spiegelman and Willett (1990)]. However, previous literature has not considered the impact of outcome misclassification on estimation of prediction accuracy. In particular, if outcomes are misclassified, then prediction accuracy summaries, as obtained from ROC curves and risk-reclassification methods, could be biased.

In this paper, we focus on the impact of outcome misclassification on estimation of prediction accuracy using ROC curves and risk-reclassification methods. Our goal is to evaluate the robustness of prediction accuracy summaries in situations in which events are not captured by an EHR system (i.e., “false negatives”). We derive estimators for sensitivity and specificity if events are incorrectly classified as nonevents and misclassification is independent of marker values. In simulation studies, we quantify the potential for bias in prediction accuracy summaries if misclassification depends on marker values. We present the results of a data application focused on 30-day all-cause hospital readmission, with readmissions to the University of Pennsylvania Health System (UPHS) captured by the UPHS EHR and readmissions to any hospital outside the UPHS network obtained from secondary data sources. Note that we do not consider “false positives” because we assume that if a hospital admission was captured by the EHR system, then that admission was a true event.

2. Methods for quantifying prediction accuracy

2.1. ROC curves

Statistical methods for prediction, or classification, are based on the fundamental concepts of sensitivity and specificity of a binary classifier for a binary disease outcome. For a marker defined on a continuous scale, an ROC curve is a standard method to summarize prediction accuracy. The ROC curve is a graphical plot of the sensitivity versus 1 − specificity across all possible dichotomizations m of a continuous marker M [Hanley and McNeil (1982)]:

$$\text{Sens}\left(m\right)=\text{P}[M>m\mid D=1],$$ (2.1)

$$\text{Spec}\left(m\right)=\text{P}[M\le m\mid D=0],$$ (2.2)

for which D = {1, 0} indicates a “case” or “control,” respectively. The marker’s prediction accuracy is quantified by the area under the ROC curve (AUC), which measures the probability that the marker will rank a randomly chosen diseased individual higher than a randomly chosen nondiseased individual. The difference in AUC, denoted by ΔAUC, can be used to contrast the prediction accuracy of different markers. Recent advances have extended ROC methods to time-dependent binary disease outcomes (or survival outcomes), which could be subject to censoring, as well as to survival outcomes that could be subject to informative censoring from competing risk events [Heagerty, Lumley and Pepe (2000), Heagerty and Zheng (2005), Saha and Heagerty (2010), Wolbers et al. (2009)].

2.2. Risk reclassification

Methods based on risk reclassification have been proposed to offer an alternative approach to contrast risk-prediction models. Risk-reclassification methods are often used to compare “nested” models: models with and without a marker or markers of interest [Cook and Ridker (2009), Pencina et al. (2008)]. Reclassification statistics quantify the degree to which an “alternative” model [i.e., a model with the marker(s) of interest] more accurately classifies “cases” as higher risk and “controls” as lower risk relative to a “null” model [i.e., a model without the marker(s) of interest]. Reclassification metrics include the integrated discrimination improvement (IDI). The IDI examines the difference in mean predicted risk among “cases” and “controls” between an “alternative” model 𝒜 and a “null” model 𝒩 [Pencina et al. (2008)]:

$$\begin{array}{cc}\hfill \text{IDI}& =\left[{\int }_0^1\text{Sens}(m;\mathcal{𝒜})dr(m;\mathcal{𝒜})-{\int }_0^1\text{Sens}(m;\mathcal{𝒩})dr(m;\mathcal{𝒩})\right]\hfill \\ \hfill & -\left[{\int }_0^1\{1-\text{Spec}(m;\mathcal{𝒜})\}dr(m;\mathcal{𝒜})-{\int }_0^1\{1-\text{Spec}(m;\mathcal{𝒩})\}dr(m;\mathcal{𝒩})\right]\hfill \\ \hfill & =\text{Difference}\text{in}\text{integral}\text{of}\text{sensitivity}\hfill \\ \hfill & -\text{Difference}\text{in}\text{integral}\text{of}(1-\text{specificity}),\hfill \end{array}$$ (2.3)

for which sensitivity and specificity are defined in equations (2.1) and (2.2), respectively; r(m; 𝒩) and r(m; 𝒜) denote the risk under the “null” and “alternative” models, respectively. The estimated IDI is obtained by averaging the estimated risk $\widehat{r}$ under the “null” and “alternative” models for “cases” and “controls” [Pencina et al. (2008)]:

$$\begin{array}{cc}\hfill \text{I}\widehat{\mathrm{D}}\text{I}& =({\overline{\widehat{r}}}_{\mathcal{𝒜},D=1}-{\overline{\widehat{r}}}_{\mathcal{𝒩},D=1})+({\overline{\widehat{r}}}_{\mathcal{𝒩},D=0}-{\overline{\widehat{r}}}_{\mathcal{𝒜},D=0})\hfill \\ \hfill & =\text{Relative}\text{improvement}\text{among}“\text{cases}”\hfill \\ \hfill & +\text{Relative}\text{improvement}\text{among}“\text{controls}.”\hfill \end{array}$$ (2.4)

Risk-reclassification methods are available for censored survival outcomes [Liu, Kapadia and Etzel (2010), Pencina, D’Agostino and Steyerberg (2011), Steyerberg and Pencina (2010), Viallon et al. (2009)], as well as for survival outcomes in the presence of competing risk events [Uno et al. (2013)].

2.3. Outcome misclassification

Prediction accuracy summaries obtained from ROC curves and risk-reclassification methods could be affected by outcome misclassification. A particular type of misclassification can arise in EHR data, in which “cases” are incorrectly classified as “controls” if an EHR system fails to capture events that occur outside the heath system’s catchment area. The misclassification of events as nonevents could be independent of or dependent on values of the marker. For example, in the context of hospital readmission, patients who have more flexible insurance coverage could be more likely to be readmitted to a hospital other than the one from which they were discharged. In this section, we derive expressions for sensitivity and specificity if events are incorrectly classified as nonevents.

Let D denote the true outcome with population prevalence π = P[D = 1], 0 ≤ π ≤ 1, and D^⋆ denote the outcome measured with error. Note that because we assume that only events can be misclassified as nonevents, $\{D^{\ast }=1\}\cap \{D=1\}=\{D^{\ast }=1\}$. The misclassification rate is denoted by p = P[D^⋆ = 0 | D = 1].

Given the observed data, the sensitivity of the marker M for the misclassified outcome D^⋆ is

$$\begin{array}{cc}\hfill {\text{Sens}}^{\ast }\left(m\right)& =\text{P}[M>m\mid D^{\ast }=1]\hfill \\ \hfill & =\text{P}[M>m\mid D^{\ast }=1,D=1]\hfill \\ \hfill & =\frac{\text{P}[M>m\mid D=1]\times \text{P}[D^{\ast }=1\mid M>m,D=1]}{\text{P}[D^{\ast }=1\mid D=1]}\hfill \\ \hfill & =\frac{\text{Sens}\left(m\right)\times \text{P}[D^{\ast }=1\mid M>m,D=1]}{1-p},\hfill \end{array}$$ (2.5)

and the specificity of the marker M for the misclassified outcome D^⋆ is Spec^⋆(m)

$$\begin{array}{cc}\hfill {\text{Spec}}^{\star }& \left(m\right)\hfill \\ \hfill & =\text{P}[M\le m\mid D^{\star }=0]\hfill \\ \hfill & =\text{P}[D=0\mid D^{\star }=0]\times \text{P}[M\le m\mid D=0,D^{\star }=0]\hfill \\ \hfill & +\text{P}[D=1\mid D^{\star }=0]\times \text{P}[M\le m\mid D=1,D^{\star }=0]\hfill \\ \hfill & =\text{P}[D=0\mid D^{\star }=0]\frac{\text{P}[M\le m\mid D=0]\times \text{P}[D^{\star }=0\mid M\le m,D=0]}{\text{P}[D^{\star }=0\mid D=0]}\hfill \\ \hfill & +\text{P}[D=0\mid D^{\star }=0]\frac{\text{P}[M\le m\mid D=0]\times \text{P}[D^{\star }=0\mid M\le m,D=1]}{\text{P}[D^{\star }=0\mid D=1]}\hfill \\ \hfill & =(1-q)\frac{\text{Spec}\left(\text{m}\right)\times \text{P}[D^{\star }=0\mid M\le m,D=0]}{\text{P}[D^{\star }=0\mid D=0]}\hfill \\ \hfill & +q\frac{\{1-\text{Sens}\left(m\right)\}\times P[D^{\star }=0\mid M\le m,D=1]}{\text{P}[D^{\star }=0\mid D=1]}\hfill \end{array}$$ (2.6)

for which

$$\begin{array}{cc}\hfill q& =\text{P}[D=1\mid D^{\star }=0]\hfill \\ \hfill & =\frac{\text{P}[D=1]\text{P}[D^{\star }=0\mid D=1]}{\text{P}[D=0]\text{P}[D^{\star }=0\mid D=0]+\text{P}[D^{\star }=0\mid D=1]}\hfill \\ \hfill & =\frac{\pi p}{(1-\pi )+\pi p},\hfill \end{array}$$

because P[D^⋆ = 0 | D = 0]= 1.

If misclassification is independent of M (e.g., P[D^⋆ = 1 | M > m, D = 1]= P[D^⋆ = 1 | D = 1]), then equations (2.5) and (2.6) reduce to

$${\text{Sens}}^{\star }\left(m\right)=\text{Sens}\left(m\right),$$ (2.7)

$${\text{Spec}}^{\star }\left(m\right)=\text{Spec}\left(m\right)+q\{1-\text{Spec}\left(m\right)-\text{Sens}\left(m\right)\},$$ (2.8)

respectively. First, the sensitivity based on the misclassified outcomes is equal to the true sensitivity. Second, note that a meaningful ROC curve is above the diagonal (i.e., 1 − specificity is always less than sensitivity). The specificity based on the misclassified outcomes is therefore an attenuated version of the true specificity. The degree of rightward horizontal shift in the corresponding ROC curve depends on the prevalence, the misclassification rate and the difference between the true sensitivity and 1 − specificity. Therefore, if the misclassification of events is independent of marker values, the ROC curve for M based on the misclassified outcomes is closer to the diagonal than the true ROC curve, which results in a reduced AUC.

For illustration, consider the use of a binary classifier C to classify individuals with respect to a binary outcome D with a prevalence of 0.5 for 200 individuals (Table 1). Based on the true outcomes, provided in Table 1(a), the sensitivity and specificity are both 0.8 (80/100). Suppose that not all of the events are captured. Thus, suppose that 20% of individuals who experience the event, denoted by D = 1 in Table 1(a), are incorrectly classified as a “control” in Table 1(b). Based on the misclassified outcomes, provided in Table 1(b), the sensitivity and specificity are 0.8 (64/80) and 0.7 (84/120), respectively. Therefore, if outcome misclassification occurs only among the “cases,” then specificity is reduced, but sensitivity is unaffected. Now suppose that C was obtained as a cut-point to a continuous marker, for which prediction accuracy could be quantified by the AUC. Reducing specificity while fixing sensitivity would result in a shifted-to-the-right ROC curve with a reduced AUC and an attenuated estimate of prediction accuracy.

Table 1.

Hypothetical data to illustrate the impact of outcome misclassification on sensitivity and specificity

	(a) True outcomes			(b) Misclassified outcomes
	D = 1	D = 0	Total	Case	Control	Total
C = 1	80	20	100	64	36	100
C = 0	20	80	100	16	84	100
Total	100	100	200	80	120	200

Given a known or assumed value for the prevalence π and the misclassification rate p, the sensitivity and specificity based on the misclassified outcomes can be used to obtain the bias-corrected sensitivity and specificity:

$$\text{Sens}\left(m\right)={\text{Sens}}^{\star }\left(m\right),$$ (2.9)

$$\text{Spec}\left(m\right)=\frac{{\text{Spec}}^{\star }\left(m\right)-q\{1-{\text{Sens}}^{\star }\left(m\right)\}}{1-q}.$$ 2.10

The bias-corrected sensitivity and specificity at each dichotomization m can then be used to obtain bias-corrected estimates of the ΔAUC and IDI, with the required integration performed using the trapezoidal rule. In practice, the true values for the prevalence and the misclassification rate are unknown. However, a priori knowledge could be used to guide sensitivity analyses. We illustrate such sensitivity analyses in our application.

If misclassification depends on the value of M, then the sensitivity and specificity depend on the magnitude and direction of the association between misclassification and the marker; see equations (2.5) and (2.6). In the following section, we use simulated data to determine how the association between a marker and the probability of misclassification affects prediction accuracy summaries.

3. Simulation study

We conducted simulation studies to evaluate the impact of outcome misclassification on estimation of prediction accuracy using the ΔAUC and IDI. We only misclassified events to emulate situations in which events are not observed. Simulations were performed under two scenarios: (1) misclassification was independent of marker values; and (2) misclassification was dependent on marker values. The focus of our analysis was the improvement in prediction accuracy associated with a new marker of interest.

3.1. Parameters

For both scenarios, we generated an “old” marker X and a “new” marker Z from a bivariate Normal distribution:

$$\left[\begin{array}{c}\hfill X\hfill \\ \hfill Z\hfill \end{array}\right]~N\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0.3\hfill \\ \hfill 0.3\hfill & \hfill 1\hfill \end{array}\right]\right).$$

We generated a binary variable D to indicate an event for a population of 10,000 individuals from a logistic regression model:

$$\text{P}[D=1\mid X=x,Z=z]=\text{expit}({\beta }_0+1.0x+1.4z).$$

in which the intercept was selected for a prevalence π = {0.2, 0.3, 0.5}, with a value of 0.3 consistent with hospital readmission rates.

To obtain the true ΔAUC and IDI associated with adding Z to a model with X alone, we fit a logistic regression model of D against X (i.e., the “null” model) and against X + Z (i.e., the “alternative” model). We specified the “null” model as

$$\text{P}[D=1\mid X=x]=\text{expit}({\beta }_0+{\beta }_{1}x)$$

and the “alternative” model as

$$\text{P}[D=1\mid X=x,Z=z]=\text{expit}({\beta }_0+{\beta }_{1}x+{\beta }_{2}z)$$

For prevalences of {0.2, 0.3, 0.5}, the true ΔAUC was {0.103, 0.110, 0.112} and the true IDI was {0.187, 0.204, 0.206}, respectively. By generating risk scores for the true outcomes, our simulations focused on the impact of outcome misclassification on estimation of prediction accuracy, and not on development of risk-prediction models. We then misclassified outcomes according to two scenarios.

3.2. Marker-independent misclassification

In scenario 1, misclassification was independent of the values of X and Z. We randomly misclassified events according to rates p = {0.05, 0.1, 0.2, 0.4}; no nonevents were misclassified. At each of 1000 iterations, we randomly selected n = 500 individuals and estimated the ΔAUC and IDI associated with adding Z to a model with X alone. We calculated the percent bias in the estimates obtained using the misclassified outcomes to those obtained using the true outcomes. Negative percent bias indicated bias toward the null.

Results

Table 2 provides the mean bias in the ΔAUC and IDI for prevalences of {0.2, 0.3, 0.5} and misclassification rates of {0.05, 0.1, 0.2, 0.4}; Supplementary Figure 1 displays additional summaries [Wang et al. (2016)]. As expected, marker-independent outcome misclassification resulted in attenuated prediction accuracy summaries, such that the estimated ΔAUC and IDI were biased toward the null. The magnitude of the estimated bias in the ΔAUC and IDI increased as the misclassification rate increased from 0.05 to 0.4. In addition, the magnitude of the estimated bias in the ΔAUC and IDI increased as the prevalence increased from 0.2 to 0.5. There were no substantial differences in the mean bias between the ΔAUC and IDI; however, ΔAUC estimates were more variable than IDI estimates (Supplementary Figure 1) [Wang et al. (2016)].

Table 2.

Mean bias (%) in the ΔAUC and IDI under marker-independent outcome misclassification

	Misclassification rate among events
	0.05		0.1		0.2		0.4
π a	ΔAUC	IDI	ΔAUC	IDI	ΔAUC	IDI	ΔAUC	IDI
0.2	−0.8	−1.4	−3.9	−2.6	−5.3	−5.4	−10.5	−9.3
0.3	−1.9	−1.8	−6.3	−4.6	−9.5	−8.3	−17.4	−17.1
0.5	−6.2	−5.6	−10.4	−8.8	−19.3	−16.4	−25.7	−26.8

^aπ denotes the prevalence.

3.3. Marker-dependent misclassification

In scenario 2, the prevalence was fixed at 0.3. We used X and Z individually and in combination to induce misclassification for events according to a logistic regression model. Let Y be an indicator of whether an outcome was misclassified. We specified the probability of misclassification as

$$\text{P}[Y=1\mid D,X=x,Z=z]=\{\begin{array}{cc}\text{expit}({\gamma }_0+{\gamma }_{1}x+{\gamma }_{2}z)\hfill & \text{if}D=1,\hfill \\ 0\hfill & \text{if}D=0,\hfill \end{array}\phantom{\}}$$ (3.1)

with values of γ₀ selected for misclassification rates of {0.05, 0.1, 0.2, 0.4}. We considered situations in which outcome misclassification depended on values of the “old” marker X, the “new” marker Z and a combination of the two. First, X and Z were positively associated with misclassification, with (γ₁, γ₂) = {(0.5, 0), (0, 0.5), (0.5, 0.5)}. In these situations, high-risk individuals (as quantified by X and Z) were more likely to be misclassified. Second, X and Z were negatively associated with misclassification, with (γ₁, γ₂) = {(−0.5, 0), (0, −0.5), (−0.5, −0.5)}. In these situations, low-risk individuals were more likely to be misclassified. Third, the direction of the association of X and Z with misclassification differed, with (γ₁, γ₂) = {(0.5, −0.5), (−0.5, 0.5)}. Note that (γ₁, γ₂) = (0, 0) corresponded to marker-independent misclassification. As above, we randomly selected n = 500 individuals and estimated the ΔAUC and IDI associated with adding Z to a model with X alone. We calculated the percent bias in the estimates obtained using the misclassified outcomes to those obtained using the true outcomes. Negative percent bias indicated bias toward the null.

Results

Table 3 provides the mean bias in the ΔAUC and IDI for values of (γ₁, γ₂) and misclassification rates of {0.05, 0.1, 0.2, 0.4}; Supplementary Figures 2–5 display additional summaries [Wang et al. (2016)]. As in scenario 1, the magnitude of the estimated bias increased as the misclassification rate increased. If only the “old” marker X was positively associated with misclassification, that is, (γ₁, γ₂) = (0.5, 0), then the estimated ΔAUC was biased toward the alternative, whereas the IDI was biased toward the null. In this situation, the AUC of the “null” model was underestimated, such that the ΔAUC between the “null” and “alternative” models was overestimated. If only the “old” marker X was negatively associated with misclassification, that is, (γ₁, γ₂) = (−0.5, 0), then both the estimated ΔAUC and IDI were biased toward the null, with greater bias for the ΔAUC.

Table 3.

Mean bias (%) in the ΔAUC and IDI under marker-dependent outcome misclassification (π = 0.3)

		Misclassification rate among events
		0.05		0.1		0.2		0.4
γ 1 a	γ 2 a	ΔAUC	IDI	ΔAUC	IDI	ΔAUC	IDI	ΔAUC	IDI
−0.5	−0.5	−1.1	0.4	−3.4	−0.1	−5.2	0.2	−6.8	4.2
−0.5	0	−5.6	−2.4	−11.7	−5.9	−21.0	−10.4	−37.6	−17.6
−0.5	0.5	−9.1	−4.9	−20.6	−12.5	−31.6	−19.7	−66.1	−39.0
0	−0.5	1.7	0.8	2.3	1.1	5.9	1.9	16.0	7.6
0	0	−1.9	−1.8	−6.3	−4.6	−9.5	−8.3	−17.4	−17.1
0	0.5	−4.7	−4.1	−12.5	−11.4	−19.7	−18.0	−39.5	−34.1
0.5	−0.5	5.1	1.7	6.5	1.6	15.9	3.9	30.3	8.3
0.5	0	1.3	−1.0	1.1	−3.5	5.2	−4.9	14.7	−5.6
0.5	0.5	−0.6	−3.0	−4.5	−9.4	−6.9	−14.7	−11.3	−27.2

^aγ₁ and γ₂ correspond to the associations between markers X and Z, respectively, and the log odds of misclassification among events.

If the “new” marker Z was positively associated with misclassification, that is, (γ₁, γ₂) = {(0, 0.5), (0.5, 0.5), (−0.5, 0.5)}, then the estimated ΔAUC and IDI were biased toward the null; the ΔAUC was substantially biased if γ₁ ≠ 0. In this situation, high-risk individuals (due to higher values of Z) were more likely to be misclassified, leading to a smaller disparity in the levels of Z between events and nonevents. Therefore, the estimated improvement in prediction accuracy associated with adding Z to X was attenuated. If the “new” marker Z was negatively associated with misclassification, that is, (γ₁, γ₂) = {(0, −0.5), (0.5, −0.5)}, then the estimated ΔAUC and IDI were biased toward the alternative. In this situation, low-risk individuals (due to lower values of Z) were more likely to be misclassified, leading to a larger disparity in the levels of Z between events and non-events. Therefore, the estimated improvement in prediction accuracy associated with adding Z to X was accentuated.

3.4. Summary

We focused on the impact of outcome misclassification on methods for evaluating improvements in prediction accuracy. If misclassification was independent of marker values, then the estimated accuracy improvement was biased toward the null. If misclassification depended on marker values, then the estimated accuracy improvement was also biased, but the direction of the bias depended on the direction of the associations between the “new” and/or “old” markers and the probability of misclassification. In particular, if the “new” marker was negatively associated with the probability of misclassification, then the estimated accuracy improvement was biased toward the alternative.

4. Application

4.1. Background

Current prognostic models for readmission among heart failure patients are based on demographic characteristics, comorbid conditions, physical assessments and laboratory values [Amarasingham et al. (2010), Chin and Goldman (1997), Felker et al. (2004), Krumholz et al. (2000), Philbin and DiSalvo (1999), Yamokoski et al. (2007)]. These models have been developed using data sourced from claims databases or collected during small randomized controlled trials. The goal of our illustrative analysis was to compare alternative prognostic models for all-cause readmission using data collected from the UPHS EHR system. Our analysis focused on the number of admissions in the previous year as the marker of interest [Baillie et al. (2013)]. Our analysis could be affected by outcome misclassification because readmissions to a hospital outside the UPHS network would not be captured by the UPHS EHR system. Readmissions to a hospital elsewhere in Pennsylvania were obtained from the Pennsylvania Health Care Containment Council (PHC4). As required by law, all hospitals in the Commonwealth of Pennsylvania must provide a discharge abstract for all patients to PHC4. In our analysis, the outcomes obtained from the UPHS EHR system represented the possibly misclassified outcomes, whereas the outcomes obtained from PHC4 represented the true outcomes.

4.2. Methods

We obtained data on 4548 Pennsylvania residents, 18 years of age or older, admitted with a primary diagnosis of heart failure to a UPHS hospital between 2005 and 2012. We limited our analysis to patients who were alive at discharge. We excluded patients who were discharged to hospice care. The outcome of interest was hospital readmission for any cause within 30 days of discharge. We formed a “null” model based on sociodemographic characteristics (age, sex, race, insurance provider) and comorbid conditions diagnosed at discharge (diabetes mellitus, chronic obstructive pulmonary disease, coronary artery disease, hypercholesterolemia and hypertension). In the “alternative” model, we additionally included the number of admissions in the previous year as a continuous variable. Logistic regression models were used to derive multi-marker risk scores for 30- day readmission under the “null” and “alternative” models [French et al. (2012)]. A leave-one-out jackknife approach was used to derive the scores [Efron and Tibshirani (1993)]. In this approach, the value of the score for each individual was calculated as a weighted combination of his/her marker values. The weights were determined by regression coefficients, which were estimated from a model fit for the data for all other individuals.

The ΔAUC and IDI were used to quantify the improvement in prediction accuracy associated with adding the number of admissions in the previous year to a model that included sociodemographic characteristics and comorbid conditions diagnosed at discharge. Confidence intervals and P values were obtained from 200 bootstrap resamples [Efron and Tibshirani (1993)]. We developed the models using the true outcomes obtained from PHC4, but evaluated the models using both the possibly misclassified outcomes obtained from the UPHS EHR system and the true outcomes obtained from PHC4.

We performed a sensitivity analysis based on the following: the sensitivities and specificities for the “null” and “alternative” models estimated from the possibly misclassified outcomes; and assumed values for the true 30-day readmission rate π = {0.2, 0.25, 0.3} and misclassification rate p = {0.2, 0.3, 0.4}. First, the estimated sensitivities and specificities, along with the assumed readmission and misclassification rates, were used to calculate bias-corrected sensitivities and specificities according to equations (2.9) and (2.10), respectively. Next, the bias-corrected ΔAUC and IDI were estimated based on the bias-corrected sensitivities and specificities, with integration performed using the trapezoidal rule. In this sensitivity analysis, we assumed that misclassification was independent of marker values.

4.3. Results

Table 4 provides summary statistics of patient characteristics at discharge, stratified by whether the patient was not readmitted within 30 days, readmitted to UPHS or readmitted to a hospital elsewhere in Pennsylvania. Of the 1143 readmitted patients, 333 were readmitted to a hospital elsewhere in Pennsylvania—a misclassification rate of 0.29. Compared to patients who were readmitted to UPHS, patients readmitted to a hospital elsewhere in Pennsylvania were younger, more likely to be insured through Medicaid and had a greater number of admissions in the previous year. These results indicated that outcome misclassification depended on both the “null” and “alternative” markers.

Table 4.

Characteristics of Pennsylvania residents discharged from UPHS with a primary diagnosis of heart failure, 2005–2012, stratified by whether the patient was not readmitted within 30 days, readmitted to UPHS or readmitted to a hospital elsewhere in Pennsylvania^a

	Not readmitted	Readmitted
	n = 3405	To UPHS n = 810	Elsewhere n = 333	P b
Sociodemographic characteristics
Age, years	69 (56, 80)	68 (55, 80)	65 (51, 76)	0.003
Male, n (%)	1529 (45)	417 (51)	190 (57)	0.09
Race, n (%)				0.73
Black	2299 (68)	530 (65)	226 (68)
White	1037 (30)	260 (32)	99 (30)
Other	69 (2)	20 (2)	8 (2)
Hispanic ethnicity, n (%)	15 (<1)	7 (1)	1 (<1)	0.45
Insurance, n (%)				0.001
Medicare	2281 (67)	543 (67)	195 (59)
Medicaid	634 (19)	163 (20)	97 (29)
Private	460 (14)	102 (13)	37 (11)
Uninsured	30 (1)	2 (<1)	4 (1)
Discharging hospital, n (%)				0.003
Pennsylvania Hospital	924 (27)	237 (29)	70 (21)
Presbyterian Medical Center	1228 (36)	287 (35)	113 (34)
University of Pennsylvania	1253 (37)	286 (35)	150 (45)
Concurrent diagonses, n (%)
Diabetes mellitus	1283 (38)	302 (37)	111 (33)	0.22
COPD	839 (25)	199 (25)	95 (29)	0.18
Coronary artery disease	1250 (37)	335 (41)	131 (39)	0.55
Hypercholesterolemia	809 (24)	167 (21)	64 (19)	0.63
Hypertension	2107 (62)	485 (60)	208 (62)	0.42
Acute stroke	8 (<1)	2 (<1)	2 (1)	0.58
Admissions in previous year, #	1 (0, 2)	2 (1, 4)	3 (1, 5)	<0.001

COPD, chronic obstructive pulmonary disease.

^aSummaries presented as median (25th, 75th percentile) unless otherwise indicated as n (%).

^bP values compare characteristics between patients readmitted to UPHS and patients readmitted elsewhere, obtained from Wilcoxon rank-sum tests for continuous variables or Fisher’s exact tests for categorical variables.

The “null” model was estimated based on sociodemographic characteristics and comorbid conditions diagnosed at discharge:

$$\begin{array}{cc}\hfill & -0.0080\times \left[\text{Age}\text{in}\text{years}\right]+0.29\times \left[\text{Male}\right]+0.069\times [\text{Race}=“\text{White}”]\hfill \\ \hfill & +0.17\times [\text{Race}=“\text{Other}”]-0.066\times [\text{Insurance}=“\text{Medicare}”]\hfill \\ \hfill & -0.29\times [\text{insurance}=“\text{Private}”]-0.83\times [\text{Insurance}=“\text{Uninsured}”]\hfill \\ \hfill & -0.045\times \left[\text{Diabetes}\text{mellitus}\right]+0.083\times \left[\text{COPD}\right]\hfill \\ \hfill & +0.21\times \left[\text{Coronary}\text{artery}\text{disease}\right]-0.21\times \left[\text{Hypercholesterolemia}\right]\hfill \\ \hfill & -0.017\times \left[\text{Hypertension}\right].\hfill \end{array}$$

The “alternative” model additionally included the number of admissions in the previous year as a continuous variable:

$$\begin{array}{cc}\hfill & -0.0015\times \left[\text{Age}\text{in}\text{years}\right]+0.28\times \left[\text{Male}\right]+0.010\times [\text{Rice}=“\text{White}”]\hfill \\ \hfill & +0.079\times [\text{Race}=“\text{Other}”]-0.087\times [\text{Insurance}=“\text{Medicare}”]\hfill \\ \hfill & -0.14\times [\text{Insurance}=“\text{Private}”]-0.044\times [\text{Insurance}=“\text{Uninsured}”]\hfill \\ \hfill & -0.068\times \left[\text{Diabetes}\text{mellitus}\right]+0.053\times \left[\text{COPD}\right]\hfill \\ \hfill & +0.11\times \left[\text{Coronary}\text{artery}\text{disease}\right]-0.14\times \left[\text{Hypercholesterolemia}\right]\hfill \\ \hfill & -0.028\times \left[\text{Hypertension}\right]+0.019\times \left[\text{Admissions}\text{in}\text{previous}\text{year}\right]\hfill \end{array}$$

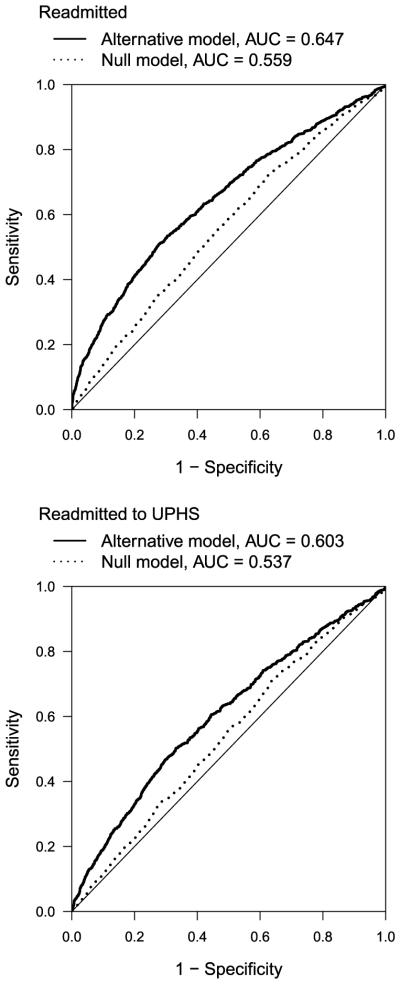
Figure 1 presents ROC curves for 30-day readmission for the “null” and “alternative” models using the true (“readmitted”) and possibly misclassified (“readmitted to UPHS”) outcomes. Outcome misclassification resulted in an underestimate of ΔAUC and IDI (Table 5). Misclassification reduced the AUC of the “alternative” model from 0.647 to 0.603 (a difference of 0.044) and that of the “null” model from 0.559 to 0.537 (a difference of 0.022). Therefore, the attenuation of the estimated ΔAUC was mainly driven by attenuation in the AUC for the “alternative” model. Recall that the estimated IDI is obtained by averaging the estimated risk under the “null” and “alternative” models for “cases” and “controls”:

$$\text{I}\widehat{\mathrm{D}}\text{I}=({\overline{\widehat{r}}}_{\mathcal{𝒜},D=1}-{\overline{\widehat{r}}}_{\mathcal{𝒩},D=1})+({\overline{\widehat{r}}}_{\mathcal{𝒩},D=0}-{\overline{\widehat{r}}}_{\mathcal{𝒜},D=0})$$

The estimated IDIs in Table 5 were calculated as follows:

$$\begin{array}{cc}\hfill \text{Readmitted:}\text{I}\widehat{\mathrm{D}}\text{I}& =(0.303-0.258)+(0.249-0.234)=0.059,\hfill \\ \hfill \text{Readmitted}\text{to}\text{UPHS:}\text{I}\widehat{\mathrm{D}}\text{I}& =(0.288-0.256)+(0.250-0.243)=0.039\hfill \end{array}$$

The attenuation in the estimated IDI was mainly driven by a decrease in the average estimated risk under the “alternative” model among “cases” (0.303 versus 0.288) and an increase in the average estimated risk under the “alternative” model among “controls” (0.234 versus 0.243).

Fig. 1.

ROC curves for 30-day all-cause readmission among Pennsylvania residents discharged from UPHS with a primary diagnosis of heart failure, 2005–2012, using the true (“readmitted”) and possibly misclassified (“readmitted to UPHS”) outcomes. The “null” model was based on sociodemographic characteristics and comorbid conditions diagnosed at discharge; the “alternative” model additionally included the number of admissions in the previous year.

Table 5.

Estimated ΔAUC and IDI for 30-day all-cause readmission among Pennsylvania residents discharged from UPHS with a primary diagnosis of heart failure, 2005–2012

	Readmitted			Readmitted to UPHS
	Estimatea	95% CI	P	Estimatea	95% CI	P
ΔAUC	0.088	0.065, 0.111	<0.001	0.066	0.042, 0.091	<0.001
IDI	0.059	0.044, 0.074	<0.001	0.039	0.025, 0.053	<0.001

CI, confidence interval.

^aEstimates quantify the improvement in prediction accuracy associated with adding the number of admissions in the previous year to a model that included sociodemographic characteristics and comorbid conditions diagnosed at discharge.

Table 6 provides the bias-corrected ΔAUC and IDI under several assumed values for the rate of 30-day hospital readmission and misclassification rate among events. Note that based on the true outcomes, the 30-day readmission rate was 0.25 and the misclassification rate was 0.29. Although the bias-corrected ΔAUC and IDI were closer to their true values (0.088 and 0.059, respectively), the bias was not completely ameliorated. The residual bias is likely due to the fact that misclassification depended on both the “null” and “alternative” markers (Table 4). In the following section, we discuss methods that can be used to correct for marker-dependent outcome misclassification.

Table 6.

Bias-corrected ΔAUC and IDI under assumed values for the rate of 30-day hospital readmission and misclassification rate among events

	Assumed misclassification rate among events
	0.2		0.3		0.4
π a	ΔAUC	IDI	ΔAUC	IDI	ΔAUC	IDI
0.2	0.070	0.041	0.071	0.042	0.073	0.043
0.25	0.071	0.042	0.073	0.043	0.075	0.044
0.3	0.072	0.043	0.075	0.044	0.078	0.046

^aπ denotes the assumed 30-day hospital readmission rate.

4.4. Summary

Our analysis focused on whether the number of admissions in the previous year improved prognostic performance for 30-day readmission compared to sociodemographic characteristics and comorbid conditions diagnosed at discharge. Using data obtained from the UPHS EHR system, ROC curves and risk-reclassification methods indicated a small but statistically significant improvement in prediction accuracy. However, the improvement in accuracy was greater if the true outcomes were used. Outcome misclassification resulted in a 25% and 34% attenuation in the ΔAUC and IDI, respectively.

5. Discussion

In this paper we focused on the impact of outcome misclassification on estimation of prediction accuracy using ROC curves and risk-reclassification methods. We focused on misclassification in which events were incorrectly classified as nonevents (i.e., “false negatives”). We derived estimators to correct for bias in sensitivity and specificity if misclassification was independent of marker values. In simulation studies, we quantified the bias in prediction accuracy summaries if misclassification depended on marker values. In this case, we found that the direction of the bias was determined by the direction of the association of the “new” and/or “old” markers with the probability of misclassification. In our application, we showed that misclassification can affect estimation of prediction accuracy in practice. Our research adds to the growing body of literature that compares and contrasts the statistical properties of ROC curves and risk-reclassification methods [Cook and Paynter (2011), Demler, Pencina and D’Agostino (2012), French et al. (2012), Hilden and Gerds (2014), Kerr et al. (2011, 2014), Pepe (2011)].

Statistical methods are available to correct for misclassification of binary outcomes. In particular, validation data provide the gold-standard measurement of outcomes and risk factors of interest, and can be used to assess the frequency and structure of the classification error [Edwards et al. (2013), Lyles et al. (2011)]. Validation data can also be used to inform statistical models that provide unbiased regression coefficients from the error-prone data [Edwards et al. (2013), Lyles et al. (2011), Magder and Hughes (1997), Neuhaus (1999), Rosner, Spiegelman and Willett (1990)]. Likelihood-based methods are available to obtain unbiased estimates of the odds ratio in the presence of outcome misclassification and marker-dependent misclassification [Lyles et al. (2011), Magder and Hughes (1997), Neuhaus (1999), Rosner, Spiegelman and Willett (1990)]. Imputation methods are available that use validation data to reduce bias caused by misclassification [Edwards et al. (2013)]. Semi-parametric and nonparametric methods have also been considered [Pepe (1992), Reilly and Pepe (1995)]. However, errors in outcomes and risk factors could be correlated due to their shared dependence on patient characteristics. Research has focused on correcting for correlated errors in covariates and continuous outcomes [Shepherd, Shaw and Dodd (2012), Shepherd and Yu (2011)]. Further research is needed to correct for correlated errors in covariates and binary outcomes.

We focused on the potential for outcomes to be misclassified in EHR data. In practice, eligibility criteria and potential risk factors can also be measured with error. For example, eligibility is typically based on codes that might not identify all events and do not account for the severity of events that are identified. In our application, the marker of interest was the number of admissions in the previous year, which could also be subject to measurement error. We used PHC4 data to count number of previous admissions, but UPHS data may undercount number of previous admissions for patients who were admitted to hospitals outside UPHS. Future research could focus on the impact of exposure misclassification on estimation of prediction accuracy. The use of EHR data in clinical research is rapidly increasing and will likely present additional analysis challenges in the future.