Abstract
Ferrofluids have demonstrated great potential for a variety of manipulations of diamagnetic (or non-magnetic) micro-particles/cells in microfluidics, including sorting, focusing, and enriching. By utilizing size dependent magnetophoresis velocity, most of the existing techniques employ single phase ferrofluids to push the particles towards the channel walls. In this work, we demonstrate a novel strategy for focusing and separating diamagnetic micro-particles by using the laminar fluid interface of two co-flowing fluids—a ferrofluid and a non-magnetic fluid. Next to the microfluidic channel, microscale magnets are fabricated to generate strong localized magnetic field gradients and forces. Due to the magnetic force, diamagnetic particles suspended in the ferrofluid phase migrate across the ferrofluid stream at the size-dependent velocities. Because of the low Reynolds number and high Péclet number associated with the flow, the fluid interface is sharp and stable. When the micro-particles migrate to the interface, they are accumulated near the interface, resulting in effective focusing and separation of particles. We investigated several factors that affect the focusing and separation efficiency, including susceptibility of the ferrofluid, distance between the microfluidic channel and microscale magnet, and width of the microfluidic channel. This concept can be extended to multiple fluid interfaces. For example, a complete separation of micro-particles was demonstrated by using a three-stream multiphase flow configuration.
I. INTRODUCTION
Microfluidics enables a diverse range of manipulations (e.g., focusing, separating, trapping, and enriching) of micrometer-sized objects, and has played an increasingly important role for applications that involve single cell biology1 and the detection and diagnosis of diseases.2 In microfluidic devices, methods that are commonly used to manipulate cells or particles include the utilization of hydrodynamic effects3–6 and externally applied field gradients that induce forces on cells/particles, such as electrical fields,7–9 optical fields,10–14 magnetic fields,15–18 and acoustic fields.19–21 Techniques that are based on hydrodynamic effects are known as passive methods, and often rely on the appropriate channel designs to direct the particles of different sizes into separate flow streamlines. The dimensions of the channels have implications for the applicable separation sizes. Among the various active methods that use external force fields, the magnetic field has advantages for applications concerning living matters, such as biological cells, because magnetic fields do not generate heat. For example, the method of dielectrophoresis-field-flow fractionation (DEP-FFF) transports particles and cells with hydrodynamic liquid flow in microchannels and fractionates particles and cells using the dielectrophoresis force generated perpendicular to the fluid flow direction.22 However, this method can lead to potential damage to living due to the temperature rise induced by electric fields. In contrast to electrical and optical fields, magnetic field has the advantage of producing low or negligible heating.23
Trapping and separation techniques that are based on the magnetic forces have become popular during the last few years.24,25 The two general methods for utilizing magnetic fields are: positive and negative magnetophoresis. In a positive magnetophoresis, magnetic particles migrate towards the regions of higher magnetic field gradient. Commonly, magnetic particles are deflected from the direction of laminar flow by a perpendicular magnetic field. The deflection velocity depends on the magnetic susceptibility, particle size, and flow rate. Thus, magnetic particles of different sizes can be separated from each other and from non-magnetic materials.26 This mechanism has been used to trap cells by labeling the target bioparticles with functionalized magnetic beads.24,27,28 However, it is both time consuming and expensive to label and remove the magnetic particles from the target cells prior to further analysis. In a negative magnetophoresis, diamagnetic particles that are suspended in magnetic solutions are repelled away from the regions of higher magnetic field gradients (e.g., magnet sources) due to magnetic buoyancy force.29 Further, most synthetic and biological particles are diamagnetic; therefore, label-free manipulation can be attained with negative magnetophoresis for practical applications.
Ferrofluids are stable colloidal suspensions of surfactant-coated magnetic nanoparticles in aqueous or organic solutions.30 Due to their large magnetic susceptibility, ferrofluids have been extensively used as magnetic solutions in negative magnetophoresis-based cell separation techniques.31 For example, to address the perceived limitation of magnetic labeling of a target cell population, Kose et al.32 developed a novel microfluidic platform that uses bio-compatible ferrofluids for the controlled manipulation and rapid separation of both microparticles and living cells. This low-cost platform exploits the differences in particle sizes and shapes to achieve rapid and efficient separation. As mentioned before, most cells are inherently diamagnetic and thus an externally applied magnetic field gradient was used to attract the magnetic nanoparticles, which caused the nonmagnetic microparticles or cells to be effectively pushed away.33 Recently, the principle of negative magnetophoresis has been applied to capture nonmagnetic microbeads between magnetic film islands in a microchannel filled with ferrofluid.34
Focusing particles into a tight stream is an essential step in many applications, such as microfluidic cell cytometry and particle sorting.35 Magnetic focusing in ferrofluid is non-invasive and well suited for handling bio-particles.16,25,36 Liang et al.37,38 proposed a method for focusing diamagnetic particles carried by a ferrofluid flow through a T-shaped microchannel using a single permanent magnet (PM). Wilbanks et al.39 and Zeng et al.40,41 presented methods for concentrating diamagnetic particles in the ferrofluid flows by means of two repulsive or attractive magnets that were positioned symmetrically or asymmetrically on either side of a particle flowing channel. In these studies, millimeter or centimeter-sized permanent magnets (PMs) helped to realize focusing. However, because these magnets were much larger than the microfluidic channel, it was difficult to align and place them precisely. A slight misalignment of the permanent magnets could lead to a relatively larger change within the fluidic channel. Further, strong and bulky magnets had to be used to provide large magnetic fields that could generate large magnetic forces. This requirement greatly increased the difficulty in integrating magnetic particle manipulation in portable and standalone lab-on-a-chip platforms. Moreover, most of the previous studies have focused the particles or cells to the wall of the microchannel.23,42 Due to the increasing friction near the wall, the velocity of the particles significantly reduced and thus hindered the throughput.
To overcome the limitations using existing techniques, we propose a simple and novel strategy to achieve focusing and separating of diamagnetic microparticles with the laminar fluid interfaces and micro-fabricated magnets. In this technique, a ferrofluid and a non-magnetic fluid co-flowing in a microfluidic channel form a stable fluid interface. Under the magnetic fields from the neighboring microscale magnet, diamagnetic particles that are suspended in the ferrofluid phase migrate towards and accumulate at the fluid interface, leading to particle focusing. This mechanism can be further exploited to separate particles of different sizes.
In our technique, both the fluid interface and microscale magnets can be precisely controlled for micrometer accuracy, and thereby achieve precise focusing. Additionally, microscale magnets provide localized high magnetic field gradients, resulting in larger magnetic forces for high-throughput operations. Moreover, focusing particles to the interface can keep particles far away from the channel wall and thus avoid the friction of the wall. The location of the interface can be additionally controlled by adjusting the flow ratios to achieve both precise focusing and separation of diamagnetic particles. In this work, we experimentally investigated the effects of several factors, including ferrofluid concentration, gap distance between the microfluidic channel and the microscale magnet, and the microfluidic channel width on the focusing performance of particles.
II. CONCEPT AND EXPERIMENT
A. Overview of the device and working principle
Fig. 1(a) presents a brief fabrication process of our microdevice. A schematic of the microdevice consisting of a microfluidic channel and a microstructure channel is displayed in step 1. The microstructure channel was fabricated parallel to the microfluidic channel with a distance of 60–100 μm. A mixture of neodymium (NdFeB) powders and Polydimethylsiloxane (PDMS) was injected into the microstructure channel in step 2. Immediately after filling the NdFeB-PDMS mixture, the microdevice was heated to cure the mixture, as in step 3. Then the microstructure channel, with the cured NdFeB-PDMS mixture, was magnetized by an impulse magnetizer to form a permanent “microscale magnet,” which can generate localized high magnetic field gradients.
FIG. 1.
Fabrication process of microdevices and basic principle of particle movement. (a) The fabrication steps of the microdevice; (b) the enlarged drawing of the microfluidic channel and the basic principle of particle movement in a ferrofluid. The microfluidic channel has a width of wc = 100 μm and a depth of dc = 35 μm; the gap distance between the microscale magnet and the microfluidic channel is wg = 60 μm; the size of the microscale magnet is w = g = h1 = h2 = 500 μm.
Fig. 1(b) illustrates the working principle of the proposed technique. Water and water-based ferrofluid, containing 7 μm and 2 μm (in diameter) diamagnetic particles, were injected from inlets 1 and 2, respectively. The flow rates of inlets 1 and 2 were kept the same in all of the following experiments. Due to the non-zero magnetic susceptibility difference between the particles and the ferrofluid, the particles experience a magnetic repulsion force, Fm, and migrate towards the fluid interface. Upon arriving at the interface, the particles will remain at the interface because, in the other phase, the water is also diamagnetic, and thus negligible magnetic force will act on the particles to induce further migration. In brief, our approach is to use the diluted ferrofluid to work as a magnetic environment that surrounds the diamagnetic microparticles within the microfluidic channel, and thus the diamagnetic microparticles inside ferrofluid experience a magnetic force under the non-uniform magnetic field induced by our microscale magnet.29 Another important force acting on the particles is the hydrodynamic drag force, Fd, due to the flow of fluids. These two forces, Fm and Fd, thereby determine the movement of the diamagnetic particle, as in Fig. 1(b). Due to the size difference, the smaller particles (2 μm) move more slowly in the y direction than the larger (7 μm) particles. At the end of the fluid channel, the larger particles are focused at the interface, while the smaller particles remain widespread throughout the ferrofluid stream.
B. Fabrication of microfluidic device
A microfluidic device was fabricated in PDMS using a soft lithography technique.43 Master molds were manufactured in a dry film photoresist (MM540, 35 μm thick, DuPont) by lithographic patterning.44 In this method, a layer of dry film resist was first laminated onto a copper plate using a thermal laminator. After ultra-violet (UV) exposure through a transparency photo mask (10 000 dpi, CAD/Art Services, Inc.), the exposed dry film was developed in a sodium carbonate solution, rinsed in water, and dried by compressed air to obtain a master mold. The PDMS base and initiator were thoroughly mixed, degassed, and then poured onto the master molds. After overnight curing at 60 °C, the PDMS replica was peeled from the master, cut and punched, and then bonded with a flat glass slide after corona surface treatment. In fact, both plasma bonding and corona surface treatment have been reported as popular strategies for PDMS.45 First, Duffy et al. introduced surface oxidation to increase the bond strength by activating layers of cross-linked PDMS in oxygen plasma.46 Surface oxidation is believed to expose silanol groups (OH) at the surface of the PDMS layers that when brought together form covalent siloxane bonds (Si–O–Si). This approach makes the channels more hydrophilic, allowing for easier fluid filling for a period of time after the oxygen plasma treatment. Second, corona discharge, first reported by Beebe's group47 for bonding PDMS, is a surface activation technique that can be implemented on fully cured PDMS to bond several layers together. A hand-held corona device generates a high voltage potential across the electrodes at the tip of the unit, ionizing the air to create the localized corona discharge. In summary, both plasma bonding and corona surface treatment are able to provide the function of bonding PDMS to PDMS or other types of material like glass with similar bond strengths, but oxygen plasma adds a significant cost to the fabrication process while limiting the flexibility with the substrates due to cleanliness requirements and the size restriction of the chamber.47 The ability to use the corona discharge unit in a non-cleanroom setting dramatically reduces the cost and complexity, so the corona discharge was chosen in our study for PDMS bonding. Using this method, microfluidic and microstructure magnet channels were fabricated with the rectangular cross sections.
Next, neodymium (NdFeB) micro-powders (MQFP-B-20076-089, Magnequench International, Inc.) were thoroughly mixed with a pre-mixed liquid PDMS. The mixture of neodymium powders and PDMS was degassed, and subsequently injected into the microscale magnet channel with a syringe pump. Immediately after being filled with the NdFeB-PDMS mixture, the microdevice was heated on a hotplate at 150 °C for 10 min to cure the mixture. The fast curing process was critical to avoid agglomeration and sedimentation of the neodymium powders. The fast curing ensured a homogeneous distribution of the neodymium powders into a composite matrix. The microfluidic device was heated in an oven at 60 °C for another 12 h to ensure complete curing and strong bonding. After the mixture was cured, the resulting solid NdFeB-PDMS microstructure was permanently magnetized by an impulse magnetizer (IM 10, ASC Scientific) and became a microscale permanent magnet, as shown in Fig. 1(a).
C. Materials
EMG 408 ferrofluid was obtained from Ferrotec (USA) Corporation with a reported initial magnetic nanoparticle concentration of 1.2% (v/v) and saturation magnetization (Ms) of 6.6 mT. The initial viscosity and magnetic susceptibility of EMG 408 ferrofluid were μ = 2 mPa s and χf = 0.5, respectively. In our experiments, the original ferrofluid was diluted to 0.6% (v/v) and 0.36% (v/v) with distilled water. Diamagnetic particles of 2 μm and 7 μm in diameter and a density of 1.05 g/ml were used as model particles. The original solutions of 2 μm and 7 μm particles (2.5% w/w) were diluted with 0.6% (v/v) or 0.36% (v/v) ferrofluid to 5000 and 200 times, respectively. The final particle concentrations were 1.14 × 106 ml−1 and 6.62 × 105 particles ml−1. Surfactant Tween 20 was added to both solutions at a concentration of 0.5% (w/w) to prevent particle adhesion to the channel walls and particle agglomeration. Tween 20 has been proved as a stable, biocompatible nonionic surfactant and widely used to prevent particles from aggregation in microfluidic systems.23,41,48,49 The ferrofluid solution with particles was injected into inlet 2 as the particle solution, and distilled water was injected into inlet 1 as the buffer solution.
D. Particle visualization and analysis
The microfluidic device was placed on an inverted microscope stage (IX73, Olympus) and illuminated by a fiber optic light for transmission of bright-field imaging. The flow rates to the inlets were controlled individually by two syringe pumps (NE-300, New Era and KDS 200, KDS Scientific). To maintain good stability of the flow, small syringes (1 ml) were used to reduce the effect of the motor's step motion. To record particle trajectories, a high-speed camera (Phantom Miro M310, Vision Research) was used to capture videos. In the experimental data analysis, ImageJ50 was used to extract the particle trajectories and positions.
III. THEORETIC BACKGROUND AND SIMULATION
A. Force and velocity analysis of microparticles
1. Magnetic force
Diamagnetic particles experience a negative magnetophoretic force, Fm, in a ferrofluid when subjected to a non-uniform magnetic field,23,40,51
| (1) |
where μ0 is the magnetic permeability of free space; Vp is the volume of the particle; the magnetization of ferrofluid Mf is collinear with a static magnetic field H produced by a microscale magnet. In general, the magnitude of Mf, Mf is determined using the Langevin function, L(α),38
| (2) |
| (3) |
where Md = 4.379 × 105 A/m is the saturation moment of the magnetic nanoparticles, as calculated from the manufacturer-provided saturation magnetization of ferrofluid; H is the magnetic field magnitude; d is the average diameter of the magnetic nanoparticles; kB is the Boltzmann constant; and T is the temperature of the ferrofluid.
Particles are repelled away from the microscale magnet owing to the negative sign in Eq. (1), suggesting that Fm is directed against the magnetic field gradient.37 In our study, the microscale magnets had larger magnetic gradients and small magnetic field strength (H ≤ 90 000 A/m); thus, the susceptibility of the ferrofluid was approximately constant. Based on the following basic relationships of and , Eq. (1) can be simplified as follows:52
| (4) |
where B is the magnetic flux density; represents the difference in the magnetic susceptibilities, between the particle (χp) and the surrounding fluid (χf); D is the diameter of the diamagnetic particle. In our study, the magnetic susceptibilities of ferrofluid χf were 0.25 and 0.15 for the ferrofluid with concentrations of 0.6% (v/v) and 0.36% (v/v), respectively. The magnetic susceptibility of polystyrene particles χp was much smaller,38 on the order of 10−6; therefore, the diamagnetic particles were repelled away from the regions of higher magnetic field strength because of Δχ < 0, which agreed with the negative sign in Eq. (1).
2. Stokes drag force
In low Reynolds number microfluidic systems, the hydrodynamic drag force, Fd, acting on the particles in microchannels, rises due to the relative motion between the particles and the surrounding fluid, and can be defined by Stokes' law,23
| (5) |
where η is the fluid viscosity; vp is the particle velocity; vf is the velocity of suspending fluid; fD is the hydrodynamic drag force coefficient. The coefficient, fD, accounts for the increased fluid resistance when the particle moves near the microfluidic channel surface.36,53 fD has the form of
| (6) |
where is the distance between the bottom of the particle and the channel surface; r = D/2 is the radius of the particle.
3. Magnetophoresis velocity
The velocity caused by magnetic force—magnetophoresis velocity—is a critical parameter influencing the time used by particles to reach the interface and focusing performance. In low Reynolds number microfluidic flows, the movement of particles can be regarded as a quasi-steady motion for each instantaneous time period because of the small mass of microparticles. Therefore, the balance between the two forces leads to
| (7) |
Based on Eqs. (5) and (7), the magnetophoresis velocity can be derived as24,26
| (8) |
B. Time scales and focusing criteria
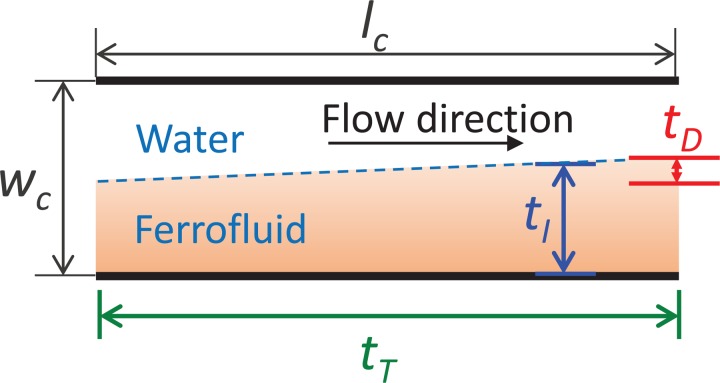
To better study the focusing of particles, the relationship between three time scales, namely, interface time, travel time, and diffusion time, are introduced in this section. The general concept of these three time scales is illustrated in Fig. 2.
FIG. 2.
Illustration of the time scales related to particle movement in a two-phase flow system: travel time, tT; interface time, tI; diffusion time, tD. wc and lc, are the width and length of the microfluidic channel, respectively.
First, interface time is defined as the time used by the particles to reach the interface between the water and ferrofluid. Interface time tI can thus be expressed as
| (9) |
where wc is the width of the microfluidic channel, and is equal to 100 μm or 150 μm in this study; is the average magnetophoresis velocity in the y direction. Based on Eqs. (4) and (8), tI can be specifically explained by the following equation:
| (10) |
where is the absolute value of the magnetic field in the y direction. This will be further discussed in Eq. (15).
Second, travel time is the time spent by the particles on moving from the inlet of the microfluidic channel to the outlet and can be written as
| (11) |
where lc = 20 000 μm is the length of the microfluidic channel; is the average fluid velocity in the x direction, where Qt is the total flow rate, and dc is the depth of the microfluidic channel and is equal to 35 μm, as shown in Fig. 1(a).
Third, diffusion will take place owing to different kinds of solutions that have different concentrations of magnetic nanoparticles. Diffusion time is defined as the time scale for nanoparticles to diffuse for distance dx,
| (12) |
where Ddiff is the diffusion coefficient and has a value of , as determined by the Einstein relation.54 To maintain a sharp interface, the diffusion distance, width dx, must be much smaller than wc/2. This criterion is equivalent to a very large Péclet number, i.e., .
The above analysis shows that the focusing of particles in a microfluidic channel can be achieved when the following two criteria are met: (a) tI ≤ tT and (b) Pe ≫ 1. In our study, Pe = 3.29 × 104 was obtained for the smallest flow rate, 3 μl/min; thus, the second criterion, to keep a sharp interface, was always met. Accordingly, the relationship between tI and tT is mainly discussed in the following analysis to explain and help the reader understand the focusing performance.
C. Numerical simulation of magnetic field
The magnetic field in the microfluidic channel was simulated with a finite element software package, Finite Element Method Magnetics (FEMM),55 to develop a deeper understanding of the magnetic forces. The geometry of the same size was constructed with experiments. The magnetic property of the ferrofluid was determined according to its concentration.38 The magnetic coercivity of the microscale magnet was determined from our measurement. Because of the small size of the microscale magnets, it is difficult to measure their magnetic field strength directly. Instead, we made a large NdFeB-PDMS cylinder (diameter = height = 0.75 in.) with the same material as the microscale magnet. We measured the magnetic field of this large magnetic cylinder with a Gauss meter with good accuracy, and compared the measurements to numerical simulations of the same geometry to determine the magnetic coercivity Hc, approximately 94 000 A/m. This value of magnetic coercivity Hc was used in the subsequent simulations of the microscale magnets in the paper.
The simulation domain was set to be at least five times of the microdevice size. The boundary condition of the simulation domain was set as an asymptotic boundary condition to solve the static Maxwell's equations.55 The magnetic flux densities Bx and By were exported by a script written in Lua programing language, and saved in a text file. The magnetic field data were later imported to the Matlab program to calculate the magnetic field distribution, which was used to understand the effects of various factors on the magnetic forces and focusing performance. According to Eq. (4), with all other material properties fixed, Fm is proportional to , which can be expressed as follows:56,57
| (13) |
In the microfluidic devices used in our experiments, changed slightly because our design is symmetric in the x direction, while in the microfluidic channel was non-uniform due to the different distance from the microscale magnet and the varying structures. Accordingly, the value of was critical to the magnetic force in Eq. (8) and the magnetophoresis velocity in Eq. (4), and thus can influence the movement of particles. In the following equation, the absolute value of , i.e.,
| (14) |
will be used to explain the focusing and separation of diamagnetic microparticles.
IV. RESULTS AND DISCUSSION
Based on the focusing criterion of tI ≤ tT, the focusing performance depends on the susceptibility of the ferrofluid and the magnetic field (and its gradients) due to the microscale magnets. These, in turn, are affected by several factors, including the concentration of ferrofluid, the gap distance between the microfluidic channel and the microscale magnet, and the width of the microfluidic channel. In this study, systematic experiments were conducted to examine the influence of these factors on focusing performance. The results are presented in Sections IV A–IV C. With a thorough understanding of the characteristics of particle focusing, a complete separation of particles of different sizes was attained with multiple fluid interfaces.
A. Effect of ferrofluid concentration on focusing performance
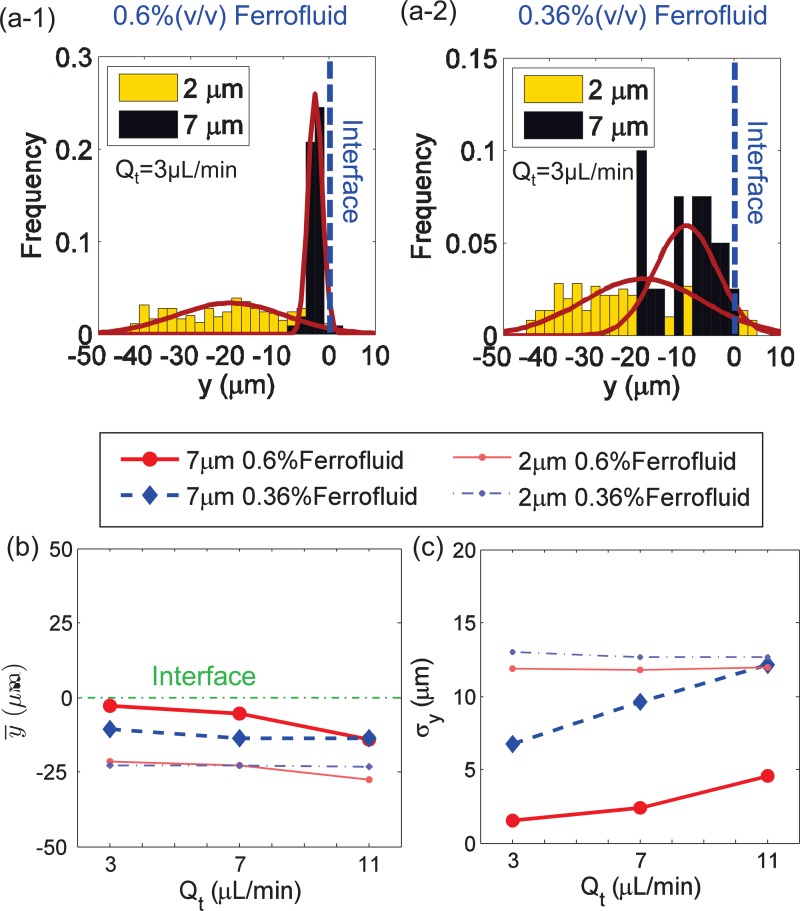
Since the ferrofluid property is critical for the interface time tI according to Eq. (10), the effect of ferrofluid concentration on focusing performance was investigated experimentally. As can be seen from Figs. 3(a-1) and 3(a-2), with 0.6%(v/v) ferrofluid at , almost all 7 μm particles were pushed onto the interface between the water and ferrofluid, while with the 0.36%(v/v) ferrofluid, the 7 μm particles spread ranged from y = −20 μm to y = 0 μm. This suggested that a high concentration of ferrofluid was beneficial for the focusing performance of particles.
FIG. 3.
Effect of ferrofluid concentration on particle focusing. (a-1) and (a-2) The Gaussian distribution of the particle's y location at the outlet when the concentration of ferrofluid is 0.6% (v/v) and 0.36% (v/v), respectively; total flow rate Qt is 3.0 μl/min for (a-1) and (a-2). (c) and (d) The mean y location of and its standard deviation σy for particles distribution at the outlet under different Qt. For each group, the flow rates of inlet 1 and inlet 2 are the same, Q1 = Q2; the width of the microfluidic channel is wc = 100 μm; the gap distance is wg = 60 μm.
From the expression of tI in Eq. (10), the time used by particles to reach the interface is inversely proportional to the susceptibility difference, , between the particles and the surrounding fluid. As mentioned before, the magnetic susceptibility χf of 0.6% and 0.36% ferrofluid is 0.25 and 0.15, respectively, so tI of 0.6% ferrofluid is smaller than that of 0.36% ferrofluid, indicating that it would be more likely to meet the focusing criterion of tI ≤ tT for higher concentration of ferrofluid, in which diamagnetic particles can be pushed towards the fluid interface more efficiently. In the meantime, almost no deflection was observed for the 2 μm particles in either 0.6% or 0.36% ferrofluid, as shown in Figs. 3(a-1) and 3(a-2). It is noted that tI was also a function of the size of particles, which was tI ∝ 1/D2. For smaller (2 μm) particles, the time needed to reach the interface was much longer than that required for the 7 μm particles, which meant that it was more difficult for the 2 μm particles to meet the focusing criterion for each concentration.
To study the overall effect of ferrofluid concentration on the focusing performance under different total flow rates Qt, the mean y location, , and the standard deviation σy of 7 μm and 2 μm particles are shown in Figs. 3(b) and 3(c). Fig. 3(b) illustrates that, for 7 μm particles, the mean y location in 0.6% ferrofluid was closer to the interface than that in 0.36% ferrofluid. Fig. 3(c) shows that the corresponding standard deviation σy of 7 μm particles in 0.6% ferrofluid was smaller, meaning that there was a more concentrated distribution. When varying the flow rate Qt, the mean y location of both 0.6% and 0.36% ferrofluid became farther from the interface and the standard deviation σy was larger, implying a worse focusing performance. The reason was that the vertical deflection distance was the result of the competition between the vertical magnetic force and the viscous drag force. With an increasing flow rate, the hydrodynamic force effect became stronger, and tT decreased. At a higher flow rate, not all of the particles were able to reach the interface before exiting the outlet. Thus, the focusing criterion tI ≤ tT set the upper flow rate limit to achieve effective focusing.
As shown in Figs. 3(b) and 3(c), the mean y location of 2 μm particles at the outlet was about 25 μm from the interface, and nearly the same at the inlet. The corresponding standard deviation was large for both ferrofluid concentrations, which agrees with the results shown in Figs. 3(a-1) and 3(a-2). Based on this observation, the 2 μm particles can almost be regarded as having no vertical deflection, owing to their small size. Therefore, in Sections IV B and IV C of this paper, the focusing performance of the large particles will be mainly discussed.
B. Effect of gap distance on focusing performance
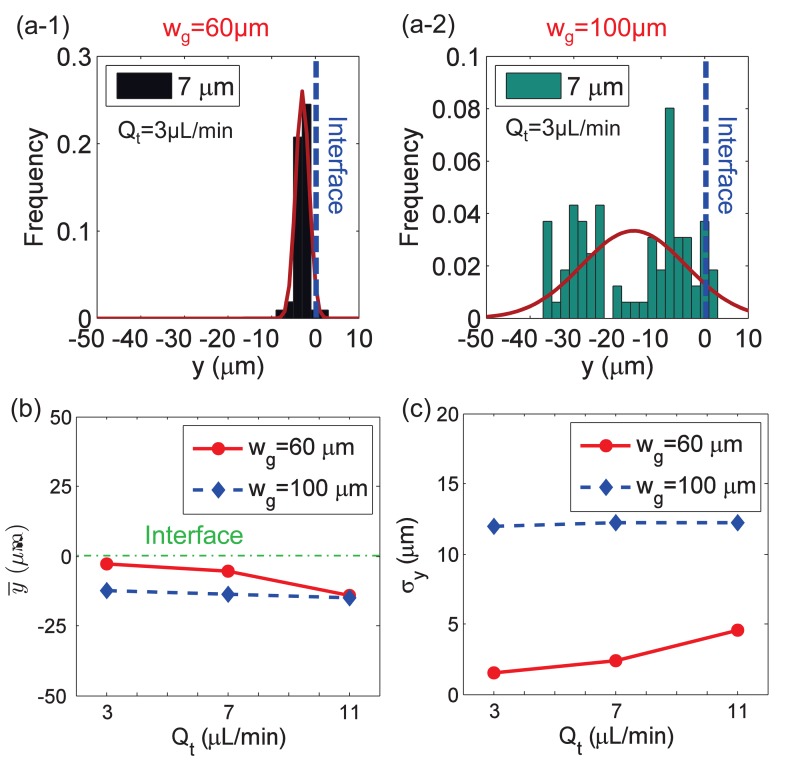
The geometric designs of microdevices have important implications on the focusing performance, according to previous studies.58 It has been shown by other researchers58 that the gap distance between the microscale magnet and the microfluidic channel can affect the magnetic field distribution, so we examined the effect of the gap distance on the focusing performance. In Fig. 4(a-1), it can be observed that the particles were pushed towards the interface when the gap distance wg = 60 μm. When wg was 100 μm, the spread range was much wider, and no obvious focusing happened, as shown in Fig. 4(a-2).
FIG. 4.
Effect of the gap distance on particle focusing. (a-1) and (a-2) The Gaussian distribution of particles y location at the outlet when the gap distance wg is 60 μm and 100 μm, respectively; total flow rate Qt is 3.0 μl/min for (a-1) and (a-2). (b) and (c) The mean y location and its standard deviation σy of particles distribution at the outlet under different Qt. For each group, the flow rates of inlet 1 and inlet 2 are the same, Q1 = Q2; the width of microfluidic channel is wc = 100 μm; ferrofluid concentration is 0.6% (v/v).
In Figs. 4(b) and 4(c), and σy of 7 μm particles are presented for different total flow rates, with two different gap distances. The smaller gap distance demonstrated better focusing for all the flow rates tested. The mean location, , was closer to the fluid interface with a smaller gap distance. The standard deviation σy of wg = 60 μm was smaller than 5 μm for each flow rate, while that of wg = 100 μm was larger than 10 μm. In Figs. 4(b) and 4(c), it is clear that, for the group of wg = 60 μm, the increase of total flow rate Qt had a negative effect on the focusing performance, including a longer distance from the interface and a larger standard deviation of particle distribution. This observation can be attributed to the decreasing tl. With a gap distance of 100 μm, neither nor σy had an obvious change as the total flow rate varied. The results suggest that the microscale magnet was too far away from the microfluidic channel, and the resulting magnetic force was too weak to cause significant particle defection in the y direction.
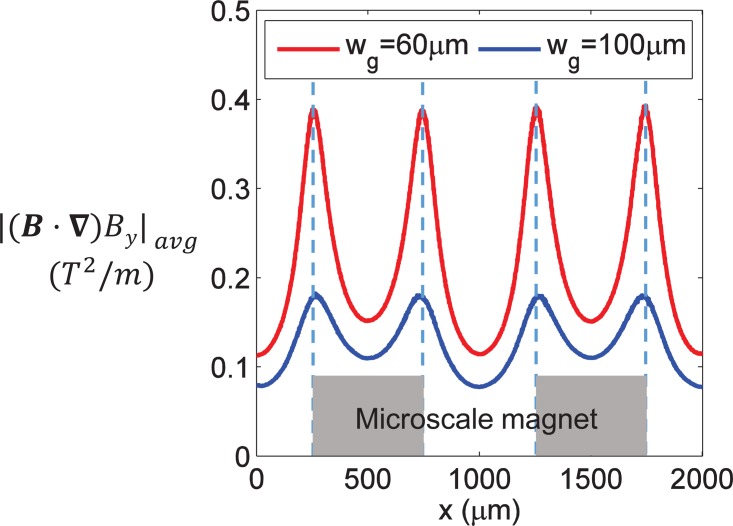
To understand the reason for a different focusing performance for each gap distance, the average value of across the fluid channel at different x locations was calculated, as shown in Fig. 5. Generally, of wg = 60 μm was larger than that of wg = 100 μm at each x location, so the magnetic force was larger and had a shorter tI according to Eq. (10). Accordingly, when wg was 60 μm, there was a greater possibility of meeting the focusing criterion of tI ≤ tT which would result in a better focusing performance of the particles.
FIG. 5.
The average value of at different x locations when wg = 60 μm and wg = 100 μm. The width of the microfluidic channel is wc = 100 μm.
C. Effect of microfluidic channel width on focusing performance
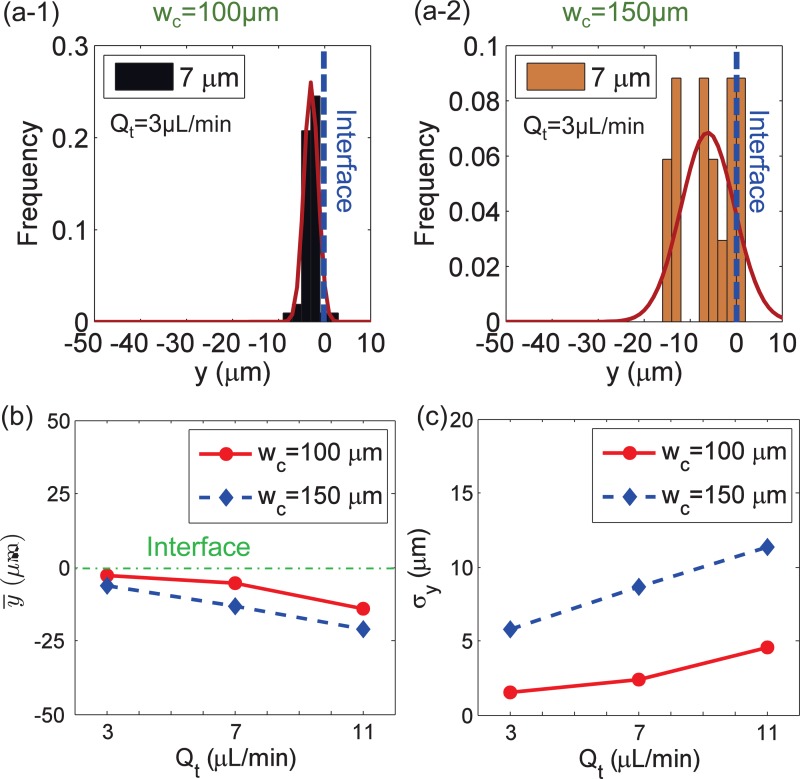
The width of the microfluidic channel is another geometric factor that can affect the focusing performance of particles in the ferrofluid flows. Figs. 6(a-1) and 6(a-2) compare the focusing of particles in two microfluidic channels with wc = 100 μm and wc = 150 μm channels under the same flow rate Qt. The microfluidic channel of wc = 100 μm had a better focusing performance than the wc = 150 μm channel, including both the smaller distance from the interface, as displayed in Fig. 6(b), and the smaller standard derivation presented in Fig. 6(c) for each total flow rate. Also, a similar trend of and σy under different Qt can be seen in Figs. 6(b) and 6(c), respectively.
FIG. 6.
Effect of the microfluidic channel width on particle focusing. (a-1) and (a-2) The Gaussian distribution of particles y location at the outlet when the channel width wc is 100 μm and 150 μm, respectively; total flow rate Qt is 3.0 μl/min for (a-1) and (a-2). (b) and (c) The mean y location and its standard deviation σy of particles distribution at the outlet under different Qt. For each group, the flow rates of inlet 1 and inlet 2 are the same, Q1 = Q2; the gap distance is wg = 60 μm; ferrofluid concentration is 0.6% (v/v).
The ratio of was analyzed to understand the reason that was responsible for the better focusing performance of a narrower microfluidic channel. The expression of can be expressed as the following equation:
| (15) |
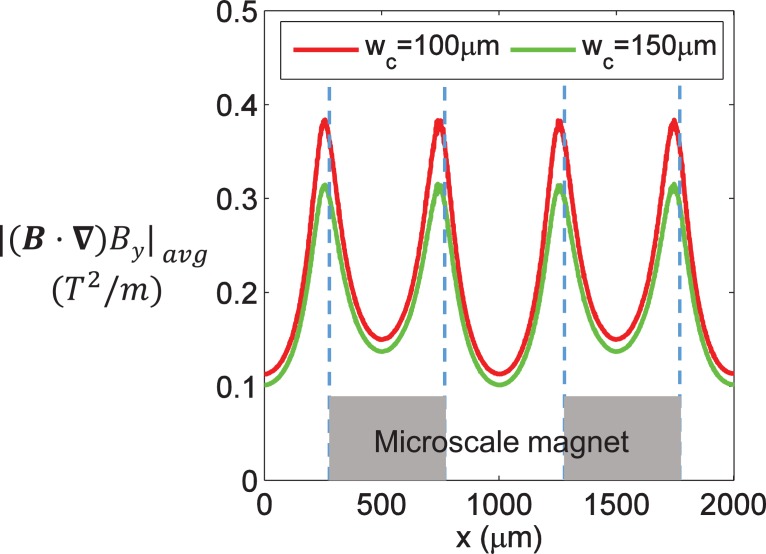
In the above equation, is proportional to the value of , when the fluid properties and total flow rate are fixed. Its values at different x locations within a structural period were chosen for magnetic field analysis to better understand the deflection of particles in channels with different widths. As can be seen in Fig. 7, value of wc = 100 μm was larger than that of wc = 150 μm at each x location. Therefore, the ratio of was larger for a narrower channel, indicating that it was easier to meet the focusing criterion of tI ≤ tT. A narrower channel was more beneficial for focusing particles onto the interface between the water and ferrofluid and increasing the throughput.
FIG. 7.
The average value of at different x locations with the different channel width wc. The gap distance wg was kept at 60 μm and the ferrofluid concentration was 0.6% (v/v).
D. Multiphase ferrofluid flows for micro-particle separation
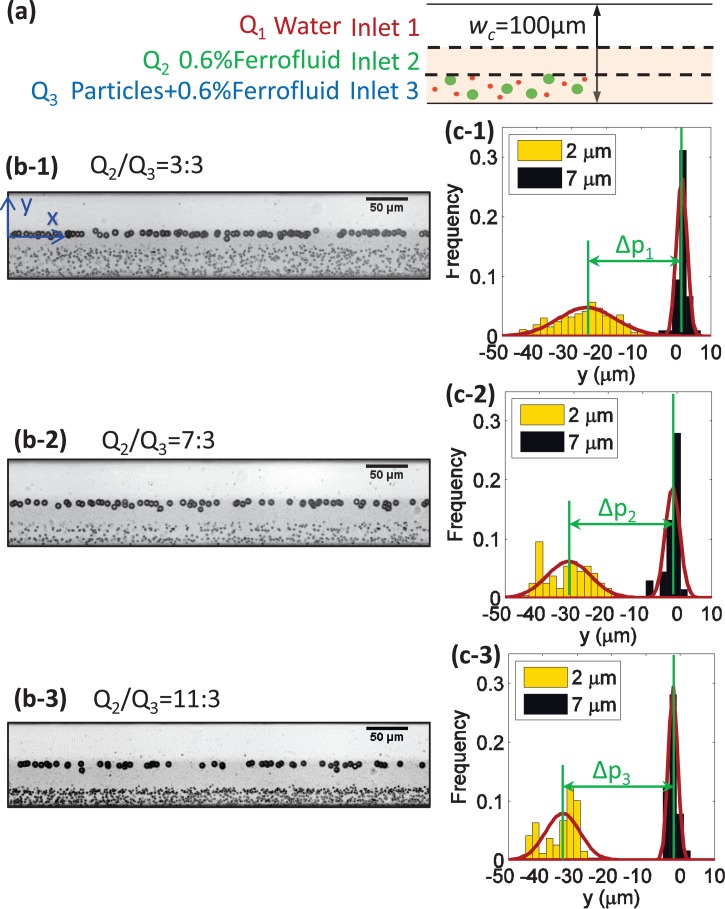
Based on the analysis presented above, large particles can be effectively focused onto the interface by choosing the correct parameters to meet the two criteria. Although the focusing of smaller particles seemed poor for all experimental conditions tested, this fact could be effectively exploited to separate particles of different sizes by using the multiple interface configurations. Here, a three inlet device was used to demonstrate the separation of different sized particles, as shown in Fig. 8(a). Water and 0.6% (v/v) ferrofluid containing 2 μm and 7 μm particles were introduced into inlets 1, 2, and 3 at flow rates Q1, Q2, and Q3, respectively. By the end of the fluidic channel, the larger particles were focused onto the water-ferrofluid interface, while the smaller particles remained near their original entry positions. Therefore, complete separation could be achieved, as in Figs. 8(b-1)–8(b-3).
FIG. 8.
Separation of microparticles of different sizes. (a) Configuration for inlet solutions of the microfluidic channel; (b-1)–(b-3) the stack images at the outlet of three different flow rate ratios; (c-1)–(c-3) the Gaussian distribution of 7 μm and 2 μm particles corresponding to (b-1)–(b-3), respectively; Δp is the peak distance between 7 μm and 2 μm particles. For each group, the width of the microfluidic channel was wc = 100 μm; the concentration of ferrofluid was 0.6% (v/v); Q1 was set at 3.5 μl/min, and Q2 + Q3 was kept at 4.0 μl/min.
To study the effect of flow rate ratio on separation performance, Q1 was set at 3.5 μl/min and the total flow rate of Q2 and Q3 was kept at 4.0 μl/min. It was clear that, when the flow rate ratio of Q2/Q3 increased, the distance between the 2 μm and 7 μm particles became larger. The Gaussian distributions of the y locations of the particles at the outlet are plotted in Figs. 8(c-1)–8(c-3). The peak distance of the three flow rate ratios had the relationship of , which suggested better separation performance with a larger flow rate ratio of Q2/Q3. As noted by other researchers, the separation distance between the peak positions alone is not sufficient to characterize the separation performance.59 To better quantify the separation performance, the parameter of separation resolution, Rs, was determined in accordance with previous studies,59
| (16) |
where pl and ps are the peak positions of 7 μm (larger) and 2 μm (smaller) particles, respectively, and dl and ds are their respective standard deviations.
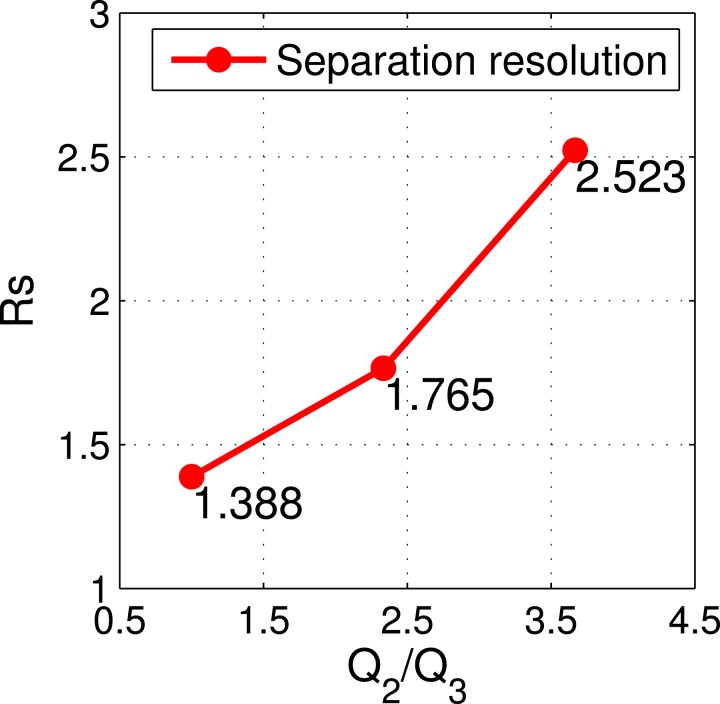
Fig. 9 shows the separation resolution under the flow rate ratio of Q2/Q3, at 3:3, 7:3, and 11:3, respectively. When the flow rate ratio of Q2/Q3 was 11:3, the separation resolution had the largest value of 2.523, suggesting the best separation performance. This result can be explained as follows. First, a larger flow rate ratio made the initial y location of both 7 μm and 2 μm particles small enough. Second, the large particles moved fast enough to reach the interface with the effect of magnetic force. Third, the 2 μm particles had almost no vertical deflection, which was identical to the previous experimental observation. Therefore, when both particles moved to the outlet, the 7 μm particles reached the interface, while the 2 μm particles remained at their original y locations. Thus, this method presents a simple way to separate particles by using multiphase ferrofluid flows.
FIG. 9.
Separation resolution corresponding to Figs. 8(b-1)–8(b-3), respectively.
V. CONCLUSIONS
This study demonstrates a simple and low-cost method for separating particles in ferrofluid by combining the multiphase laminar fluid interface and microscale magnets. The microfluidic devices integrated the NdFeB-PDMS microscale magnet next to the microfluidic channels, with a distance of tens of micrometers. The induced magnetic field gradients resulted in strong forces that could deflect magnetic particles and focus them at the interface between the water and ferrofluid. Systematic experiments were conducted to study the effects of concentrations of ferrofluid, the gap distance and the width of the fluidic channel on the focusing performance of particles. This investigation led to the following conclusions. First, when the concentration of ferrofluid increased, larger deflections of the particles were observed due to the increasing magnetic susceptibility and stronger magnetic forces. Second, a smaller gap distance between the microscale magnet and the microfluidic channel generated higher magnetic field gradients, thereby providing a better focusing performance. Third, a small channel width worked better for particle focusing.
The proposed technique is simple and offers several advantages, including a smaller footprint due to the integrated microscale magnets, accurate positioning of the interface, and thus precise focusing, as well as faster moving speeds of the focused particles. The principle of focusing particles to a fluid interface can be further extended to multiple fluid interfaces for complete separation of particles of different sizes. For practical applications, our novel technique provides an efficient method for the separation and focusing of micro-particles and (intrinsically diamagnetic) biological cells. With the rapid development of biocompatible ferrofluids in the last decade, the proposed method is expected to have broad applications involving diamagnetic biological cells, such as cytometry and cell sorting by size that are often used in biomedical diagnosis. Compared to the existing techniques using ferrofluids, the current method will allow tunable and accurate positioning of micron-sized objects to the fluid interface. In the meantime, the standalone microscale magnets are convenient to implement in a parallel format to achieve higher throughput of operations.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support from the Department of Mechanical and Aerospace Engineering at Missouri University of Science and Technology through a start-up package to C.W. The authors would like to thank Mr. F. Bai for the fruitful discussion.
References
- 1. Nilsson J., Evander M., Hammarstrom B., and Laurell T., “ Review of cell and particle trapping in microfluidic systems,” Anal. Chim. Acta 649(2), 141–157 (2009). 10.1016/j.aca.2009.07.017 [DOI] [PubMed] [Google Scholar]
- 2. Pachmann K., Camara O., Kavallaris A., Krauspe S., Malarski N., Gajda M., Kroll T., Jörke C., Hammer U., Altendorf-Hofmann A., Rabenstein C., Pachmann U., Runnebaum I., and Höffken K., “ Monitoring the response of circulating epithelial tumor cells to adjuvant chemotherapy in breast cancer allows detection of patients at risk of early relapse,” J. Clin. Oncol. 26(8), 1208–1215 (2008). 10.1200/JCO.2007.13.6523 [DOI] [PubMed] [Google Scholar]
- 3. Valero A., Merino F., Wolbers F., Luttge R., Vermes I., Andersson H., and Van Den Berg A., “ Apoptotic cell death dynamics of hl60 cells studied using a microfluidic cell trap device,” Lab Chip—Miniaturisation Chem. Biol. 5(1), 49–55 (2005). 10.1039/b415813j [DOI] [PubMed] [Google Scholar]
- 4. Zheng S., Lin H., Liu J.-Q., Balic M., Datar R., Cote R. J., and Tai Y.-C., “ Membrane microfilter device for selective capture, electrolysis and genomic analysis of human circulating tumor cells,” J. Chromatogr. A 1162(2), 154–161 (2007). 10.1016/j.chroma.2007.05.064 [DOI] [PubMed] [Google Scholar]
- 5. Tan W.-H. and Takeuchi S., “ A trap-and-release integrated microfluidic system for dynamic microarray applications,” Proc. Natl. Acad. Sci. U. S. A. 104(4), 1146–1151 (2007). 10.1073/pnas.0606625104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Tan W.-H. and Takeuchi S., “ Dynamic microarray system with gentle retrieval mechanism for cell-encapsulating hydrogel beads,” Lab Chip—Miniaturisation Chem. Biol. 8(2), 259–266 (2008). 10.1039/B714573J [DOI] [PubMed] [Google Scholar]
- 7. Pohl H., “ The motion and precipitation of suspensoids in divergent electric fields,” J. Appl. Phys. 22(7), 869–871 (1951). 10.1063/1.1700065 [DOI] [Google Scholar]
- 8. Mueller T., Gerardino A., Schnelle T., Shirley S., Bordoni F., De Gasperis G., Leoni R., and Fuhr G., “ Trapping of micrometre and sub-micrometre particles by high-frequency electric fields and hydrodynamic forces,” J. Phys. D: Appl. Phys. 29(2), 340–349 (1996). 10.1088/0022-3727/29/2/010 [DOI] [Google Scholar]
- 9. Kaler K. and Jones T., “ Dielectrophoretic spectra of single cells determined by feedback-controlled levitation,” Biophys. J. 57(2I), 173–182 (1990). 10.1016/S0006-3495(90)82520-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Molloy J. and Padgett M., “ Lights, action: Optical tweezers,” Contemp. Phys. 43(4), 241–258 (2002). 10.1080/00107510110116051 [DOI] [Google Scholar]
- 11. Moffitt J., Chemla Y., Smith S., and Bustamante C., “ Recent advances in optical tweezers,” Annu. Rev. Biochem. 77, 205–228 (2008). 10.1146/annurev.biochem.77.043007.090225 [DOI] [PubMed] [Google Scholar]
- 12. Ashkin A., “ Acceleration and trapping of particles by radiation pressure,” Phys. Rev. Lett. 24(4), 156–159 (1970). 10.1103/PhysRevLett.24.156 [DOI] [Google Scholar]
- 13. Kovac J. and Voldman J., “ Intuitive, image-based cell sorting using optofluidic cell sorting,” Anal. Chem. 79(24), 9321–9330 (2007). 10.1021/ac071366y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Grigorenko A., Roberts N., Dickinson M., and Zhang Y., “ Nanometric optical tweezers based on nanostructured substrates,” Nat. Photonics 2(6), 365–370 (2008). 10.1038/nphoton.2008.78 [DOI] [Google Scholar]
- 15. Gijs M., “ Magnetic bead handling on-chip: New opportunities for analytical applications,” Microfluid. Nanofluid. 1(1), 22–40 (2004) 10.1007/s10404-004-0010-y. [DOI] [Google Scholar]
- 16. Pamme N., “ Magnetism and microfluidics,” Lab Chip—Miniaturisation Chem. Biol. 6(1), 24–38 (2006). 10.1039/B513005K [DOI] [PubMed] [Google Scholar]
- 17. Lund-Olesen T., Dufva M., and Hansen M., “ Capture of DNA in microfluidic channel using magnetic beads: Increasing capture efficiency with integrated microfluidic mixer,” J. Magn. Magn. Mater. 311(1 SPEC. ISS.), 396–400 (2007). 10.1016/j.jmmm.2006.10.1171 [DOI] [Google Scholar]
- 18. Winkleman A., Gudiksen K., Ryan D., Whitesides G., Greenfield D., and Prentiss M., “ A magnetic trap for living cells suspended in a paramagnetic buffer,” Appl. Phys. Lett. 85(12), 2411–2413 (2004). 10.1063/1.1794372 [DOI] [Google Scholar]
- 19. Tan M. K., Friend J. R., and Yeo L. Y., “ Microparticle collection and concentration via a miniature surface acoustic wave device,” Lab Chip—Miniaturisation Chem. Biol. 7, 618–625 (2007). 10.1039/b618044b [DOI] [PubMed] [Google Scholar]
- 20. Yeo L. and Friend J., “ Ultrafast microfluidics using surface acoustic waves,” Biomicrofluidics 3(1), 012002 (2009). 10.1063/1.3056040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Friend J. and Yeo L., “ Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics,” Rev. Mod. Phys. 83(2), 647–704 (2011). 10.1103/RevModPhys.83.647 [DOI] [Google Scholar]
- 22. Lewpiriyawong N. and Yang C., “ Dielectrophoresis field-flow fractionation for continuous-flow separation of particles and cells in microfluidic devices,” in Advances in Transport Phenomena 2011 ( Springer International Publishing, 2014), pp. 29–62. [Google Scholar]
- 23. Zhu T., Marrero F., and Mao L., “ Continuous separation of non-magnetic particles inside ferrofluids,” Microfluid. Nanofluid. 9(4–5), 1003–1009 (2010). 10.1007/s10404-010-0616-1 [DOI] [Google Scholar]
- 24. Pamme N. and Wilhelm C., “ Continuous sorting of magnetic cells via on-chip free-flow magnetophoresis,” Lab Chip—Miniaturisation Chem. Biol. 6, 974–980 (2006). 10.1039/b604542a [DOI] [PubMed] [Google Scholar]
- 25. Nguyen N.-T., “ Micro-magnetofluidics: Interactions between magnetism and fluid flow on the microscale,” Microfluid. Nanofluid. 12(1–4), 1–16 (2012). 10.1007/s10404-011-0903-5 [DOI] [Google Scholar]
- 26. Pamme N. and Manz A., “ On-chip free-flow magnetophoresis: Continuous flow separation of magnetic particles and agglomerates,” Anal. Chem. 76(24), 7250–7256 (2004). 10.1021/ac049183o [DOI] [PubMed] [Google Scholar]
- 27. Adams J. D., Thevoz P., Bruus H., and Soh H. T., “ Integrated acoustic and magnetic separation in microfluidic channels,” Appl. Phys. Lett. 95(25), 254103 (2009). 10.1063/1.3275577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Plouffe B. D., Lewis L. H., and Murthy S. K., “ Computational design optimization for microfluidic magnetophoresis,” Biomicrofluidics 5(1), 013413 (2011). 10.1063/1.3553239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Rosensweig R. E., “ Fluidmagnetic buoyancy,” AIAA J. 4(10), 1751–1758 (1966). 10.2514/3.3773 [DOI] [Google Scholar]
- 30. Rosensweig R. E., “ Magnetic fluids,” Annu. Rev. Fluid Mech. 19, 437–461 (1987). 10.1146/annurev.fl.19.010187.002253 [DOI] [Google Scholar]
- 31. Plouffe B. D., Murthy S. K., and Lewis L. H., “ Fundamentals and application of magnetic particles in cell isolation and enrichment: A review,” Rep. Prog. Phys. 78(1), 016601 (2015). 10.1088/0034-4885/78/1/016601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Kose A. R., Fischer B., Mao L., and Koser H., “ Label-free cellular manipulation and sorting via biocompatible ferrofluids,” Proc. Natl. Acad. Sci. 106(51), 21478–21483 (2009). 10.1073/pnas.0912138106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Rosensweig R. E., Ferrohydrodynamics ( Cambridge University Press, 1985). [Google Scholar]
- 34. Yellen B. B., Hovorka O., and Friedman G., “ Arranging matter by magnetic nanoparticle assemblers,” Proc. Natl. Acad. Sci. U. S. A. 102(25), 8860–8864 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Kulrattanarak T., van der Sman R., Schron C., and Boom R., “ Classification and evaluation of microfluidic devices for continuous suspension fractionation,” Adv. Colloid Interface Sci. 142(1–2), 53–66 (2008). 10.1016/j.cis.2008.05.001 [DOI] [PubMed] [Google Scholar]
- 36. Gijs M. A. M., Lacharme F., and Lehmann U., “ Microfluidic applications of magnetic particles for biological analysis and catalysis,” Chem. Rev. 110(3), 1518–1563 (2010). 10.1021/cr9001929 [DOI] [PubMed] [Google Scholar]
- 37. Liang L. and Xuan X., “ Diamagnetic particle focusing using ferromicrofluidics with a single magnet,” Microfluid. Nanofluid. 13(4), 637–643 (2012). 10.1007/s10404-012-1003-x [DOI] [Google Scholar]
- 38. Liang L., Zhu J., and Xuan X., “ Three-dimensional diamagnetic particle deflection in ferrofluid microchannel flows,” Biomicrofluidics 5(3), 034110 (2011). 10.1063/1.3618737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Wilbanks J. J., Kiessling G., Zeng J., Zhang C., Tzeng T.-R., and Xuan X., “ Exploiting magnetic asymmetry to concentrate diamagnetic particles in ferrofluid microflows,” J. Appl. Phys. 115(4), 044907 (2014). 10.1063/1.4862965 [DOI] [Google Scholar]
- 40. Zeng J., Chen C., Vedantam P., Brown V., Tzeng T.-R. J., and Xuan X., “ Three-dimensional magnetic focusing of particles and cells in ferrofluid flow through a straight microchannel,” J. Micromech. Microeng. 22(10), 105018 (2012). 10.1088/0960-1317/22/10/105018 [DOI] [Google Scholar]
- 41. Zeng J., Chen C., Vedantam P., Tzeng T.-R., and Xuan X., “ Magnetic concentration of particles and cells in ferrofluid flow through a straight microchannel using attracting magnets,” Microfluid. Nanofluid. 15(1), 49–55 (2013). 10.1007/s10404-012-1126-0 [DOI] [Google Scholar]
- 42. Liang L., Zhang C., and Xuan X., “ Enhanced separation of magnetic and diamagnetic particles in a dilute ferrofluid,” Appl. Phys. Lett. 102(23), 234101 (2013). 10.1063/1.4810874 [DOI] [Google Scholar]
- 43. McDonald J., Duffy D., Anderson J., Chiu D., Wu H., Schueller O., and Whitesides G., “ Fabrication of microfluidic systems in poly(dimethylsiloxane),” Electrophoresis 21(1), 27–40 (2000). [DOI] [PubMed] [Google Scholar]
- 44. Zhou R. and Wang C., “ Acoustic bubble enhanced pinched flow fractionation for microparticle separation,” J. Micromech. Microeng. 25(8), 084005 (2015) 10.1088/0960-1317/25/8/084005. [DOI] [Google Scholar]
- 45. Eddings M., Johnson M., and Gale B. K., “ Determining the optimal PDMS bonding technique for microfluidic devices,” J. Micromech. Microeng. 18(6), 067001 (2008). 10.1088/0960-1317/18/6/067001 [DOI] [Google Scholar]
- 46. Duffy D. C., Schueller O. J. A., Brittain S. T., and Whitesides G. M., “ Rapid prototyping of microfluidic switches in poly(dimethyl siloxane) and their actuation by electro-osmotic flow,” J. Micromech. Microeng. 9(3), 211 (1999). 10.1088/0960-1317/9/3/301 [DOI] [Google Scholar]
- 47. Haubert K., Drier T., and Beebe D., “ PDMS bonding by means of a portable, low-cost corona system,” Lab Chip—Miniaturisation Chem. Biol. 6, 1548–1549 (2006). 10.1039/b610567j [DOI] [PubMed] [Google Scholar]
- 48. Cirin D. M., Posa M. M., and Krstonosic V. S., “ Interactions between sodium cholate or sodium deoxycholate and nonionic surfactant (tween 20 or tween 60) in aqueous solution,” Ind. Eng. Chem. Res. 51(9), 3670–3676 (2012). 10.1021/ie202373z [DOI] [Google Scholar]
- 49. Zeng J., Deng Y., Vedantam P., Tzeng T.-R., and Xuan X., “ Magnetic separation of particles and cells in ferrofluid flow through a straight microchannel using two offset magnets,” J. Magn. Magn. Mater. 346, 118–123 (2013). 10.1016/j.jmmm.2013.07.021 [DOI] [Google Scholar]
- 50. Abramoff M., Magalhaes P., and Ram S., “ Image processing with ImageJ,” Biophotonics Int. 11(7), 36–41 (2004). [Google Scholar]
- 51. Erb R. and Yellen B., “ Magnetic manipulation of colloidal particles,” in Nanoscale Magnetic Materials and Applications, edited by Liu J. P., Fullerton E., Gutfleisch O., and Sellmyer D. ( Springer, US, 2009), pp. 563–590. [Google Scholar]
- 52. Faivre M., Gelszinnis R., Degouttes J., Terrier N., Rivire C., Ferrigno R., and Deman A.-L., “ Magnetophoretic manipulation in microsystem using carbonyl iron-polydimethylsiloxane microstructures,” Biomicrofluidics 8(5), 054103 (2014). 10.1063/1.4894497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Han X., Feng Y., Cao Q., and Li L., “ Three-dimensional analysis and enhancement of continuous magnetic separation of particles in microfluidics,” Microfluid. Nanofluid. 18(5–6), 1209–1220 (2015). 10.1007/s10404-014-1516-6 [DOI] [Google Scholar]
- 54. Miller C. C., “ The stokes-einstein law for diffusion in solution,” Proc. R. Soc. London. Ser. A. 106(740), 724–749 (1924). 10.1098/rspa.1924.0100 [DOI] [Google Scholar]
- 55. Meeker D., Finite Element Method Magnetics (FEMM) software, 4, 32 (2010). [Google Scholar]
- 56. Yu X., Wen C.-Y., Zhang Z.-L., and Pang D.-W., “ Control of magnetic field distribution by using nickel powder@pdms pillars in microchannels,” RSC Adv. 4, 17660–17666 (2014). 10.1039/C3RA47902A [DOI] [Google Scholar]
- 57. Tennico Y. H., Hutanu D., Koesdjojo M. T., Bartel C. M., and Remcho V. T., “ On-chip aptamer-based sandwich assay for thrombin detection employing magnetic beads and quantum dots,” Anal. Chem. 82(13), 5591–5597 (2010). 10.1021/ac101269u [DOI] [PubMed] [Google Scholar]
- 58. Xia N., Hunt T., Mayers B., Alsberg E., Whitesides G., Westervelt R., and Ingber D., “ Combined microfluidic-micromagnetic separation of living cells in continuous flow,” Biomed. Microdevices 8(4), 299–308 (2006). 10.1007/s10544-006-0033-0 [DOI] [PubMed] [Google Scholar]
- 59. Jain A. and Posner J. D., “ Particle dispersion and separation resolution of pinched flow fractionation,” Anal. Chem. 80(5), 1641–1648 (2008). 10.1021/ac0713813 [DOI] [PubMed] [Google Scholar]