Abstract
Heme, the prosthetic group of hemoglobin, may be released from its host due to an intrinsic instability of hemoglobin and accumulate in the erythrocytes. Free heme is in the form of hematin (Fe3+ protoporphyrin IX OH) and follows several pathways of biochemical toxicity to tissues, cells, and organelles since it catalyzes the production of reactive oxygen species. To determine concentration of soluble free heme in human erythrocytes, we develop a new method. We lyse the red blood cells and isolate free heme from hemoglobin by dialysis. We use the heme to reconstitute horseradish peroxidase (HRP) from an excess of the apoenzyme and determine the HRP reaction rate from the evolution of the emitted luminescence. We find that in a population of five healthy adults the average free heme concentration in the erythrocytes is 21 ± 2 μM, ca. 100× higher than previously determined. Tests suggest that the lower previous value was due to the use of elevated concentrations of NaCl, which drive hematin precipitation and re-association with apoglobin. We show that the found hematin concentration is significantly higher than estimates based on equilibrium release and the known hematin dimerization. The factors that lead to enhanced heme release remain an open question.
Keywords: Human erythrocytes, Enzymatic analysis, Luminescence, Hemoglobin instability, Heme release, Hematin concentration
1. Introduction
Heme, Fe2+ protoporphyrin IX, is the prosthetic group of hemoglobin. Each hemoglobin molecule carries four hemes, one for each of its sub-chains. One or more (less likely) of the hemoglobin hemes may be released to the solution [1,2]. The release occurs predominantly after its autoxidation to methemoglobin, in which the iron is in its Fe3+ form [2,3]. Hence, the heme released from hemoglobin is in the form of hematin, i.e., Fe3+ protoporphyrin IX liganded to OH−. Hematin is a substance with proven toxicity, which triggers lyses of human erythrocytes [4–7] and other cell types [8,9]. It catalyzes the generation of toxic lipid peroxidation products by several mechanisms [10]. It generates redox reactive substances such as H2O2, superoxide radicals, and the hydroxyl radical, which directly mediates lipid peroxidation [11,12]. The heme released from hemoglobin binds to the red cell membrane causing membrane damage [13] and higher adhesion of sickle red cells to leucocytes and the endothelium [14–16]. Exposure of human B-cell lymphoma to free heme leads to high binding affinity to multiple autoantigens due to the heme’s redox potential [17]. In some of these cases, the deleterious effects of free heme are exhibited after its release during hemoglobin catabolism in malaria infected cells [11,12], in others, due to the intrinsic instability of hemoglobin [4–7].
Despite the abundant evidence of the damage inflicted by free heme, we are aware of a single determination of the concentration of free heme in malaria-free erythrocytes [18]. Most of the recent work on heme quantification has focused on the determination of the total heme content, including quantities bound to globins, often in the context of forensics [19]. The methods employed in these studies were mostly based on the spectroscopic response of heme and heme-containing proteins [20]; HPLC [21], electrochemical methods such as capillary electrophoresis [22,23], and mass-spectrometry [19,24] have been used in recent work.
The objective of the investigations reported here is to determine the concentration of the free heme in healthy human erythrocytes. For this, we developed a new sensitive and selective analytical method. We carry out extensive tests to evaluate the bias in this determination that may be introduced by continued hemoglobin dissociation and interactions between heme, apoglobin and the erythrocyte membrane. We discuss the possible reasons why our results exceed the concentrations found previously [18]. We compare the found values of free heme to the predictions of several models that assume equilibrium between free heme and methemoglobin present in the red blood cells.
2. Materials and methods
2.1. An enzymatic method with luminescent detection for heme quantification
To determine the concentration of free heme in human erythrocytes, we use donor blood drawn according to institutional and NIH regulations. We lyse the red blood cells and separate the heme from hemoglobin by dialysis. Details about these procedures and the materials and solutions used are provided as Supplementary material.
The separation of free heme from hemoglobin by dialysis has the disadvantage that it lowers the concentration of free heme to below 1 nM. At concentrations below 0.5 μM, hematin and hemin solutions are colorless. The highest absorbance of such solutions, in the Soret band near 400 nm, is below 0.1. Hence, spectroscopic determination of concentrations below this limit is prone to high error [25].
To quantify such low concentrations of hematin, we modified a recent method that relies on the reconstitution of apo-horseradish peroxidase (apo-HRP) in the presence of hemin (Fe3+ protoporphyrin IX Cl) or hematin (tests, discussed in the Supplementary Material, revealed that the method yields identical results with these two compounds) [26]. The sequence of reactions that underlie the method is:
| (1a) |
| (1b) |
| (1c) |
Reaction (1c) is accompanied by luminescence at 428 nm [27,28]. The luminescence intensity is proportional to the rate of catalytic decomposition of peroxide. This rate, in turn, is proportional to the concentration of reconstituted peroxidase. In excess of apo-HRP, the concentration of the reconstituted enzyme equals that of the initial heme. Hence, the luminescence intensity is proportional to the concentration of free heme. The transformation of the analyte to a catalyst of a reaction with a well-detectable product underlies the high sensitivity of this method. Furthermore, the luminol reaction is an example of very strong chemiluminescence [27,28]. The strong amplification of the signal allows detection and quantification of hematin or hemin levels as low as 50 pM, see tests of sensitivity below.
For experimental statistics, we used 96 well plates and filled each column of eight wells with identical solutions. Six of the columns were filled with solutions of known hemin concentration in the same buffer as the one used in the dialysis of the hemolysate and the other six—with samples of dialysate produced as discussed above. The six known concentrations were distributed in a range that bracketed the unknown dialysate concentration. The volume of standard solution added to each well varied from 0 to 40 μL so that the final heme concentrations was from 0 to 600 pM. For experimental statistics, a tested solution was divided into two, four, or six samples and each sample subdivided into the wells of one eight-well column. We added 40 μL of the tested solution to each well.
After we loaded the heme solutions, we added Tris buffer to each well in volume calculated to bring the total to 50 μL. Then we added 50 μL of apo-HRP stock solution yielding a concentration of 600 pM in each well. We incubated the microplate for 30 min at room temperature, ca. 23 °C, to reconstitute HRP [26]. The rate constant for heme binding to 35 different apoglobins is approximately kH = 1 × 108 M−1s−1, regardless of the structure or overall affinity of the apoprotein for iron-porphyrin [29]. We assume that this value applies for apo-HRP. Then, the half-time for hematin and hemin binding to apo-HRP t1/2 ≈ (kHCapo-HRP)−1 ≈ 20 s. Thus, 30 min is sufficient time for quantitative binding of free heme to apo-HRP.
After incubation, we added Immobilon (10 μL luminol and 10 μL peroxide) to the wells. The final solution volume in each well was 120 μL. We incubated the microplate for 15 min at room temperature, ca. 23 °C, and loaded it into the microplate reader. We monitored the evolution of the intensity of the luminescence emitted from each well over 30 min. For each moment of the reaction, the luminescence intensities were averaged over the eight wells with identical composition. An example of the intensity evolution over 30 min for six standard hemin concentrations is displayed in Fig. 1A.
Fig. 1.
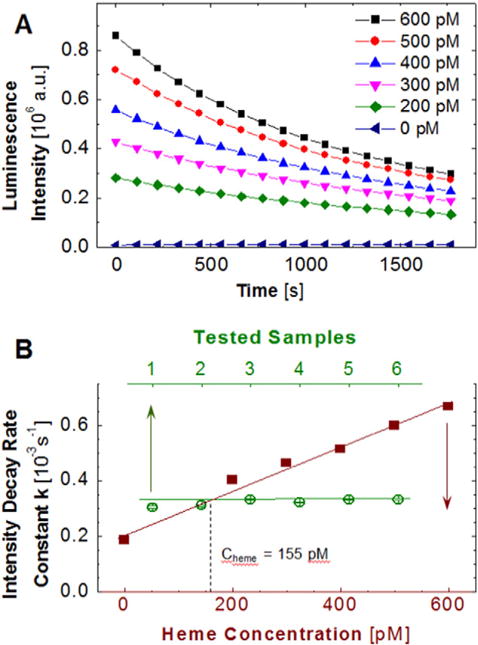
An enzymatic method for the determination of the concentration of free heme. A, The evolution of luminescence intensity emitted by the reactions in Eq. (1a,b,c) at five concentrations of heme and in its absence. B, Illustration of the determination of the concentration of free heme in the dialysate. The standard curve, shown in solid symbols, relates known concentration of heme to the rate constant k of decay of the luminescent intensity determined from evolution curves similar to those shown in A. The constant k is determined for six samples of dialysate. The unknown concentration of free heme in the dialysate is determined from the average value of k.
2.2. Definition of the calibration curve in terms of rate constants
The average luminescence intensity from a tested sample could be compared to that from solutions with known concentration at the same reaction time and the unknown concentration could be determined by interpolation between the two bracketing values [26]. We developed a new method of determination of the heme concentration based on calibration curves in terms of the rate constant for luminesce intensity decay.
The breakdown of peroxide catalyzed by HRP and other peroxidases is well described by the Michaelis–Menten rate law for the catalytic process [30]
| (2) |
| (3) |
where the Michaelis constant .
In Eqs. (2) and (3) S denotes the substrate, H2O2, and its concentration; t, time; E, the enzyme, reconstituted HRP; P, the product, OH•; ES, the enzyme-substrate complex; k1, k−1 and k2 are the respective rate constants, and the subscript 0 indicates initial values.
The Michaelis–Menten equation is integrated to
| (4) |
Independent determinations of the Michaelis constant KM for HRP have yielded values from 1.9 to 2.6 mM [31,32]. The values in this range are significantly higher than the initial concentration of H2O2 in the reaction mixture, S0 = 42 μM, determined from the dilution ratio and the concentration in the commercial product, determined as discussed in the Supplementary material We use the inequality KM ≫ (S0 − S) to simplify the integrated form of the Michaelis–Menten expression:
| (5) |
Thus, a pseudo-first order rate law obtains. Deviations from the exponential decay represented by Eq. (5) are not expected even at long reaction times, when S → 0 and (S0 − S) → S0 since KM ≫ S0.
Since the reaction of OH• with luminol, Eq. (1c), is faster than the preceding kinetic step, Eq. (1b), its rate is determined by that of the step (Eq. (1b)). With this, the luminescence intensity I is proportional to the rate of production of OH•, i.e., −dS/dt. Thus, the rate constant for the luminescence intensity evolution
| (6) |
is proportional to the initial concentration of the enzyme E0; in excess of apo-HRP, E0 is equal to the concentration of heme. Eq. (6) demonstrates that k only depends on E0, the total concentration of reconstituted HRP. On the other hand, Eq. (5) shows that the luminescence intensity also depends on S0, the initial H2O2 concentration. Thus, determinations of the rate constant k are only influenced by inconsistent concentrations of HRP in the reaction mixture, while an additional source of error of the measured intensity is the inconsistent concentration of H2O2. Hence, we use standard curves in terms of k as a basis for the determination of unknown concentrations of free heme.
We determine k from the intensity evolution I(t), similar to those plotted in Fig. 1A, employing linear regression analyses of the dependence lnI(t). Using data obtained with known hemin or hematin concentrations, we plot k(C) and use this as a standard curve. For a solution with unknown concentration, we determine k in an identical way and use this standard curve to obtain the concentration of free heme, as illustrated in Fig. 1B.
To calculate the concentration of free heme in the red cells in the analyzed blood sample, we multiply the dilution ratio of the tested dialysate in the plates (40 μL diluted to 120 μL) by the dilution ratios of the dialysate (3 mL hemolysate held in a dialysis cassette in contact with 1 L solution) and the hemolysate (computed from the concentration of hemoglobin in the hemolysate CHb assuming that the concentration of hemoglobin in the red cell cytosol is 350 mg mL−1): 3 × 334 × 350 mg mL−1/CHb. For the sample represented Fig. 1B, CHb = 2.9 mg mL−1 so that the total dilution ratio is 1.21 × 105 and Cheme = 19 μM in the erythrocytes of the analyzed blood sample.
Below, we discuss tests aimed at validation of the method and evaluation of its sensitivity and accuracy.
3. Results
3.1. Is heme released during storage of the blood and hemolysate?
Most of the blood samples used in this study were kept at room temperature, ca. 23 °C, for about 30 min after collection. However, several samples remained at this temperature for up to 4 h. Sometimes, blood samples were stored in a laboratory refrigerator for up to 4 h. We carried out two tests to judge if significant amount of heme are released in the time between blood collection and analysis, either during storage at room temperature for up to 4 h, or in the refrigerator for 2 days. Furthermore, the dissociation of heme depends on the concentration of hemoglobin [33]. The reason for this dependence is that at low concentrations, the native hemoglobin tetramers decay to dimers, which release heme faster [2]. Thus, it is possible that the heme we detect in the hemolysate was not present in the red cell cytosol, but was released after the dilution of the hemoglobin upon cell lysis. Hence, we tested if heme is released during storage of the hemolysate in the refrigerator for up to 14 days.
For the first test, we separated the tubes from one drawing into two samples. We analyzed the first sample within 30 min of delivery to the laboratory and the second—after 4 h. Both samples were kept at room temperature, ca. 23 °C, and were analyzed identically, following the procedure discussed above. Measuring the hemoglobin concentration in the hemolysate yielded ca. 2 mg mL−1 for both samples, indicating that the dilution ratios of the two hemolysate samples were similar. We observed that the decay rate constant k of the luminescence intensity was identical in both samples, i.e., storage of blood at room temperature for up to 4 h does not lead to additional amounts of heme released.
We combined the tests of heme release during blood storage in the laboratory refrigerator and upon dilution of the erythrocyte cytosol to hemolysate. As above, we separated the tubes from one blood drawing into two samples. Blood from the first sample of tubes was analyzed immediately upon delivery to the laboratory. The second sample of tubes was kept in the laboratory refrigerator at ca. 5 °C for two days. After the red blood cells were lysed, we stored in the refrigerator for 14 days both hemolysate samples. At one or two-day intervals, we took solution samples, dialyzed them to separate the free heme from the hemoglobin, and then determined the concentration of free heme in the dialysate in terms of the decay rate constant k of the luminescence intensity, defined by Eq. (6) above. The results, displayed in Fig. 2A, indicate that (i) the rate constant k is similar for both samples of tubes, i.e., heme is not released during storage of whole blood at ca. 5 °C for up to 2 days, and (ii) the rate constant does not change over 14 days of storage of the hemolysate at ca. 5 °C, i.e., no significant additional heme is released during storage of the hemolysate.
Fig. 2.
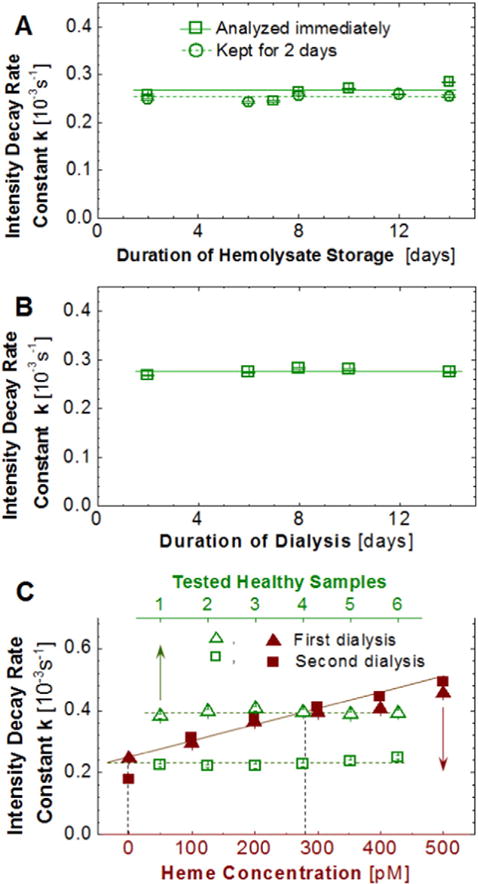
Validation of the method. A and B, Independence of found free heme concentration on duration of storage of blood and hemolysate and of dialysis. A, Hemolysate from one donor was stored at ca. 5 °C. The solution was sampled at regular intervals and the free heme was quantified. In another experiment, blood was kept for 2 days at ca. 5oC before the erythrocytes were isolated and lysed and the free heme in the hemolysate was determined. B, Hemolysate from one donor was dialyzed for 14 days. The dialysate was sampled at regular intervals and its heme concentration was evaluated. C, Arrest of heme release upon dilution at red cell lysis. A hemolysate sample was dialyzed for 14 h. The dialysate was removed and the heme concentration in it was determined. The hemolysate samples in the dialysis cassettes were placed in new dialysis buffers and, dialyzed for 14 h, and the free heme concentration in the new dialysate was determined using new standard curves.
The results of the three tests demonstrate that heme is not released in significant amounts during storage of blood at ca. 23 °C for up to 4 h, during storage of blood at ca. 5 °C for up to 2 days, and during storage of hemolysate at ca. 5 °C for up to 14 days.
3.2. Is heme released during dialysis of the hemolysate?
When we place the hemolysate in a dialysis cassette, the available free heme migrates to the dialysate solution. This lowers the chemical potential of the free heme in the hemolysate and creates a driving force for additional heme release. To test if additional heme is released as a consequence of the migration to the dialysate, we carried out two tests. First, we held a hemolysate sample in a dialysis cassette in contact with dialysate for 14 days. At one or two day intervals, we took samples of the dialysate and determined the concentration of heme. Fig. 2B demonstrates that the concentration of heme in the dialysate was steady over this period, i.e., no new heme is released in the hemolysate during dialysis.
Second, we kept a freshly prepared hemolysate sample in a dialysis cassette in contact with dialysis buffer for 14 h. After this time, the dialysate was removed and the heme concentration in it was determined using a standard curve measured simultaneously with the sample characterization. The cassette with the tested hemolysate was placed in contact with new dialysis buffer for additional 14 h. At the end of this period, the concentration of the free heme in the second dialysate was determined using a newly measured standard curve (for tests of the reproducibility of the standard curves, see below).
Fig. 2C reveals the lack of free heme in the second dialysate. This observation could either indicate that no heme is released in the hemolysate, or that heme is released in the hemolysate, but this release is arrested after the first dialysis. We analyze two processes that may provoke arrest of heme release after the first dialysis: (i) dilution of the hemoglobin concentration and (ii) chemical modification of hemoglobin leading to strong heme binding. To exclude (i), we note that we fill the dialysis bag to its capacity with 3 mL of hemolysate. Thus, the hemolysate is not diluted after the first day of dialysis. Option (ii) is also unlikely: as Fig. 2A demonstrates, if the hemolysate is stored in a container that preserves the concentration of the free heme present in it, this heme readily transfers to the dialysate even after 14 days of storage. Thus, no changes in the hemoglobin that could lead to stronger heme binding occur. Excluding options (i) and (ii) indicates that a scenario of limited duration heme release is implausible. We conclude that the release of heme is arrested in the hemolysate and all heme found after dialysis of the hemolysate comes from the erythrocyte cytosol. The reason why heme release is arrested presents an intriguing question that will be explored in future work.
3.3. Is heme bound to the erythrocyte membranes released in the hemolysate?
Hematin released from hemoglobin has been found bound to the membranes of both sickle and healthy red cells [34]. Even though the detachment of hematin from the membranes for these analyses required the application of saponin [34], it is possible that the heme that we detect does not come from the erythrocyte cytosol, but detaches from the membranes upon cell lysis in a large volume of water. We carried out two tests of this possibility:
We lysed the red blood cells from one donation in two volumes of water: 5 and 50 mL. If hematin detaches from the membranes due to its low concentration in the hemolysate, we would expect higher heme amounts in the diluted hemolysate. We found that the amount of heme did not depend on the hemolysate dilution.
We extended from 2 min (the typical length) to 30 min the time between cell lysis and centrifugation applied to remove the red cell membranes. If heme were released from the membranes, we would expect higher heme concentrations in the hemolysate that is kept in contact with the membrane ghosts for an extended period. We found that the concentration of the heme in the two ghostless hemolysates was similar.
Additional tests on the validation of the method are discussed in the Supplementary material. They include determination of the accuracy and sensitivity of the method (ca. 5% and 20 to 50 pM, respectively), justification of the choice of tubes for blood storage, and evaluation of the possible variability of the apo-HRP preparation, of the use of hemin or hematin for the standard curves, and of the effects of heme unbound to apo-HRP and hemoglobin in the dialysate on the results.
3.4. The concentration of free heme in healthy erythrocytes
Using the method discussed above, we determined the average concentration of free heme in the erythrocytes of five healthy donors. From the results in Fig. 3, the average of the population of five donors is 21 ± 2 μM. In different donors, the average free heme concentrations as high as 26 and as low as 19 μM were found. The reason for the greater variability of the free heme concentration between the four tubes donated by Donor 4 is not clear to us.
Fig. 3.
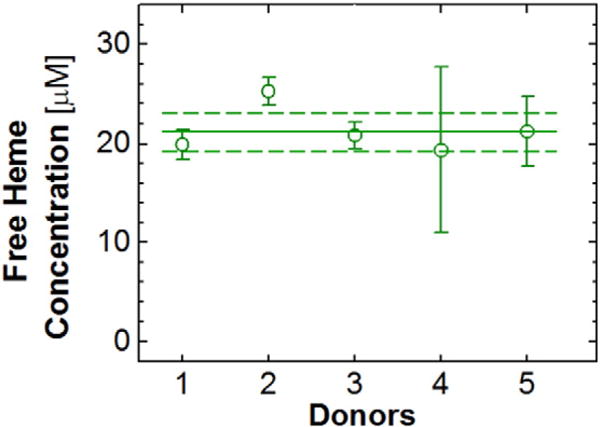
The average concentrations of free heme in blood samples of five healthy donors. Eight donations of four 4 mL tubes were obtained from donor 1 and two from donor 2 and are averaged; all other data points are averages over four tubes of a single donation. The population average, 21 μM, is marked with a horizontal solid line; the standard deviation, 2 μM, with two dashed lines.
3.5. Comparison with a previous determination of the free heme concentration
We are aware of a single previous determination of the concentration of free heme in sickle and healthy erythrocytes, [18] which found concentrations of, respectively, 0.75 and 0.15 μM. The concentration found in healthy adult erythrocytes is more than two orders of magnitude lower than the one in Fig. 3. Liu et al. separated free heme from hemoglobin by charge, using ion exchange liquid chromatography [18], in contrast to the separation by size using dialyses, employed here. To isolate the hematin, Liu et al. added 2 M NaCl to the hemolysates. At this electrolyte concentration, the hematin was retained on the column. The captured hematin was then eluted by a solution of sodium dodecyl sulfate (SDS). To validate the method, Liu et al. [18] added hematin to the hemolysate and retrieved 75% of the added amount after the SDS elution.
In the Supplementary material we discuss experiments that suggest that the high concentration of NaCl may have precipitated the hematin used in the calibration experiments as a solid residue. The residue would have been retained in the column and re-solubilized by the addition of SDS. This scenario casts doubt on the ability of the immobile phase used by Liu et al. [18] to quantitatively retain hematin from a mixture with hemoglobin and in this way on their final result. We also show that in the presence of NaCl the amount of heme released from hemoglobin is reduced, likely owing to the increased chemical potential of soluble hematin that leads to its re-association to apoglobin.
4. Discussion
4.1. The equilibrium amount of free heme
To understand the factors that may have resulted in the high concentration of free heme in Fig. 3, we first evaluate the equilibrium concentration of free heme in a solution similar to the erythrocyte cytosol. The mechanism and the relevant kinetic and thermodynamic parameters of dissociation of heme from normal hemoglobin and the reverse reaction, the association of heme to apoglobin, are well studied [1,2,29]. The main conclusions of these works are: (i) The dissociation of heme from ferrous hemoglobin is extremely slow; heme mostly dissociates from met-hemoglobin [1,3]. (ii) The dissociation of heme is ca. 10× faster from the α1β1 dimers, prevalent at low concentrations, than from the native α2β2 tetramers [2]. (iii) Most of the dissociation is from β-subunits of the dimer and tetramer since it is 25 to 60× faster than dissociation from the respective α-subunits [2]. (iv) The dissociation is reversible and the rate constant of association of hematin to apoglobin is independent of the globin and the oligomer state, tetramer or dimer [29].
With these observations, the found first order rate constant k−H(obs) of the reaction of dissociation of hematin (H) from methemoglobin (Hb+) producing apoglobin (apo-Hb).
| (7) |
is a weighted sum of the rate constants for dissociation from dimers k−H(dimer) and tetramers k−H(tetramer).
| (8) |
where γ is the fraction of hemoglobin dimer [2]. The values of k−H(dimer) and k−H(tetramer) for hematin dissociation from the respective β-subunits of normal adult hemoglobin were determined at pH = 7.0 in 0.15 M potassium or sodium phosphate buffer in the presence of 0.45 M sucrose and at 37 °C: k−H(dimer) = 4.2 × 10−3 s−1 and k−H(tetramer) = 4.2 × 10−4 s−1 [2,35].
The dimer fraction γ is higher at low hemoglobin concentrations according to the relation.
| (9) |
where K4,2 = 1.5 μM [33] is the equilibrium constant of dissociation of methemoglobin tetramers into dimers and H0 is the total heme concentration, H0 = 4CHb+ [2].
The second-order rate constant for the association of hematin to apoglobin, the reverse reaction in Eq. (7), was determined at pH = 8 in 50 mM Tris buffer and 50 mM NaCl at room temperature as kH = 1 × 108 M−1s−1 for both dimers and tetramers [2,29]. The equilibrium constant for Eq. (7) is K−H = k−H(obs)/kH. Following Hargrove et al. [2], we can calculate formal values for K−H using the above values of k−H(dimer), k−H(tetramer) and kH.
Since we expect a low concentration of released heme, corresponding to a leftward shift of the equilibrium in Eq. (7), it is safe to assume that the equilibrium concentration of methemoglobin [Hb+] is equal to its total concentration CHb+. With this assumption, from the mass balance of Eq. (7), the concentration of free heme in equilibrium with apoglobin and methemoglobin is:
| (10) |
In Table 1, we list the values of γ, k−H(obs), K−H, and the equilibrium free heme concentration Cheme for three values of CHb+ computed using the above relations and values of the relevant constants for normal hemoglobin.
Table 1.
The values of the fraction of hemoglobin dimer γ, defined by Eq. (9); the observed rate constant of dissociation of hematin from methemoglobin k−H(obs), defined by Eq. (8); the equilibrium constant for reaction (Eq. (7)) K−H = k−H(obs)/kH computed using kH = 1 × 108 M−1s−1 for both dimers and tetramers [2,29]; and the equilibrium concentration of free heme Cheme, calculated using Eq. (10) for three values of CHb+.
|
CHb+
|
γ |
k−H(obs)
|
K−H
|
Cheme
|
|
|---|---|---|---|---|---|
| mg mL−1 | mM | 10−4s−1 | pM | nM | |
| 3.5 | 0.054 | 0.077 | 7.10 | 7.10 | 20 |
| 11.5 | 0.18 | 0.045 | 5.93 | 5.93 | 33 |
| 100 | 1.55 | 0.015 | 4.73 | 4.73 | 85 |
The value of CHb+ = 3.5 mg mL−1 in the top row of Table 1 corresponds to the average fraction of methemoglobin in healthy erythrocytes of 1% [36]. CHb+ = 11.5 mg mL1 corresponds to 3% methemoglobin content, which is the upper limit of non-pathological methemoglobin concentration. CHb+ = 100 mg mL−1 corresponds to a case of severe methemoglobinemia, in which 28% of the total hemoglobin is oxidized to methemoglobin [37].
The values of Cheme in the last column of Table 1 are lower by two to three orders of magnitude than those measured in healthy individuals in Fig. 3. The pH, temperature, and solution composition, at which the rate constants for hematin association to apoglobin were determined, are different from those for dissociation of heme from methemoglobin. Moreover, some of these settings are also different from those in the erythrocytes. Still, it is unlikely that the discrepancy between the data in Fig. 3 and the predictions in Table 1 is entirely due to the disparate conditions of determination. The differences in temperature, pH, ionicity, and osmolality could lead to at most a 5× higher amount of released heme.
Both equilibrium and non-equilibrium processes can lead to the deviation of the measured erythrocyte concentration of the free heme from the predictions in Table 1. An example of a concurrent equilibrium process is the formation of dimers or higher aggregates of hematin that may delay the association of hematin to apoglobin, the reverse reaction in Eq. (7). We discuss this mechanism below.
4.2. The dimerization of hematin
In aqueous solutions, at any pH, hematin forms stable dimers. Two dimer chemical structures have been put forth and are illustrated in Fig. 4: π–π dimers, in which the Fe3+ ions are located on the outer sides of two parallel monomers bound by overlapping π electron density (Fig. 4A), and μ-oxo dimers, in which the Fe3+ ions of the constituent monomers face each other and are bound to a shared oxygen atom (Fig. 4B) [38]. Careful recent work indicates that in aqueous solvents or in the presence of protic co-solvents, at neutral and moderately basic pH’s the π–π dimer is the only hematin oligomer [39,40]. The presence of aprotic co-solvents, such as pyridine and DMSO, or ionic compounds at high concentration, induces the formation of μ-oxo dimers [39].
Fig. 4.
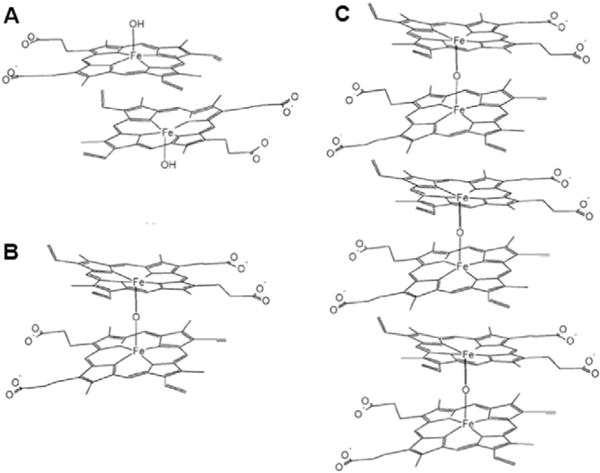
The structures of A, π–π dimer; B, μ-oxo dimer; and C, oligomers consisting of stacked μ-oxo dimers.
The μ-oxo dimers have a strong propensity to form larger oligomers bound by stacking π–π interactions [39]. In contrast, the π–π dimers, because of their structure, cannot form higher oligomers and are the terminal point in this pathway of hematin oligomerization [39,40].
Hemoglobin contains numerous polar hydrogen-containing groups on its surface and is thus a protic compound. Hence, mostly π–π hematin dimers are expected in the red cell cytosol. Because of their small size, the π–π hematin dimers easily pass through the dialysis membrane; since they are weakly bound [39]. they easily dissociate to enable hematin binding to apo-HRP. Thus, the presence of the π–π dimers should not interfere with the quantification of the free heme.
The equilibrium constant of formation of hematin dimers at pH = 7.38 has been determined as KD = 1.05 × 108 M−1. [40,41]. Straightforward mass balance calculations using the hematin dimerization constant reveal that the fraction of monomeric hematin in equilibrium with the dimers is 0.030 in solutions with Cheme = 21 μM, as in Fig. 3.
To more accurately account for the effect of hematin dimerization on its release from hemoglobin, we solve a system of equations consisting of the expressions for the equilibrium constants for heme release K−H, and hematin dimerization KD. We use two additional mass balance constraints: that the total free heme concentration is equal to that of the apoglobin, and that the initial methemoglobin concentration is equal to the sum of its equilibrium value and the apoglobin concentration. A system of four equations with four unknown emerges:
| (11) |
We apply two reasonable assumptions: that the apoglobin concentration is significantly lower than that of methemoglobin, and that the equilibrium concentration of monomeric hematin is much less than its total concentration. We obtain for the total free heme concentration
| (12) |
If the second assumption is relaxed, i.e., if both Hmonomer and Hdimer are present in significant amounts, then Cheme is the solution of a cubic equation
| (13) |
Eq. (13) has a single real root greater than zero: for Cheme = 0, the cubic polynomial on the left hand side is negative, while for sufficiently high values of Cheme, it is positive. It can be solved numerically. For the lowest methemoglobin concentration in Table 1, the difference between the values of Cheme returned by Eqs. (12) and (13), 35 and 31 nm, respectively, is about 13%. This difference decreases as CHb+ increases since greater CHb+ leads to greater Cheme and higher fraction of dimers.
In Table 2 we list values of the total concentration of free heme Cheme computed with account for hematin dimerization using Eq. (13) for the same methemoglobin concentrations as in Table 1. While the values of Cheme in Table 2 are greater than those in Table 1, they are still significantly lower than the values in the erythrocytes of normal individuals. Accounting for the disparity in temperature, pH, ionicity, and osmolality, at which the constants involved in Eq. (11) were measured, may increase Cheme to about 0.1 μM, at best, in methemoglobinemia-free individuals. Thus, a process resulting in heme release faster than the one assumed in the calculation of K−H is needed to understand the found concentrations of free heme in healthy erythrocytes.
Table 2.
The total concentration of free heme Cheme computed using Eq. (13) and the values of the heme dissociation constant from Table 1 for three values of the methemoglobin concentration CHb+.
|
CHb+
|
K−H
|
Cheme
|
|
|---|---|---|---|
| mg mL−1 | mM | M | nM |
| 3.5 | 0.054 | 7.10 × 10−12 | 35 |
| 11.5 | 0.18 | 5.93 × 10−12 | 68 |
| 100 | 1.55 | 4.73 × 10−12 | 232 |
A non-equilibrium process that could lead to faster release of heme from hemoglobin is autocatalytic acceleration of the rate of heme dissociation. The action of such mechanism is suggested by the arrested release of heme in diluted solutions, demonstrated by the data in Fig. 2. Testing a hypothetical autocatalytic heme release requires extended experimentation and is the subject of another paper.
5. Conclusions
The release of heme from hemoglobin and the accumulation of hematin in the red blood cells have numerous deleterious effects. To determine the concentration of free heme in erythrocytes, we have developed a new method based on dialytic separation of heme from hemoglobin, reconstitution of horseradish peroxidase, and determination of the peroxidase reaction rate from the released luminescence intensity. To validate the method, we demonstrate that heme is not released during the storage of red blood cells, after hemolysis, and during the dialysis. In addition, we show the heme present in the hemolysate is not released from the erythrocyte membranes. Collectively, these and several other tests suggest that the heme amounts determined by the proposed method are representative of the free heme present in the erythrocyte cytosol. We show that the error of the determination of the concentrations of free heme is about 5% and the lowest concentration of heme in the dialysate detected by this technique is between 20 and 50 pM.
Employing this method, we determine the average concentration of free heme in the red blood cells of five healthy adults. The average over the five donors is 21 μM, and the deviations from this number in individual donors are low, within 2 μM. The found concentrations are ca. 100× higher than previously determined. We test the effects of high concentrations of NaCl, used in that previous determination to separate heme from hemoglobin by charge, and find that this salt prevents the separation of heme from hemoglobin, likely be increasing the chemical potential of hematin and inducing its rebinding to apoglobin.
We compare the found concentrations of free heme to predictions of equilibrium models of heme release from met-hemoglobin. We account for the known propensity of hematin to oligomerize in aqueous solutions. This comparison indicates that heme is released at amount that significantly exceeds the model predictions. The processes leading to extraneous heme in the red blood cell cytosol are unclear at this point.
Supplementary Material
Acknowledgments
We are deeply indebted to R.C. Willson for his help with the procedure for free heme determination and for generous access to the Tecan Microplate Reader, V. Balakotaiah for insights into enzymatic kinetics and autocatalysis, Y. Li for participation in preliminary experiments, K. Waller, RN, and J. Nguyen, RN, from the UH Health Center for competent and expeditious assistance in the collection of blood from healthy donors, A. Linsey and R. Fuller from the Gulf Coast Regional Blood Center for additional blood samples, and John O’Shea from BBI Enzymes for help with apo-HRP. This work was supported by the Norman Hackerman Advanced Research Program (Grant 003652-0078-2009), NSF (Grant MCB-1244568), and NIH (U01HL114476).
Abbreviations
- HPLC
high performance liquid chromatography
- HRP
horse radish peroxidase
- Tris
Trisaminomethane, or 2-Amino-2-hydroxymethyl-propane-1,3-diol
- SDS
sodium dodecyl sulfate
Appendix A. Supplementary data
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.bcmd.2015.09.003.
References
- 1.Bunn HF, Jandl JH. Exchange of heme among hemoglobins and between hemoglobin and albumin. J Biolumin Chemilumin. 1968;243:465–475. [PubMed] [Google Scholar]
- 2.Hargrove MS, Whitaker T, Olson JS, Vali RJ, Mathews AJ. Quaternary structure regulates hemin dissociation from human hemoglobin. J Biol Chem. 1997;272:17385–17389. doi: 10.1074/jbc.272.28.17385. [DOI] [PubMed] [Google Scholar]
- 3.Hebbel RP, Morgan WT, Eaton JW, Hedlund BE. Accelerated autoxidation and heme loss due to instability of sickle hemoglobin. Proc Natl Acad Sci. 1988;85:237–241. doi: 10.1073/pnas.85.1.237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Light WR, Olson JS. Transmembrane movement of heme. J Biol Chem. 1990;265:15623–15631. [PubMed] [Google Scholar]
- 5.Chou AC, Fitch CD. Mechanism of hemolysis induced by ferriprotoporphyrin IX. J Clin Invest. 1981;68:672–677. doi: 10.1172/JCI110302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levin G, Cogan U, Levy Y, Mokady S. Riboflavin deficiency and the function and fluidity of rat erythrocyte membranes. J Nutr. 1990;120:857–861. doi: 10.1093/jn/120.8.857. [DOI] [PubMed] [Google Scholar]
- 7.Kirschner-Zilber I, Rabizadeh E, Shaklai N. The interaction of hemin and bilirubin with the human red cell membrane. Biochim Biophys Acta. 1982;690:20–30. doi: 10.1016/0005-2736(82)90234-6. [DOI] [PubMed] [Google Scholar]
- 8.Fitch C, Chevli R, Kanjananggulpan P, Dutta P, Chevli K, Chou A. Intracellular ferriprotoporphyrin IX is a lytic agent. Blood. 1983;62:1165–1168. [PubMed] [Google Scholar]
- 9.Goldstein L, Teng ZP, Zeserson E, Patel M, Regan RF. Hemin induces an iron-dependent, oxidative injury to human neuron-like cells. J Neurosci Res. 2003;73:113–121. doi: 10.1002/jnr.10633. [DOI] [PubMed] [Google Scholar]
- 10.Dutra FF, Alves LS, Rodrigues D, Fernandez PL, de Oliveira RB, Golenbock DT, Zamboni DS, Bozza MT. Hemolysis-induced lethality involves inflammasome activation by heme. Proc Natl Acad Sci. 2014;111:E4110–E4118. doi: 10.1073/pnas.1405023111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Becker K, Tilley L, Vennerstrom JL, Roberts D, Rogerson S, Ginsburg H. Oxidative stress in malaria parasite-infected erythrocytes: host–parasite interactions. Int J Parasitol. 2004;34:163–189. doi: 10.1016/j.ijpara.2003.09.011. [DOI] [PubMed] [Google Scholar]
- 12.Klouche K, Morena M, Canaud B, Descomps B, Beraud JJ, Cristol JP. Mechanism of in vitro heme-induced LDL oxidation: effects of antioxidants. Eur J Clin Investig. 2004;34:619–625. doi: 10.1111/j.1365-2362.2004.01395.x. [DOI] [PubMed] [Google Scholar]
- 13.Kuross SA, Rank BH, Hebbel RP. Excess heme in sickle erythrocyte inside-out membranes: possible role in thiol oxidation. Blood. 1988;71:876–882. [PubMed] [Google Scholar]
- 14.Wagener FADTG, Abraham NG, van Kooyk Y, de Witte T, Figdor CG. Heme-induced cell adhesion in the pathogenesis of sickle-cell disease and inflammation. Trends Pharmacol Sci. 2001;22:52–54. doi: 10.1016/s0165-6147(00)01609-6. [DOI] [PubMed] [Google Scholar]
- 15.Amin BR, Bauersachs RM, Meiselman HJ, Mohandas N, Hebbel RP, Bowen PE, Schlegel RA, Williamson P, Westerman MP. Monozygotic twins with sickle cell anemia and discordant clinical courses: clinical and laboratory studies. Hemoglobin. 1991;15:247–256. doi: 10.3109/03630269109027877. [DOI] [PubMed] [Google Scholar]
- 16.Adisa OA, Hu Y, Ghosh S, Aryee D, Osunkwo I, Ofori-Acquah SF. Association between plasma free haem and incidence of vaso-occlusive episodes and acute chest syndrome in children with sickle cell disease. Br J Haematol. 2013:702–705. doi: 10.1111/bjh.12445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mahendra A, Gangadharan B, André S, Boudjoghra M, Davi F, Lecerf M, Planchais C, Kaveri SV, Lacroix-Desmazes S, Dimitrov JD. Cryptic polyreactivity of IgG expressed by splenic marginal zone B-cell lymphoma. Mol Immunol. 2014;60:54–61. doi: 10.1016/j.molimm.2014.03.009. [DOI] [PubMed] [Google Scholar]
- 18.Liu SC, Zhai S, Palek J. Detection of hemin release during hemoglobin S denaturation. Blood. 1988;71:1755–1758. [PubMed] [Google Scholar]
- 19.Luo D, Huang J. Determination of cytochrome c and other heme proteins using the reduction wave of mercury protoporphyrin IX groups generated by a hydroxylamine induced replacement reaction. Anal Chem. 2009;81:2032–2036. doi: 10.1021/ac8023735. [DOI] [PubMed] [Google Scholar]
- 20.Appaix F, Minatchy MN, Riva-Lavieille C, Olivares J, Antonsson B, Saks VA. Rapid spectrophotometric method for quantitation of cytochrome c release from isolated mitochondria or permeabilized cells revisited. Biochim Biophys Acta Biomembr. 2000;1457:175–181. doi: 10.1016/s0005-2728(00)00098-0. [DOI] [PubMed] [Google Scholar]
- 21.Crouser ED, Gadd ME, Julian MW, Huff JE, Broekemeier KM, Robbins KA, Pfeiffer DR. Quantitation of cytochrome c release from rat liver mitochondria. Anal Biochem. 2003;317:67–75. doi: 10.1016/s0003-2697(03)00044-7. [DOI] [PubMed] [Google Scholar]
- 22.Tan SN, Hua L. Amperometric detection of cytochrome c by capillary electrophoresis at a sol–gel carbon composite electrode. Anal Chim Acta. 2001;450:263–267. [Google Scholar]
- 23.Scheller FW, Bistolas N, Liu S, Jänchen M, Katterle M, Wollenberger U. Thirty years of haemoglobin electrochemistry. Adv Colloid Interf Sci. 2005;116:111–120. doi: 10.1016/j.cis.2005.05.006. [DOI] [PubMed] [Google Scholar]
- 24.Whiteaker JR, Fenselau CC, Fetterolf D, Steele D, Wilson D. Quantitative determination of heme for forensic characterization of Bacillus spores using matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. Anal Chem. 2004;76:2836–2841. doi: 10.1021/ac034959r. [DOI] [PubMed] [Google Scholar]
- 25.Stiebler R, Hoang AN, Egan TJ, Wright DW, Oliveira MF. Increase on the initial soluble heme levels in acidic conditions is an important mechanism for spontaneous heme crystallization in vitro. PLoS One. 2010;5:e12694. doi: 10.1371/journal.pone.0012694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Takahashi S, Masuda T. High throughput heme assay by detection of chemiluminescence of reconstituted horseradish peroxidase. Comb Chem High Throughput Screen. 2009;12:532–535. doi: 10.2174/138620709788489028. [DOI] [PubMed] [Google Scholar]
- 27.Huntress E, Stanley L, Parker A. The preparation of 3-aminophthalhydrazide for use in the demonstration of chemiluminescence. J Am Chem Soc. 1934;56:241–242. [Google Scholar]
- 28.Huntress EH, Stanley LN, Parker AS. The oxidation of 3-aminophthalhydrazide (“luminol”) as a lecture demonstration of chemiluminescence. J Chem Educ. 1934;11:142. [Google Scholar]
- 29.Hargrove MS, Barrick D, Olson JS. The association rate constant for heme binding to globin is independent of protein structure. Biochemistry. 1996;35:11293–11299. doi: 10.1021/bi960371l. [DOI] [PubMed] [Google Scholar]
- 30.Guida V, Criscuolo G, Tamburino R, Malorn IL, Parente A, Di Maro A. Purification and enzymatic properties of a peroxidase from leaves of Phytolacca dioica L (Ombú tree) BMB Rep. 2011;44:64–69. doi: 10.5483/BMBRep.2011.44.1.64. [DOI] [PubMed] [Google Scholar]
- 31.Prodanović O, Prokopijević M, Spasojević D, Stojanović Ǘ, Radotić K, Knežević-Jugović Z, Prodanović R. Improved covalent immobilization of horseradish peroxidase on macroporous glycidyl methacrylate-based copolymers. Appl Biochem Biotechnol. 2012;168:1288–1301. doi: 10.1007/s12010-012-9857-7. [DOI] [PubMed] [Google Scholar]
- 32.Cooper SL, Bamford CH, Tsuruta T. Polymer Biomaterials in Solution, As Interfaces And As Solids: A Festschrift Honoring the 60th Birthday of Dr. Allan S. Hoffman. Vsp International Science Publishers; 1995. [Google Scholar]
- 33.Edelstein SJ, Rehmar MJ, Olson JS, Gibson QH. Functional aspects of the subunit association-dissociation equilibria of hemoglobin. J Biol Chem. 1970;245:4372–4381. [PubMed] [Google Scholar]
- 34.Kuross SA, Hebbel RP. Nonheme iron in sickle erythrocyte membranes: association with phospholipids and potential role in lipid peroxidation. Blood. 1988;72:1278–1285. [PubMed] [Google Scholar]
- 35.Gattoni M, Boffi A, Sarti P, Chiancone E. Stability of the heme-globin linkage in alphabeta dimers and isolated chains of human hemoglobin. A study of the heme transfer reaction from the immobilized proteins to albumin. J Biol Chem. 1996;271:10130–10136. doi: 10.1074/jbc.271.17.10130. [DOI] [PubMed] [Google Scholar]
- 36.Rodkey FL, Hill TA, Pitts LL, Robertson RF. Spectrophotometric measurement of carboxyhemoglobin and methemoglobin in blood. Clin Chem. 1979;25:1388–1393. [PubMed] [Google Scholar]
- 37.Beutler E. The effect of methemoglobin formation in sickle cell disease. J Clin Invest. 1961;40:1856–1871. doi: 10.1172/JCI104410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cannon JB. Pharmaceutics and drug delivery aspects of heme and porphyrin therapy. J Pharm Sci. 1993;82:435–446. doi: 10.1002/jps.2600820502. [DOI] [PubMed] [Google Scholar]
- 39.Asher C, de Villiers KA, Egan TJ. Speciation of ferriprotoporphyrin IX in aqueous and mixed aqueous solution is controlled by solvent identity, pH, and salt concentration. Inorg Chem. 2009;48:7994–8003. doi: 10.1021/ic900647y. [DOI] [PubMed] [Google Scholar]
- 40.de Villiers KA, Kaschula CH, Egan TJ, Marques HM. Speciation and structure of ferriprotoporphyrin IX in aqueous solution: spectroscopic and diffusion measurements demonstrate dimerization, but not mu-oxo dimer formation. J Biol Inorg Chem. 2007;12:101–117. doi: 10.1007/s00775-006-0170-1. [DOI] [PubMed] [Google Scholar]
- 41.Brown SB, Dean TC, Jones P. Aggregation of ferrihaems. Dimerization and protolytic equilibria of protoferrihaem and deuteroferrihaem in aqueous solution. Biochem J. 1970;117:733–739. doi: 10.1042/bj1170733. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


