Computational Implications of Biophysical Diversity and Multiple Timescales in Neurons and Synapses for Circuit Performance

Abstract

Despite advances in experimental and theoretical neuroscience, we are still trying to identify key biophysical details that are important for characterizing the operation of brain circuits. Biological mechanisms at the level of single neurons and synapses can be combined as ‘building blocks’ to generate circuit function. We focus on the importance of capturing multiple timescales when describing these intrinsic and synaptic components. Whether inherent in the ionic currents, the neuron’s complex morphology, or the neurotransmitter composition of synapses, these multiple timescales prove crucial for capturing the variability and richness of circuit output and enhancing the information-carrying capacity observed across nervous systems.

Introduction

To what extent can we understand the dynamics of large circuits using biophysical descriptions of single neurons and small subcircuits? In 1989 Getting suggested that the biophysical properties of individual neurons and small circuits could serve as ‘building blocks’ for a library of biological mechanisms that would aid in understanding all circuits [1]. Getting compiled a partial list of cellular, synaptic and network properties important for neural network operation (Table 1). Many of the features on this list, including intrinsic properties like spike frequency adaptation, post-burst hyperpolarization, and delayed excitation, refer to changes in temporal firing patterns that can last from milliseconds to seconds. Getting also underscored the dramatically different time courses of individual synaptic potentials, such as in the network of interneurons that generate the escape swimming motor program of Tritonia, as well as the ability of a single synaptic connection to mediate several actions with different timescales as seen in multicomponent synapses.

Table 1.

Building blocks for circuit dynamics by Peter Getting [1].

Cellular	synaptic	Connectivity
Threshold	Sign	Mutual or recurrent inhibition
F-I relationship	Strength
Spike frequency adapt.	Time course	Reciprocal or lateral inhibition
Post-burst hyperpol.	Transmission
Delayed excitation	Electrical	Recurrent inhibition
Post-inhibitory rebound	Chemical	Recurrent cyclic inhibition
Plateau potentials	Release mechanism	Parallel excit./inhib.
Bursting	Graded
Endogenous	Spike
Conditional	Multicomponent PSP

More than 25 years later, we are still struggling to understand which of the myriad of biophysical properties, such as those of Getting’s building blocks (Table 1), are crucial to include in models of brain circuits. Ideally, we should be able to identify a broad array of reusable computational mechanisms that can be combined to generate function and describe circuit dynamics. We suggest that models should capture the relevant timescales of each of the circuit components. These building blocks are often nonlinear; thus, circuit dynamics are the product of a complex spatial and temporal interaction of multiple, nonlinear processes at the cellular and synaptic levels. Therefore, multiple networks that have distinct functions can be realized by using the same constituent building blocks combined in different ways. In this review we highlight recent work that discusses the relevance of biophysical building blocks for circuit dynamics focusing on the role of multiple timescales in the intrinsic and synaptic components of neurons and circuits.

Neuronal intrinsic excitability occurs at multiple timescales

Elaborate morphologies and diverse ion channels determine the intrinsic excitability of all neurons. To reduce the potential complexity of this high-dimensional space, for many years neuroscientists have been developing strategies to extract the core features of intrinsic neuronal excitability [2•].

Many studies employ single-compartment models that simplify the neuron’s morphology but incorporate specific details of membrane conductances (Figure 1). Choosing the appropriate set of intrinsic conductances depends on the features that the model is aimed at explaining. Some models are constructed by modeling measurements from voltage clamp experiments of all known membrane currents [3, 4]. Others are more minimalist. For instance, integrate-and-fire or threshold model neurons can be successful in capturing spike initiation dynamics [5•, 6]. But adaptation and history-dependence require additional intrinsic currents [7]. To infer parameter values for these currents from observed membrane potential traces, probabilistic frameworks based on statistical inference [8, 9] and optimization techniques aimed at minimizing different objective functions have been developed [10•]. A recent study has implemented a control theoretic approach to promote alignment between the recorded and model trajectory during the fitting procedure; in addition to fitting synthetically generated data, the procedure also successfully fitted experimental traces [11•].

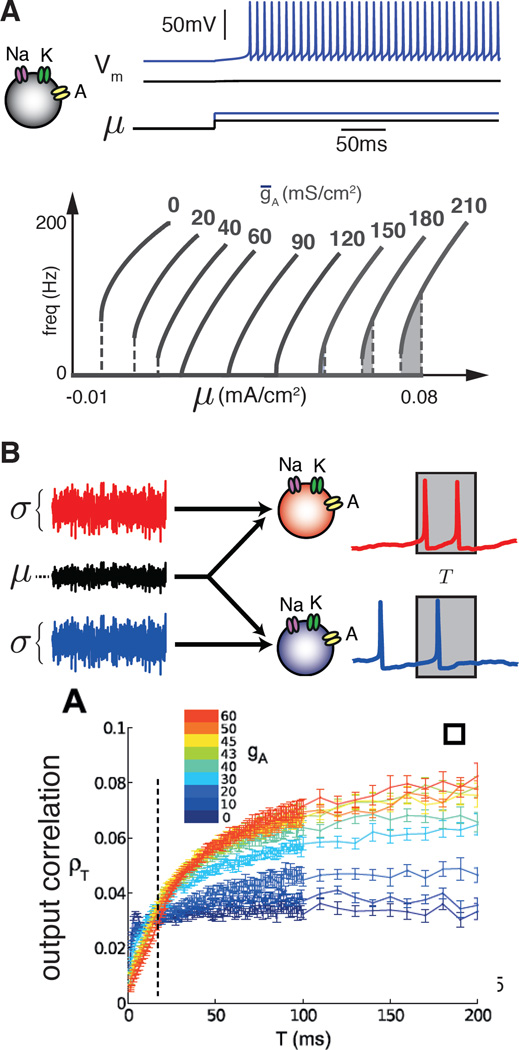
Figure 1. Single neuron biophysics impacts intrinsic properties and correlated-based population coding.

A. Firing rate vs. injected current (f-I) curves, for the Connor- Stevens model [95]. We show f-I curves for a range of g_A values yielding a range from type II to type I excitability and then to type II* excitability [37]. B. Top: A microcircuit in which two neurons receive input currents with a common component that represents correlated activity or shared afferents upstream. The mean of the input currents is μ and each fluctuates with standard deviation σ. By varying the fraction of the common component (black trace in A), relative to the independent components (red and blue traces in A), we can control the strength of the input correlation driving the microcircuit. Shared input currents lead to correlated spikes, which are quantified using the correlation coefficient of the two neurons’ spike counts counted in time windows of length T. Type II neurons with low g_A transfer more correlations at small T, while for high T the trend switches (dashed line) with type I neurons with high g_A being able to transfer more correlations [66].

Approaches for determining appropriate model parameters must overcome the following two challenges: (1) Capture the substantial variability observed in experimental measurements of voltage-dependent current densities, ion channel mRNA levels and synaptic connections, suggesting that the space of solutions is highly degenerate and multiple solutions exist for the same output [12–16, 17•]; (2) Achieve robust modulation in spite of variability and degeneracy [18•, 19, 20]. Recent studies highlight the importance of building populations of models that capture the variability of parameters seen in experimental measurements [21, 22]. Computational database approaches based on parameter exploration of experimentally identified conductances have successfully uncovered multiple and degenerate solutions [23–25, 26•]. Interesting correlations among intrinsic conductances and neuronal output have been found experimentally at the single neuron level [27], and in computational studies at the circuit level using reduction approaches like principal component analysis to find the interaction of multiple parameters [28•] or simple homeostatic rules operating at the level of the constituent neurons [29•].

Database and model reconstruction approaches have been used to fit ion channel distributions on anatomical reconstructions of known neurons [30–32, 33•]. A recent study showed that, to maintain functional properties along the dendritic tree of a neuron, mechanisms that tune the number of all ion channels collectively are more likely than those that tune the number of individual ion channels – this would not have been seen in single-compartment models [34•]. In some instances, such as the implementation of direction selectivity in the mammalian retina, the entire computation relies primarily on the spatial structure of dendrites [35••].

Methods have been developed to assess quantitatively the role of biophysical parameter variations in neuronal activity, independent of the neuron model and the set of intrinsic conductances [36••]. Dynamic input conductances (DICs) are voltage-dependent conductance curves that evolve over time, aggregating the activity of all ion channels in the generation of neuronal activity, and are a useful technique to study how diverse ion channels contribute to modulation, robustness and homeostasis in neuronal signaling in different biological systems [36••, 37•]. Although currently only applicable to single neurons, this method can also include the contribution of synaptic conductances. This should allow the characterization of network dynamics from the analysis of smaller building blocks in more principled ways than large-scale simulations.

Modeling the complexity of biological synapses

Most models of neuronal networks use simple synapse models that do not capture the full richness of use-dependent synaptic dynamics, even when they attempt to represent synaptic learning rules [38–40]. It has been long known that many different neurotransmitters are used in nervous systems, and that the same neurotransmitter can elicit a variety of postsynaptic actions, depending on the properties of the receptors on the postsynaptic membrane (Figure 2A) [41]. Moreover, many neurons contain and release cotransmitters that can act on multiple timescales [42].

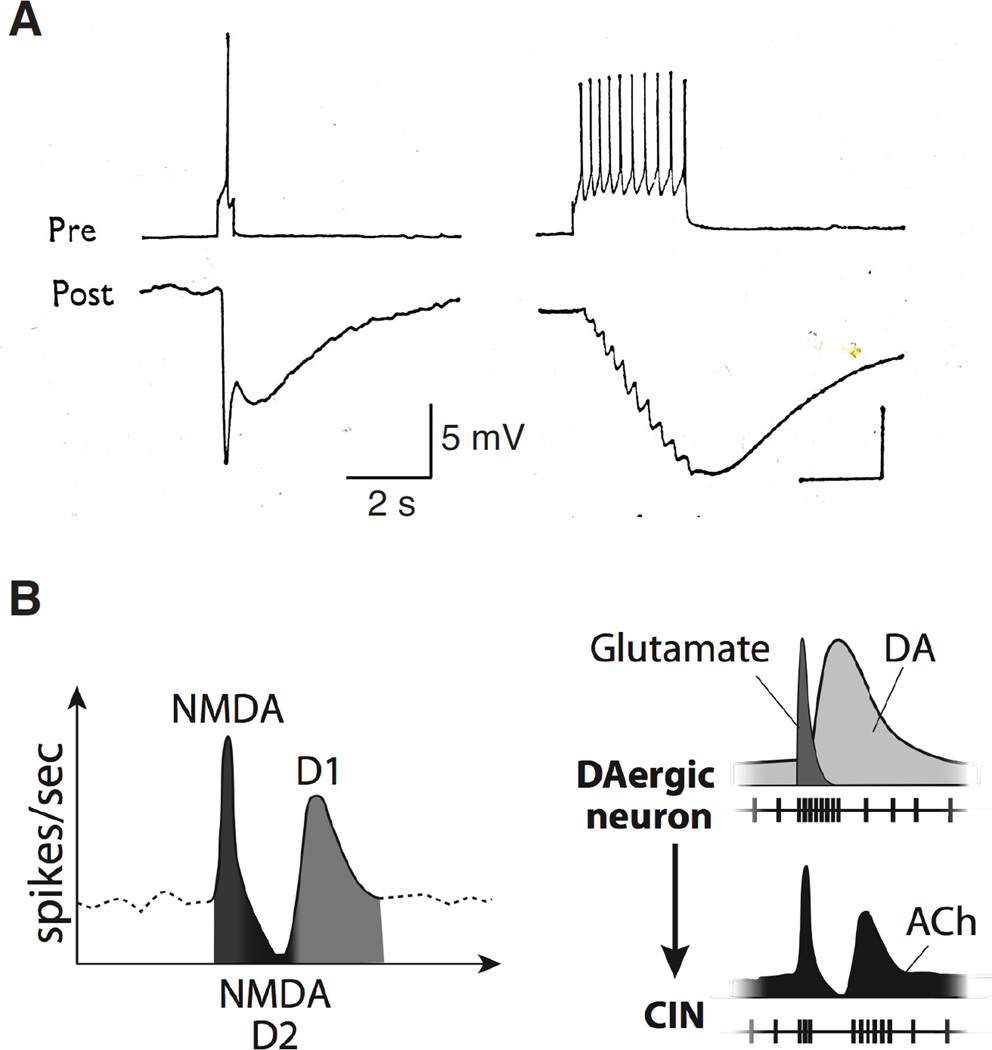
Figure 2. Synaptic transmission occurs at multiple timescales.

A. Left: A two-component inhibitory response of medial pleural neuron (in Aplysia) at resting level (Post) to a single presynaptic spike (Pre). Right: Typical response of a medial pleural neuron to repeated firing of the presynaptic neuron. A rapid IPSP is associated with each presynaptic spike, whereas the slow IPSP is only evident with repeated firing and is seen as a summated slow wave [41]. B. Phasic activation of DA controls the three different components of firing in striatal interneurons by coordinated action of glutamate and DA release: glutamate (NMDA) receptor activation evokes an initial burst followed by an afterhyperpolarlization with a firing pause, while DA elicits both a D2-type DAR-dependent firing pause and a late D1-type DAR-dependent burst. DA – dopamine, Ach – Acetylcholine, CIN – cholinergic interneuron [58].

In the last several years, a variety of exciting studies of cotransmission in the vertebrate brain are revealing additional features of synapses long-thought simpler than they really are [43–46, 47••, 48•, 49•, 50••, 51••]. Midbrain dopaminergic neurons can corelease glutamate and GABA [46, 47••, 52], which have been shown to be regionally heterogeneous [53••] and differentially affected by external perturbations such as cocaine consumption [54••]. Neurons can switch their transmitter composition over time, both during development and under different physiological conditions in the mature brain leading to changes in behavior [55, 56•, 57•].

Wieland and colleagues [58••] show that the corelease of glutamate and dopamine from midbrain dopamine neurons onto olfactory tubercle cholinergic interneurons induces a triphasic postsynaptic event composed of an early excitation due to glutamate (NMDA) receptor activation, an intermediate inhibition due to dopamine D2 receptor activation, and a late excitation due to dopamine D1 receptor activation (Figure 2B). Such multicomponent drive underlies the typical response of striatal cholinergic interneurons to relevant sensory stimuli, which can be an initial burst, a firing pause, a late burst, or a combination of the three.

Khalilov and colleagues have recently demonstrated that GABA actions in the immature hippocampal network critically depend on network state [59••]. Due to transient changes in the postsynaptic chloride driving force, GABA currents transiently switch from depolarizing to hyperpolarizing to depolarizing during giant depolarizing potentials, exerting both excitatory and inhibitory roles. This might explain the otherwise contradictory epileptogenic effect of GABA_A antagonists observed in this network.

Taken together, these recent observations suggest that the multicomponent nature of synaptic potentials is a critical property that strongly shapes neuronal activity at the network level. Due to the richness of cotransmitters and postsynaptic receptors, transient synaptic release can exert both transient and long-lasting effects on postsynaptic neuron excitability. This argues that network models that treat all synapses with a single timescale are likely to be missing important principles of how brain circuits compute.

From single neuron dynamics to circuit function

Understanding how single neuron and single synapse dynamics alter circuit behavior has classically been studied in both small and large circuits. In the former, it is possible to see directly how one or more biophysical details influence circuit function. In the latter case, it is common to ask how changes in the properties of a population influence circuit function. In both cases, the challenge is to understand the extent to which the circuit’s output is influenced either by its architecture or by the properties of its component elements.

Reciprocal inhibition in half-center oscillators has been studied for 100 years [60–63]. In modeling studies, the two constituent neurons and their synapses are usually identical. Experimental studies, however, have incorporated some variable properties of the intrinsic and synaptic components [63, 64]. In a recent modeling study, Dethier and colleagues examine the robustness of half-center oscillations made from neurons with different subsets of conductances [65••]. They find that a network with low-threshold T-type calcium current has a slow positive feedback at a timescale that endows the network with increased robustness to intrinsic and external perturbations, relative to a network with an H-conductance. This offers opportunities for reliable modulation [65••].

Information and correlation transfer also depend on the constituent neurons’ biophysical properties. Small two-neuron populations allow this feature to be studied analytically. For instance, type I neurons (with more A current) transfer correlations over longer timescales (100 ms), while type II neurons (with less A current) transfer correlations over shorter timescales (5 ms) (Figure 1) [66, 67]. The next challenge would be to take these small circuit motifs and translate them to describing the dynamics of larger networks [68••].

How biophysical properties of single neurons impact network function and coding has been addressed in the context of signal propagation through feedforward networks [69••]. Mease and colleagues have recently identified a change in the ratio of I_Na and I_K in developing mouse cortical neurons that enables these neurons to adaptively scale the gain of their response to the amplitude of the fluctuations they encounter [70•]. In a follow-up study, Gjorgjieva and colleagues examined information transmission at different timescales in networks equipped with neurons with different conductance ratios [69••]. Independent of the absolute values of the conductances, the networks either became efficient encoders of fast input fluctuations, or gained the ability to transmit slower, population-wide input variations in the network [69••]. This work underscores the significance of simple changes in conductance parameters in governing how neurons represent and propagate information across multiple timescales in networks.

Several experimental and computational studies address the role of diversity in intrinsic properties for how neuronal populations process stimuli and produce robust output. Some recent work examines the possibility that intrinsic properties are tuned to maximize the information of the neurons’ response about the stimuli they encode [71, 72•, 73••, 74•, 75]. Such theories of efficient coding, however, thus far apply most directly to sensory populations where there is a clear definition of the stimuli that the neurons represent. A future challenge will be to interpret them in the context of larger circuits where information is integrated from different brain regions and sensory modalities.

How do we know what biophysical details matter for circuit performance?

We are starting to see increasing attempts to build very large networks of neurons with biophysically “realistic” sets of conductances [76–78]. While aiming for increased biological verisimilitude, such models, even when carefully constructed and supposedly validated, can be as difficult to understand as the biological systems they are meant to represent. What is worse, these models, no matter how carefully constructed, are always “wrong,” as they fail to contain all the biological machinery that is either unknown or viewed as less fundamental by the investigator. Paradoxically, up to a point, increasing biological realism in large-scale networks probably aids understanding, while past some point, increasing biological realism impedes understanding. At present, it is unclear where the inflection point describing model complexity and increased understanding lies. Used well, with specific questions in mind, large-scale biophysically-realistic models can drive intuition [77, 78]. Otherwise, they risk adding mystery and confusion.

To understand circuit dynamics as a function of their intrinsic and synaptic properties, it is necessary to have a reliable measure of circuit output. In some cases, circuit behavior is clear. Primary sensory circuits like the retina in the visual system and the olfactory bulb in the olfactory system can be described by well-defined input-output relations. For motor circuits, it is relatively easy to quantify circuit performance.

Quantifying circuit dynamics becomes a difficult problem if circuits are degenerate so that understanding the role of any one attribute to circuit function is nontrivial because a manipulation of a single component can have different effects depending on the particular ways that circuit components are combined. Older studies on the Aplysia gill withdrawal reflex showed that variable sets of neurons can participate in the production of a given behavior and that no two trials produce the same pattern [79–81]. Sensory neurons in C. elegans exhibit stochastic responses to the repeated presentation of the same sensory stimulus [82]. This variability is present at the level of behavior as well: behavioral variability persists even when responses of sensory neurons are reproducible [83••]. Moreover, the sensitivity to specific odors shows increased variability across individual animals relative to repeated stimulation in one animal, and adaptation of response variability can be observed in multiple trials [83••].

The analysis of small rhythmic circuits can help discover principles in larger circuits. For instance, neurons can switch in and out of different oscillatory subnetworks, or participate in two rhythms at the same time [84•]. Computational and experimental studies can help us uncover degenerate mechanisms by which such switching occurs [18•, 84•, 85]. But the main challenge remains: if different neurons are active in multiple trials to repeated presentation of the same stimulus, how do we determine the role of individual biophysical properties in different states of neuronal activity?

In higher brain areas, it can be less than obvious what computations the circuits perform. Parallel results of variable output have been found in recordings of larger networks, such as the place cells in the rodent hippocampus during a virtual navigation task. The place cells exhibit location-specific firing so that their activity is confined with remarkable precision to a cell-specific part of the environment. Despite this spatial precision, the temporal firing pattern is not nearly as reliable [86, 87]. Variability across individuals is also prevalent in studies of the human cortex, as shown by functional magnetic resonance imaging [88, 89•].

Conclusions

Models of the future will need to capture more explicitly the multiple timescales shaping intrinsic and synaptic excitability. Although we can learn much from small circuits that produce well-defined outputs, the challenge will be to transfer that knowledge to understand the operation of larger brain circuits that integrate information from different sensory modalities and internal states as in the case of behaving animals. Recent studies have underscored the widely variable internal dynamics and responsiveness to external stimuli across different behavioral contexts and brain states [90]. Neuromodulators modulate intrinsic currents and thus control the excitability of cortical neurons as well as the generation of slow oscillations. These modulations occur on fast timescales that cannot be explained with processes like long-term potentiation and depression that change the strength of synaptic connections over many minutes or hours. Thus, to account for neuromodulation and homeostasis on one hand [29•, 91, 92•], and long-term synaptic plasticity on another [93, 94•] it will be necessary to build models of timescales that can account for the activity ranging from milliseconds to hours and days. Biological systems have managed to find mechanisms that allow them to function on many timescales seamlessly, but we are far from understanding the computational principles that allow this to occur.

Highlights.

• Biological neurons and synapses operate with many timescales.

• Many computational models of networks are timescale impoverished.

• Circuit operation can be understood from interacting nonlinear building blocks.