First-pass myocardial perfusion imaging with whole-heart coverage using L1-SPIRiT accelerated variable density spiral trajectories

Abstract

Purpose

To design and evaluate 2D L1-SPIRiT accelerated spiral pulse sequences for first-pass myocardial perfusion imaging with whole heart coverage capable of measuring 8 slices at 2 mm in-plane resolution at heart rates up to 125 beats per minute (BPM).

Methods

Combinations of 5 different spiral trajectories and 4 k-t sampling patterns were retrospectively simulated in 25 fully sampled datasets and reconstructed with L1-SPIRiT to determine the best combination of parameters. Two candidate sequences were prospectively evaluated in 34 human subjects to assess in-vivo performance.

Results

A dual density broad transition spiral trajectory with either angularly uniform or golden angle in time k-t sampling pattern had the largest structural similarity (SSIM) and smallest root mean square error (RMSE) from the retrospective simulation, and the L1-SPIRiT reconstruction had well-preserved temporal dynamics. In vivo data demonstrated that both of the sampling patterns could produce high quality perfusion images with whole-heart coverage.

Conclusion

First-pass myocardial perfusion imaging using accelerated spirals with optimized trajectory and k-t sampling pattern can produce high quality 2D-perfusion images with wholeheart coverage at the heart rates up to 125 BPM.

Introduction

First-pass contrast-enhanced myocardial perfusion MRI has proven to be a promising noninvasive technique for evaluating patients with known or suspected coronary artery disease (CAD), demonstrating excellent diagnostic and prognostic utility^1–5. However, the technique has not yet gained widespread clinical adoption. One challenge that continues to limit its clinical use is achieving whole-heart coverage with high spatial resolution (≤2 mm) and with minimal artifacts, such as dark-rim artifact (DRA)⁶. Currently, a two-dimensional (2D) multi-slice saturation recovery (SR) prepared acquisition with parallel imaging (PI)^7,8 has been the most commonly used clinical method. With this approach, three to four short axis slices with 2–3 mm in-plane spatial resolution can be obtained per R-R interval⁹. Several investigators have used spatial-temporal acceleration techniques (k-t SENSE¹⁰, k-t PCA¹¹) to improve slice coverage and temporal/spatial resolution. 3D techniques have become available enabling whole-heart coverage but currently suffer from poor in-plane spatial resolution and a long temporal footprint resulting in increased sensitivity to cardiac motion-induced artifacts. Recently, the nonlinear reconstruction framework of Compressed Sensing (CS)^12,13 has garnered significant interest and has been applied to first-pass perfusion imaging^14,15. By exploiting inherent data redundancy in terms of sparsity, the technique allows for the reconstruction of MR images from highly under-sampled data and may significantly shorten scan time. Several investigators have explored utilizing temporal constraints to achieve high acceleration factors.^15,16

Spiral or radial trajectories have recently been applied to first-pass myocardial perfusion imaging^17–20. Non-Cartesian pulse sequences have attractive features such as high efficiency in traversing k-space, isotropic resolution and point-spread functions, and the lack of discrete ghosting resulting from motion. Non-Cartesian approaches are also compatible with PI and CS techniques, which could further reduce imaging time and improve temporal resolution. Potential drawbacks include sensitivity to off-resonance and concomitant field gradients which can result in blurring, signal loss, and sensitivity to inconsistent data artifacts when the signal intensity varies between spiral arms due to non-equilibrium magnetization. However, by carefully optimizing the spiral trajectory and reconstruction, these artifacts can be significantly mitigated. We have previously demonstrated high image quality and excellent clinical performance of spiral-based perfusion pulse sequences for the detection of obstructive CAD⁵.

To design an optimal whole-heart coverage spiral pulse sequence for first-pass perfusion imaging, specific goals for resolution, timing, and signal-to-noise ratio (SNR) should be set and an acquisition strategy must be clearly defined. Our prior work has shown that by careful consideration of the spiral trajectory readout duration, flip angle (FA), and image reconstruction strategy, variable density (VD) spiral pulse sequences could produce high-quality first-pass perfusion images with minimal dark-rim and off-resonance artifacts, along with high signal-to-noise and contrast-to-noise ratios, and good delineation of resting perfusion abnormalities^21,22. However, that sequence was still limited to three slice locations at heart rates up to 110 beats per minute (BPM). Thus, the goal of the present study was to accelerate the spiral sequence to allow acquisition of at least eight slices covering the entire myocardium per R-R interval at heart rates up to 125 BPM using the combination of PI and CS techniques.

Methods

Design Considerations

To perform multi-slice 2D spiral perfusion imaging with whole-heart coverage, timing factors need to be considered including the total time available for imaging all slices at a given heart rate and the time required to image each slice. In order to determine the maximum number of first-pass perfusion slice positions that can be imaged during each heartbeat, the duration of the cardiac cycle (the R-R interval) under both resting and vasodilator stress conditions must be considered. Typically, heart rates vary between 60–90 BPM at rest, corresponding to R-R intervals of 667–1000 ms, and increases by approximately 20% under adenosine or regadenoson stress²³, some patients may have heart rates as high as 125 BPM, which corresponds to an R-R interval of only 480 ms. The second important consideration is the amount of time required to collect each spiral perfusion image. The total imaging time of saturation recovery based spiral sequence is determined by:

$$T_{\mathit{total}}=(T_{\mathit{sat}}+TS+TR\ast n_{\mathit{arm}})\ast n_{\mathit{slc}}=(T_{\mathit{sat}}+TS)\ast n_{\mathit{slc}}+TR\ast n_{\mathit{arms}}\ast n_{\mathit{slc}}$$ (1)

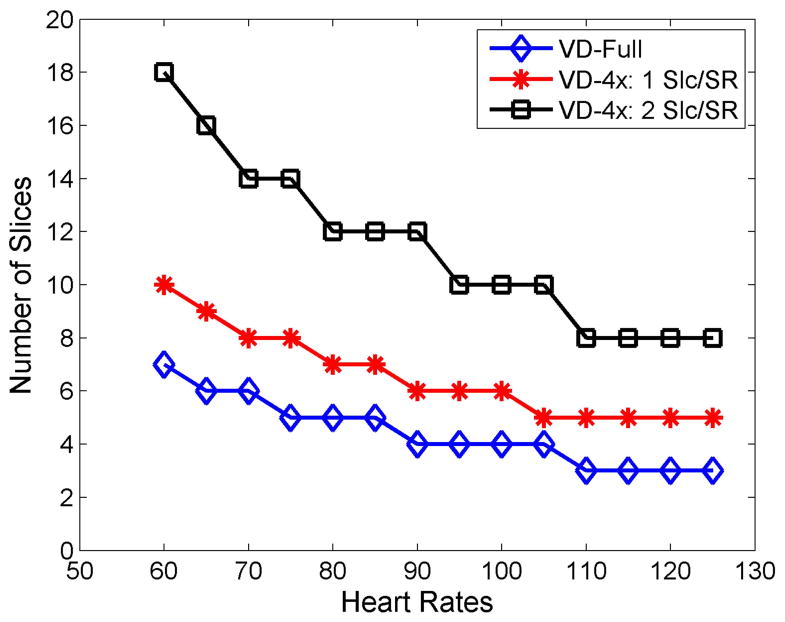
Where T_sat is the saturation pulse duration, TS is the saturation recovery time to the first readout RF pulse, TR is the time of acquiring one spiral arm, n_arm is the number of spiral arms, n_slc and is the total number of slices. For example, a pulse sequence using our previously developed VD trajectory²¹, with the parameters TS = 80 ms, TR = 9 ms, n_leave = 8, and 2 additional arms for field map estimation, can only support 3 slices up to a heart rate of 125 BPM. (Figure 1)

Figure 1.

Relationship between the maximum supported slice numbers for the VD-Full sequence, VD-4x: 1Slc/SR and VD-4x 2 Slc/SR at different heart rates. For the VD-Full sequence, only 3 slices are supported at the BPM of 125, while the accelerated VD-4x using 1 Slc/SR only acquires 5 slices. When 2 slices are imaged in one SR block, at least 8 slices can be imaged at the heart rates of 125 BPM.

As seen in Equation 1, the total imaging time per heartbeat (T_total), can only be shortened by reducing the number of arms, the readout duration per arm, or saturation recovery time. For a slew-limited spiral with a fixed spatial resolution, fixed variable density sampling pattern, and fixed total readout duration per image, the product of the number of arms and the readout duration per arm is approximately constant²¹. As the number of spiral arms increases, the SNR is reduced as the optimal FA for a given saturation time and T₁ range decreases. Conversely, reducing the number of arms at the expense of a longer readout per spiral arm does not reduce the time to image each slice. While the TS can be reduced, this comes at the expense of SNR and reduced T₁weighting. Thus, the most obvious way of shortening the T_total while maintaining the same T₁ weighting is to reduce the total number of arms by reducing the total sampling time and using parallel imaging techniques. For example, if only 2 out of 8 spirals (4x acceleration) were collected, the total readout time per image would be reduced to 18 ms instead of 72 ms. However, only 5 slices could be acquired at a heart rate of 125 BPM, as the total imaging time is dominated by the TS. For such a design, data acquisition would only occur for 18% of the R-R interval, which is very inefficient.

Therefore, the total amount of time waiting for T₁ preparation needs to be shortened. This can be achieved by acquiring multiple slices in an interleaved fashion following each saturation pulse, a concept which has previously been applied for EPI perfusion imaging.^24,25 The total imaging time collecting multiple slices per SR preparation is given by 

$$T_{\mathit{total}}=\left(T_{\mathit{sat}}+TS+TR\ast n_{\mathit{arm}}\ast \frac{n_{\mathit{slc}}}{n_{\mathit{Sat}}}\right)\ast n_{\mathit{Sat}}=(T_{\mathit{sat}}+TS)\ast n_{\mathit{Sat}}+TR\ast n_{\mathit{arm}}\ast n_{\mathit{slc}}$$ (2)

where n_Sat is the total number of SR pulses and $\frac{n_{\mathit{slc}}}{n_{\mathit{Sat}}}$ determines the number of slices acquired during each SR pulse. The total imaging time can be dramatically reduced by using this strategy. Typically, just 2 slices per SR would meet these criteria while still reducing the total time to acquire each image by 50%, further reducing sensitivity to motion induced dark-rim artifacts as compared to a fully sampled pulse sequence. Figure 1 shows the supported slice numbers of the fully sampled sequence (VD-Full), 1 slice per SR of 4x sequence (VD-4x-1 Slc/SR) and 2 slices per SR of 4x sequence (VD-4x-2 Slc/SR) at heart rate ranges from 60 to 125 BPM. A 4x accelerated VD spiral pulse sequence with 2 slices per SR pulse would support 8 slices over a total temporal window of 464 ms, thus supporting whole-heart coverage while maximizing data collection efficiency. 4x acceleration (2/8 spiral arms) is the lowest possible acceleration factor which meets criteria for the chosen spatial resolution, number of spiral arms, readout duration per spiral arm, and saturation recovery time. In order to further reduce the spiral trajectory off-resonance effects, we chose to shorten the spiral readouts (5 ms) as compared to our prior design and utilize 3 arms, as described in the following section. The above timing considerations still hold in this case.

Sequential Slice Order vs Interleaved Slice Order

When more than one slice is imaged after each SR pulse, the acquisition order could be either sequential²⁵ or interleaved²⁴ as described previously. A sequential slice order has the advantage of shorter temporal window for each slice; however, each slice would have a different effective T₁weighting time (by 21 ms), while an interleaved acquisition order would have a longer temporal window for each individual image. However, with a slice interleaved acquisition, utilizing 3 spiral arms per image, the effective temporal resolution for each slice would be 5* TR (35 ms) which includes three spiral arms from slice 1 and two spiral arms from slice 2, which is still short enough to prevent motion-induced artifacts. Secondly, the TS times would only differ by 1 TR (7 ms), which would produce a negligible difference in apparent contrast weighting. An additional benefit of the interleaved slice order is that for a given saturation time, the effective TR(TR_eff) between arms for a given slice is doubled enabling a larger FA to be utilized to further improve SNR.

SNR Considerations

To ensure that transverse magnetization evolution is the same for each spiral arm, we have previously derived an optimal constant FA (θ_c ) that exactly balances the loss in magnetization from each RF pulse²¹ to the T₁recovery of magnetization during each TR for a given TR, TS, and T₁: ${\theta }_c={\mathit{cos}}^{-1}\left(\frac{E_1-E_s}{E_1(1-E_s)}\right)$, where E₁ = exp(−TR/T₁) and Es = exp(−TS/T₁). The optimal FA for a 1 mmol/L gadolinium concentration (T₁= 175 ms in 1.5T) with the TS = 80 ms is 21° for sequential order (TR= 7 ms) and 31° for interleaved order (TR= 14 ms).

Compared with the VD-Full sequence, the SNR of the VD-4x sequence was reduced by half due to shortening of the total readout time by a factor of 4. However, the larger FA with interleaved acquisition results in 40% greater transverse magnetization compared to a sequential acquisition. Thus, the SNR of a 4x accelerated technique should only result in a 30% loss of SNR as compared to the non-accelerated sequence. Overall, these considerations indicate that the accelerated interleaved order 4x spiral sequence should have an acceptable SNR as compared to the fully sampled sequence. Furthermore, the use of compressed sensing should provide an increase in the visually apparent SNR of the image over that which is predicted by these theoretical considerations.

Spiral Trajectory Design

Slew-limited spiral gradient trajectories were created using the optimal spiral design of Meyer et al²⁶. Briefly, the k-space trajectory is defined by specifying the desired number of arms, sampling time, number of points per trajectory, field of view (FOV), maximum gradient, slew rate parameters, and a function describing the relative sampling density (compared to Nyquist) as a function of time, and then computing the minimum-time gradient waveforms corresponding to the desired k-space trajectory. In order to determine the effect of spiral trajectory on the CS reconstruction, uniform density spiral (UD), variable linear density spiral (VD), and dual density spiral using a Fermi-function shape for transition region (DD) were evaluated. The dual density spiral design used the following parameterization:

$$k(n)=k_{\mathit{start}}-\frac{k_{\mathit{start}}-k_{\mathit{end}}}{1+e^{-\tau (n-n_{fs})}}$$ (3)

Where k_start is the starting density, k_end is the ending density, n_fs = round(npts * radius)is the number of points in the fully sampled center of k-space, and steepness (tau;) is the parameter that determines the sharpness of the transition area.

For a fair comparison between strategies, all trajectories were designed to support the same spatial resolution. Furthermore, the duration of each arm is kept constant to achieve similar off-resonance performance for the different spiral trajectories.

Given the nature of VD spirals where the acceleration rate varies during the trajectory by design, the effective acceleration rate is defined as the corresponding constant acceleration factor required for a UD spiral trajectory to achieve the same desired FOV and maximum k-space radius (nominal spatial resolution) with the same number of arms and readout duration per arm. For instance, with the previously described design parameters, a UD sequence would have a density of 0.2x Nyquist corresponding to a 5 fold effective acceleration rate.

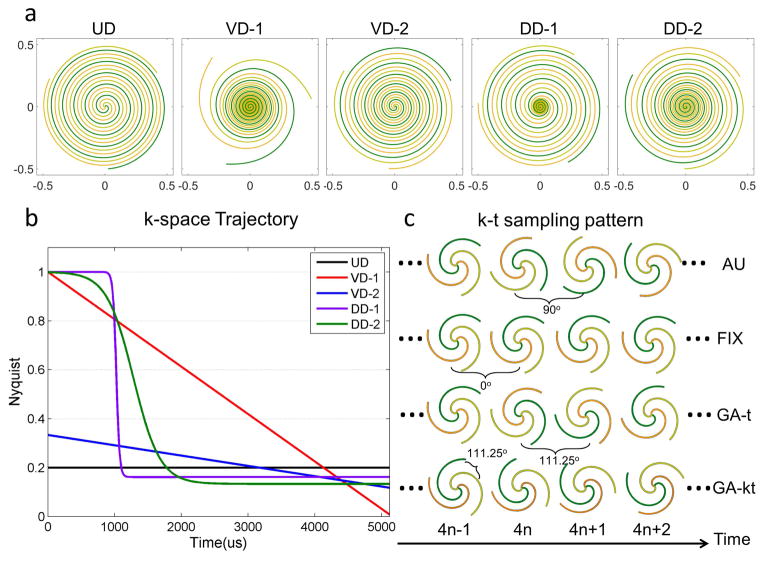
The spiral designs were chosen to span a wide range of trajectory parameters shown in Figure 2a. The UD spiral had a constant 5x under sampling factor which was advantageous from a SNR perspective, but had a coherent point-spread function (PSF), and did not fully sample low frequency high-energy data. Two VD trajectory patterns were evaluated. VD-1 had linearly decreasing density from 1x Nyquist to an under sampling density of 0.008x Nyquist at the edge of k-space. This produced very little ringing in the spatial PSF, but required a very high acceleration at the k-space edge which was least advantageous from a SNR perspective. VD-2 had less steep linearly decreasing density from 0.33x to 0.11x Nyquist and did not fully sample the center of k-space, which resulted in less non-uniform weighting of noise and a lower maximal under sampling factor as compared to VD-1. Two DD trajectory patterns were evaluated as well. The fully sampled radius was chosen to be 20% of the trajectory. In the literature the radius is typically 15–25% of the trajectory¹⁸, and the overall trajectory is similar over this range of “radius”. To evaluate the effects of the transition region between the two k-space densities, we used either a sharp transition (τ=0.08) which required a final ending density of 0.18x Nyquist, or a broad transition (τ=0.02) which required a slightly lower final ending density of 0.13x Nyquist. Of note, while specific choices of τ and radius were chosen, small variations in these parameters did not significantly impact the general appearance of the spiral trajectories. Detailed information regarding the trajectories is shown in Table 1 and Figure 2a and 2b.

Figure 2.

Combinations of k-space trajectories (a,b) and k-t sampling patterns (c). Five spiral trajectories include uniform density (UD), variable density from 1x Nyq to 0.008x Nyq (VD-1), variable density from 0.33x Nyq to 0.11x Nyq (VD-2), dual density with sharp transition (DD-1) and dual density with broad transition (DD-2). Four k-t sampling patterns include Angularly uniform (AU): within a heartbeat, 3 spirals were uniformly distributed and between heartbeats the sampling pattern was rotated by 90° with a period of 4; Fixed (FIX): 3 spirals were fixed both within and between heartbeats; Golden angle rotation in time (GA-t): 3 spirals were uniformly distributed within heartbeat and rotated by a golden angle (111.25°) between heartbeats and Golden angle rotation in both k-space and time (GA-kt): each spiral was continuously rotated by golden angle within and between heartbeats.

Table 1.

Spiral trajectories parameters

	UD	VD-1	VD-2	DD-1	DD-2
Number of arms	3	3	3	3	3
Readout duration per arm (ms)	5.12	5.12	5.12	5.12	5.12
FOV (mm)	340	340	340	340	340
Starting density	0.2	1	0.33	1	1
Ending density	0.2	0.008	0.11	0.18	0.13
Fully sample k-space center (radius)*	N/A	N/A	N/A	20%	20%
Trajectory steepness (τ)*	N/A	N/A	N/A	0.08	0.02
Resolution (mm)	2.05	2.06	2.05	2.05	2.06

^*Fully sampled k-space center and trajectory steepness is only used for dual density trajectories to determine the transition shape from starting density to ending density.

k-t Sampling Pattern

For CS reconstruction the temporal k-t sampling pattern has to be considered. The small number of spiral arms for our proposed spiral pulse sequence limits the flexibility of the sampling pattern for each acquisition. A previous study showed that a sampling pattern employing rotations of angularly-uniformly spaced arms provided better image quality compared to randomly selected arms when temporal-difference sparsity was exploited²⁷. As this pattern violates the concept of incoherent sampling in the temporal dimension which is advocated for compressed sensing, we evaluated the golden angle spiral sampling scheme²⁸. As shown in Figure 2c, 4 types of k-t sampling patterns were evaluated in the retrospective simulation experiments: 1) angularly uniform (AU): within a heartbeat, 3 spirals were uniformly distributed and between heartbeats the sampling pattern was rotated by 90° with a period of 4; 2) Fixed (FIX): 3 spirals were fixed both within and between heartbeats; 3) Golden angle in time (GA-t): 3 spirals were uniformly distributed within a heartbeat and rotated by a golden angle (111.25°) between heartbeats; 4) Golden angle in k-space and time (GA-kt): each spiral was continuously rotated by golden angle within and between heartbeats.

Pulse Sequence Design

The pulse sequence is shown schematically in Figure 3. A non-selective saturation with an adiabatic BIR-4 pulse²⁹ is used for T₁-weighting preparation. Before data acquisition, a spectrally selective fat-saturation pulse is applied. Then, 3 spirals for each image are obtained in the interleaved order for 2 different slice locations separately to create the perfusion image. Therefore, 2 slices are acquired in one SR block, and SR blocks are repeated until all the slices are imaged.

Figure 3.

Pulse sequence schematic for the whole-heart coverage SR first-pass spiral perfusion imaging. At each SR sequence block, following the BIR4 SR pulse, a fat saturation pulse is applied and then followed by interleaved spiral imaging at two slice locations. Each slice is sampled by 3 interleaved spiral readouts (boxes) each with a TR of 7 ms. Due to the slice interleaving, the effective temporal resolution of each slice is 5*TR (35 ms), and the TS times differ by 1 TR (7 ms).

Image Reconstruction

For a 2x acceleration factor non-Cartesian PI techniques such as SPIRiT or non-Cartesian SENSE perform well for spiral perfusion imaging^30,31, however their performance is inadequate at acceleration factors of 4–5x. At higher acceleration, additional prior information must be exploited to achieve high quality reconstructions. We have previously demonstrated that L1-SPIRiT using temporal finite difference as the sparsifying transform performed well at a 4x acceleration factor for this application^30,32. Therefore, images in this study were reconstructed using the combination of PI and CS techniques, L1-SPIRiT^32–34. The reconstruction problem could be formulated as:

$$\begin{array}{ll}\hfill \mathit{minimize}& {\ell }_1(\mathrm{\Psi }x)\\ \hfill s.t.& \mathit{SDFx}=y,Gx=x\end{array}$$ (4)

where F is a Fourier operator which transfers the data from image domain to k-space domain, D is the inverse gridding operator that transfers the Cartesian grid to spiral trajectory, S is the subsampling operator that chooses only acquired spiral k-space data out of the entire k-space trajectory, y is the acquired spiral k-space data, and G is an image-space SPIRiT operator that represents the k-space self-consistency convolutions in the image domain. The calibration kernel is estimated from gridding of the fully sampled k-space center using non-uniform FFT (NUFFT)³⁵. Ψ is the finite time difference transform that operates on each individual coil separately to achieve sparsity in the temporal domain of image time series.

The above equation can be reformulated as the unconstrained Lagrangian form:

$$\underset{x}{\text{argmin}}{\Vert \mathit{SDFx}-y\Vert }^2+{\lambda }_1{\Vert (G-I)x\Vert }^2+{\lambda }_2{\Vert \mathrm{\Psi }x\Vert }_1$$ (5)

where λ₁and λ₂ are parameters that balance the data acquisition consistency with calibration consistency and sparsity.

The SPIRiT calibration kernel G needs to be derived from the fully sampled, aliasing free data. Either an upfront pre-scan or temporal averaging of the under-sampled data could generate alias free images for calibration. In practice, we typically acquire fully sampled proton density images over the first 4 heart beats of the acquisition to perform calibration. This strategy results in high SNR and high spatial resolution training data without variation in signal intensity resulting from imaging during the first pass of the contrast agent.

The image reconstruction was implemented in Matlab (The MathWorks, Natick, MA). The image-based non-Cartesian reconstruction used Fessler’s NUFFT code³⁵. The nonlinear iterative conjugated gradient descent algorithm with backtracking line search was used to solve the optimization problem. The absolute value function was approximated by a smooth function as described by Lustig et al¹³.

Retrospective Study

L1-SPIRiT reconstruction performance for the 5 spiral trajectories (UD, VD-1, VD-2, DD-1,DD-2) described above and 4 different k-t sampling patterns (AU, FIX, GA-t and GA-kt) was quantitatively assessed using data from 25 multi-coil fully-sampled first-pass spiral perfusion images from previously published clinical study of adenosine stress CMR including 16 rest and 9 stress data sets⁵. The acquisition protocol and technical details of the sequence were described previously and include the following parameters: saturation recovery time of 80 ms echo time, 1 ms; repetition time, 9 ms; slice thickness, 10 mm; flip angle, 30°, field of view, 320 mm²; 8 spiral interleaves; 6.1 ms readout duration per spiral arm; and nominal spatial resolution of 2 mm²¹. Inverse gridding was performed by taking the complex image data from each coil at each time point and resampling it onto the specific non-uniformly sampled spiral k-space trajectory using reverse NUFFT³⁵. Image reconstructions of the different combinations of trajectories and sampling patterns described above were performed using L1-SPIRiT with the goal of quantitatively evaluating the reconstruction performance compared to the fully-sampled “ground-truth” datasets.

Image quality was assessed across the whole image and in the heart region using root mean square error (RMSE) and structural similarity index (SSIM), which is a comprehensive measurement of the similarity between two images, and includes measurement of structure, intensity and contrast, representing human perception more closely³⁶. The mean SSIM is defined by:

$$\mathit{SSIM}(x,y)=\frac{1}{N}\sum _{i=1}^N\frac{(2{\mu }_{xi}{\mu }_{yi}+c_{1i})(2{\sigma }_{\mathit{xiyi}}+c_{2i})}{({\mu }_{xi}^2+{\mu }_{yi}^2+c_{1i})({\sigma }_{xi}^2+{\sigma }_{yi}^2+c_{2i})}$$ (6)

where μ_xi, μ_yi and σ_xi, σ_yi are the mean and variance of images x and y at time frame i, σ_xiyi is the covariance of x_i and y_i at time frame i, c_1i and c_2i are variables which stabilize the division with a weak denominator between x_i and y_i, and are selected as described by Wang et al³⁶.

The RMSE and SSIM from the 25 simulation datasets were analyzed using a blocked two-way ANOVA factorial design to determine the best combination of the evaluated spiral trajectories and k-t sampling patterns. The model included the 2-way interactions between trajectory and sampling pattern and a p-value <0.05 was considered significant.

In addition, signal-intensity time courses were evaluated to compare the temporal fidelity between the reconstructed images and ground truth images, using 3 different manually defined regions of interest (ROI): left ventricular blood pool (LV), right ventricular blood pool (RV) and myocardium.

Prospective Study

Based on the results from the retrospective study of the spiral trajectories and k-t sampling pattern analysis, the DD-2 spiral trajectory with AU and GA-t sampling strategies were evaluated prospectively in a total of 34 subjects. Resting first-pass perfusion was performed in 24 subjects undergoing clinically ordered CMR studies using the DD-2 trajectory with either GA-t (N=8) or AU (N=16). Additionally, 2 normal subjects were imaged at rest using the DD-2 sampling pattern with both of the k-t sampling patterns (AU and GA-t) to allow for direct comparison between these two candidate sampling patterns. In these studies the same dose of contrast 0.075mmol/kg Gd-DTPA (Bayer Pharmaceuticals) was used for each injection, and the two acquisitions were separated by a 20 minute period to allow for contrast washout. As part of an ongoing clinical evaluation of the spiral perfusion sequences, 8 subjects were imaged at rest and stress during a 3 minute infusion of 140 mcg/kg/min of adenosine (Astellas Pharmaceuticals) using the AU temporal pattern. Written informed consent was obtained from all subjects, and imaging studies were performed under institutional review board (IRB) approved protocols. Imaging was performed on a 1.5T MR Scanner (Magnetom Avanto, Siemens Healthcare). The Siemens body matrix and spine matrix phased-array coils were used in triple mode yielding between twelve and eighteen effective coil channels depending on the size and positioning of the patient. The 8 studies performed under stress utilized a 32-channel phased-array receiver coil. Four proton density images were acquired at the beginning of data acquisition for calibration purpose. Fifty perfusion images covering the whole heart were obtained during injection of 0.075 mmol/kg Gd-DTPA via a peripheral IV at a rate of 4mL/s. Other pulse sequence parameters were as follows: TS 80 ms, TE 1.0 ms, 5 ms spiral and 3 spirals per slice, effective TR 14 ms, FA 30°, 8 to 10 slices to cover the whole heart, 2 slices per saturation, FOV 340mm², in-plane resolution around 2mm.

Perfusion images were reconstructed using the proposed L1-SPIRiT method. The reconstruction parameters λ₁ = 0.01 and λ₂ = 0.05 were chosen based on an analysis of the SSIM and RMSE metrics as compared to the fully sampled ground truth data and the parameters were fixed for all datasets. Image quality was graded on a 5-point scale (1-excellent, 5-poor) independently by two cardiologists. Scores from the two reviewers were analyzed using the Wilcoxon signed rank test. Image quality of the GA-t and AU k-t sampling strategies was analyzed using the Mann-Whitney U test.

Results

Simulation

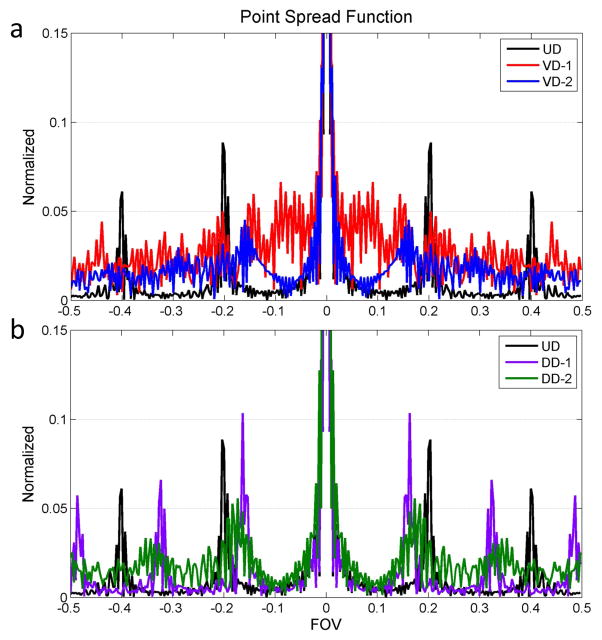
Figure 4 shows the PSF of the five evaluated k-space trajectories with 5 ms RO per arm. The UD trajectory has several very high side lobes with a peak amplitude of 8% of the main lobe. This trajectory has the least incoherent sampling pattern and is the worst case scenario for a CS type reconstruction. The VD-1 trajectory has the most incoherent side lobe energy distribution, which is good for CS type reconstruction, however the side lobe peaks are relatively high (around 5% of the main lobe), which would be unfavorable for a PI type reconstruction. The VD-2 trajectory has a similar PSF with VD-1 with the exception that there is no fully sampled region in the trajectory for calibration. In contrast to the VD trajectories, the DD has fully sampled regions in the k-space center; the broad transition trajectory DD-2 is a good trade-off solution between incoherency for CS reconstruction and calibration for PI reconstruction. Notably, the PSF only describes the spatial pattern resulting from the given trajectory at a single time point, and may not fully characterize the incoherence of the sampling pattern. However the analysis shows that the different trajectories result in different PSF which could impact the performance of the reconstruction technique.

Figure 4.

Point spread function of the k-space trajectories. The VD-1, DD-1 and DD-2 trajectories have the fully sampled k-space center which could be used for calibration kernel training. UD trajectory has strong coherent side lobes and DD-1 has a similar coherent side lobe distribution. VD-1 trajectory has the most incoherent PSF but the side lobe energy is around 5% of the main lobe. DD-2 trajectory is the trade-off between the fully sampled center calibration and incoherent side lobe distribution.

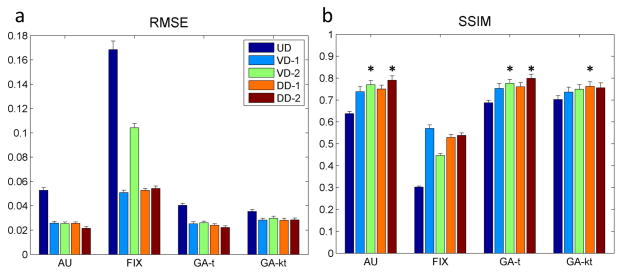
Figure 5 summarizes the RMSE and SSIM results from the heart region of the 25 datasets with all combinations of the trajectories and k-t sampling patterns. It is evident that all the k-t sampling patterns have reasonably small RMSE and high SSIM, except for the trajectories utilizing a fixed temporal sampling pattern. The main effects of trajectory type, k-t sampling pattern, and the interaction between trajectory and sampling pattern were all significant (p<0.001). When controlling for the k-t sampling pattern and interactions between trajectory and sampling pattern, DD-2 had the highest estimate for SSIM (p<0.05). When controlling for trajectory and the interaction between trajectory and sampling pattern, there was no significant difference between AU, GA-t and GA-kt, however, these patterns were all better than FIX (p<0.05). When considering the individual combinations of trajectory and k-t sampling pattern, DD-2 with AU, DD-2 with GA-t, VD-2 with AU, VD-2 with GA-t and DD-1 with GA-kt (stars indicated in Figure 5b) formed the group with the highest SSIM values with no significant difference in SSIM within the group. The DD-2 trajectory with AU and GA-t temporal sampling pattern had the smallest point estimates for RMSE, the highest SSIM, and a fully sampled k-space center for calibration, therefore were chosen for prospective evaluation. Similar results in RMSE and SSIM analysis were fund over the entire image. The UD trajectory reconstructions frequently had residual coherent aliasing resulting in higher RMSE and SSIM than the other trajectories.

Figure 5.

Quantitative analysis of the performance of combination of spiral trajectories (UD, VD-1, VD-2, DD-1and DD-2) and k-t sampling patterns (AU, FIX, GA-t and GA-kt) using L1- SPIRiT reconstruction in 25 datasets (standard error is shown as the error bar). Average root mean square error (RMSE) and structural similarity (SSIM) were compared with the ground truth reference images. The fixed k-t sampling pattern had the largest RMSE and smallest SSIM while other sampling patterns had similar performance. Stars indicated in (b) show the combinations of trajectory and k-t sampling patterns with an SSIM in the highest group of SSIM value as compared to other strategies (p<0.05). Within this group there was no statistical difference between the combinations. The DD-2 trajectory with AU and GA in time temporal sampling patterns had the lowest point estimates of RMSE and the highest point estimates of SSIM.

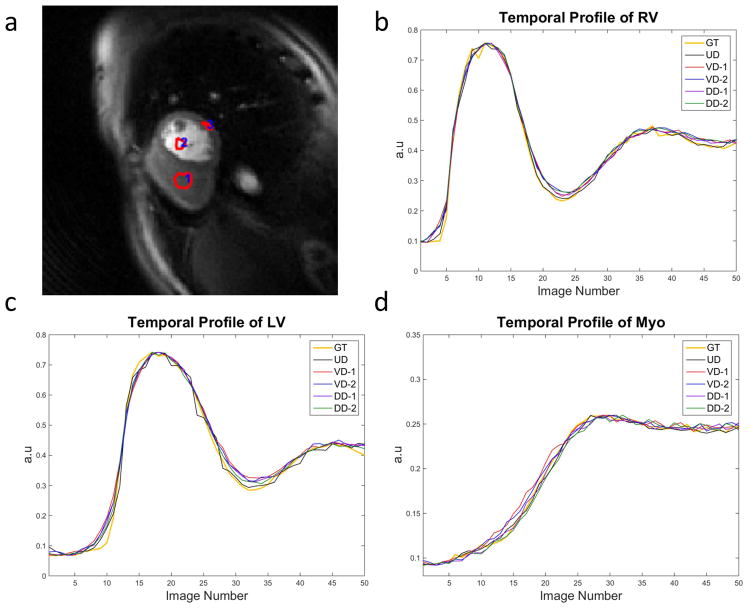
Figure 6 illustrates the representative temporal profile of the LV, RV and myocardium from a retrospective simulation dataset. All 5 trajectories using AU temporal sampling pattern were compared against the ground truth (GT). From the temporal profile, all of the trajectories demonstrate close correspondence with the GT with minimal temporal blurring in the myocardium. There is a minor loss of temporal fidelity at the arrival of contrast to the RV and LV, but the rest of the upslope and peak closely approximate the fully sampled GT.

Figure 6.

Temporal profile of the RV (b), LV (c) and myocardium(d) from one retrospective simulation dataset (a) with 5 trajectories and AU temporal sampling pattern compared with “ground truth” (GT).

Human Studies

Figure 7 shows the direct comparison of the rest perfusion images from the retrospective simulation experiment using DD-2 trajectory with the top two k-t sampling patterns, AU temporal sampling pattern (a) and GA-t (b), from the same subject in two gadolinium injections. Both of the two k-t sampling patterns demonstrated good image quality and minimal image artifacts.

Figure 7.

Whole-heart coverage resting perfusion images at a middle time frame from the same volunteer using the DD-2 trajectory with AU temporal sampling pattern (a) and GA in time (b). Both of the two k-t sampling patterns showed good image quality and minimal artifacts.

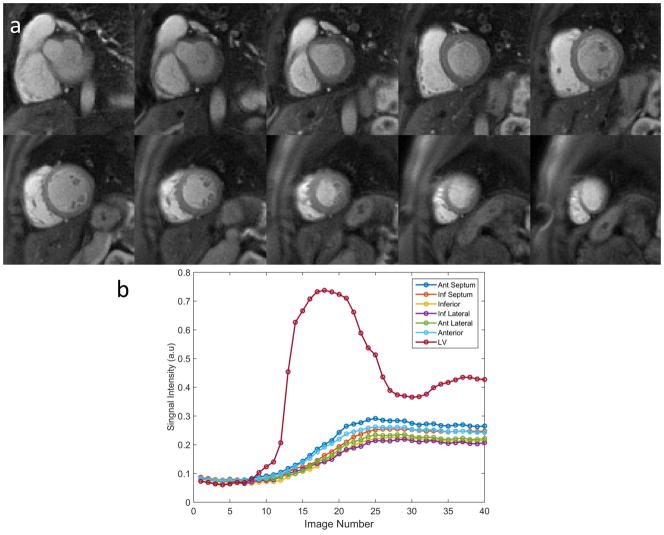
Figure 8(a) illustrates the image quality of whole-heart coverage first-pass perfusion images at the middle time frame from a healthy volunteer using the DD-2 with AU temporal sampling pattern. The images demonstrate high SNR and image quality with minimal residual aliasing outside the heart regions. Figure 8(b) shows the time-intensity curves of the LV cavity from a mid-ventricular slice and the time-intensity curves from each myocardial segment averaged across slices 3–10. The corresponding movie for this healthy volunteer is included as Supporting Movie S1 in the online Supporting Information.

Figure 8.

Example images demonstrate whole-heart coverage (10 slices) rest perfusion imaging (a) from a clinical study using the DD-2 trajectory and AU temporal sampling pattern. Time intensity curves from LV cavity of middle ventricular slice and six averaged segments of the myocardium across the whole heart from slice 3 to 10 (b).

Clinical Evaluation

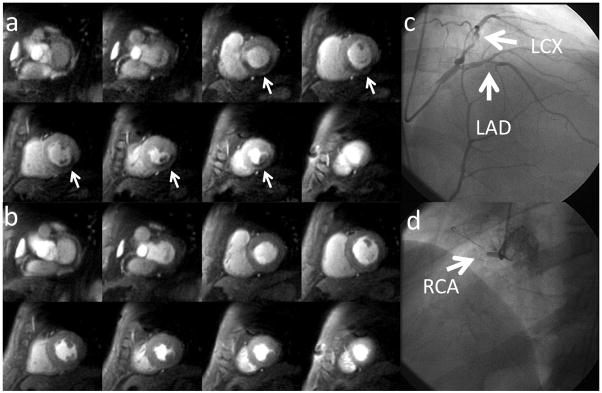
Figure 9 shows the whole-heart coverage perfusion images during adenosine stress (a) and at rest (b) from a patient undergoing adenosine stress imaging as part of a clinical research study. There are inducible perfusion abnormalities in left circumflex artery (LCx) and right coronary artery (RCA) territories. There was no evidence of infarction on the late gadolinium enhancement images. At cardiac catheterization, the patient had a high grade stenosis in the LCx (c) and a total occlusion of the RCA (d). The first-pass perfusion movies for this CAD patient are included as Supporting Movies S2 (at rest) and S3 (at stress) in the online Supporting Information.

Figure 9.

Whole-heart perfusion images obtained during adenosine stress (a) and at rest (b) from a suspected CAD patient undergoing adenosine stress imaging as part of a clinical research study. There are inducible perfusion abnormalities in left circumflex artery (LCx) and right coronary artery (RCA) territories. At cardiac catheterization, the patient had a high grade stenosis in the LCx (c) and an occluded RCA (d).

The average image quality scores (1-excellent, 5-poor) from 16 cases using the AU sampling pattern were 2.18 ± 0.75 and 1.63 ± 0.72 from two cardiologists. There was no statistical difference between the GA-t and AU sampling strategies (p = 0.74 for cardiologist 1 and p = 0.13 for cardiologist 2) showing that either technique works well for the given spiral k-space trajectory.

Discussion

The goal of this paper was to determine the best set of parameters for an interleaved spiral pulse sequence and reconstruction technique for high-resolution whole-heart perfusion imaging which is a prerequisite to a formal clinical evaluation of the technique. Fundamentally, this is a practical design study, and not a full optimization study, given the tremendous flexibility in possible spiral trajectory designs, k-t sampling strategies and reconstruction methods. We demonstrated that accelerated spiral pulse sequences with the combination of PI and CS can achieve high-quality first-pass perfusion images with whole-heart coverage (8 slices) and high in-plane resolution (2mm) at heart rates up to 125 BPM. Conventional clinical cardiac pulse sequences for first-pass perfusion are limited to 3 to 4 noncontiguous slices through the left ventricle. Achieving whole-heart coverage has a number of potential advantages. Firstly, it enables more accurate volumetric quantification of myocardial ischemic burden³⁷. This is clinically relevant as studies have demonstrated that patients with a larger ischemic burden are more likely to benefit from revascularization either by cardiac stenting or coronary artery bypass surgery³⁸. Secondly, it eliminates the need for the imaging physician/technologist to carefully plan the appropriate slice locations for the perfusion images. This reduces the time necessary to choose the appropriate slice locations for imaging, and avoids selecting slices that are too apical or basal. Finally, whole-heart coverage ensures that there is no under-sampling of ischemic myocardium in the small number of imaged slices. Recent studies have demonstrated the advantages of 3D coverage³⁷. A rapid-multi-slice approach enables higher-in plane spatial resolution and reduces the temporal footprint of the images, reducing cardiac motion-induced artifacts, and represents an alternative strategy for whole-heart coverage which may be more robust to DRA.

We evaluated the effects of spiral trajectory and k-t sampling patterns through simulation and prospective evaluation. We demonstrated that for a spiral reconstruction using L1-SPIRiT with finite-difference in time as the sparsifying transform a dual-density trajectory with a broad transition region (DD-2) provides a good balance between adequately sampling the low spatial frequencies and providing a spatially incoherent aliasing pattern while capturing sufficient energy in k-space to avoid high energy, low-frequency aliasing artifacts. The simulation used the same image datasets down-sampled onto the candidate k-space trajectories to directly compare the effects of k-space trajectory and k-t sampling pattern. Contrary to our original hypothesis, both AU and GA-t trajectories resulted in similar image quality, at least for the DD-2 trajectory and the L1-SPIRiT with finite-difference in time reconstruction.

Choosing a spiral trajectory for a combined PI and CS reconstruction requires trade-offs between factors which could affect each type of reconstruction differently. For CS based techniques a relatively incoherent sampling pattern is a necessity and adequate sampling of the low spatial frequency reduces high-energy low-frequency aliasing and generally improves image reconstruction as compared to completely random under-sampling strategies. We demonstrate through simulation and imaging experiments that DD-2, which is a dual density spiral with a broad transition, appears to provide a reasonable trade-off for a reconstruction utilizing both PI and CS.

Regarding the k-t sampling pattern, a fixed temporal pattern which is adequate for PI does not work well for an L1-SPIRiT reconstruction as it is completely coherent in the temporal domain. However, for the evaluated spiral pulse sequences, reconstruction performance between the AU, GA-t and GA-kt temporal sampling strategies was similar. The lack of difference between GA-t and GA-kt could be related to the spiral design which has 3 spiral arms that are spaced 120° apart from each other which is very close to the golden angle 111.25°. We found that the L1-SPIRiT reconstruction performance is more dependent on the particular spiral k-space trajectory pattern rather than the k-t sampling pattern. The prospective study which directly compared AU and GA-t strategies for the DD-2 trajectory in the same subjects confirmed this assertion, resulting in similar image reconstruction performance for both k-t sampling strategies.

Strictly speaking, the conclusions regarding the choice of trajectory and temporal sampling pattern apply to the L1-SPIRiT reconstruction using temporal finite difference as the sparsifying transform. We chose to use temporal finite difference as it is generally robust and errors from respiratory motion typically only affect a small temporal extent of the data series. To assess generalizability of the results we have also performed a preliminary analysis using kt-SLR³⁹ with only a temporal TV term (i.e. no spatial TV). The results with respect to the choice of k-space trajectory were similar to what we reported for L1-SPIRiT in this manuscript and images were of similar quality. With respect to temporal sampling strategy, the results for golden-angle-in-time were superior to those using the angularly uniform temporal strategy as expected.

Preservation of the temporal dynamics of the perfusion image data is essential for quantification of myocardial perfusion. Reconstruction techniques that rely on the k-t correlation of the data have the potential for affecting the fidelity of the temporal information. We show in simulation and retrospective down-sampling studies that although we are using a finite-difference in time as sparsifying transform, the temporal dynamics are preserved in the myocardium for the L1-SPIRiT based reconstruction. There is a minor loss of temporal fidelity at the time of contrast arrival at the RV and LV cavity which is due to the very high temporal-frequency content when the contrast first appears in the cavities.

This study has a few limitations. In the retrospective analysis, we utilized SSIM and RMSE as quantitative metrics for assessing image reconstruction performance. However, these parameters may not be sensitive to subtle changes in temporal dynamics and do not directly address performance for clinical detection of CAD. We chose the minimal regularization parameter for the L1 term which adequately removed aliasing to minimize losses in temporal fidelity. For 2D spiral perfusion imaging, where the SNR is limited due to heart rate constraints, non-Cartesian PI techniques work well at 2–3x acceleration factors, but performs poorly at higher acceleration factors³⁰. For perfusion studies which only acquire 3–4 slices per heart-beat, non-Cartesian PI alone at 2x acceleration may be preferable since each image is reconstructed separately and is thus robust to respiratory motion and the reconstruction does not suffer from any temporal blurring³¹. For more highly accelerated techniques required to achieve 2D whole heart coverage, we have found that reconstruction techniques which exploit prior knowledge are necessary. We did not perform a formal comparison between different reconstruction techniques which is a limitation of this paper. As most of the prospective studies were acquired during a routine clinical examination, we were only able to obtain resting perfusion images with a single pulse sequence precluding the direct comparison of spiral and Cartesian pulse sequences in the same subject. However, it does provide a real-world evaluation of the performance of the accelerated-spiral approach in patients with CAD. Resting perfusion images demonstrate both feasibility of the technique and high image quality. The example case from our ongoing study of whole-heart spiral perfusion provides preliminary evidence of the utility of the proposed pulse sequence for detecting obstructive CAD with an inducible perfusion defect matching the location of obstructive CAD by cardiac catheterization. An additional limitation is that similar to other techniques that rely on correlations in k-t space, the L1-SPIRiT reconstruction is affected by respiratory motion, and severe respiratory motion degrades image quality. We chose finite-difference in time for the L1 term, as respiratory motion artifacts which usually occur near the end of the breath-hold, tend to be localized to only this portion of the data acquisition. We have recently demonstrated a technique based on rigid-registration of the heart region⁴⁰ which improved robustness to motion, and is used to correct respiratory motion as seen in the supplemental movie. Ongoing efforts by our group and others have developed reconstruction techniques which utilize registration techniques to overcome this limitation with promising initial results.^14,41 Further clinical studies and direct comparison to existing techniques will be necessary to demonstrate the potential utility of whole-heart coverage spiral pulse sequences for this challenging application.

Conclusion

We demonstrate the successful application of whole-heart coverage first-pass myocardial perfusion imaging using accelerated spirals with optimized trajectories and k-t sampling patterns. With this technique we can acquire 8 short axis slices using a spiral trajectory designed with a nominal in-plane resolution of 2mm at heart rates up to 125 BPM. Future clinical validation studies in patients with known CAD at rest and adenosine stress will be essential to further assess and optimize performance of these sequences.

Supplementary Material

Supp MovieS1

Supporting Movie S1: Whole-heart coverage spiral first-pass perfusion imaging from a healthy volunteer at rest.

Supp MovieS2

Supporting Movie S2: First-pass perfusion of suspected CAD patient at rest 

Supp MovieS3

Supporting Movie S3: First-pass perfusion of suspected CAD patient at stress