Abstract
Age-related change in processing speed has been linked directly to increases in reasoning as well as indirectly via increases in the capacity of working memory (WM). Most of the evidence linking change in speed to reasoning has come from cross-sectional research; in this article we present the findings from a 2½-year longitudinal study of 277 6- to-13-year-olds. On three occasions, speed of information processing was assessed with Visual Matching and Cross Out; WM was assessed with reading, listening, backward digit, alphabet, and operation span tasks; and nonverbal reasoning was assessed with Raven’s progressive matrices. The results provided consistent evidence of direct links from processing speed to reasoning but inconsistent evidence for indirect links from speed to WM to reasoning. These findings suggest that variations in processing speed may constrain the development of reasoning, directly and perhaps indirectly.
When children solve arithmetic problems, determine whether two stimuli are similar perceptually, or retrieve an object’s name from long-term memory, they respond more rapidly as they develop. Speeds on these and other cognitive tasks typically increase substantially during early and middle childhood but more slowly in later childhood and early adolescence (Kail, 1991).
These age-related increases in speed have been linked to the growth of more complex cognitive processes, both directly and indirectly. Direct links are illustrated by the findings that age-related increases in processing are associated with higher scores on intelligence tests, with greater success in solving arithmetic word problems, and greater accuracy in ordering landmarks encountered during a walk (Allen & Ondracek, 1995; Coyle, Pillow, Snyder, & Kochunov, 2011; Kail & Hall, 1999). Age-related increases in processing speed have also been linked to cognitive development indirectly, via increases in WM: That is, increases in processing speed are associated with increases in the capacity of WM which, in turn, are associated with improvements in complex cognitive processing (e.g., De Alwis, Hale, & Myerson, 2014; Fry & Hale, 1996; Nettelbeck & Burns, 2010; Spanoudis et al., 2015).
Most of the aforementioned evidence comes from cross-sectional work. More compelling evidence for the cognitive consequences of age-related change in speed would come from longitudinal studies. The ideal study would assess speed, WM, and cognitive performance using similar tasks on multiple testing occasions, allowing tests of the direct effects of increased speed (e.g., speed → complex cognition) as well as tests of indirect effects (e.g., speed → WM → complex cognition).
In fact, there are few relevant studies and most fall short of the ideal. Rose et al. (2008) reported that 12-month-olds’ processing speed predicted, concurrently, their recognition memory, which predicted their mental development (as assessed by the Bayley) as 2- and 3-year-olds. Clark et al. (2014) found that 3-year-olds’ processing speed predicted their skill at mathematics as 5-year-olds (Clark et al., 2014); similarly, Rose, Feldman, and Jankowski (in press) found that 3-year-olds’ processing speed predicted their lexical proficiency as 13-year-olds. Finally, Kail (2007) showed that for 8- to 13-year-olds, more rapid processing speed was associated concurrently with greater WM, which predicted scores on a measure of fluid intelligence administered one year later. In these studies, processing speed is consistently associated with cognitive development but none was designed to provide a comprehensive evaluation of the direct and indirect effects of age-related increases in processing speed.
The study that comes closest to the ideal was reported by Demetriou et al. (2002). They administered measures of processing speed and WM as well as tasks assessing reasoning and problem solving in verbal, quantitative, and spatial domains. The participants, 8- to 14-year-olds, were tested three times over two years. Increases in speed were linked directly to greater accuracy on the reasoning and problem solving tasks and indirectly, via increases in WM.
The findings of Demetriou et al. (2002) provide the strongest longitudinal evidence for direct and indirect links between processing speed and reasoning. However, conclusions are limited by the way in which processing speed was assessed: participants named words, digits, or shapes. Speeds on such tasks are correlated with performance on psychometric measures of processing speed, but naming tasks (1) are distinct statistically from psychometric measures of processing speed, (2) are less strongly correlated with age than are psychometric measures of processing speed (Kail, 1997; Kail, Hall, & Caskey, 1999), and (3) are thought to tap naming circuits in the left hemisphere that are critical for learning to read (Lervåg & Hulme, 2009). Consequently, measures of processing speed that are more typically included in psychometric instruments would provide more compelling evidence.
The aim of the present study was to assess the direct and indirect effects of processing speed on cognitive processes, using a design similar to that of Demetriou et al. (2002) but with conventional measures of processing speed. Children and adolescents were tested multiple times over 2½ years on tasks assessing processing speed, WM, and reasoning. This design allowed us to determine whether increases in speed are linked with cognitive processes directly (i.e., increased processing speed is associated with greater reasoning), are linked indirectly (i.e., the impact of increased processing speed on reasoning is mediated by increases in WM) or both directly and indirectly.
METHOD
Participants
Participating were 277 children (137 boys, 140 girls). They were tested six times, approximately six months apart, and ranged in age from 6 to 13 years when tested initially (M = 9.25 years; SD = 1.99). They lived in cities in the XXXXXXX and were recruited via advertisements in newspapers and letters to university alumni. Most children (241) were white; 16 were African American, 7 were Asian American, and 13 were of mixed ethnicity. Most children were from middle-class homes: mothers had an average level of education of 4.06 (SD = .80) on a 5-point scale on which 3 denoted some college, 4 denoted a college graduate, and 5 denoted some graduate work.
Measures
Processing speed
Processing speed was measured with two tasks. In Visual Matching, each of 60 rows includes six digits, two of which are identical; participants circle the identical digits. In Cross Out, each of 30 rows consists of a geometric figure at the left end and 19 similar figures to the right; participants place a line through the 5 figures of the 19 that match the figure at the left. For both tasks, the score is the number of rows completed correctly in 3 min. For both tasks, across administrations, the rows were reordered randomly as were the alternatives within each row.
Working memory
WM was measured with five tasks. Reading span (from Daneman & Carpenter, 1980) included brief sentences printed on a card that ended in a noun and made assertions that were obviously true or false. Children read a sentence aloud, indicated whether it was true, then read the sentence on the next card. After the final sentence in a set, children recalled the final nouns from each sentence in order. Testing began with two 1-sentence sets, progressed to two 2-sentence sets if recall was accurate, and continued until children failed to recall the nouns in a set accurately or completed two 5-sentence sets. Listening span was analogous, but sentences were presented via audio tape. For both tasks, the child’s span was the largest set in which both sets of nouns were recalled accurately.
For operation span (modified from Turner & Engle, 1989), children were shown simple arithmetic problems of the form a ± b ± c = ? where a was a digit ranging from 2-9, b and c were either 0 or 1, and the correct answer ranged from 1-9. Children answered the problem aloud, then the next problem was presented. Following the final problem in a set, children recalled the problem answers in order. Testing began with two 1-problem sets, progressed to two 2-problem sets if recall was accurate, and continued until children failed to recall the answers in a set accurately or completed two 6-problem sets. Span was defined as the largest set in which both sets of answers were recalled accurately.
For backward digit span, children were read sequences of digits and were asked to repeat them in the opposite order (i.e., starting with the digit presented last). Testing began with two pairs of digits, progressed to two triplets of digits if recall was accurate, and continued until children failed to recall the digits in a set accurately or completed two 6-digit sets. Span was defined as the largest set in which both sets of digits were recalled accurately.
For alphabet span, children were read letters that appeared in non-alphabetic order (e.g., G Z U) and were asked to recall them in alphabetic order. Testing began with two pairs of letters, progressed to two triplets of letters if recall was accurate, and continued until children failed to recall the letters in a set accurately or completed two 6-letter sets. Span was defined as the largest set in which both sets of letters were recalled accurately.
Reasoning
To measure inductive reasoning, children were presented 30 problems taken from Raven’s (1958) Standard Progressive Matrices. Testing continued until children completed all 30 problems or erred on 4 consecutive problems. A different set of 30 problems was used at each administration.
Procedure
Children were tested in a quiet room by a research assistant. Testing began with Cross Out, followed by the Raven’s, other cognitive tasks not reported here, listening span or backwards digit span, Visual Matching, and reading span, alphabet span, or operation span. However, as noted in Table 1, not all tasks were administered at every session: to ease the burden of testing, children younger than age 8 were not administered Visual Matching, reading span, alphabet span, or operation span. (For simplicity, the four sessions of data used here are labeled Times 1-4; in fact, Times 2-4 corresponded to Times 3, 5, and 6 in the full longitudinal study.)
Table 1. Number of children participating, means, standard deviation and reliability for all measures at all time points.
| Measures | Time 1 |
Time 2 |
Time 3 |
Time 4 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | Mean (SD) | Reliability | n | Mean (SD) | Reliability | n | Mean (SD) | Reliability | n | Mean (SD) | Reliability | |
| Cross Out | 276 | 18.41 (5.68) | 244 | 21.15 (5.24) | – | 235 | 23.68 (5.42) | – | – | – | ||
| Visual Matching | 185 | 41.41 (7.71) | 201 | 43.51 (8.70) | – | 235 | 45.42 (8.95) | – | – | – | ||
| Listening Span | 277 | 1.56 (.95) | – | – | – | 234 | 2.04 (.90) | – | – | – | ||
| Reading Span | 185 | 1.85 (.74) | – | – | – | – | – | – | – | – | – | |
| Backwards | – | – | – | 244 | 3.28 (1.00) | – | – | – | – | – | – | – |
| Digit Span | ||||||||||||
| Alphabet Span | – | – | – | 201 | 3.41 (.86) | – | – | – | – | – | – | – |
| Operation Span | – | – | – | – | – | – | 232 | 3.80 (1.48) | 230 | 3.97 (1.47) | ||
| Raven | 277 | 17.82 (6.13) | .91 | 244 | 16.34 (5.05) | .87 | – | – | – | 231 | 8.55 (3.66) | .85 |
Note. Reliability = Cronbach’s alpha.
RESULTS
Descriptive statistics are shown in Table 1 and correlations between measures at all time points are shown in Table 2. The raw correlations, shown above the diagonal, reveal that age at Time 1 was highly correlated with all measures, especially performance on the measures of processing speed. Consequently, all analyses were conducted on variables residualized for age; correlations between these variables are shown below the diagonal. Also, as shown in Table 1, many children did not have complete data for all waves of testing. To determine whether missing data occurred randomly—that is, that missing data on one variable could not be predicted by values from other variables—we ran Little’s MCAR test on the age-residualized scores (Little, 1988). The outcome, χ2 (136) = 147.70, p = .233, was consistent with the null hypothesis that data were missing completely at random.
Table 2. Estimated correlations between all variables at all time points.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Cross Out_T1 | 1 | .882** | .545** | .533** | .714** | .871** | .850** | .416** | .440** | .617** | .867** | .833** | .474** | .488** | .537** | .771** |
| 2 Visual Matching_T1 | .628** | 1 | .515** | .540** | .660** | .841** | .934** | .411** | .439** | .562** | .838** | .924** | .458** | .454** | .511** | .773** |
| 3 Listening Span_T1 | .280** | .222** | 1 | .497** | .463** | .470** | .494** | .416** | .343** | .437** | .485** | .484 | .406** | .361** | .367** | .469** |
| 4 Reading Span_T1 | .171** | .194** | .316** | 1 | .545** | .541** | .495** | .324** | .369** | .517** | .456** | .469** | .435** | .406** | .434** | .507** |
| 5 Raven_T1 | .395** | .247** | .206** | .271** | 1 | .660** | .647** | .388** | .455** | .709** | .652** | .624** | .393** | .390** | .590** | .628** |
| 6 Cross Out_T2 | .671** | .582** | .170** | .225** | .326** | 1 | .852** | .439** | .391** | .569** | .881** | .827** | .439** | .409** | .528** | .709** |
| 7 Visual Matching_T2 | .580** | .822** | .199** | .134* | .264** | .638** | 1 | .434** | .448** | .506** | .832** | .930** | .450** | .400** | .463** | .740** |
| 8 Backwards Digit Span_T2 | .191** | .179** | .282** | .146* | .193** | .247** | .231** | 1 | .338** | .384** | .417** | .403** | .357** | .407** | .301** | .365** |
| 9 Alphabetic Span_T2 | .225** | .223** | .189** | .199** | .277** | .156* | .249** | .219** | 1 | .413** | .359** | .460** | .385** | .307** | .381** | .360** |
| 10 Raven_T2 | .444** | .324** | .264** | .334** | .599** | .362** | .237** | .249** | .275** | 1 | .574** | .546** | .391** | .404** | .617** | .421** |
| 11 Cross Out_T3 | .680** | .599** | .206** | .091 | .323** | .736** | .609** | .216** | .114 | .372** | 1 | .838** | .437** | .443** | .559** | .688** |
| 12 Visual Matching_T3 | .584** | .821** | .200** | .112 | .264** | .610** | .837** | .191** | .276** | .322** | .644** | 1 | .428** | .420** | .491** | .692** |
| 13 Listening Span_t3 | .232** | .201** | .244** | .264** | .157* | .191** | .198** | .229** | .261** | .235** | .196** | .178** | 1 | .334** | .338** | .411** |
| 14 Operation Span_T3 | .404** | .342** | .244** | .283** | .247** | .261** | .246** | .326** | .205** | .286** | .316** | .276** | .228** | 1 | .428** | .269** |
| 15 Raven_T4 | .431** | .373** | .228** | .283** | .496** | .403** | .293** | .186** | .272** | .529** | .450** | .339** | .214** | .337** | 1 | .310** |
| 16 Age T1 |
Note.
= p < .05;
= p < .01.
The raw correlations above the diagonal and the residualized correlations below the diagonal
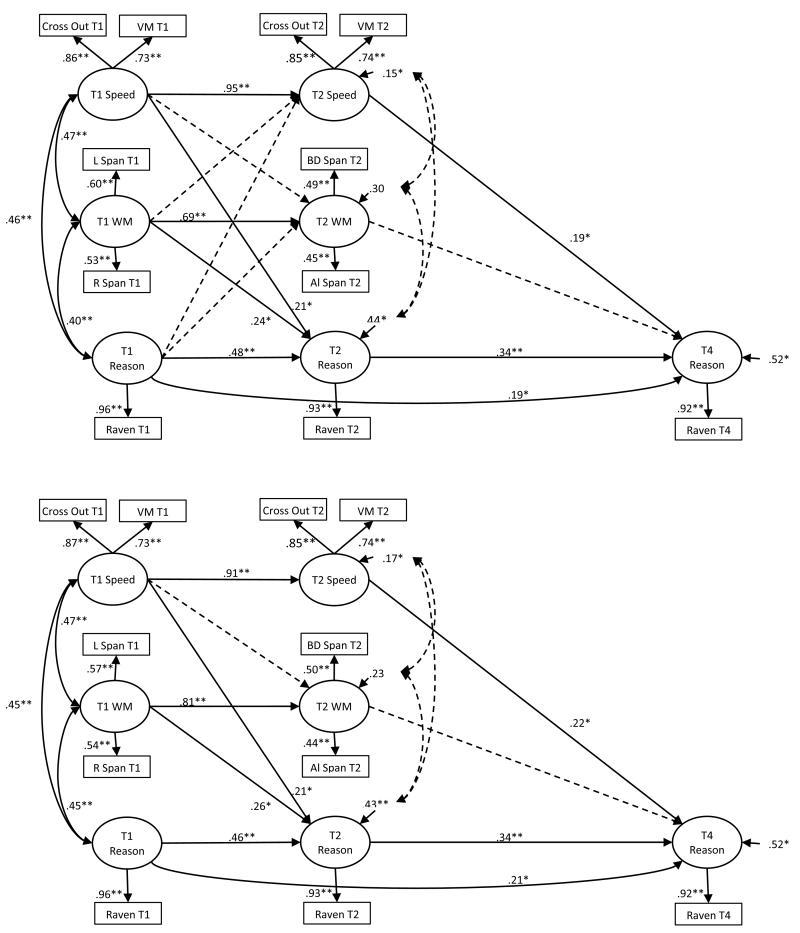
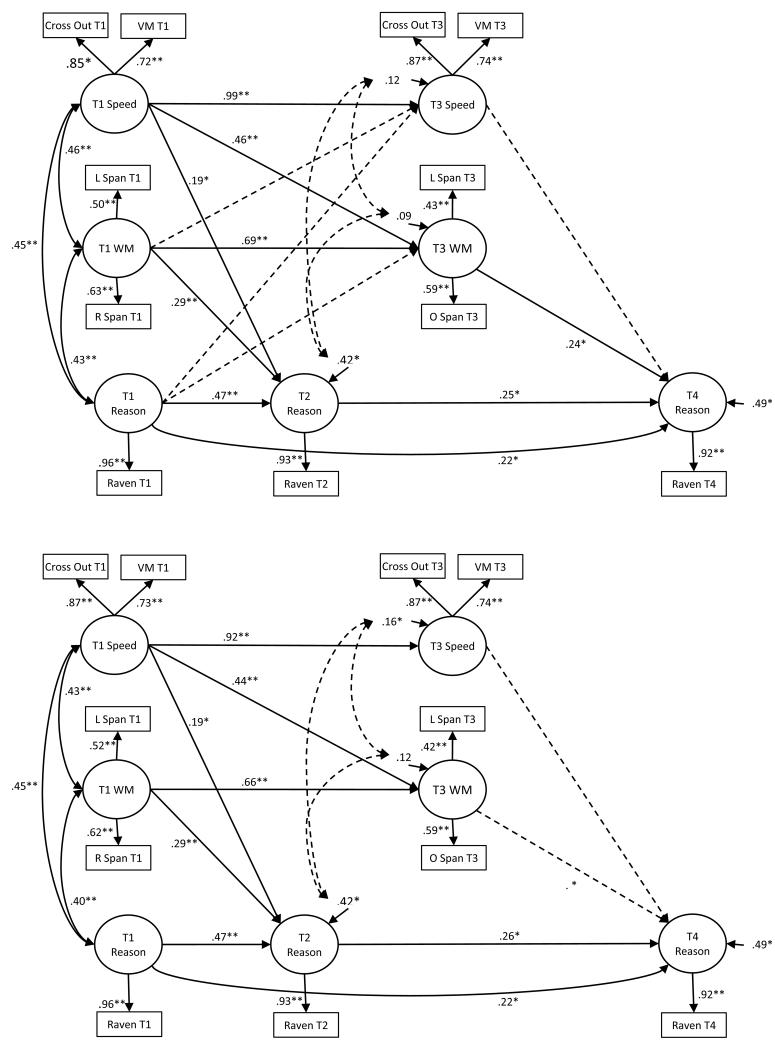
Testing hypotheses about developmental relationships between processing speed, WM and reasoning requires data from three time points and the correlations in Table 2 include two overlapping sets of such data: the data from Times 1, 2, and 4 as well as the data from Times 1, 3, and 4. For each set of data, we began with a theoretically neutral full model (Model 0) in which all three constructs were linked to the other two within each time point and each construct predicted the other two at the next time point (see Figures 1 and 2, top panels). A second model (Model 1, shown in the bottom panels of Figures 1 and 2), nested within the neutral model, evaluated the presence of direct and indirect links between processing speed and cognition. This model differed from the neutral model in that (a) processing speed predicted WM and reasoning at the next time point, (b) WM predicted reasoning but not processing speed at the next time point, and (c) reasoning predicted neither WM nor reasoning in the next time point. A third model (Model 2), nested within Model 1, evaluated the hypothesis that processing speed is linked to reasoning indirectly, via WM, but not directly. This model differed from Model 1 in omitting direct links from speed to reasoning.
Figure 1.
Models expressing relations between processing speed, WM and reasoning, using data from Times 1, 2, and 4. The top panel depicts a theoretically neutral full model (Model 0) in which all three constructs were linked to the other two within each time point and each construct predicted the other two at the next time point. The bottom panel depicts Model 1, in which change in reasoning reflects changes in speed and WM. VM = Visual Matching.
Figure 2.
Models expressing relations between processing speed, WM and reasoning, using data from Times 1, 3, and 4. The top panel depicts a theoretically neutral full model (Model 0) in which all three constructs were linked to the other two within each time point and each construct predicted the other two at the next time point. The bottom panel depicts Model 1, in which change in reasoning reflects changes in speed and WM. VM = Visual Matching. A similar version of this model with constrained paths from Speed and WM at Time 3 to Reasoning at Time 4 showed significant coefficients (β = .20, p < .001).
We evaluated these overlapping models using Mplus version 7.11 (Muthen & Muthen, 1998-2012). Missing data were handled by Full Information Maximum Liklihood, the default in Mplus. We regressed each factor at later time points on the same factor at the preceding time point to control for autoregressive effects. The speed factor reflected variation in children’s scores on the Cross Out and the Visual Matching tasks at Times 1, 2, and 3. The WM factor reflected variation on listening span plus reading span at Time 1, backward digit span plus alphabetic span at Time 2 and listening span plus operation span at Time 3. As Raven’s matrices was the only measure of reasoning, we estimated the true score variance of this measure based on its reliability.
The data from Times 1, 2, and 4 were fitted to the three models, as were the data from Times 1, 3, and 4. For both sets of data, the fit to the (neutral) Model 0 was good, χ2 (27) = 36.392, p < .107 and χ2 (27) = 21.949, p < .740, respectively for the two sets of data; CFI =.989 and 1.00, respectively; TLI = .978 and 1.01, respectively; and RMSEA =.035 and .000, respectively.
Of greater importance are the relative fits of Models 1 and 2. Model 1 fits the data well, χ2 (30) = 38.543, p < .136 and χ2 (30) = 25.954, p < .678, respectively, CFI = .990 and 1.00, respectively; TLI = .982 and 1.01, respectively; and RMSEA = .032 and .000, respectively. Critically, Model 1 fits the data as well as the neutral Model 0, χ2 difference (3) = 2.151. p = .542 and χ2 difference (3) = 4.005, p = .261, respectively for the two sets of data.
Model 2 also fits the data relatively well, χ2 (32) = 47.264, p < .040 and χ2 (32) = 33.179, p < .410, respectively; CFI = .982 and .999, respectively; TLI =.969 and .998 respectively; and RMSEA =.041 and .012, respectively. However, Model 2 fits the data significantly less well than Model 1, χ2 difference (2) = 8.721, p = .013 and χ2 difference (2) = 7.225. p = 027. In other words, a model that includes only indirect effects of speed on reasoning (via WM) fits the data less well than a model that includes direct and indirect effects of speed on reasoning.
Model 1 is shown in the bottom panels of Figures 1 and 2. For the data from Times 1, 2, and 4 (Figure 1), direct effects of speed include links from speed at T1 to reasoning at T2 as well as from speed at T2 to reasoning at T4. In these data, the indirect link between speed and reasoning (via WM) is not significant: neither the T1 speed → T2 WM path nor the T2 WM → T4 reasoning path is significant. For the data from Times 1, 3, and 4 (Figure 2), speed at T1 was linked to WM at T3 and to reasoning at T2 (already shown in Figure 1) but, surprisingly, neither the T3 speed → T4 reasoning path nor the T3 WM → T4 reasoning path is significant. However deleting these two nonsignificant paths leads to a significant decrease in model fit, χ2 difference (2) = 19.815, p < 001, suggesting colinearity between speed and WM at T3. Supporting this, a similar model, where speed and WM at T3 were put on the same scale of measurement and constrained to be equal, showed significant paths to T4 reasoning (β = .20, p < .001) and the fit of this model did not differ from the fit of the same model when the two paths were freely estimated, χ2 difference (1) = .108. p =.742.
DISCUSSION
The aim of the work reported here was to evaluate direct and indirect links between age-related changes in processing speed and reasoning. We found strong support for direct links between speed and reasoning, an outcome that replicates findings reported by Demetriou et al. (2002) in which processing speed was estimated from performance on naming tasks. We also found much weaker support for possible indirect links via WM. We first consider evidence for indirect links, then comment on the finding of direct links between speed and reasoning.
There was relatively weak evidence for an indirect path linking speed to WM and then to reasoning (such an effect was absent for the T1, T2, T4 data, but there was some support for it in the T1, T3, T4 data). This outcome might be seen as unexpected given the many demonstrations of these paths in concurrent studies. One explanation focuses on the psychometric properties of the processing speed and WM constructs. At each time, the partial correlations for the two measures of processing speed were substantially greater than those for the two measures of WM. For example, at Time 1, correlations with age partialled out were .628 between Visual Matching and Cross out but only .316 between listening span and reading span. In addition, processing speed was always estimated from the same two tasks but WM was estimated from different tasks. By this explanation, links involving processing speed were easier to detect than those involving WM because the former construct was estimated more consistently than the latter. Nevertheless, it should be noted that the WM construct was remarkably stable across waves, suggesting that the tasks were measuring a common underlying process. Furthermore, WM at T1 predicted reasoning at T2, consistent with the proposed speed → WM → reasoning pathway.
In contrast, speed was linked directly to reasoning: speed at T1 was linked to reasoning at T2, speed at T2 was linked to reasoning at T4, and at T3 speed and WM both linked to reasoning but their contribution could not be separated from each other. These findings are consistent with many cross-sectional studies (e.g., Frye & Hale, 1996) and some longitudinal work (e.g., Demetriou et al., 2002; Rose et al., 2008) in showing that greater processing speed is associated with enhanced “higher-level” cognitive processing. In other words, increases in processing speed appear to be one factor that contributes to age-related improvements in reasoning skill.
However, this conclusion comes with two caveats. First, although the present study involved a longitudinal design the effects here remain purely correlational. Consequently, it is worth noting that in one of the few relevant experimental studies, Mackey et al. (2011) found that following extensive practice on video games that emphasized rapid processing and responding, 7- to 10-year-olds responded more rapidly on psychometric measures of processing speed. However, performance did not change on measures of reasoning (or WM, for that matter); in other words, although practice led children to responded more rapidly on the Cross Out task used here, it did not increase children’s accuracy on matrix problems like those found on the Raven’s. The failure to find more accurate reasoning following practice-related increases in speed suggests it would be premature to conclude that age-related increases in speed necessarily lead to improved reasoning.
Second, the present findings were based on analyses of correlations in which age was partialled out, a procedure that assumes links between speed and reasoning are invariant throughout the ages included in the sample (6 to 13 years). However, a provocative meta-analysis of cross-sectional studies (Demetriou et al., 2014) suggests that links between speed, WM, and reasoning may change with age. In this work, at 6-8 and 11-13 years—when qualitatively more sophisticated representations are said to emerge (e.g., inference-based concepts at about 6)—speed predicted reasoning more accurately than WM did. In contrast, at ages 8-10 and 13-16—when new representations are aligned and integrated—WM predicted reasoning more accurately than speed did. These cyclical changes in the strength of links between speed, WM, and reasoning could not be evaluated here because the sample was too small to divide into the required narrow age bands. Doing so is a task for future longitudinal studies.
In summary, our findings from a large-scale longitudinal study are consistent with the idea that variations in processing speed may act directly to place constraints on the development of reasoning. Further evidence from training studies is needed to test whether such patterns reflect a causal influence of earlier variations in processing speed on later reasoning skills.
Research highlights.
This longitudinal study examined the direct and indirect effects of age-related change in processing speed on reasoning.
The findings indicate that increased speed of processing is associated longitudinally with improved reasoning.
The findings also revealed indirect influences of speed on reasoning, via working memory, but these results were less consistent.
Acknowledgments
The research described here was supported by a grant from the National Institute of Health (NICHD, R01 046927). Thanks are due to Sherry Fetterman, Megan Rockwood, Ariel Hughes, and Will Bankston for their help in collecting the data.
Contributor Information
Robert V. Kail, Purdue University
Arne Lervåg, University of Oslo.
Charles Hulme, University College London.
References
- Allen GL, Ondraceck PJ. Age-sensitive cognitive abilities related to children’s acquisition of spatial knowledge. Developmental Psychology. 1995;31:934–945. http://dx.doi.org/10.1037/0012-1649.31.6.934. [Google Scholar]
- Clark CAC, Nelson JM, Garza J, Sheffield TD, Wiebe SA, Espy KA. Frontiers in Psychology. 2014;5:107. doi: 10.3389/fpsyg.2014.00107. doi: 10.3389/fpsyg.2014.00107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coyle TR, Pillow DR, Snyder AC, Kochunov P. Processing speed mediates the development of general intelligence (g) in adolescence. Psychological Science. 2011;22:1265–1269. doi: 10.1177/0956797611418243. doi: 10.1177/0956797611418243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daneman M, Carpenter PA. Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior. 1980;19:450–466. doi:10.1016/S0022-5371(80)90312-6. [Google Scholar]
- De Alwis D, Hale S, Myerson J. Extended cascade models of age and individual differences in children’s fluid intelligence. Intelligence. 2014;46:84–93. doi: 10.1016/j.intell.2014.05.008. [Google Scholar]
- Demetriou A, Christou C, Spanoudis G, Platsidou M. The development of mental processing: Efficiency, working memory, and thinking. Monographs of the Society for Research in Child Development. 2002;67 Serial No. 268. [PubMed] [Google Scholar]
- Demetriou A, Spanoudis G, Shayer M, van der Ven S, Brydges CR, Kroesbergen E, Swanson HL. Relations between speed, working memory, and intelligence from preschool to adulthood: Structural equation modeling of 14 studies. Intelligence. 2014;46:107–121. doi:10.1016/j.intell.2014.05.013. [Google Scholar]
- Fry AF, Hale S. Processing speed, working memory, and fluid intelligence: Evidence for a developmental cascade. Psychological Science. 1996;7:237–241. doi: 10.1111/j.1467-9280.1996.tb00366.x. [Google Scholar]
- Kail R. Developmental change in speed of processing during childhood and adolescence. Psychological Bulletin. 1991;109:490–501. doi: 10.1037/0033-2909.109.3.490. http://dx.doi.org/10.1037/0033-2909.109.3.490. [DOI] [PubMed] [Google Scholar]
- Kail R. Phonological skill and articulation time independently contribute to the development of memory span. Journal of Experimental Child Psychology. 1997;67:57–68. doi: 10.1006/jecp.1997.2393. doi:10.1006/jecp.1997.2393. [DOI] [PubMed] [Google Scholar]
- Kail RV. Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning. Psychological Science. 2007;18:312–313. doi: 10.1111/j.1467-9280.2007.01895.x. doi: 10.1111/j.1467-9280.2007.01895.x. [DOI] [PubMed] [Google Scholar]
- Kail R, Hall LK. Sources of developmental change in children’s word-problem performance. Journal of Educational Psychology. 1999;91:660–668. http://dx.doi.org/10.1037/0022-0663.91.4.660. [Google Scholar]
- Kail R, Hall LK, Caskey BJ. Processing speed, exposure to print, and naming speed. Applied Psycholinguistics. 1999;20:303–314. [Google Scholar]
- Lervåg A, Hulme C. Rapid automatized naming (RAN) taps a mechanism that places constraints on the development of early reading fluency. Psychological Science. 2009;20:1040–1048. doi: 10.1111/j.1467-9280.2009.02405.x. doi: 10.1111/j.1467-9280.2009.02405.x. [DOI] [PubMed] [Google Scholar]
- Little RJA. A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association. 1988;83:1198–1202. [Google Scholar]
- Mackey AP, Hill SS, Stone SI, Bunge SA. Differential effects of reasoning and speed training in children. Developmental Science. 2011;14:582–590. doi: 10.1111/j.1467-7687.2010.01005.x. doi: 10.1111/j.1467-7687.2010.01005.x. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. Seventh Edition Muthén & Muthén; Los Angeles, CA: 1998-2012. [Google Scholar]
- Nettelbeck T, Burns NR. Processing speed, working memory, and reasoning ability from childhood to old age. Personality and Individual Differences. 2010;48:379–384. doi: 10.1016/j.paid.2009.10.032. [Google Scholar]
- Raven JC. Standard Progressive Matrices. H. K. Lewis; London, U.K.: 1958. [Google Scholar]
- Rose SA, Feldman JF, Jankowski JJ, Van Rossem R. A cognitive cascade in infancy: Pathways from prematurity to later mental development. Intelligence. 2008;36:367–378. doi: 10.1016/j.intell.2007.07.003. doi: 10.1016/j.intell.2007.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose SA, Feldman JF, Jankowski JJ. Pathways from toddler information processing to adolescent lexical proficiency. Child Development. doi: 10.1111/cdev.12415. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spanoudis G, Demetriou A, Kazi S, Giorgala K, Zenonos V. Embedding cognizance in intellectual development. Journal of Experimental Child Psychology. 2015;132:32–50. doi: 10.1016/j.jecp.2014.12.003. [DOI] [PubMed] [Google Scholar]
- Turner ML, Engle RW. Is working memory capacity task dependent? Journal of Memory and Language. 1989;28:127–154. doi: 10.1016/0749-596X(89)90040-5. [Google Scholar]