Cortical Surface-Based Construction of Individual Structural Network with Application to Early Brain Development Study

Abstract

Analysis of anatomical covariance for cortex morphology in individual subjects plays an important role in the study of human brains. However, the approaches for constructing individual structural networks have not been well developed yet. Existing methods based on patch-wise image intensity similarity suffer from several major drawbacks, i.e., 1) violation of cortical topological properties, 2) sensitivity to intensity heterogeneity, and 3) influence by patch size heterogeneity. To overcome these limitations, this paper presents a novel cortical surface-based method for constructing individual structural networks. Specifically, our method first maps the cortical surfaces onto a standard spherical surface atlas and then uniformly samples vertices on the spherical surface as the nodes of the networks. The similarity between any two nodes is computed based on the biologically-meaningful cortical attributes (e.g., cortical thickness) in the spherical neighborhood of their sampled vertices. The connection between any two nodes is established only if the similarity is larger than a user-specified threshold. Through leveraging spherical cortical surface patches, our method generates biologically-meaningful individual networks that are comparable across ages and subjects. The proposed method has been applied to construct cortical-thickness networks for 73 healthy infants, with each infant having two MRI scans at 0 and 1 year of age. The constructed networks during the two ages were compared using various network metrics, such as degree, clustering coefficient, shortest path length, small world property, global efficiency, and local efficiency. Experimental results demonstrate that our method can effectively construct individual structural networks and reveal meaningful patterns in early brain development.

1 Introduction

In the last decade, analysis of functional and structural connectivity has received increasing attentions in human brain studies, as it opens up a new approach in understanding brain development, aging and disorders. Generally, functional connectivity is identified by exploring the correlation of regional fMRI or EEG/MEG signals [1], while structural connectivity is usually established by tracking the fibers in white matters (WM) using diffusion-weighted images (DWI). Recently, there has been rising interests in studying anatomical covariance in the cortical gray matter (GM) using MR images [1]. This can help identify direct and indirect correlations between cortical regions and help reveal genetic influence on brain morphology. In contrast to the conventional studies of functional and structural connectivity that examine the correlation of brain regions within an individual, most existing studies of anatomical covariance in GM explore the correlation among morphological measures across a population [1]. To better understand the human brain, studying individual anatomical covariance in GM is also considerably indispensable. However, the methods for constructing meaningful individual anatomical networks have not been well developed yet. Although several methods based on the patch-wise similarity of image intensity have been recently proposed and reported interesting results [2-4], they all suffer from several major limitations: 1) violation of cortical topological properties, 2) sensitivity to intensity heterogeneity, and 3) influence by patch size heterogeneity.

Violation of Cortical Topological Properties

In image-patch-based methods, each patch is considered as a node in the constructed network. However, anatomically-distinct and geodesically-distant cortical regions may be included in the same patch, causing the respective node and its connections to be less meaningful. For example, as shown in Fig. 1(a), two gyral regions (x and y) are partially included in the red patch, although they are geodesically far away from each other.

Fig. 1.

Limitations of existing methods (a, b), and the advantages of the proposed method (c).

Sensitivity to Intensity Heterogeneity

Most existing methods compute the similarity between two patches based on their image intensity values. However, the intensity lacks clearly defined anatomical meanings, and the same intensity value may stand for different tissues in different MR scans, making it incomparable across subjects and longitudinal scans of the same subject. This problem is particularly pronounced in early brain development studies, where the intensity of MRI varies regionally considerably and changes temporally dynamically. For example, as shown in Fig. 1(b), the MR images of the same infant have completely different intensity levels at different ages. Thus, ‘Similarity 0’ and ‘Similarity 1’ are not comparable, though they measure the anatomical covariance in corresponding regions.

Influence by Patch Size Heterogeneity

Since the volumes of human brains are quite variable across subjects and ages, it is impossible to determine a unique size of image patch for each individual, while keeping the patches comparable across subjects. Even for the scans of the same subject at different ages, simply adjusting the patch size according to changes in brain volume still does not achieve comparable patches, as the brain develops nonlinearly and regionally heterogeneously.

To address the above limitations, this paper proposes a novel cortical surface-based method to construct individual structural networks. Specifically, in our method, the cortical surfaces are first mapped onto a standard spherical surface and aligned onto the spherical surface atlas. Then, patches on the aligned spherical surface are used to define the nodes in the individual network, as shown in Fig. 1(c). This guarantees that each surface patch strictly represents geodesically and anatomically meaningful cortical regions. Moreover, the similarity between two spherical patches is computed using cortical anatomical attributes with clear biological meanings, such as cortical thickness [5] and cortical folding. This similarity is fully comparable across subjects and also across ages for the same subject. Furthermore, since the patches are selected from aligned spherical surfaces, the size of the patch is independent from brain volume. As a result, each patch will always represent the anatomically corresponding cortical regions across different subjects and ages.

The proposed method has been applied to construct individual cortical-thickness networks for 73 healthy infants, with each infant having two MRI scans at 0 and 1 year of age. The constructed networks at the two ages were compared using various network metrics, such as degree, clustering coefficient, shortest path length, small world property, global efficiency, and local efficiency. The experimental results demonstrate that our method can effectively construct individual structural networks and reveal meaningful patterns in early brain development.

2 Methods

Subjects and Image Acquisition

MR images were acquired for 73 healthy infants (42 males and 31 females), using a Siemens head-only 3T scanner with a circular polarized head coil. For each subject, images were longitudinally collected at term birth (0-year-old) and 1 year of age (1-year-old). Both T1-weighted (resolution =1×1×1 mm³) and T2-weighted (resolution=1.25×1.25×1.95 mm³) MR images were collected.

Image Preprocessing

All MR images were processed by the following pipeline as in [6]. First, each T2-weighted image was linearly aligned onto the corresponding T1-weighted image, and then resampled to the resolution of 1×1×1 mm³. Second, skull, cerebellum and brain stem were removed automatically, and intensity inhomogeneity was corrected using N3 method [7]. Third, each image was rigidly aligned to the age-matched infant brain atlas [8]. Fourth, tissue segmentation was performed by using a longitudinally-guided coupled level-sets method [9]. Finally, non-cortical structures were filled, with each brain further separated into left and right hemispheres [10].

Cortical Surface Reconstruction and Registration

For each hemisphere of each image, topologically correct inner and outer cortical surfaces (represented by triangular meshes) were reconstructed using a deformable surface method [11]. Cortical thickness of each vertex was computed as the closest distance between the inner and outer cortical surfaces. To establish both inter-subject and left-right cortical correspondences, all cortical surfaces of the left hemisphere and mirror-flipped right hemisphere at the same age were mapped onto a spherical space and nonlinearly aligned to the age-matched unbiased surface atlases [11]. Longitudinal cortical correspondences were established by aligning the cortical surfaces at birth to the corresponding cortical surfaces at 1 year of age using Spherical Demons [12].

Construction of Individual Networks

The individual network is constructed with the following three major steps: (1) defining the nodes of the network, (2) computing similarity matrix between nodes, and (3) binarizing the similarity matrix.

In Step (1), N vertices are uniformly sampled on the aligned spherical surfaces of two hemispheres. For each sampled vertex, its neighborhood is selected and defined as a node of the network, as shown in Fig. 2(a). The size of the neighborhood (also namely node area) is constrained by two factors. First, any position on the spherical surface must be covered by at least one node area. Second, the portion of overlapping among node areas is no more than a user-specified threshold T_overlap . We experimentally set N as 1284 and T_overlap as 10% in our implementation.

Fig. 2.

Illustration of construction of individual structural network based on cortical surface.

In Step (2), as shown in Fig. 2(b), the similarity matrix is built by calculating the similarity between any two node areas. Specifically, in the area of each node i, a certain number of vertices are uniformly sampled. Then, a feature vector ${\mathit{v}}_i\in {\mathbb{R}}^n$ is constructed using the cortical morphological attributes (e.g., cortical thickness in our implementation) at all sampled vertices, where n is the number of sampled vertices in the node area. To obtain the similarity of two areas of nodes i and j, Pearson's correlation coefficient r_ij is computed using their feature vectors v_i and v_j as: $r_{ij}=\frac{{\sum }_{k=1}^n(v_{ik}-{\stackrel{‒}{v}}_i)(v_{jk}-{\stackrel{‒}{v}}_j)}{\sqrt{{\sum }_{k=1}^n{(v_{ik}-{\stackrel{‒}{v}}_i)}^2}\sqrt{{\sum }_{k=1}^n{(v_{jk}-{\stackrel{‒}{v}}_j)}^2}}$. Since the similarity of two node areas is directionally sensitive, for two nodes i and j, the Pearson's correlation coefficient r_ij is repetitively computed for every θ angle rotation of the spherical patches in its tangential plane. The maximum value is used as the similarity s_ij for these two nodes. This process can be formulated as: s_ij = max_m r_ij(mθ). In our implementation, we set θ as π/10, which indicates that 10 different correlation coefficients are computed for each pair of nodes. We also tested using the smaller θ, but the results showed no significant changes.

In Step (3), the similarity matrix is binarized using a subject-specific threshold, which is determined automatically for each subject based on an expected level of statistical significance. Specifically, the matrix of Pearson's correlation coefficients is first transformed to a p-value matrix, and then the false discovery rate (FDR) technique is applied to the p-value matrix with an expected p-value τ [13]. A corrected p-value τ′ is produced by FDR. Finally, each element in the p-value matrix is compared with τ′. If it is less than τ′, the corresponding element in the similarity matrix is set as 1; otherwise, it is set as 0. The FDR process is necessary because it can effectively control the proportion of false positives for multiple comparisons under an expected level. Generally speaking, by using FDR technique, for any subject the chance of including false correlations in its network is limited to 100τ%. We chose τ to be 0.022 since the average sparsity degree of the network for this value was 22~23%, which was similar to that of previous studies [3, 14, 15].

By using the above three steps, an individual network of cortical thickness can be established. Leveraging spherical cortical surface patches, our method generates biologically-meaningful individual networks, of which the node areas are comparable across ages and subjects. Note that, connections in the individual network may reflect the direct or indirect fiber connectivity in white matter or similar genetic influence between two regions [1] or intrinsic micro-structural connectivity in gray matter [16]. This method can also be used to construct individual networks using other cortical attributes, such as sulcal depth and cortex folding degree.

Network Metrics

The constructed individual cortical thickness network is an undirected and unweighted graph represented by a binary matrix. To measure these individual networks, we employ the following widely used metrics in graph theory, including: node degree, clustering coefficient, shortest path length, small world property, global efficiency, and local efficiency, as in [3, 17]. Specifically, in an undirected graph, node degree α_i is the number of edges of a node i. Assume the subnetwork G_i consists of all the direct neighbors of node i and their connections, the clustering coefficient c_i of the node i is defined as the number (N_Gi) of edges in G_i divided by the number of all possible connections, formulated as: $c_i=\frac{2N_{G_i}}{{\alpha }_i({\alpha }_i-1)}$. The shortest path length L_i of a node i is the average value over its shortest path lengths to all other nodes. Of note, in our network, the path length between two directly connected nodes is 1. The small world property of a network G is denoted as σ = γ/λ, where γ is defined as the sum of clustering coefficients for all nodes in G divided by the sum of clustering coefficients for all nodes in a random network G_rand, formulated as: $\gamma =\frac{{\sum }_{i\in G}{c}_i}{{\sum }_{i\in G_{rand}}{c}_i}$. And λ is defined as the sum of shortest path lengths for all nodes in G divided by the sum of shortest path lengths for all nodes in G_rand, formulated as: $\lambda =\frac{{\sum }_{i\in G}{L}_i}{{\sum }_{i\in G_{rand}}{L}_i}$. Of note, the random network G_rand is generated by reconnecting the nodes (changing the edges) in G, while preserving the node degrees [18]. A network is considered to own small world property if and only if the following two conditions are satisfied simultaneously: γ > 1 and λ ≈ 1. The global efficiency of a network G is defined as the average of the inverse of all shortest path lengths, formulated as: $E_{global}=\frac{2}{N(N-1)}{\sum }_{i\ne j\in G}\frac{1}{d_{ij}}$. Herein, d_ij is the shortest path length between nodes i and j; and N is the number of nodes in G. The local efficiency of a node i, E_g(G_i), is defined as the global efficiency of the local network G_i. Then the local efficiency of a network G is defined as the average of local efficiencies of all nodes, formulated as: $E_{local}=\frac{1}{N}{\sum }_{i\in G}{E}_g\left(G_i\right)$.

3 Results

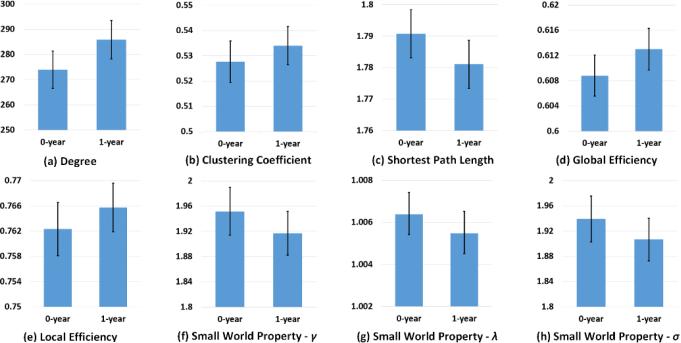
We constructed individual cortical thickness networks for 73 health infants at age 0 and age 1, and measured each individual network using the metrics introduced in Section 2. Fig. 3 reports the distributions of network measures of the whole population. As we can see, from 0 to 1 year of age, all the metrics change dramatically, indicating that our method is able to reveal network differences during early brain development. Specifically, the degree, clustering coefficient, global efficiency, and local efficiency of the cortical thickness network increase, while the shortest path length decreases in the first year. The increase of global and local efficiency is generally consistent with the results in early brain development study of population-based anatomical networks [19]. We also launched paired t-test for each metric to evaluate the difference between the networks at 0-year-old and 1-year-old. With all p-values being far less than 0.01, we can conclude that all those metrics derived from individual networks of cortical thickness are significantly different at the two time points.

Fig. 3.

Network metrics of 73 subjects at 0-year-old and 1-year-old, respectively.

We further investigated the small world property for the cortical thickness networks at age 0 and 1. Although the metric σ changes significantly during the first year as shown in Fig. 3, the cortical thickness network consistently has the small world property. Fig. 4 shows the comparison between constructed networks and their corresponding randomized networks for 10 randomly selected individuals. We can see that, at both age 0 (Fig. 4a) and age 1 (Fig. 4e), the clustering coefficient of constructed network for each individual is consistently larger than that of the randomized network, which has the same degree distribution with our constructed network. Moreover, the shortest path length of our constructed network for each individual is consistently approximately equivalent to that of the randomized network at both age 0 (Fig. 4c) and age 1 (Fig. 4g). The similar observation can also be seen from the average metrics for 73 subjects (Fig. 4b, d, f, and h). Therefore, for both ages, the metric λ is always larger than 1 and the metric is always approximately equal to 1, indicating that the small world property of the cortical thickness network constructed by our method is retained in the first year, which is consistent with results reported in early brain development study of population-based anatomical networks [19].

Fig. 4.

Comparison of constructed networks and randomized networks for 10 randomly selected individuals (a, c, e, and g) and the whole population of 73 subjects (b, d, f, and h). The first row shows the metrics of 0-year-old networks, and the second row shows the metrics of 1-year-old networks.

4 Conclusion

This paper presents a novel method for cortical surface-based construction of individual structural networks. Compared to the existing intensity patch based methods [2-4], the proposed method has three major advantages. First, surface-based patch (node area) guarantees that each patch corresponds to anatomically meaningful and geodesically neighboring cortical regions, in contrast to an image patch that might contain geodesically-distant regions. Second, the cortical morphology-defined similarity ensures that this similarity is comparable across subjects and ages, in contrast to image intensity, which is quite variable across ages and subjects and has less meaningful anatomical meanings. Third, since patches are defined on the standard spherical surface atlas space, the patch size is independent of the brain volume, which makes both the cross-subject and longitudinal comparisons more meaningful. The proposed method has been applied to 73 healthy infants at age 0 and age 1, leading to meaningful discoveries of early brain development. In the future, we will construct individual networks using other cortical attributes, e.g., sulcal depth, cortical folding and cortical local gyrification [20], and further compare them with the structural networks derived from DTI and also the functional networks derived from fMRI.