Space-Frequency Detail-Preserving Construction of Neonatal Brain Atlases

Abstract

Brain atlases are an integral component of neuroimaging studies. However, most brain atlases are fuzzy and lack structural details, especially in the cortical regions. In particular, neonatal brain atlases are especially challenging to construct due to the low spatial resolution and low tissue contrast. This is mainly caused by the image averaging process involved in atlas construction, often smoothing out high-frequency contents that indicate fine anatomical details. In this paper, we propose a novel framework for detail-preserving construction of atlases. Our approach combines space and frequency information to better preserve image details. This is achieved by performing reconstruction in the space-frequency domain given by wavelet transform. Sparse patch-based atlas reconstruction is performed in each frequency subband. Combining the results for all these subbands will then result in a refined atlas. Compared with existing atlases, experimental results indicate that our approach has the ability to build an atlas with more structural details, thus leading to better performance when used to normalize a group of testing neonatal images.

1 Introduction

Brain atlases are spatial representations of anatomical structures, allowing integral brain analysis to be performed in a standardized space. They are widely used for neuroscience studies, disease diagnosis, and pedagogical purposes [1,2].

An ideal brain atlas is expected to contain sufficient anatomical details and also to be representative of the images in a population. It serves as a non-bias reference for image analysis. Generally, atlas construction involves registering a population of images to a common space and then fusing them into a final atlas. In this process, structural misalignment often causes the fine structural details to be smoothed out, which results in blurred atlases. The blurred atlases can hardly represent real images, which are normally rich with anatomical details.

To improve the preservation of details in atlases, the focus of most existing approaches [3-7] has been on improving image registration. For instance, Kuklisova-Murgasova et al. [3] constructed atlases for preterm infants by affine registration of all images to a reference image, which was further extended in [4] by using groupwise parametric diffeomorphic registration. Oishi et al. [5] proposed to combine affine and non-linear registrations for hierarchically building an infant brain atlas. Using adaptive kernel regression and group-wise registration, Serag et al. [6] constructed a spatio-temporal atlas of the developing brain. In [7], Luo et al. used both intensity and sulci landmark information in the group-wise registration for constructing a toddler atlas. However, all these methods perform simple weighted averaging of the registered images and hence have limited ability in preserving details during image fusion. For more effective image fusion, Shi et al. [8] utilized a sparse representation technique for patch-based fusion of similar brain structures that occur in the local neighborhood of each voxel. The limitation of this approach is that it lacks an explicit attempt to preserve high frequency contents for improving the preservation of anatomical details. In [9], Wei et al. proposed to use wavelet transform to reveal detailed information from motion-corrupted diffusion-weighted images of the human heart. It is shown that pyramidal decomposition of images encodes coarse and fine image contents in different frequency subbands.

In this paper, we propose a novel image fusion approach for obtaining neonatal brain atlases with rich details. We employ information in both frequency and space domains given by wavelet transform for atlas construction.

Frequency domain

By decomposing each brain image into multiple scales and orientations using wavelet transform, fine and latent anatomical structures become more apparent in certain frequency subbands. It is hence easier to design constraints to preserve these structures.

Space Domain

The neighboring patches are group-constrained for spatial consistency during reconstruction. We apply our method to construct brain atlases for neonatal MR images, which is challenging due to the low spatial resolution and low tissue contrast. Experimental results indicate that the proposed method can generate atlases of much higher quality, compared to the existing state-of-the-art neonatal atlases.

2 Method

2.1 Overview

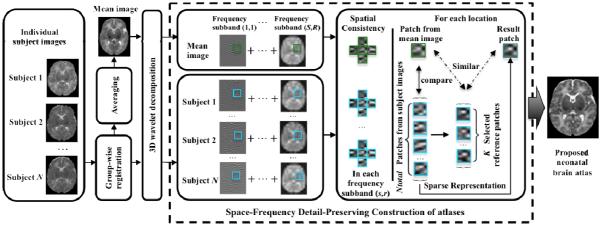
The overall pipeline of the proposed method is shown in Fig. 1. First, all individual subject images are aligned to a common space using group-wise registration to generate a mean image. Wavelet transform is then used to decompose both the aligned individual images and the mean image into the frequency domain. In each frequency subband, we then construct an atlas using patch-by-patch sparse reconstruction. To avoid inconsistency, the immediate neighbors of each patch are group-constrained to have similar sparse coefficients. Finally, the reconstructed frequency subband atlases are combined together to construct a final atlas.

Fig. 1.

Flow chart of the proposed atlas construction framework

2.2 Image Preprocessing

All images were preprocessed with a standard pipeline, including resampling, bias correction, skull stripping, and tissue segmentation. We use a publicly available group-wise registration method [10] (http://www.nitrc.org/projects/glirt) to align all images to a common space. We can then obtain a set of N registered images $\{I_n\mid n=1,\cdots ,N\},I_n\in {\mathbb{R}}^3$. These images are averaged to form a mean image $I_{mean}=\frac{1}{N}{\sum }_{n=1}^N{I}_n$.

2.3 Frequency Domain Reconstruction

We combine atlases generated from different frequency subbands of the images to better preserve high-frequency image details. We first perform pyrami decomposition using 3D wavelet on all images:

$$I=\sum _{s=1}^S\sum _{r=1}^R{I}^{(s,r)}=\sum _{s=1}^S\sum _{r=1}^R{D}^{(s,r)}\cdot a^{(s,r)}$$ (1)

where scale s = 1,…,S denotes that the image has been down-sampled s times. For each scale s , images are further decomposed into orientation subband r = 1, … , R . For each scale s , we fixed R = 8 , and the corresponding orientation subbands in 3D are denoted as ‘LLL’, ‘HLL’, ‘LHL’, ‘HHL’, ‘LLH’, ‘HLH’, ‘LHH’, and ‘HHH’ filters, where ‘L’ indicates low-pass filtering and ‘H’ indicates high-pass filtering, i.e., ‘HLH’ denotes high-pass filtering in x and z directions and low-pass filtering in y direction. D^(s,r) denotes the wavelet basis of subband (s, r), and a^(s,r) denotes the wavelet coefficients in subband (s, r). The wavelet coefficients of subband (s,r) of all images {I_n |n = 1,…, N} are denoted as $\left\{a_n^{(s,r)}\mid n=1,\cdots ,N\right\}$.

Atlas construction is performed in a patch-by-patch manner. We consider a local cubic patch $p_{mean}^{(s,r)}$ centered at location (x, y, z) in the mean image I_mean. The patch is represented as a vector of length V = v× v× v, where v is the patch diameter in each dimension. We sparsely refine the mean patch $p_{mean}^{(s,r)}$ using a dictionary, formed by including all patches at the same location in all N training images, i.e., $P^{(s,r)}=\left[p_1^{(s,r)},p_2^{(s,r)},\cdots ,p_N^{(s,r)}\right]$, thereby generating the reconstructed detail-preserving atlas patch $p_{atlas}^{(s,r)}$. To compensate for possible registration error, we enrich the dictionary by including patches from neighboring locations, i.e., 26 locations immediately adjacent to (x, y, z) . Therefore, from all N aligned images, we will have a total of N_total = 27 × N patches in the dictionary, i.e., $P^{(s,r)}=\left[p_1^{(s,r)},p_2^{(s,r)},\cdots ,p_{N_{total}}^{(s,r)}\right]$. We use this dictionary to reconstruct the refined atlas patch $p_{atlas}^{(s,r)}$ by estimating a sparse coefficient vector ${\widehat{\beta }}^{(s,r)}$, with each element denoting the weight of the contribution of a patch in the dictionary.

To further enhance robustness, we constrain the reconstructed atlas patch $p_{atlas}^{(s,r)}$ to be similar to the appearance of a small set of K (K ≤ N_total) neighboring patches $\left\{p_k^{(s,r)}\mid k=1,\cdots ,K\right\}$ from P_(s,r) that are most similar to $p_{mean}^{(s,r)}$. The reconstruction problem can now be formulated as

$${\widehat{\beta }}^{(s,r)}=\underset{{\widehat{\beta }}^{(s,r)}>0}{\text{argmin}}\sum _{k=1}^K\parallel p_k^{(s,r)}-P^{(s,r)}\cdot {\beta }^{(s,r)}{\parallel }_2^2+\lambda \parallel {\beta }^{(s,r)}{\parallel }_1$$ (2)

where λ is a non-negative parameter controlling the influence of the regularization term. Here, the first term measures the discrepancy between observations $p_k^{(s,r)}$ and the reconstructed atlas patch $p_{atlas}^{(s,r)}=P^{(s,r)}\cdot {\widehat{\beta }}^{(s,r)}$, and the second term is for L₁-regularization on the coefficients in β^(s,r). Considering that the dictionary P^(s,r) and the observations $p_k^{(s,r)}$ share the same basis D^(s,r) , we can combine Eq. (1) and Eq. (2) for a wavelet representation version of the problem:

$${\widehat{\beta }}^{(s,r)}=\underset{{\widehat{\beta }}^{(s,r)}>0}{\text{argmin}}\sum _{k=1}^K\parallel D^{(s,r)}\cdot \left(C_k^{(s,r)}-C^{(s,r)}\cdot {\beta }^{(s,r)}\right){\parallel }_2^2+\lambda \parallel {\beta }^{(s,r)}{\parallel }_1$$ (3)

where $C_k^{(s,r)}$ is a vector consisting of the wavelet coefficients of $p_k^{(s,r)}$, and $C^{(s,r)}=\left[c_1^{(s,r)},c_2^{(s,r)},\cdots ,c_{N_{total}}^{(s,r)}\right]$ is a matrix containing the wavelet coefficients of the patches in dictionary P^(s,r). Finally, the atlas is constructed as

$$I_{atlas}=\sum _{s=1}^S\sum _{r=1}^R{I}_{atlas}^{(s,r)}=\sum _{s=1}^S\sum _{r=1}^R{D}^{(s,r)}\cdot C^{(s,r)}\cdot {\widehat{\beta }}^{(s,r)}$$ (4)

2.4 Spatial Consistency

To promote local consistency, multi-task LASSO [11] is used for spatial regularization in the space-frequency domain to simultaneously estimate G neighboring atlas patches, indexed as g = 1, … , G.

We denote the dictionary, training patch, and sparse coefficient vector for the g-th neighbor respectively as $P_g^{(s,r)}$, $p_{k,g}^{(s,r)}$ and ${\beta }_g^{(s,r)}$. For simplicity, we let $B^{(s,r)}=[{\beta }_1^{(s,r)},\cdots ,{\beta }_G^{(s,r)}]$, which can also be written in the form of row vectors: $B^{(s,r)}=\left[\begin{array}{c}\hfill {\gamma }_1^{(s,r)}\hfill \\ \hfill ⋮\hfill \\ \hfill {\gamma }_M^{(s,r)}\hfill \end{array}\right]$, where ${\gamma }_m^{(s,r)}$ is the m-th row in the matrix B^(s,r) (with totally M rows).

Then, we reformulate Eq. (2) using multi-task LASSO:

$$\begin{array}{cc}\hfill & {\widehat{B}}^{(s,r)}=\underset{{\widehat{B}}^{(s,r)}>0}{\text{argmin}}\sum _{g=1}^G\sum _{k=1}^K\parallel p_{g,k}^{(s,r)}-P_{g,k}^{(s,r)}\cdot {\beta }_{g,k}^{(s,r)}{\parallel }_2^2+\lambda \parallel B^{(s,r)}{\parallel }_{2,1}\hfill \\ \hfill & =\underset{{\widehat{B}}^{(s,r)}>0}{\text{argmin}}\sum _{g=1}^G\sum _{k=1}^K\parallel D^{(s,r)}\cdot \left(C_{g,k}^{(s,r)}-C_g^{(s,r)}\cdot {\beta }_g^{(s,r)}\right){\parallel }_2^2+\lambda \parallel B^{(s,r)}{\parallel }_{2,1}\hfill \end{array}$$ (5)

where ${\parallel B^{(s,r)}\parallel }_{2,1}={\sum }_{m=1}^M{\parallel {\gamma }_m^{(s,r)}\parallel }_2$. The first term is a multi-task sum-of-squares term for all G neighboring atlas patches. The second term is for multi-task regularization using a combination of L₂ and L₁ norms. L₂ norm penalization is imposed on each row of matrix B^(s,r) (i.e., ${\gamma }_m^{(s,r)}$) to enforce similarity of neighboring patches. L₁ norm penalization is to ensure representation sparsity. This combined penalization ensures that the neighboring patches have similar sparse coefficients. The multi-task LASSO in Eq. (5) can be solved efficiently by using the algorithm described in [11].

3 Experiments

Dataset

We use neonatal brain scans to demonstrate the performance of the proposed atlas construction method. Specifically, 73 healthy neonatal subjects (42 males / 31 females) were used in this study. MR images of the subjects were scanned at postnatal age of 24±10 (9-55) days using a Siemens head-only 3T scanner. T2-weighted images were obtained with 70 axial slices using a turbo spin-echo (TSE) sequence for a resolution of 1.25×1.25×1.95mm³. All 73 images were resampled to have an isotropic resolution of 1×1×1 mm³, bias-corrected, skull-stripped, and tissue-segmented.

Implementation Details

There are several parameters in the proposed method: the patch size v, the number of nearest patches K, the regularization parameter λ, and the number of wavelet scale levels S. We performed a grid search for parameters that produced the atlas with the highest signal energy. Then we fixed the patch size as v = 6 (V = 6 × 6 × 6) and set the number of closest patches to K = 10. We also set the regularization parameter to λ = 10⁻⁴. We used ‘symlets 4’ as the wavelet basis for image decomposition. The number of scale levels for wavelet decomposition was set to S = 3. The low-frequency content of a single subject image was similar to the low-frequency content of the average atlas when using atlas when using 3 or more scales. This suggests that it is sufficient to use 3 scales.

Atlas Construction Performance Using 73 Subjects

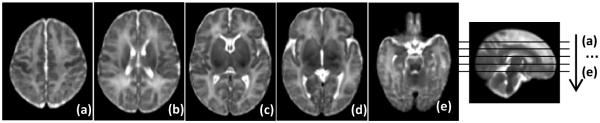
Fig. 2 (a-e) show five representative axial slices of the neonatal brain atlas built by the proposed method. Despite the large number of subjects (73) used for atlas construction, the atlas still contains clear structural details especially in the cortical regions.

Fig. 2.

Neonatal atlas constructed from 73 subjects.

Comparison with State-of-the-Art Neonatal Atlases

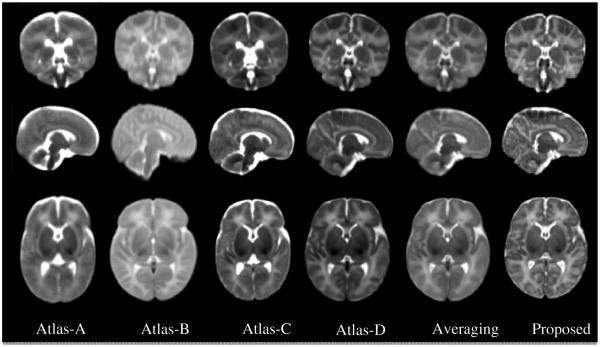
Four state-of-the-art neonatal atlases are included for visual inspection. Atlas-A: The 41-th week atlas created by Kuklisova-Murgasova et al. [3], longitudinally for each week from week 28.6 to week 47.7 using 142 neonatal subjects. Atlas-B: The atlas constructed by Oishi et al. [5] using 25 brain images from neonates of 0-4 days of age. Atlas-C: The 41-th week atlas built by Serag et al. [6] involving 204 premature neonates between 26.7 and 44.3 gestational weeks. Atlas-D: The neonatal atlas created by Shi et al. [8], involving the same neonatal brain images as used in this work. An atlas created by simply averaging the 73 aligned neonatal images is also included for comparison. One can easily observe from Fig. 3 that the atlas generated by the proposed method provides the clearest structural details. Note that, Atlas-A, Atlas-B and Atlas-C are constructed using datasets different from ours and thus may have different appearances from our atlas. Atlas-D, Averaging atlas, and the Proposed atlas are built from the same dataset.

Fig. 3.

Comparison of neonatal atlases constructed by Kuklisova-Murgasova et al. (Atlas-A, 2010), Oishi et al. (Atlas-B, 2011), Serag et al. (Atlas-C, 2012), Shi et al. (Atlas-D, 2014), simple averaging (Averaging), and our proposed method (Proposed) on the 73 aligned images. Similar slices were selected from each of these six atlases for easy comparison.

Evaluation of Atlas Representativeness

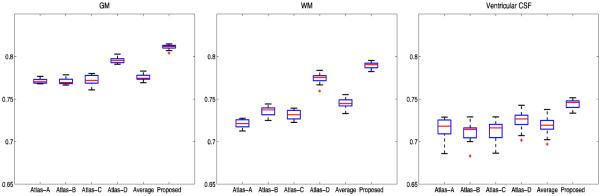
We evaluate the 6 neonatal atlases shown in Fig. 3 in terms of how well they can spatially normalize a testing population of neonatal images. MR images of 20 new healthy neonatal subjects (10 males/ 10 females) were obtained at 37-41 gestational weeks, using TSE sequences with parameters: TR=6200 ms, TE=116 ms, Flip Angle=150°, and resolution=1.25×1.25×1.95 mm³. Similar image preprocessing was performed, which includes resampling to 1×1×1 mm³, bias correction, skull stripping, and tissue segmentation. All these 20 test images are aligned to each of the 6 atlases by first using affine registration and then nonlinear deformable registration with Diffeomorphic Demons [12], respectively. For each atlas, a mean segmentation image is built by voxel-wise majority voting using all aligned segmentation images. The segmentation images of all individuals, warped to the atlas space, are then compared with this mean segmentation image by means of Dice Ratio: $DR=2\mid A\cap B\mid ∕(\mid A\mid +\mid B\mid )$), where A and B are the two segmentation maps. DR ranges from 0 (for totally disjoint segmentations) to 1 (for identical segmentations). The structural agreement is calculated in pair of each aligned image and the voted mean segmentation image, which denotes the ability of each atlas for guiding test images into a common space. Statistical analysis (Fig. 4) indicates that the proposed atlas outperforms all other atlases in GM, WM and CSF alignment. Twosample t-tests based on the Dice Ratios demonstrate that the proposed method significantly outperforms all other comparison methods (p<0.001).

Fig. 4.

Box plots for the Dice Ratio ($DR=2\mid A\cap B\mid ∕(\mid A\mid +\mid B\mid )$), where A and B are the two segmentation maps) values associated with the five state-of-the-art atlases and the proposed atlas. Red lines in the boxes mark the medians. The boxes extend to the lower and upper quartiles (i.e., 25% and 75%). Whiskers extend to the minimum and maximum values in one-and-a-half interquartile range. Outliers beyond this range are marked by red “+” symbols.

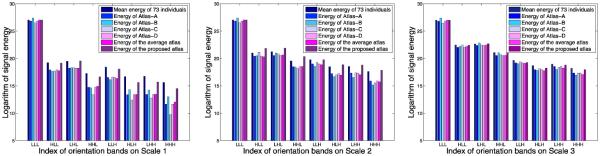
Evaluation of Energy Distribution

We assess the image energy variation across all frequency subbands for the 6 neonatal atlases shown in Fig. 3 and then compare with the individual images. For fair comparison, the intensity ranges of all atlases are normalized to interval [0,255]. Low variation of high-frequency components indicates loss of anatomical details. The energy of each frequency subband is defined as the L₂ norm of wavelet coefficients in that subband. The average energy is computed for each of the 24 wavelet subbands (including 3 scales, and 8 orientations for each scale) of the 73 neonatal subject images. Fig. 5 shows the energy distributions for different scale levels and orientations. For the atlases created with simple averaging, the energy loss is significant in the high frequency subbands (e.g., from subband ‘HLL’ to ‘HHH’ in Scale 1), compared to the atlas created using the proposed method. The energy loss can also be observed in the higher frequency subbands (e.g., subband ‘HHH’) of Scale 2 and Scale 3. The proposed atlas mitigates the energy loss problem, illustrating that the proposed atlas preserves more anatomical details from individual images and is hence more representative of the population.

Fig. 5.

Image energy distributions across orientations and scales, for the individual images, and the 6 neonatal atlases shown in Fig. 3. Higher energy values in high frequency subbands represent better preservation of anatomical details. It can be seen that the proposed atlas preserves more details from individual images, compared with state-of-the-art atlases.

4 Conclusion

In this paper, we presented a novel space-frequency domain based sparse representation method to better preserve structural details in neonatal brain atlases. Our approach employs a hierarchical strategy in reconstructing the atlas through combining atlases reconstructed from the frequency subbands using wavelet decomposition. Experimental results demonstrated that our approach preserves richer anatomical details (with better performance on neonatal image normalization) than other state-of-the-art neonatal atlases.