Abstract
Gonadotropin-releasing hormone (GnRH) neurons exhibit at least two intrinsic modes of action potential burst firing, referred to as parabolic and irregular bursting. Parabolic bursting is characterized by a slow wave in membrane potential that can underlie periodic clusters of action potentials with increased interspike interval at the beginning and at the end of each cluster. Irregular bursting is characterized by clusters of action potentials that are separated by varying durations of interburst intervals and a relatively stable baseline potential. Based on recent studies of isolated ionic currents, a stochastic Hodgkin-Huxley (HH)-like model for the GnRH neuron is developed to reproduce each mode of burst firing with an appropriate set of conductances. Model outcomes for bursting are in agreement with the experimental recordings in terms of interburst interval, interspike interval, active phase duration, and other quantitative properties specific to each mode of bursting. The model also shows similar outcomes in membrane potential to those seen experimentally when tetrodotoxin (TTX) is used to block action potentials during bursting, and when estradiol transitions cells exhibiting slow oscillations to irregular bursting mode in vitro. Based on the parameter values used to reproduce each mode of bursting, the model suggests that GnRH neurons can switch between the two through changes in the maximum conductance of certain ionic currents, notably the slow inward Ca2+ current Is, and the Ca2+ -activated K+ current IKCa. Bifurcation analysis of the model shows that both modes of bursting are similar from a dynamical systems perspective despite differences in burst characteristics.
Keywords: Mathematical model, parabolic bursting, irregular bursting, slow oscillations, slow-fast subsystem analysis, estradiol feedback
1 Introduction
Gonadotropin-releasing hormone (GnRH) neurons are neurosecretory cells of the diencephalon that regulate fertility in vertebrates through the release of GnRH in the median eminence. GnRH stimulates the release of two gonadotropins from the anterior pituitary, making GnRH neurons the apex of the hypothalamo-pituitary-gonadal axis. A pulsatile profile of GnRH release is needed for the secretion of gonadotropins, which is regulated primarily by the frequency of GnRH pulses (Belchetz et al. 1978). The interval between peaks of GnRH ranges from minutes to hours, depending on reproductive state (Moenter 2010), and differentially regulates the release of the two gonadotropins (Wildt et al. 1981).
Gonadal steroids play a role in the regulation of GnRH release. For example, estradiol is involved in the negative homeostatic feedback of GnRH in males and during much of the menstrual or estrous cycle in females, as well as in the positive feedback generation of the preovulatory GnRH surge in females (Herbison 1998; Moenter et al. 2009; Christian and Moenter 2010). Because GnRH neurons do not express detectable amounts of steroid receptors other than the beta isoform of the estradiol receptor, most steroid regulation is likely mediated via steroid-sensitive afferents (Wintermantel et al. 2006).
The mechanism(s) underlying pulsatile GnRH secretion is still an active area of research. Work on other neuroendocrine systems suggests that the electrical activity of GnRH neurons affects the profile of GnRH release (Dutton and Dyball 1979). Consistent with this, GnRH release in the median eminence is typically action potential-dependent (Glanowska and Moenter 2015). Studies of the electrophysiology of GnRH neurons have revealed sustained bursting activity with an interburst interval ranging from less than a minute (Nunemaker et al. 2002; Lee et al. 2010; Chu et al. 2012; Lee et al. 2012) to several minutes (Lee et al. 2012), which is considerably shorter than the period of hormone release. However, spectral analysis of extracellular recordings, consisting mainly of these less than a minute “short-bursting” events (Duan et al. 2011), showed a significant low frequency component with a period similar to that of hormone release (Nunemaker et al. 2003). Through long term measurement of action potential firing rate, it was suggested by this latter study that the low frequency component is attributable to slow modulation of the interburst interval.
Since bursts are a fundamental unit of activity contributing to mean firing rate, it is important to understand how they are generated in GnRH neurons. Whole-cell patch-clamp experiments have shown the existence of at least two distinct modes of bursting in GnRH neurons. The first mode is rarely observed (1–2% of cells) and referred to as “parabolic” because of its spike frequency profile during the active phase that resembles a downward-opening parabola (Chu et al. 2012). This type of bursting is also characterized by slow oscillations (10–20s) that appear to underlie the fast spiking activity, and a significant correlation between next silent duration and active phase duration. The second and more frequently observed mode is referred to as “irregular”, due to its stochastic nature that is marked by variations in its interburst interval and burst duration, no significant correlation between its active phase duration and next silent phase duration, and the absence of small-amplitude slow oscillations in membrane potential underlying its burst (Chu et al. 2012). Recordings show that irregular bursting can occur with quiescent periods on the order of minutes (Lee et al. 2012), but in this study, we will only focus on “short-bursting” (Duan et al. 2011), in which interburst interval is typically less than one minute.
Experimental evidence revealed that bursting in GnRH neurons is an intrinsic feature of these cells; meaning that bursting persists even when synaptic connections are blocked (Nunemaker et al. 2002; Lee et al. 2012). This observation indicates that bursting can occur without external stimuli, and can be generated solely by the dynamics of voltage- and calcium-gated ion channels that control the influx and efflux of ionic currents. Many of these ionic currents including the hyperpolarization-activated current Ih, small conductance calcium-activated potassium current IKCa, transient potassium current IA, and sodium current INa are affected by estradiol via positive or negative feedback loops (Chu and Moenter 2006; Pielecka and Moenter 2006; Chu et al. 2009; Pielecka-Fortuna et al. 2011). Much work has been done to quantify these and other major ionic currents (Na+, K+, Ca2+) in GnRH neurons based on recordings obtained from extracellular and patch-clamp configurations. Equipped with these electrophysiological data, we can construct biophysically detailed models to help illustrate how these different intrinsic bursting activities are generated.
In this present study, we develop a Hodgkin-Huxley-like (HH) model to illustrate the contributions of various physiologically identified ionic currents in the formation of parabolic and irregular bursts in isolated GnRH neurons. To date, no other published models for the GnRH neuron have captured both modes of bursting, while keeping the set of kinetic parameters for ionic currents invariant. The model developed for this study extends previous bursting models (LeBeau et al. 2000; Fletcher and Li 2009; Duan et al. 2011; Csercsik et al. 2012) by using an updated set of ionic currents that are based on more recent electrophysiological data. The new set of currents includes the previously excluded IA and Ih, as well as updates to the delayed rectifier potassium current IK, the high-voltage activated calcium current IHVA, and the fast and persistent sodium currents INaF/INaP. Using the updated model, we predict the ionic mechanisms required to generate both types of bursting in GnRH neurons. We demonstrate that the mode of bursting simulated by the model can be switched between the two types through minor changes in the maximum conductance of a few currents, suggesting that although the two modes of bursts have different characteristics, they possess the same underlying dynamics. In order to test the claim that the two types of bursting are similar mathematically, the dynamics of both are analyzed using bifurcation techniques. A model for the neuromodulatory effect of acutely applied estradiol is also proposed to predict the ionic currents that can be modulated for the GnRH neurons to transition between distinct electrical states under the effect of estradiol.
2 Materials and Methods
2.1 Mathematical model
A single compartment HH model (Fig. 1a) was used to describe the electrical behavior observed during whole-cell recordings of GFP-identified GnRH neurons in adult mice. The voltage equation is given by
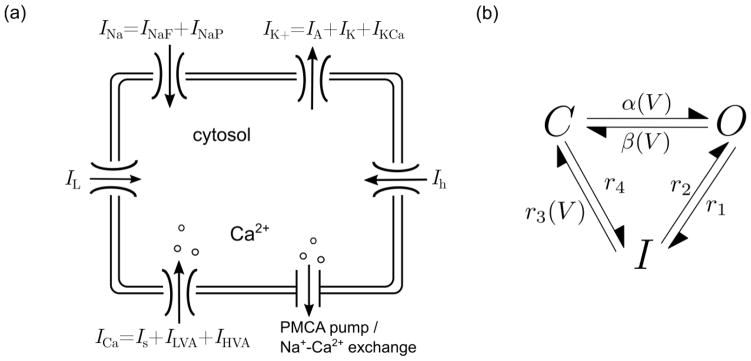
Fig. 1.
(a) Schematic of the GnRH neuron model, indicating the components contributing to ion flux through the membrane. (b) Schematic diagram of the Markov model of INaF. The voltage-dependent transition rates α(V), β(V), r3(V) all have the functional form: ai · [1 + exp[(v + bi)/ci]]−1, where i = α, β, r3 and aα = 55 ms−1, aβ = 60 ms−1, ar3 = 30 ms−1, bα = 33 mV, bβ = 32 mV, br3 = 77.5 mV, cα = −7 mV, cβ = 10 mV, and cr3 = 12 mV. The constant transition rates have the values r1 = 1.0 ms−1, r2 = 0.2 ms−1 and r4 = 0.05 ms−1
| (1) |
where Cm = 20 pF is an experimentally observed value of membrane capacitance (Pielecka-Fortuna et al. 2011), V is the voltage in mV, and t is the time in ms. INaF and INaP are fast and persistent sodium currents, IA and IK are transient and delayed-rectifier potassium currents, ILVA and IHVA are low and high voltage activated calcium currents, Is is a slow inward calcium current, Ih is a hyperpolarization activated current, IKCa is a calcium-activated potassium current, IL is a constant conductance leak current, and Iapp is the applied current (zero unless otherwise stated). The leak current was not active during bursting simulations as its inclusion suppressed the intrinsic excitability of the system. Each ionic current has the form Ij = G(V − Ej), where G (a function of the gating variables) is the conductance in nS, and Ej is the reversal potential in mV. Unless otherwise stated, the ionic current Ij is modeled using the HH formalism, given by
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where g in Eq. (2) is the maximum membrane conductance in nS, m and h are activation and inactivation gating variables, and p represents the number of independent activation gates. Equations (4) and (5) describe the kinetics of the gating variables appearing in Eq. (2), where m∞, h∞ are the voltage-dependent steady-states of (in)activation given by Eq. (6), and τm, τhi are the voltage-dependent time constants of (in)activation in ms, assumed to follow various functional forms (see caption of Table 1 for more details). The inactivation variable h is a weighted sum of gating variables hi with weights 0 ≤ fi ≤ 1, for i = 1, …, n, satisfying . From Eq. (5), each hi has the same steady-state but different voltage-dependent time constants. The weights fi represent the fraction of conducting channels that inactivate with time constant τhi (Willms et al. 1999). For some currents, we found that a value of n > 1 provided better fits of voltage-clamp traces, suggesting that these currents inactivate with multiple time constants. Table 1 provides values of kinetic parameters for currents that have gating dynamics described by Eqs. (4) and (5). The currents INaF and IKCa are not included in this table because they are modeled using different gating schemes. Maximum conductance and reversal potentials for each current are provided in Table 2.
Table 1.
Parameter values of ionic currents described by Eqs. (2)–(6). Units for time constant parameters a, b, c, d, e, f vary and are inferred from the functions τi, each of which is described by and .
| INaP | IA | IK | ILVA | IHVA | Is | Ih | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||
| m | h | m | h1 | h2 | m | m | h | m | h1 | h2 | m | h1 | h2 | |
| Vh (mV) | −41.5 | −47.4 | −15 | −69 | −69 | 15 | −56.1 | −80 | −11 | −32 | −32 | −45 | −77.4 | −77.4 |
| k (mV) | −3.0 | 8.2 | −11 | 6 | 6 | −9 | −10.7 | 4.7 | −7 | 11 | 11 | −12 | 9.2 | 9.2 |
|
| ||||||||||||||
| τ(V) (ms) | 0.4 | τ2 | τ2 | 30 | 500 | τ2 | τ2 | 20 | τ2 | 45 | 950 | 1500 | τ1 | τ1 |
| a | — | 67.3 | −40 | — | — | −43 | 50 | — | 20 | — | — | — | −89.8 | −82.6 |
| b | — | −27.5 | 26.5 | — | — | 18.5 | 9 | — | −10 | — | — | — | 11.6 | 25.7 |
| c | — | 67.3 | 43 | — | — | 144 | 50 | — | 20 | — | — | — | 35.8 | 370.9 |
| d | — | 27.5 | −8.4 | — | — | −49 | −9 | — | 10 | — | — | — | 7.6 | 54.1 |
| e | — | 574.5 | 1 | — | — | 0.38 | 7 | — | 1 | — | — | — | — | — |
| f | — | 62.6 | 0.1 | — | — | 0 | 0.5 | — | 0.6 | — | — | — | — | — |
Table 2.
Parameter values of ionic currents appearing in Eq. (1). E represents the reversal potentials, gvc the maximum current conductances obtained from voltage-clamp experiments, whenever applicable, and gp, girr, gsub, and ge the maximum current conductances used for reproducing parabolic bursting, irregular bursting, subthreshold oscillation, and estradiol-affected irregular bursting profiles, respectively
| INaF | INaP | IA | IK | ILVA | IHVA | Is | Ih | IKCa | IL | |
|---|---|---|---|---|---|---|---|---|---|---|
| E (mV) | 54 | 54 | −101 | −101 | 82.5 | 82.5 | 82.5 | −40 | −101 | −65 |
| gvc (nS) | — | 0.68 | 45 | 100 | 0.2 | 8 | — | 1 | — | 1 |
| gp (nS) | 300 | 0.68 | 45 | 115 | 0.2 | 8 | 0.58 | 0.5 | 1.96 | 0 |
| girr (nS) | 500 | 0.68 | 45 | 150 | 0.2 | 8 | 0.18 | 1 | 1.18 | 0 |
| gsub (nS) | 500 | 0.68 | 45 | 150 | 0.2 | 8 | 0.58 | 0.5 | 3.88 | 0 |
| ge (nS) | 500 | 0.68 | 35 | 150 | 0.2 | 8 | 0.2 | 0.5 | 1.18 | 0 |
The dynamics of cytosolic Ca2+ concentration in μM, denoted by Ca, were also accounted for in the model. Some previous models of the GnRH neuron assume compartmental calcium dynamics (LeBeau et al. 2000; Duan et al. 2011; Csercsik et al. 2012) but in order to minimize the number of free parameters, a single compartment model was used here. The Ca2+ submodel assumes influx of Ca2+ through voltage-gated calcium channels and efflux of Ca2+ via membrane pumps. The governing equations are given by
| (7a) |
| (7b) |
| (7c) |
where f = 0.0025 is the fraction of free (unbound) Ca2+ in the cytosol, kp = 0.265 ms−1 is the pump rate, Kp = 1.2 μM and α = 1.85 × 10−3 μM/(pA·ms) is a current to flux conversion factor. The Hill function in Eq. (7a) is assumed to capture the overall effect of the plasma membrane Ca-ATPase (PMCA) pump and the Na+/Ca2+ exchanger. A Hill coefficient of 2 was chosen based on its use in previous models to describe efflux of Ca2+ via the PMCA pump (LeBeau et al. 2000; Duan et al. 2011). The value of α was determined by Eq. (7c), where F is Faraday’s constant, the factor 2 is the valence of the Ca2+ cation, β=106 is a scaling factor that ensures the concentration is in μM, and Vcyt = 2.8 pL is the volume of the somatic compartment, estimated by digitizing a confocal image of a representative GnRH neuron (Hemond et al. 2012). The estimation of Vcyt was obtained by fitting the 2D coordinates of the soma to an ellipse and calculating the volume of the resulting ellipsoid by setting the length of the undetermined axis equal to that of ellipse’s minor axis.
2.1.1 Ionic currents
All ionic currents except for INaF, Is, and IKCa were fit to current traces from voltage-clamp experiments. For Ih, a published voltage-clamp recording was digitized to obtain estimates of its kinetic parameters using the software package NEUROFIT (Willms 2002), which implements the full-trace fitting method (Willms et al. 1999). The experimentally measured model parameters, such as the reversal potential and V1/2 of activation, were used as initial guesses for the fitting routine. The full-trace method was not used in the case of ILVA, IHVA, IA, IK, INaF, INaP, and IL, because either these currents were not of the HH form (INaF), the voltage-clamp experiments to characterize them did not follow the protocol required by NEUROFIT (INaP, IL), or the data available was insufficient (ILVA, IHVA, IA, IK). For these currents, Eqs. (2)–(6) were used as a prototype model and parametrized manually to fit the voltage-clamp data that was available. In all figures, we use the convention that inward currents are negative.
2.1.2 INaF and INaP
Two types of tetrodotoxin (TTX)-sensitive Na+ currents have been isolated experimentally in mouse GnRH neurons (Chu and Moenter 2006; Wang et al. 2010); namely, (a) the fast Na+ current INaF, primarily responsible for the generation of action potentials (Wang et al. 2010), and (b) the low-amplitude persistent Na+ current INaP identified by Wang et al. (2010) using a slow (50 mV/s) depolarizing voltage ramp. Wang et al. (2010) showed that in voltage-clamp experiments, the amplitude of INaF during an action potential reaches above 1 nA, indicating a relatively large conductance. Meanwhile, INaP is characterized by its activation at more hyperpolarized membrane potentials than INaF and the large overlap between its steady-state activation and inactivation curves (Magistretti and Alonso 1999).
A three-state Markov model by Destexhe et al. (1994), depicted in Fig. 1b, was used to describe INaF. The equation for INaF with the three-state gating scheme is given by
| (8) |
where O represents the proportion of “open” or conducting fast Na+ channels. The cubic exponent in Eq. (8) represents the number of independent subunits, analogous to the parameter p in Eq. (2). The use of standard HH formalism for INaF was excluded because (i) it does not directly take into account recovery from inactivation (Kuo and Bean 1994), and (ii) it leads to additional inconsistencies with experimental data in the GT1 cell line (Van Goor et al. 2000). Both formalisms of fast sodium, however, were tested for compatibility with the combined model by fitting it to a 20 kHz recording of spontaneously generated action potentials in the plane. This was accomplished by employing a genetic algorithm (GA) parameter search using the fitness function formulated by LeMasson and Maex (2001), which proved to be successful in parametrizing complex neuronal models (Achard and De Schutter 2006; Van Geit et al. 2007). The main advantage of this method is that by fitting to a trajectory density in the phase plane, the performance of the fitness function is not dependent on the phase between the model and observed signals. For the GA trials, we selected all parameters appearing in the INaF model to be free and assumed the presence of noise to ensure the formation of spontaneous action potentials. The conductance parameters for the other currents in the system were selected to be close to the girr-parameter values (see Table 2). For each GA iteration, the system was initially integrated for 2500 ms to eliminate transients, followed by another 6000 ms to obtain data points for evaluation of the fitness function. Overall, we found that the three-state Markov model was most successful in fitting the data because it captured more precisely the initiation and repolarization phases of the action potentials (see Online Resource 1a) when compared to that produced by the HH model. For both models, the best iteration generated by the GA consistently attained maximum voltages above the recorded value, but the AP amplitudes were still within the experimentally observed range (Chu and Moenter 2006). Based on these findings, we elected to incorporate the three-state Markov model into the combined model. Rate parameters for the three-state model are provided in the caption of Fig. 1b.
The model for INaP was based on the persistent sodium current model developed by Magistretti and Alonso (1999) for EC cells. However, the voltage-ramp simulations of INaP obtained from their model showed a more hyperpolarized activation threshold and slower inactivation at depolarized potentials compared with the GnRH neuron data of Wang et al. (2010). To address these discrepancies, we assumed that the equation for INaP has the form
| (9) |
and used the GA to fit the conductance parameter gNaP and the gating parameters of mNaP and hNaP to the digitized voltage-ramp recording of Wang et al. (2010). In this case, the fitness function was the discrete L2-norm of the difference between the interpolated-digitized recording and the voltage-ramp simulation generated by Eq. (9). The best iteration obtained from the GA produced a good fit to the digitized data (see Online Resource 2). The small time constant obtained for mNaP was consistent with the instantaneous activation term used by Magistretti and Alonso (1999).
2.1.3 ILVA and IHVA
Experimental work (Kato et al. 2003; Sun et al. 2010) has demonstrated that Ca2+ current in GnRH neurons is conducted by several types of voltage-gated Ca2+ channels that can be classified into two groups: low-voltage activated (LVA) or high-voltage activated (HVA) channels. Sun et al. (2010) isolated a low amplitude (10 pA) Ca2+ current, likely carried by T-type Ca2+ channels (Zhang et al. 2009), and a larger amplitude HVA current (0.5 nA) carried by L, N, P/Q, and R-type channels in varying proportions. Three distinct Ca2+ currents were included in the model: ILVA, accounting for the contribution from LVA channels, IHVA, accounting for the contribution from HVA channels, and Is, a slow inward Ca2+ current required for generating bursting in the model.
We assumed that ILVA has the form
| (10) |
which is the same equation used to model the T-type Ca2+ current in (LeBeau et al. 2000). The values of the kinetics parameters for mLVA and hLVA were obtained from (LeBeau et al. 2000), while the maximum conductance gLVA was allowed to vary. With this choice of parameters, we found that the voltage-clamp simulations of Eq. (10) agree qualitatively with the recordings in Fig. 7A,E of (Zhang et al. 2009). The maximum conductance of gLVA was then adjusted to make the simulation of ILVA evoke, under the voltage-clamp protocol consisting of a long pre-pulse to −100 mV followed by step to −50 mV, a current with amplitude less than 10 pA, consistent with the findings in Sun et al. (2010).
Since voltage-clamp data for isolated subtypes of HVA currents was not available, IHVA was modeled as a single current (Amini et al. 1999). The model for IHVA assumes that dominant HVA channels exhibit similar activation kinetics, but vary in their inactivation kinetics. A value of n = 2 in Eq. (3) with both fast and slow components yielded the best fit to voltage-clamp data. Based on this, the resulting current equation is
| (11) |
where fHVA = 0.2. The steady state (in)activation parameters were obtained from (Sun et al. 2010), τm was adapted from the R-type model of Miyahso et al. (2001), and τh1 and τh2 were assumed to be constant. Online Resource 3 shows the combined ILVA and IHVA model behavior when simulated under two voltage protocols used in (Sun et al. 2010) to quantify the combined LVA/HVA current. The combined model captured the rapid activation and slow inactivation of current (Online Resource 3a), reproduced the large amplitude tail-currents (Online Resource 3b), and generated a peak I − V curve (data not shown) that agrees well with experimental results (Sun et al. 2010).
2.1.4 IA and IK
GnRH neurons have been shown to conduct at least two types of voltage-gated K+ currents (DeFazio and Moenter 2002; Pielecka-Fortuna et al. 2011). The first has been identified as an A-type current (IA), because of its sensitivity only to high concentrations (mM) of the blocker 4-aminopyradine (4-AP) and its transient kinetics, whereas the second has been identified as a delayed rectifier current (IK), because of its sensitivity to tetra-ethyl-ammonium (TEA) and its very slow inactivation. Voltage-clamp recordings revealed that IA and IK have large maximum amplitudes, superseded only by the spike-generating INaF (Wang et al. 2010). Estimates for the steady-state (in)activation parameters for IA and IK were obtained from (DeFazio and Moenter 2002; Pielecka-Fortuna et al. 2011). Curves for the voltage-dependent time constants were adapted from existing models of IK and IA (Huguenard and McCormick 1992; Bekkers 2000). Maximum conductances and time constant parameters of these currents were estimated simultaneously by fitting their current-equations to the voltage-clamp recording of Fig. 1A in (Pielecka-Fortuna et al. 2011). In these recordings, the combined IA and IK currents were isolated pharmacologically using TTX (which blocks Na+ channels) and cadmium (which blocks Ca2+ channels). The current equation used for the slow-inactivating IK current is
| (12) |
In order for Eq. (12) to be consistent with the empirical steady-state activation curve for IK (Pielecka-Fortuna et al. 2011), the equation for mK,∞ (Eq. (6)) was raised to the power 1/4. For the IA current, the best fit to voltage-clamp data was attained by setting n = 2 in Eq. (3), i.e., by assuming that IA has fast and slow inactivation components. The resulting equation for IA is then
| (13) |
where fA = 0.8. The resulting fit is plotted in Online Resource 4, which shows the two important features of the combined K+ currents; namely, (i) the isolation of IK during voltage steps from pre-pulses depolarized above −40 mV to −10 mV (which effectively inactivate IA), and (ii) the generation of large amplitude transients during voltage steps from pre-pulses hyperpolarized below −40 mV to −10 mV (which effectively removes the inactivation of IA).
2.1.5 Ih and IL
The hyperpolarization-activated current Ih is an inward current generated by hyperpolarization-activated and cyclic nucleotide-gated (HCN) channels. It has been shown that this current decreases interspike interval during repetitive spiking in GnRH neurons (Chu et al. 2010). Following the formulation used by Dickson et al. (2000) to describe Ih in EC cells, we assumed that the activation of Ih has both fast and slow components (Chu et al. 2010) as follows
| (14) |
where fh = 0.364. The voltage-clamp fit obtained with NEUROFIT is shown in Online Resource 5a.
The inclusion of the leak current IL in Online Resource 5b was based on a result of Chu et al. (2010) showing that a hyperpolarizing voltage ramp from −50 mV to −130 mV evokes a linear current as a function of ramp voltage when Ih is blocked. Based on this result, we propose a leak current of the form
| (15) |
The parameters gL and VL were estimated by fitting to the current recorded from the voltage-ramp experiment mentioned above. The fitted reversal potential of −65 mV for IL suggests the presence of a background current that may be attributable to a combination of Cl− channels and non-selective cation channels (Lu et al. 2007). In Online Resource 6, we included the results from additional verification of the model for Ih.
2.1.6 Is, IKCa, and Ca
The subsystem consisting of the currents Is, IKCa, and the intracellular Ca2+ concentration Ca was essential for simulating slow membrane potential oscillations and bursting. The equations for these quantities were based on those describing the slow inward Ca2+ current, Ca2+-dependent K+ current and intracellular Ca2+ concentration in the Plant model of the R15 neuron in Aplysia (Plant 1981), which was used as a simplified model for parabolic bursting in GnRH neurons (Chu et al. 2012). The equation for Is is given by
| (16) |
Although Is has not been isolated experimentally in GnRH neurons, it was included in the present model to account for the slow depolarization of the membrane potential observed during parabolic bursting.
In the present model, IKCa accounts for the current conducted by small conductance Ca2+-activated K+ (SK) channels, which have been shown to regulate excitability in GnRH neurons (Liu and Herbison 2008). Similar to other GnRH neuronal models (Fletcher and Li 2009; Duan et al. 2011), IKCa was assumed to have instantaneous, calcium-dependent activation according to the equation
| (17) |
where K = 1.0 μM. The expressions for Is, IKCa, and Ca were parametrized simultaneously by adjusting the values of their free parameters within their physiological ranges to capture two essential features: (i) the slow oscillations in membrane potential when gNaF = gNaP = 0, and (ii) parabolic bursting with the appropriate spike count, active phase duration, period, and interburst interval when gNaF, gNaP ≠ 0. The parametrization was further constrained by ensuring that intracellular Ca2+ levels remained within its physiological range (below 1 μM) at all times. In order for the model to exhibit slow oscillations and parabolic bursting with the same properties as observed in (Chu et al. 2012), the maximum conductances of certain ionic currents were adjusted from their fitted values (gvc), to those that produce parabolic bursting (gp) (see Table 2).
2.2 Noise
The results from stochastic simulations were obtained with an exponentially correlated noise term, η(t), added to Eq. (1), which is the same approach used by Longtin (1997) in a study of stochastic resonance in the Plant model. Following (Longtin 1997), η(t) was generated by an Ornstein-Uhlenbeck process of the form
| (18) |
where tc is the correlation time, D is the noise intensity, and gw(t) is a Gaussian white noise process. For stochastic simulations of both parabolic and irregular bursting, the noise parameters were assigned the values tc = 1500 ms and D = 1 pA2/ms. A large value of tc (equal to the time constant of ms) was chosen to account for noise in the system’s slow processes (Longtin et al. 2003). The noise intensity D was selected so that simulations of irregular bursting agree with experiment in terms of interburst interval and number of action potentials per burst. The same value of D was used for parabolic bursting to obtain regularity in the interburst interval and active phase duration, as observed experimentally.
Numerical integration of stochastic differential equations was carried out in XPPAUT (Ermentrout 2002) using the Euler-Maruyama method with a time-step of dt = 0.01 ms. The white noise process gw(t) was simulated in XPPAUT using the built-in functionality.
2.3 Time-dependent effect of pharmacological agents
The application of pharmacological agents, such as estradiol and TTX, can be described by altering the values of affected parameters within the model. Letting α represent these parameters, we can describe the gradual changes in their values using the following expression involving exponential decay
| (19) |
where αi is the initial value of the parameter, Δα = αf − αi is the maximum change in parameter value due to the application of pharmacological agent, H(t) is the standard Heaviside function, t0 is the time of application, and τ is the characteristic time constant.
2.4 Afterdepolarization potentials (ADPs)
The contribution of an ionic current Ij to ADP formation was calculated using
| (20) |
where ΔIj = Ij(t) − Ij(t0), and t0 is the time at which ADPs begin to form. This formalism ensures that ADP-contribution increases positively during both an increase of an inward current or a decrease in an outward current relative to Ij(t0).
2.5 Software
Integration of differential equations was carried out using XPPAUT (Ermentrout 2002) with the adaptive Runge-Kutta or Gear solver. Bifurcation diagrams were computed with AUTO (Doedel and Oldeman 2007) and rendered using matplotlib (Hunter 2007). The genetic algorithm as implemented in MATLAB R2014b Optimization Toolbox (The MathWorks, USA) was used for the fittings of INaF and INaP. Source files for XPPAUT and AUTO are provided in Online Resource 8.
2.6 Slow-fast protocol
The protocol for conducting the slow-fast bifurcation analysis is adopted from previous studies (Rinzel and Lee 1987; Bertram et al. 1995; Izhikevich 2000) and is summarized as follows: (1) a set of slow variables are identified in the model through inspection of parameters; (2) a “fast” subsystem is formulated by treating the slow variables in the full system as quasistatic, i.e., slow variables are model parameters in the fast subsystem; (3) a single burst is simulated by the full model, and the values of the fast and slow variables are recorded; (4) at discrete time points along the burst, we compute a one-parameter bifurcation diagram for the fast subsystem with respect to one of the slow variables, and the other slow variables are set to their values obtained in step (3); and (5) for each bifurcation diagram, the phase plane solution of the full model is superimposed and the relationship between the phase trajectory and the bifurcation structure of the fast subsystem is examined.
3 Results
3.1 Parabolic Bursting
3.1.1 Burst Dynamics
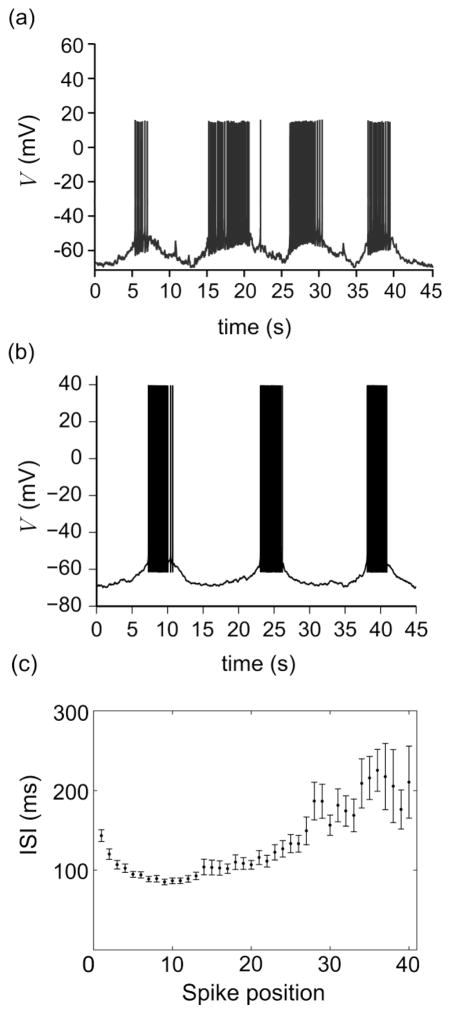
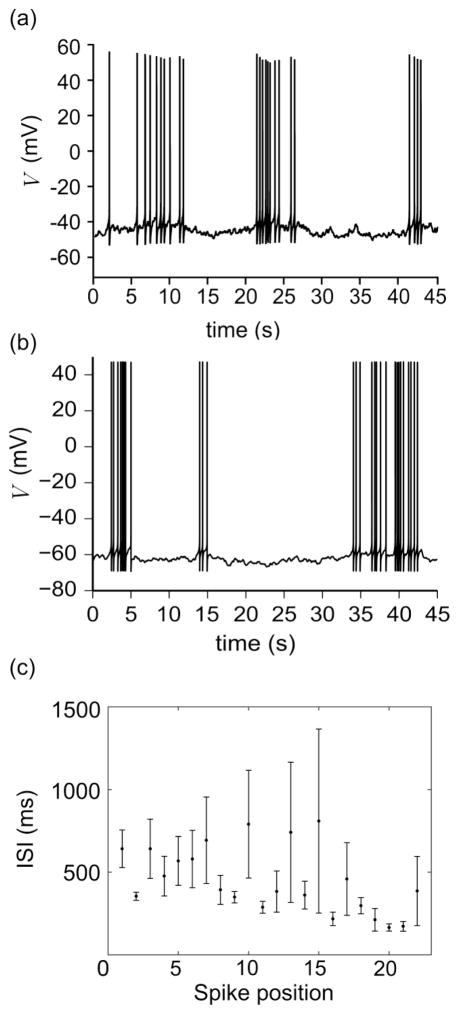
It was demonstrated experimentally that 1–2% of GnRH neurons can spontaneously generate parabolic bursts of action potentials with slow oscillations underlying the bursts (Fig. 2a). This type of bursting can be generated by the model described by Eqs. (1)–(18) using the gp-conductance parameters listed in Table 2, as demonstrated by the simulation of membrane potential in Fig. 2b and the mean interspike interval (ISI) profile for a sample of 50 simulated parabolic bursts in Fig. 2c. Notice that in Fig. 2c, the mean ISI as a function of spike position has a discernable parabolic shape. While parabolic bursts generated using the deterministic model always have approximately 30 spikes, in the stochastic model, the active phase of the burst is occasionally prolonged due to noise, yielding additional spikes. This phenomenon is clearly demonstrated in the first burst of Fig. 2b (where we see a gap near the end of the burst), and it explains why we have data points in spike positions greater than 30 in Fig. 2c.
Fig. 2.
Parabolic bursting in GnRH neurons. (a) Experimental recording of a bursting GnRH neuron. (b) Stochastic simulation of the model, defined by Eqs. (1)–(18), showing parabolic bursting behavior. Notice the qualitative agreement between the experimental and numerical results. (c) Mean and standard error of ISI at each spike position for 50 parabolic bursts recorded from a single integration of Eqs. (1)–(18). Experimental recording obtained using the methods of Chu et al. (2012)
To capture this mode of oscillations, some of the current conductances, notably gK and gh, had to be adjusted from their fitted gvc-values. In particular, the value of gK was set so that simulations were consistent with recordings showing that spikes reach a minimum voltage of 5–10 mV above the nadir of the underlying oscillation (Chu et al. 2012). Although, this behavior is compatible with the gvc-value of gK, it was still necessary to increase this conductance to its gp-value to ensure that the minimum interspike interval during the active phase of the burst is maintained close to the experimentally observed value of 100 ms. It was also necessary to decrease the conductance of Ih(gh) to make the underlying slow oscillations reach a nadir of approximately −70 mV. This phenomenon is explained in more detail later in this section. Finally, the contribution from the leak current IL was removed from model simulations since small values of gL (≥ 0.1 nS) blocked slow oscillations altogether. Using continuation methods, we investigated this phenomenon further, and found that by allowing gs and gKCa to vary, bursting (similar to that in Fig. 2b) can be still generated for gL < 0.4 nS, albeit with Ca2+-oscillations surpassing its physiological range. Similar to other conductances, the discrepancy between the fitted value of gL and that required for slow oscillations reflects a difference in the state of the cell between voltage-clamp and current-clamp recording modes. The low value of gL required for parabolic bursting suggests that increasing the conductance of the leak current is a potential mechanism for stabilizing the membrane potential, either to trigger a resting state or an irregular bursting state.
In order to test the effect of noise on the parabolic bursting model, stochastic simulations were performed by coupling a stochastic process to Eq. (1) (see Section 2.2). Figure 2b shows that the addition of noise caused some variation in the duration of the active phase and the interburst interval, but the system still exhibited a regular pattern of parabolic bursting comparable to that observed experimentally, demonstrating robustness to stochastic fluctuations at the given noise intensity. Bursting can be still generated if the noise intensity is increased beyond D = 1 pA2/ms and up to D = 5 pA2/ms, but this will lead to wide variation in interburst interval and active phase duration, an outcome that is uncharacteristic of parabolic bursting observed in GnRH neurons.
It is important to point out that, although the simulation (Fig. 2b) appears to exhibit longer silent phase duration and higher peaks of action potentials relative the experimental recording (Fig. 2a), the period of underlying oscillations produced by the model is within the reported range (Chu et al. 2012), and the large amplitude spikes reaching +40 mV are consistent with those observed in irregular bursting cells (Chu et al. 2012) and cells excited by current injection (Chu et al. 2010). Nonetheless, the discrepancy in amplitude can be resolved in the model by setting gNaF = 175 nS, gNaP = 0.3 nS, and gK = 150 nS (results not shown), i.e., by enforcing a much lower density of active Na+ channels relative to the irregular burster (see girr in Table 2). Requiring such a drastic shift in Na+ conductances to reduce spike amplitude suggests that cells capable of generating spikes reaching +40 mV or above in irregular bursting mode would also exhibit large amplitude spikes if triggered to burst in parabolic mode, under the assumption that the activation kinetics of the Na+ channels are invariant between the two modes of bursting.
3.1.2 Slow oscillations
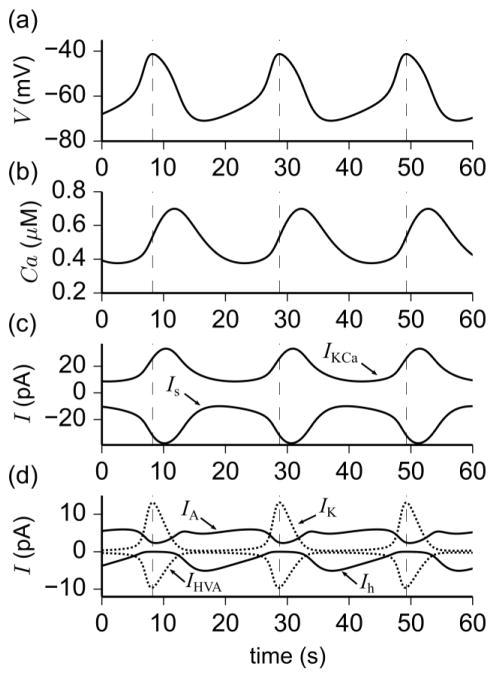
It is hypothesized that slow oscillations in membrane potential are independent of Na+ current due to the observation that TTX is not effective at suppressing them (Chu et al. 2012). Therefore, to study the currents that are active in generating the slow oscillations underlying parabolic bursting, we simulated the effect of TTX using the parameter set gp with gNaF = gNaP = 0 Under these conditions, simulations revealed that the shape of the slow oscillations underlying parabolic bursting is determined by several ionic currents that are active close to the threshold for spiking, and by the dynamics of Ca2+ (Ca). Similar to experimental recordings of intracellular Ca2+ levels obtained from bursting GnRH neurons (Lee et al. 2010), the oscillations in Ca are close to π/2 out of phase with V, due to a delay in removal of intracellular Ca2+ (compare Figs. 3a,b). As a result of the delay, intracellular Ca2+ continues to accumulate beyond the peak of the combined Ca2+ current (compare Figs. 3b–d). The latency in peak Ca2+ levels relative to V is important for the activation of IKCa, which contributes to the repolarization of the membrane potential to approximately −70 mV during the quiescent phase of parabolic bursting. In terms of absolute current amplitude, Is and IKCa are the largest during the slow oscillations (Fig. 3c), followed by IA, Ih, IK, and IHVA (Fig. 3d), suggesting that the Is, IKCa, Ca subsystem is primarily responsible for the generation of slow, oscillatory dynamics. Despite the relatively low amplitude of Ih, lowering the conductance of this current had the effect of increasing the amplitude of oscillations, because doing so attenuates its resonant behavior, i.e., the tendency of Ih to depolarize the membrane with increased hyperpolarization. Increasing the conductance of IA, on the other hand, lengthened the period of oscillations, but for high values of gA, oscillations were suppressed altogether. Furthermore, since the currents IK and IHVA activate at more depolarized potentials compared with IA and Ih, the effect of changing their maximum conductances is only apparent near oscillation peaks, as shown in Fig. 3d. In fact, simulations showed that an increase in gK lowers the maximum value of V obtained during oscillations, while an increase in gHVA leads to narrower peaks in the oscillations. Assuming that the currents underlying TTX-induced oscillations are a good approximation to those in the full bursting model, these observations indicate that IK and IHVA contribute most during the active phase of the burst rather than the quiescent phase.
Fig. 3.
Simulation of various physical quantities involved in oscillations when spiking in the parabolic bursting model is suppressed. Oscillations are obtained using the parameter set gp with gNaF = gNaP = 0. The instances of maximum voltage are marked by vertical dashed lines to illustrate the phase shift of physical quantities relative to V. (a) Slow wave in membrane potential underlying parabolic bursting. (b) Intracellular Ca2+ concentration showing π/2 phase shift relative to V. (c) Competing slow-wave currents Is (inward) and IKCa (outward). (d) Remaining currents Ih (inward, solid line), IHVA (inward, dashed line), IA (outward, solid line), and IK (outward, dotted line) contribute to shaping the oscillations in V. The current ILVA is not shown since it is close to zero during oscillations
3.1.3 Formation of afterdepolarization (ADP)
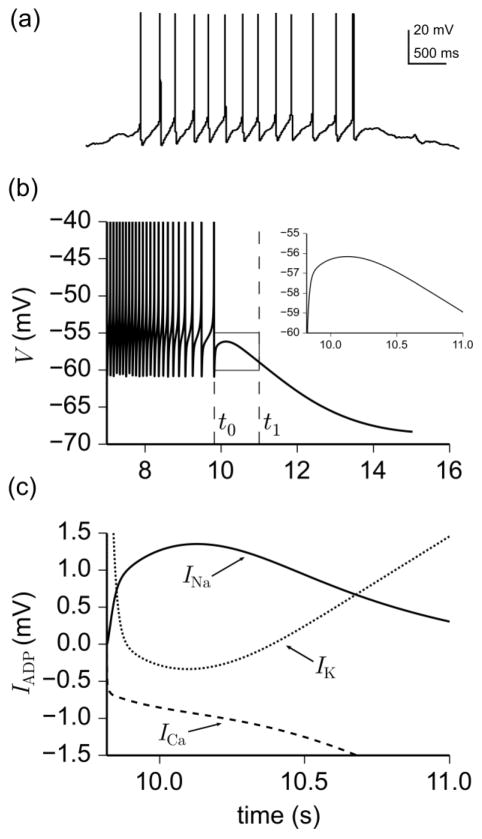
Another characteristic feature of parabolic bursting in GnRH neurons is the formation of an ADP after the final spike of the active phase, as seen in Fig. 4a. Current injection experiments by Chu et al. (2006) showed that ADPs in spontaneously firing (irregular bursting) cells were eliminated in the presence of TTX and modulated by the Ca2+ channel blocker cadmium. To investigate the potential role of Na+ and Ca2+ currents in the formation of ADPs during parabolic bursting, we analyzed the time course of individual ionic currents in a model-generated burst. Figure 4 shows that Na+ and Ca2+ currents do indeed play a central role in defining ADPs that follow parabolic bursts produced by the model. More specifically, Fig. 4b shows the simulation of an ADP after a parabolic burst, and Fig. 4c displays the contribution of Na+, Ca2+, and K+ currents (as defined in the Methods Section) to ADP-formation within the time interval [t0, t1], lying between the nadir of the last spike (t0) and some time point after the peak of the ADP (t1). The figure reveals that there is (i) a transient increase in Na+ current starting at t0, which contributes positively to ADP formation, (ii) a decrease in Ca2+ current, indicating a progressively declining positive contribution to ADPs, and (iii) a transient decrease (followed by transient increase) in K+ current starting at t0. The net effect is a small amplitude depolarization displayed in the inset of Fig. 4b. The decrease in Ca2+ current, starting at t0, is attributable to Is, whose slow activation allows the amplitude of the current to decrease as V approaches the Ca2+ reversal potential ECa = 82.5 mV. The decrease of Is in conjunction with activation of K+ currents (primarily IKCa), terminates the burst and repolarizes the membrane. The non-selective cation current Ih, on the other hand, has a negligible contribution to ADP formation because of its activation at hyperpolarized potentials and is not shown in Fig. 4c.
Fig. 4.
The role of various ionic currents in the formation of afterdepolarization (ADP) following a parabolic burst as determined by the model, Eqs. (1)–(18). (a) Magnification of the last burst in Fig. 2a reveals an ADP after the last spike. (b) Model simulation of membrane potential during a parabolic burst. The ADP occurs in the interval [t0, t1], defined as the time between the nadir of the last spike (t0) and some time after the ADP peak (t1). (c) Contribution of Na+ currents INa = INaF + INaP (solid line), Ca2+ currents ICa = ILVA + IHVA + Is (dashed line), and K+ currents IK+ = IK + IA + IKCa (dotted line) to afterdepolarization (IADP) within the interval [t0, t1], as defined by Eq. (20). Notice that while INa and ICa both contribute positively to the formation of ADPs, ICa diminishes progressively within the interval [t0, t1]. This causes the total inward current to decrease and the total outward current, led by IKCa, to dominate and terminate the burst
3.2 Irregular bursting
GnRH neurons also exhibit another mode of bursting behavior characterized by irregularity in interburst interval and active phase duration, a stable (non-oscillatory) baseline potential during quiescence, and APs undershooting the baseline (see Fig. 5a). The model was capable of reproducing this type of irregular bursting pattern by incorporating noise into the model (indicative of stochastic dynamics in both intracellular ionic concentrations and expression level of ionic channels) and by making maximum current conductances compatible with the set of parameters girr in Table 2. The increase in the value of gNaF allowed action potentials to reach +40–50 mV from a baseline potential of approximately −60 mV as recorded experimentally (Chu et al. 2012). Significant parameter shifts in gK, gs, and gKCa, relative to the set of parameters gp, were also required to transition the system to an irregular bursting mode from that of parabolic bursting. The decreases in gKCa and gs allowed the system to achieve a stable baseline potential of approximately −60 mV, which represents the average potential during quiescent phases of bursting. The increase in gK was needed for action potentials to achieve an afterhyperpolarization amplitude of approximately 10 mV. In the absence of noise (i.e., when the model is not stochastic), the parameter set girr produced a quiescent neuronal model with a stable potential of V = −61 mV. Sustained irregular bursting was then initiated from this state by activating noise within the system. Simulations of noise-induced bursting initiated from the quiescent state showed variation in active phase duration, interburst interval, and a spike frequency profile that is not necessarily parabolic. A representative simulation (Fig. 5b) provides evidence for the variation in active phase duration and interburst interval. To provide statistical evidence that irregular bursts do not necessarily have a parabolic spike frequency profile, the mean ISI profile is plotted for a sample of 50 simulated irregular bursts in Fig. 5c. Comparing Fig. 5c to Fig. 2c, we see that irregular bursts exhibit more variation in ISI and do not produce a discernable parabolic ISI profile. As a further validation of the model, simulation of TTX-induced suppression of spiking during irregular bursting showed that the membrane stabilizes at a baseline potential close to that observed experimentally (Chu et al. 2012).
Fig. 5.
Irregular bursting in GnRH neurons. (a) Experimental recording of a bursting GnRH neuron. (b) Stochastic simulation of the model, defined by Eqs. (1)–(18), showing irregular bursting behavior in qualitative agreement with the recording in (a). (c) Mean and standard error of ISI at each spike position for 50 irregular bursts recorded from a single integration of Eqs. (1)–(18). Experimental recording obtained using the methods of Chu et al. (2012)
The model also revealed that the duration of the interburst interval is dependent on the maximum conductance of IKCa. In fact, by lowering gKCa beyond a certain threshold, the deterministic model exhibits a tonic (or continuous) spiking behavior that can transition to bursting in the presence of noise. In other words, bursting can be initiated via noise applied to a deterministic quiescent or tonic spiking state, depending on the value of gKCa. Compared with irregular bursts initiated from a quiescent state (Fig. 6a), however, bursts initiated from a tonic spiking state (Fig. 6b) had, on average, an increased active phase duration (2.08 s vs 5.18 s), shorter interburst interval (11.89 s vs 6.12 s), and higher burst frequency (0.08 Hz vs 0.086 Hz). Therefore, a decrease in gKCa increases the firing rate in a manner similar to that observed by Liu and Herbison (Liu and Herbison 2008).
Fig. 6.

Effect of gKCa on the irregular bursting model. (a) Bursting initiated from a deterministic quiescent state with gKCa = 1.23 nS. (b) Bursting initiated from a deterministic tonic spiking state with gKCa = 0.95 nS. The quantities 〈AP〉, 〈IBI〉, and BF denote mean active phase duration, mean interburst interval, and burst frequency in the 300 s interval
The values of intracellular Ca2+ and total ionic current predicted by the irregular bursting model were also analyzed for physiological consistency. Figure 7 shows the time series of Ca and total ionic current during an irregular bursting simulation. Similar to the Ca2+ oscillations plotted in Fig. 3b, transients in intracellular Ca2+ are aligned with the voltage and current spikes, with a delay in Ca2+ removal after the termination of each burst. Although Ca2+ removal was modeled as a Ca2+ pump in Eq. (7a), a mechanism that is different from the IP3R mechanism presented by Duan et al. (2011), the results are consistent with experimental recordings of action currents and intracellular Ca2+ in irregular bursting cells (Nunemaker et al. 2002; Lee et al. 2010). Indeed, our simulations of total ionic current show, as in (Lee et al. 2010; Lee et al. 2012), clusters of spikes separated by regions of approximately zero current.
Fig. 7.
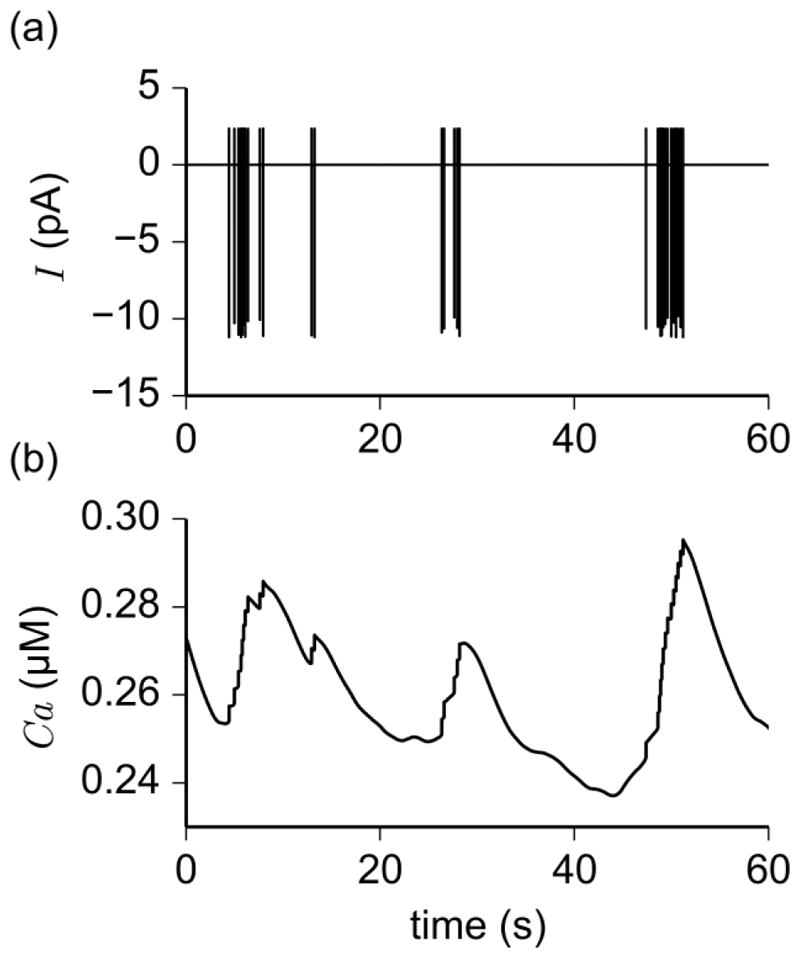
Time series of action currents and intracellular Ca2+ concentration obtained through simulation of irregular bursting model. (a) Clusters of spikes in total ionic current separated by long periods of quiescence are indicative of bursting. (b) Oscillations in intracellular Ca2+ concentration showing transients that persist after the termination of bursts of action currents
3.3 Slow-fast bifurcation analysis
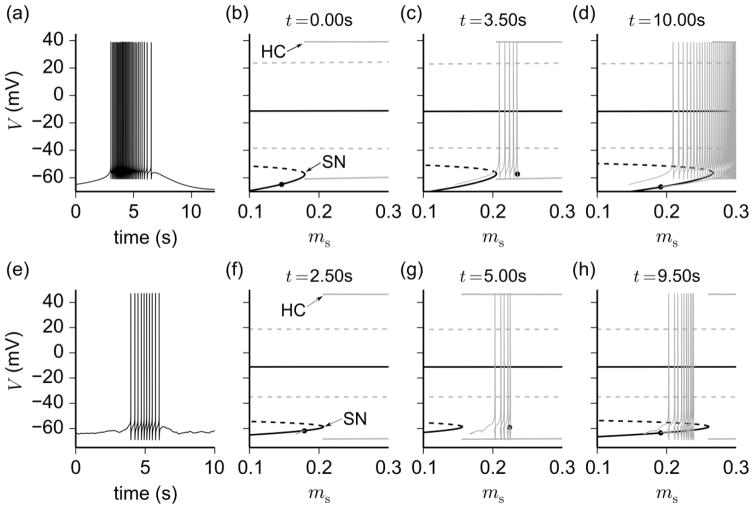
In order to understand the mathematical properties of parabolic bursting, a slow-fast subsystem analysis (Section 2.6) was performed. To conduct this analysis, we identified three slow variables within the deterministic “full” model defined by Eqs. (1)–(17): the gating variables of IHVA (h2,HVA) and Is (ms) along with Ca. The dynamic equations of these three variables constitute the “slow” subsystem, whereas the “fast” subsystem is obtained by treating the three slow variables as quasi-static. The fast subsystem has a three-dimensional critical or “slow” manifold (Bertram et al. 1995) defined in terms of the fast variable V by the surface V = V∞(ms, h2,HVA, Ca) of steady state solutions to Eq. (1). Therefore, to simplify the analysis, a series of critical manifold projections in the V − ms plane (representing a moving one-parameter bifurcation diagram) were computed for the values of Ca and h2,HVA attained along a parabolic bursting trajectory. For this series of one-parameter bifurcation diagrams, periodic solutions were extended from a subcritical Hopf bifurcation located on the upper branch of the critical manifold at a negative value of ms. By superimposing the burst solution of the full model onto the bifurcation diagrams, we found that the full model trajectory closely follows the branches of stable steady states and periodic solutions of the fast subsystem. For a representative burst (Fig. 8a), the traversal of the burst trajectory along the bifurcation structure is depicted in three bifurcation diagrams (Figs. 8b–d), and is described next. During the quiescent, depolarizing phase of the burst, the full model trajectory follows the lower stable branch (solid black line, Figs. 8b–d) of the critical manifold. The active phase of the burst is initiated by a slow increase in ms that pushes the trajectory across a saddle node (SN) bifurcation and into the fast spiking regime delineated by the stable periodic branches (thick solid gray lines, Figs. 8b–d). The trajectory moves away from the SN until reaching a turning point, that is, a point in the V − ms plane that depends on the other two slow variables, and that causes the motion of the trajectory to change directions relative to the SN. The burst is aborted when the burst solution assumes a value of ms to the left of the homoclinic bifurcation (HC), at which the stable periodic branches terminate. Once past the HC, the trajectory follows the lower branch of the critical manifold once again to repolarize the membrane. This cycle is then repeated for each subsequent parabolic burst. The phenomenon of moving back and forth relative to the SN/HC is also observed in the Chay-Cook model of parabolic bursting (Bertram et al. 1995), where the turning point for the full model trajectory depends on a single slow variable representing intracellular Ca2+ concentration. Although for our analysis, there is an additional slow variable h2.HVA, it does not add any complexity to the underlying dynamics of the burst.
Fig. 8.
Slow-fast subsystem analysis of the parabolic and irregular bursters as determined by the bifurcation diagrams of membrane potential V with respect to slow variable ms (treated as a parameter). The subplots in each row from left to right are the voltage time series of one burst cycle ((a), (e)), and the bifurcation diagrams of the parabolic and stochastic bursting models ((b)–(d),(f)–(h)). The latter show branches of (un)stable steady states, represented by thick (dashed) solid black lines, and branches of (un)stable periodic orbits, represented by thick (dashed) solid gray lines that depict the peaks and nadirs of these orbits. Superimposed on the bifurcation diagrams are the full model trajectory in the V − ms plane of the selected burst cycle up to time t (thin solid gray line), along with the phase point (black dot) at time t (specified by the legend on top of (b)–(d),(f)–(h)). Other slow variables (h2,HVA and Ca) are treated as parameters and assigned the values they attain at the phase points t. In each row, the leftmost bifurcation diagrams ((b),(f)) are computed with values of the slow variables taken during the initiation phase of the burst (i.e., before the upstroke of the first spike), the middle diagrams ((c),(g)) during active phase, and rightmost diagrams ((d),(h)) during the termination phase (i.e., after the downstroke of the last spike)
We remark that during the active phase of the burst, the interspike interval changes biphasically as the trajectory moves along the branch of periodic solutions, away from the HC and back. As suggested by Fig. 9, the period along the branch of fast spiking solutions is a decreasing function of ms (when other slow variables are fixed), which explains why the forward and backward movement of the trajectory relative to the HC causes the interspike interval during the active phase to be biphasic. We also note that the analysis above could have been carried out using one of the other slow variables (h2,HVA or Ca) as the continuation parameter; however, for the purposes of visualizing the relationship between the burst trajectory and the bifurcation structure of the fast subsystem, we found that ms is the most suitable choice as a continuation parameter.
Fig. 9.
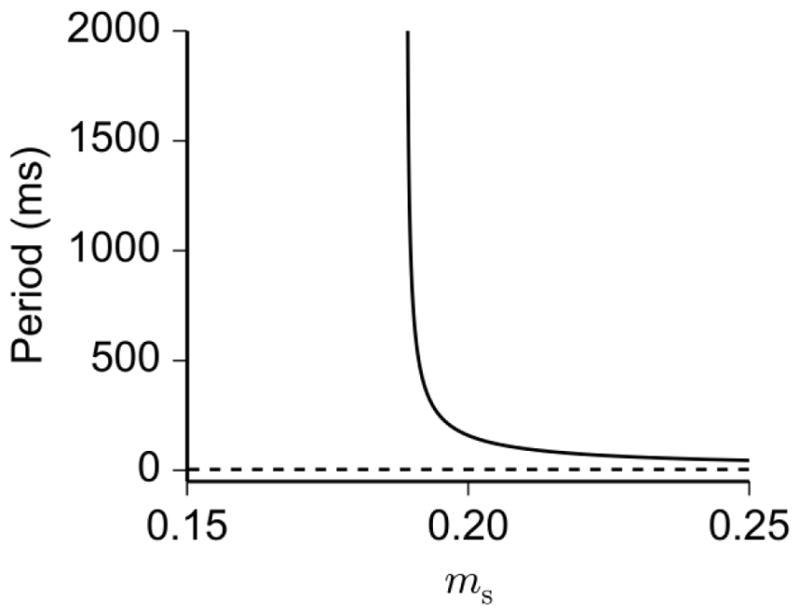
Dependence of slow variable ms (treated as a parameter) on the period of limit cycles in the fast subsystem. The period of stable (solid) and unstable (dashed) limit cycles is plotted against ms. Stable limit cycles represent spiking solutions of the fast subsystem. The other slow variables (h2,HVA and Ca) are fixed at the values they attain at t = 3 s in the burst cycle of Fig. 8a. Notice that the period of the stable limit cycle is a decreasing function of ms, indicating a decrease in interspike interval as ms approaches its peak value during the burst. The blow-up in period shows the existence of a homoclinic (HC) bifurcation
These numerical results show that the mechanism underlying this bursting behavior is similar to that of the canonical “Type II” parabolic burster, where the fast subsystem possesses a saddle-node on invariant circle (SNIC) bifurcation that defines a threshold for burst initiation and termination (Bertram et al. 1995). In the case of this bursting model, however, the fast subsystem is bistable rather than monostable in the parameter regime corresponding to the active phase of the burst. The implication of bistability is that a sufficiently strong perturbation to the system during the active phase of a burst could interrupt spiking to invoke a stable depolarized state. We did not observe any such interruptions during stochastic simulations of the model, suggesting that a large amplitude external stimulus is required to invoke the depolarized state. Note that the prediction of bistability could be tested experimentally as a means of model verification.
Mechanisms for irregular bursting were analyzed using the same bifurcation technique, but with the additional slow variable η (governed by Eq. (18)), which can be treated as quasi-static in the fast subsystem (Longtin et al. 2003). Our analysis revealed that, although the fast subsystem possesses the same dynamic structure as the parabolic burster (see Figs. 8f–h), the slow subsystem of the irregular burster causes the trajectory to repeatedly enter and exit the oscillatory regime of the fast subsystem by traversing a SNIC bifurcation in a non-deterministic manner. Indeed, Figs. 8f–h show that the slow variable ms assumes a narrow range of values within the lower stable branch during quiescence, making the system close to the threshold for firing and sensitive to “perturbations”. Such perturbations are induced by the compounding effect of noise through the variable η. This effect can be understood in the context of the full model, where the noise term η causes slow fluctuations in membrane potential directly via Eq. (1). These fluctuations then feed indirectly into the other voltage-dependent variables, such as ms, h2,HVA, and Ca, causing the system to cross the threshold for spiking in a manner similar to the parabolic burster. The termination of the burst also resembles the parabolic case, where influx of Ca2+ from ICa triggers activation of IKCa to eventually suppress spiking. However, the presence of noise affects the timing of the termination process, leading to variation in the duration of spiking. Viewed more succinctly, noise randomly causes the slow subsystem to push the trajectory past the three-dimensional surface of SN/HC points in the fast subsystem, to initiate or terminate spiking. This means that, in the irregular bursting model, noise acts in conjunction with other slow variables to reproduce the wide variation in interburst interval and burst duration observed experimentally.
3.4 Simulating the effects of estradiol and TTX
It has been shown that TTX blocks open Na+ channels with an exponential time course and that in general, the binding affinity of TTX to the resting, inactivated, and open states varies (Carmeliet 1987). As a simplification, it was assumed that a spike-suppressing dose of TTX exerts its effects on gNaF and gNaP by following an exponentially decaying function given by Eq. (19). A similar simplification was used to model the effect of estradiol applied acutely in vitro. Estradiol has been shown to decrease the maximum current density of multiple ionic currents, notably IA, IK, INaF, INaP, and IHVA (Sun et al. 2010; Wang et al. 2010; Pielecka-Fortuna et al. 2011). A reduction in the contribution of IKCa to afterhyperpolarization caused by acutely applied estradiol has also been documented (Chu et al. 2009). Estradiol also significantly affects the V1/2 of the steady state inactivation curve of IA (Pielecka-Fortuna et al. 2011). Therefore, we assume, based on the above, that acutely applied estradiol affects the dynamics of the model through time-dependent changes in the maximum conductances and parameters for the steady-state activation curves of certain currents.
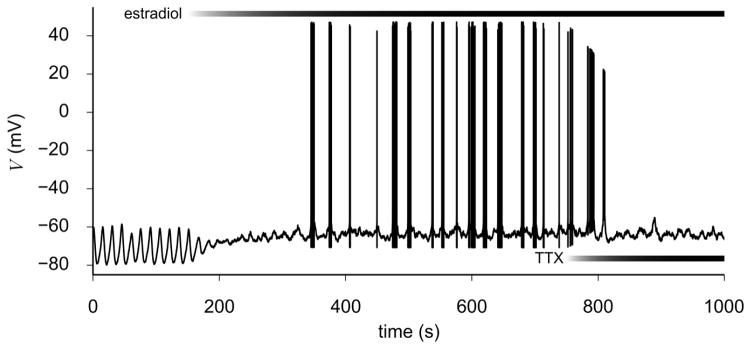
The decay model given by Eq. (19) was applied to a subset of parameters in the model to simulate an experiment by Chu et al. (2012) showing that a cell undergoing endogenous (i.e., without TTX) “subthreshold” oscillations can transition to an irregular bursting state when acute estradiol takes effect. In this context, the term “subthreshold” refers to membrane oscillations that peak below the firing threshold at which action potentials can be initiated. Since the parameter set gp was used to generate oscillations that cross the threshold for action potential firing, a new parameter set was needed for the model to reproduce the endogenous oscillations observed prior to treatment with estradiol. This set included the maximum conductance parameters gsub, listed in Table 2, and the values Vh = −65 mV and k = −6 mV for the steady state activation curve ms,∞ (Eq. (6)). The post-treatment state was modeled using the “estradiol-affected” irregular bursting parameters, which include (i) the conductance parameters ge in Table 2, and (ii) the default values of Vh and k for ms,∞ from Table 1. Furthermore, we extended the experimental protocol of Chu et al. (2012) by simulating the effect of TTX subsequent to estradiol taking full effect, i.e., when model parameters were close to irregular bursting values. Figure 10 shows the voltage time series when simulating the application of estradiol followed by TTX. This was produced by setting estradiol and TTX application times and their time constants, as defined by Eq. (19), to those listed in the caption of Fig. 10. Consistent with experiment, the slow transition from regular oscillations to irregular bursting is captured by the model, and bursting is suppressed once TTX takes full effect.
Fig. 10.
Stochastic simulation of acute application of estradiol and TTX via Eq. (19). Effectiveness of pharmacological agents was assumed to have an exponential time course and is plotted on top of the figure as a grayscale color map for each agent. Effect of estradiol was simulated using t0 = 150 s, τ = 100 s, initial parameter set αi = {gsub, Vh,ms = −65 mV, kms = −6 mV}, and final parameter set αf = {ge, Vh,ms = −45 mV, kms = −12 mV}. Effect of TTX was simulated using t0 = 750 s, τ = 50 s, αi = {gNaF, gNaP}, and αf = {0,0}
Comparing the pre- and post-treatment parameter sets used to simulate the estradiol-induced transition from subthreshold oscillations to bursting, we found that the main parameters affected by estradiol are gA, gKCa, gs, and the activation parameters Vh and k of ms,∞. These results indicate that acutely applied estradiol leads to a decrease in gs, which eliminates the slow oscillations underlying parabolic bursting neurons, and a decrease in the conductances of IA and IKCa, which depolarizes the baseline potential to approximately −65 mV. This baseline potential was maintained in the presence of TTX (Fig. 10). Decreases in gA and gKCa were consistent with the experimental observations that estradiol has a negative feedback effect on the amplitudes of IA and IKCa.
4 Discussion
In this study, a detailed ion channel model describing the electrical activities of GnRH neurons in mice is presented. The model captures the two modes of burst firing that these neurons intrinsically exhibit: parabolic and irregular bursting (Chu et al. 2012). The ionic currents described in this model were fitted to voltage- and current-clamp data from GFP-identified GnRH neurons in mice, except for the two currents (Is, IKCa) which were described based on their role in generating parabolic bursting in the R15 neuron of Aplysia (Plant 1981; Canavier et al. 1991). The transition between the two bursting modes was achieved through a shift in maximum conductance parameters only, leaving the kinetic parameters of ionic currents and parameters of the Ca2+ submodel (Eq. (7)) intact. These results indicate that the bursting modes of GnRH neurons depend on the proportions (or density) of ion channel species expressed on the cell membrane. Physiologically speaking, these densities are dynamic quantities that can be altered by the action of various neuromodulators, such as estradiol and kisspeptin (Moenter 2010). For example, in Fig. 3c, we have shown that Is and IKCa play an active role in generating the oscillations underlying parabolic bursting. However, with a certain ratio of gs to gKCa, such as that obtained with the parameter set girr, we found that the oscillations can be suppressed. This suggests that the two modes of bursting are sensitive to changes in the conductances of Is and IKCa, and that the channels conducting these currents represent potential targets for neuromodulators in controlling the burst pattern. The results from Section 3.4 provide evidence of such a claim through the estradiol-induced transition of Fig. 10, similar to that seen experimentally (Chu et. al 2012). This transition from subthreshold oscillations to bursting was primarily due to changes in the parameters of Is and IKCa.
In addition to the major results concerning Is and IKCa, exploration of the model led to the following minor observations. First, reducing the value of gKCa led to a decrease in interspike interval and an increase in duration of the active phase of the burst. However, there was a threshold of gKCa below which the active phase could no longer be terminated, leading to a continuously firing or tonic spiking state. Second, increases in gKCa led to early termination of the active phase of the burst, and an increase in interburst interval. The model showed that these effects can be counteracted by increasing the maximum conductance gs of Is.
For both parabolic and irregular bursting models, interburst interval, active phase duration, spike count, and interspike interval were within a reasonable range of the experimentally reported values (Chu et al. 2012), supporting the choice of parameter values incorporated into the model. Although each model reproduces a distinct type of bursting, a slow-fast subsystem analysis revealed that both models share the same topology in their fast subsystems. This topology is determined by a saddle node (SN) bifurcation that acts as a threshold for burst initiation and a homoclinic (HC) bifurcation that terminates it. However, despite the topological similarities, the two models differ in their slow subsystem dynamics: The parabolic burster has an oscillatory slow subsystem that is robust to noise and that causes the trajectory to move across the SN/HC in a periodic fashion. In contrast, the irregular burster has a slow subsystem that is non-oscillatory in the deterministic case, but in the presence of noise can randomly move the trajectory back and forth across the SN/HC when D (see Eq. (18)) is sufficiently large. The random movement across the SN/HC is not solely determined by the trajectory of η, but also by that of the variables ms, h2,HVA, and Ca, which depend on η through Eq. (1).
Exponentially-correlated noise with a long correlation time tc (see Eq. (18)), was required to generate irregular bursting in the model. Irregular burst patterns were also generated by the model using white noise applied to the slow gating variable ms, i.e., by using the subunit model for ion channel noise (Fox and Lu 1994) (data not shown). Therefore, it seems plausible that noise in one or more of the system’s slow processes can modulate bursting activity of the cell. Noisy slow processes may include (in)activation of voltage-dependent ion channels or intracellular Ca2+ handling. The latter would generate noise in the electrical subsystem through calcium-dependent currents such as IKCa. Note, however, that the exponentially correlated noise added to Eq. (1) can account for both scenarios and thus is a more general model for describing noise than the subunit model.
The term IKCa in Eq. (1) accounts for the current that is conducted by SK channels and that contributes to the “medium” and “slow” timescale afterhyperpolarization (AHP) (Liu and Herbison 2008; Lee et al. 2010). Two other types of Ca2+-activated K+ channels are expressed in GnRH neurons—large conductance (BK) channels that are likely active during action potential repolarization (Hiraizumi et al. 2008), and UCL2077 (UCL)-sensitive channels (Lee et al. 2010) that produce a slow AHP—but their corresponding ionic currents were not included in Eq. (1). A BK current was not included because one experimental study suggests that it is not crucial for rhythmic behavior (Chu et al. 2012), and also because there is no data quantifying its dependence on intracellular Ca2+. A UCL-sensitive current was not included because it was assumed that the SK current IKCa, which also contributes to the slow AHP (Lee et al. 2010), is sufficient for the model to reproduce the essential features of parabolic and irregular bursting. Moreover, the voltage and Ca2+ dependence of (in)activation for UCL-sensitive channels has not been confirmed, making the modeling of this current speculative.
The Ca2+ current that interacts with IKCa to sustain a slow rhythm, denoted Is in Eq. (1), is a phenomenological current, and its existence in GnRH neurons remains a conjecture. However, a study of slow ADPs in GnRH neurons (Chu and Moenter 2006) revealed that IKCa can counteract the ADP current (IADP), consistent with the existence of a slow inward Ca2+ current that activates IKCa to terminate spiking. This is further supported by the fact that the canonical parabolic bursters, i.e., “Type II” bursters classified by Bertram et al. (1995), require two slow variables to interact through a feedback mechanism to produce oscillations. Given that Ca2+ (Ca) accounts for one slow variable in the model, and knowing that blocking IKCa affects the amplitude of slow oscillations in GnRH neurons (Chu et al. 2012), it is reasonable to propose an inward Ca2+ current with slow voltage-dependent activation (ms) to account for the second slow variable.
It has been proposed that the low voltage-activated Ca2+ current (ILVA) may be active in pacemaking in GnRH neurons (Zhang et al. 2009; Sun et al. 2010). With the default parameter set gvc, the Ca2+ current ILVA had a small amplitude and negligible contribution to total ionic current during parabolic bursting. This was mainly due to its small maximum conductance gLVA compounded by the properties of the steady (in)activation curves for mLVA and hLVA. Interestingly, the model revealed that although the maximum conductance of ILVA can be adjusted to yield a larger amplitude current (5 pA), comparable to that of IA and Ih during slow oscillations, such an adjustment does not significantly alter burst dynamics. This suggests that ILVA is not essential for parabolic bursting as observed by Fletcher and Li (2009).
It is important to point out that the slow oscillations produced by the model, using the parameter values listed in the Methods Section, had a slower rate of depolarization and repolarization and a shorter plateau at the peak of oscillations when compared to experimental recordings (compare Fig. 3a and Online Resource 7a). To address these discrepancies, the parameter space of our model was further explored to determine if such oscillations, featured in Online Resource 7a and referred to as “square-wave” oscillations (Amini et al. 1999), can be reproduced by the model. Since the V1/2 for the steady state activation curve of ILVA is close to that of Is, it is plausible that the model can generate such square-wave oscillations if the conductance of Is is set to zero and the conductance of ILVA is increased. This hypothesis is motivated by the results of Zhang et al. (2009), showing the existence of a prominent ILVA current in 100% of GnRH neurons during voltage-clamp experiments, in contrast with the results of Sun et al. (2010). We tested this hypothesis by applying the proposed conditions and found that the slow oscillations obtained were still incompatible with the experimental recordings. However, by modifying the values of the conductance parameters of gsub and the parameters appearing in Eq. (7a) to those listed in the caption of Online Resource 7, the model was able to generate square-wave oscillations compatible with those observed experimentally (Online Resource 7b). Square-wave oscillations resembling the ones displayed in Online Resource 7a have been previously studied by Amini et al. (1999) and generated using a model of midbrain dopaminergic neurons where inactivation of HVA currents was assumed to be Ca2+-dependent. Interestingly, in a parabolic bursting model of Aplysia R15 developed by Canavier et al. (1991), a similar Ca2+-dependent inactivation term for the slow inward current, analogous to Is in our model, was also assumed. This suggests that Ca2+-dependent inactivation of voltage-gated Ca2+ channels could be incorporated into the model to capture this phenomenon without losing other essential features of this system. On the other hand, given that the model was able to generate square-wave oscillations with the appropriate parameters suggests that the Ca2+ pump mechanism, responsible for the long plateaus at the peaks of the oscillation (Online Resource 7), can be used to generate mathematically equivalent dynamics to those obtained with the use of Ca2+-dependent inactivation terms in Is and IHVA. It thus remains to determine how the Ca2+ model, used to generate the oscillations in Online Resource 7b, can be coupled with the electrical model to recover the two types of bursting.
An existing biophysical HH model for irregular (but not parabolic) bursting GnRH neurons was developed by Duan et al. (2011) and used as a basis for future modeling studies (Chen et al. 2013; Chen and Sneyd 2014). This model, which produces burst patterns similar to those shown in Fig. 7a, did not include a slow inward current, and incorporated a more detailed Ca2+ handling than the one presented here. The Ca2+ handling subsystem was assumed to interact with the UCL-sensitive component of IKCa to regulate interburst interval. The slow-fast subsystem analysis performed on the model shows a critical manifold closely resembling those plotted in Fig. 8, suggesting that both models are similar mathematically. Aside from the UCL current and Is, the set of ionic currents used by Duan et al. (2011) differed from the one used here in that it did not include Ih or IA, but did include inward rectifier and M-type K+ currents (Iir and IM). Our model did not include Iir because its effect is most prominent at voltages more hyperpolarized than EK (Hibino et al. 2010), and because the studies carried out here were focused on electrical activities occurring at voltages more depolarized than this range. However, voltage-clamp experiments would still be useful for confirming the role of Iir at more depolarized potentials. As for the M-type K+ current, its effects were implicitly captured by IK.
The two models developed by Roberts et al. (2009) and Chen and Sneyd (2014) are more biophysically detailed in the morphological sense; they both take into account the length of dendrites, axons and/or dendrons to further examine the electrical activities of GnRH neurons. Ionic currents for these two models were adapted from Lebeau et al. (2000) and Duan et al. (2011), respectively. These models were able to predict how ADP amplitude depends on dendritic length and determine how stochastic synaptic input along the length of the dendron affects the initiation and propagation of action potentials. In order to provide similar insights about the role of cell morphology in defining the electrophysiological properties of these cells, extensions of the model presented here should follow similar approaches by relaxing the space-clamp assumption and assuming a multi-compartmental cell. The resulting model could then be used as a building block for making realistic predictions about the ability of GnRH neurons to synchronize through synaptic interactions.
Supplementary Material
Acknowledgments
This work was supported by the Natural Sciences and Engineering Council of Canada (NSERC) discovery grant to AK.
Footnotes
Conflict of Interest:
None.
References
- Achard P, De Schutter E. Complex parameter landscape for a complex neuron model. PLoS Computational Biology. 2006;2:0794–0804. doi: 10.1371/journal.pcbi.0020094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amini B, Clark JW, Canavier CC. Calcium dynamics underlying pacemaker-like and burst firing oscillations in midbrain dopaminergic neurons: a computational study. Journal of Neurophysiology. 1999;82:2249–2261. doi: 10.1152/jn.1999.82.5.2249. [DOI] [PubMed] [Google Scholar]
- Bekkers JM. Properties of voltage-gated potassium currents in nucleated patches from large layer 5 cortical pyramidal neurons of the rat. Journal of Physiology. 2000;525(Pt 3):593–609. doi: 10.1111/j.1469-7793.2000.t01-1-00593.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belchetz PE, Plant TM, Nakai Y, et al. Hypophysial responses to continuous and intermittent delivery of hypopthalamic gonadotropin-releasing hormone. Science. 1978;202:631–633. doi: 10.1126/science.100883. [DOI] [PubMed] [Google Scholar]
- Bertram R, Butte MJ, Kiemel T, Sherman A. Topological and phenomenological classification of bursting oscillations. Bulletin of Mathematical Biology. 1995;57:413–439. doi: 10.1007/BF02460633. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Clark JW, Byrne JH. Simulation of the bursting activity of neuron R15 in Aplysia: role of ionic currents, calcium balance, and modulatory transmitters. Journal of Neurophysiology. 1991;66:2107–2124. doi: 10.1152/jn.1991.66.6.2107. [DOI] [PubMed] [Google Scholar]
- Carmeliet E. Voltage-dependent block by tetrodotoxin of the sodium channel in rabbit cardiac Purkinje fibers. Biophysical Journal. 1987;51:109–114. doi: 10.1016/S0006-3495(87)83315-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Iremonger K, Herbison A, et al. Regulation of Electrical Bursting in a Spatiotemporal Model of a GnRH Neuron. Bulletin of Mathematical Biology. 2013;75:1941–1960. doi: 10.1007/s11538-013-9877-7. [DOI] [PubMed] [Google Scholar]
- Chen X, Sneyd J. A Computational Model of the Dendron of the GnRH Neuron. Bulletin of Mathematical Biology. 2014:904–926. doi: 10.1007/s11538-014-0052-6. [DOI] [PubMed] [Google Scholar]
- Christian CA, Moenter SM. The neurobiology of preovulatory and estradiol-induced gonadotropin-releasing hormone surges. Endocrine Reviews. 2010;31:544–577. doi: 10.1210/er.2009-0023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Z, Andrade J, Shupnik MA, Moenter SM. Differential regulation of gonadotropin-releasing hormone neuron activity and membrane properties by acutely applied estradiol: dependence on dose and estrogen receptor subtype. Journal of Neuroscience. 2009;29:5616–5627. doi: 10.1523/JNEUROSCI.0352-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Z, Moenter SM. Physiologic regulation of a tetrodotoxin-sensitive sodium influx that mediates a slow afterdepolarization potential in gonadotropin-releasing hormone neurons: possible implications for the central regulation of fertility. Journal of Neuroscience. 2006;26:11961–11973. doi: 10.1523/JNEUROSCI.3171-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Z, Takagi H, Moenter SM. Hyperpolarization-activated currents in gonadotropin-releasing hormone (GnRH) neurons contribute to intrinsic excitability and are regulated by gonadal steroid feedback. Journal of Neuroscience. 2010;30:13373–13383. doi: 10.1523/JNEUROSCI.1687-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Z, Tomaiuolo M, Bertram R, Moenter SM. Two Types of Burst Firing in Gonadotrophin-Releasing Hormone Neurones. Journal of Neuroendocrinology. 2012;24:1065–1077. doi: 10.1111/j.1365-2826.2012.02313.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csercsik D, Farkas I, Hrabovszky E, Liposits Z. A simple integrative electrophysiological model of bursting GnRH neurons. Journal of Computational Neuroscience. 2012;32:119–136. doi: 10.1007/s10827-011-0343-y. [DOI] [PubMed] [Google Scholar]
- DeFazio RA, Moenter SM. Estradiol feedback alters potassium currents and firing properties of gonadotropin-releasing hormone neurons. Molecular Endocrinology. 2002;16:2255–2265. doi: 10.1210/me.2002-0155. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. Journal of Computational Neuroscience. 1994;1:195–230. doi: 10.1007/BF00961734. [DOI] [PubMed] [Google Scholar]
- Dickson CT, Magistretti J, Shalinsky MH, et al. Properties and role of I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. Journal of Neurophysiology. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- Doedel EJ, Oldeman BE. AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations. Concordia University; Montreal, Canada: 2007. [Accessed 1 Sep 2015]. http://indy.cs.concordia.ca/auto/ [Google Scholar]
- Duan W, Lee K, Herbison AE, Sneyd J. A mathematical model of adult GnRH neurons in mouse brain and its bifurcation analysis. Journal of Theoretical Biology. 2011;276:22–34. doi: 10.1016/j.jtbi.2011.01.035. [DOI] [PubMed] [Google Scholar]
- Dutton A, Dyball RE. Phasic firing enhances vasopressin release from the rat neurohypophysis. Journal of Physiology. 1979;290:433–440. doi: 10.1113/jphysiol.1979.sp012781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Society for Industrial and Applied Mathematics; Philadelphia: 2002. [Google Scholar]
- Fletcher PA, Li YX. An integrated model of electrical spiking, bursting, and calcium oscillations in GnRH neurons. Biophysical Journal. 2009;96:4514–4524. doi: 10.1016/j.bpj.2009.03.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox RF, Lu YN. Emergent collective behavior in large numbers of globally coupled independently stochastic ion channels. Physical Review E. 1994;49:3421–3431. doi: 10.1103/PhysRevE.49.3421. [DOI] [PubMed] [Google Scholar]
- Glanowska KM, Moenter SM. Differential Regulation of GnRH Secretion in the Preoptic Area (POA) and the Median Eminence (ME) in Male Mice. Endocrinology. 2015;156:231–241. doi: 10.1210/en.2014-1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemond PJ, O’Boyle MP, Roberts CB, et al. Simulated GABA Synaptic Input and L-Type Calcium Channels Form Functional Microdomains in Hypothalamic Gonadotropin-Releasing Hormone Neurons. Journal of Neuroscience. 2012;32:8756–8766. doi: 10.1523/JNEUROSCI.4188-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbison AE. Multimodal influence of estrogen upon gonadotropin-releasing hormone neurons. Endocr Rev. 1998;19:302–330. doi: 10.1210/edrv.19.3.0332. [DOI] [PubMed] [Google Scholar]
- Hibino H, Inanobe A, Furutani K, et al. Inwardly Rectifying Potassium Channels: Their Structure, Function, and Physiological Roles. Physiology Reviews. 2010;90:291–366. doi: 10.1152/physrev.00021.2009. [DOI] [PubMed] [Google Scholar]
- Hiraizumi Y, Nishimura I, Ishii H, et al. Rat GnRH neurons exhibit large conductance voltage- and Ca2+-Activated K+ (BK) currents and express BK channel mRNAs. Journal of Physiological Sciences. 2008;58:21–29. doi: 10.2170/physiolsci.RP013207. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. Journal of Neurophysiology. 1992;68:1373–1383. doi: 10.1152/jn.1992.68.4.1373. [DOI] [PubMed] [Google Scholar]
- Hunter JD. Matplotlib: A 2D graphics environment. Computing in Science and Engineering. 2007;9:99–104. doi: 10.1109/MCSE.2007.55. [DOI] [Google Scholar]
- Izhikevich EM. Neural Excitability, Spiking and Bursting. International Journal of Bifurcation and Chaos. 2000;10:1171–1266. doi: 10.1142/S0218127400000840. [DOI] [Google Scholar]
- Kato M, Ui-Tei K, Watanabe M, Sakuma Y. Characterization of voltage-gated calcium currents in gonadotropin-releasing hormone neurons tagged with green fluorescent protein in rats. Endocrinology. 2003;144:5118–5125. doi: 10.1210/en.2003-0213. [DOI] [PubMed] [Google Scholar]
- Kuo CC, Bean BP. Na+ channels must deactivate to recover from inactivation. Neuron. 1994;12:819–829. doi: 10.1016/0896-6273(94)90335-2. [DOI] [PubMed] [Google Scholar]
- LeBeau AP, Van Goor F, Stojilkovic SS, Sherman A. Modeling of membrane excitability in gonadotropin-releasing hormone-secreting hypothalamic neurons regulated by Ca2+-mobilizing and adenylyl cyclase-coupled receptors. Journal of Neuroscience. 2000;20:9290–9297. doi: 10.1523/JNEUROSCI.20-24-09290.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Duan W, Sneyd J, Herbison AE. Two slow calcium-activated afterhyperpolarization currents control burst firing dynamics in gonadotropin-releasing hormone neurons. Journal of Neuroscience. 2010;30:6214–6224. doi: 10.1523/JNEUROSCI.6156-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Liu X, Herbison AE. Burst Firing in Gonadotrophin-Releasing Hormone Neurones does not Require Ionotrophic GABA or Glutamate Receptor Activation. Journal of Neuroendocrinology. 2012;24:1476–1483. doi: 10.1111/j.1365-2826.2012.02360.x. [DOI] [PubMed] [Google Scholar]
- LeMasson G, Maex R. Introduction to Equation Solving and Parameter Fitting. In: De Schutter E, editor. Computational Neuroscience: Realistic Modeling for Experimentalists. CRC Press; 2001. pp. 1–25. [Google Scholar]
- Liu X, Herbison AE. Small-conductance calcium-activated potassium channels control excitability and firing dynamics in Gonadotropin-Releasing Hormone (GnRH) neurons. Endocrinology. 2008;149:3598–3604. doi: 10.1210/en.2007-1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longtin A, Laing C, Chacron MJ. Correlations and Memory in Neurodynamical Systems. In: Rangarajan G, Ding M, editors. Processes with Long-Range Correlations. Springer-Verlag; Berlin: 2003. pp. 286–308. [Google Scholar]
- Longtin A. Autonomous stochastic resonance in bursting neurons. Physical Review E. 1997;55:868–876. doi: 10.1103/PhysRevE.55.868. [DOI] [Google Scholar]
- Lu B, Su Y, Das S, et al. The Neuronal Channel NALCN Contributes Resting Sodium Permeability and Is Required for Normal Respiratory Rhythm. Cell. 2007;129:371–383. doi: 10.1016/j.cell.2007.02.041. [DOI] [PubMed] [Google Scholar]
- Magistretti J, Alonso A. Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons: a whole-cell and single-channel study. The Journal of General Physiology. 1999;114:491–509. doi: 10.1085/jgp.114.4.491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyasho T, Takagi H, Suzuki H, et al. Low-threshold potassium channels and a low-threshold calcium channel regulate Ca2+ spike firing in the dendrites of cerebellar Purkinje neurons: A modeling study. Brain Research. 2001;891:106–115. doi: 10.1016/S0006-8993(00)03206-6. [DOI] [PubMed] [Google Scholar]
- Moenter SM, Chu Z, Christian CA. Neurobiological mechanisms underlying oestradiol negative and positive feedback regulation of gonadotrophin-releasing hormone neurones. Journal of Neuroendocrinology. 2009;21:327–333. doi: 10.1111/j.1365-2826.2009.01826.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moenter SM. Identified GnRH neuron electrophysiology: A decade of study. Brain Research. 2010;1364:10–24. doi: 10.1016/j.brainres.2010.09.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunemaker CS, Defazio RA, Moenter SM. Episodic Firing Patterns of GnRH Neurons. Endocrinology. 2002;143:2284–2292. doi: 10.1210/endo.143.6.8869. [DOI] [PubMed] [Google Scholar]
- Nunemaker CS, Straume M, Defazio RA, Moenter SM. Gonadotropin-releasing hormone neurons generate interacting rhythms in multiple time domains. Endocrinology. 2003;144:823–831. doi: 10.1210/en.2002-220585. [DOI] [PubMed] [Google Scholar]
- Pielecka J, Moenter SM. Effect of steroid milieu on gonadotropin-releasing hormone-1 neuron firing pattern and luteinizing hormone levels in male mice. Biology of Reproduction. 2006;74:931–937. doi: 10.1095/biolreprod.105.049619. [DOI] [PubMed] [Google Scholar]
- Pielecka-Fortuna J, DeFazio RA, Moenter SM. Voltage-Gated Potassium Currents Are Targets of Diurnal Changes in Estradiol Feedback Regulation and Kisspeptin Action on Gonadotropin-Releasing Hormone Neurons in Mice. Biology of Reproduction. 2011;85:987–995. doi: 10.1095/biolreprod.111.093492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plant RE. Bifurcation and resonance in a model for bursting nerve cells. Journal of Mathematical Biology. 1981;11:15–32. doi: 10.1007/BF00275821. [DOI] [PubMed] [Google Scholar]
- Rinzel J, Lee YS. Dissection of a model for neuronal parabolic bursting. Journal of Mathematical Biology. 1987;25:653–675. doi: 10.1007/BF00275501. [DOI] [PubMed] [Google Scholar]
- Roberts CB, O’Boyle MP, Suter KJ. Dendrites determine the contribution of after depolarization potentials (ADPs) to generation of repetitive action potentials in hypothalamic gonadotropin releasing-hormone (GnRH) neurons. Journal of Computational Neuroscience. 2009;26:39–53. doi: 10.1007/s10827-008-0095-5. [DOI] [PubMed] [Google Scholar]
- Sun J, Chu Z, Moenter SM. Diurnal in vivo and rapid in vitro effects of estradiol on voltage-gated calcium channels in gonadotropin-releasing hormone neurons. Journal of Neuroscience. 2010;30:3912–3923. doi: 10.1523/JNEUROSCI.6256-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Geit W, Achard P, De Schutter E. Neurofitter: a parameter tuning package for a wide range of electrophysiological neuron models. Frontiers in Neuroinformatics. 2007;1:1. doi: 10.3389/neuro.11.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Goor F, LeBeau AP, Krsmanovic LZ, et al. Amplitude-dependent spike-broadening and enhanced Ca(2+) signaling in GnRH-secreting neurons. Biophysical Journal. 2000;79:1310–1323. doi: 10.1016/S0006-3495(00)76384-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Garro M, Kuehl-Kovarik MC. Estradiol attenuates multiple tetrodotoxin-sensitive sodium currents in isolated gonadotropin-releasing hormone neurons. Brain Research. 2010;1345:137–145. doi: 10.1016/j.brainres.2010.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wildt L, Häusler A, Marshall G, et al. Frequency and amplitude of gonadotropin-releasing hormone stimulation and gonadotropin secretion in the rhesus monkey. Endocrinology. 1981;109:376–385. doi: 10.1210/endo-109-2-376. [DOI] [PubMed] [Google Scholar]
- Willms AR, Baro DJ, Harris-Warrick RM, Guckenheimer J. An improved parameter estimation method for Hodgkin-Huxley models. Journal of Computational Neuroscience. 1999;6:145–168. doi: 10.1023/A:1008880518515. [DOI] [PubMed] [Google Scholar]
- Willms AR. NEUROFIT: Software for fitting Hodgkin-Huxley models to voltage-clamp data. Journal of Neuroscience Methods. 2002;121:139–150. doi: 10.1016/S0165-0270(02)00227-3. [DOI] [PubMed] [Google Scholar]
- Wintermantel TM, Campbell RE, Porteous R, et al. Definition of Estrogen Receptor Pathway Critical for Estrogen Positive Feedback to Gonadotropin-Releasing Hormone Neurons and Fertility. Neuron. 2006;52:271–280. doi: 10.1016/j.neuron.2006.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Bosch MA, Rick EA, et al. 17Beta-estradiol regulation of T-type calcium channels in gonadotropin-releasing hormone neurons. Journal of Neuroscience. 2009;29:10552–10562. doi: 10.1523/JNEUROSCI.2962-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.