Is Biology Destiny? Birth Weight and Differential Parental Treatment

Abstract

Time diaries of sibling pairs from the PSID-CDS are used to determine whether maternal time investments compensate for or reinforce birth-weight differences among children. The findings demonstrate that the direction and degree of differential treatment vary by mother's education. Less-educated mothers devote more total time and more educationally oriented time to heavier-birth-weight children, whereas better-educated mothers devote more total and more educationally oriented time to lower-birth-weight children. The compensating effects observed among highly educated mothers are substantially larger than the reinforcing effects among the least-educated mothers. The findings show that families redistribute resources in ways that both compensate for and exacerbate early-life disadvantages.

Now Israel loved Joseph more than any of his other sons, because he had been born to him in his old age; and he made a richly ornamented [a] robe for him.

(Genesis 37:3–4)

Introduction

Competing theories exist regarding how parents allocate resources to children who differ in terms of initial characteristics (such as cognitive abilities and health endowments) that influence future life chances. If parents are simply motivated by desires to maximize returns to their investments, resources might be disproportionately directed to higher-ability children who hold more promise for future success (Becker and Tomes 1986). If parents seek to equalize outcomes among their children, they might direct a greater share of resources to less able children (Behrman et al. 1982). Family socioeconomic circumstances may also structure the types of investment strategies parents can afford (Conley 2008). Socially advantaged families may have the luxury of pursuing compensatory strategies that seek to equalize outcomes across children, whereas socially disadvantaged families may be compelled to concentrate more limited resources on higher-ability children.

Numerous studies have sought to test whether resource allocation decisions are influenced by children's endowments, where endowments are broadly defined as genetically inherited initial traits that influence future attainment directly or indirectly. These studies have led to mixed results, with some studies finding compensatory effects (Behrman et al. 1982; Griliches 1979), others finding reinforcing effects (Behrman et al. 1994; Datar et al. 2010; Rosenzweig and Schultz 1983), and still others finding no effects of child endowment on parental investment decisions (Almond and Currie 2009). Additionally, previous studies have not examined whether investment strategies vary by socioeconomic status.¹ The use of indirect and poor proxies for children's endowments and parental investment may, in part, explain why results have been so mixed.²

This study seeks to contribute to this body of literature by analyzing a sample of sibling pairs from the Panel Study of Income Dynamics-Child Development Study (PSID-CDS). The data provide a unique opportunity to measure child endowment and parental investment directly. Birth weight is used to measure children's initial endowments. Time diaries are used to capture parental time investments in children. Both the total quantity of time mothers devote to children and the quantity of time devoted to performing activities that may more directly enhance human-capital development (such as reading, doing homework, playing together, and arts and crafts) are examined. Sibling fixed-effects models are estimated to account for family-specific heterogeneity that might bias birth-weight estimates.

The findings largely support Conley (2008), who hypothesized that the degree and direction of differential treatment vary by family socioeconomic status (SES). Specifically, the findings show that less-educated mothers tend to reinforce endowment differences by spending more total and more educational time with heavier-birth-weight children relative to lower-birth-weight children. Better-educated mothers tend to compensate for endowment differences among their children by spending more total and more educational time with their lower-birth-weight children. Additionally, the degree of differential treatment is strongest among the most highly educated mothers. For example, when both siblings are preschool-age, college-graduate mothers devote nearly 0.65 standard deviations more total time and nearly 1 standard deviation more educational time to children at the 10th percentile of birth-weight distribution relative to children at the 50th percentile of birth-weight distribution. The findings are robust to different ways of specifying birth weight and mother's education.

This study contributes to the literature in the following ways: first, it uses more direct and arguably better measures of both child endowments and parental investments. Birth weight is an ideal measure of endowments in that it is a characteristic that is assigned at birth, is correlated with outcomes throughout childhood and adulthood, and is observable by parents. Therefore, it is likely to be a trait that influences resource-allocation decisions. The type and quantity of time parents spend with children offer a novel measure of parental investments in children. Time use is an arguably better measure than the more common metric of parents’ day-to-day investments in their children. Moreover, this study pays particular attention to the time parents spend with their children performing activities that have been shown to enrich children's cognitive home environment, such as reading, playing, and doing homework together (Brooks-Gunn and Markman 2005; Davis-Kean 2005; Smith et al. 1997).

This study also contributes to the literature on the causes and consequences of birth weight for future attainment. While the short- and longer-term consequences of low-birth-weight status have been widely studied (see Black et al. (2007) for an overview of the literature), less is known about the specific pathways through which birth weight affects later status attainment. For example, are effects on future attainment due to biological destiny? Or are they due to biosocial interactions between individual health and environmental factors? This study shows that differential parental treatment may exacerbate the effects of birth weight in socially disadvantaged families and lessen such effects in socially advantaged families.

Finally, the findings offer some critiques of sibling correlation models, which have a long tradition in stratification research and have been widely used to estimate the influence of family origin on social mobility in the United States (Hauser and Mossel 1985; Hauser and Sewell 1986; Solon et al. 1991; Teachman 1995). These models use sibling resemblance in status attainment to assess the strength of family origin. They rely heavily on the assumption that family environment affects siblings in the same way. Results from this study suggest otherwise. More important, differential treatment not only exists but also varies by family SES. As a result, studies that rely on sibling resemblance in attainment outcomes to estimate the relative effect of family origin on status attainment may underestimate the influence of family origin in lower-SES families and overestimate the influence of family origin in higher-SES families.

Birth Weight and Differential Treatment

Economic theory has long argued that parents are responsive to endowment differences among children and differentially invest in children's human capital. Whether investments reinforce or compensate for endowment differences among siblings depends on several factors, including parental preferences for equity among children, resource constraints, and how endowments are distributed among siblings. Becker and Tomes (1976) introduced the first model of parental resource allocation, which posits that parents are child-neutral in that they do not favor one child over another and instead invest in all children equally. In this model, parents are concerned not about equalizing eventual outcomes among children, but rather about the level of investment each child receives. This strategy may lead to differential outcomes depending on how initial endowments are distributed among children.

In a subsequent model, Becker and Tomes (1986) argued that parents use a combination of human-capital investments and wealth transfers to maximize children's economic well-being. Human-capital investments are directed toward higher-ability children because the returns from such investments are greater than those from investing in lower-ability children. However, under this model, parents are also concerned about equalizing outcomes. Therefore, parents adopt a compensatory approach toward how income/wealth is transferred by diverting more income and wealth to lower-ability children. Like the previous model, the “separable earnings-bequest” posits that human-capital investments and income/wealth transfer are allocated differently (Behrman et al. 1982). Although wealth is transferred equally among children, the desire to ensure equality of outcomes drives parents to invest more heavily in the human-capital development of less-endowed children.

Recently, Conley (2008) proposed an alternative theory that resource-allocation decisions vary by social class. In a “strategic investments” approach, differential access to resources compels parents to respond to endowment differences among their children in different ways. When resources are limited, concentrating resources on higher-ability children may be the least risky strategy relative to alternatives that either concentrate resources on children with a lower probability of future success or spread resources equally across all children, potentially diluting resources and failing to provide any child with the means to succeed. Whereas well-off families may have the resources to take on such risks, disadvantaged families are less able to do so. For disadvantaged families, “picking a winner” and concentrating limited resources on the ablest child may be the surest way of guaranteeing positive returns for their investments. Moreover, this approach may also be the most efficient way of maximizing the economic well-being of all children if the expectation is that, down the line, high-ability children will transfer wealth to help their siblings. In contrast, socially advantaged families have more options. They have the means to ensure that high-ability children obtain the minimal level of investments to secure success while directing a higher share of resources toward lower-ability children in an effort to compensate for initial endowment differences. Conley (2008) likened the ability to strive for equality in child outcomes to a luxury good that only families of means can afford.

These theories offer insight into the factors that motivate allocation decisions. However, how families actually respond to endowment differences is an empirical question. Studies using data from the United States provide mixed results. Griliches (1979) used adult IQ as a measure of initial endowment to analyze a sample of sibling pairs and found evidence of compensatory investment strategies. Analyzing a sample of adult male twins, Behrman et al. (1982) showed that concerns regarding how earnings are distributed among children help drive allocation decisions and induce parents to adopt compensatory approaches. Behrman et al. (1994) analyzed a sample of twins from Minnesota, using adult earnings and body mass index as proxies for child endowments. They found that schooling attainment is higher for the better-endowed twin, which they interpreted as evidence of reinforcing parental behavior.

Several issues complicate previous results. First, previous studies used indirect measures of both birth endowments and parental investments. For example, educational attainment is a commonly used proxy for parental investments (see, e.g., Behrman et al. 1994; Griliches 1979). This approach requires the assumption that completed years of education are unaffected by children's initial abilities, preferences, or behavior. Second, previous studies used adult characteristics, such as adult earnings (Behrman et al. 1982) and adult IQ (Griliches 1979), as proxies for birth endowments. This approach requires the assumption that adult IQ and adult earnings capture time-invariant abilities assigned at birth that are uninfluenced by the stream of investments made by parents throughout each child's life. These simplifying assumptions are dubious, however, given the evidence showing, for example, that early cognitive abilities predict later attainment outcomes (Rouse et al. 2005; Warren et al. 2002) and that both adult earnings and IQ are affected by family environment (Blau and Duncan 1967; Jencks and Phillips 1998).

Notable exceptions are Almond and Currie (2009) and Datar et al. (2010). Both used birth weight as a direct measure of child endowments. Almond and Currie analyzed a sample of twins from the Early Childhood Longitudinal Study-Birth Cohort (ECLS-B). They used a variety of measures to capture parental investments, including breastfeeding, well-baby visits, amount of praise and affection offered, and disciplinary practices. Overall, they found that while parents voice greater concern over whether their low-birth-weight children are ready for school, they do not treat heavier-birth-weight children differently from their lower-birth-weight siblings. Datar et al. analyzed sibling pairs from the National Longitudinal Survey of Youth-Child (NLSY-C) to tackle the same question. Breastfeeding, well-baby visits, immunizations, and preschool attendance were used as direct measures of early childhood investments. Using continuous measures of birth weight, they found little evidence of differential treatment by birth weight, but when dichotomous measures were used to indicate low-birth-weight status, they found that parents are more likely to reinforce birth-weight differences.

Praise, affection, disciplinary practices, and early health investments are all different ways that parents “invest” in their children. Quantity and type of time devoted to children constitute another, arguably more direct way that parents foster children's human-capital development. Time use—particularly shared time engaged in cognitively stimulating activities—is predictive of children's cognitive development (Brooks-Gunn and Markman 2005; Davis-Kean 2005; Smith et al. 1997). Understanding the responsiveness of parental time investments to children's birth weight is critical to identifying mechanisms linking birth weight to later attainment outcomes. Additionally, in contrast with shorter-term commitments such as well-baby visits and immunizations, time use may better capture the day-to-day investments parents make in children.

Few studies have considered whether investment strategies vary over the socioeconomic conditions of the family. There are reasons to expect that parental response to differences in child endowments might depend on the socioeconomic circumstance of families. First, from the standpoint of trying to maximize returns to investments and minimize uncertainty, concentrating resources on those children who are most likely to succeed might be the optimal choice for disadvantaged families (Conley 2008). Second, social disadvantage and economic hardship reduce an individual's capacity to provide attentive and responsive care (Bradley and Corwyn 2003; Fuligni and Yoshikawa 2003; Hoff 2003). Disadvantaged parents may direct less time and attention to “difficult” children in favor of those who are “easier” to care for. On the other hand, socioeconomically advantaged parents may have access to both the economic and psychological resources to make compensatory investments in favor of higher-needs children. This study's focus on parental time use may prove better suited to identifying SES disparities in parental investments.

In conclusion, this study seeks to determine (1) whether parental investments reinforce or compensate for endowment differences among children, and (2) whether parental investment strategies vary by socioeconomic status. Birth weight is used as a direct proxy of birth endowments. Time use captures the day-to-day inputs that directly foster children's human-capital development and may offer a better means of identifying SES disparities in patterns of differential treatment.

Estimation Strategy

The empirical approach is based on sibling fixed-effect (FE) specifications, which have been widely used in the literature (Behrman et al. 1994; Conley and Bennett 2000; Datar et al. 2010). Equation 1 argues that parental investments (I) in child i from family f are a linear function of the child's birth endowment (e_if) and child and family characteristics (X_if) that influence investment decisions (e.g., mother's education, family income, and mother's age at child's birth).

$$I_{if}={\beta }_0+{\beta }_1{e}_{if}+{\beta }_2{X}_{if}+{\gamma }_f+{\epsilon }_{if},$$ (1)

γ_f represents unobserved factors that are commonly experienced by all children within the family. ε_if represents a stochastic error term. In order to examine whether parental response to endowment differences varies by social class, Eq. 1 incorporates statistical interactions between child endowment and characteristics such as mother's education or family income.

An extensive set of control variables, X_if, accounts for observable characteristics that might simultaneously determine birth endowments and parental investments. However, even after controlling extensively for such characteristics, it is likely that many aspects of the family environment that correlate with endowments remain unmeasured in X_if. For example, “negligent” mothers who smoke and drink during pregnancy may be more likely to have lower-birth-weight children.

Within a fixed-effect framework, bias attributable to unobserved family-specific heterogeneity is eliminated by γ_f, which differences out both observed and unobserved characteristics that are commonly experienced by siblings. Therefore, identification in sibling fixed-effect models is derived from within family correlations.

Birth weight is used to capture childbirth endowments, e_i. Two alternative measures of birth weight are employed. First, a continuous specification is employed using log birth weight (measured in ounces). Second, an indicator of low birth weight (LBW) is used to capture threshold effects.³ Maternal time investments are used to measure parental investments, I_if. The total time each child spends with his or her mother, and the amount of time spent on educationally oriented activities, are introduced separately to capture parental investments.

To determine whether parental response to birth-weight differences depends on the socioeconomic conditions of the family, statistical interactions between birth-weight measures and mothers’ educational attainment are included.⁴ Mothers’ education is measured using a continuous specification (i.e., years of schooling) and piecewise linear splines. The latter approach captures the possibility that education has distinct effects at different points in the distribution. In particular, one might expect mothers who go on to pursue postsecondary education to be qualitatively different from mothers who do not.⁵

While sibling fixed-effect models can eliminate bias attributable to unobserved family-specific heterogeneity, potential bias attributable to unobserved heterogeneities that are not commonly experienced by siblings remain. In order to address this problem, I include several child-specific characteristics to capture life-course events that may cause siblings within the same family to experience the family environment differently. These variables include mother's age at child's birth and marital status at birth.

Child's age and birth order are other sources of child-specific heterogeneity that should be considered. Younger children demand more time and attention than their older siblings. School-age children spend significantly less time at home than their non-school-age siblings. Therefore, the following variables are also included in the analysis: an indicator of whether the child is of school age and an indicator of whether the child is the younger within a sibling pair. To further address birth-order and age issues, additional sensitivity analyses are conducted. First, I analyze the full set of sibling pairs. Next, I analyze sibling pairs who are both preschool-age (under the age of 6) and sibling pairs who are both 6 years old or older.^6,7 Standard errors are clustered at the family level.

Data and Measures

The data come from the Child Development Supplement of the Panel Study of Income Dynamics (PSID-CDS). The Panel Study of Income Dynamics (PSID), which was begun in 1968, is a longitudinal study of a nationally representative sample of individuals and families in the United States; it oversamples low-income and immigrant families. Starting in 1997, the PSID conducted the Child Development Supplement (CDS) to collect reliable and detailed data on the early childhood development of approximately 3,600 children who were 12 years old or younger. A unique feature of the CDS is that it is the only nationally representative survey that collects children's time-diary data. Because the time diaries are child-specific, the data provide a unique opportunity to examine child-specific variation in time use within the family. Response rates for the time-diary modules were 82 % in 1997. The PSID collected time diaries and child development information for up to two randomly selected children within each family. The sample analyzed in this study is restricted to children who have siblings and whose sibling was surveyed in 1997. Only siblings who both completed time diaries were kept in the sample. These restrictions reduce the final sample to 1,516 children, or 758 sibling pairs.

Birth Weight

Two alternative measures of birth weight are examined. First, birth weight is measured in log-ounces. This approach can be estimated using the full sample of sibling pairs. The second approach measures birth weight as a dichotomous variable using an indicator for low birth weight (i.e., less than 5 pounds and 8 ounces, or less than 2,500 grams). Medical professionals and public-health researchers have placed much attention and emphasis on this birth-weight threshold. This emphasis may stigmatize children who fall into the low-birth-weight category (LBW) and influence the way that parents perceive their children. Moreover, research shows that the LBW cutoff is not without significance. Threshold effects of birth weight on both short- and longer-term attainment outcomes are well documented (Almond et al. 2005; Conley and Bennett 2001; Currie and Moretti 2007). Therefore, I also explore dichotomous measures of birth weight to better capture any potential effects.

One drawback of using dichotomous measures of birth weight, however, is that only a relatively small percentage of children fall into the LBW category. At the population level, about 8 % of children have low birth weight. Of the sample of 758 sibling pairs, only 67 pairs differ in birth weight when using dichotomous measures (i.e., one sibling is normal birth weight (NBW) and the other is LBW). For 29 pairs, both siblings are LBW; for 662 pairs, neither sibling is LBW. Therefore, estimation of birth-weight effects using dichotomous measures relies on variation within 67 sibling pairs (approximately 9 % of the sample).

Table 1 presents weighted descriptive statistics for the full sibling sample, the subsample of children with no LBW sibling, and the subsample of children with one LBW sibling. One can see that children with an LBW sibling are not socioeconomically disadvantaged relative to children who do not have a LBW sibling. There are no significant differences in terms of family income, mothers’ education, average age at birth, or maternal employment status. There are, however, some significant differences across these groups of children. Children with no LBW siblings tend to come from slightly larger families. Children without a LBW sibling also tend to be older and therefore more likely to be enrolled in school. In line with the literature, there are substantial racial differences in the prevalence of low birth weight. Its instance is higher among black and Latino sibling pairs.

Table 1.

Weighted descriptive statistics

	Full Sibling Sample	Children With No LBW Sibling	Children With 1 LBW Sibling
Parental Time Investments
Total maternal time (hrs./week)	46.12 (19.05)	45.99 (19.10)	47.31 (19.00)
Developmental time (hrs./week)	12.49 (10.34)	12.32 (10.20)	13.28 (11.33)
Child Endowment
Birth weight	119.9 (20.81)	123.27 (17.36)	93.30 (24.13)
Family Characteristics
Mother's education (yrs)	12.85 (3.07)	12.85 (3.12)	12.83 (2.60)
Prop. with high school or less	0.40 (0.49)	0.41 (0.49)	0.34 (0.48)
Log family income	10.24 (10.11)	10.25 (1.13)	10.10 (1.00)
Mother's age at child's birth	27.67 (5.34)	27.70 (5.36)	27.40 (5.80)
Prop. mothers working	0.72 (0.45)	0.79 (0.40)	0.71 (0.45)
Hrs. worked among working mothers	34.74 (13.73)	34.63 (12.69)	34.46 (15.94)
Sibship size	2.75 (0.99)	2.79 (1.02)	2.45* (0.64)
Child's age in 1997	5.96 (5.95)	6.05 (3.38)	4.91* (3.12)
School age (= 1)	0.54 (0.50)	0.55 (0.50)	0.41* (0.50)
Male (= 1)	0.50 (0.50)	0.51 (0.50)	0.51 (0.50)
Black (= 1)	0.13 (0.34)	0.12 (0.32)	0.262** (0.44)
Latino (= 1)	0.13 (0.33)	0.13 (0.33)	0.16* (0.34)
Other (= 1)	0.07 (0.07)	0.07 (0.25)	0.11 (0.37)
N	1,516	1,314	132

Notes: t test compares mean differences between children with only normal-birth-weight siblings and children with a low-birth-weight sibling. Sampling weights were used to make statistics nationally representative.

^*p < .05

^**p < .001

Still, one may question the representativeness of the 67 sibling pairs. If LBW children are more likely to be the younger sibling, then birth-weight effects might mask birth-order effects because younger children require more parental time and attention. A comparison of birth-order differences among the 67 sibling pairs (not shown in Table 1) reveals that LBW children are more likely to be the older sibling. In 43 pairs, the NBW child is the younger sibling and the LBW child is the older sibling. There are 24 cases in which the LBW child is the younger sibling and the NBW child is the older sibling. To the extent that parental time and attention are more likely to be devoted to younger siblings, the fact that LBW children tend to be the older sibling suggests that estimates of birth weight may be downwardly biased, resulting in underestimates, rather than overestimates, of birth-weight effects.⁸

Maternal Time Investments

Time diaries were collected for a random weekend and a random weekday. Information was collected on the type of activity performed and the duration of time spent on each activity within a 24-hour period. Additionally, respondents were asked to report who was present (mothers, fathers, and other siblings, for example) for each activity. Two measures of parental time investments were constructed using these data. The first measures the total hours per week that mothers spend with each child. The second captures the hours per week that mothers spend with each child performing activities that may more directly develop the child's human capital. Specifically, these activities include time spent reading, playing (e.g., playing with toys, pretend/dress-up, board games, outdoor activities), doing hobbies (e.g., arts and crafts, photography, playing musical instruments), and doing homework together.

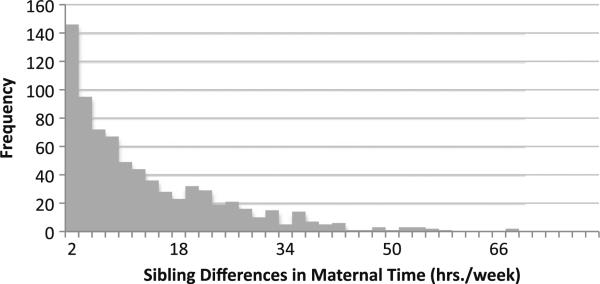
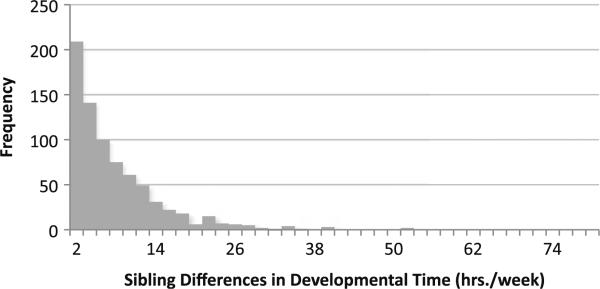
Figures 1 and 2 present histograms of the within-sibling variation in total time spent with mothers and time spent on activities that may be more educationally oriented, respectively. Both histograms show substantial differences in the amount of time each offspring receives from his or her mother weekly. Whereas approximately 175 sibling pairs report no difference in the total amount of time they receive from their mothers, the vast majority report differences. A small but nontrivial portion of siblings report a difference of 30 hours or more per week in the amount of time siblings receive. These cases consist largely of sibling pairs in which one sibling is of school age and the other is not.⁹

Fig. 1.

Histogram of within-sibling differences in maternal time investments

Fig. 2.

Histogram of within-sibling differences in maternal time in educationally oriented activities

Age effects complicate time-use data. Ideally, one would like to be able to compare time investments made in children when both siblings are the same age. Unfortunately, the data do not allow for this. As a result, analysis relies on comparisons of, for example, the time a mother devotes to her 3-year-old child with the time that the same mother devotes to her 6-year-old child during a randomly selected week in 1997. Observed differences in time investment, in this example, might reflect not only differential response to endowment differences but also differential time use because of children's age. To address this concern, all time-use variables are age-standardized (i.e., the time investment each child receives is subtracted from the average time investment other children his or her age receive and divided by its standard deviation). When time use is age-adjusted in this way, the dependent variable can be interpreted as deviations from the expected time investment each child should receive based on his or her age. This approach normalizes measures so that age effects are less likely to complicate interpretations. As discussed earlier, I also conduct an analysis restricting the sample to sibling pairs who are more comparable in age in order to address the potentially confounding effects of age.

Mother's Education

I use mother's education to measure family socioeconomic status. Mother's education is first measured using years of schooling; second, piecewise linear splines are used to capture the possibility that the relationship between birth weight, family SES, and investments is nonlinear. Given the economic and social significance of high school graduation and postsecondary schooling, I constructed splines to explore discontinuities at these particular points in the distribution. Numerous alternative specifications were examined, including cutoffs defined at 12 years and 16 years of completed schooling. Results using a piecewise linear spline with a node at 12 years of completed education offered the most significant and substantively interesting results, and are presented here. Finally, as a robustness check, I use a dummy variable for education (i.e., an indicator for some postsecondary schooling) to capture schooling effects when dichotomous measures of birth weight are also used.

Results

Table 2 reports sibling fixed-effect estimates of birth weight (measured in log-ounces) on maternal time investments using various specifications of maternal time and mother's education. Panels A, B, and C present results using the full sample of sibling pairs: siblings who are both below the age of 6 and siblings who are both 6 years or older, respectively. In Models 1, 2, and 3, the dependent variables are age-standardized measures of the total hours per week that mothers spend with children. In Models 4, 5, and 6, the dependent variables are age-standardized measures of hours per week that mothers spend performing educationally oriented activities with children. Because the dependent variables are age-standardized, they are interpreted as deviations from the expected time investments based on each child's age. Models 2 and 5 introduce statistical interactions between birth weight and mother's education measured in years of education. Models 3 and 6 include interactions between birth weight and mother's schooling, measured using a piecewise linear spline (i.e., the first segment of the spline represents schooling up to and including 12 years of education, and the second segment represents more than 12 years of education).

Table 2.

Sibling fixed-effect estimates of birth weight (log ounces) on maternal time investments, using both continuous measures and linear piecewise splines for mother's education

	Total Time			Educational Time
	(1)	(2)	(3)	(4)	(5)	(6)
A. Full Sample
Log birth weight	0.08 (0.11)	0.15 (0.11)	0.18 (0.11)	–0.08 (0.15)	–0.02 (0.16)	0.13 (0.16)
Log birth weight × Education (years)		–0.01* (0.00)			–0.00 (0.01)
Log birth weight × 1st segment of spline (≤12)			–0.00 (0.00)			–0.01* (0.00)
Log birth weight × 2nd segment of spline (≤12)			–0.09† (0.05)			–0.14† (0.08)
N	1,516	1,516	1,516	1,516	1,516	1,516
Number of sibling pairs	758	758	758	758	758	758
B. Both Siblings <6 Years Old
Log birth weight	–0.07 (0.22)	2.83* (1.13)	2.30 (1.71)	–0.10 (0.21)	2.66* (1.22)	1.06 (1.66)
Log birth weight ×Education (years)		–0.23** (0.09)			–0.22* (0.10)
Log birth weight × 1st segment of spline (≤12)			–0.17 (0.15)			–0.06 (0.14)
Log birth weight × 2nd segment of spline (≤12)			–0.29* (0.13)			–0.36* (0.16)
N	594	594	594	594	594	594
Number of sibling pairs	297	297	297	297	297	297
C. Both Siblings ≥6 Years Old
Log birth weight	0.11 (0.13)	0.17 (0.13)	0.11 (0.13)	–0.22 (0.37)	–0.23 (0.35)	–0.07 (0.38)
Log birth weight × Education (years)		–0.01* (0.00)			0.00 (0.00)
Log birth weight × 1st segment of spline (≤12)			–0.01 (0.01)			–0.01 (0.01)
Log birth weight × 2nd segment of spline (≤12)			0.04 (0.12)			–0.18 (0.18)
N	380	380	380	380	380	380
Number of sibling pairs	190	190	190	190	190	190

Notes: Sibling fixed-effect models for the full sample include the following covariates: child's sex, an indicator for whether school aged, an indicator for whether the younger child, mother's age at birth, and an indicator for whether the mother was married at the child's birth. Age-stratified models include all the preceding covariates but exclude an indicator for whether school aged. Robust standard errors are shown in parentheses.

^†p < .10

^*p < .05

^**p < .01

For the full sample of sibling pairs, Models 1 and 4 show that there is no significant main effect of birth weight on either total time or educational time. Model 2 shows that interactions between years of schooling and birth weight have a small but significant relationship with total maternal time. When splines are used to measure family SES in Models 3 and 6, the results show that interactions between birth weight and schooling among those with some postsecondary education are negative and marginally significant. Negative interactive effects show that better-educated parents spend less time with heavier-birth-weight children.

In an effort to make siblings more comparable in terms of age, in Panel B, I restrict the sample to only those siblings who are both younger than 6 years. Birth-weight effects are much stronger when both siblings are of preschool age. Models 1 and 4 show no significant main effect of birth weight on total time or educational time, respectively. Interactions with both specifications of mother's education, however, are statistically significant for both total and educational time. Models 2 and 5 show a significant negative interactive effect; in other words, better-educated parents devote less total time and educationally oriented time to heavier-birth-weight children. Results using splines in Models 3 and 6 demonstrate nonlinearities in the effect of education and birth weight on time investments. In particular, they show that the degree of differential treatment is larger for those with some postsecondary education than for those without.

Panel C in Table 2 restricts the sample to only sibling pairs in which all siblings are 6 years or older. Differential investment by birth weight is less statistically significant when all siblings are of school age. Statistical interactions between birth weight and education in Model 2 are significant and negative, which suggests that more-educated parents are more likely to compensate for endowment differences. The magnitude of these effects is small, however, relative to the effects seen when all siblings are younger than 6 years.

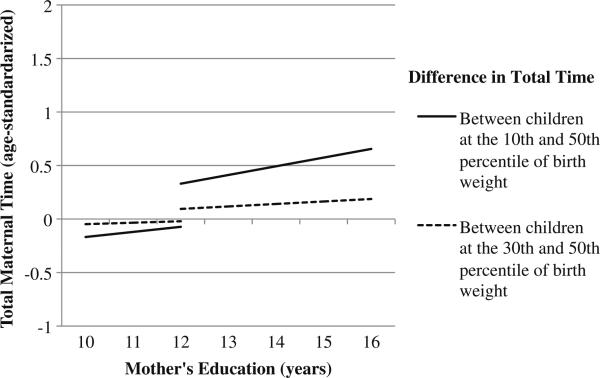
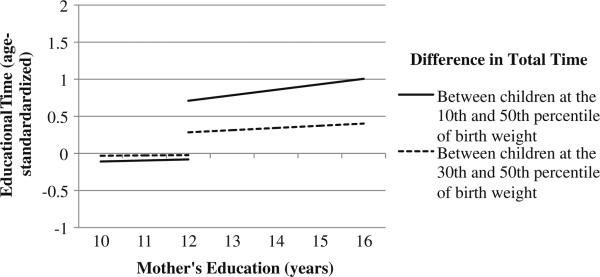
To facilitate interpretation, I graph predicted values in Figs. 3 and 4 using regression results from Models 3 and 6, respectively. All covariates are evaluated at the sample mean. Both Figs. 3 and 4 plot the difference in time investment between a child at the 10th percentile of the birth-weight distribution and a child at the 50th percentile of the birth-weight distribution by mother's education. Differences in time investment between children at the 30th and the 50th percentiles of birth distribution are also plotted by mother's education. Figs. 3 and 4 show that among mothers with 12 years of schooling or less, children at the 10th percentile receive less total time and less educationally oriented time than comparable children at the 50th percentile. Among mothers with some postsecondary education, children at the 10th percentile of the birth-weight distribution receive more total time and more educational time than their counterparts at the 50th percentile. These results suggest that socially disadvantaged families tend to adopt reinforcing investment strategies while socially advantaged families tend to compensate for endowment differences.

Fig. 3.

Predicted values of maternal time by birth weight and mother's education (using estimates from model 3 on sibling pairs younger than 6 years)

Fig. 4.

Predicted values of educational time by birth weight and mother's education (using estimates from Model 6 on sibling pairs younger than 6 years)

It is also important to note the magnitude of the effects. Reinforcing strategies among less-educated mothers are relatively small compared with the compensatory strategies adopted by the most-educated mothers. Among children of mothers with 12 years or less of schooling, NBW children (i.e., those at the 50th percentile) receive no more than 0.17 standard deviations greater total time than their lower-birth-weight siblings (i.e., those at the 10th percentile). Among children of college-educated mothers, lower-birth-weight children receive approximately 0.65 standard deviations greater total time than their normal-birth-weight siblings.

For educational time, the difference among less-educated mothers is negligible (0.10 standard deviations). Among college-educated mothers, however, nearly 1 standard deviation more educational time is devoted to children at the 10th percentile of the birth distribution relative to their siblings at the 50th percentile. Children at the 30th percentile receive nearly 0.40 standard deviations more educational time than siblings at the 50th percentile among college-educated mothers.

Table 3 reports results from sibling fixed-effect models using dichotomous measures of birth weight. Panel A presents results using the full sample. Panel B presents results for sibling pairs in which both children are younger than 6 years, and Panel C presents results in which both children are 6 years or older. Implementing these age restrictions, however, may be problematic because it further reduces the original sample of 67 sibling pairs for whom there was variation on the birth-weight indicator. Of these 67 sibling pairs, in only 31 pairs are both children younger than age 6, and in only 36 pairs are both children 6 years or older. Therefore, the results from Panels B and C should be interpreted with care.

Table 3.

Sibling fixed-effect estimates, using dichotomous measures of birth weight and both continuous and linear piecewise splines for mother's education

	Total Time			Educational Time
	(1)	(2)	(3)	(4)	(5)	(6)
A. Full Sample
LBW	0.01 (0.09)	–0.68 (0.43)	0.12 (0.12)	0.04 (0.10)	–0.54 (0.68)	0.54† (0.33)
LBW × Mother's education (years)		0.05 (0.03)			0.05 (0.05)
LBW × 1st segment of spline (≤12)			–0.03† (0.02)			–0.07* (0.03)
LBW × 2nd segment of spline (>12)			0.21** (0.07)			0.26** (0.08)
N	1,516	1,516	1,516	1,516	1,516	1,516
Number of sibling pairs	758	758	758	758	758	758
B. Both Siblings <6 Years Old
LBW	0.04 (0.14)	–0.87 (0.72)	–0.05 (0.18)	0.04 (0.14)	–0.46 (1.12)	0.90** (0.22)
LBW × Mother's education (years)		0.07 (0.05)			0.04 (0.09)
LBW × 1st segment of spline (≤12)			–0.02 (0.03)			–0.10** (0.02)
LBW × 2nd segment of spline (>12)			0.21* (0.09)			0.28* (0.11)
N	594	594	594	599	599	599
Number of sibling pairs	298	298	298	300	300	300
C. Both Siblings ≥6 Years Old
LBW	0.18 (0.15)	–0.18 (0.23)	0.02 (0.08)	0.14 (0.27)	–0.05 (0.33)	0.17† (0.09)
LBW × Mother's education (years)		0.03 (0.02)			0.02 (0.02)
LBW × 1st segment of spline (≤12)			–0.01 (0.02)			–0.03 (0.04)
LBW × 2nd segment of spline (>12)			0.15 (0.09)			0.15 (0.15)
N	380	380	380	380	380	380
Number of sibling pairs	190	190	190	190	190	190

Notes: LBW = low birth weight. Sibling fixed-effect models for the full sample include the following covariates: child's sex, an indicator for whether school aged, an indicator for whether the younger child, mother's age at birth, and an indicator for whether the mother was married at the child's birth. Age-stratified models include all the preceding covariates but exclude an indicator for whether school aged. Robust standard errors are shown in parentheses.

^†p < .10

^*p < .05

^**p < .01

Results using the full sample in Panel A tell a similar story to that derived from using continuous measures of birth weight. Mothers with 12 years of schooling or less tend to reinforce birth-weight differences by spending more total time and more educational time with NBW children relative to LBW children. Mothers with some postsecondary education tend to spend more total time and more educational time with LBW children. Additionally, the degree of differential treatment is greater among better-educated mothers than among less-educated mothers. Stratifying by age shows that the findings for the full sample are largely driven by differential treatment occurring among families in which both siblings are of preschool age. Results in Panel B are statistically significant, but results in Panel C are not. Overall, the results from models using dichotomous measures mirror those for models using continuous measures of birth weight.

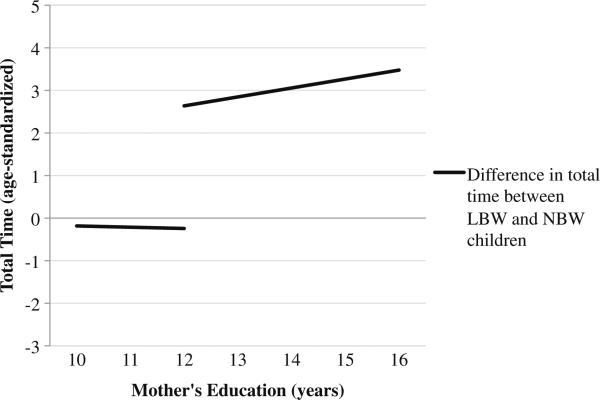
Figure 5 presents predicted values using Model 3 estimates on the full sample of siblings (all covariates are evaluated at the sample mean). Overall, the results again show that differential treatment varies by mothers’ education. Less-educated mothers tend to adopt slightly reinforcing strategies such that LBW children receive slightly less total time than their NBW siblings. Better-educated mothers tend to adopt compensatory strategies by devoting significantly more time to LBW than NBW children.

Fig. 5.

Predicted values of total time by birth weight and mother's education (using estimates from Model 3 on full sample of sibling pairs)

Figure 5 highlights a sizable difference in the degree of differential treatment by education. Whereas the degree of reinforcing strategies among less-educated mothers is relatively small (e.g., among mothers with only 12 years of schooling, LBW children receive approximately 0.25 standard deviations less total time than NBW children), the degree of compensatory strategies adopted is tremendous. LBW children receive approximately 2.5 standard deviations more total time than NBW children among those mothers with 12 years of schooling. Among children of college-graduate mothers, the gap increases to nearly 3.5 standard deviations.

Robustness Checks

In this section, I report results for robustness checks that address concerns raised by estimates using dichotomous measures of birth weight. The magnitudes of the estimates are significantly larger than estimates derived from models that use continuous measures of birth weight. Recall that models using continuous measures derive their estimates from the full sample of siblings, whereas models using LBW indicators rely on variation among 67 sibling pairs. Therefore, models using LBW indicators may be more sensitive to how it is specified.

In Table 4, results are reported for sibling fixed-effect models that use dichotomous measures for both birth weight and mother's education. Mother's education is measured as an indicator of having more than 12 years of schooling. Dichotomizing mother's education places less strain on the data because it only requires that the 67 sibling pairs for whom there is variation on the birth-weight variable can be sufficiently divided into two educational categories.

Table 4.

Sibling fixed-effect estimates, using dichotomous measures of birth weight and dichotomous measures of mother's education (>12 years)

	Total Time	Educational Time
	(1)	(2)
A. Full Sample
LBW	–0.13 (0.13)	–0.17 (0.14)
LBW × Mother's education (= 1 if >12 years)	0.28 (0.19)	0.39* (0.19)
N	1,516	1,516
Number of sibling pairs	758	758
B. Both Siblings <6 Years Old
LBW	–0.21 (0.20)	–0.14 (0.16)
LBW × Mother's education (= 1 if >12 years)	0.54* (0.27)	0.40 (0.29)
N	594	594
Number of sibling pairs	298	298
C. Both Siblings ≥6 Years Old
LBW	–0.02 (0.15)	–0.07 (0.53)
LBW × Mother's education (= 1 if >12 years)	0.34 (0.27)	0.32 (0.60)
N	380	380
Number of sibling pairs	190	190

Notes: LBW = low birth weight. Sibling fixed-effect models for the full sample include the following covariates: child's sex, an indicator for whether school aged, an indicator for whether the younger child, mother's age at birth, and an indicator for whether the mother was married at the child's birth. Age-stratified models include all the preceding covariates but exclude an indicator for whether school aged. Robust standard errors are shown in parentheses.

^*p < .05

Point estimates reported in Table 4 largely confirm the findings in Tables 2 and 3. The results show that the direction of differential treatment varies by mother's education. Better-educated mothers spend more total time and more educational time with LBW children, while less-educated mothers spend more time with NBW children. However, only the results for educational time using the full sample and results for total time when both sibling pairs are of preschool age are statistically significant.

The magnitudes of the effects are more consistent with effect sizes derived from using continuous measures of birth weight in the full sample. The point estimates show that LBW children of mothers with some postsecondary education receive 0.39 standard deviations more educational time than their NBW counterparts. When both siblings are younger than 6 years, LBW children of better-educated mothers receive 0.54 standard deviations more total time than their NBW counterparts.

Discussion and Conclusion

This article examined parental responses to endowment differences among children. In contrast to previous studies, this study uses the PSID-CDS to obtain direct and arguably better measures of children's birth endowments and parental investments. Birth weight is a characteristic that researchers could potentially use to assess children's underlying endowments because it is assigned at birth, correlated with both short- and long-term attainment outcomes, and observable to parents. Maternal time investments offer a unique way to examine the daily investments parents make toward their children's human-capital development. In addition, this study examines the possibility that investment strategies vary by family socioeconomic circumstance, a theory that has been proposed but rarely tested in the literature.

The results show that among mothers with 12 years of schooling, heavier-birth-weight children receive significantly more total time and educational time than lower-birth-weight children. Among mothers with some postsecondary education, this relationship changes such that lower-birth-weight children receive more total and more educational time than their heavier-birth-weight siblings. These patterns are most prominent when both siblings are younger than 6 years. The results hold after controlling for sibling-specific heterogeneity using sibling fixed-effect models and are robust to different ways of specifying time investments, birth weight, and mothers’ education.

Interestingly, the magnitude of differential treatment is strongest among more-educated mothers. Whereas reinforcing effects are significant but minimal among less-educated mothers, compensatory effects among the most-educated mothers are sizable. For example, among college-educated mothers with children who are both younger than 6 years, lower-birth-weight children (at the 10th percentile of birth-weight distribution) receive approximately 0.65 standard deviations more total time and 1 standard deviation more educational time than their NBW siblings (at the 50th percentile of birth-weight distribution). The results show that differential time investments seem to be driven largely by the action of those who can best afford to equalize outcomes among children.

The findings are consistent with Conley's (2008) “strategic investment” argument. This argument sees time allocation decisions as driven largely by a conscious strategy to minimize risk. Disadvantaged families concentrate resources on higher-ability children in an effort to reduce risk and maximize expected returns to human-capital investments. Advantaged families, on the other hand, adopt compensatory strategies because they can afford to devote more resources to less-endowed children while still making sure that all children receive the minimum-level investments to ensure some degree of success.

An alternative explanation that is also consistent with the findings is that differences in sociopsychological resources explain differential parental treatment by social class. Caring for LBW children may be particularly burdensome because these children tend to be more problematic along various physical, cognitive, and behavioral dimensions. Disadvantaged parents, lacking the material and psychological resources to cope with the additional responsibilities involved in the care of high-needs children, may opt to spend more time with “easier” children and less time with “problematic” children. In this case, differential treatment does not stem from conscious calculations of expected future returns but from more immediate responses to current conditions and constraints. In addition, greater awareness of the negative consequences associated with low birth weight among the better-educated might also help explain why better-educated mothers are more likely to adopt compensatory behaviors.

In the end, it is likely that a combination of all these factors motivates parents’ time investments in their children. Nevertheless, although this study cannot adjudicate between these various alternative explanations, it offers an important empirical finding: the degree and direction of parental responsiveness to children's endowment differences varies by social class.

These findings inform policy strategies aimed at reducing the long-term effects of health-related inequality and intervention programs aimed at affecting parenting behaviors. In particular, the findings provide insight into whether policies should be targeted toward individual children or toward families as a whole. If parental investments, particularly among lower-SES families, are reinforcing differences, then policies aimed at alleviating childhood disadvantage should be specifically aimed at the target child. Relying on families to distribute resources may be ineffective if the most disadvantaged families are the least likely to divert resources to less-endowed children.

Additionally, these findings also speak to a tradition of studies using sibling correlations to estimate the influence of family background on status attainment (Hauser and Mossel 1985; Hauser and Sewell 1986; Solon et al. 1991; Teachman 1995; Warren et al. 2002). This line of research relies on the assumption that shared family background implies shared family experiences. Therefore, strong sibling resemblance in attainment outcomes implies that status attainment is highly dependent on family background. Low sibling correlation would imply that family background is relatively less important for status attainment. This study shows that sibling correlation models underestimate the influence of family origin in lower-SES families and overestimates the influence of family origin in higher-SES families. Because lower-income families reinforce endowment differences among children, the influence of family origin actually acts to increase, rather than decrease, sibling resemblance over time. In this case, family background exerts its influence in unexpected ways, producing divergent rather than convergent destinies among siblings.

Finally, this study demonstrates that differential time investments may be a pathway through which initial endowments affect later attainment outcomes. The lasting effects of LBW may be due not purely to biological destiny, but to biosocial processes occurring within the family that both compensate for and reinforce early-life disadvantages.