Rheotaxis performance increases with group size in a coupled phase model with sensory noise

Abstract

Many fish exhibit rheotaxis, a behavior in which fish orient themselves relative to flow. Rheotaxis confers many benefits, including energetic cost savings and interception of drifting prey. Despite the fact that most species of fish school during at least some portion of their life, little is known about the importance of rheotactic behavior to schooling fish and, conversely, how the presence of nearby conspecifics affects rheotactic behavior. Understanding how rheotaxis is modified by social factors is thus of ecological importance. Here we present a mathematical model in the form of an all-to-all, coupled-oscillator framework over the non-Euclidean space of fish orientations to model group rheotactic behavior. Individuals in the model measure the orientation of their neighbors and the flow direction relative to their own orientation. These measures are corrupted by sensory noise. We study the effect of sensory noise and group size on internal (i.e., within the school) and external (i.e., with the flow) disagreement in orientation. We find that under noisy environmental conditions, increased group size improves rheotaxis. Results of this study have implications for understanding animal behavior, as well as for potential applications in bio-inspired engineering.

1 Introduction

Rheotaxis is a robust, multi-sensory behavior in which fish and other aquatic organisms tend to align themselves in the direction of flow [1,2]. This form of taxis is generally positive (orienting upstream), but can be negative (orienting downstream). Positive rheotaxis confers many potential benefits to fish, including capture of downstream drifting prey [3,4], orientation to currents for migration [5,6], aiding odor searches [7] and energetic cost savings for fish attempting to maintain stream-wise positions in strong currents [8].

Although rheotaxis is an important behavior in the survival of many fish and aquatic species, the benefits of group behavior have largely focused on anti-predation [9,10]. According to a review of schooling behavior by Rieucau et al. [11], there has been conflicting evidence for some of the anti-predator hypotheses, and little experimental evidence obtained for larger schools. Thus, further work is necessary to investigate other possible benefits for the evolution of schooling behavior.

While the primary focus of previous research on collective behavior has been on anti-predator benefits, there have been several studies investigating group benefits of taxis. Grünbaum [12] developed asocial and social random-walk models for chemotaxis along a gradient using attractive and repulsive forces to mimic collective behavior; this study demonstrated that collective behaviors have the potential to enhance taxis by providing a mechanism for averaging instantaneous movement decisions over neighbors rather than averaging over time. Torney et al. [13] investigated context-dependent search of a chemical gradient with fluctuating gradients defined by patchy, heterogeneous information; by including social interaction terms, a group acts as a non-local spatial gradient sensor. Berdahl et al. [14] investigated emergent environmental sampling by moving animal groups; they found that a group of fish has the ability to track a fluctuating environmental gradient.

The results of these studies support the hypothesis that group behavior enhances taxis, as compared to solitary individuals, and provide some possible mechanisms by which this benefit emerges. However, most of the previous studies on the group benefits of taxis use a repulsion, attraction, orientation (ROA) framework [15,16] to model collective behavior. In an ROA framework, individuals move closer when beyond a certain distance and move apart when too close. While widely used, the ROA framework contains a large number of parameters, including the size and shape of each behavioral zone as well as the behavioral rules in each zone. The use of simple models can still result in complex and biologically realistic dynamics. Vicsek et al. [17] previously observed emergent self motion and clustering of simulated agents using a simple model of self-driven particles with constant speed. The only rule of the model was that at each time step each particle, would assume the average direction of other particles in a given radius, with some added noise.

While rheotaxis has been extensively studied and is of interest to neuroethologists and fisheries biologists, it has yet to be fully appreciated as a group behavior, despite ample evidence of group rheotaxis in nature (e.g., the upstream migration of salmon to their natal spawning sites) and evidence of collective benefits in migration [20,21]. We hypothesize that increasing group size may enhance rheotactic behavior, particularly in noisy or turbulent flows. It has been shown that individuals in a group may gain additional information about the environment from observing the behavior of their neighbors [22–24]. During rheotaxis, individual fish may use a combination of visual and lateral-line sensing to perceive the relative motion of nearby fish in order to gain information about the directionality of the local flow field [18,19].

We investigate the effects of sensory noise and group size on rheotactic performance using a mathematical model of coupled phase oscillators based on the Kuramoto model [25]. Originally developed in physics, the Kuramoto model has been adopted in neuroscience to investigate neural control and information processing [27]. It has also been applied to the study of collective behavior in biological groups [28,29]. Phase oscillator models have motivated studies on stability analysis [30,31] and stabilization of planar collective motion [32,34]. Mahmoudian and Paley [35] investigated phase synchronization in the presence of bounded noise, based on earlier work studying noisy consensus [36].

In cooperative control theory, synchronization differs from consensus in the following sense: consensus takes place in a Euclidean space, such as the real line, whereas synchronization takes place in a non-Euclidean space, such as the circle. Synchronization is connected to the biologically relevant behaviors of alignment and rheotaxis in fish because these quantities are described by phase angles, and a phase angle is a point on a circle. In collective behavior, each fish synchronizes its orientation with that of its neighbors, so that the school heads in a common direction. In rheotaxis, individuals also synchronize with the direction of the flow.

We expand on our current understanding of the factors governing rheotaxis in flow, and on taxis in uncertain environments, by investigating synchronization of particles with sensory noise, in the context of fish behavior in a flow field. In the model, each individual obtains measurements of the relative orientation of other individuals as well as the relative orientation of an external reference direction, the flow. Sensory noise is represented by the uncertainty in each individual’s measurements. We vary the level of sensory noise, as well as the group size. Monte Carlo simulations numerically illustrate the influence of sensory noise and group size on internal (i.e., within the school) and external (i.e, with the flow) disagreement in orientation. We find that in high noise conditions, the use of neighbor cues and group size improves rheotactic behavior. By relating the model to biological processes, we generate testable predictions about fish behavior.

The contributions of this work are (1) the extension of a noisy, non-Euclidean synchronization model to include a reference direction and unbounded sensory noise; and (2) investigation of the influence of sensory noise and group size on synchronization, using novel measures of internal and external disagreement. The model generates testable experimental predictions, that may have implications for fish ecology, collective behavior, and flow sensing. While this study emphasizes schools of fish, the general model framework may be applied to other animal and engineered collectives.

2 Methods

Noisy synchronization model

Starting with random initial phases drawn from a uniform distribution on the circle, each individual gathers measurements of the relative direction of the reference direction and of its neighbors’ relative phases to determine the change in its own orientation. The measurements obtained by each individual contain additive sensory noise.

Consider a network [37] of N phase angles indexed by k = 1, …, N and coupled via an all-to-all, undirected communication graph 𝒢 = (𝒩, ℰ) with nodes 𝒩 = {1, …, N} and edges (l, k) ∈ ℰ ⊆ 𝒩 × 𝒩 such that the graph 𝒢 satisfies (l, k) ∈ ℰ for all l ≠ k. In the absence of noise, these angles synchronize with one another and with the reference direction; their dynamics are modeled below as a stochastic difference equation [38,39]. The reference direction is a special node in the graph, associated with the index k = 0 and, without loss of generality, is fixed at zero radians.

In order to sample sensory noise on the circle, we use a von Mises (VM) distribution [40]. A normal gaussian distribution when placed on the circle would lead to overlapping tail ends, increasing the probability of extreme values being selected. Thus, a distribution meant for the circle should be used. The two main options used are the wrapped Gaussian or the von Mises, which is a close approximation of the wrapped Gaussian, avoids overlapping tails, and is straightforward to implement. A VM distribution is characterized by its mean and concentration, σ^kl (roughly, the reciprocal of variance). The noise concentration depends of the values of k and l such that

$${\sigma }^{kl}=\{\begin{array}{ll}{\sigma }^0\hfill & \text{when}k=0,\hfill \\ 0\hfill & \text{when}k=l,\text{and}\hfill \\ \sigma \hfill & \text{otherwise}.\hfill \end{array}$$ (1)

Figure 1 illustrates three VM distributions with low, moderate, and high sensory noise, respectively. When individual k compares its orientation to the reference direction, the noise is sampled from a VM distribution with concentration σ⁰, and when fish k compares its orientation to another individual, the sensory noise is sampled with concentration σ. Sensory noise may be higher when visibility is poor [41] or if bulk flow interferes with inter-individual communication [42].

Fig. 1.

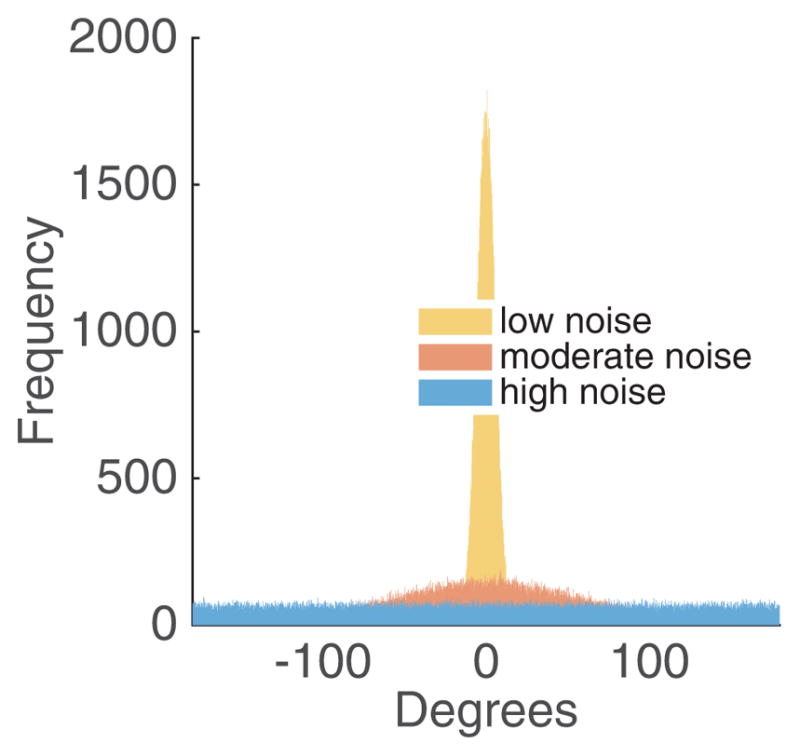
Example von Mises distributions with concentration values 10², 10⁰ and 10⁻².

Let t represent the discrete time index. The orientation of individual k at time t is denoted by ${\theta }_t^k$, k = 0, 1, …, N, where ${\theta }_t^0=0$ represents the reference direction. Each orientation is updated according to the following stochastic difference equation:

$${\theta }_{t+1}^k={\theta }_t^k+\sum _{l=0}^N{\kappa }^{kl}sin({\theta }_t^l-{\theta }_t^k+{\omega }_t^{kl}),$$ (2)

where ${\omega }_t^{kl}$ represents the sensory noise value at time t with concentration value σ^kl as above and κ^kl is the coupling gain between pair k and l. Note that the sine term linearizes to ${\theta }_t^l-{\theta }_t^k+{\omega }_t^{kl}$ when that term is sufficiently small.

The gain κ^kl is of importance for the synchronization behavior of the model (2) [25]. Namely, κ^kl > 0 yields synchronization and κ^kl < 0 yields incoherent behavior. Here we specify κ^kl > 0 to vary based on

$${\kappa }^{kl}=\{\begin{array}{ll}{\kappa }^0\hfill & \text{when}l=0,\hfill \\ 0\hfill & \text{when}l=k,\text{and}\hfill \\ \kappa \hfill & \text{otherwise}.\hfill \end{array}$$ (3)

The values κ⁰ and κ are coupled according to Nκ + κ⁰ = 1, so that as group size N increases, the influence of each neighbor decreases. We investigate several cases of κ⁰ and κ values: for κ⁰ = 1, there is no influence of the neighbors; for κ⁰ = 1/2, the influence of the reference direction is equal to that of all neighboring fish; for κ⁰ = 0, there is no influence of the reference direction, for κ⁰ = 1/3 there is slight preference for neighbors, and for κ⁰ = 2/3 there is preference for the reference direction.

Table 1 summarizes the model parameters. Each parameter combination was run for 500 Monte Carlo trials and each trial ran for 2,000 time steps. The University of Maryland supercomputing resources were used to conduct the research in this paper. Running through all group sizes for one parameter set takes twenty-four hours or more.

Table 1.

Summary of Model Parameters.

Model parameter	Symbol	Values
Group size	N	2, 4, 8, 16, 32, 64, 128
Conc., flow	σ0	102, 100, 10−2 rad.
Conc., neighbors	σ	102, 100, 10−2 rad.
Gain, flow	κ0	0, 1, $\frac{1}{2},\frac{1}{3},\frac{2}{3}$

Measures of model performance

In the coupled oscillator model introduced by Kuramoto (1975) [25], synchrony is quantified using a complex-phase order parameter $p_{\theta }\triangleq \frac{1}{N}{\sum }_{k=1}^N{e}^{i{\theta }^k}$, where i is the imaginary unit. The magnitude |p_θ| ranges from zero to one in proportion to the level of alignment, where |p_θ| = 1 is synchronized. (The magnitude of p_θ is also called vector strength [25]; the orientation of p_θ indicates the average orientation.) In the stochastic consensus literature [26], the following definition is used to characterize the asymptotic behavior in weak consensus: $\mathbb{E}{\mid {\theta }_t^k\mid }^2<\infty$ for all t and k and ${lim}_{t\to \infty }\mathbb{E}{\mid {\theta }_t^k-{\theta }_t^l\mid }^2=0$ for all pairs k, l, where 𝔼 is the expected-value operator.

Existing measures of polarization and weak consensus vary over time. Additionally, the roots of a complex number are multi-valued, as seen in the simple example of $z^{1/2}=\pm \sqrt{z}$. In order to achieve a single difference between two angles, we introduce two alternative measures of disagreement in orientation, based on chord length on the unit circle. To compute ED and ID, we use the median statistic, because the distribution of chord lengths was highly skewed, and the median captures highly skewed or bimodal data better than other statistics such as the mean or mode. The internal disagreement (ID) measure quantifies the median level of disagreement within the school, and the external disagreement (ED) measure quantifies the median level of disagreement between each fish and the reference direction. In behavioral terms, ID pertains to schooling behavior and ED to rheotaxis.

Let $z_T^{k,l}\triangleq \mid e^{i{\theta }_T^l}-e^{i{\theta }_T^k}\mid /2\in [0,1]$, where T is a sufficiently large time such that weak consensus is reached. The orientation ${\theta }_T^k$ of fish k at time step T is converted to $e^{i{\theta }_T^k}$, a complex unit phasor. When taking the difference between two angular values, there is no unique answer, thus the chord length is used instead. The value $z_T^{k,l}$ is half of the chord length between points $e^{i{\theta }_T^l}$ and $e^{i{\theta }_T^k}$ on the unit circle; the maximum chord length equals two.

For ID, we take the median of $z_T^{k,l}$ over all pairwise differences in orientation within each trial, ${\stackrel{\sim }{Z}}_T=\text{median}\{z_T^{1,2},z_T^{1,3}\dots ,z_T^{1,N},z_T^{2,2},z_T^{2,3},\dots ,z_T^{N-1,N}\}$. For ED, we compute ${\stackrel{\sim }{Z}}_T^0=\text{median}\{z_T^{0,1},z_T^{0,2},\dots ,z_T^{0,N}\}$. The number of values in the ID set is (N² − N)/2 and, in the ED set, N. Let ^mZ̃_T denote the median disagreement in synchronization for Monte Carlo trial m. The ID value is the median disagreement in orientation over all Monte Carlo trials, i.e., ID = median{¹Z̃_T, ²Z̃_T, …, ^MZ̃_T}. Similarly, the ED value is $ED=\text{median}\{{{}^1\stackrel{\sim }{Z}}_T^0,\dots ,{{}^M\stackrel{\sim }{Z}}_T^0\}$.

3 Results

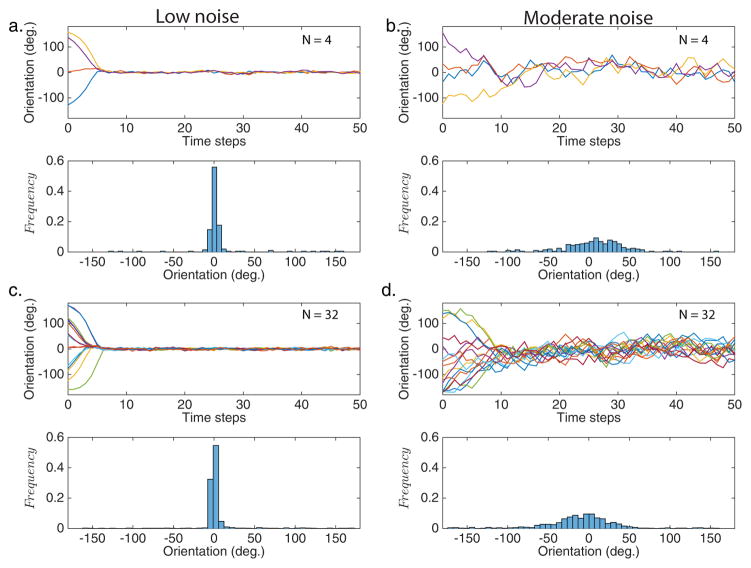
We plot the results from four typical trials to illustrate the time course of each phase angle. Figure 2 shows the orientations over time, as well as the histogram of orientation distributions for the entire trial. Figures 2a,c depict the case when there is low noise in both the neighbor orientation and the reference direction; the group size is N = 4 and 32, respectively. Both of these simulations show strong alignment with the reference direction. Figure 2b,d shows simulations with moderate noise (σ⁰ = σ = 10⁰) in both the reference direction and in neighbor orientation. In these trials, there is no qualitative difference in synchronization based on group size.

Fig. 2.

Typical runs (N=4, N=32) in the presence of low noise, σ = σ⁰ = 10² (a,c) and moderate noise, σ = σ⁰ = 10⁰ (b,d).

No gain on reference direction

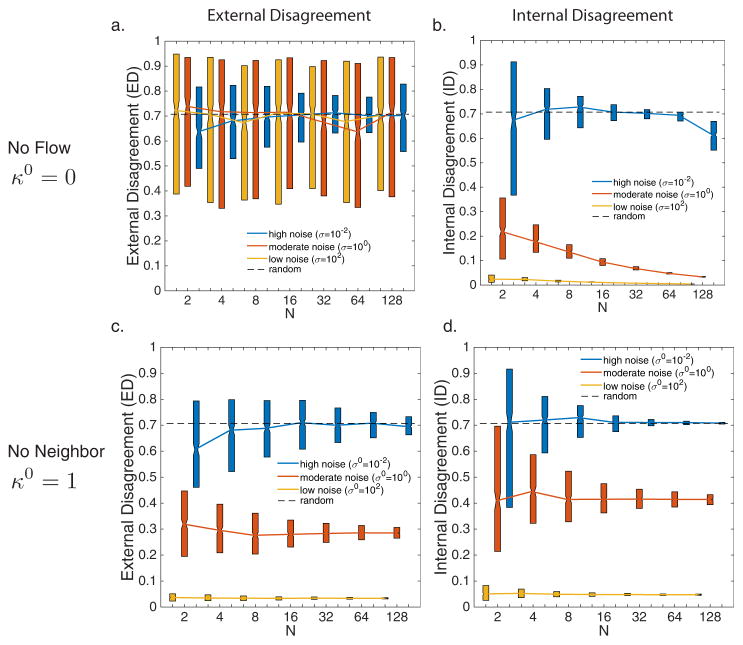
When κ⁰ = 0, the reference direction is ignored. Figures 3a,b show the internal and external disagreement measures under various levels of neighbor noise (σ = 10², σ = 10⁰, and σ = 10⁻²). With no gain on the reference direction, individuals rheotact at chance levels (the disagreement in orientation on the circle for random values is 0.7), no matter what the noise is in neighbor orientation (Fig. 3a). Internal disagreement decreases as group size increases in the presence of moderate sensory noise (Figure 3b, orange (white in print)).

Fig. 3.

(a,b) Synchronization results when the gain on flow is zero (κ⁰ = 0). (c,d) Gain on neighbors is zero (κ⁰ = 1). (a,c) ED and (b,d) ID, over all group sizes, N and noise values. Noise values are as follows: (a,b) σ = 10² and (c,d) σ⁰ = 10² (yellow online, grey in print), (a,b) σ = 10⁰ and (c,d) σ⁰ = 10⁰ (orange online, white in print), and (a,b) σ = 10⁻² and (c,d) σ⁰ = 10⁻² (blue online, black in print). Length of bars represent the upper and lower quartiles.

No gain on neighbor orientation

When κ = 0, neighbor orientation is ignored. Figures 3c,d depict the internal and external disagreement measures under various levels of noise in the reference direction (σ⁰ = 10², σ⁰ = 10⁰, and σ⁰ = 10⁻²). External and internal disagreement values increase with increasing noise levels, indicating reduced synchronization. Although there is no effect of group size on either ED or ID, performance on both measures is better than chance, because all individuals have knowledge of the reference direction.

Equal gain on reference direction and neighbor orientation

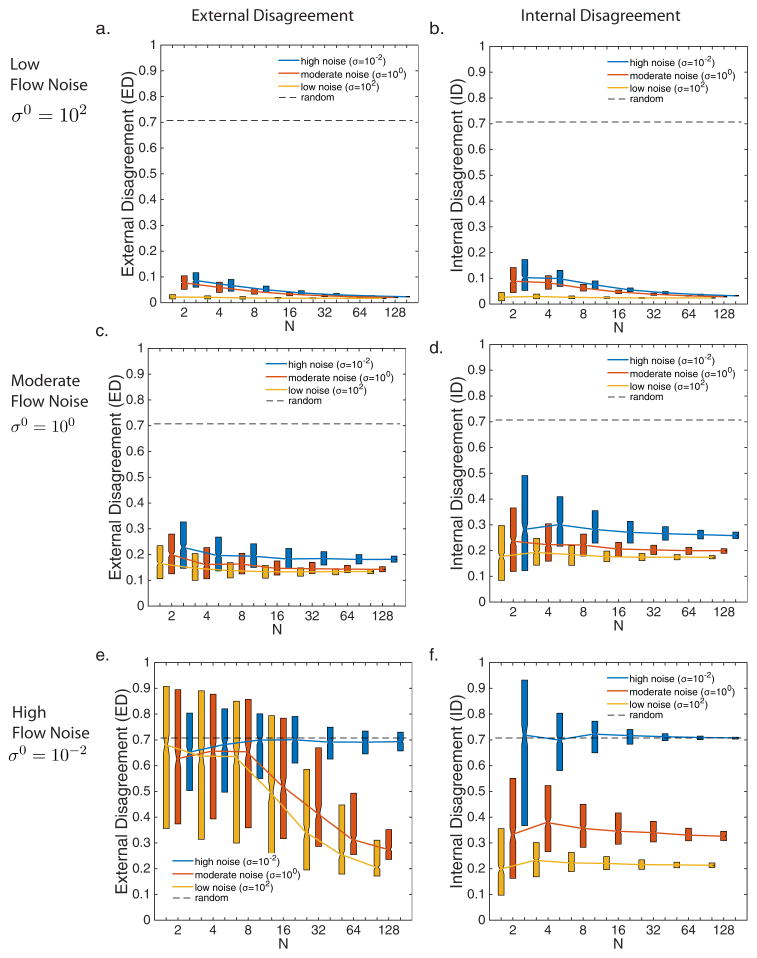
When κ⁰ = 1/2 (i.e., the influence of the reference direction equals that of all neighbors), we organize results based on the noise in the reference direction and assess how group size and noise in neighbor orientation affect the ED and ID values. There is no effect of group size when there is low noise in both the reference direction and neighbor orientation (Figs. 4a,b yellow (grey in print)). However, when there is low noise in the reference direction, and moderate to high noise in neighbor orientation (Figs. 4a,b orange (white in print) and blue (black in print)), the ED and ID values decrease with increasing group size, N. When there is moderate noise in the reference direction, there is a slight decrease in ED and no significant difference in ID values with increasing group size (Figs. 4c,d). Both ED and ID values decrease with decreasing noise levels in neighbor orientation. When there is high noise in the reference direction (Figs. 4e,f), there is a decrease in ED with increasing group size for all values of neighbor orientation noise, σ, but no difference in the ID values. Both ED and ID values decrease with decreasing noise levels in neighbor orientation.

Fig. 4.

The effect of group size on synchronization results when there is both neighbor and flow information (κ⁰ = 1/2) for low (a,b), moderate (c,d) and high (e,f) flow noise levels and for low (yellow online, grey in print), moderate (orange online, white in print) and high (blue online, black in print) levels of neighbor noise within each of these flow noise conditions. Length of bars represent the upper and lower quartiles.

Higher gain on neighbor orientation

When κ⁰ = 1/3 the results appear almost identical to the results of κ⁰ = 1/2. Agents have a slightly higher gain on neighbor orientation than the reference direction. When there is low to moderate noise in the reference direction and low noise in neighbor orientation, there is no effect of group size. When there is moderate to high neighbor noise, the ID and ED values decrease with increasing group size, N. The effect of group size in these cases is most prominent at the lowest group sizes. Both ED and ID values decrease with decreasing noise levels in neighbor orientation. When there is high noise in the reference direction, there is a decrease in ED with increasing group size for all values of neighbor orientation noise, σ, with the largest effects occurring when there is low to moderate noise in neighbor orientation. Both ED and ID values decrease with decreasing noise levels in neighbor orientation.

Higher gain on the reference direction

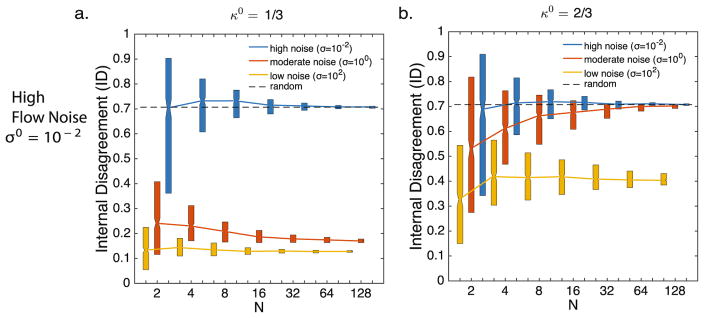
When κ⁰ = 2/3 the agents have a slightly higher gain on the reference direction than on neighbor orientation. When there is low to moderate noise in the reference direction, there is little to no effect of group size. Both ED and ID values decrease with decreasing noise levels in neighbor orientation. When there is high noise in the reference direction, there is a decrease in ED with increasing group size N only when there is the lowest value of neighbor orientation noise, σ. When there is moderate and high neighbor noise the ED values are mostly random. Conversely, the ID values increase with increasing group size with low to moderate noise in neighbor orientation, especially at lower group sizes. This is shown next to the ID values of κ⁰ = 1/3 for comparison (Fig. 5).

Fig. 5.

The effect of group size on internal disagreement (ID) when there is a slight preference for neighbor orientation (κ⁰ = 1/3) (a), or a slight preference for the reference direction (κ⁰ = 2/3) (b) in the presence of high flow noise (σ⁰ = 10⁻²). Low (yellow online, grey in print), moderate (orange online, white in print) and high (blue online, black in print) levels of neighbor noise is shown for each condition. Length of bars represent the upper and lower quartiles.

4 Discussion

Grünbaum [12] quantitatively demonstrated the effect of the many-wrongs principle [43], which states that inherent noise in a system may be damped out through multiple samples. Our results demonstrate the effects of social information on rheotaxis, a simple yet robust behavior found in fish and invertebrates. We find potential limitations of the many-wrongs principle, in the extreme cases when the individuals are randomly aligned (for very high noise) or perfectly aligned social information does not improve taxis. Additionally, when there is higher gain on a noisy reference direction and moderate to high noise in neighbor orientation, as the group size increases, rheotaxis does not improve and school alignment decreases. By introducing noise in intra-school signaling as well as in an external reference, we investigate the relative roles of each cue.

We find that (i) under environmentally plausible conditions, the use of neighbor cues in groups improves rheotactic behavior; (ii) this improvement is limited to cases when there is high sensory noise in sensing either the flow direction or neighbor cues; and (iii) when there are external cues about the flow, fish align with each other, and the addition of neighbor cues do not improve intra-school alignment.

This work extends the engineering results of [35] by analyzing weak consensus on the N-torus with additive noise. The contributions of the previous work were analytical solutions to weak consensus on the N-torus with additive noise bounded by π/2. We elaborate on this finding by numerically testing weak synchronization with unbounded noise levels, and find that with unbounded noise, individuals may still reach weak synchronization.

Effect of sensory noise on synchronization

When individuals have reliable information regarding the direction of the flow (which we take to be the reference direction), group size does not affect synchronization. However, when information regarding the flow direction is noisy, increasing group size improves synchronization to the flow. This result suggests that rheotacting fish may rely more on social information when their own information is uncertain. It has been previously shown that there may be costs to socially acquired information [44,46,47], thus when personal information is more accurate (i.e., when fish perceive the external or flow environment accurately), there may be a detriment to relying on noisy neighbor information. There is also some evidence that behaviors can change adaptively based on environmental context, including dynamically changing interactions between individuals [13,48,49].

Rheotaxis is a robust and multi-sensory behavior [50]. However, the contribution of different sensory modalities to rheotactic behavior may vary by species’ ecology. For example, fish in murky environments may rely more on other sensory modalities in order to compensate for the noisy visual information [41]. This idea could be tested experimentally using a comparative study with species of schooling fish from different habitats, or by experimentally manipulating available cues, e.g., by conducting experiments in the dark or by temporarily blocking the lateral line [51,52].

Effect of group size on synchronization

The results of this paper rely on the assumptions that there is all-to-all communication between identical individuals. Neither assumption is realistic. Although we have chosen to investigate the all-to-all interaction case, in part to match the assumptions laid out by [35], the model described here is applicable to limited interaction topologies as well [32]. Other potential directions for future research would be to investigate the case when noise values are correlated between connected individuals [53], of limited and/or time-varying interaction networks and non-independent estimates of flow direction across individuals.

Group size made the most significant improvement in our rheotaxis model when there was high noise in sensing the flow. In this case, having information from many neighbors significantly improved synchronization to the reference direction when compared to the asocial case (Figs. 3c,d), where individuals with no neighbor information orient to the reference direction at chance levels. Once the group size increases past N = 8, there is a significant effect of group size on improving rheotactic performance (Fig. 4e). Based on these results, group size has the largest benefit to schools in noisy conditions. Testing this hypothesis experimentally may yield additional insights into the roles of multi-sensory integration and group behavior in rheotaxis.

Ongoing and future work

We numerically demonstrate that weak synchronization occurs in the presence of noise, under the assumptions of an all-to-all, undirected graph. It would be interesting to perform numerical and analytical solutions when these assumptions do not hold. Skardahl et al. (2015) investigated frustrated and heterogenous networks in which synchronization is likely to erode. By characterizing the conditions that lead to the erosion of synchronization, it may be possible to mitigate these effects in both natural and unmanned systems. In biology, hypotheses may be generated when a synchronized group of fish or other animals may dissolve or break apart. Ongoing work will further test the limits of synchronization when applied to biological groups, including heterogenous networks and incomplete, directed and/or time-varying networks.

For future research involving group dynamics, it may also be interesting to explore associative memory models [54] (in addition to heterogenous populations), such that agents can dynamically associate with the other connected agents. It has been well established that fish can recognize and preferentially associate with certain individuals. Thus, a dynamic, heterogenous graph may be formed based on a memory of which agents have better knowledge of the reference direction.