A Robust and Efficient Curve Skeletonization Algorithm for Tree-Like Objects Using Minimum Cost Paths

Abstract

Conventional curve skeletonization algorithms using the principle of Blum’s transform, often, produce unwanted spurious branches due to boundary irregularities, digital effects, and other artifacts. This paper presents a new robust and efficient curve skeletonization algorithm for three-dimensional (3-D) elongated fuzzy objects using a minimum cost path approach, which avoids spurious branches without requiring post-pruning. Starting from a root voxel, the method iteratively expands the skeleton by adding new branches in each iteration that connects the farthest quench voxel to the current skeleton using a minimum cost path. The path-cost function is formulated using a novel measure of local significance factor defined by the fuzzy distance transform field, which forces the path to stick to the centerline of an object. The algorithm terminates when dilated skeletal branches fill the entire object volume or the current farthest quench voxel fails to generate a meaningful skeletal branch. Accuracy of the algorithm has been evaluated using computer-generated phantoms with known skeletons. Performance of the method in terms of false and missing skeletal branches, as defined by human experts, has been examined using in vivo CT imaging of human intrathoracic airways. Results from both experiments have established the superiority of the new method as compared to the existing methods in terms of accuracy as well as robustness in detecting true and false skeletal branches. The new algorithm makes a significant reduction in computation complexity by enabling detection of multiple new skeletal branches in one iteration. Specifically, this algorithm reduces the number of iterations from the number of terminal tree branches to the worst case performance of tree depth. In fact, experimental results suggest that, on an average, the order of computation complexity is reduced to the logarithm of the number of terminal branches of a tree-like object.

1. INTRODUCTION

Skeletonization provides a simple and compact representation of an object while capturing its major topologic and geometric information (Blum, 1967; Lam et al., 1992; Siddiqi and Pizer, 2008; Saha et al., submitted). The notion of skeletonization was initiated by Blum’s pioneering work on grassfire transform (Blum, 1967; Blum and Nagel, 1978) and has been applied to many image processing and computer vision applications including object description, retrieval, manipulation, matching, registration, tracking, recognition, compression etc. Following Blum’s grassfire propagation the target object is assumed to be a grass-field that is simultaneously lit at its entire boundary. The fire burns the grass-field and propagates inside the object at a uniform speed and the skeleton is formed by quench points, where independent fire fronts collide (Leymarie and Levine, 1992; Sanniti di Baja, 1994; Kimia et al., 1995; Kimmel et al., 1995; Siddiqi et al., 2002; Giblin and Kimia, 2004; Siddiqi and Pizer, 2008). Different computational approaches for skeletonization are available in literature, some of which are widely different in terms of their principles (Tsao and Fu, 1981; Arcelli and Sanniti di Baja, 1985; Leymarie and Levine, 1992; Lee et al., 1994; Saha and Chaudhuri, 1994; Sanniti di Baja, 1994; Kimia et al., 1995; Kimmel et al., 1995; Ogniewicz and Kübler, 1995; Saha et al., 1997; Palágyi and Kuba, 1998; Palágyi and Kuba, 1999; Siddiqi et al., 2002; Giblin and Kimia, 2004; Siddiqi and Pizer, 2008; Arcelli et al., 2011; Németh et al., 2011). Several researchers have used continuous approaches to compute skeletons (Leymarie and Levine, 1992; Kimia et al., 1995; Kimmel et al., 1995; Ogniewicz and Kübler, 1995; Siddiqi et al., 2002; Giblin and Kimia, 2004; Hassouna and Farag, 2009) while others have used purely digital methods (Tsao and Fu, 1981; Lee et al., 1994; Saha and Chaudhuri, 1994; Sanniti di Baja, 1994; Saha et al., 1997; Palágyi and Kuba, 1998; Palágyi and Kuba, 1999; Németh et al., 2011). Discussion on different principles of skeletonization algorithms has been reported by Siddiqi and Pizer, 2008, and Saha et al., submitted.

Digital skeletonization algorithms simulate Blum’s grass-fire propagation using iterative erosion (Tsao and Fu, 1981; Lam et al., 1992; Lee et al., 1994; Saha and Chaudhuri, 1996; Palágyi and Kuba, 1999; Németh et al., 2011) or geometric analysis (Arcelli and Sanniti di Baja, 1985; Sanniti di Baja, 1994; Pudney, 1998; Borgefors et al., 1999; Bitter et al., 2001; Arcelli et al., 2011) on digital distance transform (DT) field (Borgefors, 1984, 1986). In three-dimensions (3-D), a Blum’s skeleton is a union of one- and two-dimensional structures, which is referred to as a surface skeleton. However, many 3-D objects consist only of one-dimensional (1-D) elongated structures, e.g., vascular or airway trees, for which the target skeleton is a tree of 1-D branches; such skeletons are referred to as curve skeletons. There are several dedicated skeletonization algorithms, called curve skeletonization, which directly compute curve skeletons from 3-D objects (Sonka et al., 1994; Bitter et al., 2001; Greenspan et al., 2001; Wink et al., 2004; Hassouna et al., 2005; Soltanian-Zadeh et al., 2005; Serino et al., 2010) These algorithms have been broadly applied in animation (da Fontoura Costa and Cesar Jr, 2000; Wade and Parent, 2002), decomposition of objects (Serino et al., 2014), shape matching (Brennecke and Isenberg, 2004; Cornea et al., 2007), colonoscopy (He et al., 2001; Wan et al., 2002) and bronchoscopy (Mori et al., 2000; Kiraly et al., 2004), stenosis detection (Sonka et al., 1995; Greenspan et al., 2001; Chen et al., 2002; Sorantin et al., 2002; Schaap et al., 2009; Xu et al., 2012), pulmonary imaging (Tschirren et al., 2005; Jin et al., 2014a), micro-architectural analysis of trabecular bone (Saha et al., 2010; Chen et al., 2014) etc. This paper presents a new curve skeletonization algorithm for 3-D fuzzy digital objects using a minimum cost path approach.

Curve skeletonization approaches may be further classified into two major categories, namely, erosion based (Lee et al., 1994; Palágyi and Kuba, 1998; Pudney, 1998; Palágyi and Kuba, 1999; Palágyi et al., 2006) and minimum cost path based approaches. Hassouna and Farag, 2009, presented a different framework to compute the curve skeleton of volumetric objects using level sets and gradient vector flow. The erosion-based curve skeletonization algorithms keep peeling boundary voxels, while preserving object topology and its elongated structures. Pudney, 1998, used DT-based erosion to directly compute the curve skeleton where only curve-end points are preserved to capture elongated structure in a 3-D object. Also, there are a few erosion- or DT-based skeletonization algorithms which compute curve skeletons in two steps (Saha et al., 1997; Arcelli et al., 2011) – computation of surface-skeleton from a 3-D object and then computation of curve skeleton from the surface skeleton. However, the two-steps algorithms are computation less efficient as compared to dedicated algorithms which directly computes curve skeletons from 3-D objects. A major challenge with erosion-based algorithms is the generation of spurious skeletal branches caused by irregularities in object boundaries, image noise, and other digital artifacts. Although, researchers have suggested post pruning algorithms to simplify skeletons (Attali et al., 1997; Saha et al., 2010; Arcelli et al., 2011; Jin and Saha, 2013), often times, the resulting skeletons are still left with some spurious branches. This is because these pruning decisions are primarily based on local features and the global significance of a branch are not fully assessed using local features. Recently, a few curve skeletonization algorithms (Serino et al., 2010) attempted to define global significance of skeletal branches in order to improve the performance of skeletal pruning steps. In contrast, the minimum cost path approach offers a different skeletonization approach, wherein a branch is chosen as a global optimum. Therefore, the global significance of a branch is naturally utilized to distinguish a noisy branch from a true branch improving its robustness in the presence of noisy perturbations on an object.

Peyré et al., 2010, presented a thorough survey on minimum cost path methods and their applications. Minimal cost path techniques have been extensively used for centerline extraction of tubular structures in medical imaging (Cohen, 2001; Deschamps and Cohen, 2001; Wan et al., 2002; Wink et al., 2002; Staal et al., 2004; Cohen and Deschamps, 2007). These techniques involve deriving a cost metric (Cohen and Kimmel, 1997) from the image in a way such that minimal paths correspond to the centerline of a tubular structure. Li and Yezzi, 2007 developed a novel approach to simultaneously extract centerlines as well as boundary surfaces of 3-D tubular objects, e.g., vessels in MR angiography or CT images of coronary arteries, using a minimal path detection algorithm in 4-D, where the fourth dimension represents the local vessel diameter. Wong and Chung, 2007 presented another algorithm where they, first, traced the vessel axis on a probabilistic map from a gray-scale 3-D angiogram and, subsequently, delineated the vessel boundary as a minimum cost path on a weighted and directed acyclic graph derived from cross-sectional images along the vessel axis. However, such methods connects specified end points to a source point but are not designed for computation of 3-D curve skeletons. Bitter et al., 2001, presented an algorithm to compute a complete curve skeleton of a 3-D object using the minimum cost path approach. However, there are several major drawbacks and limitations and of their method, which restrict the use of minimum cost path as a popular curve skeletonization approach. These drawbacks and limitations of the previous method together with their solutions are discussed in the following.

In this paper, a comprehensive and practical solution is presented for direct computation of curve skeletons from 3-D fuzzy digital objects using a minimum cost path approach. Central challenges for curve skeletonization using a minimum cost path approach are – (1) assurance of medialness for individual skeletal branches, (2) assessment of branch significance to distinguish a true branch from a noisy one and to determine the termination condition, and (3) computational efficiency. Beside that the new algorithm is generalized for fuzzy objects, it makes major contributions to overcome each of these challenges. To assure medialness of skeletal branches, Bitter et al., 2001, suggested a penalized distance function that uses several ad-hoc and scale-sensitive parameters. However, as demonstrated in this paper, their method inevitably fails to stick to the medial axis, especially at sharp turns or large scale regions. Also, their parameters are scale-sensitive, which need to be tuned for individual objects depending on their scales. These limitations of their cost function are further exaggerated for objects containing multi-scale structures, e.g., airway or vascular trees. To solve this problem, we introduce the application of centers of maximal balls (CMBs) (Sanniti di Baja, 1994) to define path cost that is local scale-adaptive and avoids use of parameters. It can be shown that, for a compact object in R³, a minimum cost path using the new approach always sticks to the Blum’s skeleton. Moreover, in the previous approach a skeletal branch is extended up to an object boundary which contradicts Blum’s principle at a rounded surface whereby the branch of a Blum’s skeleton ends to a CMB prior to reaching an object boundary. The new method overcomes this difficulty by selecting the farthest CMB instead of object boundary points while adding a new skeletal branch. In regards to the second challenge, a local scale component is introduced while deciding the next most-significant skeletal branch, which makes a major improvement in discriminating among spurious and true branches. Finally, to reduce computational demand, a new algorithm is presented that allows simultaneous addition of multiple independent skeletal branches reducing the computational complexity from the order of the number of terminal branches to the worst-case performance of the order of tree-depth.

2. Methods and algorithms

Basic principle of the overall method is described in Section 2.1. Three major steps in the algorithm, namely, skeletal branch detection, object volume marking, and termination criterion, are described in Sections 2.2, 2.3, and 2.4, respectively. Improvements in computation performance using the new algorithm is discussed in Section 2.5. A preliminary version of our work was presented in a conference paper (Jin et al., 2014b).

2.1. Basic Principle

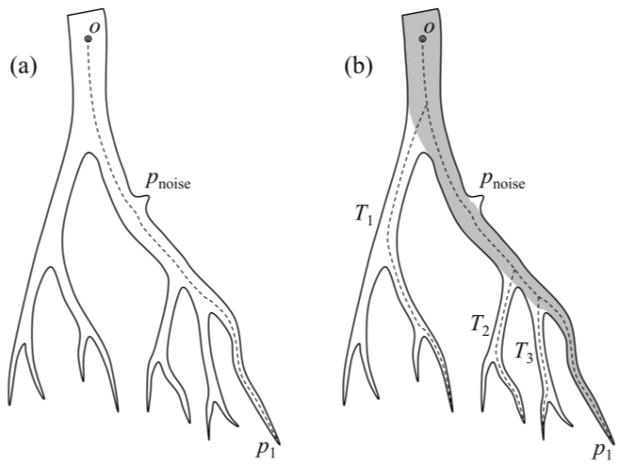
Conventional curve skeletonization algorithms are designed on the principle of Blum’s grassfire transform implemented using voxel erosions, which is subjected to constraints for preservation of object topology and local “elongatedness”. Generally, voxel erosion is controlled by local properties, limiting the use of larger contextual information while selecting the end point of a skeletal branch during the erosion process. Therefore, such methods often suffer from an intrinsic challenge while handling noisy structures or boundary irregularities, e.g., the small protrusion, denoted as p_noise in Fig. 1. The new method works for 2-D or 3-D tree-like objects (e.g., vascular or airway trees), which are simply-connected without tunnels or cavities (Saha et al., 1994; Saha and Chaudhuri, 1996). The method starts with a root voxel, say o, as the initial seed skeleton, which is iteratively grown by finding the farthest CMB and then connecting it to the current skeleton with a new branch. The iterative expansion of the skeleton continues until no new meaningful branch can be found. During the first iteration, the method finds the farthest CMB p₁ from the current skeleton o. Next, the skeleton is expanded by adding a new skeletal branch joining p₁ to the current skeleton. This step is solved by finding a minimum cost path from o to p₁ (see Fig. 1a). Here, it is important that the cost function should be chosen such that the minimum cost path runs along the centerline of the object and a high cost is applied when it attempts to deviate from the centerline. After the skeletal branch op₁ is found, the representative object volume is filled using a local scale-adaptive dilation along the new branch and marked as shown in Fig. 1b. In the next iteration, three skeletal branches are added where each branch connects the farthest CMB in one of the three sub-trees T₁, T₂, and T₃ in the unmarked region. Then the marked object volume is augmented using dilation along the three new skeletal branches. This process continues until no new meaningful branch can be found. Fig. 2 presents a color-coded illustration of the marked object volume corresponding to the branches located at different iterations.

Fig. 1.

Schematic illustration of the new curve skeletonization algorithm. (a) The algorithm starts with the root point o as the initial skeleton and finds the farthest CMB p₁. Next, p₁ is connected to the skeleton with the branch op₁ computed as a minimum cost path. (b) The object volume corresponding to the current skeleton is marked (gray region) and the three skeletal branches are added where each branch connects the farthest CMB in one of the three sub-trees T₁, T₂, and T₂ in the unmarked object region. Note that the noisy protrusion p_noise does not create any noisy branch even after all meaningful branches are added to the skeleton.

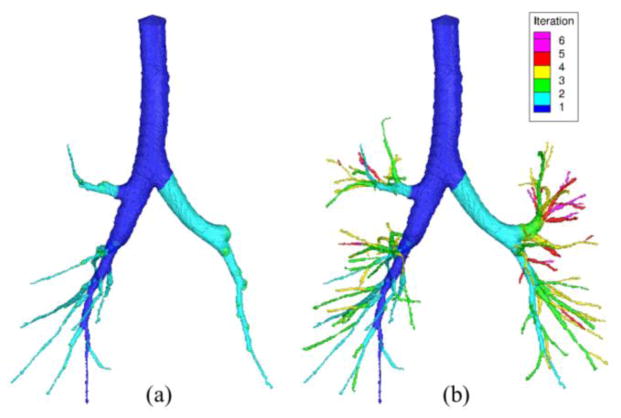
Fig. 2.

Results at different iteration of the new curve skeletonization algorithm. (a) The marked object volume on a CT-derived human intrathoracic airway tree corresponding to the skeletal branches computed after two iterations. (b) Same as (a) but at the terminal iteration.

An important feature of the new method is that the meaningfulness of an individual skeletal branch is determined by its global context. Therefore, the method is superior in stopping noisy branches. Also, the minimum cost path approach improves the smoothness of skeletal branches. Finally, depending upon the application, the initial root point may be automatically detected, e.g., (1) the point with the largest distance transform value, (2) the deepest points on topmost plane in the airway tree etc. Major steps of the algorithm are outlined in the following.

Begin Algorithm: compute-curve-skeleton

Input: the original object volume O

Output: curve skeleton S

Initialize a root voxel o as the current skeleton S and the current marked object volume Omarked

While new branches are found

Detect disconnected sub-trees T1, T2, T3, ··· in the unmarked object volume O − Omarked

For each sub-tree Ti

Find the CMB voxel vi ∈ Ti that is farthest from Omarked

If the potential branch from vi to Omarked is significant

Add a new skeletal branch Bi joining vi to the current skeleton S using a minimum cost path

Augment S = S ∪ Bi

Compute local scale-adaptive dilatation Di along Bi

Augment Omarked = Omarked ∪ Di

End Algorithm: compute-curve-skeleton

In this paper, Z³ is used to denote a cubic grid where Z is the set of integers. An element p ∈ Z³ of the grid is referred to as a voxel. A fuzzy digital object 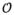= {(p, 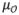(p)) | p ∈ Z³} is a fuzzy subset of Z³, where 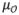: Z³ → [0,1] is the membership function. The support O of 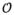is the set of voxels with non-zero membership values, i.e., O = {p | p ∈ Z³ ∧ 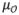(p) ≠ 0}. A voxel inside the support is referred to as an object voxel. Let 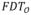(p), where p ∈ O, denote the fuzzy distance transform (Saha et al., 2002) at an object voxel p.

Sanniti di Baja, 1994, introduced the seminal notion of center of maximal ball (CMB) and counselled their use as quench voxels in a binary image. Here, we use fuzzy centers of maximal balls (fCMBs) as quench voxels in a fuzzy digital object. An object voxel p ∈ O is a fuzzy center of maximal ball (fCMB) in 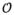if the following inequality holds for every 26-neighbor q of p

$$\mathit{FDT}(q)-\mathit{FDT}(p)<\frac{1}{2}({\mu }_{\mathcal{O}}(p)+{\mu }_{\mathcal{O}}(q))\mid p-q\mid .$$ (1)

Saha and Wehrli, 2003, introduced the above definition of fCMB which was further studied by Svensson, 2008. Also, it may be noted that the definition of fCMB is equivalent to the CMB (Sanniti di Baja, 1994) for binary digital objects.

For fuzzy objects, quench voxels are sensitive to noise generating a highly redundant set. Therefore, it is imperative to use a local significance factor (LSF) (Jin and Saha, 2013), a measure of collision impact by independent fire-fronts, to distinguish among strong and weak quench voxels. LSF of an object voxel p ∈ O in a fuzzy digital object 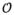is defined as:

$$\mathit{LSF}(p)=1-f_{+}\left(\underset{q\in N^{\ast }(p)}{max}\frac{\mathit{FDT}(q)-\mathit{FDT}(p)}{\frac{1}{2}\left({\mu }_{\mathcal{O}}(p)+{\mu }_{\mathcal{O}}(q)\right)\mid p-q\mid }\right),$$ (2)

where f₊(x) returns the value of x if x > 0 and zero otherwise; and N*(p) is the excluded 26-neighborhood of p. It can be shown that LSF at a quench voxel lies in the interval of (0,1] and it takes the value of ‘0’ value at non- quench voxels. A quench voxel with LSF value greater than 0.5 will be called a strong quench voxel.

2.2. Skeletal Branch Detection

During an iteration of the new algorithm, multiple meaningful skeletal branches are added to the current skeleton where each branch comes from a connected sub-tree T_i in the unmarked object volume O − O_marked. Let 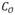⊂ O be the set of all strong quench voxels in the fuzzy digital object 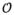. To locate the branch-end voxel in each sub-tree T_i, the geodesic distance (GD) from O_marked is computed for each voxel in 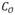∩ T_i. A path π = 〈 p₀, p₁, ···, p_l−1〉 is an ordered sequence of voxels where every two successive voxels p_i−1, p_i ∈ Z³ | i = 1, ···, l − 1, are 26-adjacent. The length of a path π is defined as

$$\mathit{length}(\pi )=\sum _{i=1}^{l-1}\mid p_{i-1}-p_i\mid .$$ (3)

The geodesic distance or GD of a voxel p ∈ 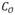∩ T_i from O_marked is computed as:

$$GD(p)=\underset{\pi \in {\mathit{\Pi }}_p}{min}\mathit{length}(\pi ),$$ (4)

where Π_p is the set of all geodesic paths from p to O_marked confined to O. The branch-end voxel in T_i is selected as farthest (in the geodesic sense) strong quench voxel v_i as follows:

$$v_i=\underset{p\in C_{\mathcal{O}}\cap T_i}{argmax}GD(p).$$ (5)

It may be noted that, unlike the algorithm by Bitter et al., 2001, the above equation ensures that a skeletal branch ends to quench voxel and thus agrees with the Blum’s principle of skeletonization.

To ensure medialness of the skeletal branch, a minimum path cost condition is imposed and the LSF measure is used to define the path-cost. First, the step-cost between two 26-adjacent voxels p, q ∈ Z³ is defined as:

$$SC(p,q)=\frac{\mid p-q\mid }{\mathrm{\epsilon }+{(\text{average}(\mathit{LSF}(p)+\mathit{LSF}(q)))}^2},$$ (6)

where the parameter ε is a small number used to overcome numerical computational difficulties. In this paper, a constant value of ‘0.01’ is used for ε. The cost Cost(π) of a path π = 〈p₀, p₁, ···, p_l−1〉 is computed by adding individual step-cost along the path, i.e.,

$$\mathit{Cost}(\pi )=\sum _{i=1}^{l-1}SC(p_{i-1},p_i).$$ (7)

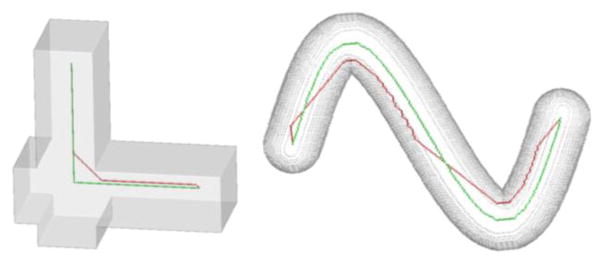
It can be shown that the new path cost function ensures that the minimum cost path between two skeletal points lies on Blum’s skeleton; see the minimum cost path (green) between two points in each of the two shapes in Fig. 3. It is encouraging to note how the new geodesic preserves the sharp corner in the first shape while the minimum cost path function by Bitter et al. fails. In the second shape, the corner cutting by Bitter et al.’s path is obvious while the new geodesic shows a smooth traversal along the centerline of the object. The final task is to connect the selected quench voxel v_i to the current skeleton S using the minimum cost path. In other words, the path B_i connecting v_i to S is computed as:

$$B_i=\underset{\pi \in {\mathit{\Pi }}_{v_i,S}}{argmin}\mathit{Cost}(\pi ),$$ (8)

where Π_viS is the set of all paths between v_i and S confined to O.

Fig. 3.

Illustration of geodesics using the new path-cost function. In the left figure, the new geodesic (green) preserves the sharp corner of the shape while the path (red) by Bitter et al. fails. In the right example, the new geodesic smoothly follows the centerline of the object while Bitter et al.’s path makes several corner cutting.

2.3. Object Volume Marking

The final step during an iteration is to mark the object volume represented by a newly added skeletal branch. After finding the minimum cost path, local volume marking is applied along the new skeletal branch B_i. Specifically, a local scale-adaptive dilation is applied to mark the object region along B_i. The local dilation scale scale(p) at a given voxel p on B_i is defined as twice its FDT value. Efficient computation of local scale-adaptive dilation is achieved along the principle of the following algorithm.

Begin Algorithm: compute-local-scale-adaptive-dilation

Input: support O of a fuzzy object

a skeletal branch Bi

local dilation scale map scale: Bi → R+

Output: Dilated object volume OBi

∀p ∈ Bi, initialize the local dilation scale DS(p) = scale(p)

∀p ∈ O − Bi, initialize dilation scale DS(p) = −max

While the dilation scale map DS is changed

∀p ∈ O − Bi, set DS(p) = maxq∈N*(p) DS(q) − |p − q|

Set the output OBi = {p | p ∈ O ∧ DS(p) ≥ 0}

Augment the marked object volume Omarked = Omarked ∪ OB

End Algorithm: compute-local-scale-adaptive-dilation

2.4. Termination Criterion

As described earlier, the algorithm iteratively adds skeletal branches and it terminates when no more significant skeletal branch can be found. Specifically, the termination is caused by two different situations – (1) the marked volume O_marked covers the entire object, or (2) none of the strong quench voxel in the unmarked region O − O_marked generates a significant branch. The first criterion characterizes the situation when the entire object is represented with skeleton branches and no further branch is needed. The second situation occurs when there are small protrusions left in the unmarked region, however, none of those protrusions warrants a meaningful skeletal branch.

The significance of a branch B_i joining an end voxel v_i ∈ 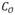∩ T_i to the skeleton S is computed by adding LSF values along the path inside the unmarked region, i.e.,

$$\mathit{significance}(B_i)=\sum _{p\in B_i-O_{\text{marked}}}\mathit{LSF}(p).$$ (9)

A local scale-adaptive significance threshold is used to select a skeletal branch. Let p_v ∈ S be the voxel where the branch B_i joining an strong quench voxel v meets the current skeleton S. The scale-adaptive significance threshold for the selection of the new branch B_i is set as 3 + 0.5 × FDT(p_v).

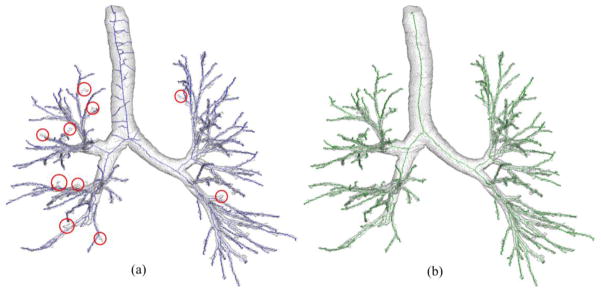
Three important features of the above termination criterion need to be highlighted. First, the significance of a new branch is computed from the current marked object volume instead of the current skeleton. Second, a measure of branch significance is used instead of simple path-length, which elegantly subtracts the portion of a path merely contributing to topological connectivity with little or no significance to object shape. Finally, the new termination criterion uses a scale adaptive threshold for significance. At large-scale object regions, it is possible to visualize a situation where a branch is long enough while failing to become significant under the new criterion. Under such a situation, a large portion of the target branch falls inside the marked object volume resulting in a low significance measure. A scale-adaptive threshold of significance further ensures that such false branch at large scale regions are arrested. Final results of skeletonization for a CT-based human intrathoracic airway tree are shown in Fig. 4b. As it appears visually, the algorithm successfully traces all true branches without creating any false branches as compared to the results using Bitter et al.’s method (Fig. 4a) which creates several false branches while missing quite a few obvious ones (marked with red circles).

Fig. 4.

Comparison of skeletal branch performance between Bitter et al.’s algorithm (a) and the new one (b) on a CT-derived human airway tree. The missing branches are marked with red circles. (a) Bitter et al.’s algorithm generates several noisy skeletal branches while already missing quite a few true branches. (b) Our method neither generates a noisy branch nor misses a visually obvious branch.

2.5. Computational Complexity

The computational bottleneck of the minimum cost path approach of skeletonization is that it requires re-computation of path-cost map over the entire object volume after each iteration. In previous methods (Bitter et al., 2001; Jin et al., 2014b), only one branch is added in each iteration. Therefore, the computational complexity is determined by the number of terminal branches N in the skeleton. The new algorithm makes a major improvement in computational complexity. As illustrated in Fig. 1, after adding the skeletal branch op₁ and finding the marked object volume along op₁, the unmarked volume generates three disconnected sub-trees T₁, T₂, and T₃ (Fig. 1b). These three sub-trees represent the object volume for which skeletal branches are yet to be detected.

An important observation is that, since these sub-trees are disconnected, their representative skeletal branches are independent. Therefore, new skeletal branches can be simultaneously computed in T₁, T₂, and T₃. In other words, in the next iteration, three branches can be simultaneously added where each branch connects to the farthest CMB within each sub-tree. After adding the three branches, the marked volume is augmented using local scale-adaptive dilation along the three new branches. This process continues until dilated skeletal branches mark the entire object volume or all meaningful branches are found. For the example of Fig. 1, algorithm terminates in four iterations while it has nine terminal branches.

This simple yet powerful observation reduces the computational complexity of the algorithm from the order of number of terminal branches to worst case performance of the order of tree-depth. For a tree with N nodes, the average depth of unbalanced bifurcating tree is $O(\sqrt{N})$ (Flajolet and Odlyzko, 1982). Thus, our average computation complexity is better than $O(\sqrt{N})$ as compared to O(N) using previous algorithms. For a complete bifurcating tree, the number of iteration by our method is O(logN). For example, the airway tree in Fig. 2 contains 118 terminal branches and the new algorithm adds twelve skeletal branches after two iterations (Fig. 2a) and completes the skeletonization process in only 6 iterations (Fig. 2b). See Section 3.4 for more experimental results demonstrating the improvement of computational efficiency of the new method.

3. Experimental Results

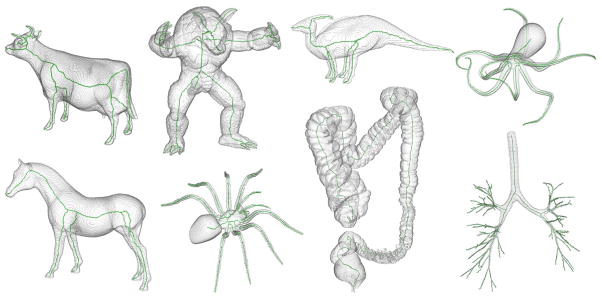
Figures 2–5 qualitatively illustrate the performance of the new method. For example, Fig. 2 illustrates the improvement by the method in terms of computation complexity where the skeleton of a tree-like object with a large number of branches is completed in a few iterations. Fig. 3 shows the superiority of the new cost function as compared to the one by Bitter et al. in tracing the center line of the target object. Fig. 4 qualitatively demonstrates the performance of the new method in handling true and noisy branches as compared to Bitter et al.’s algorithm using minimum cost path. Fig. 5 shows the robustness of the new algorithm on a variety of shapes available online, many with complex 3-D geometry. For all these figures, the method generates a skeletal branch for each visible feature while arresting noisy branches.

Fig. 5.

Results of application of the new curve skeletonization algorithm on different 3-D volume objects available online. The object volume is displayed using partial transparency and computed skeletons are shown in green. As observed from these results, the new method does not generate any noisy branch while producing branches for all major geometric features in these objects.

In the rest of this section, we present quantitative results of three experiments evaluating the method’s performance in terms of accuracy, false branch detection, and computational efficiency as compared to two leading methods (Lee et al., 1994; Palágyi et al., 2006). The method by Palágyi et al. was selected because it was designed for tubular tree objects and an optimized implementation for airways was obtained from the authors. The recommended value of ‘1’ was used for the threshold parameter ‘t’ as mentioned in Palágyi et al., 2006. Another highly cited method by Lee et al., 1994, available through ITK: The NLM Insight Segmentation and Registration Toolkit, http://www.itk.org was used for comparison. The second method represents a decision-tree based approach for curve skeletonization. The branch performance and computation efficiency of the new method was also compared with Bitter et al.’s method.

3.1. Data and Phantom Generation

The performance of the method was examined on tubular tree phantoms generated from human airway and coronary artery CT images. CT images of human airway and coronary artery were used for quantitative experiments. In vivo human airway CT images were acquired from a previous study, whereby subjects were scanned at a fixed lung volume (total lung capacity: TLC) using a volume-controlled breath-hold maneuver. Airway images were acquired on a Siemens Sensation 64 multi-row detector CT scanner using the following parameters: 120 kV, 100 effective mAs, pitch factor: 1.0, nominal collimation: 64×0.6mm, image matrix: 512×512, 0.55×0.55 mm in-plane resolution, and 0.6 mm slice thickness.

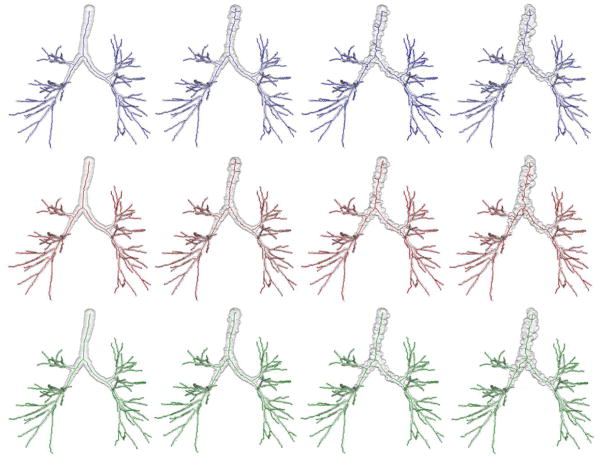
Airway phantom images with known skeletons were generated from five CT images as described below. The following steps were applied on each CT image – (1) segmentation of human airway lumen from using a region growing algorithm (Saha et al., 2000), (2) curve skeletonization (Saha et al., 1997) and computation of airway lumen local thickness (Liu et al., 2014), (3) pruning of curve skeleton beyond the 5th anatomic level of branching, (4) up-sampling of the curve skeleton and local thickness map by 2×2×2 voxels, (5) fitting of a B-spline to each individual skeletal branch, (6) smoothing of the thickness values along each skeletal branch, (7) reconstruction of a fuzzy object for the airway tree using local thickness-adaptive dilation along skeletal branches at 5 × 5 × 5 sub-voxel resolution, (8) addition of granular noisy protrusions and dents on the airway tree boundary, (9) down-sampling of each airway tree object and its skeleton at 3×3×3 voxels, and (10) filling of any small cavities or tunnels (Saha and Chaudhuri, 1996) artificially created while adding noisy protrusions and dents or down-sampling. For the step of adding noisy protrusions and dents, 1% of the airway boundary voxels are randomly selected as locations for protrusions or dents. The granular protrusion or dent were generated using local-scale adaptive blobs whose radius was randomly chosen from three different ranges depending upon the noise level. Specifically, 30±10%, 50±10% and 70±10% of the local scale were used for the three levels of noise. See Fig. 6 for the airway tree phantoms at different levels of noise.

Fig. 6.

Curve skeletonization results by different methods on airway phantom images at different levels of noise and down-sampling. Columns from left to right represent phantom images at no noise and low, medium, and high levels of noise. Top, middle, and bottom rows present curve skeletonization results using the methods by Lee et al., Palágyi et al. and the new method, respectively. It is observed from these figures that both Lee et al. and Palágyi et al.’s method produce several false branches at low, medium and high noise levels, while the new method produces no visible false branch. All methods have captured all meaningful branches.

Also, eight online (http://coronary.bigr.nl/) coronary artery datasets with known centerlines from the Rotterdam coronary centerline evaluation project (Schaap et al., 2009) were used. Steps 7 to 10 were applied to each coronary dataset to produce four test phantom images at four different noise levels. Besides these phantom data sets ten original human airway tree data sets derived from in vivo CT imaging were used for evaluating the performance of different algorithms in terms of true/false branch and computational efficiency. Finally, the new algorithm was directly applied on these fuzzy objects while a threshold of 0.5 and filling of small cavities and tunnels were applied prior to using other methods which are essentially designed for binary objects.

3.2. Accuracy

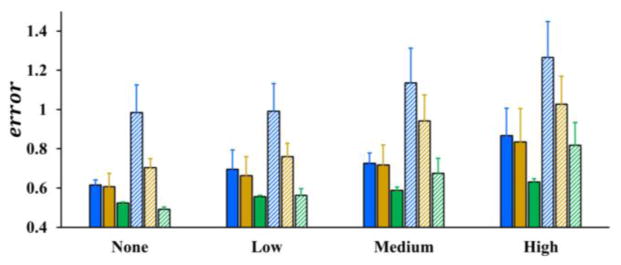
Twenty airway (5 images × 4 noise levels) and thirty two coronary artery (8 images × 4 noise levels) phantoms at different levels of noise were used to examine the accuracy of different methods. Results of application of curve skeletonization by different methods on an airway phantom data at different levels of noise are shown in Fig. 6. To quantitatively assess the performance of different methods, an error was defined to measure the difference between true and computed skeletons. As mentioned in Section 3.1, each branch in the true skeleton was represented using a B-spline. The true skeleton was expressed as a set of densely sampled points of the true skeletal branches; let S_T denote the set of N_T number of sample points on a true skeleton. Let S_C denote the set of N_C number voxels in the computed skeleton by a given method. Skeletonization error was computed as follows:

$$\mathit{error}=\frac{1}{2N_T}\sum _{p\in S_T}\underset{q\in S_{\mathrm{C}}}{min}\mid p-q\mid +\frac{1}{2N_{\mathrm{C}}}\sum _{p\in S_{\mathrm{C}}}\underset{q\in S_T}{min}\mid p-q\mid .$$

Mean and standard deviation of errors by three skeletonization algorithms (Lee et al., Palágyi et al. and the new method) for airway and coronary phantom images are presented in Fig. 7. For both airway and coronary phantoms, the average error and standard deviation using our algorithm are less than those by Lee et al. and Palágyi et al. at all noise levels and a paired t-test confirmed that these differences are statistically significant (p ≪ 0.05). Also, it is observed from the figure that the average error plus its standard deviation using our method is less than one voxel even at the highest noise level for both airway and coronary phantoms. As discussed by Saha and Wehrli, 2004, the average digitization error in a skeleton is close to 0.38 voxel. Therefore, after deducting the digitization error, the performance of the new method is promising.

Fig. 7.

Skeletonization errors by different methods on computerized phantoms at different noise levels – none, low, medium, and high. Blue, gold, and green bars represent skeleton errors by three different methods – Lee et al., Palágyi et al., and the new method. The solid bars represent the errors for airway phantoms while the bars with the slanted pattern show the errors for coronary phantoms.

In general, observed mean skeleton errors for coronary phantoms were higher than airway phantoms. A possible reason behind this observation is that the average thickness of coronary phantoms was greater than airway phantoms in voxel unit. At the noise free level, neither the algorithm by Lee et al. nor by Palágyi et al. produced visible false branches (see Table 1), however, the skeleton errors were significantly larger than the new method. A possible explanation behind this observed difference at noise free level is that the skeleton produced by the new method is spatially closer to the original centerline as compared to the other two methods.

Table 1.

Average false branches by three curve skeletonization methods on five airway phantoms at different levels of noise. None of the three algorithms missed any airway branches up to the 5th anatomic generation of tree.

Noise	Lee et al.	Palágyi et al.	our method
None	0.8	0	0
Low	4.4	3.8	0
Medium	9.2	9.8	0
High	12.8	14.6	0

3.3. False and Missing Branches

A qualitative example illustrating the difference among three skeletonization methods at various noise levels has been shown in Fig. 6. The new method successfully stopped noisy branches at all noisy granulates on the airway boundary. Although the algorithm by Palágyi et al. did not produce any false branch for no noise phantoms, it failed to do so for noisy phantoms. The algorithm by Lee et al. produced false branches even for no noise phantoms.

A quantitative experiment was carried out by two mutually-blinded experts examine the performance of different algorithms in terms of false and missing branches. Each expert independently labelled the false and missing branches in each airway skeleton by visually comparing it with the matching volume tree. The results of this experiment for airway phantoms at different noise levels are summarized in Table 1. It is worth noting that the quantitative results of Table 1 is consistent with the observation of Fig. 6. The performance of the new method in terms of false skeletal branches is always superior to the other two methods and the difference is further exacerbated at higher noise levels.

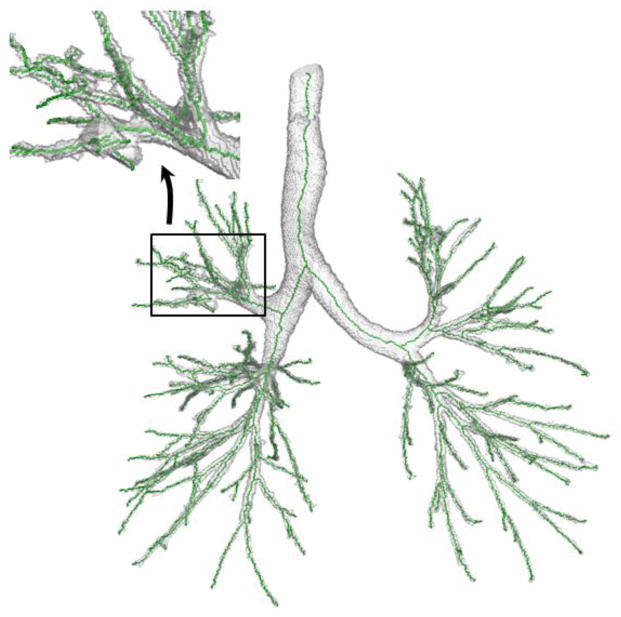
Besides the airway phantoms, ten original segmented human airway trees without down-sampling or addition of external noise were used and analyzed. The labelling of false and missing branches for these original airway trees was confined up to the fifth generation of airway branches because the confidence of labelling a false or missing branch beyond the fifth generation was low due to limited resolution even by the experts. The results are summarized in Table 2. Altogether, the new method generated five false branches among which three false branches were generated in one data set. After a careful look of the specific image data, a segmentation leakage was found at a peripheral airway branch in the right upper lobe and three false branches were generated around that leakage; see Fig. 8. On the other hand, the other two methods generated 65 and 69 false branches. Thus, both qualitative illustrations as well as results from quantitative experiments demonstrate the superiority of the new method in stopping false branches while missing no true branch.

Table 2.

Comparison of false branch performance on ten original CT-derived human airway trees without down-sampling or addition of external noise.

#false branch	Lee et al.	Palágyi et al.	our method
Average	6.5	6.9	0.5
Std. dev.	4.4	4.1	1.1
Maximum	14	15	3

Fig. 8.

Illustration of the airway tree where the new method generated three false branches. In this case, a large segmentation leakage occurs on the airway peripheral branch, which causes the generation of three false branches by the new algorithm.

3.4. Efficiency

Computational efficiency of our method was compared with Lee et al., Palágyi et al., and Bitter et al.’s methods. For this experiment, ten original CT-derived human airway tree (average image size: 368×236×495 voxels) without down-sampling, smoothing, or external noise were used. First, let us examine the relation between the computation complexity of our method and different tree-properties as discussed in Section 2.5. The average number of terminal branches observed in the tem airway trees used for this experiment was 121.7 and the average number of iterations required by our algorithm was 7.1, which is close to log₂ N = log₂ 121.7 = 6.93 and better than the observed average tree-depth of 11.6 which is close to $\sqrt{N}=\sqrt{121.7}=11.03$.

The observed average computation time by different methods for these 10 airway trees are reported in Table 3. All the algorithms are implemented in C++ and have run on a PC with a 2.0GHz Intel CPU. Although, our algorithm is slower than Palágyi et al.’s algorithm (Palágyi et al., 2006), the computation time is comparable on the order of seconds, and it is significantly faster than the other two methods. Especially, the improvement in computational complexity as compared to Bitter et al.’s algorithm, which falls under the same category of the new method, is encouraging. This improvement is primarily contributed by enabling multiple skeletal branch detection in one iteration as introduced in this paper.

Table 3.

Average computation time by different algorithms on 10 human airway trees (average image size: 368×236×495).

Lee et al.	Bitter et al.	Palágyi et al.	our method
15.4 mins	21.1 mins	6 secs	82 secs

4. Conclusion

A new algorithm of computing curve skeleton based on minimum cost path for three-dimensional tree-like objects has been presented and its performance has been thoroughly evaluated. The new method uses an initial root seed voxel to grow the skeleton, which may be computed using an automated algorithm. A novel path-cost function has been designed using a measure of local significance factor, which forces new branches to adhere to the centerline of an object. The method uses global contextual information while adding a new branch, which contributes additional power to stop false or noisy branches. Quantitative evaluative experiments on realistic phantoms with known centerlines have demonstrated that the new method is more accurate than conventional existing methods. The other experiment using airway tree data has shown that the new method significantly reduces the number of noisy or false branches as compared to two conventional methods. The new method also reduced the order of computational complexity from the number of terminal branches in a tree to the worst case performance of tree-depth. Experimental results demonstrated that, on an average, the computation complexity is reduced to O(log N), where N is the number of terminal tree branches.

Highlights.

• A comprehensive 3-D curve skeletonization algorithm using minimum cost path

• A non-parametric local significance factor for fuzzy centers of maximal balls

• A path cost function ensuring skeletal branches along object centerlines

• The new method outperforms existing ones with respect to accuracy and noisy branch

• Computation complexity reduced from the number of terminal branches to tree-depth