Recruitment of Foreigners in the Market for Computer Scientists in the United States

Abstract

We present and calibrate a dynamic model that characterizes the labor market for computer scientists. In our model, firms can recruit computer scientists from recently graduated college students, from STEM workers working in other occupations or from a pool of foreign talent. Counterfactual simulations suggest that wages for computer scientists would have been 2.8–3.8% higher, and the number of Americans employed as computers scientists would have been 7.0–13.6% higher in 2004 if firms could not hire more foreigners than they could in 1994. In contrast, total CS employment would have been 3.8–9.0% lower, and consequently output smaller.

1 Introduction

An increasingly high proportion of the scientists and engineers in the US were born abroad. At a very general level, the issues that come up in the discussion of high skilled immigration mirror the discussion of low skilled immigration. The most basic economic arguments suggest that both high-skill and low-skill immigrants: (1) impart benefits to employers, to owners of other inputs used in production such as capital, and to consumers, and (2) potentially, impose some costs on workers who are close substitutes (Borjas (1999)). On the other hand, the magnitude of these costs may be substantially mitigated if US high skilled workers have good alternatives to working in sectors most impacted by immigrants (Peri & Sparber (2011), Peri et al. (2013)). Additionally, unlike low skilled immigrants, high skilled immigrants contribute to the generation of knowledge and productivity through patenting and innovation. Doing so both serves to shift out the production possibility frontier in the US and may also slow the erosion of the US comparative advantage in high tech (Freeman (2006); Krugman (1979)).

In this paper we study the impact of high skilled immigration on the labor market for computer scientists (CS) in the US, during the Internet boom of the 1990s, and the subsequent slump in the early 2000s. During this period, we observe a substantial increase in the number of temporary non-immigrant visas awarded to high skilled workers, and individuals with computer-related occupations becoming the largest share of H-1B visa holders (US General Accounting Office, 2000). Given these circumstances, it is of considerable interest to investigate how the influx of foreigners affected the labor market outcomes for US computer scientists during this period.

In order to evaluate the impact of immigration on CS domestic workers, we construct a dynamic model that characterizes the labor supply and demand for CS workers during this period. We build into the model the key assumption that labor demand shocks, such as the one created by the dissemination of the Internet, can be accommodated by three sources of CS workers: recent college graduates with CS degrees, US residents in different occupations who switch to CS jobs, and skilled foreigners. Furthermore, firms face a trade-off when deciding to employ immigrants: foreigners are potentially either more productive or less costly than US workers, but there are extra recruitment costs associated with hiring them.

The approach we take in this paper is distinctly partial equilibrium in nature – we focus on the market for computer scientists and ignore any wider impacts that high skilled immigration might have on the U.S. economy (Nathan (2013)). While we believe this approach can potentially be used to understand the impact that the availability of high skilled foreign labor might have had for this market, this approach precludes any analysis of the overall welfare impact of the H-1B program in particular or high skilled immigration more generally.

The predictions of the model on the impacts of immigration on wages depend on the elasticity of labor demand for computer scientists. As long as the demand curve slopes downwards, the increased availability of foreign computer scientists will put downward pressure on the wages for computer scientists in the US. However, as we discuss further in Section 4.4, there are a number of considerations that might lead us to think otherwise in the case of computer scientists. First, even in a closed economy, the fact that computer scientists contribute to innovation reduces the negative effects foreign computer scientists might have on the labor market opportunities for skilled domestic workers. In addition, in an increasingly global world, we might expect that restrictions on the hiring of foreign skilled workers in the US would lead employers to increase the extent to which they outsource work. Indeed, if computer scientists are a sufficient spur to innovation, or if it is easy for domestic employers to offshore work, any negative effects that an increase in the number of foreign computer scientists working in the US might have on the domestic skilled workforce would be completely offset by increases in the domestic demand for computer scientists. In the end this issue comes down to the slope of the demand curve for computer scientists. ¹

We use data on wages, domestic and foreign employment, and undergraduate degree completions by major, during the late 1990s and early 2000s to calibrate the parameters of our model such that it reproduces the stylized facts of the CS market during the period. Next, we use the calibrated model to simulate counterfactuals on how the economy would behave if firms had a restriction on the number of foreigners they could hire. Conditional on our assumptions about the slope of the demand curve for computer scientists, our simulation suggests that had US firms not been able to increase their employment of foreign computer scientists above its 1994 level, CS wages would be 2.8–3.8% higher in 2004. Furthermore, the number of Americans working in the CS industry would be 7.0–13.6% higher, the total number of CS workers would be 3.8–9.0% lower and the enrollment levels in computer science would be 19.9–25.5% higher than the observed levels in 2004.

Within the confines of the model, the predictions of our model do not depend on the specific choice we made for non-calibrated parameters, with one important exception. The exception: crowd out in the market for computer scientists depends crucially on the elasticity of demand for their services. Ideally, we would be able to use exogenous supply shifts to identify the slope of the demand curve for computer scientists, while we use exogenous shifts in demand to identify supply curves. We believe that largely exogenous technological breakthroughs in the 1990s increased the demand for computer scientists, allowing us to identify supply curves.² In other contexts, researchers have treated the increase in foreign born workers in the US economy as exogenous. However, in the current context, immigration law in the US implies that most of the foreign born and trained individuals who migrate to the US to work as computer scientists do so because they are sponsored by US based firms. Thus, it seems implausible to treat the number of foreign born computer scientists in the US as an exogenous increase in supply. In the end, without credible sources of identifying information, we resort to parametrically varying the elasticity of the demand for computer scientists through, what we will argue is a plausible range, from −1.3 to −4.0.

This paper constitutes a contribution to two different dimensions of the research literature. First, our study can be seen as an extension of the models of the market for scientists and engineers developed by Freeman (1975, 1976) in the 1970s and refined by Ryoo & Rosen (2004) more recently. In Ryoo and Rosen’s model, employers are restricted to hiring recent graduates from US engineering programs. In our model, employers can also hire both foreigners and US based individuals not trained as computer scientists. As a result, the supply of CS workers implied by our model is substantially more elastic than implied by the Ryoo and Rosen model, especially in the short term. More importantly, the substantial number of skilled foreign workers affects how the labor and education markets adjusts to an increase in the demand for skilled labor. Second, our paper relates to the recent literature on the potential impact that the hiring of high skilled immigrants might have on the wages and employment prospects of US natives.

We review this literature in detail, and describe the market for CS workers in section 2. Section 3 presents the dynamic model we build to characterize the market for CS workers when firms can recruit foreigners. In section 4, we describe how we calibrate the parameters of the model and the counterfactual simulations where firms have restrictions on the number of foreigners they can hire. We conclude with section 5 which presents a discussion based on the results of the paper.

2 The Market for Computer Scientists in the 1990s

2.1 The Information Technology Boom of the Late 1990s

During the mid 1990s, we observe the beginning of the utilization of the Internet for commercial purposes in the United States³ and a substantial increase in the number of Internet users. One indicator of a contemporaneous change in demand for IT workers is the rise of R&D expenditure of firms in both the computer programming services, and the computer related equipment sector. Specifically, the share of total private R&D of the firms of these two industries increased from 19.5% to 22.1% between 1991 and 1998 (author’s computations using Compustat data). The entry and then extraordinary appreciation of tech firms like Yahoo, Amazon and eBay provides a further testament to the “boom” in the IT sector prior to 2001.

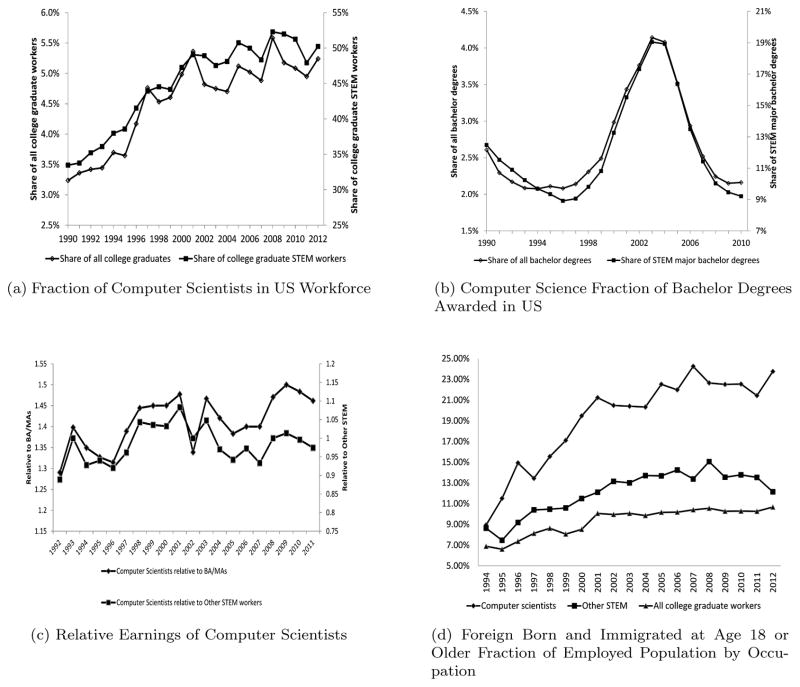
These technological innovations had a dramatic effect on the labor market for computer scientists. According to the Census, the number of employed individuals working either as computer scientists or computer software developers (CS) increased by 161% between the years 1990 and 2000. As a comparison, during the same period, the total number of employed workers with at least a bachelor degree increased by 27%, while the number of workers in other STEM occupations increased by 14%.⁴ Table 1 shows computer scientists as a share of the college educated workforce and the college educated STEM workforce. In each case, the share was rising before 1990, but rises dramatically during the 1990s. Indeed, by 2000 more than half of all STEM workers are computer scientists. In Figure 1a, we use the CPS to show a similar pattern, additionally showing that the growth of CS employment started in the second half of the decade - the same period as the dissemination of the Internet. There is no doubt this was a period of employment expansion of the CS workforce.

Table 1.

Fraction of Computer Scientists and Immigrants in the US Workforce by Occupation

Year	1970	1980	1990	2000	2010
Computer Scientists:
as a fraction of workers with a Bachelor’s/Master’s	1.68%	1.83%	3.30%	5.66%	5.28%
as a fraction of STEM college graduates	16.86%	23.60%	35.99%	53.31%	54.90%
Immigrants:
as a fraction of Bachelor’s/Master’s	2.10%	5.43%	6.86%	8.41%	12.77%
as a fraction of Computer Scientists	2.37%	7.09%	11.06%	18.59%	27.82%
as a fraction of Other STEM workers	3.63%	9.72%	10.71%	12.69%	18.21%

Note: Sample restricted to employed workers with a Bachelors or a Masters degree. Definition of Computer Scientists and STEM workers determined by occupational coding (for details see Data Appendix online). Immigrant is defined as one born abroad, and migrated to the US after the age of 18.

Source: US Census (years 1970 to 2000); ACS (2010)

Figure 1.

Major Trends (1990 to 2012)

Note: Sample restricted to employed workers with a Bachelors or a Masters degree. Definition of Computer Scientists and STEM workers determined by occupational coding (for details see Data Appendix online). STEM majors are defined as engineering, computer and math sciences and natural science. Earning are median weekly earnings. Imputed values excluded, and values are lagged by one year due to retrospective nature of the survey. Immigrant defined as one born abroad, and migrated to the US after the age of 18. Immigration status is not available in the CPS before 1994.

Sources: March CPS (for employment, earnings, and immigrants); IPEDS Completions Survey (for degrees)

On top of employment decisions, there is evidence that Internet innovation also affected educational choices of students. We show in Figure 1b that the number of bachelor degrees awarded in computer science as a fraction of both the total number of bachelor degrees and the number of STEM major degrees increased dramatically during this period. The CS share of total bachelor degrees increased from about 2% in 1995 to more than 4% in 2002. Even when compared to other STEM majors, it is clear from the figure that for college students, the decision to study computer science also responded to the Internet boom.

In addition to affecting employment and enrollment decisions, there is also empirical evidence that computer scientist wages responded to expanding Internet use. From the Census, we observe a 18% increase in the median real weekly wages of CS workers between 1990 and 2000. The CPS presents similar patterns: starting in the year 1994 we observe in Figure 1c that wages of computer scientists increased considerably when compared to both workers with other STEM occupations and all workers with a bachelor degree. In fact, while during the beginning of the 1990s, the earnings of CS workers were systematically lower than other STEM occupations, the wage differential tends to disappear after 1998.⁵

2.2 The Immigrant Contribution to the Growth of the High Tech Work-force

Employment adjustments in the market for computer scientists happened disproportionately among foreigners during the Internet boom. Evidence for this claim is found in Table 1 and Figure 1d, where we use the Census and CPS to compare the share of foreign computer scientists to the share of foreign workers in other occupations.⁶ In the second half of 1990s, the foreign fraction of CS workers increased considerably more than both the foreign fraction of all workers with a bachelor degree and the foreign fraction of all workers in a STEM occupation. In particular, foreigners were less represented among individuals working as computer scientists than in other STEM occupations in 1994. However, with the dissemination of the Internet in the later years of the decade, foreigners became a more important part of the pool of CS workers, as foreigners comprised 29.6% of the increase in CS workers.

The growth in the representation of the foreign born among the US computer scientist workforce was fueled by two developments. First, there was a truly dramatic increase in the foreign supply of men and women with college educations in science and engineering fields (Freeman (2009)). To take one important example, in India, the number of first degrees conferred in science and engineering rose from 176 thousand in 1990 to 455 thousand in 2000. Second, the Immigration Act of 1990 established the H-1B visa program for temporary workers in “specialty occupations.”⁷ The regulations define a “specialty occupation” as requiring theoretical and practical application of a body of highly specialized knowledge in a field of human endeavor including, but not limited to, architecture, engineering, mathematics, physical sciences, social sciences, medicine and health, education, law, accounting, business specialties, theology, and the arts. In addition, applicants are required to have attained a bachelor’s degree or its equivalent as a minimum.

Firms that wish to hire foreigners on H-1B visas must first file a Labor Condition Application (LCA). In LCA’s for H-1B workers, the employer must attest that the firm will pay the non-immigrant the greater of the actual compensation paid to other employees in the same job or the prevailing compensation for that occupation, and the firm will provide working conditions for the non-immigrant that do not cause the working conditions of the other employees to be adversely affected. At that point, prospective H-1B non-immigrants must demonstrate to the US Citizenship and Immigration Services Bureau (USCIS) in the Department of Homeland Security (DHS) that they have the requisite education and work experience for the posted positions. USCIS then may approve the petition for the H-1B non-immigrant for a period up to three years. The visa may be extended for an additional three years, thus a foreigner can stay a maximum of six years on an H-1B visa, though firms can sponsor H-1B visa holders for a permanent resident visa. An important feature of the H-1B visa is that the visa is for work at the specific firm. As a result, workers are effectively tied to their sponsoring firm.

Since 1990 there has been a cap in the number of H-1B visas that can be issued. Initially this cap was set at 65,000 visas per year. In the initial years of the program, the cap was never reached, By the mid-1990s, however, the allocation tended to fill each year on a first come, first served basis, resulting in frequent denials or delays on H-1Bs because the annual cap had been reached. After lobbying by the industry, at the end of the decade, Congress acted to raise the cap first to 115,000 for FY1999 and to 195,000 for FY2000–2003. The cap then reverted to 65,000.⁸ Figure 2 shows the growth in the number of H-1 visas issued over the last three decades, estimates of the stock of H-1 visas in the economy each year, and the changes in the H-1B visa cap.

Figure 2.

H-1 and H-1B Visa Population

Note: Population stock is constructed using estimations of in flow (visas granted) and out flow (deaths, permanent residency, or emigration) of H-1 workers. In later years, the number of visas granted could exceed the visa cap due to exemptions for foreigners who work at universities and non-profit research facilities.

Through the decade of the 1990s, H-1B visas became an important source of labor for the technology sector. The National Survey of College Graduates shows that 55% of foreigners working in CS fields in 2003 arrived in the US on a temporary working (H-1B) or a student type visa (F-1, J-1). Furthermore, institutional information indicates a significant increase in the number of visas awarded to computer related occupations during the 1990s. Numbers from the U.S. General Accounting Office (1992) report show that “computers, programming, and related occupations” corresponded only to 11% of the total number of H-1 visas in 1989. However, with concurrent to the Internet boom, computer scientists became a more significant fraction of individuals that received these type of working visas: according to the U.S. Immigration and Naturalization Service (2000), the number of H-1B visas awarded to computer-related occupation in 1999 jumped to close to two-thirds of the visas, and the Department of Commerce (2000) estimated that during the late 1990s, 28% of programmer jobs went to H-1B visa holders.

While H-1B visas holders represent an important source of computer scientists, they do not represent all foreigners in the country working as computer scientists. A significant number of such foreigners are permanent immigrants, some of whom may have come either as children or as students. Other foreigners enter the US to work as computer scientists in the US on L-1B visas, which permit companies with offices both in the US and overseas to move skilled employees from overseas to the US. While we know of no data showing the fraction of computer scientists working in the US on L-1B visas, substantially fewer L-1(A&B) visas are issued than are H-1Bs.

2.3 The Previous Literature on the Impact of Immigrants on the High Tech Workforce in the US

Critiques of the H-1B program (e.g. Matloff (2003)) argue that firms are using cheap foreign labor to undercut and replace skilled US workers. Even the fiercest critiques of the program do not claim that employers are technically evading the law (Kirkegaard (2005)). Rather, these authors argue that the requirement that firms pay visa holders the prevailing wage is close to meaningless. They claim that firms can describe positions using minimal qualifications for the job, thereby establishing a low “prevailing” wage, and then hire overqualified foreigners into the position. These authors conclude that given the excess supply of highly qualified foreigners willing to take the jobs, and given the lack of portability of the H-1B visa, workers on an H-1B visa are not in a position to search for higher wages.

One way to get a handle on the extent to which H-1B visa holders are being under-paid relative to their US counterparts is to compare foreigners on H-1B visas to those with “green cards,” which are portable. Available evidence suggests that computer scientists holding green cards are paid more than observationally equivalent H-1B visa holders. Using difference-in-difference propensity score matching, Mukhopadhyay & Oxborrow (2012) find that green card holders earn 25.4 percent more than observably comparable temporary foreign workers. Additionally, based on an internet survey, Mithas & Lucas (2010), found that IT professionals with green cards earn roughly 5 percent more than observationally equivalent H-1B visa holders using log earnings regressions. Comparisons between green card and H-1B holders are far from perfect, because green cards are not randomly assigned. Many high skilled workers obtain green cards by being sponsored by their employers after they have been working on an H-1B for a number of years. It seems reasonable to assume that those being sponsored are those that both want to stay in the US and are also amongst those the employer wants to hold onto. These kind of considerations lead us to suspect that, conditional on observables, green card holders are positively selected. Given these considerations, it is somewhat surprising that the observed green card premium is not larger than it is.

While there may be no incontrovertible estimate of the productivity (conditional on earnings) advantage of foreign high skilled labor, simple economic reasons suggests this advantage must exist. US employers face both pecuniary and non-pecuniary costs associated with hiring foreigners. A small GAO survey (U.S. General Accounting Office, 2011) estimated the legal and administrative costs associated with each H-1B hire to range from 2.3 to 7.5 thousand dollars. It seems reasonable to assume that employers must expect some cost or productivity advantage when hiring foreigners. This does not mean that foreign hires are always super stars. The productivity advantage could be quite small, and could involve effort, not ability. However, without some productivity advantage, it is hard to see why employers go through the effort and expense to hire foreigners.

H-1B critics are arguing that, for the reasons discussed above, employers find hiring foreign high skilled labor an attractive alternative and that such hiring either “crowds out” natives from jobs or put downward pressure on their wages. However, as far as we know, critics of the H-1B program have not tried to estimate the magnitude of either of these effects. Recent work by economists have started to fill this void. Kerr & Lincoln (2010) and Hunt & Gauthier-Loiselle (2010) provide original empirical evidence on the link between variation in immigrant flows and innovation measured by patenting - finding evidence suggesting that the net impact of immigration is positive rather than simply substituting for native employment. Kerr & Lincoln (2010) also show that variation in immigrant flows at the local level related to changes in H-1B flows do not appear to adversely impact native employment and have a small, statistically insignificant effect on their wages.

A potential issue with Kerr and Lincoln’s analysis is that the observed, reduced-form outcomes may capture concurrent changes in area specific demand for computer scientists. Kerr and Lincoln fully understand this endogeneity issue. To circumvent the problem, they construct a variable that interacts an estimate for the total number of individuals working on H-1B visas in a city with local area dependencies on H-1Bs. Their hope is that the variation in this variable is driven largely by changes in the cap on new H-1B visas that occurred over the last 20 years. That said, it is unclear the extent to which the variation Kerr and Lincoln use is being driven by variation in the visa cap. Because of the dot com bubble bust in 2000 and 2001, the variation in the H-1B cap is only loosely related to actual number of H-1Bs issued. In addition, it is hard to imagine that the cap was exogenous to the demand for IT workers. Finally, if because of local agglomeration effects, the IT boom was concentrated in areas of the country that were already IT intensive (such as Silicon Valley), then the measure of local dependency would be endogenous.

In the context of an economic model, it is difficult to generate a situation in which there is little crowd out unless labor demand is very elastic. While there are models of the labor market which could rationalize such large elasticities,⁹ this paper proposes an alternative interpretation to Kerr and Lincoln’s results, even when the labor demand is not close to perfectly elastic. If employers face costs to hire immigrant labor and are bound to pay the going wage, firms might disproportionately hire immigrants only when the demand for workers is increasing. In this case, immigrants would not replace incumbent workers or depress wages, but rather have a negative impact on the growth of wages and employment for natives. Under these circumstances, one might very well see a positive association between an increase in the utilization of foreign computer scientists and the increased utilization of their US counterparts, even though the availability of skilled foreigners is putting downward pressure on the growth in earnings and employment of native computer scientists.

3 A Dynamic Model of Supply and Demand of Computer Scientists

To gauge the impact that the availability of foreign high skilled labor has had on US workers, we construct a simple model of the labor market for computer scientists. While our model is quite stylized, we intend to capture the most salient features of the market.

In our model there are three potential sources for computers scientists. First, there are those who earn computer science bachelor’s degrees from US institutions. These individuals must complete college before they are ready to work. Second, there are US residents working in other occupations who can switch into computer science, but must pay costs to switch occupations. Third, there are foreigners who are being recruited on temporary work visas.¹⁰ There is also the group who immigrated with their parents as children, but these individuals are typically either citizens or green card holders and we assume employers do not distinguish between these individuals and the US born. We also ignore the fact that some immigrants are coming in on permanent visas. As the GAO and Department of Commerce reports cited earlier suggest, at least in the 1990s, the majority of foreigners working as computer scientists within the US who have finished their undergraduate degrees abroad, arrived on temporary work visas. In addition, the data we will use does not allow us to distinguish visa types.

In terms of the demand side of the model, we assume that firms observe the technological progress level and make decisions about whether to hire foreigners or domestic workers. We assume that foreigners are somewhat more productive than US workers but are paid the same wage due to institutional restrictions. Alternatively, we could have equally well assumed employers experience a cost advantage associated with hiring foreigners. Furthermore, firms face increasing costs for recruiting foreigners, making it non-optimal for firms to only hire foreign workers.

3.1 Labor Supply of American Computer Scientists

We model U.S computer scientists as making two types of decisions along their career in order to maximize the expected present value of their life time utility. At age 20, individuals in college choose the field of study that influences their initial occupation after graduation, and from age 22 to 65, workers choose between working as a computer scientist or in another occupation. Individuals have rational, forward looking behavior and make studying and working decisions based on the information available at each period.

3.1.1 Studying decision

We assume that students make their major decisions when they are juniors in college. At age 20, an individual i draws idiosyncratic taste shocks for studying computer science or another field: ${\eta }_i^c$ and ${\eta }_i^o$, respectively. This student also has expectations about the prospects of starting a career in each occupation after graduation (age 22), which have a values $V_{22}^c$ and $V_{22}^o$ respectively. With this information, an individual chooses between pursuing computer sciences or a different choice of major at the undergraduate level.¹¹

We model the utility of a student as a linear function of the taste shocks and career prospects in each sector. There is also a taste attractiveness parameter α_o for studying a different field from computer science and individuals discount their future with an annual discount factor β. With these assumptions, the field of study decision is represented by:

$$\mathit{max}\{{\beta }^2{\mathbb{E}}_t{V}_{22}^c+{\eta }_i^c,{\beta }^2{\mathbb{E}}_t{V}_{22}^o+{\alpha }_o+{\eta }_i^o\}$$

We assume that ${\eta }_i^c$ and ${\eta }_i^o$ are independently and identically distributed and for s = {c, o}, can be defined as ${\eta }_i^s={\sigma }_0{v}_i^s$, where σ₀ is a scale parameter and $v_i^s$ is distributed as a standard Type I Extreme Value distribution. This distributional assumption is common to dynamic discrete choice models (Rust (1987), Kline (2008)) and it is convenient because it allows the decisions of agents to be smoothed out, a desired property that will be used in the characterization of the equilibrium of the model.

Given the distributional assumption of idiosyncratic taste shocks, it follows that the probability of a worker graduating with a computer science degree can be written in logistic form:

$$p_t^c={[1+\mathit{exp}(-({\beta }^2{\mathbb{E}}_{t-2}[V_{22}^c-V_{22}^o]-{\alpha }_o)/{\sigma }_0)]}^{-1}$$

Note that the important parameter for how studying choices of workers are sensitive to different career prospects is the standard deviation of taste shocks. Small values of σ₀ imply that small changes in career prospects can produce big variations in the number of students graduating with a computer science degree.

The next step to characterize the supply of young computer scientists is to map the graduating probability described above to employment. Defining $M_t^a$ as the exogenous number of college graduates with age a in time period t,¹² the number of recent graduates with a computer science degree in year t is represented by $C_t=p_t^c{M}_t^{22}$.

3.1.2 Working Decision

The field of study determines if an individual enters the labor market as either a computer scientist or with a different occupation. However, individuals can choose to switch occupations along their careers. Specifically, at the beginning of each period, individuals between ages 22 and 65 choose to work in CS or another type of job in order to maximize the expected present value of their lifetime utility.

A feature of the model is that switching occupations is costly for the worker. A justification for this assumption is that workers have occupational-specific human capital that cannot be transferred (Kambourov & Manovskii (2009)). We assume the cost to switch occupations is a quadratic function of a worker’s age. Note that this assumption implies that it becomes increasingly harder for workers to switch occupations as they get older. Additionally, there is no general human capital accumulation and wages do not vary with the age of a worker.¹³

Finally, we assume that workers have linear utility from wages, taste shocks and career prospects. Furthermore, wages must be totally consumed in that same year and workers cannot save or borrow. The Bellman equations of worker i at age a between 22 and 64 at time t if he starts the period as a computer scientist or other occupation are respectively:

$$\begin{array}{l}{V}_{t,a}^c=\mathit{max}\{w_t^c+\beta {\mathbb{E}}_t{V}_{t+1,a+1}^c+{\epsilon }_{it}^c,w_t^o-c(a)+\beta {\mathbb{E}}_t{V}_{t+1,a+1}^o+{\epsilon }_{it}^o+{\alpha }_1\}\\ V_{t,a}^o=\mathit{max}\{w_t^c-c(a)+\beta {\mathbb{E}}_t{V}_{t+1,a+1}^c+{\epsilon }_{it}^c,w_t^o+\beta {\mathbb{E}}_t{V}_{t+1,a+1}^o+{\epsilon }_{it}^o+{\alpha }_1\}\end{array}$$

where c(a) = λ₀ + λ₁a + λ₂a², is the monetary cost of switching occupation for an age a worker, and α₁ is the taste attractiveness parameter for not working as a computer scientist. For simplicity, we assume that the current wage in the other occupation $w_t^o$ is exogenous and perfectly anticipated by the workers.¹⁴ In the model, all workers retire at age 65 and their retirement benefits do not depend on their career choices. As a consequence, workers at age 65 face the same decision problem but, without consideration for the future.

As in the college-major decision problem, idiosyncratic taste shocks play an important role in working decisions of an individual. Once more, we will assume that taste shocks are independently¹⁵ and identically distributed and for s = {c, o} can be defined as ${\epsilon }_{it}^s={\sigma }_1{v}_{it}^s$ where σ₁ is a scale parameter and $v_i^s$ is distributed as a standard Type I Extreme Value distribution.

Defining $p_{t,a}^{sS}$ as the probability that a worker at age a between 22 and 64 moves from occupation s to occupation S, it follows from the error distribution assumption that the migration probabilities can be represented as:

$$\begin{array}{l}{p}_{t,a}^{oc}={[1+\mathit{exp}(-(w_t^c-w_t^o-c(a)-{\alpha }_1+\beta {\mathbb{E}}_t[V_{t+1,a+1}^c-V_{t+1,a+1}^o])/{\sigma }_1)]}^{-1}\\ p_{t,a}^{co}={[1+\mathit{exp}(-(w_t^o-w_t^c-c(a)+{\alpha }_1+\beta {\mathbb{E}}_t[V_{t+1,a+1}^o-V_{t+1,a+1}^c])/{\sigma }_1)]}^{-1}\end{array}$$

and the migration probabilities of workers at age 65 are the same without discounting future career prospects. Note that the switching probabilities depend upon both the current wage differential and expected future career prospects at each occupation. The standard deviation of the taste shocks, the sector attractiveness constant and the cost of switching occupations will effect the extent to which changes in relative career prospects affect the movement of US residents across fields.

A feature of dynamic models with forward looking individuals is that working decisions depend upon the equilibrium distribution of career prospects. As in the dynamic choice literature with extreme value errors (Rust (1987) and Kline (2008)), we use the properties of the idiosyncratic taste shocks distribution to simplify the expressions for the expected values of career prospects. As a result, the expected value function for an individual at age a between 22 and 64 working as a computer scientists or in another occupation are respectively:

$$\begin{array}{l}{\mathbb{E}}_t{V}_{t+1,a+1}^c={\sigma }_1{\mathbb{E}}_t[\gamma +ln\{\mathit{exp}((w_{t+1}^c+\beta {\mathbb{E}}_{t+1}{V}_{t+2,a+2}^c)/{\sigma }_1)+\mathit{exp}(((w_{t+1}^o-c(a)+{\alpha }_1+\beta {\mathbb{E}}_{t+1}{V}_{t+2,a+2}^o)/{\sigma }_1)\}]\\ {\mathbb{E}}_t{V}_{t+1,a+1}^o={\sigma }_1{\mathbb{E}}_t[\gamma +ln\{\mathit{exp}((w_{t+1}^o+{\alpha }_1+\beta {\mathbb{E}}_{t+1}{V}_{t+2,a+2}^o)/{\sigma }_1)+\mathit{exp}(((w_{t+1}^s-c(a)+\beta {\mathbb{E}}_{t+1}{V}_{t+2,a+2}^c)/{\sigma }_1)\}]\end{array}$$ (1)

where gamma γ ≅ 0.577 is the Euler’s constant and the expectations are taken with respect to future taste shocks. Workers at age 65 face the same expected values but don’t discount the future.

Now we turn to transforming migration probabilities to employment. The first step is to determine the CS supply of recent college graduates. After leaving college, individuals can start their careers in the occupation correspondent to their field of study with no cost. However, we also allow workers at age 22 to pay the switching costs and get their first job in an occupation different from their field of study. As a consequence, the number of computer scientists at age 22 is a function of the number of recent graduates with a computer science degree and the migration probabilities:

$$L_t^{22}=(1-p_{t,22}^{co})C_t+p_{t,22}^{oc}[M_t^{22}-C_t]$$

where $M_t^{22}$ is the number of recent college graduates, C_t is the number of recent graduates with a computer science degree, and $M_t^{22}-C_t$ is the number of college graduates with any other degree.

In the same way, the supply of computer scientists at age a from 23–65 is a function of past employment in each occupation and the migration probabilities:

$$L_t^a=(1-p_{t,a}^{co})L_{t-1}^{a-1}+p_{t,a}^{oc}[M_{t-1}^{a-1}-L_{t-1}^{a-1}]$$

where $M_t^a$ is the exogenous total number of workers in the economy at age a in time period t. $M_t^a-L_t^a$ is the number of workers at age a working in the residual sector. For simplicity, we assume that the number of workers in the economy at age $M_t^a$ is exogenous and constant over time.¹⁶

The aggregate domestic labor supply of computer scientists is the sum of labor supply at all ages:

$$L_t={\sum }_{a=22}^{a=65}{L}_t^a$$ (2)

Note that the labor supply of computer scientists depends on past employment, new college graduates with a computer science degree and on wages through the migration probabilities.

3.2 Labor Supply of Foreign Computer Scientists

An important characteristic of our model is that firms can recruit foreigners to work as computer scientists. As it will become clear throughout the section, this possibility has implications on how the market for CS workers responds to technological shocks, such as Internet innovation, in terms of enrollment decisions, wages and employment.

We model foreign computer scientists as having a perfectly elastic labor supply. The wage that a computer scientist could obtain in India, for example, is so much lower than it is in the US that the wage premium creates a large queue of individuals ready to take jobs in the US (Clemens (2013) provides direct evidence on this point).¹⁷ Additionally, we assume that foreigners cannot switch their occupation once hired to work as computer scientists and they continue to work in the US until their visa expires.¹⁸

A simplified way to model the framework describe above is to define R_t as the number of foreigners recruited as CS in period t. Next, we assume that all CS foreigners stay in the US for 6 years, that is the maximum length of a H-1B visa contract.¹⁹ In this framework, the number of foreigners currently working as CS in the US is defined as the sum of current and the recruitment in the past 5 years:

$$F_t={\sum }_{j=0}^5{R}_{t-j}$$ (3)

3.3 Labor Demand for Computer Scientists

We model the labor demand as resulting from the decisions made by a standard representative firm in a perfectly competitive framework. In the model, firms observe both the wage and technological progress levels and choose US and foreign employment in order to maximize their intertemporal profits. While firms do not assume that their US employees will necessarily stay with them from one period to the next, given the institutional setting, firms do assume that foreign workers will continue with the firm until the workers’ visa expires six years after he or she is hired.

We assume there is only one type of firm that hires computer scientists. CS labor is the only input used in the production function and we ignore the firm’s decision about capital or other types of labor adjustments.²⁰ We further assume that computer scientists at different ages are perfect substitutes in the production function. As a consequence, firms do not distinguish workers by age when making their hiring decision, precluding the kind of issues addressed by Kerr et al. (2013).²¹ In addition, we assume that foreigners and US workers are close substitutes in the production function, but foreigners have higher marginal productivity than US workers.

A restriction we impose in the model is that all computer scientists in the market are paid the same wage independently of their age or citizenship. This assumption is in accordance with the H-1B visa regulation that requires that wages paid to foreigners must be at least the prevailing wage rate for the occupational classification in their area of employment. Finally, there are no adjustment costs for American workers but firms incur extra costs to recruit foreigners.²² This expenditure is justified by the fees and expenses directly related to the visa application process, and also the extra cost that a firm typically has for searching for workers overseas.

As it will become clear throughout the section, this framework implies that firms face a trade-off when making the decision of hiring foreigners. On one hand, foreigners have a higher marginal productivity than US workers and are paid the same wage. As a consequence, firms are willing to substitute foreign workers for their US workers. On the other hand, there are extra recruitment costs to bring foreigners to the US. This restriction implies that firms never completely substitute foreign for US workers.

3.3.1 Firm’s Decision

The forward looking firm makes decisions about the recruitment of US and foreign workers in order to maximize intertemporal profits, as represented by the Bellman equation:²³

$${\pi }_t={\mathit{max}}_{L_t,R_t}{A}_{t}Y(L_t+\theta F_t)-w_t(L_t+F_t)-C_R(R_t)+\beta {\mathbb{E}}_t[{\pi }_{t+1}]$$

subject to foreign labor supply:

$$F_t={\sum }_{j=0}^5{R}_{t-j}$$

where A_tY (.) is the production function, θ is a constant greater than 1 that represents marginal productivity differences between foreigners and US workers, and C_R(.) is the recruitment cost function of foreigners.

We represent the production function as Cobb-Douglas, such that Y (L_t + θF_t) = (L_t + θF_t)^γ, for some γ between zero and one, implying a downward sloping labor demand curve for computer scientists. This set-up can be made consistent with the Romer (1986) model of knowledge accumulation as a by-product of capital accumulation; or the Arrow (1962) learning-by-doing model, where we allow increases in employment to lead to increases in productivity. To see this, we can reformulate the production function to be Y_t = [B_t(L_t + θF_t)]^δ. If we let the technology parameter exhibit learning-by-doing, then B_t = ψ_t(L_t + θF_t)^α, giving us a production function of the form $Y_t={\psi }_t^{\delta }{(L_t+\theta F_t)}^{\delta \alpha }$. If we define, $A_t={\psi }_t^{\delta }$ and γ = αδ, then we recover the simple Cobb-Douglas production function: A_t(L_t + θF_t)^γ. The parameter, γ, should then be thought of as a reduced-form parameter that captures not just the effective labor share in output, but also the productivity gains from hiring more effective workers. As long as γ lies between 0 and 1, this parametrization guarantees a decreasing marginal return to labor and thus an interior solution for the employment decision of the firm. Furthermore, the parameter γ has a direct mapping to the long-run elasticity of labor demand with respect to effective labor (L_e = L + θF):

$${\epsilon }_{L_e,w}=\frac{1}{1-\gamma }$$

Additionally, we assume that recruitment costs of foreigners include both linear and quadratic components $C_R(R_t)=c_1{R}_t+c_2{R}_t^2$. The linear term in the foreign recruitment cost represents expenditures that are required for hiring each foreign worker, such as application fees. The quadratic term has been widely used in dynamic labor demand literature (Sargent (1978) and Shapiro (1986)). As will become clear from the first order condition of the firm, convex hiring costs, because increasing marginal recruitment costs of foreigners, prevents firms from completely substituting foreigners for domestic workers.²⁴

As in a typical dynamic labor demand problem the solution to the firm’s decision can be characterized by both the first order and envelope conditions with respect to the employment level. The first order condition of the firm’s maximization problem with respect to US employment is represented by the following equation:

$$A_t\gamma {(L_t+\theta F_t)}^{\gamma -1}=w_t$$ (4)

Note that because there is no adjustment costs for US workers, the first order condition with respect to US employment is the same as in a static maximization problem. It is simply characterized by firms equalizing the marginal product of US workers to their wage level.

In addition to choosing US worker employment, the firm also decides the number of foreign workers recruited at each period. The first order condition of the firm’s problem with respect to R_t is given by:

$$\theta A_t\gamma {(L_t+\theta F_t)}^{\gamma -1}-w_t-c_1-2c_2{R}_t+{\sum }_{j=1}^5{\beta }^j{\mathbb{E}}_{\mathrm{t}}[\frac{\partial {\pi }_{t+j}}{\partial R_t}]=0$$

where $\frac{\partial {\pi }_{t+j}}{\partial R_t}$ is defined as how profits in t+j are affected by changes in the recruitment in t. Finally, we use envelope condition to derive the shadow price of past foreign recruitment on current profits, such that:

$$\frac{\partial {\pi }_t}{\partial R_{t-j}}=\theta A_t\gamma {(L_t+\theta F_t)}^{\gamma -1}-w_t\text{for}j=1,\dots ,5$$

Rearranging the first order and envelope conditions of foreigner recruitment leads us to the useful alternative representation to the demand for foreign workers:

$${\sum }_{j=o}^5{\beta }^j{\mathbb{E}}_{\mathrm{t}}[\theta A_{t+j}\gamma {(L_{t+j}+\theta F_{t+j})}^{\gamma -1}-w_{t+j}]=c_1+2c_2{R}_t$$ (5)

Equation (5) shows the trade-off faced by firms when hiring foreigners. The left hand side can be interpreted as the present value of the expected marginal benefit of recruiting a foreigner, defined as the difference between the marginal productivity of a foreigner and wage level during the 6 years duration of his contract. Note that firms benefit from hiring foreigners because they are more productive than US workers by a constant θ but are paid the same wage. The right hand side represents the marginal cost of recruiting a foreigner. Since the marginal cost of recruiting a foreigner is increasing with R_t, firms will never completely substitute foreigners for US workers in the model.

3.4 Equilibrium

A dynamic general equilibrium can be characterized by the system of equations that represent those choice functions and the stochastic process of technological progress A_t. In particular, equation (1) characterizes the expectations of workers with respect to future career prospects, equations (2) and (3) are the dynamic labor supply of American and foreigner computer scientists respectively, and equations (4) and (5) describe the dynamic labor demand for American and foreign CS.

The last piece to characterize the equilibrium of the model is to define a stochastic process of technological progress. Note that A_t is the only source of exogenous variation to the system. We choose to specify A_t as a close to random walk process, ²⁵ such that:

$$A_t=0.999A_{t-1}+0.001\overline{A}+{\xi }_t$$ (6)

where Ā is the steady state level of progress, and ξ_t is the i.i.d. random idiosyncratic productivity shock with mean zero that is assumed to be independent of other variables of the model.²⁶

The equilibrium of the model can be expressed by a mapping from the state variables: $s=\{{\mathrm{C}}_{\mathrm{t}},L_{t-1}^{22},\dots ,L_{t-1}^{64},R_{t-1},\dots ,R_{t-5},A_{t-1}\}$ and exogenous productivity shock ξ_t to the values of L_t, w_t, R_t, and Vt, the vector of career prospects at different occupations for different ages, that satisfies the system of equations (1) to (6). We solve the system by numerically simulating the model in Dynare (a widely used software) via perturbation methods (Juillard (1996)). The policy functions are calculated using a second order polynomial approximation to the decision rules implied by the equations of the model Collard & Juillard (2001a,b).

4 Calibration and Simulation

4.1 Identification and Calibration Method

There are twelve parameters in the model {σ₀, α₀, σ₁, α₁, λ₀, λ₁, λ₂, β, γ, θ, c_R1, c_R2}. We set the foreign worker productivity²⁷ parameter θ = 1.12 based on estimations from the 2003 National Survey of College Graduates data.²⁸ This value of the wage premium earned by foreign green card holders is broadly consistent with other estimates in the literature (Mithas & Lucas (2010), Mukhopadhyay & Oxborrow (2012)). Furthermore, we set the annual discount rate of workers and firms β = 0.9. Our results are not sensitive to plausible variations of this parameter.

In our modeling we are treating the wage, employment and enrollment shifts as a response to an exogenous shift in the demand for computer scientists due to the technological developments that occurred during the period of analysis. We use this demand shift to identify the enrollment and labor supply response of natives, and the parameters affecting the hiring decision of foreigners: {σ₀, α₀, λ₀, λ₁, λ₂, σ₁, α₁, c_R1, c_R2}. At the same time, demand shifts will not identify the slope of the labor demand curve. As a result, we present the results of the paper using different assumptions about the values of γ.

To calibrate {σ₀, α₀, λ₀, λ₁, λ₂, σ₁, α₁, c_R1, c_R2}, we use observations of US and foreign employment, wages, and enrollment²⁹ between 1994 and 2004. We define other STEM occupations as the career alternative to CS jobs. The data we are using on employment and earnings is derived from the March Current Population Survey. This survey contains no indication as to the visa status of the foreign born. To approximate the population of interest, we identify the foreign born who immigrated to the US after they turned 18 as our foreign workers. We also normalize employment variables to use units of American STEM workers, and wages to use units of wages³⁰ of other STEM jobs, and thus define our key data series as:³¹

1. $L_t=\frac{\text{US}\text{computer}\text{scientists}}{\text{US}\text{workers}\text{with}\text{STEM}\text{occupations}}$

2. $F_t=\frac{\text{Foreign}\text{computer}\text{scientists}}{\text{US}\text{workers}\text{with}\text{STEM}\text{occupations}}$

3. $w_t=\frac{\text{Median}\text{weekly}\text{wages}\text{for}\text{computer}\text{scientists}}{\text{Median}\text{weekly}\text{wages}\text{for}\text{other}\text{STEM}\text{jobs}}$

4. $p_{t+2}^c=\frac{\text{US}\text{computer}\text{science}\text{Bachelor}’\mathrm{s}\text{degress}\text{awarded}(\text{lagged}2\text{years})}{\text{US}\text{STEM}\text{Bachelor}’\mathrm{s}\text{degress}\text{awarded}(\text{lagged}2\text{years})}$

5. $s_t^{a_1,a_2}=\frac{\text{US}\text{computer}\text{scientists}\text{with}\text{age}\text{between}{a}_1\text{and}{a}_2}{\text{US}\text{computer}\text{scientists}}$ For a₁and a₂ defined as the age ranges {22 to 34; 35 to 44; 45 to 65}.

Conditional on γ and θ and observations of {w_t, L_t, F_t} we are able to recover values of A_t implied by our model during the period of 1994 to 2004:

$$A_t=\frac{w_t}{\gamma {(L_t+\theta F_t)}^{\gamma -1}}$$

We assume that the economy is in steady state in 1994, such that Ā = A₁₉₉₄, and that it is hit by the series of shocks. In terms of expectations, we assume that both firms and individuals are surprised by changes in A_t.³² Note that following equation (6), firms and workers have essentially static expectations about future technology progress, such that 𝔼_t[A_t+j] = ≅ A_t for any j.

The remaining parameters {σ₀, α₀, λ₀, λ₁, λ₂, σ₁, α₁, c_R1, c_R2} are calibrated such that the model matches the observations of L_t, F_t, w_t, in two periods of time: 1994 and 2004, and the changes in the age structure $s_t^{a_1,a_2}$ in 2004.³³ We use a Nelder-Mead simplex method to find parameter values which yield solutions to the model under these data restrictions.³⁴ The intuition for the identification of the parameters comes straight from the data. For the given series of exogenous technological shocks and wages, variations of enrollment between 1994 and 2004 identify the parameters σ₀ and α₀, changes in native employment identify the parameters σ₁ and α₁, variations in foreign employment identify the recruitment cost parameters c_R1 and c_R2, and changes in the age structure of computer scientists identify the quadratic costs of switching occupations: parameters λ₀, λ₁, and λ₂.

4.2 Calibration results

We use the procedure described above to calibrate the model using three different values of γ: {0.25, 0.5, 0.75}.³⁵ We present the calibrated parameters for these different values of γ in Table 2 and a comparison of the data with the model’s output in Figures 3 – 4. We consider the demand elasticities derived from our γ’s to span a reasonable range of plausible values of this parameter, which as we describe in Section 4.4, is challenging to identify.

Table 2.

Calibrated Parameters

Parameter	Description	γ
Calibrated Parameters		0.25	0.50	0.75
		Calibrated Value
α0	Mean taste for not studying CS	0.0940	0.0943	0.0836
σ0	Std. dev. of study area taste shocks	0.0001	0.0001	0.0002
α1	Mean taste for not working in CS	0.3715	0.3486	0.3673
σ1	Std. dev. of occupation taste shocks	0.1385	0.1364	0.1439
cR1	Foreign linear recruitment cost	0.5247	0.5228	0.5221
cR2	Foreign quadratic recruitment cost	0.0102	0.0109	0.0124
λ0	Sector switching constant cost	0.1159	0.1164	0.1031
λ1	Sector switching linear cost	0.0138	0.0119	0.0151
λ2	Sector switching quadratic cost	0.0006	0.0004	0.0003
Economic Results
εLd,w	Long run effective labor demand elasticity	1.33	2.00	4.00
εLs,w	Long run US occupational labor supply elasticity	5.4612	5.5743	5.3404
εp,w	Long run US CS enrollment elasticity	11.6954	11.2624	11.7071
${\epsilon }_{L_s,w}^s$	Short run US occupational labor supply elasticity	0.5591	0.6745	0.6642
${\epsilon }_{p,w}^s$	Short run US CS enrollment elasticity	10.2834	11.3758	11.3386
ACF	Average cost of recruiting foreign worker	0.5312	0.5299	0.53

Note: The average cost of recruiting a foreign worker is measured in units of average annual US non-CS STEM worker wages. The parameter determines the labor demand elasticity to wages.

Figure 3.

Model and Counterfactual (1/2)

Note: The full model is the simulation of the economy using the calibrated parameters. The restricted model simulates the same calibrated model, but restricting firms to keep their foreign temporary worker CS employment to its 1994 value. Wages are relative to other STEM occupations. Employment and enrollment are shares of STEM workers and undergrad STEM enrollment, respectively, and are multiplied by 100. The parameter gamma determines the labor demand elasticity to wages. See Section 4 for details.

Figure 4.

Model and Counterfactual (2/2)

Note: The full model is the simulation of the economy using the calibrated parameters. The restricted model simulates the same calibrated model, but restricting firms to keep their foreign temporary worker CS employment to its 1994 value. Wages are relative to other STEM occupations. Employment and enrollment are shares of STEM workers and undergrad STEM enrollment, respectively, and are multiplied by 100. The parameter gamma determines the labor demand elasticity to wages. See Section 4 for details.

The calibrated model allows us to calculate several additional economically meaningful statistics, which we also include in the bottom segment of Table 2. We calculate the long-run occupation and enrollment elasticities with respect to wages, by replacing the demand side of the model with an exogenous wage, which we set to be permanently 1% higher than its 1994 value, and in each case, we allow the supply side to come to a new equilibrium based on the calibrated parameters. We similarly calculate the short-run occupation and enrollment elasticities, but instead of allowing the supply side to come to a new steady-state, we calculate the elasticities based off of changes in occupation and enrollment after 1 year.

In the bottom section of Table 2, we show how each of these long-run elasticities varies with γ. The long-run occupational labor supply elasticity for Americans is around 5.4. The enrollment in CS is even more elastic, with a long-run elasticity that lies around 11.6.³⁶ This result reflects the large enrollment response we witness in the data. The short-run occupation elasticity is much lower than the corresponding long-run elasticity. We expect this result, due to the supply frictions and lags in our model. In contrast, the short-run and long-run enrollment elasticities are almost exactly the same. Pre-enrollment students respond immediately to a wage shock. A fuller model which includes capacity constraints on the supply side of the higher education market, would work to slow such adjustments. Finally, the average cost of recruiting a foreign worker is about 0.53 times the average annual earnings of a non-CS STEM job.

In Figures 3–4, we report both the path predicted by our calibrated model (Full model) and the path observed in the data (Smooth data) during 1994–2009. Note that by the construction of our calibration procedure, the full model fits the data perfectly in 1994 and 2004. We use the transition period between 1995 to 2003 to evaluate how well the model fits the data, and the years 2005–2009 for out of sample prediction. These years include observed changes to relevant immigration laws, and potentially unobserved structural changes which would map to changes in our parameters, so our model has trouble fitting the data in this period for some series. Figure 3 shows that for different γ’s, the model is a fairly close fit for CS wages and American employment during the evaluation period, although CS wages in the model grow faster at first and American employment in CS grows more slowly in the model than the data. The fit of these two series is still relatively good in the out of sample prediction period, with wages slightly higher and American employment slightly lower in the model compared to the data.

Figure 4 shows that the enrollment output of the model is particularly sensitive to the choice of γ, where lower values somewhat under-predict the enrollment boom surrounding 2001. At odds with the predictions of our model, enrollment does not increase starting in 2006. Given the rising wages of computer scientists at the time, this pattern seems a bit surprising and we confess to not having a good understanding as to why enrollments do not seem to be responding to market signals. The figure also shows that foreign employment grows more slowly at first in the model than the data. In the out of sample period, foreign employment shrinks in the model instead of growing slightly, as in the data. This could be because our model assumes that after a 6-year period, foreigners return to their home country. In the Online Appendix, we calibrate a model that allows a certain fraction of H-1B workers to become permanent residents. This extension of the model does a better job of fitting the share of foreign employment in the last few years (and overall does a good job of fitting the different calibrated series).

4.3 Simulation of Fixed Foreign Worker Population Counterfactual

We use our calibrated model to simulate a counterfactual Internet boom from 1994–2004, as if firms had restrictions on the number of foreigners that they can hire. The exercise consists of hitting the calibrated model with the same technological shocks we derived before but imposing that firms cannot increase F_t above its 1994 level. The results of this simulation are also presented in Figures 3–4 (Restricted Model). There we can compare the counterfactual for different values of γ with the smoothed data.

Overall, our calibrated model implies an increase in the demand for domestic workers when firms cannot increase foreign employment above its 1994 level. As a result, we observe higher wages, US employment and computer science enrollment in the counterfactual economy. We simulate significant differences in the labor market for computer scientists during the Internet boom if firms had restrictions on the number of foreigners they could hire. While the data shows that the relative wages for CS workers increased by 3.2% between 1994 and 2004, in the simulated economy wages would have increased between 5.9% to 6.9% (decreasing with γ) during the same period. In terms of employment, we observe an increase of 41% of total CS employment during the Internet boom, while in the economy where we restrict foreign workers we find an increase of only 29.1% to 36.1% (decreasing with γ) during the same period. This change in employment results from the more inelastic labor supply curve that firms face when extra foreigners are not available.

In Table 3 we compare the 2004 levels of the variables of interest between the data and the simulated economy where firms could not increase foreign employment above its 1994 levels. We find that in 2004, CS workers wages would be 2.8% to 3.8% higher if firms had restrictions in the number of foreigners they could hire. Furthermore, the number of Americans working in the CS sector would be 7.0% to 13.6% higher in 2004, but the total employment level would be lower by 3.8% to 9.0%. Finally we find a significant difference in the number of students enrolling in computer science in the simulated counterfactual economy. Relative to other STEM fields, enrollment in CS would be 19.9% – 25.5% higher in 2004 if firms could not increase foreign employment during the Internet boom. These numbers reflect the fact that, according to our calibrations, students’ major choices are very sensitive to changes in wages.

Table 3.

Summary of Results from Counterfactual Simulation

% Differences between Simulated Economy Holding F Constant and Actual Outcomes in 2004
Variable	γ
	0.25	0.5	0.75
CS Wages	3.8%	3.2%	2.8%
CS US Native Employment	13.6%	12.5%	7.0%
CS Enrollment	25.5%	20.2%	19.9%
Total Employment	−3.8%	−4.6%	−9.0%

Note: The counterfactual simulates an economy from 1994–2009 in which the level of foreign CS workers is not allowed to increase from its 1994 value. The parameter determines the labor demand elasticity to wages. See section 4 for details.

To sum up, even when assuming a very elastic labor demand curve (high γ values) we find significant effects of foreign recruitment on wages and employment of domestic CS workers during the Internet boom. Additionally, firms would not replace all foreigners with domestic workers during this period if they were restricted to keeping the same foreign employment level of 1994, implying that industry output would be reduced.

4.4 Identification of Labor Demand

As shown previously, the labor market outcomes of the counterfactual simulations holding F_t fixed can vary with values of γ. In particular, we observe that when using a more elastic labor demand (higher γ), our simulated counterfactual economy (where we restrict foreigner workers) from section 4.3 has smaller increases in wages and US employment. The natural question is which, if any, of the 3 different γ’s yields results that are closest to what we would observe if firms had not been able to recruit foreigners during the Internet boom?

In a closed, constant returns to scale economy, the elasticity of demand for computer scientists would depend on both the substitutability between consumption of goods produced in sectors of the economy intensive in computer scientists and other goods, and on the substitutability between production of computers scientists and other factors of production. Given the fact that the share of computer scientists working in any one sector is not large,³⁷ the demand elasticity will be determined largely by the elasticity of substitution between computer scientists and other factors of production. In the relatively small window of time we are talking about, it is hard to believe these elasticities are that large.

There are two factors that mitigate this basic conclusion. First, to the extent that computer scientists contribute to innovation in the sectors of the economy intensive in computer scientist labor, the derived elasticity of demand for computer scientists in those sectors is likely to be higher than it would otherwise have been. In addition, the potential for off-shoring would drive up the derived elasticity of demand for computer scientists. However, even if, for these reasons, the derived demand for computer sciences in computer manufacturing and computer services was quite high, a small enough share of computer scientists work in these industries, that it is hard to believe either agglomeration effects or off-shoring can drive up the derived demand elasticity for computer scientists that much. Additionally, if it would have been easy for employers to outsource, CEOs like Microsoft’s Bill Gates would not have been lobbying to increase the H-1B visa cap. It is hard to reconcile the fact that the computer industry is lobbying so hard for easier access to foreigners, if it did not matter where their workforce was located.

Traditionally, exogenous shifts in supply are used to identify demand curves. In our case, while there is a plausibly exogenous component to the increased representation of the foreign born amongst the US Science and Engineering workforce, our visa system ensures that there is a large endogenous component. In theory, it might be possible to get some leverage on identifying the labor demand curve for CS workers by comparing the results of the counterfactual simulation for the different γ’s to the observations of what happened in the Information Technology (IT) sector in the the mid 1970s. Specifically, as described in Bound et al. (2013), during this earlier period, the IT sector experienced a significant transformation due to the introduction of the microprocessor, which generated an increase in the demand for IT workers. However, firms had substantially less access to foreign labor during that earlier boom than they did during the 1990s. This happened because there was a sharp increase in the supply of college graduates from overseas in the past decades, but also due to the change in the US visa system in the early 1990s that facilitated a greater inflow of high skilled foreigners via employer-sponsored visas.

Our strategy would be to use our calibrated model to simulate what would happen if firms had less access to foreign high-skilled labor in the 1990s boom and compare these simulations to the earlier boom. Comparisons between simulation results with different values of γ and what actually happened earlier would help narrow plausible values for γ. Intuitively, if demand is relatively elastic, the loss of access to foreigners would have relatively little impact on wages, but a large impact on total CS employment. Whereas a less elastic demand curve would have a large effect on wages and less of an effect on total CS employment. This kind of exercise is valid only under the strong assumptions that our economic model accurately reflects that labor market for IT workers, and that the demand and supply elasticities were the same during the two periods and that the two shocks generated shifts in the labor demand of roughly the same magnitude. However heroic such assumptions might be, the strategy fails for a simpler reason. The strategy requires comparing wage and employment changes for a small segment of the workforce across periods. Our estimates were simply not reliable enough for such exercises to be meaningful.

Given the data limitations and other complications discussed in this section, we cannot provide an estimate for the value of γ, but our discussion suggests that the elasticity of demand for computer scientists should not be too large and that the values presented in this paper cover a plausible range.

5 Discussion

The model we have developed in this paper suggests an intermediate position as the most reasonable one in the debate over the effects of high-skilled immigration, on US workers. Focusing on the tech boom of the 1990s, we develop a model that allows us to answer the counterfactual question: what would have happened to overall employment, to the employment of US residents, and to wages in the IT sector had the immigration of computer scientists been restricted to its level as of the early 1990s before the tech boom? Our results suggest a middle ground between the two sides of this debate.

First, our estimates suggest that even without foreign trained computer scientists, the supply of computer scientists to the US market is quite elastic, especially in the medium run, as the students induced to study computer science by the increased opportunities in the field begin to enter the market. For elasticities of demand that lie between −1.3 and −4.0, we show that had firms not been able to hire immigrants through the late 1990s, the wages of US trained computer scientists would have been 2.8% to 3.8% higher than they were, and there would have been 7% to 13.6% more Americans working as computer scientists.

At the same time our estimates suggest that were it not for the immigrant computer scientists that firms were able to hire, the growth in the number of computer scientists in the economy would have been significantly slowed. Our estimates suggest that total employment in the CS sector would have been 3.8–9% lower if firms were not able to hire additional immigrants during the late 1990s, thus implying that the fact that firms could hire immigrants during the 1990s increased output and lowered both input and output prices in the computer scientist intensive sectors of the economy. How much these developments benefited stock holders and consumers depends on the nature of the output market, which we have not tried to model. The increased employment of computer scientists would also have increased the demand for complementary production inputs, such as software marketing and sales workers. Furthermore, the availability of foreign CS workers made the CS labor supply curve more elastic, further enhancing this demand increase for complements.

Under the assumption that the tech boom of the 1990s exogenously increased the demand for computer scientists, we have been able to reliably estimate supply curves. Estimating the slope of the labor demand curve was substantially more difficult. In other contexts, labor economists have been willing to assume some degree of exogeneity to immigrant supplies. In the current framework, the institutional context implies that immigrant CS labor is completely endogenous to labor demand.

While we cannot reliably estimate the slope of the demand curve for computer scientists, we believe that we can reject any notion that the demand curve for computer scientists is close to perfectly elastic. Perfectly elastic demand curves are inconsistent with the rising wages for computer scientists that we observe during the 1990s. As long as the demand curve for computer scientists is downward sloping, the increased access employers had to foreign-trained, skilled immigrants during the 1990s works to lower both the wages and employment opportunities for US trained computer scientists.

Our paper should be viewed as a first-step towards modeling the US labor market for computer-scientists. In the model we incorporate features that were ignored in earlier models developed by Freeman (1976) and Ryoo & Rosen (2004). Specifically we model both the possibility that individuals might switch occupations, and the possibility that firms might hire immigrants from abroad. In the context of computer scientists both are clearly important. We focused on the market for computer scientists. In the context of other scientific fields where a masters or PhD are essential, it would also be important to model foreign participation in US graduate programs as well. Such an effort would need to model both the demand for and supply of higher education. While we believe that such an effort would be of considerable value, we leave it for future research.