Temperature response of bundle-sheath conductance in maize leaves

Highlight

Bundle-sheath conductance, g _bs , is commonly assumed to be independent of temperature. We report that temperature response of maize g _bs followed a peaked or non-peaked Arrhenius equation, triggering further investigations on this response.

Abstract

A small bundle-sheath conductance (g _bs) is essential for the C₄ CO₂-concentrating mechanism to suppress photorespiration effectively. To predict the productivity of C₄ crops accurately under global warming, it is necessary to examine whether and how g _bs responds to temperature. We investigated the temperature response of g _bs in maize by fitting a C₄ photosynthesis model to combined gas exchange and chlorophyll fluorescence measurements of irradiance and CO₂ response curves at 21% and 2% O₂ within the range of 13.5–39 °C. The analysis was based on reported kinetic constants of C₄ Rubisco and phosphoenolpyruvate carboxylase and temperature responses of C₃ mesophyll conductance (g _m). The estimates of g _bs varied greatly with leaf temperature. The temperature response of g _bs was well described by the peaked Arrhenius equation, with the optimum temperature being ~34 °C. The assumed temperature responses of g _m had only a slight impact on the temperature response of g _bs. In contrast, using extreme values of some enzyme kinetic constants changed the shape of the response, from the peaked optimum response to the non-peaked Arrhenius pattern. Further studies are needed to confirm such an Arrhenius response pattern from independent measurement techniques and to assess whether it is common across C₄ species.

Introduction

C₄ crop species have the CO₂-concentrating mechanism (CCM) in photosynthesis, which raises the partial pressure of CO₂ in bundle-sheath cells to a very high level, thereby minimizing the oxygenation activity of Rubisco and the loss by photorespiration (Hatch et al., 1995). This explains why C₄ food crops such as maize (Zea mays L.) generally have higher productivities than their C₃ counterparts (Ort and Long, 2014), at least under relatively warm conditions, and why C₄ species are preferred as a major source of sustainable bioenergy production (Heaton et al., 2008; Slattery and Ort, 2015).

The CCM mechanism in C₄ crops requires a number of biochemical, physical, and structural adaptations, especially the Kranz anatomy including the specialization of the mesophyll and bundle-sheath cells (Hatch et al., 1995; Leegood, 2002; Kromdijk et al., 2014). In C₄ photosynthesis, CO₂ is first fixed via phosphoenolpyruvate carboxylase (PEPc) in mesophyll cells into C₄ acids, which are then transported into bundle-sheath cells where the C₄ acids are decarboxylated and the released CO₂ is refixed by Rubisco. An efficient CCM would require that (i) PEPc has higher CO₂ affinity and carboxylation capacity than Rubisco; and (ii) the rate of CO₂ leakage from bundle-sheath cells back into mesophyll cells (L) is low.

This CO₂ leakage rate L depends on both the bundle-sheath conductance for CO₂ (g _bs) and the gradient between the CO₂ concentration in mesophyll cells (C _m) and that around the carboxylation sites in bundle-sheath cells (C _c): L=g _bs(C _c –C _m) (von Caemmerer and Furbankm 1999; Kromdijk et al., 2014). Therefore, g _bs is an important parameter for the effectiveness of CCM. We have previously analysed how g _bs responds to nitrogen supply, and showed that g _bs increases with increasing leaf nitrogen content (Yin et al., 2011)—a trend similar to that found for mesophyll conductance (g _m) in response to leaf photosynthetic capacity in C₃ photosynthesis (e.g. Loreto et al., 1992). It has been well established that g _m in C₃ photosynthesis responds to leaf temperature (Bernacchi et al., 2002; Warren and Dreyer, 2006; Yamori et al., 2006; Scafaro et al., 2011; Evans and von Caemmerer, 2013; Walker et al., 2013), although the effects differ greatly among species (von Caemmerer and Evans, 2015). Massad et al. (2007) have parameterized temperature dependence of some C₄ parameters such as the maximum rates of PEPc carboxylation (V _pmax), of Rubisco carboxylation (V _cmax), and of electron transport. However, there is hardly any information in the literature on whether and how g _bs responds to leaf temperature. Reports of Kubien et al. (2003) and von Caemmerer et al. (2014) on the temperature effect on leakiness (ϕ; which is defined as L/V _p, where V _p is the PEPc carboxylation rate) indirectly suggest that g _bs, among many C₄ parameters, may (co-)vary with temperature. To the best of our knowledge, only one study (Kiirats et al., 2002) has directly reported on the temperature response of g _bs: g _bs increased almost linearly with increasing leaf temperature within the range of 16–35 °C. That study used a PEPc mutant of Amaranthus edulis with a defective C₄ cycle. However, concerns have been raised about potential alterations of Rubisco kinetic constants, gas diffusion resistance, and bundle-sheath cell structure by the PEPc mutation (He and Edwards, 1996).

Given the effect of elevating atmospheric CO₂ and global warming, it is necessary to assess the production potential of C₄ species, as well as whether their relative advantages over C₃ species vary, under climate change. Like the widely used C₃ photosynthesis model of Farquhar et al. (1980), the C₄ biochemical models (Berry and Farquhar, 1978; von Caemmerer and Furbank, 1999) or their variants (Collatz et al., 1992; Chen et al., 1994; Yin and Struik, 2009a) are now increasingly coupled with stomatal conductance models and applied to a general ecosystem or crop simulation framework. However, these modelling studies all assume that g _bs does not vary with temperature, even when applied to a wide range of natural field environments. To apply the biochemical C₄ photosynthesis model to assess the (relative) production potentials and their response to climate change variables, information on the effects of temperature on g _bs is urgently needed. The objectives of this study are to assess whether or not g _bs in leaves of a maize cultivar responds to leaf temperature and, if so, to quantify the magnitude of this effect over a wide range of temperatures. To that end, we use the method of Yin et al. (2011) that can estimate g _bs by fitting a C₄ photosynthesis model to a wide range of data covering different amounts of photorespiration.

Materials and methods

Experimental set-up

An experiment was conducted in a glasshouse at Wageningen University, using maize cv. ‘Atrium’. To spread out the measurement work in time, a weekly staggered sowing was carried out on 28 August and 4, 10, and 18 September 2014, respectively, to grow plants for four replicate measurements. Plants were transplanted 7 d after sowing to pots of 12 litres, with one plant per pot. The initial soil nutrient contents were: 1.23g of nitrogen, 0.69g of phosphate, and 2.49g of potassium per pot. Extra nutrients came from 10.3g per pot of a slow-release fertilizer ‘Osmocote Pro’ (which contained 17% N, 11% P₂O₅, 10% K₂O, 2% MgO plus trace elements). Temperature in the glasshouse was 27±2 °C for daytime and 21±1 °C for night-time . Photoperiod was maintained at 12h d⁻¹ (8:00–20:00h), and relative humidity ranged between 60% and 70%. Of the photosynthetically active radiation incident on the glasshouse, 60% was transmitted to plant level. During daytime, supplemental light from 600W HPS Hortilux Schréder lamps (Monster, The Netherlands; 0.4 lamps m⁻²) was switched on automatically as soon as the global solar radiation incident on the glasshouse dropped below 400W m⁻², and then switched off if it exceeded 500W m⁻². The supplementary light largely ensured that, despite the staggered sowing, plants for measurements grew under similar light intensities.

Photosynthesis measurements

After growth in the glasshouse for ~6 weeks, plants were moved to a climate room illuminated by cool-white fluorescent tubes (~350 μmol m⁻² s⁻¹ at leaf level), where all measurements were undertaken. We used an LI-6400XT open gas exchange system with an integrated fluorescence chamber head, enclosing 2cm² areas, for combined gas exchange and chlorophyll fluorescence measurements, which were done on fully expanded leaves at the seventh leaf layer counted from below. The CO₂ response curves were taken under both 21% and 2% O₂ conditions, and the ambient CO₂ (C _a) steps were: 370, 200, 100, 85, 70, 55, 370, 370, 370, 500, 700, and 1500 μmol mol⁻¹ (~4min per step) while keeping incident irradiance (I _inc) at 1500 μmol m⁻² s⁻¹ (while measurements were done four times at 370 μmol mol⁻¹, data of only the first and fourth times were included for the analysis). For light response curves, I _inc was of the order of 2000, 1500, 1000, 500, 200, 100, 80, 60, 40, and 20 μmol m⁻² s⁻¹ (~8min per step), while keeping C _a either at 250 μmol mol⁻¹ for 21% O₂ or at 1000 μmol mol⁻¹ for 2% O₂ conditions; this was done to induce different levels of photorespiration. Gas from a cylinder containing a mixture of N₂ and required O₂ was humidified and supplied via an overflow tube to the air inlet of the LI-6400XT where CO₂ was blended with the gas, and the IRGA calibration was adjusted for O₂ composition of the gas mixture according to the manufacturer’s instructions.

Each curve was made at six set-point leaf temperatures (13.5, 18, 25, 30, 34, and 39 °C), of which extreme temperatures (13.5, 34, and 39 °C) were achieved not only by setting the temperature in the LI-6400XT measuring head but also by adjusting the temperature of the climate room. Measurement of one replicate took 5 d and was done on the same leaf for all temperatures. Any influence of different measuring days was minimized by randomizing temperatures and measuring days among the replicates. In total, 48 (i.e. 6 temperatures×4 replicates×2 O₂ levels) light response curves and 48 CO₂ response curves were generated. Leaf-to-air vapour pressure difference increased with leaf temperature, but was always within the range of 0.5–2.0 kPa, within which little impact of vapour pressure difference on stomatal conductance is expected (Bernacchi et al., 2002). The measurement flow rate was 400 μmol s⁻¹. CO₂ exchange rates were corrected for CO₂ leakage into and out of the leaf cuvette, based on measurements at specific temperatures using the same flow rate on boiled leaves across a range of CO₂ levels, and intercellular CO₂ levels (C _i) were then re-calculated.

For each step of light or CO₂ response, when the CO₂ exchange rate reached steady state, steady-state fluorescence (F _s) was measured. Dwyer et al. (2007) have shown that for C₄ leaves, the multiple-flash method is more reliable than the traditional single-flash method in measuring the maximum fluorescence (F _m′). The F _m′ was therefore obtained from using the multiphase flashes: the flash intensity was ~8000 µmol m⁻² s⁻¹ during phase 1 for a duration of 300ms, was attenuated by 35% during phase 2 for ~300ms, and was back to ~8000 µmol m⁻² s⁻¹ for phase 3 of 300ms. The intercept of the linear regression of fluorescence yields against the inverse of the flash intensity during phase 2 gives the estimate of F _m′ (Loriaux et al. 2013). The apparent operating efficiency of photosystem II (PSII) e⁻ transport was obtained as: ∆F/F _m′=(F _m′–F _s)/F _m′ (Genty et al., 1989; Schreiber et al., 1995).

The portions of the leaf used for above measurements were excised afterwards, with a punch that produced a disc of ~5cm² per leaf portion. The leaf discs were then weighed after drying at 70 °C to constant weight, and total N content was analysed using an element C/N analyser (Flash 2000, Thermo Scientific) based on the Micro-Dumas combustion method.

Modelling

The model of von Caemmerer and Furbank (1999), as modified by Yin et al. (2011), was used to estimate g _bs (see Supplementary appendix A at JXB online). The first modification was to include all four combinations of rate limitations to describe CO₂ and light response curves of the C₄ leaf CO₂ assimilation rate (A) more smoothly:

$$A=\text{min}\left(A_{\text{EE}},A_{\text{ET}},A_{\text{TE}},A_{TT}\right)$$ (1)

where A _EE is the net CO₂ assimilation rate when both C₄ and C₃ cycles are limited by enzyme activity, A _ET is the net rate when the C₄ cycle is limited by enzyme activity and the C₃ cycle is limited by e⁻ transport, A _TE is the rate when the C₄ cycle is limited by e^- transport and the C₃ cycle is limited by enzyme activity, and A _TT is the rate when both C₄ and C₃ cycles are limited by e⁻ transport. The formulation of von Caemmerer and Furbank (1999) used only two combinations, namely A=min(A _EE,A _TT). The second modification was to consider mesophyll conductance (g _m) explicitly so that A is modelled using C _i (rather than mesophyll CO₂ level C _m) as input, as C _m is not measured. The model considering g _m becomes more complicated, and Yin et al. (2011) presented an analytical solution for each of the four limitations (see Supplementary appendix A). The third modification was to use the potential rate of ATP production (J _atp), instead of the potential rate of e⁻ transport rate (J), because energy is partitioned between C₄ and C₃ cycles ultimately in terms of ATP (rather than in terms of electron) requirement. von Caemmerer and Furbank (1999) implicitly assumed that J _atp=J, whereas the analysis of Yin and Struik (2012) showed that J _atp may not equal J.

We estimated the value of J _atp empirically from chlorophyll fluorescence measurements, according to Yin et al. (2011):

$$J_{\text{atp}}=s\prime I_{\text{inc}}(\Delta F/F_{\text{m}}\prime )/\left(\text{1}-x\right)$$ (2)

where x is the fraction of ATP partitioned to the C₄ cycle (set to 0.4; von Caemmerer and Furbank 1999), and s′ is a lumped parameter resulting as the slope from the linear regression of A measured under low irradiances (≤500 µmol m⁻² s⁻¹) against I _inc(∆F/F _m′)/3 using only the data at 2% O₂ combined with high CO₂, at which photorespiration is suppressed. The intercept of the same linear regression will give the estimate of day respiration (R _d) (Yin et al., 2011). It is worth noting the importance of only using an e⁻ transport-limited range of data for estimating s′ which calibrates for the impact of any basal alternative e⁻ transport. Impacts of any additional alternative e⁻ transport, such as under high I _inc or low C _i conditions, arising from the higher J _atp than required for C₄ and C₃ cycles, are accounted for by Equation 1 via assigning to enzyme activity-limited rates.

The model of von Caemmerer and Furbank (1999) was proposed for the reference temperature 25 °C. To be applied for a range of varying temperatures, the potential variation of relative O₂/CO₂ diffusivities and solubilities with temperature needs to be quantified. This is presented in Supplementary appendix B, based on data in the literature (e.g. Frank et al., 1996; Han and Bartels, 1996).

Pre-determination of some photosynthetic parameters

To use the model to estimate g _bs, a number of other input parameter values are required (see Table 1 for parameter definitions). The Rubisco kinetic parameters (V _cmax, γ*, K _mC, and K _mO), the PEPc Michaelis–Menten constant (K _p), and R _d are expected to increase with temperature, and this is conventionally described by an Arrhenius function normalized at 25 °C:

Table 1.

Model input parameters, with their default values as derived from the literature or in this study

Symbol	Definition	Value	Source
α	Fraction of PSII activity in the bundle sheath	0.1	Chapman et al. (1980)
R m	Mitochondrial respiration in the mesophyll	0.5R d	von Caemmerer and Furbank (1999)
x	Fraction of ATP allocated to the C4 cycle	0.4	von Caemmerer and Furbank (1999)
K p25	Michaelis–Menten constant of PEPc for CO2 at 25 °C	40 μbar	Leegood and von Caemmerer (1989); Pfeffer and Peisker (1995)
K mC25	Michaelis–Menten constant of Rubisco for CO2 at 25 °C	485 μbar	Cousins et al. (2010)
K mO25	Michaelis–Menten constant of Rubisco for O2 at 25 °C	146 000 μbar	Cousins et al. (2010)
γ*25	Half the reciprocal of Rubisco specificity at 25 °C	0.0001747	Cousins et al. (2010)
E Vcmax	Activation energy for V cmax (maximum Rubisco activity)	53.4 kJ mol−1	Sage (2002); Kubien et al. (2003); Perdomo et al. (2015)
E γ*	Activation energy for γ*	27.4 kJ mol−1	Derived from data of Jordan and Ogren (1984)
E KmC	Activation energy for K mC	35.6 kJ mol−1	Perdomo et al. (2015)
E KmO	Activation energy for K mO	15.1 kJ mol−1	Derived from results of Perdomo et al. (2015)
E Vpmax	Activation energy for V pmax (maximum PEPc activity)	37.0 kJ mol−1	Derived from data of Chinthapalli et al. (2003)
D Vpmax	Deactivation energy for V pmax	214.5 kJ mol−1	Derived from data of Chinthapalli et al. (2003)
S Vpmax	Entropy term for V pmax	0.663 kJ K−1 mol−1	Derived from data of Chinthapalli et al. (2003)
E Kp	Activation energy for K p	68.1 kJ mol−1	Estimated in our report (see text)
E gm	Activation energy for g m (mesophyll conductance)	49.6 kJ mol−1	Bernacchi et al. (2002)
D gm	Deactivation energy for g m	437.4 kJ mol−1	Bernacchi et al. (2002)
S gm	Entropy term for g m	1.4 kJ K−1 mol−1	Bernacchi et al. (2002)

PEPc, phosphoenolpyruvate carboxylase; PSII, photosystem II.

$$\text{Parameter }={\text{Parameter}}_{25}\cdot e^{\frac{E}{R}\left(\frac{1}{298}-\frac{1}{273+T}\right)}$$ (3)

where R is the universal gas constant (0.008314 kJ K⁻¹ mol⁻¹) and E is the activation energy (kJ mol⁻¹) for the parameter. It is impossible to derive a complete set of in vivo kinetic constants of C₄ photosynthesis, and we mostly used in vitro values as reported in the literature. Values of γ*, K _mC, K _mO, and K _p at the reference temperature 25 °C (Table 1) were the same as those we used previously (Yin et al., 2011), based on data for maize (e.g. Cousins et al., 2010). Other parameter values are hardly available for maize, and the values used are summarized below.

• (i) Sage (2002), Kubien et al. (2003), and Perdomo et al. (2015) reported the activation energy E of V _cmax. Sage′s data on E _Vcmax for seven C₄ species range from 50.1 kJ mol⁻¹ for Cynodon dactylon and 53.5 kJ mol⁻¹ for Flaveria trinervia to 68.0 kJ mol⁻¹ for Amaranthus retroflexus. Kubien et al. (2013) reported 56.1 kJ mol⁻¹ within 18–42 °C for Flaveria bidentis. E _Vcmax values reported by Perdomo et al. (2015) for Flaveria bidentis and Flaveria trinervia were 47.6 kJ mol⁻¹ and 48.8 kJ mol⁻¹, respectively. Despite the variation of E _Vcmax even for the same species, E _Vcmax for C₄ species did not differ greatly from that for C₃ species (Sage, 2002; Perdomo et al., 2015). The average E _Vcmax of the three reports for C₄ species was used here (Table 1).

• (ii) Jordan and Ogren (1984) were the first to report on Rubisco specificity from 5 °C to 35 °C of a C₄ species Amaranthus hybridus, from which we derived the activation energy for γ* (Table 1). This estimate is quite similar to the value of Bernacchi et al. (2002) for C₃ species, and the report of Boyd et al. (2015) for a C₄ species Setaria viridis.

• (iii) The activation energy for K _mC of C₄ Rubisco was based on the recent report of Perdomo et al. (2015) on two Flaveria C₄ species (Table 1).

• (iv) Little is known for the activation energy for K _mO of C₄ Rubisco, and Table 1 gives its value that we derived from data of Perdomo et al. (2015) on activation energies for specificity (S _c/o) and K _mC, using the formula K _mO=S _c/o K _mC(V _omax/V _cmax) (where V _omax is the maximum oxygenation rate of Rubisco) and assuming that the V _omax:V _cmax ratio does not vary with temperature (i.e. activation energy for this ratio=0). The latter assumption was based on reports that the activation energy for V _omax:V _cmax of C₃ Rubisco is either small (Bernacchi et al., 2001) or inconsistent (either positive or negative) across species (von Caemmerer and Quick, 2000; Walker et al., 2013). This is in line with the C₃ photosynthesis modelling (Farquhar et al., 1980) that V _omax:V _cmax is set to be independent of temperature. The derived activation energy for K _mO (15.1 kJ mol⁻¹) is only slightly higher than 10.5 (±4.8) kJ mol⁻¹, the value that Boyd et al. (2015) published for S. viridis while we were revising our paper. Our E _KmO corresponds to a Q ₁₀ factor of ~1.23, very close to the value 1.20 that Chen et al. (1994) used. Sensitivity analysis showed that the temperature response of g _bs was least sensitive to E _KmO (see the Results).

• (v) V _pmax follows an optimum response to temperature (Chinthapalli et al., 2003; Massad et al., 2007; Boyd et al., 2015). This optimum response can be described by the peaked Arrhenius function (Medlyn et al. 2002):

  $$\text{Parameter }={\text{Parameter}}_{25}{e}^{\frac{E}{R}\left(\frac{1}{298}-\frac{1}{273+T}\right)}\frac{1+e^{\left(S-D/298\right)/R}}{1+e^{[S-D/(273+T)]/R}}$$ (4)
  where S is an entropy term (kJ K⁻¹ mol⁻¹), and E and D are energies of activation and deactivation (kJ mol⁻¹), respectively. Differentiating Equation 4 gives the optimum temperature T _opt (°C) as:

  $$T_{\text{opt}}=\frac{D}{S+R\ln (D/E-1)}-273$$ (5)

• We used the in vitro data of Chinthapalli et al. (2003) for Amaranthus hypochondriacus, which cover a very wide range of temperatures from 15 °C to 50 °C, to fit Equation 4 to derive values for S, E, and D of V _pmax (Table 1). These estimates resulted in an estimate of T _opt=44.4 °C.

• (vi) Little is known about the activation energy of K _p. We examined the initial slope of A–C _i curves at 2% O₂, since A at low C _i is limited by the PEPc activity (Sage and Kubien, 2007) and can be approximated to C _i V _pmax/(C _i+K _p)–R _m (von Caemmerer and Furbank, 1999). The first-order derivative of this equation, dA/dC _i, is K _p V _pmax/(C _i+K _p)², and was set to equal the slope value of the initial linear part of the A–C _i curve. The initial linear slope of the A–C _i curve followed an optimum response to temperature (see the Results) and this response is expected to result from temperature responses of both K _p and V _pmax. Using the pre-estimated temperature response parameters of V _pmax, we then derived the activation energy for K _p by fitting combined Equation 3 and dA/dC _i=K _p V _pmax/(C _i+K _p)² to data on the initial linear slope of the A–C _i curves over the six temperatures. We will confirm our estimate on E _Kp from fitting a full model to data of the initial part of A–C _i curves (see the Results).

• (vii) Mesophyll conductance (g _m) may be a significant limiting factor for C₄ photosynthesis (Pfeffer and Peisker, 1998), has an impact on estimation of leakiness (von Caemmerer et al., 2014), and its role in estimating g _bs has yet to be quantified. However, g _m for C₄ photosynthesis is hard to estimate (Pfeffer and Peisker, 1998; Barbour et al., 2016), let alone its temperature response parameters. We took the widely used values of Bernacchi et al. (2002) for g _m in C₃ photosynthesis, which include E, D, and S as quantified in Equation 4 (Table 1). This approach assumes that C₃ and C₄ photosynthesis have a similar relative response of g _m to temperature, although g _m in C₄ does not involve chloroplast-related resistance components. Our assumption for the same relative response of the overall g _m to temperature for C₃ and C₄ leaves will be tested through a sensitivity analysis.

Curve fitting and sensitivity analysis

With all these parameters pre-determined, we estimated g _bs of the six temperatures as well as g _m25, V _cmax25, V _pmax25 (i.e. g _m, V _cmax, V _pmax at 25 °C, respectively), by the non-linear curve-fitting using Equation 1 in combination with solutions in Supplementary appendix A. We used a dummy variable approach (Yin et al., 2009), in which we introduced six dummy variables to correspond to six temperatures, allowing us to estimate treatment-specific parameters (i.e. g _bs at six temperatures) and common parameters (i.e. g _m25, V _cmax25, and V _pmax25) simultaneously. The statistical fitting algorithms, implemented in SAS, autoassigned the range of data points to each of the four limitations as defined by Equation 1. The g _bs estimates when plotted against leaf temperature followed an optimum response (see the Results), and parameters characterizing this response were derived from fitting the estimated g _bs to Equation 4. All required curve fitting was carried out using the least-squares non-linear regression with the GAUSS method in PROC NLIN of SAS (SAS Institute Inc., Cary, NC, USA). The SAS codes for estimating g _bs parameters are available from the corresponding author upon request.

Regardless of the technique used, estimates for kinetic constants of Rubisco are full of uncertainties (Kubien et al., 2008; Cousins et al., 2010), so are the constants of PEPc (Pfeffer and Peisker, 1998) and of g _m (Silim et al., 2010; Walker et al., 2013). Also, the input values of some constants were not determined exclusively for maize. Therefore, a full sensitivity analysis on the g _bs estimates was conducted with respect to these input parameters in Table 1, except for x and α. The value of x is expected to be very invariant in terms of the ATP requirement between C₄ and C₃ cycles (von Caemmerer and Furbank, 1999), and a previous analysis (Yin et al., 2011) showed little sensitivity of g _bs to parameter α.

Results

Overall response curves of A and ∆F/F _m′ to CO₂ and irradiance

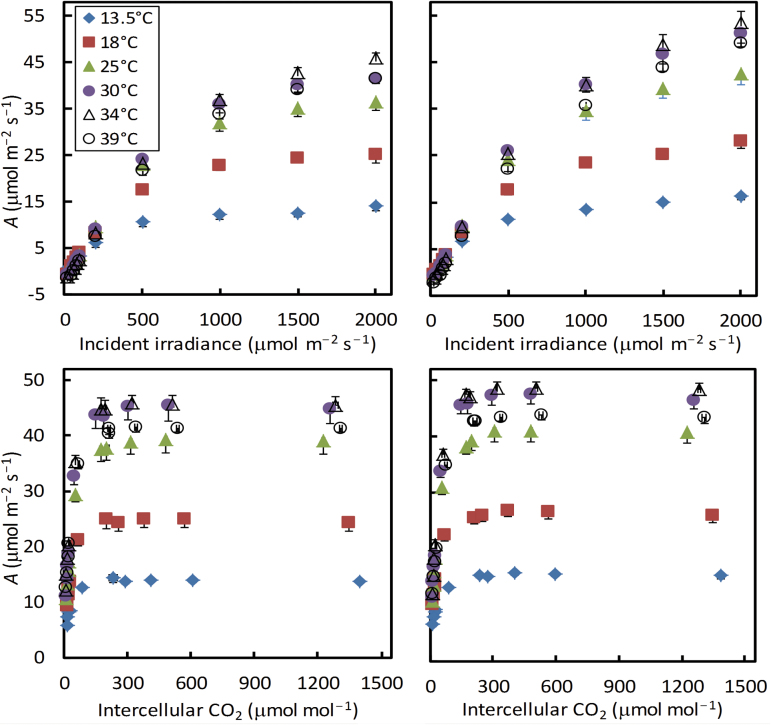
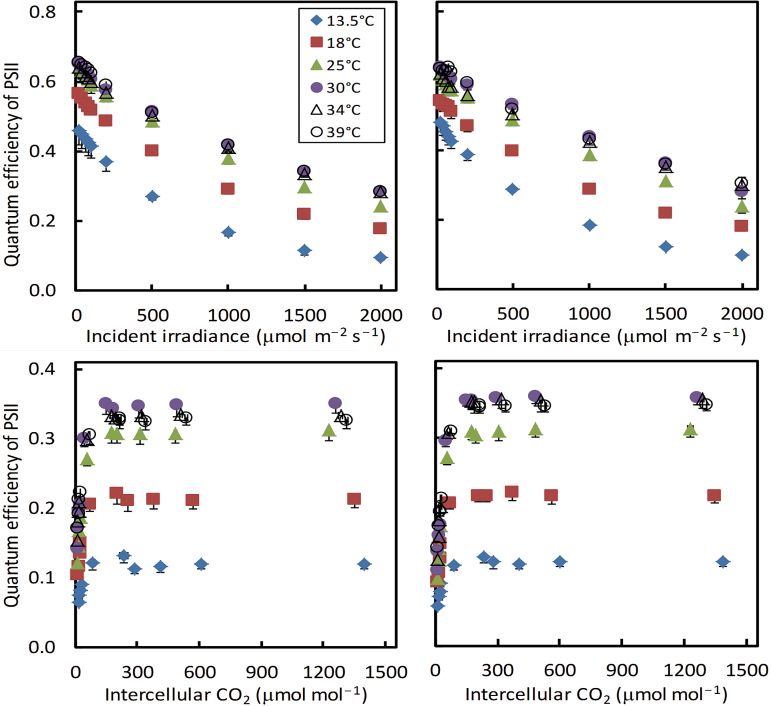
Our experimental results at the six temperatures showing typical irradiance and CO₂ responses of the C₄ photosynthesis rate were obtained (Fig. 1). The non-photorespiratory condition (2% O₂ combined with 1000 μmol mol⁻¹ C _a) had a moderate positive effect on the irradiance response curves, compared with the curves of 21% O₂ combined with 250 μmol mol⁻¹ C _a. Temperature strongly affected both irradiance and CO₂ response curves, and its effect was more significant from 13.5 °C to 25 °C than from 25 °C to 39 °C. The maximum photosynthesis was observed at ~34 °C. The effect of temperature on photosynthesis was reflected by the data for temperature effect on ∆F/F _m′, the apparent operating efficiency of PSII e⁻ transport (Fig. 2).

Fig. 1.

Net CO₂ assimilation rate A at six leaf temperatures in response to incident irradiance or to intercellular CO₂ levels under 21% (left panels) or 2% (right panels) O₂ conditions. Each symbol represents the mean of four replicated leaves (SEMs are visible in bars if larger than the symbols).(This figure is available in colour at JXB online.)

Fig. 2.

Apparent operating quantum efficiency of photosystem II (PSII) electron transport (Φ₂ or ∆F/F _m′) at six leaf temperatures in response to incident irradiance or to intercellular CO₂ levels under 21% (left panels) or 2% (right panels) O₂ conditions. Each symbol represents the mean of four replicated leaves (SEMs are visible if larger than the symbols). (This figure is available in colour at JXB online.)

Estimates of s′ and R _d

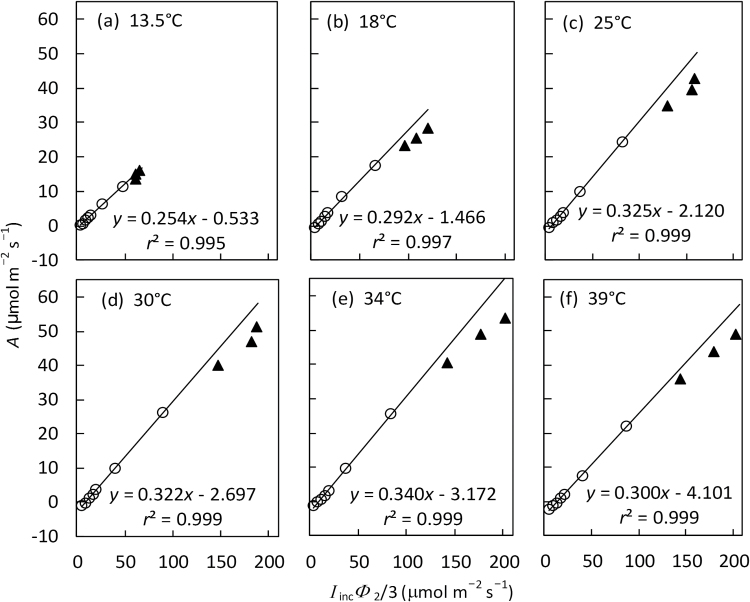
The relationship between A and I _inc(∆F/F _m′)/3 measured at low irradiances (≤500 µmol m⁻² s⁻¹) under non-photorespiratory conditions was linear for all temperatures (Fig. 3). The slope of this linear relationship gives the estimate for s′, a lumped parameter for calculating J _atp (see Equation 2), and its intercept gives the estimate of R _d (day respiration). Data points of higher irradiances (>500 µmol m⁻² s⁻¹) lay below the linear trend for all temperatures (Fig. 3), indicating that A was limited by A _EE or A _TE (see Equation 1) at high irradiances.

Fig. 3.

The relationship between net CO₂ assimilation rate A and the lumped variable I _incΦ₂/3 (mean of four replicates) from irradiance response curves under non-photorespiratory conditions (i.e. at 2% O₂ combined with high CO₂) at six leaf temperatures. Open circles are for I _inc ≤500 μmol m⁻² s⁻¹ and filled triangles come from the three levels of I _inc >500 μmol m⁻² s⁻¹. The lines represent linear regression based on data with I _inc ≤500 μmol m⁻² s⁻¹, in which the slope gives the estimate of calibration factor s′ and the intercept gives the estimate of day respiration R _d (see the text).

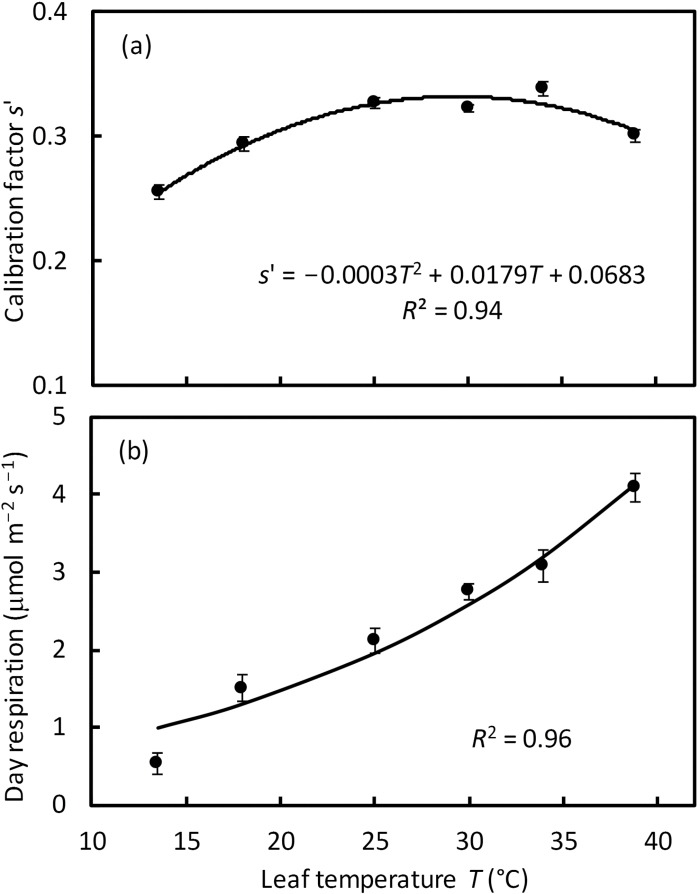
The estimated calibration factor s′ varied from 0.25 to 0.34, and its response to temperature can be empirically described by a quadratic equation with the optimum temperature at ~30 °C (Fig. 4a). As expected, the estimated values of R _d increased with increasing temperature (Fig. 4b). This response was well described by the Arrhenius equation, Equation 3, with the estimated R _d at 25 °C being 1.95 μmol m⁻² s⁻¹ and the activation energy being 41.9 kJ mol⁻¹ (Table 2).

Fig. 4.

(a) Temperature response of the estimated calibration factor s′, and (b) temperature response of the estimated day respiration R _d. Values of s′ and R _d were estimated as the slope and the intercept, respectively, of linear regression in Fig. 3. In (b), the curve represents the Arrhenius plot of Equation 3 with estimated parameter values in Table 2. Bars in (a) and (b) represent SEs of the estimates.

Table 2.

Values (standard errors of the estimates in parentheses) of parameters at the reference temperature 25 °C, activation energy E in Equation 3 for day respiration (R _d), as well as activation energy E, deactivation energy D, and entropy term S of Equation 4 for bundle-sheath conductance (g _bs) and its optimum temperature T _opt calculated from Equation 5, of maize leaves, as estimated from data in the present study

Parameter	Estimate at 25 °C	E (kJ mol−1)	D (kJ mol−1)	S (kJ K−1 mol−1)	T opt (°C)
R d	1.95(0.14) μmol m−2 s−1	41.85 (5.32)	NA	NA	NA
g m	1.33(0.06) mol m−2 s−1	–	–	–	–
V cmax	49.0(0.9)μmol m−2 s−1	–	NA	NA	NA
V pmax	119.2(4.1)μmol m−2 s−1	–	–	–	–
g bs	2.87(0.31) mmol m−2 s−1	116.77 (30.39)	264.60 (51.96)	0.86 (0.16)	33.9

NA, not applicable; –, not estimated from data of the present study, and most of them are given in Table 1, based on data in the literature, and were used as input to our present model analysis.

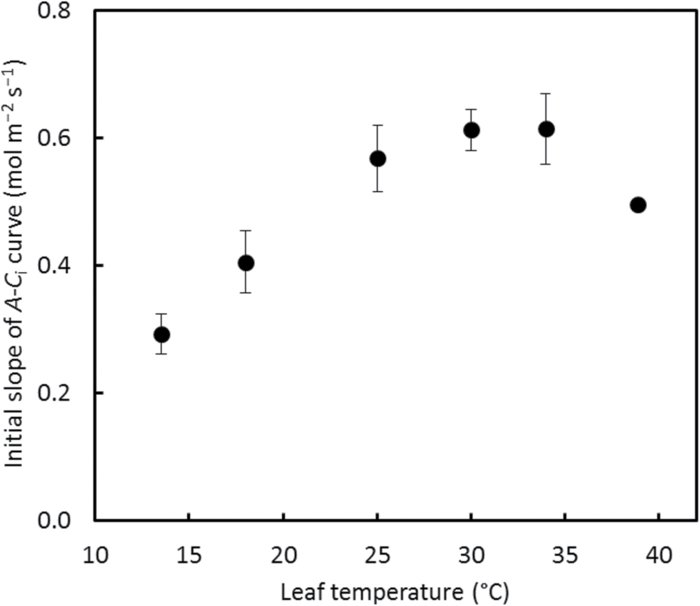
Initial slope of A– C _i curves

The A–C _i curves at 2% O₂ for the first three (for 13.5 °C) or four (for the remaining temperatures) points were essentially linear (Supplementary Fig. S1). The slope of this initial linear section of A–C _i curves at six temperatures followed an optimum response to temperature (Fig. 5), and this response is expected to result from temperature responses of both K _p and V _pmax. Using the pre-estimated temperature response parameter values of V _pmax (Table 1), we estimated the activation energy for K _p by fitting combined Equation 3 and dA/dC _i=K _p V _pmax/(C _i+K _p)² to data in Fig. 5 for the initial slope of A–C _i curves at the six temperatures. The estimated E _Kp, the activation energy for K _p, was 68.1 (SE 6.8) kJ mol⁻¹ (Table 1).

Fig. 5.

Temperature response of the initial slope of the A–C _i curve at 2% O₂. The error bar of each point indicates ±SEM of four replicated leaves. The error bar of the last point is smaller than the symbol.

Estimated response of g _bs to temperature

With s′, R _d, and E _Kp pre-fixed as presented above and other input parameters available (Table 1), we were able to estimate g _m25, V _cmax25, V _pmax25, and g _bs of the six temperatures by fitting our model (Equation 1 combined with solutions given in the Supplementary data) to all data collected in the experiment. The model described the whole data set across A–C _i and A–I _inc curves at 2% and 21% O₂, with R ²=0.98 and relative root-mean-square error rRMSE (RMSE×100/the mean of measured A)=12.0%, and a plot comparing modelled and measured A–I _inc and A–C _i curves is given in Supplementary Fig. S2 for 21% O₂. The obtained g _m25 was 1.33mol m⁻² s⁻¹, V _cmax25 was 49.0 μmol m⁻² s⁻¹, and V _pmax25 was 119.2 μmol m⁻² s⁻¹ (Table 2), meaning that the V _pmax25:V _cmax25 ratio is 2.43. We measured leaf N content, which was 1.10 (SE 0.05) g m⁻². Assuming the base leaf nitrogen content for photosynthesis is 0.24g m⁻² (Yin et al. 2011), the slope of V _cmax and V _pmax versus leaf N is 57.7 μmol and 140.3 μmol (g N)⁻¹ s⁻¹, respectively.

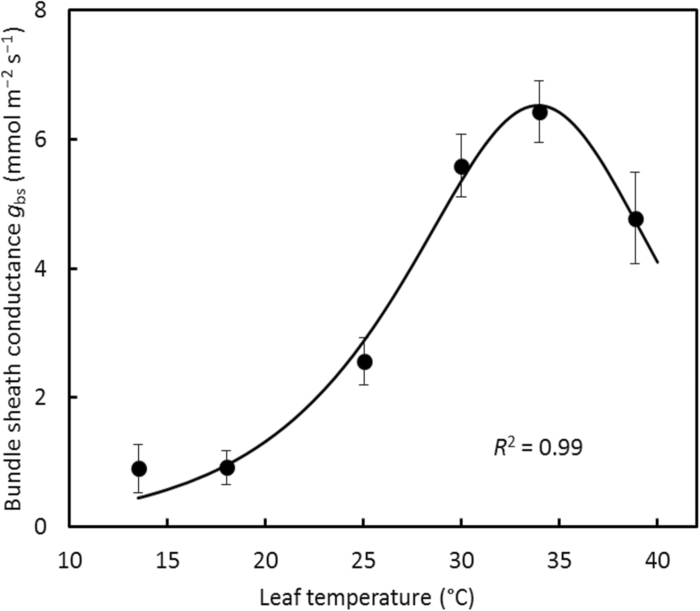
The estimated g _bs clearly varied with leaf temperature, and this response can be well described by the peaked Arrhenius equation, Equation 4 (Fig. 6). The obtained parameters of Equation 4 are: g _bs25=2.87 mmol m⁻² s⁻¹, E=116.7 kJ mol⁻¹, D=264.6 kJ mol⁻¹, and S=0.86 kJ K⁻¹ mol⁻¹ (Table 2). These parameter values of the peaked Arrhenius equation predicted, according to Equation 5, 34 °C as the optimum temperature for g _bs.

Fig. 6.

Temperature response of estimated bundle-sheath conductance g _bs in maize leaves. The error bar at each point represents ±SE of the estimate. The curve represents the peaked Arrhenius fit of Equation 4 with estimated values of the parameters in Table 2.

If we set g _bs independent of temperature, the obtained estimates from fitting to our data would be: g _m25=4.37mol m⁻² s⁻¹, g _bs=4.53 mmol m⁻² s⁻¹, V _cmax25=52.7 μmol m⁻² s⁻¹, and V _pmax25=80.0 μmol m⁻² s⁻¹, with R ²=0.98 and rRMSE=13.3%. The obtained g _m25 increased by >3-fold, V _pmax25 decreased by 33%, and, therefore, the V _pmax25:V _cmax25 ratio dropped to 1.5 and may have been underestimated (see the Discussion). Furthermore, this g _bs temperature-insensitive model statistically decreased the goodness of fit (P<0.001 based on the F-test).

If we use the original model of von Caemmerer and Furbank (1999) which predicts A as the minimum of two limiting A _TT and A _EE, we obtained the estimates: g _m25=1.53mol m⁻² s⁻¹, V _cmax25=41.9 μmol m⁻² s⁻¹, and V _pmax25=119.8 μmol m⁻² s⁻¹, with g _bs being 1.18, 0.72, 3.39, 10.60, 9.35, and 5.07 mmol m⁻² s⁻¹ at 13.5, 18, 25, 30, 34, and 39 °C, respectively. The model described the data (R ²=0.97 and rRMSE=14.3%) somewhat less adequately than our four-rates model. Also, the estimates of g _bs at 30 °C and 34 °C became higher, resulting in different parameter estimates for g _bs temperature response: g _bs25=3.54 mmol m⁻² s⁻¹, E=264.9 kJ mol⁻¹, D=385.7 kJ mol⁻¹, and S=1.27 kJ K⁻¹ mol⁻¹. This gives T _opt=31.3 °C, ~2.6 °C lower than T _opt resulting from the four-rates model. The difference stemmed from the fact that many data points were determined by A _TE (results not shown), which is excluded in the two-rates model.

Sensitivity of estimated g _bs–temperature relationships to input parameters

In Table 1, the value of E _Kp was derived from our own data using an approximate model for describing the initial slope of A–C _i curves (see earlier). This procedure may be criticized because (i) the approximate model assumes an infinite g _m; (ii) the procedure requires that the initial section of A–C _i curves is exactly linear; and (iii) the required estimates for temperature response parameters of V _pmax, which we derived from Chinthapalli et al. (2003), may actually be uncertain. To examine the uncertainties in our estimated E _Kp, we used a more complete model (Supplementary appendix C) combined with two other reports (Massad et al., 2007; Boyd et al., 2015) on temperature response parameters of V _pmax. We fitted the model to the initial section of A–C _i curves where A is expected to be limited by the PEPc activity, and the obtained E _Kp estimate was 66.3, 79.5, and 73.3 kJ mol⁻¹ if temperature response parameters of V _pmax came from Chinthapalli et al. (2003), Massad et al. (2007), and Boyd et al. (2015), respectively (Supplementary Table S1). When the E _Kp estimate was combined with their corresponding temperature response parameter values of V _pmax from the three studies, the resulting estimates of g _bs at six temperatures and of V _cmax25 were hardly affected by the use of these different sets of input for E _Kp and temperature response of V _pmax (Supplementary Table S1).

The temperature responses of g _m do not yet exist for C₄ species, and temperature responses for C₃ species differed greatly among reports for tobacco (Bernacchi et al., 2002; Evans and von Caemmerer, 2013; Walker et al., 2013), and among species (von Caemmerer and Evans, 2015), in particular between tobacco and Arabidopsis (Walker et al., 2013). The responses for tobacco ranged from the peaked Arrhenius response (Bernacchi et al., 2002; Walker et al., 2013) to a linear pattern (Evans and von Caemmerer, 2013), whereas data of Walker et al. (2013) for Arabidopsis showed virtually no effect of temperature on g _m. Despite such a contrast in the temperature response of g _m used as input, the overall response of g _bs to temperature remained similar, following a peaked Arrhenius pattern (Supplementary Fig. S3). The obtained V _cmax25 varied little, from 48.5 μmol m⁻² s⁻¹ to 51.4 μmol m⁻² s⁻¹. The obtained V _pmax25 varied to a greater extent, from 75.3 μmol m⁻² s⁻¹ (from using the Arabidopsis response) to 155.6 μmol m⁻² s⁻¹ (from using the tobacco response of Walker et al., 2013). The obtained g _m25 was mostly between 1.25mol m⁻² s⁻¹ and 1.45mol m⁻² s⁻¹, but using the Arabidopsis response gave an infinite estimate of g _m25.

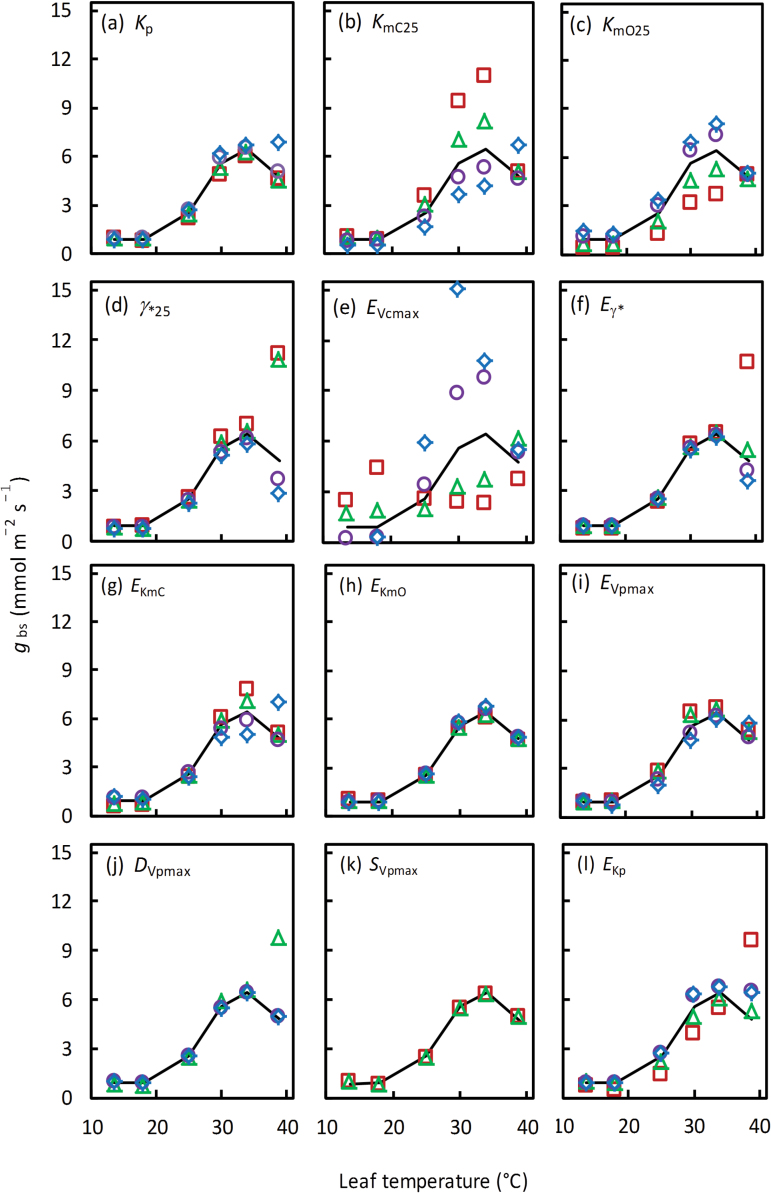
For sensitivity analyses of the estimated g _bs temperature response to 12 other parameters, the input parameters were varied by ±25% and 50% of their default values (Fig. 7). The estimated temperature response of g _bs was least sensitive to changes in K _p (Fig. 7a), E _KmO (Fig. 7h), and E _Vpmax (Fig. 7i). Overall, the sensitivity depended on the level of the parameter changes. Using extreme values of γ*₂₅, E _Vcmax, E _γ*, E _KmC, D _Vpmax, and E _Kp changed the shape of the response, from the peaked optimum response to the non-peaked Arrhenius pattern. The −50% change in D _Vpmax and +25% and +50% changes in S _Vpmax resulted in a biologically unrealistic (negative) estimate of g _bs, so their resulting response pattern is not given (Fig. 7j, k), suggesting that these changes may have reached beyond biologically realistic scopes of the two parameters. Note that Equation 5 suggests a co-determination of T _opt by E, D, and S and a much higher sensitivity to D _Vpmax and S _Vpmax than to E _Vpmax in determining T _opt of V _pmax.

Fig. 7.

Sensitivity of bundle-sheath conductance, g _bs, temperature response to changes in 12 input parameters as shown in (a–l). The input parameters and their default values are defined in Table 1. The changes were made to be 0.50 (open squares), 0.75 (open triangles), 1.25 (open circles), and 1.50 (open diamonds) times their default value. The temperature response of g _bs using the default set of input parameter values is given by the solid curve of each panel. One or two types of symbols are missing in (j) and (k) because extreme values of either D _Vpmax or S _Vpmax resulted in a biologically unrealistic negative estimate of g _bs. (This figure is available in colour at JXB online.)

The ±25% and 50% changes of the 12 parameters also resulted in changes in estimated g _m25, V _cmax25, and V _pmax25 (results not shown). Overall, the estimated V _cmax25 varied least (from 45.7 μmol m⁻² s⁻¹ to 58.4 μmol m⁻² s⁻¹), and its relative change, defined as the difference between its maximum and minimum divided by its mean, was 26%, whereas V _pmax varied most (from 67.6 μmol m⁻² s⁻¹ to 322.6 μmol m⁻² s⁻¹), and its relative change was 195%. The relative change of the estimated g _m25 was 92% (from 0.93mol m⁻² s⁻¹ to 2.05mol m⁻² s⁻¹).

Estimated leakiness, and V _o:V _c and V _c:V _p ratios

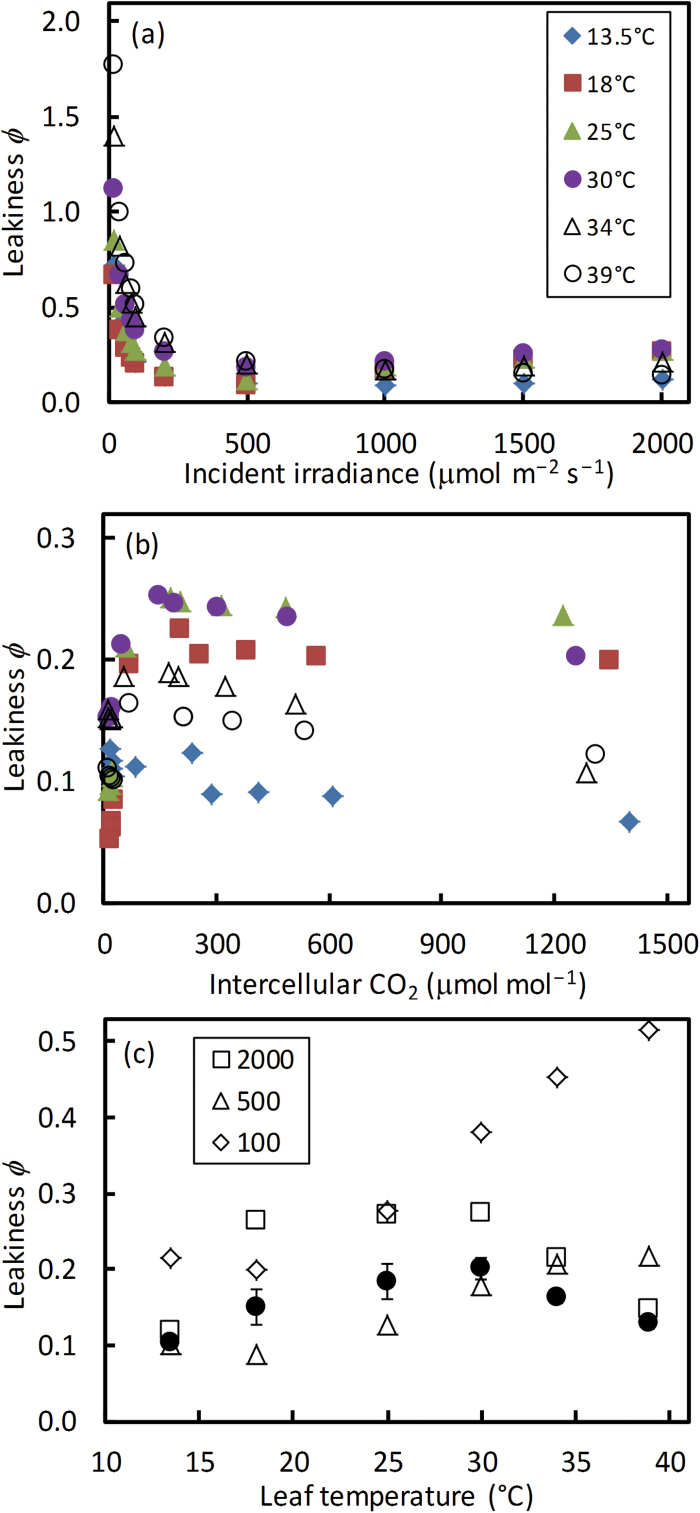
When model parameters are estimated, one can solve for leakiness ϕ (=L/V _p), V _o:V _c, and V _c:V _p ratios, using Equations A1–A6 in Supplementary appendix A. The calculated ϕ declined sharply with increasing irradiance (Fig. 8a), and increased initially and then saturated with increasing C _i (Fig. 8b). At low irradiances, ϕ values were very high, even exceeding 1.0 when the temperature was >30 °C (Fig. 8a). The temperature response of ϕ did not vary with CO₂ levels but depended strongly on the irradiance levels (Fig. 8c). The estimated ϕ at high irradiance (2000 μmol m⁻² s⁻¹) and the average ϕ of various CO₂ levels showed a peaked response to temperature (Fig. 8c).

Fig. 8.

Calculated CO₂ leakiness ϕ as a function of irradiance (a) and of intercellular CO₂ level (b) at six temperatures. The values of leakiness ϕ from (a) for three contrasting irradiance levels of 100, 500, and 2000 μmol m⁻² s⁻¹ (open symbols) and the mean ϕ (SEM in bars) across all CO₂ levels from (b) (filled circles) are shown as a function of temperature (c). The O₂ level was at 21%.(This figure is available in colour at JXB online.)

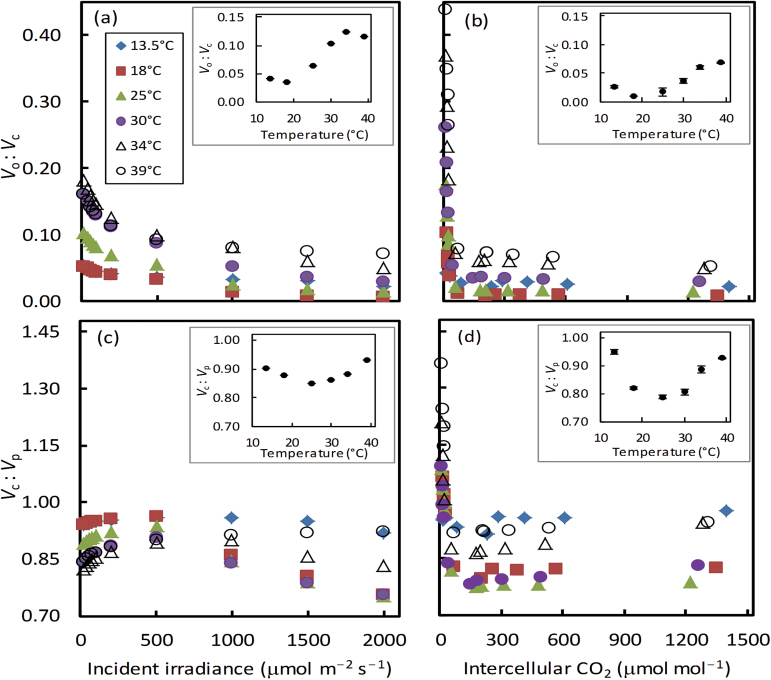
The calculated V _o:V _c ratio varied slightly with irradiance (Fig. 9a), and initially declined sharply and then became stable with increasing CO₂ levels (Fig. 9b). In accordance with this pattern, the V _c:V _p ratio responded to irradiance and CO₂ levels (Fig. 9c, d). The V _c:V _p ratio was <1.0 across irradiances (Fig. 9c), and it was also <1.0 for most CO₂ levels but became >1.0 at low C _i of 10–30 μmol mol⁻¹, especially at high temperatures (Fig. 9d). Excluding the four low CO₂ levels, the average ratios were calculated to show how these ratios under normal irradiance and CO₂ conditions responded to temperature (inset in each panel of Fig. 9). Overall, the V _o:V _c ratio increased with temperature (insets in Fig. 9a, b), and the V _c:V _p ratio had a non-linear response to temperature (insets in Fig. 9c, d).

Fig. 9.

Calculated V _o:V _c ratios (a, b) and V _c:V _p ratios (c, d) as a function of irradiance (a, c) and of intercellular CO₂ level (b, d) at six temperatures. The mean ratios (SEM in bars if larger than symbols) across all irradiance levels and across CO₂ levels with C _a ≥200 μmol mol⁻¹ against temperature during measurements are shown in the inset of each panel. The O₂ level was 21%.(This figure is available in colour at JXB online.)

Discussion

To estimate g _bs, we used the model method of Yin et al. (2011), which is based on the combined measurements of gas exchange and chlorophyll fluorescence on leaves. There are some concerns about this technique as the distribution of e⁻ transport between mesophyll and bundle-sheath cells on C₄ leaves is uncertain (von Caemmerer, 2013; Kromdijk et al., 2014). The mesophyll and bundle-sheath cells have different chloroplast populations which could result in a complex relationship between ∆F/F _m′ and the quantum yield of CO₂ fixation. However, despite a few exceptions (e.g. Fryer et al., 1998; Dwyer et al., 2007), most studies (e.g. Krall and Edwards, 1990; Edwards and Baker, 1993; Oberhuber and Edwards, 1993; Oberhuber et al., 1993; Peterson, 1994; Earl and Tollenaar, 1998; Laisk and Edwards, 1998; Siebke et al., 2003; Naidu and Long, 2004; Loriaux et al., 2013; Bellasio and Griffiths, 2014) have reported a good linear relationship for C₄ species between (quantum yields of) PSII e⁻ transport from fluorescence analysis and CO₂ fixation from gas exchange data over a wide range of conditions. This empirical evidence suggests that combined gas exchange and chlorophyll fluorescence measurements, commonly applied to estimate C₃ photosynthesis parameters, can be similarly applied for C₄ photosynthesis, as implemented by Yin et al. (2011), Bellasio and Griffiths (2013, 2014), and Bellasio et al. (2016). The way we conducted calibrations using non-photorespiratory measurements to derive s′ for calculating J _atp may also have reduced the uncertainty of applying a chlorophyll fluorescence technique to C₄ leaves.

In fact, the estimate of s′ is not just a calibration factor, but has physiological meanings and integrates a number of hard to determine parameters (Yin et al., 2011):

$$s\text{'}=\left(\text{1}-x\right)\beta {\rho }_{2}z\xi$$ (6)

where β is absorptance by leaf photosynthetic pigments, ρ₂ is the fraction of absorbed irradiance partitioned to PSII, z is the factor of converting PSII e⁻ flux into ATP flux, and ξ is the ratio of true PSII efficiency to fluorescence-measured apparent PSII efficiency. Theoretically, ρ₂ and z can be written as (Yin and Struik. 2012):

$$\rho {\text{}}_2=\frac{1-f_{\text{cyc}}}{\left(1-f_{\text{cyc}}\right)+{\Phi }_{2\text{LL}}/{\Phi }_{1\text{LL}}}$$ (7)

$$z=\frac{2+f_{\text{Q}}-f_{\text{cyc}}}{h\left(1-f_{\text{cyc}}\right)}$$ (8)

where f _cyc is the fraction of e⁻ flux at PSI that follows cyclic transport, f _Q is the fraction of e⁻ flux at reduced plastoquinone that follows the Q cycle, h is the H⁺:ATP ratio, and Φ_2LL/Φ_1LL is the PSII:PSI e⁻ transport efficiency ratio. Given recent quantitative estimation that Φ_2LL/Φ_1LL= ~0.825, f _Q=1, f _cyc= ~0.45, and h=4 (Yin and Struik, 2012), and assuming that x=0.4, β=0.9, and ξ=1, the value of s′ must be ~0.25. This theoretical value is close to our estimates for s′, 0.25–0.34 (Figs 3, 4a). Combining Equations 6–8 with the equation of Yin and Struik (2012) for the condition that the produced NADPH and ATP from e⁻ transport match the metabolic requirements (their equation 5), s′ can also be expressed as:

$$s\text{'}=\frac{3}{4}\beta \rho { }_2\xi (1+x\varphi )\left(1-\frac{f_{\text{pseudo}}}{1-f_{\text{cyc}}}\right)$$ (9)

where ϕ is leakiness, f _pseudo is the fraction of e⁻ flux at PSI that follows the basal pseudocyclic transport (e.g. nitrate reduction, and malate export from chloroplasts), and the term [1−f _pseudo/(1−f _cyc)] as a whole refers to the fraction of the PSII e⁻ flux that is used for supporting the Calvin circle and any photorespiration (Yin and Struik, 2012). Therefore, our calibration factor s′ takes into account only the part of the fluorescence signal dedicated to e⁻ sinks represented by the Calvin cycle, any photorespiration, and some energy loss due to CO₂ leakage. Our calibration procedure has excluded the effect of possible basal alternative e⁻ sinks. For example, the calibration factor s′ was found to vary with temperature (Fig. 4a), and one possible reason for this variation is that the extent of any basal alternative e⁻ transport may depend on temperature.

Kromdijk et al. (2010) and Ubierna et al. (2013) estimated g _bs by fitting the model of von Caemmerer and Furbank (1999) to carbon isotope discrimination data that were measured simultaneously with gas exchange, thereby providing an independent method to estimate g _bs. As this isotopic method has more assumptions than the fluorescence-based method (Kromdijk et al., 2014) and does not estimate J _atp and R _d, Bellasio and Griffiths (2013) compared the two methods in estimating g _bs by using J _atp and R _d estimated along the lines of our method. It is noteworthy that the fluorescence method used by Bellasio and Griffiths (2013) slightly differs from our method in that they estimated g _bs by minimizing the difference between modelled and measured J _atp, whereas our fitting method is to minimize the difference between modelled and measured A. Yin and Struik (2009b ) have shown for C₃ photosynthesis that the two minimizing targets can result in slightly different estimates of g _m, and we prefer our method because it is generally A, rather than J _atp, that is to be predicted from the general use of photosynthesis models. Nevertheless, Bellasio and Griffiths (2013) found that, compared with g _bs estimated by the isotopic method, g _bs estimated by the fluorescence method by fitting to J _atp was similar for maize leaves grown under low light conditions but was much lower for leaves from high light conditions; and the reasons for the difference are unresolved (Kromdijk et al., 2014). Bellasio and Griffiths (2013) discussed several advantages of the fluorescence method compared with the isotopic method (e.g. lower noise/signal ratio). However, since the isotopic method does not have the same problem as the fluorescence method in dealing with the two cell types, it is necessary to study further whether the relative temperature response of g _bs we obtained here (Figs 6, 7) can be confirmed using the independent isotopic method.

Our model considered only two major enzymes (i.e. PEPc for the C₄ cycle and Rubisco for the C₃ cycle). Other enzymes [e.g. pyruvate orthophosphate dikinase, C₄-acid decarboxylase, and carbonic anhydrase (CA)] are also important. The fact that detailed kinetic constants of these enzymes are rare and uncertain forces us to consider only two enzymes as in most applications of the C₄ model of von Caemmerer and Furbank (1999). Even for these two enzymes, only in vitro estimates of kinetic constants were used here as their in vivo estimates are practically impossible to obtain, and, when estimated, possibly confounded by the assumptions made on other parameters. For example, Massad et al. (2007) assumed that g _bs and γ* are independent of temperature, and obtained in vivo estimates of the peaked Arrhenius temperature response (i.e. Equation 4) for V _cmax and V _pmax, with T _opt=32.5°C and 43.3 °C, respectively. Their T _opt estimate for V _pmax is similar to our estimate of 44.4 °C based on in vitro data of Chinthapalli et al. (2003). However, the peaked temperature response for V _cmax has seldom been observed in vitro, for both C₃ and C₄ Rubisco, even when the temperature is up to 35–40 °C (e.g. Badger and Collatz, 1977; Jordan and Ogren, 1984; Sage, 2002; Kubien et al., 2003; Walker et al., 2013; Boyd et al., 2015; Perdomo et al., 2015). We believe that the low T _opt for V _cmax obtained by Massad et al. (2007) could simply be because they ignored the temperature sensitivity of g _bs and γ* when estimating V _cmax.

Our analysis showed the necessity of accounting for temperature response of g _bs. The shape of our temperature response of g _bs using default parameters (Fig. 6) followed an optimum temperature response pattern of light- and CO₂-saturated photosynthesis rates (A _max), similar to that Bernacchi et al. (2002) and others obtained for g _m in C₃ leaves. The similar temperature response of g _m and A _max is expected as g _m positively affects A _max. The similar temperature response of g _bs and A _max found here is unexpected, as g _bs negatively affects A _max in C₄ leaves. Nevertheless, given the uncertainties in all input parameters we used, our result on the temperature response of g _bs (Fig. 6) should be considered as tentative, and, as already stated, needs confirmation by other independent techniques. Our sensitivity analysis showed that the estimated temperature response of g _bs depended only slightly on the assumed temperature response of g _m (Supplementary Fig. S3), but more on Rubisco and PEPc kinetic parameters (Fig. 7). Using extreme values of some kinetic parameters occasionally caused a change from an optimum response to an accelerating response to temperature (Fig. 7). The g _bs temperature response rarely depends on g _m parameters but more on Rubisco and PEPc kinetic parameters; this is expected from the model of von Caemmerer and Furbank (1999), because the calculation of C _c is minimally affected by g _m through C _m, and V _c depends strongly on g _bs and V _cmax. However, those kinetics parameters to which the estimated temperature response of g _bs is very sensitive were either measured for maize (e.g. K _mC25, K _mO25,and γ*₂₅, reported by Cousins et al., 2010) or were relatively conserved among C₄ species (E _Vcmax and E _γ*; see above). Also uncertainties related to a set of PEPc kinetics parameters as a whole had little impact on g _bs estimates (Supplementary Table S1), although individual parameters such as D _Vpmax and S _Vpmax—when varied independently—strongly influenced the estimated g _bs (Fig. 7). Despite these uncertainties of the input parameters, the obtained g _bs–T _leaf relationship between 13.5 °C and 39.0 °C followed either a peaked or non-peaked Arrhenius pattern (Figs 6, 7). Below 35 °C, the estimated g _bs almost exclusively increased monotonously with increasing temperature (Fig. 7). The activation energy estimate based on Equation 3 for our estimates of g _bs in Fig. 6 within 35 °C was ~74.45 kJ mol⁻¹ for our study, and its corresponding Q ₁₀ value was ~2.74.

The Q ₁₀ factor for diffusion of CO₂ in water is ~1.25 (Bernacchi et al., 2002). Our higher Q ₁₀ value for g _bs suggests the possibility that some proteins/enzymes are involved in inter- and intracellular CO₂ diffusion in C₄ leaves. One candidate is CA, which facilitates the CO₂ diffusion rate (Badger and Price, 1994). CA has often been considered to play a role in mediating g _m in C₃ species (e.g. Bernacchi et al., 2002). Its role for g _m in C₄ leaves is justified since in C₄ plants CA is mainly found in the cytosol alongside PEPc (Ludwig et al., 2011), and CA activity is temperature dependent (Boyd et al., 2015). This actually gives indirect support to the use of the modified Arrhenius response for the temperature effect on g _m in our analysis. The bundle-sheath cells may contain some amount of CA isoforms (Ludwig et al., 2011), seemingly in support of its potential mediating role for g _bs as well. The other candidate may be an aquaporin that increases the CO₂ permeability of the cell membrane (Terashima and Ono, 2002). Genetic manipulation of specific aquaporins has been used to vary g _m in C₃ species (e.g. Hanba et al., 2004). Brautigam et al. (2010) showed that a 20-fold up-regulation in the abundance of an mRNA coding for an aquaporin was registered in a C₄ species. Other temperature-dependent activities may also shape our observed g _bs–temperature relationship. For example, the current model simply assumes that the rate of decarboxylation equals V _p. Recently it has been suggested that maize leaves have mixed decarboxylation pathways (Furbank, 2011). Theoretical modelling by Wang et al. (2014) showed that engaging the mixed pathways could decrease the need to maintain a high concentration gradient of metabolites between mesophyll and bundle-sheath cells, reconciling an earlier analysis of Sowinski et al. (2008) that simple diffusion-driven transport of metabolites is not adequate to explain the metabolite exchange during C₄ photosynthesis. The mixed decarboxylation pathways and associated cell to cell exchange of metabolites suggest it likely that PEPc carboxylation and the overall decarboxylation rates are not the same and have different temperature responses. In that case, such a difference will have been lumped with our estimated parameters for temperature response of g _bs.

The temperature response of g _bs, together with the temperature responses of J _atp, Rubisco, and PEPc kinetic parameters, co-determined the temperature responses of leakiness ϕ (Fig. 8), and V _o:V _c and V _c:V _p ratios (Fig. 9). In line with the trends shown by theoretical modelling (von Caemmerer and Furbank, 1999) and experimental calculation (Kromdijk et al., 2010; Pengelly et al., 2010; Yin et al., 2011; Ubierna et al., 2013; Bellasio and Griffiths, 2014), the calculated ϕ declined sharply with increasing irradiance (Fig. 8a). However, ϕ at low irradiances even exceeded 1.0 when the temperature was above 30 °C (Fig. 8a). The extreme ϕ values >1 at strictly limiting irradiances and high temperatures resulted from relatively high mitochondrial respiration in bundle-sheath cells combined with relatively high photorespiratory rates (as indicated by relatively high V _o:V _c ratios at low irradiances; Fig. 9a). As a result, the temperature response of ϕ did not vary with CO₂ levels but depended strongly on the irradiance levels (Fig. 8c). The estimated ϕ at high irradiances and the average ϕ of various CO₂ levels showed a flat peaked response to temperature (Fig. 8c), in line with the trend shown by von Caemmerer et al. (2014) with the carbon isotope method.

For an effective CCM, the V _c:V _p ratio is expected to be <1.0. However, the V _c:V _p ratio went up to >1.0 at low CO₂, especially at high temperatures (Fig. 9d). The model of von Caemmerer and Furbank (1999) (see Equations A1 and A4 in Supplementary appendix A) predicts that the V _c:V _p ratio is ≥1.0 only if L≤0.5V _o+(R _d–R _m). This condition was met at our four lowest CO₂ levels (C _i of 10–30 μmol mol⁻¹) where V _o was high. The average ratios under normal irradiance and CO₂ conditions (calculated by excluding those four low CO₂ levels) responded to temperature. Overall, the V _o:V _c ratio increased with temperature (insets in Fig. 9a, b), because increasing temperature favoured the RuBP oxygenation relative to carboxylation. However, this general temperature response of the V _o:V _c ratio seemed to be modified by the temperature response of g _bs. The temperature response of g _bs and its associated temperature response of leakiness (Fig. 8c) required V _p to vary accordingly, resulting in a non-linear response of the V _c:V _p ratio to temperature (insets in Fig. 9c, d).

Our parameter estimates can be compared with previous literature reports. Our estimate of activation energy for R _d, 41.9 kJ mol⁻¹ (Table 2), is within the range of reports for R _d in C₃ species (24.2–65.2 kJ mol⁻¹; see review by Yin et al., 2014) as well as the range reported for C₄ species (28.2–57.8 kJ mol⁻¹; Dwyer et al. 2007). Our estimate for g _m25,1.33mol m⁻² s⁻¹ (Table 2), is within the range of the earlier estimated or suggested values for maize (Pfeffer and Peisker, 1998; Kromdijk et al., 2010; Yin et al., 2011; Barbour et al., 2016), and is higher than that for C₃ leaves (for which the maximum g _m25 is ~0.6mol m⁻² s⁻¹; e.g. Loreto et al., 1992). Our estimated V _pmax25:V _cmax25 ratio, 2.43, agrees with our earlier estimate 2.5 (Yin et al., 2011). Biochemical measurements on this ratio were 2.1–2.5 (Pengelly et al., 2010), 3.1 (Kubien et al., 2003), or higher (Sage et al., 1987). The leaf N content in our experiment was on average 1.1g N m⁻². Our estimated g _bs25, 2.87 mmol m⁻² s⁻¹ (Table 2), is within the values reported for maize, 1.5 mmol m⁻² s⁻¹ (Ubierna et al., 2013), 0.37–2.35 mmol m⁻² s⁻¹ (Kromdijk et al., 2010), and 0.82–4.64 mmol m⁻² s⁻¹ (Bellasio and Griffiths, 2014), and also agrees with our previous estimate for this leaf nitrogen level (Yin et al., 2011). However, our estimates for the slope of V _cmax25 and V _pmax25 versus leaf nitrogen, 57.7 μmol and 140.3 μmol (g N)⁻¹ s⁻¹, respectively, are lower than the previous estimates [96.0 μmol and 242.2 μmol (g N)⁻¹ s⁻¹, respectively] by Yin et al. (2011). The difference between the two studies in glasshouse environments (i.e. ~1 month later in the present study than in the previous study of Yin et al., 2011), cultivars used (‘Atrium’ versus ‘2-02R10074’), and leaf ranks for measurements (the seventh versus the eighth to ninth) might have caused this disparity. It has been shown that acclimation to growing light intensities affected photosynthesis parameters in maize (Kromdijk et al., 2010; Bellasio and Griffiths, 2013) and other C₄ species (Ubierna et al., 2011).

Previously only one study (Kiirats et al., 2002) has reported the temperature response of g _bs; that is, g _bs increases almost linearly with increasing leaf temperature, in contrast to our result for the Arrhenius response. Their temperature was only up to 35 °C. If normalized to 25 °C, the response within temperatures up to 35 °C was still different between their study and ours (Supplementary Fig. S4): the activation energy estimate based on Equation 3 was ~24.92 kJ mol⁻¹ for their study, lower than 74.45 kJ mol⁻¹ for our study (see above). This may highlight species differences in temperature response of g _bs, although the impact of methodological differences between the two studies and/or the impact of uncertainty in input parameter values for our study cannot be ruled out. Temperature response of g _m for C₃ photosynthesis has recently been reported to vary greatly with plant species (Walker et al., 2013; von Caemmerer and Evans, 2015). There is a need to investigate further whether or not species diversity exists with regards to temperature response of g _bs for C₄ photosynthesis. To that end, comprehensive investigations on enzyme kinetic constants may need to be carried out across contrasting C₄ species.

In short, our study demonstrates that in contrast to existing modelling assumptions, g _bs does vary with leaf temperature. Although the presented temperature response curve still needs to be confirmed by other independent techniques, our results provide a step forward to more accurate modelling of C₄ photosynthesis and productivity, especially for maize, under changing climatic environments.

Supplementary data

Supplementary data are available at JXB online.

Appendix A. Basic equations in the C₄ photosynthesis model of von Caemmerer and Furbank (1999) and analytical solutions of the model as given by Yin et al. (2011).

Appendix B. Quantifying temperature dependence of diffusivities and solubilities of CO₂ and O₂ in water.

Appendix C. Model and data for describing PEPc-limited rates of photosynthesis within the initial section of A–C _i curves.

Table S1. Estimated values of E _Kp, V _cmax25, and g _bs at six temperatures when using three sets of V _pmax parameters.

Figure S1. The initial linear section of A–C _i curves of 2% O₂ at six measurement temperatures.

Figure S2. Comparison between modelled and measured A–I _inc and A–C _i curves at six leaf temperatures under the condition of 21% O₂.

Figure S3. Temperature response of bundle-sheath conductance, estimated using four contrasting temperature responses of mesophyll conductance.

Figure S4. Comparison of temperature response of bundle-sheath conductance normalized to 1.0 at 25 °C between Kiirats et al. (2002) for Amaranthus edulis and our study for maize.