Abstract
Executive Function (EF) has been highlighted as a potentially important factor for mathematical understanding. The relation has been well established in school-aged children but has been less explored at younger ages. The current study investigated the relation between EF and mathematics in preschool aged children. Participants were 142 typically developing 3- and 4-year-olds. Controlling for verbal ability, a significant positive correlation was found between EF and general math abilities in this age group. Importantly, we further examined this relation causally by varying the EF load on a magnitude comparison task. Results suggested a developmental pattern wherein 3-year-olds’ performance on the magnitude comparison task was worst when EF was taxed the most. Conversely, 4-year-olds performed well on the magnitude task despite varying EF demands, suggesting that EF might play a critical role in the development of math concepts.
Keywords: executive function, magnitude, mathematics, preschool children
Executive function (EF) refers to higher order cognitive abilities needed for self-control, including inhibition of incorrect responses, attention shifting, and updating information in working memory (Miyake et al., 2000; Miyake & Friedman, 2012). These skills undergo considerable development in the preschool period and beyond, and impact later abilities (Carlson, Zelazo, & Faja, 2013). In recent years it has been suggested that EF skills are important for mathematical understanding (see Raghubar, Barnes & Hecht, 2010; Yeniad, Malda, Mesman, van Ijzendoorn & Piper, 2013, for reviews). However, considerable questions remain about the causal role of EF in mathematical proficiency, and how EF skills relate to mathematical understanding at different ages, particularly as EF and mathematics skills become more automatic over the course of development. Is EF necessary for mathematical understanding? Does EF play a larger role in obtaining mathematical skills earlier in acquisition or later? How does proficiency of mathematics skills influence their relation to EF? Can improving EF skills lead to improvements in mathematical performance? These and other questions remain open.
An understanding of the relation between mathematical understanding and EF at an early age is important because both skills have an impact on later achievement. Individual differences in EF skills in preschoolers have been shown to predict better social emotional coping in adolescence, higher SAT scores, and adult outcomes such as higher sense of self-worth, higher educational achievement, better coping with stress and reduced likelihood of drug use (Ayduk et al., 2000; Moffitt et al., 2012; Shoda, Mischel & Peake, 1990). Similarly, research has consistently shown that early mathematics skill is a particularly strong predictor of later educational success. A meta-analysis showed that the relation between early performance (school entry) and academic achievement in middle school was twice as strong for mathematics than for reading skills (Duncan et al., 2007).
Despite the documented importance of EF to mathematical skills, few studies have examined the relation between EF and mathematics ability in young children, although the development of both skills has been studied separately. Some researchers have argued that basic mathematic skills (e.g., arithmetic) exist in infancy (e.g. McCrink & Wynn, 2004) and evidence suggests informal skills necessary for later math proficiency including cardinality understanding, counting skills, and basic arithmetic, develop during the preschool years (Gelman & Gallistel, 1978; Sophian, 1996). Importantly, EF skills also rapidly develop during this time as attentional and reflective abilities improve (Carlson, 2005; Garon, Bryson & Smith, 2008; Zelazo et al., 2003). It seems highly probable on a theoretical basis that these trajectories are related (Noel, 2009). For example, learning to count sequentially involves holding earlier information in mind and updating it with new information, as well as inhibiting interference from other numbers (Raghubar et al., 2010). Later, becoming flexible and proficient with new operations requires selective attention to, and inhibition of, previously learned operations (e.g., avoiding the error of answering 3 × 3 = 6; Yeniad et al., 2013).
In the few studies exploring the relation between developing trajectories in mathematics and EF, researchers have found promising associations (Bull, Espy & Wiebe, 2008; Bull, Espy, Wiebe, Sheffield & Nelson, 2011; Clark, Pritchard & Woodward, 2010; Clark, Sheffield, Wiebe, & Espy, 2013; Espy et al., 2004). In a sample of preschool children (average age 4 years), researchers found that working memory and inhibition were related to math ability (as assessed by the Woodcock Johnson Applied Problems), but only inhibition (or actively suppressing processes to better control attention, behavior, thoughts, and/or emotions) remained a unique predictor after controlling for the other EF skills and general intelligence (Espy et al., 2004). Interestingly, shifting skills at preschool were not found to be related to math skills. Using growth curve modeling starting at 4.5 years old and continuing for 3 years, researchers showed that children with higher EF scores (as assessed by a battery including working memory and attention measures) had better performance on national math tests when reading ability was controlled (Bull et al., 2008). Similarly, strong associations were shown between an EF battery measured at 3 years and math achievement in kindergarten (Clark et al., 2013). This work suggests that a unique relation between EF and mathematical development at this young age may exist, where EF might be playing a particularly important role as both these skills are undergoing important developments. However, the correlations presented in these studies are susceptible to confounds such as influences of IQ or verbal abilities, and/or variations in early educational experiences. Thus, rigorous experimental evidence is needed to better understand whether and if so, how, EF aids mathematical development.
Recent evidence suggests that EF skills are not differentiated early in development and act more like a unitary system at preschool ages (Bull & Lee, 2014; Lee, Bull & Ho, 2013; Wiebe et al., 2011). Confirmatory factor analysis has suggested that single factor models are a better fit for data from preschool aged children (Wiebe, Espy & Charak, 2008) than the three factor models (i.e. shifting, updating and inhibition) that have been found to best fit in adults (Miyake et al., 2000; Miyake & Friedman, 2012). Using this single factor of EF, researchers have found a significant relation between EF and concurrent as well as subsequent math skills at later ages (Bull et al., 2011; Clark et al., 2013).
One recent study used a brief comprehensive measure, the Minnesota EF Scale (MEFS; Carlson & Zelazo, 2014) to determine its contribution to math achievement in first grade, controlling for children’s number sense (e.g., number relations and operations) in kindergarten (Hassinger-Das, Jordan, Glutting, Irwin & Dyson, 2014). Number sense was measured by the Number Sense Brief (NSB; Jordan, Glutting, Ramineni & Watkins, 2010) which asked children to count, recognize numerals, and engage in simple verbal and nonverbal calculations. Controlling for variation in these early number skills as well as other background factors (age gender, English Language Learner status), researchers found that EF uniquely predicted mathematics scores on the Woodcock-Johnson-III subtests. Interestingly, EF was a stronger predictor of success on the Applied Problems (measuring quantitative reasoning including counting and story problems) of the Woodcock Johnson-III subtest than the Calculation subtest (measuring computation abilities on written problems) in first grade. The authors interpreted this result as EF influencing conceptual understanding (e.g. implicit or explicit understanding of principles of number relations) more than procedural learning (e.g. executing steps in a calculation problem) at this age. This study suggests that individual differences in EF predict improvements in mathematics ability from kindergarten to first grade. However, this research was still primarily correlational and did not provide insight into the causality of the relation earlier in development or look at the development of specific math skills. This leads to questions of directionality and the possibility that the contribution of EF to mathematical understanding varies based on the mathematical skill being studied.
Specifying the mathematical skill in question is important because it allows us to begin to look at questions of automaticity. It is still an open question at what point in the development of a new skill EF matters and to what extent. For example, it is possible that as concepts and procedures become more engrained and automatic, there is a smaller role of EF. When solely looking at mathematics achievement broadly, multiple skills including factual understanding, conceptual knowledge, and procedural abilities are tested simultaneously. All of these components might be contributing to successful performance, but might not all be equally related to EF, or to the same aspect of EF across different ages (Cragg & Gilmore, 2014). In an attempt to better understand the nature of the relation between EF and math skills, it is necessary to begin untangling these distinct skills and examining the impact of EF on them separately. Because of our interest in young children in particular, the skill of magnitude comparison is a compelling place to start. It has been suggested that understanding numerical magnitudes (e.g., that 5 is greater than 2) is a crucial step in mathematical skill development (Butterworth, Varma & Laurillard, 2011; Gersten, Jordan & Flojo, 2005).
Numerical Magnitude
Understanding and processing numerical magnitude information is present very early in development (Dehaene, 1997) and continues to develop, increasing in accuracy over time (Booth & Siegler, 2006). The Approximate Number System (ANS) along with the Object-Tracking System (OTS) allow humans and other species to have estimations of numerical magnitude (Gallistel & Gelman, 1992, 2000; Feigenson, Dehaene & Spelke, 2004). The OTS keeps track of individual objects in small quantities and the ANS enables rough estimation and calculation of large quantities. Both systems appear to be present in infants (Wynn, 1998; Xu & Spelke, 2000), although their precision increases from infancy to adulthood (Halberda & Feigenson, 2007; Libertus & Brannon, 2010; Wynn, 1998; Xu & Spelke, 2000). Children as young as 6-months are able to identify changes in magnitude for object sets of three or fewer and make approximate magnitude comparisons (determining which is larger when presented with two quantities) for larger numbers (Starkey, 1992; Wynn, 1995) even when quantity comparisons are controlled for volume, density, and brightness (Brannon, 2002; Xu, 2003; Xu & Spelke, 2000).
The basis of numerical magnitude is present early, and seems to be an especially important precursor for later success in math achievement. Children who met criteria for mathematics learning disability (MLD) in middle childhood showed lower performance on magnitude comparison tasks (Geary, Hoard, Nugent, Byrd-Craven, 2008). Similarly, retrospective predictive value has been shown with ninth graders’ estimation skills correlating with math achievement scores in kindergarten and with their concurrent math achievement (Halberda, Mazzocco & Feigenson, 2008; Mazzocco, Feigenson & Halberda, 2011). Additionally, magnitude understanding is related to various aspects of early numerical learning including number categorization and number comparison. More accurate magnitude knowledge is also related to more advanced math skills (Booth & Siegler, 2008; Laski & Siegler, 2007).
Despite the importance magnitude comparison plays in greater math understanding, little research exists on the underlying factors that influence variation in this ability. EF is a possible factor relating to differences in magnitude abilities, but studies exploring this possibility are lacking. Still, there is limited evidence to suggest a relation between EF and magnitude skills in school-age children. Specifically, working memory (considered a sub-skill of EF) was related to performance on a number estimation task in both first and second grades (Geary et al., 2008). A recent study with 5-year-old children also showed that children with better memory updating skills improved more on number line estimation after a period of training, suggesting that EF skills may be a prerequisite for responsiveness to intervention (Kolkman, Hoijtink, Kroesbergen & Leseman, 2013). It remains an open question how the specific skill of magnitude comparison relates to EF (in particular as a unitary measure) and what the nature of this relation is in young children when both skill sets remain underdeveloped.
Typically, magnitude skills are measured using a magnitude comparison task (Xu & Spelke, 2000) where participants are presented with two quantities and asked to determine which is more. Conveniently, a useful measure of EF abilities also asks children to determine which of two quantities is more (Less is More task; Carlson, Davis, & Leach, 2005) but with the added complexity that after determining which quantity is more, children must inhibit that response and point to the quantity that is smaller in order to receive the larger reward. Through this combination of skills we hope to explore how EF relates to magnitude understanding and to what degree it is necessary for proficient magnitude comparison performance.
Current Study
The current study had three specific aims. First, we aimed to better understand the relation between mathematical ability and EF in preschool aged children using a unitary measure of EF designed for children ages 2–7, asking if the same relation found by Hassinger-Das and colleagues (2014) exists in preschool children. We hypothesized that mathematics ability and EF would be related, even at this young age. Similar to what was demonstrated in older children, we expected that higher EF abilities would be related to better performance on a standardized measure of math achievement. Second, we aimed to move past correlational work and examined potential causal relations between EF and math using a magnitude comparison task where different degrees of EF were required for successful performance. We hypothesized that the greater the amount of EF that was required, the poorer children would perform on a magnitude comparison task, suggesting that EF is a necessary component for success on the task. For both these aims we wanted to explore the development of these skills across the preschool years. This developmental component would target questions related to how important EF is when learning new mathematical skills and if the relation between EF and math changes as mathematics skills develop and increase in automaticity. We expected to see a developmental progression such that when math skills were less developed (i.e., in younger children), poorer EF would be a greater determinant of math performance. This relates to the idea that cognitive demand would be higher overall because of the difficulty of learning a new skill, but as that skill develops and becomes more automatic (across development) the cognitive demands are attenuated and therefore EF skills would play a less prominent role in performance. Our third and final aim was to look at the directionality of the relation between EF and math. Because it is an open question if EF is influencing math, math is influencing EF, or both, this aim was exploratory and no specific hypotheses were set.
To investigate these aims, 3- and 4-year-old children were administered a battery of EF and mathematics measures including the Minnesota EF Scale (Carlson & Zelazo, 2014), the Woodcock-Johnson III Applied Problems subtest (McGrew, Schrank, & Woodcock, 2007) and a modified magnitude comparison based on the Less is More paradigm (Carlson et al., 2005). The Less is More task is a reverse-reward contingency task in which one must point to a smaller amount of treats in order to receive a larger amount. For example, when presented with a choice of 2 or 5 candies, whichever array the participant points to is removed and he or she receives the non-selected array (hence he or she must point to 2 candies in order to get 5). The task itself is a measure of EF abilities and is correlated with other preschool measures of EF (Carlson et al., 2005). To pass, and receive the larger amount of treats, children have to inhibit their natural response to choose the larger amount, and instead choose the smaller amount (e.g., 2 vs. 5). Past research has shown that 3-year-olds typically perform poorly on this task (with approximately 30% correctly pointing to the smaller amount) but 4-year-olds tend to perform significantly better (with approximately 70% correctly pointing to the smaller amount) (Carlson et al., 2005).
While this is a valid measure of EF abilities it is also fundamentally a magnitude comparison task. To increase our understanding of how EF and magnitude understanding relate to each other and to overall performance on the task, EF was differentially taxed across trials. Three magnitude pairings were established: (1) a standard EF pairing (1 vs. 2 comparison), which we expected to match the performance reported in previous work using the task, (2) a high EF pairing (1 versus 20 comparison), where the magnitude difference was the most obvious, but the temptation to select the larger amount was also the highest. We expected this condition to prove the most difficult, especially for the younger children with lower inhibitory control skills. And (3) a low EF pairing (10 versus 20 comparison) where the magnitude comparison was the same ratio as the standard task, but the temptation was lower since both magnitudes might be construed as “large.” We hypothesized that varying EF skills and increased magnitude comparison abilities (based on age) would influence the results. Specifically we hypothesized that younger children would perform worse overall, with their poorest performance being on the comparison requiring the most EF (1 versus 20). Conversely, we hypothesized that the older children would be better able to utilize their EF skills, thereby making the largest magnitude difference (1 versus 20) the easiest for them. In other words, with a stronger foundation of EF and number skills in place, older children would be able to work out the rule (less is more) and rather than being lured by the 20 in the 1 vs. 20 condition, they might actually find this to be the easiest condition because the magnitude difference is the most obvious.
Finally, given that the stimuli in the Less is More task vary on both number and volume, we included two additional conditions (volume only and number only comparisons) to explore if EF abilities influenced performance across different forms of estimation. In the volume only condition, number was controlled for but volume differences matched the ratios of the standard number + volume condition. For instance, in the volume only high EF pairings, children saw one small ball compared to one ball 20 times as large (Figure 1). Similarly, in the number only condition, volume was controlled for, but again, the number differences matched the ratios of the standard number + volume condition. For instance, in number only high EF pairings, children saw one ball compared to an equal volume divided into 20 balls (Figure 1.).
Figure 1.
Schematic representation of stimuli presentations for standard EF, high EF and low EF trials in each condition (Volume and Number, Volume only and Number only)
In general, these magnitude manipulations are not thought to impact children’s comparison abilities (Brannon, 2002; Xu, 2003; Xu & Spelke, 2000) but it seemed possible that they would recruit varying amounts of EF. The exploratory aim of these conditions was to further isolate the source of children’s difficulty with the task to primarily number or volume comparisons, and to provide additional instantiations of the Less-is-More task that might yield results that could be generalized across different kinds of magnitude comparisons.
Methods
Participants
Participants were 142 typically developing preschoolers, including 76 3-year-olds (M = 43.72 months, SD = 1.55, range = 38 to 47; 52% females) and 66 4-year-olds (M = 55.03 months, SD = 1.31, range = 53 to 58; 41% females) recruited from a family database at a large metropolitan university in the Midwestern United States. Exclusion criteria included developmental delays (e.g. autism, ADHD) premature birth (more than three weeks early), non-English speaking (although bilingual children were accepted), physical disabilities affecting vision or hearing, or a disorder or disease that influenced physical growth (e.g., Prader-Willi Syndrome). The sample was primarily white, non-Hispanic (93.7%) although other ethnicities, including Asian (2.1%), Hispanic (.7%) and biracial (4.2%) also were represented. The sample was primarily upper-middle class with 5.8% of families earning under $50,000, 34.1% earning between $50,000 and $100,000, and 60.1% earning over $100,000. Primary caregivers were well educated with 83.1% having completed at least a bachelor’s degree. Participants were given a $5 gift card and a lab T-shirt as compensation.
Participants were assigned to one of three comparison type conditions: standard number and volume magnitude comparison (50% female; 53% 3-year-olds; n = 68), volume only magnitude comparison (24% female; 55% 3-year-olds, n = 37), and number only magnitude comparison (26% female; 52% 3-year-olds; n = 37). The standard condition was conducted first as it most closely matched both the previously used Less is More protocols and typical magnitude comparison tasks. The volume only and number only conditions were conducted later to account for possible variations in performance based on stimuli manipulations. The procedure remained the same across conditions and all children were presented with standard EF pairing trials, high EF pairing trials and low EF pairing trials (Figure 1) with order counterbalanced across trial types.
Procedure
Each child was tested individually in a laboratory playroom at a small table. Sessions were approximately 45-min and were videotaped. Tasks were administered in a fixed order with the modified magnitude task (Less is More) administered first followed by the Minnesota EF Scale and the Stanford-Binet Verbal Reasoning subtest. A standardized order was used to control for possible priming effects of introducing number concepts or EF skills earlier in the administration sequence. For example, we did not want participants to become experienced pointing to and sorting based on certain rules (MEFS task) before being asked to point to various quantities on the Less is More task. A subsample (66 children) was then administered the Woodcock Johnson-III Applied Problems subtest. This measure was added to better link our work to the extant literature because related research, published while our study was underway, had included it (Hassinger-Das et al., 2014). This subsample did not differ significantly from the rest of the sample in their demographic characteristics or performance on the magnitude comparison test (caregiver education: t(140) = .46, p = .64, family income level: t(136) = 1.56, p = .12, ethnicity: t(140) = 1.50, p = .14, magnitude comparison (total proportion correct): t(140) = .86, p = .39).
Magnitude Task (Less is More)
Before beginning the magnitude task, the experimenter (E) showed children three Play-Doh toys (a cupcake maker, movie food maker, and dentist office) and asked which one they would like to play with. E then gave children a small piece of Play-Doh to try with the toy. The amount of Play-Doh was too small to make full use of the toy. E then explained that the child could get lots of Play-Doh in the next game, and return to the toy again later. The toy was put away after the child agreed.
Next, children were introduced to the magnitude comparison Less is More task (Carlson et al., 2005). The task was introduced by showing children two containers with identically colored and sized balls of Play-Doh (2 balls in one container and 5 balls in the other). E said, “Look, this container has some Play-Doh and this container has some Play-Doh. Which container do you want?” (All indicated the larger.) E then introduced a puppet and explained, “This is a naughty monkey named Chris. He likes to get all the Play-Doh for himself, that’s why he’s naughty.” E then placed the puppet next to a clear box and said, “This is Chris’ box.” Next she pointed to a similar box near the child and said, “This is your box.” After clearly indicating the boxes E returned to the treat arrays in the middle of the table saying: “Today we’re going to play a silly game. In this game every time you point to a container, Chris gets the Play-Doh in that container and they’ll go into his box (pointing to Chris’ box) and the Play-Doh in the other container will go into your box (pointing to the child’s box.)” For practice, E said, “Point to a container.” After children made a selection E dumped the Play-Doh from the selected container into the puppet’s box, and dumped the Play-Doh from the non-selected container in the child’s box. A verbal rule check followed where E asked, “So when you point to a container, who gets that Play-Doh? You or Chris?” The experimenter gave feedback and repeated the question as needed (up to four times). Nearly all of the children (98%) answered this question correctly.
Each child received a total of 18 test trials, 6 per magnitude pairing. The order of the magnitude pairings was counter-balanced, as were left/right positions. After 9 trials, regardless of performance, E gave a verbal rule reminder (“When you point to a container, that Play-Doh goes to Chris, and you get the Play-Doh in the other container.”) Children received no feedback during test trials apart from the implicit feedback of seeing the Play-Doh transferred to the respective containers. Each child received three final scores, computed as the proportion correct (out of 6) for each of the pairings (standard EF (1 vs. 2), low EF (10 vs. 20) and high EF (1 vs. 20)).
Minnesota EF Scale (MEFS; Carlson & Zelazo, 2014)
This table-top, early childhood version of the Minnesota EF Scale requires children to sort a variety of cards based on the dimensions of the target cards (e.g., color and shape) that are graded in difficulty level. The MEFS has been used with over 5,000 children and been found to be reliable (Beck, Schaefer, Pang, & Carlson, 2011) and valid (Carlson & Harrod, 2013). This measure also has been validated in clinical populations (Doom et al., 2014; Fuglestad et al., 2014) and at-risk preschoolers (Chu, VanMarle, & Geary, 2013; VanMarle, Chu, Li, & Geary, 2014), is related to emotion understanding in preschoolers (Martins, Osorio, Verissimo & Martins, 2014), and predicts kindergarten readiness and first-grade math achievement over and above IQ (Carlson & Harrod, 2013; Hassinger-Das et al., 2014). Individual items consisted of the child correctly or incorrectly sorting cards into two equidistant boxes affixed with target cards specified by level. The current rule was stated at each trial (e.g., “Stars go here, Trucks go here”) and the relevant dimension was highlighted (e.g., “Here’s a truck”). After 5 trials, E announced that the rules had changed (e.g., to the color game) and 5 more trials ensued. Testing began at an age appropriate starting point as determined by test norms and progressed in a forward manner if a criterion (80%) score was met for each level and continued until the child failed a level. If the criterion score was not met at the first level, E moved backward until a lower level was passed (basal). Scoring was based on the highest level that the child passed (range of 0–7).
Woodcock-Johnson III Applied Problems (WJ-III; McGrew et al., 2007)
This test of general mathematics abilities was included in order to align the present study with the current literature (Hassinger-Das et al., 2014). Testing followed the standardized procedure with age-appropriate starting points. Children were asked to count objects in pictures (both with and without distractors), do basic arithmetic, answer verbally presented story problems (both with without pictures), and other simple mathematics procedures. Testing continued until 5 consecutive scores of 0 were obtained. A raw score was calculated based on the number of correct responses and this score was converted to an age-equivalence score.
Stanford-Binet Early 5 Verbal Abilities (Roid, 2005)
General verbal abilities were measured using the verbal abilities subtest following the standardized procedures. Children were asked to identify objects and describe common words. Children received as score of 0, 1 or 2 based on the quality of their response according to the testing manual. Testing continued until 4 consecutive scores of 0 were obtained. Final scores based on the number of correct responses were calculated.
Results
Consistent with prior research (Brannon, 2002; Xu, 2003; Xu & Spelke, 2000), no significant differences were found between the standard number and volume, number only, and volume only magnitude comparison conditions for proportion of correct responses on the Less is More trials (F(4, 278) = .78, p = .539), thus the conditions were collapsed.
Mean scores for all measures are presented in Table 1. Across all measures, 4-year-olds performed better than 3-year-olds as would be expected developmentally.
Table 1.
Descriptive Statistics and Age Effects
| Measure | All Ages Mean (SD) |
3-Year-Olds Mean (SD) |
4-Year-Olds Mean (SD) |
t (140)a | p |
|---|---|---|---|---|---|
| Executive Function (MEFS) Range = 1–7 |
4.37 (.87) | 3.98 (.88) | 4.81 (.60) | 6.46 | .001 |
| Math Abilities (WJ-III Applied Problems) Range = 36–68 |
52.15 (7.50) | 47.60 (6.04) | 57.29 (5.41) | 6.84a | .001 |
| Magnitude Score – Overall (Percent Correct) Range = 0–100 |
65.51 (25.22) | 55.85 (23.03) | 76.63 (23.10) | 5.36 | .001 |
| Magnitude Score – Standard EF (Percent Correct) Range = 0–100 |
63.50 (29.63) | 56.78 (26.40) | 71. 46 (29.19) | 3.19 | .002 |
| Magnitude Score – High EF (Percent Correct) Range = 0–100 |
64.44 (35.29) | 50.44 (33.43) | 80.55 (30.32) | 5.59 | .001 |
| Magnitude Score – Low EF (Percent Correct) Range = 0–100 |
66.44 (28.62) | 57.09 (26.55) | 77.20 (26.95) | 4.47 | .001 |
| Verbal Ability (Stanford-Binet) Range = 7–30 |
19.82 (3.47) | 18.64 (3.38) | 21.18 (3.07) | 4.65 | .001 |
Degrees of freedom for all comparisons was 140 except for the WJ-III Applied Problems comparison which had 64 degrees of freedom.
The first aim, to investigate the relation between math and EF in this young age group, was explored using correlation analyses (Table 2). Controlling for age and verbal ability, a significant positive correlation was found between WJ-III Applied Problems scores and MEFS scores. Significant correlations also were found between the scores for each age group separately, controlling for verbal ability. These correlations suggest a strong relation between math ability and EF skills in preschool aged children that is similar to that seen in older children
Table 2.
Partial Correlations among the Minnesota EF Scale (MEFS), Woodcock Johnson-III (WJ-III) Applied Problems, and Magnitude tasks, Controlling for Verbal Ability
| Measure | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1. Executive Function (MEFS) | -- | ||||
| 2. Math Abilities (WJ-III Applied Problems) (n = 66) | .53*** .35a* .43b** |
-- | |||
| 3. Magnitude Score – Standard EF | .09 | .17 | -- | ||
| 4. Magnitude Score – High EF | .26** | .44*** | .46*** | -- | |
| 5. Magnitude Score – Low EF | .15 | .31** | .55*** | .55*** | -- |
Note.
3-year-olds;
4-year-olds; Verbal ability assessed using the Stanford-Binet Early 5;
p < .05.
p < .01.
p < .001
Scores on the magnitude Less is More task were also were correlated with the MEFS (controlling for verbal ability), with the high EF (1 vs. 20) condition showing the strongest correlation.
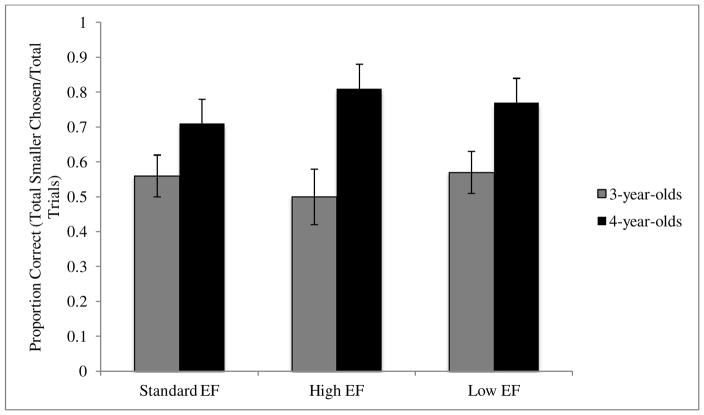
The second aim, investigating the causal role of EF on magnitude comparison abilities was analyzed through a 2 (age; 3-year-olds, 4-year-olds) × 3 (magnitude; standard EF (1 vs. 2), high EF (1 vs .20), and low EF (10 vs. 20)) mixed design repeated measures ANOVA. Proportion of correct responses (out of 6 trials per EF pairing) was chosen as the dependent variable for all analyses. There was a significant main effect of age, F(1, 140) = 30.76, p = .0001, ηp2 = .18, with 4-year-olds performing significantly better than 3-year-olds. Across all magnitudes, 4-year-olds averaged 76.63% (SD = 23.10) trials correct (pointing to the smaller amount) whereas 3-year-olds averaged 55.85% (SD = 23.03) correct, although the performance of both groups were above chance (3-year-olds: t(75) = 2.21, p = .03, 4-year-olds: t(65) = 9.37, p = .001). The main effect of magnitude was not significant, as expected, F(2, 139) = .78, p = .460, ηp2 = .006. However, the repeated measures ANOVA also revealed a significant interaction between age and magnitude pairing, F(2, 139) = 4.77, p = .009, ηp2 = .033. A test of within-subjects contrasts showed a significant quadratic interaction with age F(1, 140) = 6.95, p = .009, ηp2 = .047. Post hoc tests revealed a trending difference for 3-year-olds between the high and low EF pairings, t(75) = −1.82, p = .07, suggesting the high EF (1 vs. 20) pairing had the lowest proportion correct (M = .50, SE = .04) and the low EF (10 vs. 20) pairing had the highest (M = .57, SE = .03) (see Figure 2). Among 4-year-olds, a significant difference was found between the high EF (1 v. 20) and standard EF (1 vs. 2) pairings, t(65) = −2.38, p = .02, as well as a trending difference between the low EF (10 v. 20) and standard EF (1 vs. 2) pairings, t(65) = −1.69, p = .09. However, in this older age group, the high EF (1 vs. 20) pairing had the highest score (M = .81, SE = .04) and the standard EF (1 vs. 2) pairing had the lowest (M = .71, SE = .04) (see Figure 2). No other contrasts were significant (ps = .12 – .86). These results show that 3-year-olds perform worse than 4-year-olds on a magnitude comparison task, in particular when their EF skills are taxed most heavily.
Figure 2.
Proportion correct for 3- and 4- year-olds on 3 magnitude pairings. Bars represent 95% confidence interval.
Finally, an exploratory analysis in the form of a regression was conducted to look at the directionality of the relation between EF and mathematics skills. The results are presented in Table 3. Math ability (WJ-III Applied Problems) scores significantly predicted EF scores (MEFS), but magnitude comparison (Less is More) scores were not a significant predictor. Math ability scores also explained a significant proportion of variance controlling for age and verbal ability. Looking at the reverse, both MEFS and magnitude comparison (Less is More) scores uniquely predicted math ability scores on the WJ-III Applied Problems. Interestingly, controlling for age and verbal ability, only math ability (WJ-III Applied Problems) significantly predicted magnitude comparison Less is More scores. Domain-general EF (MEFS) scores were not a significant predictor.
Table 3.
Standardized Regression Coefficients from Regression Analyses for Variables Predicting EF and Math Outcomes
| Executive Function | Math Ability | Magnitude | |
|---|---|---|---|
| Block 1 | |||
| Age (months) | .30** | .58*** | .35** |
| Verbal ability (Stanford Binet) | .51*** | .20* | .11 |
| R2 | .44*** | .46*** | .17** |
| Block 2 | |||
| Math Ability (WJ-III Applied Problems) | .43*** | -- | .32* |
| Magnitude | −.01 | .21* | -- |
| ΔR2 | .10*** | .04* | .06* |
| Block 3 | |||
| Executive function (MEFS) | -- | .40*** | −.02 |
| ΔR2 | -- | .09*** | .00 |
p<.05.
p<.01.
p<.001
To piece apart the findings seen on the magnitude task outcome, a final analysis was done to further explore the role of EF on the magnitude skills across age groups (Table 4). Rather than looking at magnitude comparison scores as a whole, the high EF comparison was chosen as the outcome variable. This was done because the greatest variation across age groups was seen here, and we hypothesized that the recruitment of EF was most varied on this comparison. Regression analyses showed that for 3-year-olds, EF was a significant predictor of magnitude comparison performance controlling for verbal abilities, but for 4-year-olds EF was not a significant predictor.
Table 4.
Standardized Regression Coefficients for Variables Predicting Magnitude Comparison Less is More Task Outcomes by Age-Group
| High EF Magnitude 3-year-olds |
High EF Magnitude 4-year-olds |
|
|---|---|---|
| Block 1 | ||
| Verbal ability (Stanford Binet) | −.11 | .12 |
| R2 | .01 | .02 |
| Block 2 | ||
| Executive Function (MEFS) | .32* | .01 |
| ΔR2 | .07* | .00 |
p < .05
p < .01
p < .001
In terms of directionality, we can see that EF scores predict math abilities and the reverse (math abilities predict EF scores) for broad measures of math abilities. However, the same pattern of bi-directionality was not seen when looking at the specific skill of magnitude comparisons. Instead, it seems EF are contributing differently depending on the developmental age of the participant.
Discussion
This study aimed to explore the relation between EF and mathematical abilities in preschool aged children. This relation has been established in older children (Raghubar et al., 2010; Yeniad et al., 2013) but questions remained about the relation in younger children, and whether the relation changes across development.
The first aim of this study was to build on the relation found in older children by Hassinger-Das and colleagues (2014), showing that even in younger children, who have not entered formal schooling, the same unitary measure of EF (MEFS) was significantly related to mathematics performance on the Woodcock Johnson-III Applied Problems subtest. These correlations were robust, and independent of verbal ability, in both 3- and 4-year-old participants. Our results are among the first to demonstrate the presence of this relation in this age group using a comprehensive measure of EF. It is likely that as the component skills of EF differentiate with age, their relation to math changes, making it necessary to establish and understand the earliest connection first seen in this younger age group.
In looking at this relation between EF and mathematics in younger children both correlationally and experimentally, it is important to highlight the types of skills being studied. Again, the majority of studies investigating mathematics and EF have used standardized measures that encompass many different mathematics skills. As Hassinger-Das and colleagues suggested, the significant correlation found between EF and the Applied Problems subtest could relate to the conceptual understanding (rather than the procedural knowledge) present in the test. For example, seeing the relation between and among numbers for skills like mental arithmetic, quantity comparisons and manipulation of larger numbers, requires children to think flexibly about previous mathematical knowledge, combine knowledge sets and maintain problem information in mind (Bull & Lee, 2014). Still, it remains difficult to distinguish the specific skills being utilized on a broad measure of mathematics ability.
By looking at the specific skill of magnitude comparison in isolation, as we did for the second aim in this study, we are able to better understand the role that EF may play in its development. This is a first step in better understanding the unique relation between EF and specific skills that may be included in broad measures of math achievement. Magnitude understanding is an important place to start because understanding in this area is related to a variety of other mathematical understandings including number categorization, number comparison, and other more advanced math skills (e.g. addition, multiplication; Booth & Siegler, 2008; Laski & Siegler, 2007).
We found that children at different ages seem to be depending on EF in varying amounts when making magnitude comparisons. Results showed that 3-year-olds performed the worst on the magnitude comparison task when their EF skills were taxed most heavily, whereas this same comparison (1 v. 20) was the easiest for 4-year-olds, suggesting once children had worked out the “less is more” concept, their EF abilities became less coupled with their magnitude comparison skills. Past research has suggested that the more automatic a skill becomes, the less EF is recruited (Cragg & Gilmore, 2014). For example, mathematical ability has been shown to affect 10- to 12-year-old children’s reliance on EF skills for problem solving (Imbo & Vandierendonck, 2007). Based on the present study, it seems older children had a better conceptual understanding of the Less is More task, causing them to need less EF recruitment when comparing the magnitude quantities and thereby showing less impaired performance on the High-EF (1 vs. 20) trials.
Relatedly, in our third aim, the exploratory regression analyses suggested that general math abilities, rather than EF, predicted performance on the magnitude comparison task in the full sample. It is important to note that the WJ-III as our measure of general math abilities did not include direct magnitude comparison questions, but instead targeted other early numeracy skills. Furthermore, in this analysis, EF was a significant predictor of magnitude comparison skills for 3-year-olds, but not for 4-year-olds. This supports the conclusion that if well-developed mathematical skills exist, EF is less necessary for successful task performance. Still, in looking at the reverse prediction, both EF skills and magnitude comparison scores were significantly predictive of general math abilities. This begins to suggest that EF is necessary to obtaining broader math understanding but as that understanding matures, and specific skills become more concrete, less deployment of EF is needed for their successful expression.
Limitations
Although we believe that this study offers important advancements in our understanding of how EF and mathematics skills are related in a preschool age group, it does have several limitations. The primary limitation of this study relates to the sample. Our participants were largely Caucasian and of upper-middle socio-economic status. Both their EF (as measured by the MEFS) and mathematics abilities (as measured by the WJ-III Applied Problems) were above the level predicted by their age. Therefore, it is unknown how our results would differ for children who showed poorer mathematics or EF skills. It has been shown that children from more disadvantaged backgrounds tend to have lower EF skills as well as lower academic achievement (e.g., Hackman & Farah, 2009), so a more diverse sample would likely show greater variation in ability level, perhaps performing similarly to the 3-year-old participants in our sample. However, EF has also been found to be a unique predictor of resilience in homeless and highly mobile children, where those children with higher EF are more likely to reach academic standards (Óbradovic, 2010). It is possible that if EF skills are less developed and therefore less easily deployed, it may change how they relate to mathematics understanding. Perhaps children in these circumstances would show a unique response pattern not demonstrated by the participants in our study. It is possible that children in this environment have found unique ways to overcome deficits in EF, developing different strategies when learning and understanding mathematics that rely less on skills like attention, working memory and inhibition.
Another limitation of the current study was that not all participants were given the WJ Applied Problems subtest. Although there were no significant differences between those participants who received this measure and those who did not, our study would have been methodologically stronger if all participants were given this measure.
Conclusions and Future Directions
A primary aim of this study was to look at how EF relates to the specific skill of magnitude comparison. While this skill is especially relevant to a preschool age group, it is by no means the only skill that should be analyzed in relation to EF. Future research should continue to tease apart how EF skills differentially affect various components of mathematics. This next step will also help to elucidate how the relation between EF and math changes across development. Is EF causally related to addition and subtraction? Is it important for fractional understanding? While it seems likely that the answer is yes, future studies should look at the skills in isolation to better understand how, why, and what components of EF are important.
Additionally, within the specific skill of magnitude comparison, future studies can investigate strategy use and its role in overall performance. Again, the Less is More task is particularly well suited for this exploration because of its combination of EF and magnitude skill demands. Effectively choosing and using a certain strategy is an important component of mathematical problem solving and it seems to be a skill that is substantially affected by EF (Cragg & Gilmore, 2014). How EF might impact strategy use, how the relation develops over time as more complex and multiple strategies are required, and how these skills might be improved to shape overall mathematical performance, are further questions of interest.
While causal evidence is currently sparse, necessary next steps in understanding this relation also include training studies. Highlighting the importance that EF may play in mathematics learning in young children suggests a possible pathway for intervention. If EF is necessary for early conceptual understanding as well as preliminary number skills, then access points for intervention abound. For example, EF could be incorporated more fully into early math exercises, adding switching and inhibition components to tasks like number identification and early counting. It seems likely that improving EF at young ages both in the context of math instruction and independently will have large downstream benefits for math achievement. Relatedly, for children struggling to understand and/or express specific number skills at any age or grade level, EF interventions may be an important area to address.
As a first step, this study offers new evidence of the relation between EF and mathematical skills in preschool aged children, and suggests that the nature of this relation changes with development, as children’s number skills improve.
Highlights.
Executive function has been highlighted as an important factor for mathematical understanding.
A significant relation was found between executive function (EF) and general math abilities in preschool aged children.
A causal exploration of the relation suggested a developmental pattern where younger children’s mathematical performance was worst when EF demands were highest.
Older children performed well on mathematical tasks when EF demands where both high and low.
Acknowledgments
Support for this study was provided by NIH Grant: T32 HD00715 (to E.O.P.), NSF Doctoral Fellowship 00039202 (to E.O.P.) and by R01HD1495 (to S.M.C.). Many thanks to the research assistants involved in testing, the members of the Developmental Social Cognitive Neuroscience Lab, and to the children and families who participated in this research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Apperly IA, Carroll DJ. How do symbols affect 3- to 4-year-olds’ executive function? Evidence from a reverse contingency task. Developmental Science. 2009;12:1070–1082. doi: 10.1111/j.1467-7687.2009.00856.x. [DOI] [PubMed] [Google Scholar]
- Ayduk O, Mendoza-Denton R, Mischel W, Downey G, Peake PK, Rodriguez M. Regulating the interpersonal self: Strategic self-regulation for coping with rejection sensitivity. Journal of Personality and Social Psychology. 2000;79:776. doi: 10.1037//0022-3514.79.5.776. [DOI] [PubMed] [Google Scholar]
- Beck DM, Schaefer C, Pang K, Carlson SM. Executive function in preschool children: Test-retest reliability. Journal of Cognition and Development. 2011;12:169–193. doi: 10.1080/15248372.2011.563485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth JL, Siegler RS. Developmental and individual differences in pure numerical estimation. Developmental Psychology. 2006;42:189–201. doi: 10.1037/0012-1649.41.6.189. [DOI] [PubMed] [Google Scholar]
- Brannon EM. The development of ordinal numerical knowledge in infancy. Cognition. 2002;83:223–40. doi: 10.1016/s0010-0277(02)00005-7. [DOI] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA. Short-term memory, working memory, and executive functioning in preschoolers: Longitudinal predictors of mathematical achievement at age 7 years. Developmental Neuropsychology. 2008;33:205–28. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R, Espy KA, Wiebe SA, Sheffield TD, Nelson JM. Using confirmatory factor analysis to understand executive control in preschool children: Sources of variation in emergent mathematic achievement. Developmental Science. 2011;14:679–92. doi: 10.1111/j.1467-7687.2010.01012.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R, Lee K. Executive functioning and mathematics achievement. Child Development Perspectives. 2014;8:36–41. [Google Scholar]
- Butterworth B, Varma S, Laurillard D. Dyscalculia: From brain to education. Science. 2011;332(6033):1049–53. doi: 10.1126/science.1201536. [DOI] [PubMed] [Google Scholar]
- Carlson SM. Developmentally sensitive measures of executive function in preschool children. Developmental Neuropsychology. 2005;28:595–616. doi: 10.1207/s15326942dn2802_3. [DOI] [PubMed] [Google Scholar]
- Carlson SM, Davis AC, Leach JG. Less is more: Executive function and symbolic representation in preschool children. Psychological Science. 2005;16:609–616. doi: 10.1111/j.1467-9280.2005.01583.x. [DOI] [PubMed] [Google Scholar]
- Carlson SM, Harrod J. Validation of the executive function scale for early childhood. In: Griffin J Chair, editor. Developing the next generation of preschool outcome measures: The interagency school readiness measurement consortium; Poster symposium presented at the biennial meeting of the Society for Research in Child Development; Seattle, WA. 2013. Apr, [Google Scholar]
- Carlson SM, Zelazo PD. Minnesota Executive Function Scale - Test Manual. Reflection Sciences; Saint Paul, MN: 2014. [Google Scholar]
- Carlson SM, Zelazo PD, Faja S. Executive function. In: Zelazo PD, editor. The Oxford handbook of developmental psychology, Vol. 1: Body and mind. New York: Oxford University Press; 2013. pp. 706–743. [Google Scholar]
- Chu FW, VanMarle K, Geary DC. Quantitative deficits of preschool children at risk for mathematical learning disability. Frontiers in Psychology. 2013;4:1–10. doi: 10.3389/fpsyg.2013.00195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark CAC, Pritchard VE, Woodward LJ. Preschool executive functioning abilities predict early mathematics achievement. Developmental Psychology. 2010;46:1176–91. doi: 10.1037/a0019672. [DOI] [PubMed] [Google Scholar]
- Clark CAC, Sheffield TD, Wiebe SA, Espy KA. Longitudinal associations between executive control and developing mathematical competence in preschool boys and girls. Child Development. 2013;84:662–677. doi: 10.1111/j.1467-8624.2012.01854.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cragg L, Gilmore C. Skills underlying mathematics: The role of executive function in the development of mathematics proficiency. Trends in Neuroscience and Education. 2014;3:63–68. [Google Scholar]
- Dehaene S. The number sense. New York: Oxford University Press; 1997. [Google Scholar]
- Doom J, Gunnar MR, Georgieff MK, Kroupina MG, Frenn K, Fuglestad AJ, Carlson SM. Beyond stimulus deprivation: Iron deficiency and cognitive deficits in post-institutionalized children. Child Development. 2014;85:1805–1812. doi: 10.1111/cdev.12231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, … Japel C. School readiness and later achievement. Developmental Psychology. 2007;43:1428–46. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Espy KA, McDiarmid MM, Cwik MF, Stalets MM, Hamby A, Senn TE. The contribution of executive functions to emergent mathematic skills in preschool children. Developmental Neuropsychology. 2004;26:465–86. doi: 10.1207/s15326942dn2601_6. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Fuglestad AJ, Whitley ML, Carlson SM, Boys CJ, Eckerle JK, Fink BA, Wozniak JR. Executive functioning deficits in preschool children with Fetal Alcohol Spectrum Disorders. Child Neuropsychology. 2014 doi: 10.1080/09297049.2014.933792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: From reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Garon N, Bryson SE, Smith IM. Executive function in preschoolers: A review and integrative framework. Psychological Bulletin. 2008;134:31–60. doi: 10.1037/0033-2909.134.1.31. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, Byrd-Craven J. Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology. 2008;33:277–99. doi: 10.1080/87565640801982361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman R, Gallistel CR. The child’s understanding of number. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Gersten R, Jordan NC, Flojo JR. Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities. 2005;38:293–304. doi: 10.1177/00222194050380040301. [DOI] [PubMed] [Google Scholar]
- Hackman DA, Farah MJ. Socioeconomic status and the developing brain. Trends in Cognitive Sciences. 2009;13:65–73. doi: 10.1016/j.tics.2008.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the “number sense”: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology. 2008;44:1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Hassinger-Das B, Jordan NC, Glutting J, Irwin C, Dyson N. Domain-general mediators of the relation between kindergarten number sense and first-grade mathematics achievement. Journal of Experimental Child Psychology. 2014;118:78–92. doi: 10.1016/j.jecp.2013.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imbo I, Vandierendonck A. The development of strategy use in elementary school children: Working memory and individual differences. Journal of Experimental Child Psychology. 2007;96:284–309. doi: 10.1016/j.jecp.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Glutting J, Ramineni C, Watkins MW. Validating a number sense screening tool for use in Kindergarten and first grade: Prediction of mathematics proficiency in third grade. School Psychology Review. 2010;39:181–185. [Google Scholar]
- Kolkman ME, Hoijtink HJa, Kroesbergen EH, Leseman PPM. The role of executive functions in numerical magnitude skills. Learning and Individual Differences. 2013;24:145–151. [Google Scholar]
- Laski AV, Siegler RS. Is 27 a big number? Correlational and causal connections among numerical categorization, number line estimation, and comparison. Child Development. 2007;78:1723–1743. doi: 10.1111/j.1467-8624.2007.01087.x. [DOI] [PubMed] [Google Scholar]
- Lee K, Bull R, Ho RMH. Developmental changes in executive functioning. Child Development. 2013;84:1933–53. doi: 10.1111/cdev.12096. [DOI] [PubMed] [Google Scholar]
- Libertus ME, Brannon EM. Stable individual differences in number discrimination in infancy. Developmental Science. 2010;13:900–906. doi: 10.1111/j.1467-7687.2009.00948.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins EC, Osorio A, Verissimo M, Martins C. Emotion understanding in preschool children: The role of executive functions. International Journal of Behavioral Development 2014 [Google Scholar]
- Mazzocco MMM, Feigenson L, Halberda J. Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS ONE. 2011b;6(9):e23749. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mccrink K, Wynn K. Large-number addition and subtraction by 9-month-old Infants. Psychological Science. 2004;15:776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- McGrew KS, Schrank FA, Woodcock RW. Woodcock-Johnson III normative update. Rolling Meadows, IL: Riverside Publishing; 2007. [Google Scholar]
- Miyake A, Friedman NP, Emerson MJ, Witzki AH, Howerter A, Wager TD. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology. 2000;41:49–100. doi: 10.1006/cogp.1999.0734. [DOI] [PubMed] [Google Scholar]
- Miyake a, Friedman NP. The nature and organization of individual differences in executive functions: Four general conclusions. Current Directions in Psychological Science. 2012;21:8–14. doi: 10.1177/0963721411429458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moffitt TE, Arseneault L, Belsky D, Dickson N, Hancox RJ, Harrington H, … Caspi A. A gradient of childhood self-control predicts health, wealth, and public safety. Proceedings of the National Academy of Sciences. 2011;108:2693–2698. doi: 10.1073/pnas.1010076108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noel MP. Counting on working memory when learning to count and to add: A preschool study. Developmental Psychology. 2009;45:1630–1643. doi: 10.1037/a0016224. [DOI] [PubMed] [Google Scholar]
- Obradović J. Effortful control and adaptive functioning of homeless children: Variable-focused and person-focused analyses. Journal of Applied Developmental Psychology. 2010;31:109–117. doi: 10.1016/j.appdev.2009.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghubar KP, Barnes MA, Hecht SA. Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences. 2010;20:110–122. [Google Scholar]
- Roid GH. Stanford–Binet Intelligence Scale. 5. Itasca, IL: Riverside Publishing; 2005. [Google Scholar]
- Shoda Y, Mischel W, Peake PK. Predicting adolescent cognitive and self-regulatory competencies from preschool delay of gratification. Developmental Psychology. 1990;26:978–986. [Google Scholar]
- Sophian C. Children’s numbers. Boulder, CO: Westview; 1996. [Google Scholar]
- Starkey P. The early development of numerical reasoning. Cognition. 1992;43:93–126. doi: 10.1016/0010-0277(92)90034-f. [DOI] [PubMed] [Google Scholar]
- VanMarle K, Chu FW, Li Y, Geary DC. Acuity of the approximate number system and preschoolers’ quantitative development. Developmental Science. 2014;17:492–505. doi: 10.1111/desc.12143. [DOI] [PubMed] [Google Scholar]
- Wiebe SA, Espy KA, Charak D. Using confirmatory factor analysis to understand executive control in preschool children: Latent structure. Developmental Psychology. 2008;44:575–87. doi: 10.1037/0012-1649.44.2.575. [DOI] [PubMed] [Google Scholar]
- Wiebe SA, Sheffield T, Nelson JM, Clark C, Chevalier N, Espy KA. The structure of executive function in 3-year-olds. Journal of Experimental Child Psychology. 2011;108:436–52. doi: 10.1016/j.jecp.2010.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wynn K. Psychological foundations of number: Numerical competence in human infants. Trends in Cognitive Sciences. 1998;2:296–303. doi: 10.1016/s1364-6613(98)01203-0. [DOI] [PubMed] [Google Scholar]
- Wynn K. Infants possess a system of numerical knowledge. Current Directions in Psychological Science. 1995;4:172–177. [Google Scholar]
- Xu F. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Yeniad N, Malda M, Mesman J, van Ijzendoorn MH, Pieper S. Shifting ability predicts math and reading performance in children: A meta-analytical study. Learning and Individual Differences. 2013;23:1–9. [Google Scholar]
- Zelazo P, Muller U, Frye D, Marcovitch S, Argitis G, Boseovski J, … Carlson SM. The development of executive function in early childhood. Monographs for the Society for Research in Child Development. 2003:68. doi: 10.1111/j.0037-976x.2003.00260.x. [DOI] [PubMed] [Google Scholar]