Phase Imaging Using Focused Polycapillary Optics

Abstract

Conventional radiographic techniques depend on attenuation, which provides low contrast between soft tissues. However, X rays can accumulate large differential phase delays even in weakly absorbing materials. This can produce significantly higher contrast. One technique for taking advantage of phase effects, propagation-based phase imaging, can yield marked edge enhancement but requires spatially coherent intense sources. Microfocus sources have sizes on the order of tens of microns but necessarily are low power and hence require long exposures. In this project, X-ray optical and computational techniques were explored to develop both edge-enhancement and phase imaging using a large spot conventional source. A polycapillary optic was employed to create a small secondary source from a large spot rotating anode X-ray generator. The secondary spot created by the focusing polycapillary optic was 114 µm ± 50 µm. Images of a 1.6 mm polyethylene rod were taken at varying distances from the optic. Edge enhancement was observed with a maximum edge-enhancement-to-noise ratio of 6.5. Insect images were also acquired and analyzed. Phase reconstructions were computed using two different approaches, weak attenuation and phase attenuation duality. Pure phase images were successfully reconstructed from the phase contrast images by employing the weak attenuation model.

1. Introduction

Since the discovery of X rays by Roentgen, absorption-based images have utilized the attenuation properties of the object being imaged to generate a two dimensional attenuation map. Such images produce high contrast for objects where the electron density differences are substantial, e.g., bone and flesh, but result in poor contrast for soft tissue imaging where the tissues exhibit similar attenuation, e.g., glandular tissue and infiltrating ductal carcinoma in breast imaging.¹ However, X rays can accumulate significant differential phase delay even in weakly absorbing materials, so that the image contrast produced by a phase delay offers significant enhancement over attenuation-based contrast. Phase contrast imaging renders the different phase delays as intensity variation in the detector plane. The amount of attenuation and phase delay of a given material can be described by its complex-valued index of refraction,

$$\mathrm{n}=1-\mathrm{\delta }+\mathrm{i}\mathrm{\beta }$$ (1)

where β and δ are real-valued parameters describing the absorption and phase delay of X rays, respectively. For X-ray energies of 10 to 100 KeV, δ for soft tissue is about 10⁻⁶ to 10⁻⁸ and β is about 10⁻⁹ to 10⁻¹¹, so the phase delay term is approximately 1000 times greater than the absorption term. Additionally, because δ remains relatively large at high energies where absorption is low, phase imaging may give the possibility of dose reduction by allowing the use of higher photon energies. A number of techniques can be used to extract phase information from intensity measurements.² Grating- and crystal-based interferometric techniques have shown particular promise, but rely on precise, stable alignment of the gratings or crystals.^3,4 Techniques based on using analyzer crystals to detect X ray deflection have also received considerable interest, but rely on the precise alignment and stability of analyzer crystals.^5,6 In this work, we consider propagation-based phase contrast, which uses propagation of beams through air to generate phase contrast, and is therefore relatively robust to misalignments or vibrations in the system. However, this method requires significant spatial coherence of the X-ray beam and sufficient brightness. Outside of synchrotrons, which are unsuitable for widespread clinical use, coherence for propagation imaging is typically achieved through the use of low-power microfocus sources which produce an X-ray focal spots on the order of 10 µm diameter, and thus require long exposure times. Here we consider an alternative method of generating coherence with a conventional X-ray source by employing focusing optics to produce an X-ray focal spot of the required size for propagation-based imaging.

The phase accumulated by an X ray traversing a sample, assuming the sample is weakly scattering, is simply proportional to the integral of δ along the ray trajectory through the sample. It can be denoted by

$${\mathrm{\varphi }}_0(\mathrm{x})=-\mathrm{k}\int \mathrm{\delta }\mathrm{d}\mathrm{l},$$ (2)

where the integral is taken over the path of X rays traversing the sample, x is a vector in a plane transverse to the beam axis at the exit face of the sample, k=2π/λ is the wavenumber and λ the wavelength of the X rays. For simplicity, it is assumed in the following that the beam is monochromatic, but it can be shown that propagation-based phase imaging is relatively unaffected by the X-ray spectrum. At the exit face of the sample the X-ray beam is described by the field

$$\mathrm{E}(\mathrm{x},\mathrm{z}=0)=\sqrt{{\mathrm{I}}_0(\mathrm{x})}\text{exp}[\mathrm{i}{\mathrm{\varphi }}_0(\mathrm{x})],$$ (3)

where z denotes the primary direction of the beam’s propagation, z=0 is chosen to correspond to the exit face of the sample, I₀ is the intensity of the beam exiting sample and ϕ is the phase imparted by the sample. This geometry is illustrated in Figure 1. Note that in general the beam may have a non-negligible phase imparted by the source, but since this is present without the sample in place, it can be characterized a priori and is not relevant to measuring sample phase.^7,8 In particular, the phase of a cone beam is due to its divergence and can be accounted for by introducing appropriate magnification factors in phase measurements.

Figure 1.

Diagram of X-ray illumination of a sample. X rays passing through the sample exit at z=0 where they have been attenuated and deflected by phase variations.

After exiting the sample, the beam propagates according to the paraxial wave equation

$$\frac{\partial }{\partial \mathrm{z}}\mathrm{E}(\mathrm{x},\mathrm{z})=\frac{\mathrm{i}}{2\mathrm{k}}{\nabla }_{\mathrm{x}}^2\mathrm{E}(\mathrm{x},\mathrm{z}),$$ (4)

where ${\nabla }_{\mathrm{x}}^2$ denotes the Laplacian in the plane transverse to the z axis. The variation of intensity upon propagation can be readily found by inserting the field in Eq. (3) into Eq. (4) and separating out the real-valued portion of the result, yielding the transport of intensity equation (TIE)^9,10

$$\frac{\partial }{\partial \mathrm{z}}\mathrm{I}(\mathrm{x},\mathrm{z})=-{\nabla }_{\mathrm{x}}·[\mathrm{I}(\mathrm{x},\mathrm{z})\frac{{\nabla }_{\mathrm{x}}\mathrm{\varphi }(\mathrm{x},\mathrm{z})}{\mathrm{k}}],$$ (5)

where ∇_x denotes the gradient operator in the transverse plane, and the quantity ∇_xϕ/k describes the angle and transverse direction of deflection of the X rays by the sample. Since intensity can be directly measured, this presents a linear, second order, elliptic partial differential equation for phase ϕ in terms of measurable intensities.¹¹ In practical use, one approximates the axial derivative of intensity on the left-hand side as a finite difference between the contact image intensity I₀(x) and a intensity captured at a displaced position z=z_d. Under cone beam illumination, the displaced image must be demagnified for comparison with the contact image by introducing a magnification factor M. The finite difference form of the TIE can then be expressed as¹²

$${\mathrm{M}}^2\mathrm{I}(\mathrm{M}\mathrm{x},{\mathrm{z}}_{\mathrm{d}})\approx {\mathrm{I}}_0(\mathrm{x})-{\nabla }_{\mathrm{x}}·\{{\mathrm{I}}_0(\mathrm{x})[\frac{{\mathrm{z}}_{\mathrm{d}}}{\mathrm{M}}\frac{{\nabla }_{\mathrm{x}}{\mathrm{\varphi }}_0(\mathrm{x})}{\mathrm{k}}\left]\right\},$$ (6)

where x, and ϕ₀ are the position and phase in the contact/sample plane. In this form, it is clear that the TIE describes propagated intensity as a perturbation of the contact intensity by the phase contrast term on the right-hand-side of Eq. (5). This phase contrast term depends on the gradient of phase and so tends to produce high contrast in regions where the phase varies rapidly, such as at the edges of structures, resulting in images that tend to show significant edge-enhancement-Tthis term increases linearly with z_d, so taking a second image further from the sample improves contrast. However, the approximations inherent in the finite difference approximation to the axial derivative, ∇_x, require that z_d be small enough that the transverse displacement of the ray is also small (the displacement is, up to magnification factors, the quantity in square brackets) on the right-hand side of Eq. (6)). Because of the small wavelengths of X rays, k is large and distances z_d on the order of 1 meter can typically be used without significant error.

Practically, computing phase by taking two images displaced in z is problematic. As the phase features in the images are fine structures, the lateral shift in the detector position must be kept less than one pixel (~10 to 50 µm) as it is displaced by distances on the order of 1 m. Image registration may be employed to overcome this, but the effective pixel size is smaller for the magnified image, which requires accounting for magnification. Further the phase contrast also differs between the two images, complicating the registration. Even a shift of a single pixel can produce severe artifacts in the reconstructed images, and so techniques comparing two displaced images are of limited utility. There are several phase retrieval techniques that circumvent this problem by reconstructing phase from a single image captured at z_d. This amounts to leaving both I₀(x) and ϕ₀(x) as unknowns in Eq. (6), and so with one equation and two unknowns this cannot be uniquely solved for phase. Single-image techniques rely on making strong assumptions on the contact phase and intensity so that Eq. (6) can be reduced to a form that depends on only one unknown. Two such techniques are considered here: weak attenuation (WA), in which I₀(x) is assumed to be approximately constant (so that attenuation contrast is assumed negligible compared to phase contrast) and phase-attenuation duality (PAD) in which Compton scattering is assumed to dominate the attenuation so that phase and attenuation are proportional to each other, leaving only one unknown.

In the WA model, it is assumed that the attenuation variations across the object are negligible compared to phase variations so that the exit face intensity I_o can be assumed to be approximately constant, yielding

$$\mathrm{g}(\mathrm{x})\equiv \frac{\mathrm{k}\mathrm{M}}{{\mathrm{z}}_{\mathrm{d}}}[\frac{{\mathrm{M}}^2\mathrm{I}(\mathrm{M}\mathrm{x},{\mathrm{z}}_{\mathrm{d}})}{{\mathrm{I}}_0}-1]\approx -{\nabla }_{\mathrm{x}}^2{\mathrm{\varphi }}_0(\mathrm{x}),$$ (7)

where g is used here to denote the combination of measured intensities, geometric parameters and wavenumber, and I₀ represents the constant exit intensity. Formally, this equation can be solved if an inverse Laplacian operator ${\nabla }_{\mathrm{x}}^{-2}$ is introduced such that

$${\mathrm{\varphi }}_0(\mathrm{x})\approx -{\nabla }_{\mathrm{x}}^{-2}\mathrm{g}(\mathrm{x})$$ (8)

A particularly efficient method of inverting this equation is by employing Fourier transforms, which renders the Laplacian as multiplication by a transfer function H_wa = (2π)²u², where u is the magnitude of the spatial frequency vector in the Fourier domain. The phase can then be obtained by division by H_wa

$${\mathit{\varphi }}_{\mathbf{0}}(\mathit{x})\approx {\mathbf{ℱ}}^{-\mathbf{1}}{\mathit{H}}_{\mathit{w}\mathit{a}}^{-\mathbf{1}}\mathbf{ℱ}\mathit{g}(\mathit{x})$$ (9)

where ℱ is the Fourier transform and ℱ⁻¹ is the inverse Fourier transform. The the inverse transfer function is

$${\mathit{H}}_{\mathit{w}\mathit{a}}^{-\mathbf{1}}=\frac{\mathbf{1}}{{(\mathbf{2}\mathit{\pi })}^{\mathbf{2}}{\mathbf{u}}^{\mathbf{2}}}.$$ (10)

Because ${\mathit{H}}_{\mathit{w}\mathit{a}}^{-\mathbf{1}}$ diverges at u = 0, the phase component at that frequency must be removed from the reconstruction, which corresponds to insensitivity to a constant, global phase. Additionally, as u → 0, low frequency content in g is significantly amplified when Eq. (9) is solved. As illustrated in Figure 2, this means that low spatial frequency phase features produce weak measurements that are easily corrupted by noise, and that when solving for phase, the noise is strongly amplified.

Figure 2.

The inverse transfer function diverges at low spatial frequencies.

To suppress the low frequency component around the origin, Tikhonov regularization can be used. The net effect is to replace the inverse transfer function used in Eq. (9) with a Tikhonov regularized inverse transfer function ${\mathit{H}}_{\mathit{\text{Tik}}}^{-\mathbf{1}}$,

$${\mathit{H}}_{\mathit{\text{Tik}}}^{-\mathbf{1}}=\frac{{(\mathbf{2}\mathit{\pi }\mathit{u})}^{\mathbf{2}}}{{(\mathbf{2}\mathit{\pi }\mathit{u})}^{\mathbf{4}}+{(\mathbf{2}\mathit{\pi }\mathit{\alpha })}^{\mathbf{4}}},$$ (11)

where α is a regularization parameter that effectively damps low spatial frequency content in the reconstructed phase. The behavior of the reconstruction can be inferred from plots of ${\mathit{H}}_{\mathit{\text{Tik}}}^{-\mathbf{1}}$ for different regularization parameters, illustrated in Figure 3. Notice that the effect of Tikhonov is to reduce low frequency components while closely matching the exact inverse transfer function (for which α=0) for higher spatial frequencies.

Figure 3.

Tikhonov regularization is used to suppress low spatial frequencies in phase reconstruction. Curves show three Tikhonov-regularized transfer functions for phase reconstructions with different values of the regularization parameter, α.

While the WA model eliminates the contact intensity as a variable by assuming it is constant, the PAD method assumes that Compton scattering is the primary cause of attenuation, in which case the contact intensity can be written as I₀(x) = I_b exp[−σ_KNρ(x)], where σ_KN is the Klein-Nishina total cross-section for Compton scattering from a single electron, ρ(x) is the projected electron density through the sample, and I_b is the intensity of the incident beam (assumed to be constant).¹³ Phase is also proportional to projected electron density, ϕ₀(x) = −2πr_eρ(x)/k where, r_e is the classical electron radius. As a result, ρ is the only unknown in Eq. (6), and this equation can be solved for electron density (and therefore phase) using a single image. Note that although electron density could be obtained from a contact image alone, the phase contrast image can offer improved signal to noise performance, especially for small features, due to edge enhancement. Using the above definitions of contact intensity and phase, I₀(x)∇_x ϕ₀(x) = γ∇_xI₀(x), where γ = 2πr_e/kσ_KN. Using this in Eq. (6) yields an equation for I₀(x) in terms of constants and the measured intensity at z_d

$${\mathit{M}}^{\mathbf{2}}\mathit{I}(\mathit{M}\mathit{x},{\mathit{z}}_{\mathit{d}})\approx (\mathbf{1}-\frac{\mathit{\gamma }{\mathit{z}}_{\mathit{d}}}{\mathit{k}\mathit{M}}{\mathit{\nabla }}_{\mathit{x}}^{\mathbf{2}}){\mathit{I}}_{\mathbf{0}}(\mathit{x}).$$ (13)

This can again be solved simply using Fourier transforms where ${\mathit{\nabla }}_{\mathit{x}}^{\mathbf{2}}\to -{(\mathbf{2}\mathit{\pi })}^{\mathbf{2}}{\mathit{u}}^{\mathbf{2}}$. Dividing the resulting transfer function from both sides to solve for I₀ yields

$${\mathit{I}}_{\mathbf{0}}(\mathit{x})=\mathit{\text{exp}}[\frac{\mathbf{1}}{\mathit{\gamma }}{\mathit{\varphi }}_{\mathbf{0}}(\mathit{x})]\approx {\mathbf{ℱ}}^{-\mathbf{1}}\{\frac{\mathbf{1}}{\mathbf{1}+\frac{{(\mathbf{2}\mathit{\pi })}^{\mathbf{2}}\mathit{\gamma }{\mathit{z}}_{\mathit{d}}{\mathit{u}}^{\mathbf{2}}}{\mathit{k}\mathit{M}}}\mathbf{ℱ}[{\mathit{M}}^{\mathbf{2}}\mathit{I}(\mathit{M}\mathit{x},{\mathit{z}}_{\mathit{d}})]\}.$$ (14)

This can be expressed in a form similar to Eq. (9) by setting g(x) ≡ M²I(Mx,z_d) and letting

$${\mathbf{H}}_{\mathbf{p}\mathbf{a}}=\mathbf{1}+\frac{{(\mathbf{2}\mathbf{\pi })}^{\mathbf{2}}\mathbf{\gamma }{\mathbf{z}}_{\mathbf{d}}{\mathbf{u}}^{\mathbf{2}}}{\mathbf{k}\mathbf{M}},$$ (16)

such that

$${\mathbf{\varphi }}_{\mathbf{0}}(\mathbf{x})\approx \mathbf{\gamma }\mathbf{\text{ ln}}({\mathbf{ℱ}}^{-\mathbf{1}}\{{\mathbf{H}}_{\mathbf{p}\mathbf{a}}^{-\mathbf{1}}\mathbf{ℱ}[{\mathbf{M}}^{\mathbf{2}}\mathbf{I}(\mathbf{M}\mathbf{x},{\mathbf{z}}_{\mathbf{d}})]\}).$$ (17)

As can be readily seen from Eq. (16) and Figure 4, the transfer function is non-zero for all spatial frequencies, and so PAD does not cause the extreme low frequency noise that is evident in the WA model.

Figure 4.

Inverse transfer function for phase attenuation duality, $\frac{{\mathbf{z}}_{\mathbf{d}}}{\mathbf{M}}=\mathbf{2.5}\mathbf{m}$ and an X-ray mean energy of 20 keV.

The preceding analysis was based on a spatially coherent, monochromatic, point-like source. If dispersion in the sample refractive index can be neglected, the accrued phase and k are proportional, and the WA model predicts similar phase contrast images for all x-ray energies. The effect of energy on the PAD model is more subtle, but it also proves relatively robust to the spectral bandwidth of the source if the phase is reconstructed using the mean energy. Spatial coherence, on the other hand, is critical to the performance of propagation-based phase contrast imaging. The edge enhancement that is a signature of phase contrast degrades quickly as the spatial coherence of the beam is reduced. Traditionally, high coherence is obtained for tabletop sources by using long source-to-object distances and a very small X-ray spots (with diameters on the order of microns), both of which lead to long exposure times for imaging. In this work, a polycapillary optic was used to generate a sufficiently small secondary source from a large spot rotating anode Mo X-ray source by focusing through a pinhole.¹⁴ Polycapillary optics are a collection of small hollow glass tubes through which X rays are guided as long as the incidence angle is less than the critical angle, as shown in Figure 5(b). The exiting beam is convergent to create a small, intense, secondary source of X rays. If this focal spot is small enough, it can provide sufficient coherence for propagation-based phase contrast imaging. For an isotropic source, the coherence length is $\lambda \frac{{\mathbf{R}}_{\mathbf{1}}}{\mathbf{s}}$, where s is the source size. For these experiments that would yield a coherence length of around or less than 1 µm at the sample. The polycapillary optics may provide enhanced coherence by restricting the divergence of the beam emitted from any part of the optic face.

Figure 5.

(a) Scanning electron micrograph of a polycapillary optic. (b) A single fiber with diameter. The X rays reflected down the channel only if the incidence angle is less than the critical angle for the fiber.¹⁵

The primary benefit of a polycapillary optic is to produce a secondary spot that is brighter than would be achievable with a conventional microfocus source. Rotating anode sources are typically are about a factor of 10 brighter (allow more current per millimeter of electron spot than microfocus tubes), but have spot sizes which are too large to employ in phase systems. The use of a focusing optic increases the intensity of the secondary spot produced by the pinhole by a gain factor of

$$\mathbf{\text{Gain}}=\left(\frac{{\mathbf{d}}_{\mathbf{\text{in}}}^{\mathbf{2}}}{{\mathbf{f}}_{\mathbf{\text{in}}}^{\mathbf{2}}}\right)\mathbf{T}{\left(\frac{\mathbf{L}}{\mathbf{\sigma }}\right)}^{\mathbf{2}},$$ (18)

where d_in is the input diameter of the optic, T is its transmission, f_in is the input focal length, L is the distance from the conventional source and σ is the diameter of the pinhole.¹⁵

2. Materials and Methods

A 5 KW Molybdenum (Mo) rotating anode X-ray source with a source size of 3×0.3 mm¹⁶ was used at a takeoff angle of 12°. As shown in Figure 6, the polycapillary optic collected radiation from the divergent source and focused it onto a small spot. The input and output focal lengths of the optic were 81 and 5.5 mm, as given in Table 1. A solid state CdZe Amptek XR-100 CR X-ray detector was used for alignment. For imaging, a Fuji Computed Radiography plate M1040019 with an active area of 10 cm × 12 cm and 50 µm resolution or a phosphor coated CCD camera with an active area of 3 cm × 4 cm and a pixel size of 22 µm were employed. A 1.6 mm polyethylene rod was imaged to test edge enhancement. Insect images were also taken to determine the feasibility of phase imaging on a biological specimen.

Figure 6.

Schematic diagram of experimental set-up. The optic was translated horizontally and vertically at each point along z-axis to align it with the x-ray source.

Table 1.

Characteristics of Polycapillary Optic 690

Manufacturer	X-ray Optical System Inc.
ID Number	690
Input Focal Length (mm)	81
Output Focal Length (mm)	5.5
Channel Diameter (µm)	9.4

Results and Discussion

In order to align the optic for maximum transmission, it was first placed as close to the source as possible and translated iteratively in the horizontal and then in the vertical directions to achieve the best alignment. The optic was then translated away from the source and same procedure was repeated. At each distance, the data of the scan along the x and y axes was fit to a Gaussian distribution

$$\mathbf{y}={\mathbf{y}}_{\mathbf{o}}+\mathbf{A}{\mathbf{e}}^{-\frac{\mathbf{2}{(\mathbf{x}-{\mathbf{x}}_{\mathbf{c}})}^{\mathbf{2}}}{{\mathbf{w}}^{\mathbf{2}}}},$$ (19)

using Origin 6.0 software as shown in Figure 7 for the horizontal case. The variation of the horizontal scan width with the distance is shown in Figure 8. At the input focal point, the $\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}=\mathbf{w}\sqrt{\mathbf{2}\mathbf{\text{ln}}(\mathbf{2})}$ was minimum with a value of 0.34 ± 0.02 mm, as shown in Figure 8. The vertical width was the same to within the uncertainty.

Figure 7.

Graph resulted from the scan of optic. The red line is the Gaussian fit to data. The width at the input focal point is 0.34 ± 0.02 mm.

Figure 8.

Alignment of optic with the x-ray source. At the input focal point, the scan width is minimum.

The minimum expected value of the beam scan FWHM_calc at the input focal point is approximately¹⁷

$$\mathbf{F}\mathbf{W}\mathbf{H}{\mathbf{M}}_{\mathbf{\text{calc}}}=\sqrt{{\mathbf{s}}^{\mathbf{2}}+{(\mathbf{1.5}{\mathbf{f}}_{\mathbf{\text{in}}}{\mathbf{\theta }}_{\mathbf{c}})}^{\mathbf{2}}},$$ (20)

where s is the source size s = 300 µm, f_in is the input focal length, and θ_c is critical angle for total reflection, which for the borosilicate glass is

$${\mathbf{\theta }}_{\mathbf{c}}=\frac{\mathbf{30}\mathbf{e}\mathbf{V}}{\mathbf{E}}.$$ (21)

For an X-ray energy of 20 KeV, the critical angle is 1.5 mrad. The expected scan width is 0.35 mm, which is in agreement with the measured value.

An image plate was used to estimate the output spot size. The image plate (Fuji M1040019) was placed close to the optic focal spot and the resulting image was then read in film reader (Fuji Films BAS-1800) using Image Gauge software. The smallest resolution of 50 µm was selected during reading of the image plate. Figure 9(a) shows the magnified view of the spot at a distance of 5.5 mm from the optic. The profile across the focal spot size drawn in Figure 9(a) gave a fit Gaussian distribution with a width of 114 ± 50 µm at the output focal point as shown in Figure 9(b). The variation of spot size with the distance from the optic is shown in Figure 10. The spot was round, and the horizontal and vertical widths were similar.

Figure 9.

(a) Magnified image of the source (b) shows the graph of (a). Profile taken across the line in (a). The red line is the Gaussian fit to the data.

Figure 10.

The output spot size is a minimum at the output focal point.

The expected output focal spot size of the optic¹⁵ is

$$\mathbf{s}\approx {\mathbf{w}}_{\mathbf{\text{calc}}}=\sqrt{{\mathbf{c}}^{\mathbf{2}}+{(\mathbf{1.5}{\mathbf{f}}_{\mathbf{\text{out}}}{\mathbf{\theta }}_{\mathbf{c}})}^{\mathbf{2}}}$$ (22)

where c is the channel size of a single fiber and f_out is the output focal length of the optic. For the optic used here, the expected value of the spot size is 15 µm. The difference between the measured and expected focal spot size may be due to an error in manufacturing of the optic. For short focal length optics it can be difficult to cut the optic at the position for which the channels are directed toward a single point. This optic was designed to be used with the short focal length side facing the source, to enable efficient source capture, in which case it was not as important that all of channels be precisely aligned.

To reduce the spot size, 25–100 µm diameter, pinholes were placed at the output focal point of the optic and carefully aligned to maximize the output. Assuming a typical polycapillary transmission of 10%, and using the anode-to-window distance of 60 mm to set a minimum value for L, the gain is about 40 for the measured spot size and would be several hundred for an optic manufactured to produce a smaller output spot, and even higher for an optic with a larger input area

After aligning the optics and pinhole with the X-ray source, the output beam was used to form phase contrast enhanced images.

3. Images of Rod

3.1. 100 µm Pinhole

3.1.1. Image Plate

A cylindrical 1.6 mm diameter polyethylene rod was imaged using a 100 µm diameter pinhole. The rod was placed 17 cm from the pinhole (R₁ in Figure 6) and the image plate was positioned at a distance of 64 cm from the rod (R₂). The magnification,

$$\mathbf{M}=\frac{{\mathbf{R}}_{\mathbf{1}}+{\mathbf{R}}_{\mathbf{2}}}{{\mathbf{R}}_{\mathbf{1}}},$$ (23)

was 4.7.

The image shown in Figure 11 presents a dark region within the body of the rod due to attenuation, and a white band at the rod edge which is edge enhancement due to the phase imparted by the rod. For quantitative analysis of the rod profile, a background correction was first performed by dividing by an image taken without the rod in place in order to remove intensity variations induced by the optic. Next, a vertical line, five pixels wide, was drawn through the rod. This line was summed over the five horizontal pixels at each vertical position to reduce noise and produce a single line plot. The resulting line plot is shown in Figure 12. Both the intensity dip due to attenuation, and the intensity peak due to phase are evident in this plot, although the peak is rather obscured by noise. The presence of noise in the image diminishes the strength of the phased enhanced signal. The conspicuity of the edge enhancement¹⁸ can be described by the edge-enhancement to noise ratio (EE/N) ratio

$$\frac{\mathbf{E}\mathbf{E}}{\mathbf{N}}=\frac{\mathbf{P}-\overline{\mathbf{B}}}{{\mathbf{\sigma }}_{\mathbf{B}}},$$ (24)

where P is the peak intensity, B̅ is the average intensity over a region of background labeled B in Figure 12, and σ_B is the standard deviation of intensity over region B. The edge-enhancement to noise ratio was 0.9 ± 1, where the uncertainty in the peak height was assumed to be equal to the noise.

Figure 11.

Image of a 1.6 mm diameter rod taken with a 100 micron pinhole. The white lines illustrate edge enhancement. A profile is shown in Figure 12.

Figure 12.

Profile of the 1.6 mm diameter rod taken with a 100 µm pinhole. The small peaks on both sides of the valley are due to edge enhancement

The image in Figure 11 was acquired at 30 kVp and 30 mA for two and a half minutes. The product of current and exposure time is higher than the normally used for soft tissue imaging in clinical settings,¹⁹ however, the intensity loss occurs before the object and would not create additional patient dose. In addition, an optic²⁰ which is designed for this application would have a larger input area and produce a smaller spot without a pinhole and thus would have a much higher intensity and shorter exposure time. The optic used in this measurement has a relatively large input focal length, 81 mm, and a small input diameter, of about 4 mm. It also had a very sharp output focus, which, combined with the pinhole, gave a small effective transmission, probably less than 1%. Changing to a standard optic with a 15 mm diameter, a transmission of 20%, and an input focal length of 40 mm, all parameters within measured values for standard optics, would, according to equation 16, increase the intensity by a factor of 500, which would decrease the exposure time to less than 1 second. Increasing the source power from 900 W to 5 kW would allow exposures of less than 1 second, even with a reduced pixel size of 25 µm.

3.2. 25 µm Diameter Pinhole

3.2.1. Image Plate

The 1.6 mm diameter polyethylene rod was then imaged using a 25 µm diameter pinhole, shown in Figure 13. The rod was placed at a distance of 25 cm from the output focal point of the optic (R₁) and the image plate was placed approximately 80–81 cm from the rod (R₂), giving a magnification of 4.2. The distances were increased in order to increase the beam coherence. The rod was exposed for 6 minutes with voltage of 30 kVp and a current of 40 mA. The exposure was increased to accommodate the large distance and loss of intensity in using the 25 µm diameter pinhole.

Figure 13.

Image of a 1.6 mm rod taken with a 25 µm pinhole. The white line along the length of rod shows edge enhancement. A profile is shown in Figure 14.

As with the 100 micron pinhole, the captured image shows attenuation through the rod body with edge enhancement due to phase at the rod edges. The normalized resulting profile is shown in Figure 14. The peaks on both sides of the valley show edge enhancement. The edge-enhancement to noise ratio was 2.6 ± 1.

Figure 14.

Profile of the image of Figure 13. Edge enhancement is evident from the two peaks. Background division was applied to remove nonuniformity in the beam.

3.2.2. Charged Coupled Device (CCD) Camera

The previous rod images were taken with the image plate that had a pixel size of 50 µm. A higher resolution digital detector (CCD camera) with a pixel size of 22 µm was used to test whether the edge enhancement would be improved. Flat field and dark field images were acquired with no rod in place and were applied to the rod images.

The rod-to-pinhole distance was increased to 40 cm, and an image of the rod was taken with a detector-to-rod distance of 67 cm, for a magnification of 2.6. As the exposure per frame was restricted to 30 seconds, the average of 30 frames was taken to increase the exposure time to 15 minutes. A bright line along the length of the rod could be seen on both sides of the rod as shown in Figure 15. The conspicuity for this image was 6.5 ± 1.

Figure 15.

A 1.6 mm diameter rod image taken with CCD camera after flat-field correction. Two bright lines along the length of rod are clearly seen.

Additional images were taken at varying object-to-detector distances. The effect of increased magnification on edge enhancement is shown in Figure 16. The edge enhancement increases approximately linearly with increasing detector-to-object distance, as expected from the work of other investigators⁶ using a small spot microfocus source with no optic. The secondary source provided by a polycapillary optic and pinhole performed as a microfocus source.

Figure 16.

The effect of distance R₂ on edge enhancement. The edge enhancement to noise ratio increases with distance.

4. Insect Images

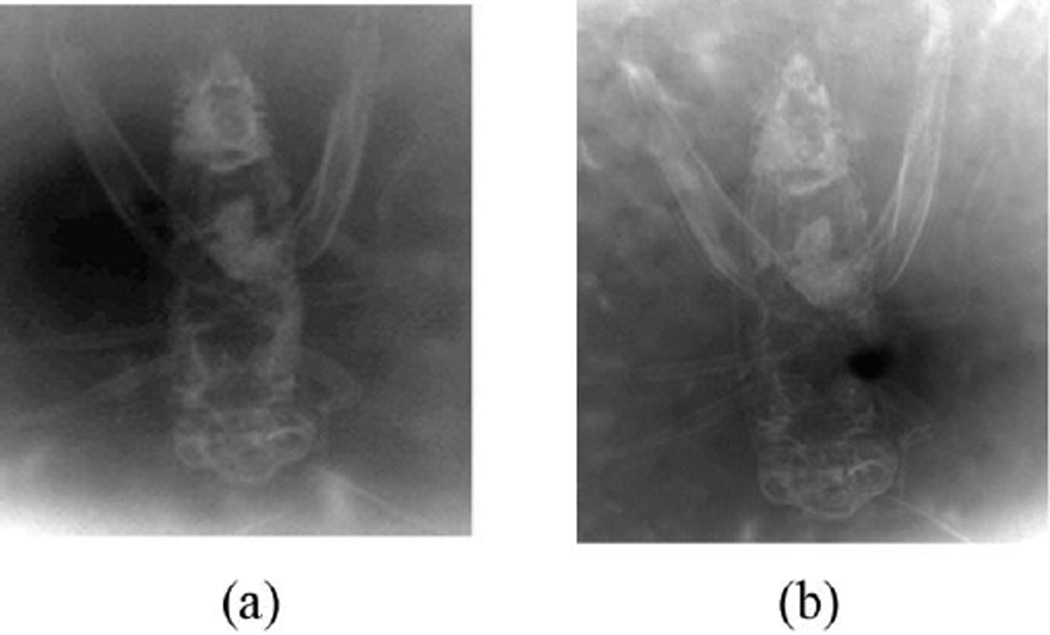
A conventional absorption image, shown in Figure 17(a), was acquired with an insect at a distance of R₁ = 40 cm from the source, with the image plate placed just behind the object at a distance of R₂= 2 cm. The phase contrast image shown in Figure 17(b) was taken with the detector displaced to a distance of 67 cm from the insect, keeping R₁ = 40 cm.

Figure 17.

(a) Contact image of the cricket (detector placed against the insect). (b) Phase-contrast image of a cricket with detector placed 67 cm from the insect. The edges of internal structures are clearly visible even though a low-resolution detector was employed

The phase contrast image shows not only the internal structures (due to absorption) but also shows clearly defined boundaries evidencing edge enhancement. Some of the improvement is due to the smaller effective pixel size due to the magnification; however there is visible edge enhancement.

5. Quantitative Phase Retrieval

In addition to simple edge enhancement, additional information about the material in the object could be extracted if a quantitative phase can be calculated. Quantitative phase retrieval was performed for the rod image shown in Figure 15 using the WA model. The mean X-ray energy was approximated as 20 keV. Each reconstruction (from image b to d in Figure 18) shows the phase at each pixel, calculated using Eqs. (9) & (10). Tikhonov regularization was used with a range of regularization parameters α =0.5–2 mm⁻¹. The parameter α provides a cutoff below which spatial frequencies are excluded from the reconstruction, i.e. only features of physical dimensions smaller than a certain cutoff value are preserved. For α = 0.5 mm⁻¹, which corresponds to a maximum allowed feature size of about 2 mm, the rod itself is visible in the reconstruction, but the edge is poorly defined and low frequency (blob-like) noise dominates the reconstructed phase values, which are an order of magnitude too large. For α = 1 mm⁻¹, feature sizes up to roughly 1 mm are preserved in the reconstruction, which sharpens the rod’s edges and excludes the larger noise features. However, since the rod is 1.6 mm in diameter, it is not properly reconstructed and a bright strip appears in its central region. The highest value of α = 2 mm⁻¹ reconstructs features on the order of 0.5 mm or smaller and so clearly cannot reconstruct the bulk of the rod, but does capture the bright edge enhancement while removing low frequency noise. None of the values of the regularization parameter captures both the shape and the numerical value of the rod accurately, which is primarily due to inaccuracy in the WA approximation. The rod itself is clearly visible in Figure 18(a), and so does not present the negligible attenuation assumed by the WA model. Additionally, although the image is background corrected, residual background structure due to the polycapillary optic is still present and produces significant low frequency artifacts in the reconstructed image, which are evident in the blob-like background structures in Figure 18(b).

Figure 18.

(a) The raw image. (b) Images processed with the value of regularization parameters: (b) α=0.5, (c) α=1, (d) α=2 mm⁻¹. As the value of α increases, the low spatial frequencies are removed from the phase reconstruction. Color bar on (b)–(d) indicates reconstructed phase value.

The same rod image of Figure 15 was also processed using the phase attenuation duality model Equation 13 and 14 with the results shown in Figure 19.

Figure 19.

Rod processed using PAD model.

Phase attenuation duality assumes that phase and attenuation can be considered proportional, which is true if Compton scattering is the dominant attenuation process. Although this is also not an accurate approximation at the mean photon energy of 20 keV used here (photoelectric absorption is expected to be the dominant attenuation process), it is still considerably more accurate than WA as it accounts (albeit improperly) for the rod attenuation. The shape of the rod is reconstructed accurately, although the reconstructed phase is still about 5 times too large.

The phase of the insect shown in Figure 17 was also reconstructed using the same two approaches. Figure 20 (a) shows the background corrected phase contrast image of the insect. Figure 20(b) and (c) show the WA phase reconstructions α = 1.25 mm⁻¹ and α = 2 mm⁻¹, respectively. Note that the WA approximation works considerably better in this case than for the rod, as the insect is significantly more weakly absorbing, and the internal structure of the insect is much finer than the background non-uniformities and therefore a suitable value of α can remove background artifacts from the reconstruction without removing the insect structure. Figure 20(d) shows the phase reconstructed image using phase attenuation duality approach. All processed images show an enhanced image contrast along with improved noise reduction. The WA model in Figure 20(c) shows enhanced edges due to the regularization parameter removing image features larger than the edges, while the WA model with too small of a regularization parameter shows blurring and a halo about the body of the insect due primarily between the inaccuracy of the WA model (the insect presents non-negligible attenuation). The PAD model does not obviously suffer from this inaccuracy due to absorption since the model accounts (although somewhat inaccurately) for attenuation.

Figure 20.

(a) The phase contrast image of a cricket from Figure 17 with background correction. (b) WA phase reconstruction with α=1.25 mm⁻¹. (c) WA phase reconstruction with α=2 mm⁻¹. (d) PAD phase reconstruction.

Conclusion

Propagation-based phase imaging was successfully tested with a large spot rotating anode X-ray source aligned with polycapillary optic. The polycapillary optic accepts radiation from a large X-ray source and converges it to create a small spot. A rod of 1.6 mm diameter was imaged with different geometric configurations using an image plate and CCD camera. An edge enhancement-to-noise ratio up to a value of 6.5 was obtained. Conventional absorption and phase images of an insect were acquired to determine the feasibility of phase imaging in biological tissues using this technique. A pure phase object was obtained using phase attenuation duality and weak attenuation approaches with a single image. Additional optimization of the optical system is required to reduce the exposure time.

Highlights.

• Phase contrast in x-ray imaging can be significantly higher than conventional absorption contrast, but requires coherent sources. Coherence in the x-ray regime requires small source sizes, and hence low power (to avoid melting the anode), which translates to long exposure times.

• In this project a focused polycapillary optic was employed to create a small secondary source from a large spot rotating anode X-ray generator. Rotating anode systems have higher power per source area, but are too large to be coherent for reasonable source-to-object distances.

• Edge enhancement was observed, and increased as expected with object-to-detector distance, with a maximum edge-enhancement-to-noise ratio of 6.5.

• Phase reconstructions were computed using two different approaches, weak attenuation and phase attenuation duality. Pure phase images were successfully reconstructed from the phase contrast images by employing the weak attenuation model.