Abstract
Delayed-enhancement magnetic resonance imaging (DE-MRI) is an effective technique for detecting left atrial (LA) fibrosis both pre and postradiofrequency ablation for the treatment of atrial fibrillation. Fixed thresholding models are frequently utilized clinically to segment and quantify scar in DE-MRI due to their simplicity. These methods fail to provide a standardized quantification due to interobserver variability. Quantification of scar can be used as an endpoint in clinical studies and therefore standardization is important. In this paper, we propose a segmentation algorithm for LA fibrosis quantification and investigate its performance. The algorithm was validated using numerical phantoms and 15 clinical data sets from patients undergoing LA ablation. We demonstrate that the approach produces good concordance with expert manual delineations. The method offers a standardized quantification technique for evaluation and interpretation of DE-MRI scans.
Keywords: Delayed-enhancement MRI, left atrium, image segmentation, fibrosis
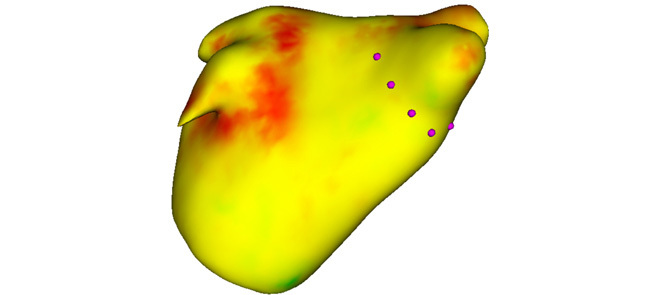
Standardization of quantification for left-atrial scar will allow the select of patients who are predicted to respond well to ablation procedures for cardiac arrhythmias. This could improve the success rate of such procedures and reduce recurrence of arrhythmias. An algorithm to standardize quantification is proposed. Figure shows a heat map of the left atrium, generated from the algorithm, showing likely areas of scar. Purple stylized dots represent potential sites of ablation based on the scar distribution.
I. Introduction
Atrial fibrillation (AF) affects approximately 2.3 million people in the USA with significant comorbidity and mortality [1], [2]. It is a condition that increases the risk of stroke by a factor of six-fold and doubles the mortality rate of patients when compared to age-matched controls. Since it was shown that ectopic beats from the pulmonary veins (PV) give rise to AF [3] the treatment of AF using radiofrequency catheter ablation (RFCA) has become an important and common procedure. In this procedure, ablation lesions are created in a circular fashion around the PV ostia to electrically isolate the PVs, and thus the ectopic focal points, from the rest of the left atrium (LA). This treatment can provide a cure for the majority of patients and prevent the requirement for long-term pharmacotherapy. However, for a high proportion of patients (15%–46%) [4]–[6], there is recurrence of AF. This normally requires a second or third re-do ablation procedure and thus has a high burden on health care.
It is important to select patients who will respond better to RFCA to reduce recurrence rates. Several studies have shown that it is possible to predict the outcome of RFCA procedures from the fibrosis extent in LA [7]–[10]. A scoring system based on the degree of fibrosis has been developed, leading to treatment stratification [8]. Other recent studies have also highlighted the significance of the extent of fibrosis or scar in LA post-ablation for predicting outcome [11], evaluate effectiveness of ablation technologies [12] and helping to gain a better understanding of the left atrial substrate [13]. In this context, magnetic resonance imaging (MRI) has been shown to be effective for non-invasive imaging of the LA. In particular, Gadolinium delayed-enhancement (DE) MRI has the ability to detect changes that take place in the LA both pre- and post-ablation and recent studies have shown that it could potentially be useful for selecting suitable candidates for RFCA [8]. DE-MRI is acquired with an inversion-recovery gradient echo sequence performed after administration of Gadolinium yielding an image at an inversion time which is chosen to null the signal from healthy myocardium. Due to the differential washout kinetics of Gadolinium, scar or fibrotic areas are differentiated from heatlhy tissue. Fibrotic or scar tissues in the myocardium appear with a signal intensity (SI) above normal myocardium. Fig. 1 shows some examples of DE-MRI with intensities significantly higher than myocardium.
Fig. 1.
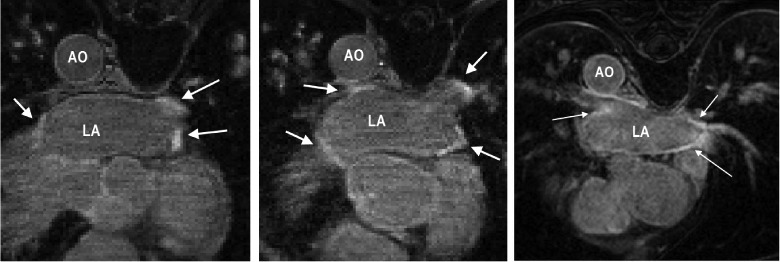
DE-MRI images from three separate patients taken 3 months post-ablation. Arrows indicate areas of enhancement. Abbreviations: AO—aorta, LA—left atrium.
Quantification of scar or fibrosis from DE-MRI is challenging due to various reasons [14]. The thin myocardium of the LA wall leads to low singal-to-noise ratio. Contrast variation in these images can be an issue due to choice of inversion time. Also the complex geometry of the LA results in some transverse slices where a very small section of the anatomy is visible, making manual quantification in these areas highly observer-dependent. Finally, patients suffering from AF often have an irregular heart rate and breathing making it hard to acquire good quality respiratory- and cardiac-gated images. Quantification from such images become difficult to automate and manual quantification tends to be highly observer-dependent.
In this work, a scar quantification approach is proposed and investigated. The method exploits a well-known image segmentation approach known as graph-cuts [15]. Segmentation is achieved using a combination of scar intensity model priors and Gaussian-fitting to tissues in the unseen image to be segmented. The final labelling is achieved by optimizing a cost function using graph-cuts.
A. Previous Works
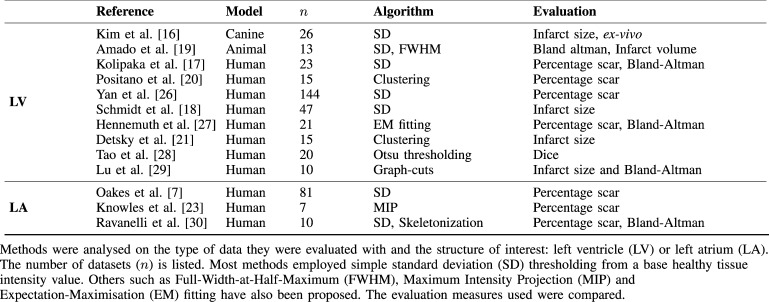
Quantification and segmentation of ventricular scar from DE-MRI images have been studied in several investigations. Refer to Table I for a brief summary. A common method for detecting scar or fibrosis is to use a fixed model of thresholding between two and six standard deviations (SD) above the mean intensity of healthy myocardium [16]–[19]. This requires the user to manually outline remote or healthy myocardium. Another common method is the Full-Width-At-Half-Maximum (FWHM) which sets scar to be intensities greater than 50% of manually outlined hyper-enhanced myocardium [19]. Other approaches exist to compute the threshold automatically [17] or by applying clustering [20], [21], or with graph-cuts [22].
TABLE I.
Overview of Previously Published Methods for Scar Detection, Quantification and Segmentation.
The aforementioned works were primarily developed for the left ventricle. For the LA, methods have been proposed for endocardial surface-based segmentation [23] and threshold-based volumetric segmentation [7], [14], [24]. In [23], the maximum intensity projection (MIP) of the DE-MRI SI on the segmented LA shell is used to visualise enhancing intensities on the surface. This technique has an important drawback: it is only a visualisation of intensities and thus not a segmentation technique with no volumetric segmentation as output. In [7], a volumetric segmentation of pre-ablation LA fibrosis is proposed by obtaining suitable measurements from the intensity histogram within atrial wall. This has a disadvantage that the LA wall is thin and thus its manual segmentation can have significant inter-observer variation. Other methods have employed fixed models for pre-ablation fibrosis [24] and post-ablation scar [25] with variable thresholding.
In summary, a fixed thresholding model cannot handle all the different variabilities encountered in LA DE-MRI and these are both from the varied internal factors (size, distribution and heterogeneity of scar) and varied external factors (resolution, image noise, inversion time, surface coil intensity variation). The inversion time choice can generate the appearance of more or less scar, and change the appropriate scar threshold. Motion blurring also reduces the appearance of scar.
B. Contributions
In this work, we present a method for segmenting and thus quantifying LA fibrosis in DE-MRI. It is based on a probabilistic tissue intensity model of DE-MRI data, which is derived from both training and the unseen data. It offers two advantages: 1) It does not require manual outlining of base-line healthy myocardium, and 2) It provides greater accuracy than fixed models with no inter-observer variation. The algorithm was evaluated and compared with existing clinically-used methods using local pixel overlap measures. Performance was analyzed by exploring various scar contrast levels.
An abbreviated version of this work was published in [31] and [32]. In this current version, we present the approach with more details including additional experiments and validation. We also include an automated adaptive step that allows for variation in the scar signal level and avoids sub-optimal scar intensity models. Furthermore, we present a much more comprehensive validation of the algorithm on a larger clinical cohort. The algorithm was also used recently in a segmentation challenge [33], segmenting sixty DE-MRI datasets from three imaging centres.
II. Clinical and Imaging Protocols
A. Patients
15 patients were followed up at 6 months following their first ablation for the treatment of paroxysmal AF. The procedures were carried out in the cardiac catheterization laboratory at St. Thomas Hospital, London, U.K. All patients gave written permission to take part in this local ethics committee approved study.
B. Ablation Procedure
A catheter was placed in the coronary sinus to provide a reference for electroanatomic mapping and to enable LA pacing. Two trans-septal punctures were made to access the LA using standard long sheaths (St. Jude Medical, MN, USA). A three-dimensional (3D) LA geometry was created using either Ensite NavX (St. Jude Medical, MN, USA) or CARTO (Biosense Webster, Diamond Bar, CA, USA). A circular mapping catheter was then placed in each PV in turn while the corresponding LA-PV ostium was targeted with wide area circumferential ablation. Energy was delivered through a 3.5 mm irrigated tip catheter with flow limited to 17 ml/min, power limited to 30 W on the anterior wall and 20 W on the posterior wall and temperature limited to 50 . Ablation lesions were marked on the LA geometry when there had been an 80% reduction in the local electrogram voltage or after 30 seconds of energy delivery. The clinical endpoint was electrical isolation of all PVs.
. Ablation lesions were marked on the LA geometry when there had been an 80% reduction in the local electrogram voltage or after 30 seconds of energy delivery. The clinical endpoint was electrical isolation of all PVs.
C. MRI Scanning Procedure
MRI scanning was performed before and after the ablation procedure. Pre-ablation scanning was performed 24 hours prior to the procedure and post-ablation scanning was performed 6 months after the procedure. The proposed algorithm in this work was developed and evaluated primarily for post-ablation images.
All scanning was performed on a 1.5T Achieva scanner (Philips Healthcare, The Netherlands). The examination began with a survey and reference scans, and an interactive scan to determine the four-chamber orientation of the heart. For anatomical information, a 3D magnetic resonance angiography (MRA) scan with whole-heart coverage (1 1
1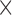 2
2  acquired, 1
acquired, 1 1
1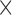 1
1  reconstructed, 20 secs duration) was acquired following the injection of 0.4 ml/kg double dose of a gadolinium-diethylenetriaminepentaacetate (Gd-DTPA) contrast agent. This scan was not cardiac-gated. This scan was followed by a 3D respiratory navigated and cardiac-gated, 3D balanced steady-state free precession (b-SSFP) acquisition in a sagittal orientation with whole-heart coverage (1.3
reconstructed, 20 secs duration) was acquired following the injection of 0.4 ml/kg double dose of a gadolinium-diethylenetriaminepentaacetate (Gd-DTPA) contrast agent. This scan was not cardiac-gated. This scan was followed by a 3D respiratory navigated and cardiac-gated, 3D balanced steady-state free precession (b-SSFP) acquisition in a sagittal orientation with whole-heart coverage (1.3 1.3
1.3 2.6
2.6 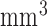 acquired, 1.3
acquired, 1.3 1.3
1.3 1.3
1.3  reconstructed, 6 mins duration). The scan for the visualization of delayed-enhancement was a 3D ECG-triggered, free breathing inversion recovery (IR) turbo field echo (TFE) with respiratory-navigated and cardiac-gated with whole heart coverage (0.6
reconstructed, 6 mins duration). The scan for the visualization of delayed-enhancement was a 3D ECG-triggered, free breathing inversion recovery (IR) turbo field echo (TFE) with respiratory-navigated and cardiac-gated with whole heart coverage (0.6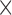 0.6
0.6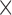 4
4  acquired, 0.6
acquired, 0.6 0.6
0.6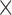 2
2 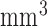 reconstructed, 3 mins duration). Data were acquired within a window of 150 ms every one RR interval, with a low-high k-space ordering and spatial pre-saturation with inversion recovery (SPIR) fat suppression. The IR time delay was determined from the Look-Locker sequence, and was set at an inversion time (TI) intermediate between the optimal TIs to null myocardium and blood. This scan was performed approximately 20 mins after contrast administration. The slices were set for complete coverage of both left and right atria. Slice orientation was in the four-chamber view for AF ablation to optimize visualization of the pulmonary veins. Note that the scan times quoted above are actual scan times. Typical respiratory gating efficiency is 50% but this varies considerably in this particular patient population.
reconstructed, 3 mins duration). Data were acquired within a window of 150 ms every one RR interval, with a low-high k-space ordering and spatial pre-saturation with inversion recovery (SPIR) fat suppression. The IR time delay was determined from the Look-Locker sequence, and was set at an inversion time (TI) intermediate between the optimal TIs to null myocardium and blood. This scan was performed approximately 20 mins after contrast administration. The slices were set for complete coverage of both left and right atria. Slice orientation was in the four-chamber view for AF ablation to optimize visualization of the pulmonary veins. Note that the scan times quoted above are actual scan times. Typical respiratory gating efficiency is 50% but this varies considerably in this particular patient population.
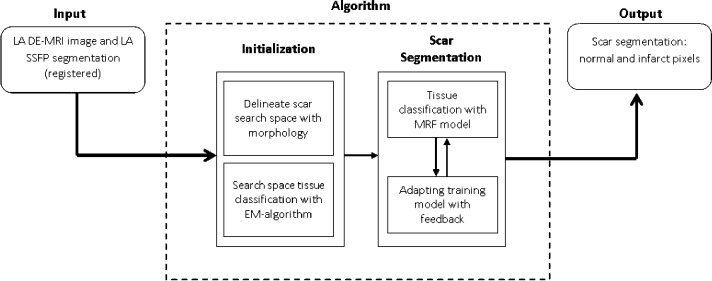
D. Segmentation Algorithm
Fig. 2 shows an overview of the algorithm. The inputs were a DE-MRI image and a segmentation of the LA from an anatomical scan. The LA segmentation was obtained from the b-SSFP whole-heart scan by an automatic approach based on a statistical shape model [34], and was followed where necessary by manual correction by a human rater (throughout this paper, the terms human rater or observer refer to someone who has experience viewing tomographic images and can correctly identify the LA endocardium and fibrosis in the LA myocardium). The b-SSFP image was chosen over MRA as it was acquired at the same phase in the cardiac cycle as the DE-MRI. The MRA, though it provides better anatomical visualization, was not cardiac gated and it can be difficult to resolve the differences between this and the DE-MRI with registration. The anatomical images were registered to the DE images using the DICOM header data, and then refined by rigid and affine registration steps [35]. Affine registration was necessary to account for the differing PV angles in the scans. This defined the endocardial LA boundary in the DE images.
Fig. 2.
An overview of the steps involved in the segmentation process. The pipeline takes as input MRI images and outputs binary segmentations (rounded boxes). The processing pipeline is illustrated here with each separate stage in the algorithm. Smaller boxes represent sub-stages. The scar segmentation stage is iterative as indicated by the bi-directional arrows.
E. Scar Segmentation
Segmentation of scars from DE-MRI images can be defined as assigning a label 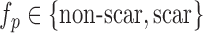 for every voxel
for every voxel 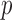 in the search space of the image. The search space is defined as a region
in the search space of the image. The search space is defined as a region 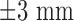 from the endocardial border obtained from the atrial geometry extraction. This is within the limits of atrial wall [23]. Given the observed intensities in the atrial wall and prior knowledge of scars, the segmentation problem is solved using a probabilistic framework where the maximum a posteriori (MAP) estimate is computed using Bayes' theorem:
from the endocardial border obtained from the atrial geometry extraction. This is within the limits of atrial wall [23]. Given the observed intensities in the atrial wall and prior knowledge of scars, the segmentation problem is solved using a probabilistic framework where the maximum a posteriori (MAP) estimate is computed using Bayes' theorem:
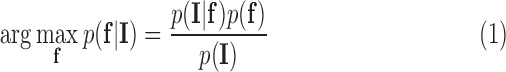 |
where 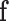 is the total label configuration and
is the total label configuration and 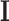 are all observed intensities in the image. The image likelihood
are all observed intensities in the image. The image likelihood 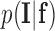 describes how likely is the observed image given a label configuration
describes how likely is the observed image given a label configuration 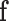 . The prior
. The prior  encodes any prior knowledge of the healthy and scar tissue classes.
encodes any prior knowledge of the healthy and scar tissue classes.
The MAP estimate allows to determine the most likely label configuration 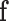 of the observed image
of the observed image 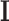 . To make numerical computation more convenient, the MAP formulation is transformed to one involving only summations. This is possible by taking the negative logarithm of (1):
. To make numerical computation more convenient, the MAP formulation is transformed to one involving only summations. This is possible by taking the negative logarithm of (1):
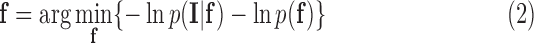 |
where 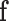 is the optimal labelling. The prior probability
is the optimal labelling. The prior probability 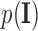 can be ignored as it is independent from the labelling
can be ignored as it is independent from the labelling 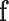 . Note that the segmentation problem is now an energy minimization problem, following from (2):
. Note that the segmentation problem is now an energy minimization problem, following from (2):
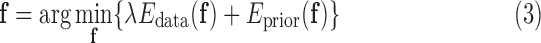 |
where 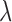 weights the influence of the two terms. The intensity energy
weights the influence of the two terms. The intensity energy 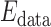 measures the disagreement between a probabilistic tissue model and the observed data, and
measures the disagreement between a probabilistic tissue model and the observed data, and 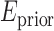 is a smoothness term penalizing any discontinuities within a tissue class. In Sections III–VI, the intensity models that contribute towards
is a smoothness term penalizing any discontinuities within a tissue class. In Sections III–VI, the intensity models that contribute towards 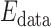 and
and 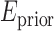 are described in Sections III–VI.
are described in Sections III–VI.
F. Intensity Models
The likelihood 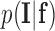 of the observed intensities in the image can be estimated. Assuming that the voxel intensities are independent, the total likelihood for the image is given as:
of the observed intensities in the image can be estimated. Assuming that the voxel intensities are independent, the total likelihood for the image is given as:
 |
The negative logarithm or the log-likelihood gives the total intensity energy contributed by each voxel:
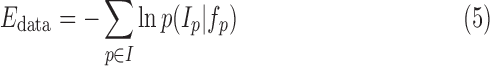 |
We first consider the intensity energy contribution from the scar tissue class, i.e., for the function 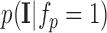 and then for the non-scar class.
and then for the non-scar class.
1). Intensity Model for Scar Tissue
Enhancements in DE-MRI can vary greatly depending on a number of reasons: choice of inversion time, scanner vendor, protocol, operator experience, motion-blurring and patient breathing. Modelling variation in enhancement is thus important. When examining atrial DE-MRI images, the contrast-to-noise ratio (CNR) of scar to left atrial blood pool is often compared. This is simply due to the fact that normal atrial myocardium is not sufficiently visible to the naked eye in DE-MRI. Atrial blood pool is the single largest neighbouring tissue block sufficiently visible to the naked eye in the axial view. In this work, to exploit the nature of scar-blood CNR in DE-MRI, the scar to blood pool (SC-BP) intensity ratio is modelled and in the rest of paper we refer to normalization of DE-MRI intensities in this context as taking the ratio of DE-MRI voxel's intensity to blood pool.
To model enhancement, human raters delineated scar in training images. The blood pool was also delineated. The scar to blood pool ratio was determined for every voxel labelled as scar. This ratio could be modelled suitably with a Gaussian distribution:
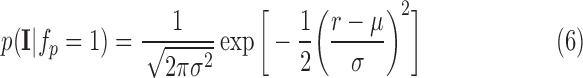 |
Here 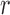 is normalized intensity of labelled scar. Re-training this model allows it to adapt to images from a different source which may exhibit different scar-blood CNR levels due to its inversion times.
is normalized intensity of labelled scar. Re-training this model allows it to adapt to images from a different source which may exhibit different scar-blood CNR levels due to its inversion times.
2). Intensity Model for Non-Scar Tissue
This is based on some prior knowledge about different tissue classes that could possibly interface with scar. As scar tissue normally borders with blood pool, normal myocardium and pericardial regions, a multi-modal mixture distribution is used:
 |
where  is a Gaussian distribution for non-scar tissue
is a Gaussian distribution for non-scar tissue  with mean
with mean 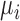 and variance
and variance 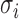 for some mixture proportion
for some mixture proportion 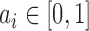 .
.
The model parameters were obtained from the image to be segmented (i.e., unseen image). However, as scar tissue is also part of myocardium, the mixture most likely to correspond to scar was identified and eliminated. This was the mixture with the highest mean. Following the elimination of the mixture 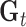 , the weights of the remaining Gaussians of the mixture model were normalized to sum to one. The non-scar tissue model is given by:
, the weights of the remaining Gaussians of the mixture model were normalized to sum to one. The non-scar tissue model is given by:
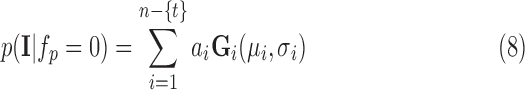 |
where 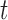 is the eliminated distribution. The parameters of the Gaussian mixture model
is the eliminated distribution. The parameters of the Gaussian mixture model 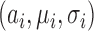 were obtained using the Expectation-Maximization (EM)-algorithm [36]. The number of tissue classes used was 4 pertaining to: blood pool, myocardium, scar and pericardial region. Starting with an initial estimate of the mean and variance for the four classes, the EM-algorithm iteratively computed the multimodal distribution parameters until convergence. This was followed by a truncation of the distribution pertaining to scar.
were obtained using the Expectation-Maximization (EM)-algorithm [36]. The number of tissue classes used was 4 pertaining to: blood pool, myocardium, scar and pericardial region. Starting with an initial estimate of the mean and variance for the four classes, the EM-algorithm iteratively computed the multimodal distribution parameters until convergence. This was followed by a truncation of the distribution pertaining to scar.
In summary, the algorithm extracted and incorporated knowledge both from the training dataset and the unseen image. The SC-BP contrast ratio was modelled from the training and intensity distributions of non-scar tissue were modelled from the unseen. This made the algorithm better equipped to handle contrast variations commonly encountered in DE-MRI.
G. Smoothness Constraint
To ensure smoothness and avoid discontinuities in the final segmentation, the 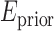 term of the MRF energy function in (3) penalised for assigning different labels to neighbouring voxels sharing similar intensity levels. The Lorentzian error norm was employed, which is a robust metric for measuring intensity differences within a neighbourhood:
term of the MRF energy function in (3) penalised for assigning different labels to neighbouring voxels sharing similar intensity levels. The Lorentzian error norm was employed, which is a robust metric for measuring intensity differences within a neighbourhood:
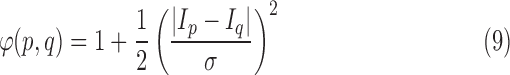 |
The scale 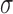 can be estimated from the DE-MRI image and depends on the variance of the actual scar and non-scar tissue class intensity distributions. With decreasing scale, the algorithm becomes less forgiving to small differences in intensities. Given that it is technically challenging to acquire high quality DE-MRI scans that show a clear distinction between scar and non-scar tissue, a larger value for the scale
can be estimated from the DE-MRI image and depends on the variance of the actual scar and non-scar tissue class intensity distributions. With decreasing scale, the algorithm becomes less forgiving to small differences in intensities. Given that it is technically challenging to acquire high quality DE-MRI scans that show a clear distinction between scar and non-scar tissue, a larger value for the scale 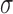 is almost always preferred. For convenience, to bound
is almost always preferred. For convenience, to bound  above and below by [1] it is re-adjusted by
above and below by [1] it is re-adjusted by 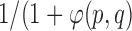 . This allows, if necessary, some adaptation of the training model to the unseen image.
. This allows, if necessary, some adaptation of the training model to the unseen image.
H. Optimization
The optimization of the MRF energy function in (2) yields the desired image segmentation for scar. In [15], it was shown that it is possible to find the global optimum of functions of this type using the graph-cut method. In the graph-cut method, the MRF energy function is converted to a directional graph and the minimum 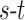 cut gives the desired segmentation. A graph
cut gives the desired segmentation. A graph 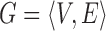 with two terminal nodes
with two terminal nodes 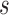 and
and 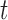 representing the scar and healthy segmentation labels. The graph has a set of nodes
representing the scar and healthy segmentation labels. The graph has a set of nodes 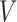 for every voxel in the image and
for every voxel in the image and 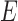 is the set of edges connecting these nodes (see Fig. 3). There are edges connecting every voxel to the two terminal nodes also known as the
is the set of edges connecting these nodes (see Fig. 3). There are edges connecting every voxel to the two terminal nodes also known as the 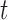 -links. There are also edges connecting neighbouring nodes called the
-links. There are also edges connecting neighbouring nodes called the  -links. Each of these edges has a non-negative weight assigned to it. The
-links. Each of these edges has a non-negative weight assigned to it. The  -link edge weights are obtained from the non-scar and scar tissue intensity priors in (8) and 6 respectively. The
-link edge weights are obtained from the non-scar and scar tissue intensity priors in (8) and 6 respectively. The  -link edge weights are obtained from (9). An
-link edge weights are obtained from (9). An  cut on
cut on  partitions the nodes into two disjoint sets belonging to either the foreground or the background classes. Every
partitions the nodes into two disjoint sets belonging to either the foreground or the background classes. Every  cut incurs a cost and corresponds to a segmentation labelling
cut incurs a cost and corresponds to a segmentation labelling  . The total cost of an
. The total cost of an  cut is equivalent to the sum of the edge weights the cut passes through. Fig. 3 illustrates how an
cut is equivalent to the sum of the edge weights the cut passes through. Fig. 3 illustrates how an  cut in a simple graph of an image with only 3 voxels computes a possible segmentation. Note how the
cut in a simple graph of an image with only 3 voxels computes a possible segmentation. Note how the  -links are assigned a value based on the affinity of the node to the particular class label. In a similar way, the
-links are assigned a value based on the affinity of the node to the particular class label. In a similar way, the  -links represent affinity for neighbouring voxels, holding nodes with similar intensities together and resisting to a cut passing through them resulting in a labelling of neighbouring voxels into two separate tissue classes.
-links represent affinity for neighbouring voxels, holding nodes with similar intensities together and resisting to a cut passing through them resulting in a labelling of neighbouring voxels into two separate tissue classes.
Fig. 3.
An illustration of an  cut through a simple graph that represents the energy functional of an image containing only 3 voxels.
cut through a simple graph that represents the energy functional of an image containing only 3 voxels.
1). Adaptive Feedback
The algorithm iteratively improved the segmentation result by incorporating new intensity information about scar. This step is shown in Fig. 2 as ‘Adapting training model’. Starting from the initial training model for scar (see Section II-F-I), this prior model may be sub-optimal since scar-blood CNR typically varies between DE-MRI images. It was iteratively adapted by incorporating the mean and SD of intensities in the segmentation:
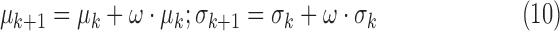 |
where 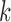 is the
is the 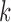 -th iteration of adapting the scar training model with present parameters
-th iteration of adapting the scar training model with present parameters 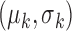 and those obtained from the new segmentation
and those obtained from the new segmentation 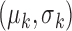 ;
; 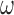 is the learning rate and empirically set to 0.2. The iterative process was stopped when the difference in consecutive means was small:
is the learning rate and empirically set to 0.2. The iterative process was stopped when the difference in consecutive means was small: 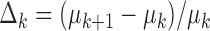 .
.
III. Experiments
The algorithm was evaluated on both numerical phantom and real patient MRI datasets as described below.
A. Numerical Phantom Data
In the rest of the paper, the true location of scar is referred to as the ground-truth for scar. The extent of scarring during ablation is non-deterministic and there is also confounding pre-ablation fibrosis. Therefore, identifying locations where ablations were made is not sufficient to be a surrogate for the ground truth for scar. Moreover, there is a high degree of inter- and intra-observer variability in manual segmentations of scar. These make evaluating algorithms more difficult and challenging. To overcome these issues, numerical phantoms were employed to extensively validate the algorithm.
1). Phantom Construction
The phantom was constructed in a four step process. The result of some steps is shown in Fig. 4. In the first step the LA geometry was extracted from a typical patient dataset. In the second step, a 2.5 mm wall was constructed around the LA. This represented LA wall. In a third step, regions were manually drawn within the constructed LA wall; these regions represented scar. In the final fourth step, intensities were sampled randomly from pre-determined distributions. These distributions belong to LA wall and blood-pool, and are measured and obtained from real MRI data. This ensured likeness of the phantoms to real MRI. Scar was filled with intensities from blood-pool but multiplied by a factor of 1.0 or above, and thus an SC-BP ratio of at-least 1.0 was maintained. This ratio emulated the selection of different inversion times for nulling the blood pool and was varied in experiments that follow. It is important to simulate partial voluming, anisotropic voxel sizes and noise in the phantoms. An anisotropic blur was applied with a kernel size of 2 mm in the through-plane direction and 1 mm in the in-plane direction. Gaussian white noise 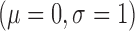 was added to the image.
was added to the image.
Fig. 4.

Images of a single-slice through a phantom taken at each stage of its construction process: (a) the phantom template with blood pool (BP) and atrial wall (AW) outlined semi-automatically using morphological dilation; scar (SC) drawn manually. (b) Assignment of intensity levels drawn randomly from pre-defined Gaussian distributions, with separate distributions for each tissue class. (c) In-plane and through-plane blurring followed by the addition of Gaussian white noise. Abbreviations: L—left side, R—right side.
2). Phantom Experiments
Numerical phantoms were generated by varying the SC-BP contrast ratio between 1.0 to 3.0. Some instances of these phantoms can be seen in Fig. 5. This evaluated the algorithm's performance on scar with varying contrast in relation to blood pool. The noise in the phantoms was maintained at signal-to-noise (SNR) of 9.0. This was the average SNR observed on a cohort of clinical datasets. Training 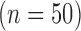 and testing
and testing 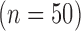 data sets were generated accordingly. To make training as realistic as possible, it was separately trained on SC-BP ratios: 1.5–1.8 and 1.8–2.1. The algorithm was compared to ground-truth using the Dice overlap co-efficient [37].
data sets were generated accordingly. To make training as realistic as possible, it was separately trained on SC-BP ratios: 1.5–1.8 and 1.8–2.1. The algorithm was compared to ground-truth using the Dice overlap co-efficient [37].
Fig. 5.
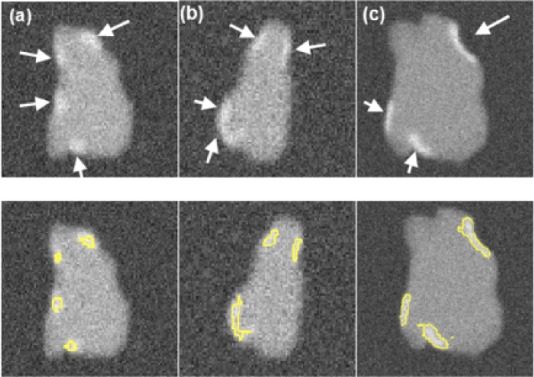
Single slices through three different phantoms with numerically generated scars indicated by the arrows (Top row). SC-BP contrast is varied keeping SNR constant at 9.0. SC-BP: (a) 1.4, (b) 1.6 and (c) 1.8. The segmentations from the algorithm are also shown (Bottom row).
In a separate experiment, the SNR was varied from 4 to 16 along with the SC-BP contrast ratios. A single instance of the algorithm was tested and this was trained on the SC-BP range 1.8–2.1. The Dice overlap of the segmentation with ground truth was compared.
In addition to the above experiments on scar enhancement and noise variation, the performance of the algorithm and fixed models (FWHM and 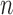 -SD) were compared on the same dataset. Five separate phantoms were used from which 200 different scarred regions were identified and their SC-BP contrast ratio noted. The accuracy with each method segmented each of the 200 regions was measured with Dice and reported.
-SD) were compared on the same dataset. Five separate phantoms were used from which 200 different scarred regions were identified and their SC-BP contrast ratio noted. The accuracy with each method segmented each of the 200 regions was measured with Dice and reported.
3). Clinical Data
A total of 15 clinical human datasets were available. In these set of experiments, segmentations from the algorithm were compared to the combined manual segmentations of three observers. In addition to this, the algorithm was also compared to fixed models: FWHM and 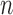 -SD methods. Training for the algorithm was accomplished using the leave-one-out principle, where 14/15 datasets were used for training and 1/15 used for testing. In the test scan, segmentation performance was measured both locally and globally for the image. For local comparison, performance on individual sections of scar was measured (a total of 155 regions were considered) and for a global comparison, total scar volume was measured. The pre-processing (left atrium geometry extraction and registration) was the same for each approach.
-SD methods. Training for the algorithm was accomplished using the leave-one-out principle, where 14/15 datasets were used for training and 1/15 used for testing. In the test scan, segmentation performance was measured both locally and globally for the image. For local comparison, performance on individual sections of scar was measured (a total of 155 regions were considered) and for a global comparison, total scar volume was measured. The pre-processing (left atrium geometry extraction and registration) was the same for each approach.
Three experienced observers manually segmented scars in each DE-MRI scan. They were combined to generate a consensus segmentation or pseudo-ground truth for each scan. This is necessary in order to consolidate inter-observer variabilities. Segmentations were combined using the STAPLE algorithm described in [38]. For each voxel, a probability estimate for the scar label could be computed. The STAPLE ground-truth was then be obtained by considering voxels to be scar if their probability is greater than 0.7, or 70%. This is a reasonable threshold capable of generating a strong consensus segmentation (In [38] the authors chose a lower consensus at 50%). To explore this threshold further, an experiment was performed by varying the threshold. Segmentations were available from five experienced observers on a random subset of the clinical datasets. The segmentations were combined using STAPLE and three thresholds were considered: 1) 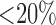 , 2)
, 2) 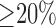 and 3)
and 3) 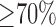 . This generated different consensus segmentations with varying degrees of consensus against which the algorithm's performance was measured. Finally, to further explore whether better training of the algorithm leads to better segmentations and thus better performance, different instances of the algorithm are evaluated by incrementing the number of training set.
. This generated different consensus segmentations with varying degrees of consensus against which the algorithm's performance was measured. Finally, to further explore whether better training of the algorithm leads to better segmentations and thus better performance, different instances of the algorithm are evaluated by incrementing the number of training set.
It is important to note that segmentations from the proposed algorithm were obtained without any user interaction necessary at any step of the algorithm. The most computationally demanding step was that of graph-cuts. On images of the resolution described above, there are typically 50000–100000 nodes that require processing. However, each step of the iterative process took less than a minute. The total running time of the proposed approach is less than a minute on a 2.5 GHz PC.
B. Evaluation Metrics
To our experience, there is no single metric which works best for comparing segmentation overlaps. We chose two different metrics to quantify segmentation overlap.
1). Regional Overlap
The Dice co-efficient of similarity is a well-known metric [37]. It is given by:
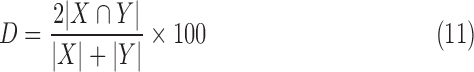 |
where 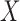 is the region in ground-truth and
is the region in ground-truth and 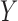 is the region in the algorithm.
is the region in the algorithm. 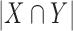 is total overlapping pixels and
is total overlapping pixels and 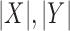 are total number of pixels in each region. A Dice of 100 denotes perfect overlap.
are total number of pixels in each region. A Dice of 100 denotes perfect overlap.
2). Sensitivity and Specificity
The proportion of true positives and true negatives in the detection process was analyzed by means of Receiver Operating Characteristic (ROC) curves where possible.
3). Total Scar Volume
Segmentations were also compared by measuring the total scar volume. This is mostly how scar is quantified and interpreted in clinical studies [39] and also serves as an important indicator for the total scar burden on the atrium.
IV. Results
A. Numerical Phantoms
1). Scar Contrast
Fig. 6 show results from testing the algorithm on phantoms generated by varying the SC-BP contrast. Segmentation overlap with known true location of scar was measured using Dice. The algorithm performs well within its training range with median Dice 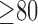 in both ranges:
in both ranges: 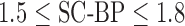 [Fig. 6(a)] and
[Fig. 6(a)] and 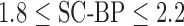 [Fig. 6(b)]. Outside its training area, the algorithm showed that it is able to adapt to excellent SC-BP contrast
[Fig. 6(b)]. Outside its training area, the algorithm showed that it is able to adapt to excellent SC-BP contrast 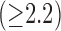 and good segmentations were achieved. Values of SC-BP explored in this experiment included realistic DE-MRI values but
and good segmentations were achieved. Values of SC-BP explored in this experiment included realistic DE-MRI values but 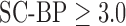 is very difficult to achieve in practice. To summarise, this experiment evaluated the algorithm across a wide dynamic SC-BP contrast range and the algorithm's approximation of ground truth was found to be good.
is very difficult to achieve in practice. To summarise, this experiment evaluated the algorithm across a wide dynamic SC-BP contrast range and the algorithm's approximation of ground truth was found to be good.
Fig. 6.
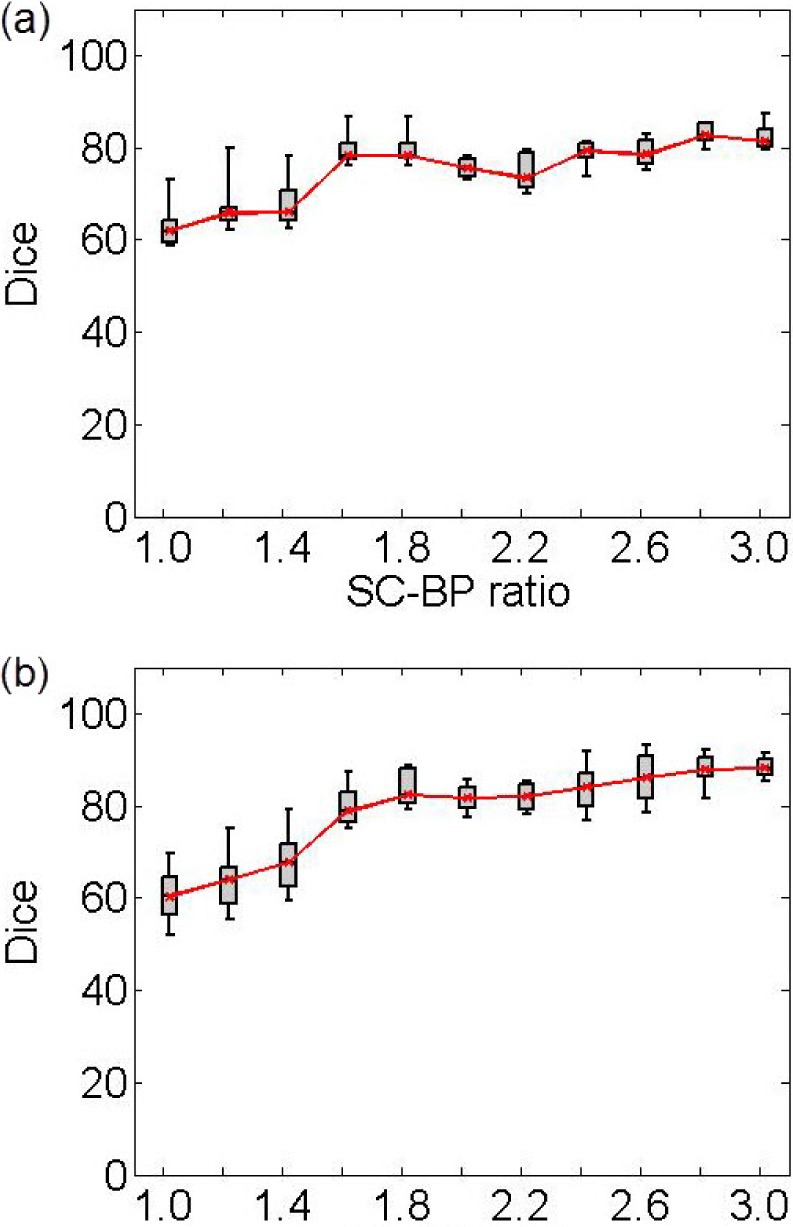
Performance of algorithm on numerical phantoms with increasing SC-BP contrast and SNR fixed at 9.0. Each graph is an instance of the algorithm: (a) trained on 1.5 to 1.8, and (b) trained on 1.8 to 2.1. The trend-lines show the median. Boxes in the plot indicate the 9th, 25th, 50th, 75th and 91st percentiles.
2). Noise Variation
Fig. 7 show results from testing the algorithm on phantoms generated by varying SNR. The SNR is varied between 4 and 16. The algorithm is trained on datasets generated with SC-BP ranging between 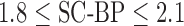 . Results show that SC-BP dictates over SNR for achieving good segmentations. Note segmentations are poor with
. Results show that SC-BP dictates over SNR for achieving good segmentations. Note segmentations are poor with 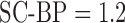 when
when 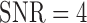 and with
and with 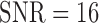 . But this is improved when
. But this is improved when 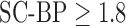 demonstrating that the algorithm is robust to noise. SNR in actual DE-MRI is typically around 9.0 and the algorithm is seen to perform well in this range.
demonstrating that the algorithm is robust to noise. SNR in actual DE-MRI is typically around 9.0 and the algorithm is seen to perform well in this range.
Fig. 7.
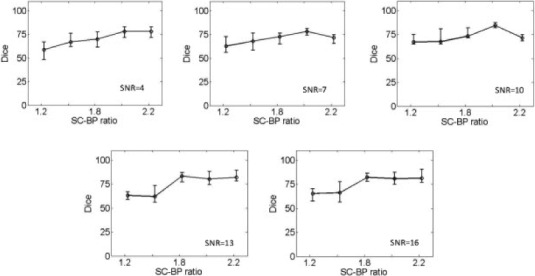
Performance of algorithm on numerical phantoms with varying SNR. The SNR is varied between 4 to 16. The median Dice segmentation overlap is plotted for the trend line shown.
3). Comparison With Fixed Models
Fig. 8 show how the algorithm and fixed models performed on the same datasets. A total of 200 scarred regions were identified in five anatomically-unique phantoms. Their SC-BP contrast were computed and the overlap accuracy noted for each method. This allowed each method to be evaluated on specific SC-BP ratios and the plots in Fig. 8 show the segmentation accuracy trend. Fixed models 3,4,6-SD generated better segmentations than FWHM when scar contrast is between 1.2 to 2.2. However, FWHM improved substantially with higher scar contrast (SC-BP 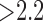 in Fig. 8), which is when the 50 percent cut-off was more reasonable. Overall, as illustrated in Fig. 8, the algorithm maintained good accuracy when compared to fixed models in numerical phantoms.
in Fig. 8), which is when the 50 percent cut-off was more reasonable. Overall, as illustrated in Fig. 8, the algorithm maintained good accuracy when compared to fixed models in numerical phantoms.
Fig. 8.
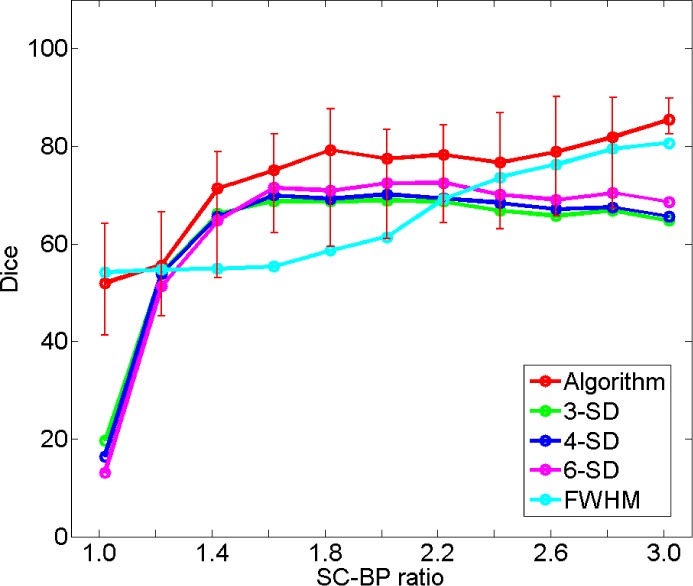
Comparing performance of algorithm with fixed models on numerical phantoms. Fixed models namely 3-SD, 4-SD, 6-SD and FWHM were evaluated. The trend-lines show the median Dice computed from 200 different scarred regions obtained from 5 separate phantoms.
The failure of FWHM revealed in this experiment is further illustrated in Fig. 9 (see columns 1 and 2). When the contrast in scar is not high, 50 percent of maximal signal as considered in FWHM, is not optimal and leaks in segmentation are inevitable [Fig. 9 (row 3)].
Fig. 9.
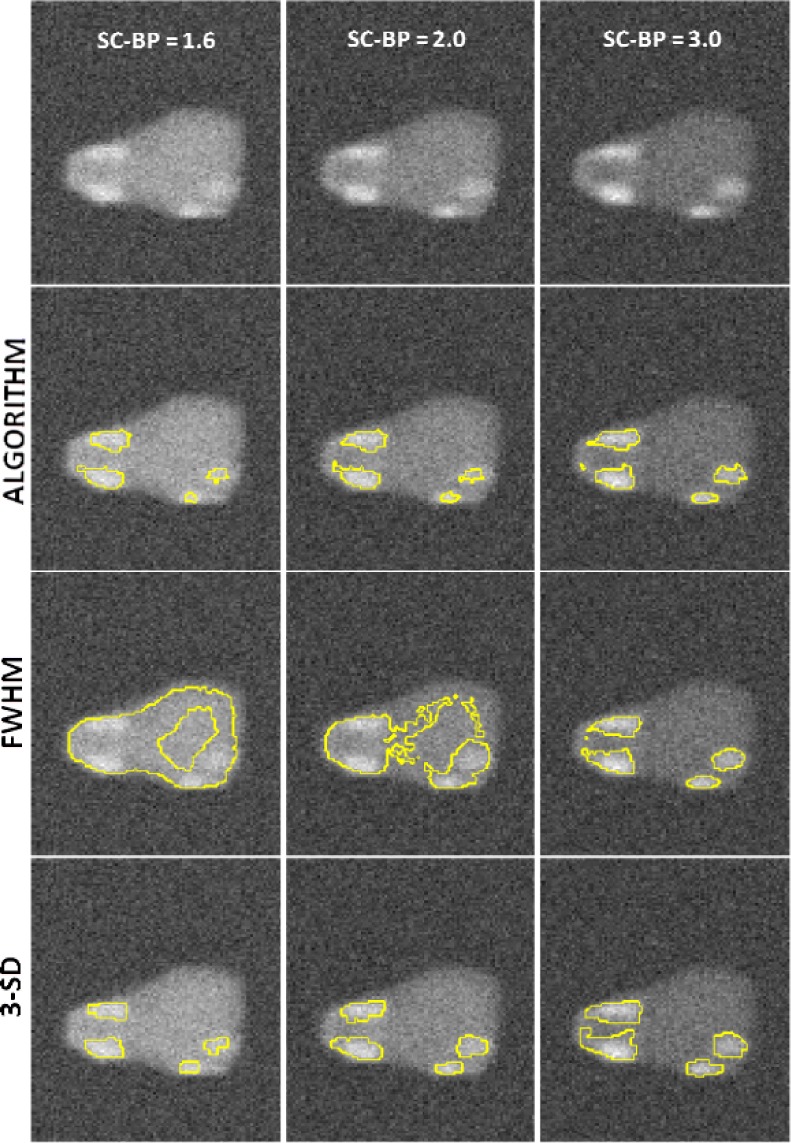
Instances where 50% cut-off in FWHM is not optimal. First row: Original images of phantom with variable scar contrast. Second row: Algorithm's segmentation. Third row: Segmentation from FWHM with leaks. Fourth row: Segmentation from 3-SD.
B. Clinical Data
1). Comparison With Fixed Models Using Overlap Metric
In the clinical datasets, performance of algorithm and fixed models were tested by measuring overlap with pseudo ground-truth (STAPLE) and comparing segmentation outputs in terms of scar volumes. For assessing performance based on overlap, each method was tested on individual SC-BP contrast levels: 1.0, 1.4, 1.8, 2.2, 2.6 and 3.0. This was possible by sampling 155 individual scarred regions from the clinical scans, measuring their SC-BP contrast ratio and testing how well each method segmented it. Results are given in Fig. 10.
Fig. 10.
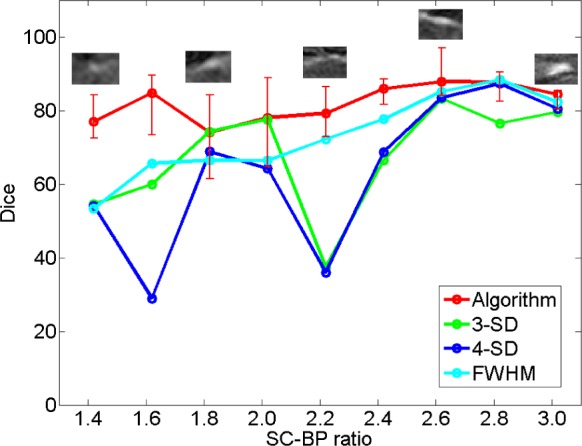
Comparing performance of fixed models with algorithm on patient scans. The performance over a total of 155 scarred regions are shown here. The trend-lines show the median. Five example snapshots of scar are also given to illustrate SC-BP contrast levels. Note SC-BP ratios analysed range from 1.4 to 3.0.
Fixed models perform less accurately than the algorithm when SC-BP is less than 2.5. At excellent and rarely attainable SC-BP levels 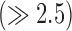 , this trend changes and all models perform equally well. FWHM and the algorithm perform consistently across the entire SC-BP range used in this experiment, with 3- and 4-SD models outputting less accurate segmentations on scar at certain SC-BP contrast levels (1.6, 2.2). This is because scar is not adequately segmented by 3- or 4-SD due to non-overlapping intensities between model and actual. These results highlight that the algorithm performs consistently on actual DE-MRI and across realistic SC-BP levels. Performance of fixed models is found to be variable.
, this trend changes and all models perform equally well. FWHM and the algorithm perform consistently across the entire SC-BP range used in this experiment, with 3- and 4-SD models outputting less accurate segmentations on scar at certain SC-BP contrast levels (1.6, 2.2). This is because scar is not adequately segmented by 3- or 4-SD due to non-overlapping intensities between model and actual. These results highlight that the algorithm performs consistently on actual DE-MRI and across realistic SC-BP levels. Performance of fixed models is found to be variable.
2). Comparison With Fixed Models Using Quantified Volume
Assessment of performance using total scar volume reported by each method is important as this is mostly how scar is quantified and interpreted for clinical studies. Results obtained from scar volume quantified by each 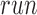 of method is given in Fig. 11 for six clinical datasets. Each method was run three separate times with inputs (i.e., normal and hyper-enhanced myocardium) fed from three independent observers. Volume reported by each method was compared to the volume reported by three independent experienced observers (see Manual method in Fig. 11). The algorithm correlated well with manual scar volumes. All three runs of the algorithm produced the same result as depicted by the single bar in Fig. 11. All other methods showed variations in the quantified volume. This variation was primarily due to observer variability in selecting normal or hyper-enhanced tissue required for fixed models. This highlights that a standardized quantification for scar using a fixed model approach (FWHM and SD) can be difficult to achieve.
of method is given in Fig. 11 for six clinical datasets. Each method was run three separate times with inputs (i.e., normal and hyper-enhanced myocardium) fed from three independent observers. Volume reported by each method was compared to the volume reported by three independent experienced observers (see Manual method in Fig. 11). The algorithm correlated well with manual scar volumes. All three runs of the algorithm produced the same result as depicted by the single bar in Fig. 11. All other methods showed variations in the quantified volume. This variation was primarily due to observer variability in selecting normal or hyper-enhanced tissue required for fixed models. This highlights that a standardized quantification for scar using a fixed model approach (FWHM and SD) can be difficult to achieve.
Fig. 11.
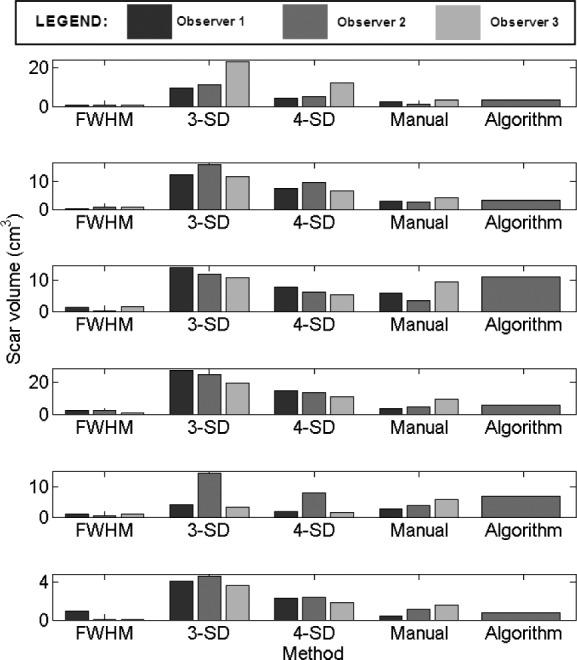
Assessment of inter-observer variation in fixed models, manual segmentation and algorithm. Six clinical cases are illustrated here.
3). Qualitative Comparison on DE-MRI Scans
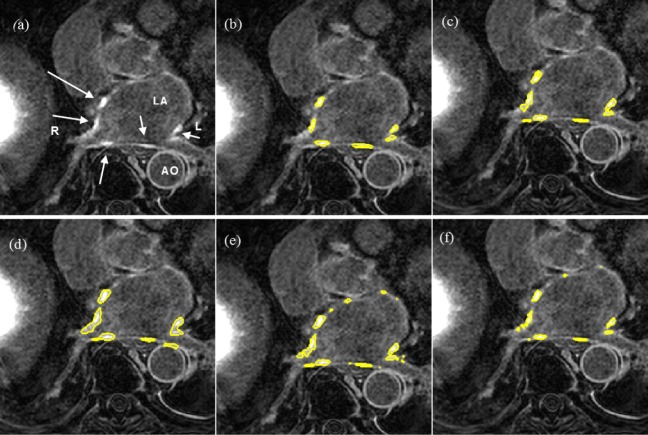
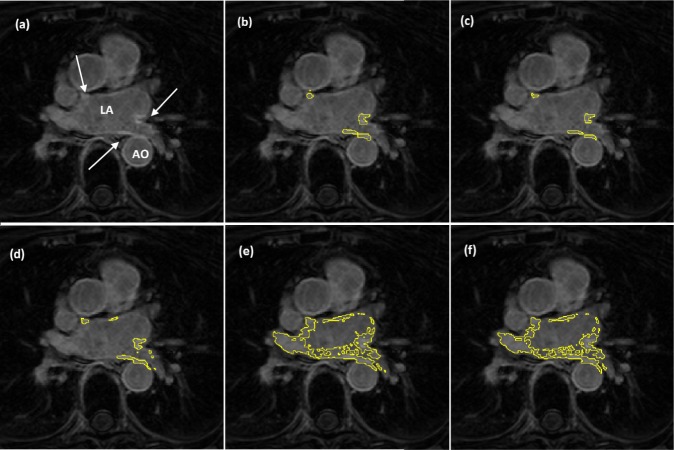
Segmentation quality was assessed by overlaying region contours over the original DE-MRI slices. It was generally observed that in images with excellent SC-BP contrast, contours followed scar boundaries accurately in both algorithm and fixed models. Fixed models 3 and 6-SD were less accurate. An example is shown in Fig. 15 where segmentations similar to the consensus segmentation [Fig. 15(b)] could be obtained. Fixed models showed poor correlation when the SC-BP contrast is not sufficiently high. An example is shown in Fig. 16 where FWHM and the algorithm fared well with the algorithm providing a better approximation to the consensus segmentation. Fixed models 3 and 6-SD have gross errors in their segmentations due to a large overlap of intensities between their scar model and actual healthy tissue. Such segmentations are not usable for clinical studies and the operator would require to resort to threshold re-adjustment.
Fig. 15.
Segmentations on clinical scans I: (a) original scan, (b) consensus STAPLE segmentation, (c) Algorithm, (d) FWHM, (e) 3-SD, (f) 6-SD. Arrows show enhancement. This scan has excellent SC-BP contrast and all methods except 3-SD and 6-SD demonstrate good accuracy. Abbreviations: AO—Aorta, LA—Left atrium, R—Right side, L—left side.
Fig. 16.
Segmentations on clinical scans II: (a) original scan, (b) consensus STAPLE segmentation, (c) Algorithm, (d) FWHM, (e) 3-SD, (f) 6-SD. Arrows show enhancement. This scan has excellent SC-BP contrast and all methods except 3-SD and 6-SD demonstrate good accuracy. Abbreviations: AO—Aorta, LA—Left atrium, R—Right side, L—left side.
4). Analyzing Algorithm Performance by Varying Consensus Levels of Pseudo Ground Truth
The algorithm's performance on a subset of clinical datasets was evaluated by varying the STAPLE threshold and thus the level or strength of the consensus segmentation. Results are plotted in Fig. 12 showing segmentation overlap on three consensus levels. There was a small difference in the algorithm's performance noted when SC-BP contrast levels were low. With higher SC-BP the performance was nearly similar. When SC-BP contrast is poor, the consensus or agreement between observers can be low. By lowering the acceptable consensus threshold (to 20%), dubious pixels are included in the ground truth where 2/10 observers would agree that it is scar. As the algorithm generally selects pixels which have close affinity to its models and priors, dubious pixels are omitted by the algorithm. There is a decrease in performance when segmentations with low consensus are presented.
Fig. 12.
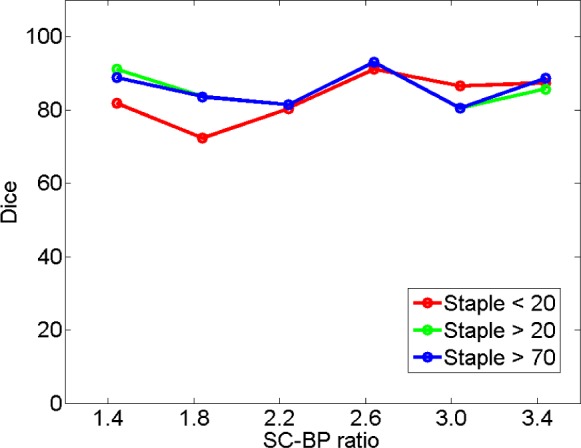
Performance trends of the algorithm on STAPLE consensus ground truths. Each curve represents performance on consensus segmentations, with consensus varied from 20% (weak) to 70% (strong).
5). Analyzing Algorithm Performance by Varying Strength of the Training Set
The algorithm's training set was incrementally increased and its segmentation overlap performance was noted. There was little notable difference in the performance. Results are plotted in Fig. 13. Training had an impact on performance only when the training set and test set had similar SC-BP contrast levels. If these vastly differ, initial iterations of the algorithm generate poor segmentations and these progressively become better in later iterations when the scar intensity model is continuously adapted with feedback from previous iterations (refer to ‘adapting training step’ in Fig. 2).
Fig. 13.
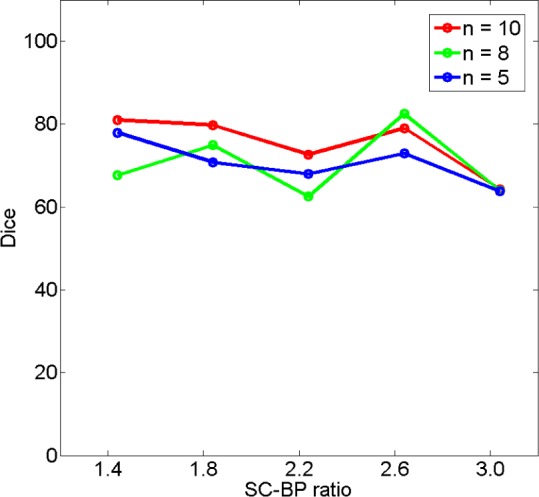
Performance trends of the algorithm by increasing the training set. Each curve represents an instance of the algorithm trained on  , 7, 5 datasets.
, 7, 5 datasets.
6). ROC Analysis
The true positive and true negatives rates were analyzed by looking at sensitivity and specifity of the algorithm and the fixed-models. A ROC curve between sensitivity and specificity was only plotted, where each point on the curve represented a decision threshold. The plots are given in Fig. 14 for the  -SD fixed model's ROC curve, where the decision threshold was varied between
-SD fixed model's ROC curve, where the decision threshold was varied between 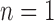 to
to 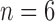 . Since both the algorithm and FWHM do not require a decision threshold for obtaining segmentations, their overall sensitivity and specificity on all datasets was plotted. The
. Since both the algorithm and FWHM do not require a decision threshold for obtaining segmentations, their overall sensitivity and specificity on all datasets was plotted. The 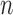 -SD fixed model approach has low specificity for
-SD fixed model approach has low specificity for 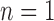 , 2, 3 and increasingly mis-labelled healthy tissues as scar. However, its higher sensitivity indicated that scar tissues are mostly labelled correctly. This reversed with
, 2, 3 and increasingly mis-labelled healthy tissues as scar. However, its higher sensitivity indicated that scar tissues are mostly labelled correctly. This reversed with 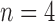 , 5, 6 and the trade-offs between sensitivity and specificity was seen to be optimal when
, 5, 6 and the trade-offs between sensitivity and specificity was seen to be optimal when 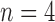 , 5. Overall, the algorithm maintained both higher sensitivity and specificity than the fixed models as indicated in the ROC plot. The FWHM fell behind in this global ROC analysis and this is in-line with earlier tests on individual regions where it was shown that its 50% cut-off is too low for scar with low SC-BP, but more suitable for high SC-BP ratios.
, 5. Overall, the algorithm maintained both higher sensitivity and specificity than the fixed models as indicated in the ROC plot. The FWHM fell behind in this global ROC analysis and this is in-line with earlier tests on individual regions where it was shown that its 50% cut-off is too low for scar with low SC-BP, but more suitable for high SC-BP ratios.
Fig. 14.
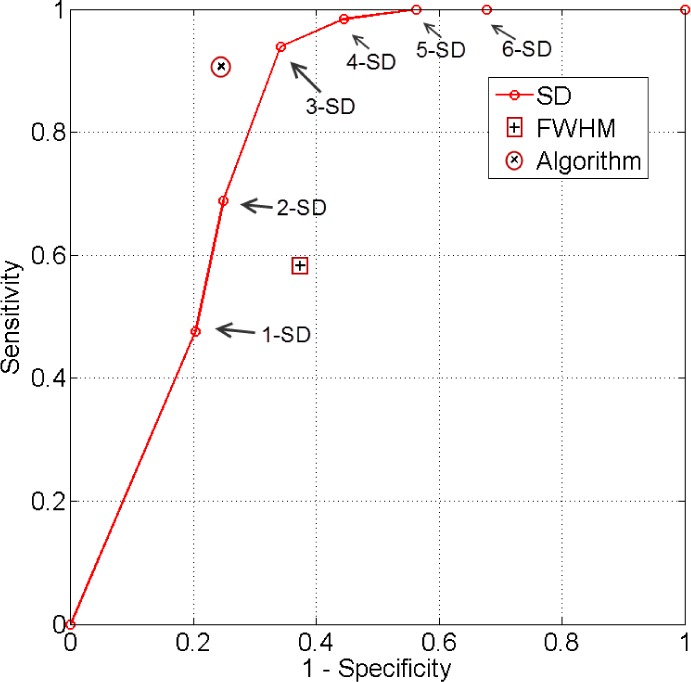
ROC analysis of the algorithm, FWHM and 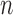 -SD method. The ROC curve is only plotted for the
-SD method. The ROC curve is only plotted for the 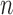 -SD method and the overall sensitivity and specificity is plotted for the parameter-less proposed algorithm and FWHM.
-SD method and the overall sensitivity and specificity is plotted for the parameter-less proposed algorithm and FWHM.
V. Discussion
In this work a segmentation algorithm was investigated for fast quantification of fibrosis in DE-MRI scans. The proposed algorithm offers the following advantages: 1) Segments fibrosis without requiring a manual outline of remote or healthy myocardium. This is beneficial since remote myocardium tends to have low SNR and manual selection suffers from high observer variability. 2) The algorithm does not routinely generate false positives as was observed in existing fixed model methods: FWHM and  -SD. 3) The algorithm is developed particularly for left atrial fibrosis segmentation and all present approaches were developed for ventricle scans. 4) Analysis of DE-MRI scans was shortened to an average of 30 seconds when compared to existing semi-automatic approaches requiring 2 minutes per scan on average.
-SD. 3) The algorithm is developed particularly for left atrial fibrosis segmentation and all present approaches were developed for ventricle scans. 4) Analysis of DE-MRI scans was shortened to an average of 30 seconds when compared to existing semi-automatic approaches requiring 2 minutes per scan on average.
The algorithm along with existing approaches was tested on both numerical phantoms and clinical datasets. Numerical phantoms provided with a wide dynamic range of variation in scar contrast otherwise not possible in clinical datasets. Furthermore, in present literature, methods were validated on images using global overlap measures and not on individual regions and nor on individual SC-BP ratios. In this work, these together have allowed existing approaches to be investigated more thoroughly and results have revealed where they fail to perform. Both FWHM and SD methods can have gross errors in its segmentations when scar contrast is not high enough causing significant overlap of intensities between the scar and healthy tissue. On the clinical datasets, the variability in scar volume from FWHM and SD when operated by three different experienced operators meant no standard quantification was possible. The algorithm reported the same volume in each run and this was also consistently found to be close to the consensus segmentation of experienced observers.
The algorithm incorporates knowledge both from its training dataset and the unseen image. The SC-BP contrast ratio is modelled from the training and intensity distributions of non-scar tissue is modelled from the unseen. The SC-BP model is automatically adapted iteratively where necessary. These made the algorithm better equipped to handle contrast variations commonly encountered in DE-MRI. Built-in smoothness constraints and the graph-cuts approach allow it to consider neighbouring regions for inclusion or exclusion even when they do not fit the model. This enabled it to produce accurate scar boundaries.
The absence of ground truth for scar in DE-MRI is an important issue for segmentation methods and this has not been properly addressed in literature. One approach is to use voltage as a surrogate for scar [30]. In this work, three experienced observers manually segmented scars in each DE-MRI scan. These were then combined to generate a consensus segmentation or pseudo-ground truth for each scan using a statistical approach. This consolidated inter-observer variabilities commonly encountered in such scans. The degree of agreement of the consensus was also varied to show that a strong consensus was needed, especially when SC-BP levels were poor. A 70% threshold was overall deemed appropriate and this meant pixels with 7/10 consensus or above were included in the pseudo ground truth on which all tests were performed. Furthermore, numerical phantoms are employed in this work to evaluate the algorithm, FWHM and SD over a wider dynamic range of SC-BP contrast ratios.
The training step is also further explored in this work. A decrease in algorithm performance was noted when a small training set was used. However, there might come a point where increasing the training set would not substantially increase the accuracy of the algorithm but this is dependent on the variation of the image population. The algorithm was evaluated using the leave-one-out approach, with 14/15 of the datasets used for training and 1/15 for testing. This would always be applicable with unseen data always being left out of the training and any previous data being added to the training.
A. Clinical Translation and Application
Several recent studies [7]–[11] have highlighted the importance of quantifying LA fibrosis in DE-MRI and these include its use in deciding treatment strategy and thus selecting patients who will respond better to RFCA procedures. Quantifying using fixed models such as FWHM and SD is frequently utilised clinically due to its simplicity. In this work, both SD and FWHM were shown to have several disadvantages. The FWHM had overall equally low sensitivity and specificity than SD; it is more reliable in segmenting scar with high SC-BP than low SC-BP. The SD fixed model was overall more sensitive with a higher true positive rate than FWHM, but this comes at the expense of reduced specificity. In scar detection, a higher true positive rate and thus detecting most scar pixels is more desirable. This is because rectifying quantified volumes by manually removing mis-labelled healthy pixels is relatively simpler and less time-consuming than manually labelling and including scar pixels that are missed. The algorithm is shown to have good true positive and true negative rates in the ROC analysis, and higher than FWHM in all decision thresholds explored for SD. Moreover, standardization is impossible to achieve in fixed models such as SD with several choices of thresholds left to the operator to tweak. The clinical translation of the proposed algorithm thus becomes clear—it aims to provide a reliable and standardized method of quantifying scar.
Quantification algorithms such as the one proposed, which can potentially be used in deciding treatment strategy, should be evaluated on a wide randomized spectrum of datasets from different imaging centres. To this end, the algorithm was recently evaluated in a segmentation challenge organized to compare quantification algorithms from seven different centres [33]. It was evaluated on sixty datasets obtained from three different imaging centres. A similar level of performance was achieved in these datasets. Dice segmentation overlap scores were comparable to those obtained from semi-automatic methods.
B. Other Applications
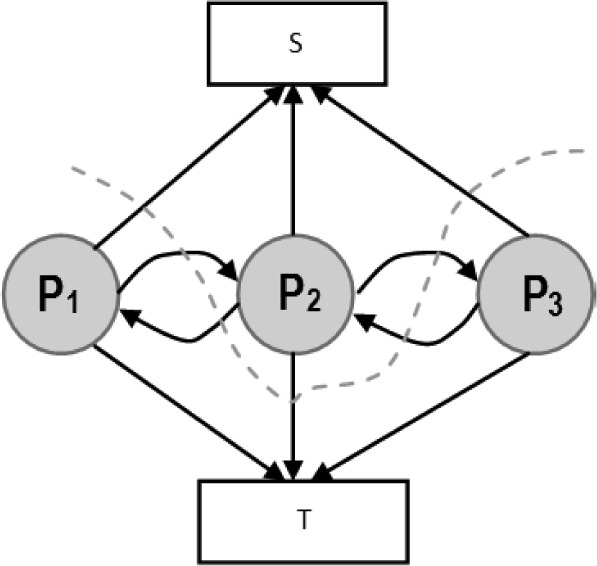
The proposed algorithm generates binary images of scar and this can be mapped and represented on the segmented LA surface model in two ways: 1) Maximum Intensity Projection (MIP) maps, and 2) Probabilistic maps. The former can be used to visualise scar on LA geometry and potential uses include predicting gaps in ablation patterns (see Fig. 17). A recent algorithm [40] also allows them to be visualized on two-dimensional flattened maps of the LA. Gaps play an important role in reconnection of re-entrant circuits in AF-cured patients. The latter can be used to obtain confidence levels on each region of scar extracted by the algorithm (i.e., a probability value between 0 and 1 of the chance of it being scar). An example of such a map can be seen in Fig. 18.
Fig. 17.
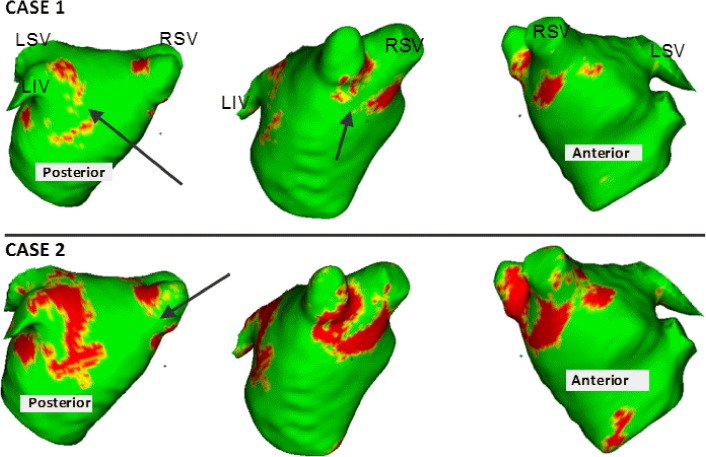
Clinical applications I: Two clinical cases with scar quantified by the algorithm and projected on left atrial surface using MIP. Potential gaps are indicated using arrows. Gaps have important implications in re-do procedure planning.
Fig. 18.
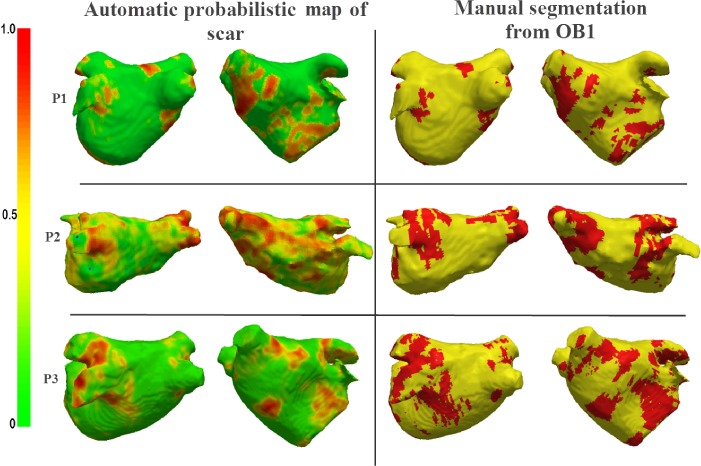
Clinical applications II: Probabilistic map generated from the algorithm for three clinical cases (P1, P2, P3) shown alongside Maximum Intensity Projections (MIP) of manually outlined scar.
C. Limitations
One of the limitations of the study is the absence of ground truth in the clinical datasets. To overcome this consensus segmentations from three observers were generated using probabilistic methods. Furthermore, numerical phantoms were used and ground truth was readily available in these cases. A second limitation is in the Dice co-efficient used to measure overlap between segmentations. Dice can be highly sensitive to small translational errors between the test and true regions. To overcome this, clinical datasets were also evaluated by comparing segmentation volumes.
VI. Conclusion
DE-MRI is becoming a preferred method for non-invasive imaging of myocardial scar. The amount of scar predicts whether a patient will respond to RFCA procedures. Thus accurately quantifying scar is important and has implications in patient selection for RFCA. Currently, SD and FWHM fixed thresholding models are frequently utilized clinically to quantify scar due to their simplicity. Present literature has only evaluated these methods using global image measures and thus their deficiences could not be noted. In this work, there are two important contributions: 1) SD and FWHM fixed models are evaluated on individual regions of scar and thus various scar contrast ratios are examined to show they fail when some contrast levels do not suit the selected threshold in SD or 50% cut-off in FWHM. This is further confirmed and validated in numerical phantoms. 2) the proposed algorithm has the potential to standardize quantification of scar from routine clinical scans; it requires no threshold selection and is shown to be more sensitive and specific than SD and FWHM in scar detection.
Accurate and standardized quantification will allow appropriate selection of patient candidates for RFCA. This could considerably reduce the recurrence rates, procedure risk and high financial burden associated with unsuccessful RFCA treatment. Patients not deemed appropriate for RFCA based on their scar assessment could be treated far less invasively using drug therapy. A standardized quantification of scar in DE-MRI is thus necessary.
Acknowledgment
The authors would like to thank members of the Division of Biomedical Engineering and Imaging Sciences, King's College London who assisted with this study. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.
Biographies

Rashed Karim received the B.Sc. degree in computer science from the University of Toronto, the M.Sc. (Hons.) degree from Queen Mary, University of London, and the Ph.D. degree in computer science from Imperial College London working under Prof. Daniel Rueckert. Since 2010, he has been a Post-Doctoral Research Fellow with the King's College London Medical Engineering Centre. His current research interests include myocardial scar classification from MR, image-guided robotics, and left atrial surface parameterization.

Aruna Arujuna received the M.B.Ch.B. degree from the University of Bristol and the M.D. degree from the King's College London, in 2002 and 2013, respectively. Following gaining membership into the Royal College of Physicians in 2006, he pursued a career in cardiology. From 2009 to 2012, he was a Clinical Research Fellow with the Department of Imaging Sciences and Biomedical Engineering, King's College London. He was involved in image-guided interventions, robotic catheter-based electrophysiology procedures, and cardiac MR imaging. His research interests include image-guided cardiovascular interventions, cardiac electromechanical modeling, advanced pacing, and advanced imaging.

Richard James Housden received the B.A. and M.Eng., and M.A. degrees in engineering and the Ph.D. degree in ultrasound imaging from the University of Cambridge, U.K., in 2004, 2007, and 2008, respectively. From 2008 to 2011, he was with the Department of Engineering, University of Cambridge, where he was involved in ultrasound elasticity imaging. He is currently a Post-Doctoral Researcher with the Division of Imaging Sciences and Biomedical Engineering, King's College London, involved primarily in image guidance systems for minimally invasive cardiac catheterization. His research interests include ultrasound imaging, image processing, and surgical guidance systems.
Jaspal Gill, photograph and biography not available at the time of publication.

Hannah Cliffe is in her penultimate year of reading medicine at King's College, London, having received a Distinction for Pre-clinical Sciences. She received a First with Honours in her intercalated degree in Imaging Sciences, also at King's College, London. She is currently studying for a Diploma in Conflict and Catastrophe Medicine at the Worshipful Society of Apothecaries of London, and is a Medical Cadet, sponsored through her studies by the Royal Air Force.
Kavir Matharu, photograph and biography not available at the time of publication.
Jaswinder Gill, photograph and biography not available at the time of publication.
Christopher Aldo Rindaldi, photograph and biography not available at the time of publication.

Mark O'Neill is a Consultant Cardiologist and Electrophysiologist with the St. Thomas' Hospital London, and a Reader of clinical cardiac electrophysiology with the King's College London. He received the Hons. Degree from the University College Dublin Medical School, and the D.Phil. degree in physiology from Oxford University in 1995. From 2005 to 2006, he completed a clinical research fellowship in Bordeaux with Prof. M. Hassaguerre and Prof. P. Jas, where he gained particular expertise in atrial fibrillation. He was a Senior Lecturer with the Imperial College and an Honorary Consultant Cardiologist with the St. Mary's Hospital in 2008. In 2009, he joined St. Thomas' Hospital and King's College London, Department of Cardiology, Division of Imaging Sciences and Biomedical Engineering, and was promoted to Reader in 2011. He is a Clinical Lead of the King's Health Partners Clinical Academic Group, Departmental Lead for Arrhythmias in Adult Congenital Heart Disease, and the Divisional Research Lead for electrophysiology. His primary research interests are the development and use of advanced signal processing and imaging technologies to improve arrhythmia characterization and treatment in patients with heart rhythm disturbances.

Daniel Rueckert is a Professor of Visual Information Processing and heads the Biomedical Image Analysis Group with the Department of Computing, Imperial College London. He received the Diploma (M.Sc.) degree in computer science from Technical University Berlin and the Ph.D. degree in computer science from the Imperial College London. Before moving to Imperial College, he was a Post-Doctoral Research Fellow with the Division of Radiological Sciences and Medical Engineering, King's College London, where he has been involved in the development of nonrigid registration algorithms for the compensation of tissue motion and deformation. During his doctoral and post-doctoral research, he has authored more than 300 journal and conference articles in medical image computing. He is an Associate Editor of the IEEE Transactions on Medical Imaging, an Editorial Board Member of Medical Image Analysis, Image and Vision Computing, and a Referee for a number of international medical imaging journals and conferences. He has served as a member of organizing and program committees at numerous international conferences.

Reza Razavi received the M.D. degree in MR-guided cardiac catheterization from the King's College London, London, U.K, and studied medicine from the St. Bartholomew's Hospital Medical School, University of London, London. He trained in pediatrics and pediatric cardiology with Guy's and St. Thomas' Hospital London. He was a Clinical Research Fellow. He was appointed as a Lecturer and an Honorary Consultant of pediatric cardiology in 2001, and a Professor of pediatric cardiovascular science in 2004. He has been the Deputy Head of the Division of Imaging Sciences since 2005 and the Head of Division since 2007. He is the Director of the KCL Centre for Excellence in Medical Engineering funded by the Welcome Trust and the Engineering and Physical Sciences Research Council. His current research interests include cardiovascular magnetic resonance imaging and MR-guided cardiac catheterization.

Tobias Schaeffter studied electrical engineering in Berlin and received the Ph.D. degree in magnetic resonance imaging (MRI) from the University of Bremen (Prof. Leibfritz), Bremen, Germany. From 1996 to 2006, he was a Principal Scientists with the Philips Research Laboratories, Hamburg, Germany. In 2006, he was the Philip Harris Professor of imaging sciences with the Kings College London, London, U.K. His current research interests include the investigation of new acquisition and reconstruction techniques for cardiovascular and quantitative MRI. In particular, he is involved in new techniques for MR-guided electrophysiology procedures and the quantitative assessment of ablation procedures. He is interested in minimally invasive surgery and robotics. He has also pioneered a technique for Botulinum toxin injection for the treatment of overactive bladders.

Kawal Rhode received the bachelor's degree in basic medical sciences and radiological sciences from the King's College London and the Doctoral degree from the Department of Surgery, University College London, investigating quantitative blood flow analysis using X-ray angiography, in 1992 and 2001, respectively. From 2001 to 2007, he was with the Division of Imaging Sciences, King's College London, as a Post-Doctoral Research Fellow, involved in image-guided interventions, in particular, catheter-based electrophysiology procedures. In 2007, he was a Lecturer of image processing with the King's College London and a Senior Lecturer in 2011. His research interests include image-guided cardiovascular interventions, cardiac electromechanical modeling, computer simulation of minimally invasive procedures, and medical robotics. He specializes in translation of novel technologies into the clinical environment via collaborative research programs with leading clinical and industrial partners. He has authored 125 peer-reviewed papers in journals and conference proceedings, and 100 conference abstracts.
Funding Statement
This work was supported in part by the Kings College London Centre, Excellence in Medical Engineering through the Welcome Trust and EPSRC under Grant WT088641/Z/09/Z, and in part by the National Institute for Health Research, Biomedical Research Centre Award to Guy's and St Thomas' NHS Foundation Trust and King's College London.
References
- [1].Go A. et al. , “Prevalence of diagnosed atrial fibrillation in adults,” J. Amer. Med. Assoc., vol. 285, no. , pp. 2370–2375, 2001. [DOI] [PubMed] [Google Scholar]
- [2].Piccini J. P. et al. , “Incidence and prevalence of atrial fibrillation and associated mortality among medicare beneficiaries: 1993–2007,” Circulat., Cardiovascular Qual. Outcomes, vol. 5, no. 1, pp. 85–93, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Haissaguerre M. et al. , “Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins,” New England J. Med., vol. 339, no. 10, pp. 659–666, 1998. [DOI] [PubMed] [Google Scholar]
- [4].Pappone C. et al. , “Circumferential radiofrequency ablation of pulmonary vein ostia: A new anatomic approach for curing atrial fibrillation,” Circulation, vol. 102, no. 21, pp. 2619–2628, 2000. [DOI] [PubMed] [Google Scholar]
- [5].Oral H., et al. , “Circumferential pulmonary-vein ablation for chronic atrial fibrillation,” New England J. Med., vol. 354, no. 9, pp. 934–941, 2006. [DOI] [PubMed] [Google Scholar]
- [6].Karch M. et al. , “Freedom from atrial tachyarrhythmias after catheter ablation of atrial fibrillation: A randomized comparison between 2 current ablation strategies,” Circulation, vol. 111, no. 22, pp. 2875–2880, 2005. [DOI] [PubMed] [Google Scholar]
- [7].Oakes R. et al. , “Detection and quantification of left atrial structural remodeling with delayed-enhancement magnetic resonance imaging in patients with atrial fibrillation,” Circulation, vol. 119, no. 13, pp. 1758–1767, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Akoum N. et al. , “Atrial fibrosis helps select the appropriate patient and strategy in catheter ablation of atrial fibrillation: A DE-MRI guided approach,” J. Cardiovascular Electrophysiol., vol. 22, no. 1, pp. 16 22, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Vergara G. R. and Marrouche N. F., “Tailored management of atrial fibrillation using a LGE-MRI based model: From the clinic to the electrophysiology laboratory,” J. Cardiovascular Electrophysiol., vol. 22, no. 4, pp. 481–487, 2011. [DOI] [PubMed] [Google Scholar]
- [10].Daccarett M., McGann C. J., Akoum N. W., MacLeod R. S., and Marrouche N. F., “MRI of the left atrium: Predicting clinical outcomes in patients with atrial fibrillation,” Expert Rev. Cardiovascular Therapy, vol. 9, no. 1, pp. 105–111, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Arujuna A. et al. , “Acute pulmonary vein isolation is achieved by a combination of reversible and irreversible atrial injury after catheter ablation: Clinical perspective evidence from magnetic resonance imaging,” Circulat., Arrhythmia Electrophysiol., vol. 5, no. 4, pp. 691–700, 2012. [DOI] [PubMed] [Google Scholar]
- [12].Sohns C. et al. , “Quantitative magnetic resonance imaging analysis of the relationship between contact force and left atrial scar formation after catheter ablation of atrial fibrillation,” J. Cardiovascular Electrophysiol., vol. 25, no. 2, pp. 138–145, 2014. [DOI] [PubMed] [Google Scholar]
- [13].Malcolme-Lawes L. et al. , “Automated analysis of atrial late gadolinium enhancement imaging that correlates with endocardial voltage and clinical outcomes: A 2-center study,” Heart Rhythm, vol. 10, no. 8, pp. 1184–1191, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Peters D. et al. , “Detection of pulmonary vein and left atrial scar after catheter ablation with three-dimensional navigator-gated delayed enhancement MR imaging: Initial experience 1,” Radiology, vol. 243, no. 3, pp. 690–695, 2007. [DOI] [PubMed] [Google Scholar]
- [15].Boykov Y., Veksler O., and Zabih R., “Fast approximate energy minimization via graph cuts,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 23, no. 11, pp. 1222–1239, Nov. 2001. [Google Scholar]
- [16].Kim R. et al. , “Relationship of MRI delayed contrast enhancement to irreversible injury, infarct age, and contractile function,” Circulation, vol. 100, no. 19, pp. 1992–2002, 1999. [DOI] [PubMed] [Google Scholar]
- [17].Kolipaka A., Chatzimavroudis G. P., White R. D., O'Donnell T. P., and Setser R. M., “Segmentation of non-viable myocardium in delayed enhancement magnetic resonance images,” Int. J. Cardiovascular Imag., vol. 21, nos. 2–3, pp. 303–311, 2005. [DOI] [PubMed] [Google Scholar]
- [18].Schmidt A. et al. , “Infarct tissue heterogeneity by magnetic resonance imaging identifies enhanced cardiac arrhythmia susceptibility in patients with left ventricular dysfunction,” Circulation, vol. 115, no. 15, pp. 2006–2014, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Amado L. et al. , “Accurate and objective infarct sizing by contrast-enhanced magnetic resonance imaging in a canine myocardial infarction model,” J. Amer. College Cardiol., vol. 44, no. 12, pp. 2383–2389, 2004. [DOI] [PubMed] [Google Scholar]
- [20].Positano V. et al. , “A fast and effective method to assess myocardial necrosis by means of contrast magnetic resonance imaging,” J. Cardiovascular Magn. Resonan., vol. 7, no. 2, pp. 487–494, 2005. [DOI] [PubMed] [Google Scholar]
- [21].Detsky J., Paul G., Dick A., and Wright G., “Reproducible classification of infarct heterogeneity using fuzzy clustering on multicontrast delayed enhancement magnetic resonance images,” IEEE Trans. Med. Imag., vol. 28, no. 10, pp. 1606–1614, Oct. 2009. [DOI] [PubMed] [Google Scholar]
- [22].Lu Y., Wright G., and Radau P. E., “Automatic myocardium segmentation of LGE MRI by deformable models with prior shape data,” J. Cardiovascular Magn. Reson., vol. 15, no. 1, p. P14, 2013. [Google Scholar]
- [23].Knowles B. et al. , “3-D visualization of acute RF ablation lesions using MRI for the simultaneous determination of the patterns of necrosis and edema,” IEEE Trans. Biomed. Eng., vol. 57, no. 6, pp. 1467–1475, Jun. 2010. [DOI] [PubMed] [Google Scholar]
- [24].Wylie J., Peters D., Essebag V., Manning W., Josephson M., and Hauser T., “Left atrial function and scar after catheter ablation of atrial fibrillation,” Heart Rhythm, vol. 5, no. 5, pp. 656–662, 2008. [DOI] [PubMed] [Google Scholar]
- [25].Peters D. et al. , “Recurrence of atrial fibrillation correlates with the extent of post-procedural late gadolinium enhancement: A pilot study,” J. Amer. College Cardiol., Cardiovascular Imag., vol. 2, no. 3, pp. 308–316, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Yan A. et al. , “Characterization of the peri-infarct zone by contrast-enhanced cardiac magnetic resonance imaging is a powerful predictor of post-myocardial infarction mortality,” Circulation, vol. 114, no. 1, p. 32, 2006. [DOI] [PubMed] [Google Scholar]
- [27].Hennemuth A. et al. , “A comprehensive approach to the analysis of contrast enhanced cardiac MR images,” IEEE Trans. Med. Imag., vol. 27, no. 11, pp. 1592–1610, Nov. 2008. [DOI] [PubMed] [Google Scholar]
- [28].Tao Q. et al. , “Automated segmentation of myocardial scar in late enhancement MRI using combined intensity and spatial information,” Magn. Reson. Med., vol. 64, no. 2, pp. 586–594, 2010. [DOI] [PubMed] [Google Scholar]
- [29].Lu Y., Yang Y., Connelly K. A., Wright G. A., and Radau P. E., “Automated quantification of myocardial infarction using graph cuts on contrast delayed enhanced magnetic resonance images,” Quant. Imag. Med. Surgery, vol. 2, no. 2, pp. 81–86, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Ravanelli D. et al. , “A novel skeleton based quantification and 3D volumetric visualization of left atrium fibrosis using late gadolinium enhancement magnetic resonance imaging,” IEEE Trans. Med. Imag., vol. 33, no. 2, pp. 566–576, Feb. 2014. [DOI] [PubMed] [Google Scholar]
- [31].Karim R. et al. , “Validation of a novel method for the automatic segmentation of left atrial scar from delayed-enhancement magnetic resonance,” in International Workshop on Statistical Atlases and Computational Models of the Heart. New York, NY, USA: Springer Verlag, 2012, pp. 254–262. [Google Scholar]
- [32].Karim R. et al. , “Automatic segmentation of left atrial scar from delayed-enhancement magnetic resonance imaging,” in International Workshop on Functional Imaging and Modeling of the Heart. New York, NY, USA: Springer Verlag, 2011, pp. 63–70. [Google Scholar]
- [33].Karim R. et al. , “Evaluation of current algorithms for segmentation of scar tissue from late gadolinium enhancement cardiovascular magnetic resonance of the left atrium: An open-access grand challenge,” J. Cardiovascular Magn. Reson., vol. 15, no. 105, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Peters J. et al. , “Automatic whole heart segmentation in static magnetic resonance image volumes,” in Proc. MICCAI, 2007, pp. 402–410. [DOI] [PubMed] [Google Scholar]
- [35].Schnabel J. et al. , “A generic framework for non-rigid registration based on non-uniform multi-level free-form deformations,” in Proc. MICCAI, 2010, pp. 573–581. [Google Scholar]
- [36].Dempster A., Laird N., and Rubin D., “Maximum likelihood from incomplete data via the EM algorithm,” J. R. Statist. Soc. Ser. B, vol. 39, no. 1, pp. 1–38, 1977. [Google Scholar]
- [37].Dice L., “Measures of the amount of ecologic association between species,” Ecology, vol. 26, no. 3, pp. 297–302, 1945. [Google Scholar]
- [38].Warfield S., Zou K., and Wells W., “Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation,” IEEE Trans. Med. Imag., vol. 23, no. 7, pp. 903–921, Jul. 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Flett A. S. et al. , “Evaluation of techniques for the quantification of myocardial scar of differing etiology using cardiac magnetic resonance,” JACC, Cardiovascular Imag., vol. 4, no. 2, pp. 150–156, 2011. [DOI] [PubMed] [Google Scholar]
- [40].Karim R. et al. , “Surface flattening of the human left atrium and proof-of-concept clinical applications,” Comput. Med. Imag. Graph., Feb. 2014, to be published. [DOI] [PMC free article] [PubMed]