Novel Method to Track Soft Tissue Deformation by Micro-Computed Tomography: Application to the Mitral Valve

Abstract

Increasing availability of micro-computed tomography (μCT) as a structural imaging gold-standard is bringing unprecedented geometric detail to soft tissue modeling. However, the utility of these advances is severely hindered without analogous enhancement to the associated kinematic detail. To this end, labeling and following discrete points on a tissue across various deformation states is a well-established approach. Still, existing techniques suffer limitations when applied to complex geometries and large deformations and strains. Therefore, we herein developed a non-destructive system for applying fiducial markers (minimum diameter: 500μm) to soft tissue and tracking them through multiple loading conditions by μCT. Using a novel applicator to minimize adhesive usage, four distinct marker materials were resolvable from both tissue and one another, without image artifacts. No impact on tissue stiffness was observed. μCT addressed accuracy limitations of stereophotogrammetry (inter-method positional error 1.2±0.3mm, given marker diameter 1.9±0.1mm). Marker application to ovine mitral valves revealed leaflet Almansi areal strains (45±4%) closely matching literature values, and provided radiographic access to previously inaccessible regions, such as the leaflet coaptation zone. This system may meaningfully support mechanical characterization of numerous tissues or biomaterials, as well as tissue-device interaction studies for regulatory standards purposes.

Introduction

To fully understand the complex function of a biological tissue, it is vital to define its material properties and the deformations it experiences. Increased arterial stiffness, for example, can induce hypertension and numerous co-morbidities.²⁷ Perturbed tissue deformations alter mechanotransduction pathways, as in stretch-related calcification of the aortic valve.¹ Of equal importance, these characteristics are central to the computational study of biological systems. Whether by fluid-structure interaction, finite element, or other methods, spatiotemporal boundary conditions and mechanical moduli govern dynamic simulations.

Numerous efforts are ongoing to improve material and kinematic characterizations of soft tissues and engineered biomaterials.^{7, 17, 19} To this end, earlier idealized geometric models are giving way to those with unprecedented structural detail.^{9, 17, 25} These pursuits are facilitated by the increased availability of micro-computed tomography (μCT), which, with voxel resolution as fine as 9–17 μm,¹¹ has rapidly become a gold-standard against which other structural imaging modalities are evaluated.^{2, 5, 15, 30} Yet standalone structures, though necessary, are insufficient to fully characterize the finer aspects of a tissue’s mechanics. As one solution, critical insights into its local material properties and deformation fields can be gained by tracking movement of points on its surface across time.

Indeed, in harder tissues such as bone or wood, recent studies have computed strain fields and/or material stiffness using μCT-based digital volume correlation (DVC) approaches.^{6, 18, 29} However, DVC is less applicable to soft tissues, which generally lack identifiable, porous internal structures,²¹ and which undergo large displacements and strains. Previously, we have successfully tracked the motion of heart valve leaflets ex vivo using optical stereophotogrammetry (SP),^{24, 28} whereby a series of fiducial markers on the leaflet surface is observed by a pair of high-speed cameras, and three-dimensional coordinates are computed through direct linear transformation (DLT). This approach is effective for tracking rapidly moving markers, and has provided valuable insights into leaflet strains throughout the cardiac cycle.^{22, 28} However, SP suffers key limitations, both generally^{3, 4} and specifically to this application. These include a need to optimize the field of view relative to marker size, and limited optical access to some valvular structures. They also include post-processing error due to image-observed shape changes as markers change position and angle, user variability in manual processing, and/or inaccuracy in automatic point recognition algorithms.

Therefore, the present study aimed to develop a system for applying fiducial markers to soft tissue and tracking them across large tissue deformations by μCT. We hypothesized that this system could yield novel insights about mitral valve (MV) material properties and mechanics. A systematic investigation was conducted to (a) design an effective, efficient technique for applying markers of minimum possible size, (b) identify a series of marker materials that could be differentiated both from the tissue and from one another during reconstruction, and (c) demonstrate proof of concept by applying the system to MV specimens.

Materials and Methods

μCT Imaging and Data Visualization

All μCT imaging was performed using a Siemens Inveon scanner and Inveon Acquisition Workplace software (Siemens Medical Solutions USA, Inc., Malvern, PA), with settings optimized for soft tissue visualization (80 kV voltage, 500 μA, 650 ms integration time). Volumes were composed of 43.29 μm isotropic voxels. Following data acquisition, raw images were converted to DICOMs (Inveon Research Workplace), and surface meshes and volume renderings were computed using InVesalius 3.0 (InVesalius, São Paulo, Brazil) and/or Avizo 8.1 (FEI, Hillsboro, OR). Mesh refinement and marker centroid extraction were performed using Geomagic Studio (3D Systems, Cary, NC). Marker mesh sensitivity analysis was performed, with the criteria of volume convergence to within 2%, and centroid convergence to within 43.29 μm. This criteria was met at 240 elements; all markers in this study were meshed with >500 elements.

To verify the positional accuracy of the μCT scanner, a calibration cube was measured, first with precision calipers. In parallel, the cube was scanned in the μCT system, and the three dimensions of the resulting segmented image of the cube were measured. Worst-case positional error was 20 μm; this was within the positional uncertainty of the 43.29 μm scan resolution, and was therefore acceptable. In the context of the 2 mm marker spacing used in this study, standard uncertainty analysis suggests this would propagate to a worst-case of 3.4% areal strain error.

Marker Application

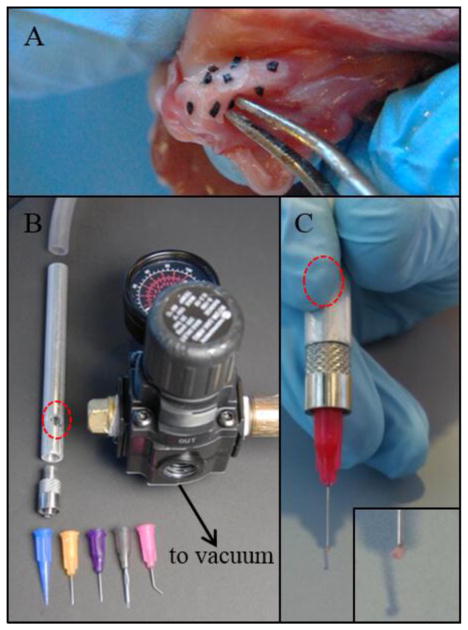
To attach a given marker, it was picked up, dredged through tissue adhesive (Loctite 4014, Henkel Corporation, Westlake, OH), and lightly pressed against the soft tissue. Stable attachment resulted within 2–3 seconds, and was confirmed by gentle manipulation with the applicator. The first application technique took a trivial approach, using fine forceps to carefully grip and maneuver markers (Figure 1A). A vacuum-based technique, developed to improve on the forceps’ limitations, was employed in all subsequent studies. For this technique, a novel device was designed and fabricated, consisting of a hollow shaft to be held by the operator. The shaft was connected on the distal end to a blunt-end needle tip of preferred size/shape (Nordson EFD, East Providence, RI) (1B). On the distal end it was connected to an airflow regulator and a vacuum source in series. A simple secondary air inlet was positioned for the operator’s finger. After setting the airflow regulator for a given function, the operator actuated the tip suction by covering the secondary inlet, and in this way could lift the marker (1C). Finally, to release the marker, the operator removed their finger from the secondary inlet, relieving the vacuum from the primary tip inlet.

FIGURE 1.

(a) Forceps-based marker application to mitral valve tissue led to significant tissue stiffening due to excess adhesive carried by the forceps tips. (b) A novel marker applicator (patent pending; shown disassembled) uses vacuum suction and a series of interchangeable, disposable tips. (c) Novel applicator in use. By covering the finger actuator (red circles) the user generates increased suction through the tip, enabling lift and release of a marker without excess adhesive (inset, zoomed view of marker).

To assess the impact of the adhesive on tissue stiffness, a simple experiment was conducted. Ovine hearts were acquired from a local market, and circumferential strips of the MV anterior leaflet were excised (dimensions: 12 × 5 μm; N=5). Each was loaded in a uniaxial tensile tester (Electroforce 3200, TA Instruments, Eden Prairie, MN) with a 25 N load cell (SMT1-22; Interface, Scottsdale, AZ). Samples were preconditioned with 20 sinusoidal cycle at 1 Hz, as per previous work with this tissue.⁸ The chosen peak stretch ratio of 1.3 was observed to induce an exponential stress response, as previously shown.¹⁶ Next, a 1 mm/sec linear displacement to a peak stretch ratio of 1.3 was conducted; load response was recorded at 50 Hz to ensure no tissue damage or slippage. Clay markers were then added to the atrial face of the tissue, and the test was repeated. Successive tests were conducted with 4 mm, 2 mm, and as dense as possible (<1 mm) marker spacing. Terminal loads from each test were recorded. For data processing, these loads were normalized by the no-bead test from that sample.

Material Viability Test

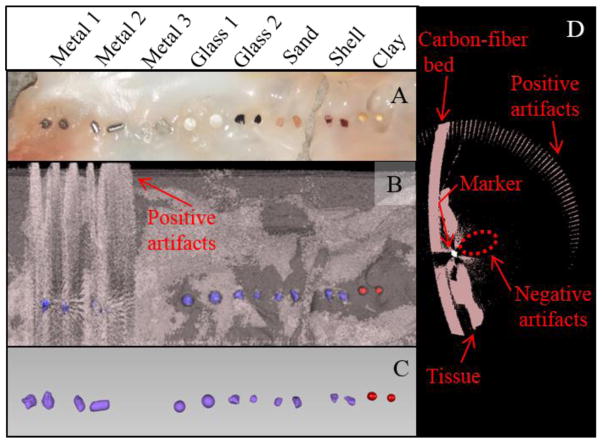
Material testing included three metallic markers and two glass markers, as well as sand, seashell, and clay (Table 1). The clay was from IMPAK Corporation (Los Angeles, CA). Mitral leaflets were excised from an ovine heart. Markers (N=2) of each material were applied to the leaflets, aligned axially so that the orbiting X-ray scanner would image each marker independently (Figure 2A). The sample was then subjected to μCT imaging. During postprocessing, the optimal x-ray intensity thresholds were identified for each material, to maximize segmentation clarity while minimizing overlap with other materials (including tissue) where possible.

Table 1.

Marker Materials Tested

Material	Mass Composition	X-ray Intensity Thresholds	Result	Remark
Metal 1	Fe (98%), C (2%)	−230:26000+	Artifacts	-
Metal 2	Sn (60%), Pb (40%)	−230:18000	Artifacts	-
Metal 3	Al (100%)	< −230	Unresolvable from tissue	Thin foil (~200 μm thickness)
Glass 1*	O (46%), Si (35%), Na (10%), Ca (8%)	−230:1000	Poor adhesion	Minimum diameter 1 mm
Glass 2	O (46%), Si (35%), Na (10%), Ca (8%)	−230:3850	Effective	-
Sand	O (53%), Si (35%), Na (10%), Ca (8%)	−230:2200	Effective	-
Seashell	O (48%), Ca (40%), C (12%)	−230:3250	Effective	-
Clay*	O (45%), Si (20%), Al (19%), Na (16%)	−230:320	Effective	Absorbs water (22% w/w)

Composition: major elements with mass >1% (trace elements do not contribute significantly to radiopacity); Unless otherwise specified, average diameters as small as 500 μm were available for each material.

^*Spherical shape, which makes registering individual markers across deformation states more difficult. In all other materials, each individual marker’s shape was unique.

FIGURE 2.

Eight materials were tested for viability as markers on mitral valve tissue. (a) Photograph of testing setup. (b) Raw surface meshes of markers, tissue, and carbon-fiber scan bed, generated by intensity thresholding (pink, −800:−230; red, −230:320; purple, 320:22000). (c) Refined meshes of markers isolated from other material. Metal 3 was not resolvable from the tissue. (d) Heavier metals (1 and 2) caused artifacts in the soft tissue threshold range, rendering them nonviable. Both positive artifacts (high-intensity voxels suggesting physical material that was not actually present) and negative artifacts (low-intensity voxels suggesting absence of physical material that was present) were observed.

Positional Uncertainty Quantification

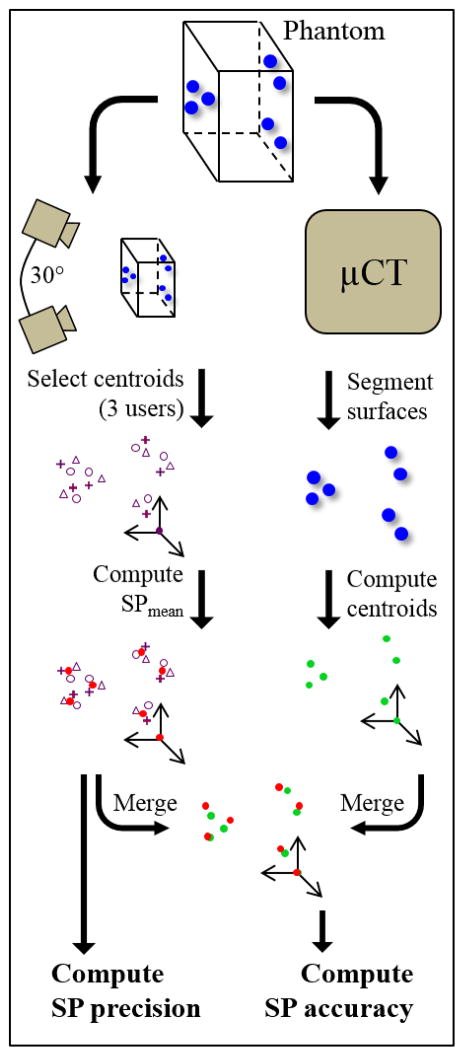
Although μCT is commonly regarded as the superior imaging technique for geometric reconstruction,^{2, 5, 15, 30} until now SP has been the best available means of tracking markers on soft tissue. To demonstrate the need for an improved methodology, precision and accuracy of SP were evaluated against μCT. A schematic of this approach is shown in Figure 3. A series of glass markers (N=7) was attached to points around an optically clear, low-radiopacity plastic phantom. The markers were spread across all three spatial dimensions of the phantom, such that errors in all directions could be quantified. Although the applicator could manipulate markers with diameter as small as 500 μm, larger markers were used here to ensure visibility by SP over the necessary field depth.

FIGURE 3.

Schematic of quantification of positional uncertainty associated with centroid identification by SP. A transparent, low-radiopacity phantom was tagged with 7 glass markers and imaged by SP and μCT. Precision and accuracy were quantified by separate processes as shown.

Synchronized stereoscopic imaging used two high-speed cameras (A504k, Basler AG, Ahrensburg, Germany) and XCAP acquisition software (Epix Inc., Buffalo Grove, IL) separated by an angle of approximately 30°. Each camera had resolution of 1024 × 1280 pixels. Positional calibration was performed by imaging a cube of known dimensions. Three-dimensional coordinates corresponding to each marker’s centroid were computed from the image pair by DLT, using a custom MATLAB program (MathWorks, Natick, MA).^{23, 28} Identification of calibration cube vertices and marker centroids relied on manual selection via a graphical user interface. Given the equipment and processing techniques employed here, 3D positions of selected points could be determined to an accuracy of <100μm.^{12, 23} To quantify the precision associated with manual centroid selection process, these steps were repeated by three users.

Following SP, the marked phantom was imaged by μCT and marker centroids were extracted. Euclidean distances between marker centroids and average marker diameters were based on μCT. Volume (mm³), V, was computed in SolidWorks (3DS, Waltham, MA) from the reconstructed surface mesh. Average diameter (mm), D_avg, was then derived by

$$D_{\mathit{avg}}=2\ast \sqrt[3]{\frac{3}{4\pi }V}$$ (1)

After image processing, all centroid datasets (one from μCT plus one from each of three SP users) were re-oriented to a common coordinate system defined by the same three points. One point was constrained to the origin, leaving six unconstrained. A mean SP-derived centroid (SP_mean) was also computed for each marker based on the locations identified by each SP user. Therefore, for the purposes of this study, SP precision was defined as the average Euclidean distance between any single user’s SP-derived centroid and the corresponding SP_mean. Accuracy was defined as the average Euclidean distance between SP_mean positions and their corresponding μCT-derived centroids.

Functional MV Simulation

An additional whole MV, including chordae tendineae and papillary muscles, was excised from an ovine heart. It was mounted in the extensively validated Georgia Tech Left Heart Simulator (GTLHS) and positioned to a healthy geometry using previously described methods.^{9, 20, 24} To assess the positional tracking capacity of the new method, a dense marker mesh (target: 2 mm between markers) was attached across the annulus and both leaflets. This was imaged twice by μCT: first open and relaxed, then statically closed under steady systolic air pressure (120 mmHg), using recently developed methods.⁹ The air used to pressurize the model left ventricle was first humidified by passing through warm water; this prevented tissue dehydration during imaging.

To assess the method’s utility for strain computation, a 4×4 subset of these markers was analyzed. This subset was located in the central anterior leaflet. In terms of material behavior, this is the most well-described region of the MV; focusing on this subset enabled direct comparison to previous studies of strain in this region.^{10, 13, 22} These studies have employed spacing between 1.5–2.5 mm. Following image processing and marker centroid extraction and triangulation, Almansi areal strain, ε_a, was computed within each triangular element as

$${\epsilon }_a=\frac{a_{\mathit{systolic}}-A_{\mathit{diastolic}}}{a_{\mathit{systolic}}}$$ (2)

where a_systolic and A_diastolic correspond to the area (mm²) in the closed and open MV states, respectively. Strains were calculated and averaged using a custom MATLAB code, and visualized in TecPlot 360 (TecPlot, Inc., Bellevue, WA).

Results

Marker Application

Application of markers by the trivial forceps method was only possible using markers with maximum dimension >1 mm. Below this level, human error in handling was insurmountable. Even with markers sized near this lower limit, manipulation was extremely slow, and marker slippage and placement error were significant. Furthermore, dredging markers through the liquid adhesive led to excess adhesive being carried by the forceps tips. This excess easily transferred to the tissue during marker attachment, causing tissue adjacent to the marker contact zone to stiffen (Figure 1A).

The suction-based device addressed each limitation of the trivial method. Beads as small as 500 μm could be placed accurately. With constant vacuum pressure, markers did not slip, making application quick and free of major errors. With the applicator tip positioned behind the marker, it did not contact the liquid adhesive. If the adhesive did contact the tip accidentally, it would be rapidly pulled into the applicator barrel, such that no excess could transfer to the tissue. Any incidental uptake of tissue adhesive into the applicator could be resolved easily: tips could be quickly discarded and replaced, while the barrel could be stored in acetone between uses for complete dissolution of any buildup.

Uniaxial testing pulled each tissue strip to a stretch ratio of 1.3, with successive increases in marker density. At every density, mean normalized terminal load differed from that of the control case (no markers) by under 6%. One-tailed, one-sample t-tests comparing each marker density to the control gave p-values of 0.76 or higher. That is, no significant changes in stiffness were observed, even when markers were packed as densely as possible.

Material Viability Test

In total, eight marker candidates were tested (Figure 2A). MV tissue was reconstructed at an intensity threshold of −800:−230, while each marker was reconstructed in a different intensity range. Marker characteristics, including intensity thresholds, are detailed in Table 1. As expected from clinical experience,²⁶ both heavier metallic markers were ineffective due to generation of artifacts in the soft tissue threshold range (2B, 2D). Positive artifacts (ie, high intensity voxels suggesting physical material that was not actually present) were created, such as in the form of a ‘halo effect’ in the empty space surrounding the sample. Negative artifacts (ie, low intensity voxels suggesting absence of physical material that was present) were also created; an empty region was clearly seen in a portion of both the carbon-fiber bed and the tissue, in close proximity to the marker. In contrast, Metal 3, an extremely thin aluminum foil, could not adequately be resolved from the soft tissue, due to its low radiopacity. All other markers could be clearly resolved from the tissue without artifacts, although the larger glass beads were found to detach more easily. This was likely due to the smooth, non-porous surface bonding more weakly with the adhesive/tissue, as well as the higher out-of-plane profile exposing the marker to greater shearing forces. The clay beads, despite a similar round shape, had no adhesion issues. This was likely due to their 22 %w/w water adsorption capacity (per manufacturer documentation), which may have facilitated a stronger bond with the adhesive.

Intensities of glass, sand, and seashell all fell between −230:3850, depending on material and depth within the marker. Their intensities overlapped to the extent that unique reconstruction thresholds did not exist for any of these. Clay, however, exhibited weaker x-ray attenuation, with intensities between −230:320. A two-step reconstruction was therefore possible: by thresholding once in the −230:320 range, and once with a lower threshold of 320, clay was clearly distinguished from other marker types at the post-processing stage (2C).

Positional Uncertainty Quantification

Positional accuracy of the novel μCT marker tracking technique was assessed versus SP using markers on a plastic phantom (Figure 3). An average marker occupied 136±35 pixels by SP (0.010±0.003% of one camera’s field of view), and had diameter 1.9±0.1 mm. Although the vacuum-based applicator enabled use of smaller markers, this size was chosen to ensure visibility to both cameras, given the field of view. The minimum and maximum Euclidean distances between markers were 8.9 and 49.8 mm, respectively. After re-orienting all datasets to a common coordinate system, SP precision and accuracy were computed based on the six unconstrained centroids. SP precision was 1.0±0.4mm, and SP accuracy was 1.2±0.3mm.

Functional MV Simulation

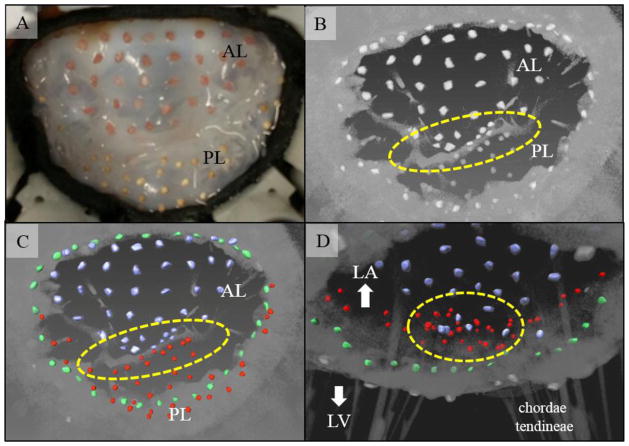
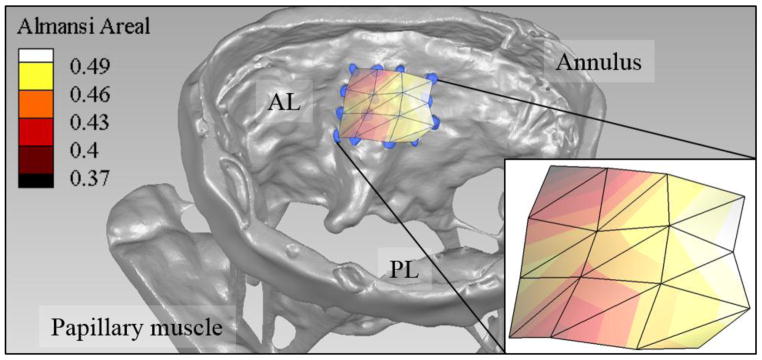
After configuring an ovine MV to a healthy configuration in the GTLHS, a marker grid was applied across the surfaces of the valve’s annulus and leaflets. In total, 73 sand and 41 clay markers were applied (Figure 4A). These had minimum diameter of approximately 500 μm. Average distance between a marker’s centroid and that of its closest neighbor was 2.2±0.5 mm. The estimated cumulative mass of the markers was 70 mg, whereas combined leaflet and annular mass was 2865 mg. The markers therefore added 2.4% to the total mass. After imaging, during volume rendering (4B), 99.1% of the markers were recaptured during volume rendering (one marker likely fell off during handling). By selectively attaching sand and clay markers to the anterior and posterior leaflet, respectively, markers in the coaptation zone could be distinguished on the basis of their shapes and/or intensity thresholds (4C–D). Finally, using the 4×4 sub-grid of sand markers located in the central anterior leaflet, Almansi areal strains were computed between the open and closed MV configurations (Figure 5). Based on the centroids of these markers, average Almansi areal strain in this region was 45±4%.

FIGURE 4.

73 sand and 41 clay markers were attached to the leaflets and annulus of a MV mounted in the GTLHS. (a) and (b) Atrial en face images of the MV when closed under systolic pressure, viewed by optical camera and μCT (raw volume rendering), respectively. (c) and (d) Surface meshes of markers from atrial and ventricular view (overlaid on volume rendering), respectively. Key features not visible by optical camera can be distinguished, such as the annulus (green) and coaptation zone (yellow ovals). Blue: anterior leaflet (AL); red: posterior leaflet (PL).

FIGURE 5.

Almansi areal strain field associated with MV closure, calculated from nine marker centroids extracted from μCT. The strain field is superimposed over the open MV tissue and markers. Mean±SD strain was 45±4%. AL, anterior leaflet; PL, posterior leaflet.

Discussion

This study aimed to develop an improved method for capturing the large deformations and strains experienced by soft tissues, such that these data could be coupled to high-resolution μCT-derived geometries. We have reported a non-destructive technique to precisely apply fiducial markers as small as 500 μm to soft tissue. As compared to the trivial approach using forceps, the novel tool developed herein enables application of smaller markers, with a complete reduction of excess glue, and with minimal risk of handling error. Moreover, despite minimal adhesive usage and negligible impact on tissue stiffness, the markers adhere strongly even under large deformations and strains (99.1% were recaptured during surface reconstruction). The markers identified in this study have mass sufficiently low to be neglected for most applications (114 markers added 2.4% to MV tissue mass in our trial). Four unique materials were identified that adhere durably to tissues undergoing large strains and that can be resolved from soft tissue and from one another under μCT imaging. For studies in which marked surfaces move into contact with one another, availability of multiple unique materials enables unambiguous registration of each marker to its associated surface.

Quantification of the positional errors associated with our previous technique, SP, highlighted some of the advantages of the μCT method. Variability among three users processing the same set of SP images was 1.0±0.4 mm. μCT-based centroid extraction eliminates this precision error by removing the user input altogether. μCT is increasingly recognized as a gold-standard for positional accuracy,^{2, 5, 15, 30} and in this study was considered ground-truth for marker centroid position. The average error between SP_mean and μCT was 1.2±0.3 mm. This disparity in accuracy likely resulted from a combination of well-characterized SP error sources,^{3, 4} including limits on lighting, calibration accuracy, and camera positioning/resolution, in addition to difficulty identifying a marker’s 3D centroid from 2D images. It is worth noting that both precision and accuracy were within the size range of the markers themselves (diameter: 1.9±0.1 mm). Improved precision would be expected by using smaller or more uniform markers with a more focused field of view. μCT, by contrast, provides uniform voxel resolution as fine as 9–17 μm,¹¹ allowing for diverse marker sizes and shapes independent of the selected field of view.

As further validation, marker application to ovine MVs highlighted potential for novel explorations into valve kinematics. The observed average areal strain was 45±4%, which is in good agreement with previous ex vivo measurements of anterior leaflet areal strain conducted by Sacks et al (47±10%),²² He et al (42±20%),¹⁰ and Jimenez et al (36±14%).¹³ Given the success of this technique as demonstrated, strain measurements in previously unexplored regions of the MV represent an exciting new frontier. The leaflet coaptation zone, for example, could not be visualized during systole until now. More generally, placement of a dense marker mesh can offer unique boundary conditions for dynamic, μCT-based computational models of valves or other tissues. Already, application of this technique in the GTLHS is enabling validation of finite element simulations of MV closure.¹⁴

With respect to future applications, insofar as the subject(s) can be experimentally held in static configurations of interest, this workflow can be applied as shown here. It may also lend well to dynamic processes that move on a sufficiently slow time scale (e.g. tissue growth & remodeling), although this was not explored in this study. Potential settings where this technique could meaningfully contribute include stages of device and/or biomaterial development where the interaction with tissue dynamics is investigated. The biomechanical impact of any device can be derived by observing the difference between soft tissue deformation prior to and following implantation. Currently, regulatory guidelines on mechanical interaction between device and soft tissue are vaguely described. Calibrated force information available in literature is currently being used in the design of valve repair devices, for example. High-resolution information about the impact of such devices on tissue deformation would directly inform more rigorous standards, as well as assessment of safety factors for specific designs. In addition, this information can empower computational models of the soft tissue that the devices interact with. Once these models are validated, tissue response to repair or device implantation procedures can be more faithfully recreated in silico, using both idealized and patient-specific geometries.

In any future application of this technique, experimental design must be optimized. This includes choice of marker type, size, and density, as well as μCT acquisition settings; each of these may impact measurement uncertainty. Post-processing algorithms may also prove useful. Digital Volume Correlation techniques, applied to the markers themselves, may save manual processing time. Sub-voxel interpolation techniques may further improve spatial resolution. Follow-up studies should investigate the applicability of these techniques.

Limitations

A few key limitations must be considered with this methodology. First, though the necessary volume of adhesive and mass of markers are both sufficiently small to be negligible over most scales to be investigated, a slight effect on the sample’s mechanics is inevitable. Additionally, μCT bore size may preclude certain applications that are more compatible with SP or clinical CT. Finally, it must be remembered that rapidly moving materials cannot be clearly imaged by most computed tomography systems. Thus this technique is largely limited to scenarios in which the deformations occur over a sufficiently long time scale, or can be experimentally halted at a state of interest, as shown here. Looking forward, the potential for adverse interactions between markers, adhesive, and living tissues should be evaluated. Should a method be developed to stably implant these markers in living tissues, a wealth of new applications may result.