Predictive Value Tools as an Aid in Chemopreventive Agent Development

Abstract

Background:

Over 25 years, the National Cancer Institute’s Division of Cancer Prevention has entered some 800 agents into a chemopreventive agent testing program. Two critical steps involve: 1) in vitro/in vivo morphologic assays and 2) animal tumor assays (incidence/multiplicity reduction). We sought to determine how accurately the earlier-stage (morphologic) assays predict efficacy in the later-stage (animal tumor) assays.

Methods:

Focusing on 210 agents tested in both morphologic and animal tumor assays, we carried out statistical modeling of how well the six most commonly used morphologic assays predicted drug efficacy in animal tumor assays. Using multimodel inference, three statistical models were generated to evaluate the ability of these six morphologic assays to predict tumor outcomes in three different sets of animal tumor assays: 1) all tumor types, 2) mammary cancer only, and 3) colon cancer only. Using this statistical modeling approach, each morphologic assay was assigned a value reflecting how strongly it predicted outcomes in each of the three different sets of animal tumor assays.

Results:

We demonstrated differences in the predictive value of specific morphologic assays for positive animal tumor assay results. Some of the morphologic assays were strongly predictive of meaningful positive efficacy outcomes in animal tumor assays representing specific cancer types, particularly the aberrant crypt focus (ACF) assay for colon cancer. Moreover, less strongly predictive assays can be combined and sequenced, resulting in enhanced composite predictive ability.

Conclusions:

Predictive models such as these could be used to guide selection of preventive agents as well as morphologic and animal tumor assays, thereby improving the efficiency of our approach to chemopreventive agent development.

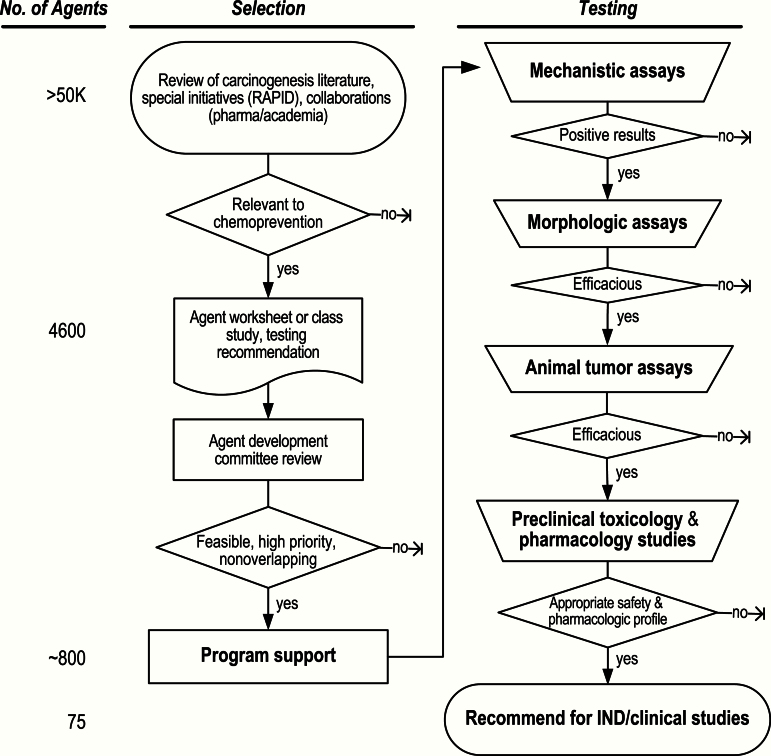
For over 25 years, the National Cancer Institute’s (NCI’s) Division of Cancer Prevention (DCP) has followed a conventional drug development process similar to one used for treatment. This program is the only large-scale endeavor focusing on the development of agents to prevent or reduce the risk of cancer. Approximately 800 promising agents have been brought into the program through a variety of venues. Of these, 750 candidate agents were tested first in mechanistic and/or morphologic (in vitro and in vivo) assays (Figure 1). The latter were then considered for preclinical in vivo testing in animal tumor assays and ultimate advancement to successive phases of clinical trials. The results reported here arise from a project designed to investigate whether DCP’s cancer prevention drug development process is achieving its ultimate goal of enhancing public health by preventing cancer or substantially decreasing its risk in a resource-efficient manner. In the current evaluation of two of the early stages of agent testing—morphologic and animal tumor assays—we updated a similar 1996 analysis (1), using a more quantitative approach. Our approach is timely, given the current climate of increasingly constrained research resources.

Figure 1.

Decision-gate agent selection and testing process. Although ideas for chemopreventive agents come from a variety of sources, most agents are suggested from preclinical data presented in peer-reviewed published articles. 1) Prevention efficacy may be suggested by epidemiologic data on cancer incidence from population studies of widely used approved drugs for nonmalignant diseases, suggesting the possibility of “repurposing” drugs to cancer prevention. 2) Nutritional components are also suggested as having preventive properties based on observational data associating specific diets or use of individual nutrients with cancer incidence. 3) Retrospective analyses of secondary cancer endpoints or even nonprospectively collected cancer data from trials of noncancer drugs also offer hypotheses regarding cancer prevention effects. 4) Prevention of second primary cancers within treatment trials of existing cancers, breast cancer being the most obvious example, also has supported the testing of treatment agents for prevention. IND = investigational new drug.

Methods

General Approach

We tracked outcomes at each stage of testing (morphologic assays, animal tumor assays, clinical trial phases, including investigational new drug [IND]–enabling safety trials), relating successes and failures to those of the preceding stage, simulating a “screening” approach. Definitions of positive and negative outcomes were formulated for each stage of testing, with success at a given stage based on composite outcomes of multiple assays. “Positivity” at an earlier stage in the screening process generally favored progression to the next stage (morphologic to in vivo, for example) (Figure 1), conditional on resource availability and other factors related to infrastructure. “Negativity” at the morphologic assay stage generally did not support testing an agent in the later, animal tumor assay stage. However, the data collected were diverse in morphologic assay outcomes, encouraging us to estimate positive and negative predictive values for the earlier assay stage relative to the later stage using statistical modeling. In the current paper, this “decision-gate” approach is applied to the morphologic-to-in vivo transition. The critical decision is whether to progress from the earlier to the next, more resource-intense, stage.

For the current project, predictive models were generated based on quantitative measures of morphologic outcomes for individual assays and for composites of multiple assay types. The actual outcomes at each stage are not strictly quantitative, however, and therefore are transformed into a quantitative value. Net success at the morphologic screening assay stage was interpreted as general “positivity.”

To investigate whether efficacy in commonly used morphologic assays predicts cancer prevention efficacy in our animal tumor assays, a statistical modeling approach was developed to evaluate the relationship between quantitative results on each side of the morphologic-to-animal tumor assay transition. The implementation of such statistical models as a tool in evaluation of the earlier-stage assays allows the generation of “predictive values” that can guide our decisions whether to proceed to the next stage at each transition.

Morphologic and Animal Tumor Assays

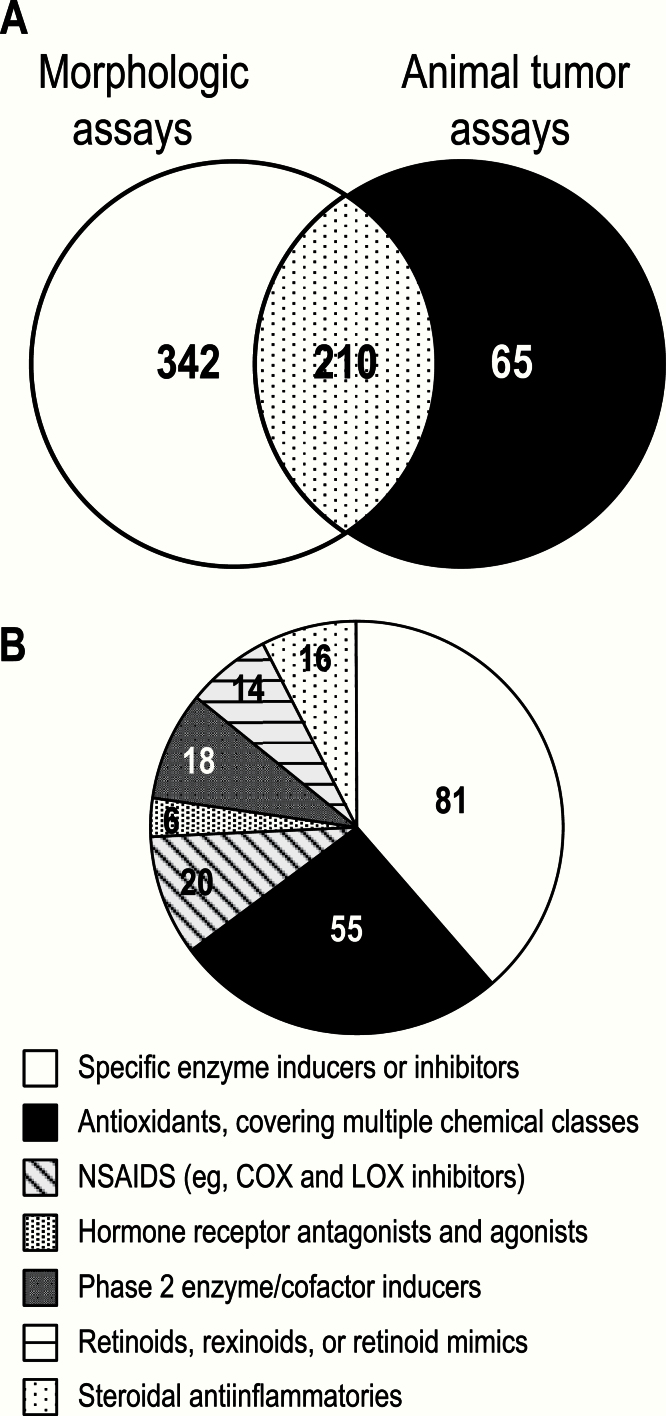
The results from DCP-sponsored studies, maintained in relational databases, indicated that 617 agents had been evaluated in morphologic assays and/or tumor efficacy assays in animals. Among these, the 210 agents tested in both assay types were used in this analysis (Figure 2A). These 210 agents are distributed among seven functional/biological categories (Figure 2B).

Figure 2.

Agents tested in Division of Cancer Prevention assays. A) Number of agents tested in morphologic and animal tumor assays. B) Classes of agents tested. The 210 agents were representative of many functional or biological categories. To illustrate, each agent was assigned to the “best” category, where the best category was considered the more specific or more common category. For example, many agents with antioxidant activity were reported under specific enzyme or pathway activities.

Datasets

The six selected morphologic assays span several tissue types and follow various criteria for determining efficacy (Table 1) (2). Of note, the aberrant crypt focus (ACF) assay does not assess tumor prevention and is considered a morphological assay despite taking place in vivo. Data generated from these assays were classified into ordered categories of efficacy (Table 2). The best result for each agent in each assay was used in fitting the statistical model. This approach was used in order to optimize the chance to retain a true positive signal and avoid false negative results. Although this was done at the expense of possible false positive signals, this approach is a first pass at estimating agent efficacy. In general, a false negative (discarding a useful agent) is considered less desirable than a false positive in early drug screening phases.

Table 1.

Characteristics of morphologic assays and percent of agents that tested positive*

Assay	Model/inducer	Criteria for a positive result†	Positive/total agents (% positive)
ACF	F344 rats/AOM	Statistically significant (P < .05) decrease in ACF	152/244 (62)
A427	Human lung carcinoma cells/NA	≥20% inhibition of anchorage-independent colony formation at one or more concentrations	253/336 (75)
HFE	Neonatal human foreskin epidermal cells/PS	≥30% growth inhibition; or ≥20% involucrin induction; or ≥20% PCNA† expression inhibition – at two consecutive, nontoxic concentrations	57/65 (88)
JB6	Mouse epidermal cells/TPA	Statistically significant (P < .05) decrease in anchorage-independent colony formation	60/110 (54)
MMOC	BALBc mammary glands/DMBA	≥60% decrease of hyperplastic nodules	184/350 (53)
RTE	F344 tracheal epithelial cells/B[a]P	≥20% inhibition of transformed foci at two or more nontoxic concentrations	283/388 (73)

* The six morphologic assays comprise five in vitro assays: rat tracheal epithelial cell (RTE), human lung tumor A427 cell (A427), mouse mammary organ culture (MMOC), mouse JB6 epidermal cell (JB6), and human foreskin epithelial cell (HFE); and one in vivo assay: aberrant crypt foci (ACF) in rats (1). The best result for each agent in each assay was incorporated into the statistical model. To fit a good statistical model, a reasonable percent of agents should test negative as well as positive in a given morphologic assay. If the percent testing positive is too high, less discrimination is achieved among tested agents. A427 = human lung tumor A427 cell; ACF = aberrant crypt foci; AOM = azoxymethane; B[a]P = benzo[a]pyrene; DMBA = 7,12-dimethylbenz[a]anthracene; HFE = human foreskin epithelial cell; JB6 = mouse JB6 epidermal cell; MMOC = mouse mammary organ culture; RTE = rat tracheal epithelial cell; NA = not applicable; PS = propane sultone; PCNA = proliferating cell nuclear antigen; TPA = tetradecanoylphorbol acetate.

† Each endpoint is evaluated in comparison with the vehicle or solvent control. Of the 552 agents, 484 were positive in at least one assay.

Table 2.

Result rank definitions*

Rank integer	General definition	Inhibition ranges	HFE	MMOC
0	Not efficacious (NE)	<20%	< Minimum criterion for a positive result	<60%
1	Weak positive (+)	20 – <50%	Minimum positive criterion – <50%	60 – <75%
2	Moderate positive (++)	50 – <75%	50 – <75%	75 – <90%
3	Strong positive (+++)	≥75%	≥75%	≥90%

* Results were normalized by assignment of a rank integer corresponding to the strength of positivity of the result. All animal efficacy and most morphologic assays used the general inhibition ranges shown in the third column. Human foreskin epithelial cell (HFE) and mouse mammary organ culture (MMOC) assays used slightly different scales (columns 4 and 5) based on the less quantitative nature of weak positive results (HFE) or an increased stringency for MMOC results that better correlates with animal mammary results. HFE = human foreskin epithelial cell; MMOC = mouse mammary organ culture.

Statistical Methods

The most commonly used animal tumor assays are the carcinogen-induced assays, which represent distinct tumor sites: azoxymethane (AOM) rat colon, methyl nitrosourea (MNU) rat mammary, hydroxyl butyl(butyl) nitrosamine (OH-BBN) rat bladder, benzo[α]pyrene (B[a]P) mouse lung, and ultraviolet (UV) mouse skin (3). As with the morphologic assays (Table 2), tumor results (incidence, multiplicity) were classified into ordered categories. The best result for each agent and site-specific tumor model was selected, again in order to err on the side of positivity. The current analysis addressed three classes of animal tumor assays: 1) the general tumor model using all the data from all animal assays, 2) the colon, and 3) the mammary assays; the latter two were restricted to data for the indicated tumor sites.

In constructing models to predict outcomes of animal tumor assays from morphologic assay results, separate analyses were performed for each class of animal tumor assay (general, colon, mammary). Both animal tumor and morphologic assays generated ordinal data (values of 0, 1, 2, 3) (Table 2), so ordinal logistic regression was applied. Under this model, if Y is the potential outcome of the animal tumor assay and X _ACF , X _A427 , X _HFE , X _JB6 , X _MMOC , and X _RTE are the observed outcomes of the morphologic assays, the logarithm of the odds that Y will be at most j, where j ranges from 0 to 2, is a _j + b _ACF X _ACF + b _A427 X _A427 + b _HFE X _HFE + b _JB6 X _JB6 + b _MMOC X _MMOC + b _RTE X _RTE. Note that the slope coefficients (the bs) do not change with j; only the intercept a changes.

When considering predictive models, we allowed for options in which certain morphologic assays would not be used, which is equivalent to setting their slope coefficients to 0. The set of all possible such options consists of 63 models (Supplementary Table 1, available online). Because a relatively small number of outcomes of animal tumor assays had associated results from all six morphologic assays, multiple imputation was performed to generate multiple complete datasets having close concordance with the observed data (4). For each of the 100 imputed datasets, each of the 63 ordinal logistic regression models was fitted. The SAS procedure MIANALYZE was applied to every model to obtain combined estimates (with standard errors) of the coefficients over the 100 datasets. The 63 models were then compared using a bias-corrected version (AICc) of the Akaike Information Criterion (AIC), which discourages overfitting. The AICc values were used to obtain coefficient estimates that were weighted averages over all 63 models, a technique known as multimodel inference (5). This part of the analysis was performed in Mathematica, version 8.0.1.0 for Mac (Wolfram Research - Champaign, Illinois). The remainder was done with the use of SAS/STAT, version 9.2 of the SAS System for Linux (SAS Institute, Inc. - Cary, North Carolina).

Results

Predictive Values of Individual Morphologic Assays for Animal Tumor Efficacy Outcomes

The estimated coefficients in the predictive models are provided in Table 3. The magnitude (absolute value) of a slope coefficient indicates how strongly the outcome of the associated morphologic assay predicts the outcome of the tumor assay. The sign of a slope coefficient indicates whether the relationship of the outcome of the morphologic assay to the odds of the outcome of the tumor assay being at most j (j = 0, 1, 2) is a direct one (positive slope) or an inverse one (negative slope). Most of the slope coefficients in Table 3 being negative shows that this relationship is generally an inverse one, with larger outcomes of morphologic assays associated with smaller odds, which is equivalent to larger outcomes of the animal tumor assay. The two positive slopes in the table are too small to be of any consequence in the models. These estimated model coefficients are used in the equations in Figure 3 (colon model) and Supplementary Figures 1 and 2 (available online), from which the graphs in Figure 4, A, B, and C, are generated. The strongest predictor is ACF for animal tumor assays of colon cancer. In the mammary tumor model, the MMOC assay is strongest, ACF having little effect on the outcome. These relationships between morphologic assays and tumor assays suggest disease site–specific connections.

Table 3.

Predictive model coefficients*

Assay	General model (all sites)	Colon model	Mammary model
Slopes (standard error)
ACF	−0.559 (0.184)	−0.698 (0.205)	−0.031 (0.094)
A427	0.019 (0.060)	−0.092 (0.164)	−0.205 (0.174)
HFE	−0.159 (0.204)	−0.015 (0.135)	−0.329 (0.255)
JB6	−0.031 (0.095)	−0.076 (0.220)	−0.010 (0.077)
MMOC	−0.288 (0.168)	0.002 (0.073)	−0.428 (0.177)
RTE	−0.153 (0.139)	−0.075 (0.124)	−0.111 (0.140)
Intercepts (standard error)
Y=0	0.849 (0.526)	0.410 (0.648)	1.521 (0.668)
Y=1	1.849 (0.554)	1.594 (0.659)	2.891 (0.713)
Y=2	2.538 (0.576)	2.942 (0.702)	4.065 (0.772)

* Slopes and intercepts in the ordinal logistic regression models are presented, where Y is the potential outcome of the animal tumor assay. An example of using the coefficients in the general model is shown in Figure 3. A427 = human lung tumor A427 cell; ACF = aberrant crypt foci; HFE = human foreskin epithelial cell; JB6 = mouse JB6 epidermal cell; MMOC = mouse mammary organ culture; RTE = rat tracheal epithelial cell.

Figure 3.

Colon-specific model for predicting the outcome of the animal tumor assays from the results of the morphologic assays.

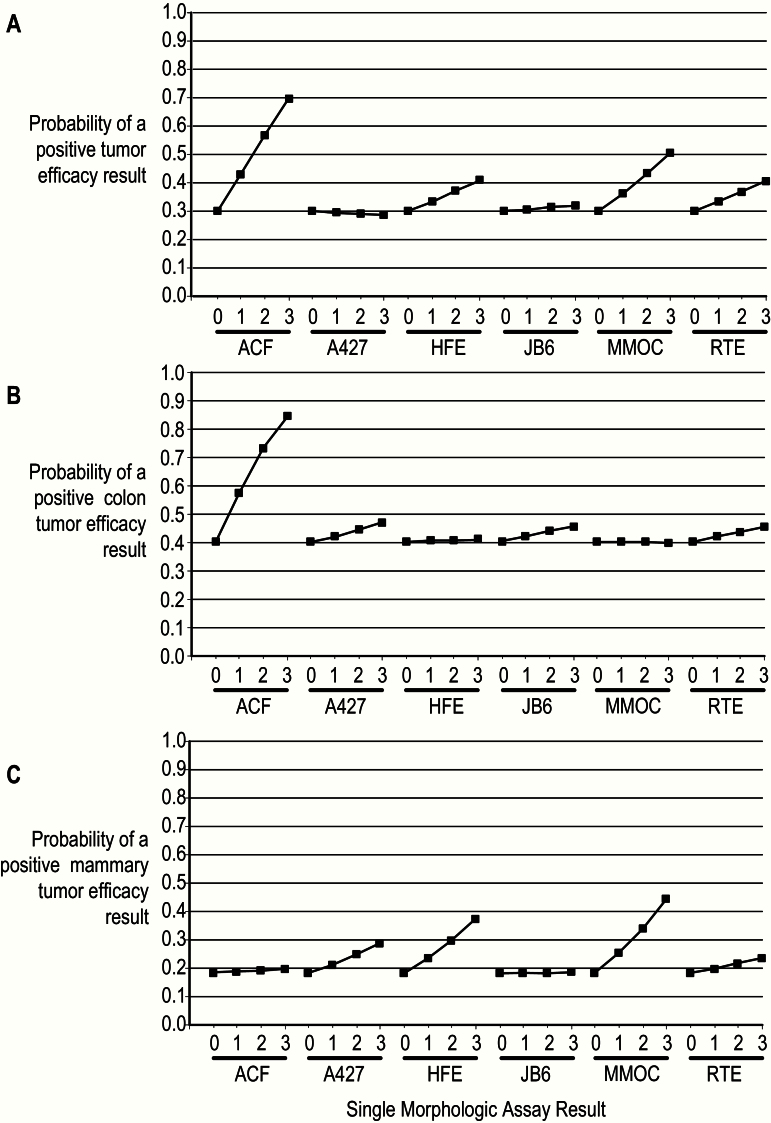
Figure 4.

Predictive model graphs. For each tumor class, the graph for any positive result is shown. This presentation is a visual version of the coefficients. For each morphologic assay, the possible results are shown on the x-axis, and the results for the other five assays are set to 0. Each graphed line depicts the probability of a tumor efficacy result of 1, 2, or 3 (y-axis) in at least one tumor endpoint (incidence, multiplicity, tumor burden). A427 = human lung tumor A427 cell; ACF = aberrant crypt foci; HFE = human foreskin epithelial cell; JB6 = mouse JB6 epidermal cell; MMOC = mouse mammary organ culture; RTE = rat tracheal epithelial cell.

Figure 4 displays the predictive value of each morphologic assay for a positive outcome in each animal tumor assay, using the model coefficients in Table 3. Any outcome of an animal tumor assay exceeding 0 is considered positive. Each plotted point on a graph gives the minimum estimated probability of a positive outcome of the animal tumor assay (vertical coordinate) at the specified outcome of the morphologic assay (horizontal coordinate). The estimated probability shown on the graph is a minimum because the outcomes of all other morphologic assays have been set to 0. The maximum probability for a positive outcome in an animal tumor assay is 0.84, when the ACF assay outcome is 3. The predictive value of the MMOC assay does not reach this level, peaking at 0.44. A high predictive value provides support for advancing an agent to the next stage of testing according to the “decision-gate” process depicted in Figure 1.

Combinations of Morphologic Assays to Improve Predictive Ability

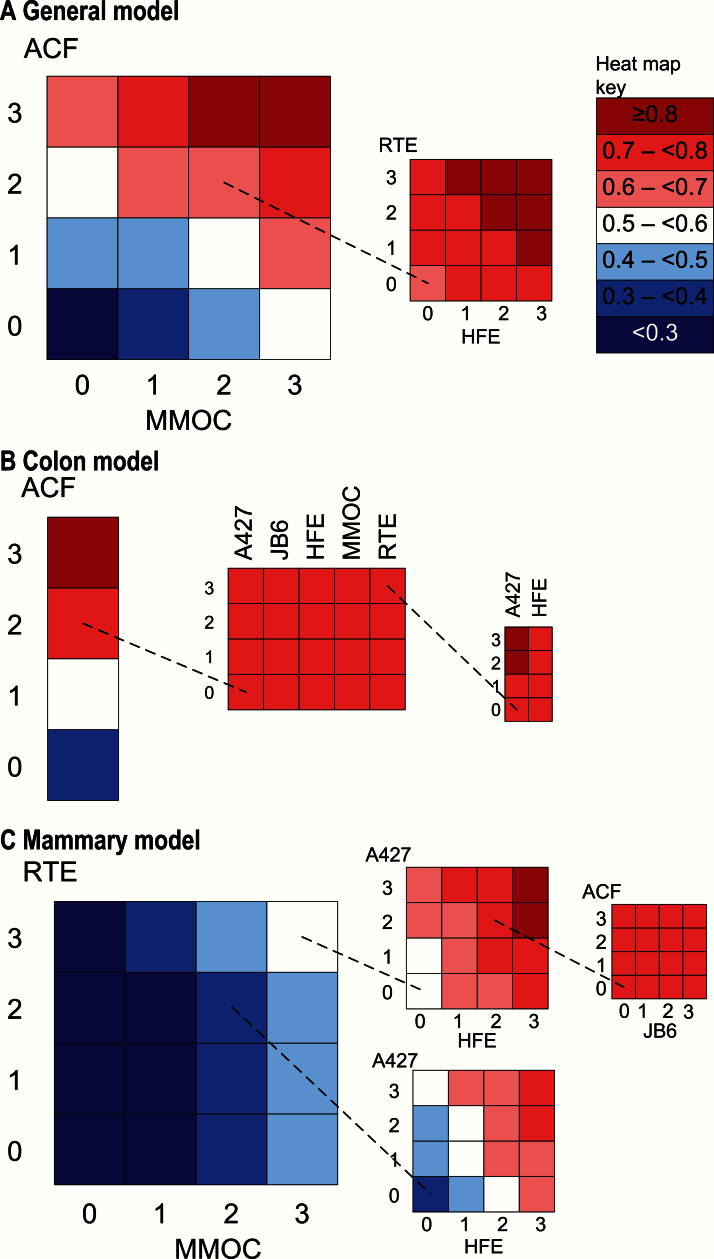
Given the limited value that individual morphologic assays have in predicting positivity in tumor assays, we investigated the extent to which predictive values of morphologic assays improved when they were used in combination (Figure 5). This approach as applied to the general model (Figure 5A) illustrates the value of combining results from independent assays in a systematic manner. Although the ACF and MMOC assays yield moderate results (both 2), adding results for two more assays, RTE and HFE, improves the predictive probability that an animal tumor assay will be positive so that it exceeds 80% if the results of the latter two assays sum to more than 4. With respect to the colon tumor model, an ACF morphologic assay result of 3 is sufficient for a probability of a positive colon tumor assay outcome in excess of 0.8 (Figure 5B). With a moderate ACF result of 2, experimentally more common, a predictive value of 0.8 can be achieved when at least two additional morphologic assays yield adequate results. An ACF result of 2 (first grid) combined with an RTE result of 3 (middle grid) and an A427 result of 2 or 3 (third grid) yields at least a 0.8 probability that the agent in question will exhibit positive efficacy in a colon tumor assay. As shown, a similarly high result (2 or 3) in the HFE assay will not guarantee attainment of this threshold probability. As indicated earlier, the MMOC assay has a predictive value at least between 0.4 and 0.5 for a positive mammary tumor assay outcome when its result is 3. Results of 3 in both MMOC and RTE raise the predictive value to at least between 0.5 and 0.6 (Figure 5C, first grid). When these maximal MMOC and RTE results are combined with a maximal HFE result (3) and a moderate-to-strong A427 result (2 or 3), a predictive value of at least 0.8 can be achieved (Figure 5C, second grid, top). Moderate results (2) for both MMOC and RTE combined with a maximal HFE result (3) and a moderate-to-strong A427 result (2 or 3) yield a predictive value at least between 0.7 and 0.8 (Figure 5C, second grid, bottom).

Figure 5.

Tumor model heat maps. Additive value of additional morphologic assays is illustrated in the following sets of heat maps. A) For the general tumor model, given moderate aberrant crypt foci (ACF) and mouse mammary organ culture (MMOC) results (both 2), the effect of adding results for two more assays, rat tracheal epithelial cell (RTE) and human foreskin epithelial cell (HFE), is shown. The inset shows that any positive result in the additional assays is sufficient to bring the probability of a positive tumor assay result to 0.7 or above, but combined results adding to 4 or above are needed to bring the probability of a positive tumor result to 0.8 or above. B) An ACF result of 3 gives a probability of a positive colon tumor result of 0.8 or above. If a moderate ACF result (2) is obtained (experimentally more common), a probability of 0.8 cannot be achieved using a single additional assay (middle grid). With a moderate ACF result (2) and a strong RTE result (3), the addition of a moderate or strong result (2 or 3) in the human lung tumor A427 cell (A427) is sufficient to bring the probability to 0.8 or above. In contrast, the addition of HFE results will not increase the probability of a positive colon tumor result. C) Given moderate MMOC and RTE results (both 2), adding A427 and HFE results may give a positive tumor assay probability of 0.7 or above. A probability over 0.8 is possible with strong positive results for MMOC, RTE, and HFE (all 3) and moderate to strong results for A427 (2 or 3). Under these conditions, neither mouse JB6 epidermal cell nor ACF has a substantial influence on the probability of a positive mammary tumor result. A427 = human lung tumor A427 cell; ACF = aberrant crypt foci; HFE = human foreskin epithelial cell; JB6 = mouse JB6 epidermal cell; MMOC = mouse mammary organ culture; RTE = rat tracheal epithelial cell.

Discussion

The current drug development approach is resource-intensive, posing considerable challenges in many diseases. Oncology drugs have fared worse than pharmaceuticals in other therapeutic areas. For oncology agents that entered the clinic from 1993 to 2004, the success rate for drug approval was less than 20% (6). Only 5% of drugs that show anticancer activity in preclinical models are sufficiently efficacious in phase 3 trials to progress to being approved (7), in contrast to 20% of cardiovascular agents. These factors contribute to an increasingly unprofitable return on investment (6–8). Agent development in cancer prevention faces even greater hurdles. Relevant clinical endpoints, specifically cancer incidence, are rare events, and concerns about toxicity in healthy individuals are paramount. Even early stages of preventive agent development often prove disappointing, with agents that show positive outcomes in morphologic assays not performing with the same efficacy in the more resource-intensive animal assays.

The NCI/DCP has had qualified success in its chemopreventive agent development program. To optimize resource use, DCP periodically evaluates the ability of early-stage efficacy outcomes to predict outcomes at subsequent stages, with a goal of developing statistical models to guide the decision-making process. The first such analysis, in 1996, examined the predictive capabilities of five morphologic assays used to screen the efficacy of potential chemopreventive agents (1). The greater the number of positive morphologic assays, the greater their ability to predict at least one positive animal tumor assay. The current evaluation aimed to update the 1996 analysis, because many more agents have been tested and additional assays at both morphologic and animal tumor stages have been implemented. Furthermore, in 1996 the criteria for positivity at both the morphologic and the animal tumor stages were coarse and did not allow for degrees of variation. A positive morphologic assay was one in which inhibition of the endpoint reached a threshold, often 20%, depending on the assay. This cutoff was used to generate a dichotomous outcome, positive or negative. In the current evaluation, we employed criteria of a finer grain. The outcome of each combination of agent and assay was assigned an integer ranging from 0 to 3, depending on the percent inhibition (Table 2). Any result greater than 0 was positive. In addition to the coarseness of its positivity definition, the earlier analysis did not weight morphologic assays on the basis of predictive ability. One positive assay was as good as any other. In contrast, our current statistical modeling approach weighted the six selected morphologic assays on the basis of predictive value.

The most predictive morphologic test was the ACF assay, likely attributable to its being the only in vivo morphologic assay recapitulating the live animal setting used in the later-stage tumor assays. The ACF prediction was also very specific for colon cancer assays, showing no impact on breast tumor assays. In contrast, the in vitro MMOC morphologic assay only mildly predicted efficacy in mammary tumor assays. Thus, identity of tissue type between morphologic and animal tumor assays is not entirely associated with a strong predictive value of the former for the latter.

Our statistical models addressing breast and colon cancers provide quantitative decision support tools for the future development of chemopreventive agents for these diseases. They suggest a stepwise approach to performing morphologic assays in gathering evidence to support further testing in animal tumor assays. In this approach, one begins by performing the morphologic assay that is most predictive of the outcome of the animal tumor assay, based on having the slope coefficient of greatest magnitude in the model. For example, for colon cancer, this morphologic assay would be ACF. One then inserts the result of this assay into the model and computes the highest probability of a positive animal tumor assay that could be attained. Such a probability is achieved when all morphologic assays that have not yet been performed are assumed to yield integer values of 3. If this probability is sufficiently large (exceeding, for example, an arbitrary threshold of 0.8), the motivation exists to continue to the morphologic assay that is the next most predictive of the outcome of the animal tumor assay. If not, no further morphologic assays are performed, and the conclusion is ineffectiveness of the chemopreventive agent. The procedure continues in this fashion until either it is clear that further testing will not result in the threshold probability ever being reached, or the morphologic assays done so far have yielded values that result in the threshold probability being crossed irrespective of what values the other morphologic assays may produce. The value of the threshold probability may be selected to provide a specified assurance that an agent with a certain high probability of positivity will proceed to testing in an animal tumor assay. This approach would reduce the number of morphologic assays performed, allowing optimization of resources supporting the research. The full complement of morphologic assays would be performed only on rare occasions. Performance characteristics of this approach will be further studied in future work.

Several features limit the generalizability of our analysis. First, the data came out of an actual research endeavor in which agents were prioritized for further, more expensive testing. In general, agents that did not perform well in a subset of the six available morphologic assays were not tested further, a decision based on pragmatic considerations. Consequently, the data were incomplete, and combinations of outcomes of morphologic assays were not evenly represented. Data incompleteness was addressed through multiple imputation. We did not assume that data were missing completely at random (MCAR), in which case missingness is entirely independent of data, observed or unobserved. Rather, we made the missing-at-random (MAR) assumption, according to which unobserved data provide no additional information about missingness over that given by observed data. We believe that, given the process by which the data were generated, this is a reasonable assumption. With regard to representation of morphologic assay outcomes, we remark that negative morphologic results were sometimes pursued with follow-up animal tumor assays based on other considerations, such as mechanistic observations. The net result was animal tumor assay follow-up to both negative and positive morphologic assays in our dataset. Among the 210 agents tested in both morphologic and animal tumor assays, 56 agents had negative ACF, 43 had negative A427, eight had negative HFE, 36 had negative JB6, 66 had negative MMOC, and 45 had negative RTE assays. Furthermore, there were 78 agents with negative animal tumor assays, tempering potential concerns about bias toward positive outcomes.

Second, the current analysis did not address the transition from animal tumor assays to human clinical trials. Thus, we were unable to deduce the applicability of drug efficacy to humans from this analysis. The juxtaposition of animal tumor assay results against data from human clinical trials will comprise the next steps of our overall prediction value project. Finally, our study is retrospective and does not represent a planned prospective analysis.

Two key observations emerged from this investigation. First, some of the morphologic assays are strongly predictive of meaningful positive efficacy outcomes in specific animal tumor assays. This is particularly true of the ACF assay, which in future drug development projects should play a major role when colon cancer is the ultimate prevention target. The second observation is that even less strongly predictive assays can be combined, resulting in enhanced composite predictive ability. This approach should facilitate rational selection of agents for progression from morphologic to animal tumor assays. The next step will be to expand our statistical modeling to animal assays of additional cancer sites, including bladder and lung cancers. We will also apply the same statistical modeling approach to evaluating the ability of animal tumor assays to predict outcomes in humans, specifically in clinical trials. Our goal is to achieve more efficient use of increasingly scarce research resources.